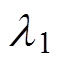 等于2倍的相邻导线间距,即
等于2倍的相邻导线间距,即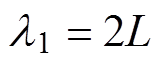 。
。摘要 电磁超声换能器(EMAT)激励的Lamb波中经常存在多种模式,给波形分析造成困难,甚至会干扰对缺陷信息的判断,从而导致误判。常规的EMAT线圈空间波数谱中含有谐波,谐波是造成多模式现象的重要原因。该文提出试件涡流密度分布(洛伦兹力分布)相当于对线圈电流密度分布的空间低通滤波,通过对线圈空间域进行有效设计从而抑制空间域谐波,进而实现激发单波数正弦形式的涡流密度分布。结合正弦脉冲宽度调制(SPWM)技术的特点,提出将时域中的SPWM技术应用于空间域以实现线圈参数设计。通过建立有限元仿真模型,仿真证明了正弦形式的涡流密度空间分布可以被激励。该文以激励S0模态Lamb波为例进行实验,实验结果表明,由波数谱中的3次谐波激励的A0模态被极大地抑制,抑制比为21dB。
关键词:电磁超声换能器 Lamb波 模态抑制 空间域谐波控制 正弦脉冲宽度调制
电磁超声换能器(Electromagnetic Acoustic Transducers, EMAT)通过电磁耦合的方式产生超声波[1-3],由于无需耦合剂的优点,使得其在无损检测和无损评估中得到广泛研究和应用。
EMAT是产生超声Lamb波的一种有效方式。Lamb波的多模式现象会给波形分析造成一定的困难,甚至会干扰对缺陷信息的判断,导致误判。因此,Lamb波模态抑制方法一直是研究的热点。刘素贞等根据对称模式和反对称模式两种模式波结构的特点,利用双EMAT实现了单一模态Lamb波的激发和接收;该团队还研究了电磁超声换能器激发方式对Lamb波模态的影响,并通过对加载方式的选择实现了Lamb波模态控制[4-5]。M. Seher等通过有限元仿真的方式,利用遗传算法优化了磁铁直径和磁铁提离,得到了较为纯净的A0模式,S0模式的抑制比达30dB[6]。
P. Khalili等研究了在中、高频厚积Lamb波模式下,压电换能器和曲折线圈EMAT对单一波模式激励的相对能力,说明了EMAT激发单一模式的导波需要同时考虑频率和波数[7]。李明亮等建立了电磁超声Lamb波位移和线圈参数的关系模型[8],根据模型可以得出,曲折线圈激发的Lamb波的声波位移幅值与表面洛伦兹力的波数谱幅值成正比。在此基础上,Li Mingliang和Sun Wenxiu等在线圈参数固定的情况下,通过选择合适的工作点实现了模态抑制和单一模态Lamb波的激发[9-10]。Zhai Guofu等将曲折线圈等效为空间横向滤波器,设计了可抑制谐波的滤波函数,并根据滤波函数设计了一种特殊参数的曲折线圈,实现了多模态现象的抑制[11]。
研究者们主要通过改变工作点、时域信号激励或EMAT结构等方式实现Lamb波模态抑制,设计方法大多较为复杂,实际使用时较为不便或适用范围小。
EMAT激励的Lamb波模态和试件表面洛伦兹力的空间波数谱直接相关。因此,可以通过控制空间域中的波数谱的方式实现Lamb波模态抑制。常规EMAT线圈波数谱中,除了基波外,还存在奇次谐波[11],这是造成多模式现象的重要原因。因此,若能重新对EMAT线圈进行有效设计,使得其激发的洛伦兹力在空间域中仅含基波(也就是仅有单一波数),则可有效抑制因谐波而产生的多模态现象。
本文将对EMAT模型进行分析,提出新的EMAT线圈设计方法以抑制空间域谐波,最终实现Lamb波模态抑制。
EMAT包括线圈、磁铁和被测试件,结构如图1所示,Bs为磁感应强度。激励Lamb波的EMAT所使用的线圈为曲折线圈,线圈每根导线的宽度为l,相邻导线间距为L。EMAT产生的超声Lamb波的波长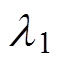 等于2倍的相邻导线间距,即
等于2倍的相邻导线间距,即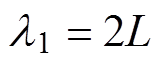 。
。
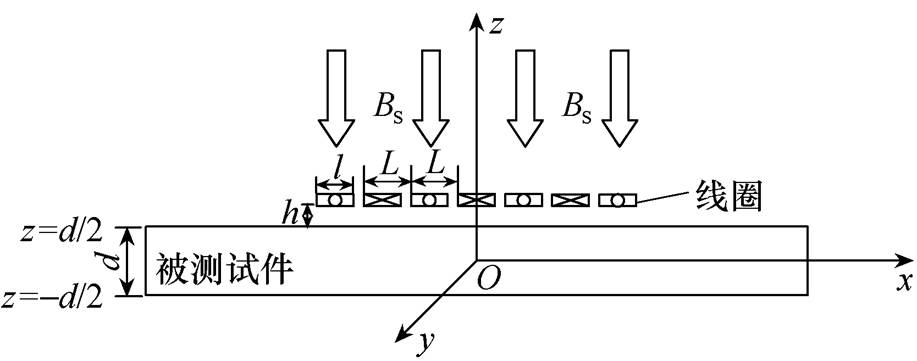
图1 电磁超声换能器结构
Fig.1 EMAT structure
假设曲折线圈的电流密度空间分布函数为g(x)。对空间周期为2L的线圈在空间上进行延拓,得到无限大的周期性电流密度分布。此时,函数g(x) 可进行傅里叶级数展开,有
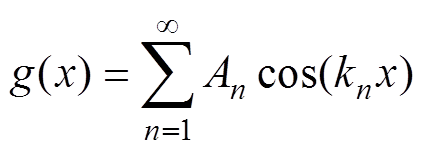 (1)
(1)式中,An为各次谐波的幅值;kn为第n阶Lamb波的波数。波数kn与第n阶Lamb波波长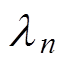 的关系为
的关系为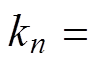
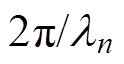 。
。
试件中被感应的涡流密度Je大小[8, 12]为
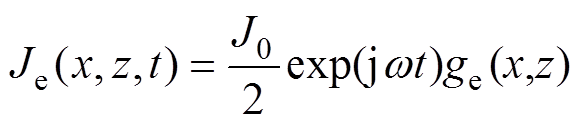 (2)
(2) (3)
(3)
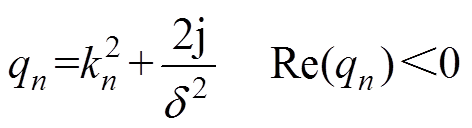 (4)
(4)
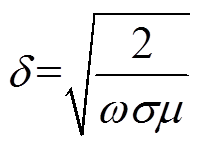 (5)
(5)式中,J0为导线中的电流密度;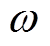 为电流角频率;h为线圈提离高度;d为试件厚度;
为电流角频率;h为线圈提离高度;d为试件厚度;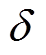 为趋肤深度;
为趋肤深度;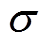 为试件电导率;m 为试件磁导率;
为试件电导率;m 为试件磁导率;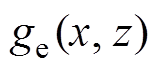 为涡流密度空间分布函数;x、z为坐标。
为涡流密度空间分布函数;x、z为坐标。
对比式(1)和式(3)可以看出,对于某一纵坐标z,涡流密度分布函数比电流密度分布函数多出了系数项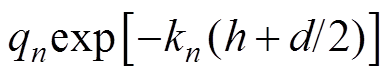 。由于趋肤深度很小,qn随着n的变化很小,因此,随着n的增加,整个系数值呈指数下降。可以得到结论:涡流密度分布相当于对电流密度分布进行了空间的低通滤波。滤波函数为
。由于趋肤深度很小,qn随着n的变化很小,因此,随着n的增加,整个系数值呈指数下降。可以得到结论:涡流密度分布相当于对电流密度分布进行了空间的低通滤波。滤波函数为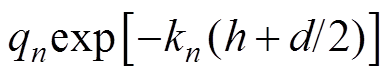 。具体表现为:①涡流密度的空间分布函数和电流密度的空间分布函数的波数谱中的谐波次数一致;②随着谐波次数升高、提离距离增大,涡流密度空间谐波幅值相对电流密度空间谐波幅值呈指数趋势下降;③试件涡流密度分布和线圈电流密度分布的相位相同,且相位不随波数的改变而改变。由于洛伦兹力的空间分布和涡流密度的空间分布是一致的,EMAT可激发的Lamb波的各波模式可以由试件表面的涡流密度空间分布或线圈中电流密度空间分布的波数谱分析出。
。具体表现为:①涡流密度的空间分布函数和电流密度的空间分布函数的波数谱中的谐波次数一致;②随着谐波次数升高、提离距离增大,涡流密度空间谐波幅值相对电流密度空间谐波幅值呈指数趋势下降;③试件涡流密度分布和线圈电流密度分布的相位相同,且相位不随波数的改变而改变。由于洛伦兹力的空间分布和涡流密度的空间分布是一致的,EMAT可激发的Lamb波的各波模式可以由试件表面的涡流密度空间分布或线圈中电流密度空间分布的波数谱分析出。
第1节的分析中,线圈在空间域上是无限大的,实际的线圈电流密度和试件涡流密度空间分布函数应该是被窗函数调制的。传统曲折线圈对应的窗函数为矩形窗。矩形窗并不会改变各谐波的次数和幅值,仅会产生主瓣和旁瓣。
由第1节分析可得,若想抑制因谐波而产生的Lamb波模态,涡流密度分布的波数谱中不应包含谐波。不包含谐波的涡流密度分布应该为单波数正弦波,其表达式为
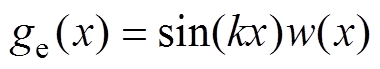
式中,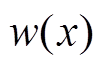 为窗函数;k为波数。
为窗函数;k为波数。
由于试件涡流密度分布是对线圈电流密度分布的空间低通滤波,且谐波次数越高,滤波效果越好。因此,为了能抑制涡流密度分布的空间域谐波,结合EMAT线圈的特点,提出以下线圈设计要求: ①线圈空间域中必须包含基波;②线圈空间域中可以包含谐波,谐波幅值尽可能低,谐波次数尽可能大;③线圈各导线的电流密度相等或电流相等。
正弦脉冲宽度调制(Sinusoidal Pulse Width Modulation, SPWM)技术是控制领域的一项技术,只应用在时域中,并且要求系统是惯性环节[13]。EMAT的电流密度分布在空间域,而且试件涡流密度分布和线圈电流密度分布的关系并不是空间域中的惯性环节。但是,SPWM技术应用于电磁超声领域有其独特性:①SPWM脉冲序列幅值相等,可以实现线圈各导线的电流密度相等;②SPWM脉冲序列的幅度谱中,除基波外,还有一些高次谐波[14],满足2.1节提出的线圈设计要求。SPWM技术中,载波比越大,则谐波次数越高。幅值比Ac/Am>1时,幅值比越小,基波分量越大,谐波相对基波的幅值越低[14]。因此,只要幅值比大于1,并且尽可能小,载波比尽可能大,则满足SPWM脉冲序列分布的线圈可以激发出近似正弦的涡流密度空间分布。因此,综合考虑SPWM技术的特点和电磁超声的独特性,时域中的SPWM技术可以应用于空间域中的EMAT线圈设计,且能很好地符合本文的线圈设计要求。
SPWM基本原理如图2所示。本文中,输出信号就是最终的电流密度分布。输出信号中每个的1或-1的宽度对应着线圈的宽度(正负号代表电流流向,电流正方向可自定义),每个0的宽度对应着导线间距。使用此方法可以得到线圈的参数。
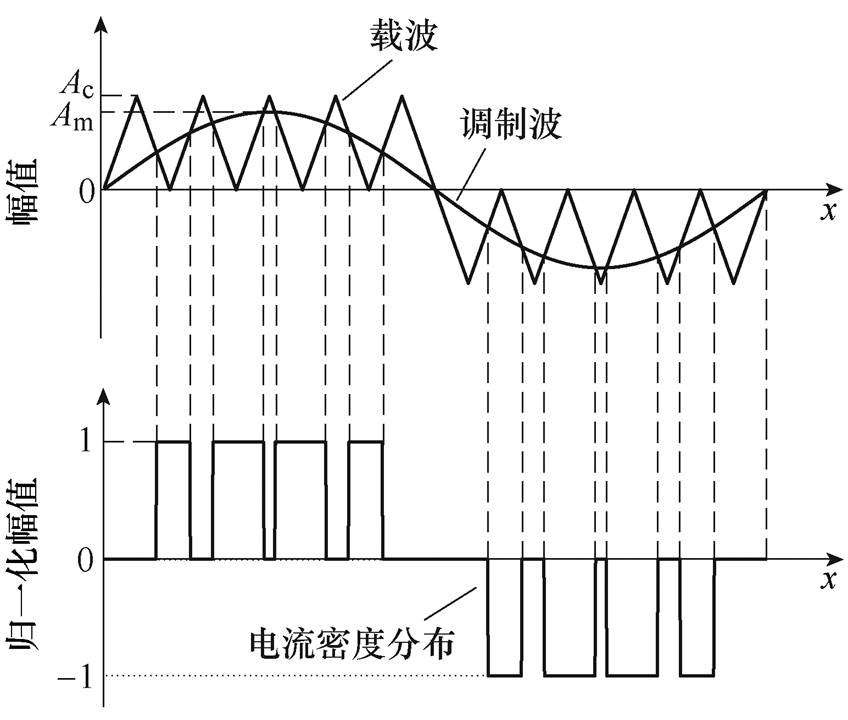
图2 SPWM基本原理
Fig.2 SPWM fundamental
本文以在1mm厚度的铝板上激发波长为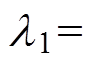
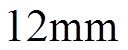 的S0模态Lamb波为例说明线圈设计方法。Lamb波波长为12mm时,L=6mm。实际应用中,EMAT线圈可使用印制电路板(Printed Circuit Board, PCB)工艺加工,由于加工工艺的限制, PCB线圈加工时需保证每根导线的宽度和导线间距要大于0.1mm。因此,本文取幅值比为Ac/Am=1.2,载波比为20,使用图2的方式进行线圈设计。此时,线圈宽度最低为0.15mm,导线间的间距最低为0.114mm,满足实际的加工工艺要求。基于SPWM技术得到的单个空间周期的线圈参数如图3a所示,l1~l5代表每根导线的宽度,s1~s5代表导线的间距,线圈具体参数见表1。实际绘制的4空间周期PCB线圈如图3b和图3c所示。发射线圈的各导线需要并联连接,这样可以最大程度地保证各导线内的电流密度基本相等。而接收线圈中,各导线串联连接,因为接收线圈中各导线电流是被试件内的振动感应的,这样可以使各导线产生的电压串联连接,提高接收电压,增强信噪比。
的S0模态Lamb波为例说明线圈设计方法。Lamb波波长为12mm时,L=6mm。实际应用中,EMAT线圈可使用印制电路板(Printed Circuit Board, PCB)工艺加工,由于加工工艺的限制, PCB线圈加工时需保证每根导线的宽度和导线间距要大于0.1mm。因此,本文取幅值比为Ac/Am=1.2,载波比为20,使用图2的方式进行线圈设计。此时,线圈宽度最低为0.15mm,导线间的间距最低为0.114mm,满足实际的加工工艺要求。基于SPWM技术得到的单个空间周期的线圈参数如图3a所示,l1~l5代表每根导线的宽度,s1~s5代表导线的间距,线圈具体参数见表1。实际绘制的4空间周期PCB线圈如图3b和图3c所示。发射线圈的各导线需要并联连接,这样可以最大程度地保证各导线内的电流密度基本相等。而接收线圈中,各导线串联连接,因为接收线圈中各导线电流是被试件内的振动感应的,这样可以使各导线产生的电压串联连接,提高接收电压,增强信噪比。
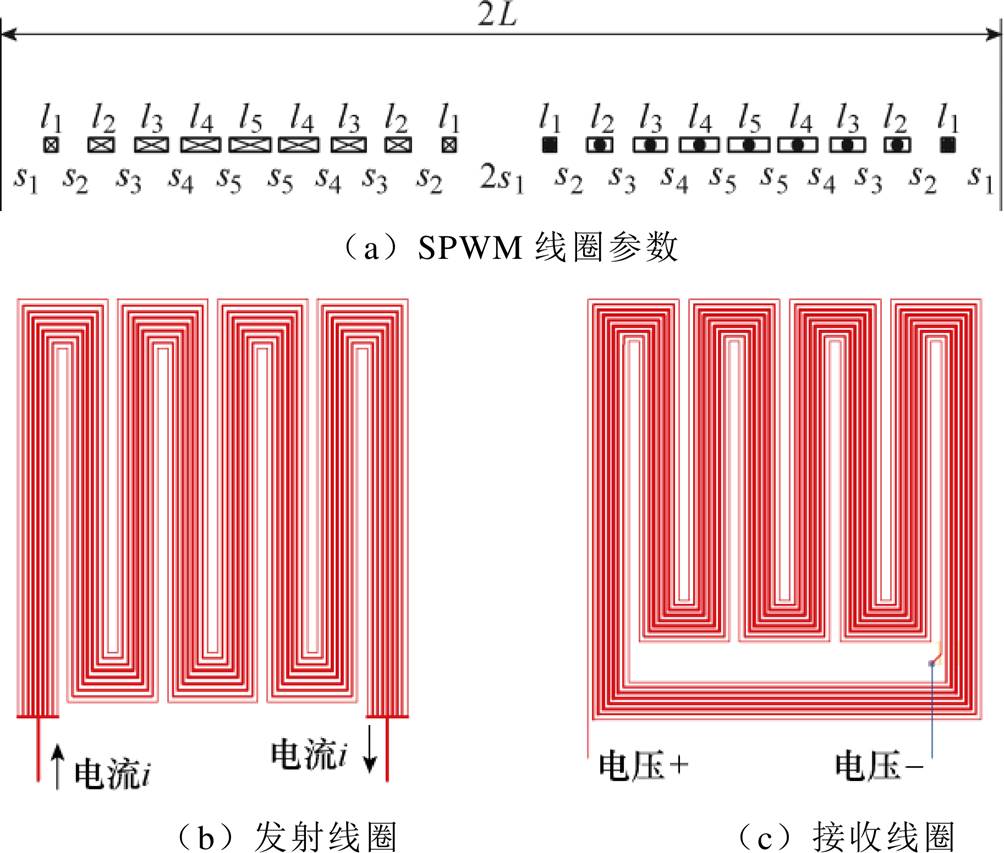
图3 线圈参数和实际绘制的PCB线圈
Fig.3 Coil parameters and PCB coils
表1 线圈具体参数
Tab.1 Coil parameter value
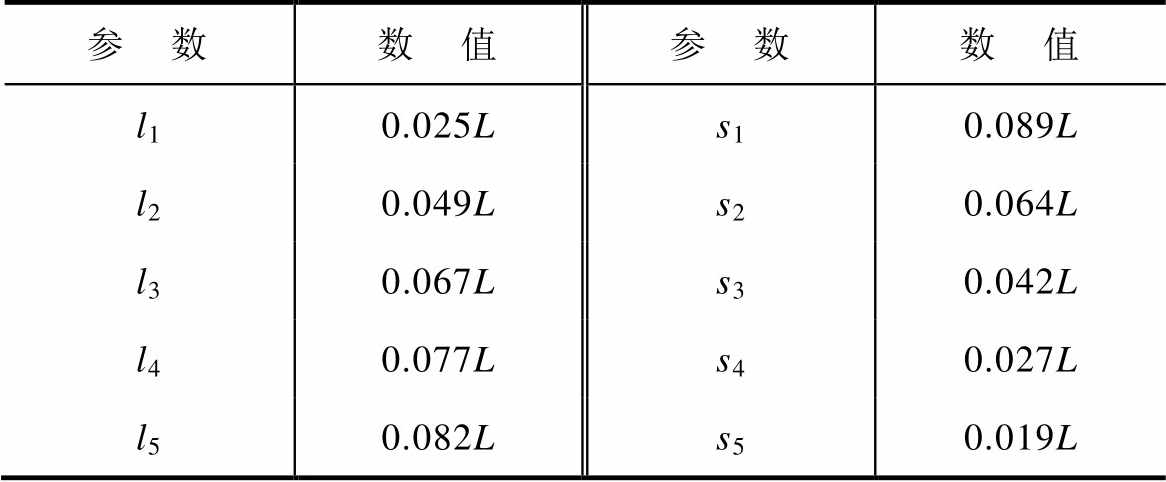
参 数数 值参 数数 值 l10.025Ls10.089L l20.049Ls20.064L l30.067Ls30.042L l40.077Ls40.027L l50.082Ls50.019L
本文首先使用COMSOL软件建立二维频域电磁场仿真模型,验证SPWM线圈的有效性。建立如图4所示的有限元法(Finite Element Analysis, FEA)仿真模型,模型参数见表2。板材选用铝板,换能器处于铝板中心位置。EMAT中的线圈总宽度为4个空间周期。仿真模型中线圈激励方式设置为电压激励,电压为100V。为了保证电流密度一致,每根导线设置为多匝线圈。
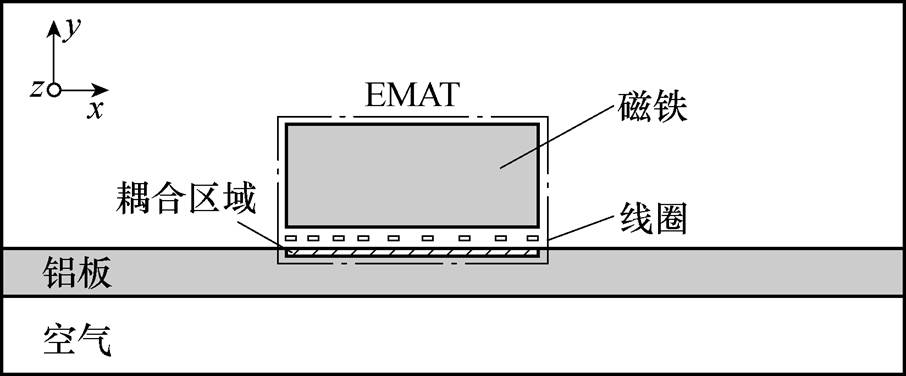
图4 有限元法仿真模型
Fig.4 FEA simulation model
表2 模型参数
Tab.2 Model parameters
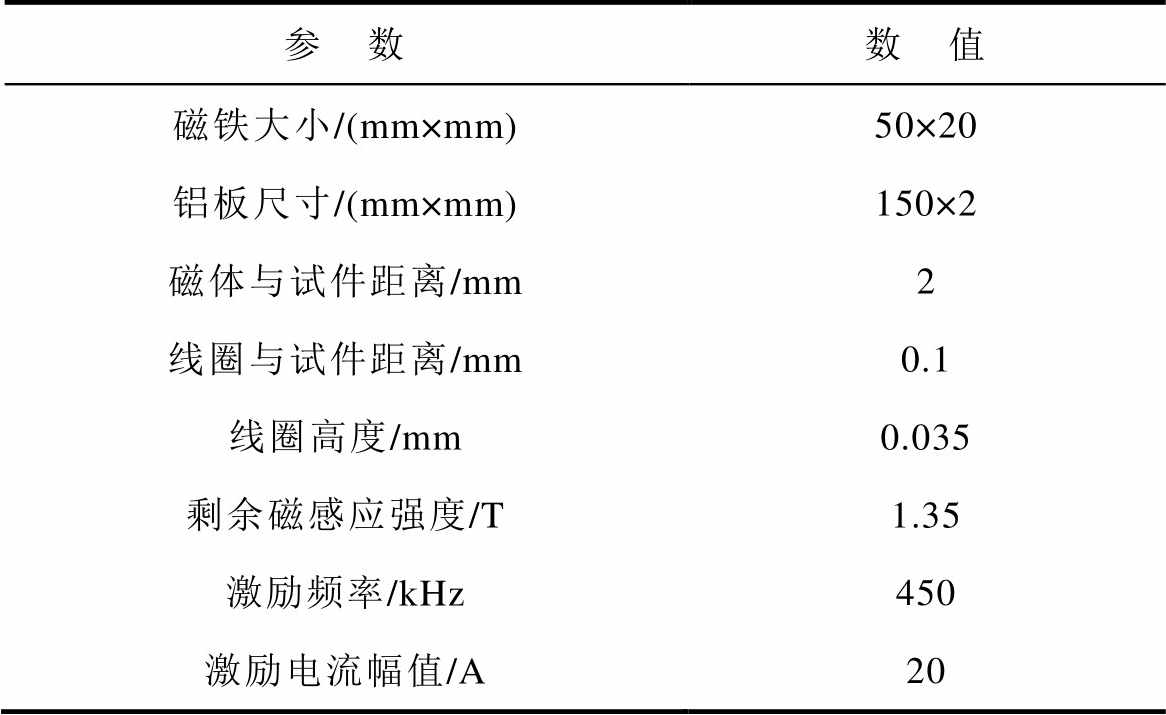
参 数数 值 磁铁大小/(mm×mm)50×20 铝板尺寸/(mm×mm)150×2 磁体与试件距离/mm2 线圈与试件距离/mm0.1 线圈高度/mm0.035 剩余磁感应强度/T1.35 激励频率/kHz450 激励电流幅值/A20
将SPWM线圈参数代入仿真模型中,提取换能器下方铝板表面沿x轴方向的洛伦兹力和涡流密度如图5a所示。计算图5a中洛伦兹力、涡流密度的波数谱和SPWM线圈电流密度的波数谱如图5b所示。
由图5a可知,洛伦兹力分布几乎呈正弦形式,但是存在幅值很小的高次谐波,高次谐波的波数和载波的波数接近。对比涡流密度和洛伦兹力可以发现,洛伦兹力的边缘幅值要大于中间部分的幅值,这是因为磁铁边缘的磁感应强度要大于磁铁中心的磁感应强度。
由图5b可知,在低波数部分,洛伦兹力波数谱的旁瓣幅值要高于SPWM线圈电流密度波数谱的旁瓣幅值,而涡流密度波数谱的旁瓣幅值和线圈电流密度波数谱的旁瓣幅值几乎一致。因此可以确定,洛伦兹力分布的高旁瓣幅值是由于磁场分布不均匀造成的。而在高波数部分,洛伦兹力和涡流密度波数谱几乎一致,谐波次数和线圈电流密度波数谱的谐波次数一致,但是幅值要低很多。说明实际的涡流密度分布会对高次谐波产生抑制效果,与理论分析一致。

图5 洛伦兹力、涡流密度、线圈电流密度及其波数谱
Fig.5 Lorentz force, eddy current density, coil current density and their wavenumber spectrum
由于导线内的趋肤效应会造成各导线内的电流密度并不严格一致,为了明确线圈导线内的趋肤效应的影响,将仿真模型中各导线设置改为单导线。单导线激励下的涡流密度分布的波数谱如图6所示。由图可知,导线内的趋肤效应会导致涡流密度分布中存在3次谐波,幅值为基波幅值的5.5%。由于此幅值很小,并且接收换能器有更进一步的空间滤波作用,因此,可以认为导线内趋肤效应造成的影响可以忽略。
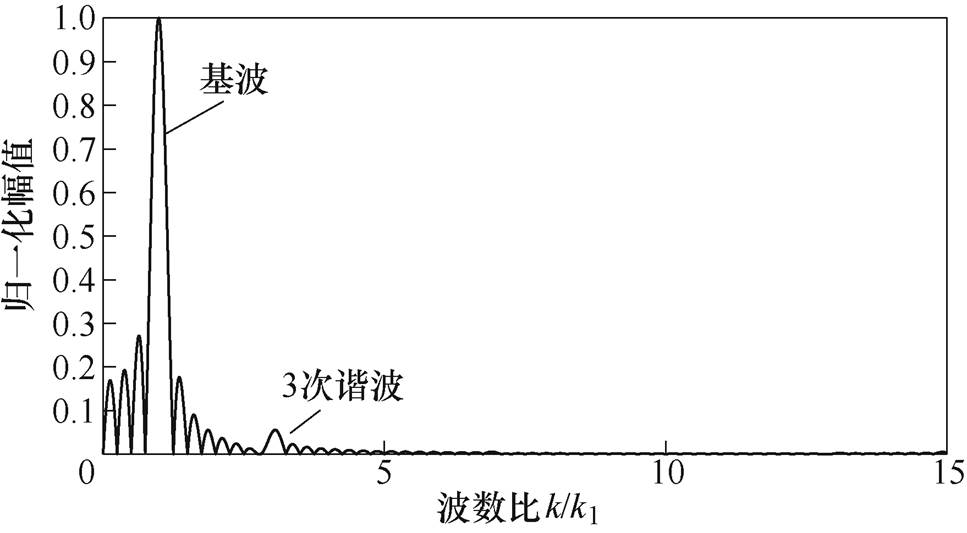
图6 考虑导线内的趋肤效应时,涡流密度分布的波数谱
Fig.6 Wavenumber spectrum of the eddy density when skin effect in wire is considered
Lamb波频散曲线和工作点如图7所示。由频散曲线可得,当波长为12mm(即波数为k1= 0.52mm-1),板材厚度为1mm时,S0模态的激励频率为f0=450kHz。此时,频厚积为450kHz·mm,A0模式的波数约为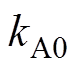 =1.57mm-1,A0模式的波数为S0模式波数的3倍。因此,在激发波长为12mm的S0模态时,Lamb波中也会同时包含波长约为4mm的A0模式。
=1.57mm-1,A0模式的波数为S0模式波数的3倍。因此,在激发波长为12mm的S0模态时,Lamb波中也会同时包含波长约为4mm的A0模式。
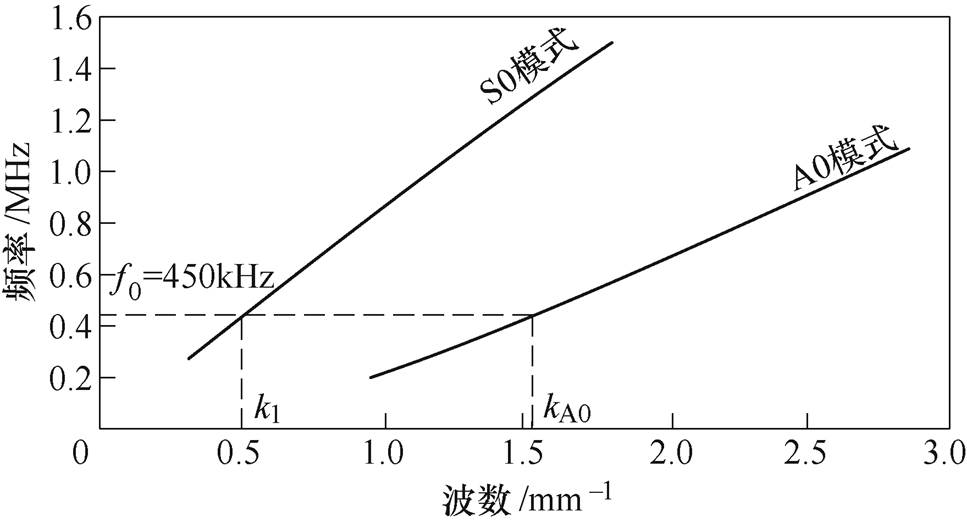
图7 Lamb波频散曲线和工作点
Fig.7 Dispersion curves and working point of Lamb waves
搭建实验装置如图8所示。EMAT的激励和信号处理设备为零声科技(苏州)有限公司研制的EMAT-2000便携式电磁超声探伤仪,主要技术参数见表3,参数完全满足实验要求。被测试件为1mm厚的6061铝板。换能器为一发一收,发射接收EMAT的参数完全一致,中心间距为s=200mm。EMAT中的磁铁为50mm×50mm×25mm的N35型钕铁硼磁铁。实验使用SPWM线圈和常规线圈作为对比,SPWM线圈参数如图3所示,常规线圈参数为:l=0.5mm,L=6mm,线圈匝数为8。实验中探伤仪和EMAT之间未添加阻抗匹配电路,这在一定程度上会降低信噪比,但不会影响实验结果。
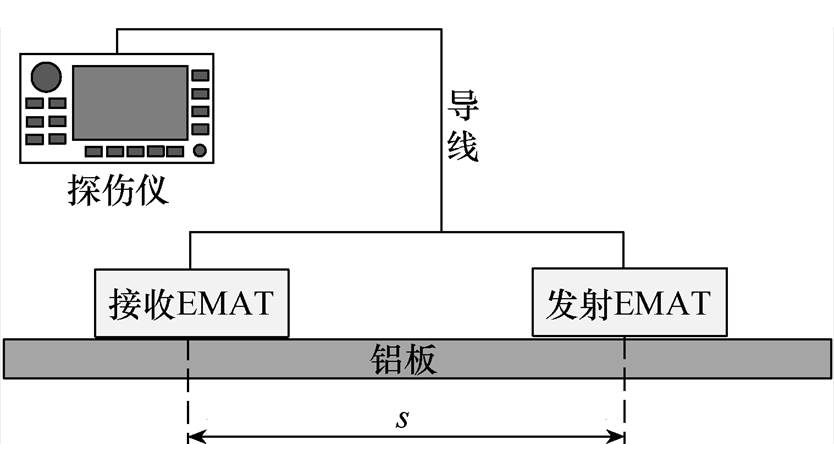
图8 实验装置
Fig.8 Experiment platform
表3 探伤仪参数
Tab.3 Instrument parameters
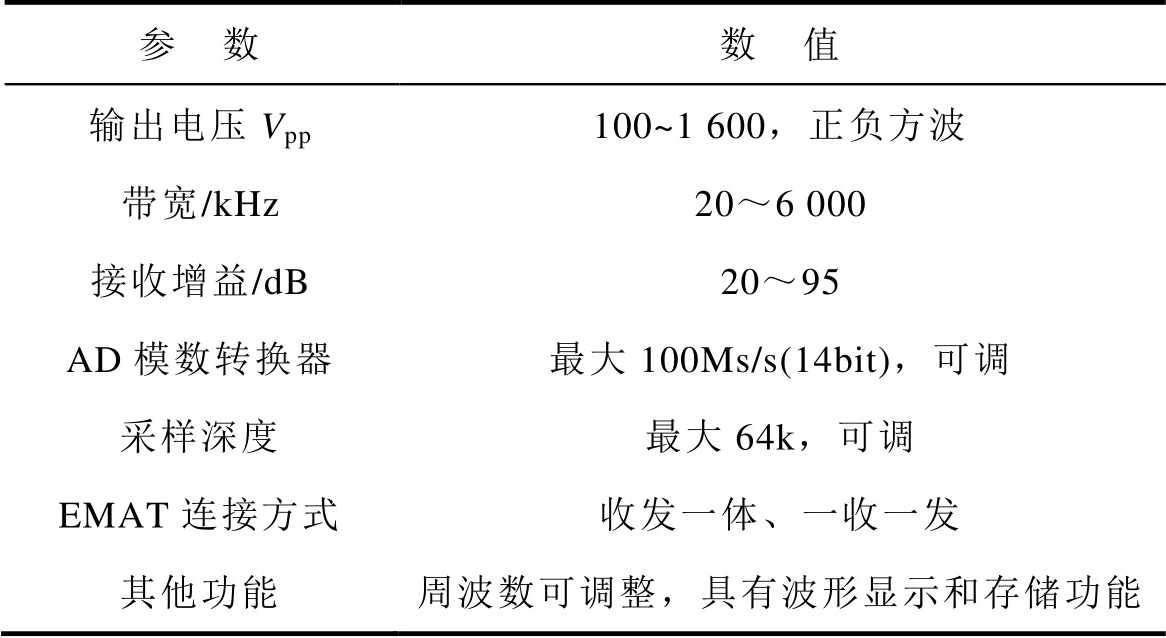
参 数数 值 输出电压Vpp100~1 600,正负方波 带宽/kHz20~6 000 接收增益/dB20~95 AD模数转换器最大100Ms/s(14bit),可调 采样深度最大64k,可调 EMAT连接方式收发一体、一收一发 其他功能周波数可调整,具有波形显示和存储功能
设置探伤仪激励参数为周波数4,发射强度50%(约800Vpp),激励频率450kHz。设置接收参数为采样率20MHz,采样深度8k,平均次数64。首先使用常规线圈进行实验,接收增益为83dB,得到的实验结果如图9a所示。
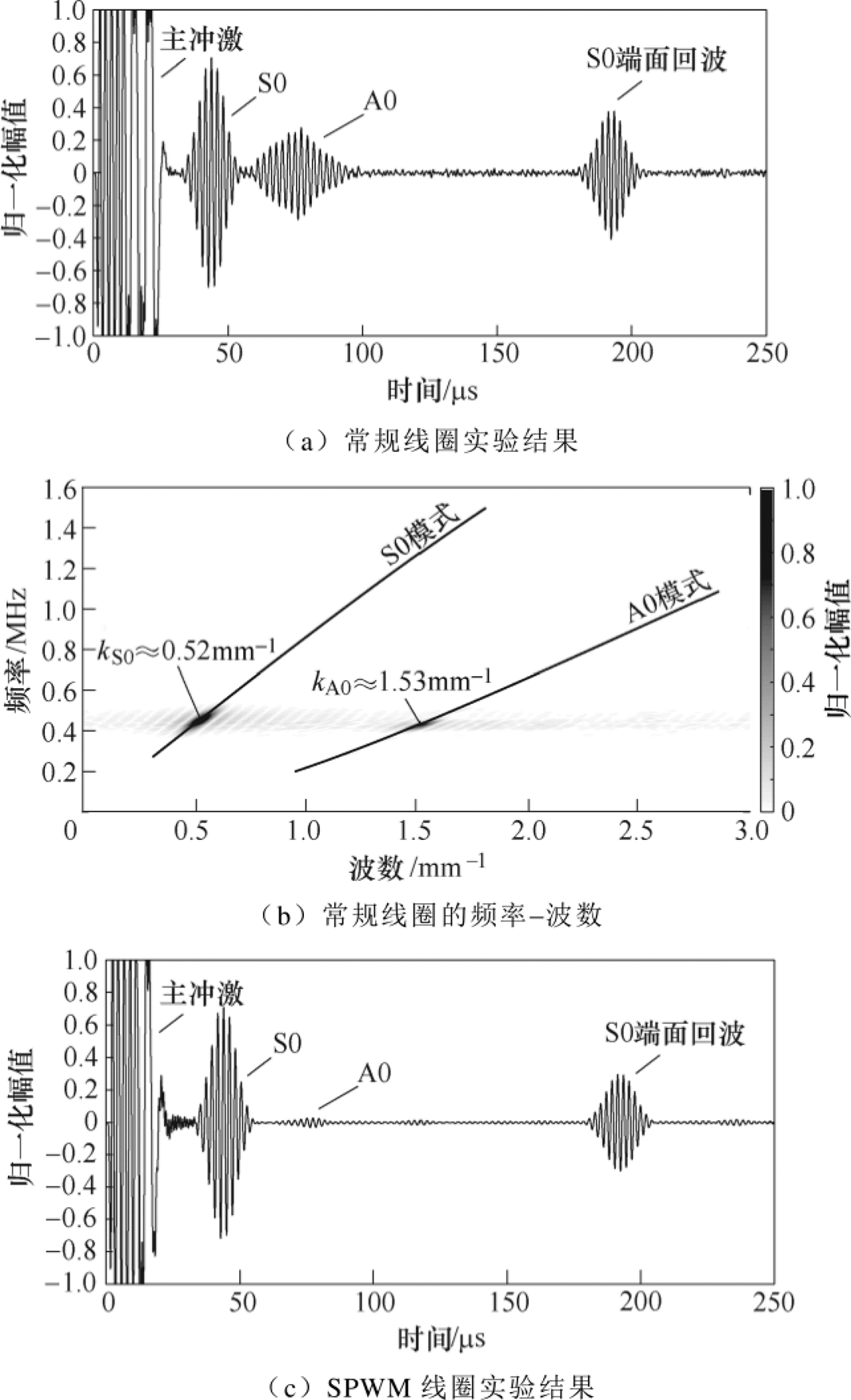
图9 实验结果
Fig.9 Experimental results
根据Lamb波群速度曲线可以计算,S0模态的群速度约为5 420m/s,A0模态的群速度约为2 880m/s。S0模态的理论到达时间约为29.2ms,A0模态的理论到达时间约为54.9ms。图9a中第一个波包的实际到达时间为31.4ms,第二个波包的实际到达时间为56.9ms。考虑到电路延时、计算误差、测量误差以及Lamb波成型需要一段距离等因素,可以判定图中前两个波包分别为S0模态和A0模态。A0模态与S0模态的幅值比约为0.4。
为进一步判断S0模态和A0模态的波数,移动发射EMAT位置,在s=200~300mm之间,每2mm进行一次测量,得到51组数据。对数据进行时间和空间二维傅里叶变换,得到频率-波数如图9b所示。由图9b可以证实,S0模态和A0模态被激发。S0模态的中心波数约为0.52mm-1,而A0模态的中心波数约为1.53mm-1。A0模态的波数约为S0模态波数的3倍,与理论分析相一致,证明A0模态确实是由波数谱中的3次谐波激励的。
使用SPWM线圈进行实验,发射接收EMAT间距s=200mm,接收增益为67dB(和常规线圈EMAT接收增益不一致的原因是线圈参数发生了改变,导致EMAT换能效率存在较大差异),结果如图9c所示。A0模态得到了极大的抑制,幅值接近0。A0模态与S0模态的幅值比约为0.036。相对传统线圈,抑制比达21dB。证明了该线圈有较好的Lamb波模态抑制效果。
对于仍存在的幅值很小的A0模态,本文认为,这并非是导线内的趋肤效应引起的。由于Lamb波理论模型是基于稳态情况下建立的,而Lamb波成型需要经历一个暂态过程。稳态模型不能100%地还原这个暂态过程,导致了A0模态无法被完全消除,只能被抑制。
谐波是造成多模式现象的重要原因,本文提出了基于空间域谐波控制的电磁超声Lamb波模态抑制方法,并将时域中的SPWM技术应用于空间域线圈参数设计,仿真和实验证明了该方法的有效性,模态抑制比达21dB。
本文分析了电磁超声理论模型,指出试件中涡流密度分布和洛伦兹力分布一致,均是对EMAT线圈电流密度分布的空间低通滤波。涡流密度分布和电流密度分布的谐波次数和相位是一致的,但是随着谐波次数升高、提离距离增大,涡流密度分布的谐波幅值相对电流密度分布的谐波幅值呈指数趋势下降。
为了实现对涡流密度空间域谐波的控制,本文指出线圈需能够激励出单波数正弦形式的涡流密度分布,并提出了新的线圈设计要求:线圈空间域中必须存在基波,可以存在幅值尽可能低、次数尽可能高的谐波,且线圈各导线的电流密度或电流必须相等。结合SPWM技术的特点,指出SPWM技术符合本文的线圈设计要求,可以实现线圈参数设计。
被EMAT激励的Lamb波模态是由线圈空间波数谱决定的,本文所述的基于空间域谐波控制的电磁超声Lamb波模态抑制方法解决了波数谱中的谐波问题,从根本上解决了因谐波产生的多模态现象。该设计方法适用范围广,且简单易行。
参考文献
[1] 翟国富, 梁宝, 贾文斌, 等. 横波电磁超声相控阵换能器设计[J]. 电工技术学报, 2019, 34(7): 1441- 1448.
Zhai Guofu, Liang Bao, Jia Wenbin, et al. Design of the shear wave electromagnetic ultrasonic phased array transducer[J]. Transactions of China Electro- technical Society, 2019, 34(7): 1441-1448.
[2] 孙文秀, 刘国强, 夏慧, 等. 非铁磁材料的电磁超声接收过程数值模拟及实验研究[J]. 电工技术学报, 2018, 33(19): 4443-4449.
Sun Wenxiu, Liu Guoqiang, Xia Hui, et al. Numerical simulation and experimental study of electro- magnetic acoustic transducer receiving process in nonferromagnetic material[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4443-4449.
[3] 刘素贞, 王淑娟, 张闯, 等. 钢板电磁超声表面波的仿真分析及缺陷定量检测[J]. 电工技术学报, 2020, 35(1): 97-105.
Liu Suzhen, Wang Shujuan, Zhang Chuang, et al. Simulation analysis of electromagnetic acoustic surface wave of steel plate and quantitative defect detection[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 97-105.
[4] 刘素贞, 张严伟, 张闯, 等. 基于电磁超声双换能器的单模态Lamb波激励方法研究[J]. 电工技术学报, 2018, 33(1): 140-147.
Liu Suzhen, Zhang Yanwei, Zhang Chuang, et al. Research on excitation method of single-mode Lamb wave based on electromagnetic acoustic double transducer[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 140-147.
[5] 刘素贞, 董硕, 张闯, 等. 电磁超声加载方式对Lamb波模态的影响[J]. 电工技术学报, 2018, 33(19): 4426-4433.
Liu Suzhen, Dong Shuo, Zhang Chuang, et al. The influence of electromagnetic acoustic transducer loading way on the mode of Lamb wave[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(19): 4426-4433.
[6] Seher M, Huthwaite P, Lowe M J S, et al. Model- based design of low frequency Lamb wave EMATs for mode selectivity[J]. Journal of Nondestructive Evaluation, 2015, 34(3): 22.
[7] Khalili P, Cawley P. Relative ability of wedge coupled piezoelectric and meander coil EMAT probes to generate single mode Lamb waves[J]. IEEE Transa- ctions on Ultrasonics Ferroelectrics & Frequency Control, 2018, 64(4): 648-656.
[8] 李明亮, 邓明晰, 高广健. 电磁超声换能器激发超声兰姆波的模式展开分析[J]. 声学学报, 2014, 39(3): 385-391.
Li Mingliang, Deng Mingxi, Gao Guangjian. Modal expansion analyses of ultrasonic Lamb waves generated by electromagnetic ultrasonic trans- ducers[J]. Acta Acustica, 2014, 39(3): 385-391.
[9] Li Mingliang, Deng Mingxi, Gao Guangjian. Selective generation of ultrasonic Lamb waves by electromagnetic acoustic transducers[J]. Chinese Physics B, 2016, 25(12): 124301.
[10] Sun Wenxiu, Liu Guoqiang, Xia Hui, et al. Lamb wave signal selective enhancement by an improved design of meander-coil electromagnetic acoustic trans- ducer[J]. Chinese Physics B, 2018, 27(8): 084301.
[11] Zhai Guofu, Jiang Tao, Kang Lei. Analysis of multiple wavelengths of Lamb waves generated by meander-line coil EMATs[J]. Ultrasonics, 2014, 54(2): 632-636.
[12] Hirao M, Ogi H. Electromagnetic acoustic trans- ducers: noncontacting Ultrasonic measurements using EMATs[M]. 2nd. Japan: Springer, 2018.
[13] 王兆安, 刘进军. 电力电子技术[M]. 5版. 北京: 机械工业出版社, 2013.
[14] 邵江富. 逆变器脉宽调制输出电压的谐波分析[J]. 机车电传动, 1980(4): 26-32.
Mode Suppression Method of Lamb Wave Excited by Electromagnetic Acoustic Transducers Based on Spatial Harmonic Control
Abstract Lamb waves excited by electromagnetic acoustic transducers (EMAT) often have multiple modes, which make waveform analysis difficult and even interfere with the judgment of defect information, leading to misjudgment. Harmonics of conventional EMAT coils in the space wavenumber spectrum are the important cause of the multi-mode phenomena. This paper proposes that the eddy current density distribution (or the Lorentz force distribution) in the specimen is equivalent to the spatial low-pass filtering of the coil current density distribution. By effectively designing the coil, the harmonics in the space domain can be suppressed, and the sinusoidal (that is, single wavenumber) eddy current density distribution can be excited. Combining the characteristics of sinusoidal pulse width modulation (SPWM) technology, it was proposed to apply the time domain SPWM technology to the space domain to design the coil parameters. A finite element simulation model was established, and the simulation proved that the sinusoidal eddy current density distribution can be excited. The experiment was conducted by taking the S0 mode Lamb wave as an example. It is shown that the A0 mode excited by the third harmonic in the wavenumber spectrum is greatly suppressed, and the suppression ratio is 21dB.
keywords:Electromagnetic acoustic transducers (EMAT), Lamb, mode suppression, spatial harmonic control, sinusoidal pulse width modulation (SPWM)
DOI: 10.19595/j.cnki.1000-6753.tces.200467
中图分类号:TM15
翟国富 男,1964年生,教授,博士生导师,研究方向为高可靠电器设计理论与技术、产品质量一致性稳健设计理论与技术、电子系统及装备可靠性和可测性设计及健康管理、电磁超声无损检测技术。E-mail: gfzhai@hit.edu.cn
李永虔 男,1991年生,博士研究生,研究方向为电磁超声无损检测技术。E-mail: 15B906029@hit.edu.cn(通信作者)
国家自然科学基金(51977044)和民用航天技术预先研究(JZKGJ20190004)资助项目。
收稿日期 2020-05-07
改稿日期 2020-06-16
(编辑 崔文静)