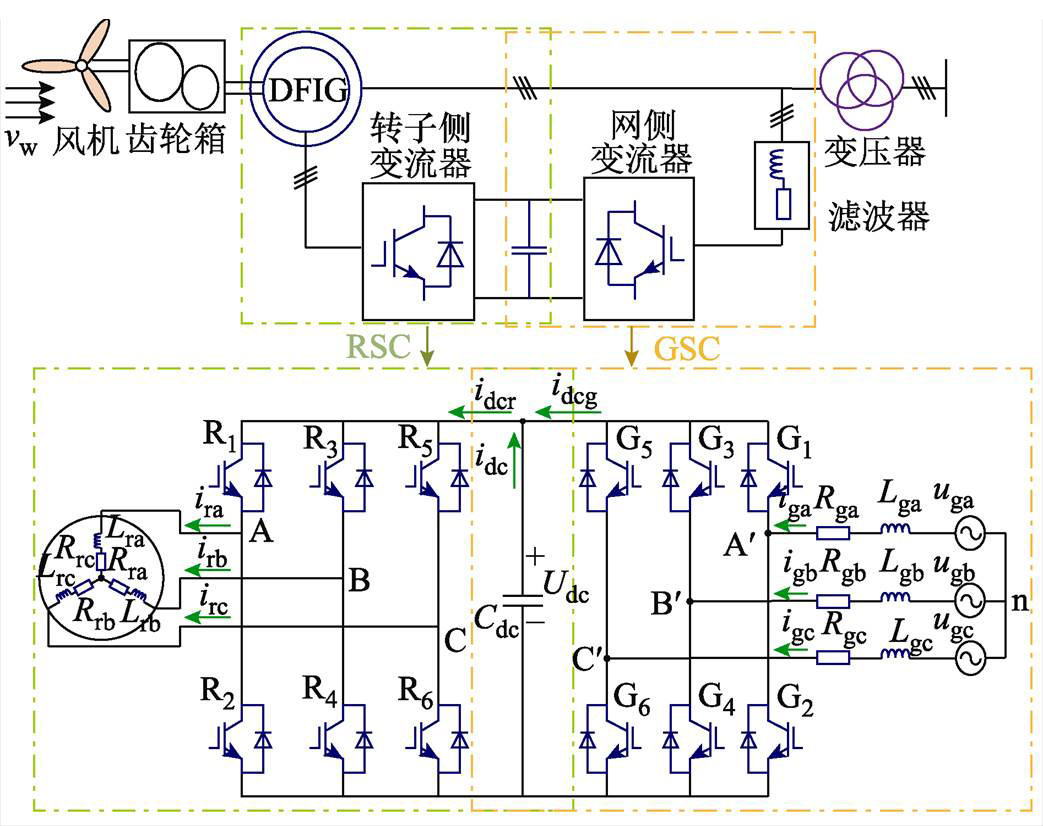
图1 双馈风电机组结构 Fig.1 Structure of the doubly-fed wind turbine
摘要 变流器功率器件开路故障监测与识别对提高双馈风电系统智能运维至关重要。针对现有基于变流器电压或电流单一特征以及固定阈值的方法难以同时实现功率器件故障诊断监测与识别问题，该文提出一种基于变流器直流母线电压的故障监测与基于转子电流故障识别的综合诊断方法。首先，理论分析变流器功率器件开路故障对直流母线电压的影响，基于累积和（CUSUM）算法，提出基于直流母线电压特征的故障监测方法；其次，针对转子输出电流非平稳特性和阈值固定问题，提出基于归一化输出电流平均值和绝对平均值为故障特征量及自适应阈值的故障识别方法；最后，仿真模拟不同功率器件先后开路，验证所提方法的有效性，以风速随机及电网电压跌落为场景验证所提方法的鲁棒性。同时，以功率器件典型开路故障实验数据验证仿真分析的准确性。仿真与实验结果表明，所提方法能准确实现变流器功率器件开路故障诊断。
关键词：双馈风电变流器 功率器件开路故障 累积和算法 自适应阈值 故障综合诊断
近年来，由于具备功率可调、控制独立及并网灵活等优势，基于双馈感应发电机（Doubly-Fed Induction Generator, DFIG）的风电机组一直是备受欢迎的机组类型之一。然而，变流器的高故障率与运维成本问题制约了其发展[1-2]。变流器故障通常分为短路与开路两种，前者故障时间极短（一般小于10μs）难以直接进行诊断，主要通过植入熔丝将其演化为开路故障[3-5]，因此开路故障为现有变流器故障诊断方法研究的重点。据统计，变流器发生单管与双管开路故障的概率较高，同时，相对于网侧变流器（Grid-Side Converter, GSC），转子侧变流器（Rotor-Side Converter, RSC）因承受多时间尺度热载荷而导致故障率更高 [2,6]。因此研究双馈RSC单管与双管开路故障的在线诊断方法对风电系统智能运维与容错控制具有重要意义。
目前变流器开路故障诊断方法通常基于电压[7-13]或电流[14-25]信号。文献[7-10]提取变流器电压特征量作为神经网络的输入，由智能体输出故障诊断结果，然而该方法需大量历史数据对智能体进行预训练。文献[12]则利用正常状态与故障状态下的线电压偏差进行永磁风机变流器的故障诊断与定位，该方法采用电压幅值和时间宽度的双重检测标准以提高故障诊断的可靠性，然而其只能有效诊断和定位变流器单管及同桥臂双管开路故障情况，对于不同桥臂双管故障则往往难以识别。文献[13]对比分析了直流母线电压故障前后的能量谱以实现变流器故障诊断。虽然直流母线电压特征量提取算法简单，便于实现故障的快速诊断，但是存在不同故障类型下电压特征量差异小而难以实现故障定位问题。文献[14-15]结合信号处理与人工智能技术对变流器进行故障诊断，对变流器输出电流信号基于主成分分析，提取各频带能量值特征量训练支持向量机模型，然而此类方法仍然存在数据获取困难和模型难以验证问题。文献[17]分析了逆变器故障前后电流矢量瞬时频率与角度特征的变化，实现故障快速定位，但其只能针对单管故障场景。文献[18-19]利用输出电流Park矢量相位斜率实现风电背靠背机/网侧变流器开路故障检测，同时分别通过电流极性与平均电流误差识别网/机侧变流器单功率管故障位置，由于风电变流器输出电流矢量斜率大小随风速的改变而变化，而基于固定参数的故障诊断阈值，往往使得该方法的适用性与鲁棒性不强。文献[20]通过电压源PWM驱动器主控电路电流参考值与实测值的误差构建故障特征量，阈值由最恶劣工况下的特征量波动值所确定，仍然面临诊断阈值固定带来的缺陷。文献[24-25]则针对双馈风电变流器输出电流信号，通过归一化电流均值构建了无负载依赖特性的故障诊断变量与自适应阈值，提高了故障诊断方法的适用性，但该方法存在诊断延迟问题。综上所述，现有变流器功率器件开路故障诊断方法通常基于单一的电压或电流信号，虽然变流器电压信号独立于负载和控制策略，便于实现故障诊断，但是却难以识别多故障类型，而单一的电流信号易于实现变流器故障识别却又存在阈值固定与诊断延迟问题。
基于此，为提高双馈风电RSC功率器件故障诊断的能力，提出一种基于变流器直流母线电压的故障监测与基于转子电流故障识别的综合诊断方法。本文首先建立RSC直流母线电压数学模型，利用累积和（Cumulative Sum, CUSUM）算法捕捉直流母线电压故障特性，实现基于直流母线电压特征的故障监测；其次，通过RSC转子电流构建和设计故障特征量与自适应阈值，实现基于转子电流特征的故障识别；最后，对所提方法的有效性及鲁棒性进行仿真分析，并通过功率器件典型开路故障实验数据验证仿真分析的有效性。
双馈风电机组主要由风机、齿轮箱、滤波器、变压器、双馈感应发电机、背靠背变流器等部分组成，结构如图1所示。其中背靠背变流器通过直流母线电压连接两个两电平电压型PWM变换器作为DFIG的交流励磁环节，其中与DFIG转子相连的是转子侧变流器（RSC），实现直流侧电压和电网侧无功功率控制功能的为网侧变流器（GSC）[26]。
图1 双馈风电机组结构 Fig.1 Structure of the doubly-fed wind turbine
图1中，R1～R6分别为RSC各功率器件，Lrm、Rrm分别为DFIG转子各相绕组电感及电阻，m= a, b, c，irm为RSC交流侧电流，idcr为RSC直流侧电流，G1～G6分别为GSC各功率器件，Lgm、Rgm分别为GSC三相并网电感及电阻，igm为GSC交流侧电流，idcg为GSC直流侧电流，Udc为直流母线电压，Cdc为其电容值，idc为电容电流。
1.2.1 直流母线电压数学建模
为了提取RSC功率器件开路故障时的直流母线电压特征量，以RSC超同步运行（此时风速vw= 13m/s，转子电流基频fr=11.5Hz）为例，建立直流母线电压故障前后动态数学模型。考虑GSC通常以单位功率因数运行[26]，为简化分析，将GSC视为负载Rg[12]，构建RSC等效电路如图2所示。
根据欧姆定律，Udc应满足
（1）其中
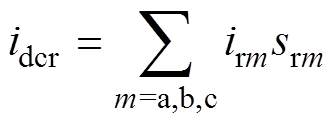（2）式中，Req为直流母线电容Cdc与Rg的等效并联负载；srm为RSC各相桥臂开关函数。
图2 RSC等效电路
Fig.2 Equivalent circuit of RSC
假设RSC交流侧电流的初始相位为qr0，则各相电流表达式为
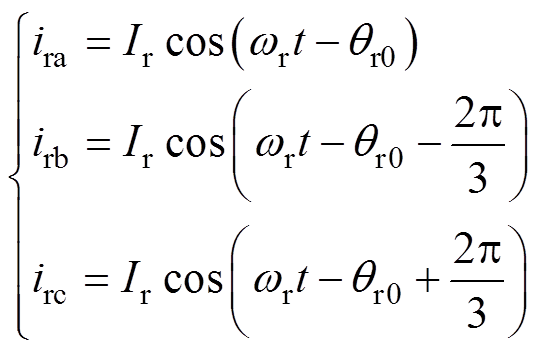（3）式中，Ir、wr分别为RSC交流侧电流幅值与角频率。
忽略PWM下RSC开关函数的高频分量，采用占空比描述RSC一般数学模型，则RSC各相开关函数的平均值定义[27]为
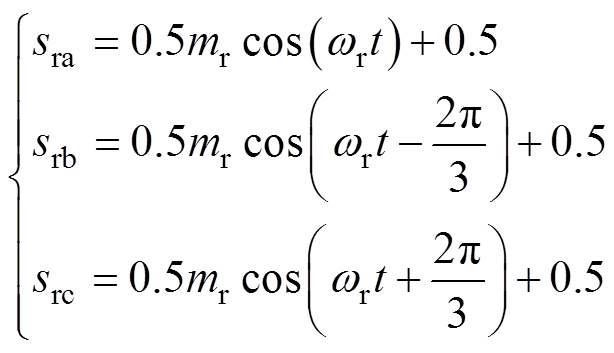（4）式中，mr为PWM调制比（mr＜1）；srm＞0.5时，上桥臂导通，srm＜0.5时，则下桥臂导通。
结合式（1）～式（4），得到Udc数学表达式为
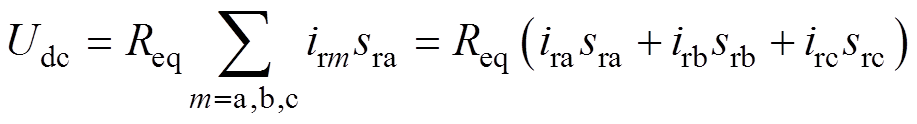（5）1）RSC无开路故障时，有
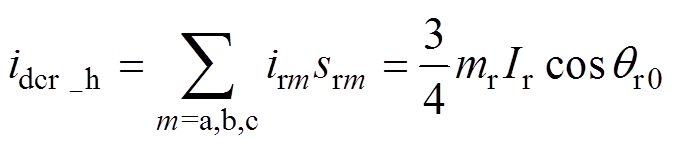（6）则
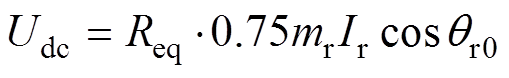（7）式中，idcr_h为RSC无开路故障的直流侧输出电流。
由式（7）可知，当RSC未发生开路故障时，直流母线电压为定值。
2）RSC发生开路故障时（以R1开路为例，如图2所示），有
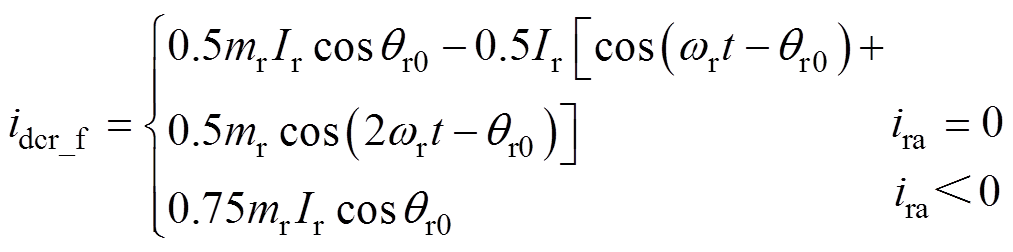（8）则
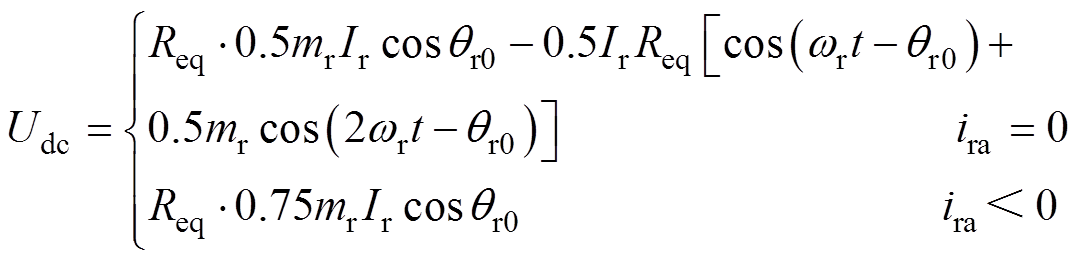（9）式中，idcr_f为RSC故障时的直流侧输出电流。
由式（9）可知，RSC功率管R1开路将导致Udc产生转子电流基频及其两倍频的脉动。同理可知，若RSC发生多管开路故障，则Udc将产生转子电流基频及其倍频的脉动。
为验证理论推导的正确性，以风速vw=13m/s及功率管R1开路故障为例，设置故障时刻tf =1.23s，对故障Udc进行快速傅里叶变换（Fast Fourier Trans- formation, FFT），结果如图3所示。由FFT分析结果可知，故障Udc主要产生了转子电流基频及其两倍频的脉动，同时伴随部分更高次基波倍频的波动，但所占比例较小，仿真与理论分析结果基本一致，验证了仿真结果的有效性。
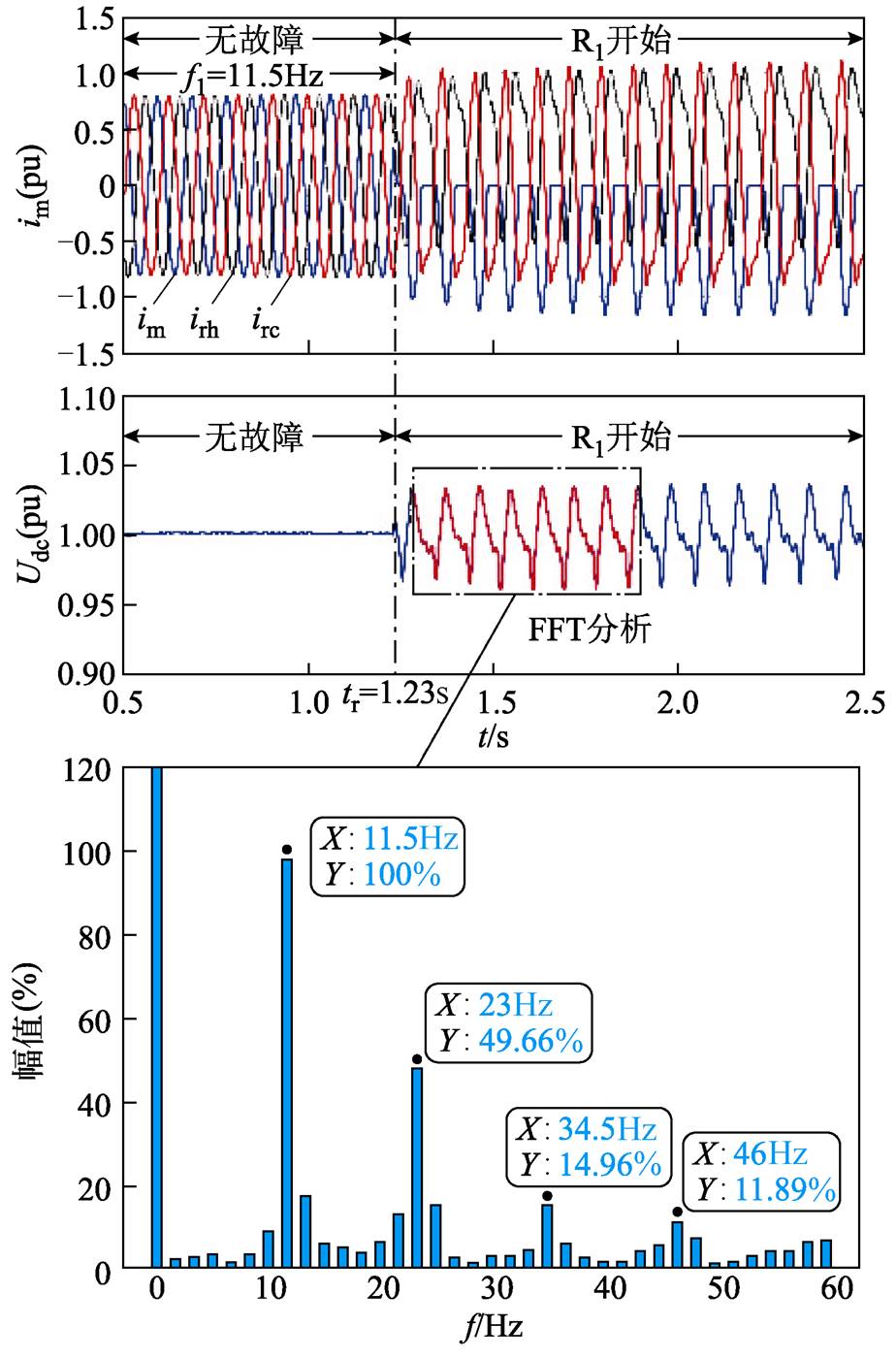
图3 故障Udc的FFT分析
Fig.3 FFT analysis of faulty Udc
1.2.2 基于直流母线电压特征的故障监测
基于Udc数学模型的准确性，对RSC功率管R1故障前后的Udc仿真数据集进行概率分布检验，得到故障前后Udc的分布特性与正态分布较拟合，如图4所示。由图4知，功率管R1故障前Udc的正态分布均值与方差分别为m0=1，s0=8.488×10-4，而故障后均值与方差分别为m1=0.998，s1=2.5×10-2。对比Udc故障前后的分布特性可知，故障前后其分布类型不变，但分布参数发生了改变，即均值几乎不变（偏差在1%以内），但方差变化显著。
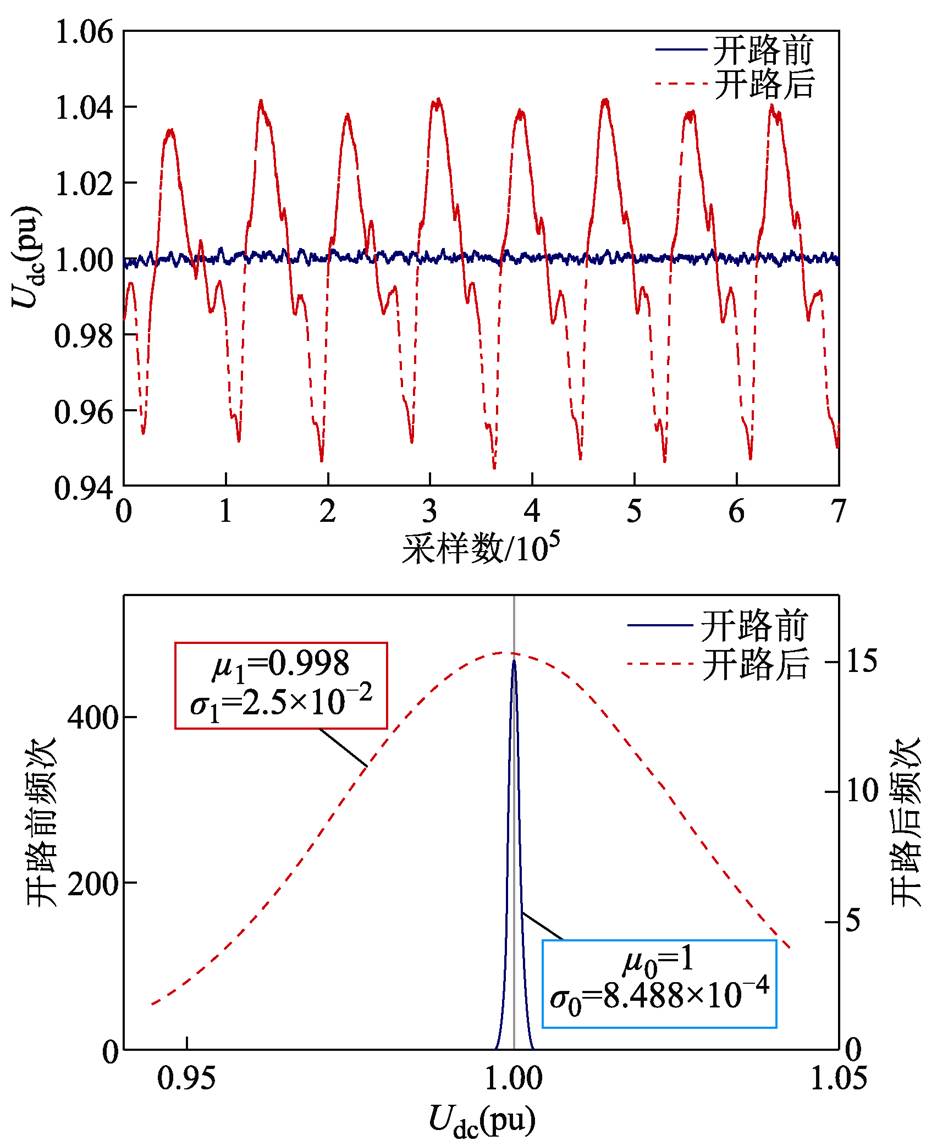
图4 直流母线电压故障前后分布特性
Fig.4 Distribution characteristics of the DC-bus voltage before and after fault
而累积和算法是一种常用于在线监测数据异常波动的统计学手段，其对Udc故障前后分布特性变化具有较好的捕捉能力[28-29]。其核心思想为被监测量（假设为x）的对数似然比L(x)，定义为
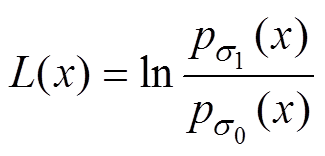（10）式中，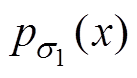
、
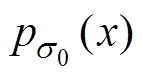分别为变量x对应分布参数s1、s0的概率密度函数（Probability Density Function,PDF）。
而对于服从正态分布的变量x，对应的PDF表示为
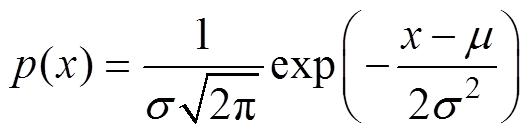（11）式中，m、s 分别为变量x的均值与偏差。
当变量x的偏差由s0演化到s1时，其似然比定义为
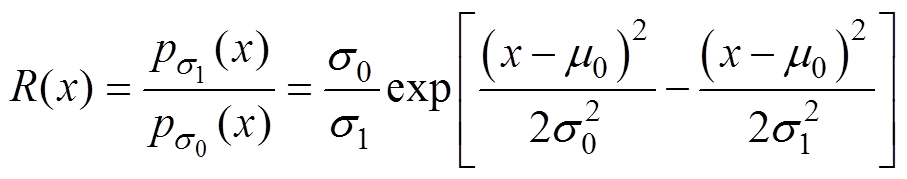（12）将式（12）代入式（10）中得
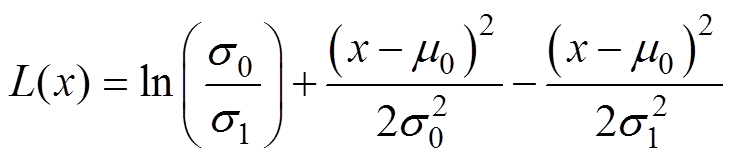（13）根据式（13），定义偏差累积和函数为
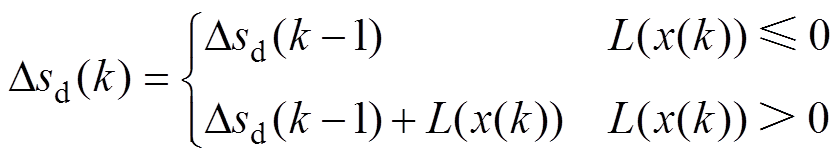（14）式中，Dsd(k)为变量x第k（k≥1）次采样的偏差累积和，且有Dsd(0)=0。
根据最大似然估计原理，当变量x未发生异常波动时，m0、s0为对应变量最大PDF值的最佳参数，故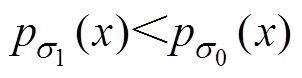
，0＜R(x)＜1，此时L(x)＜0, Dsd(k)保持原值；而当变量x异常波动时，变量最大PDF值的最佳参数将变为m1与s1，故
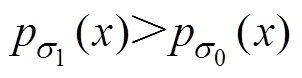，R(x)＞1，此时L(x)＞0，Dsd(k)进行累加。
根据式（13）和式（14），利用RSC开路故障前后Udc对数似然比的变化特性，定义Udc异常监测标识值为
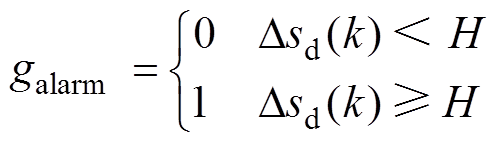（15）式中，galarm=0，表示Udc正常，galarm=1，表示Udc异常；H为Udc异常的偏差累积和阈值。当Udc第k次采样的Dsd(k)超出阈值H时，galarm由0变为1。
根据式（15），当Udc正常运行时，对应的L(Udc)＜0，此时Dsd(Udc)保持不变；而当Udc异常波动时，则有L(Udc)＞0，此时Dsd(Udc)在上一次的基础上进行累积。一旦Dsd(Udc)超出阈值H时，系统警报触发。本文综合故障监测的速度与精度，阈值H选取约为Udc额定值的一半，即H=600，同时为了防止Dsd(Udc)数值过大数据溢出，对其进行限幅处理，取其最大值为5倍Udc额定值左右，即(Dsd(Udc))max=6 000。
基于Udc特征仅能实现RSC功率器件开路故障监测，却无法定位不同开路故障位置。而与Udc故障特征不同，RSC发生单管或双管开路故障时，故障相电流出现半波或全波缺失现象，即RSC不同开路故障类型对应故障相电流输出波形不同。故可通过RSC输出电流特征实现开路故障类型识别。
根据恒幅值变换得到RSC转子电流Park矢量及其幅值为
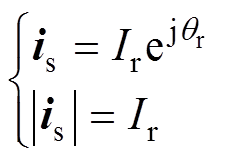（16）式中，is、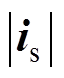
、qr分别为电流Park矢量及其幅值与相位。
由式（16）得RSC各相输出电流归一化值为
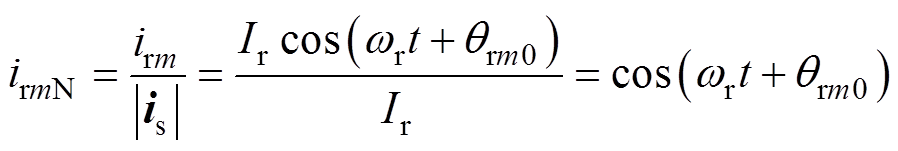（17）式中，qrm0、irmN分别为RSC各相初始相位与归一化电流值。
由式（17）可知，RSC归一化相电流是幅值恒为1的正弦信号，大小与风电载荷无关。由式（17）进一步得到RSC输出电流的归一化平均值与绝对平均值为
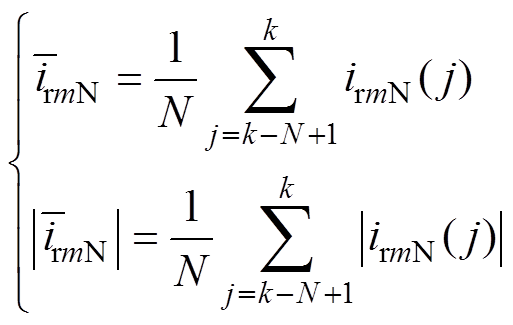（18）式中，N为RSC相电流单周期内的采样数；j为采样时刻。
在一个周期内，若采样点数N趋于无穷大，则式（18）可表示为
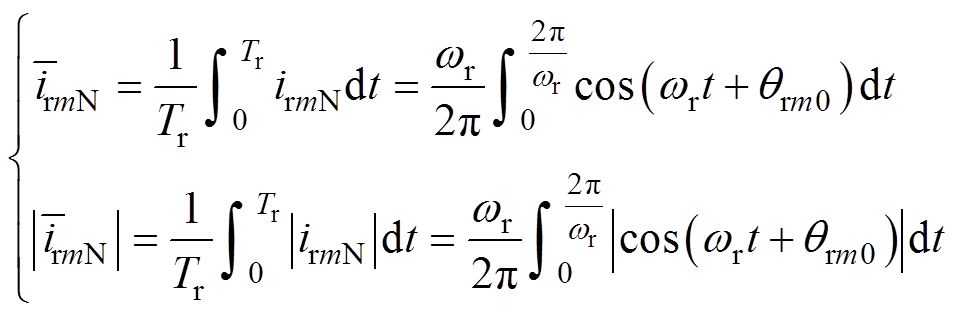（19）当RSC未发生开路故障时，有
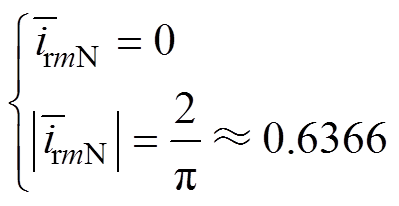（20）利用逆变器输出电流均值与绝对均值的比值，构建故障特征量[14]为
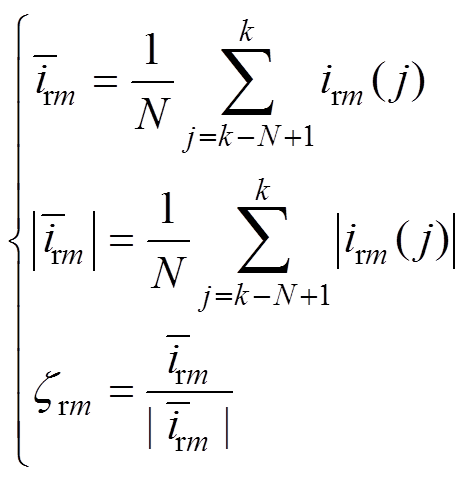（21）故障特征量zrm忽略了故障相对非故障相电流的影响。当RSC发生开路故障时，非故障相因直流分量的增加而导致自身特征参量实际值不为零（理论为零）。为减小故障相对非故障相电流的干扰，同时保证故障相特征量原有特性，鉴于两个非零且绝对值小于1的数相乘具有相互抑制作用，故利用特征量zrm绝对值与RSC归一化电流均值的乘积来构建新故障特征量，即
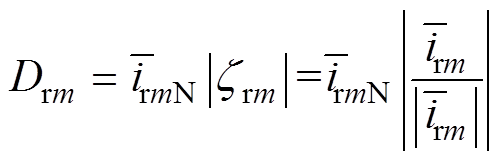（22）式中，Drm为本文所构建的故障电流特征量。
由式（22）可知，当RSC发生开路故障时，非故障相的zrm属于(0, 1)或(-1, 0)，对应相的归一化电流均值也属于(0, 1)或(-1, 0)，可知两者的乘积既能有效削弱故障相对非故障相电流的影响，还能保证故障相特征不变。
由式（22）可知，RSC不同开路故障情况对应的故障电流特征量不同。若阈值恒定，则降低故障识别方法的普适性。针对该问题，本文设计随故障情况变化而改变的自适应阈值以提高故障诊断系统的可靠性。
根据式（19），RSC不同故障情况所对应的电流归一化绝对均值不同。鉴于RSC输出电流归一化绝对均值可有效区分不同开路故障情况，考虑到其值与相应的故障电流特征量绝对值相近，为提高故障识别的鲁棒性，故利用RSC输出电流归一化绝对均值与偏移常量共同构建故障识别自适应阈值，即
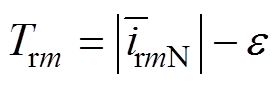（23）式中，Trm为故障识别自适应阈值；e 为偏移常量。
对于RSC单管开路故障情况，故障电流特征量绝对值由零增加至非故障电流归一化绝对均值的一半，而对应的故障相阈值则减半，同时对于RSC同桥臂双管开路故障情况，故障电流特征量绝对值趋近于零值，而此时故障相阈值也减小至零。根据式（23），若e 取零，则存在因故障电流特征量与其阈值相近而难以实现故障识别的问题。基于此，e 取值需大于零以增加两者之间的差值。考虑系统干扰与计算误差，对故障识别速度与鲁棒性进行折中，本文选取e 值为0.32，即非故障电流归一化绝对均值的一半。
RSC不同开路故障情况对应不同的故障电流特征量与阈值，对比故障特征量与相应的阈值，得到RSC开路在不同故障情况下的标识值为
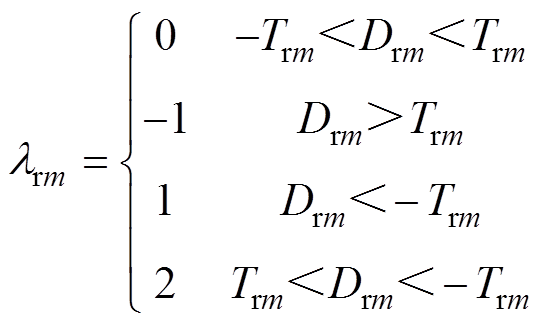（24）根据式（24），当RSC处于健康状态下，各相电流满足-Trm＜Drm＜Trm，故lrm始终为0。当RSC发生下桥臂单管开路故障时，故障相电流负半波缺失，故障相Drm由0逐渐增加至原归一化绝对电流均值的一半，而Trm减半，此时Drm＞Trm，lrm变为-1；同理，当发生上桥臂单管开路故障时，RSC对应故障相电流正半波缺失，故障相Drm由0逐渐减小至原归一化绝对电流均值的一半的负值，Trm也减半，此时Drm＜-Trm，lrm变为1。对于RSC同桥臂上、下两管开路的故障类型（类型Ⅱ），故障相电流全波缺失，此时故障相Drm为0，Trm变为-e，满足Trm＜Drm＜-Trm，lrm变为2。
双馈风电RSC单管与双管开路共有21种不同的情况，归纳为以下三种主要类型：Ⅰ单管故障（6种）；Ⅱ同桥臂双管故障（相故障）（3种）；Ⅲ不同桥臂双管故障（12种）。
RSC开路故障类型Ⅰ、Ⅱ、Ⅲ中，故障类型Ⅰ和Ⅱ只涉及RSC某一相输出电流波形缺失，增加的直流分量由两非故障相共同承担，非故障相电流波形受故障相的影响相对较小。而对于故障类型Ⅲ，其导致RSC某两相输出电流波形缺失，根据KCL定律，此时非故障相将产生与故障相相反的波形缺失。综上所述，RSC不同开路故障类型对应的故障识别标识值见表1。
通过上述分析可知，基于CUSUM算法，捕捉双馈风电变流器直流母线电压故障特性，实现基于直流母线电压特征的故障监测。同时，同双馈RSC转子电流进行归一化处理，基于转子电流归一化绝对值及绝对归一化绝对值构建故障识别特征量及其自适应阈值，实现基于转子电流特征的故障识别。利用双馈风电机组直流母线电压与转子电流特征实现RSC功率器件开路故障综合诊断具体流程如图5所示。
表1 RSC功率管开路故障识别标识值
Tab.1 Identification signs of the open-circuit fault of RSC power switches
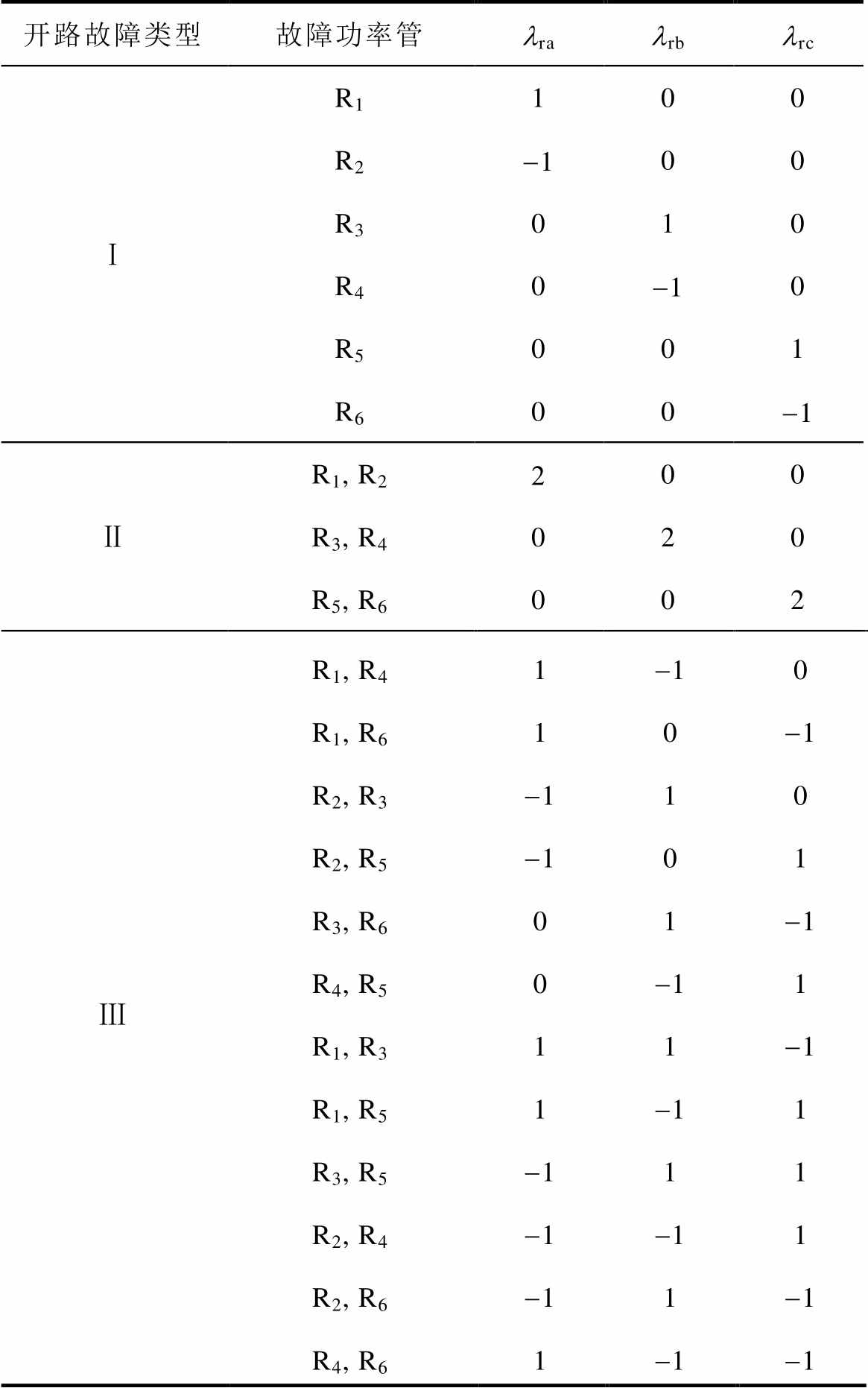
开路故障类型故障功率管lralrblrc ⅠR1100 R2-100 R3010 R40-10 R5001 R600-1 ⅡR1, R2200 R3, R4020 R5, R6002 ⅢR1, R41-10 R1, R610-1 R2, R3-110 R2, R5-101 R3, R601-1 R4, R50-11 R1, R311-1 R1, R51-11 R3, R5-111 R2, R4-1-11 R2, R6-11-1 R4, R61-1-1
为验证本文所提方法的有效性，基于Matlab/ Simulink平台，以容量1.5MW的双馈风电机组为例，通过驱动信号缺失来模拟RSC功率器件开路，同时假设各功率器件的反并联二极管均正常工作。仿真相关参数见表2。
不失一般性，本文假设任意时刻tf1发生某单管开路故障，而后任意时刻tf2又发生另一功率管开路故障，以模拟RSC单管故障演变至双管故障的过程。本文选定tf1=1.23s，tf2=1.85s，对RSC不同功率器件先后开路故障进行仿真，结果如图6～图8所示。
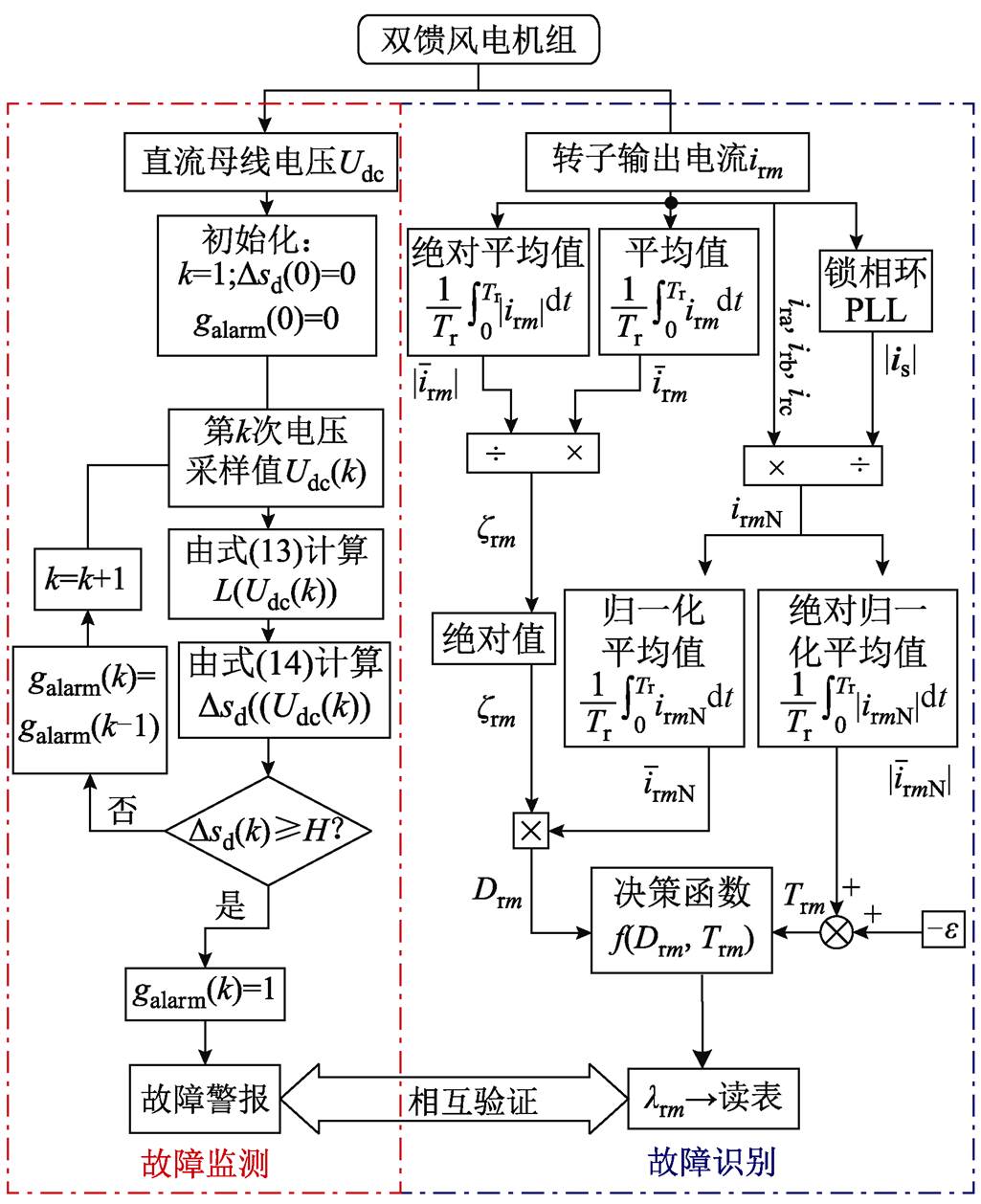
图5 RSC功率器件开路故障综合诊断流程
Fig.5 Flow chart of the open-circuit fault comprehensive diagnosis of RSC power switches
表2 DFIG主要仿真参数
Tab.2 The main parameters of the DFIG
参 数数 值 输出有功功P/MW1.5 输出无功功率Q/var0 输出电压U/V575 基准频率fb/Hz50 直流母线电压Udc/V1 150 直流母线电容Cdc/mF10 定子电阻Rs/mΩ5.069 定子电感Ls/mH0.105 转子电阻Rr/mW3.527 转子电感Lr/mH0.279 励磁电感Lm/mH1.696 极对数p3
图6展示了RSC功率管R1、R2先后开路故障监测与识别仿真结果。在tf1=1.23s时刻，RSC功率管R1发生开路故障，Udc波动，ira正半波形缺失，当Dsd(Udc)＞H时，警报触发。而Dra由0渐变为负值，同时Tra减半，此时满足Dra＜-Tra，lra由0变为1。在tf2=1.85s时刻，R2开路，RSC由a相单管故障演变为a相故障，此时Dra由负值变为0，而Tra继续减小至-e，有Tra＜Dra＜-Tra，lra由1变为2。
图6 RSC功率管R1、R2先后开路故障监测与识别
Fig.6 Fault monitoring and identification for R1, R2 successive open-circuit fault of RSC
图7与图6仿真结果的分析类似，在tf1=1.23s与tf2=1.85s时刻先后发生了功率管R2与R3开路故障。R2开路导致Dsd(Udc)超出阈值H，系统触发警报，此时Dra由0渐变为正值，Tra减半，满足Dra＞Tra，lra由0变为-1。当R3开路，此时RSC发生a、b两相上桥臂单管开路故障，Drb由0渐变为负值，Trb减半，有Drb＜-Trb，故lrb由0变为1。
图8为RSC功率管R1、R5先后开路故障仿真结果。同理，功率管R1开路引发系统警报，同时ira正半波形缺失，Dra由0渐变为负值，Tra减半，满足Dra＜-Tra，lra由0变为1。在tf2=1.85s时刻，R5开路，此时RSC发生a、c两相上桥臂单管开路故障，Drc由0渐变为负值，Trc减半，有Drc＜-Trc，故lrc也由0变为1。但与前两种故障情况所不同，因此时非故障相b受故障相a、c的影响较大，导致irb对应的Drb也超出了阈值Trb，使得Drb＞Trb，进而lrb由0变为1。
为验证本文所提方法对外界干扰的免疫性能。以风速随机、电网电压跌落这两种常见的场景来验证本文所提方法的鲁棒性。
图7 RSC功率管R2、R3先后开路故障监测与识别
Fig.7 Fault monitoring and identification for R2, R3 successive open-circuit fault of RSC
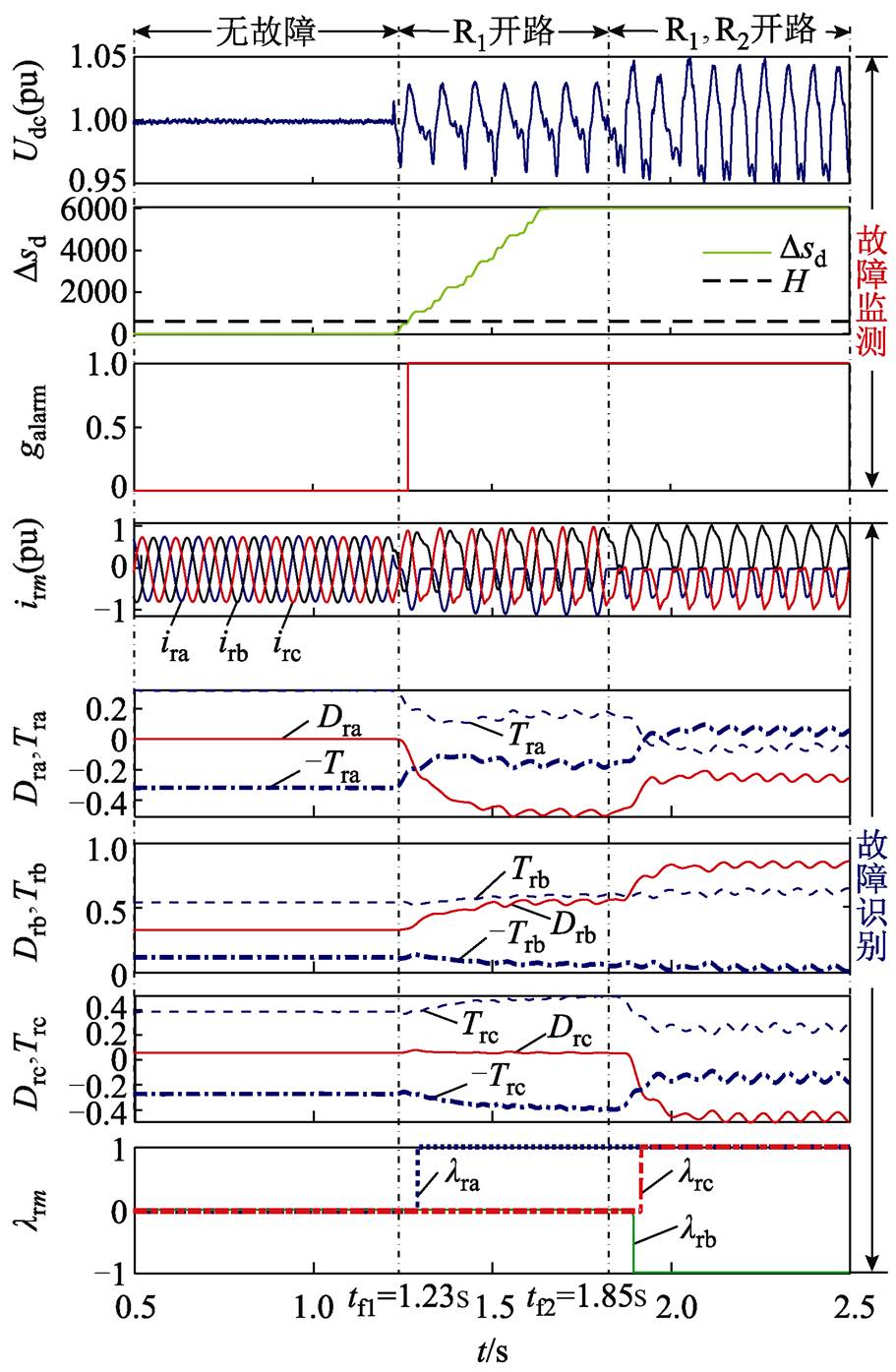
图8 RSC功率管R1、R5先后开路故障监测与识别
Fig.8 Fault monitoring and identification for R1, R5 successive open-circuit fault of RSC
3.2.1 风速随机情况
为更好地模拟风电场实际风况，仿真输入随机风由基本风分量、阵风分量、渐变风分量及随机风分量叠加而成，基本风速设置为10m/s[30]。仿真结果如图9所示。可知随机风速对Udc影响较小，因Dsd(Udc)始终小于H，故galarm始终保持为0。虽随机风速使RSC各相电流故障诊断量与阈值产生一定波动，但各相特征量仍然处于阈值范围内，可知，本文所提方法对随机风工况仍适用。
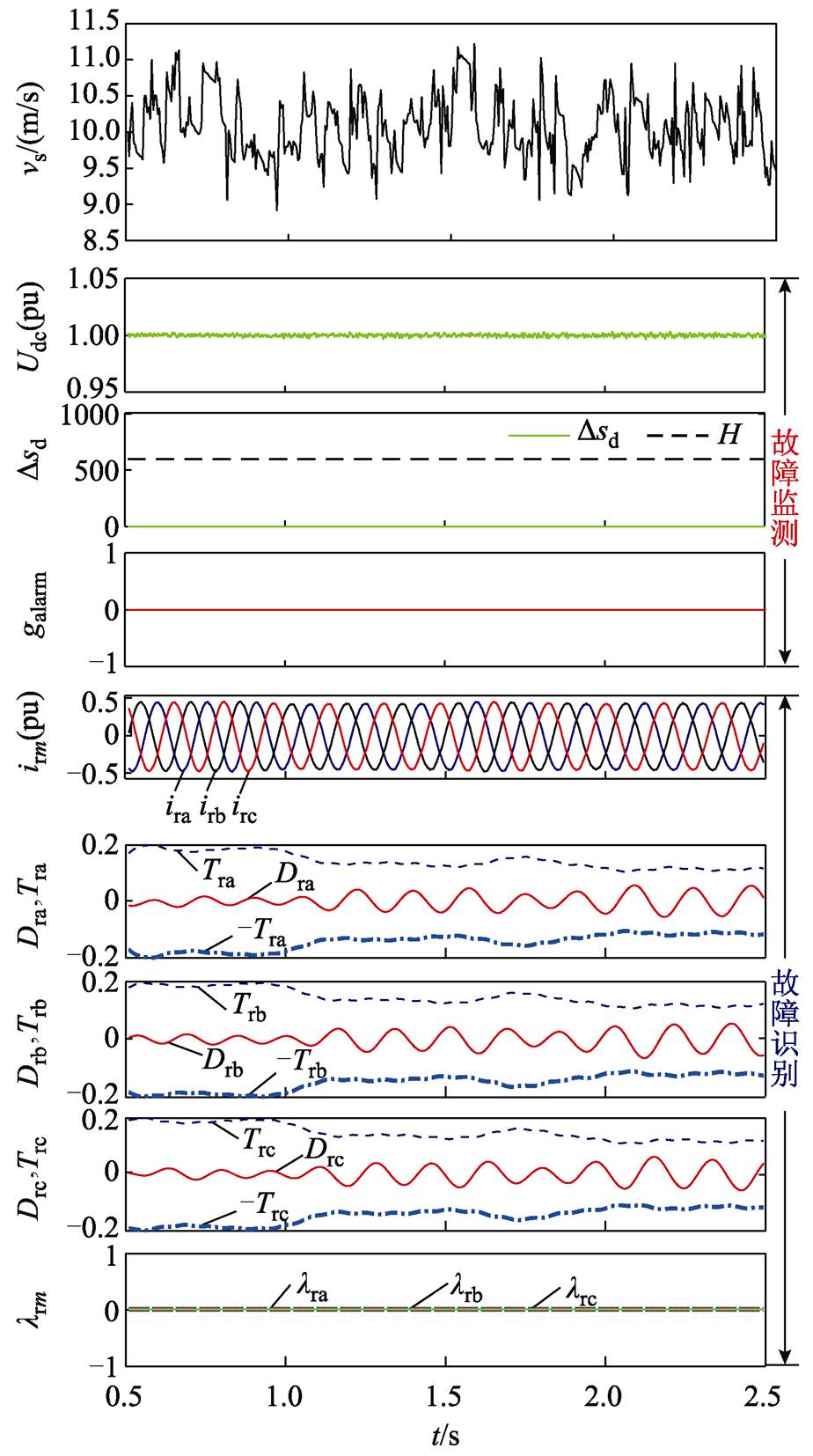
图9 随机风速下的故障监测与识别
Fig.9 Fault monitoring and identification under stochastic wind
3.2.2 电网电压跌落情况
设置网侧电压幅值Ug在不同时刻先后发生变化。假设在t1=1.5s时刻Ug跌落50%，在t2=1.8s时刻，恢复原值。仿真结果如图10所示。Ug跌落瞬间，Udc产生较大冲击，致使Dsd超出阈值，galarm由0变为1，此时系统产生误警报。但Ug跌落对RSC故障识别产生了有利影响。Ug跌落使电流变大，但因电流形状仍为正弦，故RSC转子电流的增大对Drm基本无影响，却使Trm变大。而Drm不变，Trm增大，反而增加故障识别系统的稳定裕度。Ug跌落虽致使系统产生误警报，但故障识别却未动作，因此可将故障监测与故障识别进行相互验证以综合判断系统是否误诊断。
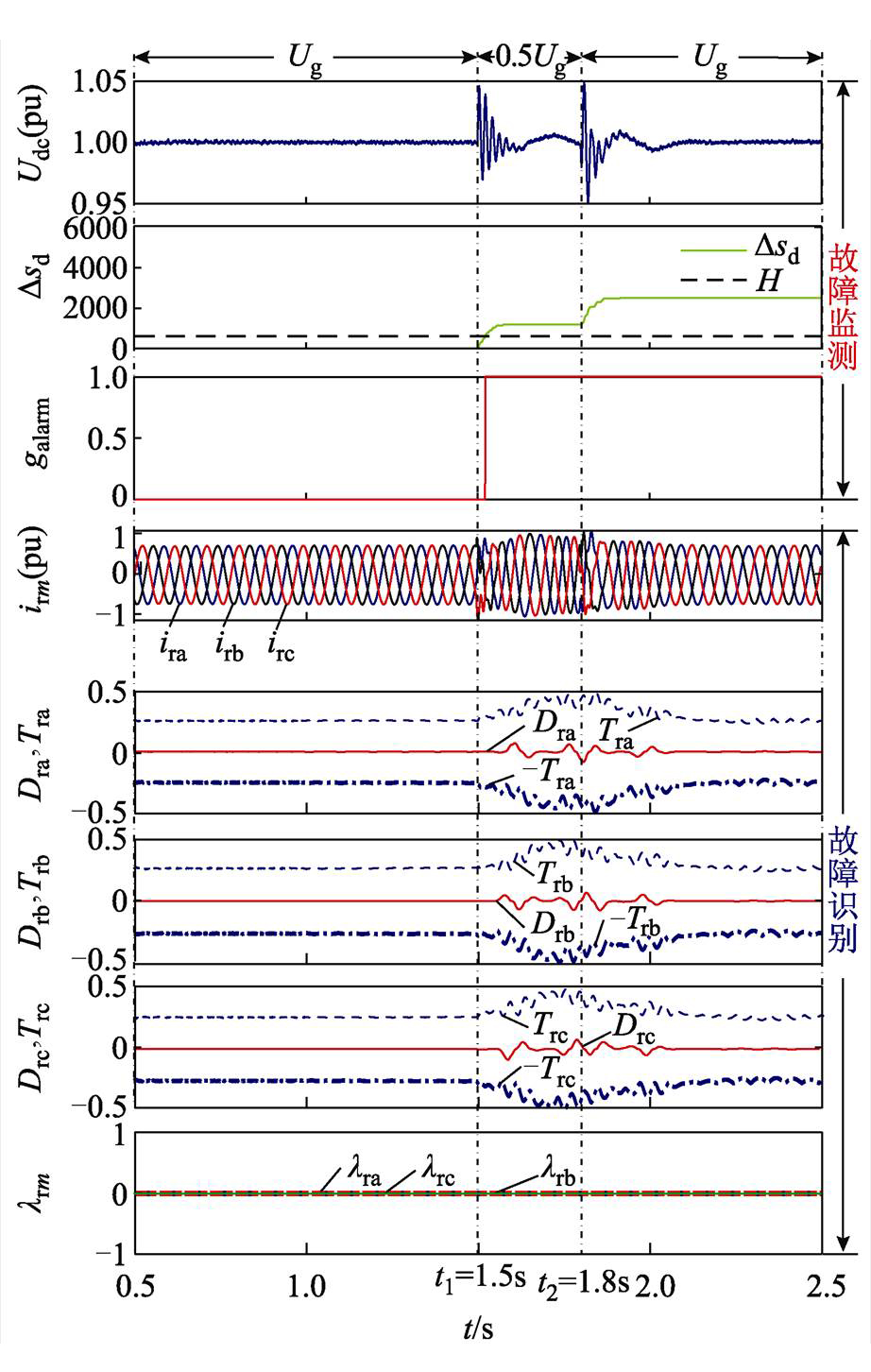
图10 电压跌落下的故障预警与识别
Fig.10 Fault monitoring and identification with voltage drop
实验平台主要由三相调压器、直流母线电容、滤波电感、DC-AC变流器功率模块、RL串联负载组成，如图11所示。实验相关参数见表3。
为更真实地模拟仿真情景，实验时保持变流器故障前后控制方式不变。为验证仿真结果的准确性，实验主要以变流器功率器件三种典型开路故障为例进行验证。通过上位机程序平台控制各功率器件脉冲的输出，以模拟不同功率器件先后开路情况，同时设置输出电流基波为10Hz（模拟超同步运行状态），测量变流器不同故障情况下的直流侧电压与输出电流。分别对故障直流电压与输出电流的实验数据进行FFT分析与绝对均值计算处理，结果分别如图12、图13～图15所示。
图12以功率管R1与R4开路故障时的直流侧电压Udc进行FFT分析，由图可知，故障Udc产生了输出电流基频及其倍频的脉动，实验分析与理论推导基本相符。
图11 功率器件故障诊断实验平台
Fig.11 Experiment setup for fault diagnosis of power switches
表3 主要实验参数
Tab.3 The main parameters of the experiment
参 数数 值 开关频率fs/kHz10 输出频率fr/Hz10 直流输入电压Udc/V100 直流母线电容Cdc/mF3.3 滤波电感L/mH3 负载电阻Rr/W11 负载电感Lr/mH0.2
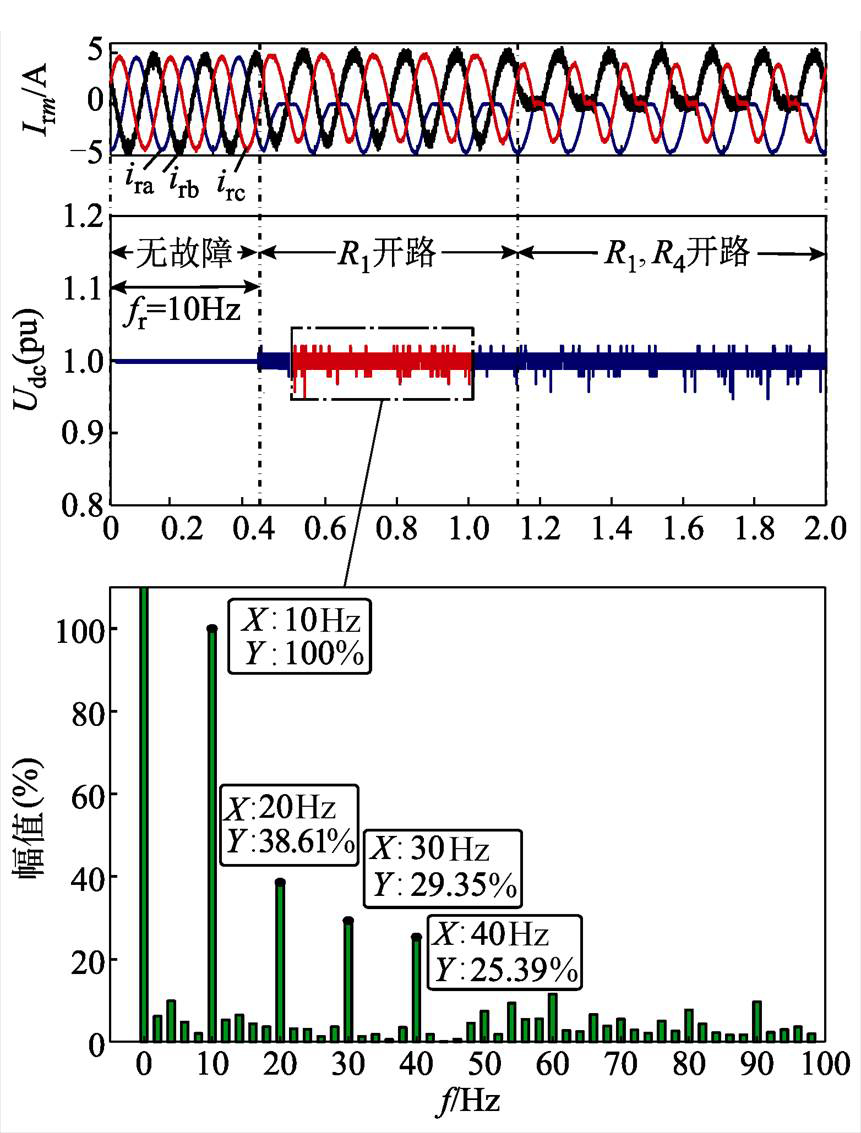
图12 故障Udc的FFT分析
Fig.12 FFT analysis of faulty Udc
图13 功率管R1、R2先后开路故障识别
Fig.13 Fault identification for R1, R2 successive open-circuit fault
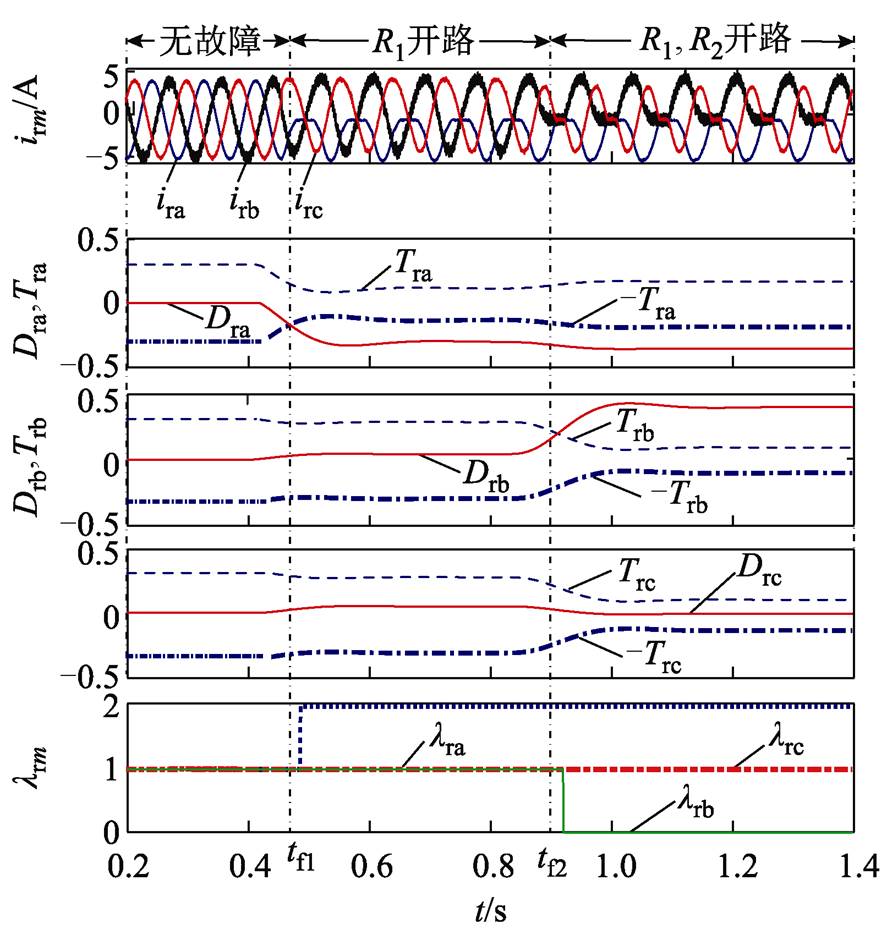
图14 功率管R1、R4先后开路故障识别
Fig.14 Fault identification for R1, R4 successive open-circuit fault
对图13～图15的分析可知，实验分别设置在时刻tf1与tf2发生功率器件先后开路，电流产生相应的波形缺失，实验现象与仿真结果基本吻合。同时，实验数据分析的故障识别结果与表1一致。
为了提高双馈风电变流器功率器件开路故障监测与识别能力，本文提出了一种基于直流母线电压与转子电流特征的故障综合诊断方法。基于RSC功率器件典型开路故障诊断及鲁棒性验证的结果，得出如下结论：
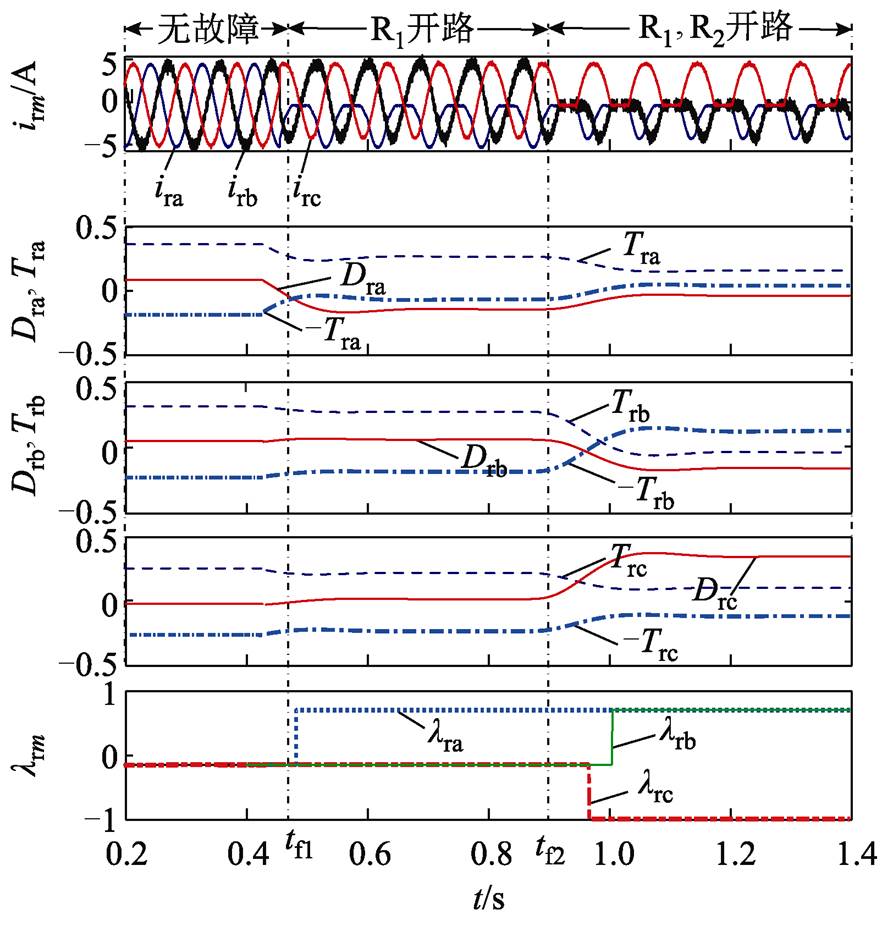
图15 功率管R1、R3先后开路故障识别 Fig.15 Fault identification for R1, R3 successive open-circuit fault
1）CUSUM算法简单，易于在线实现，基于该算法的直流母线电压异常捕捉实现了RSC功率器件开路故障在线监测。
2）通过对比RSC转子电流特征量及其阈值，实现了RSC单管与双管开路故障的准确识别。
3）以随机风与电网电压跌落为场景仿真验证了本文所提方法的鲁棒性，通过变流器功率器件开路故障实验验证了本文所提方法的有效性。
参考文献
[1] Hahn B, Durstewitz M, Rohrig K. Reliability of wind turbines[M]. New Jersey: Wind Energy, 2007.
[2] Yang Zhimin, Chai Yi. A survey of fault diagnosis for onshore grid-connected converter in wind energy conversion systems[J]. Renewable and Sustainable Energy Reviews, 2016, 66: 345-359.
[3] Richardeau F, Baudesson P, Meynard T A. Failures tolerance and remedial strategies of a PWM multi-cell inverter[J]. IEEE Transactions on Power Electronics, 2002, 17(6): 905-912.
[4] 孟云平, 周新秀, 李红, 等. 基于四桥臂拓扑的永磁同步电机断相容错控制策略[J]. 电工技术学报, 2019, 34(15): 3158-3166.
Meng Yunping, Zhou Xinxiu, Li Hong, et al. Fault tolerant strategy of four-leg for permanent magnet synchronous motor in case of open circuit fault[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3158-3166.
[5] 谢东, 葛兴来. 基于残差变化率的单相级联H 桥整流器IGBT 开路故障诊断[J]. 电工技术学报, 2018, 33(16): 3822-3834.
Xie Dong, Ge Xinglai. Residual-changing-rate based open-circuit fault diagnosis for a single-phase cascaded H-bridge rectifier[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3822-3834.
[6] 高兵, 陈民铀, 杨帆, 等. 考虑机侧变流器复杂热载荷特性的寿命评估[J]. 电工技术学报, 2017, 32(13): 88-99. Gao Bing, Chen Minyou, Yang Fan, et al. Life estimation of generator side converter considering the comprehensive mission profiles[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 88-99.
[7] Khomfoi S, Tolbert L M. Fault diagnosis and recon- figuration for multilevel inverter drive using AI-based techniques[J]. IEEE Transactions on Industrial Elec- tronics, 2007, 54(6): 2954-2968.
[8] 陈丹江, 叶银忠. 基于多神经网络的三电平逆变器器件开路故障诊断方法[J]. 电工技术学报, 2013, 28(6): 120-126.
Chen Danjiang, Ye Yinzhong. Fault diagnosis of three level inverter based on multi neural network[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 121-126.
[9] 于生宝, 何建龙, 王睿家, 等. 基于小波包分析和概率神经网络的电磁法三电平变换器故障诊断方法[J]. 电工技术学报, 2016, 31(17): 102-112.
Yu Shengbao, He Jianlong, Wang Ruijia, et al. Fault diagnosis of electromagnetic three-level inverter based on wavelet packet analysis and probabilistic neural networks[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 102-112.
[10] 李兵, 崔介兵, 何怡刚, 等. 基于能量谱熵及小波神经网络的有源中性点钳位三电平逆变器故障诊断[J]. 电工技术学报, 2020, 35(10): 2216-2225.
Li Bing, Cui Jiebing, He Yigang, et al. Fault diagnosis of active neutral point clamped three-level inverter based on energy spectrum entropy and wavelet neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2216-2225.
[11] Li Zhan, Ma Hao, Bai Zhihong, et al. Fast transistor open-circuit faults diagnosis in grid-tied three-phase VSIs based on average bridge arm pole-to-pole voltages and error-adaptive thresholds[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 8040-8051.
[12] 杭俊, 张建忠, 程明, 等. 基于线电压误差的永磁直驱风电系统变流器开路故障诊断[J]. 中国电机工程学报, 2017, 37(10): 2933-2943.
Hang Jun, Zhang Jianzhong, Cheng Ming, et al. Fault diagnosis of open-circuit faults in converters of direct-driven permanent magnet wind power generation systems based on line voltage errors[J]. Proceedings of the CSEE, 2017, 37(10): 2933-2943.
[13] 沈艳霞, 周文晶, 纪志成, 等. 基于小波包分析的风力发电系统中变流器的故障识别[J]. 电网技术, 2013, 37(7): 242-248.
Shen Yanxia, Zhou Wenjing, Ji Zhicheng, et al. Fault identification of converter used in wind power generation based on wavelet packet analysis[J]. Power System Technology, 2013, 37(7): 242-248.
[14] 梅樱, 孙大南, 韦中利, 等. 一种基于矢量控制的变流器故障诊断方法[J]. 电工技术学报, 2010, 25(3): 177-182.
Mei Ying, Sun Danan, Wei Zhongli, et al. An approach to converter faults diagnosis based on vector control[J]. Transactions of China Electro- technical Society, 2010, 25(3): 177-182.
[15] 褚召伟, 李春茂, 何登, 等. 基于小波神经网络的风电变流器故障诊断系统[J]. 电气技术, 2012, 13(9): 34-37.
Chu Zhaowei, Li Chunmao, He Deng, et al. Fault diagnosis system of wind power converter based on wavelet neural network[J]. Electrical Engineering, 2012, 13(9): 34-37.
[16] 郝振洋, 徐子梁, 陈宇, 等. 航空Vienna整流器故障诊断与容错控制[J]. 电工技术学报, 2020, 35(24): 5152-5163.
Hao Zhenyang, Xu Ziliang, Chen Yu, et al. Fault diagnosis and fault tolerant control for aviation Vienna rectifier[J]. Transactions of China Electro- technical Society, 2020, 35(24): 5152-5163.
[17] 陈勇, 刘志龙, 陈章勇. 基于电流矢量特征分析的逆变器开路故障快速诊断与定位方法[J]. 电工技术学报, 2018, 33(4): 883-891.
Chen Yong, Liu Zhilong, Chen Zhangyong. Fast diagnosis and location method of open-circuit fault in inverter based on current vector character analysis[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 883-891.
[18] 黄科元, 刘静佳, 黄守道, 等. 永磁直驱系统变流器开路故障诊断方法[J]. 电工技术学报, 2015, 30(16): 135-142.
Huang Keyuan, Liu Jingjia, Huang Shoudao, et al. Converters open-circuit fault-diagnosis methods research for direct-driven permanent magnet wind power system[J]. Transactions of China Electro- technical Society, 2015, 30(16): 135-142.
[19] Freire N M A, Estima J O, Marques Cardoso A J. Open-circuit fault diagnosis in PMSG drives for wind turbine applications[J]. IEEE Transactions on Indu- strial Electronics, 2013, 60(9): 3957-3967.
[20] Estima J O, Marques Cardoso A J. A new algorithm for real-time multiple open-circuit fault diagnosis in voltage-fed PWM motor drives by the reference current errors[J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 3496-3505.
[21] Tiancheng S, Yigang H, Fangming D, et al. Online diagnostic method of open-switch faults in PWM voltage source rectifier based on instantaneous AC current distortion[J]. IET Electric Power Appli- cations, 2018, 12(3): 447-454.
[22] Huang Zhanjun, Wang Zhanshan, Zhang Huaguang. A diagnosis algorithm for multiple open-circuited faults of microgrid inverters based on main fault component analysis[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 925-937.
[23] Khojet El Khil S, Jlassi I, Marques Cardoso A J, et al. Diagnosis of open-switch and current sensor faults in PMSM drives through stator current analysis[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 5925-5937.
[24] Duan Pan, Xie Kaigui, Zhang Li, et al. Open-switch fault diagnosis and system reconfiguration of doubly fed wind power converter used in a microgrid[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 816-821.
[25] Zhao Hongshan, Cheng Liangliang. Open switch fault diagnostic method for back to back converters of doubly fed wind power generation system[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 3452-3461.
[26] 贺益康, 胡家兵, 徐烈. 并网双馈异步风力发电机运行控制[M]. 北京: 中国电力出版社, 2012.
[27] Wu R, Dewan S B, Slemon G R. Analysis of an AC-to-DC voltage source converter using PWM with phase and amplitude control[J]. IEEE Transactions on Industry Applications, 1991, 27(2): 355-364.
[28] Li Yongbo, Xu Minqiang, Wei Yu, et al. Health condition monitoring and early fault diagnosis of bearings using SDF and intrinsic characteristic- scale decomposition[J]. IEEE Transactions on Instru- mentation and Measurement, 2016, 65(9): 2174-2189.
[29] Flynn T, Yoo S. Change detection with the kernel cumulative sum algorithm[C]//IEEE 58th Conference on Decision and Control (CDC), France, Nice, 2019: 6092-6099.
[30] 李辉, 胡玉, 柴兆森, 等. 随机风载荷对双馈风电机组轴系扭振响应分析[J]. 太阳能学报, 2020, 41(5): 180-187.
Li Hui, Hu Yu, Chai Zhaosen, et al. Analysis on shaft torsional vibration responses of doubly fed induction generators under stochastic wind load[J]. Acta Energiae Solaris Sinica, 2020, 41(5): 180-187.
Comprehensive Diagnosis of Open-Circuit Fault for Power Devices of Doubly-Fed Wind Power Converter Based on the Features of Voltage and Current
Abstract Open-circuit fault monitoring and identification for power converter devices are of the utmost importance for improving the intelligence operations for doubly-fed wind power system. Aiming at the problems that the existing diagnosis methods are difficult to achieve fault monitoring and identification simultaneously for power devices based on the converter voltage or current single feature and fixed threshold, a comprehensive diagnosis method of fault monitoring based on converter DC-bus voltage and fault identification based on the rotor current is proposed. First of all, theoretical analysis of the influence of power device failure of the converter on the DC-bus voltage. According to the cumulative sum (CUSUM) algorithm, an open-circuit fault monitoring method of power devices based on the feature of DC-bus voltage is put forward. Secondly, in view of the non-stationary characteristic and fixed threshold of the rotor current, a fault identification method based on the normalized output current average value and absolute average value as the fault feature and adaptive threshold is presented. Finally, to verifythe effectiveness of the proposed method with the different power devices open-circuit faults simulation, and the robustness is validated by the scenes of stochastic wind and grid voltage drop. At the same time, the accuracy of the simulation analysis is verified by testing the typical open-circuit fault of the power device. The simulation and experimental results show that, the proposed method could accurately realize the comprehensive diagnosis of the power converter devices open- circuit fault.
keywords：Doubly-fed wind power converter, power device open-circuit fault, cumulative sum algorithm, adaptive threshold, comprehensive fault diagnosis
DOI:10.19595/j.cnki.1000-6753.tces.L90287
中图分类号：TM46
李 辉 男，1973年生，教授，博士生导师，研究方向为风电发电技术，新型电机及系统分析，功率器件可靠性。E-mail：cqulh@163.com（通信作者）
杨 甜 女，1995年生，硕士研究生，研究方向为风电变流器故障诊断与容错控制。E-mail：yt_0727_6080@163.com
国家高技术船舶科研项目（MC-202025-S02）、国家自然科学基金重点项目（U1966213）和重庆市技术创新与应用发展专项（cstc2019jscx-msxmX0004）资助。
收稿日期 2020-07-09
改稿日期 2021-03-05
（编辑 赫 蕾）