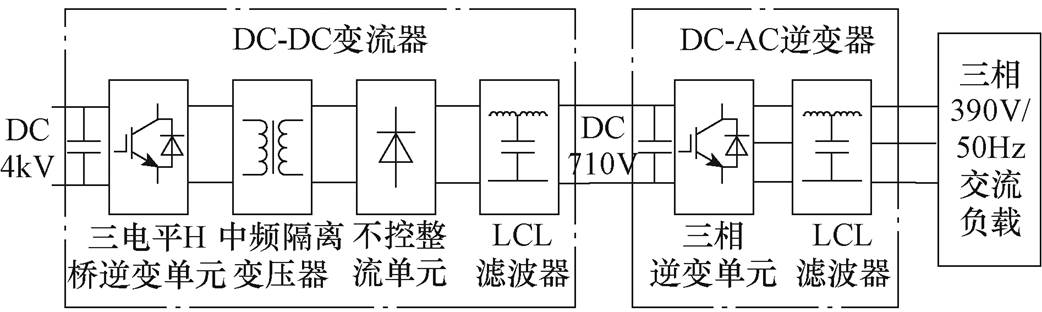
图1 变流器-逆变器级联示意图
Fig.1 Schematic diagram of the system cascaded by DC-DC converter and DC-AC inverter
摘要 舰船低压变配电系统中的大容量电力电子设备级联后，可能由于阻抗不匹配而导致电压振荡失稳。为了探究影响电力电子级联系统静态稳定性的因素，该文针对大容量DC-DC变流器进行建模和阻抗特性分析。首先，基于开关网络平均法建立变流器的小信号模型，推导出相应的输出阻抗模型。在此基础上，根据阻抗比判据进行稳定性原理分析，明确变流器输出阻抗幅值的峰值是造成阻抗不匹配的主导因素。进一步地，通过探究不同运行模式下变流器控制方式、控制参数和滤波器参数对输出阻抗幅值的影响，为改善系统静态稳定性找准优化的方向。最后，通过PSCAD/EMTD仿真和试验验证了该文稳定性分析的正确性。
关键词：DC-DC变流器 输出阻抗 级联系统 静态稳定性
随着电力电子技术在电能变换方面的成熟应用，采用“模块化、集成化、系统化”思想的舰船综合电力系统成为未来的发展方向[1]。在综合电力系统中，低压变配电子系统是实现中压直流到低压交流电能转换的关键组成部分。变流器-逆变器级联示意图如图1所示，DC-DC变流器（以下简称变流器）将主网中压直流转换成低压直流，DC-AC逆变器（以下简称逆变器）将低压直流转换成低压交流。由于变流器和逆变器都是强非线性的电力电子设备，级联后相互影响，若级联变换器阻抗不匹配，将会使系统的静态稳定性退化，容易产生低频振荡和电压失稳现象[2]。若采用Middlebrook阻抗比判据评估电力电子变换器级联系统的稳定性，首先需要分析级联系统源侧变换器的输出阻抗。
图1 变流器-逆变器级联示意图
Fig.1 Schematic diagram of the system cascaded by DC-DC converter and DC-AC inverter
源侧变换器输出阻抗受滤波器结构参数、控制方式等因素影响[3]。通过对分布式供电、微电网、不间断电源等系统的研究表明，滤波器对变换器输出阻抗的影响不尽相同：不考虑寄生参数时，滤波电感和电容的加入有利于减小变换器输出阻抗[2, 4-6]；若考虑寄生参数，滤波电容并不是越大越好[7]，电容性质过强将导致系统更易失稳[8]。可见，滤波器参数对输出阻抗的影响根据变换器拓扑而定，需视情况分析。通过研究控制方式对输出阻抗的影响，表明闭环控制系统较开环系统有更小的输出阻抗。例如，在加入有源阻尼控制[9-10]、虚拟阻抗控制[11-14]等阻抗补偿策略后，有效地减小了变换器的输出阻抗。又如，文献[15]使用电感电流的高频分量直接注入占空比对PWM环节进行补偿，减小了Buck变换器的输出阻抗。在研究控制参数对输出阻抗影响因素方面，文献[16]通过优化锁相环控制参数降低了并网侧逆变器的正负序阻抗，但并未以控制参数对阻抗的影响为依据。文献[17]研究双闭环控制参数对车网耦合系统输出阻抗的影响时，选取参数变化范围窄，不足以全面体现对输出阻抗的影响趋势。然而现有文献中，鲜有对DC-DC变换器控制参数的研究。本文所研究的变流器控制策略是综合多因素确定的，若改变控制策略可能会削弱系统动态性能，因此有必要在原有控制策略下分析控制参数对输出阻抗的影响。另外，由于变流器稳态工作模式分为电感电流连续导通模式（Continuous Conduction Mode, CCM）和电感电流断续导通模式（Discontinuous Conduction Mode, DCM），两种运行模式下输出阻抗不同，需要分析各自的特性。
本文以变流器为研究对象，通过小信号动态建模推导对应的输出阻抗模型，根据阻抗比判据确定变流器输出阻抗是造成级联系统阻抗不匹配的关键所在；然后分析不同模式下控制方式、控制参数和滤波器参数对变流器的输出阻抗的影响，进而探究影响级联系统静态稳定性的影响因素；最后通过仿真和试验验证了稳定性分析的正确性。
变流器由三电平逆变桥、中频隔离变压器、不控整流桥和滤波器组成[18]，实现主网DC 4kV到DC 710V的变换，变流器主电路拓扑结构如图2所示。
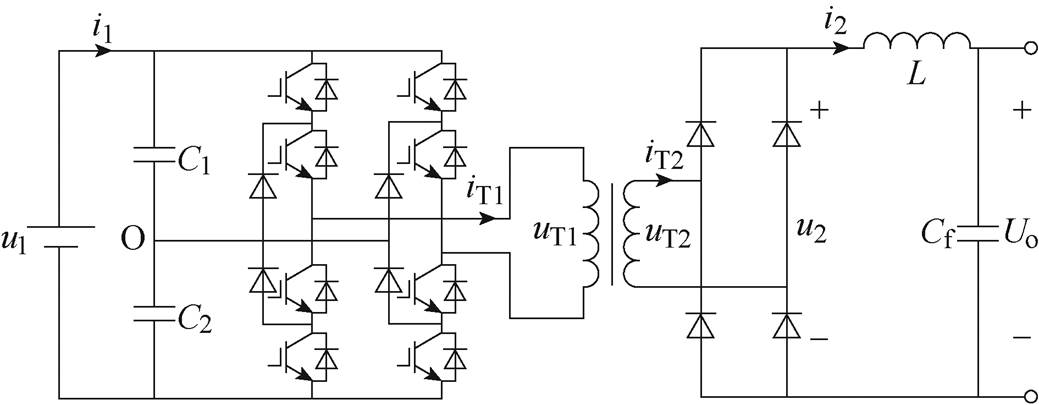
图2 变流器主电路拓扑结构
Fig.2 Main circuit structure diagram of DC-DC Converter
文献[19]初步建立了变流器的小信号模型，然而其组成器件多、非线性强，要探究影响输出阻抗的主要因素，就要在建模时合理简化。本文基于开关网络平均法改进变流器CCM小信号模型。
假设变流器所有开关器件均为理想器件，带电阻负载R运行于CCM，其一个周期内的波形如图3所示。图中，Ud、Uo、uT1、u2和i2分别为额定输入电压、额定输出电压、变压器一次电压、不控整流桥输出电压和滤波电感L电流，IC1～IC4为CCM下电感电流i2各阶段数值，dq、dg、da 分别为导通角q、钳位角g、移相角a 的占空比形式。
将稳态时的开关网络的输入、输出电压平均值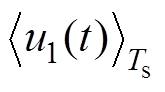
、
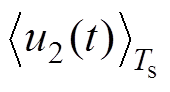作为变流器的输入、输出电压的开关周期平均值。分别计算出分段时间内流经电感的电流与电感压降的关系，即
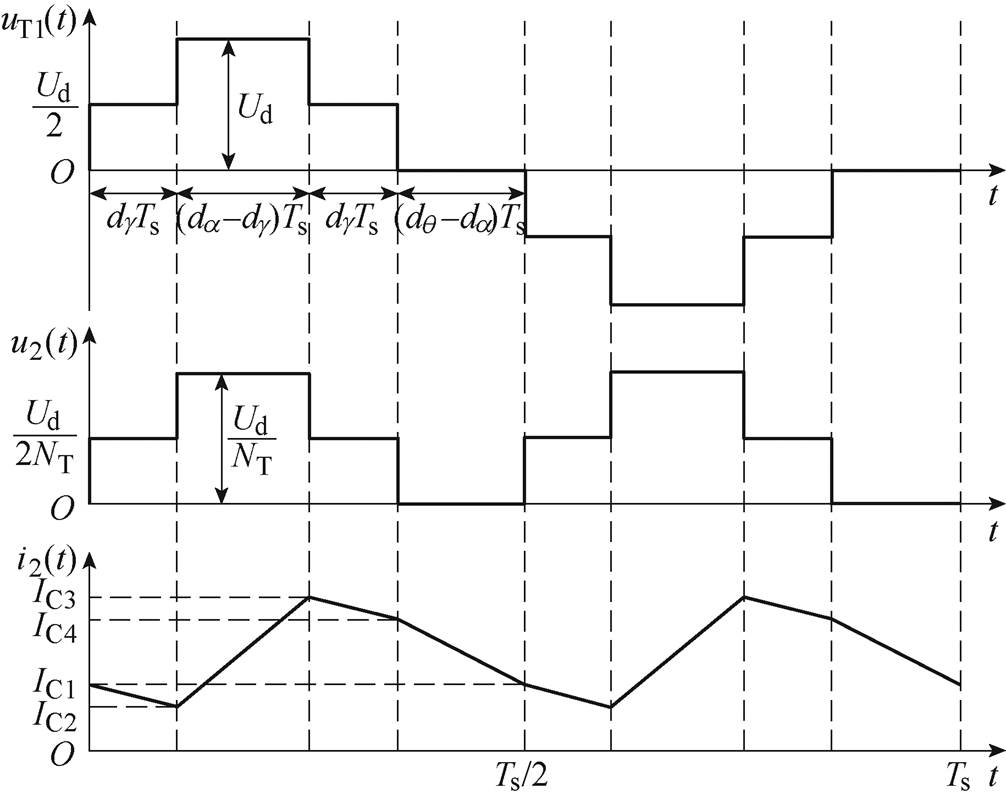
图3 变流器CCM下一个周期内的波形
Fig.3 Waveforms in a cycle of DC-DC converter in CCM
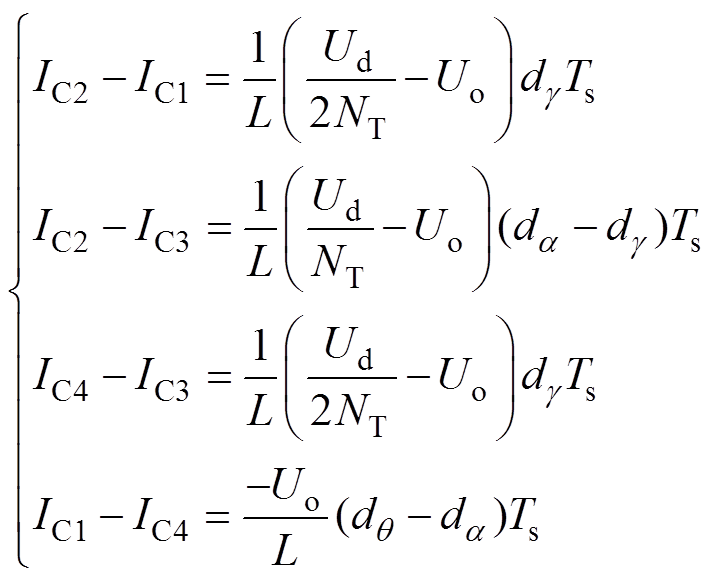（1）式中，Uo为额定输出电压；NT为变压器匝数比；Ts为开关周期。
将式（1）中四式相加得
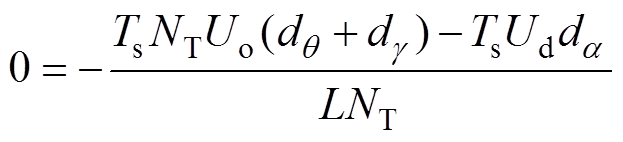（2）由于导通角和钳位角之和为p，即dq+dg=0.5，则变流器输入输出电压比M为
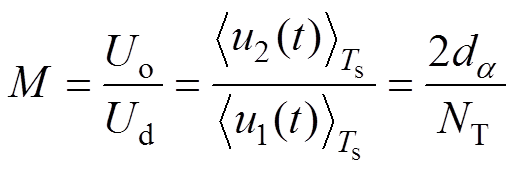（3）
开关网络输入、输出端口的关系为
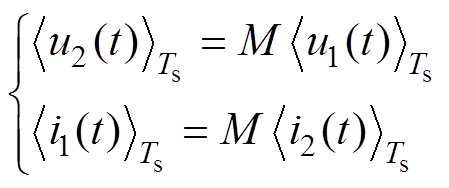（4）在静态工作点进行小扰动处理，得
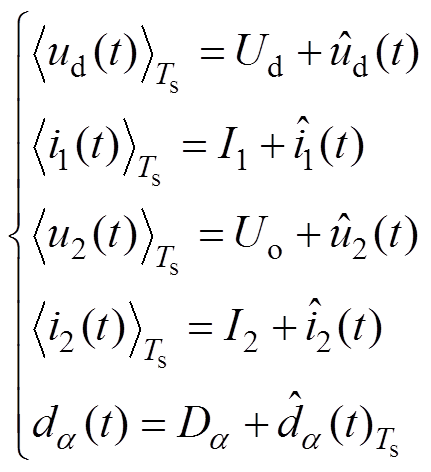（5）
将式（4）线性化得到开关网络输入、输出的小信号关系为
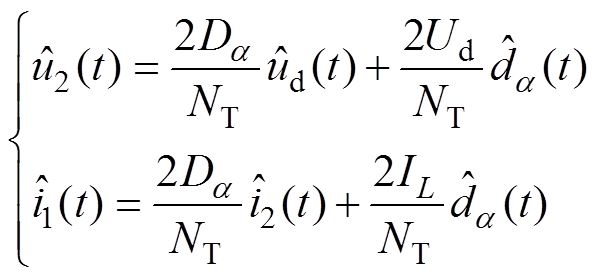（6）设输入无扰动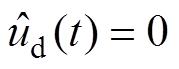
，则变流器CCM下的小信号模型为
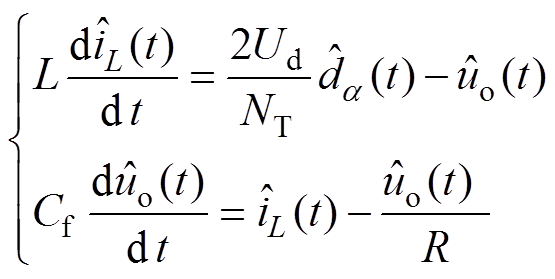（7）
上述小信号建模过程可推广至DCM，详见文献[20]。
变流器输出直流电作为逆变器的输入电源，考虑到变流器在负载突变时波动较大，设计较大的逆变器输入侧支撑电容以抑制直流电压纹波。因此，为了厘清级联系统的阻抗关系，不妨将支撑电容与变流器输出滤波电容Cf合并为等效电容C。结合文献[20]，两种模式的小信号模型等效电路如图4所示。
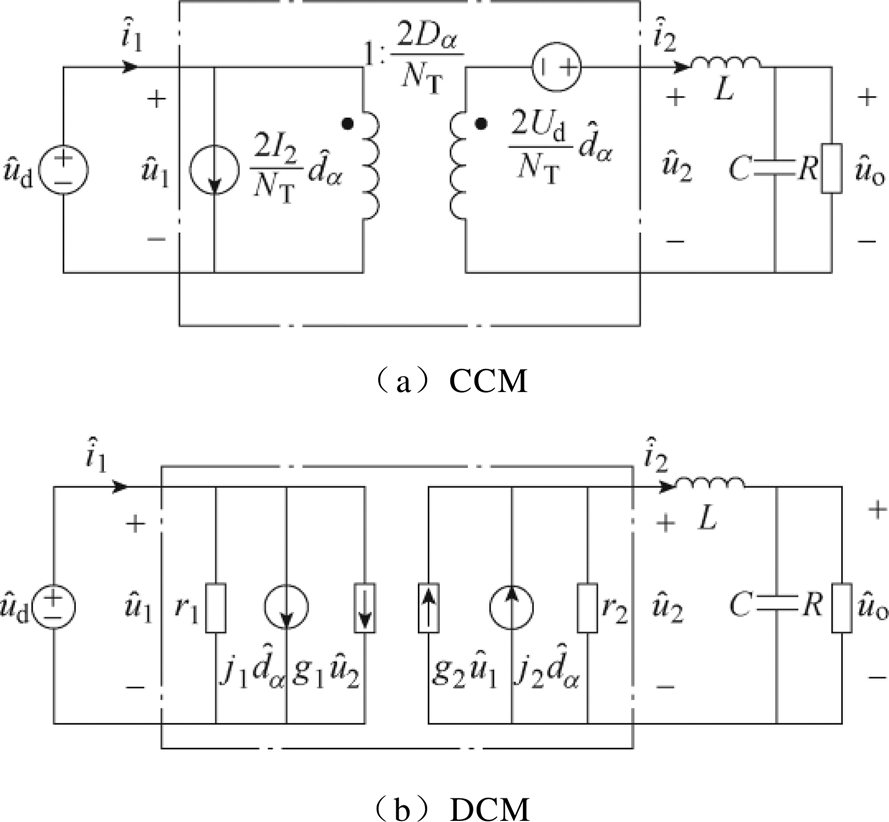
图4 变流器小信号交流电路模型
Fig.4 Small signal AC circuit model
单独计算变流器的输出阻抗时，可认为变流器空载。变流器开环时移相占空比扰动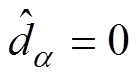
，令输入电压扰动
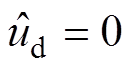，根据小信号模型等效电路（见图4）列写节点电压方程，可以得到CCM下输出阻抗ZCCM_oo、DCM下输出阻抗ZDCM_oo分别为
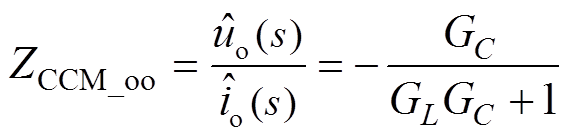（8）
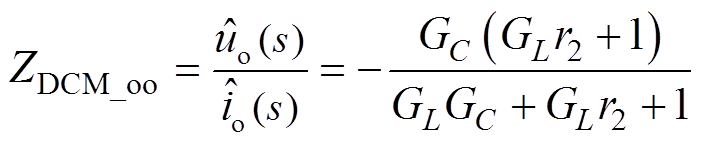（9）
式中，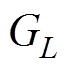
为考虑滤波电感的导纳传递函数，
；
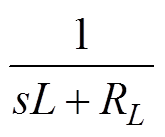为考虑等效电容阻抗传递函数，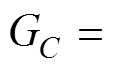
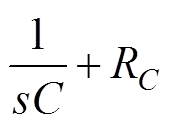，RL和RC分别为滤波电感L和电容C的等效串联电阻（Equivalent Series Resistance, ESR）。
结合电流内环电压外环控制策略[21]，易知其对应的控制框图如图5所示。Ub、Ib分别为电压、电流标幺值；Kpu、Kiu分别为电压环的比例、积分系数，Kpi、Kii分别为电流环的比例、积分系数。
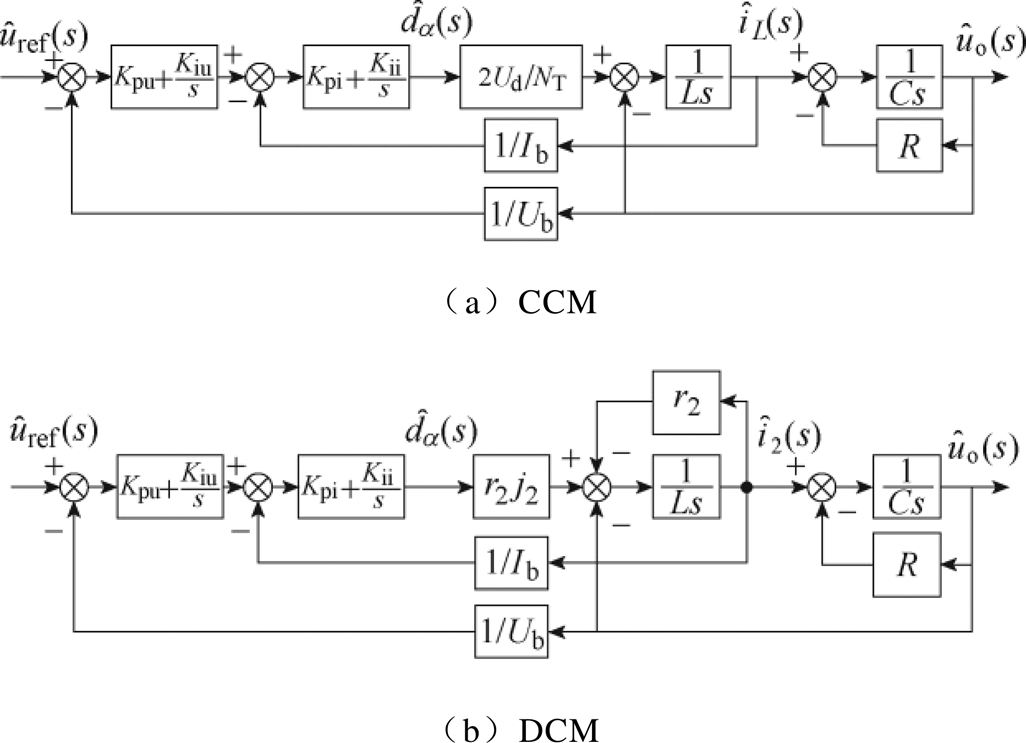
图5 变流器控制框图
Fig.5 Control block diagram of DC-DC inverter
根据输出阻抗的定义，结合图5所示的变流器闭环控制框图，令输入参考电压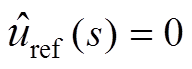
，分别推导变流器在CCM和DCM下输出电流到输出电压的传递函数，即得到对应的闭环输出阻抗分别为
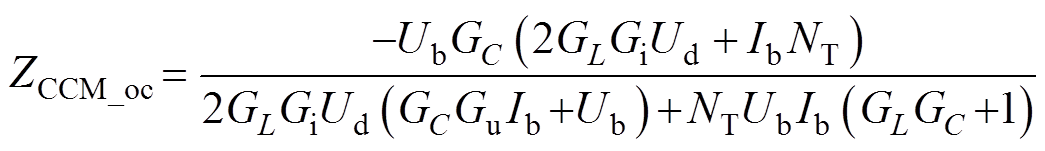（10）
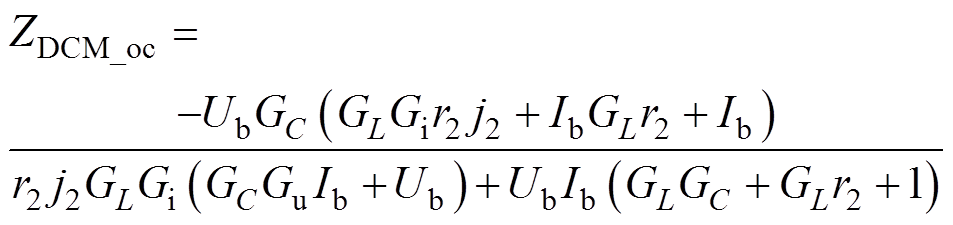（11）
式中，
、
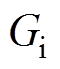分别为电压环、电流环PI控制的传递函数，
、
。
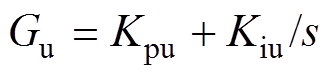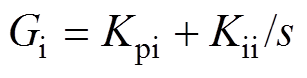通过电压扰动法在变流器输出端口施加不同频率的电压扰动，记录每个频率下的输出电压、电流数据，两者之比即为输出阻抗测量值，再通过傅里叶分析解到所测输出阻抗的幅频、相频曲线。变流器主回路和控制回路参数见表1。
表1 变流器参数
Tab.1 DC-DC converter parameter values
参 数数 值 主回路额定输入电压Ud/V4 000 额定输出电压Uo/V710 额定输出电流Io/V1 050 变压器电压比NT3.77 滤波电感L/mH250 等效电容C/mF28 滤波电感ESR RL/mW1.288 等效电容ESR RC/mW1.6 控制回路电压基准值Ub/V710 电流基准值Ib/V1 050 电压环比例系数Kpu3 电压环积分系数Kiu150 电流环比例系数Kpi0.06 电流环积分系数Kii10
将表1数据代入式（7）～式（10）和仿真测量模型，得到理论推导的阻抗值与仿真测量值，变流器输出阻抗验证如图6所示。
输出阻抗的理论计算与仿真结果在高频段（f＞300Hz）吻合度较弱，这是由于建模时对滤波元件的简化所致，但影响较小。因此，可以看出，无论变流器运行在CCM还是DCM，理论计算的开环、闭环输出阻抗都能够反映出仿真系统的输出阻抗的幅值和相位随频率变化的趋势，从而验证了理论计算的正确性。
变流器与逆变器组成的配电系统级联运行时，变流器运行模式取决于逆变器所带负载Po的大小：负载较大（128kW≤Po≤750kW）时，变流器运行在CCM；负载较小（0＜Po＜128kW
时，则处于DCM。由于逆变器的输入阻抗幅值随着功率增大而减小，根据阻抗比判据可知：变流器输出最大功率（750kW）时，处于CCM的级联系统最有可能发生静态失稳；输出功率为DCM下最大功率（128kW）时，处于DCM的级联系统最有可能发生静态失稳。
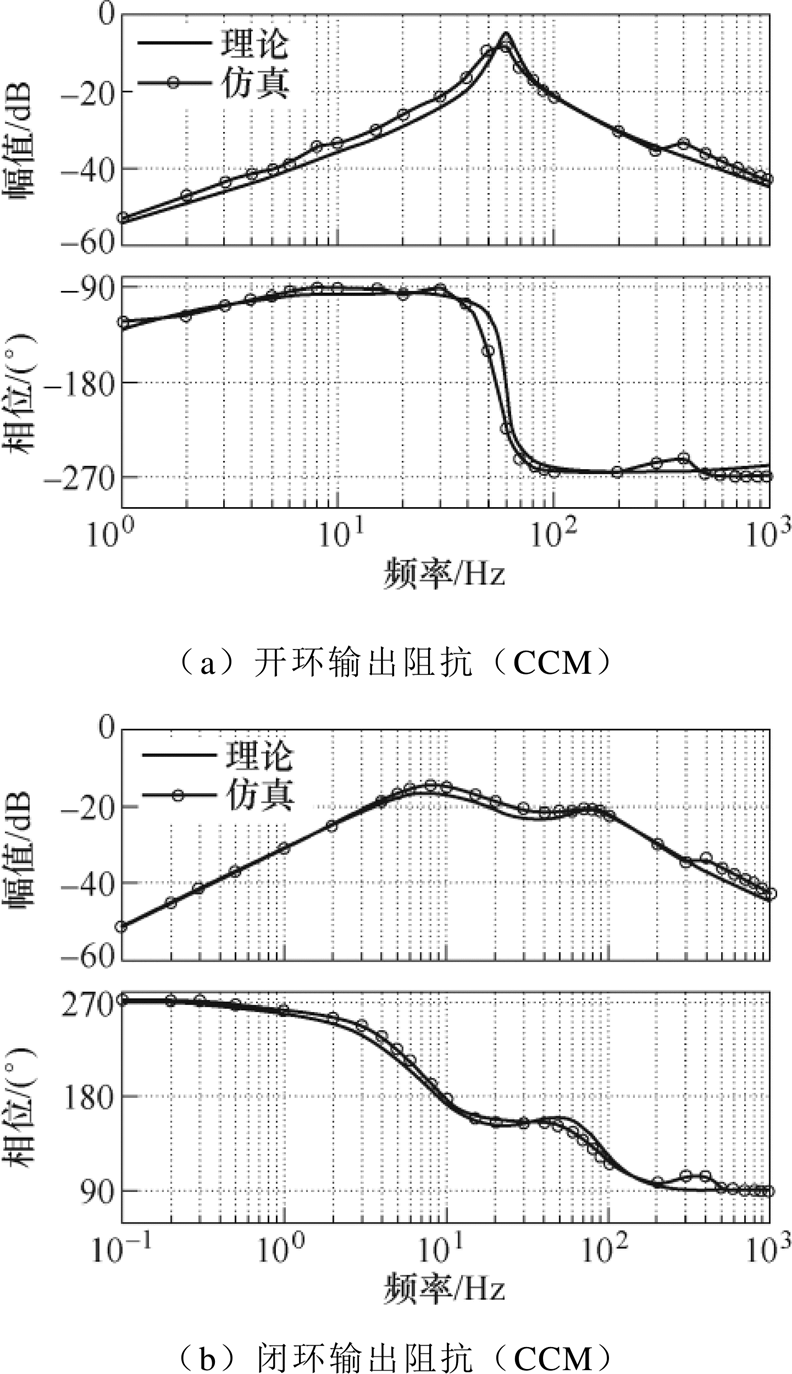
图6 变流器输出阻抗验证
Fig.6 Verification of output impedance of DC-DC converter
Po=750kW时，变流器闭环输出阻抗ZCCM_oc(s)及逆变器闭环输入阻抗Zic(s)[22]的特性曲线如图7a所示；而Po=128kW时，两变换器的阻抗特性曲线如图7b所示。
由图7可知：最大功率时，CCM下变流器与逆变器级联，在全频域有|ZCCM_oc|＜|Zic|成立，级联系统稳定，也就说明在CCM功率范围内，级联系统都能保持静态稳定；而DCM下，级联系统在f = 7.04Hz附近，变流器输出阻抗尖峰穿越了逆变器输入阻抗，即|ZDCM_oc|＞|Zic|，有可能发生静态失稳。
图7 级联系统输入输出阻抗Bode图
Fig.7 Bode diagram of output and input impedance
由于两种变换器的阻抗特性曲线最有可能在中低频段交叉，而逆变器在中低频段体现出负阻抗特性，幅值在特定功率下为常数，因此，影响级联系统静态稳定的最大不确定因素在于变流器。要探究级联系统能否保持稳定，就要对影响变流器输出阻抗幅值的因素进行分析。
分别绘制变流器CCM和DCM下开环和闭环输出阻抗如图8所示。
为了便于分析，不妨将频率分段，设低频段范围为f ＜1Hz、中频段范围为1Hz≤f ≤100Hz、高频段范围f ＞100Hz。从图8可知，在同一组PI参数下，变流器CCM和DCM下的闭环输出阻抗幅频特性曲线走势类似：闭环输出阻抗幅值在低频段随频率升高而增大，在高频段随频率升高而减小，而且高频段闭环输出阻抗幅值与开环输出阻抗幅值相等。另外，两种模式下的闭环输出阻抗都存在谐振峰值（对应相位分别为180°和0°）。特别地，DCM的闭环输出阻抗谐振峰值为正（7.04Hz，22.7dB），在该频率附近有两个截止频率wc1、wc2，在wc2处相位裕度g =-71.3°，易给级联系统带来静态稳定性问题。
图8 变流器输出阻抗Bode图
Fig.8 Output impedance Bode diagram of DC-DC converter
值得注意的是，闭环控制对两种模式下的输出阻抗的影响有所区别，闭环控制减小了CCM下输出阻抗谐振峰值和峰值所处的频率；然而闭环控制的加入增大了DCM的阻抗谐振峰值，并提高了峰值所处的频率。
上述分析表明，变流器的闭环输出阻抗的谐振峰出现在1～100Hz频段，为了明确影响变流器闭环输出阻抗峰值的因素，下文从控制参数和滤波器参数两个方面展开探究。
3.2.1 1≤Kpu≤10，Kiu、Kpi、Kii不变
CCM下，电压环比例系数Kpu=1时，闭环输出阻抗幅值的谐振峰值最大；Kpu越大，谐振峰值越小，如图9a所示。DCM下，当Kpu=3.2时，输出阻抗幅值在f =7.1Hz处有最大值；Kpu取值远离3.2时有利于减小阻抗峰值，如图9b所示。
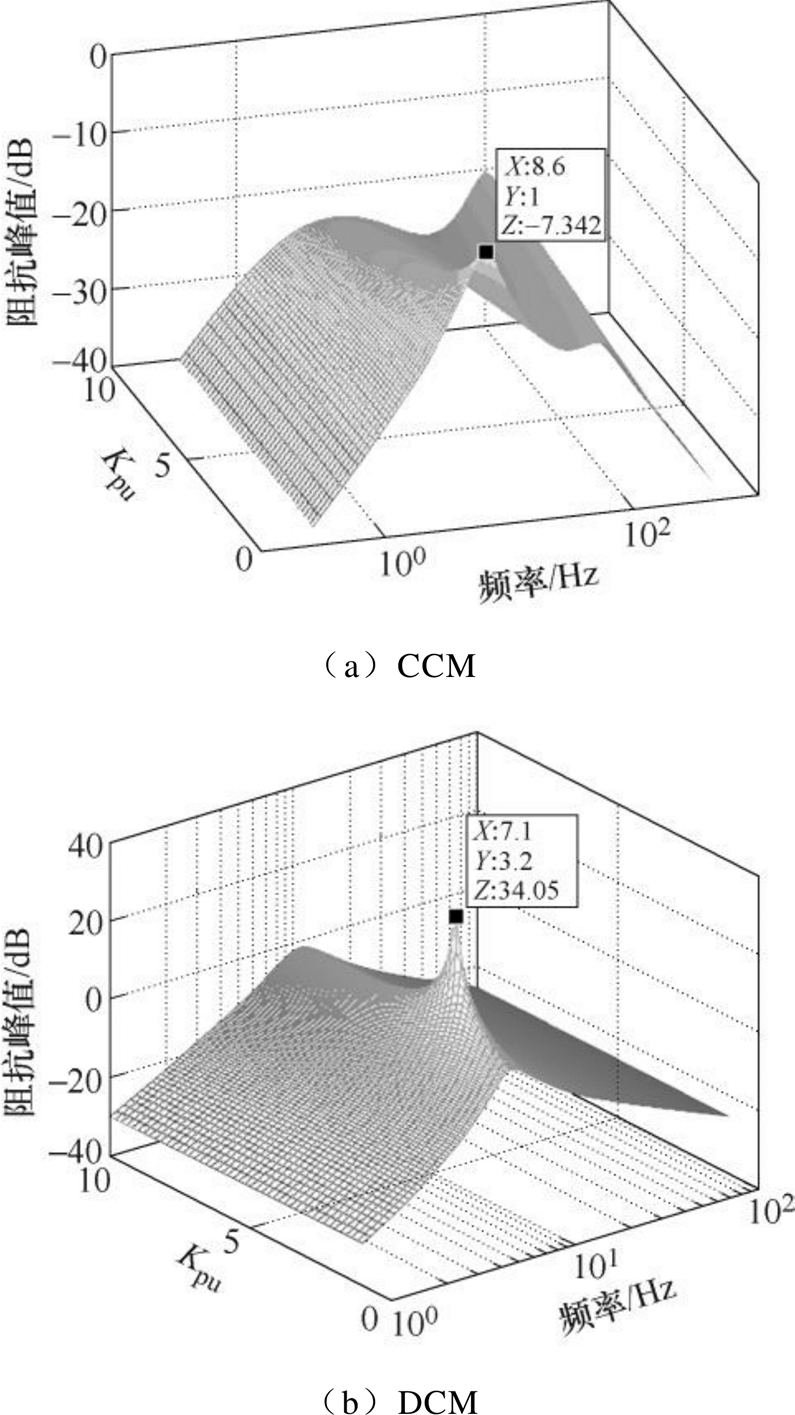
图9 1≤kpu≤10时变流器闭环输出阻抗幅频特性
Fig.9 Amplitude-frequency characteristic of closed loop output impedance when 1≤kpu≤10
3.2.2 10≤Kiu≤200，Kpu、Kpi、Kii不变
CCM下，电压环积分系数Kiu对输出阻抗的峰值影响不大，如图10a所示。DCM下，当Kiu=138时，输出阻抗幅值在f =6.9Hz处有最大值32.82dB；Kiu取值远离138则有利于减小阻抗峰值，如图10b所示。
3.2.3 0.01≤Kpi≤0.5，Kpu、Kiu、Kii不变
CCM下，当电流环比例系数取值为0.01≤Kpi≤ 0.5时，输出阻抗的最大幅值几乎不变；但Kpi不宜取0.01，此时输出阻抗幅值有最大值-3.462dB，如图11a所示。DCM下，当Kpi=0.07时，输出阻抗幅值在f =7Hz处有最大值32.88dB；Kpi越大越利于减小阻抗峰值，如图11b所示。
图10 10≤kiu≤200时变流器闭环输出阻抗幅频特性
Fig.10 Amplitude-frequency characteristic of closed loop output impedance when 10≤kiu≤200
图11 0.01≤kpi≤0.5时变流器闭环输出阻抗幅频特性
Fig.11 Amplitude-frequency characteristic of closed loop output impedance when 0.01≤kpi≤0.5
3.2.4 1≤Kii≤40，Kpu、Kiu、Kpi不变
CCM下，电流环积分系数Kii的变化对输出阻抗的峰值影响较小，如图12a所示。DCM下，Kii=5和Kii=19时，输出阻抗有两个较大的峰值点，对应的频率分别为5.4Hz和9Hz，因此Kii取5和19附近的数时不利于减小阻抗峰值，如图12b所示。
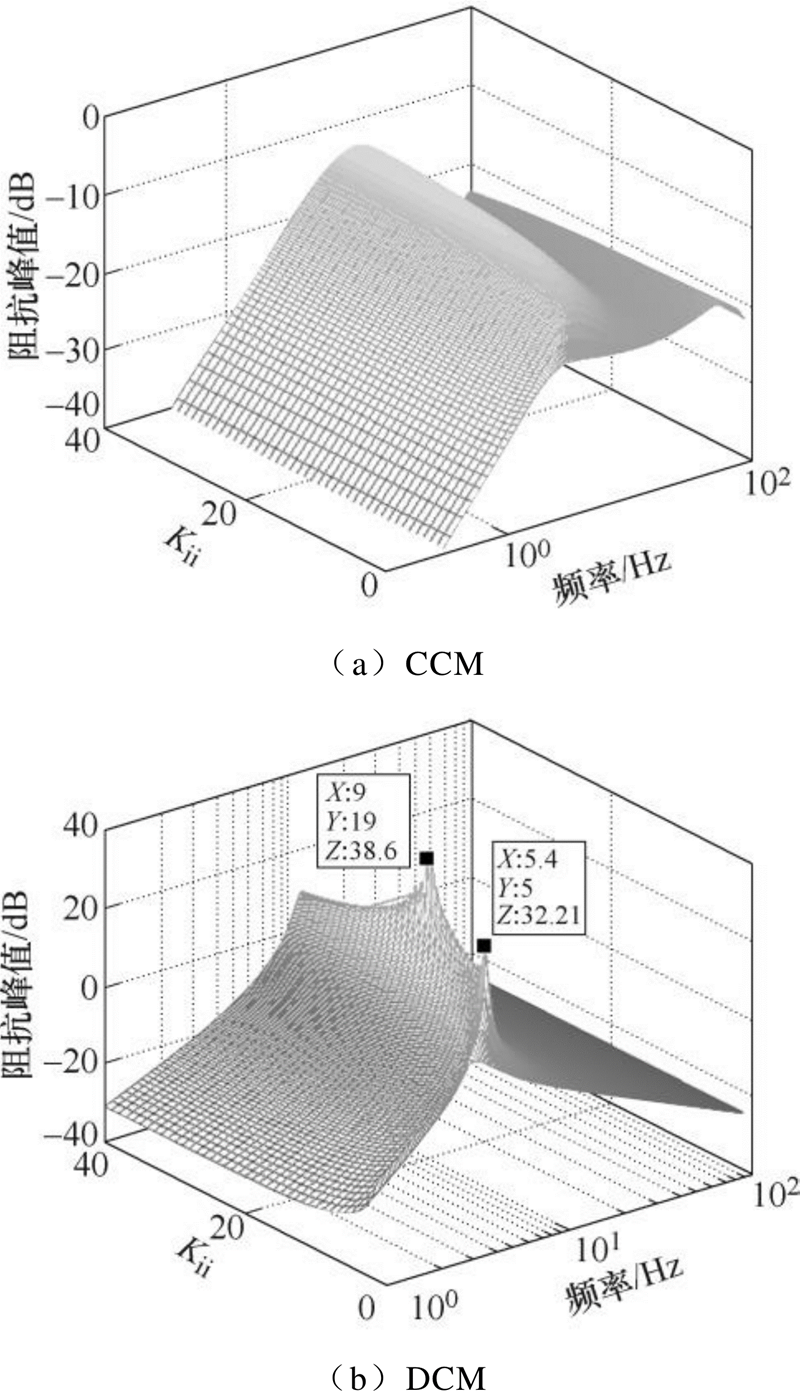
图12 1≤kii≤40时变流器闭环输出阻抗幅频特性
Fig.12 Amplitude-frequency characteristic of closed loop output impedance when 1≤kii≤40
3.3.1 等效电容及其ESR对闭环输出阻抗的影响
固定其他参数，同时改变C和RC的值，绘制两种模式下闭环输出阻抗峰值随C和RC的关系曲线，等效电容及ESR对变流器闭环输出阻抗的影响如图13所示。从图13a可以看出，在RC不变的情况下，等效电容C越小，其CCM下的输出阻抗峰值越大。从图13b可以看出，RC较小（RC＜0.2W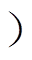
，电容C取值在20～50mF时，DCM的闭环输出阻抗峰值会很大，不利于系统稳定，C取值远离这一区间才有利于阻抗峰值减小；RC较大时（RC＞0.2W），电容C越大，输出阻抗峰值越小。
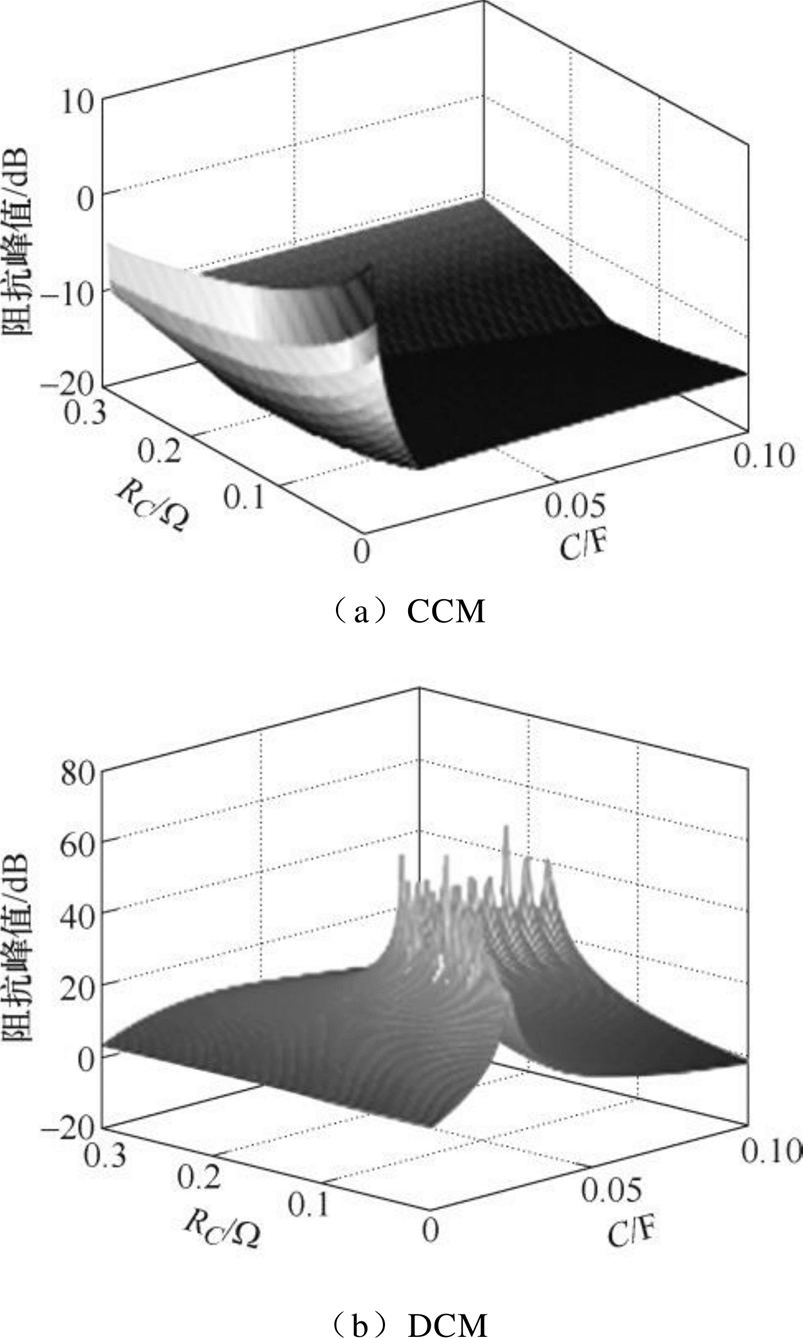
图13 等效电容及ESR对变流器闭环输出阻抗的影响
Fig.13 Influence of equivalent capacitance and its ESR on output impedance of DC-DC converter
3.3.2 滤波电感及其ESR对闭环输出阻抗的影响
固定其他参数不变，同时改变滤波电感L和等效串联电阻RL的值，两种模式下闭环输出阻抗峰值分布如图14所示。对比图14a和图14b，若RL不变，两种模式的输出阻抗峰值几乎不受L的影响；若L不变，CCM下闭环输出阻抗峰值随RL增大而增大，DCM则相反，即增大RL有利于DCM的阻抗峰值减小。
图14 滤波电感及ESR对变流器闭环输出阻抗的影响
Fig.14 Influence of inductance and its ESR on closed loop output impedance of DC-DC converter
当逆变器输出功率Po=710kW时，变流器输出电流Io=1 050A，变流器运行在CCM；当逆变器输出功率Po=99.4kW时，变流器输出电流Io=140A，变流器运行在DCM。t =1.5s前，变流器的输出电压稳定，在t =1.5s时刻，逆变器突加10kW负载。
级联系统受小扰动时母线电压波形如图15所示。当级联系统的负载小幅增加时，运行于CCM下的变流器输出母线电压在短时间内调整至新的稳态，具有较好的静态稳定性，如图15a所示。运行于DCM下的变流器母线电压会出现增幅振荡，系统静态失稳，如图15b所示。
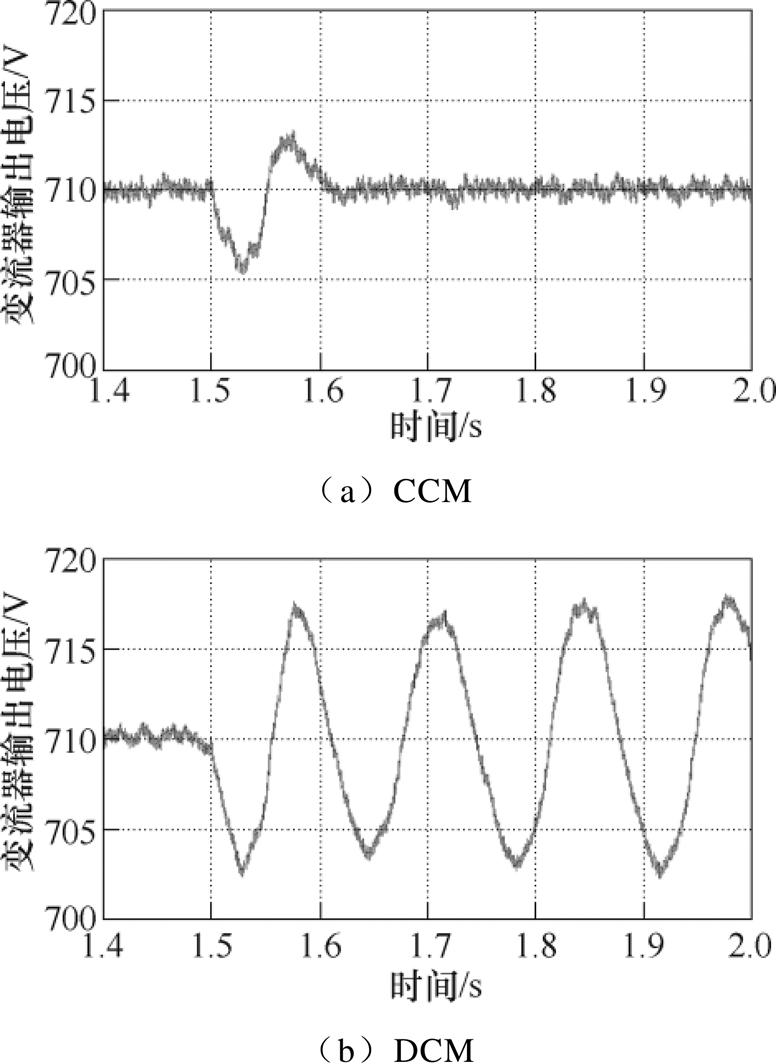
图15 级联系统受小扰动时母线电压波形
Fig.15 Voltage waveforms when cascaded system is disturbed
在DC-DC变流器带电阻负载单机试验、逆变器电源为恒压源单机试验中，两者皆能稳定运行。在级联试验中，逆变器作为变流器的负载，逆变器空载起动后分级加载。当变流器输出电流在140A左右时，变流器处于DCM，继续增大负载，输出电压出现低频振荡，如图16a所示。当变流器带最大负载（Io=1 050A）时，变流器处于CCM，其输出电压在负载波动下能保持平稳的输出，如图16b所示。可见，CCM下变流器具有较好的静态稳定性，而变流器处于DCM时易受负载扰动而使级联系统静态失稳。
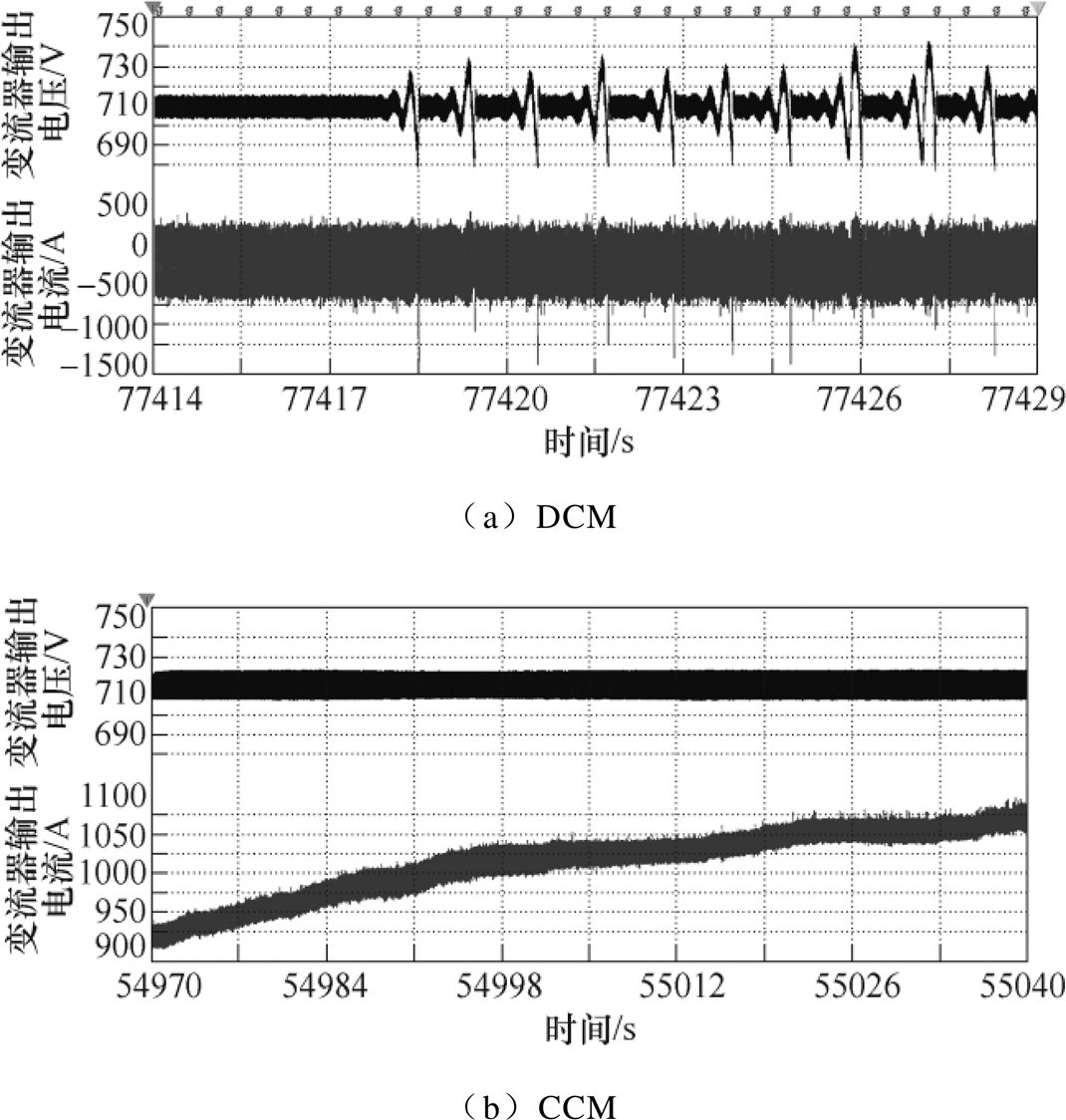
图16 级联系统增大负载时母线波形
Fig.16 Bus waveforms when cascaded system is disturbed
本文主要建立了大容量变流器小信号输出阻抗模型，以阻抗比判据为理论依据，通过研究不同工作模式下变流器输出阻抗随控制参数和滤波器参数的变化趋势，分析了变流器输出阻抗的影响因素。主要结论如下：
1）闭环控制并非一定能减小变流器的输出阻抗。当前控制策略减小了CCM输出阻抗幅值时，同时也增大了DCM阻抗幅值。处于CCM的变流器与逆变器级联能保持静态稳定性，而DCM下级联稳定裕度不足，更容易引起静态失稳。
2）滤波器参数对变流器的输出阻抗的影响是多方面的，CCM下，电容越大输出阻抗峰值越小，越有利于级联系统稳定。但DCM下，电容在特定区间会增大输出阻抗峰值，从而增加级联系统失稳风险。电感对两种模式下的输出阻抗影响均较小，而增大电感等效电阻能减小DCM下级联系统的失稳风险。
3）控制参数对变流器输出阻抗的影响呈现区间性：特定区间内的控制参数将导致变流器输出阻抗急剧增大，不利于级联系统保持静态稳定性。
综上所述，要减小变流器的输出阻抗，需综合多因素评估，滤波器参数和控制参数对输出阻抗的影响趋势为改善级联系统静态稳定性提供了方向。
参考文献
[1] 马伟明. 电力电子在舰船电力系统中的典型应用[J]. 电工技术学报, 2011, 26(5): 1-7.
Ma Weiming. Typical applications of power elec- tronics in naval ship power systems[J]. Transaction of China Electrotechnical Society, 2011, 26(5): 1-7.
[2] 佟强, 张东来, 徐殿国. 分布式电源系统中变换器的输出阻抗与稳定性分析[J]. 中国电机工程学报, 2011, 31(12): 57-64.
Tong Qiang, Zhang Donglai, Xu Dianguo. Output impedance and stability analysis of converters in distributed power systems[J]. Proceedings of the CSEE, 2011, 31(12): 57-64.
[3] 吴涛, 阮新波. 分布式供电系统中源变换器的输出阻抗的研究[J]. 中国电机工程学报, 2008, 28(3): 66-72.
Wu Tao, Ruan Xinbo. Output impedance analysis of source converters in the DC distributed power system[J]. Proceedings of the CSEE, 2008, 28(3): 66-72.
[4] 蔡久青, 陈昌松, 段善旭, 等. 模块化不间断电源自适应均流控制技术[J]. 电工技术学报, 2017, 32(24): 153-159.
Cai Jiuqing, Chen Changsong, Duan Shanxu, et al. Adaptive current-sharing control technique for modular uninterruptible power supply[J]. Transaction of China Electrotechnical Society, 2017, 32(24): 153-159.
[5] Wu Mingfei, Lu Dylan Dah-Chuan. A novel stabili- zation method of LC input filter with constant power loads without load performance compromise in DC microgrids[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4552-4562.
[6] 庄绪州, 张勤进, 刘彦呈. 基于负阻抗特性补偿的船舶DC/DC变换器控制策略[J]. 电力系统及其自动化学报, 2019, 31(5): 27-32.
Zhuang Xuzhou, Zhang Qinjin, Liu Yancheng. Control strategy for DC/DC converter in ship based on negative impedance compensation[J]. Proceedings of the CSU-EPSA, 2019, 31(5): 27-32.
[7] 姚雨迎, 张东来, 徐殿国. 级联式DC-DC变换器输出阻抗的优化设计与稳定性[J]. 电工技术学报, 2009, 24(3): 147-152.
Yao Yuying, Zhang Donglai, Xu Dianguo. Output impedance optimization and stability for cascade DC/DC converter[J]. Transaction of China Electro- technical Society, 2009, 24(3): 147-152.
[8] 胡鹏, 艾欣, 肖仕武, 等. 静止无功发生器序阻抗建模及对次同步振荡影响因素的分析[J]. 电工技术学报, 2020, 35(17): 3703-3713.
Hu Peng, Ai Xin, Xiao Shiwu, et al. Sequence impedance of static var generator and analysis of influencing factors on subsynchronous oscillation[J]. Transaction of China Electrotechnical Society, 2020, 35(17): 3703-3713.
[9] 庄绪州, 张勤进, 刘彦呈, 等. 船舶全电力推进系统恒功率负载有源阻尼控制策略[J]. 电工技术学报, 2020, 35(增刊1): 101-109.
Zhuang Xuzhou, Zhang Qinjin, Liu Yancheng, et al. An active damping control of constant power load for all-electric ships[J]. Transaction of China Electro- technical Society, 2020, 35(S1): 101-109.
[10] 贾鹏宇, 李艳, 郑琼林. 电压型级联系统中减小源变换器输出阻抗的有源阻尼控制方法[J]. 电工技术学报, 2015, 30(8): 71-82.
Jia Pengyu, Li Yan, Zheng Qionglin. An active damping method to reduce output impedance of converters in voltage source cascaded system[J]. Transaction of China Electrotechnical Society, 2015, 30(8): 71-82.
[11] 郭春义, 赵剑, 刘炜, 等. 一种适用于混合多馈入直流输电系统的附加虚拟电阻阻尼控制方法[J]. 中国电机工程学报, 2019, 39(12): 3400-3408.
Guo Chunyi, Zhao Jian, Liu Wei, et al. A supple- mentary virtual-resistor damping control for hybrid multi-infeed HVDC system[J]. Proceedings of the CSEE, 2019, 39(12): 3400-3408.
[12] 伍文华, 周乐明, 陈燕东, 等. 海上MVDC供电系统的正阻尼重构稳定控制策略[J]. 中国电机工程学报, 2019, 39(3): 696-710.
Wu Wenhua, Zhou Leming, Chen Yandong, et al. Stability control strategy with positive-damper reconstructed for the maritime MVDC power supply system[J]. Proceedings of the CSEE, 2019, 39(3): 696-710.
[13] 汪春江, 孙建军, 宫金武, 等. 并网逆变器与电网阻抗交互失稳机理及阻尼策略[J]. 电工技术学报, 2020, 35(增刊2): 503-511.
Wang Chunjiang, Sun Jianjun, Gong Jinwu, et al. Mechanism and damping strategy of interactive instability between grid-connected inverter and grid impedance[J]. Transaction of China Electro technical Society, 2020, 35(S2): 503-511.
[14] 周兵凯, 杨晓峰, 李继成, 等. 一种用于优化LC-DAB级联系统稳定性的虚拟阻抗控制技术[J].电工技术学报, 2020, https://doi.org/10.19595/j.cnki. 1000-6753.tces.200063.
Zhou Bingkai, Yang Xiaofeng, Li Jicheng, et al. Virtual impedance control technology for stability optimization of LC-DAB cascaded system[J]. Transa- ction of China Electrotechnical Society, 2020, https:// doi.org/10.19595/j.cnki.1000-6753.tces.200063.
[15] 庞圣钊, 皇甫宜耿, 郭亮, 等. 基于Lyapunov间接法分析的功率负载电源变换器宽稳定控制策略[J]. 电工技术学报, 2017, 32(14): 146-154.
Pang Shengzhao, Huangfu Yigeng, Guo Liang, et al. A novel wide stability control strategy of constant power load power converter based on the analysis of Lyapunov indirect method[J]. Transaction of China Electrotechnical Society, 2017, 32(14): 146-154.
[16] 张冲, 王伟胜, 何国庆, 等. 基于序阻抗的直驱风电场次同步振荡分析与锁相环参数优化设计[J]. 中国电机工程学报, 2017, 37(23): 6757-6767.
Zhang Chong, Wang Weisheng, He Guoqing, et al. Analysis of sub-synchronous oscillation of full- converter wind farm based on sequence impedance and an optimized design method for PLL para- meters[J]. Proceedings of the CSEE, 2017, 37(23): 6757-6767.
[17] 邓睿, 刘碧, 宋文胜. 牵引供电网-多台机车耦合系统的低频振荡分析与抑制[J]. 电工技术学报, 2019, 34(增刊1): 327-335.
Deng Rui, Liu Bi, Song Wensheng. Low-frequency- oscillation analysis and suppression of the coupling system between traction network and multi- locomotives[J]. Transaction of China Electrotechnical Society, 2019, 34(S1): 327-335.
[18] Yang Guorun, Xiao Fei, Fan Xuexin, et al. Three- phase three-level phase shifted PWM DC/DC con- verter for electric ship MVDC application[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2016, 5(1): 162-170.
[19] 谢桢, 魏建勋, 付立军, 等. 三电平H桥直流换流器电流连续模式下的建模与控制器设计[J]. 电网技术, 2013, 37(5): 1230-1236.
Xie Zhen, Wei Jianxun, Fu Lijun, et al. Modeling and controller design of three-level H-bridge DC/DC converter under continuous conduction mode[J]. Power System Technology, 2013, 37(5): 1230-1236.
[20] 范学鑫, 彭方成, 王瑞田, 等. 大容量变流器DCM模式下带逆变器级联系统静态稳定性分析[J]. 海军工程大学学报, 2020, 32(3): 18-25.
Fan Xuexin, Peng Fangcheng, Wang Ruitian, et al. Modeling and static stability analysis of cascaded system with high-capacity converter in DCM[J]. Journal of Naval University of Engineering, 2020, 32(3): 18-25.
[21] 杨国润, 肖飞, 范学鑫, 等. 中压大容量三重化三电平直流变换器冗余容错控制[J]. 电工技术学报, 2017, 32(增刊1): 186-195.
Yang Guorun, Xiao Fei, Fan Xuexin, et al. Redundant and fault tolerant control of a medium-voltage high- power three-phase three-level DC-DC converter[J]. Transaction of China Electrotechnical Society, 2017, 32(S1): 186-195.
[22] 彭方成, 陈金萌, 刘明. 三相逆变器小信号输入阻抗特性分析[J]. 电气应用, 2020, 39(7): 43-49.
Peng Fangcheng, Chen Jinmeng, Liu Ming. Analysis of small signal input impedance characteristics of three-phase inverter[J]. Electrotechnical Application, 2020, 39(7): 43-49.
Analysis and Application of Output Impedance Characteristics of High-Capacity DC-DC Converter
Abstract Voltage oscillation may be caused by impedance mismatch after cascading the high-capacity power electronic converters in the low-voltage power transformation and distribution subsystem of the ship. In order to explore the factors that affect static stability of the cascaded system with high-capacity DC-DC converter, this paper mainly focused on modeling and analyzing of output impedance. Firstly, the small signal model of the high-capacity DC-DC converter was established, and correspondingly, the output impedance models was derived. Secondly, the system stability according to the impedance ratio criterion was analyzed. It is clear that the peak value of the output impedance of the high-capacity DC-DC converter is the dominant factor causing the impedance mismatch. Thirdly, by exploring the influence of the control strategy, control parameters and filter parameters on the converter’s output impedance amplitude under different operation modes, the parameter optimization direction was found for improving the static stability of the system. Finally, the theoretical analysis was verified by PSCAD/EMTDC simulation and test.
keywords：DC-DC converter, output impedance, cascaded system, static stability
DOI: 10.19595/j.cnki.1000-6753.tces.L90059
中图分类号：TM46
彭方成 男，1993年生，硕士，研究方向为电力电子与电力传动。E-mail: pfc1993@163.com
范学鑫 男，1977年生，研究员，硕士生导师，研究方向为电力电子与电力传动。E-mail: fxxdldz@163.com（通信作者）
国家自然科学基金资助项目（51707200, 51490680）。
收稿日期 2020-06-20
改稿日期 2020-10-20
（编辑 陈 诚）