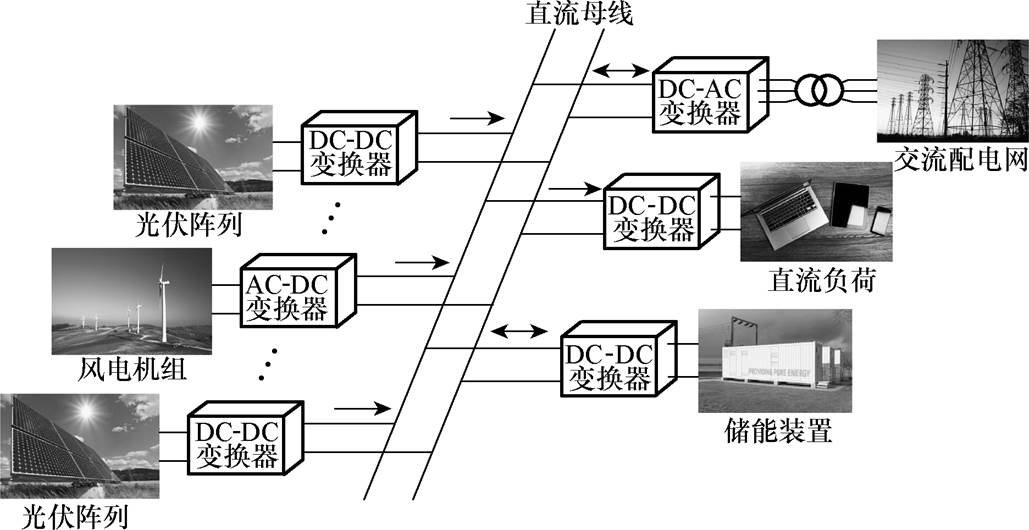
图1 直流微电网典型拓扑示意图
Fig.1 Typical topology diagram of DC microgrid
摘要 直流微电网并联系统多采用下垂控制实现功率分配，但线路阻抗的存在会降低其分配精度，传统均流策略基于高带宽通信网络采集电压或电流信息实现功率补偿，制造成本偏高、可靠性较低，同时通信线路存在通信延时，会对均流效果产生影响。为实现直流微电网并联系统变换器输出功率自主均分控制，提出一种无高带宽通信线路的直流微电网并联光储变换器均流策略。该策略通过分析恒压运行模式与下垂运行模式下，线路阻抗对并联变换器功率分配特性的影响规律，设计虚拟阻抗补偿环节，根据变换器自身输出电气特性，对变换器输出功率进行调节，实现输出功率的自主均分。仿真和实验结果表明，所提控制策略能够提高并联变换器的功率自主分配精度。
关键词：直流微电网 自主均流策略 虚拟阻抗补偿
直流微电网作为分布式发电系统的重要组成部分，具有结构简单、控制灵活等优点[1]。以直流母线为主要能量传输通路的直流微电网架构是未来分布式发电技术中一个重要的发展方向。直流微电网中发电设备和用电设备均通过电力电子变换器并联在直流母线上，协调各微源之间的出力，实现并联系统分布式能量的管理与控制，对直流微电网的稳定运行具有重要的意义[2-3]。
微电网并联变换器功率均分控制策略主要分为集中控制与分布式控制两种[4-6]。集中控制包括主从控制、最大电流功率均分控制、平均电流功率均分控制等[7-9]；分布式控制主要采用具有即插即用特性的下垂控制实现功率分配[10]，控制方式简单灵活，是目前应用较为广泛的一种控制策略[11-13]。但由于电能传输线路阻抗及传感器采样误差的存在，导致传统下垂控制功率分配精度不高[14]。
为提升下垂控制的功率均分精度，文献[15-16]提出电压补偿功率均分策略，通过高带宽通信线路采集系统内各变换器电气信息，计算平均功率，再以各变换器输出功率与平均功率的偏差作为二次电压补偿环节，产生电压补偿量，调节电压给定值产生功率交叉点达到功率均分目的。文献[17-21]采用自适应下垂控制，通过调节下垂系数减小工作点功率偏差。主要分为两种：一种是通过对下垂系数进行自适应的改进，基于通信线路采集各变换器输出功率，将各变换器输出功率与平均功率偏差代入下垂系数计算中，在重载时采用较大的下垂系数来保证功率均分的精度，轻载时采用较小的下垂系数保证母线电压的稳定，达到功率均分的目的，但该控制策略存在可靠性低或协调策略在全工况下通用性差等缺陷；另一种通过构造一个电气控制指标，例如，虚拟损耗与功率均分精度的价值指标函数，选取指标最优点对应的下垂系数作为实际控制下垂系数，实现虚拟损耗最小且功率均分精度最高的最优控制。文献[22]提出虚拟负阻抗对消法，通过将线路阻抗引入下垂控制中产生虚拟负阻抗，从而消除线路阻抗的影响，达到功率均分控制的目的。引入虚拟负阻抗可以有效地将线路阻抗的影响减小甚至消除，但其功率均分精度取决于线路阻抗估计精度，可靠性较低。
综上，现有均流方法多采用高带宽通信线路通过交换各变换器自身电气信息，对下垂控制进行调节，提升变换器间功率分配的精度，实现直流微电网内功率平衡。但基于高带宽通信线路的控制方法，增加了制造成本、降低了可靠性，同时通信线路存在通信延时，影响均流效果。
本文提出一种无通信网络的直流微电网并联系统自主均流控制策略，通过对恒压工作模式和下垂工作模式功率分配偏差机理的分析，设计虚拟阻抗补偿环节，从而减少线路阻抗带来的功率分配误差，提升功率分配精度，实现直流微电网的稳定运行。
直流微电网典型拓扑示意图如图1所示，直流微电网通常由光伏、风电等分布式电源、储能装置、并网逆变器及直流负荷组成，发电装置和用电装置均通过电力电子变换器并联到直流母线上。
图1 直流微电网典型拓扑示意图
Fig.1 Typical topology diagram of DC microgrid
对图1的发电设备、用电装置及线路阻抗进行等效，其源荷分布示意图如图2所示。图2中，uoi、iloadi分别为第i台变换器输出电压及负载电流；rlineij为第i台与第j台变换器间线路阻抗。
图2 直流微电网源荷分布示意图
Fig.2 Source and load distribution schematic diagram of DC microgrid
由图2可知，微源与微源间，微源与负荷间均存在阻值不定的线路阻抗，直接采用下垂控制会影响功率的分配精度。为分析线路阻抗对功率分配精度的影响，简化图2的直流微电网源荷分布，分别对恒压运行模式与下垂运行模式下的变换器进行建模，并联变换器等效示意图如图3所示。图3中，恒压工作模式微源等效为一个电压源Udci；下垂控制模式微源等效为电压源Udci和阻性下垂系数rdi的串联。由图3可得，各分布式电源微源输出功率表达式为
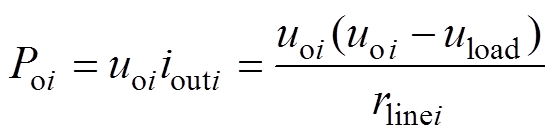（1）式中，Poi为第i台变换器输出功率；uoi、uload分别为第i台变换器输出电压及负载电压；rlinei为第i台变换器输出线路阻抗。
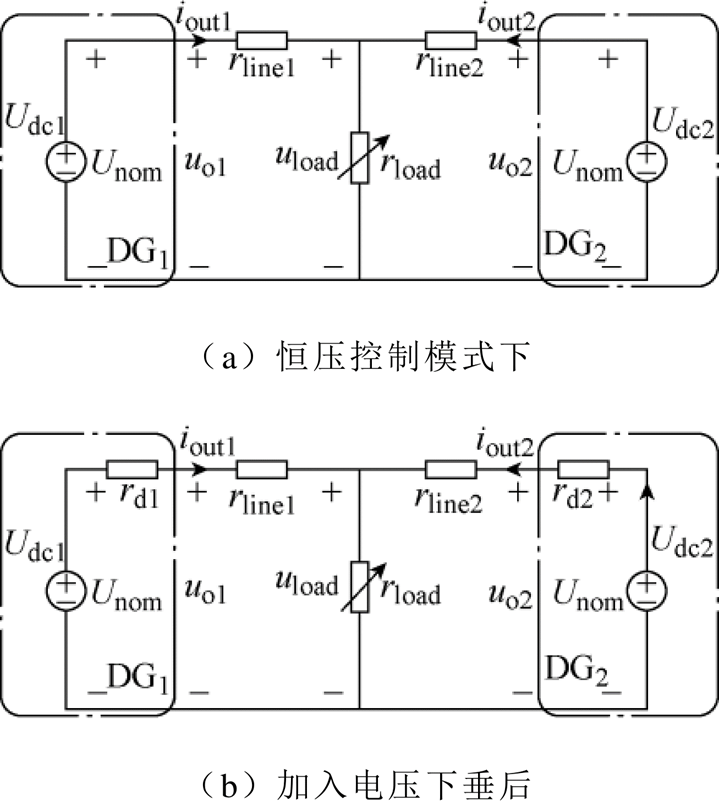
图3 并联变换器等效示意图
Fig.3 Equivalent schematic diagram of parallel converter
图3a为恒压控制模式下并联变换器等效示意图。采用恒压控制模式的变换器输出电压uoi跟踪初始给定电压Unom，当达到稳态时，有
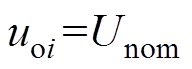（2）将式（2）代入式（1），恒压模式下各变换器输出功率为
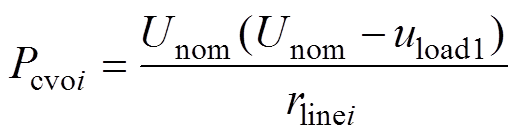（3）
式中，Pcvoi为恒压模式下各变换器输出功率；uload1为恒压控制下负载电压。
图3b为加入电压下垂后并联变换器等效示意图，图中，rd1、rd2分别为电压-电流下垂特性的下垂系数，对应等效电压-功率下垂关系为
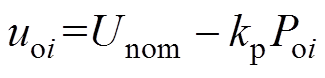（4）式中，kp为电压-功率下垂系数，其表达式为
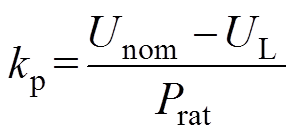（5）
式中，UL为直流母线电压最小值；Prat为功率变换器额定功率。则各变换器输出功率为
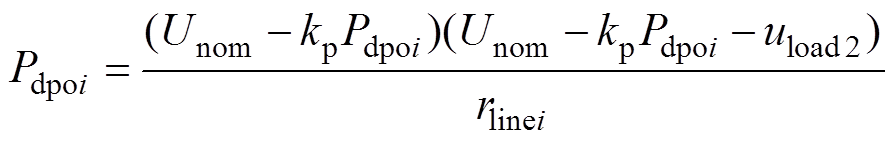（6）式中，Pdpoi为下垂控制模式下各变换器输出功率；uload2为下垂控制模式下负载电压。
在线路阻抗不等的工况下，由式（3）与式（6）可得各变换器输出功率示意图如图4所示。
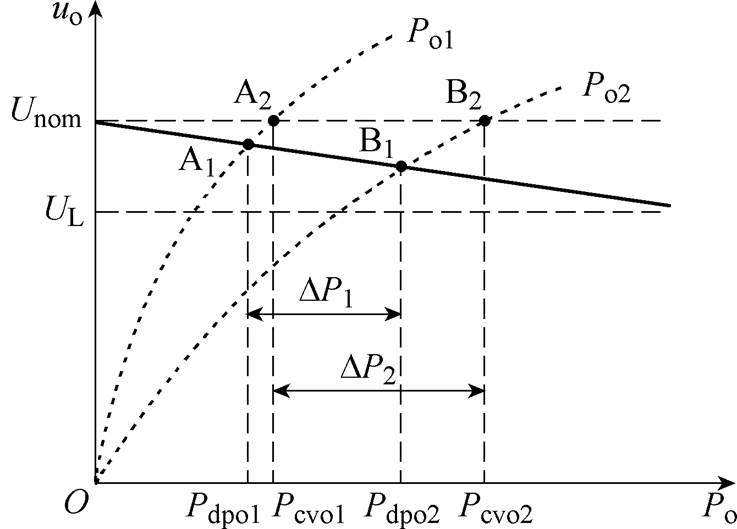
图4 各变换器输出功率示意图
Fig.4 Schematic diagram of output power of each converter
图4中，点线为两台并联变换器输出功率Po曲线，实线为下垂曲线。由图4可以看出，线路阻抗越大，功率曲线斜率越大，对应的输出功率越小。例如，当采用恒压模式即变换器输出电压为下垂初始电压Unom时，变换器1工作在A2点，输出功率为Pcvo1；相对地，变换器2工作在B2点，输出功率为Pcvo2，两者功率偏差为DP2，变换器输出功率存在功率偏差。
为使并联变换器能够在无高带宽通信的情况下，依据本地信息实现变换器自主功率均分，对下垂控制及恒压控制功率偏差进行积分补偿，得到如图5所示补偿后变换器输出功率波形。
由于线路阻抗的影响，当变换器1工作在下垂模式时（A1点），变换器2在相同下垂特性下，工作点为B1，两者存在DP1的功率偏差；当变换器1工作在恒压控制模式，即变换器输出电压取恒定值
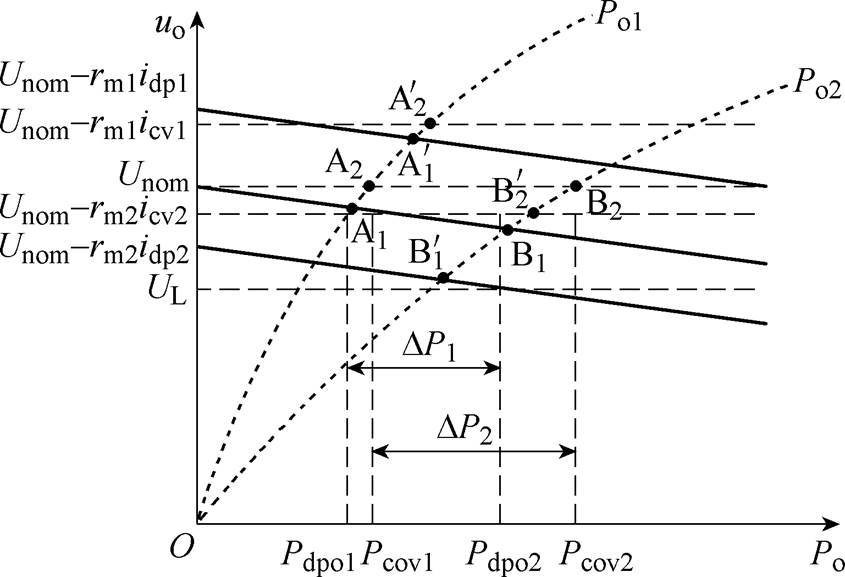
图5 补偿后变换器输出功率波形
Fig.5 Converter output power waveforms after compensation
Unom时，变换器1工作在A2点，变换器2工作在B2点，两者存在功率偏差DP2。设计积分补偿环节，其表达式为
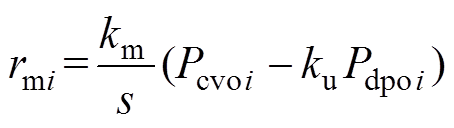（7）式中，rmi为补偿量；km为积分时间常数；ku为比例系数，其表达式为
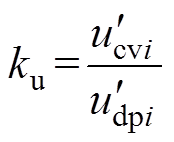（8）
式中，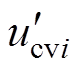
为补偿后恒压控制给定电压，其表示为
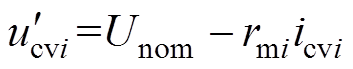（9）式中，icvi为恒压控制下变换器输出电流。通过对下垂初始电压Unom的补偿，得到补偿后恒压控制给定电压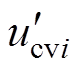，其初始值取
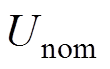后，进行迭代，而式（8）
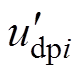为补偿后下垂控制变换器输出电压，其表达式为
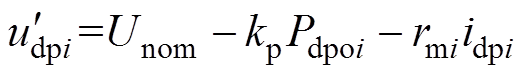（10）
通过在下垂与恒压模式间进行切换得到两种模式下变换器输出功率，求解积分补偿量，对下垂控制及恒压控制指令电压的补偿，实现变换器输出功率调节，如图5所示。初始时刻当变换器1在下垂控制模式下，其工作点位于A1，而切换至恒压模式时其工作点位于A2，两种模式对应的输出功率分别为Pdpo1、Pcvo1，代入式（7）得到积分补偿量rm1，依据式（9）、式（10），可得补偿后下垂初始电压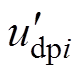及恒压控制电压给定值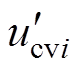，下垂曲线与恒压曲线上移，实现对变换器输出功率的调节。
通过在并联系统控制中加入虚拟阻抗补偿环节对各变换器输出功率进行调节后，各变换器输出功率逐步趋于稳态功率均分点。本节分别对稳态点两种控制模式下稳态功率均分特性进行分析，验证自主均流策略稳态点并联系统的功率均分特性。
2.2.1 下垂模式下并联变换器功率均分特性分析
将式（9）与式（10）分别代入式（7）与式（8）中，可得各变换器输出功率表达式为
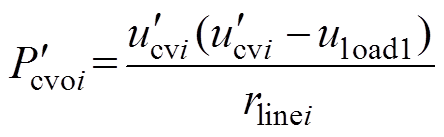（11）
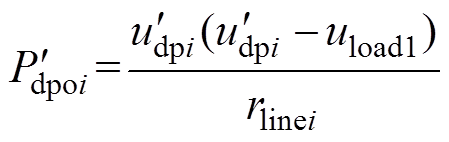（12）
式中，
为补偿后恒压控制下变换器输出功率；
为经过补偿后下垂控制模式下变换器输出功率。将式（11）与式（12）分别代入式（7）中，可得积分补偿量等效关系式为
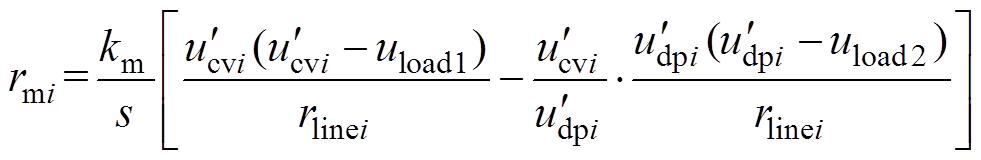（13）当恒压模式输出功率与下垂控制模式输出功率比例偏差为零时，积分补偿量达到稳态固定值，即
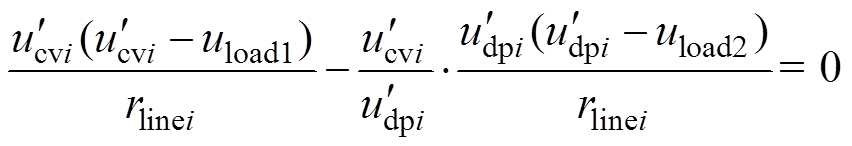（14）
化简式（14）可得
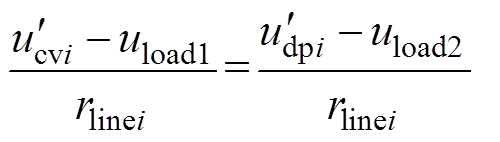（15）依据图3，变换器输出电压与负载电压差值为线路阻抗压降，因此式（15）可进一步简化为
（16）
由式（16）可知，积分补偿达到稳态值时，变换器在恒压模式与下垂模式下输出电流相等，即
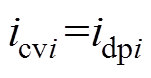（17）变换器输出电流示意图如图6所示。图中实线与三角实线分别为采用恒压模式与下垂模式下变换器输出电流特性曲线，两种模式下变换器初始工作点为A1、A2，经过积分补偿后工作点移动到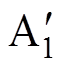
、
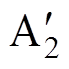，多次补偿后系统达到稳态点，虚拟阻抗补偿值也同时达到稳态值。
稳态点变换器输出电流示意图如图7所示。工作点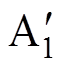、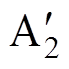处变换器输出电流在两种模式下相等，达到稳态。
同时，由图3可知，当两台变换器并联运行时，负载电压相同，因此可得并联变换器电压关系式为
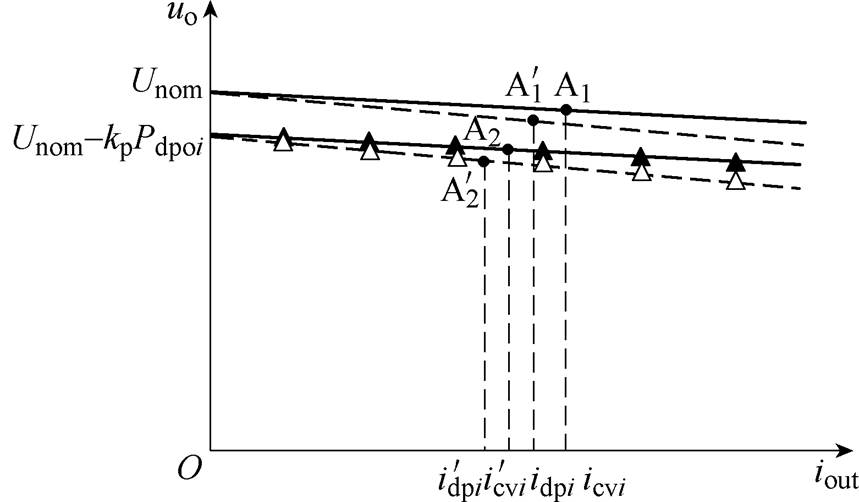
图6 变换器输出电流示意图
Fig.6 Schematic diagram of converter output current
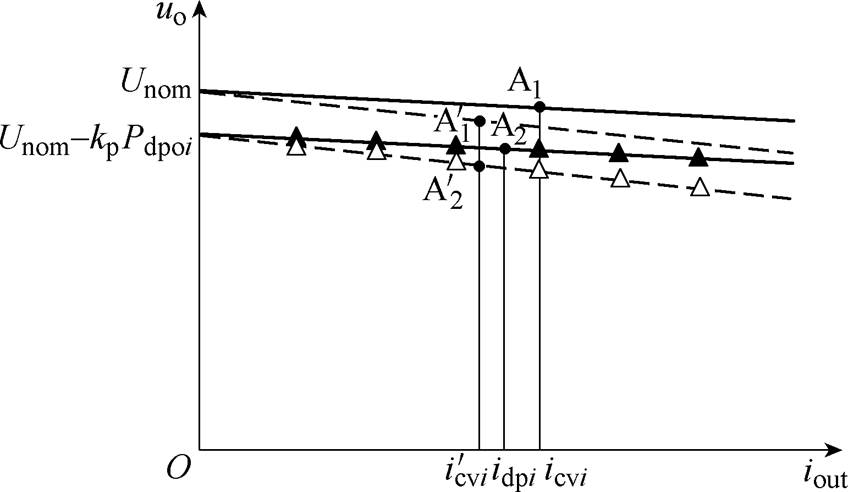
图7 稳态点变换器输出电流示意图
Fig.7 Schematic diagram of output current of steady-state point converter
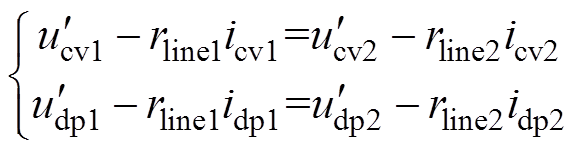（18）将式（9）与式（10）代入式（18）并进行化简后得到
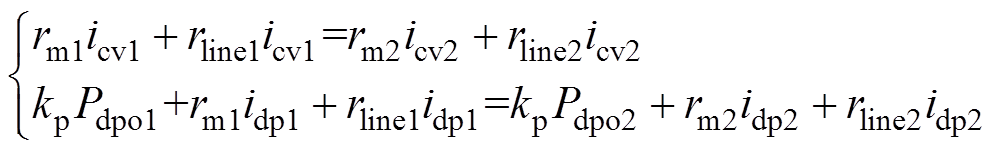（19）
将式（17）代入式（19）中可得
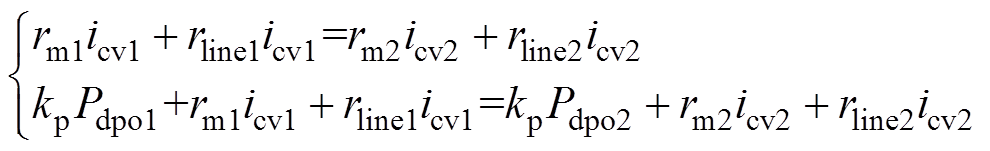（20）对式（20）进行化简可得
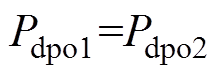（21）
由式（21）可以看出，当变换器输出电流在恒压模式与下垂模式下保持恒定时，即积分补偿环节达到稳态时，并联变换器在下垂控制模式下实现输出功率均分。
2.2.2 恒压模式下并联变换器功率均分特性分析
由式（19）可知，当变换器输出电流在下垂模式与恒压模式下保持恒定时，可以得到
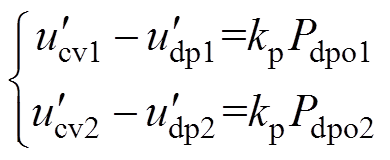（22）对式（22）进行化简可得
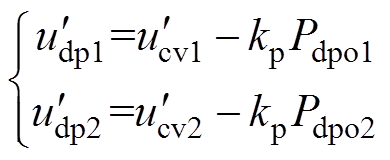（23）
由式（23）与式（4）可知，稳态时，并联变换器输出下垂特性与初始下垂曲线相平行，示意图如图8所示。此时恒压控制指令电压与下垂初始电压重合，简化后可得图9所示稳态点变换器输出功率示意图。
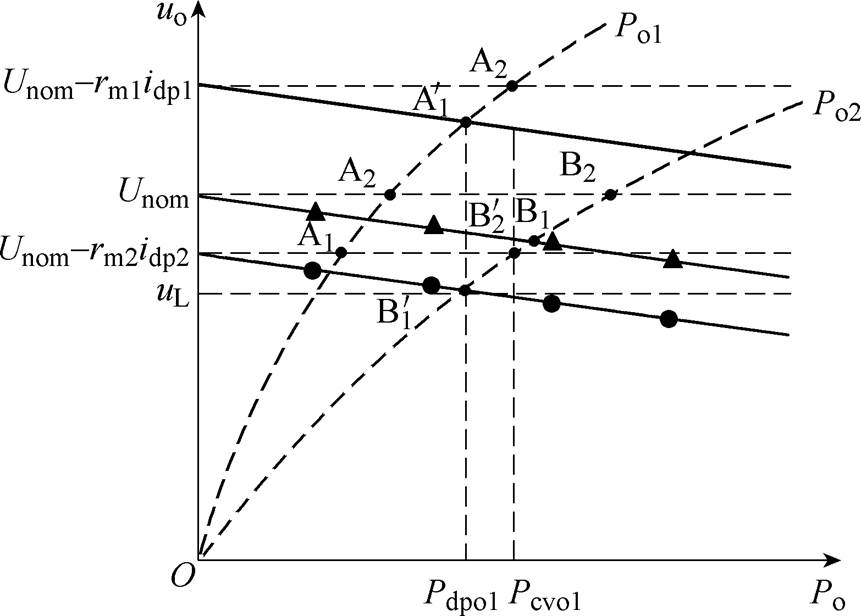
图8 稳态点变换器输出功率示意图
Fig.8 Schematic diagram of output power of steady-state converter
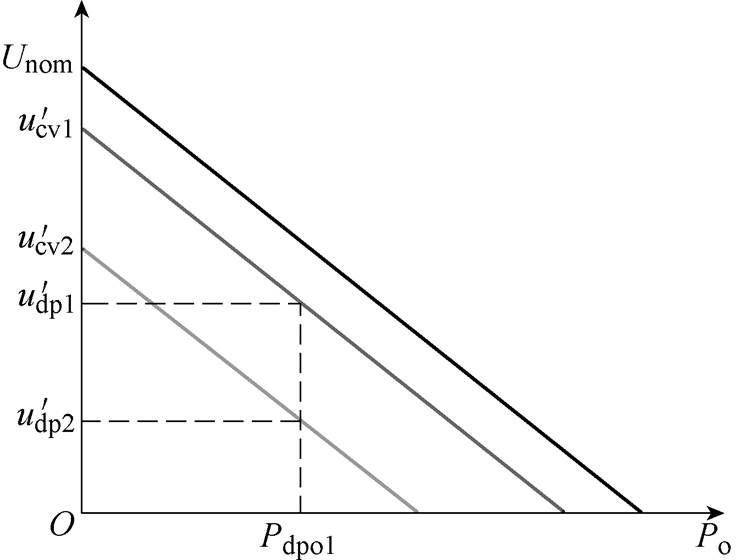
图9 稳态点变换器下垂特性简化示意图
Fig.9 Simplified schematic diagram of the droop characteristic of the converter at steady state
图9中，各变换器恒压控制的指令电压作为下垂特性曲线初始电压，由图9可得
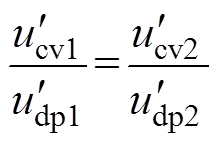（24）由式（24）可知，此时并联变换器恒压控制指令电压与下垂电压比值相等，因此结合式（7）可知，当系统达到稳态时，变换器恒压控制模式下输出功率与下垂控制模式下输出功率比例偏差为零，即
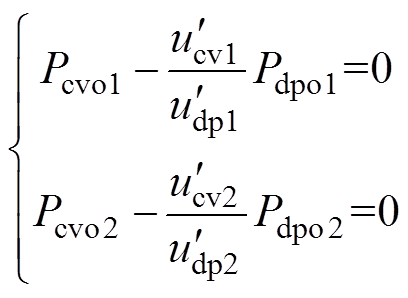（25）
而由前述证明可知，稳态时并联变换器下垂模式下输出功率均分，因此将式（24）代入式（25）中可得
（26）由式（26）可以看出，稳态时并联变换器恒压控制模式下，输出功率均分，结合式（21）与式（26）可得，稳态时变换器输出功率在两种模式下都能够实现功率均分。因此所提并联直流变换器自主功率均分控制策略，在无高带宽通信线路情况，仅通过采集变换器本地电气信息，实现并联变换器输出功率均分控制。
自主均流策略控制框图如图10所示。主要包括微源输出功率提取单元、虚拟阻抗调节单元、下垂控制单元、模式选择单元和电压电流双环跟踪单元五个部分。该策略首先通过功率提取单元对变换器输出功率进行提取，送入虚拟阻抗调节单元中，根据式（7）求解积分补偿量，对恒压控制与下垂控制指令电压进行补偿，在时基信号作用下，模式选择单元确定变换器工作模式，得到电压电流双环跟踪环节输入的指令电压，而图中
为经补偿后的下垂初始电压，表示为
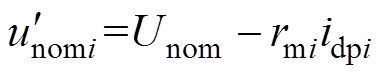（27）
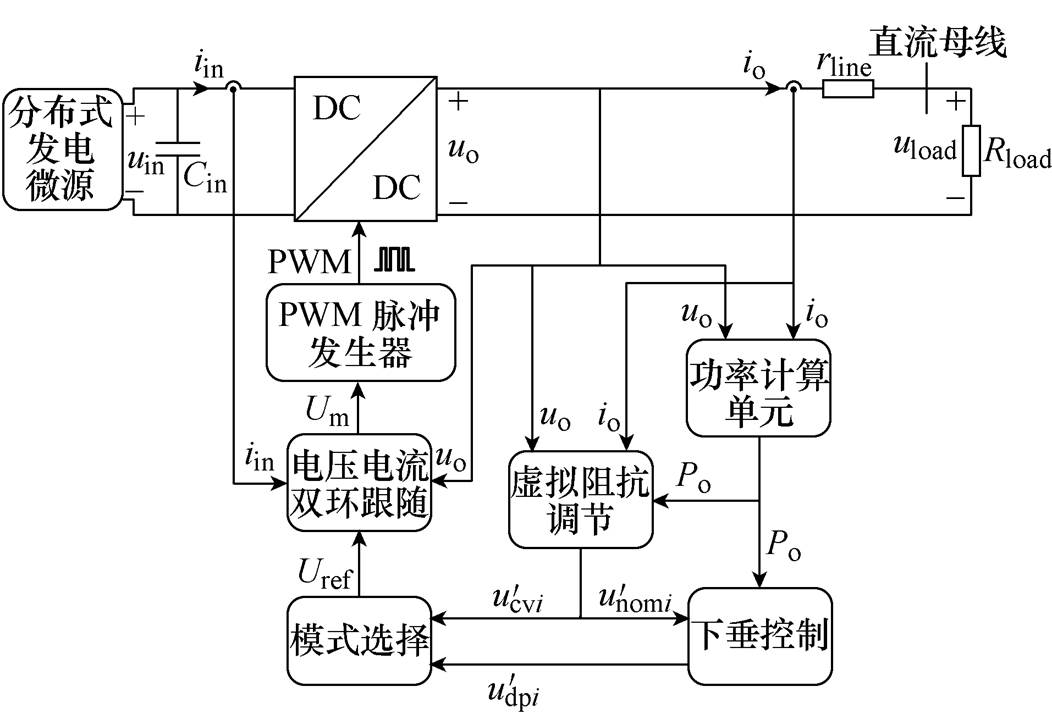
图10 自主均流策略控制框图
Fig.10 Block diagram of autonomous current sharing strategy control
模式选择环节工作示意图如图11所示。图11中，模式选择单元根据时基信号确定变换器工作模式，当并联变换器时基信号实现同步后，控制器发出启动信号，时基信号启动，模式选择环节在时基信号作用下，通过在不同时基周期内给定电压的选择实现其控制模式的切换。经过虚拟阻抗调节环节对恒压控制及下垂控制的指令电压进行补偿，调节变换器输出功率，最终达到稳态点，实现并联变换器输出功率均分控制，策略运行程序流程如图12所示。
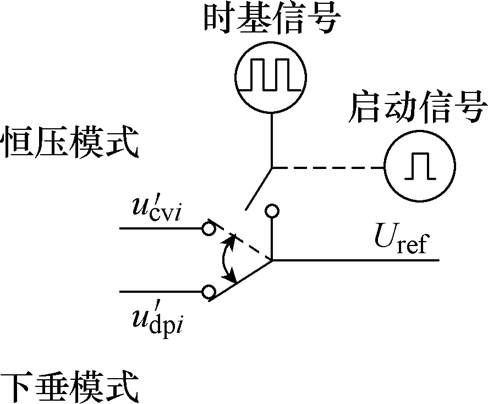
图11 模式选择环节工作示意图
Fig.11 Schematic diagram of mode selection
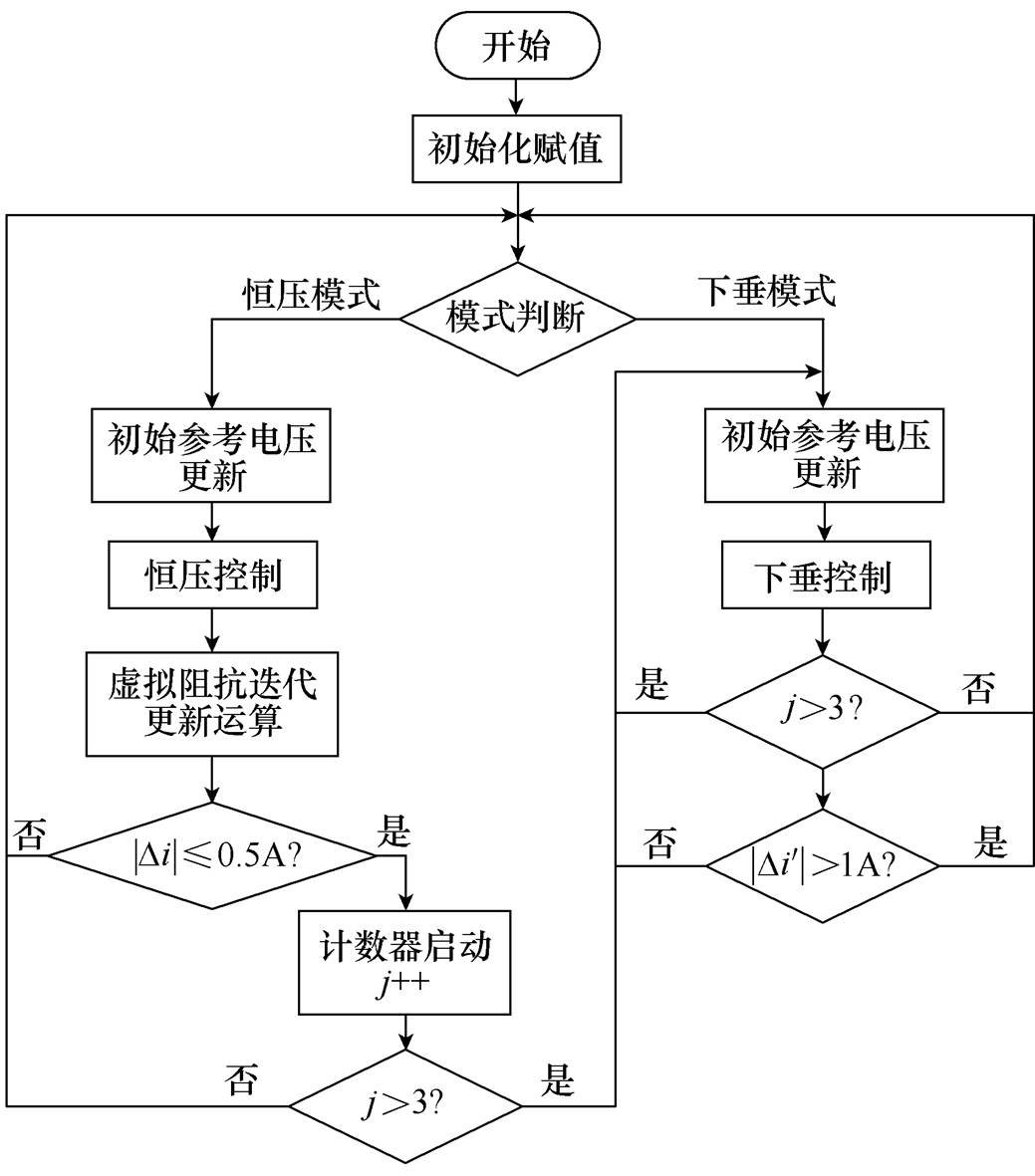
图12 策略运行程序流程
Fig.12 Flow chart of strategy operation procedure
图12中，
为恒压模式与下垂模式电流偏差，
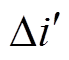为电流前后两拍差值，j为系统处于稳态后的时基周期计数值。
为验证所提策略的有效性，搭建如图13所示并联变换器仿真模型，各分布式微源无高带宽通信线路连接。功率均分控制仿真参数见表1，采用表1仿真参数得到图14～图18仿真结果。
图13 自主均流策略仿真模型
Fig.13 Autonomous current sharing strategy simulation model
表1 功率均分控制仿真参数
Tab.1 Simulation parameter table of power sharing control
参 数数 值 空载电压Unom/V400 直流VSC额定功率Prate/kW5 变换器输出侧电容Cpvout/mF1 200 变换器输入侧电感Lpv/mH2 开关频率fs/kHz10 线路阻抗rline1, rline2, rline3 /W0.2, 0.6, 0.8 下垂系数kp0.002 电压环PI比例系数kpu2 电压环PI积分系数kiu200 电流环PI比例系数kpi10 电流环PI比例系数kii100
图14为未加入均流策略各变换器输出功率波形，可以看出，由于线路阻抗的存在，各变换器输出功率不均分。未加入均流策略各变换器输出功率偏差波形如图15所示，初始功率偏差大于20%，且当2s、8s、13s及16s发生负载功率投切及变换器投入运行时，误差始终大于3%。
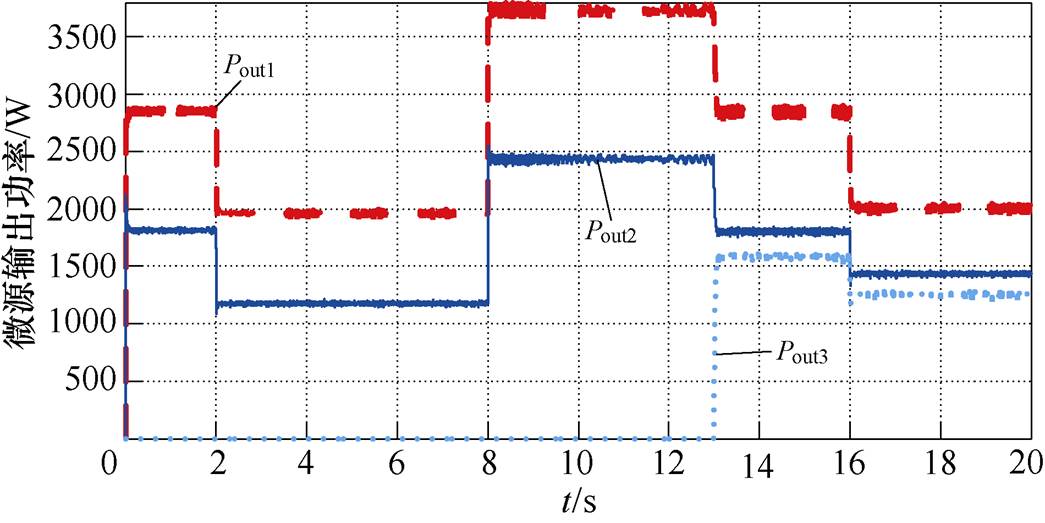
图14 未加入均流策略各变换器输出功率仿真波形
Fig.14 The output power simulation waveforms of each converter without the current sharing strategy
图15 未加入均流策略各变换器输出功率偏差波形
Fig.15 The output power deviation waveforms of each converter without the current sharing strategy
图16为自主均流策略变换器1输出电压波形，在时基信号作用下，模式切换产生的电压波动幅值远小于5%额定电压的电压质量要求范围。图17为自主均流控制各变换器输出功率波形。初始时刻，由于线路阻抗存在，两台并联变换器功率偏差较大，各变换器输出功率偏差波形如图18所示。可以看出，其功率偏差达到平均功率的20%。随着积分补偿环节逐步对给定电压的补偿，各变换器输出功率逐步趋近平均功率，如图17所示。
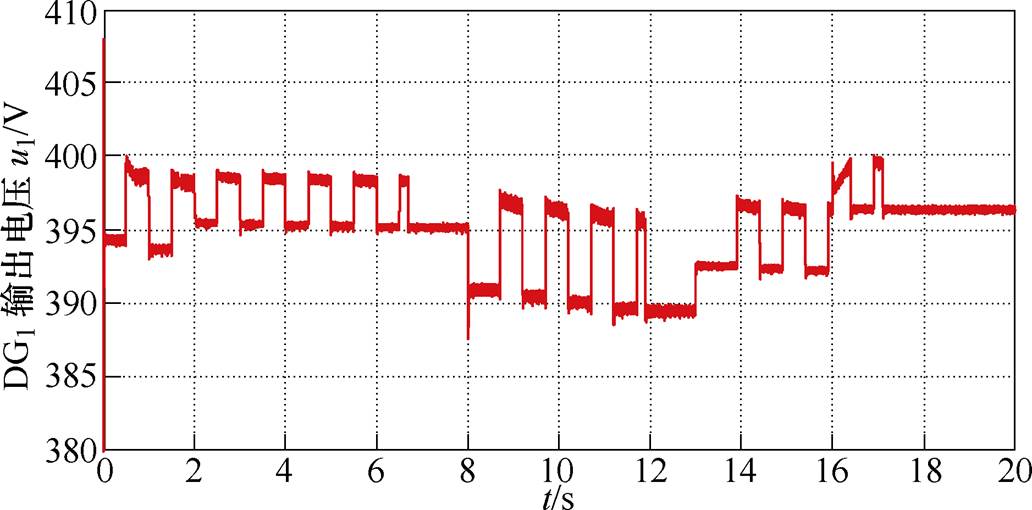
图16 变换器1输出电压波形
Fig.16 Converter 1 output voltage waveform
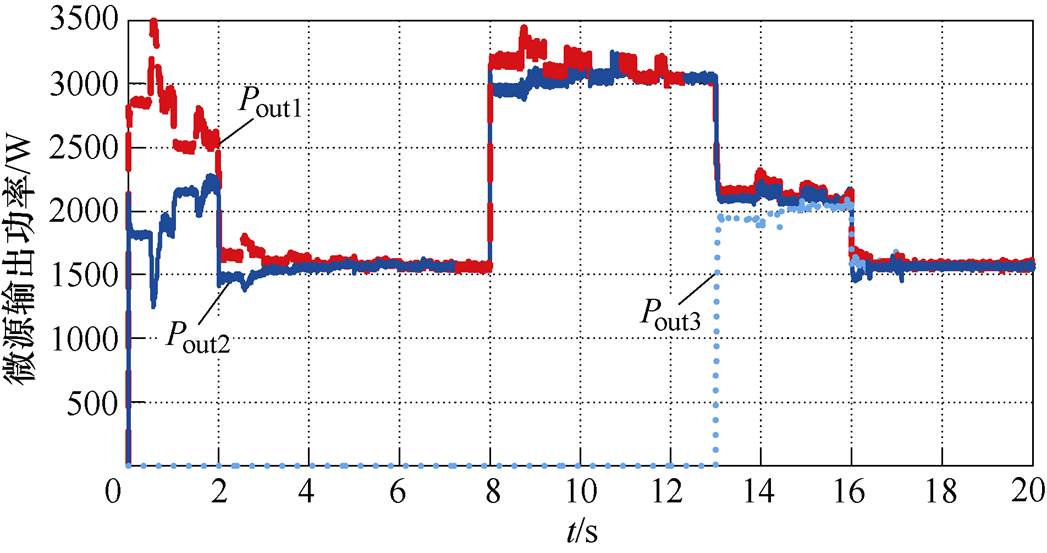
图17 加入均流策略各变换器输出功率波形
Fig.17 Adding current sharing strategy to the output power waveforms of each converter
图17中，2s时负载功率突减，积分补偿环节仍保持调节过程；6.3s时各变换器功率达到平衡，变换器固定工作在下垂模式，稳态示意图如图18所示；8s时负载功率突增，均流策略积分补偿环节重新启动，经过逐步补偿，使系统重新达到稳态；13s时第3台变换器投入运行，在积分补偿环节的调节作用下，3台变换器在17.2s时输出功率实现均分。
图18 各变换器输出功率偏差波形
Fig.18 Output power deviation waveforms of each converter
由图18变换器输出功率偏差波形可以看出，自主均流控制策略通过逐步对变换器输出功率的调节，使得变换器输出功率偏差由初始时刻20%逐步减小到稳态点3%以下，调节过程中在8s负载投切及13s变换器投入时出现功率偏差，最终经过调节仍能回到稳态点，实现变换器输出功率均分控制。
以上仿真结果表明，自主均流策略在线路阻抗1
3工况及各类复杂突变工况下，仍能够保持良好的补偿调节效果，实现并联变换器功率均分控制。
为更进一步验证所提自主均流策略的有效性，采用如图19所示的RT-box半实物平台，搭建如图13所示直流微电网并联系统实验平台，实验参数见表1。
图20为未采用均流策略下变换器输出功率实验波形，由波形可以看出，未采用均流策略，线路阻抗使得下垂控制下垂特性产生偏移，各变换器输出功率分配不均，存在1.6kW功率偏差，随负载投切其仍存在较大偏差。而采用自主均流策略后，各变换器输出功率波形如图21所示，各变换器输出功率由初始偏差1.6kW自主调节，逐步趋于稳态功率均分点，且在调节过程中负载功率突降1.6kW时，自主均流策略仍能稳定工作，实现各变换器输出功率均分控制。
图19 RT-box半实物平台
Fig.19 RT-box semi-physical platform
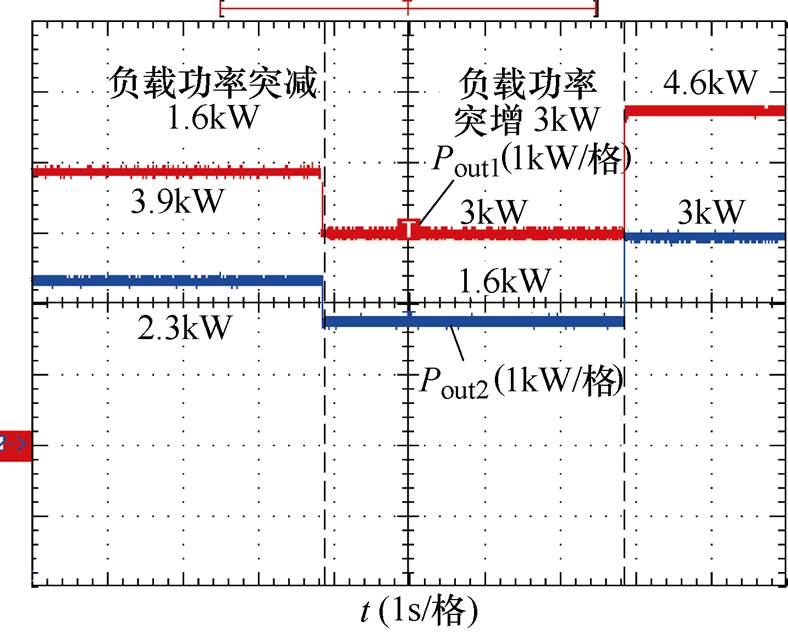
图20 未采用均流策略下变换器输出功率实验波形
Fig.20 The experimental waveforms of putput power without using current sharing strategy
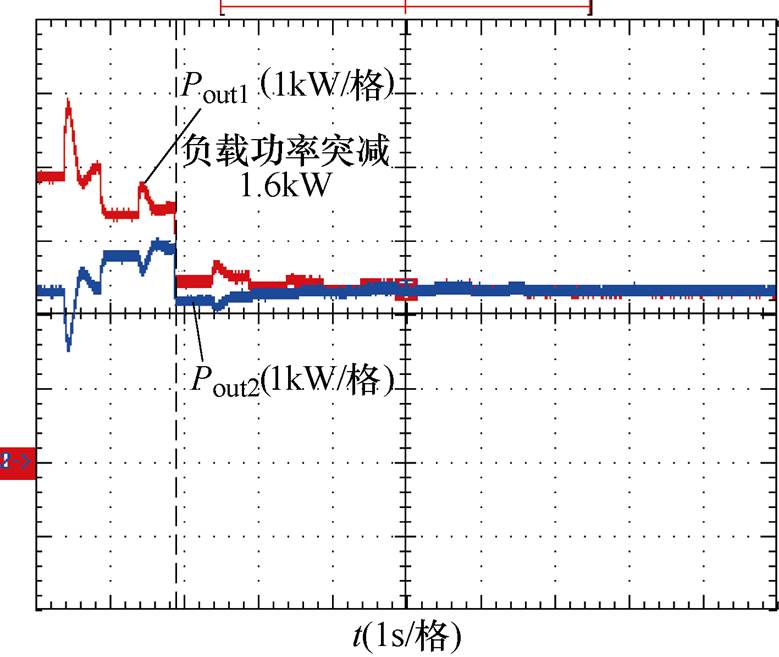
图21 切载工况下变换器输出功率波形
Fig.21 Converter output power waveforms under load shedding
图22为系统稳定运行，各变换器达到稳态功率均分点，负载功率突增3kW时各变换器输出功率波形，由图中可以看出，当稳态点出现3kW负载功率突变时，自主均流策略无需通信线路，即可及时启动进行自主调节，实现变换器输出功率均分控制。
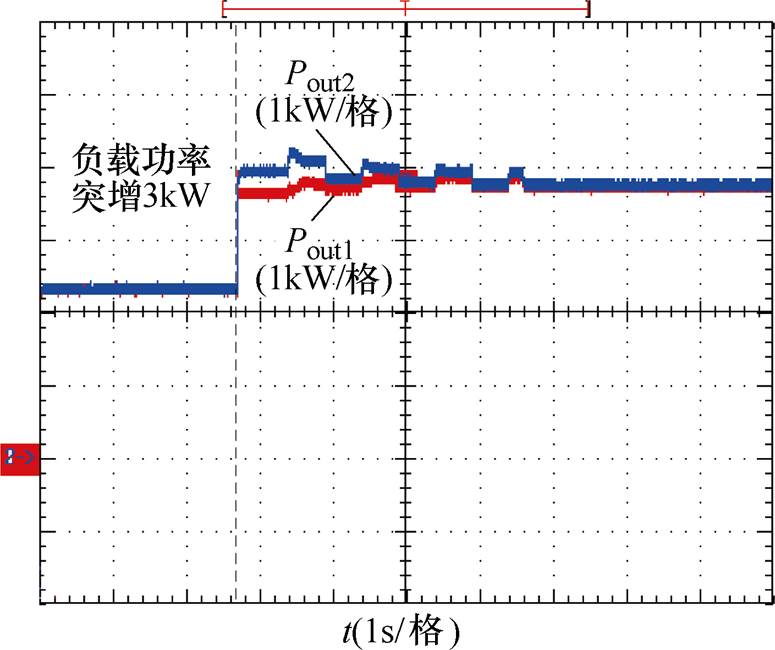
图22 投载工况下变换器输出功率波形
Fig.22 Converter output power waveforms under load connection
图23在稳态点突降3kW负载功率工况下，仍能自主启动对各变换器输出功率进行调节，实现并联系统自主均流控制。图24为稳态功率均分点投入第三台变换器工况下，各变换器输出功率波形。由波形可以看出，在稳态点突然投入第三台变换器，自主均流策略自主启动调节各变换器输出功率实现并联系统自主均流控制。
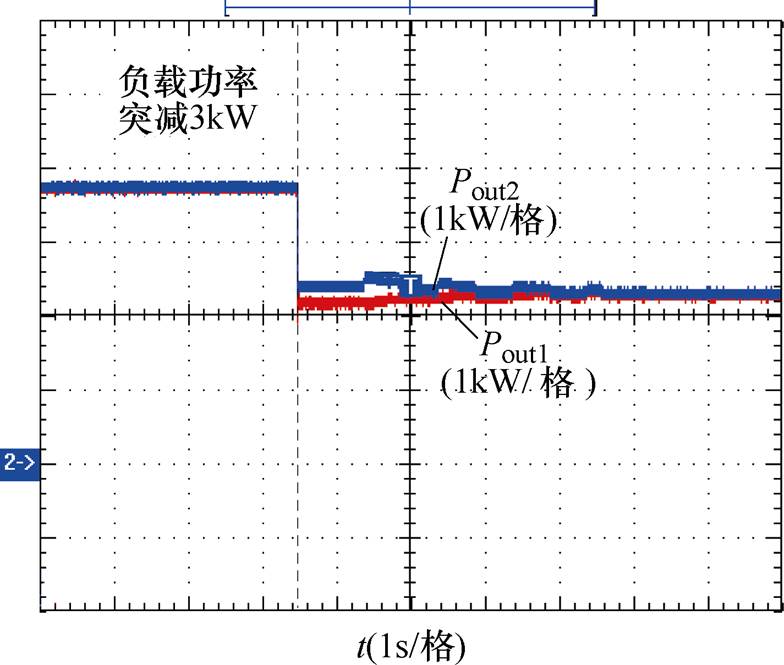
图23 切载工况下变换器输出功率波形
Fig.23 Converter output power waveforms under load shedding
图24 投入第三台变换器工况下变换器输出功率波形
Fig.24 The output power waveforms of the converter under the working condition of the third converter
通过以上实验验证了所提自主均流策略在不同工况下，能够可靠地自主调节变换器输出功率实现各变换器输出功率均分的能力，有效地提升了并联系统运行的可靠性。
直流微电网并联变换器均流算法多基于高带宽通信线路，其成本高、可靠性差，本文提出一种并联系统自主均流策略，变换器依据自身输出的电气特性，通过积分补偿环节改变下垂控制初始电压，从而调节微源输出功率，实现微源输出功率均分控制。建立并联系统下垂控制与恒压控制模式下的数学模型，理论分析了自主均流策略稳态点下垂控制与恒压控制模式微源输出功率均分特性，并利用功率差设计积分补偿环节。仿真和实验结果表明，该控制策略能够提升并联变换器的功率均分精度。
参考文献
[1] 郭伟, 赵洪山. 基于事件触发机制的直流微电网多混合储能系统分层协调控制方法[J]. 电工技术学报, 2020, 35(5): 1140-1151.
Guo Wei, Zhao Hongshan. Coordinated control method of multiple hybrid energy storage system in DC microgrid based on event-triggered mechanism[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1140-1151.
[2] 徐宏健, 赵涛, 朱爱华, 等. 直流微电网的改进型下垂控制策略[J]. 电气技术, 2019, 20(7): 14-17.
Xu Hongjian, Zhao Tao, Zhu Aihua, et al. Research on a new improved droop control method for DC micro- grid[J]. Electrical Engineering, 2019, 20(7): 14-17.
[3] 支娜, 张辉, 肖曦. 提高直流微电网动态特性的改进下垂控制策略研究[J]. 电工技术学报, 2016, 31(3): 31-39.
Zhi Na, Zhang Hui, Xiao Xi. Research on the improved droop control strategy for improving the dynamic characteristics of DC microgrid[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 31-39.
[4] Cai Hongda, Xiang Ji, Wei Wei, et al. V-dp/dv droop control for PV sources in DC microgrids[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7708-7720.
[5] 佟子昂, 武建文, 马速良, 等. 一种基于主动电压扰动的直流微网负载均流控制策略[J]. 电工技术学报, 2019, 34(24): 5199-5208.
Tong Ziang, Wu Jianwen, Ma Suliang, et al. A load current-sharing control strategy for DC microgrid converters based on active voltage disturbance[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5199-5208.
[6] 孟建辉, 邹培根, 王毅, 等. 基于灵活虚拟惯性控制的直流微网小信号建模及参数分析[J]. 电工技术学报, 2019, 34(12): 2615-2626.
Meng Jianhui, Zou Peigen, Wang Yi, et al. Small- signal modeling and parameter analysis of the DC microgrid based on flexible virtual inertia control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2615-2626.
[7] Federico I, Jose E, Luis F. Master-slave DC droop control for paralleling auxiliary DC/DC converters in electric bus applications[J]. IET Power Electronics, 2017, 10(10): 1156-1164.
[8] 芦思晨, 潘再平. 无储能风电微网系统的下垂控制策略[J]. 电工技术学报, 2016, 31(18): 169-175.
Lu Sichen, Pan Zaiping. Droop control strategy of wind power microgrid system without energy storage device[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 169-175.
[9] 陆晓楠, 孙凯, Josep Guerrero, 等. 适用于交直流混合微电网的直流分层控制系统[J]. 电工技术学报, 2013, 28(4): 35-42.
Lu Xiaonan, Sun Kai, Josep Guerrero, et al. DC hierarchical control system for microgrid applica- tions[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 35-42.
[10] Cai Hongda, Xiang Ji, Wei Wei. Decentralized coordination control of multiple photovoltaic sources for DC bus voltage regulating and power sharing[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5601-5610.
[11] Chen Xia, Shi Mengxuan, Sun Haishun, et al. Distributed cooperative control and stability analysis of multiple DC electric springs in a DC microgrid[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5611-5622.
[12] Cook M D, Parker G G, Robinett R D, et al. Decentralized mode-adaptive guidance and control for DC microgrid[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 263-271.
[13] 喻礼礼, 张兆云, 刘艺涛. 基于改进自适应下垂的直流微电网稳定分析与研究[J]. 电气技术, 2020, 21(5): 28-32.
Yu Lili, Zhang Zhaoyun, Liu Yitao. Stability analysis and research of DC microgrid based on improved adaptive drooping[J]. Electrical Engineering, 2020, 21(5): 28-32.
[14] Cingoz F, Elrayyah A, Sozer Y. Optimized settings of droop parameters using stochastic load modeling for effective DC microgrids operation[J]. IEEE Transa- ctions on Industry Applications, 2017, 53(2): 1358- 1371.
[15] Shehata E G, Thomas J, Mostafa R M, et al. An improved droop control for a low voltage DC micro- grid operation[C]//Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 2018: 850-855.
[16] Dam H D, Lee H H. A power distributed control method for proportional load power sharing and bus voltage restoration in a DC microgrid[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3616-3625.
[17] Prabhakaran P, Goyal Y, Agarwal V. Novel nonlinear droop control techniques to overcome the load sharing and voltage regulation issues in DC microgrid[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4477-4487.
[18] Shirazul, Islam, Shyam, et al. Ideal current-based distributed control to compensate line impedance in DC microgrid[J]. IET Power Electronics, 2018, 11(7): 1178-1186.
[19] Augustine S, Mishra M K, Lakshminarasamma N. Adaptive droop control strategy for load sharing and circulating current minimization in low-voltage standalone DC microgrid[J]. IEEE Transactions on Sustainable Energy, 2015, 6(1): 132-141.
[20] Ingle A A, Shyam A B, Sahoo S R, et al. Quality index based distributed secondary controller for low voltage DC microgrid[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7004-7014.
[21] Lu Xiaonan, Guerrero Josep M, Sun Kai, et al. An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing accuracy[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 1800-1812.
[22] Tah A, Das D. An enhanced droop control method for accurate load sharing and voltage improvement of isolated and interconnected DC microgrids[J]. IEEE Transactions on Sustainable Energy, 2016, 7(3): 1194- 1204.
An High Precision Autonomous Current Sharing Control Strategy without High Bandwidth Communication Line
Abstract The DC microgrid parallel systems mostly use droop control to achieve power distribution. However, the line impedance will reduce power distribution precision. The traditional current sharing strategy is based on high-bandwidth communication lines, which has high manufacturing cost and low reliability. In addition, the communication delay in the communication line will affect the power distribution precision. In this paper, an optical autonomous current sharing strategy of parallel storage converters in the DC microgrid is proposed. This strategy analyzes the influence of line impedance on the power distribution characteristics of the converter in constant voltage operation mode and droop operation mode. A virtual impedance compensation link is designed to adjust the output power of the converter according to the output electrical characteristics of the converter, and then, the output power of each converter is equally shared. The effectiveness of the proposed parallel system autonomous current sharing strategy is verified by simulation and experiment.
keywords：DC microgrid, autonomous current sharing strategy, virtual impedance compensation
DOI: 10.19595/j.cnki.1000-6753.tces.200738
中图分类号：TM727
支 娜 女，1976年生，博士，副教授，研究方向为新能源发电及微电网控制。E-mail: zhina@xaut.edu.cn
丁 可 男，1995年生，硕士研究生，研究方向为直流微电网及其协调控制。E-mail: 1597436271@qq.com（通信作者）
国家自然科学基金面上项目（51877175）、陕西省重点项目（2017ZDXM-GY-003）和陕西省自然基金项目（2017JM5100）资助。
收稿日期 2020-06-30
改稿日期 2020-09-14
（编辑 陈 诚）