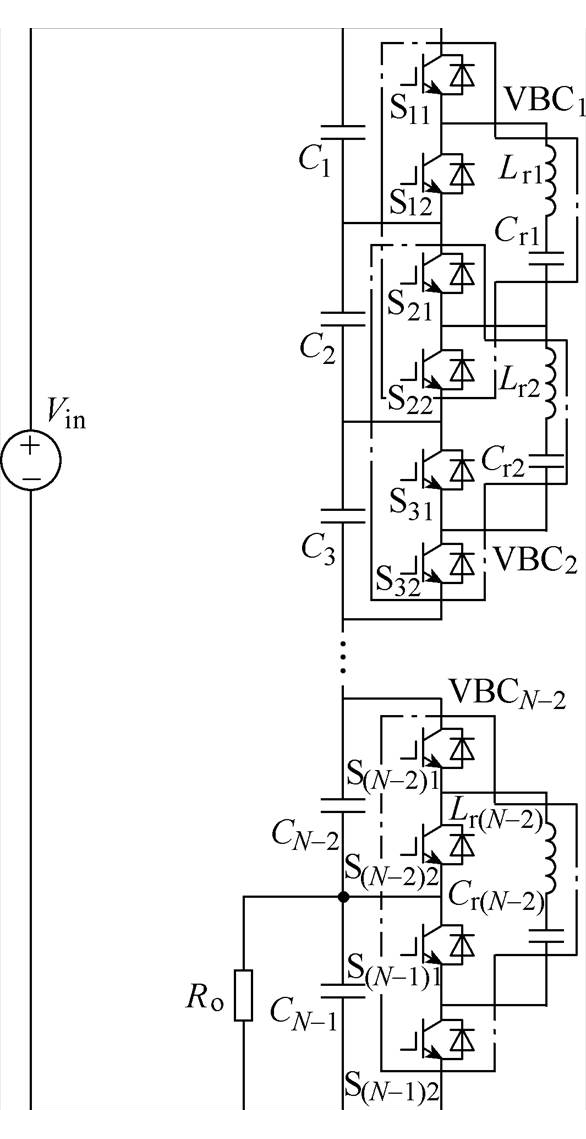
图1 N电平C-MVBDC拓扑
Fig.1 Configuration of N level C-MVBDC
摘要 多电平均压型直流变换器(MVBDC)在中高压直流变换领域具有良好的应用前景,然而随着电平数的提高,MVBDC中谐振单元数目增加,易引起较大的输入电流纹波,进而影响变换器效率和器件寿命。该文以常见的耦合型和解耦型MVBDC为例,在分析MVBDC输入电流纹波与各级谐振电流之间关系基础上,提出一种输入电流纹波抑制策略。通过调整各谐振电流之间的相位,可有效降低MVBDC输入电流纹波、提高变换器效率。最后,通过搭建仿真模型和实验平台验证了上述理论分析的正确性和有效性。
关键词:多电平均压型直流变换器 中高压直流变换 电流纹波 效率 谐振
多电平变换器凭借其开关器件电压应力低、容量大、控制简单等优点,在中高压直流变换领域具有良好的应用前景,并且得到了广泛研究[1-2]。然而由于电平数增加、寄生参数、器件特性不一致等因素影响,多电平变换器不可避免地存在电压均衡问题,严重时甚至威胁到变换器的正常运行[3-4]。
为解决上述电压均衡问题,硬件均压方法因其简单可靠而受到广泛关注。文献[5-6]提出了传统型均压电路(Voltage-Balancing Circuit, VBC),即通过开关电容充放电来实现直流支撑电容电压均衡,但是该电路器件数量多、电流应力大。文献[7-8]提出了谐振型VBC,即通过谐振单元替换传统型VBC中充放电电容进行能量传递,进而有效降低器件的电流应力,更适合大功率场合应用。
利用直流支撑电容和VBC来实现直流能量变换的装置,可统称为多电平均压型DC-DC变换器(Multilevel Voltage-Balancing DC-DC Converter, MVBDC)。此时MVBDC主要包含若干直流支撑电容和VBC,具有高电压比、控制简单和结构模块化等优点[9]。且根据谐振型VBC中各谐振单元间耦合关系,可将MVBDC进一步划分为耦合型MVBDC[10-12](Coupled MVBDC, C-MVBDC)和解耦型MVBDC(Decoupled MVBDC, D-MVBDC)[1, 13]。前者所需的开关数量少,但由于耦合关系而使得控制策略较为单一,且对谐振参数一致性要求较高;后者通过增加开关数量而实现各谐振单元间的解耦,进而为扩展多种控制策略提供可能。
MVBDC在中高压大功率场合应用中,随着电平数的增大,谐振单元数也随之增大。然而多个谐振单元同时工作可能使得MVBDC输入电流纹波增大,该电流纹波不仅会带来一定损耗,降低效率,还会降低器件使用寿命,严重时甚至影响系统稳定性,因此MVBDC输入电流纹波抑制就显得尤为必要。对于输入电流纹波抑制,可分为增加辅助电路的硬件解决方案和改进控制策略的软件解决方案。文献[14]采用无源纹波抑制电路来减小输入电流纹波,响应快,但结构复杂,导致系统体积增大。文献[15]通过有源钳位辅助电路,消除了钳位电容电流纹波对输入电流纹波的影响。文献[16-18]则引入辅助电感和辅助电容抑制电流纹波,同样会增大系统的体积与成本。文献[19-21]使用耦合电感降低输入电流纹波,但对耦合电感的耦合系数敏感,设计难度大。文献[22-23]使用交错并联技术抑制输入电流纹波,但是仅在特定占空比下才能实现零纹波,控制难度高。文献[24]基于开关器件复用抑制输入电流纹波,但纹波抑制能力取决于直流母线电容大小。文献[25]采用输入电流随耦合电感相移的方法抑制输入电流纹波,但也存在耦合电感的不足。文献[26-27]综合使用硬件与软件方案来减小输入电流纹波,适用于由多个电力电子装置串联组成的综合系统。综上所述,硬件解决方案由于辅助电路引入而通常会增大MVBDC的体积与成本,并且局限于特定的MVBDC电平数,不同电平之间需单独设计;而现有的交错并联技术、开关器件复用等软件解决方案也无法直接应用于MVBDC,故MVBDC需要开展适应其自身拓扑的纹波抑制策略研究。
为此,本文深入研究C-MVBDC与D-MVBDC拓扑,提出了D-MVBDC输入电流纹波抑制策略,并与C-MVBDC进行详细对比研究。纹波抑制策略通过对D-MVBDC中各VBC谐振电流分别进行相位控制,有效地降低了D-MVBDC的输入电流纹波,进而减小纹波带来的损耗、提高变换器的效率。本文首先介绍C-MVBDC 和D-MVBDC拓扑结构和工作原理,并重点研究输入电流和各谐振电流之间关系。同时,分析和推导MVBDC输入电流最小纹波方案,实现理想情况下输入电流零纹波。最后,通过搭建仿真模型和实验平台验证上述理论分析的正确性和有效性。
典型N电平C-MVBDC 拓扑如图1所示,主要包含N-1个直流支撑电容与N-2个VBC单元,且每个VBC单元均包含4个开关管和1个由谐振电容与谐振电感串联组成的谐振单元。C-MVBDC中相邻VBC单元存在耦合关系,即相邻VBC单元中部分开关管复用,如图1中VBC1和VBC2共用开关管S21、S22,此时N电平C-MVBDC共包含2(N-1)个开关管与N-2个谐振单元。

图1 N电平C-MVBDC拓扑
Fig.1 Configuration of N level C-MVBDC
典型N电平D-MVBDC拓扑如图2所示,同样包含N-1个直流支撑电容与N-2个VBC单元,且每个VBC单元均包含4个开关管和1个谐振单元。但与C-MVBDC相比,D-MVBDC通过额外增加开关管,使得相邻VBC单元相互独立,不存在上述开关管复用情况。此时N电平D-MVBDC共包含4(N-2)个开关管与N-2个谐振单元,即相对于C-MVBDC,D-MVBDC额外增加2(N-3)个开关管。
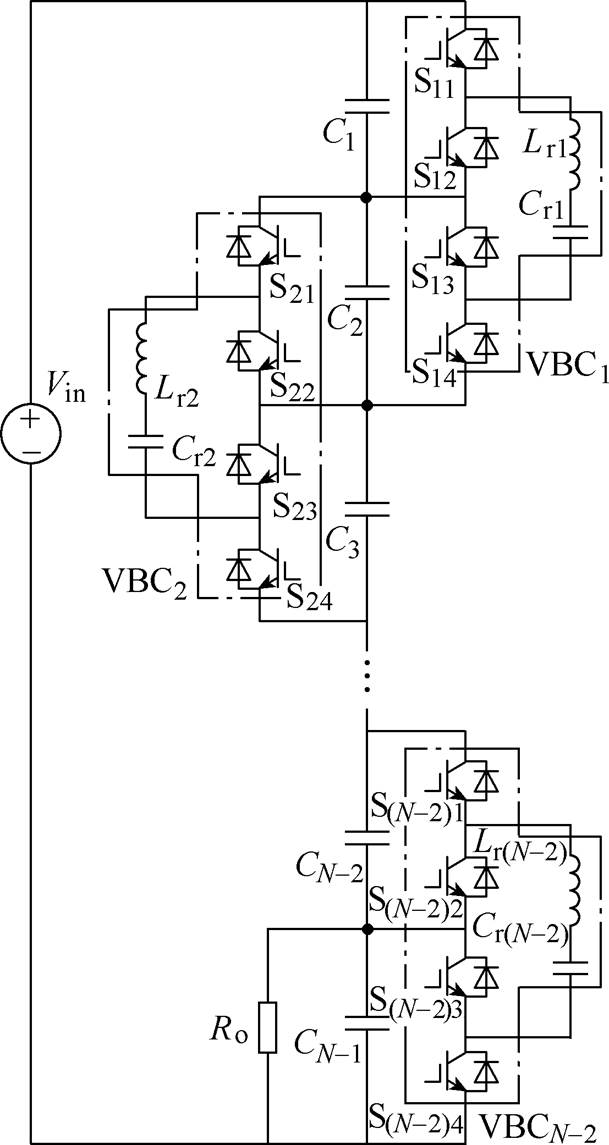
图2 N电平D-MVBDC拓扑
Fig.2 Configuration of N level D-MVBDC
C-MVBDC和D-MVBDC中相邻VBC单元耦合与否,使得其工作原理存在较大差异。以直流支撑电容Ck-1、Ck、Ck+1、VBCk-1和VBCk所构成的局部电路为例,此时C-MVBDC和D-MVBDC的典型工作模态分别如图3、图4所示。
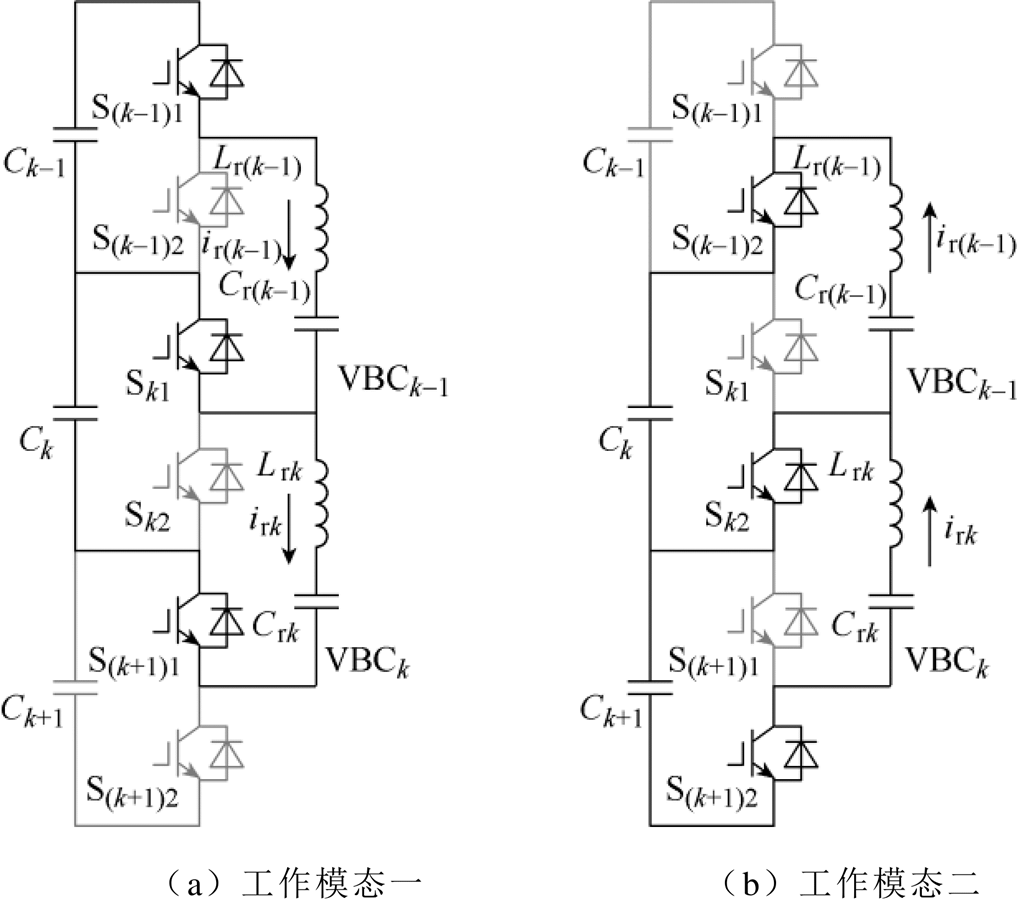
图3 C-MVBDC典型工作模态
Fig.3 Typical operating modes of C-MVBDC

图4 D-MVBDC典型工作模态
Fig.4 Typical operating modes of D-MVBDC
C-MVBDC工作模态一如图3a所示,开关管Si1导通(i=k-1, k, k+1),开关管Si2关断,此时各谐振电流从零开始正向谐振,直流支撑电容Ck-1向谐振电容Cr(k-1)传递能量,直流支撑电容Ck向谐振电容Crk传递能量。理想情况下,各VBC谐振频率均与开关频率相同,故在谐振电流过零时,开关管Si1关断,开关管Si2导通,此时C-MVBDC进入如图3b所示的工作模态二。此时各谐振电流从零开始反向谐振,谐振电容Cr(k-1)向直流支撑电容Ck传递能量,谐振电容Crk向直流支撑电容Ck+1传递能量。同样谐振电流过零时,开关管Si1导通,开关管Si2关断,此时C-MVBDC进入工作模态一,如此循环往复,即可通过VBC在各直流支撑电容间能量传递而实现直流支撑电容电压均衡。
同理,D-MVBDC典型工作模态如图4所示,电容间能量传递与C-MVBDC典型工作模态相同,仅各工作模态下各开关管状态存在些许差别。此时D-MVBDC在如图4a所示的工作模态一时,开关管Sj1、Sj3导通(j=k-1, k),开关管Sj2、Sj4关断;而在如图4b所示的工作模态二时,开关管Sj1、Sj3关断,开关管Sj2、Sj4导通。
显然由于D-MVBDC解耦关系,相邻VBC单元之间不存在开关管复用,电容间能量传递不再局限于如图3所示的C-MVBDC固定开关状态,进而使得D-MVBDC工作模态得到进一步扩展,则此时D-MVBDC可存在如图5所示的新型工作模态,而这种能量传递路径是在C-MVBDC无法实现的。
D-MVBDC新型工作模态一如图5a所示,开关管S(k-1)1、S(k-1)3、Sk2和Sk4导通,其余开关管关断,此时直流支撑电容Ck-1向谐振电容Cr(k-1)传递能量,谐振电容Crk向直流支撑电容Ck+1传递能量;而在如图5b所示的新型工作模态二时,开关管S(k-1)2、S(k-1)4、Sk1和Sk3导通,其余开关管关断,此时谐振电容Cr(k-1)向直流支撑电容Ck传递能量,而直流支撑电容Ck进一步向谐振电容Crk传递能量。
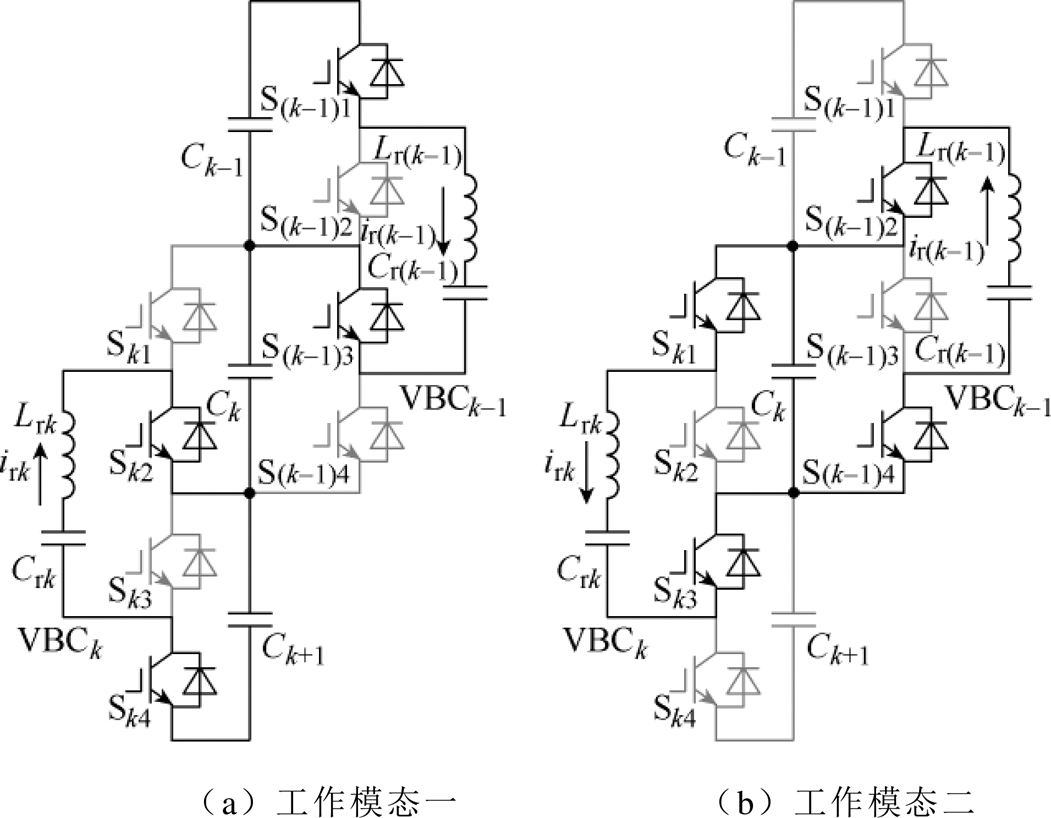
图5 D-MVBDC新型工作模态
Fig.5 New operating modes of D-MVBDC
由上述理论分析可见,C-MVBDC控制策略相对单一,即当C-MVBDC某个开关管导通关断状态确定时,其余开关管状态均可根据该开关管状态来确定,此时所有VBC工作模态同步、谐振电流相位均相同,同时也限制了移相控制在C-MVBDC中应用[7]。此外,C-MVBDC相对单一的控制策略也使得其对谐振单元的参数一致性要求较高,各谐振频率应均与开关频率相等,以免开关管关断时谐振电流仍未谐振到零或已反向谐振,使得开关管存在硬关断问题而带来额外的损耗。而D-MVBDC通过解耦使得其控制策略多样化,各VBC单元工作模态可互不相同,移相控制亦可引入D-MVBDC中,且利用特定开关管提前关断可阻断反向谐振电流进而扩展谐振频率选取范围。随着电平数的提高,D- MVBDC可选的控制策略更为多样化,而如何在众多控制策略中选取最适用的D-MVBDC成为目前MVBDC研究中的重点问题。本文正是从输入电流纹波抑制角度入手,通过选取合适的控制策略来减小输入电流纹波,进而提高MVBDC的性能。
N电平D-MVBDC和C-MVBDC均可由如图6所示的简化模型表示,任意VBC单元在工作模态一或工作模态二下均与某个直流支撑电容相连。对于VBCk(k=1, 2, 3,…, N-2),选取从上到下为参考方向,其谐振电流记为irk。在前半个开关周期内(见图6a所示的工作模态一),VBCk与直流支撑电容Ck构成回路,直流支撑电容Ck电流为iin-irk,其中iin为输入电流;在后半个周期内(见图6b所示的工作模态二),VBCk与直流支撑电容Ck+1构成回路,直流支撑电容Ck+1电流为iin-ik-1。因此,无论MVBDC处于何种工作模态,VBCk所连接的直流支撑电容(输出电容除外)电流始终等于输入电流iin与VBCk谐振电流irk之差。此外,对于输出电容CN-1,还应该考虑到输出电流Io,此时输出电流Io可以视为恒定值。
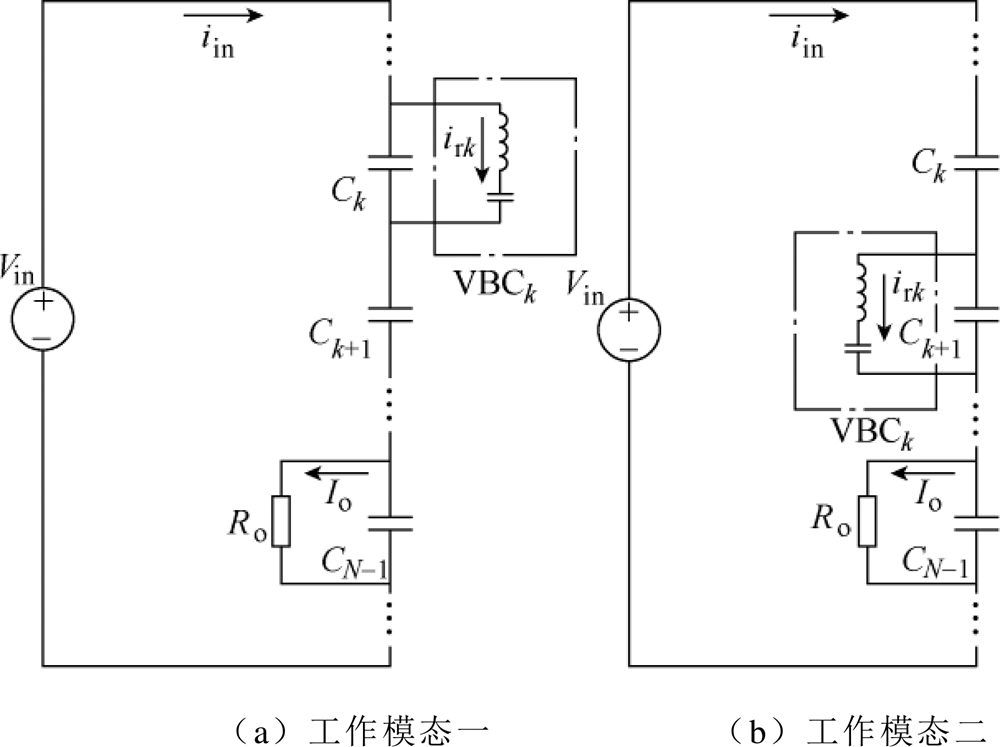
图6 MVBDC简化模型
Fig.6 Simplified model of MVBDC
对于N电平MVBDC,假设输入源为理想电压源,所有直流支撑电容值相等,谐振支路参数完全一致。显然各直流支撑电容电压纹波之和为零,并且根据各直流支撑电容电压电流关系i=Cdv/dt,即可得到
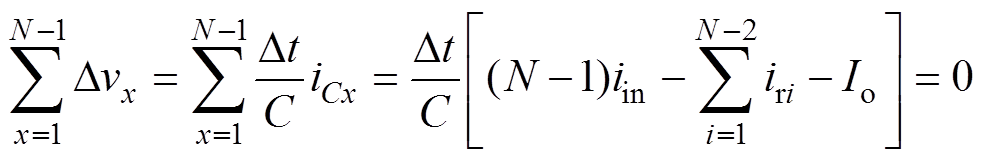 (1)
(1)式中,Dvx和iCx(x=1, 2, 3,…, N-1)分别为直流支撑电容Cx电压纹波和电流。由式(1)可化简得到
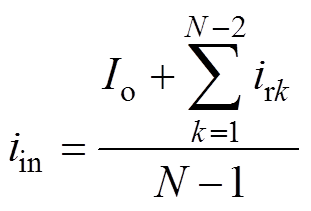 (2)
(2)
显然,式(2)中可分离出输入电流iin的直流分量(即输入电流平均值)和交流分量(即输入电流纹波)。同时,由式(2)可知,输入电流纹波与各谐振电流之和、电平数有关。当电平数一定时,各谐振电流之和越大,输入电流纹波越大。
假定各谐振频率与开关频率相等,则MVBDC的各VBC中谐振电流可根据电容充放电关系得到
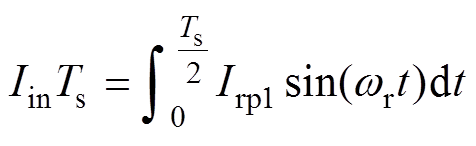 ()
()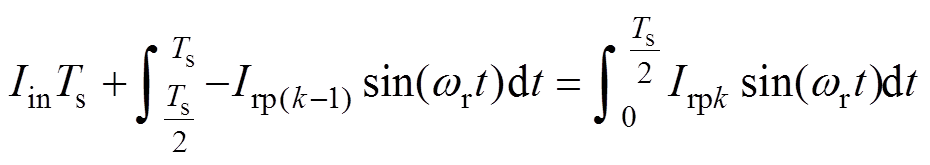
 (4)
(4)
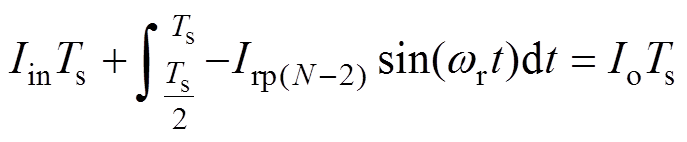 (5)
(5)式中,Iin为输入电流的平均值;Ts为开关周期;wr为谐振角频率;Irpk为VBCk的谐振电流峰值,Irpksin(wrt)为VBCk的理想谐振电流。结合式(3)~式(5),可以得到
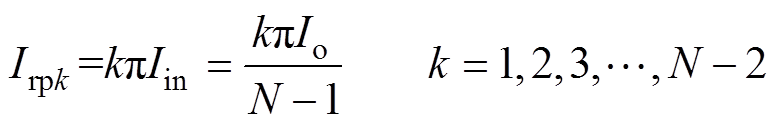 (6)
(6)
对于C-MVBDC,相邻谐振单元互相耦合,控制策略单一,所有谐振电流的相位相等,此时将式(6)代入式(2)中,可以得到输入电流为
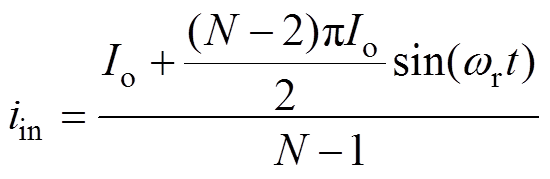 (7)
(7)对于D-MVBDC,相邻谐振单元互相解耦,谐振电流之间的相位可以各不相同。当使用如图4所示的典型工作模态时,谐振电流相位相等,输入电流表达式与式(7)相同。此时,典型工作模态下MVBDC电流纹波峰-峰值与谐振电流峰值关系为
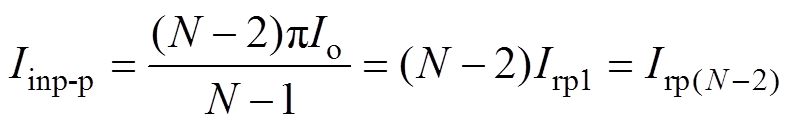 (8)
(8)
此外,当考虑MVBDC输入侧寄生参数,如输入侧串联寄生电感Ls与串联寄生电阻Rs时,典型工作模态下输入电流纹波幅值会减小,纹波相对于谐振电流的相位f 也会发生变化,但纹波频率保持不变,即始终与开关频率相等。此时幅值B与相位f 可以根据s域中方程式(9)求得。
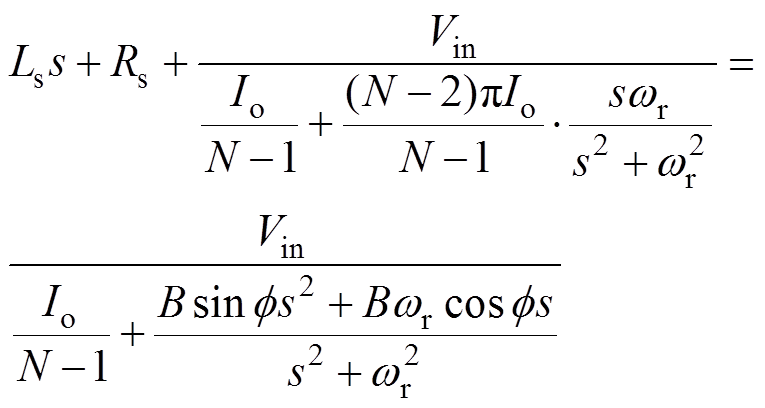 (9)
(9)由式(2)可知,当MVBDC的谐振电流之和为零或达到最小值时,输入电流纹波为零或达到最小。然而,C-MVBDC由于谐振单元的耦合关系,控制策略单一,所有谐振电流的相位相同,无法调整控制策略来降低输入电流纹波;而D-MVBDC的谐振单元互相解耦,可以调整谐振电流之间的相位,从而使得谐振电流之和最小,进而大幅降低输入电流纹波,使D-MVBDC中谐振电流之和为零或达到最小值的控制策略即为纹波抑制策略。MVBDC纹波抑制策略如图7所示。
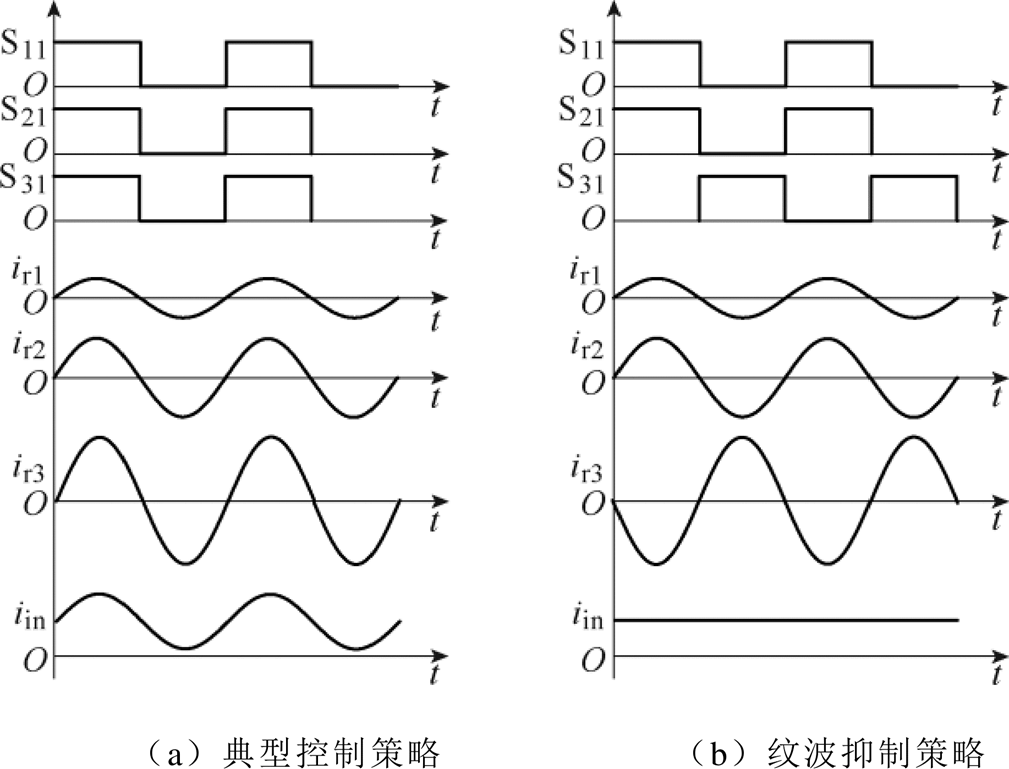
图7 MVBDC纹波抑制策略
Fig.7 The ripple suppression strategy of MVBDC
以五电平D-MVBDC为例,其纹波抑制策略如图7b所示,此时VBC1与VBC2的谐振电流ir1和ir2相位相同,VBC3中谐振电流ir3的相位与ir1相差p/2。此时,理想情况下谐振电流之和为0,故五电平D-MVBDC的输入电流可表示为
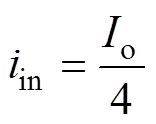 (10)
(10)当MVBDC采用典型控制策略时,输入电流表达式如式(7)所示,此时输入电流有效值为
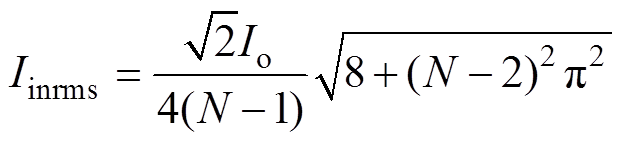 (11)
(11)而当MVBDC采用纹波抑制策略实现零纹波时,此时输入电流有效值为
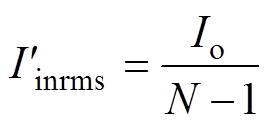 (12)
(12)
假设MVBDC输入侧等效寄生电阻为Rs,则采用纹波抑制策略可以减小的损耗为
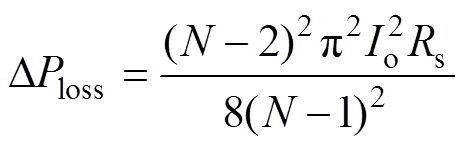 (13)
(13)进而系统效率可提高为
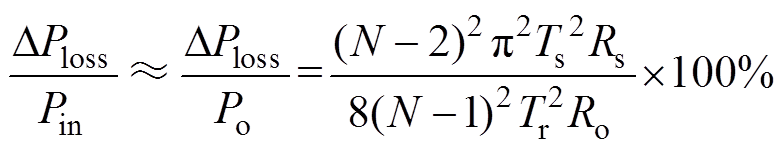 (14)
(14)
式中,Ro为MVBDC输出电阻阻值。显然,由式(13)与式(14)可知,纹波抑制策略能够有效地降低线路导通损耗,进而提高变换器效率。
为了验证上述理论,基于PSIM软件分别搭建了如图8所示五电平C-MVBDC和D-MVBDC仿真模型,MVBDC仿真参数见表1。
图8 五电平MVBDC拓扑
Fig.8 Configurations of the 5-level MVBDC
表1 MVBDC仿真参数
Tab.1 Simulation parameters of MVBDC

参 数数 值 输入电压Vin/V1 000 输出电压Vout/V250 系统功率P/kW2.8 开关频率fs/kHz5 支撑电容C/mF5 600 谐振电容Cr/mF50 谐振电感Lr/mH20
典型控制策略下C-MVBDC与D-MVBDC的谐振电流和输入电流的理想仿真波形分别如图9和图10所示。显然,各谐振电流和输入电流相位相同,输入电流存在较大纹波。此时C-MVBDC和D-MVBDC的输入电流大小相等,且纹波峰-峰值的理论值为27.22A。而采用纹波抑制策略时D-MVBDC谐振电流和输入电流理想仿真波形如图11所示。此时谐振电流ir3与谐振电流ir1和ir2存在p/2的相位差,输入电流近似实现零纹波。此时MVBDC各谐振电流峰值、输入电流纹波峰-峰值的仿真结果与理论值对比见表2,显然各仿真结果与理论值基本相同。此时谐振电流逐级递增,典型控制下输入电流纹波峰-峰值与谐振电流ir3峰值相等;而采用纹波抑制控制后,各谐振电流峰-峰值大小与典型控制策略基本相同,但输入电流纹波由谐振电流ir3峰值近乎降低至零纹波,即降低至原纹波的0.2%,进而验证了理论分析的正确性。
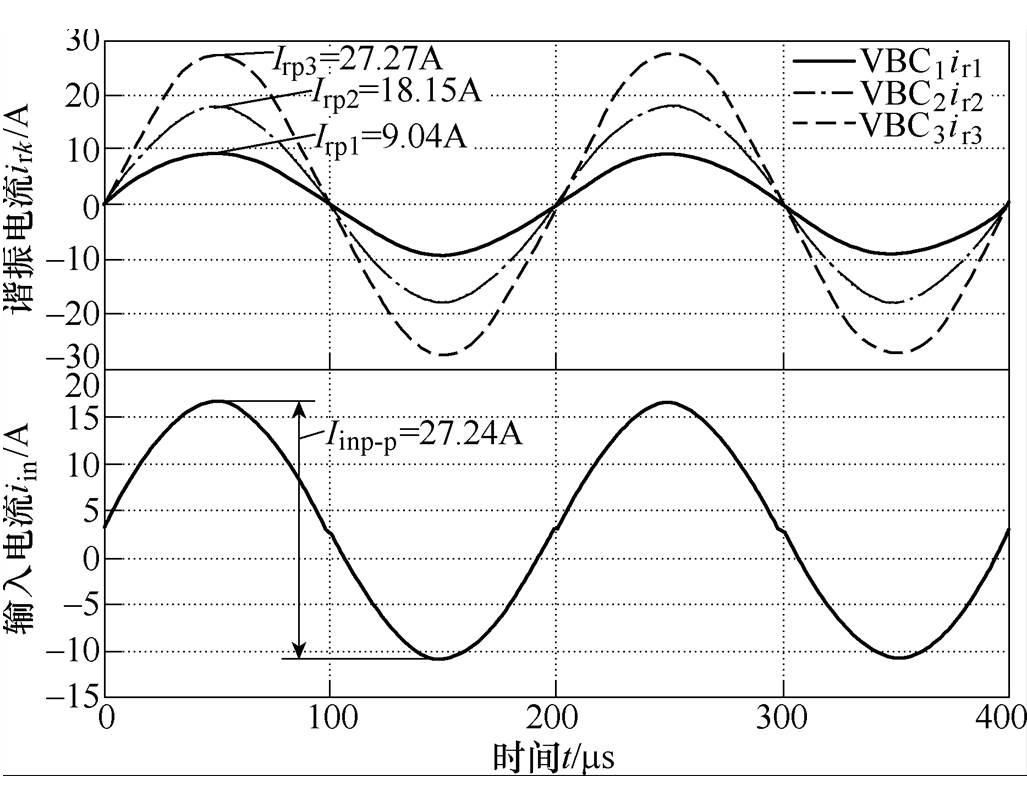
图9 典型控制策略下C-MVBDC理想仿真波形
Fig.9 Ideal simulation waveforms of C-MVBDC with the typical control strategy

图10 典型控制策略下D-MVBDC理想仿真波形
Fig.10 Ideal simulation waveforms of D-MVBDC with the typical control strategy
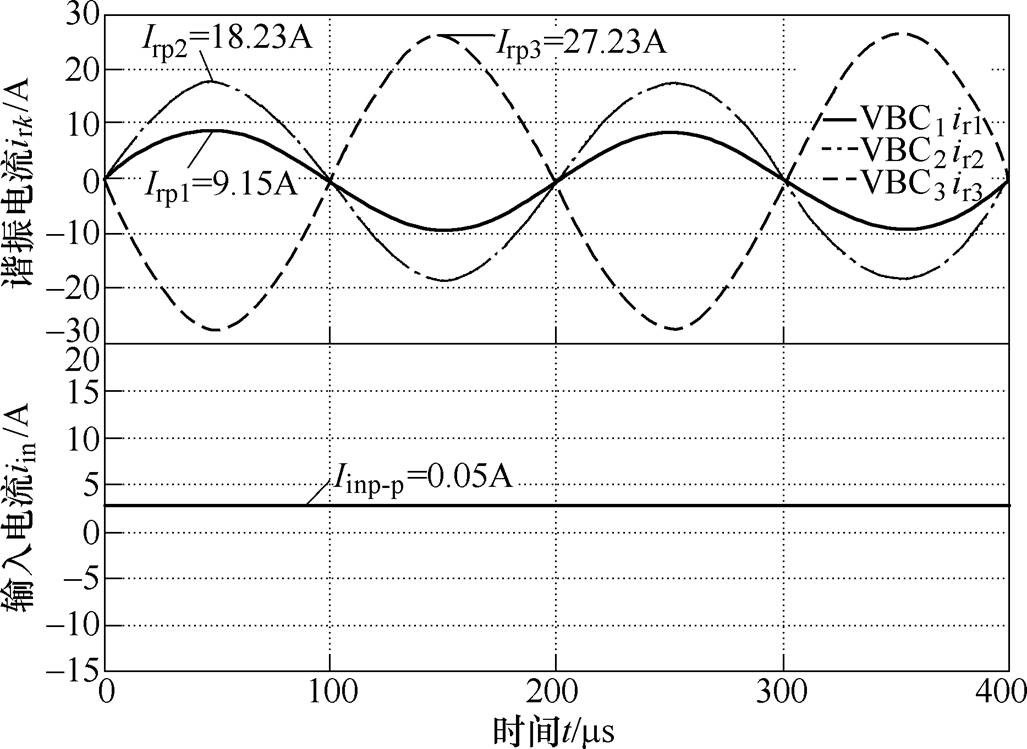
图11 纹波抑制策略下D-MVBDC理想仿真波形
Fig.11 Ideal simulation waveforms of D-MVBDC with the minimum ripple suppression strategy
表2 MVBDC理想仿真结果
Tab.2 Ideal simulation results of MVBDC (单位: A)

电流C-MVBDC典型控制D-MVBDC典型控制D-MVBDC纹波抑制理论值 Irp19.049.069.159.07 Irp218.1518.1618.2318.15 Irp327.2727.2827.2327.22 Iinp-p27.2427.260.0527.22
为评估寄生参数的影响,上述理想仿真模型中加入以下寄生参数:输入侧串联寄生电阻Rs=0.1W,串联寄生电感Ls=0.1mH。
此时典型控制策略下C-MVBDC和D-MVBDC的仿真波形分别如图12和图13所示,纹波抑制策略下的D-MVBDC仿真波形如图14所示。显然在寄生参数影响下,各谐振电流无明显变化,但输入电流纹波在幅值和相位均存在明显改变。此时典型控制策略下C-MVBDC和D-MVBDC的输入电流纹波相位分别滞后0.44p 和0.4p,纹波峰-峰值分别降低至6.00A和5.98A;纹波抑制策略下D-MVBDC的输入电流纹波峰-峰值为2.60mA,降低至原纹波的0.04%,从而验证纹波抑制策略的正确性。
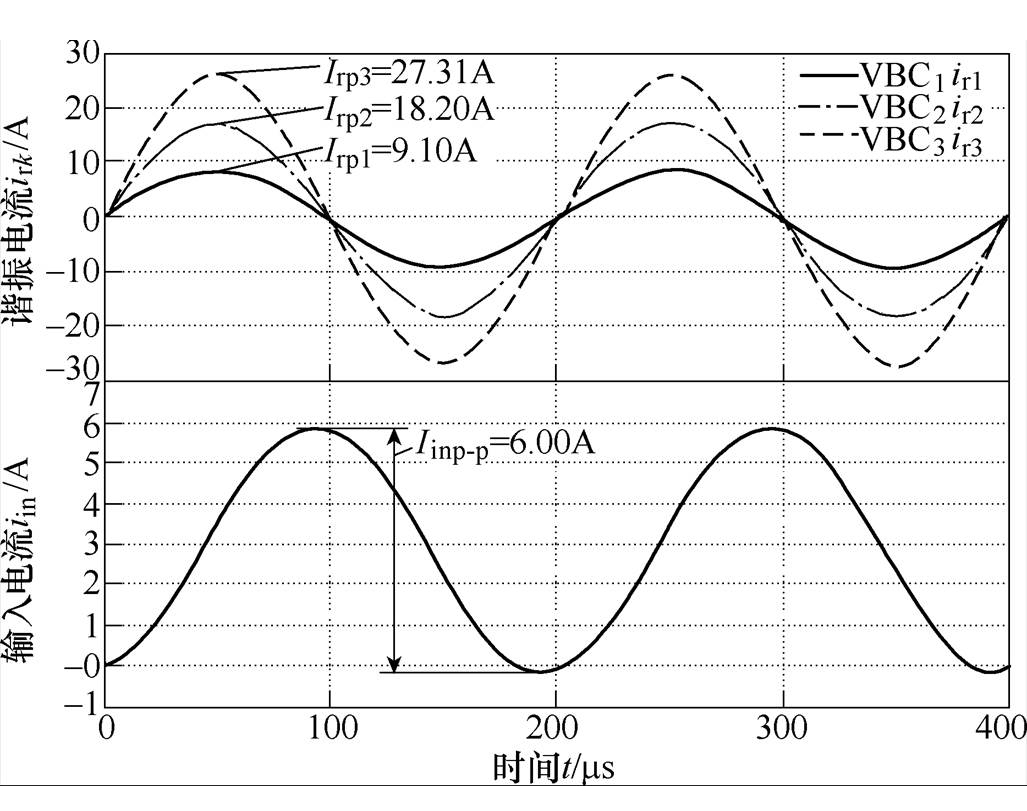
图12 典型控制策略下C-MVBDC仿真波形
Fig.12 Simulation waveforms of C-MVBDC with the typical control strategy
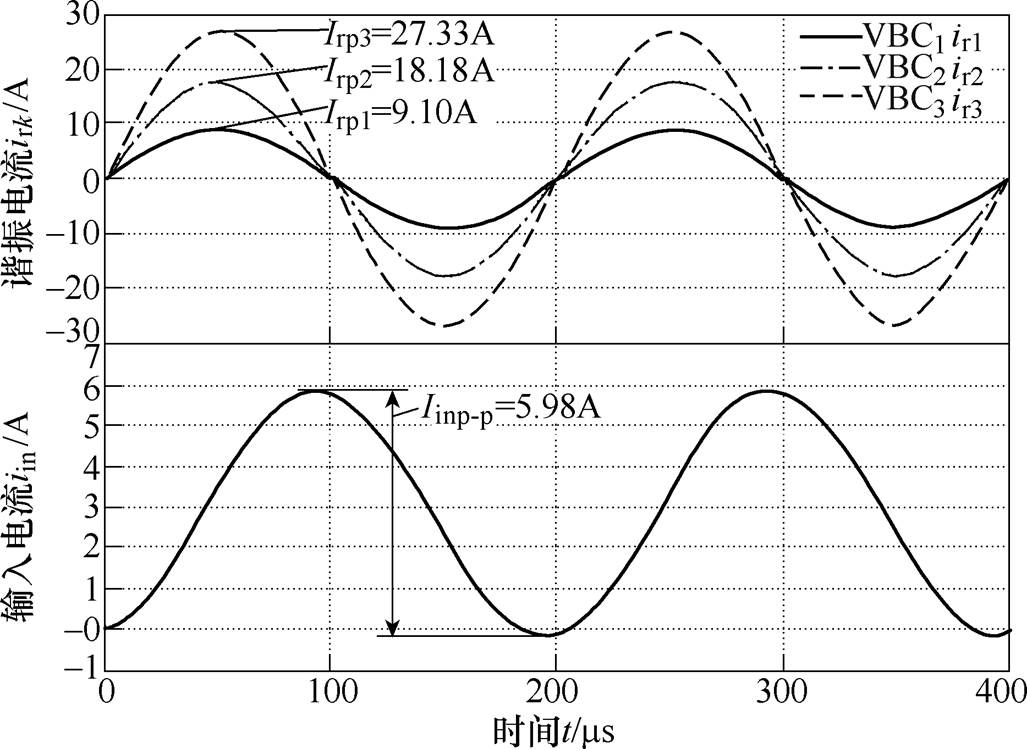
图13 典型控制策略下D-MVBDC仿真波形
Fig.13 Simulation waveforms of D-MVBDC with the typical control strategy
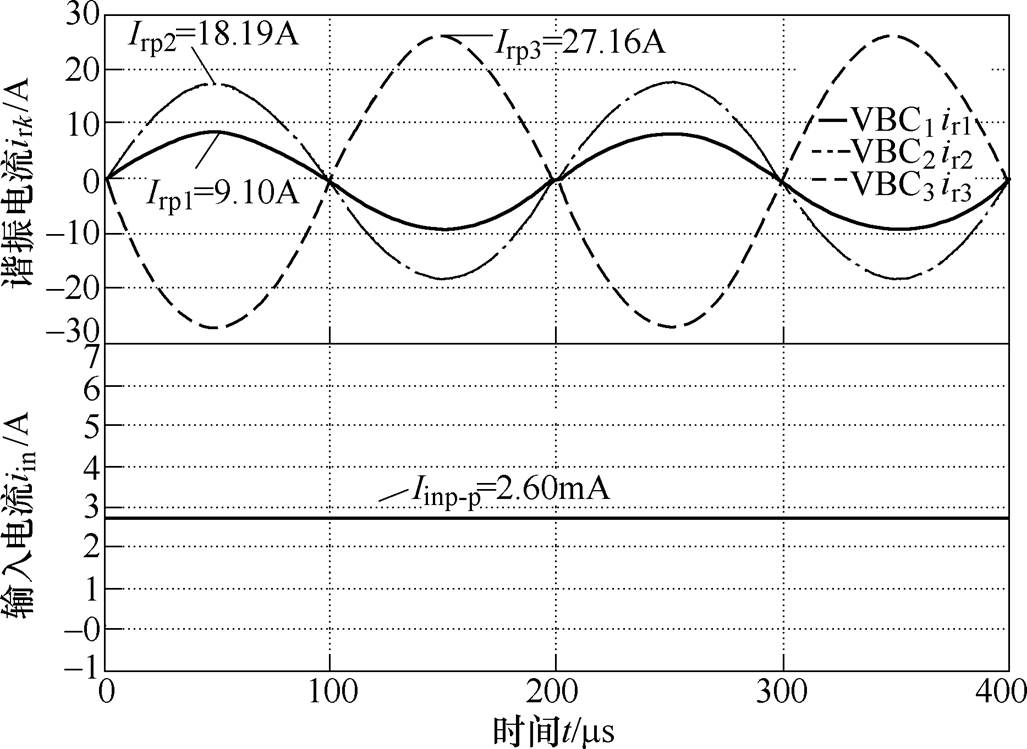
图14 纹波抑制策略下D-MVBDC仿真波形
Fig.14 Simulation waveforms of D-MVBDC with the minimum ripple suppression strategy
当负载或输入电压发生变化时,各VBC单元中的谐振电流幅值发生相应改变,且由于电容电压和电感电流无法突变,接近负载处的谐振电流率先发生变化。在此过程中开关脉冲保持不变,即各谐振电流相位保持不变,输入电流和各谐振电流、输出电流之间仍满足式(2)。因此,纹波抑制策略在负载变化时刻仍有效,无需额外的相位调整策略,但动态过程中纹波抑制效果降低,当变换器进入稳态后即可达到最佳抑制效果。
图15为纹波抑制策略下D-MVBDC负载切换仿真波形。显然当负载由满载切换至空载时,输出电容C4无对外能量输出,电容电压升高,进而使得电容C4与相邻VBC3中谐振电容Cr3电压差值降低,VBC3中谐振电流幅值逐渐降低至零,但由于开关脉冲恒定使得谐振电流相位保持不变。电容C4能量输出降低导致谐振电容Cr3传递能量降低、谐振电流降低,进而也使得与谐振电容Cr3相连的电容C3输出能量降低。以此类推,各VBC中谐振电流幅值均逐渐降低,此时输入电流也随之降低为零。同时,当负载由空载切换至满载时,输出电容C4对外输出能量增大,电容电压降低,与相邻VBC3中谐振电容Cr3电压差值增大,VBC3中谐振电流也随之增大。此时各VBC中谐振电流幅值均逐渐增大、且相位保持不变,输入电流逐步升高至额定值Iin。
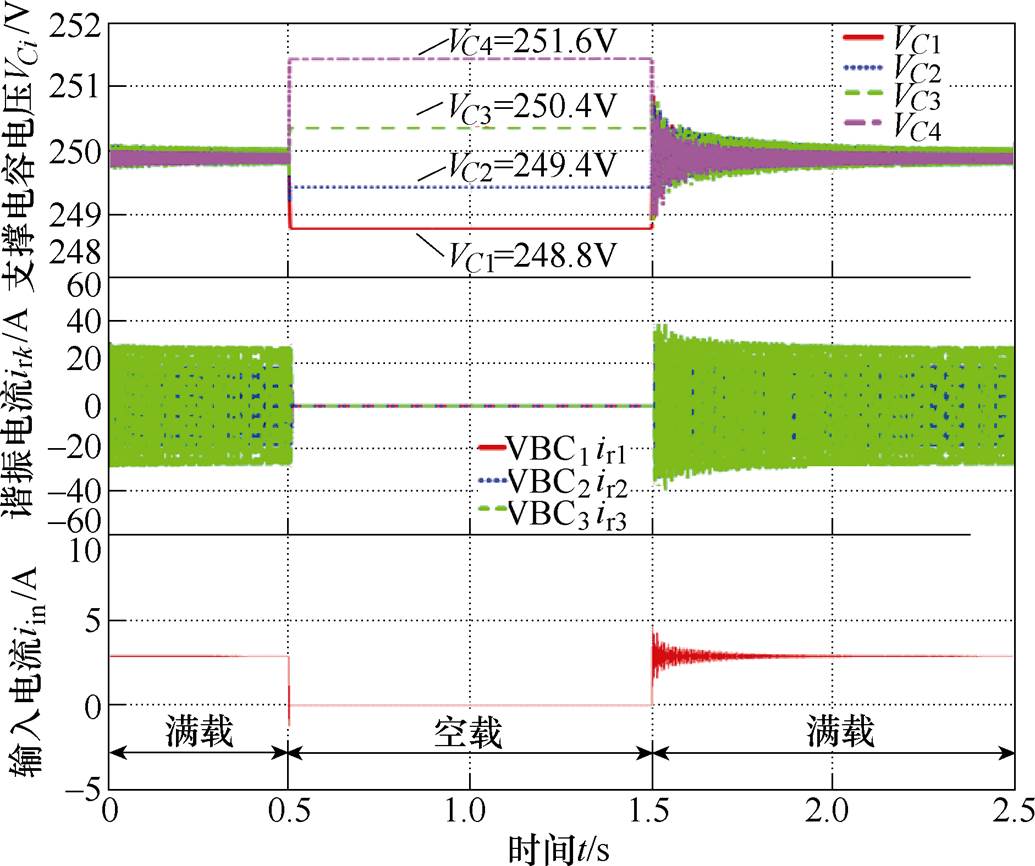
图15 纹波抑制策略下D-MVBDC负载切换仿真波形
Fig.15 Simulation waveforms of D-MVBDC with the minimum ripple suppression strategy in load switching mode
为进一步验证上述理论和仿真分析,根据如图8所示的五电平MVBDC拓扑搭建了如图16所示的MVBDC原理样机,此时实验参数与表1的仿真参数相同。该实验平台通过调整主电路接线,可以分别构建出C-MVBDC和D-MVBDC电路拓扑。

图16 MVBDC原理样机
Fig.16 MVBDC prototype
典型控制策略下C-MVBDC实验波形如图17所示,各谐振电流相位完全相同,输入电流与谐振电流相位偏差为滞后0.27p,C-MVBDC的谐振电流幅值分别为9.40A、21.58A、28.30A,输入电流峰-峰值为6.29A。典型控制策略下D-MVBDC实验波形如图18所示,各谐振电流相位也完全相同,输入电流相位与谐振电流相位偏差为滞后0.29p,D-MVBDC的谐振电流幅值为9.45A、21.20A和27.90A,输入电流峰-峰值为6.35A。

图17 典型控制策略下C-MVBDC实验波形
Fig.17 Experimental waveforms of C-MVBDC with the typical control strategy
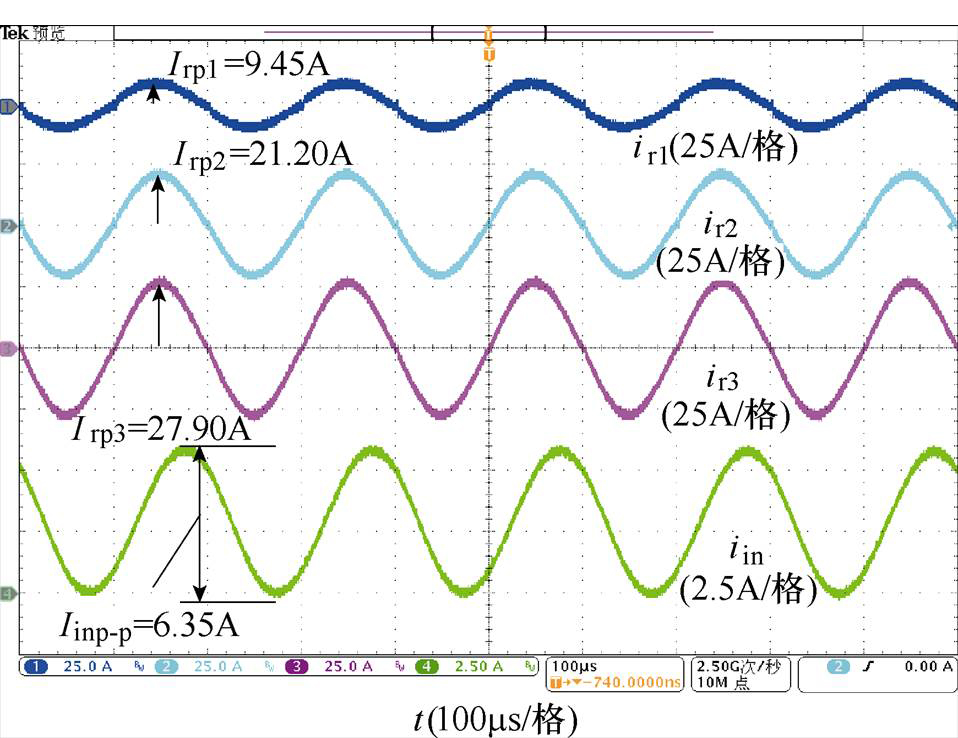
图18 典型控制策略下D-MVBDC实验波形
Fig.18 Experimental waveforms of D-MVBDC with the typical control strategy
纹波抑制策略下D-MVBDC实验波形如图19所示,此时谐振电流ir3相位与谐振电流ir1和ir2的相位相差p/2;D-MVBDC的谐振电流幅值为9.99A、21.20A、29.50A,输入电流峰-峰值为0.46A。显然,相对于典型控制策略下输入电流纹波6.35A,采用纹波抑制策略后纹波降低至7.2%。因此,实验结果表明,纹波抑制策略能大幅降低输入电流纹波,进而验证了理论分析与仿真的正确性和有效性。
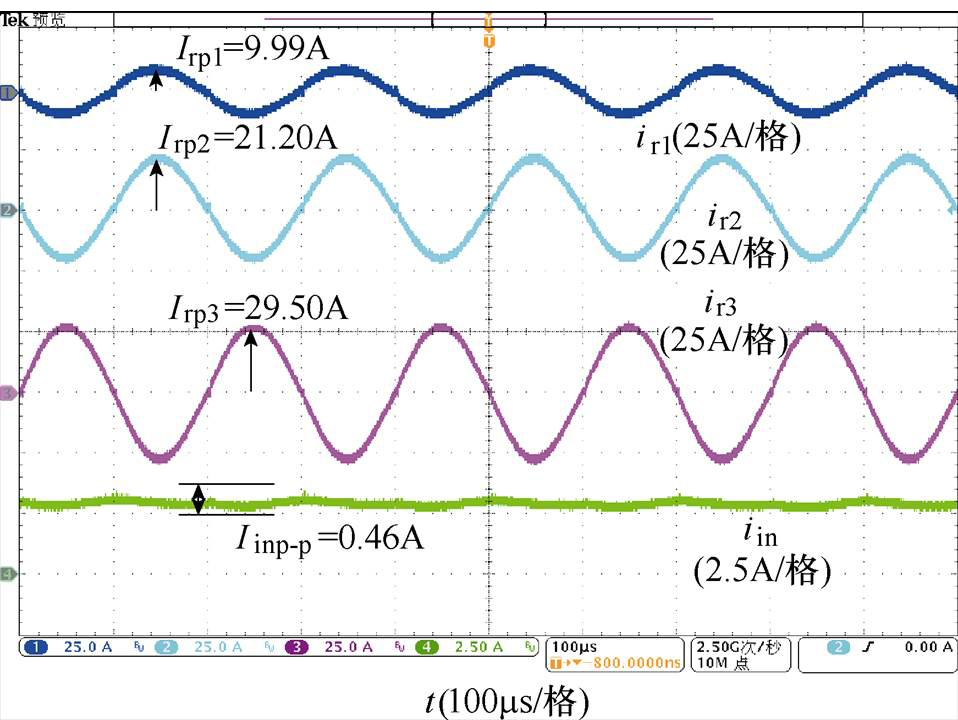
图19 纹波抑制策略下D-MVBDC实验波形
Fig.19 Experimental waveforms of D-MVBDC with the minimum ripple suppression strategy
纹波抑制策略下D-MVBDC负载切换实验波形如图20所示。显然,当负载由满载切换至空载时,各谐振电流逐渐降低,输入电流也随之降低。而当负载由空载切换至满载时,各谐振电流均由零逐渐增大,输入电流也增大。上述动态过程中,输入电流与各谐振电流、输出电流之间始终满足式(2),输入电流纹波随谐振电流之和变化而变化,且当变换器进入稳态后输入电流可达到最小纹波。

图20 纹波抑制策略下D-MVBDC负载切换实验波形
Fig.20 Experimental waveforms of D-MVBDC with the minimum ripple suppression strategy in load switching mode
采用纹波抑制策略前后D-MVBDC效率对比如图21所示。此时典型控制策略下的D-MVBDC最高效率为95.31%,而纹波抑制策略下最高效率为95.54%。故相对于典型控制策略,纹波抑制策略下D-MVBDC效率提高了0.23%。因此,实验结果表明,采用纹波抑制策略可以有效地降低MVBDC损耗,进而提高变换器效率。
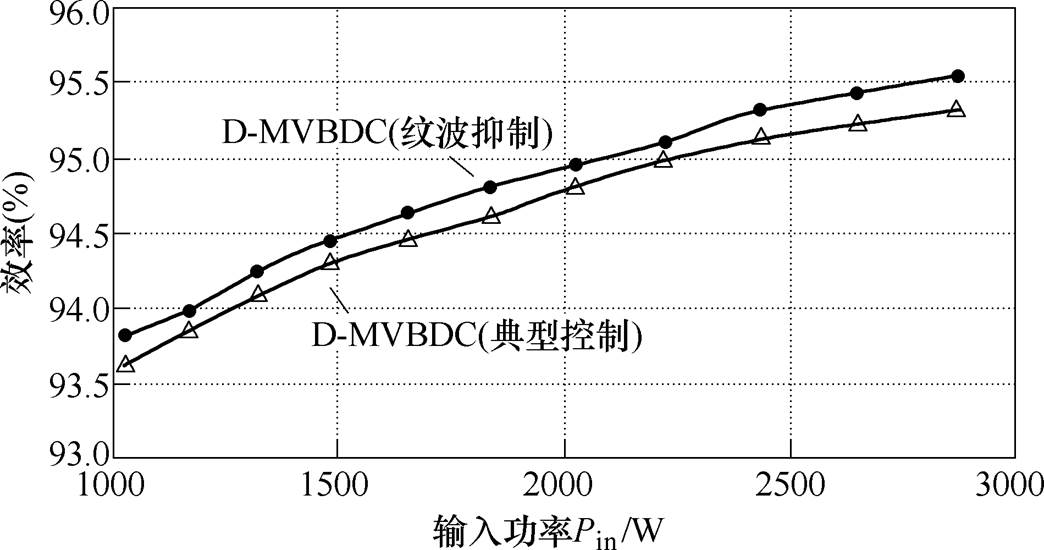
图21 采用纹波抑制策略前后D-MVBDC效率对比
Fig.21 Efficiency comparison of D-MVBDC with/without the minimum ripple suppression strategy
本文通过对比D-MVBDC与C-MVBDC的拓扑与工作原理,研究耦合关系对MVBDC性能的影响。同时,推导输入电流纹波与各谐振电流、输出电流间关系,并提出MVBDC的输入电流纹波抑制策略,并通过仿真和实验对理论分析进行验证。结果表明:
1)C-MVBDC和D-MVBDC输入电流纹波仅与各谐振电流有关。
2)D-MVBDC通过纹波抑制策略来调整VBC单元的电流相位,使得各谐振电流之和等于零,进而可有效降低输入电流纹波;且在负载动态变化时,无需对纹波抑制策略进行额外相位控制,稳态后输入电流仍能实现最小纹波。
3)D-MVBDC通过降低输入电流纹波可以提高变换器效率。
参考文献
[1] Hassan W, Lu Dylan Dah-chuan, Xiao Weidong. Single-switch high step-up DC-DC converter with low and steady switch voltage stress[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(12): 9326- 9338.
[2] 任强, 肖飞, 孙驰, 等. 新型模块化多电平DC-DC变换器拓扑及其工作机理分析[J]. 电力系统自动化, 2017, 41(10): 141-147.
Ren Qiang, Xiao Fei, Sun Chi, et al. Topology and mechanism analysis of novel modular multilevel DC-DC converter[J]. Automation of Electric Power Systems, 2017, 41(10): 141-147.
[3] Kouro S, Rodriguez J, Wu Bin, et al. Powering the future of industry: high-power adjustable speed drive topologies[J]. IEEE Industry Applications Magazine, 2012, 18(4): 26-39.
[4] Busquets-Monge S, Alepuz S, Bordonau J, et al. Voltage balancing control of diode-clamped multi- level converters with passive front-ends[J]. IEEE Transactions on Power Electronics, 2008, 23(4): 1751-1758.
[5] Peng Fangzheng. A generalized multilevel inverter topology with self voltage balancing[J]. IEEE Transa- ctions on Industry Applications, 2001, 37(2): 611- 618.
[6] Shu Zeliang, He Xiaoqiong, Wang Zhiyong, et al. Voltage balancing approaches for diode-clamped multilevel converters using auxiliary capacitor-based circuits[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2111-2124.
[7] Sano K, Fujita H. Voltage-balancing circuit based on a resonant switched-capacitor converter for multilevel inverters[J]. IEEE Transactions on Industry Appli- cations, 2008, 44(6): 1768-1776.
[8] Preindl M. A battery balancing auxiliary power module with predictive control for electrified transportation[J]. IEEE Transactions on Industrial Electronics, 2018, 65(8): 6552-6559.
[9] 王淼, 杨晓峰, 郑琼林, 等. 一种高效率多电平均压型DC-DC变换器[J]. 中国电机工程学报, 2020, 40(11): 3622-3633.
Wang Miao, Yang Xiaofeng, Zheng Trillion Q, et al. A high-efficiency multilevel voltage-balancing DC- DC converter[J]. Proceedings of the CSEE, 2020, 40(11): 3622-3633.
[10] Gitau M, Kala-Konga C L. Compact energy efficient switched-capacitor multilevel DC-DC converters for interfacing DC-buses with common ground[C]//2011 IEEE International Symposium on Industrial Elec- tronics, Gdansk, Poland, 2011: 1845-1850.
[11] Xiong Song, Tan Siew-Chong. Family of cascaded high-voltage-gain bidirectional switched-capacitor DC-DC converters[C]//2015 IEEE Energy Conversion Congress and Exposition, Montreal, Canada, 2015: 6648-6654.
[12] 张捷频, 王淼, 郑琼林, 等. 基于单谐振支路的多电平均压型DC-DC变换器[J]. 电工技术学报, 2017, 32(增刊2): 119-127.
Zhang Jiepin, Wang Miao, Zheng Trillion Q, et al. Single resonant cell based multilevel voltage-sharing DC-DC converter[J]. Transactions of China Electro- technical Society, 2017, 32(S2): 119-127.
[13] Huang Yongshan, Zheng Trillion Q, Yang Xiaofeng, et al. Four-level step-down soft-switching DC-DC converter for electric locomotives[C]//2015 IEEE 2nd International Future Energy Electronics Conference, Taipei, 2015: 1-6.
[14] Pan Ching-Tsai, Cheng Ming-Chieh, Lai Ching-Ming, et al. Current-ripple-free module integrated converter with more precise maximum power tracking control for PV energy harvesting[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 271-278.
[15] Zhang Yuedong, Guo Youguang, Zhu Jianguo, et al. Performance comparison of input current ripple reduction methods in UPS applications with hybrid PEM fuel cell/supercapacitor power sources[J]. Inter- national Journal of Electrical Power & Energy Systems, 2015, 64: 96-103.
[16] Fukushima K, Norigoe I, Shoyama M, et al. Input current-ripple consideration for the pulse-link DC-AC converter for fuel cells by small series LC circuit[C]// IEEE Applied Power Electronics Conference and Exposition, Washington DC, America, 2009: 447-451.
[17] 曾汉超, 许俊阳, 陈道炼. 带低频纹波抑制的单级充放电高频环节DC-AC变换器[J]. 电工技术学报, 2018, 33(8): 1783-1792.
Zeng Hanchao, Xu Junyang, Chen Daolian. Single- stage charging/discharging high-frequency link DC- AC converter with low-frequency harmonic supper- ssion[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1783-1792.
[18] 梁文娟, 谭国东, 陈浩, 等. 一种零纹波耦合电感高增益DC-DC 变换器[J]. 哈尔滨理工大学学报, 2019, 24(4): 14-21.
Liang Wenjuan, Tan Guodong, Chen Hao, et al. A zero-ripple high voltage gain convertor with coupled- inductors[J]. Journal of Harbin University of Science and Technology, 2019, 24(4): 14-21.
[19] Gu Yu, Zhang Donglai, Zhao Zhongyang. Input/ output current ripple cancellation and RHP zero elimination in a Boost converter using an integrated magnetic technique[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 747-756.
[20] 陈章勇, 许建平, 吴建雪. 基于耦合电感倍压单元的零输入电流纹波高增益非隔离变换器[J]. 电工技术学报, 2015, 30(18): 25-34.
Chen Zhangyong, Xu Jianping, Wu Jianxue. Zero- input-current-ripple non-isolated high voltage gain converter based on coupled inductor voltage-doubler cell[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 25-34.
[21] 高伟, 罗全明, 张阳, 等. 一种零输入电流纹波高增益DC-DC变换器[J]. 电工技术学报, 2018, 33(2): 284-292.
Gao Wei, Luo Quanming, Zhang Yang, et al. A high step-up DC-DC converter with zero input current ripple[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 284-292.
[22] Hosoki R, Koizumi H. High-step-up DC-DC con- verter using voltage multiplier cell with ripple free input current[C]//IECON 2013-39th Annual Con- ference of the IEEE Industrial Electronics Society, Vienna, Austria, 2013: 834-839.
[23] Zhang Saijun, Yu Xiaoyan. Control strategy to achieve minimum/zero input current ripple for the interleaved Boost converter in photovoltaic/fuel cell power conditioning system[C]//2012 IEEE Energy Conversion Congress and Exposition, Raleigh, America, 2012: 4301-4306.
[24] Kan Jiarong, Xie Shaojun, Wu Yunya, et al. Single- stage and Boost-voltage grid-connected inverter for fuel-cell generation system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5480-5490.
[25] Jafarian M S A, Karshenas H R. Current ripple reduction in single-input, multiple-output converters using phase-shift and coupled inductors[C]//2016 24th Iranian Conference on Electrical Engineering, Shiraz, Iran, 2016: 816-821.
[26] 刘斌, 贺建军, 粟梅, 等. 两级式单相逆变输入端纹波电流双反馈抑制[J]. 电工技术学报, 2013, 28(8): 187-193, 217.
Liu Bin, He Jianjun, Su Mei, et al. Input ripple current active mitigating for two-stage single-phase inverter based on double channel current feedback[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 187-193, 217.
[27] 汪飞, 雷志方, 梁东, 等. 单相逆变器低频脉动电流抑制机理分析与方法综述[J]. 电力自动化设备, 2017, 37(2): 184-191.
Wang Fei, Lei Zhifang, Liang Dong, et al. Analysis of mechanism and review of methods for low-frequency ripple current suppression of single-phase inverter[J]. Electric Power Automation Equipment, 2017, 37(2): 184-191.
Input Current Ripple Suppression Strategy of Multilevel Voltage-Balancing DC-DC Converter
Abstract Multilevel voltage-balancing DC-DC converter (MVBDC) shows good application prospect in medium and high voltage DC conversion field. However, with the increase of output levels, the resonant current may introduce large input current ripple, which affects the converter efficiency and device life. This paper takes coupling and decoupling MVBDC as examples to analyze the relationship between MVBDC input current ripple and resonance currents at various levels, and the input current ripple suppression strategy is proposed. By controlling the phases of the resonant currents, zero ripple of the MVBDC input current can be achieved, which improves the converter efficiency. Finally, the correctness of the above theory is verified by experimental results.
keywords:Multilevel voltage-balancing DC-DC converter (MVBDC), medium and high voltage DC conversion, current ripple, efficiency, resonance
DOI: 10.19595/j.cnki.1000-6753.tces.L90233
中图分类号:TM46
倪梦涵 男,1995年生,硕士研究生,研究方向为多电平均压型直流变换器、城轨交通牵引供电系统、地铁杂散电流治理等。E-mail: 18121481@bjtu.edu.cn
杨晓峰 男,1980年生,副教授,博士生导师,研究方向为模块化多电平换流器及应用、电力电子技术在轨道交通中的应用等。E-mail: xfyang@bjtu.edu.cn(通信作者)
收稿日期 2020-07-04
改稿日期 2020-10-29
国家自然科学基金(51737001)和中央高校基本科研业务费(2019JBM058)资助项目。
(编辑 陈 诚)