Lo，Pupper为上钳位电容输入功率；Plower为下钳位电容输入功率。图1中，钳位电容电流iC1、iC2所表示的方向为正方向。摘要 针对全桥三电平（FBTL）DC-DC变换器两个占空比协调优化控制、传输功率太小以及钳位电容电压平衡等问题，该文提出一种基于查表法的FBTL DC-DC变换器优化控制策略。首先，详细分析FBTL DC-DC变换器输入、输出特性，并设计一种钳位电容电压自平衡调制策略。其次，在所设计的钳位电容电压自平衡调制策略基础上，提出一种抗钳位电容电压扰动控制策略，并根据钳位电容输入功率差与电压最大调节能力的关系计算出占空比必须满足的条件。然后，建立一种以变压器输入电压谐波为目标函数，功率传输能力、钳位电容电压调节能力等为约束条件的优化模型，进而得到FBTL DC-DC变换器的优化控制策略。优化占空比离线计算，然后存储在数字控制系统里，控制时直接采用查表法得到最优占空比。所提出的方法无需变换器精确模型，控制过程简单、高效，控制效果优于传统控制策略。最后，在Matlab/Simulink平台和一台实验样机上验证了所设计的优化控制策略的正确性和有效性。
关键词：直流输电 全桥三电平DC-DC变换器 钳位电容电压控制 优化控制
随着陆地风力发电的饱和，海上风电特别是直流海上风电和柔性直流输电技术受到了国内外专家学者越来越多的关注[1-3]。基于中频变压器（Medium Frequency Transformer, MFT）的高压、高电压增益、大容量（High voltage, High voltage gain, Large capacity, HHL）全桥DC-DC变换器是直流海上风电场和高压直流电网的关键装备，是DC-DC变换器研究的热门[1-9]。
文献[10]研究了基于LCC串并联谐振的全桥两电平DC-DC变换器归一化分析与设计方法，这是一种应用非常广泛的拓扑结构，但是无法应用在高压、大容量场合。文献[11]提出了一种具备软开关能力的半桥三电平DC-DC变换器，不同于全桥两电平DC-DC变换器，这种变换器的隔离变压器输入端的一个端子直接连接钳位中点，因此两个变压器输入端的电位变化不对称，且一个端子电位变化是相同电压等级的全桥DC-DC变换器中相应电位变化的两倍，对应的绝缘要求也要提高两倍。文献[12]提出了一种不对称全桥多电平DC-DC变换器，这种变换器一个桥臂为三电平，另一个桥臂为两电平，三电平桥臂开关管的电压应力为输入电压的一半且能在宽负载范围内实现零电压开关，两电平桥臂开关管的电压应力为输入电压。该变换器的输入电流脉动小、输出整流电压交流分量小，因此，可减小输入、输出滤波器尺寸。但是由于电路不对称，这种变换器中的开关管电压应力、开关损耗不对称且输入端承受电压应力的能力不足。文献[13]提出了基于二极管钳位型三电平的单相逆变器优化调制方法，该逆变器能够实现高压、大容量电能变换，但是无法连接MFT。
文献[14]提出了一种全桥三电平（Full-Bridge Three Level, FBTL）DC-DC变换器并对其调制策略进行了研究，这种变换器结构简单，但是调制策略复杂，变压器输入电压少了一个零电平电压且IGBT的电压应力大，同时，这种变换器的传输功率能力被削弱。文献[15]提出了一种变压器输入端接有源滤波的FBTL DC-DC变换器，这种变换器能够显著减小变压器的谐波电压、电流畸变率，但是有源滤波电路增加了系统的复杂性且变换器的电能传输能力被显著削弱，同时，文中的调制策略表述不清楚。文献[16-17]提出了一种具有软开关能力的FBTL DC-DC变换器并设计了一种不同于传统二极管钳位型三电平变换器的调制策略，当采用这种调制策略时，变换器能够实现IGBT的软开关，并且钳位电容电压能够自平衡，但是，此时变压器输入电压的波形不对称且无法达到五电平电压要求。文献[18-19]提出了一种三相三电平相移DC-DC变换器，这种变换器在低开关频率情形下具有很好的动态特性和容错能力，但其结构和调制策略复杂。文献[20]对FBTL DC-DC变换器测试电路进行了深入研究，成功解决了开关管动作双脉冲测试方法不能模拟开关器件实际开关动作时序的问题，这种方法增加了变换器的可靠性，但是没有对其两个占空比的协调控制展开研究。变压器输入电压谐波越大，磁滞损耗和涡流损耗越大。因此优化变压器输入电压谐波就是优化变压器损耗[21]。文献[22]对双向FBTL DC-DC变换器占空比的协调优化控制进行了深入的研究，提出了基于变压器基波、3次谐波之和代替总谐波的无需变换器精确模型的优化控制方法，这种方法简单、有效，但是在变压器输入电流不是标准正弦波的FBTL DC-DC变换器中，基波、3次谐波很难求取，因此这种方法很难实现。同时，单向FBTL DC-DC变换器调制度少且运行方式与双向FBTL DC-DC变换器不一样，因此这种方法不 适合。
综上所述，本文设计了一种简单、高效的FBTL DC-DC变换器优化控制策略，分析了变换器的特征变量波形，设计了钳位电容电压的自平衡控制策略和抗扰控制策略，基于所设计的钳位电容电压抗扰控制策略得出两个占空比的一个约束条件。在FBTL DC-DC变换器输入电压环、输出电压环控制系统基础上，设计了一种只需测量变换器的传输功率以及输入、输出电压的优化控制策略。该优化控制策略存在如下优势：无需复杂的谐波电流计算；在钳位电容输入功率不同时，能够保证钳位电容电压的平衡；在保证FBTL DC-DC变换器功率传输能力前提下，能够实现占空比的协调优化控制；无需变换器精确模型，实现方法简单、有效；综合性能优于传统控制策略。最后，在基于Matlab/Simulink的仿真模型和样机实验平台上对本文所设计的优化控制系统进行了仿真和样机实验验证。仿真和样机实验结果显示，所设计的优化控制系统简单、稳定且有效。
图1a为输入并联输出串联（Input Parallel Output Series, IPOS）DC-DC变换器拓扑结构，其中的子模块拓扑结构如图1b所示，是本文所研究的FBTL DC-DC变换器拓扑结构。图1b中，Lf为变压器的漏电感与变压器串联电感之和，Lo为输出电感，且Lf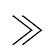Lo，Pupper为上钳位电容输入功率；Plower为下钳位电容输入功率。图1中，钳位电容电流iC1、iC2所表示的方向为正方向。
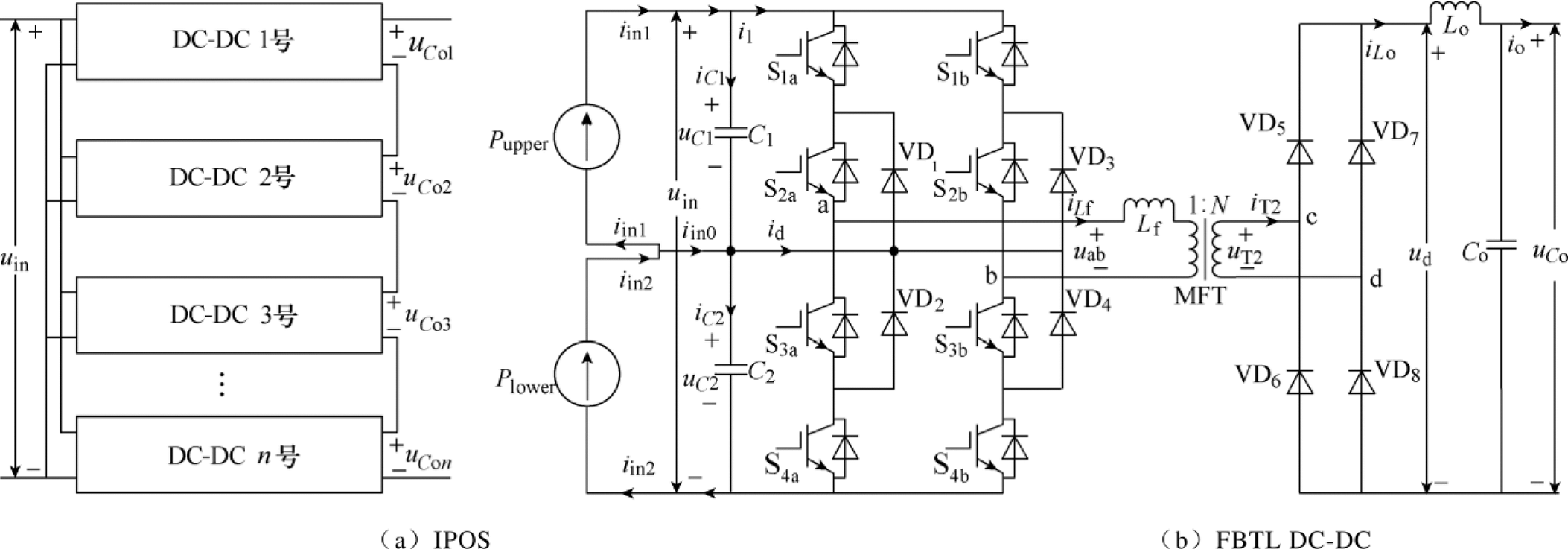
图1 IPOS FBTL DC-DC电路拓扑
Fig.1 Circuit of IPOS FBTL DC-DC converter
图2是采用钳位电容电压自平衡调制策略时，FBTL DC-DC变换器特征变量波形。图2中，S1a、S4a、S1b、S4b分别为S1a、S4a、S1b、S4b的触发脉冲，uin为变换器输入电压，uab为FBTL逆变器输出电压，iLf为变压器输入电流，iLo为变换器输出电流；d1为高电平电压占空比的一半，d2为中间电压占空比，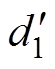
为高电平电压中电流反向阶段的占空比。
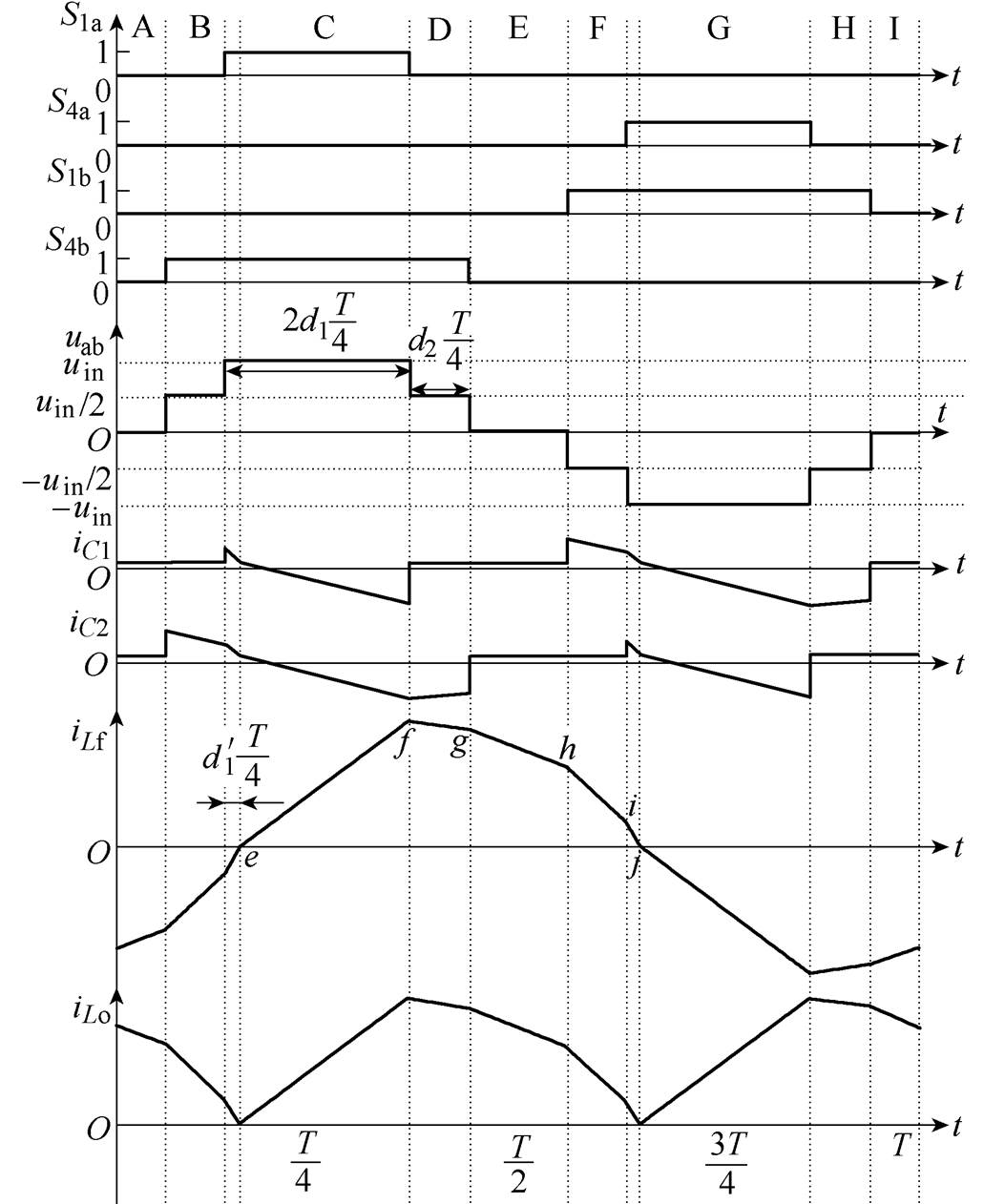
图2 FBTL DC-DC变换器特征变量波形
Fig.2 Characteristics variables waveforms of the FBTLDC-DC converter
图2中，FBTL DC-DC变换器一个周期被分成9个阶段（A～I），9个阶段相继周期性地工作得到对称五电平电压uab。为了得到对称五电平uab，开关S1a～S3a，S2a～S4a，S1b～S3b和S2b～S4b必须成对互补导通，则图2中4个IGBT的触发脉冲可以得到8个IGBT的触发脉冲。在uCo高的场合，uin＞uCo＞0.5uin，输出电感电流iLo在变压器输入电压uab的高电平结束，中电平开始时刻取得最大值或最小值。
为了简化计算，假设在一个周期内，FBTL DC-DC的两个钳位电容电压相等，输入电压uin恒定。图2中，电流iLf波形上线段ef、fg、gh、hi、ij斜率的绝对值分别为m1、m2、m3、m4和m5，且m1～m5的计算式分别为
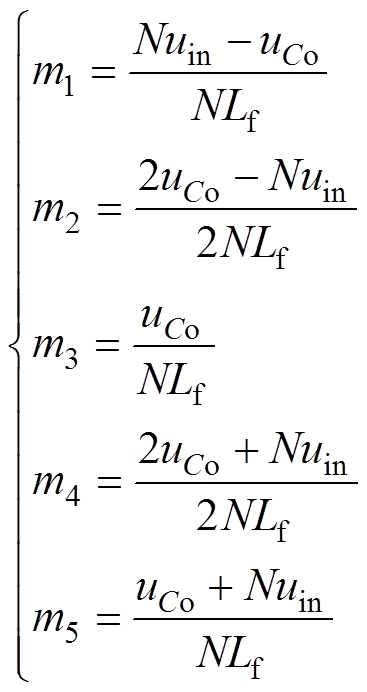（1）图2中，假设uC1=uC2=uin/2，忽略FBTL DC-DC 变换器钳位电容输入功率对两个钳位电容与i1的影响。阶段B，iC1＜iC2；阶段D，iC1
iC2；阶段F，iC1＞iC2；阶段H，iC1
iC2；阶段B和F，钳位电容C1、C2传输到负载的能量相等；阶段D和H，C1、C2传输到负载的能量相等。又因为，阶段A、C、E、G和I，C1、C2传输到负载的能量相等，则在一个周期内，C1、C2传输到负载的能量相等。因此，uC1、uC2在一个周期内保持不变及钳位电容电压能够实现自平衡。
为了最大限度地利用FBTL DC-DC变换器的功率传输能力，本文研究的变换器工作模式与文献[15]中变换器的工作模式不同，本文只研究该变换器在如图2所示的连续导通模式（Continuous Conduction Mode, CCM）下的特性，此时有
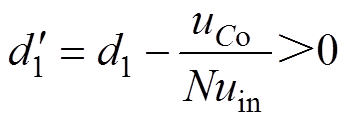（2）当两个钳位电容电压受到较大的扰动时，自平衡调制策略无法快速平衡钳位电容电压，因此本文提出了一种抗钳位电容电压扰动控制策略，该控制策略在模式Ⅰ、Ⅱ之间切换运行，保证钳位电容电压的平衡[15]。图3为该抗扰控制策略下，IGBT的触发脉冲、uab、钳位电容电流波形示意图。
假设uC1、uC2在一个周期保持恒定，忽略FBTL DC-DC变换器输入功率对两个钳位电容与i1的影响。如图3a所示，在模式Ⅰ，阶段B，iC1＞iC2；阶段D，iC1iC2；阶段F，iC1＜iC2；阶段H，iC1iC2。阶段B、D、F和H，相比于C1，C2将提供更多的能量到负载。又因为，阶段A、C、E、G和I，C1、C2传输到负载的能量相等，则在一个周期内，相比于C1，C2将提供更多的能量到负载。因此，uC1＞uC2。
假设uC1、uC2在一个周期保持恒定，如图3b所示，在模式Ⅱ，阶段B，iC1＞iC2；阶段D，iC1iC2；阶段F，iC1＞iC2；阶段H，iC1iC2。阶段B、D、F和H，相比于C2，C1将提供更多的能量到负载。又因为，阶段A、C、E、G和I，C1、C2传输到负载的能量相等，则在一个周期内，相比于C2，C1将提供更多的能量到负载。因此，uC1＜uC2。
图3 抗扰控制策略下FBTL DC-DC特征变量
Fig.3 Characteristics variables of the FBTLDC-DC converter under the disturbance rejection control strategy
本文所提出的抗扰控制策略为：当uC1＜uC2时，在下一个周期，采用模式Ⅰ的调制策略；反之，在下一个周期则采用模式Ⅱ的调制策略。由图3可知，在一个周期内，模式Ⅰ、Ⅱ调制策略产生的钳位电容电压差相等。
由图3可知，在模式Ⅰ，阶段B、F和D、H，中间电平电压由uC2提供；在模式Ⅱ，阶段B、F和D、H，中间电平电压由uC1提供。uC1与uC2之间的电压差由iC1与iC2之间的电流差决定，且iC1与iC2之间电流差的大小决定uC1与uC2的电压调节能力大小。阶段A、C、E、G和I，iC1、iC2之间的电流差相等；阶段B、F和D、H，iC1、iC2之间的平均电流差的计算公式为
（3）式中，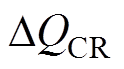
为一个周期内C1、C2的电荷量之差。
联立式（2）、式（3）并化简可得
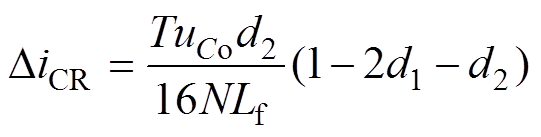（4）假设在一个周期内，两个钳位电容电压相等，阶段B、F和D、H，电容C1、C2之间的平均输入功率差必满足
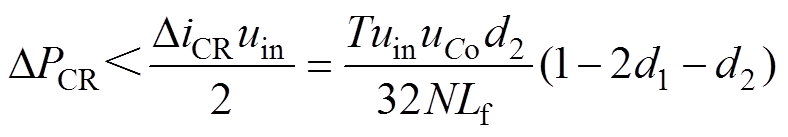（5）
式（5）为两个占空比的一个约束条件。
由图1可知，为了实现功率的稳定传输和子模块功率的平衡，IPOS DC-DC变换器的输入电压必须稳定在一个定值，子模块输出电压必须相等[23]。各子模块输出电压控制无需解耦，直接采用子模块输出电压控制能保证各子模块输出电压相等[23]。综上所述，本文设计了一种优化控制策略，其控制策略框图如图4所示。
图4 FBTL DC-DC控制策略框图
Fig.4 Control block diagram of the FBTL DC-DC converter
图4中
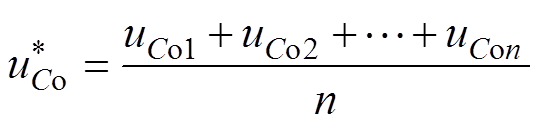（6）式中，uCon为第n个子模块输出电压；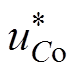
为第n个子模块输出电压控制系统的给定，该电压控制环能使子模块输出电压平衡。
图4中，FBTL DC-DC输入电压环与输出电压环之和相加得到d，d与变换器的输出功率Po、变换器输出端接入直流电网点电压UN在优化控制率作用下得到优化占空比d1、d2，然后根据测得的钳位电容电压和本文所提出的调制策略即可得出8个全控型开关的触发脉冲。
忽略FBTL DC-DC变换器损耗，在一个周期内，uLf的平均值等于0，因此，电压uCo、ud的平均值与占空比d1、d2的关系为
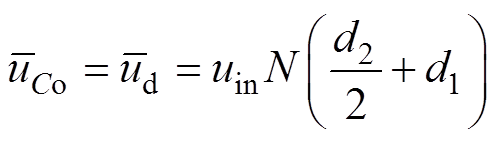（7）在一个周期内，iCo的平均值等于0，电流iLo、io的平均值之间的关系为
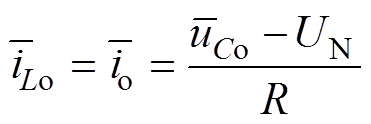（8）
式中，R为变换器输出端到直流电网接入点电压之间的传输线电阻。
FBTL DC-DC变换器输出功率为
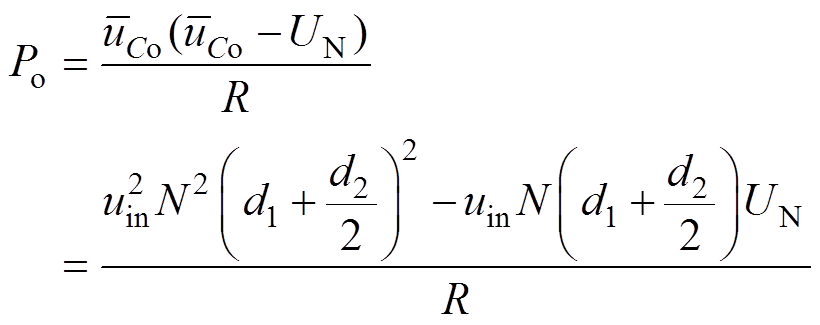（9）化简式（9），得到
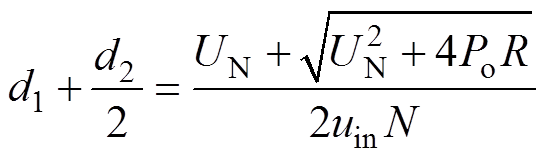（10）
uab的有效值为
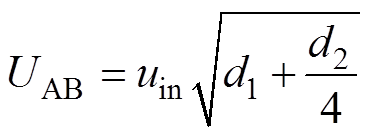（11）uab的基波电压有效值为
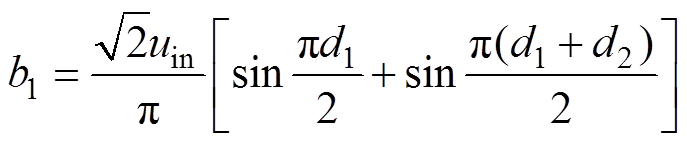（12）
联立式（11）、式（12），得到uab的总谐波畸变率uTHD为
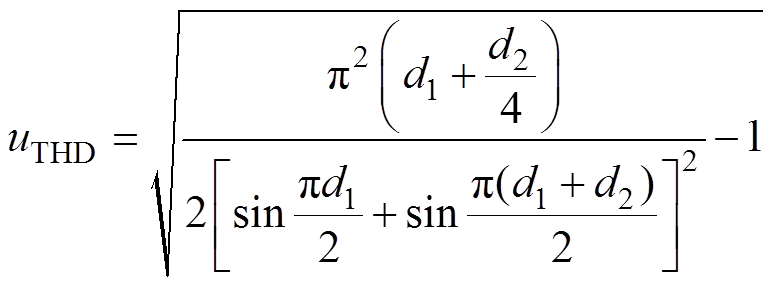（13）联立式（2）、式（5）、式（10）、式（13），得到以uTHD最小为目标函数的占空比优化模型为
（14）
联立式（1）、式（14）可得占空比优化模型。式（14）的在线计算过程复杂且耗时，因此，本文采用粒子群优化算法离线计算得到优化占空比[24-25]，然后将计算所得优化占空比存储在数字控制器的存储器中，在线运行时根据测得的变换器输出功率、直流电网接入点电压，采用查表法直接得到最优占空比。
本文采用式（15）定义变换器的效率h[26]，h 越大，变换器的效率越高。
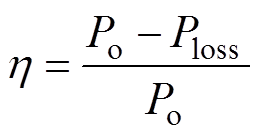（15）式中，Po为变压器的输入功率；Ploss为变换器的损耗，主要包括全控型开关器件损耗、电感与MFT损耗、二极管损耗等。
由文献[27]可知，变压器谐波损耗不容忽视，当谐波含量为10%时，变压器的损耗比不存在谐波时增大10%。由文献[28-30]可知，变压器的损耗主要由铜耗和谐波损耗组成，谐波损耗可以占到60%～80%，且输入电压的频率越高、谐波损耗越大。变压器输入电压谐波越大，那么输入电流谐波越大，变压器谐波损耗越大且变压器谐波的二次方与谐波损耗大致成正比[29-31]。考虑到开关管可以实现软开通和软关断，则开关管的开、关损耗相对较低，本文予以忽略。由文献[31]可知，软开关全桥DC-DC变换器中变压器损耗约占系统总损耗的70%，且全控型开关管的导通损耗只占了很小一部分，因此FBTL DC-DC变换器中变压器损耗约占系统总损耗的50%～70%。综上所述，变压器谐波损耗可以占到FBTL DC-DC变换器损耗的50%～60%。
为了证明本文所设计的FBTL DC-DC变换器优化控制策略的正确性和有效性，本文搭建了基于Matlab/Simulink的仿真模型，并进行了仿真实验。基于Matlab/Simulink的FBTL DC-DC变换器参数见表1。
当FBTL DC-DC变换器的输入功率扰动发生时，图5为模块化FBTL DC-DC变换器输入、输出电压波形，显然，电压uin、uCo1、uCo2在输入功率扰动情形下具有很好的抗扰动能力。
当钳位电容的输入功率差扰动发生即Pupper＞Plower一个特定的值时，图6是电压uin、uCo1、uCo2的波形，显然电压uin、uCo1、uCo2在钳位电容的输入功率差扰动情形下具有很好的抗扰动能力。
表1 基于Matlab/Simulink的FBTL DC-DC变换器参数
Tab.1 The parameters of the FBTL DC-DC converter in Matlab/Simulink
参 数数 值 输入电压/V3 000 钳位电容C1, C2/mF60 000 变压器电压比11 电感Lf/mH0.6 电容Co/mF132 直流网电压uN/V5 000 负载电阻/W0.5 开关频率/kHz1 子模块数2
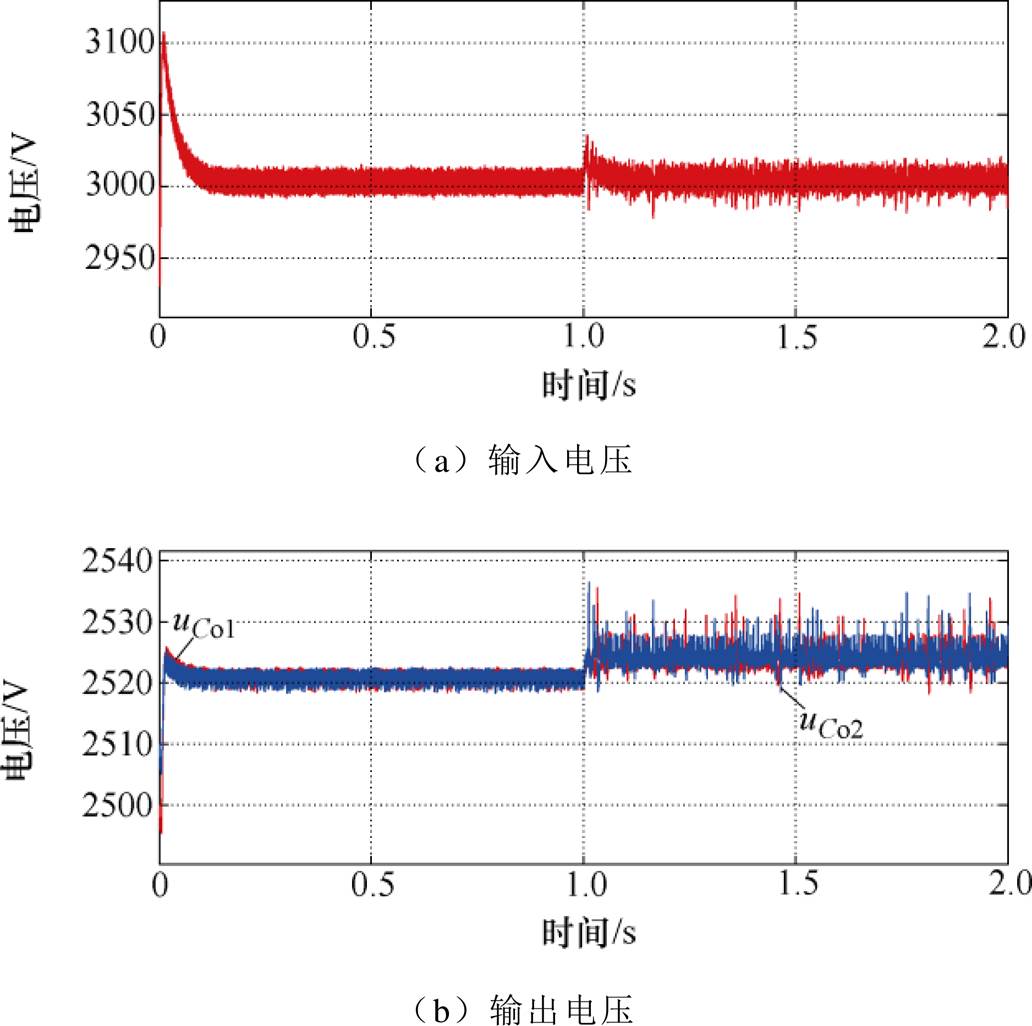
图5 输入功率变化时模块化FBTL DC-DC变换器输入、输出电压波形
Fig.5 Input and output voltages waveforms of the modular FBTL DC-DC converters with different input power
钳位电容电压波形如图7所示。在钳位电容的输入功率差扰动发生时，图7a是采用自平衡调制策略时，钳位电容电压uC1、uC2的波形；图7b是采用钳位电容电压抗扰控制策略时uC1、uC2的波形。显然采用自平衡调制策略时，钳位电容电压无法平衡；采用钳位电容电压抗扰控制策略时，钳位电容电压能够快速地保持平衡，表明抗钳位电容电压扰动控制策略具有很好的抗扰性。
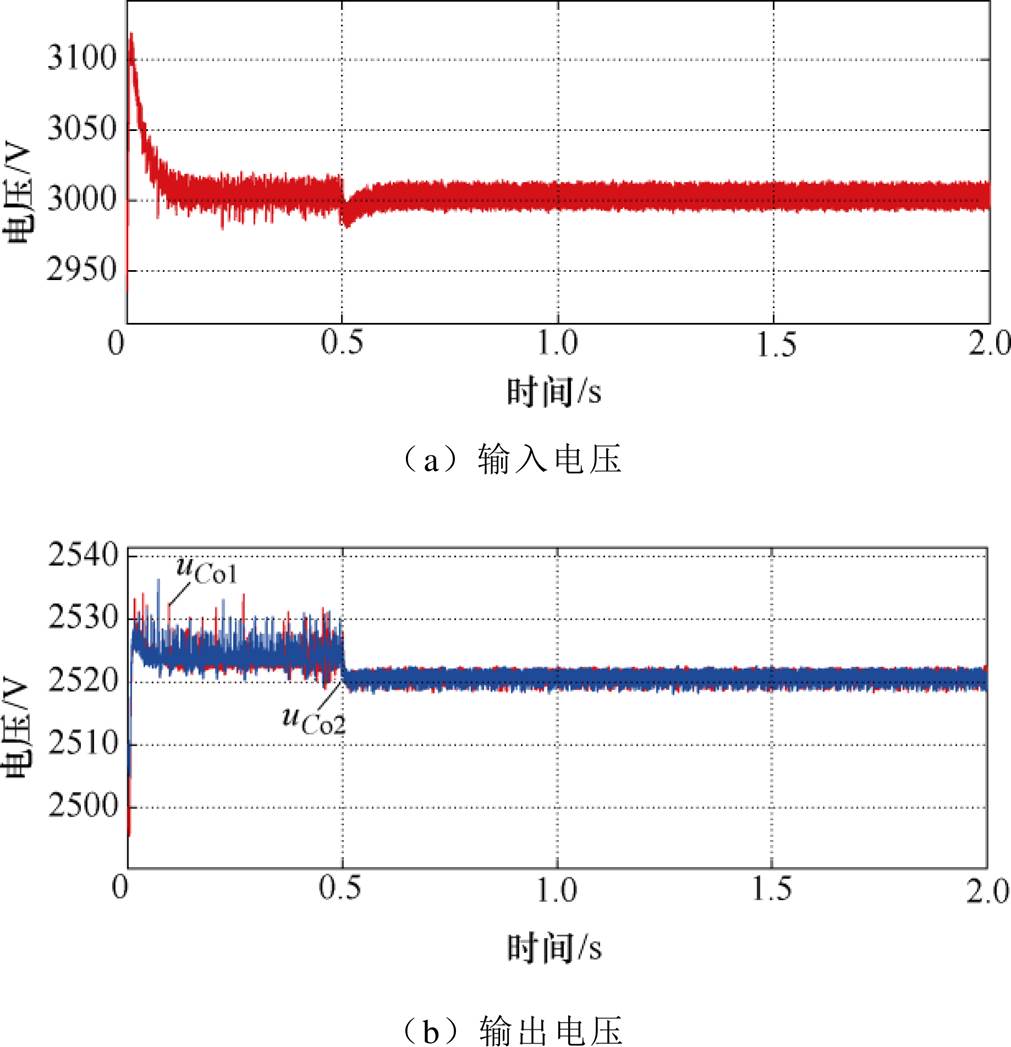
图6 钳位电容输入功率不一致时模块化FBTL DC-DC变换器输入、输出电压
Fig.6 Input and output voltages of the modular FBTL DC-DC converters with different clamped capacitors input power
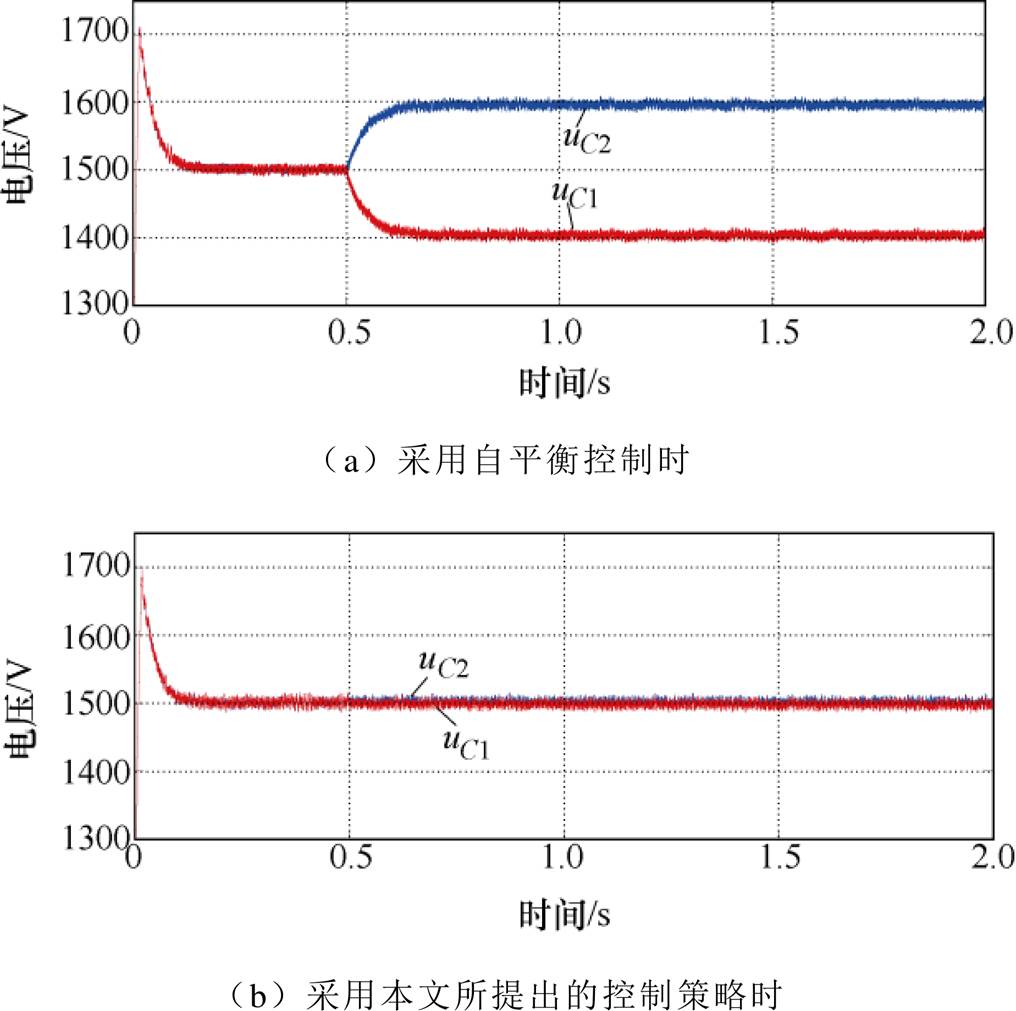
图7 钳位电容电压波形
Fig.7 Voltages waveforms of the divided capacitors
在仿真平台上，根据本文所设计的优化控制方法，得到关键变量之间的特征关系曲线如图8所示。图8a为优化占空比与变换器输出功率之间的关系，图8b为图8a在d1、d2坐标轴上的投影，表示优化的占空比d1、d2之间的关系。由图8a、图8b可知，优化的占空比d1、d2近似呈比例关系且输出功率对最优占空比有一定影响。图8c为采用优化控制策略时，变压器输入电压总谐波畸变率与输出功率的关系，由图可知，输出功率越大，变压器输入电压总谐波畸变率越大、损耗越大。图8d为逆变器输出电压谐波与变压器谐波损耗之间的关系，由图可知，变换器传输功率越大、谐波越大、损耗越大。图8e为变换器效率与输出功率之间的关系，其中变压器谐波损耗在变压器损耗中的比重取为70%，变压器损耗在FBTL DC-DC变换器损耗中的比重为60%。由图8e可知，变换器传输功率越大、谐波损耗越大。显然，当FBTL DC-DC变换器采用文献[14]所提控制策略时，变换器的功率传输能力明显小于采用本文所提出的控制策略时变换器的功率传输能力。因此采用本文所提出的优化控制策略在减小变换器损耗的前提下能显著提升变换器的功率传输能力。
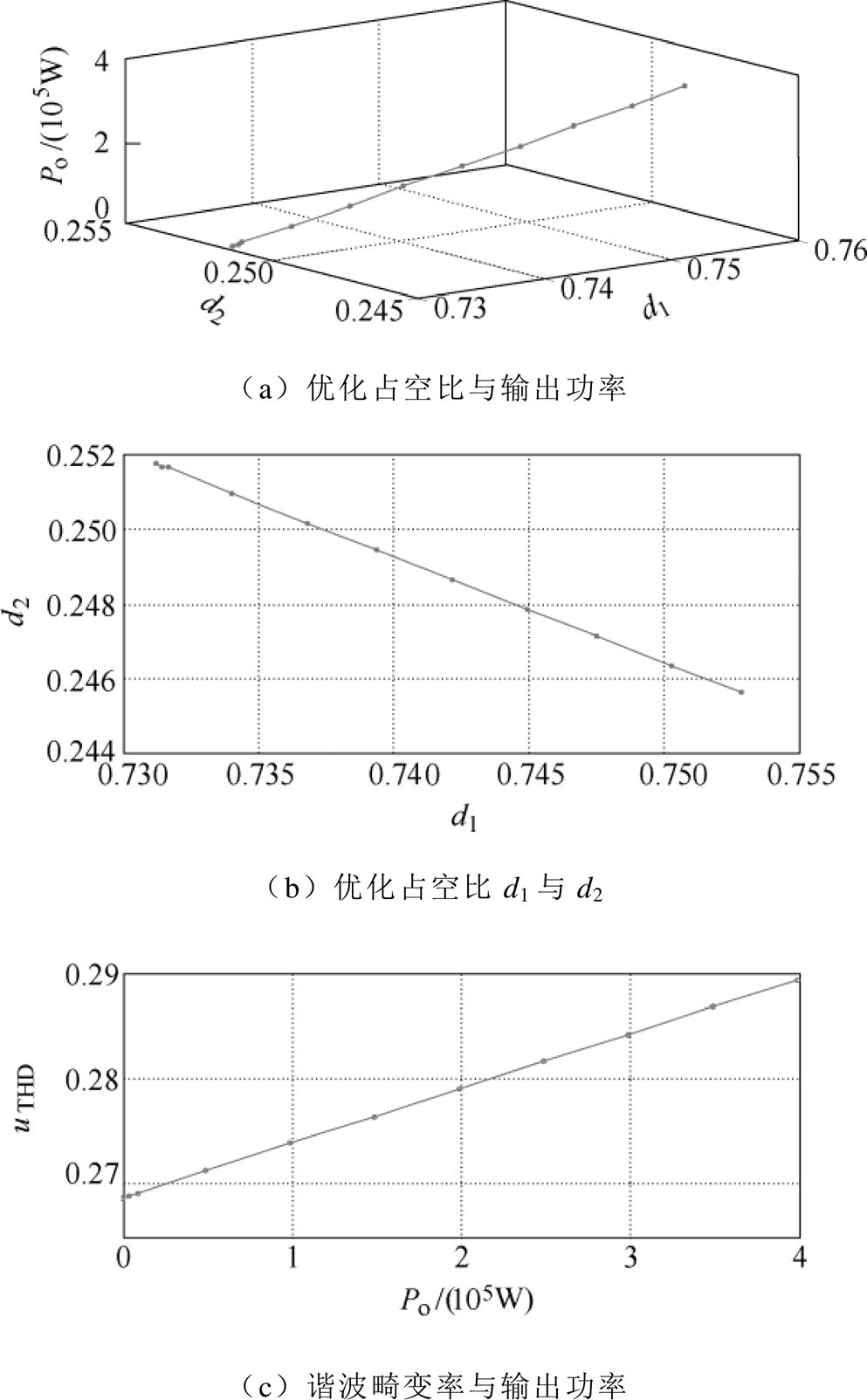
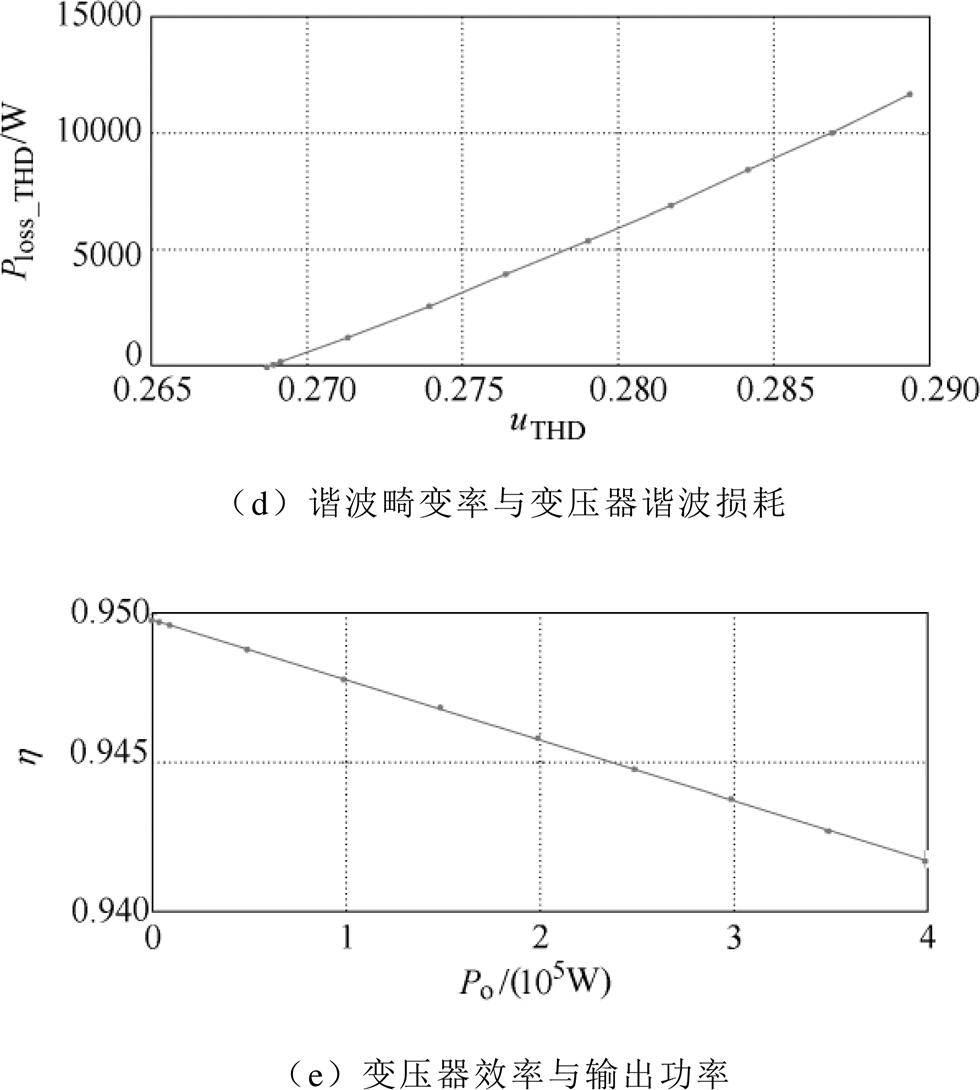
图8 特征关系曲线
Fig.8 Curves of the characteristic relationship
本文在一台小功率FBTL DC-DC实验装置上验证了本文所提出的优化控制理论。实验样机参数见表2。
表2 FBTL DC-DC变换器样机参数
Tab.2 The parameters of the FBTL DC-DC converter experimental prototype
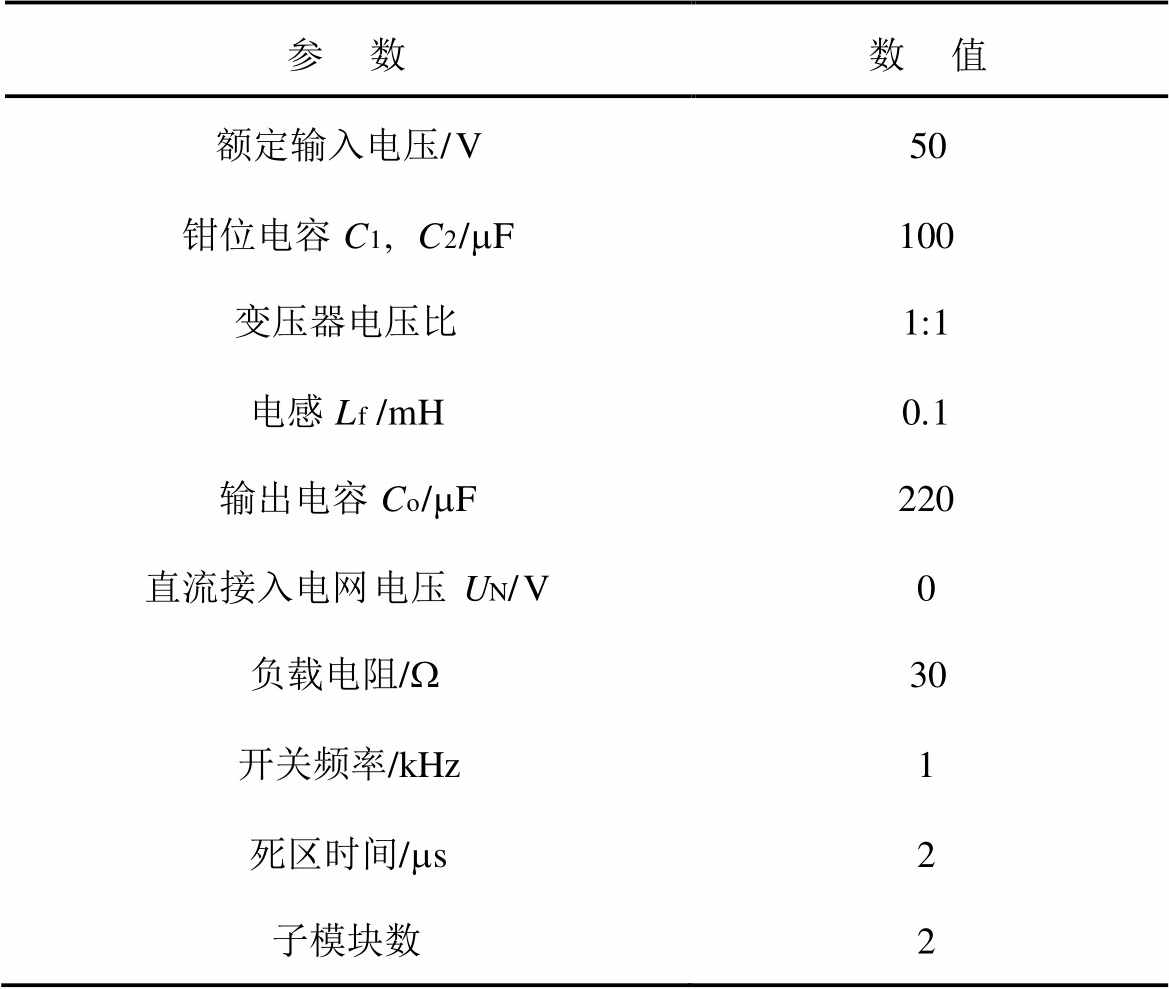
参 数数 值 额定输入电压/V50 钳位电容C1, C2/mF100 变压器电压比1:1 电感Lf/mH0.1 输出电容Co/mF220 直流接入电网电压UN/V0 负载电阻/W30 开关频率/kHz1 死区时间/ms2 子模块数2
图9a是采用钳位电容电压自平衡调制策略时，电压uab、uC1、uC2的波形，其中，占空比d1=0.82、d2=0.13，稳态输入电压为40V，稳态钳位电容电压uC1、uC2为20V，uab为对称五电平，显然相比于三电平、四电平电路，五电平电路显著地减小了变压器输入端电压的变化率。同时，采用钳位电容电压自平衡调制策略时，两个钳位电容电压近似相等，表明钳位电容电压具有很好的自均压特性。图9b、图9c是采用钳位电容电压抗扰控制策略时，uab、uC1、uC2的波形，其中模式Ⅰ与模式Ⅱ之间的转换时间是10个周期。图9b、图9c对应的占空比d1分别为0.70、0.65，d2分别为0.06、0.10。显然图9c中的钳位电容电压差大于图9b中的钳位电容电压差。表明d1越小、d2越大，钳位电容电压抗扰控制策略的调节能力越大，与本文的理论分析一致。
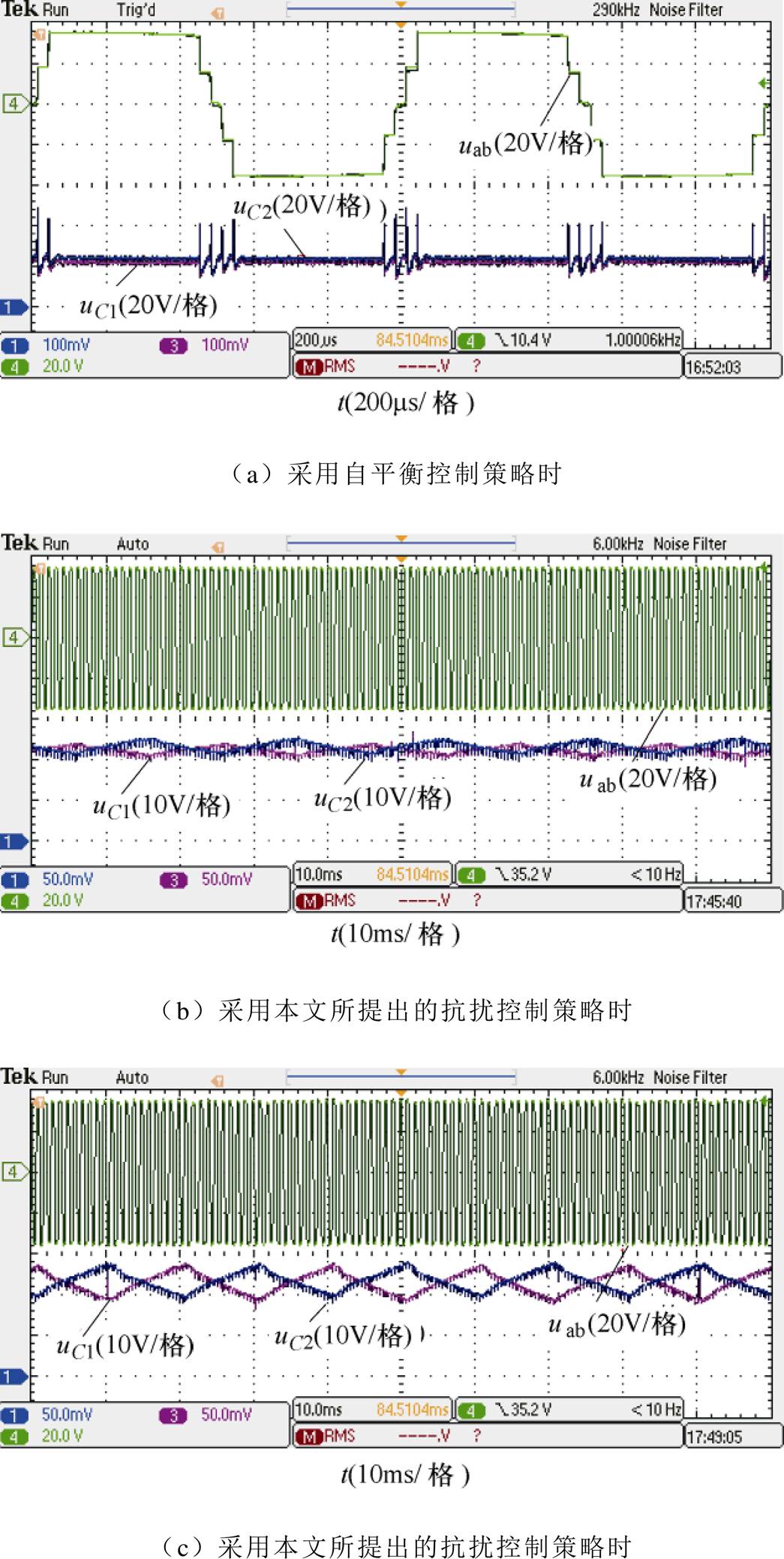
图9 uab与钳位电容电压波形
Fig.9 Voltages waveforms of divided capacitors and uab
图10是采用输入电压控制、子模块输出电压控制策略时，IPOS连接的两个FBTL DC-DC变换器输入电压、输出电压波形，图中子模块稳态输入电压为-30V，实际值为30V，稳态输出电压为20V。
由图10可知，采用本文所提出的控制策略时，变换器输入电压uin、FBTL逆变器输出电压uab具有很好的稳定性，子模块输出电压uCo1、uCo2能够保持平衡，实验结果与理论分析一致。
在实验平台上，根据本文所设计的优化控制方法，得到优化的占空比与传输功率、两个优化占空比、变压器谐波畸变率、变压器谐波损耗、效率之间的关系如图11所示。与仿真模型类似，由图11a、图11b可知，优化的占空比d1、d2近似呈比例关系，优化占空比受输出功率的影响较大。由图11c可知，输出功率越大，基于优化控制策略的变压器输入电压总谐波畸变率越大、损耗越大且该谐波畸变率的变化范围较广。
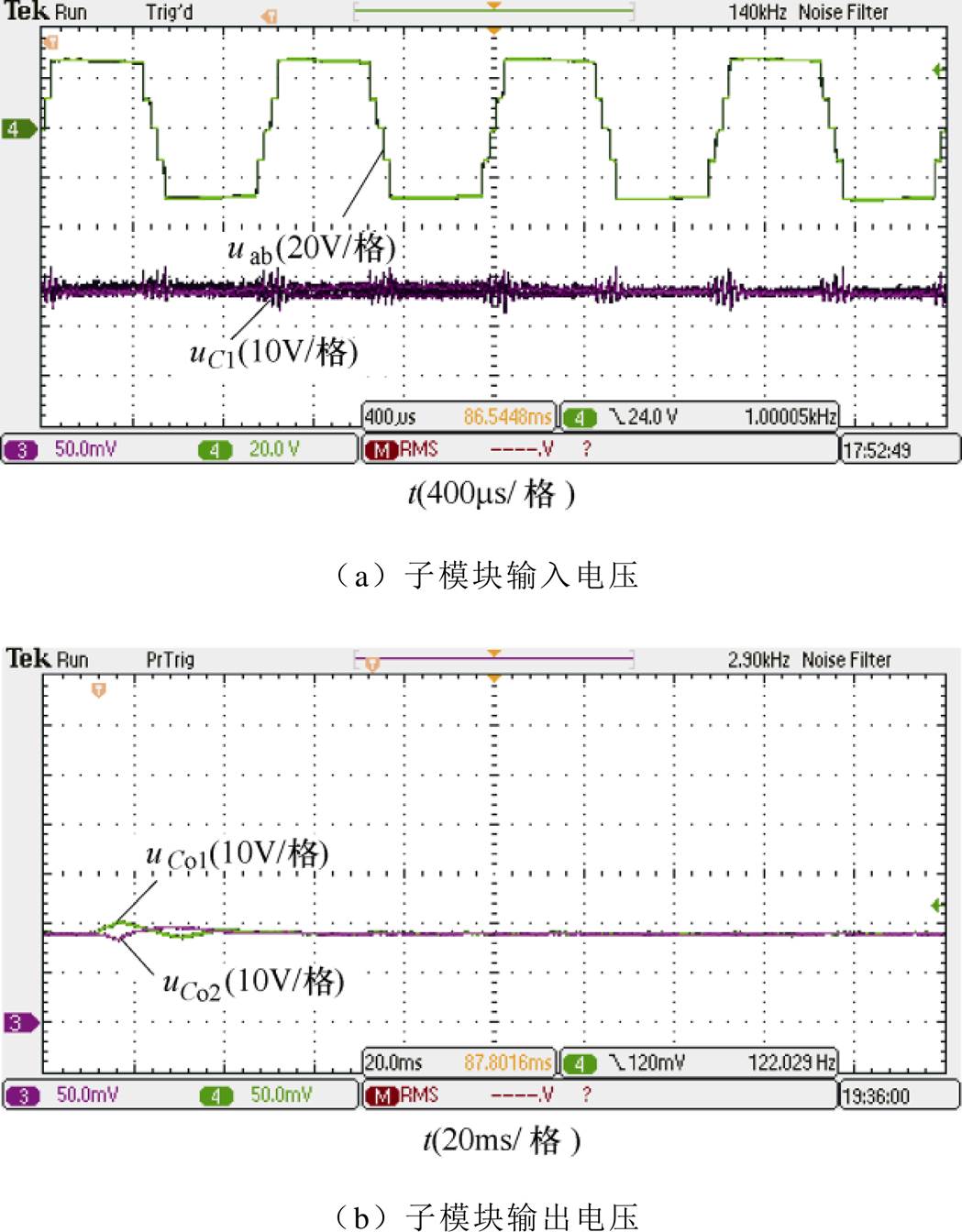
图10 uab与子模块输入、输出电压波形
Fig.10 Input voltage, output voltage and uab waveforms of DC-DC converters
图11d为电压谐波与变压器铁耗之间的关系，由图可知，谐波越大，变压器谐波损耗越大。图11e为系统效率，其中，变压器谐波损耗在变压器损耗中的比重取为70%，变压器损耗在FBTL DC-DC变换器损耗中的比重为60%。
图12是采用本文所提出的优化控制方法得到的变压器输入电压THD，此时d1=0.65、d2=0.25，THD=21.28%，传输功率为135W，与曲线得到的结果一致。
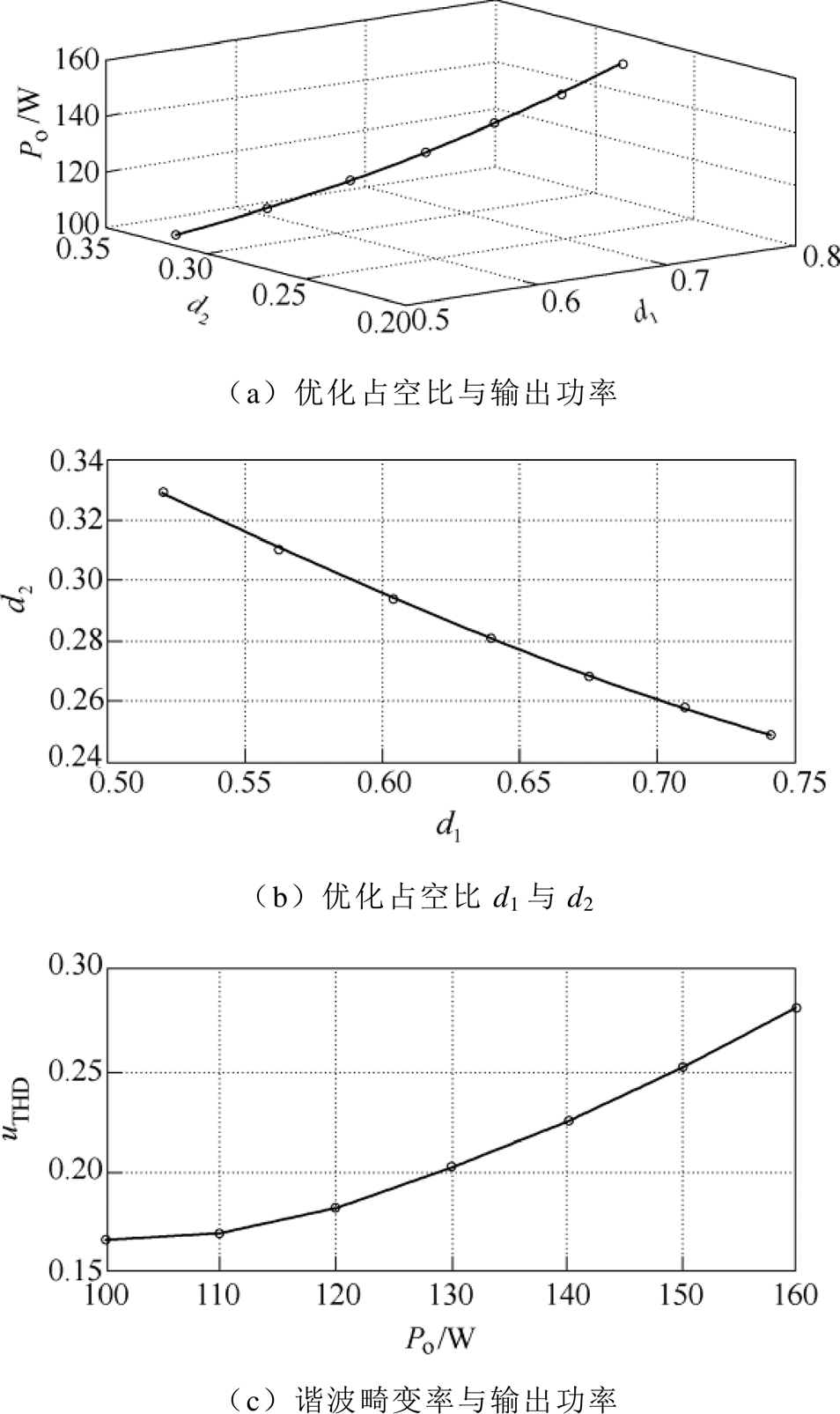
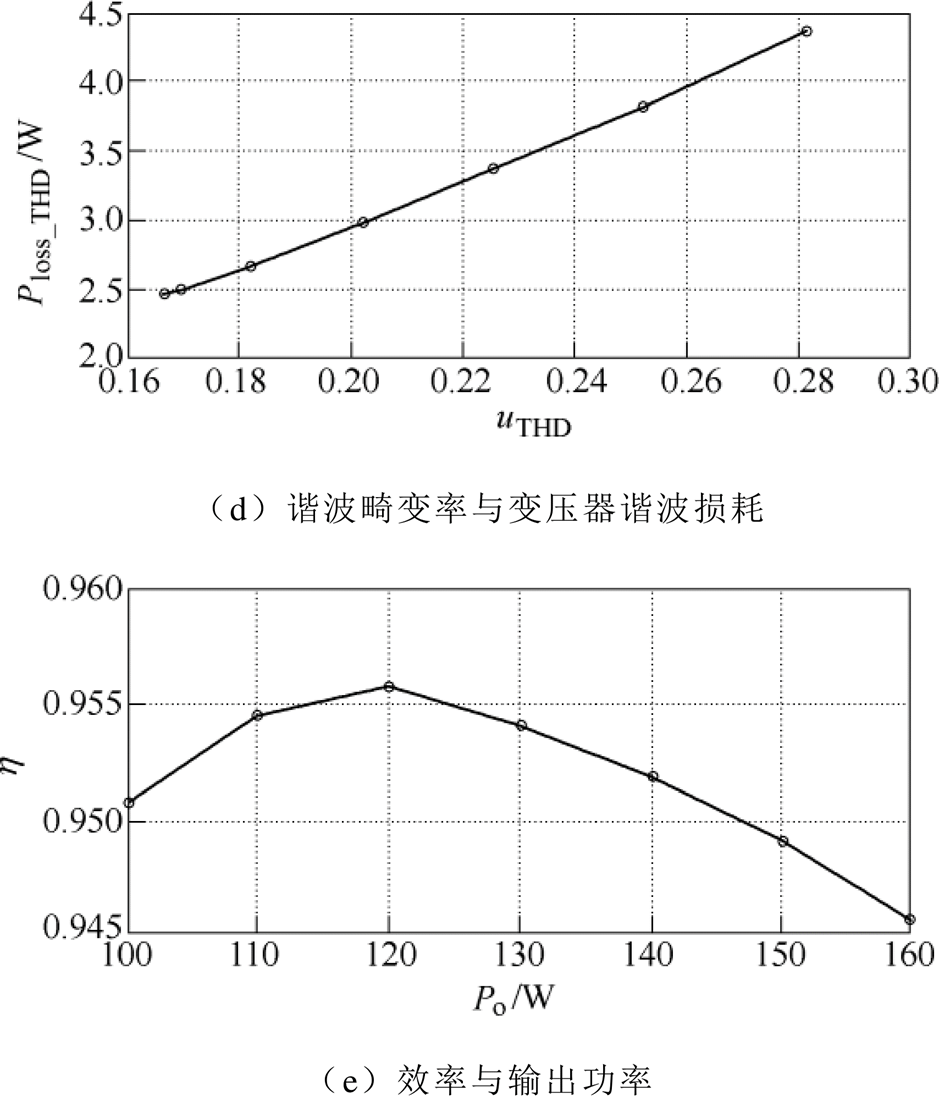
图11 实验样机的特征曲线
Fig.11 Curve of the characteristic relationship in prototype
对比图8和图11可知，图11中优化占空比、uTHD变化范围大。由式（10）可知，在实验电路中，UN=0，优化占空比受传输功率变化的影响很大，导致优化占空比的变化范围广。图8e和图11e表明，实验效率比仿真效率高，这是因为本文采用的高压大功率中频变压器的效率是工业用高压大功率中频变压器效率的一个近似平均值，这个值低于本文采用的小功率中频变压器的效率[26-34]。
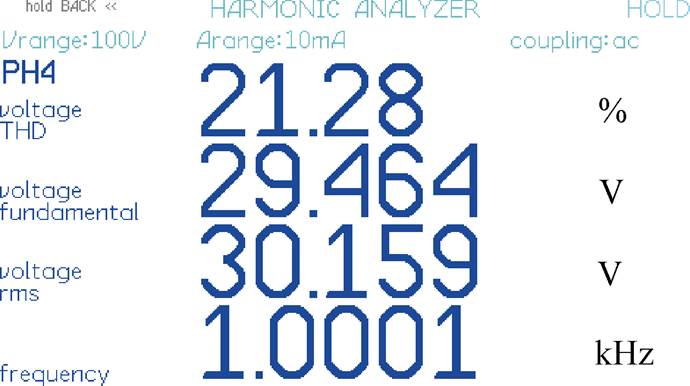
图12 变压器输入电压总谐波畸变率
Fig.12 THD for the input voltages of the MFT
本文针对FBTL DC-DC变换器中两个占空比配置不同、变换器传输功率不同导致变压器输入电压谐波含量不同、损耗不同的问题，展开了深入研究。在详细分析变换器钳位电容电压、输入电压、输出电压、变压器输入电压谐波、变换器传输功率特性的基础上提出了一种占空比优化控制策略。该控制策略以变压器输入电压谐波最小为目标函数，传输功率、钳位电容电压调节能力为约束条件。本文从理论和实验分析得出如下结论：
1）通过本文所设计的自平衡调制策略，钳位电容电压能够实现自均衡。本文所设计的抗扰调制策略能够增加钳位电容电压抗扰动能力，且这种能力与两个占空比的取值大小有关。
2）相比于传统优化控制方法，所提出的优化控制保证了变压器输入电压为对称五电平，从而减小了变压器电压的变化率；采用本文所提出的优化控制策略时，相同拓扑结构的FBTL DC-DC变换器在保证低损耗的前提下能显著提升功率传输能力。所提出的优化控制策略无需变换器精确模型，控制算法简单、有效。
3）本文初步研究发现，当FBTL DC-DC变换器运行在本文所示CCM和对称五电平模式时，只需通过增加辅助电容，采用本文所提出的调制策略，该变换器的8个全控型器件可以实现软开关，下一步将对其软开关特性进行深入的研究。
参考文献
[1] 张亚超, 黄张浩, 郑峰, 等. 基于风电出力模糊集的电-气耦合系统分布鲁棒优化调度[J]. 电力系统自动化, 2020, 44(4): 44-53.
Zhang Yachao, Huang Zhanghao, Zheng Feng, et al. Distributionally robust optimal dispatch for power- gas coupled system based on fuzzy set of wind power output[J]. Automation of Electric Power Systems, 2020, 44(4): 44-53.
[2] Dong Huanfeng, Xu Zheng, Song Pengcheng, et al. Optimized power redistribution of offshore wind farms integrated VSC-MTDC transmissions after onshore converter outage[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 8948-8958.
[3] 王新颖, 汤广福, 贺之渊, 等. 远海风电场直流汇集用 DC-DC 变换器拓扑研究[J]. 中国电机工程学报, 2017, 37(3): 837-847.
Wang Xinying, Tang Guangfu, He Zhiyuan, et al. Topology research of DC-DC converters for offshore wind farm DC collection systems[J]. Proceedings of the CSEE, 2017, 37(3): 837-847.
[4] 魏晓光, 王新颖, 高冲, 等. 用于直流电网的高压大容量 DC-DC 变换器拓扑研究[J]. 中国电机工程学报, 2014, 34(20): 218-224.
Wei Xiaoguang, Wang Xinying, Gao Chong, et al. Topologies research of high voltage and high-power DC-DC converters used in DC grids[J]. Proceedings of the CSEE, 2014, 34(20): 218-224.
[5] Juan David Páez, David Frey, Jose Maneiro, et al. Overview of DC-DC converters dedicated to HVDC grids[J]. IEEE Transactions on Power Delivery, 2019, 34(1): 119-128.
[6] 鲁静, 同向前, 张嘉翔, 等. L-LLC谐振型双向DC-DC变换器的复合最优轨迹控制策略研究[J]. 电工技术学报, 2020, 35(增刊1): 60-69.
Lu Jing, Tong Xiangqian, Zhang Jiaxiang, et al. Research on the hybrid optimal control principle based on the L-LLC resonant bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 60-69.
[7] 杨惠, 晁凯悦, 孙向东, 等. 基于矢量作用时间的双向DC-DC变换器预测电流控制方法[J]. 电工技术学报, 2020, 35(增刊1): 70-80.
Yang Hui, Yao Kaiyue, Sun Xiangdong, et al. Predictive current control method for bidirectional DC-DC converter based on optimal operating time of vector[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 70-80.
[8] 何圣仲, 代东雷. 开关变换器数字双功率控制技术[J]. 电机与控制学报, 2020, 24(3): 38-44.
He Shengzhong, Dai Donglei. Digital bi-power control technique for switching converters[J]. Electric Machines and Control, 2020, 24(3): 38-44.
[9] 王强, 单瑞香, 王天施, 等. 单相全桥谐振直流环节软开关逆变器[J]. 电机与控制学报, 2017, 21(3): 38-47.
Wang Qiang, Shan Ruixiang, Wang Tianshi, et al. Single-phase full-bridge resonant DC-link soft-switching inverter[J]. Electric Machines and Control, 2017, 21(3): 38-47.
[10] 张洪寅, 童朝南, 王泽庭, 等. 基于临界模态的DCM-LCC谐振变换器的归一化分析与设计[J]. 电工技术学报, 2019, 34(1): 103-115.
Zhang Hongyin, Tong Chaonan, Wang Zeting, et al. Normalized analysis and design of DCM-LCC resonant converter based on critical current mode[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 103-115.
[11] 阮新波, 严仰光. 软开关PWM三电平直流变换器[J]. 电工技术学报, 2000, 15(6): 24-34.
Ruan Xinbo, Yan Yangguang. Soft-switching PWM three-level converters[J]. Transactions of China Electrotechnical Society, 2000, 15(6): 24-34.
[12] 陈志英, 阮新波. 零电压开关PWM复合式全桥三电平变换器[J]. 中国电机工程学报, 2004, 24(5): 24-29.
Chen Zhiying, Ruan Xinbo. Zero-voltage-switching PWM hybrid full-bridge three-level converter[J]. Proceedings of the CSEE, 2004, 24(5): 24-29.
[13] 宋文胜, 冯晓云. 一种单相空间矢量脉宽调制优化方法[J]. 电工技术学报, 2011, 26(4): 107-113.
Song Wensheng, Feng Xiaoyun. A single phase SVPWM optimized method[J]. Transactions of China Electrotechnical Society, 2011, 26(4): 107-113.
[14] 刘计龙, 肖飞, 陈伟, 等. 一种多电平全桥直流变换器新型控制策略研究[J]. 中国电机工程学报, 2014, 34(33): 5854-5860.
Liu Jilong, Xiao Fei, Chen Wei, et al. Research on a novel control scheme for three-level full-bridge converter[J]. Proceedings of the CSEE, 2014, 34(33): 5854-5860.
[15] Deng Fujin, Chen Zhe. Control of improved full- bridge three-level DC-DC converter for wind turbines in a DC grid[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 314-324.
[16] Liu Peng, Duan Shanxu. Analysis of the neutral-point voltage self-balance mechanism in the three-level full-bridge DC-DC converter by introduction of flying capacitors[J]. IEEE Transactions on Power Electro- nics, 2019, 34(12): 11736-11747.
[17] 刘朋, 陈昌松, 段善旭, 等. 带飞跨电容的三电平全桥直流变换器输入中点电压的自平衡分析[J]. 电工技术学报, 2018, 33(18): 4335-4344.
Liu Peng, Chen Changsong, Duan Shanxu, et al. Self-balance mechanism analysis of the neutral point voltage in three-level full bridge DC-DC converter with flying capacitors[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4335-4344.
[18] Yang Guorun, Xiao Fei, Fan Xuexin, et al. Three- phase three-level phase-shifted PWM DC-DC converter for electric ship MVDC application[J]. IEEE Transactions on Power Electronics, 2017, 5(1): 162-170.
[19] 杨国润, 肖飞, 范学鑫, 等. 中压大容量三重化三电平直流变换器冗余容错控制[J]. 电工技术学报, 2017, 32(1): 186-195.
Yang Guorun, Xiao Fei, Fan Xuexin, et al. Redundant and fault tolerant control of a medium-voltage high- power three-phase three-level DC-DC converter[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 186-195.
[20] 杨国润, 肖飞, 范学鑫, 等. 一种四管动作的高压大功率三电平变流器双脉冲测试方法[J]. 中国电机工程学报, 2015, 35(3): 695-701.
Yang Guorun, Xiao Fei, Fan Xuexin, et al. A novel four-switch action double-pulse test method for high-voltage high-power three-level converters[J]. Proceedings of the CSEE, 2015, 35(3): 695-701.
[21] 刘成君, 杨仁刚. 变压器谐波损耗的计算与分析[J].电力系统保护与控制, 2008, 36(13): 33-36.
Liu Chengjun, Yang Rengang. Calculation and analysis of transformer’s harmonic loss[J]. Power System Protection and Control, 2008, 36(13): 33-36.
[22] Liu Peng, Chen Changsong, Duan Shanxu, et al. An optimized modulation strategy for the three-level DAB converter with five control degrees of free- dom[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 254-264.
[23] Chen Wu, Ruan Xinbo, Yan Hong, et al. DC-DC conversion systems consisting of multiple converter modules: stability, control, and experimental verifi- cations[J]. IEEE Transactions on Power Electronics, 2009, 24(6): 1463-1474.
[24] 石季英, 凌乐陶, 薛飞, 等. 领地粒子群算法在光伏最大功率跟踪的应用[J]. 太阳能学报, 2019, 40(9): 2554-2559.
Shi Jiying, Ling Yuetao, Xue Fei, et al. Application of territorial PSO in global MPPT for PV array[J]. Acta Energiae Solaris Sinica, 2019, 40(9): 2554-2559.
[25] Wu Jiangling, Sun Xiaodong. Accurate torque modeling with PSO-based recursive robust LSSVR for a segmented-rotor switched reluctance motor[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 96-104.
[26] 张弛, 曾杰, 曾嵘, 等. 应用于储能系统的双向DC-DC效率模型研究[J]. 电气传动, 2019, 49(8): 38-42.
Zhang Chi, Zeng Jie, Zeng Rong, et al. Research on efficiency model of bidirectional DC-DC applied to energy storage system[J]. Electric Drive, 2019, 49(8): 38-42.
[27] 李国栋, 李培, 徐永海, 等. 变压器谐波损耗计算方法比较与仿真[J]. 电力系统保护与控制, 2010, 38(18): 63-68.
Liu Guodong, Li Pei, Xu Yonghai, et al. Comparison and simulation of calculation methods for transformer harmonic losses[J]. Power System Protection and Control, 2010, 38(18): 63-68.
[28] 唐海燕, 李建泉. DC-DC 变换器中25kW高频功率变压器的设计[J]. 大功率变流技术, 2010, 2(5): 26-30.
Tang Haiyan, Li Jianquan. Design of 25kW high frequency power transformer for DC-DC converter[J]. High Power Converter Technology, 2010, 2(5): 26-30.
[29] 汤厚涛. DC-DC充电机功率损耗分析及电路设计[D]. 成都: 电子科技大学, 2016.
[30] 李琼林, 邹磊, 刘会金, 等. 电力变压器谐波损耗仿真计算与实验研究[J]. 电网技术, 2013, 37(12): 3521-3527.
Li Qionglin, Zou Lei, Liu Huijin, et al. Simulation calculation and experimental research on harmonic losses in power transformers[J]. Power System Technology, 2013, 37(12): 3521-3527.
[31] 贺威.电力电子变压器 DC-DC变换器的设计[D]. 徐州: 中国矿业大学, 2016.
[32] 郭云翔. 大功率中频变压器特性研究与优化设计[D]. 保定: 华北电力大学, 2017.
[33] 王瑞田, 赵治华, 肖飞, 等. 中频变压器并联绕组环流的频率特性及其对等效电阻的影响分析[J]. 电工技术学报, 2020, 35(1): 251-258.
Wang Ruitian, Zhao Zhihua, Xiao Fei, et al. Investigation of frequency characteristics and effect on winding equivalent resistance of circulating current in medium-frequency transformer[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(1): 251-258.
[34] 黄佩. 大功率中频变压器电磁分析与优化设计[D]. 武汉: 华中科技大学, 2018.
Optimal Control for the Full-Bridge Three-Level DC-DC Converter
Abstract In this paper, an optimal control strategy was proposed according to the problems of the full-bridge three level (FBTL) DC-DC converter, such as coordinated control of two duty cycles, small output power of the FBTL DC-DC converter and voltage balance of divided capacitors. First, the characteristics of the FBTL DC-DC converter was analyzed in detail and a self-balance modulation scheme for divided capacitor voltage was investigated. Second, a strategy to resist the voltage disturbance of the divided capacitor was proposed. At the same time, a restraint condition for the duty cycles was investigated. Third, taking the harmonics of the transformer input voltage as the objective, and taking the power of the FBTL DC-DC converter and the voltage regulation capacity of the divided capacitor as the constraints, an optimization model for the duty cycles was established. The optimal duty cycles were calculated offline and stored in the digital control system. The look-up table method was adopted to get the optimal duty cycles. The proposed method does not require an accurate model of the converter, and the control process is simple and efficient. Finally, a FBTL DC-DC converter model in Matlab/Simuink and a FBTL DC-DC converter experimental prototype were built to verify the theoretical analysis.
keywords：HVDC, full-bridge three-level DC-DC converter, voltages control of the divided capacitors, optimal control
DOI: 10.19595/j.cnki.1000-6753.tces.200535
中图分类号：TM464
李 伟 男，1989年生，博士研究生，研究方向为电能变换与控制技术、DC-DC变换器及其控制技术。E-mail: 13517487551@163.com
王 辉 男，1960年生，教授，博士生导师，研究方向为电力电子与电力传动系统、新能源发电控制技术。E-mail: Hwang1960@163.com（通信作者）
收稿日期 2020-05-25
改稿日期 2020-06-19
国家自然科学重点基金资助项目（51737004）。
（编辑 陈 诚）