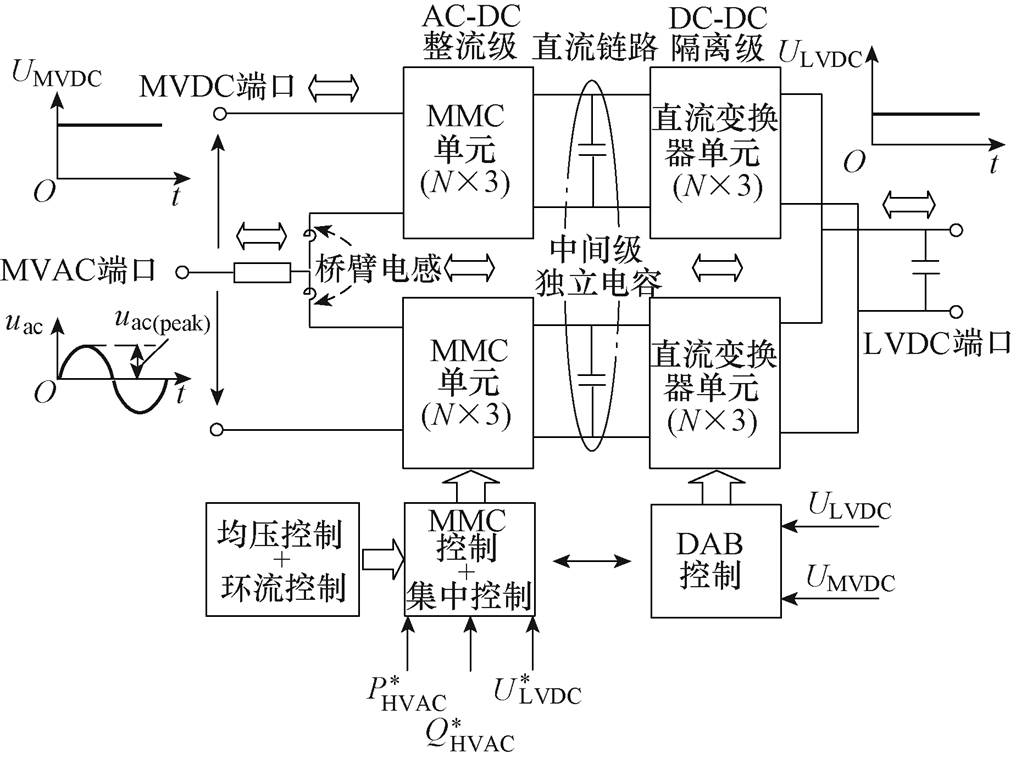
图1 MMC型PET运行原理
Fig.1 The schematic of MMC based PET
摘要 基于模块化多电平变换器(MMC)的电力电子变压器(PET)因其多端口接入、模块化结构、易实现电压拓展、输出波形质量高等优点受到广泛关注。但由于该PET中压交流侧电压由中压直流母线产生,使其中压交流端口电压始终限制在中压直流端口电压以下。该文结合模块化拓扑结构与单级式功率变换思想,提出一种混合式隔离型模块化多电平变换器(HI-MMC)。首先,分析HI-MMC结构以及组成HI-MMC两种隔离型子模块的拓扑结构及调制策略,通过不同子模块的组合配置可使HI-MMC突破交/直流电压比的限制,实现各端口电压等级的灵活设计;同时,所提出的HI-MMC还具有单级式功率变换、控制系统简单、节约电容等优点;其次,研究不同电压比下各类子模块相应的配置方案,并建立单相HI-MMC系统平均等效模型;最后,通过搭建的一套10kW实验室HI-MMC样机验证了所提拓扑结构的有效性。
关键词:电力电子变压器 混合式隔离型模块化多电平变换器 单级式功率变换 电压比
近年来,随着我国分布式能源占比逐年递增,作为可再生能源柔性并网系统充分消纳及高效利用的关键装备,电力电子变压器(Power Electronic Transformer, PET)受到了广大学者的关注[1-4]。由于它具有很高的可控性,以及谐波抑制、功率分配等功能,因此是未来柔性配电网能源路由的有效载体。同时,具有高频链隔离功能的PET可实现多端口交/直流混合功率变换,大大减少铁心、绕组的体积,在提高系统功率密度的同时减少设备的安装和维护成本,业已应用于电力牵引机车[5-6]及能源互联网[7-8]等诸多领域。目前,基于模块化结构的隔离型PET常采用“DC-DC隔离级+AC-DC整流级”的双级式系统结构,有级联H桥(Cascade H-Bridge, CHB)型PET[9-10]和模块化多电平变换器(Modular Multilevel Converter, MMC)型PET[11-12]两种形式。CHB型PET与中性点钳位或飞跨电容多电平等结构相比,可避免因增加电平数而带来的控制复杂性问题,但是由于缺少中压直流(Medium-Voltage DC, MVDC)端口使其在实际应用中存在局限性,如中压交/直流柔性并网的可再生能源发电系统、MVDC供电系统的电力船舶[13-14]。此外,CHB型PET一般需要多绕组移相变压器为各子模块提供隔离独立的直流电源[15],增加了系统的成本和体积。MMC型PET具备MVDC端口,为分布式能源的接入提供便利接口,有助于提高新能源占比。同时,多台PET构建的基于MVDC多馈线互联环网,不仅可以提高配电网的可靠性和灵活性,还能缓冲大型储能电站、电动汽车充电站等新型冲击性负荷。
MMC型PET运行原理如图1所示,该结构具有模块化结构、多电平输出、交/直流混合功率变换等优点。然而,该结构仍然存在一些问题。其中压交/直流侧功率变换由MMC半桥子模块电容的充放电过程实现,各子模块工作在期望电压值是MMC型PET稳定工作的前提下。因此,子模块电容均 压[16-17]、预充电及环流抑制[18-19]等问题导致MMC型PET需要复杂的控制策略。由于MMC型PET属于双级式拓扑结构,需要大量的独立电容来缓冲交流侧固有的二倍频功率波动,因此也显著地增加了装置的体积与成本,限制了MMC型PET功率密度的提高。

图1 MMC型PET运行原理
Fig.1 The schematic of MMC based PET
由MMC工作原理可知,中压交流(Medium- Voltage AC, MVAC)端口电压由MVDC母线产生。在传统的MMC型PET中,其电压比K(pu)表示直流母线中用于产生交流电压的比例,所以K(pu)不会大于1。图中,UMVDC为MVDC端口电压值,uac(peak)为MVAC端口峰值电压。在不考虑相电压的3次谐波前提下,该电压比K(pu)可定义为
 (1)
(1)考虑到装置安全裕度与子模块冗余设计,传统MMC型PET中K(pu)<1。当K(pu)较小时,表明MVDC母线利用率较低,结合变换器谐波特性与工作效率多目标优化设计,大多数MMC型PET的K(pu)=0.85为最宜选择。这意味着MMC存在MVAC侧电压峰- 峰值永远小于MVDC侧电压,会影响PET在某些特定场景的应用。
文献[20]提出了一种基于隔离型模块化多电平变换器(Isolated Modular Multilevel Converter, I-MMC)的单级式PET结构,本文在此拓扑结构基础上提出了一种混合式隔离型模块化多电平变换器(Hybrid Isolated Modular Multilevel Converter, HI-MMC),该结构不仅克服了传统MMC型PET存在的问题,例如,它能够实现从低压到中压的单级式变换、完全消除了独立电容、无需复杂的控制策略以及减少功率半导体器件数量,还能够打破传统PET中压交/直流侧电压比K(pu)的约束条件。本文首先介绍HI-MMC拓扑结构及其优势;其次分别介绍构成HI-MMC的隔离型斩波子模块(Isolated Chopper Cell, I-CC)与隔离型全桥子模块(Isolated Bridge Cell, I-BC)的拓扑结构和调制策略;然后给出HI-MMC实现不同交/直流电压比K(pu)时桥臂子模块数量的设计方案;接着建立HI-MMC单相平均等效模型;最后介绍了三相HI-MMC实验样机,并给出了相关实验波形。
HI-MMC采用单级式功率变换结构,具有低压直流(Low-Voltage DC, LVDC)、MVDC和MVAC三个基本端口,可实现三端口间能量自由流动。三相HI-MMC拓扑结构及两种子模块示意图如图2所示,每相由上、下桥臂以及交流端口的滤波电感构成。其采用模块化设计,每个桥臂由若干隔离型子模块以及1个桥臂电感组成,隔离型子模块包括I-CC和I-BC,且在三相6个桥臂中两种隔离型子模块的配置数量一致,各子模块采用低压侧并联,中压侧串联的连接方式。其中所有隔离型子模块一次侧并联构成公共LVDC端口;三个相单元上、下桥臂的连接点引出后串联滤波电感构成MVAC端口,三个相单元上桥臂的正极连接点与下桥臂的负极连接点作为MVDC端口。
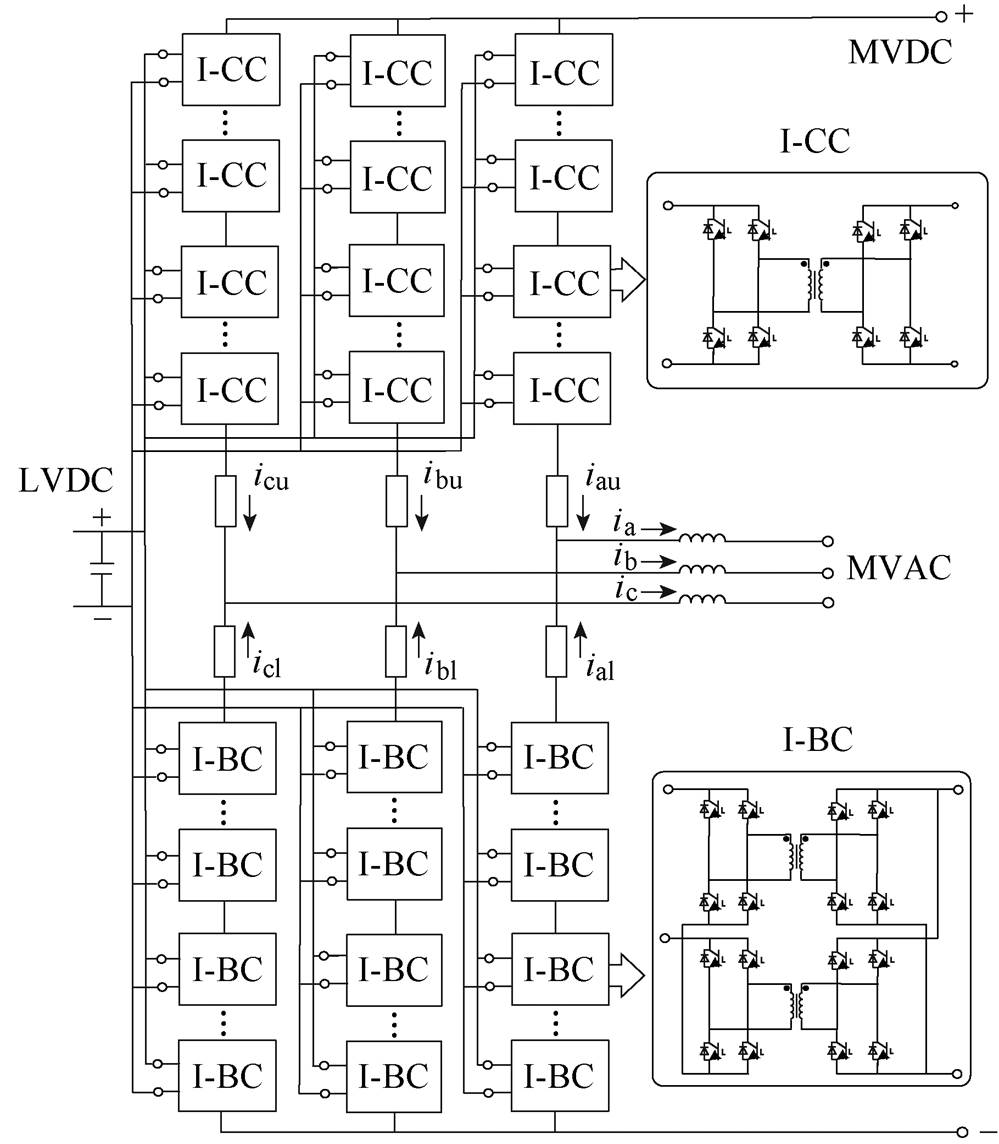
图2 三相HI-MMC拓扑结构及两种子模块示意图
Fig.2 The topology of proposed three-phase HI-MMC and two types sub-modules
与传统MMC型PET相比,HI-MMC在拓扑结构及控制策略方面均具有显著优势。
在拓扑结构方面:HI-MMC属于单级式功率变换结构,可以实现从LVDC到MVAC-DC的混合功率变换,与双级式结构相比更加紧凑,有利于提升功率密度;HI-MMC可以完全消除双级式PET中用于缓冲二倍频功率波动的独立电容,从而降低设备体积,节约成本;在三相HI-MMC系统中,各相二倍频功率波动通过隔离型子模块的高频变压器汇集到公共LVDC侧相互抵消,进一步减少了电容的使用;HI-MMC打破了中压交/直流电压等级的约束条件,可以构建更高电压等级的MVAC端口,无需前级工频变压器调压作用,减少了额外设备使用。
在控制策略方面:HI-MMC属于单级式控制,无需考虑双级式PET两级间的协调控制;由于消除了设备中间级的独立电容,HI-MMC无需复杂的子模块均压和环流抑制等控制策略;HI-MMC采用基于交/直流双调制自由度(da/D)的控制策略,可以完成交流、直流端口的直接解耦控制,从而实现各端口间的协调运行。
本节主要介绍构成HI-MMC的I-CC与I-BC两种隔离型子模块,包括其拓扑结构、调制策略和平均等效模型。
HI-MMC中的I-CC拓扑结构及调制策略如图3所示,其由一次侧全桥(Q1~Q4)、二次侧全桥(S1~S4)以及具有等效漏感Lr的高频变压器(High- Frequency Transformer, HFT)组成。HFT可以提供电平转换及电气隔离功能。根据输出电流io的流动方向,可将I-CC的工作模式分为升压模式(io<0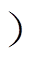 和降压模式(io>0),且无论I-CC在何种模式下工作,均可采用如图3b所示的统一调制策略。
和降压模式(io>0),且无论I-CC在何种模式下工作,均可采用如图3b所示的统一调制策略。
图3中,UdcL为子模块输入侧电压,即LVDC端口电压;uo为子模块输出侧电压;iin、io分别为子模块输入侧与输出侧电流;u1、u2为HFT一次与二次电压;Lr为HFT的等效漏感;k为HFT的电压比;iL为流过漏感的电流。
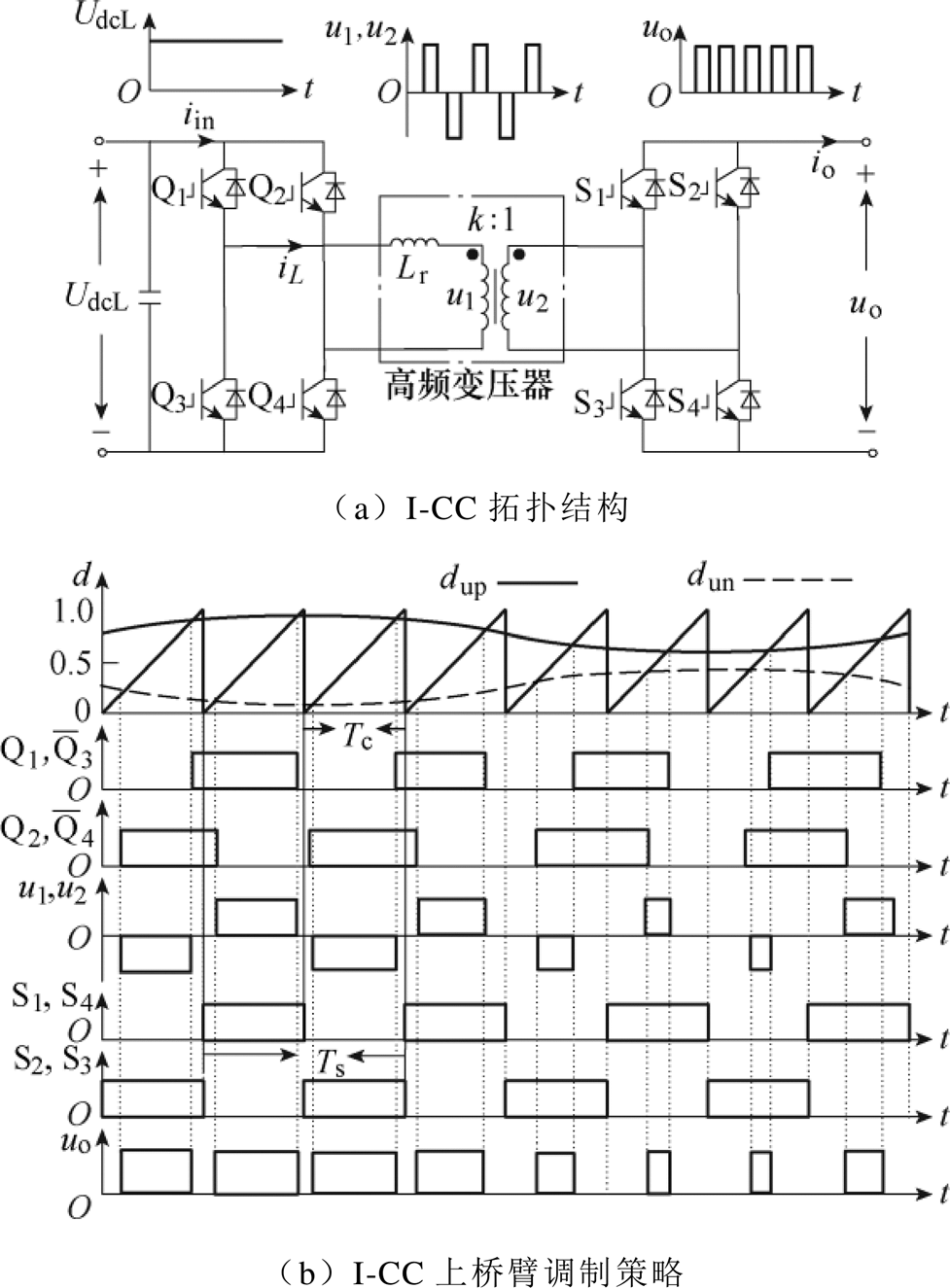
图3 I-CC拓扑结构和上桥臂调制策略
Fig.3 The topology structure of I-CC and modulation strategy of I-CC in the upper arm
当I-CC工作在降压模式下,其工作过程与传统移相全桥类似,因此其具体工作过程不予赘述。在图3b中所描述的统一调制策略中,当子模块二次侧开关动作时,一次侧始终处于续流阶段,因此可以避免电流换相过程中出现的电压尖峰和振荡。
上、下桥臂I-CC的调制信号分别为
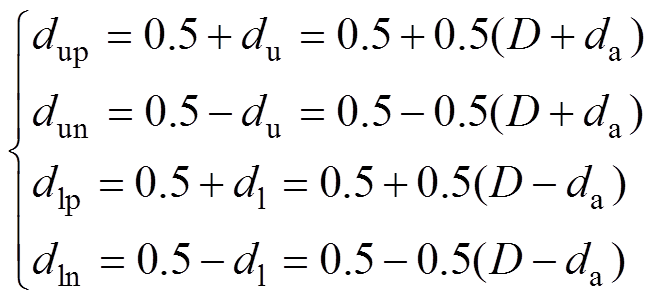 (2)
(2)式中,dup(un)为上桥臂I-CC超前(滞后)桥臂的调制信号;dlp(ln)为下桥臂I-CC超前(滞后)桥臂的调制信号。且上、下桥臂调制信号du和dl需同时满足
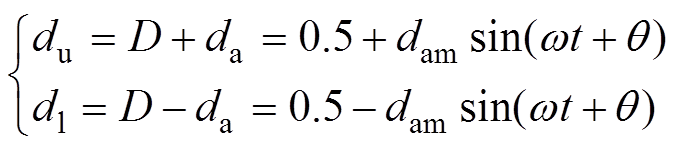 (3)
(3)
式中,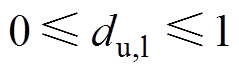 ;直流调制比D通常设置为0.5[21],而交流调制比da应满足0≤da≤0.5,以保证输出电
;直流调制比D通常设置为0.5[21],而交流调制比da应满足0≤da≤0.5,以保证输出电
压极性为正;dam为交流调制比最大值。
为分析HI-MMC中I-CC端口功率特性,本文建立了平均等效模型。由于I-CC无需改变调制策略即可实现功率双向自由流动,因此其平均等效模型同时适用于降压模式和升压模式。为简化分析,本文做如下假设:
(1)理想开关,开关无寄生效应。
(2)负载恒定,负载变换可加入额外电流源。
(3)理想电感,不考虑其内阻值。
I-CC平均等效模型推导过程如图4所示。当I-CC工作在降压模式下,在其半个工作周期中有两种不同的工作状态。当Q1和Q4导通时,功率从一次侧转移到二次侧,其等效电路如图4a所示。该时段内子模块输出电压uo(14)及输入电流iin(14)可表示为
 (4)
(4)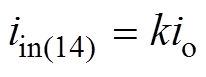 (5)
(5)
式中,Ts=1/fs为切换周期。Q1、Q4导通的持续时间为(D+da)Ts/2。
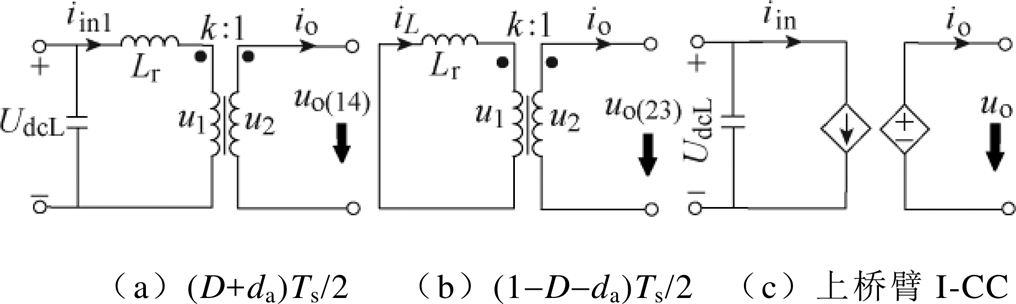
图4 平均等效模型推导过程
Fig.4 The deduction process of average equivalent model
当Q3和Q4导通时,一次电流通过开关Q3和Q4的反并联二极管续流,导通的持续时间为(1-D-da)Ts/2,其等效电路如图4b所示。该时段内子模块输出电压uo(23)及输入电流iin(23)表示为
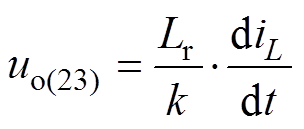 (6)
(6)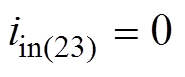 (7)
(7)
在半个开关周期中的输出电压uo和输入电流iin的平均值分别为
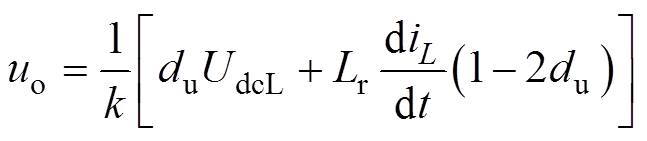 (8)
(8)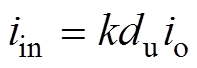 (9)
(9)
从式(9)可知,I-CC输出电压具有交流和直流分量。一次侧等效为电流源、二次侧等效为电压源。上桥臂I-CC等效电路如图4c所示。
若使PET在无需外接工频变压器情况下突破电压约束则需要在HI-MMC中增设I-BC。I-BC的拓扑结构及调制策略如图5所示,由两个ICC单元通过一次侧并联,二次侧反向串联构成。I-BC输出端口由两个具有不同调制比的ICC单元输出电压叠加产生,其中ICC1的调制比与2.1节中上桥臂I-CC相同,ICC2的调制比与2.1节中下桥臂I-CC相同,具体可由式(2)得出。
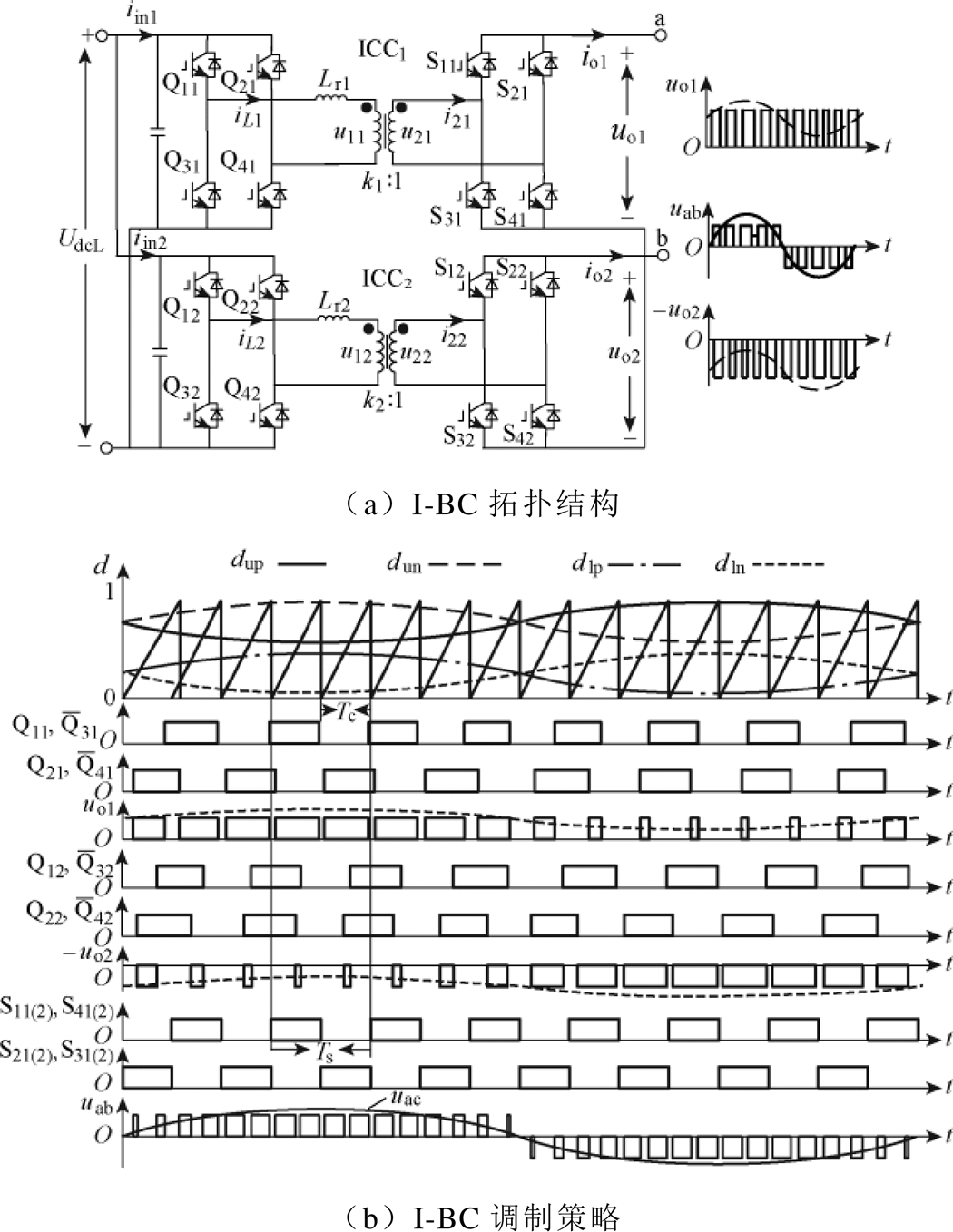
图5 I-BC拓扑结构和调制策略
Fig.5 The topology structure and detailed modulation strategy of I-BC
根据叠加原理,可由I-CC推导出I-BC的平均等效模型如图6所示。根据I-BC中ICC1的平均等效模型可知,将式(8)、式(9)中ICC1调制信号替换为ICC2的调制信号,即可得出I-BC中ICC2的平均等效模型。ICC1与ICC2的平均输出电压uo1和uo2以及输入电流iin1和iin2分别表示为
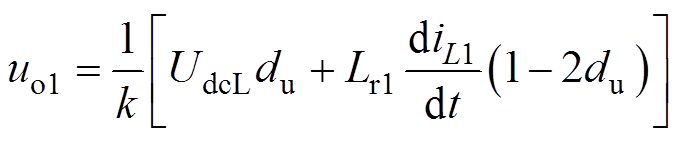 (10)
(10)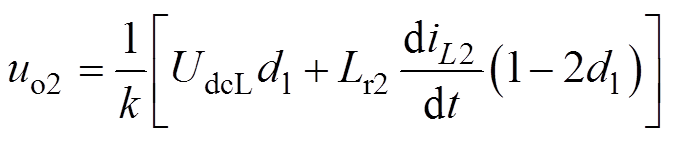 (11)
(11)
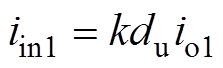 (12)
(12)
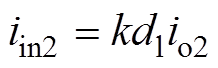 (13)
(13)式中,Lr1为ICC1内HFT的等效漏感;Lr2为ICC2内HFT的等效漏感;iL1为流过ICC1内漏感的电流;iL2为流过ICC2内漏感的电流;io1为ICC1的输出电流;io2为ICC2的输出电流。
通常可以假设Lr1=Lr2=Lr, iL1=iL2=iL, io1=-io2。根据基尔霍夫电压定律和电流定律可以得到I-BC的简化平均模型,如图6b所示。因此,上桥臂I-BC的等效受控电压源及等效受控电流源可表示为
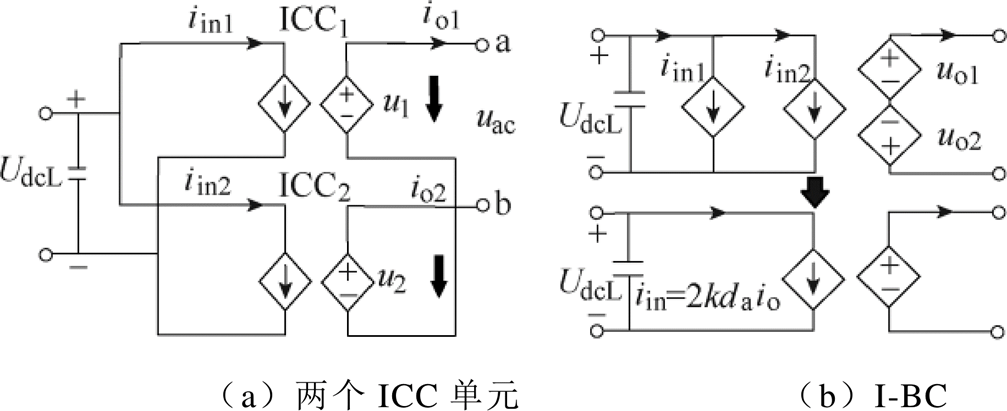
图6 I-BC平均等效模型
Fig.6 The deduction process of average equivalent model
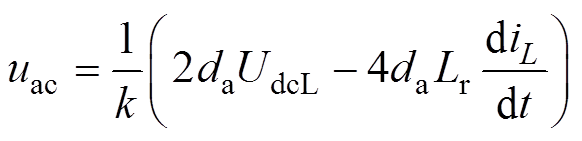 (14)
(14)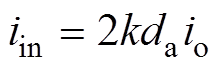 (15)
(15)
从I-BC的平均等效模型可知,其输出端口电压呈现交流特性。与传统单级式DC-AC矩阵变换器相比,ICC单元端口均为正极性,无需双向开关且避免了双向开关管换流时出现电压尖峰等问题。在HI-MMC拓扑结构中,可以通过提高I-BC的占比来提升MVAC的电压等级。随着I-BC数量的增加,电压比K(pu)的取值会超过约束值1。
基于第2节所述两种构成HI-MMC的隔离型子模块,可以构造出如图7所示的三种类型的级联桥臂,即I-CC级联桥臂、I-BC级联桥臂以及由I-CC与I-BC组合成的混合式级联桥臂,这些桥臂结构各自具有不同特点。以I-BC级联桥臂为例,它具有两个不同电压等级的MVAC端口,可实现不同频率输出,另一个公共LVDC端口可为电动汽车充电桩、储能电池等直流负荷提供接口。
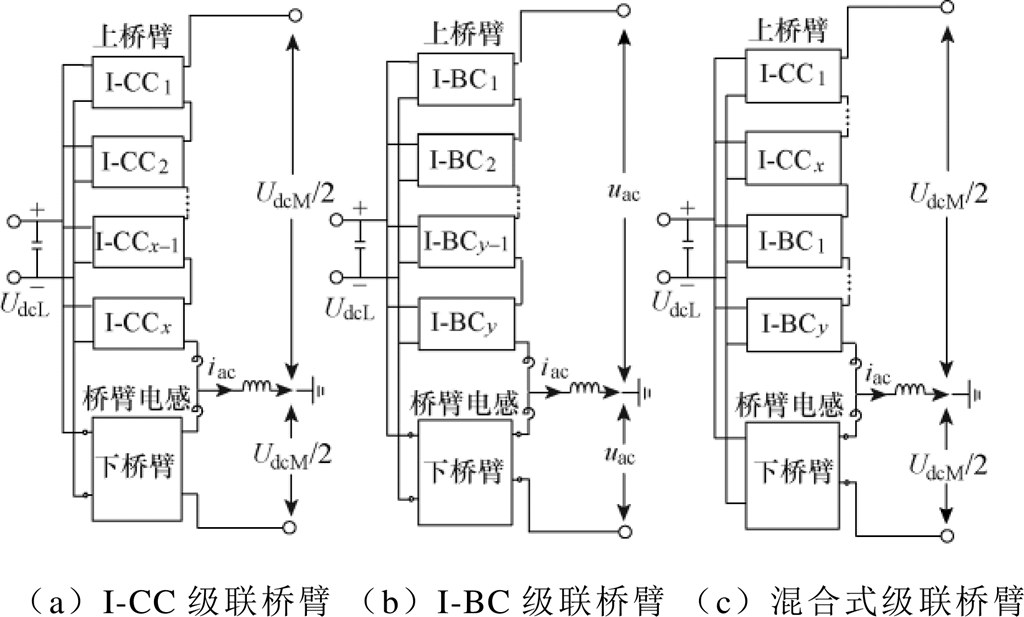
图7 由I-CC和I-BC组成的三种HI-MMC级联桥臂
Fig.7 Three types of HI-MMC cascaded legs consisting of I-CC and I-BC
本文介绍的HI-MMC拓扑结构基于I-CC和I-BC混合式级联桥臂构成。该结构的主要特点是可以实现更高的电压比K(pu),这意味着HI-MMC可以在无需工频变压器等设备进行升压的情况下应用于MVAC需要更高电压等级的场景,本节将介绍单相HI-MMC实现不同K(pu)的工作原理及过程。
在不考虑HFT的漏感情况下,可得到调制比与输出电压的关系,即
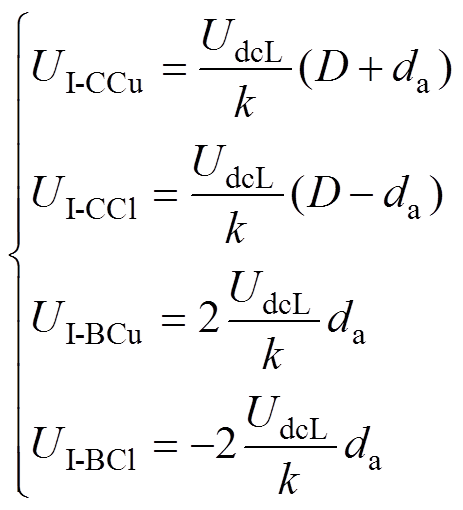 (16)
(16)式中,UI-CCu(l)为上(下)桥臂I-CC的输出电压;UI-BCu(l)为上(下)桥臂I-BC的输出电压。
根据回路电压方程可知,如果每个级联桥臂中有x个I-CC和y个I-BC,则MVDC和MVAC端口的输出电压可表示为
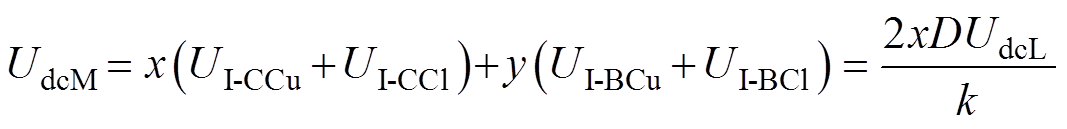 (17)
(17)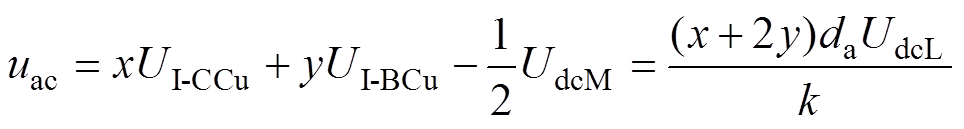 (18)
(18)
式中,UdcM为MVDC端口输出电压;uac为MVAC端口输出电压。
若需在不改变MVAC电压等级条件下获得更高电压等级的MVDC端口,则可在级联桥臂中增加I-CC(DC)。I-CC(DC)中仅使用直流调制比D,功能类似于传统的DC-DC变换器。此时每个I-CC(DC)所产生的直流分量为I-CC两倍。由式(16)可知,若每个桥臂只有1个I-CC,则上、下桥臂I-CC输出电压和为2DUdcM/k,因此上、下桥臂只有1个I-CC(DC)时,输出电压和为4DUdcM/k。如果每个桥臂中配置z个I-CC(DC),则
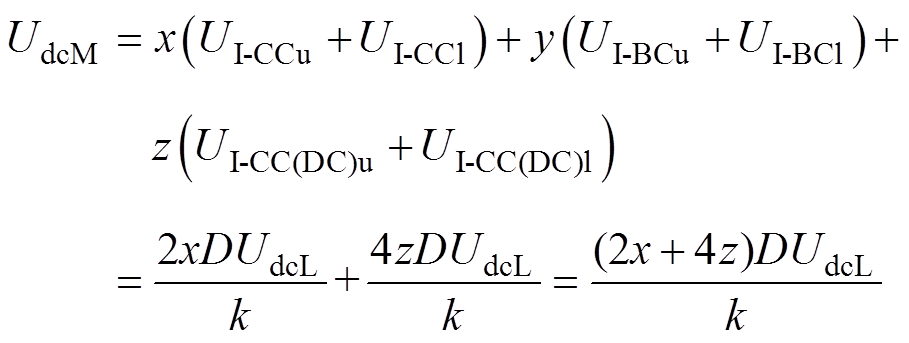 (19)
(19) 式(18)表明,通过增加I-BC的数量可以提高MVAC端口电压等级。为进一步说明电压比K(pu)的值,本文分别将y/x定义为p1,将z/x定义为p2。如果交流调制比最大值dam及直流调制比D均为0.5,则K(pu)与p1、p2的关系如图8所示。如果级联桥臂仅有I-CC,则K(pu)的值可以取到1,这与传统PET类似。随着I-BC或I-CC(DC)数量的增加,K(pu)的取值将呈现出不同的趋势,从而拓宽了MVAC端口与MVDC端口之间电压比范围。
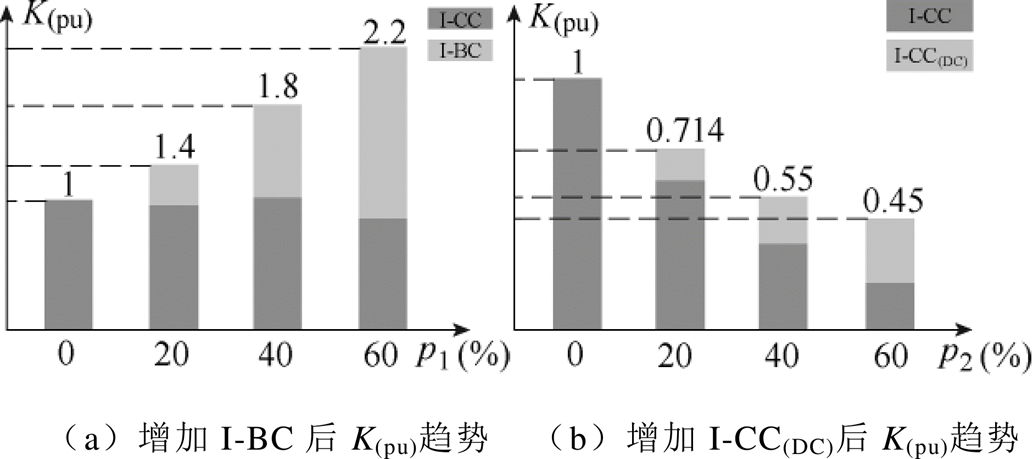
图8 增加不同数量的I-BC或I-CC(DC)后得出的K(pu)值
Fig.8 The value of K(pu) with different p1 and p2
在某些应用场景中,当MVAC端口的峰-峰值电压与MVDC端口电压值不匹配时,会采用工频变压器来匹配MVAC及MVDC端口电压。例如,电力船舶供电系统中36MW发电机的机端电压为4.1kV,传统的MMC型PET需要8kV的MVDC电压才能使其接入系统,然而船舶供电系统最适宜使用的中压直流电压等级为5kV,无法直接与发电机机端电压匹配。通常采用电压比为41 25的工频变压器实现机端电压等级变换,既满足了发电机机端电压,又能够实现中压直流电压等级最优设计。但是传统工频变压器存在一些问题,如系统故障或过载时需要复杂的保护策略、谐波影响较大、变压器油带来的环境污染以及直流偏置负载不平衡下导致的性能降低等问题。
25的工频变压器实现机端电压等级变换,既满足了发电机机端电压,又能够实现中压直流电压等级最优设计。但是传统工频变压器存在一些问题,如系统故障或过载时需要复杂的保护策略、谐波影响较大、变压器油带来的环境污染以及直流偏置负载不平衡下导致的性能降低等问题。
本文提出的HI-MMC可通过改变隔离型级联桥臂中I-CC和I-BC的数量,实现更高电压等级需求的MVAC端口。此过程中无需额外设备,提供了一种匹配MVAC和MVDC间不同电压等级的新方法。
在设计过程中为简化分析,可假设:①系统中各子模块参数均相同,且无误差;②HFT的匝数比为1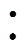 1;③忽略桥臂电感上的压降。
1;③忽略桥臂电感上的压降。
首先设公共LVDC端口电压值为1kV,当K(pu)= 2时,交流调制比dam及直流调制比D均为0.5。可根据式(18)、式(19)求出I-CC和I-BC的数量,计算结果为x=10, y=5, z=0。此时不同电压比下的HI-MMC结构如图9所示。HI-MMC结构如图9a所示,MVDC和MVAC端口电压均为10kV。
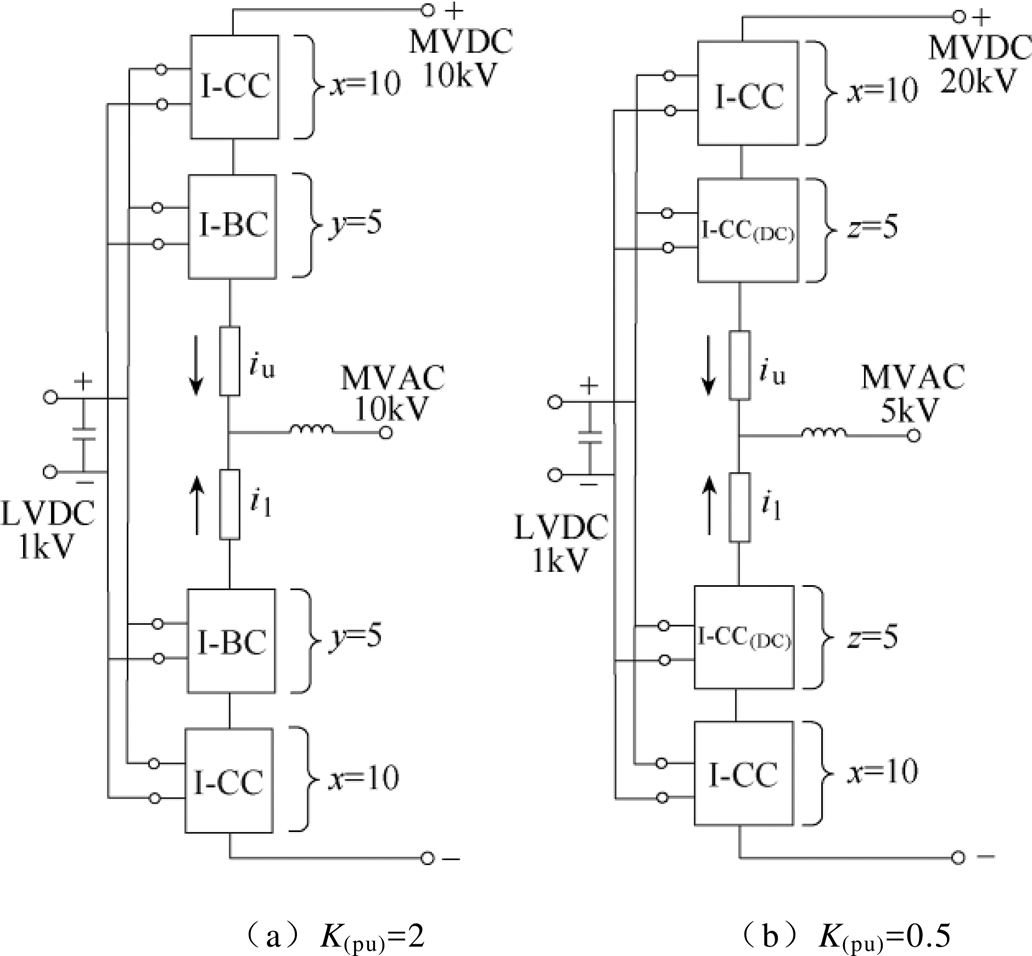
图9 不同电压比下的HI-MMC结构
Fig.9 The design of HI-MMC under different voltage ratios
I-BC数量增加可以提升混合型级联桥臂中压交/直流端口K(pu)的数值,但三相系统所用的变压器额定容量也随之增加。当p1>50%时,HI-MMC将需要更多的变压器容量。因此,为节约设备变压器额定容量,x与y应满足y/x<0.5,即I-BC的使用数量通常不超过I-CC使用数量的一半。满足该条件的HI-MMC在突破电压比限制的情况下,还可节约变压器容量。
当K(pu)=0.5时,同样设公共LVDC端口电压值为1kV,交流调制比dam及直流调制比D均为0.5。根据式(18)、式(19)求出I-CC和I-CC(DC)的数量,计算结果为x=10, y=0, z=5,在该级联桥臂中应配置20个I-CC和10个I-CC(DC)。此时HI-MMC结构如图9b所示,MVDC和MVAC端口电压分别为20kV和5kV。
HI-MMC通过公共LVDC侧的电容替代了双级式PET中间级的独立电容。在三相系统中,每相的二倍频功率波动可通过HFT汇集到公共LVDC侧的电容中。三相系统中二倍频功率波动总和几乎是恒定不变的,因此在公共LVDC侧的电容使用数量可以进一步降低。
另外,HI-MMC中压侧有HFT电压钳位作用。在相同桥臂中每个子模块HFT匝数比与调制比相同,因此每个子模块输出端口电压也相同,无需考虑各个子模块的均压控制,这在极大程度上降低了系统控制的复杂性。
以三相HI-MMC中的A相为例,介绍单相HI- MMC的平均等效模型,如图10所示。各端口电流参考方向已在图10中给出。
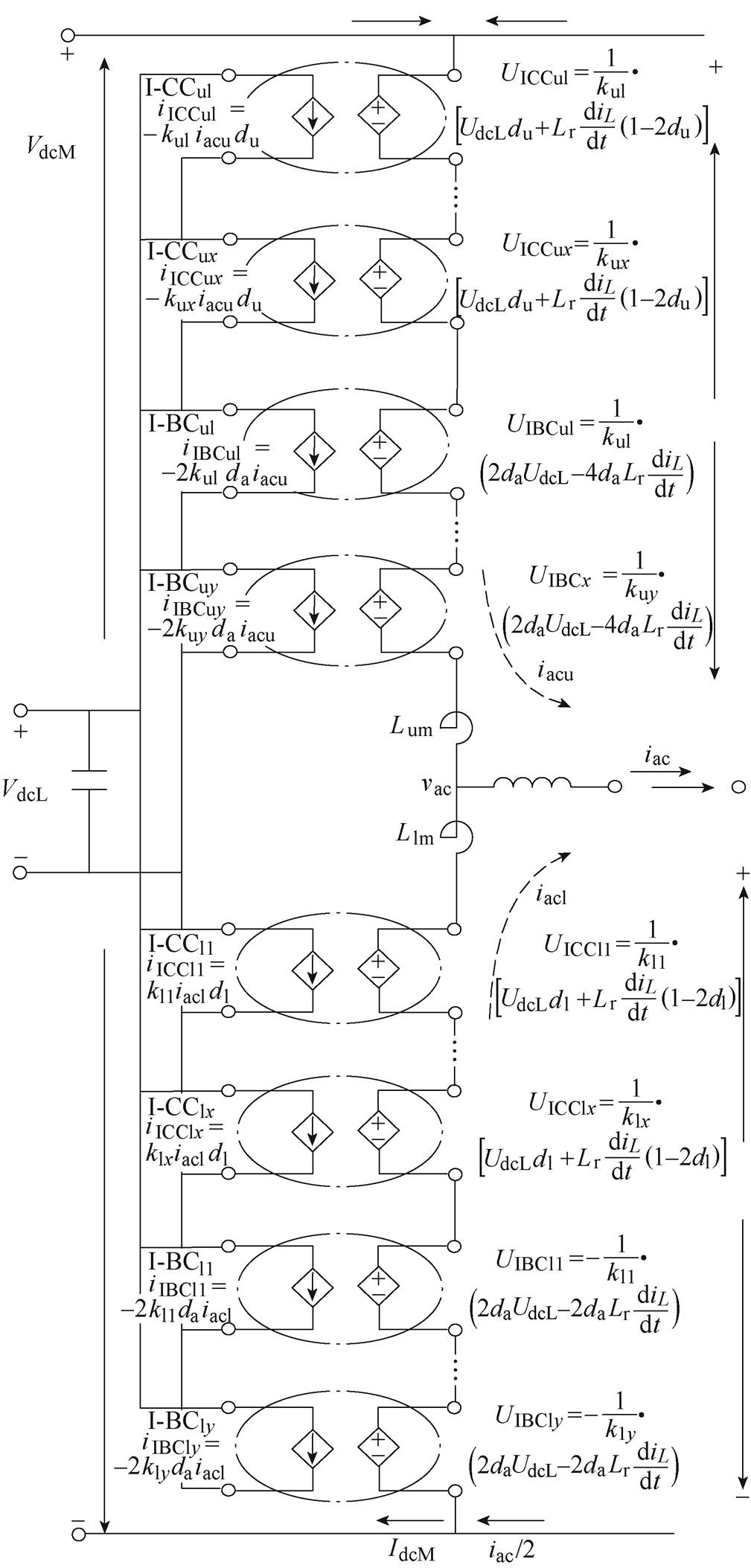
图10 单相HI-MMC平均等效模型
Fig.10 The average equivalent model of single-phase HI-MMC is established
为简化分析,本节给出了I-CC(DC)数量为0条件下HI-MMC相关计算公式与数学模型。若级联桥臂中存在I-CC(DC),则每增加一个额外的I-CC(DC),式(20)中的直流分量系数将加1,交流分量系数将减1。子模块中压侧由具有交/直流混合调制比的受控电压源UI-CCu(l)i(i=1,…, x)或UI-BCu(l)j(j=1,…, y)等效形成,调制比参考式(2)。
上、下桥臂电流iacu和iacl与MVD-AC端口电流IdcM和iac关系为
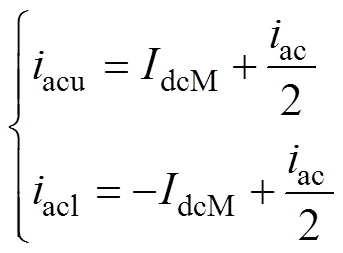 (20)
(20)根据式(16)和式(20),可得出上、下桥臂两种基本子模块的瞬时输出功率为
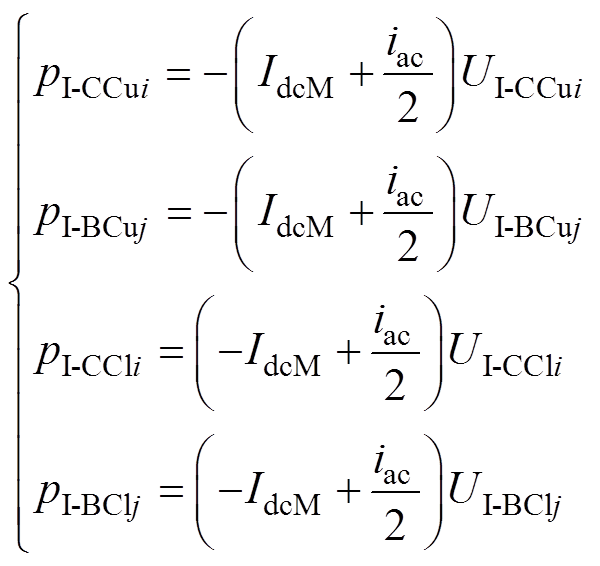 (21)
(21)
式中,pI-CCu(l)i为上(下)桥臂第i个I-CC的瞬时输出功率;pI-BCu(l)j为上(下)桥臂第j个I-BC的瞬时输出功率。
由式(22)、式(23)可知,I-CC的平均功率由直流分量PMVDCu(l)i与交流分量PMVACu(l)i两部分组成(i=1,…, x)。I-BC的平均功率仅由PMVACu(l)j(j=1,…, y)组成,即
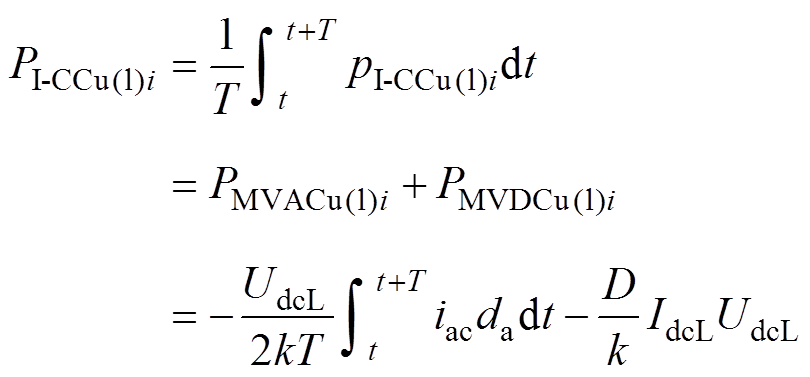 (22)
(22)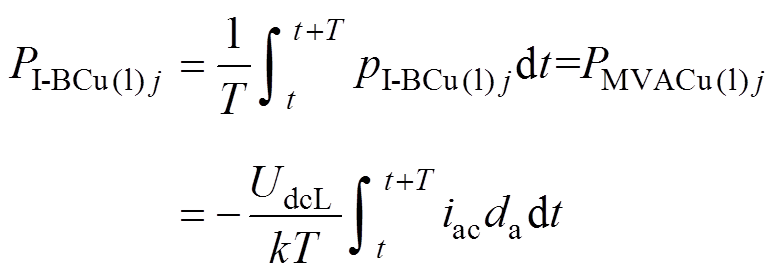 (23)
(23)
式中,T为工频周期。
根据式(9)和式(15)可知,单相HI-MMC的公共LVDC侧的平均等效模型的推导过程如图11所示,瞬时电流idcL等于公共LVDC侧所有受控电流源的总和。根据叠加定理,它可以等效为受控电流源iedc和ieac,即
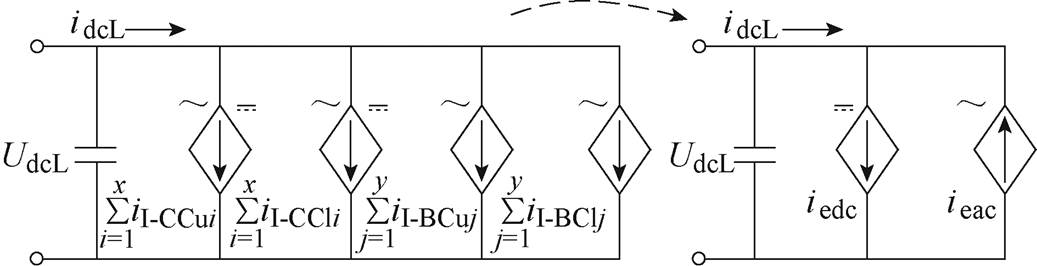
图11 平均等效模型的推导过程
Fig.11 The deduction process of average equivalent model in the LVDC
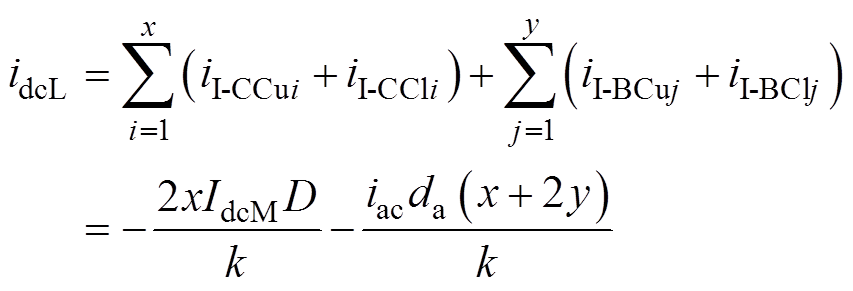 (24)
(24)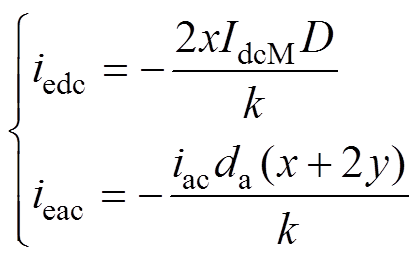 (25)
(25)
公共LVDC侧电流IdcL为iedc+ieac的平均值,即
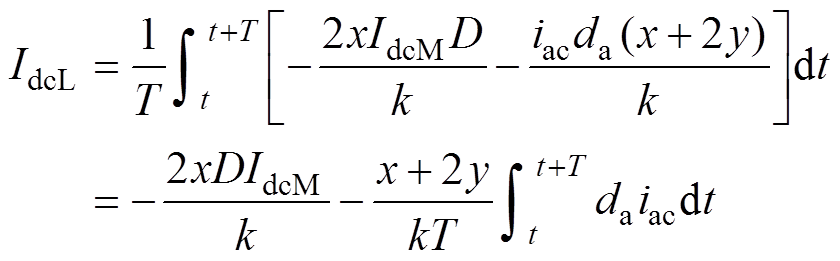 (26)
(26)为验证所提HI-MMC拓扑结构及工作原理的正确性,本文搭建了一套三相HI-MMC样机。该样机容量根据实验室最大负载条件设定为20kW,交流侧额定功率10kW,子模块输入额定电压为100V。图12展示了三相HI-MMC实验的拓扑示意图以及用于验证所提拓扑结构的实验样机。图12a中参数如下:①K(pu)=1.63, x=4, y=1;②K(pu)=0.4, x=3, z=2, D=0.45, da=0.45。
三相HI-MMC系统中子模块的输入端均在LVDC端口处并联,并与一台直流电压源相连。MVDC端口和MVAC端口分别连接直流负载和三相交流负载。三相HI-MMC实验样机的主要参数见表1。
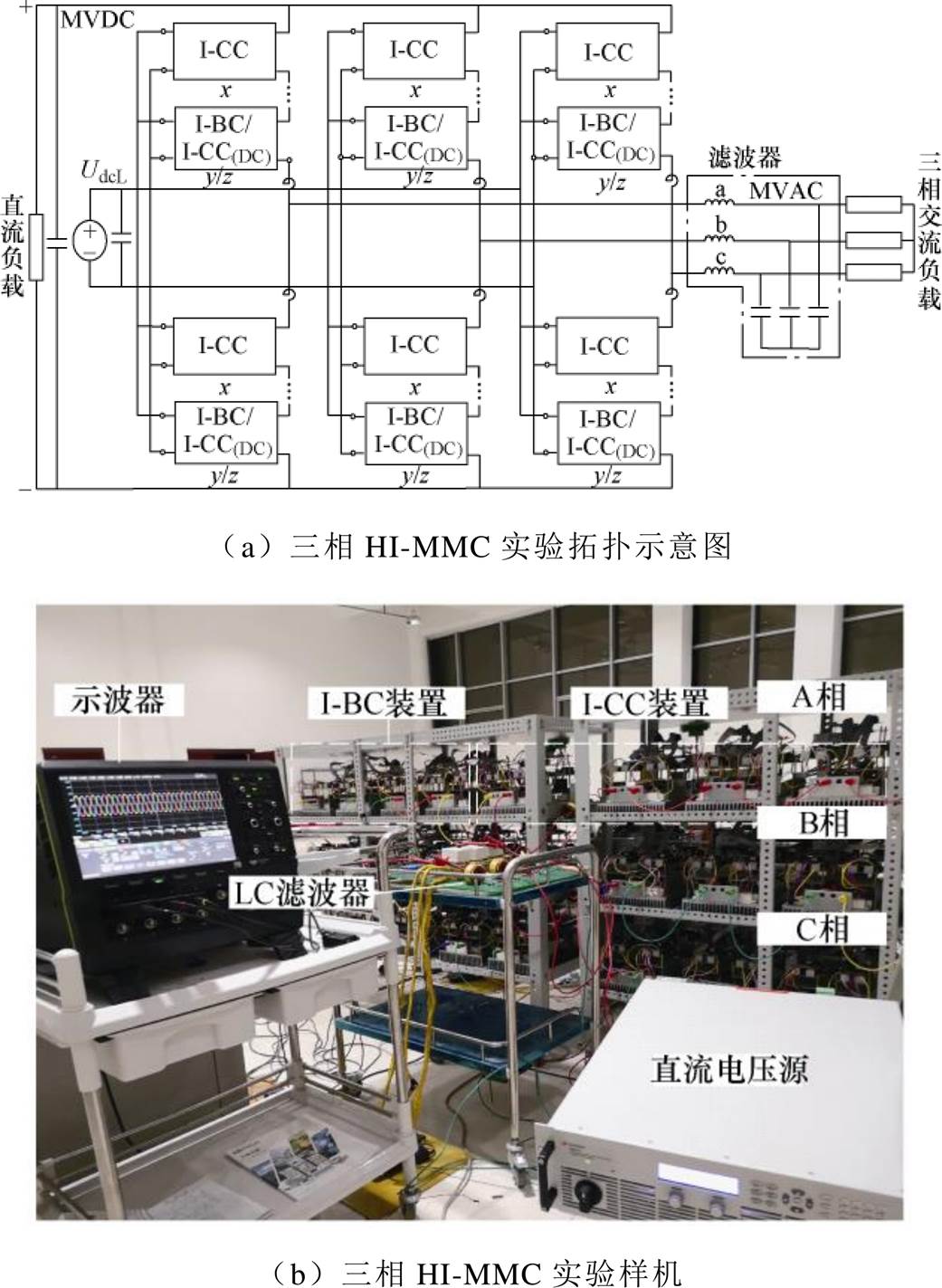
图12 三相HI-MMC实验原理及实验样机
Fig.12 The schematic diagram of three-phase HI-MMC experiment and the hardware setup
表1 三相HI-MMC实验样机电路参数
Tab.1 Circuit parameters of three-phase HI-MMC prototype

参 数数 值 低压直流侧电压UdcL/V100 低压直流侧电容CdcL/mF500 高频变压器漏感Lr/mH3 开关频率fs/kHz10 变压器电压比k1718 直流调制比D0.45 交流调制比da0.45 滤波电感Lf/mH0.5 滤波电容Cf/mF2 中压直流侧电容CdcM/mF250
该实验工况为MVAC侧电压高于MVDC侧电压。在实验中每个桥臂配置3个I-CC和1个I-BC。由第3节式(17)、式(18)可计算出此时MVDC和MVAC电压峰值。K(pu)=1.67工况下稳态过程波形如图13所示。LVDC侧电压源输入电压为100V,D和da均为0.45,x=3, y=1, k=17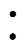 18。此时MVDC端口和MVAC端口的理论电压峰值分别为285V和238V。如图13a所示,MVDC和MVAC的实验电压峰值为283V和232V。实验值与理论值基本一致,验证了本文电压式(17)、式(18)的正确性。
18。此时MVDC端口和MVAC端口的理论电压峰值分别为285V和238V。如图13a所示,MVDC和MVAC的实验电压峰值为283V和232V。实验值与理论值基本一致,验证了本文电压式(17)、式(18)的正确性。
经过Matlab/Simulink计算,输出电压波形THD=0.47%,说明HI-MMC具有良好的波形质量。图13b显示了HI-MMC中的上桥臂波形,UI-BCu为上桥臂I-BC的输出电压,UI-CC(1-3)u为上桥臂3个I-CC输出电压的和,Uarmu为上桥臂的桥臂电压,Iarmu为上桥臂的桥臂电流。从图中可以看出,UI-BCu波形是具有正负双极性的脉宽电压,这表示在上桥臂中存在I-BC。UI-CC(1-3)u波形为具有正极性的四电平波形,这表示在上桥臂中存在3个I-CC。HI-MMC因其模块化拓扑设计使其可以采用载波移相(Carrier Phase Shifting, CPS)调制策略。在图13b中,UI-CC(1-3)u的等效频率为载波频率fs的3倍。即使开关在低频模式下工作,也会使输出电压获得较高的等效频率。
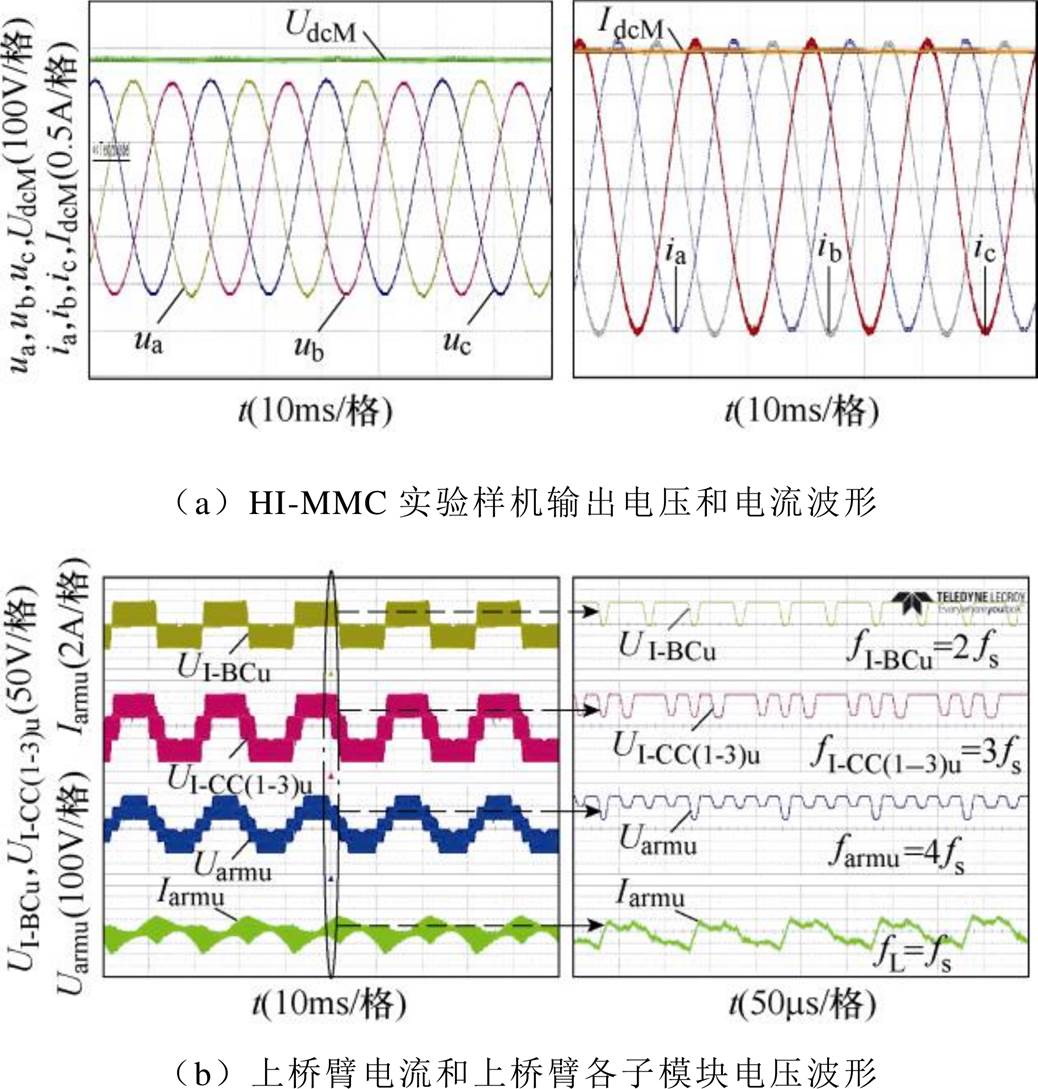
图13 K(pu)=1.67工况下稳态过程波形
Fig.13 The stable waveforms with K(pu)=1.67
该实验工况为MVAC侧电压低于MVDC侧电压。在实验中每个桥臂配置3个I-CC和2个I-CC(DC)。由第4节式(18)、式(19)可计算出MVDC和MVAC电压峰值。K(pu)=0.4工况下稳态过程波形如图14所示。LVDC侧电压源输入电压为100V,D和da均取0.45,x=3, z=2, k=17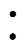 18,此时MVDC和MVAC的理论电压峰值分别为667V和142V。如图14a所示,MVDC和MVAC的实验电压峰值分别为642V和135V。实验值与理论值基本一致,验证了本文所推电压式(18)、式(19)的正确性。
18,此时MVDC和MVAC的理论电压峰值分别为667V和142V。如图14a所示,MVDC和MVAC的实验电压峰值分别为642V和135V。实验值与理论值基本一致,验证了本文所推电压式(18)、式(19)的正确性。
经过Matlab/Simulink计算,输出电压波形总谐波畸变率(Total Harmonic Distortion, THD)为0.21%,表明HI-MMC具有良好的波形质量。图14b显示了HI-MMC中的上桥臂波形,UI-CC(1-3)u为上桥臂3个I-CC的电压之和,UI-CC(DC)(1-2)u为上桥臂两个I-CC(DC)的电压,Uarmu为上桥臂电压。在这种情况下也可以使用CPS调制策略。输出电压的等效频率提高了5倍。在图14b中,UI-CC(1-3)u的等效频率为fs的3倍。
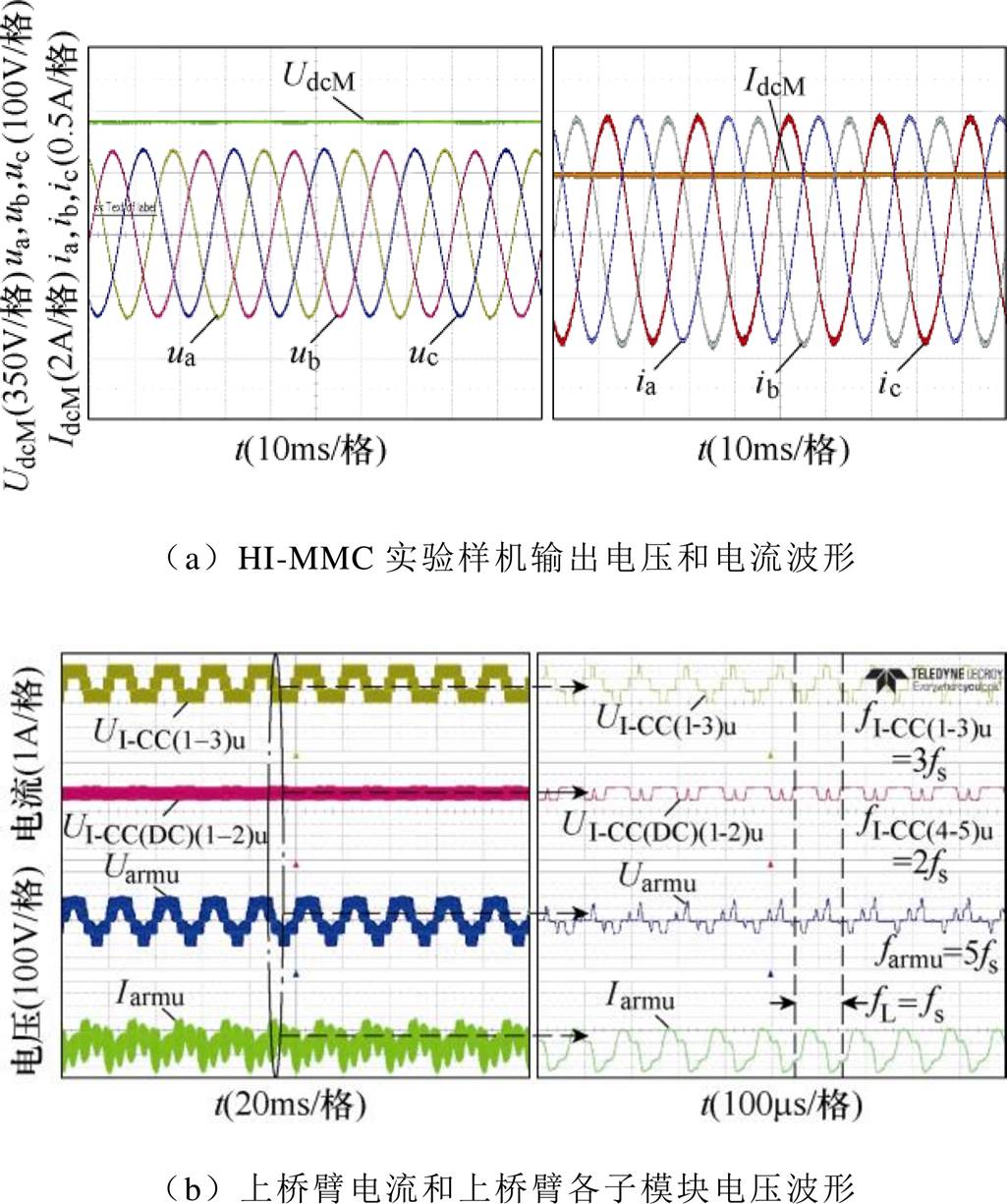
图14 K(pu)=0.4工况下稳态过程波形
Fig.14 The stable waveforms with K(pu)=0.4
以上实验给出了HI-MMC在K(pu)=1.67或K(pu)= 0.4工况下的实验波形。从实验结果可以看出,各个端口具有质量良好的输出波形。同时,不同工况下的实验结果验证了本文HI-MMC拓扑结构实现不同电压比K(pu)的可行性。由于采用了CPS调制策略,开关管可以在相对较低的开关频率下获得较高等效频率的输出波形,从而减小了滤波装置体积。
基于两个I-CC反向串联可以构成输出电压仅有交流分量的I-BC,通过I-BC与输出电压存在交直流分量的I-CC组合可形成HI-MMC,该结构可打破传统PET中压交/直流端口间电压约束条件,实现电压比K(pu)的任意选取,使PET各端口电压等级设计不再受限。
本文详细地分析了HI-MMC的工作原理、调制策略、数学模型以及子模块数量设计方法。搭建了一套10kW三相HI-MMC样机,并验证了所提出结构的正确性。本结构具有高电压比、单级式功率变换、无独立电容以及控制策略简单等优势,为未来单级式PET拓扑结构的探索提供了一种新的方案。
参考文献
[1] Ji Shiqi, Zhang Zheyu, Fred Wang. Overview of high voltage sic power semiconductor devices: deve- lopment and application[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(3): 254- 264.
[2] 涂春鸣, 黄红, 兰征, 等. 微电网中电力电子变压器与储能的协调控制策略[J]. 电工技术学报, 2019, 34(12): 2627-2636.
Tu Chunming, Huang Hong, Lan Zheng, et al. Coordinated control strategy of power electronic transformer and energy storage in microgrid[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2627-2636.
[3] 刘晋源, 吕林, 高红均, 等. 计及分布式电源和电动汽车特性的主动配电网规划[J]. 电力系统自动化, 2020, 44(12): 41-49.
Liu Jinyuan, Lü Lin, Gao Hongjun, et al. Planning of active distribution network considering characteri- stics of distributed generator and electric vehicle[J]. Automation of Electric Power Systems, 2020, 44(12): 41-49.
[4] 李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274-1289.
Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer techno- logies[J]. Proceedings of the CSEE, 2018, 38(5): 1274-1289.
[5] Dieckerhoff S, Bernet S, Krug D. Power loss-oriented evaluation of high voltage IGBTs and multilevel converters in transformerless traction applications[J]. IEEE Transactions on Power Electronic, 2005, 20(6): 1328-1336.
[6] 王婷, 王广柱, 张勋. 基于模块化多电平矩阵变换器的电力电子变压器控制策略[J]. 电工技术学报, 2016, 31(18): 108-115.
Wang Ting, Wang Guangzhu, Zhang Xun. The control strategy of power electronic transformer based on modular multilevel matrix convertors[J]. Transaction of China Electrotechnical Society, 2016, 31(18): 108-115.
[7] 盛万兴, 段青, 梁英, 等. 面向能源互联网的灵活配电系统关键装备与组网形态研究[J]. 中国电机工程学报, 2015, 35(15): 3760-3769.
Sheng Wanxing, Duan Qing, Liang Ying, et al. Research of power distribution and application grid structure and equipment for future energy Internet[J]. Proceedings of the CSEE, 2015, 35(15): 3760-3769.
[8] Feng Jianghua, Chu W Q, Zhang Zhixue, et al. Power electronic transformer-based railway traction systems: challenges and opportunities[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 1237-1253.
[9] 张雪垠, 徐永海, 肖湘宁. 适用于中高压配电网的高功率密度谐振型级联H桥固态变压器[J]. 电工技术学报, 2018, 33(2): 310-321.
Zhang Xueyin, Xu Yonghai, Xiao Xiangning. A highpower density resonance cascaded H-bridge solid-state transformer for medium and high voltage distribution network[J]. Transactions of China Elec- trotechnical Society, 2018, 33(2): 310-321.
[10] 叶满园, 宋桂智, 康翔, 等. Ⅱ型不对称CHB多电平逆变器SHEPWM功率均衡控制策略[J]. 电机与控制学报, 2020, http://kns.cnki.net/kcms/detail/23. 1408.thm.20200106.1317.002.html.
Ye Manyuan, Song Guizhi, Kang Xiang, et al. Type II asymmetric CHB multilevel inverter SHEPWM power balance control strategy[J]. Electric Machines and Control, 2020, http://kns.cnki.net/kcms/detail/23.1408. thm.20200106.1317.002.html.
[11] 艾欣, 荣经国, 吕正, 等. 一种新型的能量路由器结构及其控制策略的研究[J]. 电网技术, 2019, 43(4): 1202-1210.
Ai Xin, Rong Jingguo, Lü Zheng, et al. Research on structure and control strategy of a novel energy router[J]. Power System Technology, 2019, 43(4): 1202-1210.
[12] Briz F, Lopez M, Rodriguez A, et al. Modular power electronic transformers: modular multilevel converter versus cascaded H-bridge solutions[J]. IEEE Indu- strial Electronics Magazine, 2016, 10(4): 6-19.
[13] Chen Yu, Zhao Shanshan, Li Zuoyu, et al. Modeling and control of the isolated DC-DC modular multilevel converter for electric ship medium voltage direct current power system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 124-139.
[14] Chen Yu, Li Zuoyu, Zhao Shanshan, et al. Design and implementation of a modular multilevel converter with hierarchical redundancy ability for electric ship MVDC system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 189-202.
[15] Rahim N A, Elias M F M, Hew W P. Transistor- clamped H-bridge based cascaded multilevel inverter with new method of capacitor voltage balancing[J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 2943-2956.
[16] 谷恭山, 郑祥杰, 高明, 等. 两级结构模块化ISOP组合的DC-DC变换器均压控制策略[J]. 电工技术学报, 2019, 34(15): 3175-3185.
Gu Gongshan, Zheng Xiangjie, Gao Ming, et al. Research on voltage sharing control strategy of a combined two-stage modular input-series output- parallel DC-DC converter[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3175-3185.
[17] 黄守道, 彭也伦, 廖武. 模块化多电平型换流器电容电压波动及其抑制策略研究[J]. 电工技术学报, 2015, 30(7): 62-71.
Huang Shoudao, Peng Yelun, Liao Wu. Study of capacitor voltage fluctuation and its suppression for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2015, 30(7): 62-71.
[18] 张臣, 叶华, 韦凌霄, 等. 不平衡状态下MMC双回路环流抑制策略[J]. 电工技术学报, 2019, 34(9): 1924-1933.
Zhang Chen, Ye Hua, Wei Lingxiao, et al. Double- loop circulating current suppressing strategy for modular multilevel converter under unbalanced conditions[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1924-1933.
[19] 李凯, 赵争鸣, 袁立强. 模块化多电平变换器上、下桥臂不对称运行环流重复控制[J]. 电工技术学报, 2016, 31(20): 122-129.
Li Kai, Zhao Zhengming, Yuan Liqiang. Repetitive control of circulating current in MMC with asymmetrical operation of upper and lower arms[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 122- 129.
[20] 裴忠晨, 林霖, 应鸿, 等. I-M2C型单级式电力电子变压器[J]. 电网技术, 2020, 44(9): 3565-3574.
Pei Zhongchen, Lin Lin, Ying Hong, et al. Single- stage power electronic transformer based on isolated modular multilevel converter (I-M2C)[J]. Power System Technology, 2020, 44(9): 3565-3574.
[21] 罗永捷, 宋勇辉, 熊小伏, 等. 高压大容量MMC换流阀损耗精确计算[J]. 中国电机工程学报, 2020, 40(23): 7730-7742.
Luo Yongjie, Song Yonghui, Xiong Xiaofu, et al. Accurate loss calculation method for bulk-power MMCs[J]. Proceedings of the CSEE, 2020, 40(23): 7730-7742.
Hybrid Isolated Modular Multilevel Converter
Abstract Thanks to the advantages such as multi-ports, modular topology, easy to achieve voltage level expansion and high quality of output waveform, the power electronic transformer (PET) based on modular multilevel converter (MMC) has
receivedwidespread attention. However, because the voltage on the MVAC (medium-voltage alternating current) side is created by the MVDC (medium voltage direct current) bus, the voltage of MVAC port is always lower than the MVDC port voltage. Combining with the modular topology and single-stage power conversion ideas, this paper proposed a hybrid isolated modular multilevel converter (HI-MMC). Firstly, the HI-MMC structure as well as the topology and modulation strategy of two isolated sub-modules in HI-MMC was analyzed. Through the combination of two different sub-modules, HI-MMC could break through the limitation of voltage ratio and realize the flexible design of the voltage level in each port. Moreover, HI-MMC has main advantages of single-stage power conversion, simple control system and capacitance saving. Secondly, the corresponding configuration schemes of various sub-modules under different voltage ratios were studied, and the average equivalent model of single-phase HI-MMC system was established. Finally, the experimental results on a scaled-down 10kW HI-MMC prototype show that the proposed circuit topology is feasible and effective.
keywords:Power electronics transformer (PET), hybrid isolated modular multilevel converter (HI-MMC), single-stage power conversion, voltage ratio
DOI: 10.19595/j.cnki.1000-6753.tces.200703
中图分类号:TM46
林 霖 男,1996年生,硕士研究生,研究方向为电力电子柔性功率变换技术及其在能源互联网中的应用。E-mail: LLin0718@foxmail.com
刘 闯 男,1985年生,教授,博士生导师,研究方向为电力电子柔性功率变换技术在电力系统中的应用等。E-mail: victorliuchuang@163.com(通信作者)
国家自然科学基金资助项目(51877035)。
收稿日期 2020-06-23
改稿日期 2020-10-16
(编辑 陈 诚)