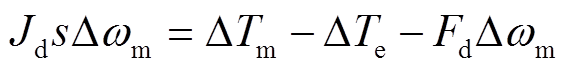 (1)
(1)摘要 随着风电渗透率的增加,风电机组参与电力系统调频已成为间歇式风电消纳的共识。为实现含高比例风电电力系统频率特性的高效准确分析,该文首先建立了附加频率控制下双馈异步风电机组(DFIG)双输入(风速、频率)-单输出(并网功率)频率响应模型,并通过劳斯近似,依次建立了DFIG频率响应4阶和2阶模型;进而针对双馈风电场整体频率响应特性的建模需求,结合矩阵束法和最小二乘法,设计了采用数据重构的双馈风电场频率响应降阶模型参数辨识算法;最后,基于DFIG单机并网系统和含双馈风电场的扩展IEEE 30节点系统,通过对比Matlab/Simulink电磁暂态仿真结果,分别验证了频率响应降阶模型和所提参数辨识算法的准确性和有效性。
关键词:双馈风场 附加频率控制 频率响应 模型降阶 参数辨识
近年来,随着风力发电机组的大规模建设,风电正逐步成为我国电能生产的主要来源之一[1-2]。然而,无论是双馈异步风电机组(Doubly-fed Induction Generator, DFIG)还是永磁直驱风电机组,均经过电力电子换流器接入电网,风力机的转速与电网频率之间不直接耦合,对系统转动惯量的增加作用有限[3],导致风电场发电容量增加替代常规同步发电机组的同时,系统转动惯量和频率调节能力却呈降低趋势[4]。在风电高渗透率接入背景下,风电机组参与系统调频已成为风电安全消纳的共识,被各国电网标准所采纳。
风电机组参与系统调频主要通过附加频率控制器实现,大致可分为超速控制、桨距角控制、惯性控制等[5],其中惯性控制可在全风速工况下提供惯性支撑,因而被广泛运用。由于风机机组动态过程包含电磁、机电暂态和机械动态,多时间尺度完整建模会导致系统级频率特性分析效率的严重低下,因此,对于含高比例风电的电力系统而言,风机(场)合理的频率响应特性建模成为系统频率特性高效分析的基础。文献[6]在忽略定子磁链和转子侧电流及控制器暂态的基础上,建立了小干扰稳定分析用的DFIG 2阶模型,由于不涉及机械暂态过程,模型不适用于系统频率特性分析。针对虚拟惯性控制,文献[7]将全功率换流器简化为惯性环节,虽然降低了模型的复杂度,但并未给出惯性环节参数简化方法。文献[8]假设DFIG输出功率等于参考功率,进而在转子运动方程上直接附加频率控制,但该频率响应建模方式的准确度难以保证。文献[9]针对超速控制,采用线性增量法建立了DFIG的3阶频率-功率响应模型,但未给出所涉及等效参数的确定方法,且无法考虑风速变化对并网功率的影响,属于单输入-单输出模型。文献[10]建立了考虑虚拟惯性控制的DFIG3阶模型,但仅适用于描述转子角速度和电网角频率之间的互作用关系。
对于含多台机组的风电场,各机组的运行状态不一,若以机组为基本单元进行风场整体频率响应特性的集成,维数灾问题会极为显著。为简化建模,文献[11]将参与调频的风电场等效为1阶惯性环节,进而建立了含风电参与调频的电力系统整体频率响应模型,但该模型忽略了风电场的机电暂态特性,准确性较差。文献[12]基于额定风速以下和以上的两台等值风机,建立了风场参与一次调频时动态响应的状态空间模型,但其输入为风力机功率补偿指令,输出为并网功率增量,因而无法直接用于系统级的频率特性分析。虽然原理上可根据风速情况对风场进行多机动态等值,然后建立参与系统调频的降阶模型[13],但模型参数将经过多机等值和单机降阶2次处理。
在风场等值建模过程复杂和参数适用性差的情况下,通过仿真或者监测数据进行直接参数辨识成为简化建模过程的有效替代方案。常用的参数辨识算法主要有最小二乘法、递推最小二乘法、梯度校正法、极大似然估计法、Prony估计法及粒子群等智能算法[14-19],在虚拟同步机控制并网逆变器、永磁同步电机等同步系统频率响应特性辨识中已有较多应用[20-21]。然而,双馈风场具有显著的非同步和受风速影响的特征,附加频率控制后,风场并网功率对频率、风速扰动的响应之间存在相关性,这给参数辨识增加了困难。目前,针对风场的辨识多是对单机或者多机等值参数[22-23],对频率响应特性的简化建模和参数获取却鲜有文献讨论。文献[24]以单机等值前后输出功率偏差的二次方和作为评判目标函数,采用遗传算法,寻求定转子阻抗、励磁电抗、转子惯性时间常数等最优等值参数。文献[25]则采用粒子群算法辨识影响机组输出功率的主导参数,包括控制参数、发电机参数和锁相环参数等。文献[26]采用风电场公共并网点相量测量单元数据,提出了基于轨迹灵敏度的等值风机参数辨识方法。就应用范围而言,风电场单机或多机等值模型主要用于系统暂态特性研究,而频率响应模型则适用于系统频率特性分析;从模型复杂度上看,单机或多机等值以机组为单元,保留了完整的物理特征,而经简化得到的频率响应模型复杂度则远低于单机或多机等值,但其参数无直接的物理意义,因此在辨识上与等值机参数辨识存在差异,且依赖合理的模型简化结构。
为获得较为准确的双馈风电场频率响应模型与特性参数,本文首先建立了完整的附加频率控制DFIG双输入(风速、频率)-单输出(并网功率)频率响应线性化模型,并采用劳斯近似,分别推导了DFIG频率响应4阶和2阶模型,实现了单个机组等效参数的严格获取。进而针对风电场频率响应建模的需求,以DFIG频率响应2阶模型为基础,结合矩阵束法与最小二乘法,设计了基于数据重构的双馈风电场频率响应特性参数辨识算法。最后,采用DFIG单机并网系统和含双馈风电场的扩展IEEE30节点系统,通过对比Matlab/Simulink电磁暂态仿真,验证了频率响应降阶模型和所提参数辨识算法的有效性和准确性。
DFIG转子动态过程主要体现在运动方程上,其小信号方程为
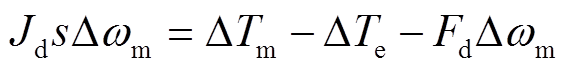 (1)
(1)式中,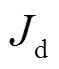 为风力机和异步电机转动惯量之和;
为风力机和异步电机转动惯量之和;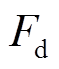 为DFIG摩擦系数;
为DFIG摩擦系数;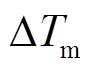 与
与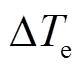 分别为机械转矩和电磁转矩增量;
分别为机械转矩和电磁转矩增量;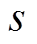 为拉普拉斯算子;
为拉普拉斯算子;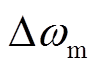 为机械角速度增量。
为机械角速度增量。
机械转矩由风力机提供,即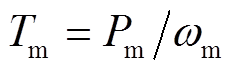 ,
,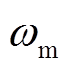 为转子机械角速度,
为转子机械角速度,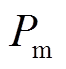 为风力机捕获的机械功率,
为风力机捕获的机械功率,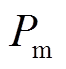 为
为
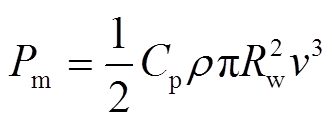 (2)
(2)式中,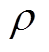 为空气密度;
为空气密度;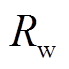 为风轮叶片半径;
为风轮叶片半径;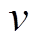 为进入风力机扫掠面之前的空气流速;
为进入风力机扫掠面之前的空气流速;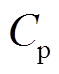 为风能利用系数,其经典的计算公式为[27]
为风能利用系数,其经典的计算公式为[27]
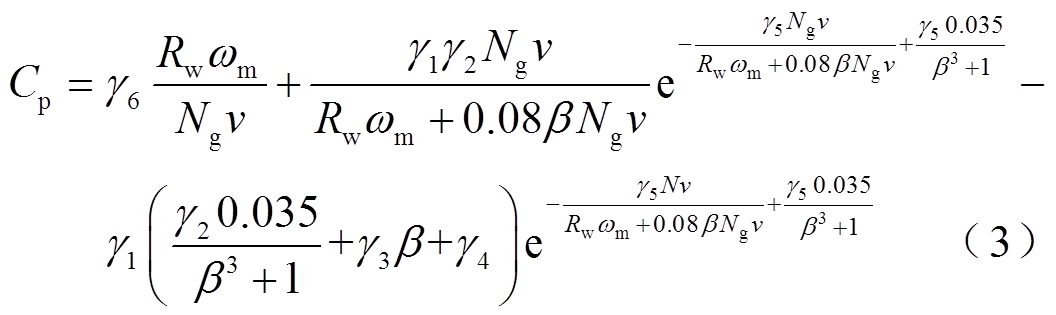
式中,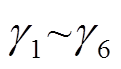 为风能利用系数曲线的拟合参数;
为风能利用系数曲线的拟合参数;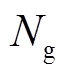 为齿轮箱变速比;
为齿轮箱变速比;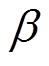 为桨距角。
为桨距角。
当机械角速度与风速分别增加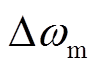 和
和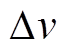 时,机械功率增量为
时,机械功率增量为
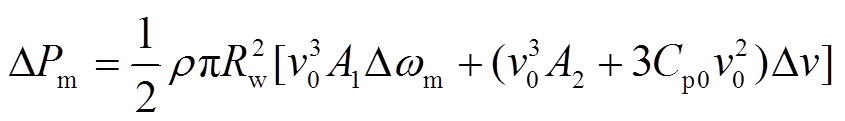 (4)
(4)式中,下标“0”表示状态量稳态值;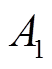 与
与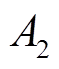 分别为
分别为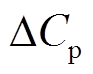 关于
关于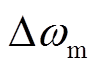 和
和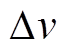 的系数。限于篇幅,不再详细列出。
的系数。限于篇幅,不再详细列出。
由式(4),机械转矩增量可表示为
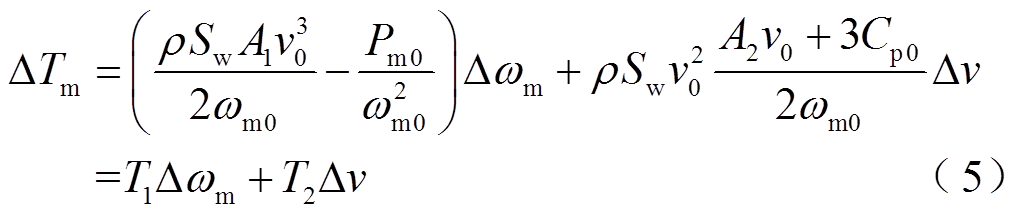
式中,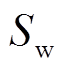 为风轮扇叶扫过的面积。
为风轮扇叶扫过的面积。
由异步电机的转矩方程,电磁转矩可描述为
 (6)
(6)式中,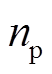 为异步发电机极对数;
为异步发电机极对数;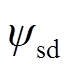 与
与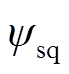 分别为定子dq坐标系下d轴与q轴的磁链;
分别为定子dq坐标系下d轴与q轴的磁链;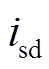 、
、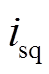 为定子d、q轴电流。
为定子d、q轴电流。
对于常用的定子电压定向矢量控制,异步电机定子电压可近似为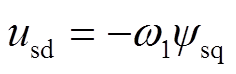 ,
,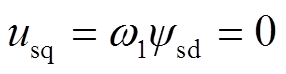 ,其中
,其中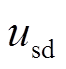 为定子d轴电压,
为定子d轴电压,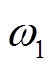 为电网角频率。将磁链替换后可得电磁转矩增量的近似表达式为
为电网角频率。将磁链替换后可得电磁转矩增量的近似表达式为
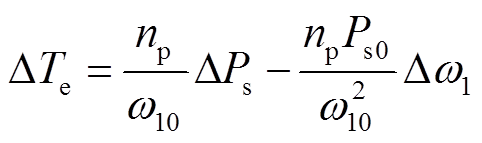 (7)
(7)式中,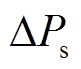 为定子侧有功功率的增量;
为定子侧有功功率的增量;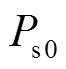 为定子有功功率稳态值。
为定子有功功率稳态值。
基于定子电压定向矢量控制,DFIG定子功率对控制指令的增量可表示为
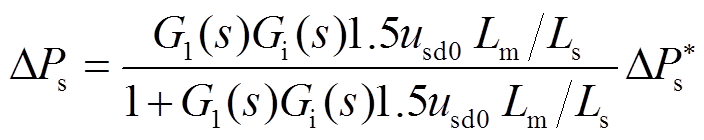 (8)
(8)式中,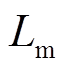 为定、转子间的互感;
为定、转子间的互感;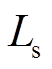 为定子绕组的电感;
为定子绕组的电感;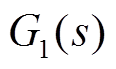 为转子侧换流器外环PI调节器;
为转子侧换流器外环PI调节器;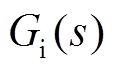 为电流内环传递函数,即
为电流内环传递函数,即
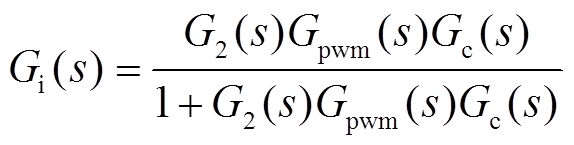 (9)
(9)式中,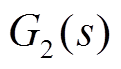 为转子侧换流器电流内环PI调节器;
为转子侧换流器电流内环PI调节器;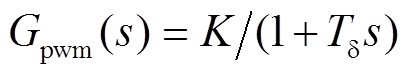 ,
,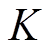 为PWM的调制增益,
为PWM的调制增益,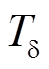 为开关周期;
为开关周期;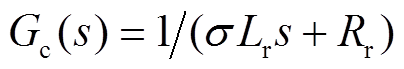 ,
,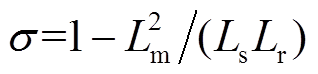 为漏磁系数,
为漏磁系数,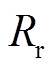 、
、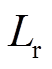 分别为转子绕组的电阻和电感。
分别为转子绕组的电阻和电感。
为不失一般性,本文考虑的附加频率控制包含频率变化回路和频率偏差回路。频率变化率回路用于调整频率变化峰值;频率偏差回路用于增加调频的快速性。系统频率扰动引起的DFIG有功出力增量为
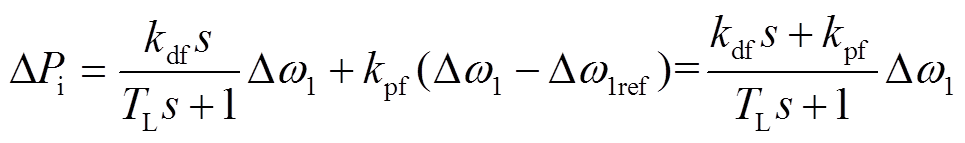 (10)
(10)式中,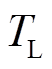 为低通滤波器的时间常数;
为低通滤波器的时间常数;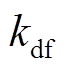 为虚拟惯性系数;
为虚拟惯性系数;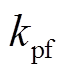 为下垂控制系数。
为下垂控制系数。
为保证DFIG参与调频的能力,附加频率控制一般需要同时采用限功率减载策略实现有功备用,因此,功率外环有功参考值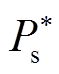 可根据最大功率点跟踪(Maxium Power Point Tracking, MPPT)最佳运行点
可根据最大功率点跟踪(Maxium Power Point Tracking, MPPT)最佳运行点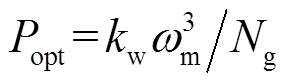 和附加频率控制器的有功出力
和附加频率控制器的有功出力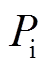 联合给出,其小信号增量可描述为
联合给出,其小信号增量可描述为
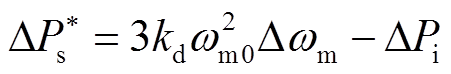 (11)
(11)式中,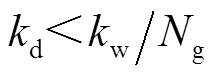 ,
,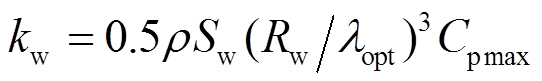 。
。
忽略定、转子的铜损,DFIG并网功率与其电磁功率近似相等,即
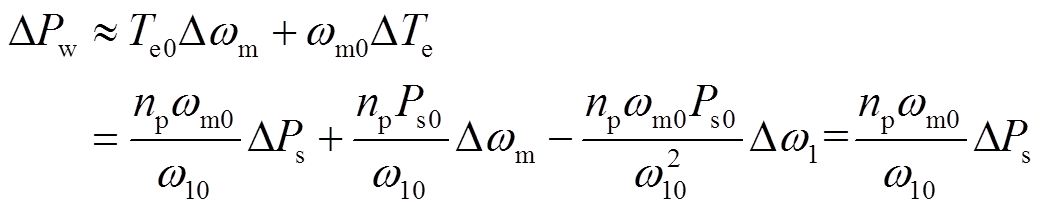 (12)
(12) 综合上述推导,可得如图1所示附加频率控制下DFIG双输入-单输出频率响应模型。
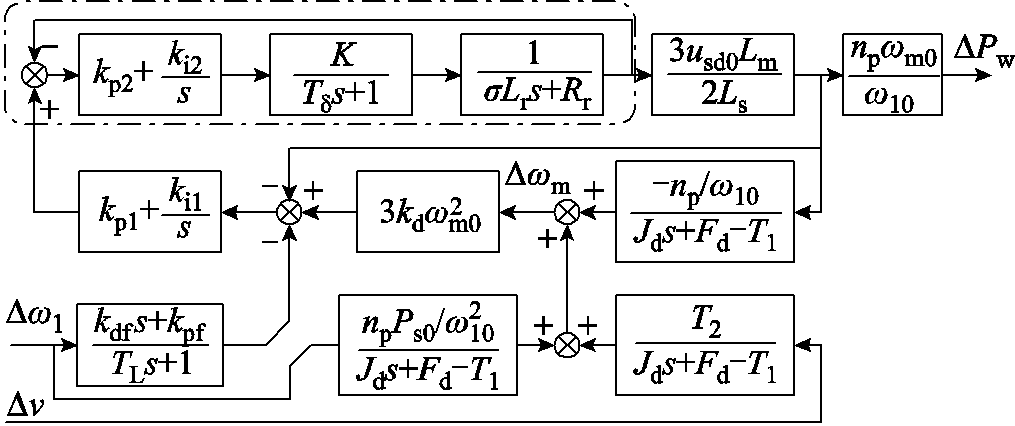
图1 DFIG频率响应模型
Fig.1 Model of frequency response applied to DFIG
对于含高比例风电的电力系统,以上述模型进行系统频率特性分析易造成模型维数灾问题,建立简化的频率响应解析模型十分必要。
上述DFIG频率响应模型涉及附加频率控制、矢量控制、转子机械动态过程,其中矢量控制贡献了4阶。考虑到PWM调制过程等效时间常数较小,带宽较大,对于低频段的频率响应特性建模而言,可等效为增益环节,从而电流内环开环传递函数为
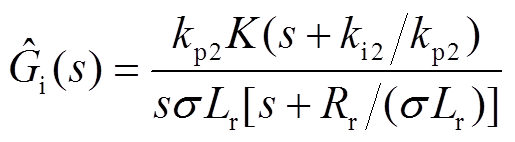 (13)
(13)当按照典型的I型系统设计电流内环的PI参数时[28],即式(13)的极点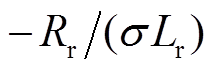 和零点
和零点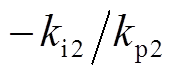 对消,电流内环可近似为
对消,电流内环可近似为
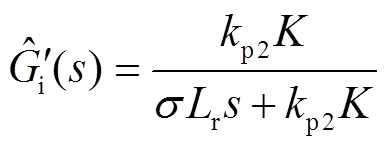 (14)
(14)
从而转子侧控制器的有功传递特性可表示为
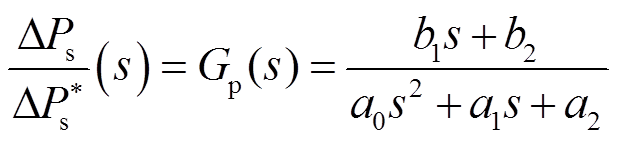 (15)
(15)式中
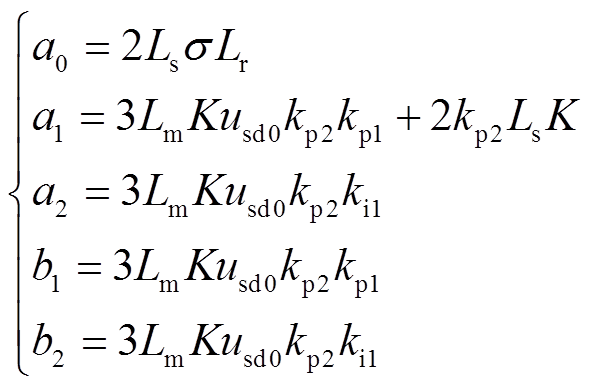 (16)
(16)
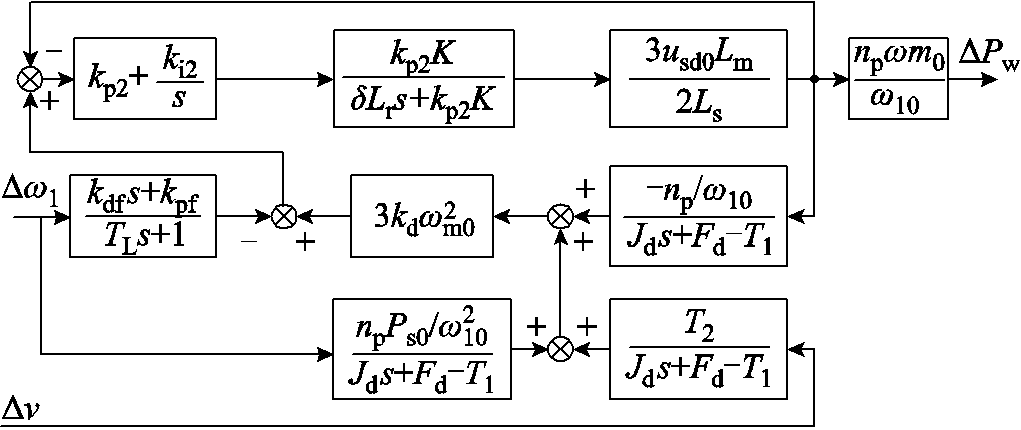
图2 DFIG频率响应降阶模型(4阶)
Fig.2 Reduced-order model of frequency response applied to DFIG (4th-order)
结合附加频率控制器,可得图2所示DFIG频率响应4阶模型,其传递函数如式(17)与式(18)所示。
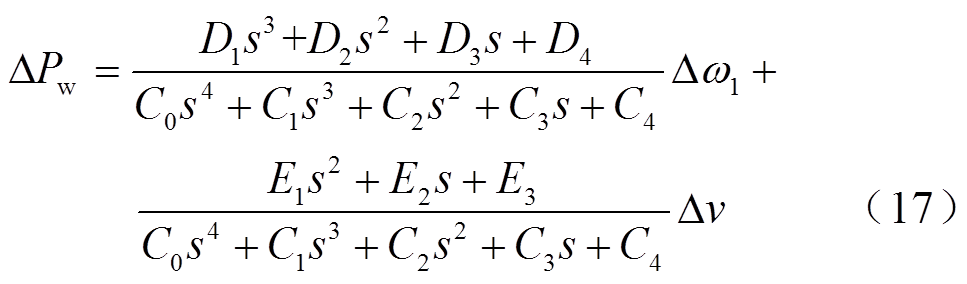
式中
 (18)
(18)
为在复杂度上匹配常规发电机的2阶模型,采用劳斯近似[29]对式(15)所示DFIG的有功传递特性进行二次降阶
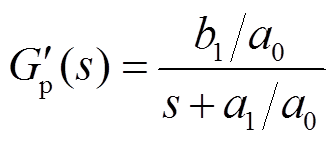 (19)
(19)式(19)表明降阶后的功率传递特性的极点为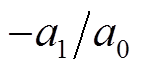 。为确保获取低频段的近似,对式(15)进行倒数变换,即
。为确保获取低频段的近似,对式(15)进行倒数变换,即
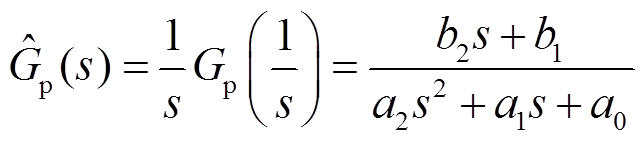 (20)
(20)
对式(20)采用劳斯近似处理并再次进行倒数变换,可得一阶近似为
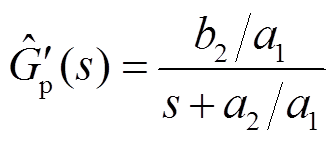 (21)
(21)式(21)的极点为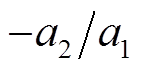 ,由风机典型控制参数,
,由风机典型控制参数,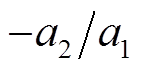 更靠近虚轴,表明式(21)照顾了近似对象的低频性能,而式(19)保留了近似对象的高频特性。因此,选择式(21)作为DFIG有功传递特性的一阶近似,从而
更靠近虚轴,表明式(21)照顾了近似对象的低频性能,而式(19)保留了近似对象的高频特性。因此,选择式(21)作为DFIG有功传递特性的一阶近似,从而
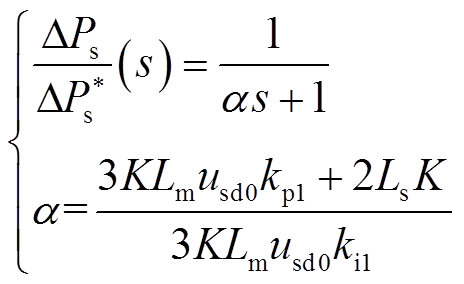 (22)
(22)
由于低通滤波器时间常数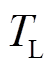 的数量级在
的数量级在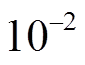 左右,其带宽可覆盖系统频率波动所在频段,从而
左右,其带宽可覆盖系统频率波动所在频段,从而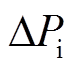 可近似为
可近似为
 (23)
(23)综合上述近似,可得图3所示DFIG频率响应双输入-单输出2阶模型,即
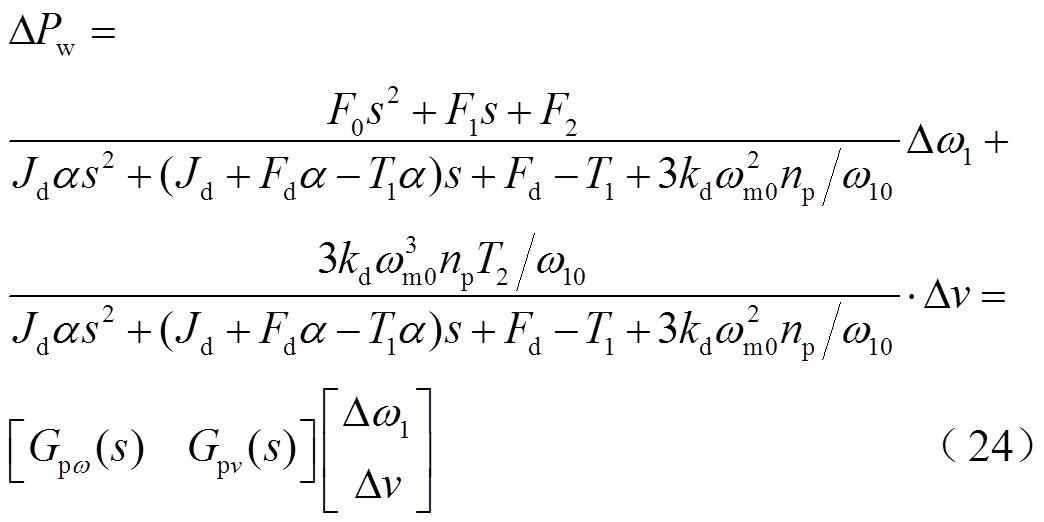
式中,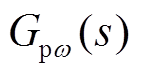 与
与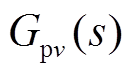 分别为并网功率对电网频率扰动与风速扰动的响应特性;
分别为并网功率对电网频率扰动与风速扰动的响应特性;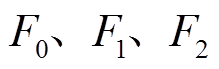 分别为
分别为
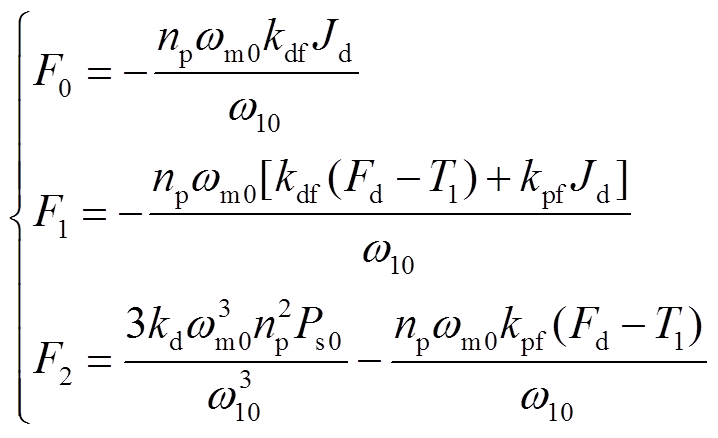 (25)
(25)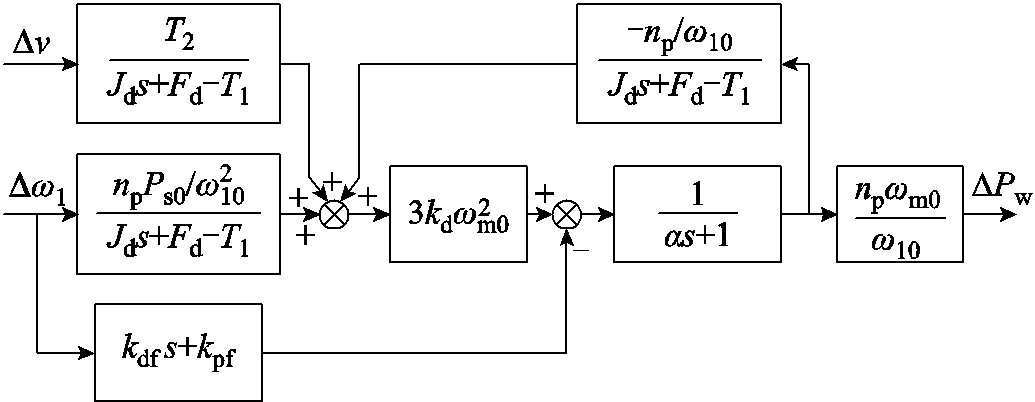
图3 DFIG频率响应降阶模型(2阶)
Fig.3 Reduced-order model of frequency response applied to DFIG (2th-order)
式(24)与式(25)确定了含附加频率控制的DFIG频率响应模型的2阶形式,具体参数可通过代入实际机组数据导出。然而,对于含多DFIG的风电场,由于各机组不同运行点和集电网络的影响,风电场整体频率响应特性难以推导获得,通过仿真或实际监测数据进行风电场频率响应模型的参数辨识成为另一可行途经。
考虑到仿真和监测数据的离散性,采用后向差分法对式(24)进行z变换,即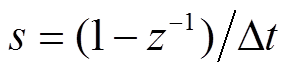 ,其中
,其中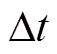 为采样时间间隔,离散后的z域传递函数可表示为
为采样时间间隔,离散后的z域传递函数可表示为
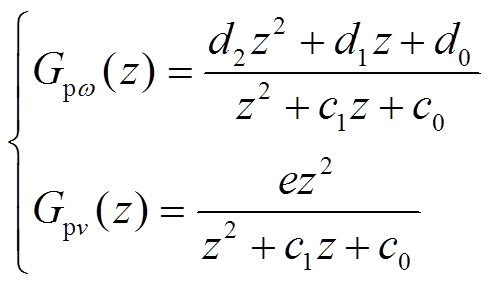 (26)
(26)式中,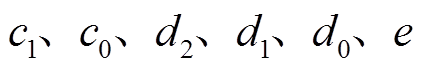 为z域传递函数待辨识系数。
为z域传递函数待辨识系数。
若令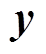 为并网功率的采样数据序列,
为并网功率的采样数据序列,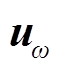 与
与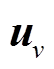 分别为电网频率和风速的采样数据序列,待辨识参数与采样数据序列之间均应满足[14]
分别为电网频率和风速的采样数据序列,待辨识参数与采样数据序列之间均应满足[14]
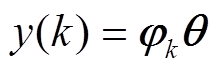 (27)
(27)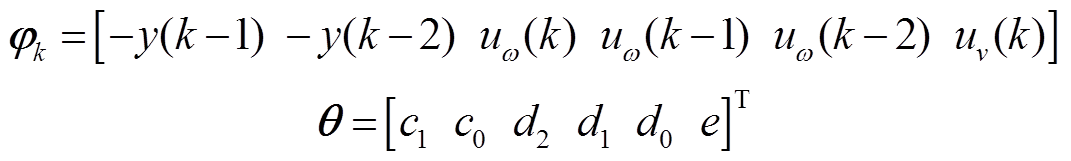
式中,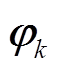 为观测向量。
为观测向量。
考虑数据噪声或异常值的影响,对于N次观测下,待辨识参数向量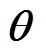 的准确度可用式(28)所示误差二次方和进行度量。
的准确度可用式(28)所示误差二次方和进行度量。
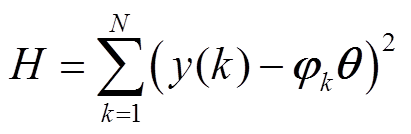 (28)
(28)由函数极值定理可知,当满足式(29)时,式(28)具有最小值,即
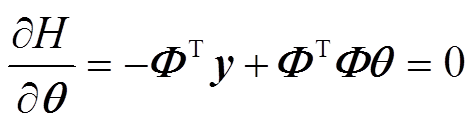 (29)
(29)
其中
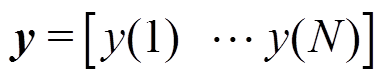 T
T 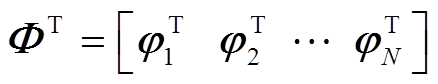
若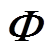 满秩,则待辨识参数向量
满秩,则待辨识参数向量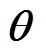 的最小二乘估计解为
的最小二乘估计解为
 (30)
(30)
由式(30),可得双馈风电场频率响应特性的z域传递函数。对于式(26)所示s域传递函数,可通过以下逆变换得到。
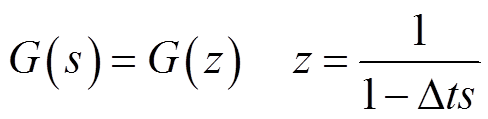 (31)
(31)式(27)~式(31)为双馈风电场频率响应特性参数辨识提供了可遵循的基本流程,但在实际应用时仍存在以下难点:
(1)风场风速波动会引起并网功率变化,进而导致背景交流系统频率的变化,而附加频率控制后DFIG转子转速与电网频率相互作用,促使并网功率出现新的动态过程。风速、功率和频率三者之间的耦合表现在式(29)则是不定方程存在多解,不易厘清并网功率中对应于风速变化和频率变化的部分,从而导致辨识上的困难。
(2)双馈风电场中普遍存在转子侧/网侧换流器开关频率附近的谐波,对于低频段的风场频率响应特性辨识而言,相应高次谐波表现为数据噪声。最小二乘估计对有色数据噪声的适应性差,尤其体现在噪声导致的功率采样数据序列直流分量偏差上。
针对难点(1),可通过分步辨识的方式进行处理,即风速平稳时先估计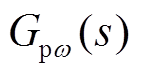 ,然后通过线性近似和叠加抵消的方式辨识
,然后通过线性近似和叠加抵消的方式辨识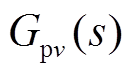 ,但采样数据序列需要经过合理筛选。针对难点(2),可通过矩阵束法和奇异值分解[30]预处理,通过重构获得低频主导分量表示为
,但采样数据序列需要经过合理筛选。针对难点(2),可通过矩阵束法和奇异值分解[30]预处理,通过重构获得低频主导分量表示为
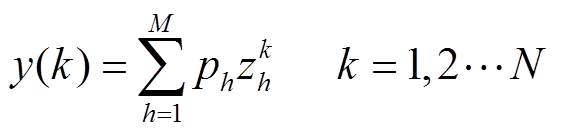
其中
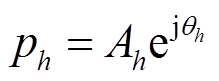
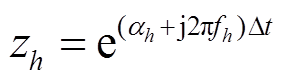
式中,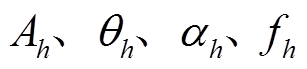 分别为分量
分别为分量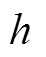 幅值、初始相位、衰减因子和频率;Dt为采样时间间隔。综合上述处理方式,风场频率响应特性辨识算法的主流程如图4所示。
幅值、初始相位、衰减因子和频率;Dt为采样时间间隔。综合上述处理方式,风场频率响应特性辨识算法的主流程如图4所示。

图4 频率响应特性辨识算法主流程
Fig.4 Main process of identification algorithm for frequency response
(1)辨识所需风场数据采集。设置采样间隔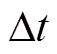 和采样总时长
和采样总时长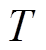 ,采集风电场各监测点风速、并网点处频率和并网功率数据,构成平均风速(各点取平均)、电网频率和并网功率序列
,采集风电场各监测点风速、并网点处频率和并网功率数据,构成平均风速(各点取平均)、电网频率和并网功率序列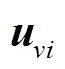 、
、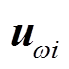 和
和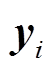 ,
,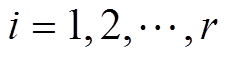 ,各序列长度为
,各序列长度为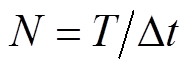 ,r为采集次数。保留m段风速序列初始状态相近的序列
,r为采集次数。保留m段风速序列初始状态相近的序列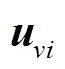 及其对应的
及其对应的 和
和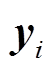 ,
,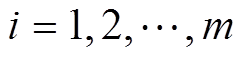 。初始状态相近的判定条件为
。初始状态相近的判定条件为
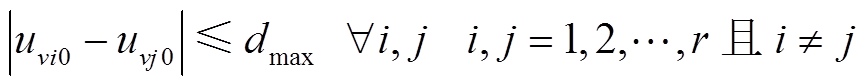
式中,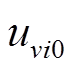 为序列
为序列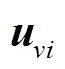 的初始状态;
的初始状态;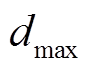 为判定阈值。
为判定阈值。
(2)序列状态判定与筛选。对平均风速和电网频率子序列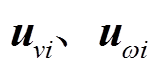 进行归一化处理。若
进行归一化处理。若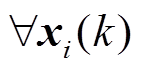 ,
,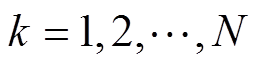 ,满足
,满足 则判定为平稳序列
则判定为平稳序列 ,否则为非平稳序列
,否则为非平稳序列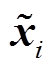 ,其中
,其中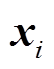 表示归一化后子序列
表示归一化后子序列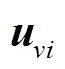 或
或 ,
,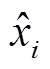 表示序列均值,上标“-”或“~”分别用于标识平稳与非平稳序列。风速与频率序列按平稳与否可划分为
表示序列均值,上标“-”或“~”分别用于标识平稳与非平稳序列。风速与频率序列按平稳与否可划分为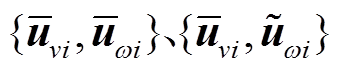 和
和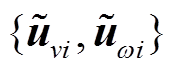 三类组合。
三类组合。
(3)功率序列滤波预处理。对归属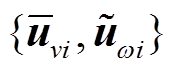 和
和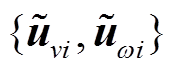 的任一并网功率序列
的任一并网功率序列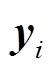 ,构造Hankel矩阵
,构造Hankel矩阵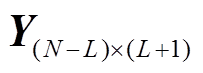 进行SVD分解,并保留前M个奇异值对应的右酉矩阵
进行SVD分解,并保留前M个奇异值对应的右酉矩阵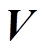 ,束参数
,束参数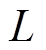 通常取
通常取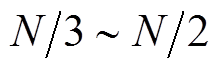 。
。
(4)功率序列低频主导分量参数估计。计算SVD分解和去噪后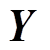 矩阵束的广义特征值,即求解
矩阵束的广义特征值,即求解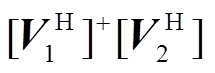 的特征值
的特征值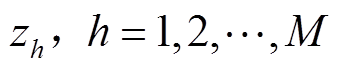 ,其中
,其中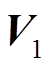 和
和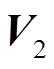 分别由
分别由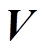 去除最后一行和第一行获得。从而,低频主导分量特征参数可由式(32)的最小二乘解获得
去除最后一行和第一行获得。从而,低频主导分量特征参数可由式(32)的最小二乘解获得
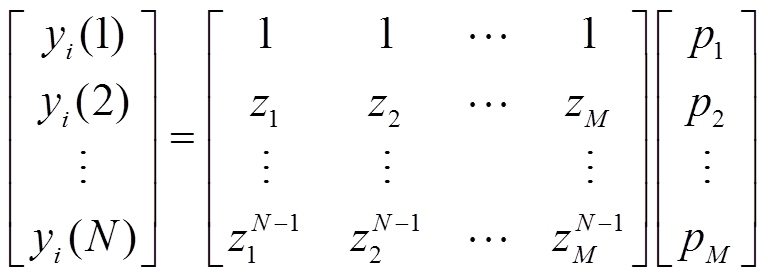 (32)
(32)(5)功率序列数据重构。按序列衰减指数和形式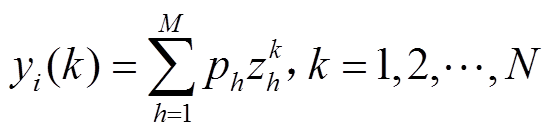 重构
重构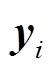 ,分量
,分量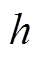 的幅值、初始相位、衰减因子和频率参数分别为
的幅值、初始相位、衰减因子和频率参数分别为
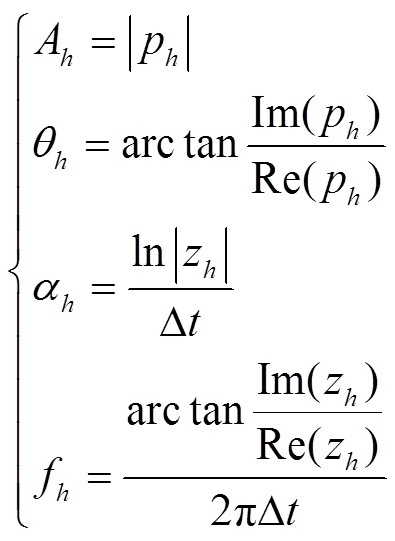 (33)
(33)
从而,可得重构后的并网功率序列为
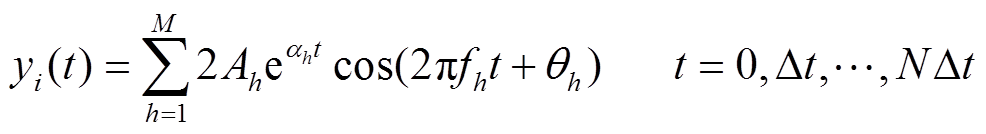 (34)
(34)便于论述,将对应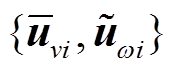 的重构功率序列记为
的重构功率序列记为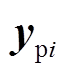 ,而对应
,而对应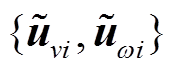 的重构功率序列记为
的重构功率序列记为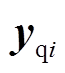 。
。
(6)单一频率响应特性估计。对归属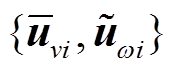 类型的序列组合,以
类型的序列组合,以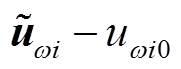 和
和 分别作为输入和输出,其中
分别作为输入和输出,其中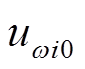 、
、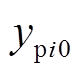 分别为频率和并网功率序列的初始值。忽略风速子序列,式(28)改写为
分别为频率和并网功率序列的初始值。忽略风速子序列,式(28)改写为
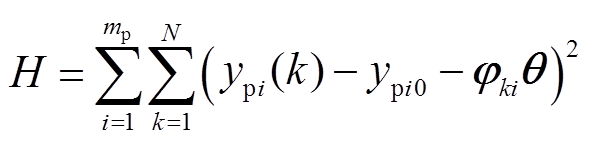 (35)
(35)其中
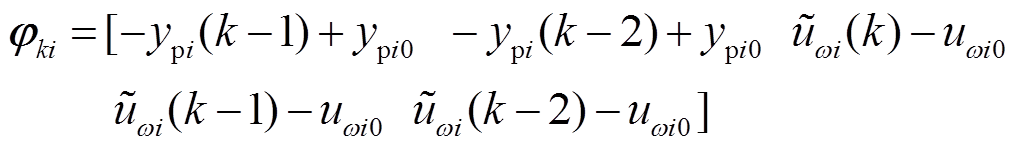
式中,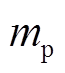 为序列组合
为序列组合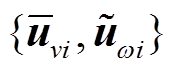 的总数。按
的总数。按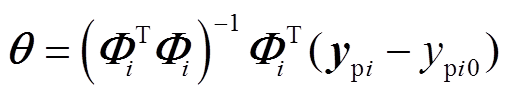 估计
估计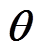 的最小二乘解,其中
的最小二乘解,其中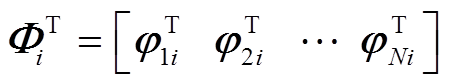 ,从而可初步确定单一频率响应特性
,从而可初步确定单一频率响应特性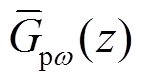 。
。
(7)风速与频率响应特性统一辨识。令输入为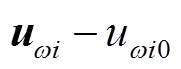 和
和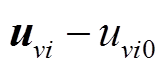 ,且当
,且当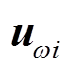 归属
归属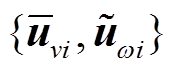 类型时,
类型时,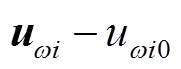 用0替代。令输出为
用0替代。令输出为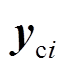 ,构造方式为
,构造方式为
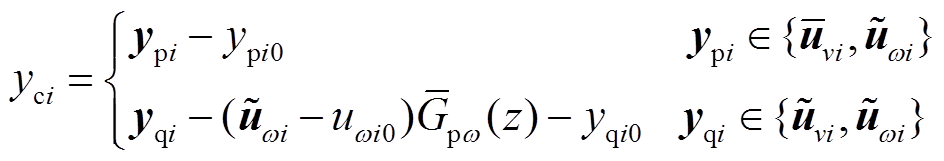 (36)
(36)从而,式(28)可扩展为
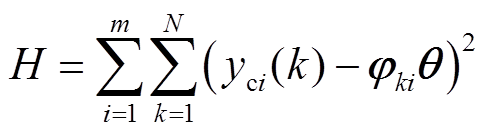 (37)
(37)
其中
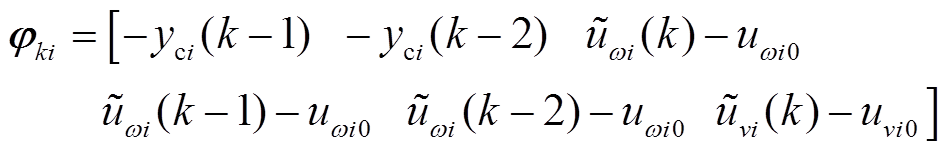
按式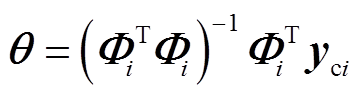 估计
估计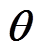 的最小二乘解,其中
的最小二乘解,其中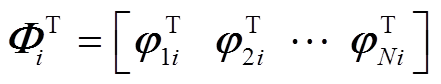 ,可得极点分布一致的风速与频率响应特性离散传递函数
,可得极点分布一致的风速与频率响应特性离散传递函数 和
和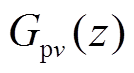 ,进而按式(31)对其进行反变换,可最终确定
,进而按式(31)对其进行反变换,可最终确定 和
和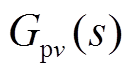 。
。
需要指出:①上述步骤给出了风场频率响应特性辨识的基本算法框架,对于重构、辨识等环节,可按实际对效率与精度的不同需求选用其他方法替换;考虑到实施的简单性,仍选择最小二乘法作为分步辨识工具,在线应用时该环节也可替换为实时性更好的递推最小二乘法。②风电场数据采集时需考虑数据异常值问题,配置相应的数据清洗步骤。③低频分量数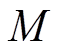 可由
可由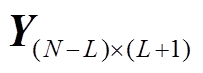 的奇异值确定,若
的奇异值确定,若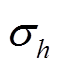 满足式(38),则
满足式(38),则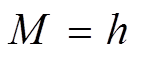 。
。
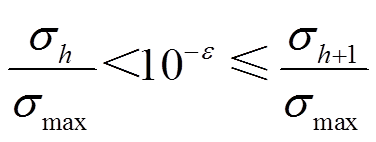 (38)
(38)式中,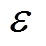 为筛选阈值,表示比值低于10-e的
为筛选阈值,表示比值低于10-e的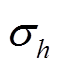 被认为是噪声奇异值;
被认为是噪声奇异值;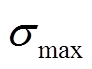 为最大奇异值。
为最大奇异值。
DFIG频率响应降阶模型是双馈风电场频率响应特性参数辨识的基础。为直接验证所推导的附加频率控制DFIG频率响应模型的准确性,在Matlab/Simulink搭建了DFIG单机并网系统,其基本参数见表1。背景交流系统由容量100MV×A等值发电机构成,其转动惯量为6 500kg×m2,频率扰动由系统负荷投入切出产生。
4.1.1 频率响应降阶模型推导结果
由表1中参数,按图2和图3可分别得到附加频率控制后DFIG频率响应的4阶和2阶降阶模型。在给定频率扰动和风速扰动下,DFIG频率响应降阶模型输出与电磁暂态(Electro-Magnetic Transient, EMT)仿真的对比结果如图5所示。图6给出了4阶模型和2阶模型输出相较于EMT仿真轨迹(换流器采用平均建模)的误差。就精度而言,频率响应2阶模型的精度与4阶模型相近,两者均与电磁暂态模型保持了较好的一致性,表明所推导的频率响应降阶模型能保留DFIG在频率特性方面的主要特征。
表1 DFIG单机并网系统参数
Tab.1 Parameters of DFIG grid-connected system

参数数值 额定功率P/MW2 定子额定电压V/kV0.575 风力机和异步电机转动惯量和Jd/(kg×m2)580 定、转子绕组电阻Rs, Rr/mW23,16 定、转子绕组漏感Lls, Llr/mH0.18,0.16 定转子之间互感Lm/mH2.9 电流内环PI [kp ki][1.6 80] 功率外环PI [kp ki][0.2 20] 虚拟惯性系数kdf 下垂系数kpf
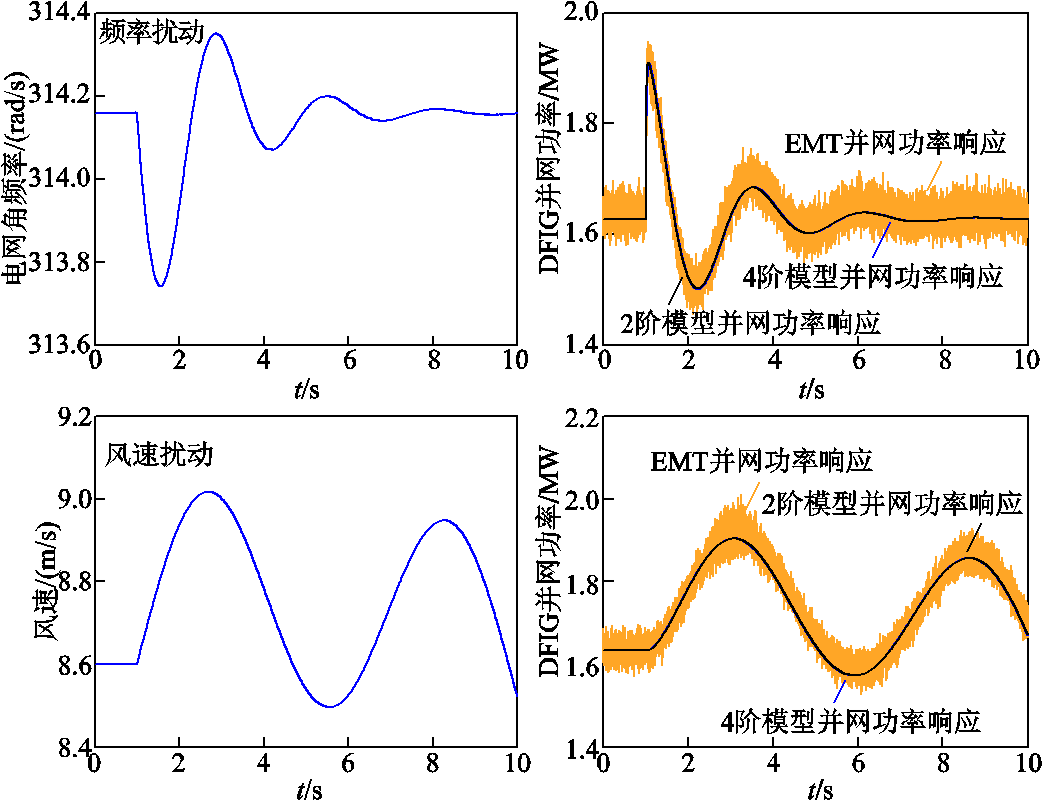
图5 频率/风速扰动下DFIG频率响应降阶模型(推导结果)输出与EMT仿真对比
Fig.5 Comparison of frequency response between reduced-order model(derived results) and EMT simulation under frequency/wind disturbance
结合发电机2阶模型,分别以DFIG频率响应4阶和2阶模型构建系统频率特性分析模型,表2给出了不同复杂度的系统频率特性分析模型与EMT仿真的分析耗时对比(仿真总时长为10s),计算机配置为Intel i7-9700 CPU 3.00GHz。采用频率响应模型的仿真耗时远小于EMT仿真耗时,4阶模型的仿真时长约为2阶模型的1.6倍,考虑到两者精度相近,在含分散式风场参与调频的电力系统中,应用2阶模型的仿真效率优势会更加显著。
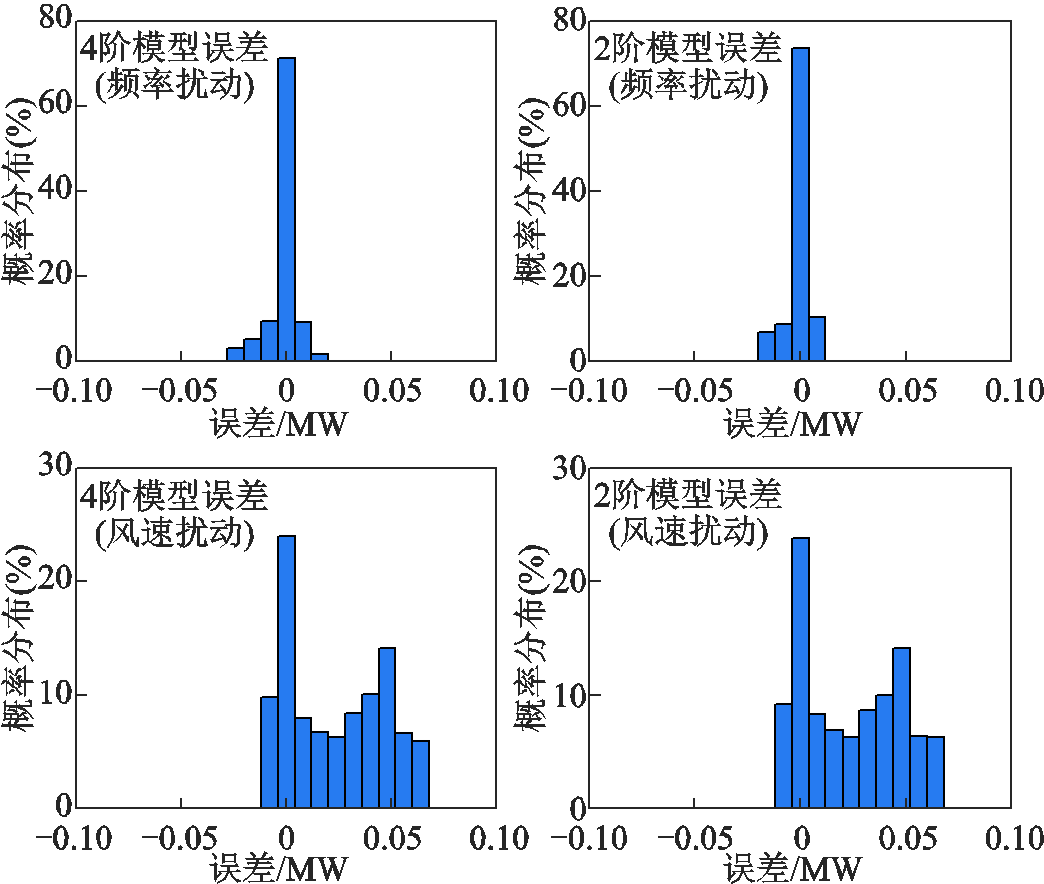
图6 频率/风速扰动下DFIG频率响应降阶模型(推导结果)输出误差分布
Fig.6 Error distribution of DFIG reduced-order frequency response model (derived results) under frequency/wind disturbance
表2 仿真耗时对比
Tab.2 Comparison of simulation time cost

单机并网系统仿真模型仿真耗时/s EMT详细模型202.48 2阶发电机模型+4阶DFIG频率响应模型12.16 2阶发电机模型+2阶DFIG频率响应模型7.56
4.1.2 频率响应降阶模型辨识结果
为了验证频率响应参数辨识方法有效性,仍以单机系统为测试对象。采样间隔设置为2ms,采样时间为10s,筛选出图7所示4段数据,采用所提基于矩阵束重构和最小二乘法的分步辨识算法,辨识结果见表3。
表3 不同算法参数辨识结果
Tab.3 Identification results of different identification algorithms

辨识算法辨识结果 矩阵束重构+最小二乘法 低通滤波+最小二乘法 矩阵束重构+Prony估计
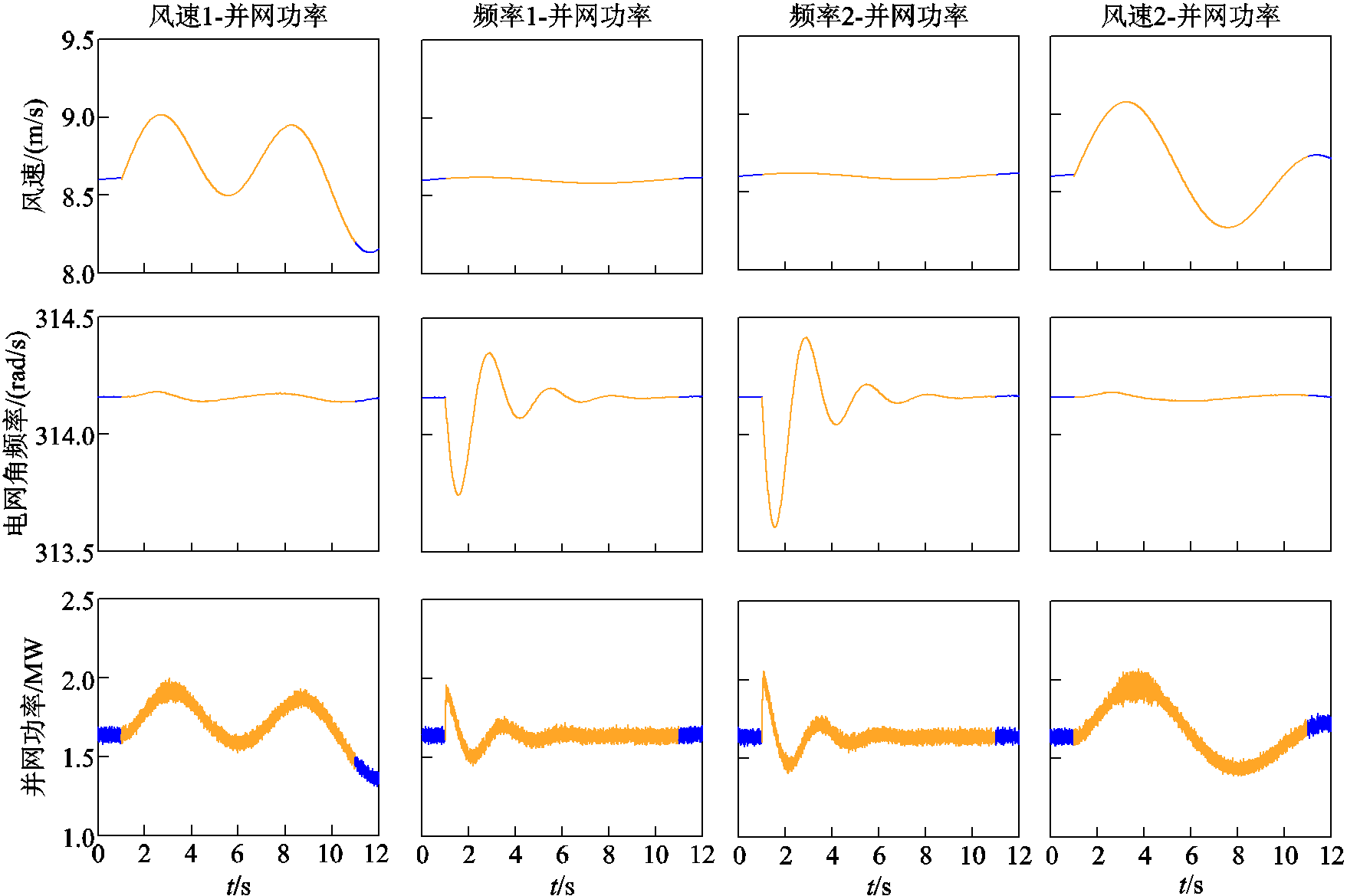
图7 DFIG单机并网系统采样数据序列
Fig.7 Sampling data of DFIG grid-connected system
以频率扰动和风速扰动作为输入,辨识出的频率响应模型的输出与EMT仿真的对比及其误差分布如图8所示,其中误差是以EMT平均值模型仿真轨迹为基准,两者相减获得。图中,由频率响应辨识模型得到的并网功率动态轨迹与EMT仿真轨迹具有较好的一致性。频率扰动下的误差分布在±0.002MW范围内,而风速扰动下输出误差分布在±0.09MW范围内,若以峰值功率2MW为基值,相对误差分布范围分别是±0.1%与±4.5%,说明所提算法对DFIG频率扰动-功率响应特性的辨识结果具有更高的精度。
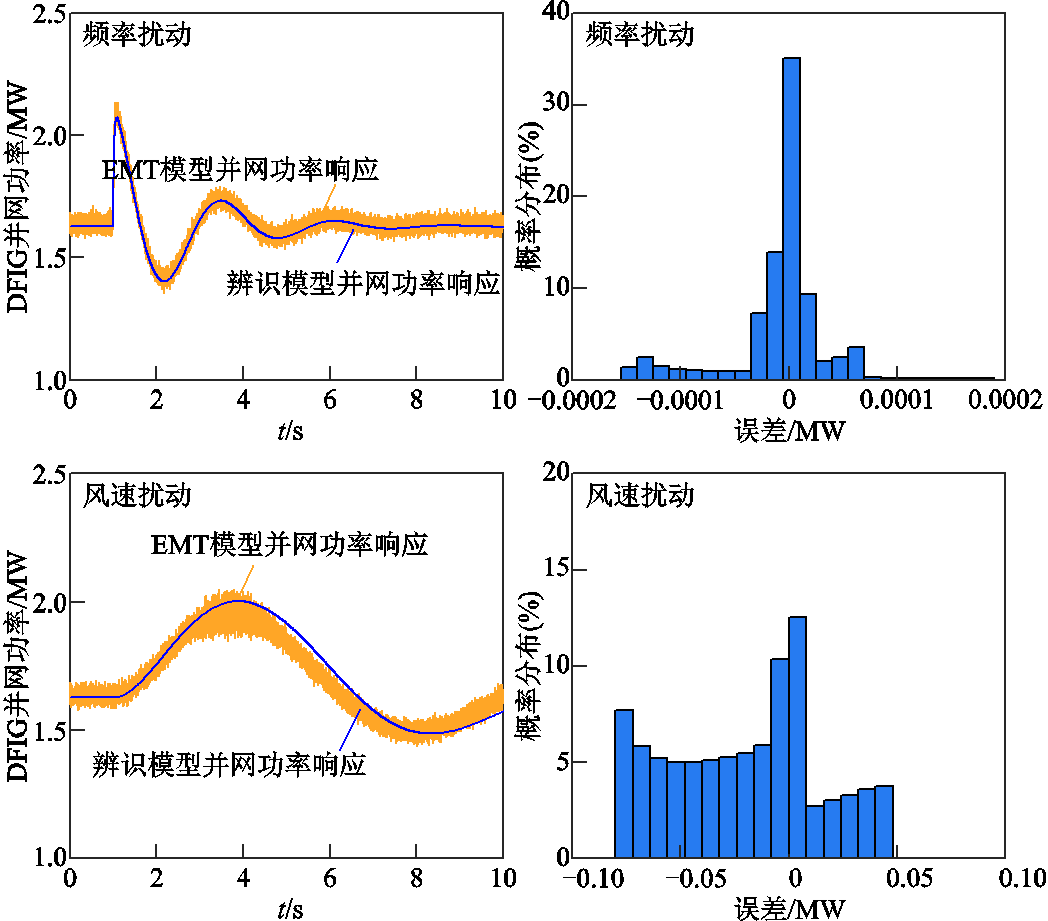
图8 频率/风速扰动下DFIG频率响应降阶模型(辨识结果)输出与EMT仿真对比
Fig.8 Comparison of power between estimated model and EMT detailed model under frequency/wind disturbance
设置稳态风速分别为8.3m/s和8.9m/s,对辨识出的频率响应模型进行适用范围测试。在频率与风速扰动下,与EMT仿真轨迹的对比结果如图9所示。在不同稳态风速的运行工况下,辨识模型的输出和EMT仿真得到的动态轨迹基本一致,说明了线性化与多重降阶方式获得的频率响应模型及其参数辨识结果在较宽风速范围下的适用性。
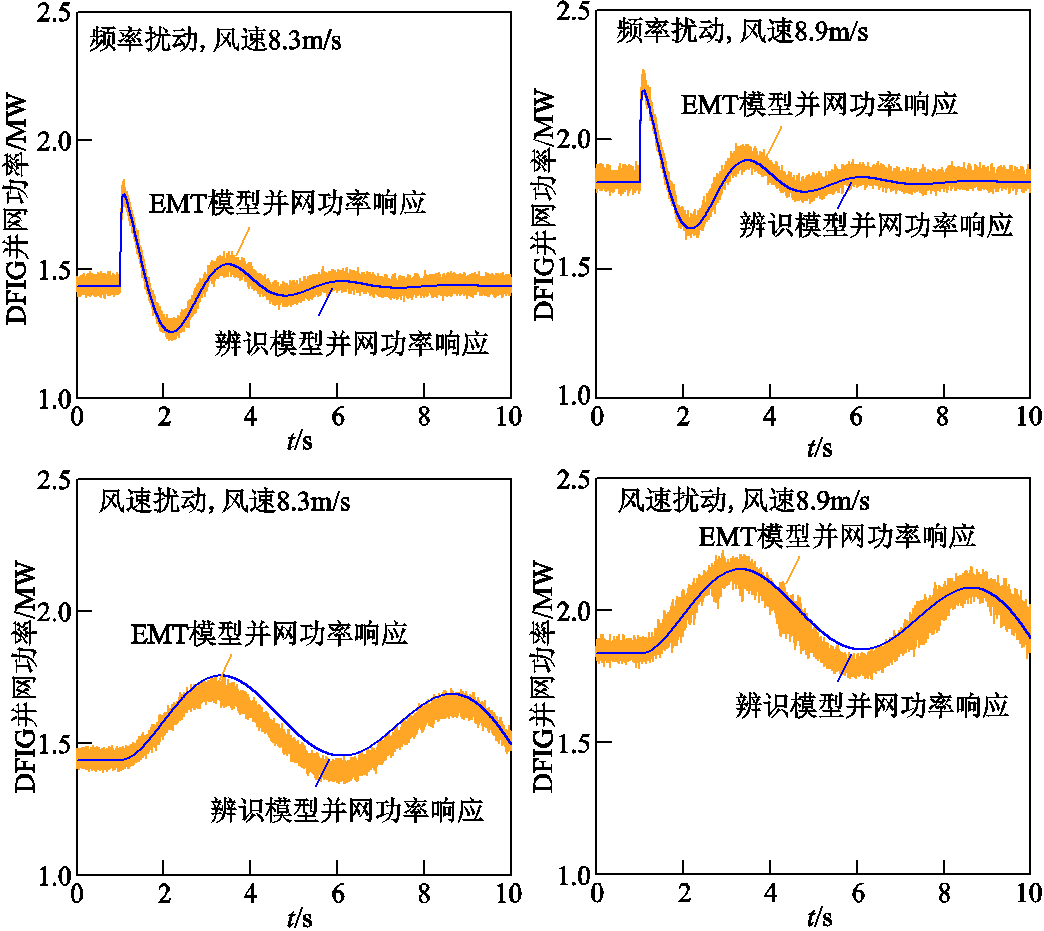
图9 频率/风速扰动下DFIG频率响应降阶模型(辨识结果)输出与EMT仿真对比(其他风速)
Fig.9 Comparison of frequency response between estimated model and EMT simulation under frequency/wind disturbance (other wind speeds)
4.1.3 与其他辨识方式的对比
本文所提算法为风场频率响应特性的辨识提供了基本框架。为了验证算法的辨识性能,将重构与分步辨识环节分别采用的矩阵束法与最小二乘法分别替换为低通滤波[14]与Prony估计法[19],从而构成低通滤波+最小二乘法(该方法被用于虚拟同步机惯性和阻尼的辨识)与矩阵束重构+Prony估计法(被用于汽轮机参数辨识)两种算法,其中低通滤波截止频率设为50Hz。两种算法的辨识结果可参见表3,平均耗时分别为0.099 5s和11.160 8s。仅就算法效率而言,基于低通滤波的最小二乘法最优,而基于矩阵束重构的Prony估计法效率最低。
图10和图11分别展示了在给定频率扰动和风速扰动下,两种算法得到的频率响应模型输出和EMT仿真轨迹的对比结果。对比图8可见,由于低通滤波存在延时现象,本文所提算法辨识出的频率响应模型,在频率扰动下其并网功率输出比经低通滤波辨识的频率响应模型更加贴合EMT仿真结果,误差分布也更为集中。矩阵束重构+Prony估计的辨识精度与本文所提算法类似,但分步辨识环节的计算复杂度显著提升。对于风速扰动响应,三种算法辨识结果的精度基本一致,误差大多分布在±0.05MW范围内。综上,矩阵束重构对数据噪声的消去效果优于低通滤波;相较于Prony估计法,采用最小二乘法分步辨识能产生极点分布一致的DFIG频率响应特性,符合式(24)所示DFIG频率响应模型特征。
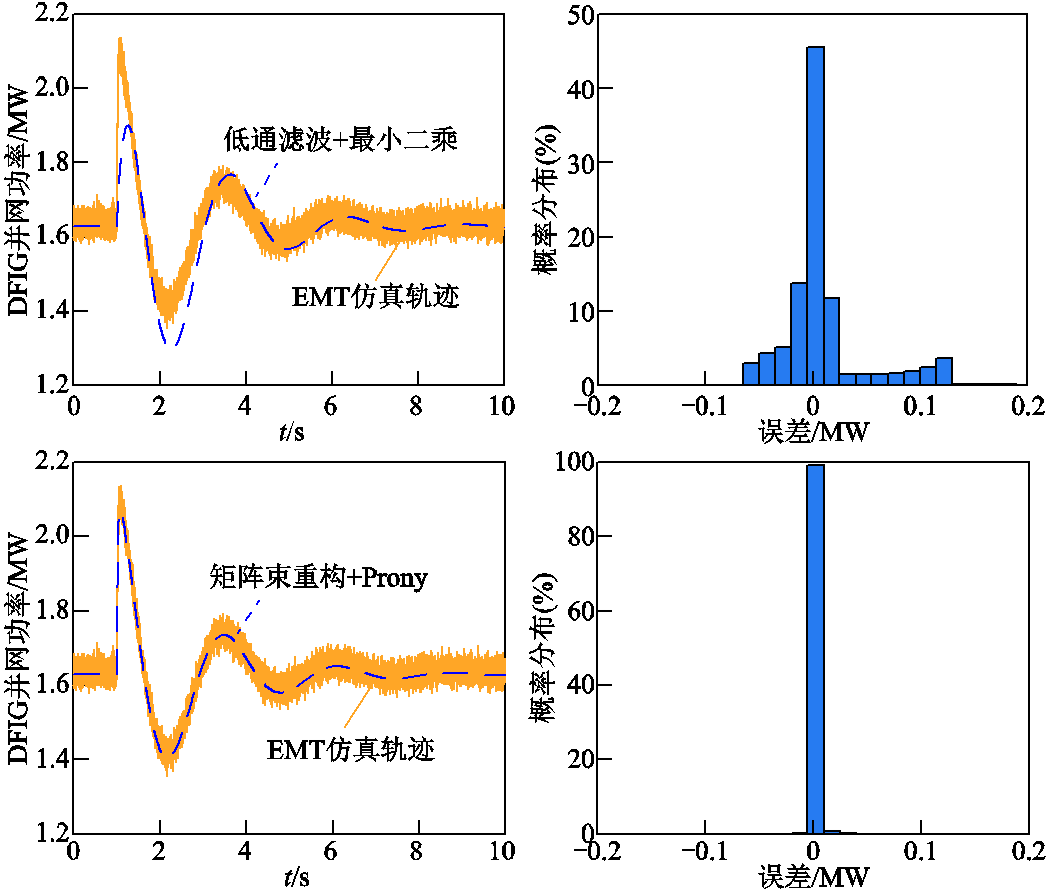
图10 频率扰动下DFIG频率响应降阶模型(其他算法辨识结果)输出与EMT仿真对比
Fig.10 Comparison of frequency response between estimated model (other algorithms) and EMT simulation under frequency disturbance
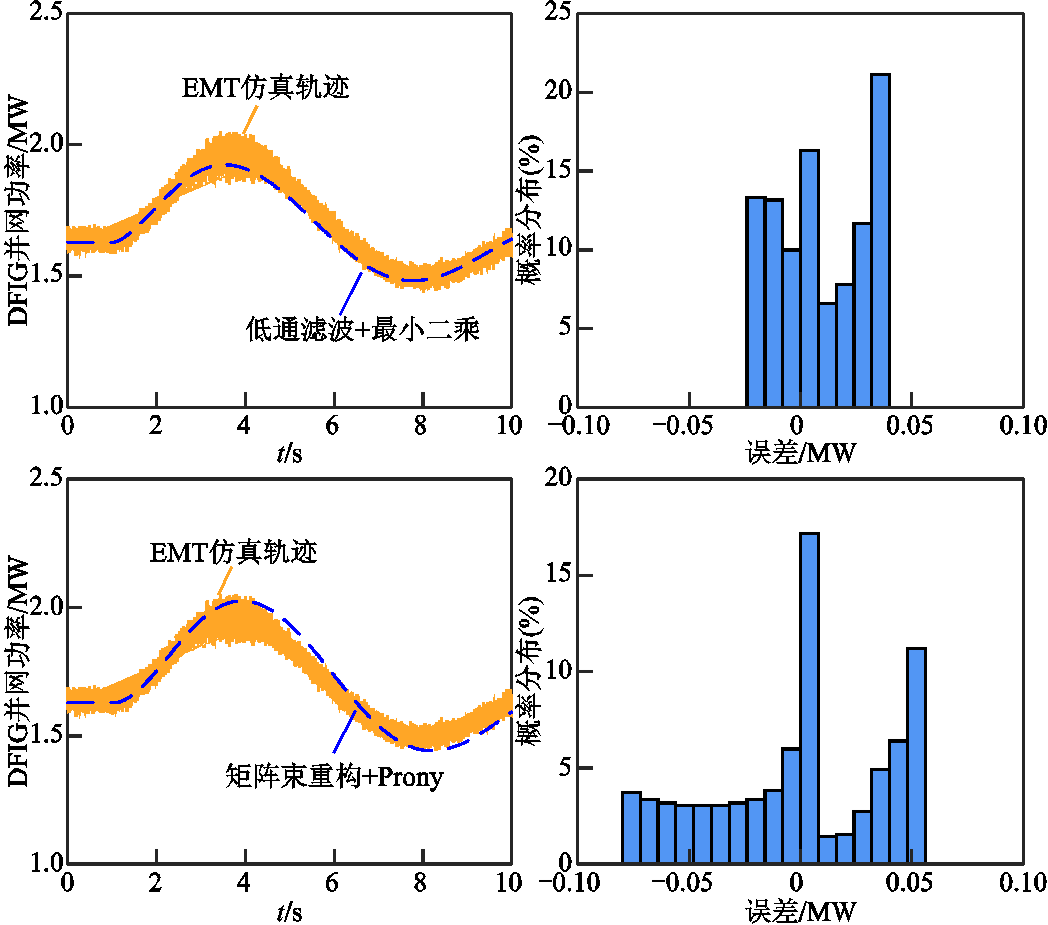
图11 风速扰动下DFIG频率响应降阶模型(其他算法辨识结果)输出与EMT仿真对比
Fig.11 Comparison of frequency response between estimated model (other algorithms) and EMT simulation under wind disturbance
为进一步验证频率响应降阶模型及其辨识算法对双馈风电场的适用性,以图12所示扩展IEEE 30节点系统为测试对象。局限于Matlab/Simulink的电磁暂态仿真能力,风场选择由3台10MW等值风机构成,换流器采用平均建模,系统中同步发电机和等值风机的部分关键参数见表4。
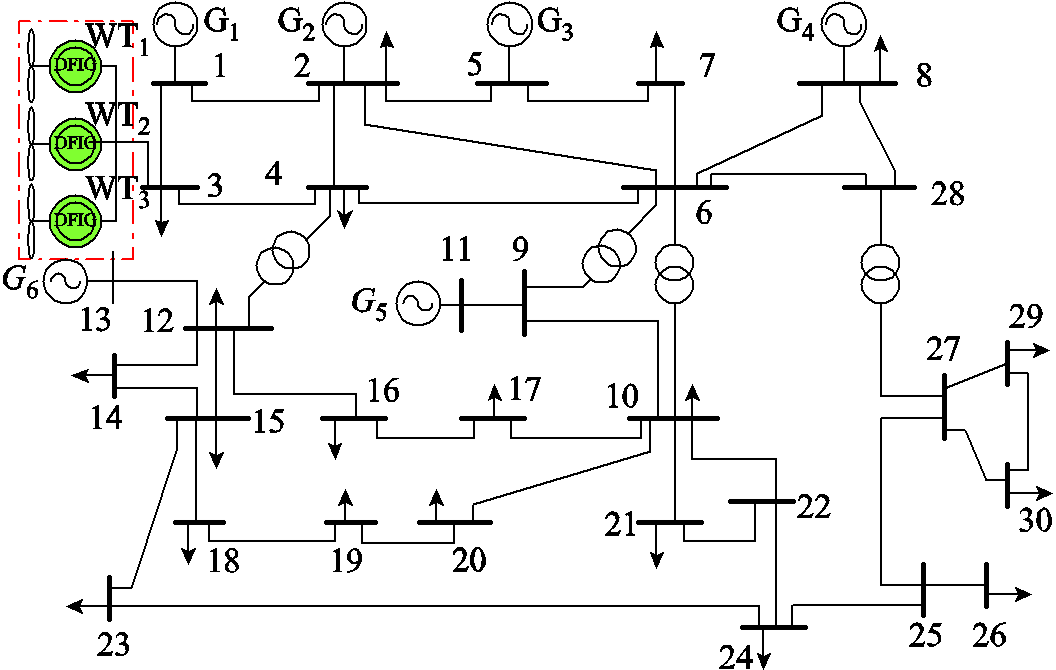
图12 含风场的扩展IEEE 30节点系统
Fig.12 Modified IEEE 30-node system with wind farm
表4 IEEE-30节点系统关键参数
Tab.4 Key parameters of IEEE 30-node system

参数数值 同步发电机G1~6G1额定功率P/MW200 G1转动惯量J/(kg×m2)13 000 G2~6额定功率P/MW100 G2~6转动惯量J/(kg×m2)6 500 等值风机WT1~3额定功率P/MW10 转动惯量和Jd/(kg×m2)960 虚拟惯性系数kdf0.8 下垂系数kpf0.8
4.2.1 风场频率响应模型辨识结果
采样间隔、时长设置与上节相同,在风电机组全部参与调频的运行模式下,风场各监测点风速、并网母线角频率(由锁相环锁相得到)和并网点功率的4段采样序列如图13所示。囿于篇幅,对于部分机组参与调频的运行模式,其数据不再列出。
对各监测点风速取平均作为输入,本文所提算法辨识出的不同运行模式双馈风电场频率响应特性结果见表5。
图14展示了给定频率和风速扰动情况下双馈风电场辨识模型的输出,其与EMT仿真轨迹高度一致。频率扰动下并网功率的响应误差主要分布在±0.03MW范围内,风速扰动下并网功率的响应误差在±0.025MW范围内。若以峰值功率20MW为基值,相对误差分布范围分别是±0.15%与±0.13%,表明了风电场频率响应特性采用二阶传递函数近似描述与所提辨识算法的准确性,同时也表明:即使风电场内部各机组的运行点不一,但风电场的整体频率响应特性仍可用二阶传递函数集中近似表示。
表5 基于矩阵束重构的最小二乘算法参数辨识结果
Tab.5 Identification results of least-square algorithm based on matrix pencil
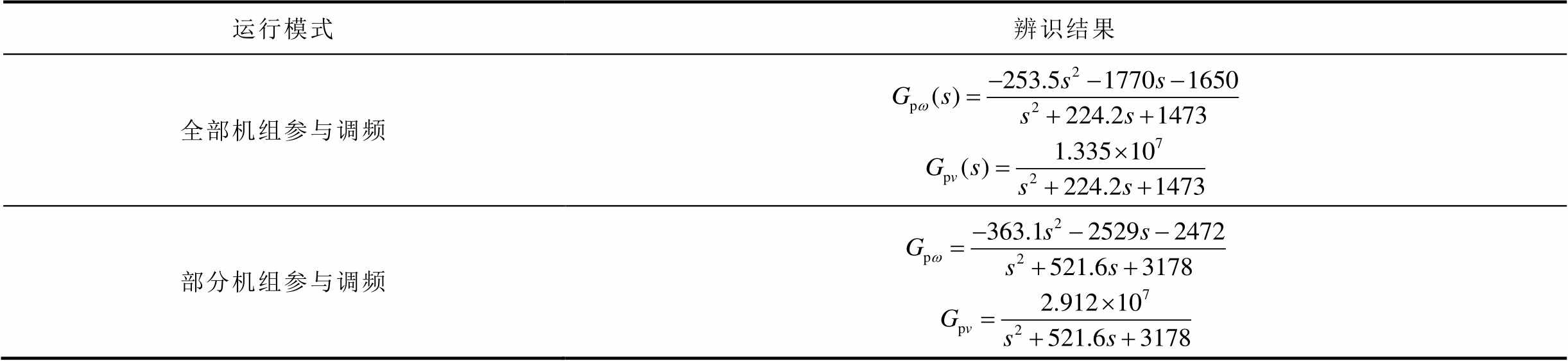
运行模式辨识结果 全部机组参与调频 部分机组参与调频
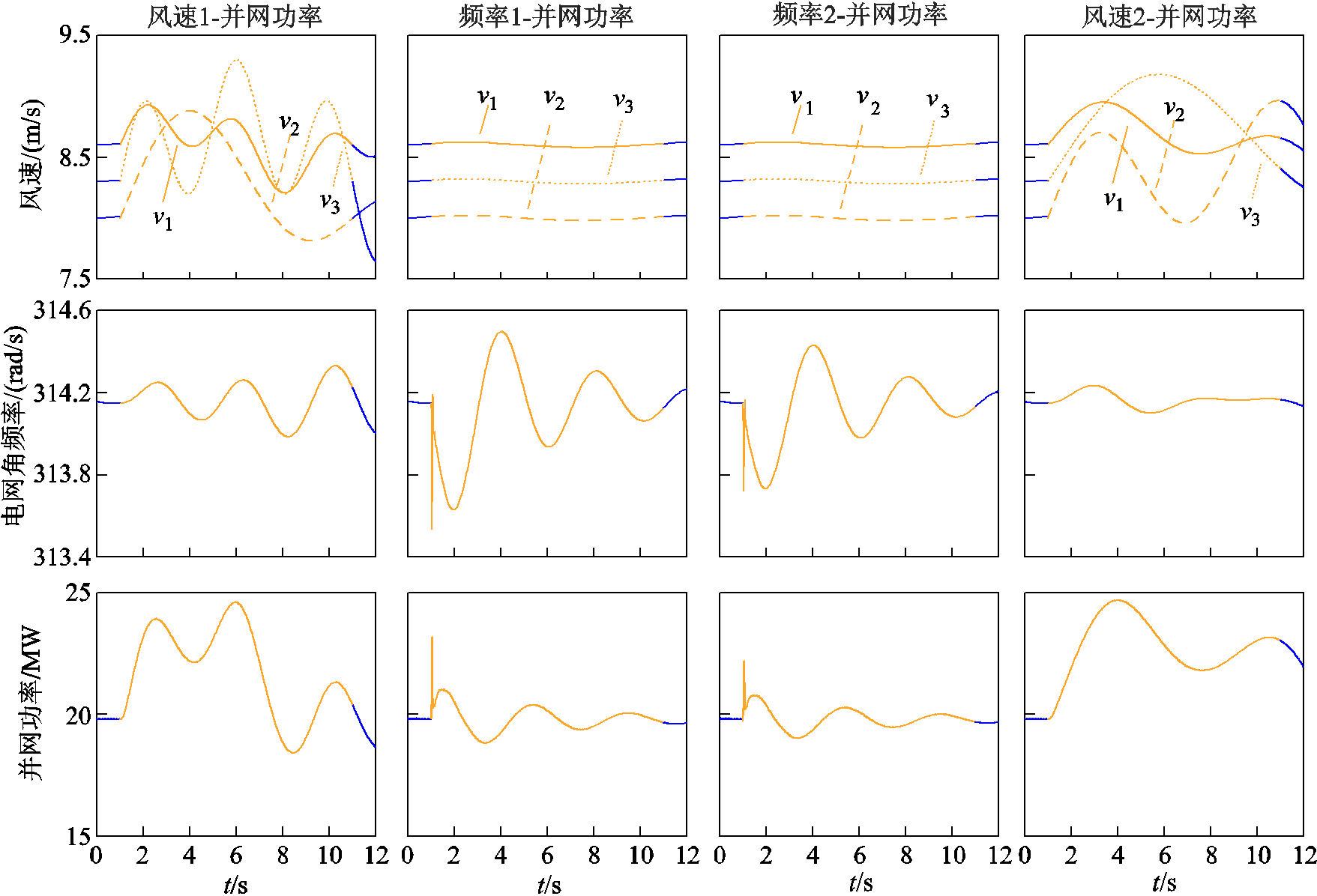
图13 双馈风电场采样数据序列(全部参与调频)
Fig.13 Sampling data of doubly-fed wind farm(all participation)
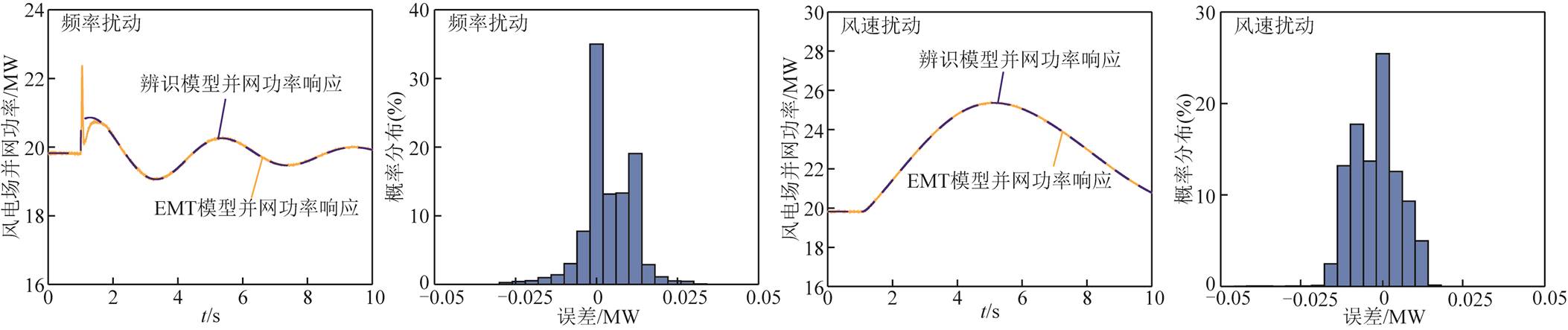
图14 频率/风速扰动下双馈风电场频率响应辨识模型输出与EMT仿真对比(全部参与调频)
Fig.14 Comparison of frequency response between estimated model and EMT detailed model under frequency/wind disturbance(all participation)
图15进一步给出了其他稳态风速及扰动下(稳态平均风速分别为8.0m/s与8.6m/s)依旧采用上述频率响应辨识模型的并网功率输出轨迹。对比EMT仿真轨迹,两者的一致性说明所辨识出的频率响应模型可以表征宽风速输入下风电场频率响应特性。这意味着在平均风速相近时,所辨识的风电场频率响应模型可以被重复利用,在简化建模过程的同时,提高了辨识模型的应用价值。
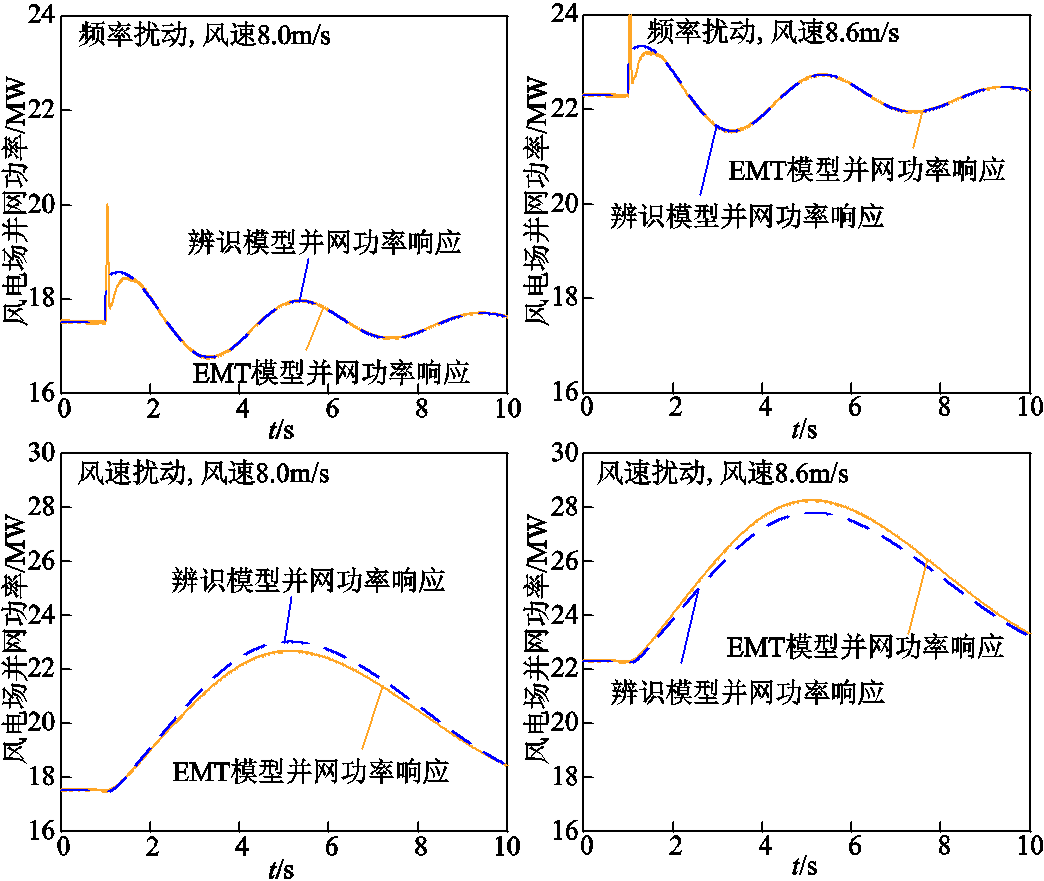
图15 频率/风速扰动下双馈风电场频率响应辨识模型输出与电磁暂态仿真对比(全部参与调频,其他风速)
Fig.15 Comparison of frequency response between estimated model and EMT simulation under frequency/wind disturbance(all participation, other wind speed)
针对双馈风电场部分机组参与一次调频的运行模式,图16对比了频率/风速扰动下频率响应辨识模型的输出轨迹与EMT仿真轨迹。频率扰动输出误差集中在±0.03MW范围内,风速扰动下输出误差也在±0.025MW范围内。与图15类似,图17给出了其他稳态风速与扰动下(稳态平均风速分别为8.0m/s与8.6m/s)依旧采用上述频率响应辨识模型的并网功率输出轨迹。与EMT仿真的一致性表明参数辨识建模方式不依赖风场的具体运行模式,且所提基于矩阵束重构的最小二乘分步辨识算法对不同调频参与模式、风速情况下均有较好的辨识精度,具备算法稳定性。
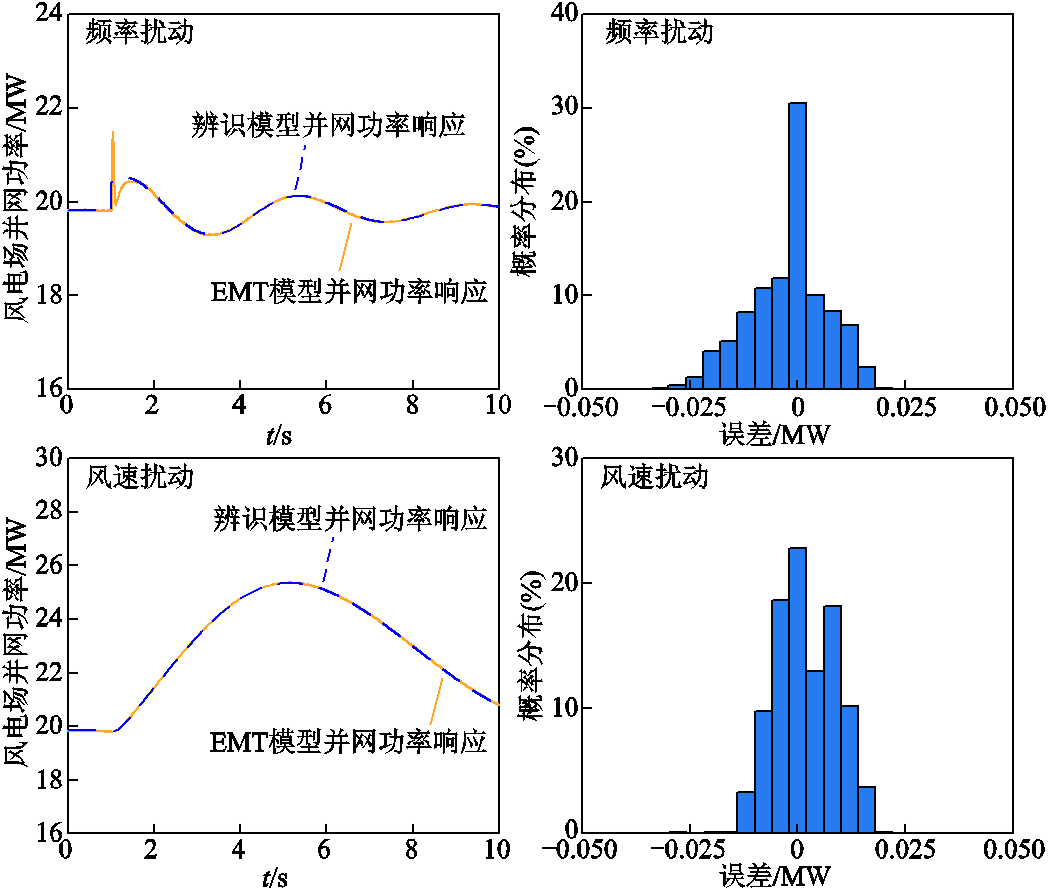
图16 频率/风速扰动下双馈风电场频率响应辨识模型输出与EMT仿真对比(部分参与调频)
Fig.16 Comparison of frequency response between estimated model and EMT simulation under frequency/wind disturbance(part participation)
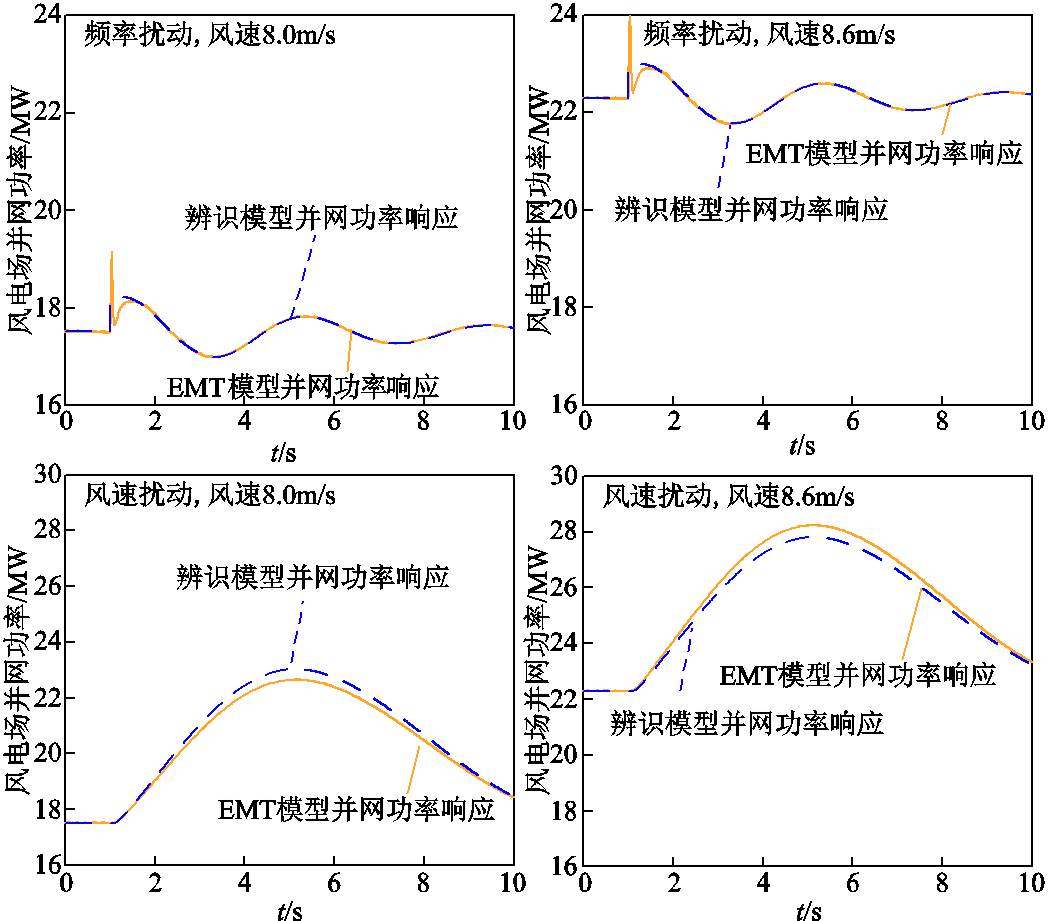
图17 频率/风速扰动下双馈风电场频率响应辨识模型输出与EMT仿真对比(部分参与调频,其他风速)
Fig.17 Comparison of frequency response between estimated model and EMT simulation under frequency/ wind disturbance(all participation, other wind speed)
表6给出了所提算法各步骤的平均耗时(10次辨识取平均值)。算法的主要耗时体现在数据处理过程,当采样间隔扩大,算法效率会明显提升。采样间隔取2ms,辨识总体耗时为8.723 2s,完全可以满足在线应用要求。
表6 辨识算法的平均耗时
Tab.6 Average time cost of estimation algorithm

算法步骤平均耗时t/s Dt=1msDt=2msDt=3ms 数据采集(步骤(1)~(5))84.436 88.609 22.777 6 频率响应估计(步骤(6)~(7))0.126 60.1140.094 总耗时84.563 48.723 22.871 6
4.2.2 与其他辨识方式的对比
为说明所提算法在风电场频率响应特性辨识上的优势,与单机系统测试类似,表7给出了全部参与调频模式下不同辨识算法对风电场2阶频率响应模型的辨识结果。
表7 其他算法参数辨识结果(全部参与调频模式)
Tab.7 Identification results of different identification algorithms(all participation)
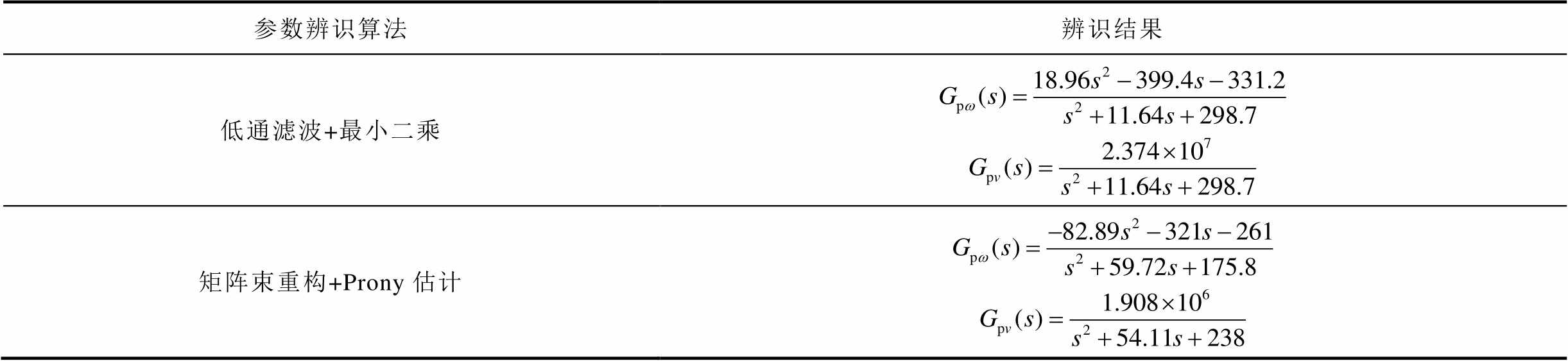
参数辨识算法辨识结果 低通滤波+最小二乘 矩阵束重构+Prony估计
根据表7所示算法辨识出的风场频率响应模型,在给定频率扰动下,不同模型输出轨迹及误差分布如图18所示。对比图14可以发现,所提基于矩阵束重构的最小二乘法分步辨识算法得到的频率响应模型,误差分布在±0.025MW范围内,更为集中。图19进一步给出了风速扰动下不同模型输出与EMT仿真轨迹的对比结果。各机组稳态风速不同,各风速扰动对风场频率响应特性存在差异化影响。由于低通滤波存在延时现象,而Prony估计法可能存在过拟合问题,误差相对显著,而对比图14,所提算法的并网功率响应误差分布在0附近,精度要优于另外两种算法。
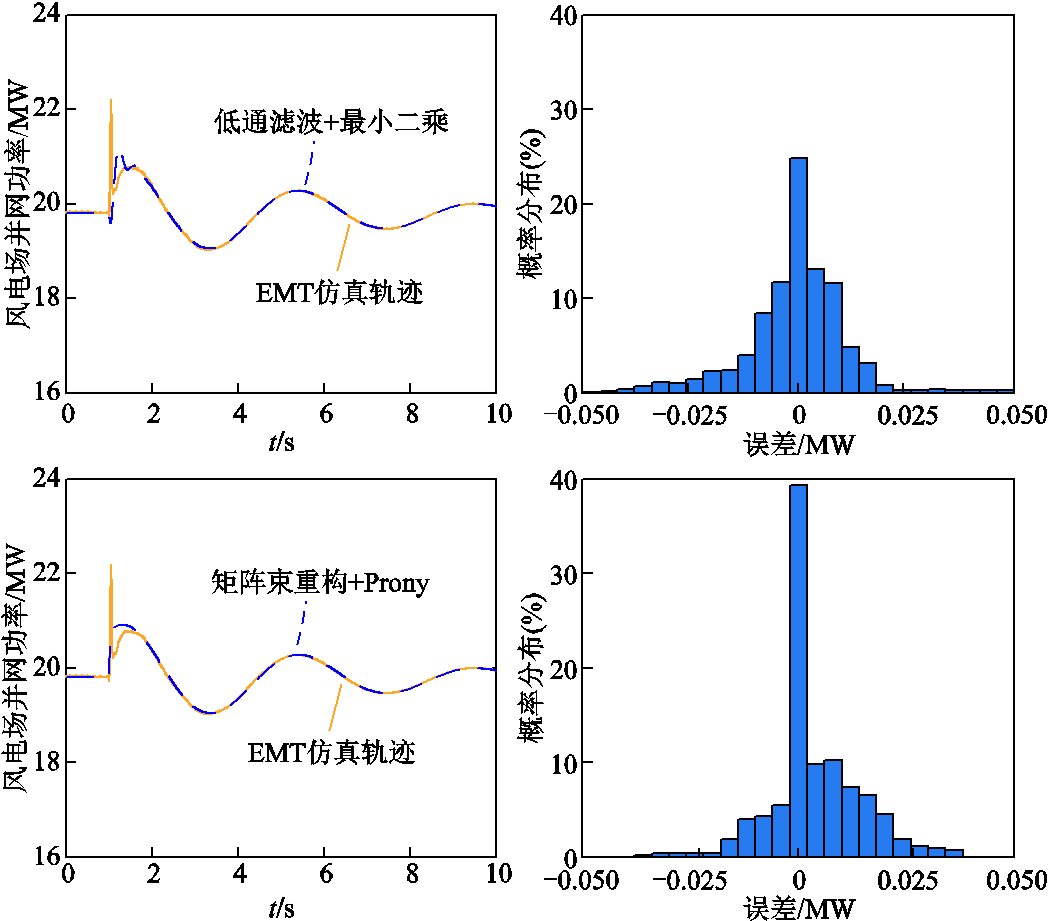
图18 频率扰动下双馈风电场频率响应辨识模型(其他算法辨识结果)输出与EMT仿真对比(全部参与调频)
Fig.18 Comparison of frequency response between estimated model (other algorithms) and EMT simulation under frequency disturbance(all participation)
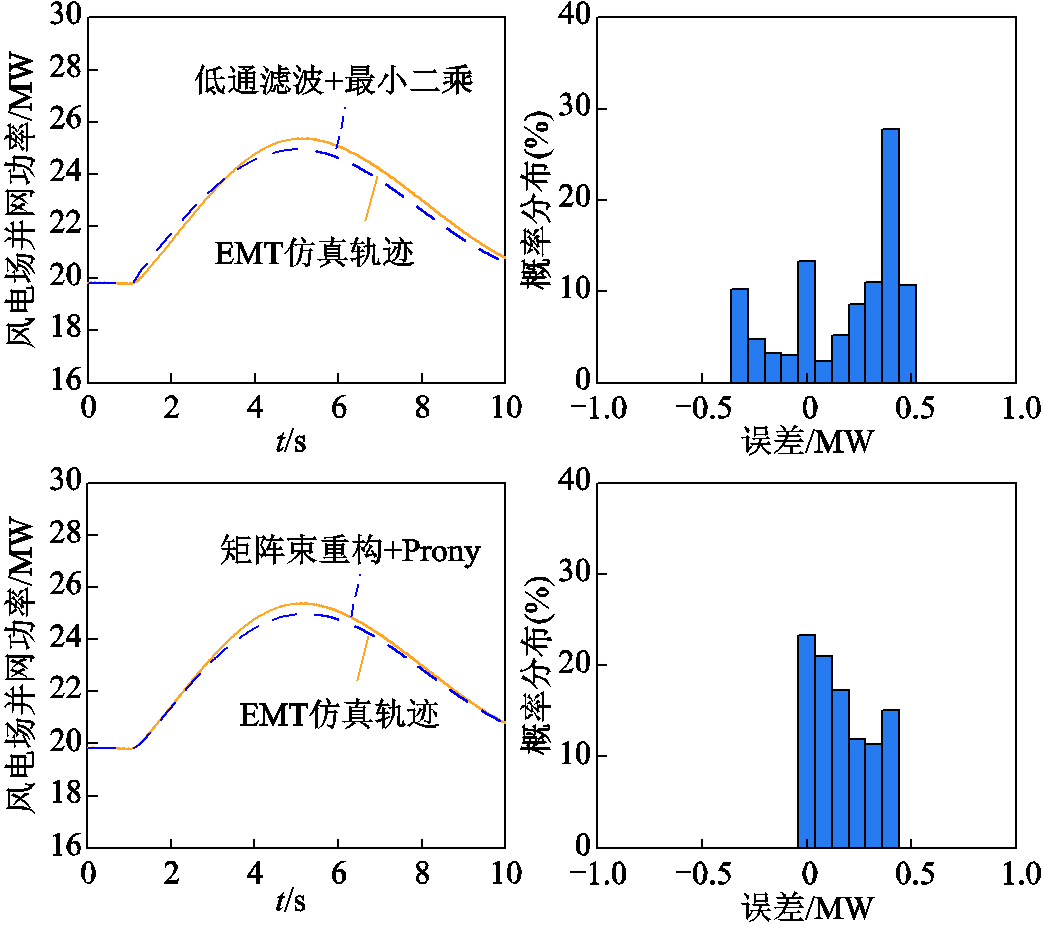
图19 风速扰动下双馈风电场频率响应辨识模型(其他算法辨识结果)输出与EMT仿真对比(全部参与调频)
Fig.19 Comparison of frequency response between estimated model and EMT detailed model under wind disturbance(all participation)
为准确获得附加频率控制下双馈风电场的频率响应特性,本文基于推导的DFIG双输入(风速、频率)-单输出(并网功率)频率响应降阶模型,提出了结合矩阵束重构和最小二乘法分步辨识的双馈风电场频率响应特性参数辨识算法。采用DFIG单机并网系统和含双馈风电场的扩展IEEE 30节点系统,通过对比Matlab/Simulink电磁暂态仿真结果,验证了频率响应降阶模型和所提参数辨识算法的有效性和准确性,并得到结论如下:
1)所推导的线性化DFIG频率响应4阶和2阶模型对附加频率控制的DFIG响应特性具有准确的描述能力,等效参数可直接由机组参数导出;就仿真效率而言,2阶模型具有明显的效率优势,结合交流系统简化模型,可提高含分散式风场参与调频的电力系统频率特性的分析效率。
2)所设计的基于数据重构的参数辨识算法能较好解决附加频率控制后双馈风电场整体频率响应特性耦合情况下的建模问题,避免了以机组为单元的特性集成和推导过程;辨识算法对风场不同调频参与模式均具有表征能力,而辨识结果可适用于宽风速运行范围。
参考文献
[1] 颜湘武, 崔森, 常文斐. 考虑储能自适应调节的双馈感应发电机一次调频控制策略[J]. 电工技术学报, 2021, 36(5): 1027-1039.
Yan Xiangwu, Cui Sen, Chang Wenfei. Primary fequency rgulation control strategy of doubly-fed induction generator considering supercapacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.
[2] 李少林, 王伟胜, 张兴, 等. 风力发电对系统频率影响及虚拟惯量综合控制[J]. 电力系统自动化, 2019, 43(15): 64-70.
Li Shaolin, Wang Weisheng, Zhang Xing, et al. Wind power on system frequency and combined virtual inertia control[J]. Automation of Electric Power System, 2019, 43(15): 64-70.
[3] He Jiafa, Huang Linbin, Wu Di, et al. Frequency support from PMSG-based wind turbines with reduced DC-link voltage fluctuation[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(3): 296-302.
[4] 颜湘武, 宋子君, 崔森, 等. 基于变功率点跟踪和超级电容器储能协调控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2020, 35(3): 530-541.
Yan Xiangwu, Song Zijun, Cui Sen, et al. Primary frequency regulation strategy of doubly-fed wind turbine based on variable power point tracking and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 157-163.
[5] Chang-Chien L, Lin Weiting, Yin Yaoching. Enhacing frequency response control by DFIGs in the high wind penetrated power system[J]. IEEE Transactions on Power System, 2011, 26(2): 710-718.
[6] 张宝群, 张伯明, 吴文传. 基于小干扰稳定的双馈感应电机电磁模型降阶分析[J]. 电力系统自动化, 2010, 34(10): 51-55.
Zhang Baoqun, Zhang Boming, Wu Wenchuan. Small singal based reduced electromagnetic model analysis of double fed induction generator[J]. Automation of Electric Power System, 2010, 34(10): 51-55.
[7] Mauricio J M, Marano A, Gomez-Exposito A, et al. Frequency regulation contribution through variable speed wind energy conversion system[J]. IEEE Transactions on Power System, 2009, 24(1): 173-180.
[8] Vidyanandan K V, Senroy N. Primary frequency regulation by deloaded wind turbines using variable droop[J]. IEEE Transactions on Power System, 2013, 28(2): 837-846.
[9] 李世春, 黄悦华, 王凌云, 等. 基于转速控制的双馈风电机组一次调频辅助控制系统建模[J]. 中国电机工程学报, 2017, 37(24): 7077-7086.
Li Shichun, Huang Yuehua, Wang Lingyun, et al. Modeling primary frequency regulation auxiliary control system of doubly fed induction generator based on rotor speed control[J]. Proceedings of the CSEE, 2017, 37(24): 7077-7086.
[10] 李世春, 邓长虹, 龙志君, 等. 风电场等效虚拟惯性时间常数计算[J]. 电力系统自动化, 2016, 40(7): 22-29.
Li Shichun, Deng Changhong, Long Zhijun, et al. Caculation of equivalent virtual time constant of wind farm[J]. Automation of Electric Power System, 2016, 40(7): 22-29.
[11] 薄其滨. 含风电的电力系统频率动态分析[D]. 成都: 西南交通大学, 2015.
[12] 姚琦, 刘吉臻, 胡阳, 等. 含异步变速风机的风电场一次调频等值建模与仿真[J]. 电力系统自动化, 2019, 43(23): 185-192.
Yao Qi, Liu Jizhen, Hu Yang, et al. Equivalent modeling and simulation for primary frequency regulation of wind farm with asynchronous variable-speed wind turbines[J]. Automation of Electric Power System, 2019, 43(23): 185-192.
[13] 黄梅, 万航羽. 在动态仿真中风电场模型的简化[J]. 电工技术学报, 2009, 24(9): 147-152.
Huang Mei, Wan Hangyu. Simplification of wind farm model for dynamic simulation[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 147-152.
[14] 曾正, 邵伟华. 基于线性化模型的虚拟同步发电机惯性和阻尼辨识[J]. 电力系统自动化, 2017, 41(10): 37-43, 81.
Zeng Zheng, Shao Weihua. Estimation of inertia and damping for virtual synchronous generator based on linearized model[J]. Automation of Electric Power System, 2017, 41(10): 37-43, 81.
[15] 谢文超, 赵延明, 方紫微, 等. 带可变遗忘因子递推最小二乘法的超级电容模组等效模型参数辨识方法[J]. 电工技术学报, 2021, 36(5): 996-1005.
Xie Wenchao, Zhao Yanming, Fang Ziwei, et al. Variable forgetting factor recursive least squares based parameter identification method for the equivalent circuit model of the supercapacitor cell module [J]. Transactions of China Electrotechnical Society, 2021, 36(5): 996-1005.
[16] Tahir M, Moazzam A, Ali K. A stochastic optimization approach to magnetometer calibration with gradient estimates using simultaneous perturbations[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(10): 4152-4161.
[17] Hu Chaofang, Liu Qizhi. Online identification for hypersonic vehicle using recursive maximum likelihood method based on interior-point algorithm[C]// 2013 25th Chinese Control and Decision Conference (CCDC), Guiyang, 2013: 1862-1867.
[18] Smith J R, Fatehi F, Woods C S, et al. Transfer function identification in power system applications[J]. IEEE Transactions on Power Systems, 1993, 8(3): 1282-1290.
[19] 陈龙, 易琼洋, 贲彤, 等. 全局优化算法在Preisach磁滞模型参数辨识问题中的应用与性能对比[J]. 电工技术学报, 2021, 36(12): 2585-2593, 260.
Chen Long, Yi Qiongyang, Ben Tong, et al. Application and performance comparison of global optimization algorithms in the parameter identification problems of the preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2585-2593, 260.
[20] 于鸿儒, 苏建徽, 徐华电, 等. 并网逆变器虚拟惯性与阻尼的等效及辨识[J]. 中国电机工程学报, 2019, 39(20): 6034-6043, 6184.
Yu Hongru, Su Jianhui, Xu Huadian, et al. Equivalent and identification of virtual inertia and damping of grid-connected inverter[J]. Proceedings of the CSEE, 2019, 39(20): 6034-6043, 6184.
[21] 荀倩, 王培良, 李祖欣, 等. 基于递推最小二乘法的永磁伺服系统参数辨识[J]. 电工技术学报, 2016, 31(17): 161-169.
Xun Qian, Wang Peiliang, Li Zuxin, et al. PMSM parameters identification based on recursive least square method[J]. Transactions of China Electrote-chnical Society, 2016, 31(17): 161-169.
[22] Wang Yinfeng, Lu Chao, Zhu Lipeng, et al. Comprehensive modeling and parameter identification of wind farms based on wide-area measurement systems[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(3): 383-393.
[23] Lin Jin, Cheng Lin. Model parameters identification method for wind farms based on wide-area trajectory sensitivities[J]. International Journal of Emerging Electric Power Systems, 2010, 11(5): 2.
[24] 李辉, 王荷生, 史旭阳, 等. 基于遗传算法的风电场等值模型的研究[J]. 电力系统保护与控制, 2011, 39(11): 1-8, 16.
Li Hui, Wang Hesheng, Shi Xuyang, et al. Study on equivalent model of wind farms based on genetic algorithm[J]. Power System Protection and Control, 2011, 39(11): 1-8, 16.
[25] Cheng Xueyang, Lee W, Sahni M, et al. Dynamic equivalent model development to improve the operation efficiency of WPP[J]. IEEE Transactions on Industry Applications, 2016, 52(4): 2759-2767.
[26] 张剑, 何怡刚. 基于轨迹灵敏度分析的永磁直驱风电场等值模型参数辨识[J]. 电工技术学报, 2020, 35(15): 3303-3313.
Zhang Jian, He Yigang. Parameters identification of equivalent model of permanent magnet synchronous generator wind farm based on analysis of trajectory sensitivity[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3303-3313.
[27] 李颖颖. 限功率运行条件下双馈风电机组参与电网一次调频控制策略研究[D]. 成都: 西南交通大学, 2019.
[28] Amirnaser Yazdani, Reza Iravani. Voltage-source converters in power system[M]. New Jersey: John Wiley & Sons, Inc., Hoboken, 2010.
[29] Hsieh C S, Hwang C. Model reduction of continuous-time systems using a modified Routh approximation method[J]. IEE Proceedings D- Control Theory and Applications, 1989, 136(4): 151-156.
[30] Tapan K. Sarkar, Odilon Pereira. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials[J]. IEEE Antennas and Propagation Magazine, 1995, 37(1): 48-55.
Frequency Response Modeling and Parameter Identification of Doubly-Fed Wind Farm with Additional Frequency Control
Abstract With the increasing penetration of wind power into power system, wind turbines participating in frequency regulation has become a consensus for wind power consumption. In order to realize the efficient and accurate analysis of frequency response characteristic in power system with high proportion wind power, the paper firstly establishes the double input(the wind speed and frequency) and single output(the grid-connected power) frequency response model of doubly-fed induction generator (DFIG). Then by using Routh approximation method, the fourth-order and second-order reduction models of DFIG frequency response are sequentially derived. Furthermore, to satisfy the need of building the frequency response model for doubly-fed wind farm, a parameter identification algorithm for the frequency response characteristics of doubly-fed wind farm is designed by combining matrix pencil method and least square method. Finally, the test results based on the DFIG grid-connected system demonstrate the accuracy of the derived frequency response reduce-order model. The effectiveness of parameter identification method is verified by comparing the electromagnetic transient simulation results of MATLAB/Simulink in DFIG grid-connected system and modified IEEE 30 node system with wind farm.
keywords:Doubly-fed wind farm, additional frequency control, frequency response, model reduction-order, parameters identification
DOI:10.19595/j.cnki.1000-6753.tces.210117
中图分类号:TM614
陈鹏伟 男,1992年生,博士,讲师,硕士生导师,研究方向为直流配电系统不确定性建模与优化控制。E-mail:chenpw2019@nuaa.edu.cn(通信作者)
戚陈陈 男,1996年生,硕士研究生,研究方向为新能源发电与并网技术,直流配电系统建模与优化控制等。E-mail:qichenchen@nuaa.edu.cn
国家自然科学基金(51877105)和国家电网专项科技项目(SGTYHT/18-JS-206)资助。
收稿日期 2021-01-22
改稿日期 2021-03-26
(编辑 郭丽军)