图1 Buck降压斩波电路
Fig.1 Diagram of Buck chopper circuit
摘要 在由多个降压斩波器各自驱动独立负载的某军事应用场景中，要求各个降压斩波器的输出电流在启动阶段和稳态阶段均具有良好的一致性。如果不加以控制，电流的一致性会受负载差异和启动通信延时等因素的严重影响。该文基于多智能体协同控制思想设计了一种相邻电流协同控制策略，用相邻电流值实时补偿电流设定值的方式实现了系统的控制目标。通过对实际多降压斩波器系统进行实验，引入工业以太网EtherCAT进行信息交互以满足控制系统的实时性要求，从而验证了相邻电流协同控制算法对解决多斩波器电流协同问题具有良好的效果。
关键词：多斩波器控制系统 协同控制 系统稳定性 工业以太网
包含多个直流斩波器的现代工业控制系统如直流电源控制系统等多存在非线性、高耦合等经典控制理论无法解决的难题。在由多个降压斩波器各自驱动独立负载的某军事应用场景中，要求各个降压斩波器的输出电流在启动阶段和稳态阶段均具有良好的一致性，保证每个斩波器输出电流产生的磁场稳定一致，从而得到良好的消磁效果，若输出电流不一致，消磁效果将受到严重影响。因此为了获得满意的实际控制效果，必须采用控制策略对多个直流斩波器的输出进行协同控制。
协同控制最早是从大自然中获得灵感，比如鸟的列队而飞、昆虫的蜂拥而至等[1]。为了解决多智能体的一致性问题，近年来国内外提出许多协同控制策略，在不同的应用场景取得了不同的控制效果。文献[1]将图表化的思想应用于多个直流变换器的建模控制中，大大简化了控制系统的设计，从而更便于控制策略的研究。文献[2]基于黄金分割自适应控制的思想提出基于多智能体系统的一主多从协调跟踪控制策略，在简化信息交互的同时使系统响应迅速，取得了良好的控制效果。在直流微电网系统中，文献[3]提出一种混合储能三端口直流微电网母线电压控制器及多目标控制方法；文献[4]提出一种考虑微电网参与的主动配电网（Active Distribution Networks, ADN）无功电压分区与控制策略；文献[5]提出一种面向多台直流变换器并联运行，基于主动电压扰动的负载均流控制策略；文献[6]提出一种基于事件触发机制的多个混合储能系统（Hybrid Energy Storage System, HESS）的分层协调控制方法；文献[7]提出一种基于多时间级垂直分层思想与模型预测控制（Model Predictive Control, MPC）理论相结合的风电场无功电压分层协调控制策略。这些研究均对多个直流斩波器的电流协同控制具有指导意义。在直流斩波器的控制上，文献中提出的基于脉冲宽度调制（Pulse Width Modulation, PWM）的数字控制、自适应滑模控制及基于AD采样的预测控制等控制策略均取得了满意的实际控制效果[8-11]。
对于多个直流斩波器并联的功率不均衡问题，文献[12]基于一致性理论，提出电流共享控制，通过总线共享电流信息，取得了满意的控制效果；文献[13]提出基于有限时间的输出反馈控制，取得了较好的仿真效果；文献[14]在滑模控制的基础上提出基于分数阶的滑模控制，在解决功率不均衡问题的同时显著提高了系统的输出效率。文献[15-19]提出基于比例积分观测器的反演控制，基于状态空间模型的预测控制、主从电流共享控制、主从电流共享滑模控制以及基于CAN总线的主从电流跟踪控制策略，成功实现了多直流斩波器的并联协同控制。
对于多智能体的一致性问题，相对于稳态一致性，人们越来越关注有限时间内的一致性问题及一致性收敛速度问题[20]。针对多智能体系统，文献[21]使用最小阶观测器和积分器进行动态牵制控制，显著提高了系统达到一致性的速度；文献[22]针对含有不确定动力学的高阶非线性多智能体系统提出一种实现有限时间一致性的分布式控制算法，验证了提出的控制算法能够在有限时间内以较高的精度达到一致；文献[23]提出一种主从式预测编队控制架构，为实现多智能体动态一致性提供了新的思路。
上述协同控制理论的实现大都基于多个直流斩波器给同一负载供电的情况，较多应用于直流电源控制系统中。然而在由多个降压斩波器各自驱动独立负载的某军事应用场景中，每个斩波器的负载不尽相同，且不同负载之间的距离较远，普通的通信方式如CAN、RS485等不能满足实时性和远距离的要求。
为了解决由多个降压斩波器各自驱动独立负载的控制系统的电流协同一致性问题，本文基于一致性理论提出相邻电流协同控制策略，并对其稳定性和一致性进行分析研究。在实际四降压斩波器系统中取得了较好的电流协同控制效果。
对于图1所示的单个Buck降压斩波电路，假设其工作在连续导通模式（Continuous Conduction Mode, CCM）下，图中u0表示输入电压，d0表示控制PWM占空比，i0表示输出电流，L0表示功率电感，C表示输出侧电容，R和L表示负载为阻感负载。通过PWM信号控制开关管导通关断，便可调节输出电流的大小。
图1 Buck降压斩波电路
Fig.1 Diagram of Buck chopper circuit
由多个负载不同的降压斩波器通过工业以太网互相连接共享信息，得到本文研究的多降压斩波器控制系统，如图2左半部分所示。设网络中有n个斩波器，分别用A1, A2,
,An表示，其中u1, u2,, un分别表示n个斩波器的输入直流电压，d1, d2,, dn分别表示n个斩波器的控制PWM占空比，L1, L2,, Ln分别表示n个斩波器的功率电感，C1, C2,, Cn分别表示n个斩波器的输出侧电容，r1, r2,, rn分别表示n个斩波器的负载。不同斩波器通过工业以太网主站A0共享信息，形成了如图2右半部分所示的系统网络层结构。
图2 系统网络拓扑
Fig.2 System network topology
通过网络连接的多斩波器控制系统必须是稳定的，假设电流设定值为
，第i个斩波器在t时刻的输出电流为
，则当时间趋近于无穷大时，网络中的每一个斩波器输出电流都必须稳定在，并且不同斩波器的输出电流保持一致，值得注意的是，传统的PID控制器就可以满足这一控制目标。然而本文所研究的电流协同控制系统要求输出电流在动态过程中也能保证一致性，因此在理想状态下系统的控制目标可描述为：①在任意时刻t，不同斩波器i和j的输出电流和
满足
，其中
；②当时间趋于无穷大时，
。这两个条件又可称为控制系统的动态一致性目标和稳定性目标。
当斩波器数量增大时，控制系统不能同时满足斩波器之间完全信息共享的要求和控制的实时性要求。为了减少传输的信息量，提高系统的控制效率，提出相邻电流协同控制策略，每个斩波器输出电流只需要保持与相邻斩波器输出电流协同一致，那么整个系统就可以实现其控制目标。
对于每一个斩波电路，将输出电流与相邻斩波器的输出电流之差定义为相邻电流误差。相邻斩波器电流从工业以太网中获得，相邻电流误差经过协同控制器，将得到的误差值作为斩波电路主控制器的输入，相当于用电流误差来补偿电流设定值，这一过程如图3所示，因此控制器输入描述为
（1）
图3 PI控制策略框图
Fig.3 Block diagram of PI control strategy
式中，
为主控制器的输入；
为本斩波器输出电流；
和
分别为相邻斩波器输出电流；为设定电流值；
和
为协同控制比例系数。
由于斩波器电源干扰较多，引入微分环节容易引起高频振荡，所以主控制器仅采用PI控制，则由式（1）得到控制器输出为
（2）
，kp、ki分别为比例、积分系数。由于
表示第i个斩波器的占空比，作用于开关管，因此
。
在图3所示单个斩波器控制策略的基础上，通过网络连接实现信息的快速共享，得到相邻电流协同控制系统的框图如图4所示，其中yi表示第i个从站的输出电流值，y0表示设定电流值，k1,k2,…,k2n表示协同控制比例系数，在补偿电流设定值的基础上，主控制器输出占空比控制斩波电路的输出电流，使相邻从站的输出电流协同一致。
图4 电流协同控制系统框图
Fig.4 Diagram of current cooperative control system
当时间趋于无穷大时，若控制系统满足以下两个条件，便可认为该系统具有稳定性和输出电流一致性：①斩波器i输出电流满足
；②不同斩波器i和j的输出电流和
满足
，其中
。
对于如图1所示的单个Buck斩波器，将传递函数离散化，加入式（2）所述离散化PI控制器，得到第i个斩波器控制系统的离散传递函数，由离散传递函数得到系统的离散状态空间模型为
（3）式中，xi(k)、ui(k)、yi(k)分别为第i个斩波器的状态变量、输入变量（采样时刻的输入占空比d0）、输出变量（采样时刻的输出电流i0）；Ai、Bi、Ci为第i个斩波器的系统矩阵。
为了更好地说明系统的稳定性和一致性问题，定义状态变量为
（4）
（5）
（6）
第i个斩波电路的控制器的输入变量为，由式（1）可得控制系统输入ui(k)为
（7）由式（1）得输入ui(k)的增量
为
则单个斩波器控制系统状态变量的增量可以表示为
式中，
。
（10）
（11）
（12）
由式（9）～式（12）可知，该多斩波器控制系统可用状态变量增量的方程描述为
（13）其中，0和1分别表示合适维数的零矩阵和单位阵。
为了便于说明，令
（14）如果式（12）所描述的系统具有稳定性，则所描述的系统状态变量的增量是递减的，当时间趋于无穷大时，系统的状态变量保持不变，由此可知该系统是稳定的，并且
、
、
、
均趋于零，由式（4）～式（6）可知，当时间无穷大时
（15）
显然斩波器输出满足系统稳定性和一致性的两个条件。结合式（13）所描述的系统稳定的充分必要条件是Z矩阵的所有特征值均在单位圆内，得到以下引理。
引理1 基于式（2）所描述的控制策略，图4所表示的多降压斩波器控制系统具有稳定性和输出一致性的充分必要条件是Z矩阵的所有特征值均在单位圆内。
对于由式（12）所描述的n个斩波器控制系统来说，每个包含离散控制器的斩波器本身具有四个状态变量，因此
是
阶方阵。式（4）～式（6）定义了描述系统一致性的三个状态变量，因此每个斩波器有七个状态变量，Z矩阵就是一个
阶的方阵，有7n个特征值。
为了便于说明，本节以四个斩波器控制系统为例，计算实际系统的Z矩阵及其特征值，并分析Z矩阵的特征值分布，以此来说明设计协同控制算法的稳定性和一致性。
对于图1所示的Buck斩波电路，输入为占空比D，输出为负载电流I，其传递函数可表示为
（16）式中，
为输入电压；L0为功率电感；C为输出侧电容；R和L分别为负载的电阻和电感，具体参数见表1。
表1 Buck电路元器件参数值
Tab.1 The parameters of Buck chopper
参数数值 u0/V160 L0/mH0.1 L/mH0.5 C/μF1 000 R/Ω0.5
代入表1所示元器件参数值得系统传递函数为
（17）通过零阶保持器将传递函数离散化，加入离散化PI控制器，控制器离散传递函数可描述为
（18）
式中，Ts为采样时间间隔，取采样频率为1kHz，则采样时间间隔Ts为1ms。为了便于说明，设其中比例系数kp=0.000 1，积分系数ki=0.3，由式（17）、式（18）得到单降压斩波器的离散传递函数为
（19）由式（19）得系统的离散状态空间模型为
（20）由式（16）～式（20）可以得到其他三个斩波电路的状态空间模型，因此可以计算四个降压斩波器控制系统的A、B、C矩阵，得到四个降压斩波器的离散状态空间模型，每个降压斩波器有七个状态变量，因此四个降压斩波器控制系统的Z矩阵是一个28×28阶的矩阵，具体见附录。
为了研究负载差异对系统稳定性和一致性的影响，基于表2设计了三组不同电阻，负载差异分别为0.1Ω，0.2Ω和0.3Ω。其中R1、R2、R3和R4分别表示四个斩波电路的输出负载，取k1=-0.5，k2=-0.5，分别计算Z矩阵的特征值，并在单位圆中表示出来，结果如图5所示。
表2 负载差异影响实验参数
Tab.2 The parameters of the experiment on the influence of load differences
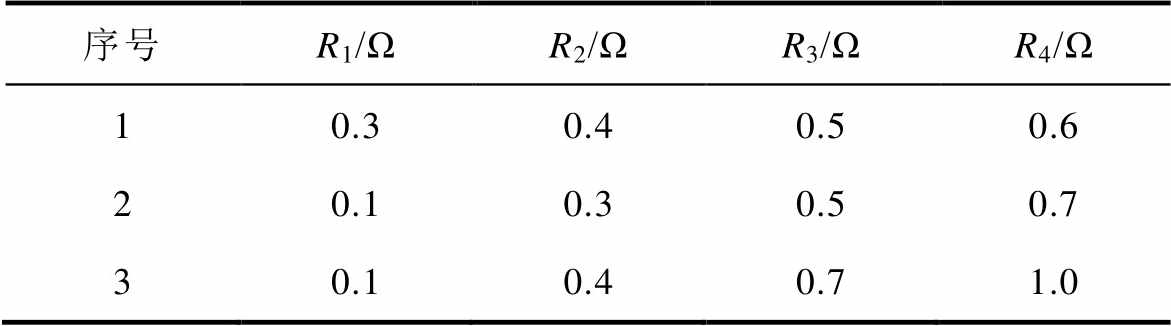
序号R1/ΩR2/ΩR3/ΩR4/Ω 10.30.40.50.6 20.10.30.50.7 30.10.40.71.0
图5 负载不同条件下Z矩阵特征值分布
Fig.5 Eigenvalues of Z matrix under different load conditions
由图5可知，不同负载差异情况下Z矩阵的28个特征值均位于单位圆内，由此说明基于相邻电流协同控制算法的四个斩波器控制系统具有稳定性和一致性。
随着负载差异的增大，Z矩阵的部分特征值有向单位圆外扩散的趋势，系统的状态变量增量衰减的速度变慢，状态变量更难趋于稳定，系统达到稳定状态所需要的时间更长，系统的稳定性和一致性更差，这与实际情况一致。
为了进一步探究第1节所设计的协同控制算法对实际控制系统控制效果的改善，本节基于四个直流斩波器控制系统，用三相三重降压斩波器给不同感性负载供电，通过EtherCAT进行变换器之间的通信及人机交互，实时显示负载电流曲线，并对不同参数下电流的动态响应曲线进行对比分析，从而验证了相邻电流协同控制策略具有良好的实际控制效果。
为了让斩波器的输出电流更加平稳，本实验采用三相三重斩波电路，相当于每个斩波器都由三个降压斩波单元并联而成，总输出电流为三个斩波单元的电流之和。主控制器采用STM32+FPGA的架构，实际每个斩波单元的控制占空比相位相差120°，由于三个斩波单元输出电流的脉动幅值互相抵消，因此总输出电流的脉动幅值将变得很小。
为了解决实际系统的远距离传输问题，将工业以太网EtherCAT总线技术引入多斩波器控制系统，从而构建基于EtherCAT一主多从的多直流斩波器数据交互系统，如图6所示。
图6 多直流斩波器数据交互系统
Fig.6 Data interaction system of multiple DC choppers
在每一个数据传输周期内，由主站发送定义了不同从站配置信息的下行报文，报文经过第一个从站，由从站控制器读取其相邻电流值及电流设定值信息并写入本从站当前时刻的电流值，然后转发报文给下一个从站进行相关数据的读写，在报文遍历了所有从站后，返回一个上行报文给主站，上行报文中包含了所有从站需要的数据信息，并且可以通过修改通信协议的方式来获取需要的数据。
EtherCAT主站选用创龙AM5728开发板，板载多核异构CPU，双核浮点DSP，具有强大的运算控制和信息交互能力，集成双核PRU-ICSS工业实时控制子系统，支持EtherCAT等多种工业协议。从站控制器采用STM32+LAN9252的硬件架构，STM32作为SPI上位机与LAN9252之间通过四线SPI进行电流等信息的交互。
负载采用绕制线圈，四个斩波器控制系统（设为C1～C4）的负载不同，其余参数均相同，四个斩波器具体实验参数见表3。至此完成了四个斩波器电流协同控制系统的硬件实现。具体实物如图7所示。
表3 实验斩波器系统参数
Tab.3 The parameters of the experiment on multiple chopper systems
斩波系统u0/VL0/mHL/mHC/mFR/Ω C11600.10.4010.20 C21600.10.5710.25 C31600.10.7410.31 C41600.10.7710.33
图7 四个降压斩波器控制系统实物图
Fig.7 The experimental system with 4 Buck choppers
对于四个实际斩波器控制系统，设定电流值
，为了更好地进行分析比较，考虑以下几种情况进行实验。
1）无相邻电流协同控制策略，即
，控制器输入
。在t=100ms时设定电流值为50A，2s后设定电流值变为0，在这一过程中，斩波器的输出电压V1、V2、V3、V4和输出电流
随时间变化曲线如图8所示。由图8可知，该四斩波器控制系统是稳定的并且能较好地跟随电流设定值。斩波器C1的某一相开关管的驱动波形如图9所示，开始启动时驱动电压波形如图9左下方所示，稳定时的驱动电压波形如图9右下方所示，驱动电压占空比在启动过程中逐渐增大。
图8 情况1输出电压和电流变化波形
Fig.8 The output voltage and current waveforms of case 1
图9 情况1电压驱动波形
Fig.9 Driver signal of case 1
为了分析输出电流的动态一致性，考虑电流上升阶段，斩波器的输出电流随时间变化曲线如图10所示。在电流上升阶段，不同斩波器电流差异较大，不能满足动态一致性的控制目标，因此需要引入电流协同控制策略。
图10 情况1输出电流上升曲线
Fig.10 The output current curves of case 1
2）加入第1节所述相邻电流协同控制策略，调整
和
参数至合适值，控制器输入如式（1）所描述，考虑上升阶段，斩波器的输出电流
随时间变化曲线如图11所示。由图11可知在误差允许的范围内，系统实现了动态一致性和稳定性的控制目标。
图11 情况2输出电流上升曲线
Fig.11 The output current curves of case 2
3）在情况2的基础上，考虑到不同斩波器信息交互过程中存在延时，设置延时启动时间ts，四个斩波器的延时启动时间ts分别设为6ms、9ms、0ms和3ms，在电流上升阶段观察斩波器的输出电流y1、y2、y3、y4随时间变化曲线如图12所示。时间t=20ms之前，由于延时启动，输出电流之间有差异；20ms之后在控制的作用下电流变化曲线与图11基本一致。然而实际系统工业以太网传输延时基本小于1ms，由此带来的对输出电流一致性影响可忽略不计。
图12 情况3输出电流上升曲线
Fig.12 The output current curves of case 3
4）实际控制系统中不同斩波器的控制频率可能不同，因此需要考虑开关管控制频率对控制系统的影响。在情况2的基础上，设置斩波器C1、C2、C3、C4的PWM控制频率分别为5kHz、6kHz、8kHz、10kHz，观察启动阶段斩波器的输出电流y1、y2、y3、y4随时间变化曲线如图13所示。电流输出曲线与图11基本一致，由此说明在一定范围内控制频率的变化对控制效果基本无影响。
图13 情况4输出电流上升曲线
Fig.13 The output current curves of case 4
比较图10和图11可知，基于式（2）所描述的控制策略能够很好地实现系统的控制目标。由图11～图13对比可知系统传输延时，不同控制频率对控制效果基本无影响，基于式（2）所描述的控制策略，图4所表示的多降压斩波器控制系统对延时和频率具有较好的抗干扰性。
本文针对由多个降压斩波器各自驱动独立负载的控制系统提出了一种相邻电流协同控制策略，对其稳定性和一致性进行分析，并通过实验验证了提出的相邻电流协同控制策略具有良好的电流协同效果。
1）在多降压斩波器控制系统中引入工业以太网EtherCAT，构建实时信息交互系统，解决了不同斩波器远距离信息传输时延大的问题。
2）多个降压斩波器输出动态一致性差异主要是负载电阻差异引起的，电感大小对电流动态一致性影响不大。在一定负载差异范围内，本文提出的协同控制策略能够较好地实现不同斩波器输出电流的动态一致性。
3）增大协同控制器的比例系数可以加快不同斩波器的协同速度，然而过大的比例系数会破坏系统的稳定性，导致输出振荡。
4）相较于无协同控制算法，引入相邻电流协同控制策略对通信延时具有一定的抗干扰性。在一定范围内，斩波器的控制频率对协同控制效果基本无影响，因此该协同控制算法可应用于不同频率场合。
5）当负载差异过大时，受控制器性能和通信速率的影响，输出电流达到动态一致性的收敛速度变慢，系统的调节时间变长，因此需要使用速率更高的通信方式来扩展本控制策略的应用范围，从而保证在较大负载差异情况下仍能实现较好的输出动态一致性。
附录 四降压斩波器系统Z矩阵
由式（13）所描述的四个斩波器控制系统的实际Z矩阵如下所示，其中四个降压斩波器的电路参数见表1，负载参数见表2中1组实验，协同控制比例参数
。
参考文献
[1] Behjati H, Davoudi A, Lewis F. Modular DC-DC converters on graphs: cooperative control[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6725-6741.
[2] Wu You, Liu Guoping. A coordinated tracking control of multi-agent systems using data-driven methods[C]// 37th Chinese Control Conference, Wuhan, 2018: 6866-6871.
[3] 李微, 周雪松, 马幼捷, 等. 三端口直流微网母线电压控制器及多目标控制[J]. 电工技术学报, 2019, 34(1): 92-102.
Li Wei, Zhou Xuesong, Ma Youjie, et al. Three-port DC microgrid bus voltage controller and multi-objective control[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 92-102.
[4] 潘舒扬, 李勇, 贺悝, 等. 考虑微电网参与的主动配电网分区自动电压控制策略[J]. 电工技术学报, 2019, 34(21): 4580-4589.
Pan Shuyang, Li Yong, He Li, et al. Automatic voltage control strategy based on zone-division for active distribution network with microgrids[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4580-4589.
[5] 佟子昂, 武建文, 马速良, 等. 一种基于主动电压扰动的直流微网负载均流控制策略[J]. 电工技术学报, 2019, 34(24): 5199-5208.
Tong Ziang, Wu Jianwen, Ma Suliang, et al. A load current-sharing control strategy for DC microgrid converters based on active voltage disturbance[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5199-5208.
[6] 郭伟, 赵洪山. 基于事件触发机制的直流微电网多混合储能系统分层协调控制方法[J]. 电工技术学报, 2020, 35(5): 1140-1151.
Guo Wei, Zhao Hongshan. Coordinated control method of multiple hybrid energy storage system in DC microgrid based on event-triggered mechanism[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1140-1151.
[7] 张哲, 王成福, 董晓明, 等. 基于分层模型预测控制的风电场电压协调控制策略[J]. 电力系统自动化, 2019, 43(11): 34-42.
Zhang Zhe, Wang Chengfu, Dong Xiaoming, et al. Coordinated voltage control strategy of wind farms based on hierarchical model predictive control[J]. Automation of Electric Power Systems, 2019, 43(11): 34-42.
[8] NguyenM K, Tran T T, Lim Y C. A family ofPWMcontrolstrategiesforsingle-phase quasi-switched-Boost inverter[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1458-1469.
[9] Calderon-Lopez G, Villarruel-Parra A, Kakosimos P, et al. Comparison of digital PWM control strategies for high-power interleaved DC-DC converters[J]. IET Power Electronics, 2018, 11(2): 391-398.
[10] Pandey S K, Patil S L, Phadke S B. Comment on “PWM-based adaptive sliding-mode control for Boost DC-DC converters”[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 5078-5080.
[11] Yan Xingda, Shu Zhan, Sharkh S M. Prediction-based sampled-data control for DC-DC Buck converters[C]//2015 First Workshop on Smart Grid and Renewable Energy (SGRE), Doha, 2015: 1-6.
[12] Jiang Congrang, Du Haibo, Wen Guanghui. Current sharing control for parallel DC-DC Buck converters based on consensus theory[C]//2017 13th IEEE International Conference on Control & Automation, Ohrid, 2017: 536-540.
[13] Xu Yeyuan, Du Haibo. Finite-time output feedback control for DC-DC Buck power converters system[C]//Proceedings of the 36th Chinese Control Conference, Dalian, 2017: 732-736.
[14] Bouarroudj N, Boukhetala D, Benlahbib B, et al. Sliding mode control based on fractional order calculus for DC-DC converters[J]. International Journal of Mathematical Modelling & Computations, 2015, 5(4): 319-333.
[15] Wang Zuo, Li Shihua, Wang Junxiao, et al. Generalized proportional integral observer based backstepping control for DC-DC Buck converters with mismatched disturbances[C]//IEEE International Conference on Industrial Technology (ICIT), Taipei, 2016: 1783-1789.
[16] Shekhar A, Mackay L, Elizondo L R, et al. State space model for n-parallel connected DC-DC converters with predictive current control strategy[C]//PCIM Europe 2016-International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, 2016: 1-8.
[17] Chen Zongxiang, Guo Yanan, Chen Mingxing, et al. Study on PI sliding mode controller for paralleled DC-DC converter[C]//Power Electronics & Motion Control Conference, Hefei, 2016: 3079-3083.
[18] Khalil A, Wang J, Mohamed O. Networked control of parallel DC-DC Buck converters[C]//2015 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies, Amman, 2015: 1-6.
[19] Ashiebi A, Khalil A, Wang J. Networked control of parallel DC-DC converters over CAN bus[C]//2016 IEEE International Conference on Power System Technology, Wollongong, 2016: 1-6.
[20] Tian Bailing, Zuo Zongyu, Wang Hong. Leader-follower fixed-time consensus of multi-agent systems with high-order integrator dynamics[J]. International Journal of Control, 2017, 90(7): 1420-1427.
[21] Sakaguchi A, Ushio T. Dynamic pinning consensus control of multi-agent systems[J]. IEEE Control Systems Letters, 2017, 1(2): 340-345.
[22] Wang Yujuan, Song Yongduan, Krstic M, et al. Adaptive finite time coordinated consensus for high-order multi-agent systems: adjustable fraction power feedback approach[J]. Information Sciences, 2016, 372(C): 392-406.
[23] 张天勇, 刘国平. 网络化多智能体主从式预测编队控制[J]. 控制与决策, 2017, 32(10): 1864-1870.
Zhang Tianyong, Liu Guoping. Master-slave predictive formation control of networked multi-agents[J]. Control and Decision, 2017, 32(10): 1864-1870.
Research on Multi-Chopper Current Cooperative Control
Abstract In a military application scene where multiple buck choppers independently drive independent loads, the output current of each buck chopper is required to have good consistency in the start and steady process. If it is not controlled, the consistency of the current will be severely affected by factors such as load differences and delays in starting communication. Based on the cooperative control of multi-agent systems, this paper designs a cooperative control strategy based on neighbor currents, and utilizes the neighbor current values to compensate the desired current value in real time to achieve the control goals of the system. Furthermore, the actual experiments on multi-buck chopper system are performed and industrial Ethernet EtherCAT for information exchange to meet the real-time requirements of the control system is introduced, thus verifying the effectiveness and excellent performance of the neighbor current cooperative control algorithm on solving the multi-chopper current cooperative problem.
keywords：Multi-chopper control system, cooperative control, system stability, EtherCAT
DOI:10.19595/j.cnki.1000-6753.tces.200815
中图分类号：TM76; TP13
邓其军 男，1975年生，教授，博士生导师，研究方向为无线电能传输、电力系统及其自动化等。E-mail：dqj@whu.edu.cn
曾文彬 男，1996年生，硕士研究生，研究方向为多智能体协同控制、电力系统及其自动化。E-mail：1157833257@qq.com（通信作者）
国家自然科学基金资助项目（51977151）。
收稿日期 2020-07-09
改稿日期 2020-10-30
（编辑 赫蕾）