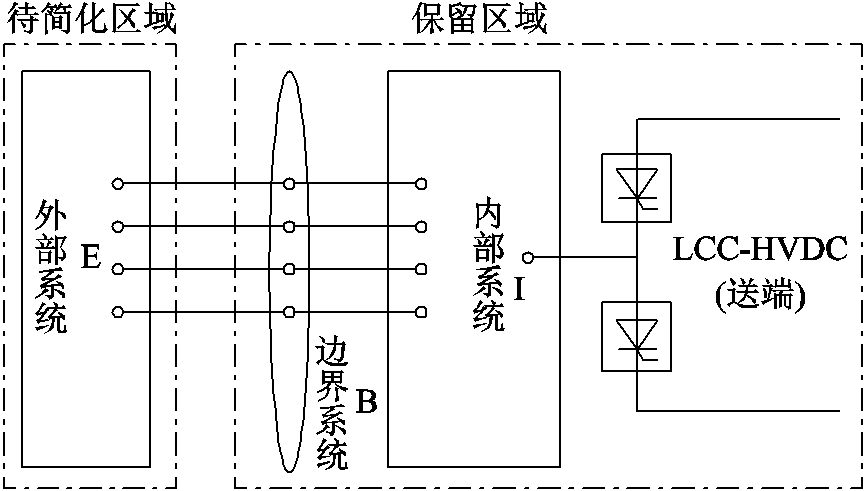
图1 系统划分结构
Fig.1 Structure of system after division
摘要 大规模新能源经电网换相高压直流输电（LCC-HVDC）送出时，极易引发送端电网暂态过电压。通过建立LCC-HVDC及送端等值电网电磁暂态仿真模型，可以详细分析其暂态过电压特性，进而优化其控制策略。目前，针对LCC-HVDC送端电网等值的相关研究较少。结合工程需求，给出一种适用于LCC-HVDC送端电网的等值方案。首先，根据主干网各梯级断面点节点残压大小与LCC-HVDC电气耦合强弱的关系，提出一种基于节点残压的内部系统主干网确定方法。该方法在快速确定内部系统范围的同时，可有效避免等值过程中可能因人为因素而引起的等值误差；然后，以梯级断面点为依据划分拓扑区域，以等值前后各拓扑区域电气特性一致为原则，提出内部系统中包括新能源电源在内的等值电源、负荷及变压器等元件的详细参数确定方法；最后，给出LCC-HVDC送端电网多端口戴维南等值方法，简化了外部系统。基于国内某LCC-HVDC送端电网等值方案实际算例，验证了所提等值方案的有效性。
关键词：电网换相高压直流输电 送端电网 等值 主干网 节点残压
根据我国能源战略规划，西北和东北地区的新能源电力需通过电网换相高压直流输电（Line-Commutated-Converter Based High Voltage Direct Current, LCC-HVDC）送至东部负荷地区，实现新能源更大范围的消纳[1-4]。大规模风电、光伏等新能源电力经LCC-HVDC外送时，直流功率大扰动（如交流短路、换相失败、直流闭锁等故障）极易造成送端电网暂态过电压，从而引发风机脱网及联锁反应，严重威胁系统的安全稳定运行[5-8]。目前，由于送端电网接入大量新能源机组，以扎鲁特-青洲±800kV HVDC工程为代表的多个LCC-HVDC工程，均面临着严峻的暂态过电压问题[9]。
大规模风电、光伏接入的LCC-HVDC送端电网属于含高比例可再生能源和高比例电力电子装备的“双高”电力系统[10]。电力电子装备不仅具有微秒级的响应速度，而且呈现出显著的非线性、切换性和离散性等特征[11]。因此，在采用时域分析方法研究LCC-HVDC送端电网暂态过电压问题时，为了充分体现LCC-HVDC及送端电网的暂态过程，必须采用仿真步长为μs级的电磁暂态仿真分析方法[12-14]。电磁暂态仿真分析方法虽然能够计及元件的非线性特征，实现电力电子装备的精确建模，但是，电磁暂态仿真所能模拟的系统规模较小。为了减轻电磁暂态仿真压力，在建立LCC-HVDC及送端电网电磁暂态仿真模型前，需首先在机电暂态仿真环境中，以等值前后系统动态特性不畸变为前提，对LCC-HVDC送端电网进行等值简化[15-20]。
目前，已有国内外学者在交流系统等值方面开展了相关研究，并取得了一定的进展。文献[19]提出了一种基于物理等效且适用于电力系统电磁暂态分析的动态等值方法；文献[21-22]分析了Ward等值方法的优缺点，并结合优缺点分析了该方法的使用场景。文献[23]通过引入边界缓冲网，扩大内部系统范围，进而提高外网动态等值精度。上述文献所涉及的交流系统中，水/火电机组为系统主力机组，新能源机组占比小，暂态过电压问题对交直流系统的稳定运行影响小。在评估交直流等值系统有效性时，以往研究侧重于交流系统故障下的系统功角稳定问题，而对LCC-HVDC故障下系统的电压响应特性，特别是送端电网的过电压问题关注甚少。随着国内LCC-HVDC送端电网暂态过电压问题的不断凸显，针对该问题，研究LCC-HVDC送端电网等值方法愈加迫切。
针对LCC-HVDC送端电网的等值问题，内部系统范围、内部系统详细参数确定及外部系统简化方法是其研究重点。现有的交流系统等值研究中，内部系统通常由研究人员依照经验确定。由于等值系统的主要动态特性由内部系统体现，依据经验人为确定内部系统时，可能造成内部系统过小以致大量动态特性丢失，从而产生较大的等值误差。为了提高等值系统精度，文献[23]提出了引入边界缓冲网间接扩大内部系统规模的方法，但是并未给出具体的边界缓冲网确定方法。此外，扩大内部系统的同时可能导致等值系统规模过大，浪费计算资源。客观有效的内部系统确定方法，可以避免因研究人员主观判断造成的不确定性，从而大幅度提高等值系统的精确度。
等值系统中各元件详细参数的确定方法是否合理，同样会影响整个系统等值工作的精度。文献[24]基于电气距离识别同调机群进而对不同的同调机群进行等值简化；文献[25]提出一种基于容量加权法的相关机群详细模型参数聚合方法，并对不同型号的发电机进行了聚合；文献[26]提出一种按照短路电流贡献率确定具有主导成分的发电机类型作为等值机机型的方法。上述研究工作中将水电/火电等传统同步机组作为影响等值系统动态特性的主导因素，只针对同步机组的等值方法进行了研究，而忽略了新能源电源对等值系统动态特性的影响。当新能源大规模接入LCC-HVDC送端电网后，交直流系统动态特性，特别是送端电网的暂态过电压特性，将发生很大程度的改变。故在LCC-HVDC送端电网等值过程中，新能源电源的动态特性不可忽视[27]。
在LCC-HVDC送端电网等值系统中，详细建模的内部系统主导整个等值系统的全部动态特性，而外部系统动态特性可忽略不计。在等值系统的建立过程中，通常只需保留外部系统原有的静态潮流及短路容量等特性，故可大规模简化外部系统。现有研究在简化外部系统时多采用WARD等值方法，但采用该方法获得的等值结果中易出现不符合电力系统实际情况的参数，无法在电磁暂态仿真中实现，且无法保证等值前后系统短路容量的一致[28]。
结合工程需求，本文给出一种适用于LCC-HVDC送端电网的等值方案。首先，分析LCC-HVDC送端电网特性，制定送端电网等值原则，并给出送端电网等值结构及等值系统建立流程；其次，提出一种基于节点残压的内部系统主干网确定方法，该方法以节点残压为基本量化指标，可以有效确定内部系统主干网范围；再次，充分考虑新能源电源对系统动态特性的影响，给出等值系统中包括新能源电源在内的等值电源、负荷及变压器等元件详细参数确定方法；最后，引入多端口戴维南等值方法，对外部系统进行大规模简化。应用该方案对某LCC-HVDC送端电网进行等值，仿真验证等值方案的有效性。
根据系统等值需要，将LCC-HVDC送端电网划分为内部系统、边界系统和外部系统三部分。其中，内部系统为详细建模部分；外部系统是待简化部分；边界系统是建立内、外部系统连接的全部节点集合。图1给出了划分后的LCC-HVDC送端电网结构。
图1 系统划分结构
Fig.1 Structure of system after division
由图1可知，内部系统直接与LCC-HVDC连接，主导交直流系统动态特性，是所要重点研究的系统部分。外部系统与LCC-HVDC电气距离远，无功耦合度低，故在分析LCC-HVDC送端电网暂态过电压特性时可忽略该部分的动态特性。在建立LCC-HVDC送端电网等值系统时，需对内部系统详细建模，而对外部系统进行简化。LCC-HVDC送端电网等值系统的建立，应遵循以下原则。
（1）当LCC-HVDC发生故障时，故障所引起的功率冲击将通过LCC-HVDC送端电网主干网进行传递，即LCC-HVDC的动态稳定性在很大程度上取决于LCC-HVDC送端电网主干网[29-30]。内、外部系统间耦合也主要体现在主干网层面，二者一般不存在其他电压等级的电气耦合，故复现LCC-HVDC送端电网等值系统中交直流交互特性的关键在于等值系统应保留足够规模的LCC-HVDC送端电网主干网。
（2）根据LCC-HVDC送端电网暂态过电压仿真需要，保留对交直流系统动态特性有重要影响的水/火电及新能源电源。
（3）为充分保留LCC-HVDC运行特性，满足换流站设备调试和直流控制策略优化等相关要求，保留LCC-HVDC送、受端换流站内所有交直流电气设备。
为了直观、清晰地反映LCC-HVDC与送端电网各母线间的电气耦合情况，可在主干网层面对送端电网进行梯级化划分。给出LCC-HVDC送端电网梯级化划分过程中所涉及名词的具体释义。
1）主干网：指在LCC-HVDC送端电网中，由全部最高电压等级交流母线及输电线路共同构成的电网结构。
2）路径：指在主干网层面，由某一主干网母线出发经若干输电线路和母线到达第一梯级断面点，且输电线路和母线均不可重复出现，将经过的所有输电线路组成的集合称为该母线至第一梯级断面点的一个路径，其中，包含母线数最少的路径为最短路径。
在此基础上，介绍LCC-HVDC送端电网梯级化划分具体过程。首先，定义LCC-HVDC送端电网换流母线为第一梯级断面点；然后，以第一梯级断面点作为划分起始，按照各主干网母线至第一梯级断面点的最短路径所包含的母线数n，确定相应母线为第n梯级断面点；最后，将两端分别连接于第a、b（a≤b）梯级断面点的输电线路划入第a梯级断面，完成LCC-HVDC送端电网的梯级化划分。图2所示为梯级化划分后的LCC-HVDC送端电网结构，图2中标出了全部第二梯级断面点，并以不同线型分别标出了第一、第二、第三梯级断面。
以环网l4-l5-l6内母线及输电线路的梯级化划分为例，说明上述LCC-HVDC送端电网梯级化划分的具体过程。母线N2至第一梯级断面点T1共有l4-l1、l6-l5-l1、l6-l3-l2三条路径，其中，l4-l1为最短路径，该路径中包含母线N1、N2和T1，即n=3，故N2为第三梯级断面点。输电线路l4两端分别与第二梯级断面点N1和第三梯级断面点N2相连，故l4划入第二梯级断面；输电线路l5两端分别与第二梯级断面点N1和第三梯级断面点N3相连，故l5划入第二梯级断面；输电线路l6分别与N2、N3相连，N2、N3均为第三梯级断面点，故l6划入第三梯级断面。
图2 LCC-HVDC送端电网梯级化划分
Fig.2 Cascade division of AC system in sending-end of LCC-HVDC
随着梯级断面点级数增大，其与第一梯级断面点的电气距离随之增加，电气耦合随之减弱。各同级数梯级断面点与第一梯级断面点的电气距离一般差异不大。当LCC-HVDC发生故障时，同一梯级内各梯级断面点电气特性基本一致。通过选定某一梯级断面作为边界系统，可以简化边界系统确定过程。当选定所有第z梯级断面点为边界系统后，梯级断面数小于z的交流系统结构为内部系统，梯级断面数大于z的交流系统为外部系统。
根据1.1节所给出的等值原则建立LCC-HVDC送端电网等值系统。LCC-HVDC送端电网等值系统建立的主要流程如图3所示，等值系统的建立可以分为Step1～Step4四个阶段。
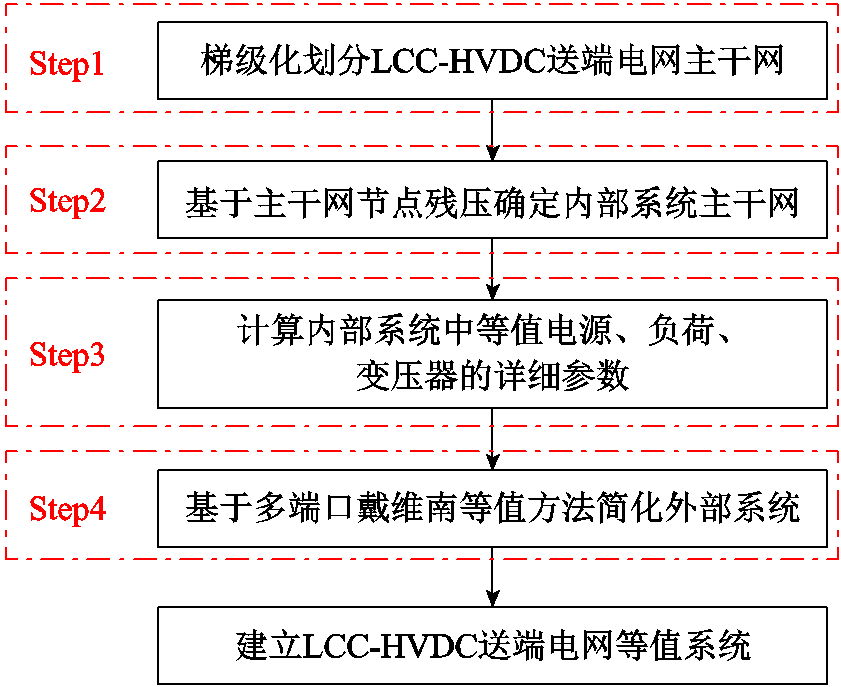
图3 等值系统建立流程
Fig.3 Establishment process of equivalent system
确定内部系统主干网时，以第一梯级断面点为起始，按照梯级递增的顺序依次拓展至某一与LCC-HVDC弱耦合的梯级断面，将该梯级断面与第一梯级断面之间的电网结构作为内部系统主干网。本节提出基于节点残压的内部系统主干网确定方法。该方法以各梯级断面点节点残压水平表征其与LCC-HVDC间的电气耦合程度，通过选择与LCC-HVDC强电气耦合的梯级断面点集合构成内部系统主干网。
定义当第一梯级断面点发生三相短路故障且达稳态后，各梯级断面点电压有效值为该梯级断面点节点残压。第一梯级断面点故障期间，并网于非主干网（下称“下级电网”）的各电源经主干网向第一梯级断面点提供短路电流。随着梯级断面点级数的增大，经下级电网连接于各梯级断面点的电源与LCC-HVDC间的等效阻抗变大，与此同时，梯级断面点节点残压值随之增大。由此可知，当以第一梯级断面点作为研究中心时，随着梯级断面点节点残压值的增大，连接于各梯级断面点的电源与LCC-HVDC间的等效阻抗变大，电气耦合逐渐变小。
各梯级断面点节点残压的大小，由LCC-HVDC送端电网中各电源所提供的短路电流和全系统阻抗矩阵决定。节点残压的表示方法如图4所示。图4中节点α为第一梯级断面点，各类电源经下级电网与相应的梯级断面点相连。当α发生三相短路故障时，LCC-HVDC送端电网中并网于各下级电网的电源经不同梯级断面点向主干网注入短路电流，并最终馈入第一梯级断面点。由此可知，在一定程度上，节点残压可以综合反映各下级电网对LCC-HVDC送端电网的电气影响。当系统处于稳态时，依据式（1）可计算得到各梯级断面点节点残压值。
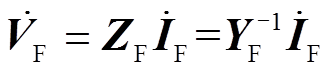（1）式中，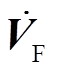
为梯级断面点节点残压矩阵；
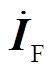为节点注入短路电流矩阵，如式（2）所示，节点注入短路电流矩阵由注入各梯级断面点的短路电流所构成；ZF为LCC-HVDC送端电网主干网节点阻抗矩阵，YF为相应的节点导纳矩阵。
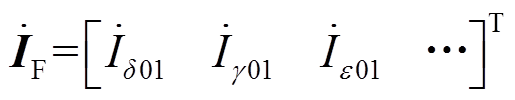（2）
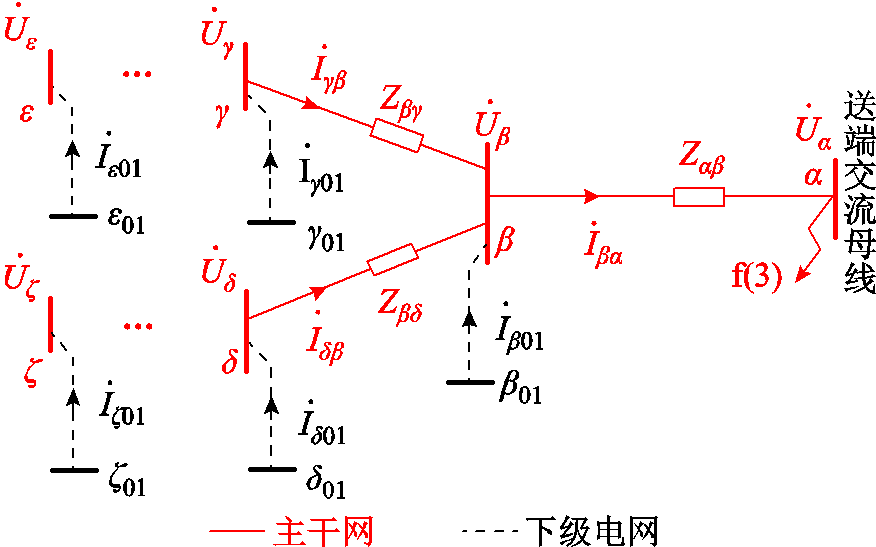
图4 节点残压表示方法
Fig.4 Represententation of residual voltage of node
如图4所示，当α发生三相短路故障时，短路电流由各电源经各梯级断面点逐级汇集并最终馈入α，各输电线路流过的短路电流在上一级梯级断面点汇集，形成上一级梯级断面电流。由α逆电流方向，随着梯级断面点级数的增大，梯级断面点节点残压值逐级升高。由于支路的分流作用，随着梯级断面级数变大，相应断面支路电流逐渐减小。当梯级断面等级增大到一定值时，同一梯级断面点相邻的两梯级断面线路上的短路电流值较小且近似相等。此时，该断面内输电线路所连的两梯级断面点之间的节点残压差与该支路导纳值成反比。当梯级断面等级高于一定值时，即当梯级断面点节点残压高于一定值后，即使很小的梯级断面点节点残压差也意味着相应梯级断面点之间较远的电气距离。
基于上述分析，通过在第一梯级断面点设置三相短路故障，求取各梯级断面点节点残压值便可得到同一输电线路两端梯级断面点间的电气耦合程度。进一步，以节点残压值表征各梯级断面点与第一梯级断面点间的电气耦合程度。通过设定节点残压阈值θ，选出节点残压值小于等于阈值θ的全部梯级断面点，构成内部系统主干网。
基于节点残压的内部系统主干网确定流程如图5所示。首先，在第一梯级断面点处设置三相短路故障，计算各梯级断面点节点残压值，并根据节点残压计算结果，设定最小节点残压阈值θ=θmin。其次，选出节点残压值小于等于阈值θ的全部梯级断面点，构成内部系统主干网。再次，建立内部系统，简化外部系统，构建节点残压阈值θ所对应的等值系统。最后，验证等值系统有效性；若所建立的等值系统有效性不满足要求，增大节点残压阈值θ，重复上述步骤，直至等值系统满足要求。
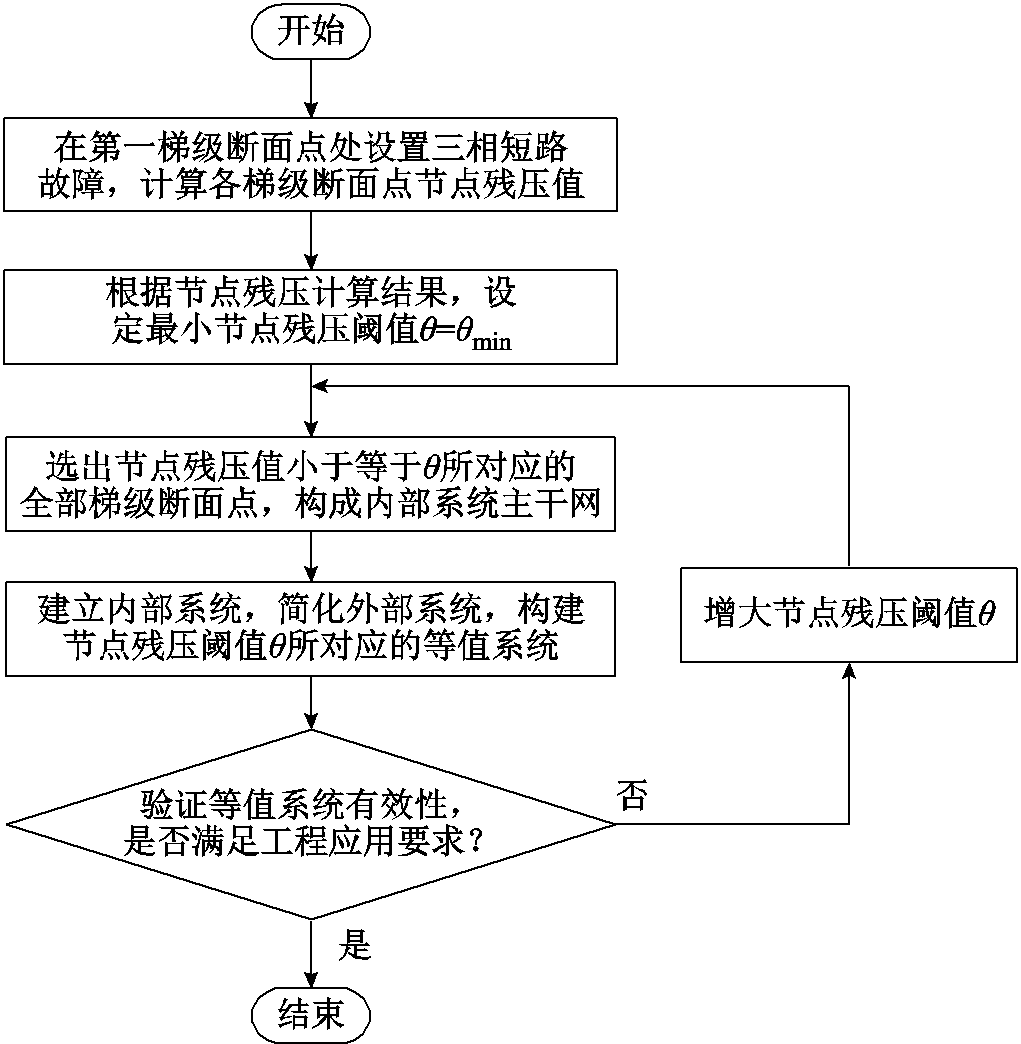
图5 基于节点残压的内部系统主干网确定流程
Fig.5 Process of determining internal system backbone based on residual voltage of node
考虑到LCC-HVDC送端电网中可能存在环网结构，需根据所确定内部系统主干网的实际结构进行调整。基于节点残压确定的内部系统主干网中，可能存在“所确定的内部系统节点所在环网未能完全包含于内部系统主干网”。针对这一情况，对于某一环网，若存在至少两个梯级断面点位于所确定内部系统主干网内，则将整个环网划入内部系统主干网中；若仅存在至多一个梯级断面点位于所确定内部系统主干网内，则不再改变所确定的内部系统主干网结构。
节点残压阈值θ的选取主要从等值系统仿真规模和有效性两个方面考虑。在保证等值系统有效性的前提下，所建立的等值系统规模应尽可能小。此外，在验证等值系统有效性时，本文建立了相应的有效性评价体系：①等值前后内部系统主干网稳态潮流特性一致；②等值前后内部系统主干网各主要梯级断面点短路容量误差在10%以内；③等值前后系统的交流系统故障响应特性基本一致；④等值前后系统的功角响应特性基本一致；⑤等值前后送端电网过电压特性基本一致。
在第2节确定的内部系统主干网基础之上，本节将给出内部系统中等值电源、负荷及变压器的详细参数计算方法。通过构建等值电源、负荷及变压器等元件模型，以复现原LCC-HVDC送端电网的系统特性。
为了尽可能保留原系统的电源动态特性，在建立LCC-HVDC送端电网等值系统模型时，除了要尽可能保留水/火电等同步机组动态特性，还应充分保留风电、光伏等新能源机组动态特性[20]。
3.1.1 水/火电机组参数确定
根据水/火电接入电网位置的不同，可以将其分为以下两种类型，针对不同类型给出不同的等值机组参数确定方案。
1）类型1，通过升压变直接接入主干网的大容量主力机组，对于此类型机组而言，采用加权法将同一电厂内的所有机组等效为1台等值机。
加权法是一种可以应用于大规模系统暂态稳定分析的等值聚合方法，该方法以各个待聚合机组的额定容量与等值机组额定容量之比为权值，对需要聚合的发电机各参数进行加权计算[25]。加权法不仅操作简单，而且能够保证等值前后系统的功角响应特性基本一致、等值效果明显，被广泛地应用于大规模系统等值之中。利用式（3）所示加权法，即等值机组各参数（以等值机容量为基值）等于等值前各机组相应参数（以各自容量为基值）的标幺值的加权平均值，对包括原动机、发电机、励磁调节系统及电力系统稳定器等组成部分在内的等值机组参数进行确定。
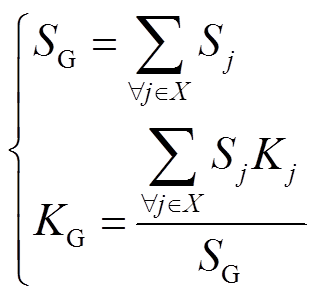（3）式中，X为待聚合机组集合；SG为等值机组额定容量；Sj为等值前各机组额定容量；KG为聚合后等值机的惯性常数、原动功率、电磁功率、dq轴同步电抗、暂态电抗、次暂态电抗、励磁系统各环节增益及时间常数等参数；Kj为等值前各机组相应的参数。
2）类型2，分散接入其他电压等级电网的机组，对于此类型机组而言，按照各个梯级断面点划分主干网拓扑区域，将属于同一区域的各机组等效为1台机。各等值机通过等值变压器连接到相应的梯级断面点上，等值机参数依旧按照式（3）所示的加权法进行确定。等值机与所属梯级断面点的连接关系
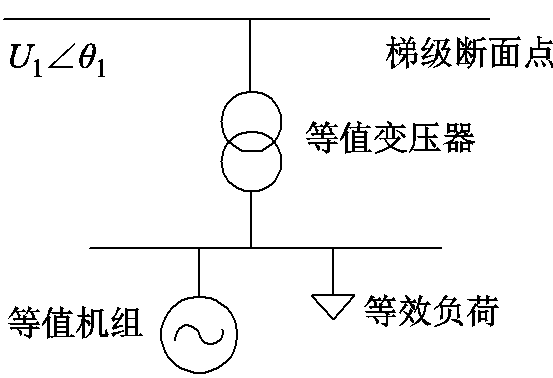
图6 同一区域，等值机组与主干网连接关系
Fig.6 Connection relationship between equivalent source and backbone network in the same area
如图6所示。
3.1.2 新能源机组参数确定
随着大规模新能源逐渐接入电网，尤其是大容量、高电压等级的风电、光伏并网，并通过LCC-HVDC集中外送。为了保证等值系统动态特性不发生畸变，在制定等值方案时应充分考虑新能源机组给系统电压稳定性带来的影响。同样，针对新能源机组接入电网位置的不同，将新能源机组分为以下两种类型，针对两种类型给出相应的等值方案。
1）类型1，通过升压变压器直接接入主干网的大容量新能源机组，对于此类型机组而言，采用文献[31]提出的单机聚合等值方法将位于同一新能源场站内的所有机组聚合为1台等值机。单机聚合等值方法对新能源机组中的变流器环节进行了详细的建模，可以充分复现原系统中新能源机组与交流系统间的动态响应关系。
2）类型2，分散接入其他电压等级电网的新能源机组，对于此类型机组而言，按照传统的针对新能源机群处理方案，将其等值为功率为负的负荷，忽略其动态特性[20]。
依据原系统潮流数据确定等效负荷，等值系统中负荷采用静态负荷与动态负荷组合的形式。静态负荷即为式（4）所示的恒功率、恒电流和恒阻抗负荷的组合形式，动态负荷即为电动机负荷。
（4）式中，PLoad为恒功率负荷部分；ALoadV为恒电流负荷部分；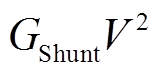
为恒阻抗负荷部分。
等值系统中引入电动机负荷是为了还原原系统中负荷所表现的暂态特性，同时，保证等值前后各主干网节点短路容量不变。
在等效负荷的确定中，采用类似式（3）所示的加权法求取恒功率、恒电流和恒阻抗负荷所占总负荷的比例，即等效负荷中恒功率、恒电流和恒阻抗负荷的占比为
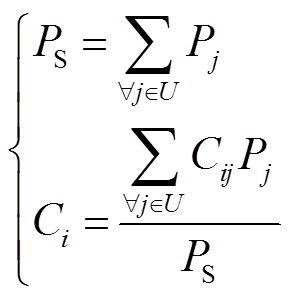（5）式中，U为待等效负荷集合；PS为等效负荷值；Pj为等值前各下级母线负荷值；Ci(i=1、2、3)分别为等效负荷中恒功率、恒电流、恒阻抗负荷所占等效负荷的比例；Cij分别为各下级母线负荷中恒功率、恒电流、恒阻抗负荷所占比例。同样电动机负荷参数计算式为
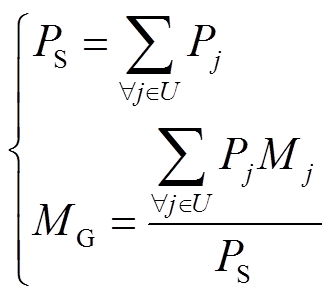（6）式中，MG为等值电动机负荷定子阻抗、转子阻抗和励磁阻抗等参数；Mj为等值前各下级母线电动机负荷相应的参数。
得到了等值机组和等效负荷的详细参数后，建立等值机组和等效负荷模型。采用文献[17]提出的等效变压器参数确定方法求解位于各主干网拓扑区域中各等效变压器的详细参数。该方法通过对比等值前后各梯级断面点的静态潮流特性和短路容量，以等值前后各个梯级断面点短路容量和相应的静态潮流特性一致为原则，确定变压器详细参数。
LCC-HVDC送端电网边界系统由多个梯级断面点组成。多端口戴维南等值方法通过对所有梯级断面点进行两两之间的组合，形成多个端口，然后以各个端口作为研究对象将外部系统简化为等值电动势和等值阻抗的串联模型[32]。该等值方法能够保证等值前后边界系统中各个梯级断面点短路容量的一致。由于外部系统与LCC-HVDC在动态特性方面的电气耦合可忽略不计，故利用多端口戴维南等值方法简化外部系统可以满足本文对送端电网等值系统的电压响应特性的要求。
结合图7所示的LCC-HVDC送端电网划分结构，说明应用多端口戴维南等值方法简化外部系统的具体过程。图7中，所有第三梯级断面点作为边界系统；第三及以上梯级断面作为外部系统，即待简化系统部分。
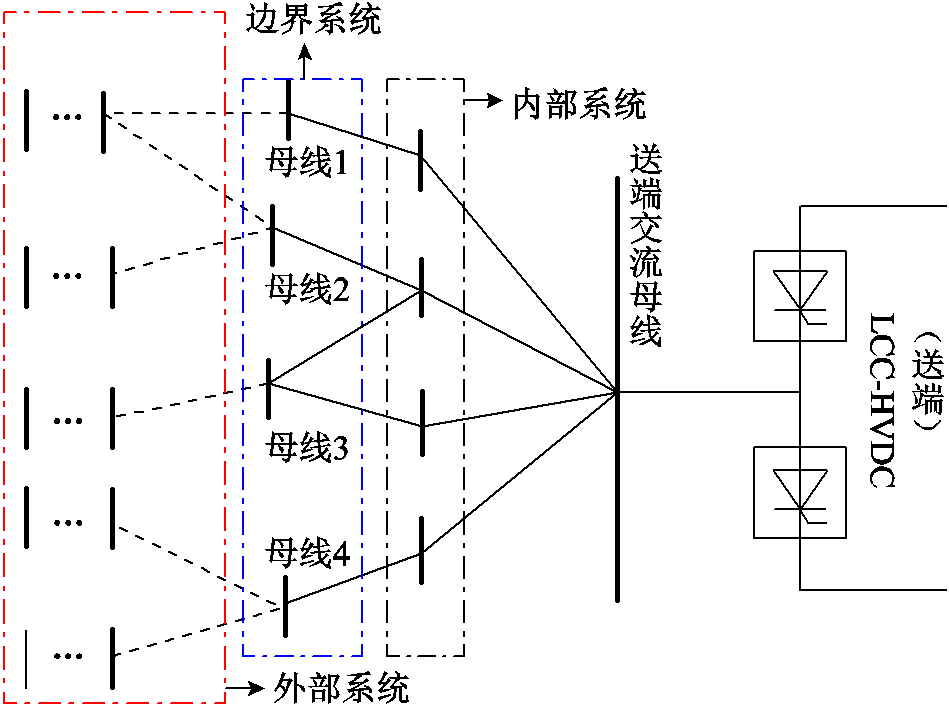
图7 LCC-HVDC送端电网划分结构
Fig.7 Structure of sending-end after division
以分块矩阵的形式构建图7所示LCC-HVDC送端电网导纳矩阵Y为
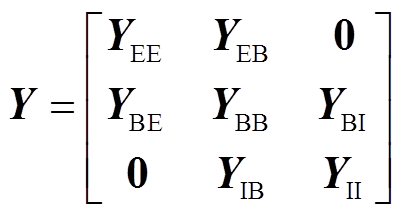（7）式中，YEE为外部系统自导纳矩阵块；YEB、YBE为外部系统与边界系统互导纳矩阵块；YBB为边界系统自导纳矩阵块；YBI、YIB为边界系统与内部系统互导纳矩阵块；YII为内部系统自导纳矩阵块。YEB与YBE互为对称矩阵块，YBI与YIB互为对称矩阵块。
由LCC-HVDC送端电网导纳矩阵Y可相应地推得其系统阻抗矩阵Z为
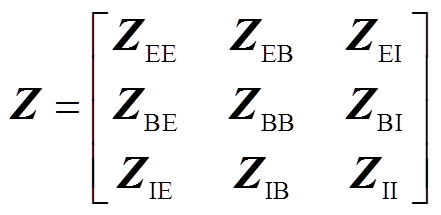（8）将边界系统中母线1～4依次进行编号形成边界系统节点集合B
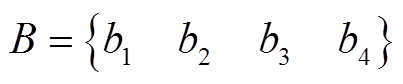（9）
集合B包含了所有边界系统节点的全部信息，在此基础上，确定多端口戴维南等值过程中的端口情况，任意边界节点bx与其他边界节点均形成网络端口，即总网络端口数为n(n-1)/2。
建立任意两个节点bp、bq组成端口m关联矩阵为
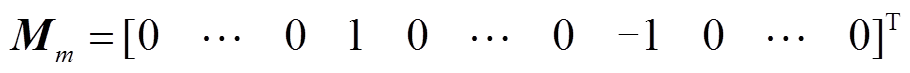（10）式中，1、-1分别对应矩阵中第p、q列元素。
将所有端口关联矩阵分别写出，建立边界系统节点关联矩阵为
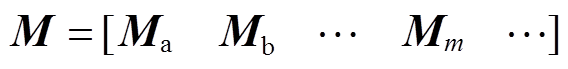（11）根据边界系统节点关联矩阵和原系统阻抗矩阵求得等值系统阻抗矩阵为
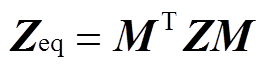（12）
等值系统Yeq为
（13）
各端口开路电压矩阵为
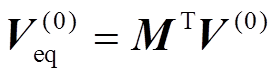（14）
式中，V(0)为原系统节点电压矩阵。
至此，求得LCC-HVDC送端电网等值系统如图8所示。所有边界系统节点两两组合，形成母线1、2，母线1、3，母线1、4，母线2、3，母线2、4和母线3、4相组合的共计6个端口。与LCC-HVDC电气弱耦合的外部系统被简化，简化后，各个边界系统节点均连接一个等值电动势和等值阻抗串联模型。原系统中各个边界系统节点间由于存在一定的电气耦合，故等值过程中不同边界系统节点间将形成类似图8中Z12所示的互联阻抗以反映原系统中互异节点间的电气耦合。
图8 LCC-HVDC送端电网多端口戴维南等值系统结构
Fig.8 Structure of multi-ports thevenin equivalent system for the sending-end of LCC-HVDC
由于简化过程严格依托数学计算，简化外部系统后，所获得的各等值电势、等值阻抗及互联阻抗等相关参数中可能存在以下两类问题。
1）个别边界节点等值电势的数值远超主干网额定电压值，与电网实际运行情况不符。此时，可在保证该边界节点短路容量不变的前提下，通过修改相应边界节点等值电势及等值阻抗值来解决该问题。
2）某两个边界节点间互联阻抗值数量级可能达102，甚至更高，进而造成等值系统潮流在边界系统中的异常分布。这是由原LCC-HVDC送端电网中边界节点间的弱电气耦合所造成的，可以通过忽略边界节点间的弱电气耦合，删除数值异常互联阻抗的方法，来解决该类等值系统潮流异常的问题。
以国内某LCC-HVDC送端电网为源数据，采用本文所提等值方案对该系统进行等值。该送端电网中共包含各种电压等级母线8 712条，发电机1 258台，发电总容量达297 770MW，其主干网电压等级为750kV。根据该LCC-HVDC的换流站落点位置及送端电网特性，确定内部系统范围，最终建立等值系统。基于PSD-BPA对该系统进行等值简化，仿真对比系统等值前后的相关电气特性。
在LCC-HVDC送端电网中第一梯级断面点设置三相短路故障，计算各梯级断面点节点残压值；设定节点残压阈值θ为0.7UN（UN为主干网电压基准），在该阈值下确定内部系统主干网。表1所示为构成内部系统主干网的全部梯级断面点节点残压。内部系统主干网结构如图9中实线所示，待研LCC-HVDC落点于第一梯级断面点A处。第四梯级断面点J、K、L、M等组成边界系统，即内部系统主干网为包括第四梯级断面点在内的主干网部分。
表1 内部系统各梯级断面点节点残压
Tab.1 Residual voltage of each node of the internal system
梯级断面点梯级数节点残压值(pu) A一0.002 5 B二0.097 8 C三0.125 1 D二0.323 0 E三0.292 9 F三0.362 3 G三0.426 3 H三0.597 7 I四0.688 1 J四0.596 2 K四0.597 0 L四0.660 0 M四0.688 1
建立内部系统主干网后，计算内部系统中等值电源、负荷及变压器等详细参数，并采用多端口戴维南等值方法简化外部系统。如图9所示为运用本文所提出的等值方案所建立的LCC-HVDC送端电网等值系统。该等值系统中共含7座光伏场站、8座由风电场站、1座火电厂和6座水电厂。图9可知，外部系统被简化为分别连接于J、K、L、M各边界节点的等值电势和等值阻抗串联模型，及各边界节点间连接的互联阻抗（为了更好地呈现等值系统结构，图中未给出互联阻抗连接情况）。
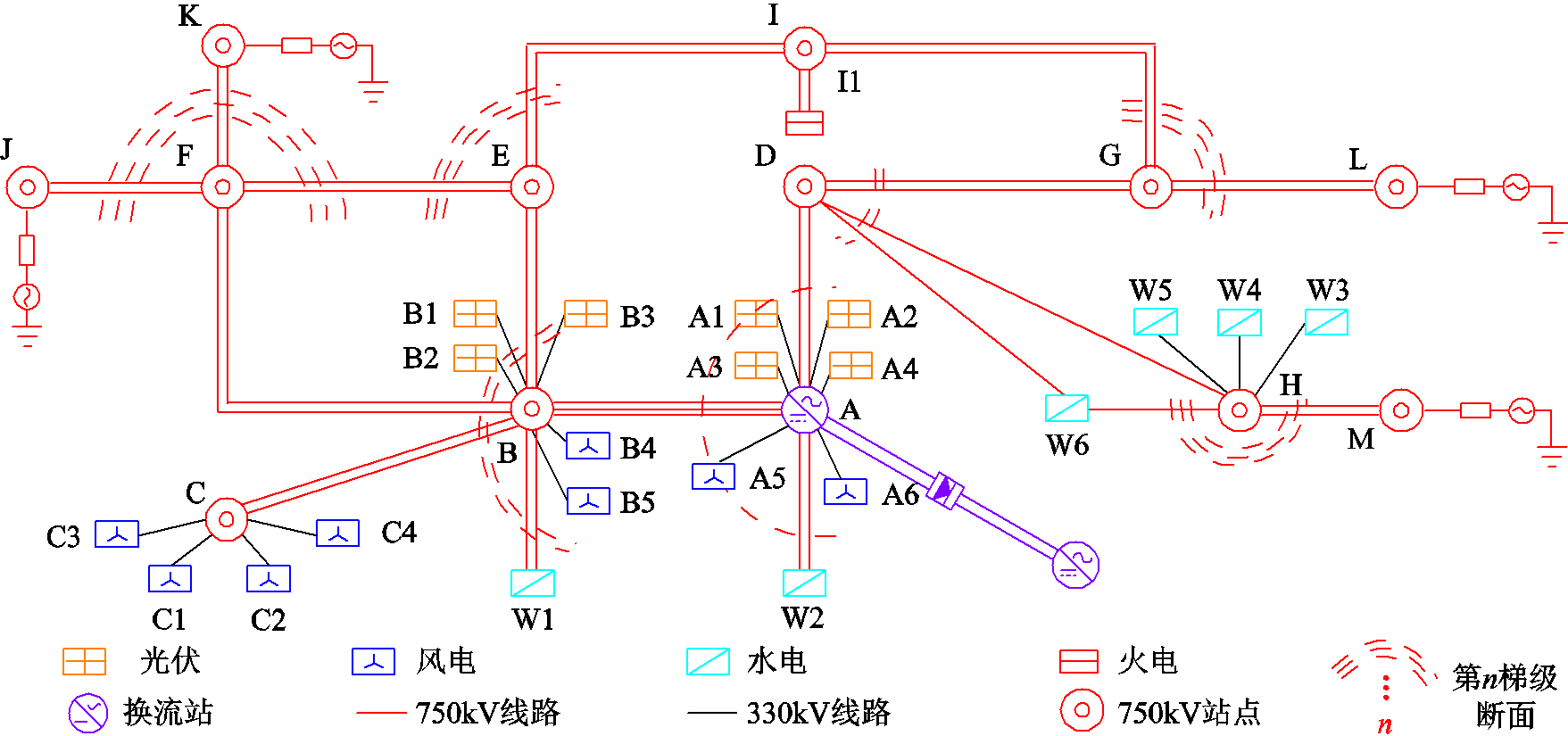
图9 等值系统结构
Fig.9 The structure of equivalent system
分别对比等值前后LCC-HVDC送端电网中母线和电源数量，以评估等值系统的等值效果。
定义母线等值比率为
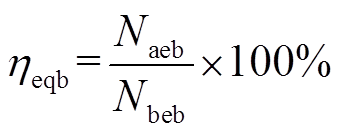（15）式中，ηeqb为母线等值比率；Naeb、Nbeb分别为等值系统和原LCC-HVDC送端电网中母线总数。表2给出了各电压等级所对应的母线等值比率。
表2 等值前后系统母线等值比率
Tab.2 Equivalent ratio of buses before and after equivalence
电压等级/kVNbeb/条Naeb/条ηeqb(%) 3511991109.17 110895313.46 330637446.91 7505048216.27 总计32352678.25
定义如式（16）所示的电源等值比率为
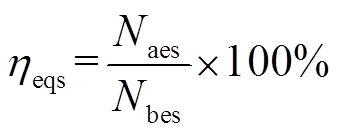（16）式中，ηeqs为电源等值比率；Naes、Nbes分别为等值系统和原LCC-HVDC送端电网电源总数。表3给出了各类型电源的电源等值比率。
表3 等值前后系统电源等值比率
Tab.3 Equivalent ratio of sources before and after equivalence
电源类型Nbes/座Naes/座ηeqs(%) 火电（含热电、自备电厂）21110.47 水电10665.67 风电78810.26 光伏（含光热）69710.14 总计464224.74
ηeqb和ηeqs的大小可以在一定程度上反映LCC-HVDC送端电网等值效率的大小，ηeqb和ηeqs越小，所建立的等值系统中母线和电源的规模越小，等值效率越高。由表2和表3可知，运用本文所提等值方案对该LCC-HVDC送端电网进行等值后，母线等值比率为8.25%，电源等值比率为4.74%。由上述分析可知，本文所提等值方案可以显著降低LCC-HVDC送端电网仿真规模，大幅提高仿真效率。
本节将依据2.2节所给出的等值系统有效性评价体系，从主干网稳态潮流、主要梯级断面点短路容量、交流系统故障响应特性、功角响应特性及送端电网过电压特性等方面，验证所构建LCC-HVDC
送端电网等值系统的有效性。
5.4.1 稳态潮流对比
通过时域仿真，对比分析了等值前后LCC-HVDC送端电网的静态潮流特性。表4为等值前后内部系统各梯级断面点电压有效值对比，表5为等值前后所有第一、第二梯级断面内输电线路传输有功功率对比。
表4 等值前后节点电压有效值对比
Tab.4 Comparison of node voltages before and after equivalence
相关节点节点电压计算结果(pu)节点电压相对误差(%) 等值前等值后 A0.9750.9750 B0.9770.9770 D0.9740.9740 C0.9790.9800.1 E0.9670.9680.1 F0.9640.9650.1 G0.9760.9760 H0.9760.964-1.23
表5 等值前后线路有功功率对比
Tab.5 Comparison of active power of lines before and after equivalence
相关线路传输有功功率计算结果/MW有功功率相对误差(%) 等值前等值后 B-A7 731.207 735.960.06 D-A-4 758.30-4 749.00-0.20 E-B-1 188.50-1 174.10-1.21 F-B2 690.002 680.60-0.35 G-D-203.00-220.400.09 H-D-1 824.50-1 752.80-3.93
通过分析表4和表5数据可知，采用本文所提出的等值方案，LCC-HVDC送端电网等值前后内部系统各节点电压相对误差均在1.5%以内，主要输电线路传输有功功率相对误差均在4%以内。因此，采用本文提出的等值方案可以保证等值前后LCC-HVDC送端电网静态潮流特性的一致。
5.4.2 短路容量对比
短路容量的大小在一定程度上可以反映电力系统电压稳定等相关运行特性，因此保证等值前后内部系统短路特性的一致至关重要。表6为等值前后内部系统全部梯级断面点短路容量对比。
表6 等值前后节点短路容量对比
Tab.6 Comparison of node short circuit capacities before and after equivalence
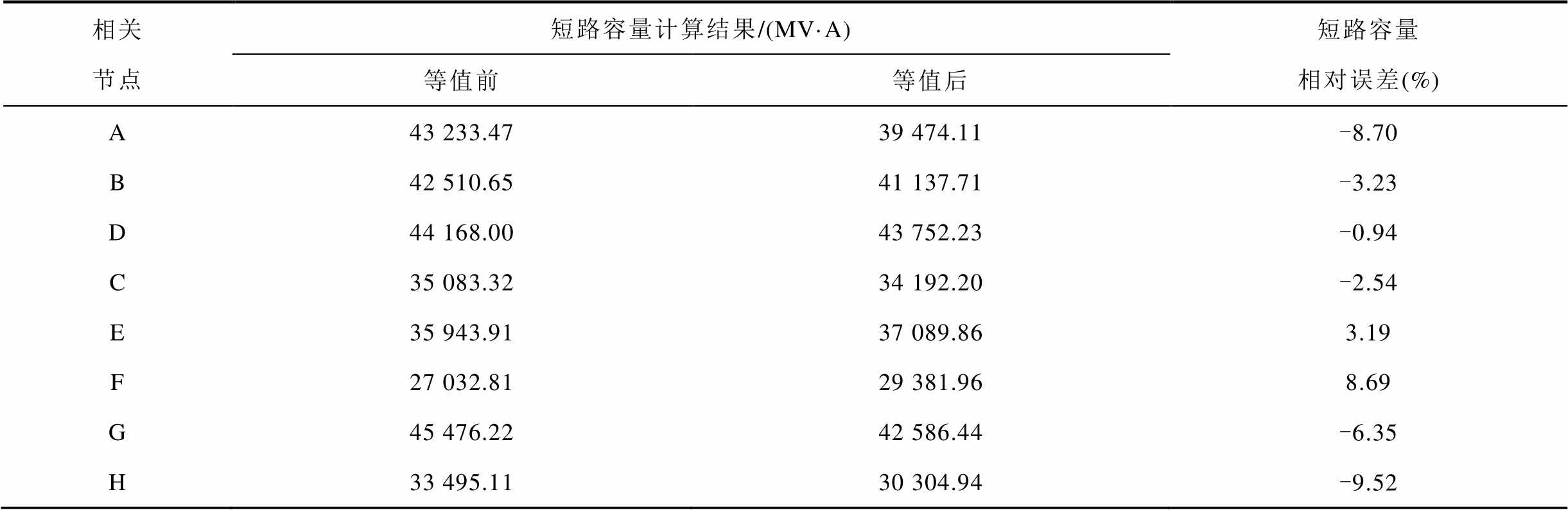
相关节点短路容量计算结果/(MV·A)短路容量相对误差(%) 等值前等值后 A43 233.4739 474.11-8.70 B42 510.6541 137.71-3.23 D44 168.0043 752.23-0.94 C35 083.3234 192.20-2.54 E35 943.9137 089.863.19 F27 032.8129 381.968.69 G45 476.2242 586.44-6.35 H33 495.1130 304.94-9.52
由表6可知，采用本文提出的等值方案，LCC-HVDC送端电网等值前后短路容量相对误差均在10%以内，该方案可以保证等值前后系统短路特性的一致。
5.4.3 交流系统故障响应特性对比
为考察等值前后LCC-HVDC送端电网动态特性的变化，在相同工况下，校核系统等值前后故障响应特性。校核内容为第一梯级断面点A和第二梯级断面点B、D电压故障响应。
0.5s时换流母线发生三相短路故障，100ms后故障切除。等值前后A、B、D各梯级断面点电压响应对比曲线如图10所示。
0.4s时送端电网发生N-1故障，B-A中一回线路发生三相短路故障，100ms后该回线路切出。等值前后A、B、D各梯级断面点电压响应对比曲线如图11所示。
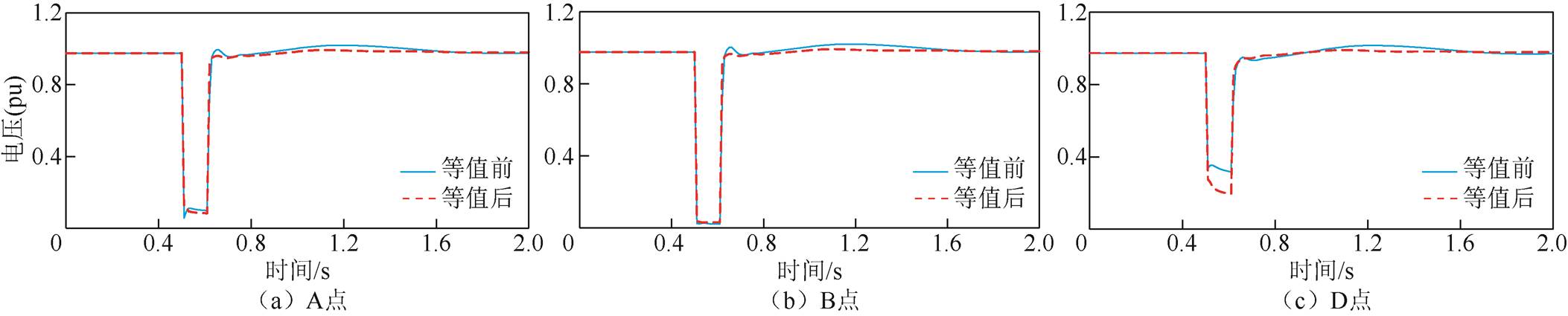
图10 换流母线A三相短路故障下，送端电网各节点电压对比
Fig.10 Comparison of each node voltage on sending-end under three-phase fault on bus A
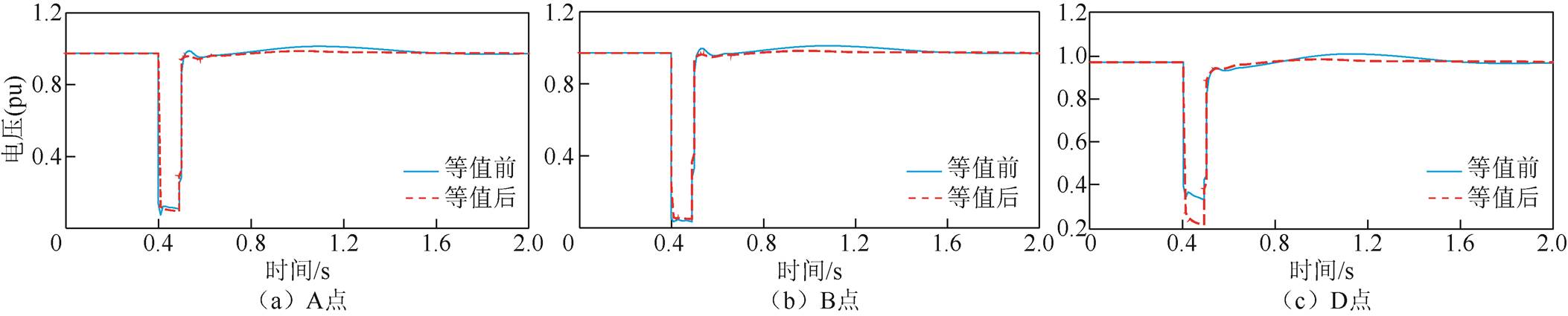
图11 N-1故障下，送端电网各节点电压对比
Fig.11 Comparison of each node voltage on sending-end under N-1 fault
由图10和图11可知：等值前后，换流母线发生三相短路故障和送端电网发生N-1故障时，梯级断面点A、B、D的电压响应曲线基本一致，等值前后的LCC-HVDC送端电网具有相似的故障响应特性。
5.4.4 功角响应特性对比
分别对等值前后的LCC-HVDC送端电网功角响应特性进行仿真分析。设置总仿真时长为8s，1s时换流母线发生三相短路故障，100ms后故障切除。以机组W1作为参考机组，等值前后机组I1和W2功角摇摆曲线如图12所示。
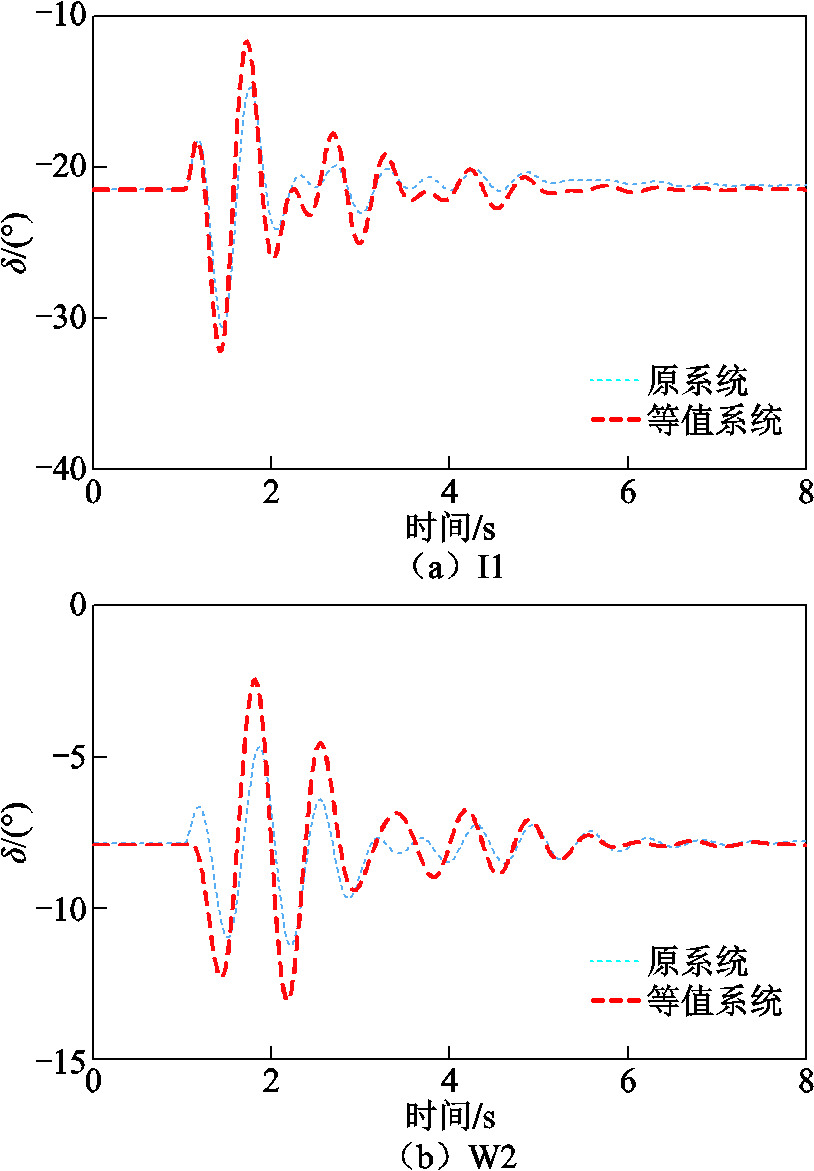
图12 等值前后，各机组功角摇摆曲线
Fig.12 Power angle curve of each generator before and after equivalence
由图12可知，在8s的系统仿真时间内，LCC-HVDC送端电网等值前后，机组I1和W2的功角摇摆曲线具有较高的相似度，表明LCC-HVDC送端电网等值系统效果良好。
为了进一步对比系统等值前后，机组I1和W2功角摇摆曲线的相似程度。利用Prony算法，辨识出系统等值前后，机组I1和W2的功角摇摆曲线所对应的阻尼比，见表7。
表7 等值前后，各功角摇摆曲线对应阻尼比
Tab.7 Damping ratio of each power angle curve before and after equivalence
水/火电机组系统属性阻尼比误差(%) I1原系统0.1133.54 等值系统0.117 W2原系统0.1936.74 等值系统0.206
由表7可知，系统等值前后，机组I1和W2功角摇摆曲线所对应的阻尼比基本一致，进一步验证了LCC-HVDC送端电网等值前后具有相同的功角响应特性。
5.4.5 送端电网过电压特性对比
分别对原系统和等值系统LCC-HVDC换相失败过程进行仿真分析，等值前后送端电网换流母线电压响应曲线如图13所示，送端电网主要新能源汇集母线电压响应曲线如图14所示。
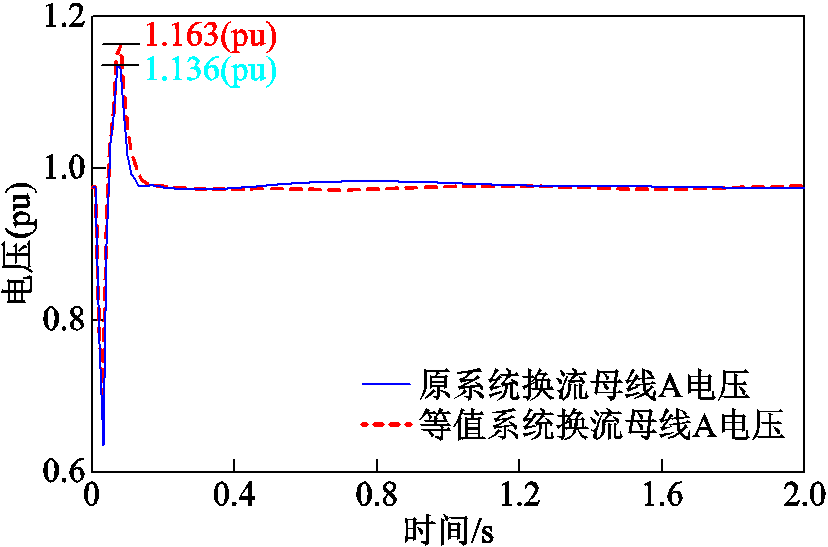
图13 换流母线A电压对比
Fig.13 Voltage comparison of node A
为了更加直观、清晰地反映系统等值前后的过电压特性，对比了换相失败过程中原系统与等值系统各母线电压的最大值Vpea（后称“尖峰电压”），并以原系统尖峰电压为基准，采用式（17）所示计算方法对等值系统过电压响应特性误差进行量化。
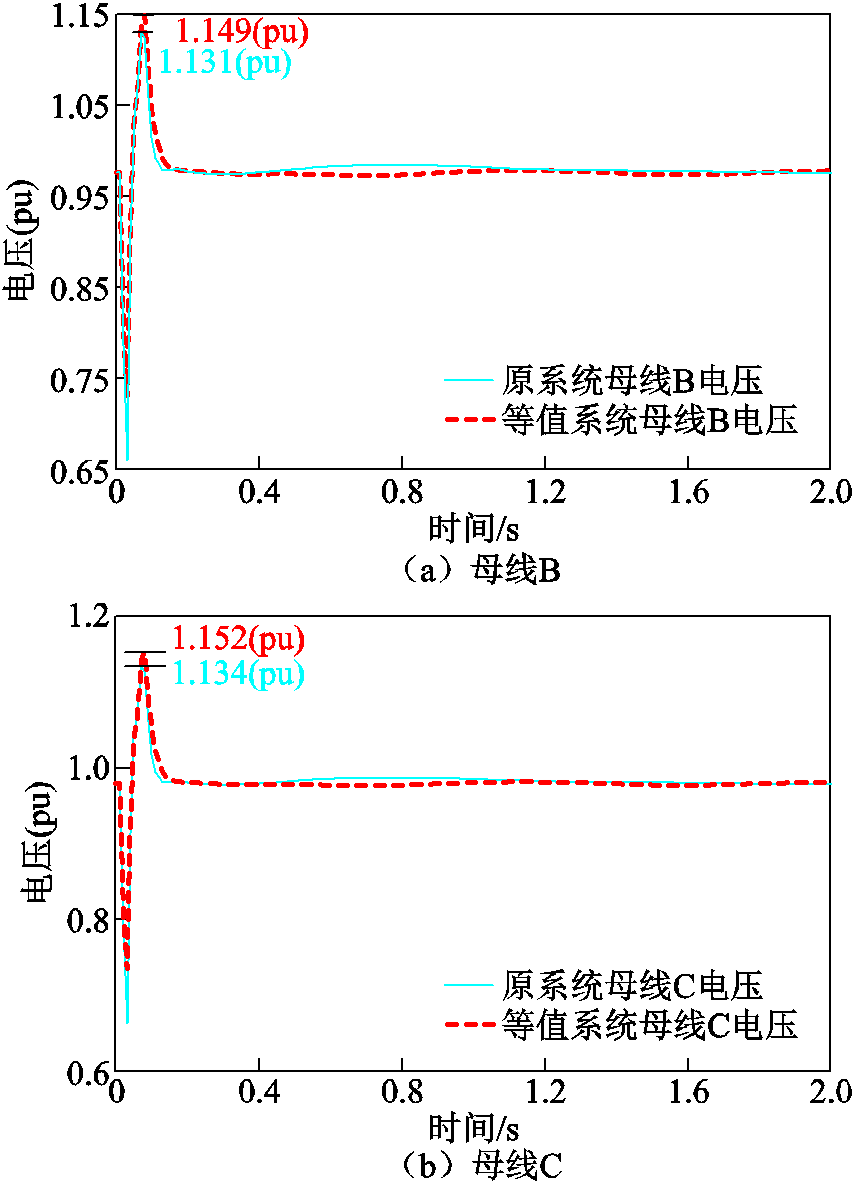
图14 新能源汇集母线电压对比
Fig.14 Voltage comparison of new energy collection buses
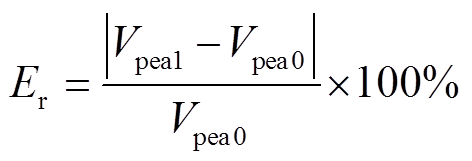（17）式中，Vpea1为等值系统某母线的尖峰电压值；Vpea0为原LCC-HVDC送端电网中相应母线的尖峰电压值。
图13和图14中分别标示了各母线的尖峰电压，表8对等值系统中各母线的尖峰电压响应特性误差进行了计算。
表8 等值前后主要母线尖峰电压响应误差
Tab.8 Overvoltage response error of main buses before and after equivalence
母线原系统等值系统Er(%) A1.1361.1632.38 B1.1311.1491.59 C1.1341.1521.59
由图13和图14可知，原系统和等值系统中LCC-HVDC发生换相失败期间，送端电网中各主要母线电压变化趋势一致。故障清除后直流进入恢复过程，等值系统和原系统中各主要母线均能够快速达到稳态。且由表8可知，LCC-HVDC换相失败过程中，等值系统换流母线和主要的新能源汇集母线的尖峰电压响应误差均在3%以内。因此，LCC-HVDC送端电网等值前后具有相同的过电压特性。
通过仿真，本节对比分析了该LCC-HVDC送端电网等值前后稳态特性、故障响应特性、功角响应特性及过电压特性。仿真结果表明，运用本文所提出的等值方案对LCC-HVDC送端电网进行等值时具有较好的等值效果。
为了建立适用于LCC-HVDC过电压抑制研究的送端电网等值系统模型，给出了一种LCC-HVDC送端电网等值方案。首先，以节点残压可反映各梯级断面点与LCC-HVDC间电气耦合关系为依据，在梯级化划分LCC-HVDC送端电网的基础上，提出了一种基于节点残压的内部系统主干网确定方法。该方法以节点残压为量化指标，通过设定节点残压阈值，进而确定内部系统主干网，有效避免了可能因人为确定内部系统范围而引起的等值误差。然后，以梯级断面点为依据，将内部系统划分为不同拓扑区域，在保证等值前后各梯级断面点电气特性一致的原则下，计算得到了各拓扑区域等值电源、负荷及变压器详细参数。最后，针对LCC-HVDC送端电网结构特点，给出了LCC-HVDC送端电网多端口戴维南等值方法，简化了外部系统。同时，指出了简化过程中可能存在的问题并给出了相应的解决方法。
应用本文所提方案对某LCC-HVDC送端电网进行了等值。等值前后系统的稳态特性、故障响应特性、功角响应特性及过电压特性表明，等值系统较好地保留了原LCC-HVDC送端电网系统特性。该等值系统的建立，为后续的LCC-HVDC及送端电网电磁暂态建模工作提供了有益支撑。
参考文献
[1] 李明节, 陈国平, 董存, 等. 新能源电力系统电力电量平衡问题研究[J]. 电网技术, 2019, 43(11): 3979-3986.
Li Mingjie, Chen Guoping, Dong Cun, et al. Research on power balance of high proportion renewable energy system[J]. Power System Technology, 2019, 43(11): 3979-3986.
[2] 丁平, 安宁, 赵敏, 等. 一种实用的电压源型换流器及直流电网机电暂态建模方法[J]. 电工技术学报, 2017, 32(10): 69-76.
Ding Ping, An Ning, Zhao Min, et al. A practical modeling method of VSC-HVDC and DC-grid electromechanical transient[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 69-76.
[3] 盛逸标, 林涛, 陈宝平, 等. 面向新能源外送系统次/超同步振荡的控制器参数协调优化[J]. 电工技术学报, 2019, 34(5): 983-993.
Sheng Yibiao, Lin Tao, Chen Baoping, et al. Coordination and optimization of controller parameters for subsynchronous/super-synchronous oscillation in new energy delivery systems[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 983-993.
[4] 高本锋, 刘毅, 宋瑞华, 等. 双馈风电场经LCC-HVDC 送出的次同步振荡特性研究[J]. 中国电机工程学报, 2020, 40(11): 3477-3489.
Gao Benfeng, Liu Yi, Song Ruihua. Study on sub-synchronous oscillation characteristics of DFIG-based wind farm integrated with LCC-HVDC system[J]. Proceedings of the CSEE, 2020, 40(11): 3477-3489.
[5] 李辉, 王震, 周挺, 等. 含同步调相机的直流受端换流站全工况下多模式协调控制策略[J]. 电工技术学报, 2020, 35(17): 3678-3690.
Li Hui, Wang Zhen, Zhou Ting, et al. Multi-mode coordinated control strategy for DC receiving converter station with synchronous condenser under full operating conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3678-3690.
[6] 冀肖彤. 抑制HVDC送端交流暂态过电压的控制系统优化[J]. 电网技术, 2017, 41(3): 721-728.
Ji Xiaotong. Optimization of HVDC control system for mitigating AC transient overvoltage on rectifier station[J]. Power System Technology, 2017, 41(3): 721-728.
[7] 陈厚合, 鲁华威, 王长江, 等. 抑制直流送端系统暂态过电压的直流和风电控制参数协调优化[J]. 电力自动化设备, 2020, 40(10): 46-55.
Chen Houhe, Lu Huawei, Wang Changjiang, et al. Coordinated optimization of HVDC and wind power control parameters for mitigating transient overvoltage on HVDC sending-side system[J]. Electric Power Automation Equipment, 2020, 40(10): 46-55.
[8] 王长江, 姜涛, 刘福锁, 等. 基于轨迹灵敏度的暂态过电压两阶段优化控制[J]. 电工技术学报, 2021, 36(9): 1888-1900, 1913.
Wang Changjiang, Jiang Tao, Liu Fusuo, et al. Two-stage optimization control of transient overvoltage based on trajectory sensitivity[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1888-1900, 1913.
[9] 岳涵, 邵广惠, 夏德明, 等. 考虑过电压抑制的特高压直流弱送端系统无功控制策略[J]. 电力系统自动化, 2020, 44(15): 172-182.
Yue Han, Shao Guanghui, Xia Deming, et al. Reactive power control strategy for UHVDC weak sending-end system considering overvoltage suppression[J]. Automation of Electric Power Systems, 2020, 44(15): 172-182.
[10] 谢小荣, 贺静波, 毛航银, 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475.
Xie Xiaorong, He Jingbo, Mao Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power electronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-475.
[11] Sajadi A, Kolacinski R M, Clark K, et al. Transient stability analysis for offshore wind power plant integration planning studies—part I: Short-term faults[J]. IEEE Transactions on Industry Applications, 2018, 55(1): 182-192.
[12] 张炎, 丁明, 韩平平, 等. 直流闭锁后风电送端系统暂态稳定及控制策略研究[J]. 电工技术学报, 2020, 35(17): 3714-3726.
Zhang Yan, Ding Ming, Han Pingping, et al. Study on the transient stability and control schemes of the sending-end system involving wind power after UHVDC block[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3714-3726.
[13] 骆悦, 姚骏, 张田, 等. 大规模风电直流外送系统单极闭锁场景下送端系统协调控制策略[J]. 电工技术学报, 2019, 34(19): 4108-4118.
Luo Yue, Yao Jun, Zhang Tian, et al. Coordinated control strategy of large-scale wind power generation sending system under mono-polar block fault[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4108-4118.
[14] 尹纯亚, 李凤婷, 周识远, 等. 基于无功功率短路比的直流闭锁暂态过电压计算方法[J]. 电力系统自动化, 2019, 43(10): 150-157, 161.
Yin Chunya, Li Fengting, Zhou Shiyuan, et al. Calculation method of transient overvoltage due to DC blocking based on short circuit ratio of reactive power[J]. Automation of Electric Power Systems, 2019, 43(10): 150-157, 161.
[15] 汤涌. 交直流电力系统多时间尺度全过程仿真和建模研究新进展[J]. 电网技术, 2009, 33(16): 1-8.
Tang Yong. New progress in research on multi-time scale unified simulation and modeling for AC/DC power systems[J]. Power System Technology, 2009, 33(16): 1-8.
[16] 刘文焯, 汤涌, 万磊, 等. 大电网特高压直流系统建模与仿真技术[J]. 电网技术, 2008, 32(22): 1-3, 7.
Liu Wenchao, Tang Yong, Wan Lei, et al. Modeling and simulation technologies for large UHVDC power grid[J]. Power System Technology, 2008, 32(22): 1-3, 7.
[17] 杨福, 梁军, 牛庆达. 一种适用于交直流互联系统电磁暂态仿真的动态等效方法[J]. 电力系统保护与控制, 2012, 40(16): 70-76.
Yang Fu, Liang Jun, Niu Qingda. A dynamic equivalent method for electromagnetic transient simulation of AC/DC interconnected power system[J]. Power System Protection and Control, 2012, 40(16): 70-76.
[18] 顾丹珍, 戴海锋, 崔勇, 等. 基于BPA的大规模电力系统工程应用的同调动态等值方法[J]. 水电能源科学, 2019, 37(3): 176-180.
Gu Danzhen, Dai Haifeng, Cui Yong, et al. Homologous dynamic equivalence method for large scale power system engineering application based on BPA[J]. Water Resources and Power, 2019, 37 (3): 176-180.
[19] 徐政, 杨靖萍, 段慧. 一种适用于电磁暂态仿真的等值简约方法[J]. 南方电网技术, 2007(1): 37-40.
Xu Zheng, Yang Jingping, Duan Hui. An equivalent reduction method for electromagnetic transient simulation of large-scale power systems[J]. Southern Power System Technology, 2007(1): 37-40.
[20] 朱林, 陈达, 张健, 等. 计及特征约束的南方电网主网架动态等值方案[J]. 电力自动化设备, 2019, 39(9): 206-212.
Zhu Lin, Chen Da, Zhang Jian, et al. Dynamic equivalence scheme for main grid of China southern power grid considering feature constraints[J]. Electric Power Automation Equipment, 2019, 39(9): 206-212.
[21] 楼霞薇, 王威, 王波, 等. 基于WARD等值的电网限流运行方式优化方法[J]. 电力系统保护与控制, 2017, 45(18): 128-136.
Lou Xiawei, Wang Wei, Wang Bo, et al. A grid operation mode optimization method for controlling short-circuit current level based on WARD equivalence[J]. Power System Protection and Control, 2017, 45(18): 128-136.
[22] 林济铿, 闫贻鹏, 刘涛, 等. 电力系统电磁暂态仿真外部系统等值方法综述[J]. 电力系统自动化, 2012, 36(11): 108-115.
Lin Jikeng, Yan Yipeng, Liu Tao, et al. Review on external system equivalent method for electromagnetic transient simulation of power systems[J]. Automation of Electric Power Systems, 2012, 36(11): 108-115.
[23] 王刚, 张伯明. 电力系统外网在线动态等值方案[J].电网技术, 2006, 30(19): 21-26.
Wang Gang, Zhang Boming. External online dynamic equivalents of power system[J]. Power System Technology, 2006, 30(19): 21-26.
[24] Jardim J I, Leite DA Silvaam. A methodology for computing robust dynamic equivalents of large power systems[J]. Electric Power Systems Research, 2017, 143: 513-521.
[25] 胡杰, 余贻鑫. 电力系统动态等值参数聚合的实用方法[J]. 电网技术, 2006, 30(24): 26-30.
Hu Jie, Yu Yixin, A practical method of parameter aggregation for power system dynamic equivalence[J]. Power System Technology, 2006, 30(24): 26-30.
[26] 朱琳, 葛俊, 吴学光, 等. 一种工程实用的电力系统等值方法[J]. 电力自动化设备, 2017, 37(9): 178-184.
Zhu Lin, Ge Jun, Wu Xueguang, et al. Power system equivalence for practical engineering[J]. Electric Power Automation Equipment, 2017, 37(9): 178-184.
[27] 李明节. 大规模特高压交直流混联电网特性分析与运行控制[J]. 电网技术, 2016, 40(4): 985-991.
Li Mingjie. Characteristic analysis and operational control of large-scale hybrid UHV AC/DC power grids[J]. Power System Technology, 2016, 40(4): 985-991.
[28] 倪以信, 陈寿松, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[29] 徐政. 交直流电力系统动态行为分析[M]. 北京: 机械工业出版社, 2004.
[30] 孙景强, 郭小江, 张健, 等. 多馈入直流输电系统受端电网动态特性[J]. 电网技术, 2009, 33(4): 57-60, 87.
Sun Jingqiang, Guo Xiaojiang, Zhang Jian, et al. Dynamic characteristics of receiving-end of multi-infeed HVDC power transmission system[J]. Power System Technology, 2009, 33(4): 57-60, 87.
[31] 黄梅, 万航羽. 在动态仿真中风电场模型的简化[J].电工技术学报, 2009, 24(9): 147-152.
Huang Mei, Wan Hangyu. Simplification of wind farm model for dynamic simulation[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 147-152.
[32] 张伯明, 陈寿松, 严正. 高等电力网络分析[M]. 北京: 清华大学出版社, 2007.
Study on Equivalence Method of AC System in Sending-End of LCC-HVDC
Abstract When the sending-end of line-commutated-converter based high voltage direct current (LCC-HVDC) contains large-scale new energy, the risk of overvoltage on the sending-end will aggravate. It is necessary to establish the electromagnetic transient model of LCC-HVDC and its equivalent AC system in sending-end. Then the control strategy of LCC-HVDC can be optimized by analyzing its overvoltage characteristics. Atpresent, there are few researches on the equivalence of AC system in sending-end. According to the engineering requirements, an equivalent scheme suitable for LCC-HVDC is proposed. First, the residual voltage of each node in the main network can reflect the coupling between LCC-HVDC and the sending-end. A method for determining the internal system backbone network based on the residual voltage is proposed. The method can quickly determine the scope of the internal system and effectively avoid the human error during the equivalence. Then, based on the node of backbone network, the topology area is divided, and the detailed parameter determination method of equivalent sources, loads and transformers in the internal system are given based on the principle of consistent electrical characteristics of each topology area before and after equivalence. Finally, the multi-port thevenin equivalent suitable for the sending-end of LCC-HVDC is used to simplify the external system. Based on a domestic LCC-HVDC, the effectiveness of the proposed equivalent scheme is verified.
keywords：Line-commutated-converter based high voltage direct current(LCC-HVDC), AC system in sending-end, equivalence, backbone network, residual voltage of node
DOI：10.19595/j.cnki.1000-6753.tces.201328
中图分类号：TM743
高本锋 男，1981年生，副教授，研究方向为高压直流输电和电力系统次同步振荡。E-mail：gaobenfeng@126.com
王 刚 男，1997年生，硕士，研究方向为电力系统分析与控制。E-mail：15996296521@163.com（通信作者）
国家电网公司总部科技研究资助项目（SGZB0000TGJS1900747）。
收稿日期 2020-10-09
改稿日期 2020-11-25
（编辑 郭丽军）