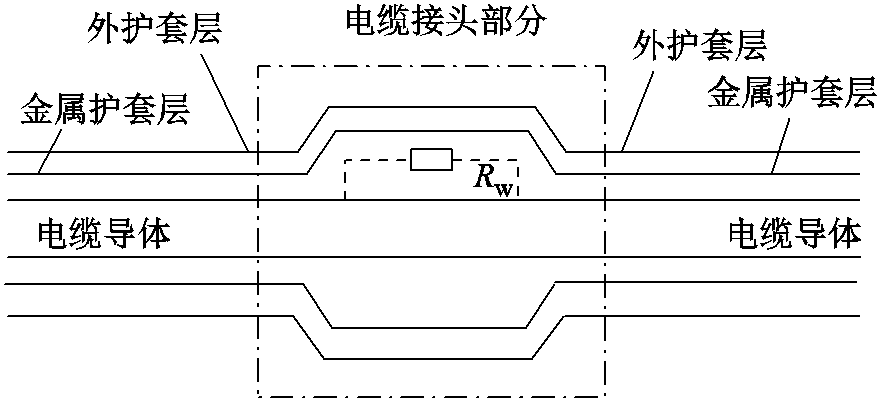
图1 电缆接头物理结构简图
Fig.1 Physical structure diagram of cable joint
摘要 为缓解高温天气及负荷高位运行情况下线路接头异常温升引起的持续发热,该文提出一种计及线路接头温升约束的受端电网转供优化模型。首先在电热耦合理论基础上分析了线路接头温升等效热模型及其参数估计方法,并以潮流变化量为中间变量,推导了在当前运行点负荷变化时线路接头温升线性方程。然后,结合220kV/110kV受端电网拓扑,构建了潮流转移下的线路接头温升约束,并与有功功率平衡约束、线路最大允许载流量动态约束和电网辐射型结构组成约束集,以电网运行方式调整的开关动作总次数为优化目标,提出计及线路接头温升约束的受端电网转供优化模型,该模型为混合整数线性规划问题,采用CPLEX工具箱进行求解。最后,通过对实际220kV/110kV受端电网进行仿真分析,验证了该模型的有效性。
关键词:受端电网 电热耦合 线路接头温升 潮流转移 转供优化
在迎峰度夏期间,大型中心城市负荷中心的220kV/110kV电网线路长时间高负荷运行。在极端高温天气的持续作用下,架空线线夹、电缆线路的接头、电缆穿墙导管、变压器导管、绝缘子、隔离开关等发热现象会非常严重。其中,架空线耐张线夹耐受高温能力较低[1]、电缆线路的接头工艺不良[2]或者电流过大引起的发热最为常见,其温升也较高、较快。在恶劣天气或者负荷高位运行下,由于长期运行的线路接头存在老化现象,其温升将持续异常升高,导致线路绝对温度超过其最大允许温度,严重影响线路的运行安全[3-5]。在负荷高位运行期间,电网调度中心为保证输变电设备的运行安全,会对电网进行一定方式的调整,将部分负荷进行转供[6-8]。
随着动态热定值方法(Dynamic Thermal Rating, DTR)的研究和发展[9],电力系统可以通过测量得到导线实际运行的表面风速、光照、环境温度等数据,并根据IEEE标准[10]和CIGRE标准[11],计算线路最大允许载流量及温度[12-13]。为反映线路温度动态变化,文献[14]利用电热协调,基于电缆具体结构,提出了电缆的热特性模型以挖掘电缆的载荷潜力。文献[15]通过半参数平差模型对线路在不同温度下的交流电阻进行精确估计,并结合热平衡方程进行线路温度估计。文献[16]对自然对流条件下架空线的径向温度计算方法进行了研究。文献[17]进一步考虑了强迫对流,建立架空线径向和周向温度热网络模型。上述文献在电热耦合及热路模型基础上,对线路温度的动态变化进行了研究,但并未与电网运行调度结合起来以充分挖掘线路的输电能力。
针对电热耦合理论在电网运行与优化调度中的应用,文献[18]将架空线电阻视为与温度相关的变量,提出一种考虑电热耦合的架空线功率传输限值计算方法。文献[19]将电热耦合关系引入传统最优潮流中,考虑线路电阻和线路温度的关系,建立基于电热协调的电力系统温度最优潮流模型。文献[20]考虑输电元件热惯性效应,对故障后最优潮流的校正控制允许时间提供了依据,有效避免了在电网元件故障后引发连锁故障的安全风险。文献[21]计及架空线的电热耦合关系,提出一种风电系统输电阈值估计方法,以确定系统能吸收的可用风力。动态增容技术通过对线路温度的测量计算线路的动态载流量,结合电网运行调度可以充分利用线路可输送容量[22-23]。文献[24]针对高风电渗透率系统中正常运行的线路,提高线路的动态输送容量上限来解决风电消纳问题。文献[25]计及线路的热惯性效应,将线路载流量动态约束引入安全经济调度模型以最大化利用导线载荷能力。文献[26]提出一种增强型安全约束最优潮流模型,提高线路动态容量以应对事故后可能出现的潮流越限问题,保证电网安全运行。文献[27]在导线载流量的实时计算基础上,考虑系统的安全稳定性,提出一种基于输电线路阻塞分析的动态增容方案。
上述研究在线路温度层面,已经将线路DTR物理建模成果及电热耦合理论与电网优化运行充分结合。但在当前实际电网还未应用DTR提升输电断面容量条件下,其对应允许的传输载荷还比较保守。虽然计及导线温度显著提升了线路载荷能力,但是同一负荷条件下,架空线耐张线夹和电缆线路接头处比线路本体的运行温度更高[28-29],在负荷高位运行期间,即使进行了负荷转供,仍发生了多次由架空线耐张线夹温度长时间过高引起引流线断股导致的断线故障,以及由电缆线路接头高温发热引发爆炸起火导致的短路故障[30]。为避免线路接头在异常温升情况下持续发热引起的电网安全问题,有必要在现有线路温度层面研究基础上,进一步开展计及线路接头温升约束的受端电网转供理论研究。
基于以上考虑,本文提出一种计及线路接头温升约束的受端电网转供优化模型。首先,对架空线耐张线夹和电缆接头温升进行建模,并在DTR环境获取实时参数的基础上,建立线路接头温升线性化约束;然后,引入线路接头温升约束,与有功功率平衡约束、线路最大允许载流量动态约束和电网辐射型结构约束共同组成约束集,以电网运行方式调整的开关动作总次数为优化目标,建立转供优化模型;最后,用实际算例分析验证了本文提出模型方法的有效性。
在电缆线路运行中,由于电缆接头压接处存在接触电阻,导致电缆接头高温发热严重,且运行过程中接触电阻值会随温度升高而增大,造成电缆接头长期温升异常。电缆接头热量主要包括电流经过导体压接处接触电阻的电能损耗、金属护套内涡流及环流损耗、各静电屏蔽层和绝缘层的介质损耗[3]。电缆接头物理结构简图如图1所示。电缆导体部分以电缆导芯、绝缘层为主,电流流经接触电阻产生热量,在线路运行中成为电缆接头发热的主要热源,热量经过以金属护套层为主的电缆接头内部密封护套层,再通过外护套层散热到环境中。

图1 电缆接头物理结构简图
Fig.1 Physical structure diagram of cable joint
对于架空线来说,在实际运行中发热最严重的主要是耐张线夹。架空线耐张线夹主体部分由钢锚和铝管组成,用钢锚锚固线路导体钢芯部分并穿插进铝管内,通过压接工艺使导线与线夹成为一体。与电缆接头类似,架空线耐张线夹的热源主要为流经导体电流在接头部分接触电阻处产生的热量损耗,经过钢锚与铝管压接层,径向散热到外界环境中。因此,可将架空线耐张线夹温升与电缆接头温升等效用线路接头温升热路模型来表示。
采用热电类比法可以建立起线路接头温升的等效热模型,其二阶简化等效热模型如图2所示[3]。电流源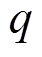 主要为线路接头压接处接触电阻
主要为线路接头压接处接触电阻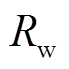 产生的电能损耗;
产生的电能损耗;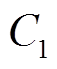 、
、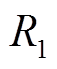 分别为线路导体与外表层的等效热容和等效热阻,
分别为线路导体与外表层的等效热容和等效热阻,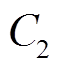 、
、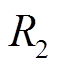 分别为外表层向外界环境散热的等效热容和等效热阻;
分别为外表层向外界环境散热的等效热容和等效热阻;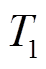 、
、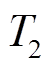 分别为线路导体温度和接头外表层温度,环境温度等效为电压源
分别为线路导体温度和接头外表层温度,环境温度等效为电压源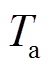 。
。
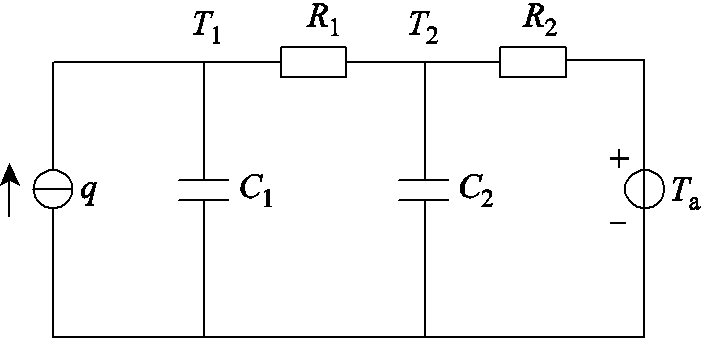
图2 线路接头温升等效热模型
Fig.2 Temperature model of transmission line joint
图2中,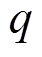 为线路接头的等效热源,即为流经线路电流的
为线路接头的等效热源,即为流经线路电流的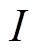 在接头接触电阻
在接头接触电阻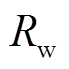 处产生的电能损耗,即
处产生的电能损耗,即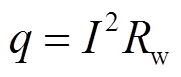 ,代入简化等效热模型可得线路接头温度的状态方程为
,代入简化等效热模型可得线路接头温度的状态方程为
 (1)
(1) (2)
(2)式中,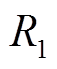 、
、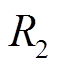 、
、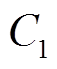 、
、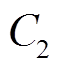 由线路结构参数决定;接触电阻
由线路结构参数决定;接触电阻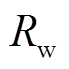 的值难以直接得到,在暂态过程中,可视为常数。根据DL/T 664—2016带电设备红外诊断应用规范[30],可通过红外热像仪显示线路热像,从而判断其缺陷程度。对应地,可对每一缺陷级别的线路接触电阻采用GB/T 25840—2010《规定电气设备部件允许温升的导则》中触头电阻的测量方法进行试验测量[31],在接头处通直流电流并测量接头两端电压降得到该级别下线路接头电阻估计值。在进行运行状态线路热路建模时,通过红外热像仪检测其缺陷状态并对照试验数据,可得到该线路接头接触电阻的估计值。
的值难以直接得到,在暂态过程中,可视为常数。根据DL/T 664—2016带电设备红外诊断应用规范[30],可通过红外热像仪显示线路热像,从而判断其缺陷程度。对应地,可对每一缺陷级别的线路接触电阻采用GB/T 25840—2010《规定电气设备部件允许温升的导则》中触头电阻的测量方法进行试验测量[31],在接头处通直流电流并测量接头两端电压降得到该级别下线路接头电阻估计值。在进行运行状态线路热路建模时,通过红外热像仪检测其缺陷状态并对照试验数据,可得到该线路接头接触电阻的估计值。
为计算在当前温度和当前线路流经电流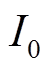 下随负荷条件改变的线路接头温升,将式(2)代入式(1),并在当前线路接头温度运行点处线性化得到
下随负荷条件改变的线路接头温升,将式(2)代入式(1),并在当前线路接头温度运行点处线性化得到
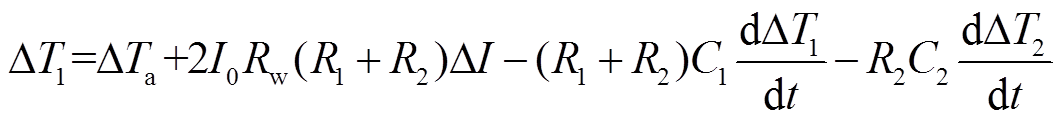 (3)
(3)实际运行中,通常会在电缆外表皮安装监测单元如传感光纤等进行测温,以得到电缆外护套层温度,并由载流量监测软件进行电缆导体温度的计算。而对于架空线来说,通过导线温度采集单元可直接获取监测点导线及金具的温度。因此,在各线路的温度监测、采集单元获取温度数据后,从电网实时数据采集与监视控制(Supervisory Control And Data Acquisition, SCADA)系统中可以得到线路接头处导体温度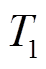 、接头外表层温度
、接头外表层温度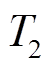 、环境温度
、环境温度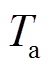 及流经电缆的电流值监测数据
及流经电缆的电流值监测数据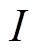 ,由此可计算它们的温升
,由此可计算它们的温升 、
、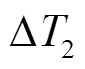 、
、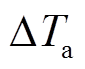 和
和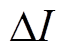 ,以及线路接头温升斜率
,以及线路接头温升斜率 、外表层温升斜率
、外表层温升斜率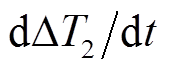 和当前流经电缆电流值
和当前流经电缆电流值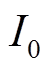 的时序数据。将上述时序数据代入式(3),可得到以
的时序数据。将上述时序数据代入式(3),可得到以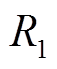 、
、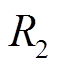 、
、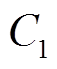 、
、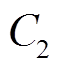 为未知量的方程组,再采用非线性最小二乘法可计算得到线路接头温升模型的参数估计值。
为未知量的方程组,再采用非线性最小二乘法可计算得到线路接头温升模型的参数估计值。
线路接头与线路本体的具体结构虽然有差别,但两者散热原理大致相同,均为径向散热到环境中,故线路本体温升也可以用图2所示的二阶等效热模型简化表示。其中,线路本体的发热源主要为线路导体电阻而非接触电阻,结构层等效热阻、热容参数也与线路接头不同。对同一线路的接头及本体分别进行参数估计,由温升等效热模型计算可得到相同负荷条件下线路接头处的温升 及线路本体温升
及线路本体温升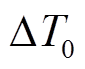 。线路接头及线路本体温升示意图如图3所示。t0时刻前,线路温度已达到稳态,设t0时刻为初始时刻,此时负荷条件改变,线路载流量由0.5(pu)变为1.0(pu),线路温升随载流量改变而变化。
。线路接头及线路本体温升示意图如图3所示。t0时刻前,线路温度已达到稳态,设t0时刻为初始时刻,此时负荷条件改变,线路载流量由0.5(pu)变为1.0(pu),线路温升随载流量改变而变化。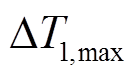 、
、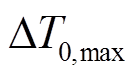 表示线路载流量为1.0(pu)时对应的线路接头及线路本体温升限值,由线路运行温度限值减去t0时刻初始温度值计算得到。t1时刻,线路本体温升仍在安全约束范围内,但线路接头温升已越限。若按线路本体温升约束条件运行,线路接头将持续超过其最大允许温度运行,可能会导致线路接头损毁并引发停电事故。因此,为保证电网运行安全,在电网实际运行与调度中应考虑引入线路接头温升约束条件。
表示线路载流量为1.0(pu)时对应的线路接头及线路本体温升限值,由线路运行温度限值减去t0时刻初始温度值计算得到。t1时刻,线路本体温升仍在安全约束范围内,但线路接头温升已越限。若按线路本体温升约束条件运行,线路接头将持续超过其最大允许温度运行,可能会导致线路接头损毁并引发停电事故。因此,为保证电网运行安全,在电网实际运行与调度中应考虑引入线路接头温升约束条件。
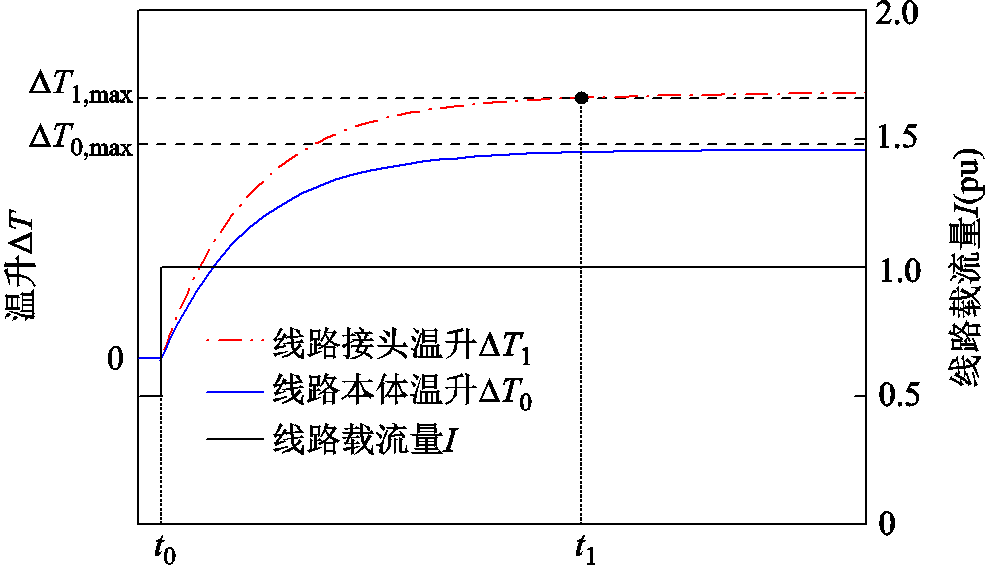
图3 线路接头及线路本体温升示意图
Fig.3 Schematic diagram of transmission line joint and transmission line temperature rise
在220kV/110kV受端电网中,线路接头温度通过线路潮流与负荷建立起联系,且线路潮流变化量与负荷变化量存在线性关系。为获取负荷变化引起的线路接头温升变化,以线路潮流变化量作为中间变量,对接头温度和线路潮流量进行分段线性化处理,得到线路接头温升计算模型。假设第t个时段线路潮流大小为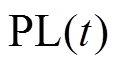 时,线路潮流变化
时,线路潮流变化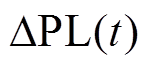 后,线路接头温升为
后,线路接头温升为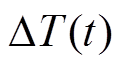 ,那么当前时段的斜率
,那么当前时段的斜率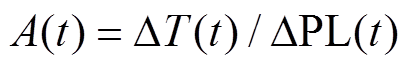 ,该斜率可由线路接头温度在当前运行点线性化后得到。由式(3)可得,线路接头温升
,该斜率可由线路接头温度在当前运行点线性化后得到。由式(3)可得,线路接头温升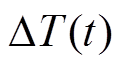 在第t个时段线路潮流大小为
在第t个时段线路潮流大小为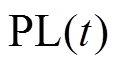 时的线性化方程为
时的线性化方程为
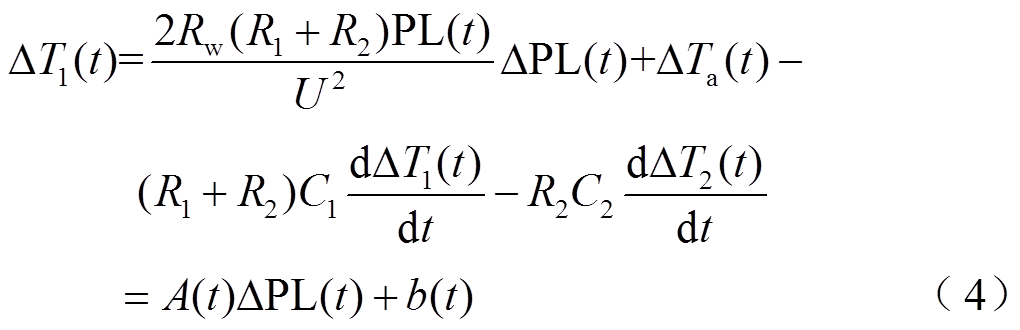
式中,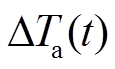 为环境温度变化量,
为环境温度变化量,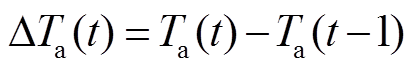 ;
; 为线路电压;线路接头温升变化率为
为线路电压;线路接头温升变化率为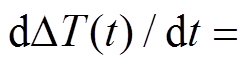
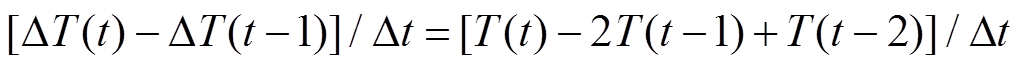 ,其中
,其中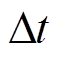 为相邻时段时间间隔。式(4)函数斜率
为相邻时段时间间隔。式(4)函数斜率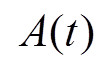 和系数
和系数 与当前线路潮流量、线路接头温度、环境温度有关,在确定转供方案时,由电网监控系统可获取当前受端电网线路运行数据,以得到线路接头温升线性方程的参数即
与当前线路潮流量、线路接头温度、环境温度有关,在确定转供方案时,由电网监控系统可获取当前受端电网线路运行数据,以得到线路接头温升线性方程的参数即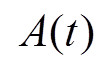 、
、 ,进而建立受端电网转供时线路接头温升线性化约束。由式(4)可得,负荷转供时线路潮流量变化
,进而建立受端电网转供时线路接头温升线性化约束。由式(4)可得,负荷转供时线路潮流量变化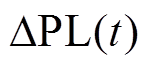 后,线路接头温度为
后,线路接头温度为
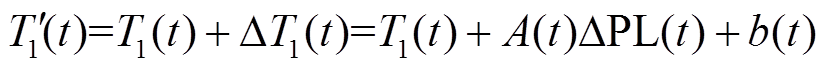 (5)
(5)
在220kV/110kV受端电网中,出于对电网稳定性和可靠性的考虑,一般不对220kV电网进行方式调整。由于220kV线路潮流与其所带110kV站运行状态相关,对于220kV线路接头温度越限,可对其所带110kV站进行运行方式调整,进而调节220kV站主变压器下网功率,对应的220kV主供线路功率随之减少,线路接头过热问题得以缓解。而对于110kV线路接头温度越限,一般可采用两种方式进行调整:①将110kV站主供备供线路互换,将过热主供线路直接转为热备用;②对110kV站所供10kV线路进行转供,降低110kV主供线路输电功率,从而减少线路发热。考虑电网供电可靠性,不考虑220kV、110kV站全站分裂运行方式,据此可建立计及线路接头温升约束的受端电网转供优化模型。
结合220kV/110kV受端电网的调整方式,当第t个时段进行负荷转供时,应考虑110kV线路开关的总动作次数最少和10kV线路开关及环网柜刀开关等操作次数最少,尽可能减少改变和恢复电网运行方式总操作次数。对于110kV线路开关远方操作次数,目标函数表示为
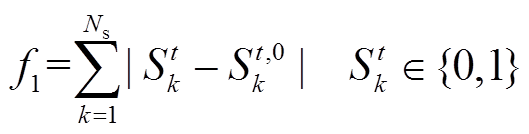 (6)
(6)式中, 为第t时段优化后110kV线路开关k的状态,0表示开关是拉开状态,1表示开关是运行状态;
为第t时段优化后110kV线路开关k的状态,0表示开关是拉开状态,1表示开关是运行状态;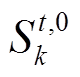 为第t时段优化前的110kV线路开关的状态;Ns为总的110kV线路开关个数。该目标函数为非线性,为便于求解,通过线性松弛对其进行线性化处理。令变量
为第t时段优化前的110kV线路开关的状态;Ns为总的110kV线路开关个数。该目标函数为非线性,为便于求解,通过线性松弛对其进行线性化处理。令变量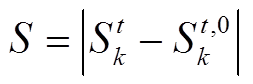 ,且S需满足
,且S需满足
 (7)
(7)由此,该目标函数线性化为
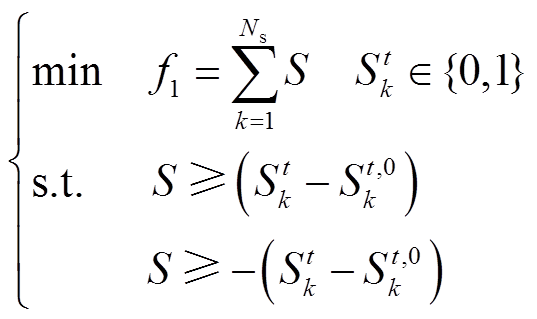 (8)
(8)对于10kV线路开关和环网柜刀开关等操作次数,由于其过程涉及的开关、刀开关操作较110kV线路开关操作更加复杂,为简化问题及统一多电压等级的转供目标函数,本文采用归算至220kV站的总10kV负荷转供量作为目标函数,负荷转供量越少代表需要进行的转供操作越少,可间接代表其所供110kV站的10kV负荷转供时开关操作次数最少,即
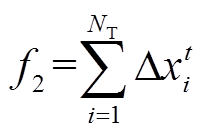 (9)
(9)式中,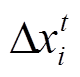 为第t时段归算至第i个220kV变电站的10kV负荷转供量;NT为220kV变电站总数量。
为第t时段归算至第i个220kV变电站的10kV负荷转供量;NT为220kV变电站总数量。
由式(8)、式(9)可将多电压等级的转供操作成本统一为总目标函数F,即
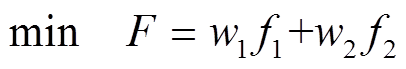 (10)
(10)式中,w1为110kV线路开关成本系数,根据国家电网公司发布的2019年第一季度电网工程设备材料信息价进行选取;w2为归算到220kV站的10kV负荷转供成本系数。设转供时段的间隔时间为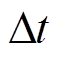 ,每一时间间隔的10kV负荷成本为p,则10kV负荷转供成本系数为
,每一时间间隔的10kV负荷成本为p,则10kV负荷转供成本系数为
 (11)
(11)
2.2.1 有功功率平衡约束
受端电网转供后,线路开关状态需满足110kV电网的有功平衡约束,设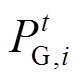 为时段t时第i个220kV站主变下网有功功率,
为时段t时第i个220kV站主变下网有功功率,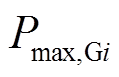 为主变允许传输的最大有功功率,
为主变允许传输的最大有功功率,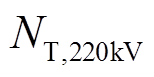 为所有220kV站主变压器个数;
为所有220kV站主变压器个数;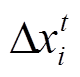 为时段t时归算至第i个220kV变电站的10kV负荷转供量,
为时段t时归算至第i个220kV变电站的10kV负荷转供量,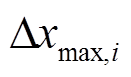 为归算后负荷转供量最大值。则有功功率平衡约束为
为归算后负荷转供量最大值。则有功功率平衡约束为
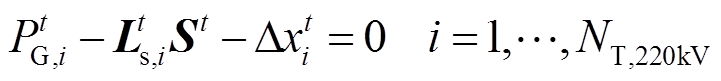 (12)
(12)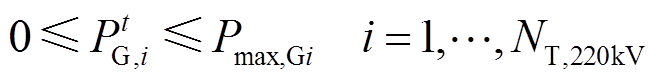 (13)
(13)
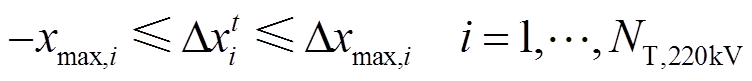 (14)
(14)
式中,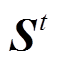 为110kV线路开关状态列向量;
为110kV线路开关状态列向量;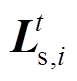 为在t时段第i个220kV站与110kV开关存在拓扑关系的负荷系数行向量。由文献[6]可得,220kV/110kV受端电网主要为110kV变电站直供和串供的接线方式,将线路两端的联络开关以一个联络等效开关表示,即图4中
为在t时段第i个220kV站与110kV开关存在拓扑关系的负荷系数行向量。由文献[6]可得,220kV/110kV受端电网主要为110kV变电站直供和串供的接线方式,将线路两端的联络开关以一个联络等效开关表示,即图4中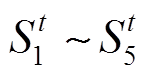 ,仅当线路两侧联络开关均为运行状态时,对应联络等效开关等于1,则110kV变电站接线方式的等效拓扑结构如图4所示。
,仅当线路两侧联络开关均为运行状态时,对应联络等效开关等于1,则110kV变电站接线方式的等效拓扑结构如图4所示。
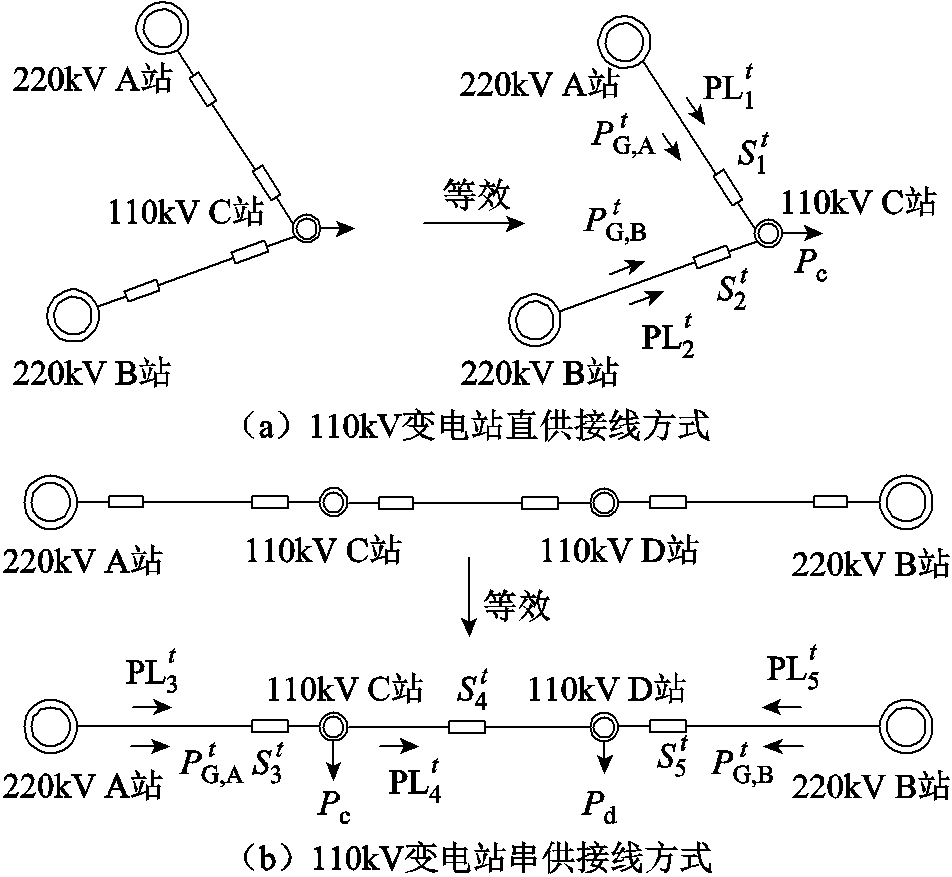
图4 110kV变电站的主要接线方式
Fig.4 Main wiring modes of 110kV substations
由图4a可得,直供接线方式下,220kV变电站主变压器下网量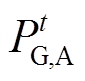 、
、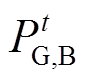 与110kV C站负荷
与110kV C站负荷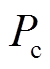 及开关状态满足有功平衡方程,即
及开关状态满足有功平衡方程,即
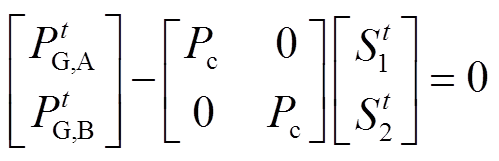 (15)
(15)定义负荷系数矩阵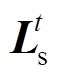 为220kV变电站主变压器下网量与110kV线路开关拓扑状态的系数,则直供接线方式的负荷系数矩阵为
为220kV变电站主变压器下网量与110kV线路开关拓扑状态的系数,则直供接线方式的负荷系数矩阵为
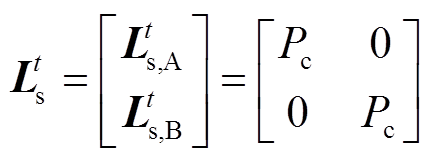 (16)
(16)
由图4b可得,串供接线方式下,220kV变电站主变压器下网量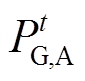 、
、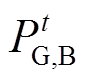 与110kV C站负荷
与110kV C站负荷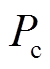 、110kV D站负荷
、110kV D站负荷 及开关状态满足有功功率平衡方程,即
及开关状态满足有功功率平衡方程,即
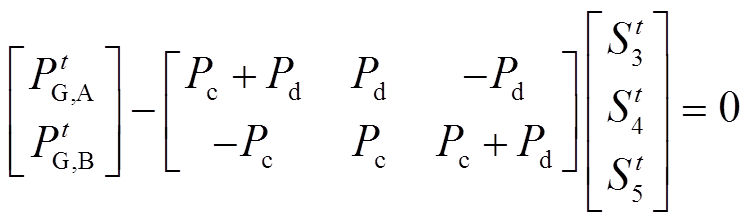 (17)
(17)则串供接线方式的负荷系数矩阵为
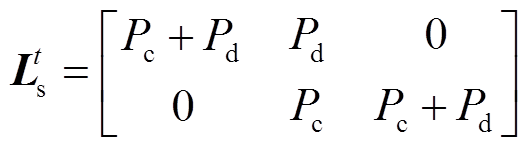 (18)
(18)
2.2.2 潮流转移下的线路接头温升约束
220kV/110kV受端电网中,如果架空线耐张线夹或者电缆接头的异常温升引致温度越限持续时间较短,并不会对电网运行安全造成太大影响;当线路接头温度越限时间过长时,则需要进行负荷转供以降低线路输送的功率或将线路由运行转热备用,故引入第j条线路接头温度越限允许持续时间常数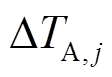 。由于DTR环境下测量数据以时段为单位,为保证转供时段线路接头温度越限时间尚未超过其最大允许持续时间,对
。由于DTR环境下测量数据以时段为单位,为保证转供时段线路接头温度越限时间尚未超过其最大允许持续时间,对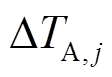 以数据测量的一个时段为单位向下取整得⌊
以数据测量的一个时段为单位向下取整得⌊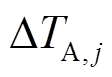 ⌋,当DTR环境下测得t时段线路接头温度满足式(19)、式(20),则在t时段进行转供。
⌋,当DTR环境下测得t时段线路接头温度满足式(19)、式(20),则在t时段进行转供。
 (19)
(19)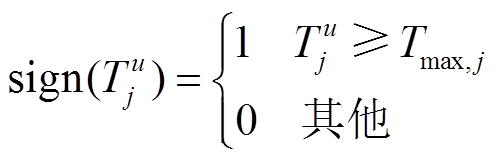 (20)
(20)
式中, 、
、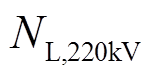 分别为受端电网中110kV线路与220kV线路条数;
分别为受端电网中110kV线路与220kV线路条数;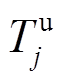 为第t个时段第j条线路接头温度;
为第t个时段第j条线路接头温度; 为线路接头温度上限;
为线路接头温度上限;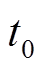 为
为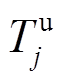 大于
大于 的第一个时段。转供后,线路接头温度不再越限,则转供优化模型中线路接头温升约束可表示为
的第一个时段。转供后,线路接头温度不再越限,则转供优化模型中线路接头温升约束可表示为
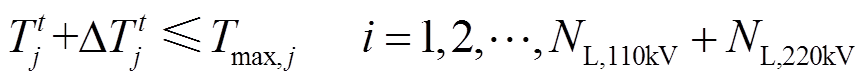 (21)
(21)式中, 为t时段负荷变化下第j条线路接头温升,可在获取线路潮流变化量后由式(4)计算得到。
为t时段负荷变化下第j条线路接头温升,可在获取线路潮流变化量后由式(4)计算得到。
对于110kV线路来说,不同接线方式下110kV线路潮流大小与110kV站负荷及线路开关状态满足有功功率平衡方程。与负荷系数矩阵定义相似,110kV线路潮流量与110kV线路开关状态的关系可用潮流系数矩阵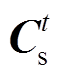 来表示。由图4a可得,直供接线方式下,110kV线路潮流量与220kV主变压器下网量相等,则直供接线方式下110kV线路潮流与线路开关状态的潮流系数矩阵同式(16)。如图4b所示,串供接线方式下,110kV线路潮流与线路开关、110kV变电站主变压器负荷满足
来表示。由图4a可得,直供接线方式下,110kV线路潮流量与220kV主变压器下网量相等,则直供接线方式下110kV线路潮流与线路开关状态的潮流系数矩阵同式(16)。如图4b所示,串供接线方式下,110kV线路潮流与线路开关、110kV变电站主变压器负荷满足
 (22)
(22)即串供接线方式下110kV线路潮流与线路开关状态的潮流系数矩阵为
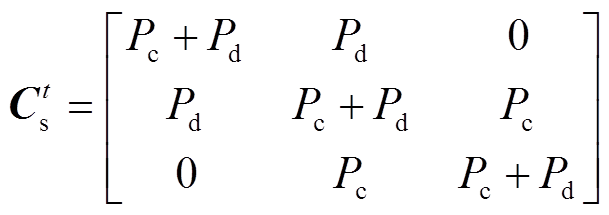 (23)
(23)
则由t时段转供前后开关状态可得110kV线路潮流变化量可表示为
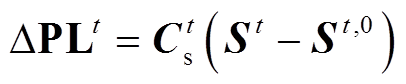 (24)
(24)代入式(4)可计算转供后110kV线路接头温升,则110kV线路接头温升约束为
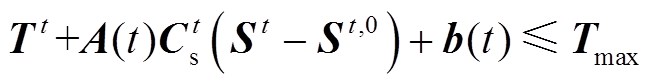 (25)
(25)
对于220kV线路来说,实际运行中220kV电网均为环网、电磁环网运行方式,如图5所示,则220kV线路潮流变化量与220kV站主变压器负荷变化量之间的线性关系与潮流方向相关。在220kV电网内机组起停方式确定、220kV电网运行方式确定的前提下,潮流方向确定,据此可得到220kV线路潮流变化量与该线路所供220kV站主变压器负荷变化量的关系。
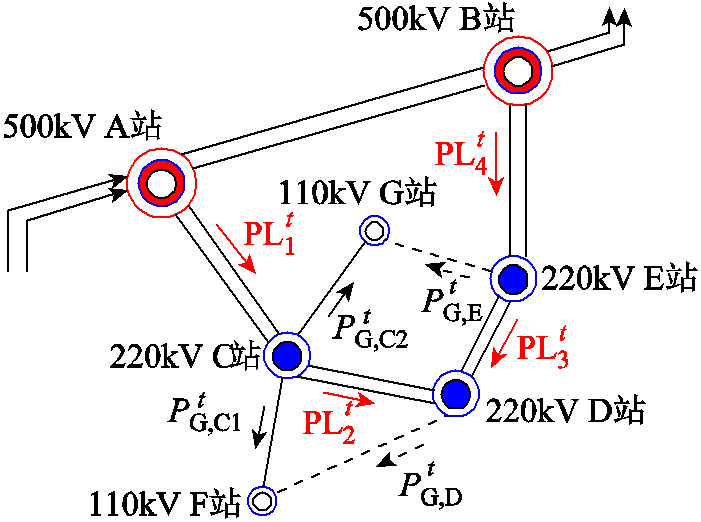
图5 220kV环网潮流示意图 Fig.5 Diagram of 220kV network power flow
设受端电网中有NT个220kV站和NL条220kV线路,且满足NL=NT+1,在SCADA线路潮流方向量测基础上,可建立220kV线路潮流方向矩阵D,且矩阵元素满足
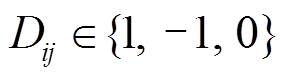 (26)
(26)
式中,i为220kV变电站, ;j为220kV线路,
;j为220kV线路,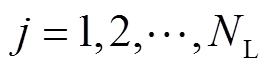 ;矩阵元素
;矩阵元素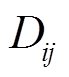 为1表示潮流方向为线路j流入变电站i,
为1表示潮流方向为线路j流入变电站i,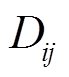 为-1表示潮流方向为线路j流出变电站i,
为-1表示潮流方向为线路j流出变电站i,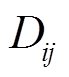 为0表示线路j与变电站i不相接。图5所示电网有3个220kV站C站、D站、E站,有4条220kV线路,线路潮流量分别为
为0表示线路j与变电站i不相接。图5所示电网有3个220kV站C站、D站、E站,有4条220kV线路,线路潮流量分别为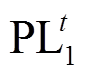 、
、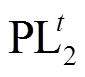 、
、 、
、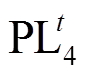 ,则图5中电网220kV线路潮流方向矩阵为
,则图5中电网220kV线路潮流方向矩阵为
 (27)
(27)由220kV/110kV电网有功平衡关系可得,流入及流出220kV变电站的220kV线路潮流变化量应与该站主变压器下网功率变化量保持平衡,则220kV变电站主变压器下网功率变化量ΔPG与220kV线路潮流变化量ΔPL可表示为线性关系为
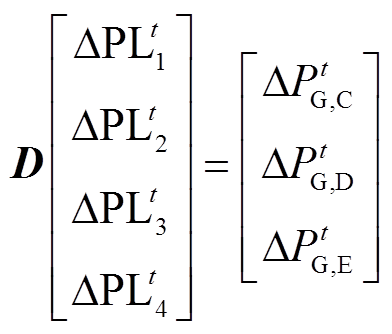 (28)
(28)
由于220kV电网为环网运行方式,故存在220kV变电站为有功功率分解点,即该站潮流方向恒为流入,其供电线路潮流变化量按照当前成分负荷比例进行分配。图5中,220kV D站为有功功率分解点,其两条主供线路分别为第2条线路与第3条线路,设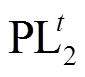 与
与 潮流比例为
潮流比例为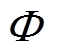 ,则220kV线路潮流变化量还需满足
,则220kV线路潮流变化量还需满足
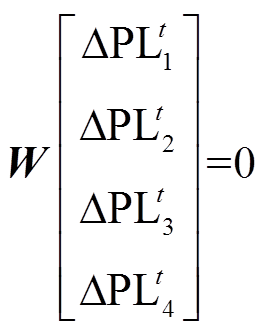 (29)
(29)
式中,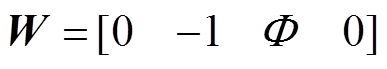 。联立式(28)、式(29)可得220kV线路潮流变化量与220kV站主变压器下网功率变化量满足线性关系,即
。联立式(28)、式(29)可得220kV线路潮流变化量与220kV站主变压器下网功率变化量满足线性关系,即
 (30)
(30)由式(12)可将220kV变电站主变压器负荷表示为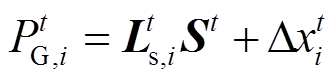 ,则t时段优化前后220kV变电站主变下网功率变化量可表示为
,则t时段优化前后220kV变电站主变下网功率变化量可表示为
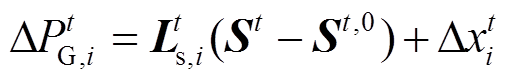 (31)
(31)
由式(31)得转供前后220kV站主变压器下网功率变化量,结合式(30)可得220kV线路潮流变化量,代入式(4)即可计算得到转供后220kV线路接头温升,则220kV线路接头温升约束为
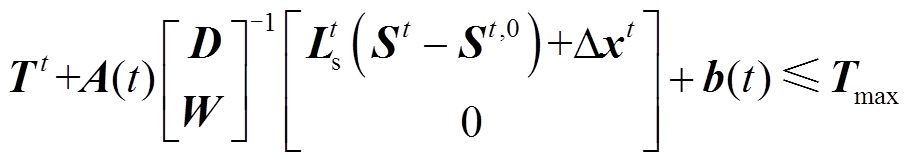 (32)
(32)由上述可知,负荷转供时110kV站运行方式的调整,虽然能缓解自身线路接头温度过热问题,但有可能使转供后220kV线路接头温度不满足约束条件。为避免220kV线路和110kV线路接头温升约束出现互斥矛盾,本文引入10kV负荷转供量作为松弛变量,可解决此问题。
2.2.3 线路载流量动态约束及电网辐射型约束
线路最大允许载流量动态约束在不同导线表面风速、光照、环境温度等因素和电缆绝缘介质、金属护套等因素条件下,在时段t下的线路最大允许载流量动态约束可表示为
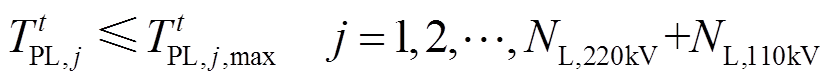 (33)
(33)式中,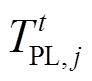 和
和 分别为第t个时段下第j条220kV/110kV线路当前电热载流量对应温度和最大允许电热载流量对应临界温度。
分别为第t个时段下第j条220kV/110kV线路当前电热载流量对应温度和最大允许电热载流量对应临界温度。
由文献[4]可得110kV电网辐射型约束为
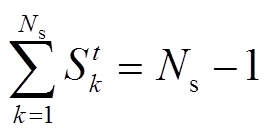 (34)
(34)
该转供优化模型为混合整数线性规划问题,求解过程如下:
1)从实时SCADA数据中获取线路j的耐张线夹、电缆接头温度以及线路接头温度越限允许时间常数取整[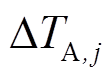 ]。当其线路接头温度越限时,计越限的第1个时段为
]。当其线路接头温度越限时,计越限的第1个时段为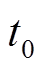 ,通过式(19)、式(20)进行判断,当持续时间超过允许持续时间常数取整[
,通过式(19)、式(20)进行判断,当持续时间超过允许持续时间常数取整[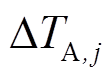 ]时,开始进行时段t的转供优化计算。
]时,开始进行时段t的转供优化计算。
2)获取受端电网在第t时段的负荷数据及线路接头温度、环境温度等,并由负荷数据得到当前线路潮流量大小,由式(4)计算出电网内线路在当前运行点的接头温升函数斜率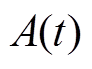 和系数
和系数 。
。
3)结合直供和串供接线方式下的220kV主变负荷、110kV线路潮流与110kV线路开关状态间系数矩阵式(16)、式(18)、式(23),根据220kV站、110kV线路开关和负荷的网络拓扑关系,生成110kV电网的负荷系数矩阵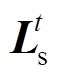 及潮流系数矩阵
及潮流系数矩阵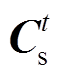 。
。
4)形成第t时段220kV线路潮流方向矩阵D,并获取220kV线路功率分解点的两条220kV线路的潮流比例Φ,形成矩阵W,根据式(30)计算得到220kV线路潮流量和220kV站主变下网功率变化量的系数矩阵。
5)根据各条线路的导线表面风速、光照、环境温度等因素和电缆绝缘介质、金属护套等实时数据,获取该时段的线路最大允许载流量动态约束(式(33))。
6)获取第t时段转供前的110kV线路开关状态0-1组合St,0,用CPLEX工具箱求解计及线路接头温升约束的受端电网转供优化模型。
7)通过计算,求解出所建模型第t时段的110kV线路开关状态0-1最优组合St*,以及归算至220kV站的最优10kV总转供量Δx*。
8)根据所得最优转供方案St*和Δx*,对110kV电网运行方式进行调整,并完成对220kV所供110kV站的10kV负荷进行转供,整个转供优化调度过程结束。
在Matlab R2012a上对某220kV/110kV受端电网[32-33]进行了计及线路接头温升约束的受端电网转供测试分析,如图6所示。该220kV/110kV电网共有8座220kV变电站,15座110kV变电站,网内电源点均为220kV变电站,网内没有任何上网电源,并且110~500kV架空线、电缆线路分别用不同颜色予以表示。220kV MJW、CS和TP站所带全部负荷均只有110kV站,其10kV母线不带10kV用户负荷。220kV WH站、SY站所供110kV站与本地区电网没有直接电气联系,仅体现220kV网络关系,故在本算例中不予考虑。
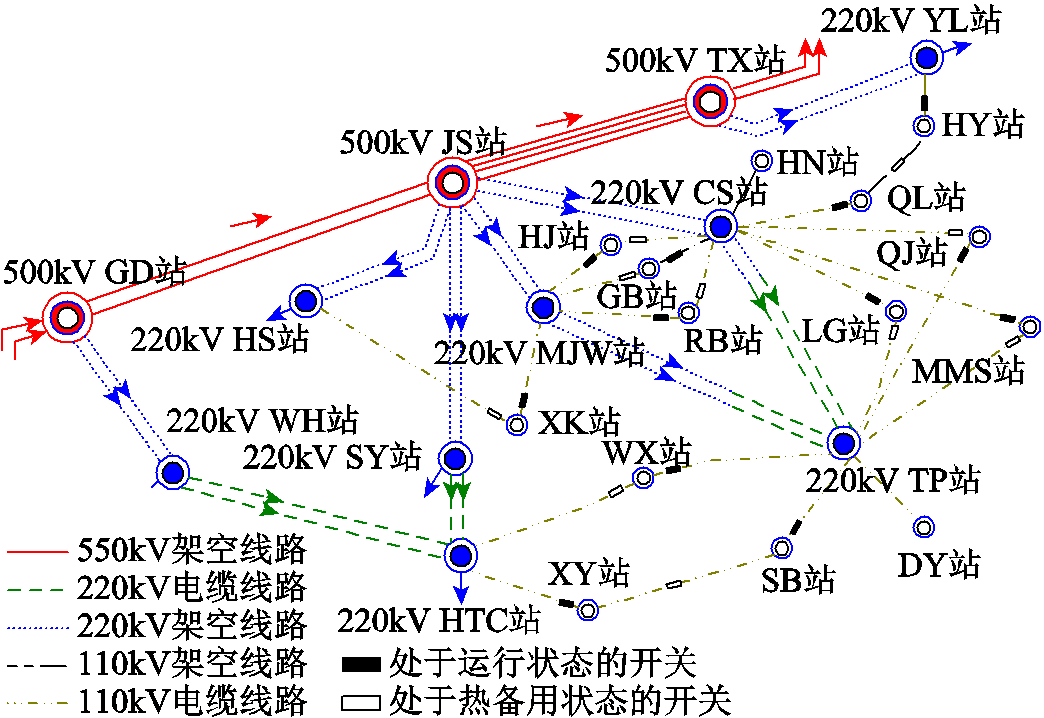
图6 某实际220kV/110kV电网接线潮流
Fig.6 Diagram of a practical 220kV/110kV network power flow
图6中,所有110kV变电站接线方式均为串供和直供两种方式,其中串供线路两侧联络开关等效为一个开关,如HY站与QL站之间为串供线路、XY站与SB站之间为串供线路。各条线路开关状态构成为该地区电网的标准运行方式。
算例测试中取各个110kV站于2016年7月22日和23日,以15min为1个时间断面的SCADA负荷数据。在标准运行方式下,网内没有接入发电机组,故电网的潮流方向均不发生变化,其220kV线路潮流方向矩阵D为已知常数矩阵,220kV WT线和ST线同时对TP站供电,其两条220kV线路的潮流比例Φ为2:1。
根据实际运行统计,选出具有大负荷、高温、耐热能力较差的线路进行重点监测,各条重点监测的线路最大允许温度Tmax和线路温度越限允许持续时间常数ΔTA见表1。在表1中,ST线表示CS站至TP站的220kV双回线路,其余以此类推。ST双回、WT双回为架空、电缆混合的线路,其ΔTA和Tmax取电缆参数和架空线参数中最小的一个。表2给出了归算至220kV站的10kV可转供负荷量Δx。
表1 重点监测的架空和电缆线路Tmax、ΔTA数据
Tab.1 Tmax and ΔTA of monitoring overhead and cable lines

变量ST线WT线JC线JW线YH线SQ线SG线 Tmax/℃80809090808080 ΔTA/15min2.52.322222
表2 归算至220kV站的10kV可转供负荷量Δx
Tab.2 The max transferred 10kV load to 220kV substation Δx

220kV站MJW站CS站TP站HTC站 Δxmax/MW21.222.128.827.3
在本算例中,导线表面吸收系数为0.5,导体表面黑体辐射系数为0.6,风速为0.5m/s、光照强度为1kW/m2、环境温度在28~37℃。
4.2.1 1个线夹超温时电网转供结果分析
当调控中心接收到重点监测的架空线夹的测温上送数据后,根据表1的架空线温度越限允许持续时间常数ΔTA,对其取整后,按照其温度越上限持续时间进行监控。假设在11:30发现220kV JC线40号耐张线夹温度高达92℃,并且高于其最大温度上限90℃长达30min,需要对其降低负荷运行。采用CPLEX进行转供优化模型求解,得到转供方案如图7所示,图中所示开关运行状态为转供后状态。图7中未画出电网部分,没有进行方式调整。

图7 1个线夹超温时转供方案
Fig7 Transfer plan with one clamp temperature over limit
表3给出了按照本文所提电网有功平衡约束和耐张线夹、电缆接头温升限制约束计算方法,获取转供前后220kV JC双回的温度最高的40号转角塔上耐张线夹、220kV JW双回的温度最高的32号转角塔上耐张线夹和110kV YH线电缆接头1的温度数据。表4给出了转供前后,220kV MJW、CS和YL站的主变压器负载数据。
表3 转供前后线夹、接头温度数据
Tab.3 Temperature data of each clamp and joint before and after power transfer

线路线夹、接头温度/℃潮流变化量ΔPL/MW 转供前转供后 220kV JC双回40号耐张线夹92.286.3-94.2 220kV JW双回32号耐张线夹72.474.334.1 110kV YH线电缆接头167.376.548.2
表4 转供前后220kV站主变压器负载变化情况
Tab.4 Load ratio variation of 220kV substations before and after power transfer

220kV站负荷率(%)转供后主变压器下网负荷/MW 转供前转供后 CS站89.179.437.9 MJW站56.262.329.2 YL站56.357.327.5
由图7可以看出,该转供方案进行了三次转供操作,分别为110kV GB站、QL站转供及归算到220kV CS站的10kV配电网负荷转供。220kV JC线潮流变化量为110kV QL站和GB站分别倒由220kV YL站和MJW站供电的负荷转供量,且220kV CS站需要10kV配电网配合转供12MW的负荷。由表1和表3可知,转供后220kV JC双回40号耐张线夹温度满足90℃安全要求,且转供后会引起负荷增加的220kV JW线路双回32号耐张线夹、110kV YH线电缆接头1温度均没有超上限90℃和80℃。另外,由表4可知,转供后各220kV站均未超载,该方案满足所建模型的220kV有功功率平衡约束。
由此可见,针对220kV架空线单个耐张线夹持续超温问题,采取本文所建转供模型能够及时调整运行方式,减少设备故障发生的概率,尽可能避免长时间高温运行可能造成的断线故障。
4.2.2 多个线夹、接头超温时电网转供结果分析
根据该电网地理信息,已知图6中的220kV ST双回和WT双回的部分电缆线路位于同一个电缆地下通道中。现在监测到ST双回的电缆接头1和WT双回电缆接头2温度达到83℃和84℃,且两条线路接头均高于其最大温度上限80℃超过长达30min,需要降低这两条220kV双回电缆线路负荷以降低线路接头温度。
为比较多个线路接头超温时,计及线路接头温升约束与忽略接头温升约束的转供方案消除接头温度越限的效果,分别按计及线路接头温升约束的转供优化模型(M1)、仅考虑载流量动态约束的转供优化模型(M2)进行求解。M2忽略线路接头温升约束,其余约束条件及目标函数与M1相同。采用CPLEX进行M1及M2求解,M1转供方案如图8所示,图中所示开关运行状态为转供后状态。图8中未画出电网部分,未进行方式调整。
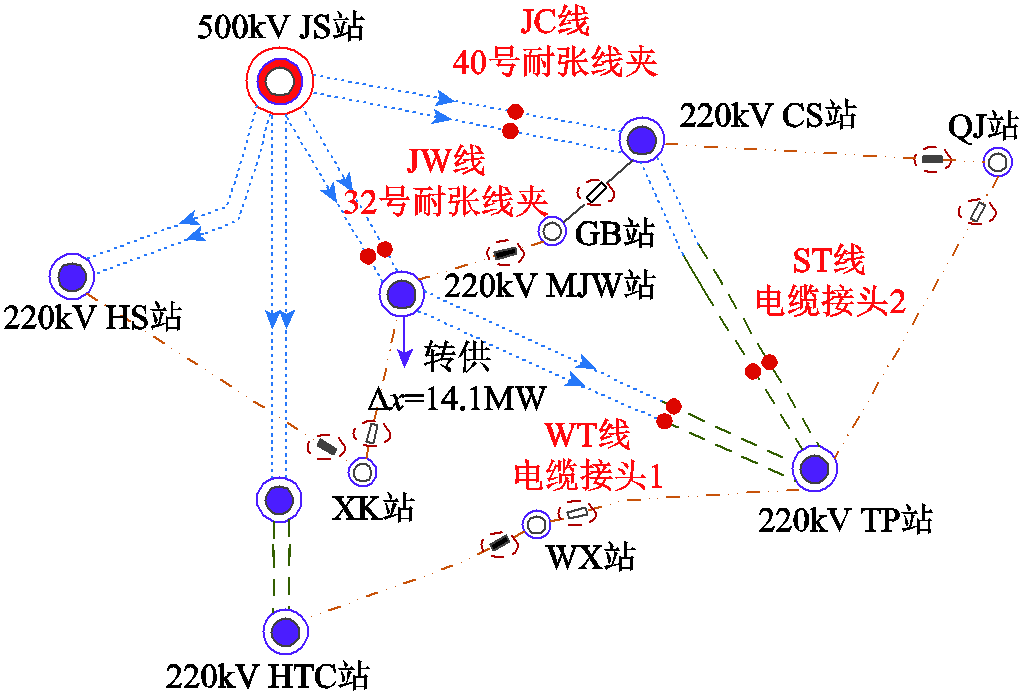
图8 多个线夹、接头超温时转供方案
Fig.8 Transfer plan with multiple joints temperature over limit
表5给出了按照本文所提电网有功平衡约束计算方法,计算出转供前后220kV站主变压器负,其中,10kV配网负荷转供量为归算至220kV MJW站的10kV配网转供。表6给出了按照本文所提耐张线夹和电缆接头温升限制约束,计算出转供前后各条220kV线路耐张线夹和电缆接头温度的变化情况。
表5 转供前后220kV站主变压器负载变化情况
Tab.5 Load ratio variation of 220kV substations before and after power transfer
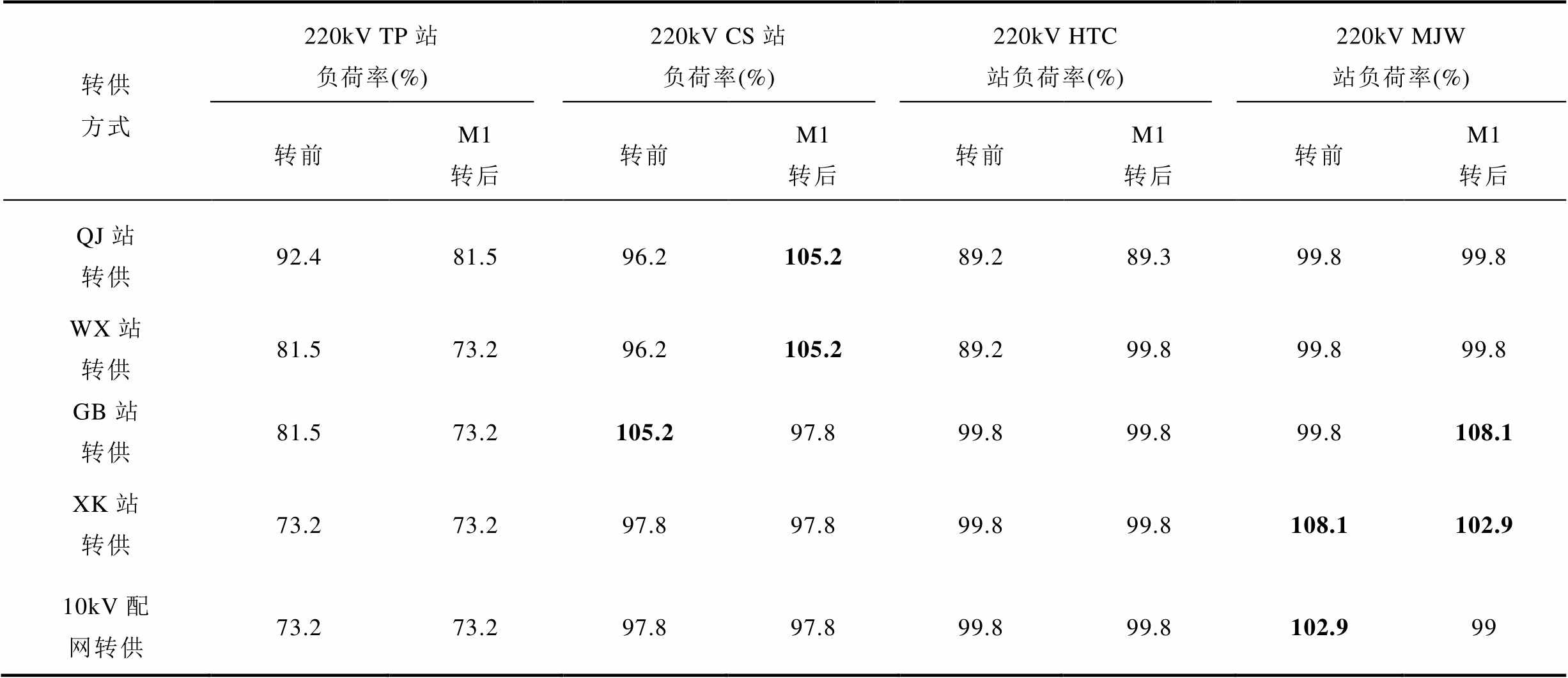
转供方式220kV TP站负荷率(%)220kV CS站负荷率(%)220kV HTC站负荷率(%)220kV MJW站负荷率(%) 转前M1转后转前M1转后转前M1转后转前M1转后 QJ站转供92.481.596.2105.289.289.399.899.8 WX站转供81.573.296.2105.289.299.899.899.8 GB站转供81.573.2105.297.899.899.899.8108.1 XK站转供73.273.297.897.899.899.8108.1102.9 10kV配网转供73.273.297.897.899.899.8102.999
表6 转供前后220kV线路线夹和接头温度变化情况
Tab.6 Temperature variation of the joint and clamp points of 220kV lines before and after power transfer

转供方式ST、WT电缆接头温度/℃ 转前M1转后M2转后 QJ站转供83、8481、81.581、81.5 WX站转供81、81.578.8、79.178.8、79.1 GB站转供78.8、79.178.8、79.178.8、79.1 XK站转供78.8、79.178.8、79.178.8、79.1 10kV配网转供78.8、79.178.8、79.1— 转供方式JW双回32号耐张线夹温度/℃ 转前M1转后M2转后 QJ站转供89.389.389.3 WX站转供89.389.389.3 GB站转供89.391.191.1 XK站转供91.190.190.1 10kV配网转供90.189.8— 转供方式JC双回40号耐张线夹温度/℃ 转前M1转后M2转后 QJ站转供72.172.272.2 WX站转供72.272.272.2 GB站转供72.273.873.8 XK站转供73.873.173.1 10kV配网转供73.172.8—
如图8所示,M1转供方案共进行了五次转供操作,分别为110kV QJ站、WX站、GB站、XK站转供及归算到220kV MJW站的10kV配电网负荷转供。由表5及表6可知,110kV QJ站和WX站转供能够减少220kV TP站主变压器下网负荷,减少对220kV TP站供电的ST、WT线负荷,达到降低其电缆接头运行温度的目的。但是这样将造成220kV CS站和HTC站下网负荷增加,进而导致220kV CS站主变压器超载约5%。为消除超载,220kV CS站将所供110kV GB站倒至220kV MJW站供电,但是此时220kV MJW站主变压器负荷已达到100%满载,故又将其所供110kV XK站倒至主变压器负荷较低的220kV HS站供电,此时220kV JW双回线路32号耐张线夹温度上升后将出现越限,为保证其不越限,从配电网转移14.1MW的负荷。由表1及表6可得,按M1转供方案进行五次转供操作后,所有线路接头温度均未越限。如表6所示,M2转供方案中,前四次转供操作与M1一致,但由于M2不考虑线路接头温升约束,四次转供后所有线路温度满足载流量动态约束,故M2提供的转供方案不进行第5次的配电网负荷转供操作。因此,M2转供方案实施后,JW双回32号耐张线夹温度保持在90.1℃,超过其最大允许温度90℃,威胁220kV JW双回线路安全运行。
由上述可得,M1计算得到的转供方案既解决了220kV ST、WT线电缆接头温度超限问题,又能保证转供后,220kV CS站和MJW站不会出现超载情况,且其他线路接头温度不会越限。而M2转供方案只考虑了线路本体的载流量动态约束,在消除原有线路接头温度越限后,可能导致新的接头温度越限问题,影响线路的运行安全。
由此可见,针对同沟多条电缆的接头温度越限问题,本文提出计及线路温升约束的转供优化模型协调考虑了转供后不能引起其他线路、设备出现温度超限或超载问题,从电网全局层面上给出最优的转供方案。
本文建立了一种计及线路接头温升约束的受端电网转供优化模型。通过某220kV/110kV电网测试结果表明,当220kV线路或者110kV线路的耐张线夹、电缆接头异常温升持续发热时,仅考虑线路载流量动态约束并不能解决线路接头发热问题。本文计及线路接头温升约束的模型,能够在保证不拉限负荷的前提下最大化利用受端电网的供电网络,从全局层面实现操作成本最少的转供方案,消除线路接头温度超限。本文所建模型是从实际运行的角度,将线路接头温升线性化约束引入了负荷转供中,在线路载流量允许温度的基础上进一步考虑接头处的温升安全约束,构建实时转供优化模型。本文通过对线路潮流变化量与主变压器下网功率变化量的有功平衡推导,以潮流变化量为中间变量得到负荷变化时线路接头温升的线性变化量,并建立线性化的转供优化模型。在保证电网安全运行的基础上,本文模型进一步从实际运行角度深挖了线路的供电潜力,为全面提升受端电网的转供互供能力提供了科学依据。
参考文献
[1] 林杰, 刘刚, 张海鹏, 等. 架空线路并沟线夹温度分布研究[J]. 电力系统保护与控制, 2013, 41(24): 88-94.
Lin Jie, Liu Gang, Zhang Haipeng, et al. Research of temperature distribution of overhead lines parallel groove clamp[J]. Power System Protection and Control, 2013, 41(24): 88-94.
[2] 周纹霆, 董守龙, 王晓雨, 等. 电磁脉冲焊接电缆接头的装置的研制及测试[J]. 电工技术学报, 2019, 34(11): 2424-2434.
Zhou Wenting, Dong Shoulong, Wang Xiaoyu, et al. Development and test of electromagnetic pulse welding cable joint device[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2424-2434.
[3] 高云鹏, 谭甜源, 刘开培, 等. 电缆接头温度反演及故障诊断研究[J]. 高电压技术, 2016, 42(2): 535-542.
Gao Yunpeng, Tan Tianyuan, Liu Kaipei, et al. Research on temperature retrieval and fault diagnosis of cable joint[J]. High Voltage Engineering, 2016, 42(2): 535-542.
[4] 林晨炯, 林珍, 吴雅琳. 电缆接头温度在线监测方法研究综述[J]. 电气技术, 2019, 20(5): 1-4, 9.
Lin Chenjiong, Lin Zhen, Wu Yalin. Summary of research on online monitoring method of cable joint temperature[J]. Electrical Engineering, 2019, 20(5): 1-4, 9.
[5] 刘家军, 杜智亮, 李娟绒, 等. 铁路10kV电力电缆头发热分析与安全监测[J]. 电力系统保护与控制, 2019, 47(24): 131-138.
Liu Jiajun, Du Zhiliang, Li Juanrong, et al. Thermal analysis and safety monitoring of railway 10 kV power cable joints[J]. Power System Protection and Control, 2019, 47(24): 131-138.
[6] 王强钢, 李钰双, 雷超, 等. 计及主变上层油温约束的受端电网转供优化模型[J]. 中国电机工程学报, 2018, 38(16): 4747-4758.
Wang Qianggang, Li Yushuang, Lei Chao, et al. A power transfer optimization model of receiving-end power systems considering transformer top-oil temperature constraints[J]. Proceedings of the CSEE, 2018, 38(16): 4747-4758.
[7] 周念成, 谷飞强, 雷超, 等. 考虑合环电流约束的主动配电网转供优化模型[J]. 电工技术学报, 2020, 35(15): 3281-3291.
Zhou Niancheng, Gu Feiqiang, Lei Chao, et al. Apower transfer optimization model of activedistribution networks in consideration of loop closingcurrent constraints[J]. Transactions of ChinaElectrotechnical Society, 2020, 35(15): 3281-3291.
[8] Yang Tianshu, Guo Ye, Deng Lirong, et al. A linear branch flow model for radial distribution networks and its application to reactive power optimization and network reconfiguration[J]. IEEE Transactions on Smart Grid, 2021, 12(3): 2027-2036.
[9] Zhan Junpeng, Liu Weijia, Chung C Y. Stochastic transmission expansion planning considering uncertain dynamic thermal rating of overhead lines[J]. IEEE Transactions on Power Systems, 2019, 34(1): 432-443.
[10] IEEE Std 738—2012IEEE standard for calculation of bare overhead conductor temperatures[S]. IEEE, 2013.
[11] CIGRE Working Group B2.43. Guide for thermal rating calculation of overhead lines[S]. International Council on Large Electric Systems, 2014.
[12] 王孟夏, 韩学山, 韦志清, 等. 电网运行环境下基于电热耦合潮流的架空线路应力预估[J]. 电工技术学报, 2019, 34(5): 1078-1087.
Wang Mengxia, Han Xueshan, Wei Zhiqing, et al. Tension prediction of overhead transmission line based on electrothermal coupling power flow in operating power systems[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1078-1087.
[13] 王艳玲, 莫洋, 韩学山, 等. 考虑气象时空分布特性的输电线路模型和分析方法[J]. 电工技术学报, 2020, 35(3): 636-645.
Wang Yanling, Mo Yang, Han Xueshan, et al. Transmission line model and analysis method considering the time and space distribution characteristics of meteorology[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 636-645.
[14] Olsen R, Holboell J, Gudmundsdottir U S. Electrothermal coordination in cable based transmission grids[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4867-4874.
[15] 陈芳, 查浩, 韩学山, 等. 基于半参数平差模型的线路温度估计[J]. 电力系统自动化, 2015, 39(21): 81-86.
Chen Fang, Cha Hao, Han Xueshan, et al. Transmission line temerperture estimation based on semi-paramettric adjustment model[J]. Automation of Electric Power Systems, 2015, 39(21): 81-86.
[16] 应展烽, 杜志佳, 冯凯, 等. 高压架空导线径向热路模型及其参数计算方法[J]. 电工技术学报, 2016, 31(4): 13-21.
Ying Zhanfeng, Du Zhijia, Feng Kai, et al. Radial Thermal circuit model and parameter calculation method for high voltage overhead transmission line[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 13-21.
[17] 胡剑, 熊小伏, 王建. 基于热网络模型的架空输电线路径向和周向温度计算方法[J]. 电工技术学报, 2019, 34(1): 139-152.
Hu Jian, Xiong Xiaofu, Wang Jian. Radial and circumferential temperature calculation method of overhead transmission lines based on thermal network model[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 139-152.
[18] Zhan Junpeng, Liu Weijia, Liang Jun, et al. Calculation of power transfer limit considering electro-thermal coupling of overhead transmission line[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1503-1511.
[19] 高沁, 卫志农, 孙国强, 等. 计及线路电阻随温度变化影响的电力系统最优潮流[J]. 电力系统自动化, 2015, 39(16): 76-80.
Gao Qing, Wei Zhinong, Sun Guoqiang, et al. Temperature-dependent power system optimal power flow[J]. Automation of Electric Power Systems, 2015, 39(16): 76-80.
[20] 王孟夏, 韩学山, 黄金鑫, 等. 计及输电元件热惯性效应的安全约束最优潮流[J]. 中国电机工程学报, 2016, 36(5): 1181-1189.
Wang Mengxia, Han Xueshan, Huang Jinxin, et al. Security constrained optimal power flow considering thermal inertia effect of transmission component[J]. Proceedings of the CSEE, 2016, 36(5): 1181-1189.
[21] Dong Xiaoming, Kang Chongqing, Ding Yuanyuan, et al. Estimating the wind power integration threshold considering electro-thermal coupling of overhead transmission lines[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3349-3358.
[22] 侯宇, 王伟, 韦徵, 等. 输电线路动态增容技术研究及应用[J/OL]. 电力系统自动化: 1-13[2021-03-09]. http: //kns.cnki.net/kcms/detail/32.1180.TP. 20201221.0959.004.html.
Hou Yu, Wang Wei, Wei Zheng, et al. Research and application of dynamic rating technology of transmission lines[J]. Automation of Electric Power Systems: 1-13[2021-03-09].http: //kns.cnki.net/kcms/ detail/32.1180.TP.20201221.0959.004.html.
[23] Dawson L, Knight A M. Applicability of dynamic thermal line rating for long lines[J]. IEEE Transactions on Power Delivery, 2018, 33(2): 719-727.
[24] Teng Fei, Dupin R, Michiorri A, et al. Understanding the benefits of dynamic line rating under multiple sources of uncertainty[J]. IEEE Transactions on Power Systems, 2018, 33(3): 3306-3314.
[25] 冯凯, 应展烽, 陈汹, 等. 计及线路热惯性效应的模型预测控制安全经济调度模型[J]. 电工技术学报, 2018, 33(8): 1875-1883.
Feng Kai, Ying Zhanfeng, Chen Xiong, et al. Model predictive control security economic dispatch model considering transmission line thermal inertia effect[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1875-1883.
[26] 楼贤嗣, 王橹裕, 郭创新, 等. 考虑输电线路动态增容的增强型安全约束最优潮流[J]. 电力系统自动化, 2019, 43(18): 26-36.
Lou Xiansi, Wang Luyu, Guo Chuangxin, et al. Enhanced security-constrained optimal power flow considering dynamic thermal rating of transmission lines[J]. Automation of Electric Power Systems, 2019, 43(18): 26-36.
[27] 徐伟, 鲍颜红, 周海锋, 等. 基于阻塞分析的输电线路动态增容[J]. 电力系统保护与控制, 2016, 44(6): 15-22.
Xu Wei, Bao Yanhong, Zhou Haifeng, et al. Transmission line dynamic capacity-increase based on congestion analysis[J]. Power System Protection and Control, 2016, 44(6): 15-22.
[28] 董选昌, 曲烽瑞, 李艳飞, 等. 架空线路耐张线夹三维温度场仿真分析及验证[J]. 西南交通大学学报, 2019, 54(5): 997-1004.
Dong Xuanchang, Qu Fengrui, Li Yanfei, et al. Simulation analysis and verification on three-dimensional temperature field of strain clamps for overhead lines[J]. Journal of Southwest Jiaotong University, 2019, 54(5): 997-1004.
[29] 刘刚, 王鹏宇, 毛健琨, 等. 高压电缆接头温度场分布的仿真计算[J]. 高电压技术, 2018, 44(11): 3688-3698.
Liu Gang, Wang Pengyu, Mao Jiankun, et al. Simulation calculation of temperature field distribution in high voltage cable joints[J]. High Voltage Engineering, 2018, 44(11): 3688-3698.
[30] 国家能源局. DL/T 664-2016 带电设备红外诊断应用规范[S]. 2016.
[31] 中华人民共和国国家质量监督检验检疫总局、中国国家标准化管理委员会. GB/T 25840-2010规定电气设备部件(特别是接线端子)允许温升的导则[S]. 2010.
[32] 周念成, 何宽, 王强钢, 等. 高压配电网与天然气管网互联的转供优化模型[J]. 中国电机工程学报, 2020, 40(5): 1432-1443.
Zhou Niancheng, He Kuan, Wang Qianggang, et al. An energy transfer optimization model of interconnected energy systems with high voltage distribution networks and natural gas networks[J]. Proceedings of the CSEE, 2020, 40(5): 1432-1443.
[33] 国网四川省电力公司天府新区供电公司. 国网四川省电力公司天府新区电力系统2020年度运行方式[R]. 成都: 国网四川省电力公司天府新区供电公司, 2020.
A Power Transfer Optimization Model of Receiving-End Power Systems Considering Line Joint Temperature Rise Constraints
Abstract To relieve the continuous heating problem of transmission line joint caused by abnormal temperature rise under heavy load and high temperature conditions, this paper proposes an power transfer optimization model of receiving-end power system considering line joint temperature rise constraints. Firstly, based on electro-thermal coupling theory, the equivalent thermal model of line joint temperature rise and its parameter estimation method are studied. And using power flow variation as the intermediate variable, the linearized equation of line joint temperature rise with load changes under a certain operation point is derived. Combining with the topology of 220kV/110kV receiving-end power system, the linear constraints of the line joint temperature rise with power flow transferring is constructed. And then a power transfer optimization model is proposed in the constraints of line joint temperature rise, electro-thermal flow security, active power balance and radial grid structure, for the objective function of minimum switching number. The model is a mixed integer linear programming problem, so CPLEX tools are used for solving. Finally, a practical 220kV/110kV receiving-end power system is used for simulating and verifying that the proposed model is effective.
keywords:Receiving-end power system, electro-thermal coupling theory, line joint temperature rise, power flow transfer,power transfer optimization
DOI:10.19595/j.cnki.1000-6753.tces.201018
中图分类号:TM712
周念成 男,1969年生,博士,教授,研究方向为电力系统自动化和电能质量。E-mail:cee_nczhou@cqu.edu.cn
莫复雪 女,1997年生,硕士,研究方向为电力系统优化运行和电能质量。E-mail:mofuxue@hotmail.com(通信作者)
国家自然科学基金联合基金资助项目(U1866603)。
收稿日期 2020-08-11
改稿日期 2021-03-10
(编辑 赫蕾)