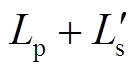 即为归算至一次侧的等效漏感。
即为归算至一次侧的等效漏感。摘要 中频变压器作为反激直流变换器的核心部件,变压器漏感过大时产生的尖峰电压对开关器件的影响是不可忽视的。另外在谐振直流变换器中,变压器漏感需要与谐振电容、频率匹配才能使电路达到理想工作状态。因此,在设计直流变换器时,对变压器漏感进行精确的计算变得尤为重要。现有计算漏感的数值法无法灵活地运用于变压器设计中,解析法得到广泛的推广。目前中频圆导线变压器漏感的解析计算法大多基于面积等效法,但是等效后会使变压器窗口处绝缘区域面积偏大,漏感计算结果不够准确。另外也有对中频圆导线的频率效应进行直接分析,但忽略了匝间的不规则空隙,导致漏感计算结果偏小。为此,该文提出一种更加精确的漏感解析计算方法,不仅对圆导线的频率效应进行分析,而且考虑了匝间不规则空隙,以提高漏感的解析计算精度。最后基于搭建的变压器样机进行实验,验证了所提方法的正确性和有效性。
关键词:中频圆导线变压器 漏感 圆导线频率效应 匝间不规则空隙 解析计算法
作为直流变换器核心器件的中频变压器,其漏感过大会给开关器件带来不可忽略的影响。在反激变换器中,开关器件关断的瞬间,漏感上存储的能量会被瞬间释放,此时开关器件两端承受尖峰电压,从而有可能导致开关器件损坏[1-2]。若能在反激变换器设计时降低变压器漏感,以减小开关管关断时的尖峰电压,则可对开关器件进行有效的保护。另外,在谐振直流变换器中,变压器漏感需要与谐振电容,电路工作频率相匹配,才能使电路工作在最佳谐振状态,以提高变换器的传输效率[3-4]。为此,对变压器漏感进行准确的计算和控制对直流变换器的设计具有重要的指导意义。
目前,计算中频圆导线变压器漏感的计算方法主要分为两种:数值法和解析法。数值法例如有限元仿真,在求解漏感时有足够高的精度[5-6],但是该方法会因施加激励的频率升高而导致计算时间过长,并且在变压器设计中不易灵活使用;解析法是一种考虑变压器磁心结构、绕组分布情况、绕组频率效应等因素以解析式计算变压器漏感的方法,并且便于工程师在制造变压器的过程中对漏感进行设计以达到漏感期望值[7-9]。目前常用的解析法为磁场能量解析法,通过计算变压器窗口处的磁场能量来求解变压器漏感。
以磁场能量解析法提高圆导线变压器漏感计算精度是许多研究者一直在研究的内容。现在广泛使用的方法为Dowell的圆导线面积等效法[10],将圆导线等效为铜箔导线从而进行铜箔变压器漏感的计算[11-12]。但是该方法没有考虑圆导线的频率效应,缺乏一定的理论基础,并且等效后使得变压器窗口处绝缘区域的面积计算不够准确,导致漏感计算结果偏大。之后,有研究者针对利兹线变压器漏感计算提出了一种考虑导线频率效应的计算方法,这可类比进行圆导线变压器漏感的计算,但是这种类比方法忽略了匝间的不规则空隙,导致计算出来的漏感偏小[13]。
为此,本文提出一种更加准确的中频圆导线变压器漏感计算方法。该方法基于变压器窗口处的磁场分布和圆导线的频率效应,间接地将匝间不规则空隙的漏磁场能量计算在内,使得中频下圆导线变压器漏感的计算精度得以提高。
在理想变压器中,变压器一次侧交变的磁链全部通过变压器的磁心与二次绕组相交链,二次侧也同样如此。但是,实际中变压器任意一侧磁链不可能全部通过磁心与另一侧绕组交链,如图1所示。其中泄漏出的磁通可用归算至变压器某一侧的漏感来等效,如图2,图中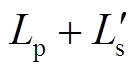 即为归算至一次侧的等效漏感。
即为归算至一次侧的等效漏感。
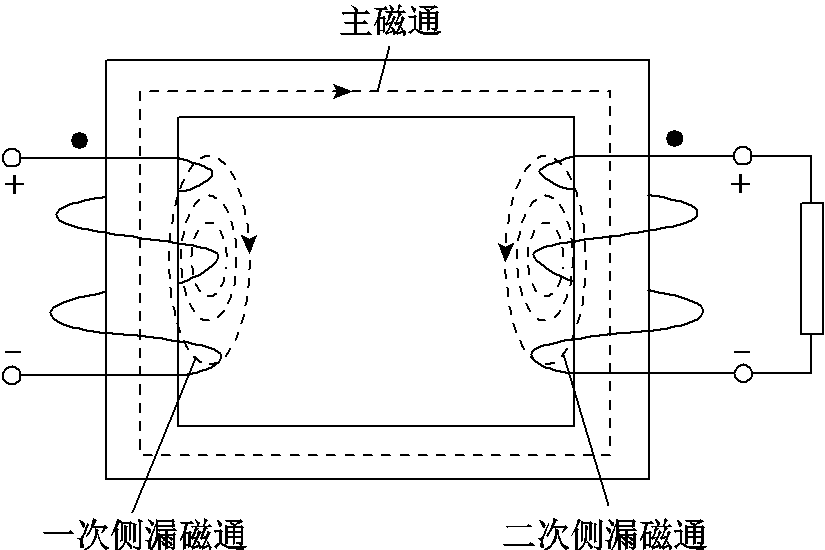
图1 漏感的定义
Fig.1 Definition of leakage inductance
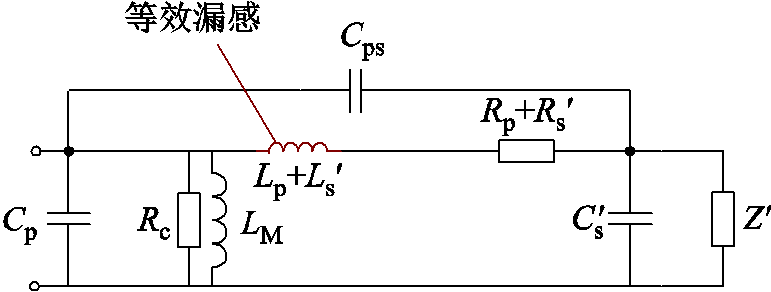
图2 变压器等效电路
Fig.2 The equivalent circuit of transformer
若变压器二次侧短路,磁心中的一、二次侧磁动势会相互抵消,只留下存在于窗口处的漏磁场。磁场能量解析法就是计算出此时窗口处的总磁场能量Wleakage,并结合式(1)求出归算至一次侧的漏感。
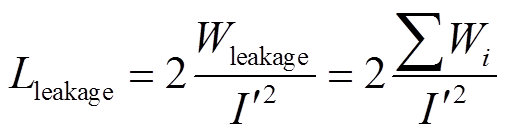 (1)
(1)式中,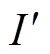 为漏感归算侧电流的有效值;Wi为变压器窗口处不同区域的磁场能量。
为漏感归算侧电流的有效值;Wi为变压器窗口处不同区域的磁场能量。
因为变压器窗口处结构复杂,求解总磁场能量Wleakage需将变压器窗口处划分成不同的区域分别计算Wi。图3为圆导线变压器截面图,图中将变压器窗口分为两类形状规则的区域:一类称为规则混合区域,由圆导线区域和不规则空隙区域组成;另一类称为规则绝缘区域,用于层间绝缘,其中无导电介质。求解总磁场能量Wleakage即为求一次和二次侧规则混合区域、一次和二次侧规则绝缘区域及一次和二次侧隔离处规则绝缘区域的磁场能量之和。

图3 圆导线变压器截面图
Fig.3 Window section of round conductor transformer
圆导线的几何形状及绝缘的存在使得圆导线无法紧密排布,所以在圆导线变压器绕制过程中,窗口处必然会存在空隙。其中相邻导体层之间的空隙可归为规则绝缘区域来处理;而在一层导体层中,即一层规则混合区域中,导线之间会存在不规则空隙区域。但是因为该不规则空隙区域结构复杂,一般在计算规则混合区域磁场能量时将其忽略。为了说明忽略不规则空隙区域磁场能量对规则混合区域磁场能量的影响,进行了忽略与考虑不规则空隙磁场能量的有限元仿真对比,仿真模型参数见表1。
表1 变压器仿真案例的具体参数
Tab.1 The parameters of the transformer simulation case

磁心E55/28/21 一次、二次侧规则混合区域层数mreg_mix_p/s2/1 圆导线直径D/mm1 每层匝数N28 一次侧每匝电流的幅值Ip/A1 一次、二次侧规则绝缘区域层数mreg_ins_p/s1/0 一次、二次侧隔离处规则绝缘区域层数mreg_ins_g1 规则绝缘区域厚度dins/mm1 频率f/kHz50,70,90
仿真条件为一次侧每匝导体施加幅值为1A的电流,二次侧短路。此时仿真模型中变压器磁心处的一、二次磁动势相互抵消,只留下变压器窗口处的漏磁场。通过有限元仿真可以将变压器窗口处不同区域的磁场能量计算出来。
仿真结果如图4所示,从每组频率点的对比图可以发现:若在计算规则混合区域磁场能量时忽略不规则空隙区域能量,大约会少考虑一半的规则混合区域磁场能量。对比不同频率下两者仿真的相对误差可以发现:随着频率的升高,忽略不规则空隙磁场能量带来的相对误差也会随之增大,从47%上升到52%。所以,不规则空隙区域的磁场能量在漏感计算中是不可忽略的。
为此,本文提出一种解析法,通过分析变压器窗口处的磁场分布和圆导线的频率效应,将不规则空隙区域的磁场能量考虑在内,以提高变压器的漏感计算精度。
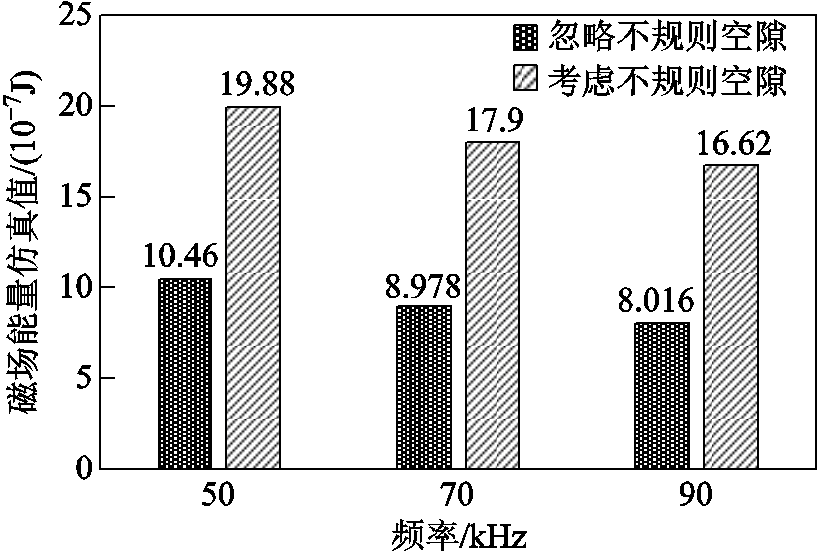
图4 忽略不规则空隙区域对规则混合区域磁场能量的影响
Fig.4 The infulence of ignoring the magnetic energy of irregular gap area on the magnetic energy of regular mixed area
基于磁场能量解析法求解漏感,需要分别计算规则混合区域和规则绝缘区域磁场能量。但变压器工作在不同频率下,窗口处的磁场分布不同,导致磁场能量的计算结果也不相同。由于变压器中规则绝缘区域和不规则空隙区域无电流流过,可以认为基本不受频率效应影响,但圆导线区域通过中频交流电,其磁场分布受频率效应的影响相对较大。基于各区域的频率效应影响情况,可进行以下两点理想假设:①低频下变压器窗口处磁场分布不受频率效应影响;②中频下频率效应只对圆导线区域的磁场分布有影响。
基于上述理想假设,中频和低频下规则绝缘区域的磁场分布不受频率效应影响,可以按低频下恒定的磁场分布对该区域磁场能量进行计算。而对于中频下规则混合区域磁场能量的计算,不仅需要合理地考虑圆导线区域的频率效应,还需要计算出不规则空隙区域处的磁场能量。但是直接计算不规则空隙区域的磁场能量较为困难,为此提出计算中频下规则混合区域磁场能量的方法如图5所示。

图5 中频下规则混合区域磁场能量求解提出的解析法
Fig.5 The proposed analytical method for enery calculation of regular mixed area under the medium frequency
中频下规则混合区域的磁场能量可以看作是低频下规则混合区域的磁场能量减去由于频率效应导致圆导线区域磁场能量的衰减量。由假设①可求出低频下规则混合区域的磁场能量;由假设②可知,中频下的频率效应只会影响圆导线区域的磁场分布,导致圆导线中磁场能量发生衰减,由此可求出中频下规则混合区域的磁场能量。所以提出的方法间接地考虑了不规则空隙区域的磁场能量,规避了直接计算带来的困难。基于上述提出的方案,下面具体介绍低频下规则绝缘区域及中频下规则混合区域的磁场能量计算。
2.2.1 低频下变压器窗口处各区域磁场能量计算
根据Dowell的一维磁场模型[14]及圆导线内部产生的磁场,低频下圆导线变压器窗口处的磁场分布如图6所示。其中Hext为规则混合区域的电流所产生并施加在外部区域的磁场强度,可根据安培定律求出,并且在窗口处只有一维z向分量。Hint为每匝圆导线内部通过电流时在其导线内部产生的环形磁场。并根据假设①,这两种磁场强度在低频下均呈线性分布。其中规则混合区域不仅要受到外部磁场强度Hext的影响,还要受到内部磁场强度Hint的影响。其中第k层规则混合区域在Δx处受的外部磁场强度Hext(k, Δx)为
 (2)
(2)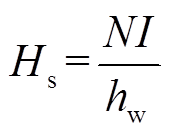 (3)
(3)
式中,D为圆导线的直径,同时也为规则混合区域厚度;Hs为变压器窗口处每一层规则混合区域产生的磁场强度;N为每一层规则混合区域中圆导线的数量;I为每匝圆导线通入电流量的有效值;hw为变压器窗口高度。
在式(2)中,当Δx=D时,Hext(k, D)=kHs为外部相邻规则绝缘区域的磁场强度。
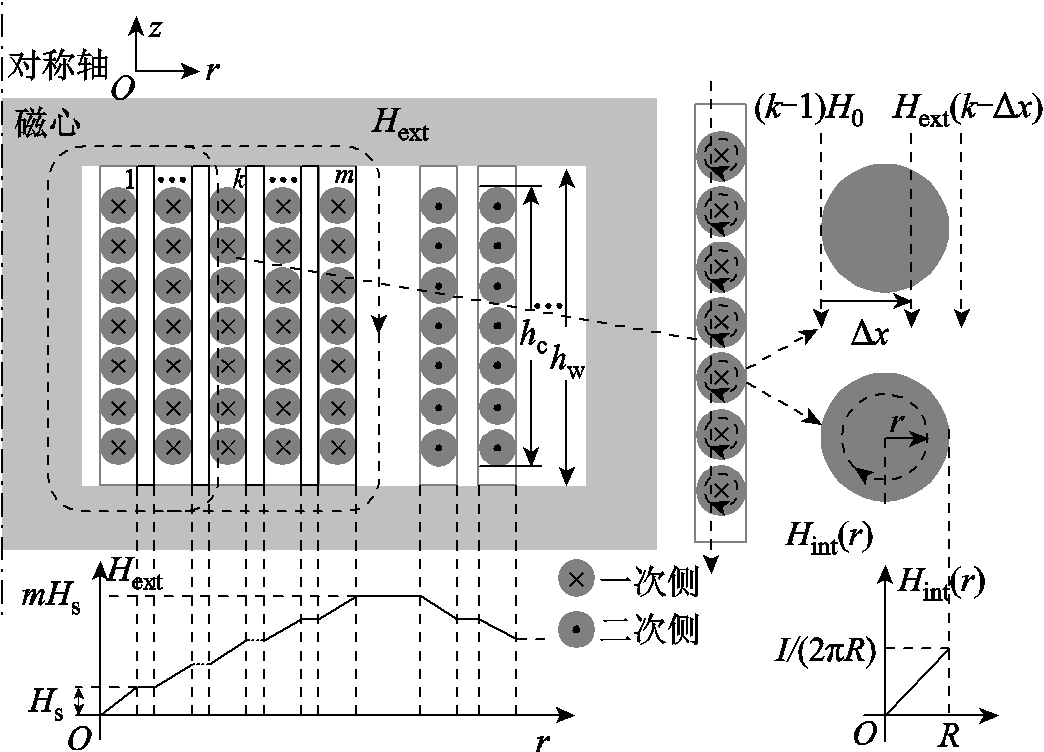
图6 低频下变压器窗口处的磁场分布
Fig.6 Distribution of magnetic field in transformer window under the low frequency
每匝圆导线内部磁场强度Hint(r)可根据安培定律求出,即
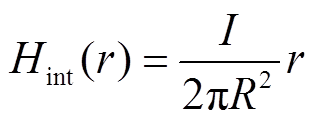 (4)
(4)式中, R为圆导线半径,R=D/2。
现已知规则混合区域的磁场分布和磁场强度表达式(2)、式(4),可求得其磁场能量为
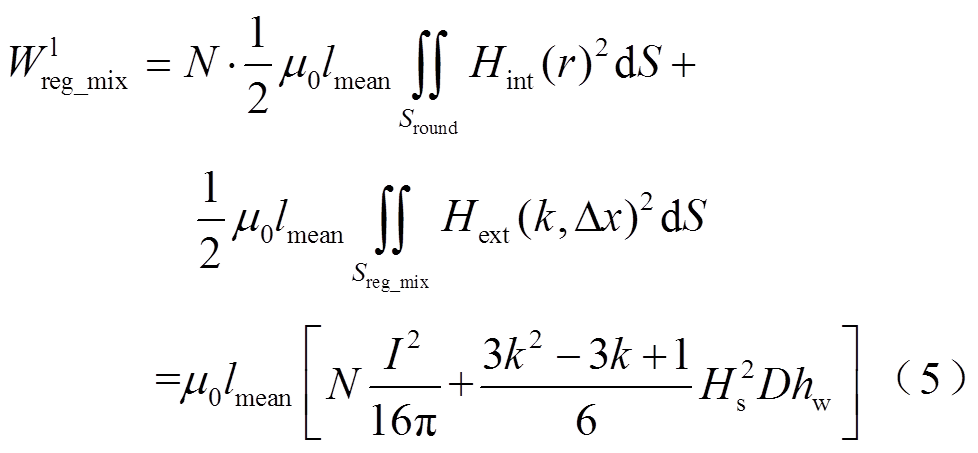
式中,Wlreg_mix为低频下一层规则混合区域的磁场能量;lmean为平均匝长;Sround为每匝圆导线面积,Sround=πR2;Sreg_mix为规则混合区域的横截面积,Sreg_mix=Dhw。
由于已知规则绝缘区域的磁场强度,也可求出相应的磁场能量为
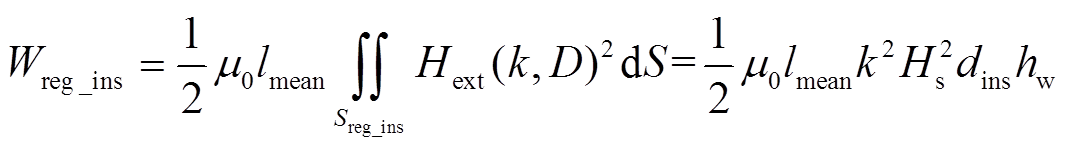 (6)
(6)式中,Sreg_ins为规则绝缘区域的横截面积,Sreg_ins= hwdins;dins为规则绝缘区域的宽度。
根据假设②,频率效应会影响圆导线区域的磁场能量,为方便后期求解每匝圆导线的磁场能量,需要将式(7)代入式(2)中,得到Hext(k,Δx)在每匝圆导线中的极坐标表达式(8)。
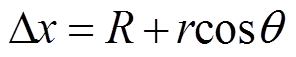 (7)
(7)
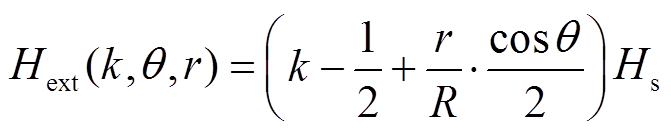 (8)
(8)2.2.2 中频下圆导线区域磁场能量衰减量
当变压器工作在中频下,频率效应会影响圆导线区域的磁场分布,导致圆导线区域的磁场能量发生衰减。为精确计算中频下圆导线变压器的漏感,需要计算衰减的磁场能量。电流的频率效应可具体分为趋肤效应与邻近效应,根据这两者的正交性[15],可分别分析两种效应对低频下圆导线区域磁场能量造成的衰减影响。
1)趋肤效应衰减率
圆导线内中频电流产生的趋肤效应会影响导线内部磁场Hint,导致Hint作用下的圆导线磁场能量发生改变。为了定量说明趋肤效应对磁场能量的衰减影响,以图7来举例说明。在半径为R0的圆导线中通入角频率为ω,电流峰值为I0的交流电,并根据Maxwell方程求解圆导线内部的磁场强度。

图7 圆导线趋肤效应分析案例
Fig.7 Analysis of skin effect for round conductor
根据文献[16],角频率ω=2πf下圆导线内的磁场强度为
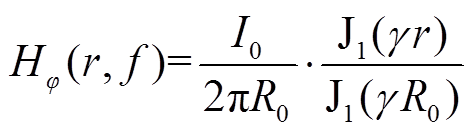 (9)
(9)其中
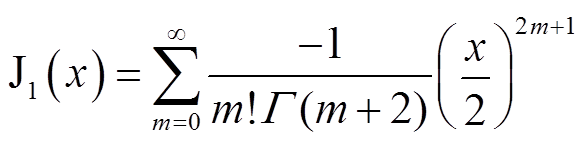 (10)
(10)
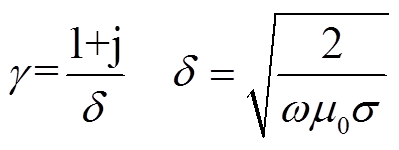 (11)
(11)式中,J1(x)为第一类1阶贝塞尔函数;δ为圆导线渗透率;σ为圆导线电导率;γ为复传播常数。
现已知不同频率下圆导线内磁场强度解析式,可用趋肤效应衰减率ηs来表示由趋肤效应所导致的圆导线磁场能量衰减情况,即
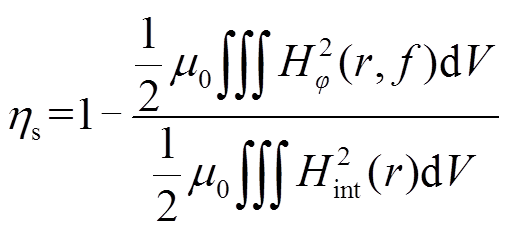 (12)
(12)以直径为1mm的圆导线为例,相应的趋肤效应衰减率曲线如图8所示,其中横坐标为通入的交流电频率。从图8中可知,随着频率的上升,由趋肤效应导致低频下圆导线中衰减的磁场能量也会增加。
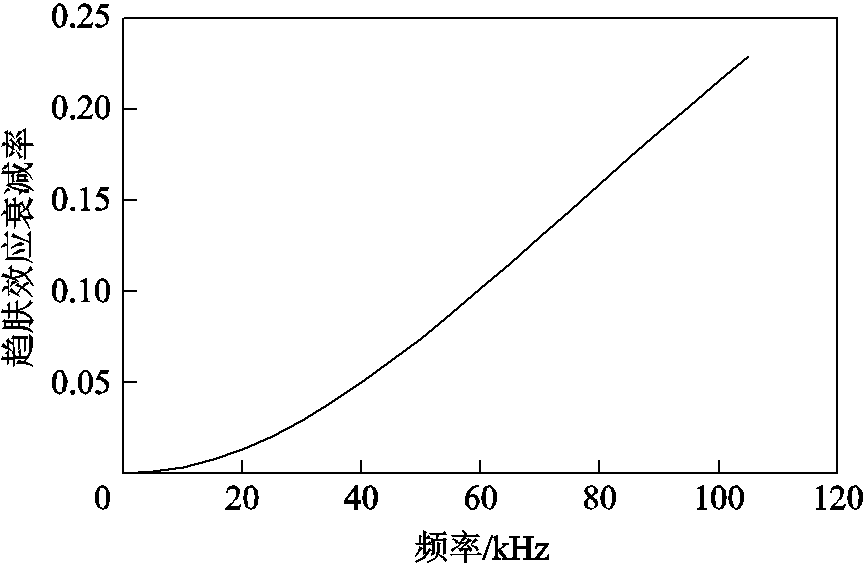
图8 圆导线趋肤效应衰减率曲线
Fig.8 The curve of attenuation rate of skin effect for round conductor
2)邻近效应衰减率
外部规则混合区域施加的中频时变磁场会使得每匝圆导线的电流产生邻近效应,影响每匝圆导线上的外部磁场Hext。为了定量分析该磁场强度的变化情况及磁场能量的衰减量,以图9举例说明。在半径为R0在圆导线上施加幅值为H0、角频率为ω的时变磁场,根据Maxwell方程计算圆导线中的磁场强度。
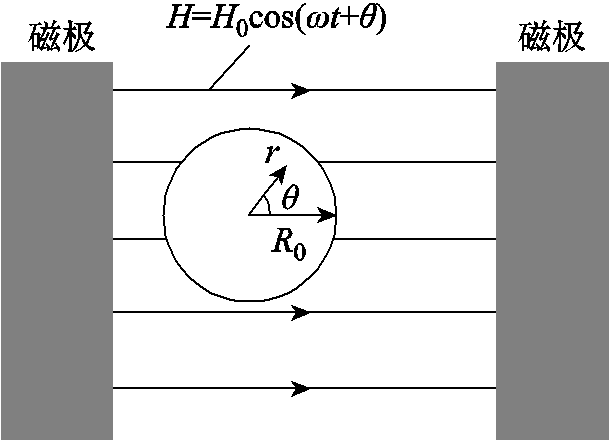
图9 圆导线邻近效应分析案例
Fig.9 Analysis of proximity effect for round conductor
根据文献[17],求出外加角频率ω=2πf磁场下圆导线中的磁场强度为
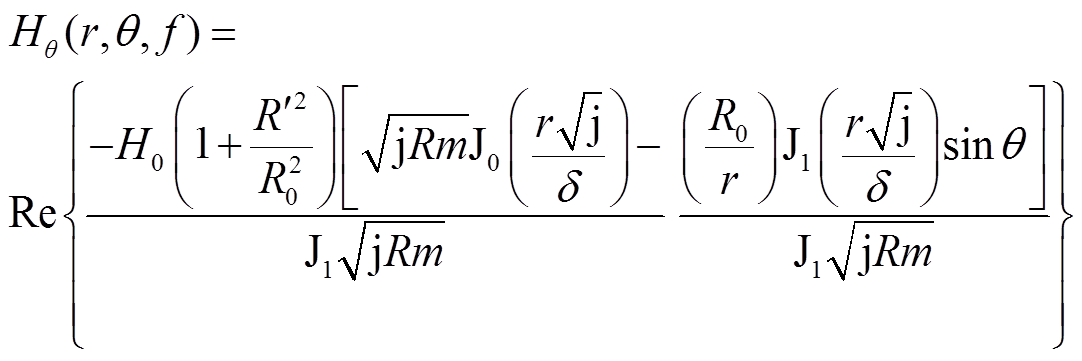 (13)
(13)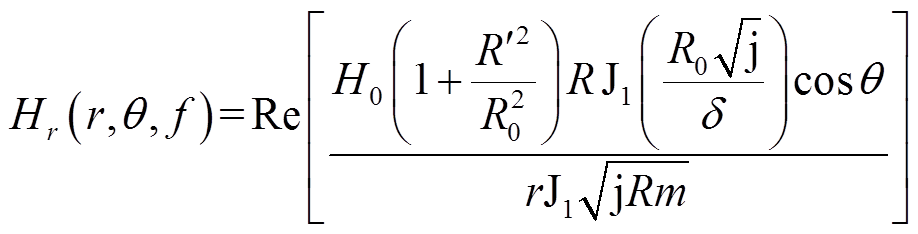 (14)
(14)
式中,J0(x)为第一类0阶贝塞尔函数;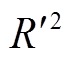 与磁雷诺数Rm分别为
与磁雷诺数Rm分别为
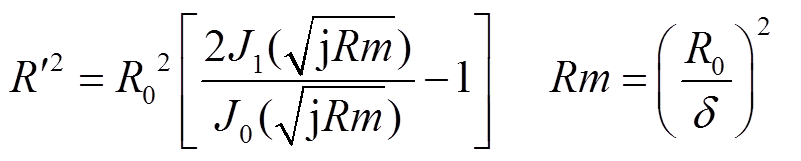 (15)
(15)根据上述磁场强度表达式,可求出受邻近效应影响导致低频下圆导线内衰减的磁场能量,用邻近效应衰减率ηp表示为
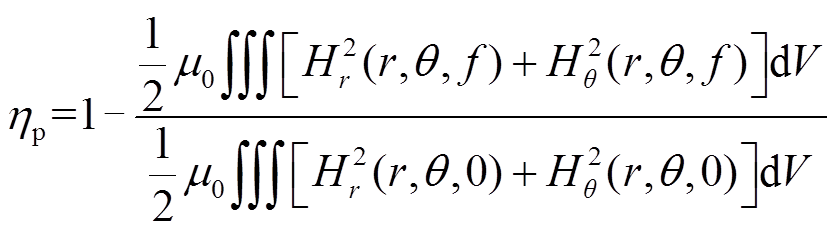 (16)
(16)
以直径1mm的圆导线为例,求出相应的邻近效应衰减率曲线如图10所示,图中横坐标为外加时变磁场的频率。由图10可知,随着频率的上升,邻近效应对圆导线磁场能量的衰减影响会逐渐加剧,然后趋于平缓。
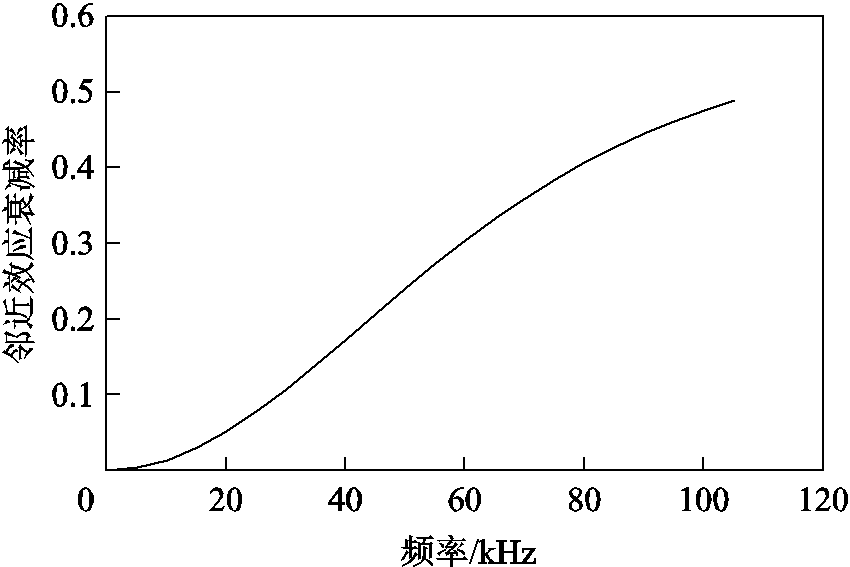
图10 圆导线邻近效应衰减率曲线
Fig.10 The curve of attenuation rate of proximity effect for round conductor
3)频率效应下圆导线区域磁场能量衰减量
趋肤效应和邻近效应分别改变的是圆导线区域中每匝圆导线所受的内部磁场Hint和外部磁场Hext,所以趋肤效应衰减率和邻近效应衰减率仅分别影响Hint和Hext作用下的磁场能量。结合趋肤效应衰减率ηs和式(4)求出趋肤效应导致一匝圆导线衰减的磁场能量为
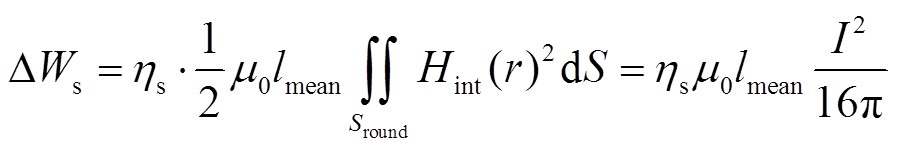 (17)
(17)同理,结合邻近效应衰减率ηp和式(8),求出邻近效应导致一匝圆导线衰减的磁场能量为
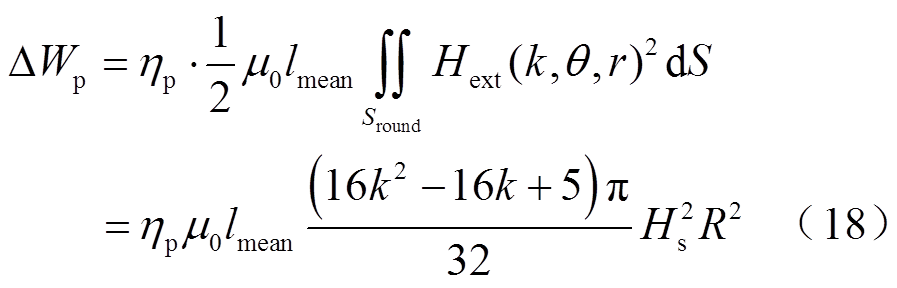
现已知低频下规则混合区域的磁场能量以及中频下每匝圆导线磁场能量的衰减量,结合所提出的解析方法可求出中频下一层规则混合区域的磁场能量,即式(19),其中间接地将不规则空隙区域的磁场能量考虑在内。
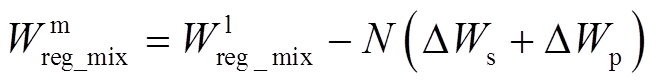 (19)
(19)为简化漏感计算,可假设变压器窗口处一次侧和二次侧的规则混合区域有统一的厚度,一次侧、二次侧和一、二次侧隔离处的规则绝缘区域也有统一的厚度。通过各区域层数累加分别求出中频下变压器窗口处一次侧、二次侧规则混合区域磁场能量Wreg_mix_p/s,以及一次侧、二次侧和一、二次侧隔离处规则绝缘区域的磁场能量Wreg_ins_p/s、Wreg_ins_g分别为
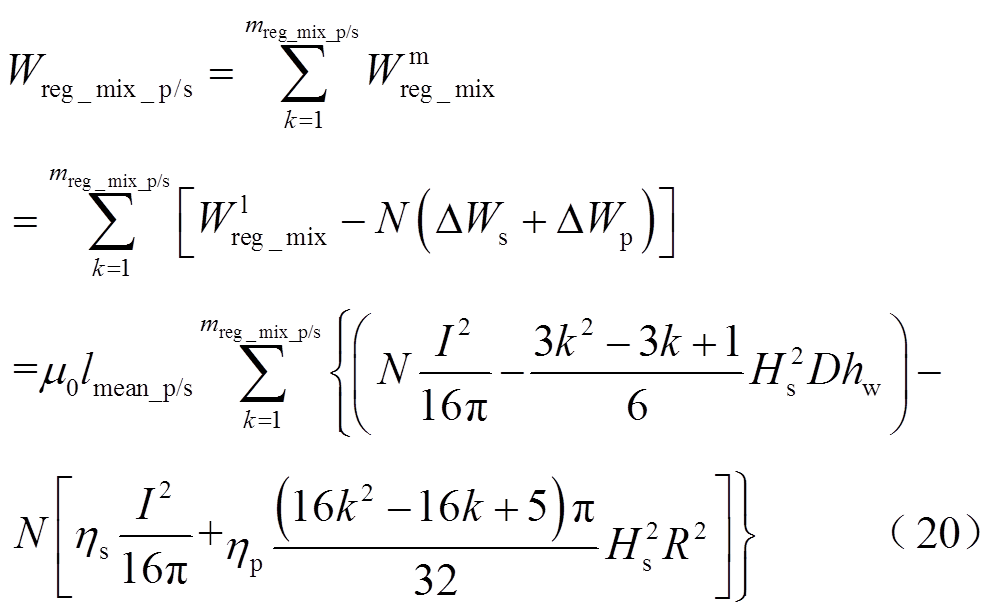
 (21)
(21) (22)
(22)
式中,mreg_mix_p/s分别为一次侧、二次侧规则混合区域的层数;mreg_ins_p/s分别为一次侧、二次侧规则绝缘区域层数,另外令一、二次侧隔离处规则绝缘区域层数为1;lmean_p/s/g分别为一次侧、二次侧及一、二次侧隔离处规则混合区域的平均匝长。分别将式(20)~式(22)代入式(1),求出中频下圆导线变压器的漏感解析式为
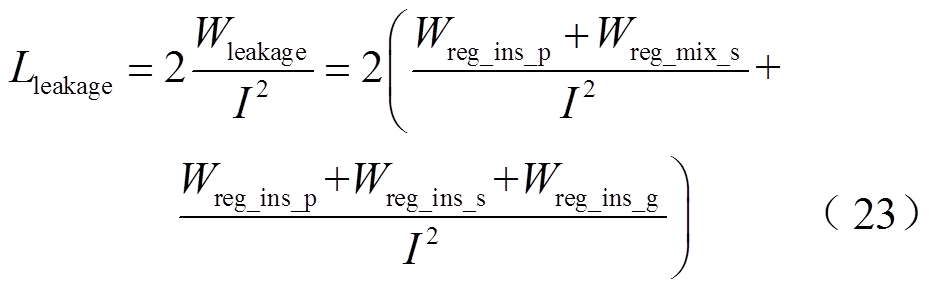
由于受变压器骨架与爬电距离的影响,变压器绕组高度hc会小于变压器窗高hw,此时绕组上、下处会存在非一维分布磁场,导致磁场能量计算出现偏差。为此,可以通过洛氏系数对变压器窗口高度进行修正,以考虑非一维分布磁场对磁场能量计算的影响[18]。修正后的变压器等效绕组高度为heq,即式(24),以替代式(3)、式(20)~式(22)中的hw。
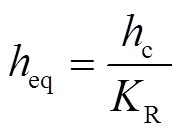 (24)
(24)
其中,KR为洛氏系数,即
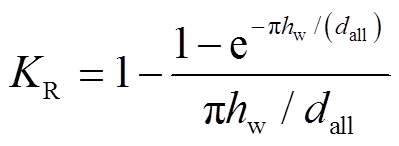 (25)
(25)式中,dall为总绕组宽度,即
 (26)
(26)
已知不规则空隙区域的磁场能量不可忽略,但不规则空隙区域的大小与圆导线孔隙率有密切的联系,基于文献[11]对圆导线变压器的孔隙率重新定义为
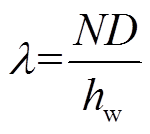 (27)
(27)
其中孔隙率越大,说明在一层规则混合区域中圆导线填充的越密集,不规则空隙区域越小。为了验证提出的解析法在不同孔隙率下对规则混合区域磁场能量计算有足够的精度,基于仿真案例即表1进行了相应的解析和仿真结果对比。其中解析方法分为考虑规则空隙所提出的解析法及忽略不规则空隙的解析法,对比结果如图11所示。
由图11可知,在不同孔隙率下,本文提出的解析法能准确地对规则混合区域的磁场能量进行计算,与仿真的最大相对误差在6%以下,和忽略不规则空隙的解析法相比,具有更高的计算精度。这说明该解析法能在不同孔隙率情形下将不规则空隙区域的磁场能量考虑在内,计算出准确的磁场能量。
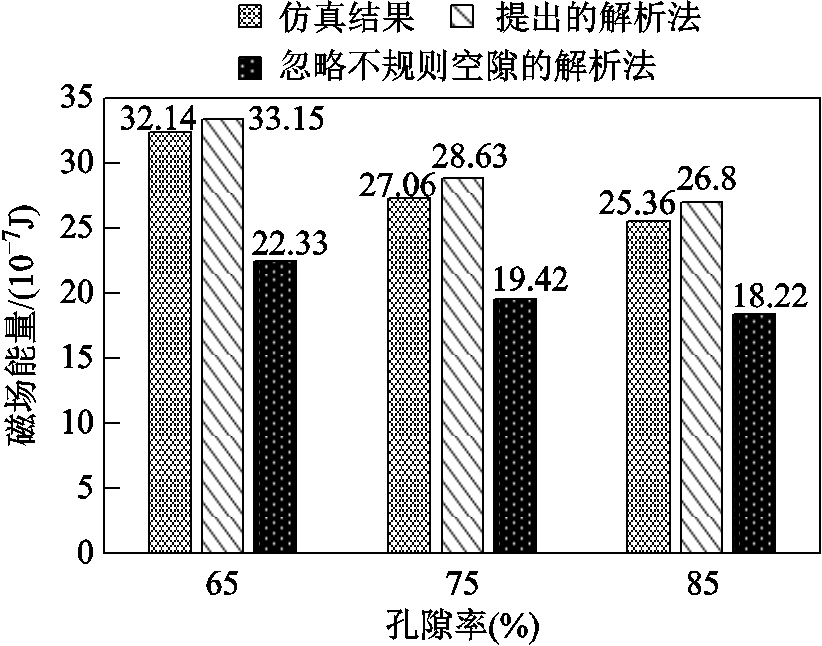
图11 不同孔隙率下规则混合区域磁场能量的仿真与解析计算对比
Fig.11 Comparison between simulation and analytic calculation of magnetic energy in regular mixed area under different porosity
另外,对比不同孔隙率下忽略不规则空隙的解析法与仿真的相对误差可以发现:在孔隙率为85%时,相对误差为28.1%;当孔隙率降为65%时,相对误差增大为30.5%。这说明当孔隙率下降时,一层规则混合区域中的不规则空隙区域会增加,若此时仍用忽略不规则空隙的解析法计算规则混合区域能量,则必然会导致相对误差的增加。
为了验证提出方案的合理性,搭建了两台具有不同孔隙率的变压器样机。两组变压器的具体参数见表2。
表2 变压器样机参数
Tab.2 Parameters of transformer prototypes

参数数值 变压器Ⅰ变压器Ⅱ 磁心RM14Z-12 磁心窗口高度hw/mm21.38 规则混合区域层数mreg_mix_p/s1/1 规则混合区域匝长lmean_p/s/g/mm55.418/61.198/66.979 圆导线直径D/mm0.84 规则绝缘区域厚度dins/mm1 频率f/kHz10~90 孔隙率(%)6371 绕组高度hc/mm13.515.3 一次、二次侧每层匝数Np/s1618
漏感测量设备为Chroma的自动变压器测试系统3250。将变压器二次侧短路后,设定测试系统的测试频率和输入电压,然后将测量夹具夹在变压器一次侧引出的导线上可进行漏感的测量,实验设备如图12所示。
以90kHz下变压器Ⅱ的漏感计算为例,详细介绍所提出解析法的计算过程和对应的实验测量结果。其中磁场能量求解以幅值为1A的一次侧每匝电流为基础,趋肤效应衰减率ηs与邻近效应衰减率ηp分别为0.111 3和0.324 3,求解内容见表3。

图12 实验设备展示
Fig.12 Experimental equipment display
表3 变压器Ⅱ在90kHz下漏感详细解析计算与实验测量结果对比
Tab.3 Comparsion between the detailed analytic calculation and experimental results of leakage inductance under 90kHz in TransformerⅡ

待求量公式计算结果 中频下一次侧规则混合区域能量Wreg_mix_p/J8.68×10-8 中频下二次侧规则混合区域能量Wreg_mix_s/J10.5×10-8 规则绝缘区域能量Wreg_ins_g/J3.23×10-7 总窗口能量Wleakage/J5.14×10-7 漏感解析值Lleakage/μH2.059 漏感实验测量Le/μH2.126
由前面分析可知,表3中,中频下一、二次侧规则混合区域的磁场能量计算不仅将不规则空隙区域的能量间接考虑在内,而且考虑了圆导线频率效应造成的衰减影响。这两者使得提出解析法的计算结果基本上与实验测量结果相吻合。考虑测量结果比提出解析法的计算结果略大,这是因为窗口处磁场的非理想一维特性和测量漏感时一次侧引线所造成的误差。
基于本文提出的解析法,在频率为10~90kHz的条件下解析计算、建模仿真和测量两台圆导线变压器的漏感值,并与忽略空隙解析法和运用面积等效解析法[12]进行对比,结果如图13和图14所示。
由图中可以看出:在不同孔隙率的变压器漏感测量过程中,本文提出的解析法、仿真结果与实验结果三者基本吻合,并且该解析法与实验结果的相对误差维持在4%下。而忽略空隙解析法由于忽略不规则空隙区域的磁场能量,导致计算出的漏感值偏小。另外,由于面积等效解析法是基于导线面积等

图13 不同频率下变压器Ⅰ的漏感实验测量、仿真与各解析法计算结果对比
Fig.13 Comparison between experiment, simulation and various analytic methods for leakage inductance under different frequency in TransformerⅠ
效来求解漏感,会使得等效后绝缘区域的面积过大,导致计算出的漏感值偏大。而本文提出的解析法基于圆导线频率效应,能更合理地分析变压器窗口处磁场的分布,求出准确的窗口处磁场能量和变压器漏感值。
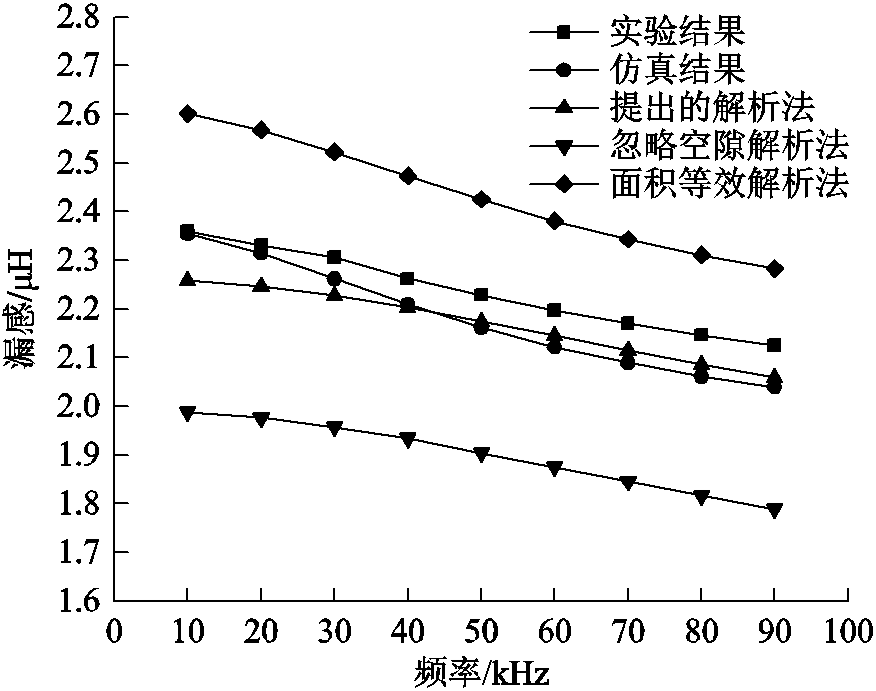
图14 不同频率下变压器Ⅱ的漏感实验测量、仿真与各解析法计算结果对比
Fig.14 Comparison between experiment, simulation and various analytic methods for leakage inductance under different frequency in TransformerⅡ
直流变换器在设计过程中,需要对变压器漏感进行准确的计算和控制。目前对圆导线变压器漏感计算的方法大多基于圆导线面积等效法,但该方法没有考虑圆导线的频率效应,缺乏一定的理论基础,并且该方案使得等效后绝缘区域的面积偏大,导致漏感求解不够准确。基于现有利兹线变压器漏感计算方法,可类比对圆导线变压器漏感计算进行圆导线频率效应分析,并在此基础上考虑了常被忽略的匝间不规则空隙处能量,以提高整体的变压器漏感计算精度。
通过对不同频率下变压器窗口处磁场分布的分析,得出圆导线变压器窗口处不同区域的磁场强度表达式及频率效应带来的影响,最终得出漏感的解析表达式。为了验证提出方案在不同孔隙率下的有效性,进行了相应的实验。实验证明所提出的方法相比现有方法可进一步提高漏感的计算精度,为后面扩展为大功率直流变换器中变压器的设计提供可靠的理论依据。
参考文献
[1] 章治国,刘俊良, 郭强, 等. 基于脉冲频率调制的高增益隔离软开关直流变换器[J]. 电工技术学报, 2019, 34(2): 297-305.
Zhang Zhiguo, Liu Junliang, Guo Qiang, et al. A high step-up isolated soft-switching DC-DC converter with pulse frequency modulation[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 297-305.
[2] 张峰, 谢运祥, 胡炎申, 等. 临界模式混合光伏微型逆变器的特性分析[J]. 电工技术学报, 2020, 35(6): 1290-1302.
Zhang Feng, Xie Yunxiang, Hu Yanshen, et al. Characteristics analysis for a boundary conduction mode hybrid-type photovoltaic micro-inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1290-1302.
[3] 吴琨, 钱挺. 一种高效率高增益的谐振型直流功率变换器[J]. 电力电子技术, 2018, 52(1): 33-35.
Wu Kun, Qian Ting. A novel high-efficiency high step-up resonant DC/DC converter[J]. Power Electronics, 2018, 52(1): 33-35.
[4] 杨玉岗, 吴晗, 关婷婷. 交错并联LLC谐振变换器的磁集成均流特性[J]. 电工技术学报, 2019, 34(12): 2530-2538.
Yang Yugang, Wu Han, Guan Tingting. Magnetic integrated current sharing characteristics of interleaved LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2530-2538.
[5] 李朋, 郝治国, 张保会, 等. 基于有限元法的变压器漏感计算在绕组变形中的应用[J]. 电力自动化设备, 2007, 27(7): 49-53.
Li Peng, Hao Zhiguo, Zhang Baohui, et al. Leakage inductance calculation based on finite element method for power transformer and its application to winding deformation analysis[J]. Electric Power Automation Equipment, 2007, 27(7): 49-53.
[6] Hameed K R. Finite element calculation of leakage reactance in distribution transformer wound core type using energy method[J]. Journal of Engineering and development, 2012, 16(3): 297-320.
[7] Hurley W G, Wilcox D J. Calculation of leakage inductance in transformer windings[J]. IEEE Transactions on Power Electronics, 1994, 9(1): 121-126.
[8] Wilson P R, Wilcock R. Frequency dependent model of leakage inductance for magnetic components[J]. Advanced Electromagntics, 2012, 1(3): 99-106.
[9] Maria K. High-frequency magnetic components [M]. 2nd ed. Chichester: John Wiley & Sons, 2014.
[10] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the Institution of Electrical Engineers, 1966, 113(8): 1387-1394.
[11] 律方成, 郭云翔, 李鹏. 大功率中频变压器漏感计算及其校正方法[J]. 高电压技术, 2016, 42(6): 1702-1707.
Lv Fangcheng, Guo Yunxiang, Li Peng. Calculation and correction method for leakage inductance of high-power medium-frequency transformer[J].High Voltage Engineering, 2016, 42(6): 1702-1707.
[12] Bahmani M A, Thiringer T. Accurate evaluation of leakage inductance in high-frequency transformers using an improved frequencydependent expression[J]. IEEE Transactions on Power Electron, 2015, 30(10): 5738-5745.
[13] Zhang Ke, Chen Wu, Cao Xiaopeng. Accurate calculation and sensitivity analysis of ieakage inductance of high-frequency transformer with Litz wire winding[J]. IEEE Transcations on Power Electronics, 2020, 35(4): 3951-3962.
[14] Ouyang Z, Zhang J, Hurley W G. Calculation of leakage inductance for high-frequency transformers[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5769-5775.
[15] Ferreira J A. Improved analytical modeling of conductive losses in magnetic components[J]. IEEE Transactions on Power Electronics, 1994, 9(1): 127-131.
[16] Lammeraner J, StaflM. Eddy currents[M]. Cleveland, Ohio: CRC Press, 1966.
[17] Perry M, Jones T. Eddy current induction in a solid conducting cylinder with a transverse magnetic field[J]. IEEE Transactions on Magnetics, 1978, 14(4): 227-232.
[18] Marko M, Drazen D. 100 kW, 10 kHz medium-frequency transformer design optimization and experimental verification[J]. IEEE Transactions on Power Electronics, 2019, 32(4): 1696-1708.
Accurate Analytical Calculation of Leakage Inductance of Round Conductor Transformer under the Medium Frequency
Abstract As the critical power component of fly-back DC/DC converter, excessive leakage inductance of the medium-frequency transformer causes the peak voltage on the switching device which can not be ignored. In addition, in resonant DC/DC converter, the leakage inductance needs to be matched with resonant capacitance and frequency, so that the circuit can reach the ideal working state. So it is very important to calculate the leakage inductance of transformer accurately when designing DC/DC converter. The existing numerical methods for calculating leakage inductance cannot be flexibly applied in transformer design, so analytical methods are widely used. At present, most analytical methods for leakage inductance of round conductor transformer under medium frequency are based on the equivalent method. However, after equivalence, the insulation area of transformer window is larger, and the calculation result of leakage inductance is not accurate enough. In addition, there is an analytical method proposed to directly analyze the frequency effect of round conductor under medium frequency, but the irregular gap between turns is ignored, resulting in inaccurate leakage inductance calculation result. Therefore, a more accurate analytical calculation method of leakage inductance is proposed in this paper, which not only analyzes the frequency effect of the round conductor, but also takes the irregular gap between turns into account, so as to improve the analytical calculation accuracy of leakage inductance. Finally, based on the transformer prototypes, the experiment verified the correctness and effectiveness of the proposed method.
Keywords:Round conductor transformer under medium frequency, leakage inductance, frequency effect of round conductor, irregular gap between turns, analytical calculation method
DOI:10.19595/j.cnki.1000-6753.tces.201024
中图分类号:TM432
尹 浩 男,1996年生,硕士研究生,研究方向为变压器设计与寄生参数计算。E-mail:yinhao_hfut@163.com
赖纪东 男,1981年生,博士,副教授,硕士生导师,研究方向为新型电力变换节能技术、分布式发电与微电网技术。E-mail:laijidong@126.com(通信作者)
国家重点研发计划(2018YFB0904100)和国家电网公司科技(SGHB0000KXJS1800685)资助项目。
收稿日期2020-08-11
改稿日期 2021-01-23
(编辑 赫蕾)