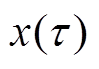 ,在
,在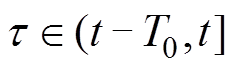 区间可通过具有时变系数的傅里叶级数表示为
区间可通过具有时变系数的傅里叶级数表示为摘要 通常采用窗口快速傅里叶变换(WFFT)对电力电子化配电网中快速变化时域波形进行谐波分析,但WFFT易出现误差从而无法准确获得谐波暂态特性。为此,该文提出一种可用于配电网谐波暂态分析的频变输电线动态相量(DP)模型。采用矢量匹配法对模域频变输电线模型中特征导纳和传播系数进行有理函数拟合,在频变输电线状态空间方程表示基础上建立其DP模型,同时对输电线末端晶闸管控制电抗器(TCR)建立DP模型,将TCR与电网间谐波动态耦合描述为以各阶相量为状态量的解析式。基于Matlab对简单测试系统的DP模型进行计算,能够直接分析系统中各节点电压和支路电流的谐波暂态特性,还可获取瞬时电能质量参数。基于EMTP搭建的仿真系统暂稳态结果验证了DP模型的有效性和准确性。
关键词:谐波分析 频变输电线 矢量匹配法 动态相量 电能质量
随着配电系统电力电子化程度的不断提高,大量具有冲击性、非线性特征的电力电子设备运行时会产生大量谐波,导致电能质量恶化[1-3],甚至会产生谐振。同时当配电系统发生扰动、故障的情况时,电网中会存在丰富的暂态与稳态谐波分量[4-5],这对配电网安全可靠运行及谐波抑制措施提出了新要求。因此对于含电力电子开关的配电系统中谐波暂态特性研究显得尤为重要。
目前的研究方法主要有时域仿真法和频域分析法[6-7]。时域仿真法使用范围广且准确度高,但计算量大且运行时间长,此外在处理快速变化波形的谐波分析时,利用窗口快速傅里叶变换(Windowed Fast Fourier Transform, WFFT)很难做到同步采样和整数周期截断,易造成频谱泄露和栅栏效应[8-9]。频域分析法通常利用谐波潮流计算确定系统中节点电压和支路电流的谐波分量,但谐波潮流计算是以稳态建模为基础的,结果不具有瞬时特性[10-11]。为准确获取谐波暂态特性,有必要考虑结合时域与频域对电力电子器件和输电线建立动态模型。
基于状态空间平均理论的动态相量(Dynamic Phasor, DP)法可比较准确地反映系统动态特性,且该方法采用状态变量对应的时变傅里叶级数具有更宽的频带[12]。目前关于动态相量模型研究多集中在逆变型分布式电源微电网[13]、柔性交流输电[14]、高压直流输电[15-16]等含电力电子器件系统建模仿真,或将动态相量原理应用于谐波测量单元提高测量精度[17]。上述文献研究可以较好地反映电力电子器件在较宽频谱下响应特性,但建模主要集中在源侧,对于网侧输电线建模研究较少,频变输电线具有分布特性及频率相关性,从而呈现出高度非线性,使其建模难度增加。文献[18-20]对输电线的动态相量模型展开研究:文献[18]基于动态相量法对三相分布参数线路建模,为大系统快速仿真提供新方法,但模型仅考虑参数为定值情况;文献[19]对集中参数交流线路进行动态相量建模,实现对短路电流的高精度计算,但该模型不能够分析线路的波动过程;文献[20]提出基于行波法的半波长输电线路动态相量模型,但其研究场景仍是工频分量下输电线的仿真分析。以上输电线动态相量模型为理论研究含输电线系统暂稳态特性指明了方向,但没有考虑输电线路参数的频变特性,无法适用于电力电子化配电系统的谐波暂态分析。
利用时域状态方程描述频变输电线的波动过程是其动态相量建模的前提,目前能准确分析频变输电线波动过程是频率相关的分布参数模型[21],但计算过程复杂且很难处理与频率有关的复函数。文献[22]提出了矢量匹配概念,通过对线路参数进行有理函数拟合,提高了计算效率。在此基础上,文献[23]将输电线端口的电压电流各变量间解析关系线性化,分析输电线的端口电流动态响应特性,该文献尽管讨论内容未涉及含输电线的电力系统中谐波暂稳态分析,但为输电线动态建模研究提供了思路。因此,本文提出一种频变输电线动态相量建模方法,采用矢量匹配法将频变输电线的复频域模型转换为状态空间形式,在频变输电线状态空间方程基础上建立其动态相量模型,同时对晶闸管控制电抗器(Thyristor Controlled Reactor, TCR)也建立动态相量模型,分析谐波电流在输电线路中传播的谐振放大机理并获取频变输电线的谐振放大频率点。通过Matlab对简单测试系统的动态相量模型进行计算,分析系统中谐波电压和电流的暂稳态特性并应用于瞬时电能质量参数求解,基于EMTP时域仿真验证所提出模型的有效性和准确性。
动态相量法是选取宽度为T0的时间窗内主要傅里叶级数建立动态模型。对于时域中以T0为周期的函数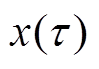 ,在
,在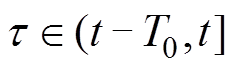 区间可通过具有时变系数的傅里叶级数表示为
区间可通过具有时变系数的傅里叶级数表示为
 (1)
(1)式中,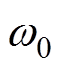 为基波角频率,
为基波角频率,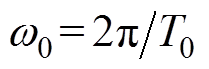 ;
;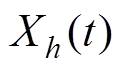 为h次时变傅里叶系数,在动态相量法中定义为“相”。第h阶动态相量为
为h次时变傅里叶系数,在动态相量法中定义为“相”。第h阶动态相量为
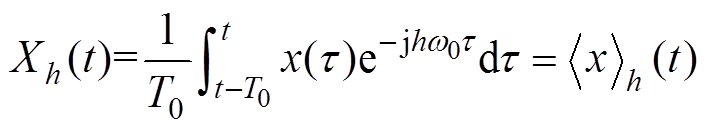 (2)
(2)
式中, 表示第h阶动态相量。
表示第h阶动态相量。
动态相量运算具备如下两个重要特性:
1)h阶相量微分特性。
 (3)
(3)2)卷积特性,两个时域变量x(t)和y(t)乘积的h阶相量为每个变量对应的相量离散卷积,则
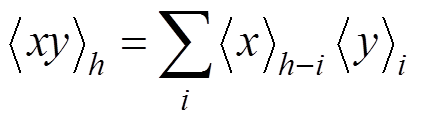 (4)
(4)
将动态相量法应用于含电力电子开关的配电系统谐波暂态分析时,可选取系统状态变量对应的时变傅里叶级数中重要的项,在时域模型基础上建立以各次傅里叶系数为变量的动态相量模型。
矢量匹配法可快速有效地对频域响应曲线f(s)进行有理函数逼近,获取有理函数的零极点。假设f(s)用有理函数近似表示为
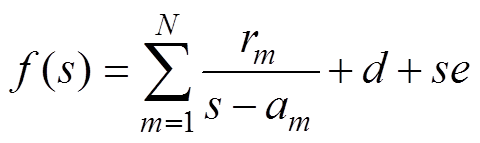 (5)
(5)式中,留数rm和极点am为实数或共轭复数对;d、e为实数,且视情况选用。
矢量匹配法利用线性约束最小二乘法来确定f(s)的极点,引入辅助函数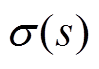 ,得到
,得到
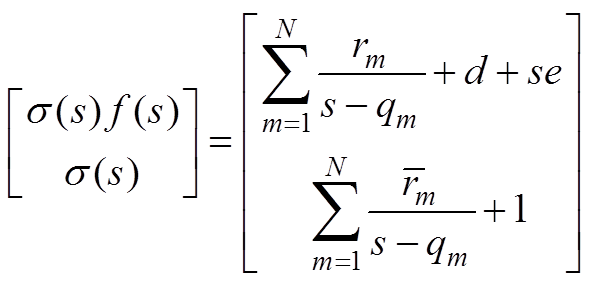 (6)
(6)式中,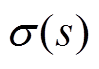 和
和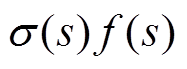 具有相同的极点qm。通过设定初始极点
具有相同的极点qm。通过设定初始极点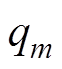 ,给s赋予不同的频率采样数值,形成一组关于
,给s赋予不同的频率采样数值,形成一组关于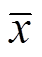 参数
参数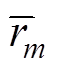 、
、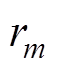 、d、e为未知数的线性方程。将
、d、e为未知数的线性方程。将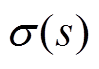 的零点作为f(s)的极点进行迭代计算,直到误差满足要求为止。
的零点作为f(s)的极点进行迭代计算,直到误差满足要求为止。
文献[22]提出了改进的矢量匹配法(Modified Vector Fitting, MVF),提高了收敛性且降低了初始极点对拟合精度的影响。本文采用MVF对输电线特征导纳和传播系数进行有理函数拟合。
三相频变输电线的数学模型建立在求解电报方程的基础上,利用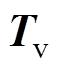 、
、 变换矩阵将相域耦合方程组转换为模域解耦方程组,即
变换矩阵将相域耦合方程组转换为模域解耦方程组,即
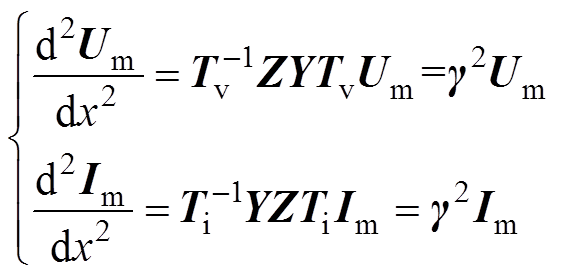 (7)
(7)式中,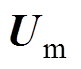 、
、 为电压、电流的模量;
为电压、电流的模量;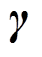 为传播系数矩阵,且为对角阵;Z、Y分别为单位长度阻抗和导纳矩阵,其中,
为传播系数矩阵,且为对角阵;Z、Y分别为单位长度阻抗和导纳矩阵,其中,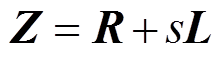 ,
,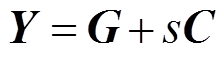 ,
, 、
、 分别为单位长度电阻、电感矩阵,C、G分别为单位长度电容、电导矩阵。由于趋肤效应,实际线路参数
分别为单位长度电阻、电感矩阵,C、G分别为单位长度电容、电导矩阵。由于趋肤效应,实际线路参数 、
、 与频率有关,而在电磁暂态计算频率范围内,可认为参数C、G为常数,G数值很小可忽略不计。
与频率有关,而在电磁暂态计算频率范围内,可认为参数C、G为常数,G数值很小可忽略不计。
输电线相域模型中特征导纳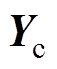 和传播系数矩阵
和传播系数矩阵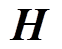 的表达式[24]为
的表达式[24]为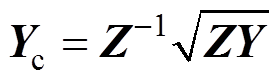 和
和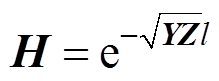 ,l为线路长度。将式(7)求解得到的电压电流模量进行相模反变换后代入电报方程,可推导得
,l为线路长度。将式(7)求解得到的电压电流模量进行相模反变换后代入电报方程,可推导得
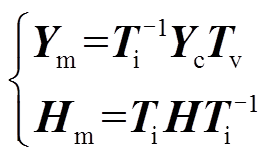 (8)
(8)
式中,Ym和Hm分别为模域特征导纳矩阵和传播系数矩阵。如果三相输电线完全换相,则模域模型中每个方程都可看作单相输电线路以简化求解过程,下文中Ym和Hm分别表示单相输电线的特征导纳和传播系数。
图1为基于行波法的输电线示意图,下标f、b表示输电线的前向行波和反向行波,uk、ik为端口k的电压、电流,um、im为端口m的电压、电流。
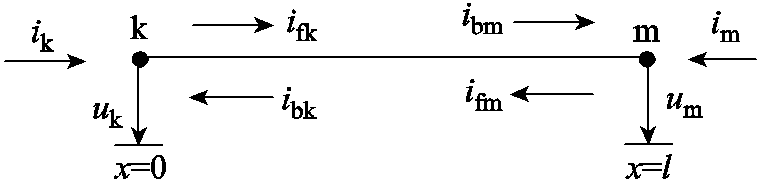
图1 基于行波法的输电线示意图
Fig.1 Schematic diagram of transmission line based on traveling wave method
结合式(7)的解,端口k、m的频域行波方程为
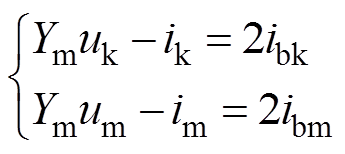 (9)
(9)输电线端口k、m的电压电流及传播系数Hm间关系在频域中可表示为
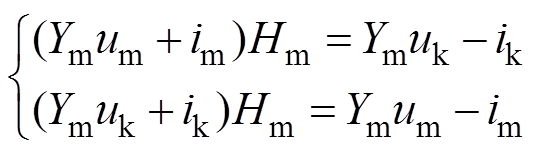 (10)
(10)
式中,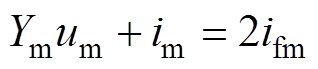 ,
,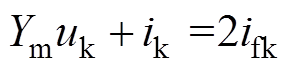 ,则
,则
 (11)
(11)
式(9)~式(11)为基于行波法的输电线端口电压、电流关系式,其中Ym和Hm都与频率有关,采用矢量匹配法对Ym和Hm做有理函数近似并转换为状态空间方程。假设u为输入量,y为输出量,G(s)为矢量拟合的n阶矩阵传递函数,得
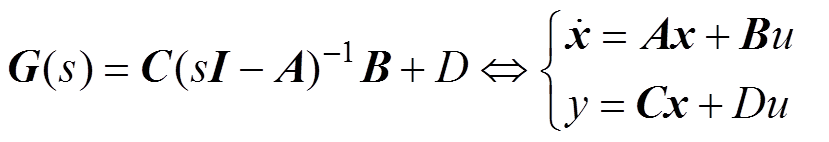 (12)
(12)式中,A为拟合的极点组成的对角阵;B为元素均为1的列向量;C为留数组成的行向量;D为常数。
考虑输电线的趋肤效应影响时,线路参数将会随频率发生变化。随着频率的增加,导体中的电流趋向它的表面从而减小导体的有效截面积,此时沿线路的等效串联电阻(Equivalent Series Resistance,ESR)将会占主导[24],因此可利用ESR随频率的变化来描述线路参数的频变特性,ESR的计算公式见文献[24]。三相输电线的型号为LGJ—185,单位参数为电感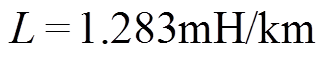 、电容
、电容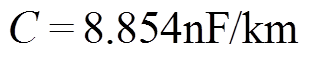 ,等效串联电阻在频率为20Hz时
,等效串联电阻在频率为20Hz时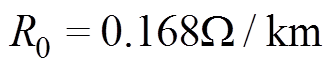 ,线路长度l=100km。采用MVF对频变输电线特征导纳Ym和传播系数Hm在10Hz~10kHz频率范围内数据进行拟合,设定Hm、Ym拟合阶数分别为14和6阶,Hm和Ym的拟合曲线如图2所示,需要注意的是Ym拟合的有理函数中D不能等于零,以便于后续的编程求解。
,线路长度l=100km。采用MVF对频变输电线特征导纳Ym和传播系数Hm在10Hz~10kHz频率范围内数据进行拟合,设定Hm、Ym拟合阶数分别为14和6阶,Hm和Ym的拟合曲线如图2所示,需要注意的是Ym拟合的有理函数中D不能等于零,以便于后续的编程求解。
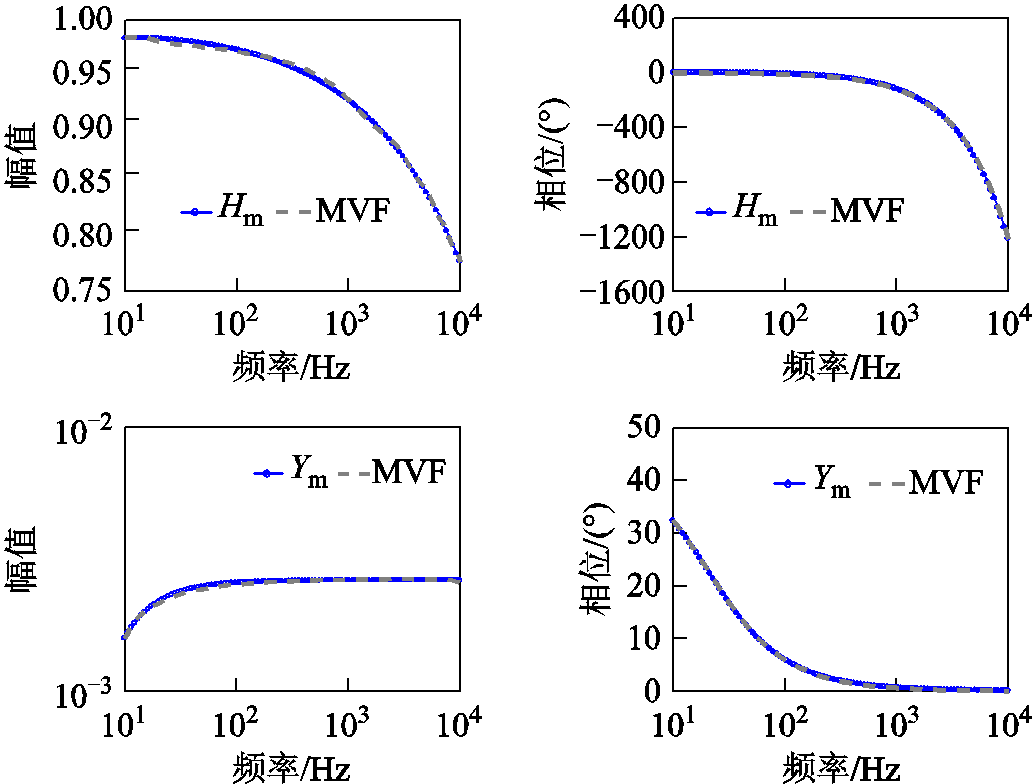
图2 Hm和Ym的拟合曲线
Fig.2 Fitting curves of Hm and Ym
根据式(9)得频域k、m端口电压电流间关系式,利用矢量匹配法对特征导纳Ym进行有理函数拟合,结合式(12),则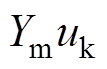 和
和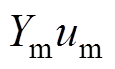 可转换为传递函数矩阵,得
可转换为传递函数矩阵,得
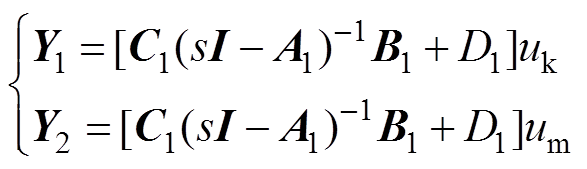 (13)
(13)式中,对角阵A1由拟合的6个极点组成;B1为元素均为1的列向量;C1为留数组成的行向量;D1为常数。将式(13)转换为状态空间方程,代入式(9),得
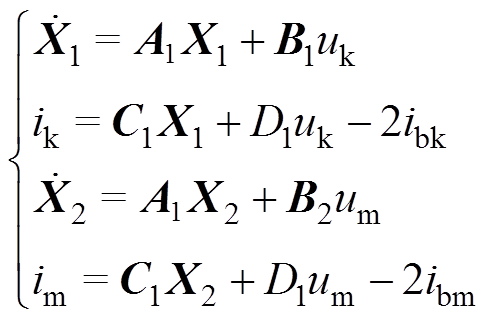 (14)
(14)
利用动态相量微分特性,其动态相量表达式为
 (15)
(15)式中,N1为元素为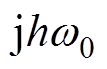 的6阶对角矩阵。
的6阶对角矩阵。
根据式(11)推导频域端口k、m的电流前向行波和反向行波间关系式,利用矢量匹配法对传播系数Hm进行有理函数拟合,结合式(12),得
 (16)
(16)式中,对角阵A2由拟合的14个极点组成;B2为元素均为1的列向量;C2为留数组成的行向量;D2为常数。将式(16)转换为状态空间方程,得
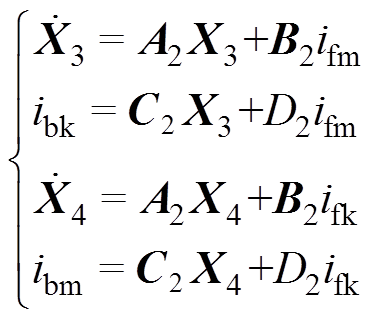 (17)
(17)
利用动态相量微分特性,其动态相量表达式为
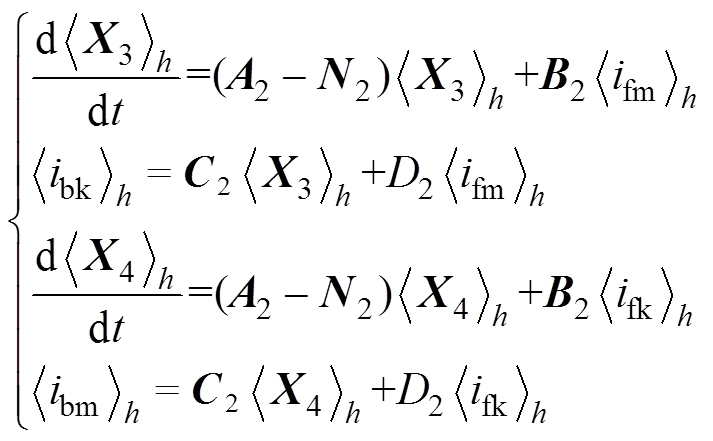 (18)
(18)式中,N2为元素为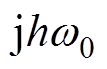 的14阶对角矩阵。
的14阶对角矩阵。
输电线端口k、m的电流与行波电流间关系式可表示为
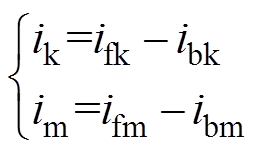 (19)
(19)
式(19)的动态相量表达式为
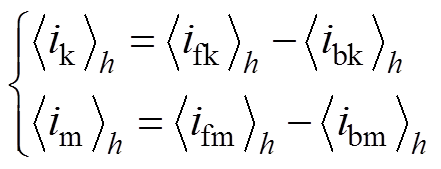 (20)
(20)由式(15)、式(18)及式(20)组成的频变输电线动态相量模型中h的取值为-H~H,H为截取谐波次数。虽然该动态相量模型阶数较高,但DP模型可采用较大的仿真步长和截取主导谐波次数来减少模型阶数,故该模型仍具有较高的仿真效率。
TCR在无功功率调节中具有瞬时响应速度,但从电能质量方面考虑,TCR运行过程中将大量谐波电流注入配电系统,导致电能质量恶化。图3为三相TCR电路图,三相TCR通常按三角形联结,3及3的倍数次谐波经三相电感环流而不注入配电系统中。

图3 三相TCR电路图
Fig.3 Three phase TCR circuit diagram
三相对称情况下,以AB相为例,BC和CA相同理,AB相中电抗器为L,其等效电阻为RL,以电抗器电流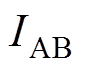 为状态变量,可得时域微分方程为
为状态变量,可得时域微分方程为
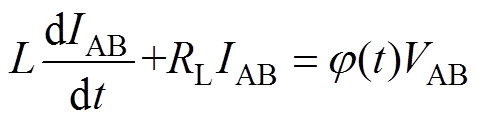 (21)
(21)式中,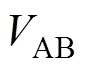 为AB相电抗器的端电压;
为AB相电抗器的端电压;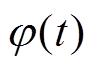 为开关函数,其傅里叶级数展开式为
为开关函数,其傅里叶级数展开式为
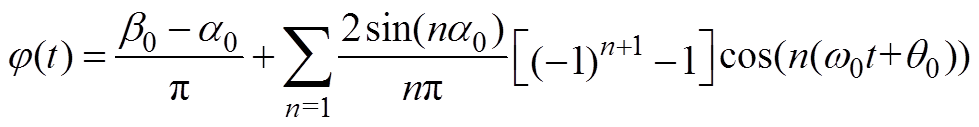 (22)
(22)
式中,n为整数;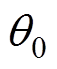 为电压VAB的初始相角;触发延迟角
为电压VAB的初始相角;触发延迟角 ;关断角
;关断角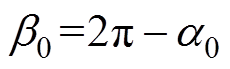 。
。
根据动态相量微分特性和卷积特性,式(21)的动态相量表达式为
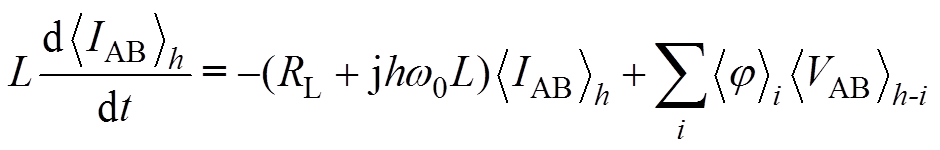 (23)
(23)三相TCR的AB相电流方程为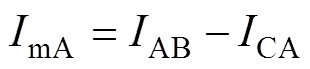 ,则其动态相量表达式为
,则其动态相量表达式为
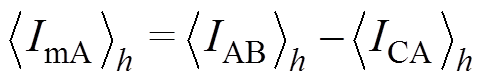 (24)
(24)
可将式(23)及式(24)扩展为三相TCR的动态相量模型,其中式(23)中开关函数和端电压乘积的卷积特性会导致TCR产生的各次谐波间存在耦合,故模型需要考虑足够的谐波次数来确保精确性。此外当TCR端口电压发生较大畸变时,实际关断角 会发生变化,可能不等于固定关断角
会发生变化,可能不等于固定关断角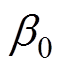 ,因此有必要考虑关断角
,因此有必要考虑关断角 的变化对TCR电抗器电流的影响,具体参考文献[25]。
的变化对TCR电抗器电流的影响,具体参考文献[25]。
当配电系统中谐波电流频率等于输电线的串并联谐振频率时,会导致谐波电流在输电线路中传播发生谐振放大现象。此时,输电线末端放大的谐波电压与谐波电流存在交互作用,加剧输电线末端谐波电流的畸变。
图4为电压源、输电线及TCR组成的配电系统结构。TCR等效为谐波电流源It并联导纳Yt,电源等效为电压源Vs串联阻抗Zg。图4a为含谐波源的输电线模型。根据末端谐波源特性分析,谐波导纳仅衰减末端谐波源,不影响谐波电流在输电线路中传播特性。故谐波导纳所在支路可视为开路,同样电压源对谐波电流可视为短路,图4b为含谐波源的输电线简化模型。
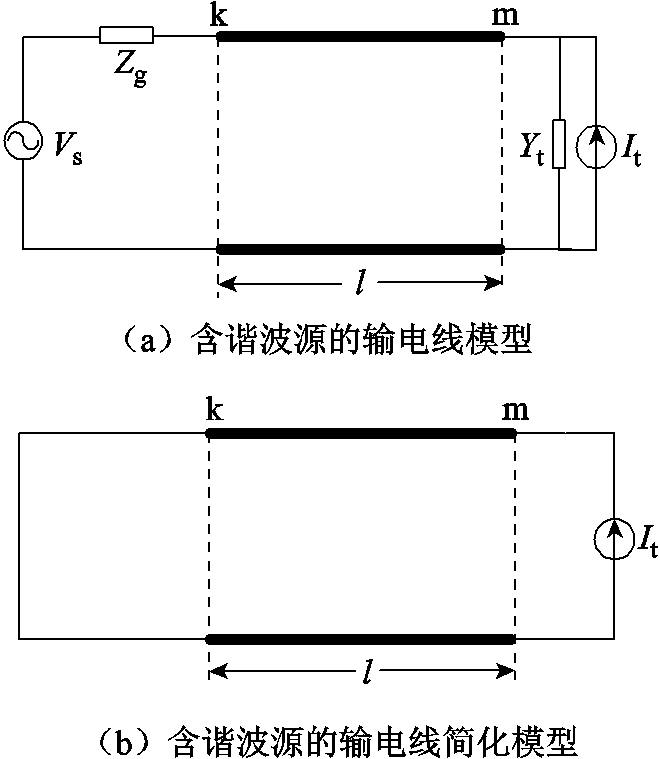
图4 配电系统结构
Fig.4 Distribution system structure diagram
输电线端口m、k间电压电流的关系式为
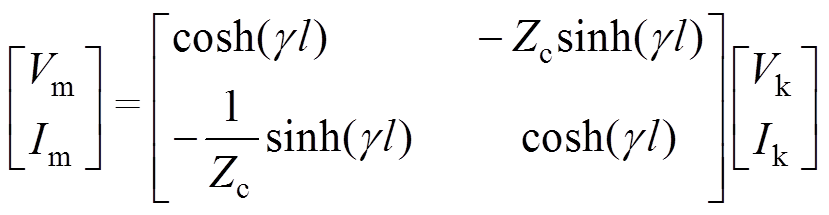 (25)
(25)式中,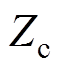 为特征阻抗。结合图4b,由式(25)可得输电线的首末端电流放大系数
为特征阻抗。结合图4b,由式(25)可得输电线的首末端电流放大系数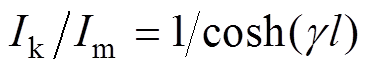 。
。
采用上节输电线路参数,利用MVF对放大系数在100Hz~10kHz的频率范围进行拟合分析,图5为频变输电线首末端电流放大系数拟合曲线。
由MVF拟合的极点值虚部为谐波谐振放大角频率值,实部则表示该频率点瞬态分量包络线衰减系数。由图5可看出,谐振放大频率增大而对应幅值却逐渐减小,这是由于线路参数的频变特性,谐振放大频率点主要集中在742Hz、2227Hz、 3 713Hz等,同时这些间谐波也是输电线路高频振荡频率点。
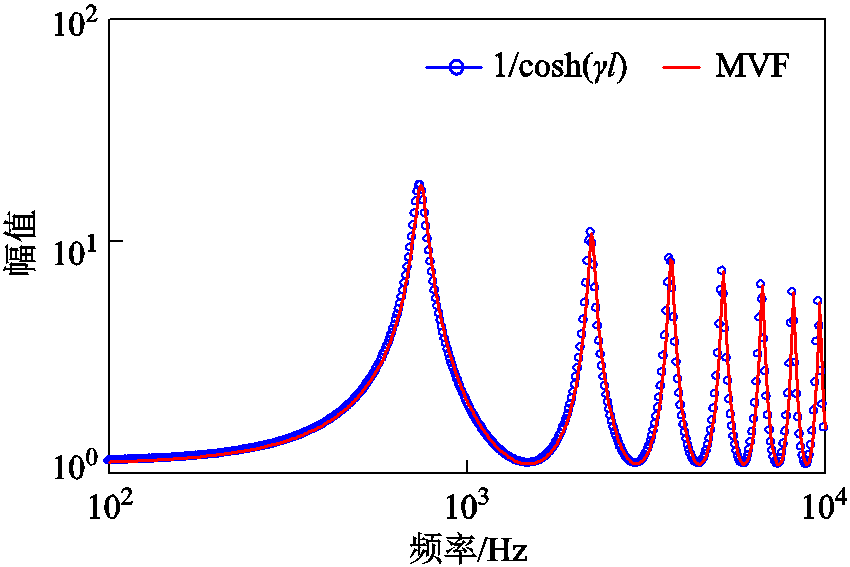
图5 放大系数拟合曲线
Fig.5 Fitting curve of amplification coefficient
在EMTP软件中搭建三相频变输电线接TCR的简单测试系统仿真,如图4a所示。在Matlab中编写以各次谐波为状态量的微分-代数方程组,采用ode15s解法计算DP模型结果。通过EMTP时域仿真与该模型计算结果对比来验证DP模型的准确性并分析输电线末端电压和电流谐波瞬态特性。
频变输电线采用上文输电线路参数,输电线末端TCR中电抗器L为538.7mH,RL为1Ω,触发延迟角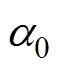 =150°。输电线始端的三相电源幅值为1kV,阻抗Zg=1mΩ,DP模型的计算程序中截取谐波次数H取45次,两者仿真步长均设定为10ms。
=150°。输电线始端的三相电源幅值为1kV,阻抗Zg=1mΩ,DP模型的计算程序中截取谐波次数H取45次,两者仿真步长均设定为10ms。
假设DP模型和EMTP仿真的初始条件都为零,将DP模型计算的各次随时间变化谐波瞬时值相加重构时域波形与EMTP仿真波形作比较。图6为输电线末端三相电压和电流瞬态波形的EMTP仿真和DP模型对比图。从图6可看出,EMTP仿真和DP模型计算的电压电流波形基本吻合,不同之处在于DP模型计算的电压电流波形纹波稍大,这是由于截取谐波次数有限而表现出吉布斯效应,尤其在晶闸管关断电抗器电流降为零时表现明显。通过两者结果比较,DP模型可准确地反映系统的高频振荡,并在一定程度上分析输电线路的波动过程。
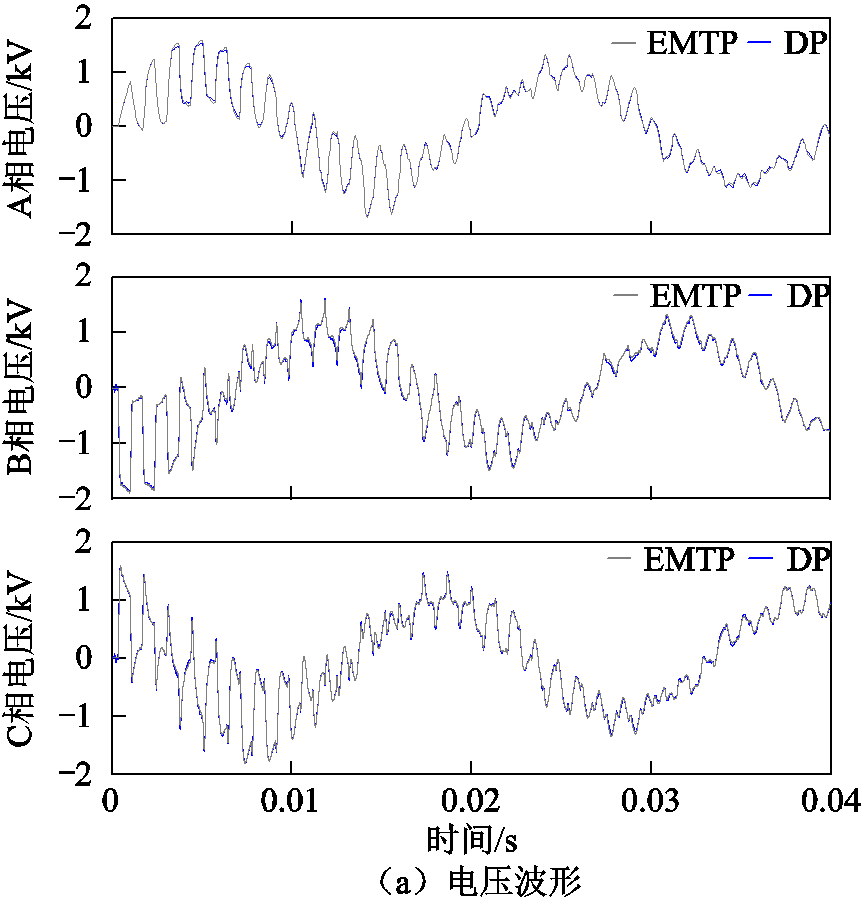
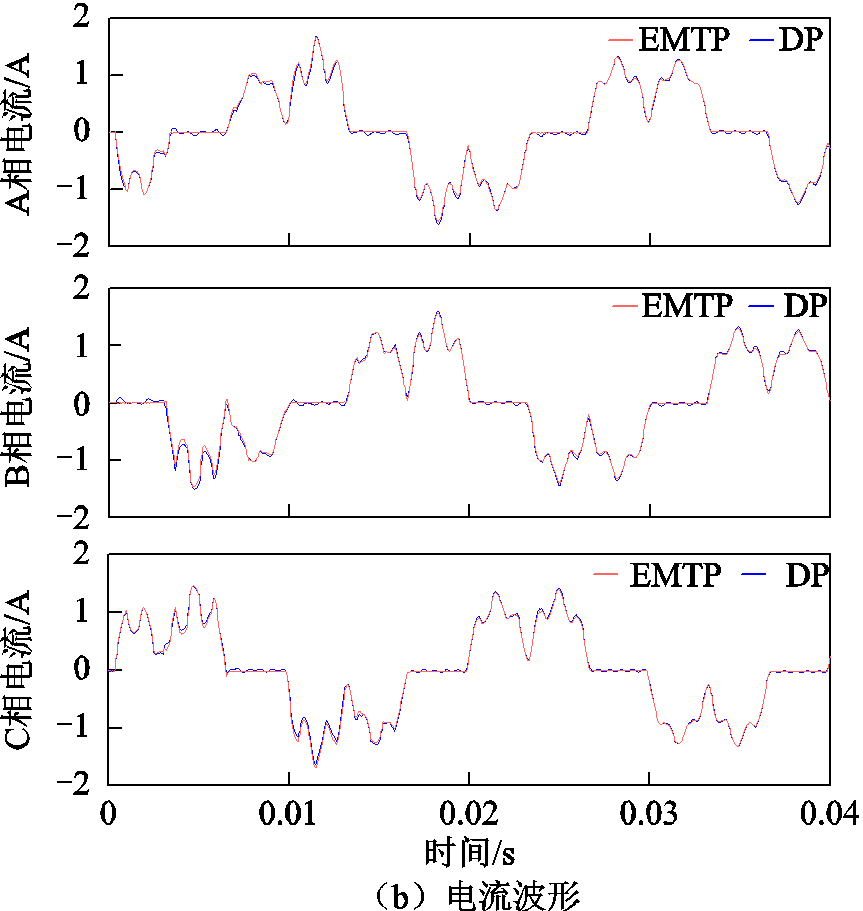
图6 三相电压和电流波形
Fig.6 Three phase voltage and current waveforms
令DP模型中状态变量的导数为零,可实现系统稳态值的直接求解,这将有利于系统稳态初始条件计算,减少时域仿真获取稳态值的时间。求解DP模型构成的代数方程组可获得系统各节点稳态电压谐波值,同时采用FFT程序对EMTP仿真稳态电压波形进行谐波分析。图7为输电线末端三相稳态电压谐波的EMTP仿真和DP模型对比图,为更好地凸显各次谐波量,将基波进行缩放。从图7可看出,EMTP仿真和DP模型的稳态电压谐波含量基本相同,较大差异是15次谐波在EMTP仿真中存在而DP模型中极小,这种差异在于DP模型中晶闸管开关函数的线性化,在谐波相位图中可观察到存在差异的是谐波含量极小的3的倍数次谐波。图中还可观察到13、17次谐波大于11次谐波,这是由于13、17次谐波在输电线路中传播被放大导致。
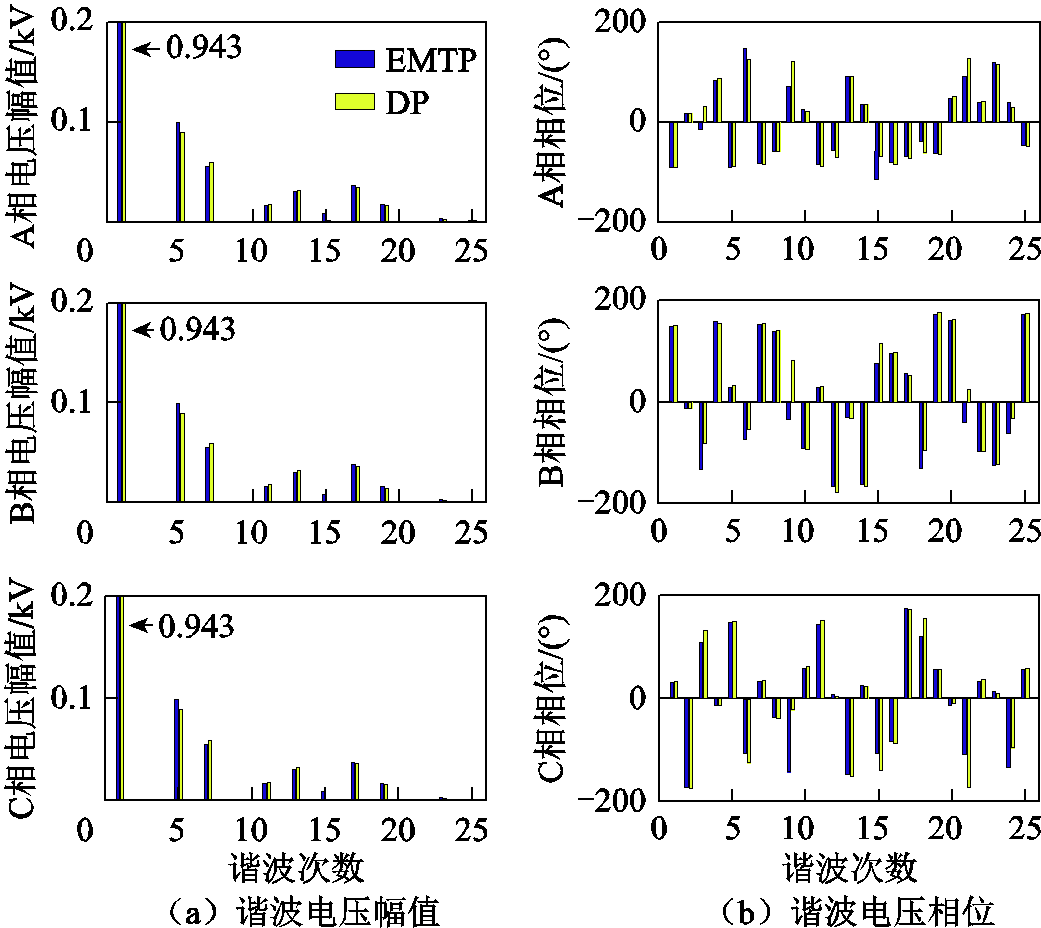
图7 三相稳态电压谐波柱状图
Fig.7 Three phase steady-state voltage harmonic histogram
系统处于稳态时在0.02s给电源注入10%的2次谐波用来模拟网侧背景谐波,图8为输电线末端A、B相电压瞬态波形的EMTP仿真和DP模型对比图。从图8可看出,DP模型中A、B相电压瞬时值与EMTP仿真结果基本一致,虽然在个别时间点上电压瞬时值有一定差别,其原因是系统谐波畸变严重导致TCR的开关函数关断时刻有偏差,但总体上可准确地反映电源注入2次谐波后各相电压阶跃响应过程。同样系统处于稳态时在0.02s将A相通过小电阻接地,模拟单相接地故障,持续0.04s后,在0.06s接地故障被清除并将电源电压幅值增加一倍。图9为输电线末端A相电压瞬态波形EMTP仿真和DP模型对比图。为了更好地对比,将时间压缩到0.06s,其中局部放大图为接地故障后的A相电压瞬态波形。从图9可看出,当A相出现接地故障时,DP模型可以很好地和EMTP仿真结果相吻合,能够用来分析三相频变输电线在故障后的电磁暂态过程。以上对比结果表明DP模型可有效描述扰动及故障下的系统瞬态特性。
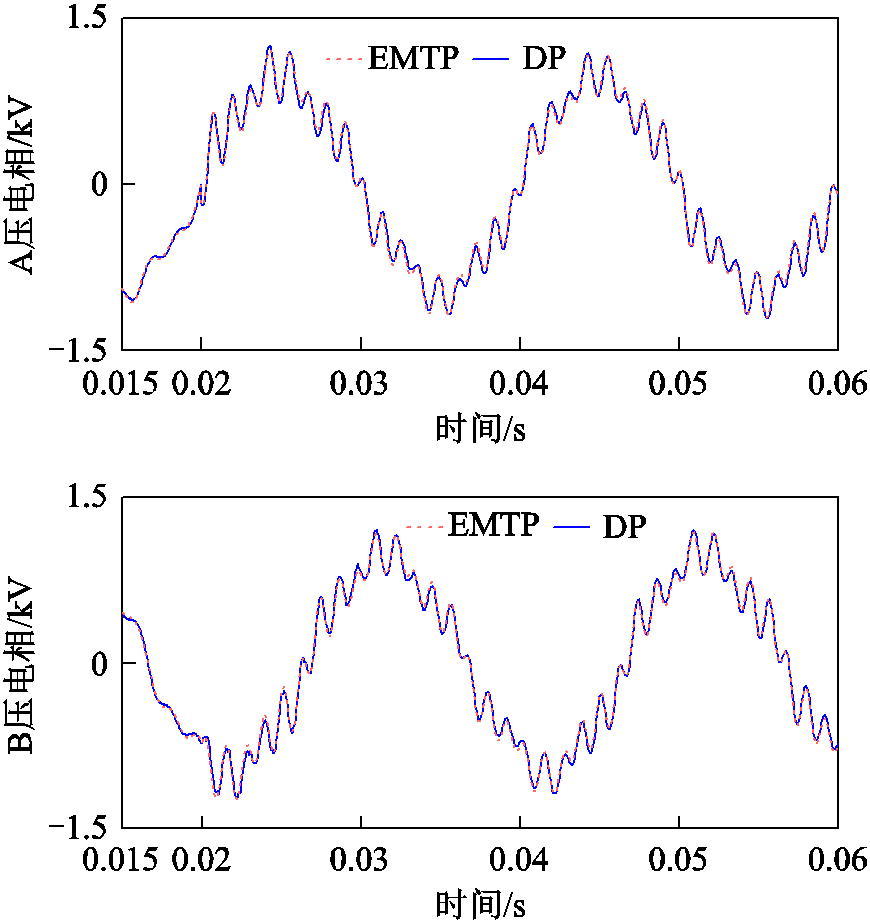
图8 注入2次谐波的A、B相电压波形
Fig.8 Phases A、B voltage waveform injected with the second harmonic

图9 接地故障后A相电压波形
Fig.9 Phase A voltage waveform after ground fault
通过对简单测试系统DP模型求解,能够直接获得系统中电压电流的各次谐波瞬态波形,其中DP模型计算的偶次谐波及3和3的倍数次谐波基本为零,通常可以忽略。图10为图6中A相电压电流的基频、5次及7次谐波瞬态波形,由于篇幅有限,选取前9次谐波中较大量。从图10可看出,电压电流的基频、5次及7次谐波在前0.04s都处于快速变化,但各次谐波波形变化趋势都是逐渐达到稳态。其中,电流谐波波形的幅值变化与其对应频次相符合,而电压谐波波形则处于快速振荡,其原因在于输电线路的高频振荡,可观察到基频电压波形的包络线呈现近似二次振荡。系统稳态下在0.02s给电源注入10%的2次谐波,图11为输电线末端A相电压电流谐波瞬态波形,选取前9次谐波中较大量。从图11可看出,基频、5次及7次谐波量基本不变,而2次、4次谐波量变化较大,表明DP模型中2次谐波电压在开关函数调制下仅会导致输电线末端的电压电流偶次谐波发生变化,其偶次谐波暂态特性分析与图10相同。
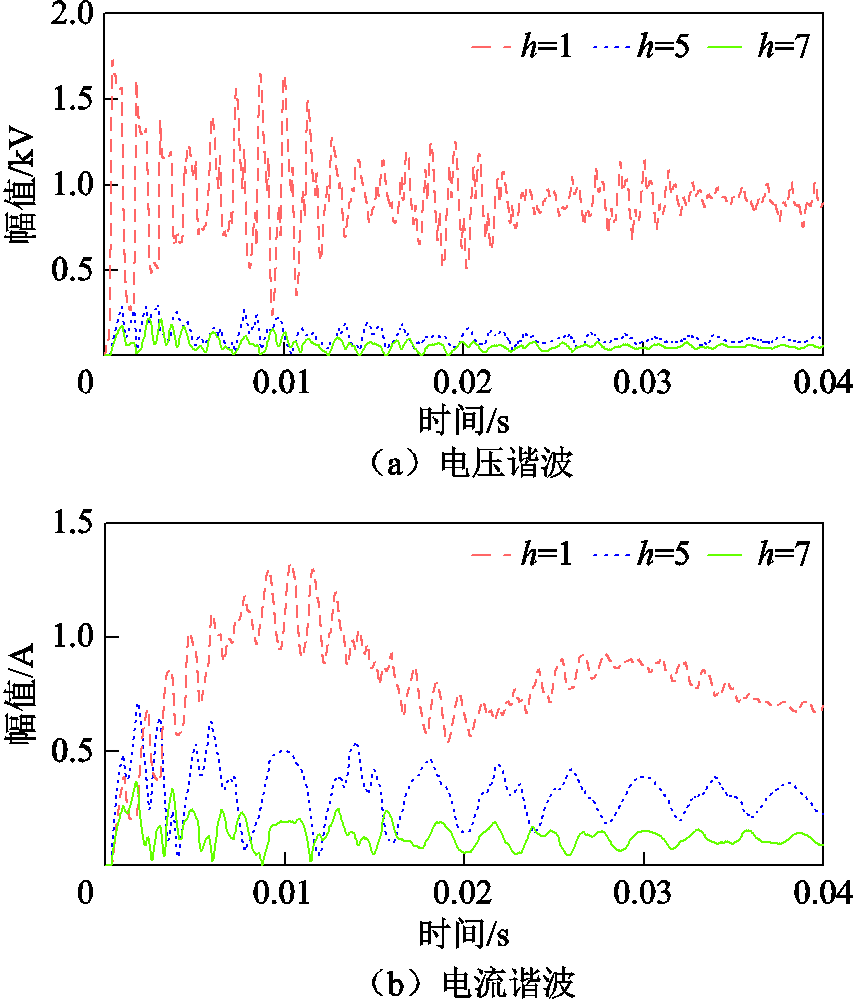
图10 A相电压和电流谐波
Fig.10 Phase A voltage and current harmonic
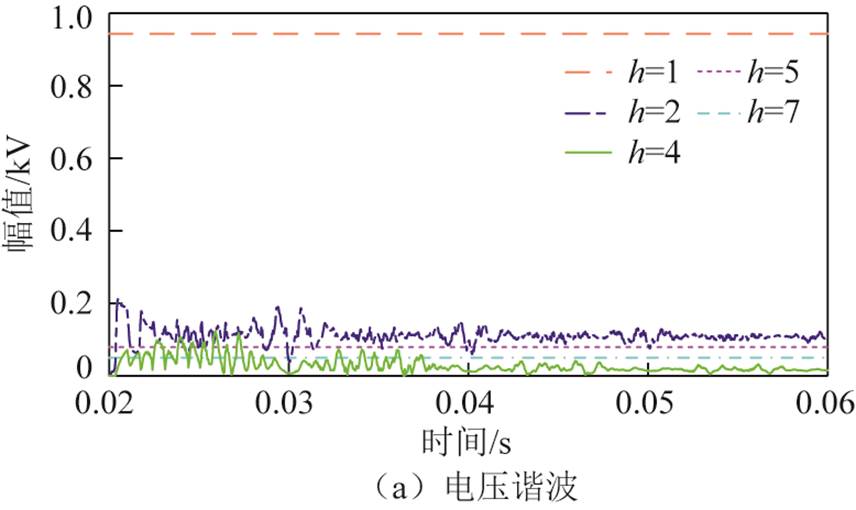

图11 注入二次谐波的A相电压和电流谐波
Fig.11 Phase A voltage and current harmonic injected with the second harmonic
对图10a中基频电压波形进行傅里叶分析,图12为基频电压波形的频谱图。从图12可看出,除含直流分量外,其余较大幅值频率点是742Hz、2227Hz、3713Hz等,与上文谐波谐振分析的频率点是一致的,由此说明DP模型中基频电压的时变相量可准确反映输电线路的高频振荡频率。
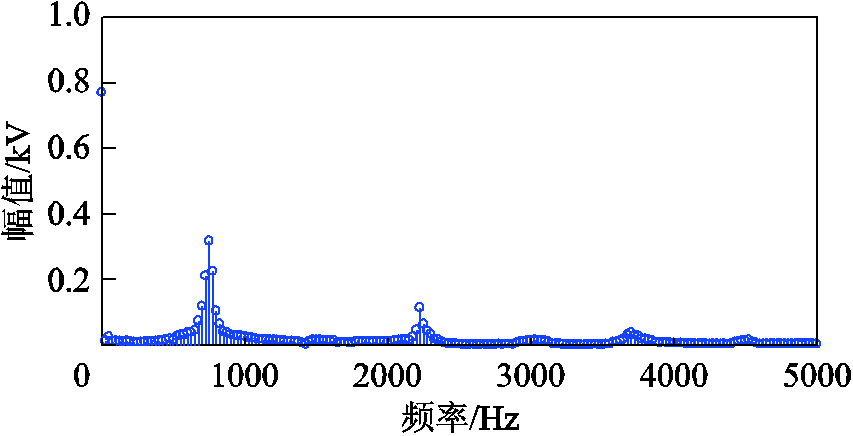
图12 基频电压波形的频谱
Fig.12 Frequency spectrum of fundamental transient voltage waveform
瞬态情况下的电能质量评估对系统安全稳定运行及滤波器设计有重要影响。目前WFFT方法很难精确获取各次谐波瞬时值,因此无法计算瞬时电能质量参数。而DP模型可精确获取仿真步长下各次谐波的瞬时值,采用传统公式可求得瞬时电能质量参数,如有效值、视在功率等。图13是图11中谐波电压电流计算出的瞬时有效值及视在功率。从图13可看出,电压电流有效值和视在功率的瞬时值随谐波幅值变化而产生较大变化。
对频变输电线与电力电子装置的DP模型构成的微分-代数方程组求解可直接获取系统各节点电压和支路电流的谐波幅值和相位,避免WFFT对谐波暂态分析产生的误差,其仿真分析表明:①DP模型可快速确定系统稳态量,也可通过模型中各阶相量的变化来验证系统是否达到稳态;②DP模型中各阶相量在系统扰动下会发生变化,其各阶相量的时变情况即为谐波暂态特性;③DP模型不仅可获取系统中电力电子开关产生的特征次谐波暂态特性,同时能反映输电线路的高频振荡频率。
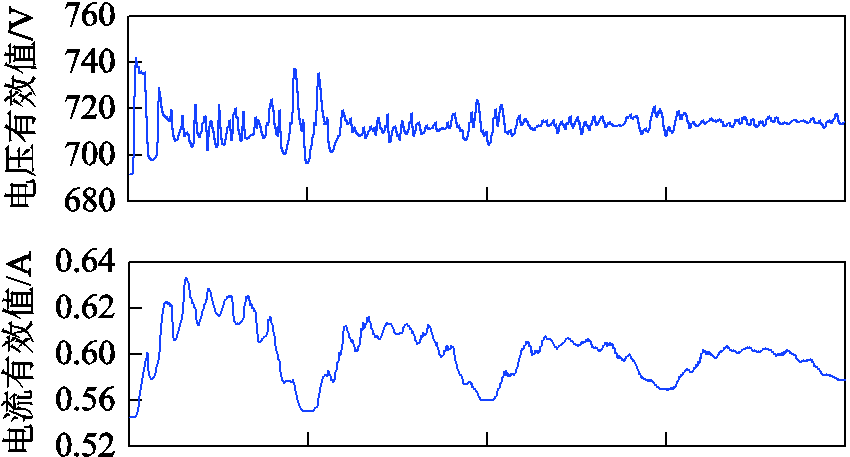
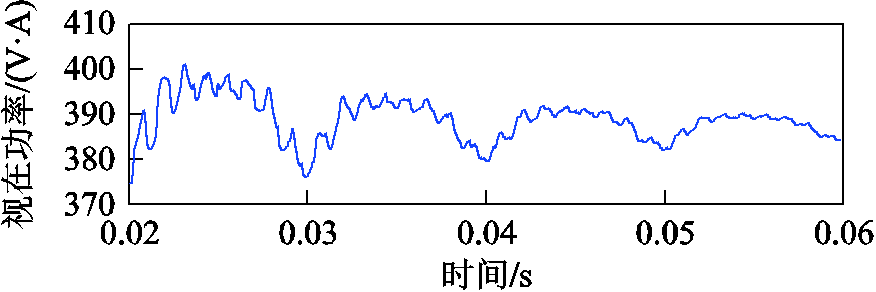
图13 A相有效值和视在功率
Fig.13 Phase A RMS and apparent power
输电线的DP模型虽然能够用于配电网谐波暂稳态特性分析,但模型的精度和仿真时间问题仍待研究。DP模型的精度主要取决于仿真步长和截取谐波次数,根据采样定理可知,仿真步长对应的频率一般为信号频率的10倍,因此仿真步长上限可依据截取的最高次数谐波来确定。目前还没有可预设的精度标准来衡量模型截取的谐波次数,因此截取的谐波次数通常由电源谐波含量、开关函数傅里叶展开式及输电线振荡频率等确定。本文为进一步分析截取谐波次数对模型精度的影响,采用误差e(i)的最大值(MAX)和方均根(RMS)两个指标对图6a中EMTP仿真和DP模型计算的A相电压值进行对比,从而量化DP模型的精度,对DP模型截取不同谐波次数的仿真时间也进行比较,计算结果见表1。
表1 不同谐波次数的模型性能对比
Tab.1 Model performance comparison of different harmonic orders

谐波次数RMS(e)/VMAX(e)/V仿真时间/s 1556.531 8102.342 5483 2527.761 661.110 51 056 3521.508 948.564 22 619 4513.961 225.267 44 186 5512.675 923.186 27 356 6512.458 623.056 49 249
表1给出不同谐波次数的模型性能对比,由表1可知,随着截取谐波次数的增加,其RMS(e)和MAX(e)值逐渐减少,则表明仿真精度相应提高,其中当谐波次数截取45、55、65时,相应的RMS(e)和MAX(e)值已很小且非常接近,但当谐波次数取值为45、55、65时,其仿真时间却大大增加,因此综合考虑文中DP模型的截取谐波次数为45次。此外,由表1可知,DP模型的仿真时长相比时域仿真不具有优势,尤其当特征导纳和传播系数拟合阶数较高及截取较多次数谐波时,仿真时长将会大大增加,此时建议采用改进计算方法如多频段动态相量法[26]或对模型进行简化来缩短仿真时间如三相对称系统可简化为单相模型进而通过相移准确分析另外两相。
本文基于矢量匹配法推导出频变输电线的状态空间形式,在频变输电线状态空间方程形式基础上提出其动态相量模型。基于Matlab对简单测试系统的DP模型进行仿真计算,可直接观察系统中电压和电流各次谐波的暂稳态谐波特性并获取瞬时电能质量参数,同时输电线末端基频电压的时变相量可准确地反映输电线路的高频振荡频率。通过与EMTP搭建的仿真系统暂稳态时域结果进行对比,验证了该模型可适用于电力电子化配电系统谐波暂态特性分析。
本文虽然只针对输电线和TCR的三相简单模型进行谐波暂稳态分析,但该建模方法同样适用于参数不对称的多相耦合输电线路及其他电力电子设备在电网中谐波传播特性,为电力系统数字仿真提供了新方法。基于本文已有的工作,后续可开展的研究有:①继续研究所提动态相量模型的简化工作及三相不对称配电系统中谐波暂稳态特性研究;②基于动态相量理论研究含控制器的电力电子装置和输电线路间谐波交互特性。
参考文献
[1] Bollen M H J, Das R, Djokic S, et al. Power quality concerns in implementing smart distribution-grid applications[J]. IEEE Transactions on Smart Grid, 2016, 8(1): 1-8.
[2] 肖湘宁, 廖坤玉, 唐松浩, 等. 配电网电力电子化的发展和超高次谐波新问题[J]. 电工技术学报, 2018, 33(4): 707-720.
Xiao Xiangning, Liao Kunyu, Tang Songhao, et al. Development of power-electronized distribution grids and the new supraharmonics issues[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 707-720.
[3] 陶顺, 罗超, 肖湘宁, 等. 电流物理分量理论改进方法及其在电能质量评估中的应用[J]. 电工技术学报, 2019, 34(9): 1960-1970.
Tao Shun, Luo Chao, Xiao Xiangning, et al. A modified current physical components theory and its application in power quality assessment[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1960-1970.
[4] 严静, 邵振国. 电能质量谐波监测与评估综述[J]. 电气技术, 2020, 21(7): 1-7.
Yan Jing, Shao Zhenguo. Summary of harmonic monitoring and evaluation[J]. Electrical engineering, 2020, 21(7): 1-7.
[5] 谢宁, 罗安, 陈燕东, 等. 大型光伏电站动态建模及谐波特性分析[J]. 中国电机工程学报, 2013, 33(36): 10-17.
Xie Ning, Luo An, Chen Yandong, et al. Dynamic modeling and characteristic analysis on harmonics of photovoltaic power stations[J]. Proceedings of the CSEE, 2013, 33(36): 10-17.
[6] Medina A, Segundo J, Ribeiro P, et al. Harmonic analysis in frequency and time domain[J]. IEEE Transactions on Power Delivery, 2013, 28(3): 1813-1821.
[7] 程佩芬, 李崇涛, 傅闯, 等. 基于状态空间法的高压直流输电系统电磁暂态简化模型的解析算法[J]. 电工技术学报, 2019, 34(6): 1230-1239.
Cheng Peifen, Li Chongtao, Fu Chuang, et al. An analytic solution for simplified electromagnetic transient model of HVDC transmission system based on state space method[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1230-1239.
[8] 王保帅, 肖霞. 一种用于谐波分析的高精度多谱线插值算法[J]. 电工技术学报, 2018, 33(3): 553-562.
Wang Baoshuai, Xiao Xia. A high accuracy Multi-spectrum-line interpolation algorithm for harmonic analysis[J]. Transactions of China Electrotechnical Society,2018, 33(3): 553-562.
[9] 李建闽, 林海军, 梁成斌, 等. 基于双分辨率S变换和学习向量量化神经网络的电能质量扰动检测方法[J]. 电工技术学报, 2019, 34(16): 3453-3463.
Li Jianmin, Lin Haijun, Liang Chengbin, et al. Detection method of power quality disturbances based on double resolution s transform and learning vector quantization neural network[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3453-3463.
[10] Gallo D, Langella R, Luiso M, et al. A new test procedure to measure power electronic devices frequency coupling admittance[J]. IEEE Transactions on Instrumentation & Measurement, 2018, 67(10), 2401-2409.
[11] 谢桦, 任超宇, 郭志星, 等. 基于聚类抽样的随机潮流计算[J]. 电工技术学报, 2020, 35(23): 120-128.
Xie Hua, Ren Chaoyu, Guo Zhixing, et al. Stochastic load flow calculation method based on clustering and sampling[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 120-128.
[12] Shu Dewu, Xie Xiaorong, Dinavahi V, et al. Dynamic phasor based interface model for EMT and transient stability hybrid simulations[J]. IEEE Transactions on Power Systems, 2017, 33(4): 3930-3939.
[13] 姜宽, 王慧芳, 林达, 等. 面向逆变器型分布式电源的快速建模与仿真方法[J]. 电力系统自动化, 2017, 41(12): 13-19.
Jiang Kuan, Wang Huifang, Lin Da, et al. Rapid modeling and simulation method for inverter interfaced distributed generators[J]. Automation of Electric Power System, 2017, 41(12): 13-19.
[14] E Zhijun, Fang D Z, Chan K W, et al. Hybrid simulation of power systems with SVC dynamic phasor model[J]. International Journal of Electrical Power & Energy Systems, 2009, 31(5): 175-180.
[15] 王童辉, 贾科, 毕天姝, 等. 基于动态相量理论的高压直流系统换相失败暂态特性[J]. 电力系统自动化, 2018, 42(23): 78-86.
Wang Tonghui, Jia Ke, Bi Tianshu, et al. Transient characteristics of commutation failure of HVDC system based on dynamic phasor theory[J]. Automation of Electric Power System, 2018, 42(23): 78-86.
[16] 许汉平, 杨炜晨, 张东寅, 等. 考虑换相失败相互影响的多馈入高压直流系统换相失败判断方法[J]. 电工技术学报, 2020, 35(8): 178-188.
Xu Hanping, Yang Weichen, Zhang Dongyin, et al. Commutation failure judgment method for multi-infeed HVDC systems considering the interaction of commutation failures[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 178-188.
[17] 刘洁波, 黄纯, 江亚群, 等. 基于强跟踪泰勒-卡尔曼滤波器的动态相量估计算法[J]. 电工技术学报, 2018, 33(2): 433-441.
Liu Jiebo, Huang Chun, Jiang Yaqun, et al. Dynamic phasor estimator based on strong tracking Taylor-Kalman filter[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 433-441.
[18] 应迪生, 张明, 陈家荣. 三相分布参数线路动态相量法的建模与仿真[J]. 中国电机工程学报, 2007, 27(34): 46-51.
Ying Disheng, Zhang Ming, Chan K W. Modeling and simulation of 3-phase distribution parameter line using dynamic phasor[J]. Proceedings of the CSEE, 2007, 27(34): 46-51.
[19] 邱丽萍, 张彦涛, 王蒙, 等. 适用于交流长线路的动态相量时域短路电流计算方法研究[J]. 中国电机工程学报, 2019, 39(13): 3736-3744.
Qiu Liping, Zhang Yantao, Wang Meng, et al. Dynamic phasor time domain short-circuit current calculation method for power systems with long ac transmission lines[J]. Proceedings of the CSEE, 2019, 39(13): 3736-3744.
[20] 张彦涛, 秦晓辉, 汤涌, 等. 输电线路工频动态相量模型在半波长交流输电系统机电暂态仿真中的应用研究[J]. 中国电机工程学报, 2017, 37(18): 5294-5302.
Zhang Yantao, Qin Xiaohui, Tang Yong, et al. Half-wavelength system transients stability simulation using dynamic phasor model of AC transmission line[J]. Proceedings of the CSEE, 2017, 37(18): 5294-5302.
[21] Marti J, Tavighi A. Frequency dependent multiconductor transmission line model with collocated voltage and current propagation[J]. IEEE Transactions on Power Delivery, 2017, 33(1): 71-81.
[22] Gustavsen B. Improving the pole relocating properties of vector fitting[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1587-1592.
[23] Semlyen A, Gustavsen B. Phase-domain transmission-line modeling with enforcement of symmetry via the propagated characteristic admittance matrix[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 626-631.
[24] Zhang Shao, Jiang Shuai, Lu Xi, et al. Resonance issues and damping techniques for grid-connected inverters with long transmission cable[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 110-120.
[25] Mercado M A C, Orillaza J R. Harmonic state space model of a closed-loop balanced thyristor controlled series compensator[C]//2016 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 2016: 1-6.
[26] 刘博宁, 姚蜀军, 张慧媛, 等. 多频段-动态相量法电磁暂态仿真研究[J]. 中国电机工程学报, 2019, 39(19): 5772-5781.
Liu Boning, Yao Shujun, Zhang Huiyuan, et al. A research on multi-frequency band dynamic phasor for electromagnetic transients simulation[J]. Proceedings of the CSEE, 2019, 39(19): 5772-5781.
Modeling and Simulation of Dynamic Phasor Harmonic Analysis for Frequency-Dependent Transmission Line
Abstract The windowed fast Fourier transform (WFFT) is widely used for harmonic analysis on rapidly changing time domain waveforms in power electronic distribution network, but WFFT is prone to errors so that the harmonic transient characteristics cannot be obtained accurately. In this paper, a dynamic phasor (DP) model of frequency-dependent transmission line is proposed for harmonic transient analysis in distribution network. The characteristic admittance and propagation coefficient are fitted in rational function by adopting vector fitting method, which exist in the model domain frequency-dependent transmission line model. The DP model of frequency-dependent transmission line is established based on state space equation, the DP model is also established for the thyristor controlled reactor (TCR) at receiving end of the transmission line, the harmonic dynamic coupling between TCR and power grid is described by the analytical formula with phasors of each order as state variables. The DP model of the simple test system is calculated based on Matlab, which can directly analyze harmonic transient characteristics for the voltage of each node and current in each branch in the system, and the instantaneous power quality parameters can also be obtained. The transient steady state results of the simulation system based on EMTP verify the effectiveness and accuracy of the model.
keywords:Harmonic analysis, frequency-dependent transmission line, vector fitting method, dynamic phasor, power quality
DOI:10.19595/j.cnki.1000-6753.tces.201021
中图分类号:TM743
解润生 男,1990年生,博士研究生,研究方向为电力电子化配电系统谐波分析。E-mail:runsheng_xie314@hotmail.com
张国荣 男,1963年生,教授,博士生导师,研究方向为电力化电子配电系统谐波分析、电力电子变换技术。E-mail:zhanggrcao@163.com(通信作者)
(编辑 赫蕾)