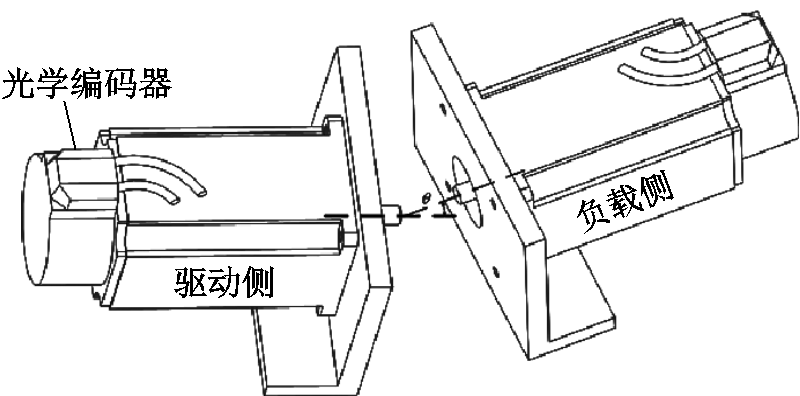
图1 角度不对中示意图
Fig.1 Schematic diagram of angle misalignment
摘要 为了提高电机运行的安全性和可靠性，减少电机首次安装中存在的角度不对中现象，提出一种基于电机转速信号的电机首次安装角度不对中故障检测方法。该方法不需要任何健康数据及历史数据信息，更不需要额外安装振动传感器。该文首先分析了角度不对中故障影响转速信号的机理；然后利用快速傅里叶变换及最小二乘法对转速信号进行处理，根据其二倍转频幅值随转速变化所拟合曲线的二次项系数，并结合S型分布隶属度函数，综合评判电机的首次安装不对中程度；最后搭建了永磁同步电机角度不对中故障的仿真模型和实验平台，仿真及实验结果证明了该方法用于永磁同步电机首次安装角度不对中故障检测的可行性与有效性，具有广阔的应用前景。
关键词：永磁同步电机 首次安装 不对中 转速信号
近年来，针对转子轴承系统进行的不对中故障诊断与监测方面的研究非常普遍。旋转机械的不对中故障会对整个系统的可靠运行构成严重威胁，往往会导致停机甚至带来巨大的经济财产损失和人员伤亡[1]。据统计，工业界每年大约要花费维护费用的40%来解决旋转机械的不对中问题[2-3]。不对中故障主要包括轴承不对中和联轴器不对中，联轴器不对中又分为平行不对中和角度不对中两大类[4]。在电机安装环节，由于电机安装误差而导致的驱动和从动机械轴偏心是联轴器角度不对中故障的主要来源，其示意图如图1所示。
图1 角度不对中示意图
Fig.1 Schematic diagram of angle misalignment
目前国内外学者对不对中故障诊断已经取得了一定的研究成果。文献[5]发现由于联轴器不对中而产生的振动是由联轴器刚度随轴旋转而变化引起的，并且此现象随联轴器类型而变化。文献[6]基于模态综合法建立了不对中故障的广义系统运动方程，得出联轴器安装不对中产生的故障频率是转频的两倍这一结论。文献[7]从联轴节的变形和受力角度分析了角度不对中故障的扭振特性，得出当轴系存在角度不对中故障时，其附加扭矩与偏角的二次方成正比这一结论。文献[8]基于有限元建模的方法分析了不对中故障对转子轴承系统的振动响应，研究结果表明二倍转频幅值大小可作为评判不对中故障程度的一个关键指标。文献[9]在谐波平衡法的理论基础上对角度不对中进行了研究，得出角度不对中故障会使系统出现工频与振动频率二者相耦合的频率这一结论。上述关于不对中故障的研究都是基于振动信号，但振动信号的获取需要额外安装传感器，传感器不仅价格昂贵而且还会受到实际工作条件的限制，后期维护也不方便，并不能很好地适用于电机初始安装环节的不对中检测。
近年来，基于电气法的机械故障诊断作为一种非入侵式的手段而备受关注。文献[10]基于电机的起动电流信号对不对中故障进行了诊断与辨识，初步的研究结果表明采用电机电流信号来实现机械故障诊断与监测具有良好的应用前景。文献[11]表明电流信号和负载转矩信号在不同类型的联轴器下对角度不对中故障的诊断效果不尽相同，且随负载的变化而变化。文献[12]通过采用快速傅里叶变换（Fast Fourier Transformation, FFT）并结合小波变换分析了转矩信号的频谱特性，初步实现了对不对中故障的检测，并表明转矩信号用于不对中故障诊断的有效性。文献[13]基于转速信号的特征分析法对电机轴承进行故障诊断，初步表明转速信号特征分析法用于典型性机械故障诊断的可行性。目前基于电气法的不对中故障诊断大多基于电流信号，但电流信号的采集会受到嵌入式系统采样偏置、电流基频分量和谐波的干扰，需要配合一定的数字信号处理方法才能提取到有用的故障信息。相比而言，从编码器采集的转速信号获取方便且采样精度较高，成本较低，能够实现实时状态监测，有很好的应用前景。
为了能够有效地对不对中故障进行诊断、监测与预测，在上述理论研究的基础上，国内外已经开发出各种用于状态监测的定量和定性模型，各种定量模型基于线性和非线性技术，包括主成分回归（Principal Component Regression, PCR）、偏最小二乘（Partial Least Squares, PLS）、核回归（Kernel Regression, KR）、支持向量机（Support Vector Regression, SVR）和人工神经网络（Artificial Neural Network, ANN）。两种常见的定性模型是专家系统（Expert System, ES）和定性趋势分析（Qualitative Trend Analysis, QTA）。文献[14]使用主成分回归和偏最小二乘来预测轴平行度和角度未对准。文献[15]提出一种基于转矩信号自回归（Autoregressive, AR）模型的不对中故障诊断方法，将AR模型结合自组织神经网络、最小冗余和最大相关性进行故障模式判别。但状态监测通常是基于连续收集的数据，在实际中样本量通常很少。此外，状态监测的学习概念会随着时间而变化。
目前针对转子轴承系统角度不对中的故障诊断及状态监测都是通过比较和分析故障及健康状况所获得的振动信号或电流信号，传统的角度不对中故障诊断、监测和预测始终无法摆脱对健康状态下运行数据或历史数据信息的依赖，但在实际的工业应用中几乎不存在完全健康的数据或者很难获取相对健康的数据，而且健康状态的数据还会随着时间、工作环境及其他外界因素的变化而变化。健康数据的获取对测量仪器的精度有一定的要求，还需要不定期地对数据进行更新，这就需要耗费大量的人力和物力成本。在工业领域，通常使用百分表、应变仪等仪器指导电机的首次安装过程。虽然这类方法能够在一定程度上减少电机的安装误差且成本较低，但在实际操作中十分依赖工人的经验，而且会耗费大量时间。随着传感器等测量仪器精度的提高，出现了像激光对中仪等光学仪器来辅助电机的首次安装。虽然这类仪器大大降低了对技术人员的经验要求，但其对设备的工作环境要求更高，而且存在价格昂贵和操作复杂等诸多问题。所以，如何得出一个有效的方法来检测和评价电机的初始安装不对中情况就显得至关重要。
基于此研究现状，本文提出一种基于永磁同步电机转速信号的电机首次安装角度不对中故障检测方法。主要针对转子系统中弹性联轴器的角度不对中故障，提出一种适用于中小功率伺服电动机首次安装环节的角度不对中故障检测。该方法不需要安装额外的传感器，通过电机驱动系统本身作为传感器采集转速信号，在没有健康数据或历史数据信号的前提下，可以诊断出电机是否存在角度不对中故障，用于指导电机的首次安装过程。该方法降低了监测成本且诊断效果良好，节约了大量的人力和物力资源。仿真和实验的结果验证了该方法的有效性。
当两个轴之间通过弹性联轴器错位连接时，就会出现与万向节效应有关的某些故障。为了研究转子系统的角度不对中对电机运行的影响，首先分析角度不对中产生的附加转矩。如图2所示，该系统由电机、弹性联轴器和Jeffct转子组成，建立x-y-z空间直角坐标系，电机轴与转轴之间形成的偏角为α，其中z轴与传动轴轴线重合，电机的转矩Te经弹性联轴器传递到转子轴，可以分为沿着z轴驱动转轴的转矩分量Tz和垂直于转子轴的弯矩分量Ts。
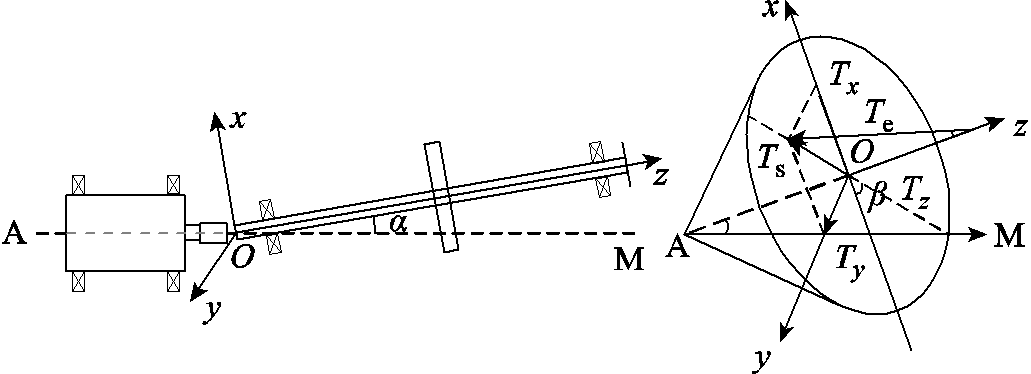
图2 角度不对中模型
Fig.2 Angular misalignment model
为了分析角度不对中故障对电机的转速信号的影响，这里仅考虑沿z轴方向的转动[6]，可得
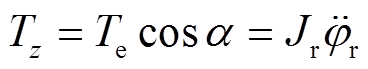（1）式中，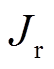
为转子系统的转动惯量；
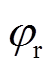为转子的旋转角度，
，
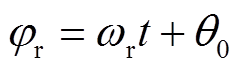为转子的旋转角位移，
为转子的旋转角速度。
对于偏角为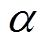
的电机转子系统，二者的角速度满足[16]
（2）式中，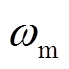
为电机的角速度；
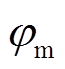为电机的旋转角度，
，
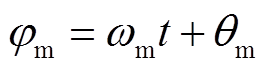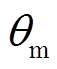为电机的扭转角。
将式（2）泰勒展开可得
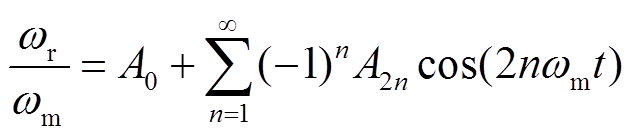（4）其中
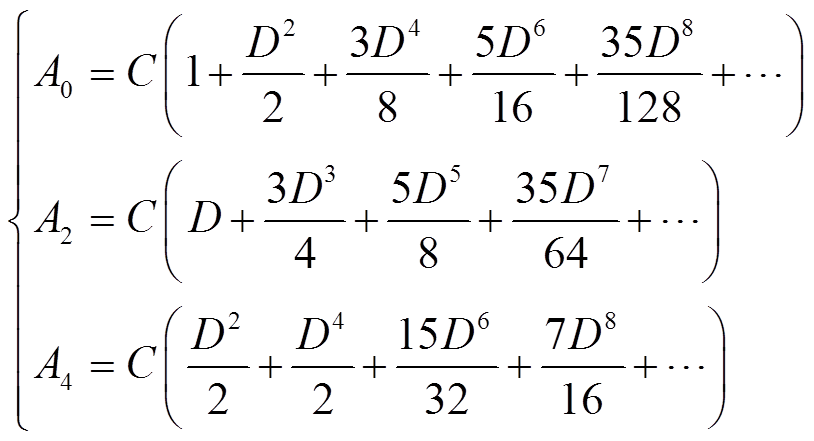（5）
对式（4）进行微分，得
（6）其中
（7）
由于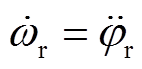
，所以将式（6）代入式（1）可得电磁转矩为
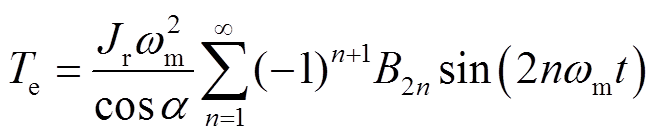（8）由式（8）可以看到，此时的电磁转矩表达式中含有偶数倍转频的正弦成分，在此模型中转矩的大小还与转速的二次方、偏角α大小及转子系统的参数有关，转速越高，转矩越大。
文献[13]的研究结果表明基于转速信号的电气法机械故障诊断有着很好的效果，而转速与转矩之间关系十分密切。为了研究方便，这里忽略高倍频的扭转振动，主要考虑二倍转频的正弦成分[7]，可以进一步将式（8）简化为
（9）式中，
为电机旋转频率；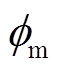
为电磁转矩的初始相位。当带负载运行时，根据经典传动系统的动力学公式，即
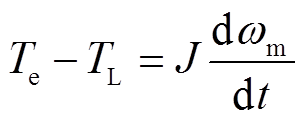（10）
式中，J为电机侧的转动惯量；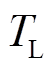
为负载转矩的大小。
可以知道，在角度不对中产生的附加转矩的作用下，转速信号也会受到一定的影响。
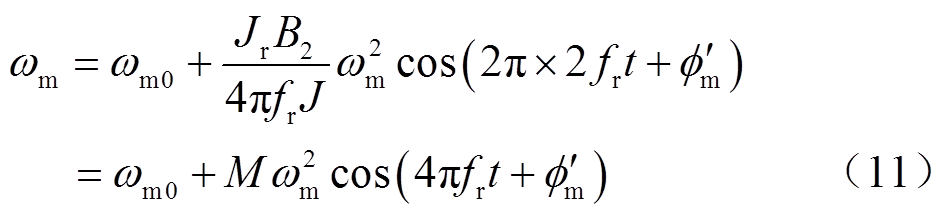
式中，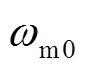
为电机正常条件下运行的转速；M为与转子系统和偏角大小有关的参数；
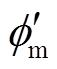为转速的初始相位。
所以，角度不对中故障作用在电机转速中反映出来的故障特征频率也应为2fr。由式（11）可知，当存在角度不对中故障时，随着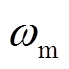的逐渐增大，转速信号中二倍转频的幅值2fr也会明显升高，理论上二者应该近似成二次方关系。
由1.1节和1.2节的分析结果可知，当偏角a为零时，产生的附加转矩也为零，转速信号中也不存在2fr的正弦成分。当a不为零时，转速信号的频域中主要表现为2fr的特征频率，且该特征频率的幅值随着转速的升高而明显增大。在上述理论基础上，提出电机初始安装故障检测算法，具体的流程如图3所示。
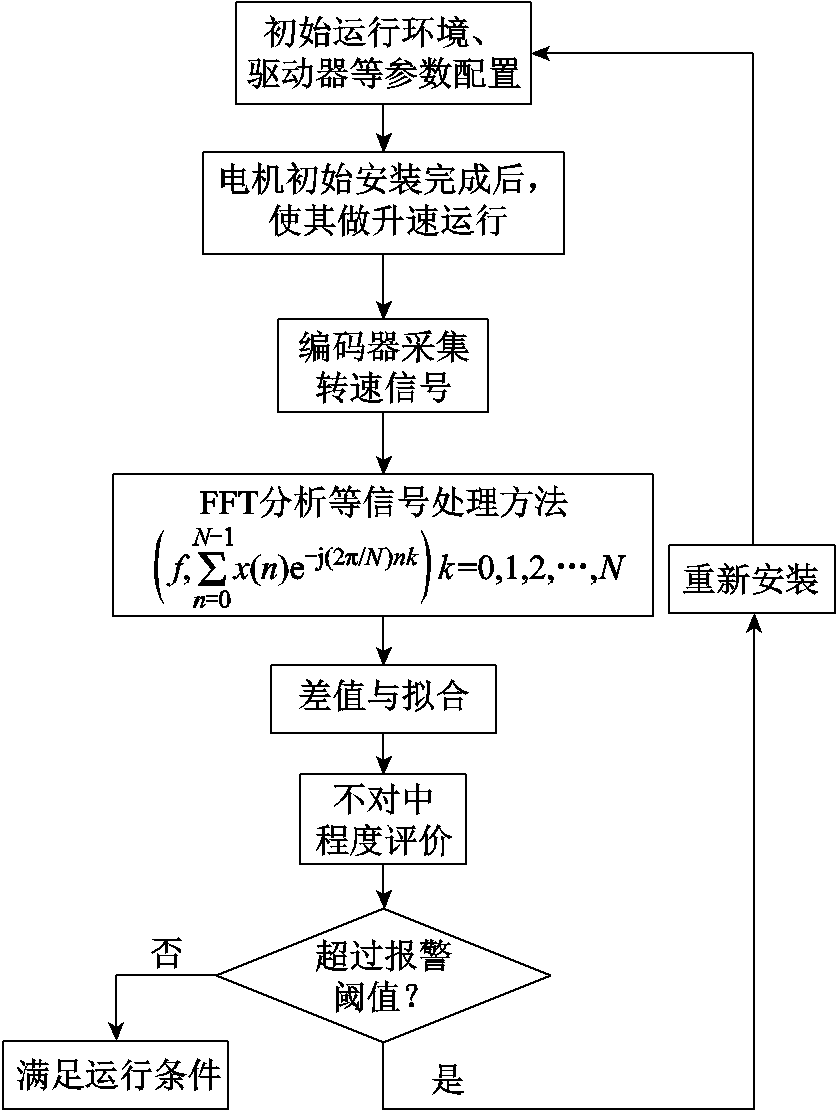
图3 不对中故障检测流程
Fig.3 Flow chart of alignment fault detection
在电机的初始安装环节，首先对电机从低到高做均匀升速，间隔100r/min；接着通过增量式编码器获取转速信号并去除暂态过程；最后采用FFT等数字信号处理方法得到二倍转频2fr的幅值，利用最小二乘法对其进行差值与拟合，得到2fr幅值随转速的变化趋势。可以发现当存在角度不对中故障时，2fr幅值随转速从低到高逐渐增大，而正常情况下的2fr幅值基本不变。当电机初始安装完成后，若随转速升高，2fr幅值呈增大趋势，则可初步判断电机存在一定的角度不对中故障。所得到的2fr幅值随转速变化曲线的二次项系数大小可表征不对中程度。
当检测到电机的初始安装环节存在一定程度的不对中故障时，如何对其不对中程度进行评价对于报警阈值的设定非常关键。不对中程度是一个相对模糊的概念，所以可以尝试将模糊评价的方法引入实际的工程中。
为了解决不对中程度大小这一模糊概念建模的基本问题，首先应该确定其隶属度函数。由式（11）可知，角度不对中故障的特征频率2fr的幅值与转速成明显的二次方关系。在没有任何历史数据的前提下，当用所拟合曲线的坡度大小来刻画角度不对中的故障程度时，“故障程度”模糊集的论域应选择能表征曲线斜率变化的指标K，即所拟合曲线的二次项系数大小。为了便于分析和研究，可将所关心的论域范围缩减为[0,kmax]，在[0,kmax]区间中又设定了k1和k2两个阈值，且满足0＜k1＜k2＜kmax。当K值极小时，电机安装存在不对中故障的概率也很小；只有当K值大于某一阈值时才能确定其存在一定程度的角度不对中故障。因此隶属度函数的整体结构应该选为偏大型。
若电机的初始安装情况良好，此时曲线的K值很小，靠近零附近，论域中[0,k1]的元素对“故障”的隶属度为0，该情况下电机可长期稳定运行，此时认定系统处于健康状态。当K∈[k2,kmax]区间时，则对于故障的隶属度为1，此时电机应立刻停机重新安装。至此，确定了隶属度为0和1的元素区间，临界论域为k1和k2。显然，当电机安装情况良好时，K值大小应该在0附近，当K值越来越大，则出现不对中故障的概率越大，系统运行的稳定性也越来越差。当K∈[k1,k2]时，则可以认为电机的初始安装存在一定程度的角度不对中故障，此时电机可稳定运行一段时间，但长期运行则可能引起设备损坏。但不能简单判定当K值属于[k1,k2]时电机的初始安装情况不合格，事实上，此时整个系统仍然能够继续运行，只是运行情况有所不同，而且不同的K值对应的故障程度明显不同。因此，[k1,k2]这个区间可被确定为过渡带。在过渡带中，根据K值大小与整个系统的关系可以知道，当K值大小偏离允许范围时，K值越小则其变化对整个系统的运行影响就越小，而在靠近允许范围时这种影响就越大。所以过渡带不应该是线性的，而应该是非线性的过渡。
综合以上分析结果，可以选择S型分布隶属度函数，其解析表达式为
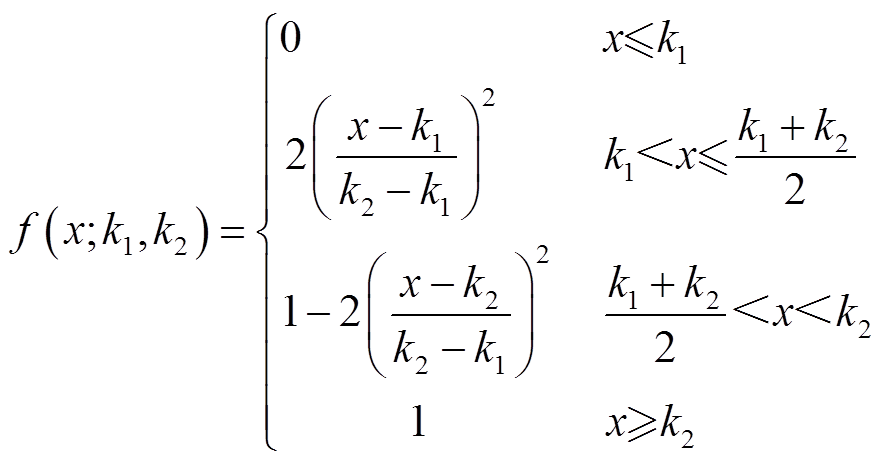（12）式中，x为所选取的表征曲线变化趋势的参数。
在此基础上参照国标ISO7919（GB/T11348）和ISO/TC10816（GB/T6075）中的有关评价准则，进一步将故障程度划分为A、B、C、D四个区域，结合对安装精度和误差的具体要求，以及仿真所得结果初步设定k1和k2的数值。当确定相应的k1、k2等参数之后，选取隶属度函数值作为报警阈值，记为Z。对于初始安装的电机，若计算出的隶属度函数值大于Z，则认为安装情况不合格，需要重新调整；若小于Z，则认为安装情况良好。在实际的工程应用中，报警阈值Z的选取应该根据具体的安装精度和报警灵敏度的要求综合考虑。
为了验证本文提出的电机初始安装角度不对中故障检测方法的正确性与算法的有效性，在Simulink中搭建了永磁同步电机的仿真模型，如图4所示。仿真部分所涉及的永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）基本参数见表1。
图4 仿真模型
Fig.4 Simulation model
表1 PMSM伺服系统仿真参数
Tab.1 PMSM servo system simulation parameters
参数数值 额定功率/kW0.75 额定转矩/(N·m)2.39 额定电流/A3 额定转速/(r/min)3 000 电机轴转动惯量/(kg·m2)1.82×10-4 负载惯量/(kg·m2)7.2×10-4 电机极对数4
在仿真中，还搭建了角度不对中故障的模型，用以模拟不同程度的角度不对中故障。结合式（1）和式（9）可得在空载条件下由角度不对中故障产生的附加转矩表达式为
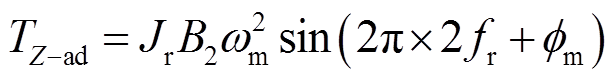（13）在保证精度的前提下，仿真模拟时只取式（7）中的前两项进行计算，因为其高次项越来越小，可忽略不计。据此，在Matlab的Simulink中搭建了附加转矩的传递函数表达式（S-function），以传递函数的输出结果作为附加转矩输入，来模拟由角度不对中故障产生的附加转矩对电机转速的影响。当n=1 000r/min，不同故障程度下附加转矩的时域波形如图5所示。
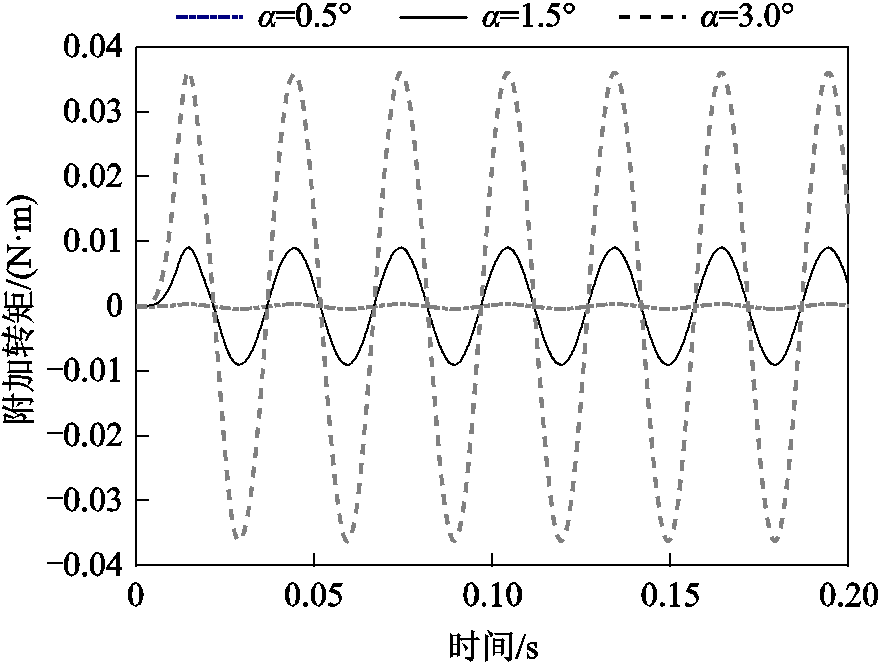
图5 附加转矩时域波形
Fig.5 Time domain waveform of additional torque
为了更直观地显示附加转矩的周期性变化情况，这里只给出了0.2s的时域波形情况，仿真结果中进行的FFT频谱分析需要采用2s的数据量。
设定仿真时间为2s，电机给定转速大小的范围为100～2 000r/min，间隔100r/min，偏角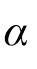
分别设为0°、0.5°、1.5°、3°，代表四种不同程度的角度不对中故障。仿真的结果如图6和图7所示。n=1 000r/min时不同故障程度下转速信号的频谱如图6所示。不同故障程度下二倍转频的幅值大小随转速的变化趋势如图7所示。
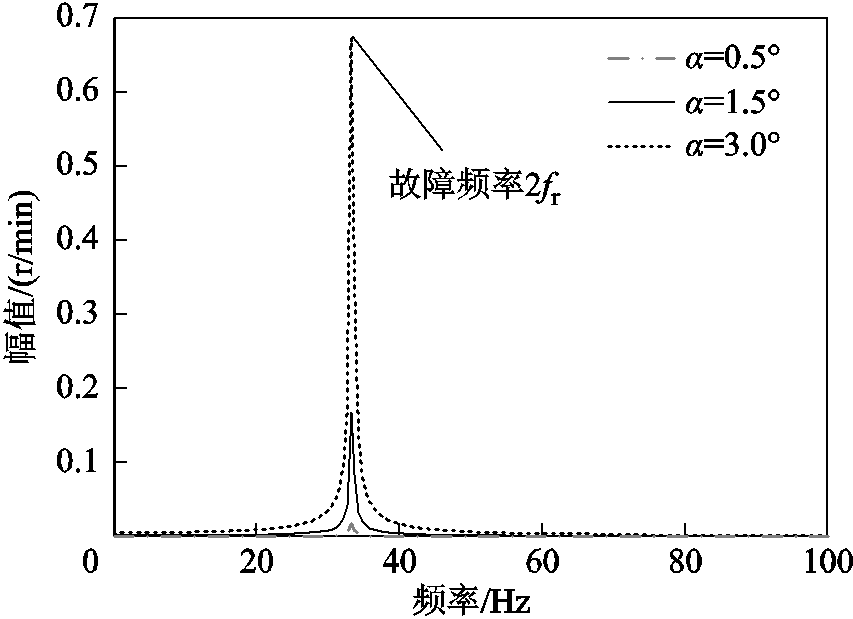
图6 转速信号频谱图
Fig.6 Speed signal spectrum
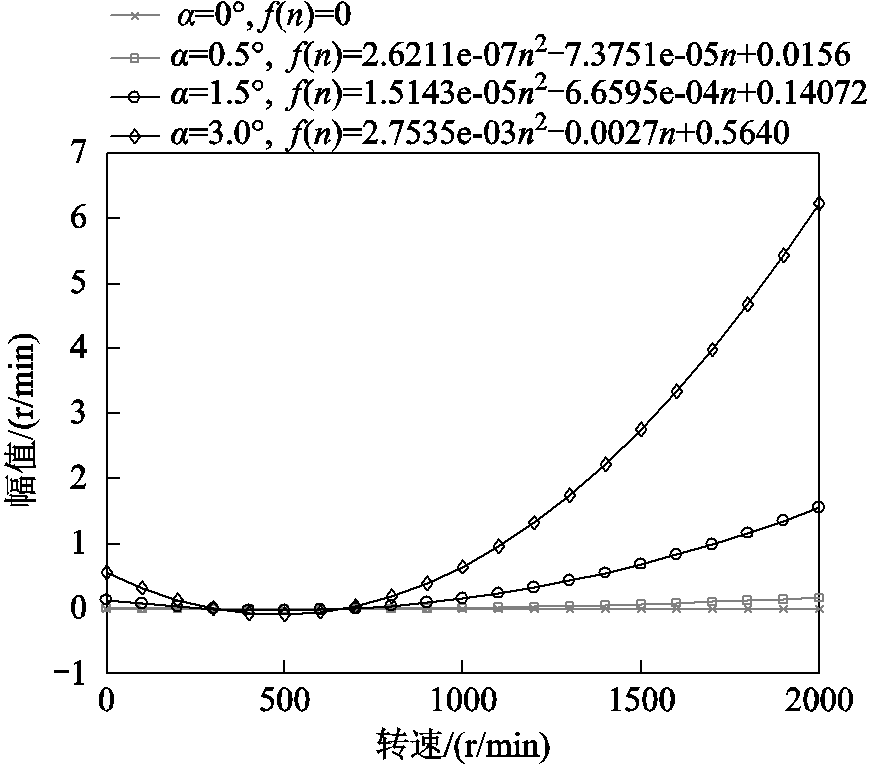
图7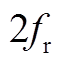 
幅值随转速变化趋势
Fig.7 The trend of 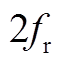amplitude with rotating speed
对仿真所得的转速信号做FFT处理，由图6可知，由角度不对中故障产生的附加转矩对转速信号的影响在其频谱图中表现为二倍转频的特征频率，这与1.1节所得的结论相吻合。随着不对中程度的增大，转速信号的故障特征频率2fr的幅值也明显增大。采用最小二乘法对不同转速下2fr的幅值做差值与拟合，如图7所示，可以发现当存在角度不对中故障时，随着转速的升高2fr的幅值呈现出明显的上升趋势，二者之间表现出很明显的二次方关系，不对中程度越大，上升趋势越明显，而健康状态下，2fr幅值几乎不变，所以1.4节中用所拟合曲线的二次项系数大小来表征故障程度大小是具有一定的依据所在的。
本实验平台主要由电机驱动系统和转子系统两部分组成。转子系统由额定功率为750W的米格80ST-M02430LB型永磁同步电机通过弹性联轴器带动转子系统运行，通过增量式编码器获取电机转速信号，驱动程序由上位机操作的Xilinx软件执行。实验平台如图8所示。在该实验中，针对角度不对中故障的检测在电机的初始安装状态下进行，所以应该保证带载情况为空载或轻载。通过SKF激光对中仪进行角度不对中的定量实验，如图9所示。
图8 实验平台示意图
Fig.8 Schematic diagram of experimental platform
图9 SKF激光对中仪示意图
Fig.9 SKF laser alignment instrument
特别需要说明的是激光对中仪上的界面参数与不对中偏角大小的换算关系，如图10所示。
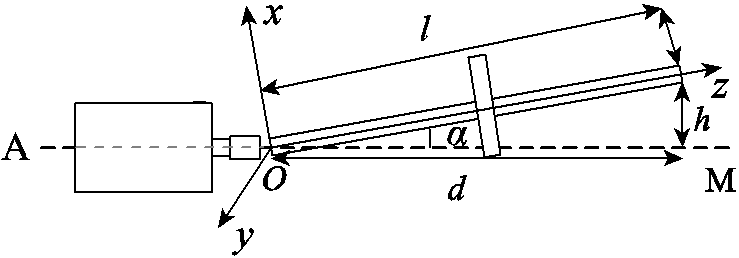
图10 参数换算关系示意图
Fig.10 Parameter conversion relationship
参照该型号的激光对中仪的使用说明，图9中的0.05mm/100mm的对应到图10中的几何关系应为h/d，所以若要设置不对中偏角为α，则在激光对中仪上的输入参数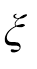
需调整为
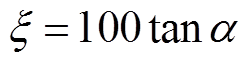（14）与仿真参数相对应，分别设置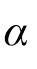=0°、0.5°、1.5°、3°，从低速到高速，间隔100r/min，设定电机运行时间为10s，采样频率为2kHz，实验电机的基本参数见表2。
表2 PMSM伺服系统实验参数
Tab.2 The basic parameters of the experiment motor
参数数值 额定功率/kW0.75 额定转矩/(N·m)2.39 额定电流/A3 额定转速/(r/min)3000 电机轴转动惯量/(kg·m2)1.82×10-4 负载惯量/(kg·m2)7.2×10-4 电机极对数4
在该实验平台下，选取所拟合曲线的二次项系数K来表征不对中故障的严重程度，K值越大，不对中的程度越大。在参照和借鉴振动法的国标标准ISO7919(GB/T11348)和ISO/TC10816(GB/T6075)中有关评价准则的基础上，首先，将故障程度划分为健康、轻度不对中、中度不对中、严重不对中四个区域，在仿真所得结果的基础上先人为确定了几个故障程度区间，包含三个数据点。由于仿真所得的结果与实验又必不可少地会存在一定差异，所以最后又使用对中仪器——激光对中仪，离线测量了几个数据点，并结合实际工程经验对所得数值进行修正处理，而其他的数据点是根据隶属度函数进行模糊插值计算得来。
设定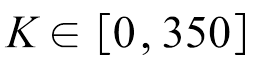
，并将二次项系数同等放大108倍，设定k1=5，k2=200，选取隶属度函数值大小作为报警阈值，设为0.5。所得隶属度函数曲线如图11所示。
图11 隶属度函数曲线
Fig.11 Membership function curve
实验采集到的转速信号（以n=1 000r/min为例）稳态情况下的时域波形如图12a所示，可以发现随着不对中偏角的增大，转速信号在时域中的周期性转速脉动幅值也随之增大。通过对其进行FFT分析，如图12b所示，每组谱线均为同一转速条件下的实验结果。当电机的给定转速为1 000r/min，在电机侧引入不同程度角度不对中故障时，转速信号中的2fr幅值相对于健康状态明显升高，而一倍转频fr的幅值变化不大，且没有明显的变化规律和趋势。
图12 转速信号的频谱图
Fig.12 Frequency spectrum of speed signal
对采集到的实验数据依次进行处理可以得到不同故障程度下不同转速的特征频率2fr的幅值，记录并保存。采用最小二乘法对其进行差值与拟合，进而可得故障的特征频率2fr随转速的变化趋势如图13所示。
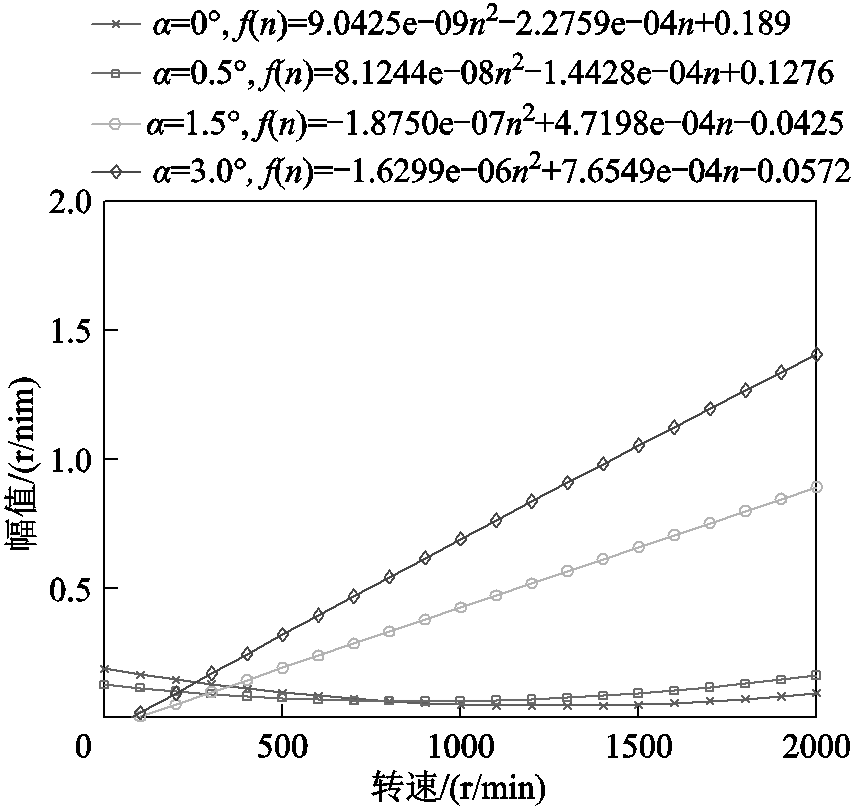
图13 2fr随转速变化趋势一
Fig.13 The amplitude of 2fr changed trend(Ⅰ) with speed
由图13可知，对中小功率伺服电机而言，当不对中程度较小时，在低速区间，2fr的幅值随转速升高有减小的趋势，这是因为在低速运行时，由于逆变器的非线性特性等因素导致的电机转速脉动较大，使得有用的故障信息被淹没。当速度增大到800r/min以上时，2fr幅值又开始增大。重新拟合该速度区间下的数据，如图14所示。图15是2fr的幅值随不对中程度和转速变化的综合效果立体图。
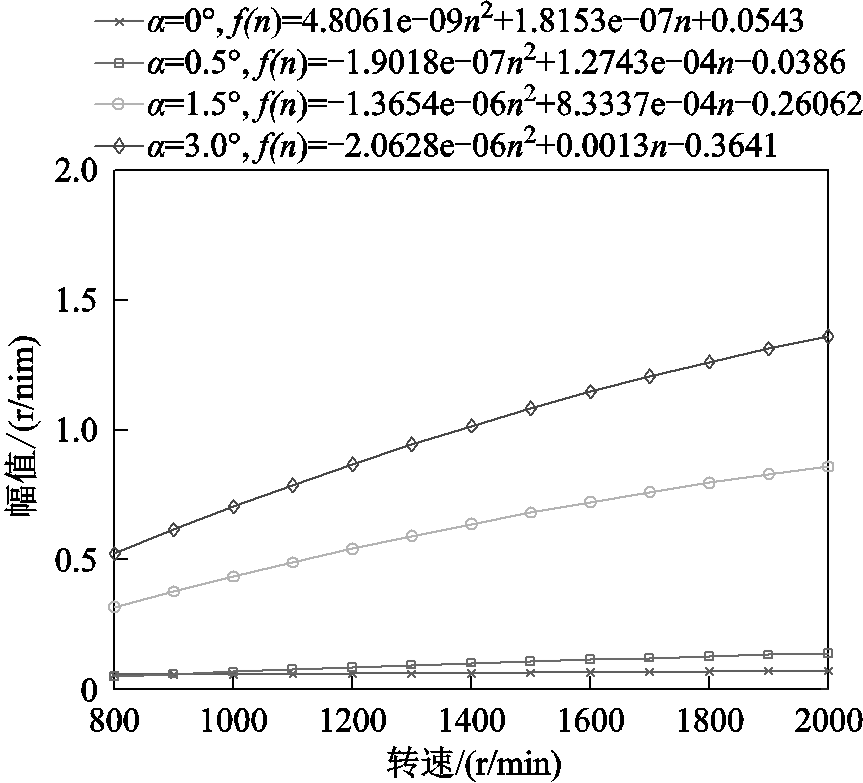
图14 2fr随转速变化趋势二
Fig.14 The amplitude of 2fr changed trend(II) with speed
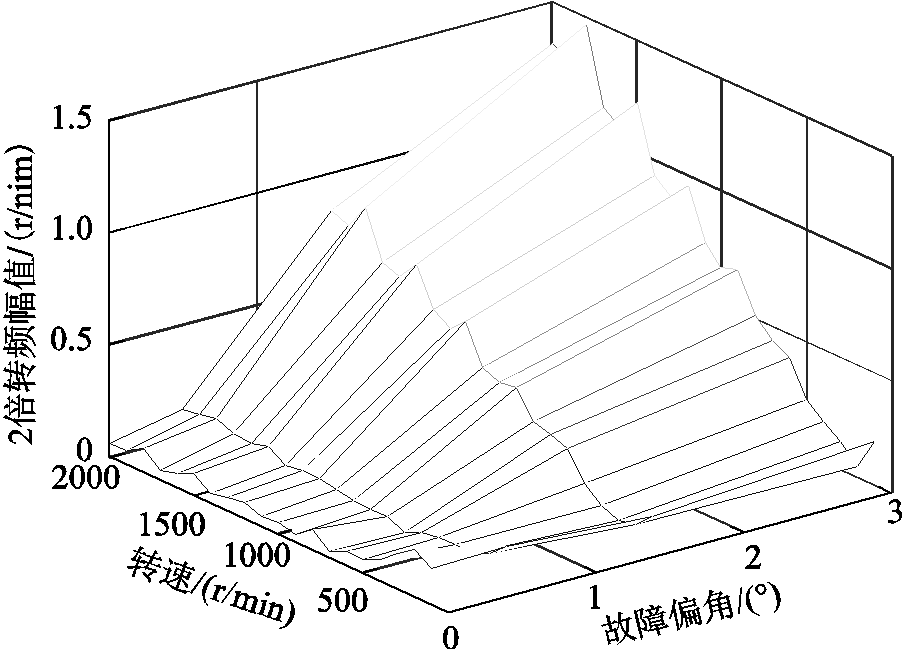
图15 2fr幅值变化综合效果立体图
Fig.15 2fr change trend with misalignment and speed
根据图14，可以发现当存在角度不对中故障时，随着不对中程度的进一步增大，从低速到高速，2fr的幅值呈现出明显的上升趋势，不对中程度越大，2fr的幅值变化越快，即所拟合曲线的二次项系数越大。所以，可以选取所拟合曲线的二次项系数的绝对值来刻画不对中程度。由图15可得，当不对中程度在0.5°以内时，2fr的幅值变化随转速和不对中程度变化都不明显；当α超过0.5°时，转速越高，2fr幅值的变化越明显。
由2.3节和3.2节内容可知，仿真与实验的结果与理论分析基本相吻合，初步验证了本文所提出的首次安装不对中检测方法的可行性。实验与仿真所得到的结果有部分差异，这是由整个电机驱动与传动系统本身非线性因素及不可避免的传动误差所导致的，其误差大小在合理的范围内，不会影响该方法的可行性。根据图14所示结果，结合式（12），得出当α=0°、0.5°、1.5°、3°时的隶属度函数值分别为0、0.043 4、0.696 6、1，对应的评判结果依次为健康、轻度不对中、中度不对中、严重不对中状态，只有中度不对中和严重不对中状态会报警，与实际结果相吻合。
本文提出了一种基于永磁同步电机转速信号的电机初始安装角度不对中故障检测方法。该方法可以不依赖任何健康数据和历史信息，也不需要额外安装传感器，能够在电机的初始安装环节检测电机是否存在角度不对中故障。并结合模糊综合评价中的隶属度函数来评价电机的初始安装不对中情况，将电机对中情况划分为健康、轻度不对中、中度不对中、严重不对中四种状态。理论推导、仿真及初步的实验结果表明：
1）根据转速信号中2fr的幅值随转速的变化趋势可以检测电机的初始安装环节是否存在角度不对中故障，即当电机存在角度不对中故障时，2fr的幅值随转速的升高而增大，整体呈上升趋势。
2）根据所拟合曲线的二次项系数并结合隶属度函数可以评价电机的初始安装不对中程度，并结合模糊综合评价对不同故障程度做了区分；不对中程度越大，相对应的隶属度函数值越大。
该方法不依赖于任何的健康数据和历史数据信息，也不需要额外安装传感器，仅需要永磁同步电机的转速信号，成本较低，且算法简单易实现，用于指导电机的安装环节，有着广阔的应用前景。对于如何将振动法的标准与电气法准确对应起来，也是后期工作的重点和研究难点。
参考文献
[1] Reddy M C S, Sekhar A. Detection and monitoring of coupling misalignment in rotors using torque measurements[J]. Measurement, 2015, 61: 111-122.
[2] Wowk V. Machinery vibration alignment[M]. New York: McGraw-Hill Education, 2000.
[3] Umbrajkaar A, Krishnamoorthy A. Vibration analysis using wavelet transform and fuzzy logic for shaft misalignment[J]. Journal of Vibroengineering, 2018, 20(8): 2855-2865.
[4] 夏松波, 张新江, 刘占生, 等. 旋转机械不对中故障研究综述[J]. 振动·测试与诊断, 1998, 18(3): 157-161.
Xia Songbo, Zhang Xinjiang, Liu Zhansheng, et al. A survey of research on misalignment of rotary machinery[J]. Vibration. Test and Diagnosis, 1998, 18(3): 157-161.
[5] Saavedra P, Ramirez D. Vibration analysis of rotors for the identification of shaft misalignment part1: theoretical analysis[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2004, 218(9): 971-985.
[6] Xu M, Marangoni R. Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance, part I: theoretical model and analysis[J]. Journal of Sound and Vibration, 1994, 176(5): 663-679.
[7] 黄典贵, 蒋滋康. 交角不对中轴系的扭振特性分析[J]. 汽轮机技术, 1995, 37(3): 150-152.
Huang Diangui, Jiang Zikang. Analysis of torsional vibration characteristics of shaft system with angular misalignment[J]. Steam Turbine Technology, 1995, 37(3): 150-152.
[8] 刘杨, 太兴宇, 姚红良, 等. 双盘转子轴承系统不对中-碰摩耦合故障分析[J]. 振动·测试与诊断, 2013, 33(5): 819-823.
Liu Yang, Tai Xingyu, Yao Hongliang, et al. Analysis of misalignment rub impact coupling fault of double disk rotor bearing system[J]. Vibration, Test and Diagnosis, 2013, 33(5): 819-823.
[9] 李明. 转角不对中故障的转子系统非线性动力学特征[J]. 振动·测试与诊断, 2011, 31(5): 552-556.
Li Ming. Nonlinear dynamic characteristics of rotor system with angular misalignment fault[J]. Vibration, Test and Diagnosis, 2011, 31(5): 552-556.
[10] Antonino-Daviu J, Popaleny P. Detection of induction motor coupling unbalanced and misalignment via advanced transient current signature analysis[C]// 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 2018: 2359-2364.
[11] Verucchi C , Bossio J , Bossio G , et al. Misalignment detection in induction motors with flexible coupling by means of estimated torque analysis and MCSA[J]. Mechanical Systems and Signal Processing, 2016, 80(12): 570-581.
[12] Reddy M C S, Sekhar A S. Detection and monitoring of coupling misalignment inrotors using torque measurements[J]. Measurement, 2015, 61: 111-122.
[13] Yang Ming, Chai Na, Liu Zirui, et al. Motor speed signature analysis for local bearing fault detection with noise cancellation based on improved drive algorithm[J]. IEEE Transactions on Industrial Electronics, 2020, 67(5): 4172-4182.
[14] Bhattacharya I, Getoor L. A latent dirichlet model for unsupervised entity resolution[C]//Proceedings of the 2006 SIAM International Conference on Data Mining, Bethesda, MD, USA, 2006: 47-58.
[15] Haroun S, Seghir A N, Touati S. Misalignment fault detection and diagnosis using AR model of torque signal[C]//IEEE International Symposium on Diagnostics, Guarda, Portugal, 2015: 322-326.
[16] 刘杨, 李炎臻, 石拓, 等. 转子-滑动轴承系统不对中-碰摩耦合故障分析[J]. 机械工程学报, 2016, 52(13): 79-86.
Liu Yang, Li Yanzhen, Shi Tuo, et al. Analysis of rotor sliding bearing system misalignment rub impact coupling fault[J]. Journal of Mechanical Engineering, 2016, 52(13): 79-86.
Angle Misalignment Fault Detection Method of Motor's First Installation Based on Speed Signal
Abstract In order to improve the safety and reliability of the motor operation and reduce the misalignment phenomenon in the first installation of the motor, this paper proposed a method to detect the angular misalignment fault in the first installation of the motor based on the speed signal. This method does not require any health data and historical information, nor does it need to install additional vibration sensors. Firstly, the influence of the angular misalignment fault on the speed signal was analyzed. The fast Fourier transform and the least square method were used to analyze the speed signal. According to the coefficient of the quadratic term of the curve fitted by the change of the twice frequency amplitude with the rotation speed, and combined with the S-type distribution membership function, then the first installation misalignment of the motor was comprehensively evaluated. Finally, the simulation model and experimental platform of permanent magnet synchronous motor (PMSM) were built. The results show that the method is feasible and effective for the detection of angle misalignment fault in the first installation of PMSM, and has a great application prospect.
keywords：Permanent magnet synchronous motor, first installation, misalignment, speed signal
DOI:10.19595/j.cnki.1000-6753.tces.200179
中图分类号：TM315
杨 明 男，1978年生，博士，教授，博士生导师，研究方向为电力电子技术及交流伺服系统与智能控制。E-mail：yangming@hit.edu.cn（通信作者）
黄 旭 男，1997年生，硕士研究生，研究方向为电气法伺服驱动链机械故障诊断。E-mail：tszshuangxu@163.com
国家自然科学基金资助项目（51677037, 51690182）。
收稿日期 2020-02-23
改稿日期 2020-06-28
（编辑 赫蕾）