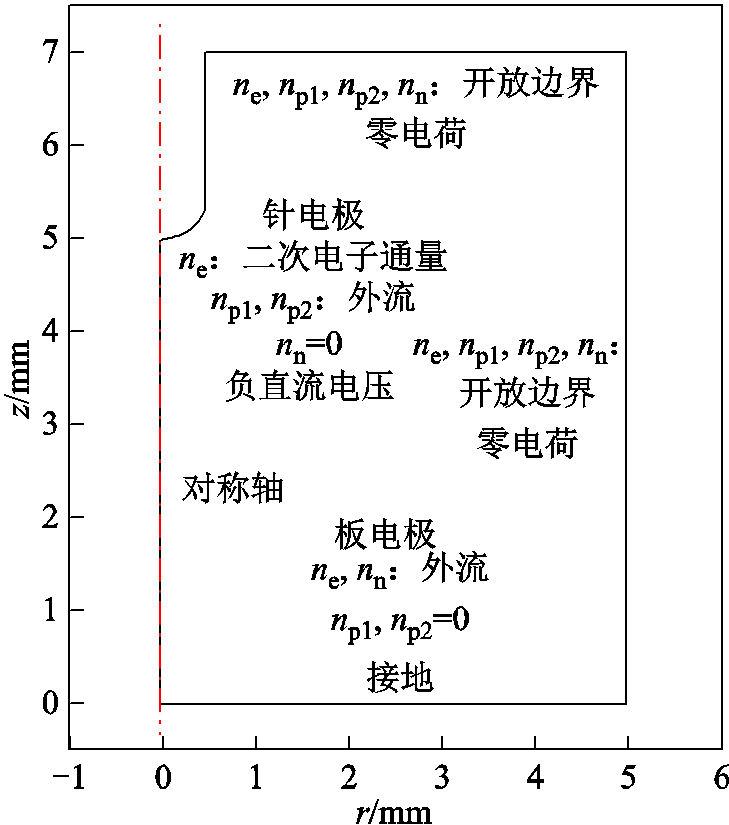
图1 负电晕放电仿真几何模型
Fig.1 Simulation geometry of the negative corona discharge model
摘要 为了研究SF6/N2混合气体负直流电晕电流脉冲特性,建立SF6/N2混合气体二维轴对称针-板几何模型,对不同电场不均匀系数下的负直流电晕放电进行了仿真计算。通过将放电过程中正离子、负离子和电子的连续性方程与泊松方程耦合,研究负电晕电流脉冲的形成机制,分析了电场不均匀系数对带电粒子变化过程和电流脉冲特征参数的影响,并通过针-板模型电晕放电实验平台验证了仿真模型的有效性。仿真结果表明,电流脉冲形成过程中,电子数密度远小于离子数密度,且正离子数密度大于负离子数密度;每个电流脉冲对应一个负离子云的形成和迁移,随着电场不均匀系数减小,由于针电极和负离子云之间的静电排斥,负电晕会呈现先偏离针尖发展、而后又向针尖回移的趋势;电流脉冲幅值整体呈增大趋势,初始电流脉冲宽度增大,脉冲上升时间和下降时间增长,同时脉冲重复率减小。
关键词:负直流电晕 电流脉冲 电场不均匀系数 SF6/N2混合气体 针-板模型
由于高介电强度和高稳定性等优点,SF6气体被广泛应用于气体绝缘电力设备。然而,SF6是一种会对自然环境造成巨大危害的温室气体,其全球变暖潜能值(Global Warming Potential, GWP)是CO2的23 900倍,同时较高的液化温度限制了SF6在高寒地区的使用[1-2]。近年来,SF6替代气体的研究引起了世界范围内关注,目前SF6/N2混合气体被认为是可以降低SF6气体消耗的一种有效方法,并且已经在第二代气体绝缘输电线路(Gas Insulated transmission Line, GIL)中得到应用[3-4]。
随着直流技术的大幅发展,此类SF6或SF6/N2混合气体绝缘电力设备在直流输电工程领域得到广泛使用。在制造、运输和装配过程中,设备内部难免会出现不同程度和类型的绝缘缺陷,由尖端缺陷或导电微粒污染而引起的电晕放电会降低绝缘气体的性能,从电晕起始到间隙击穿的放电模式转换更会严重损坏设备的内绝缘[5]。脉冲放电是其中一个复杂且重要的放电模式,通常将负电晕起始电压定义为气体击穿判据[6],因此研究直流电压作用下SF6/N2混合气体负电晕电流脉冲特性,对于完善SF6/N2混合气体电晕放电微观机理,优化电力设备的绝缘设计具有重要意义。
针-板电极作为一种典型电极结构已在电晕放电实验和仿真研究中得到较为成熟的应用[7-10]。针电极曲率半径决定了电场不均匀系数,会影响针尖附近电场以及带电粒子漂移扩散,对电晕放电发展造成不可忽视的影响。早在20世纪70年代,N. H. Malik等[11]最先研究了电场不均匀系数和气体组分对SF6/N2混合气体负电晕起始电压的影响,同时给出了负电晕起始电压的计算公式。邱毓昌等[12]提出需在不均匀电场的电晕起始电压计算中引入混合气体优异值(M值),并给出了不同类型不均匀电场的M值计算方法。近年来,汪沨等[13]仿真研究了电场不均匀系数和SF6含量对流注电晕放电发展的影响,发现由于电极半径或电极间距变化而改变的电场不均匀系数,会对放电稳定性产生相反影响。陈会利等[14]研究了电场不均匀系数对SF6/N2混合气体击穿特性的影响,发现电场不均匀系数的变化对混合气体正负击穿电压差值的改变极小。庞培川等[15]研究了电场不均匀系数对SF6/N2混合气体电晕起始特性的影响,结果表明电场畸变严重时,正负极性下均存在混合气体起始电压高于纯SF6起始电压的情况。因此,针对电场不均匀系数对SF6/N2混合气体负电晕放电的影响,目前研究主要集中在电晕起始特性和击穿特性上,而对于电晕电流脉冲特性的研究较少,尤其是电流脉冲形成中的微观物理过程鲜有报道。
本文在0.3MPa气压和300K环境温度中,采用二维轴对称针-板几何模型,模拟了不同针电极曲率半径下SF6/N2混合气体的负直流电晕放电。通过将放电过程中正离子、负离子和电子的连续性方程与泊松方程耦合,研究了负电晕电流脉冲的形成机制和电场分布情况,分析了不同电场不均匀系数下脉冲幅值、脉冲时间参数和脉冲重复率等电流脉冲特征参数的变化规律。通过搭建针-板模型电晕放电实验平台,在与仿真条件相同的环境中进行了实验验证。
基于流体动力学理论建立了SF6/N2混合气体二维轴对称针-板几何模型,并采用有限元软件COMSOL进行计算。负电晕放电仿真几何模型如图1所示,其中,气压p为0.3MPa,气体混合比为j(SF6):j(N2)=2:8,针-板间距d为5mm,针电极曲率半径r0分别设置为50μm、100μm、200μm、300μm和500μm,并且在针电极上施加负直流电压。

图1 负电晕放电仿真几何模型
Fig.1 Simulation geometry of the negative corona discharge model
SF6/N2混合气体电晕放电过程中会涉及上百种粒子和化学反应,然而模型中考虑过多的粒子和化学反应会使计算过程繁杂且非常昂贵。如已有研究中指出的[16-17],考虑放电过程中正离子、负离子和电子的连续性方程与泊松方程耦合,就可以很好地描述电晕放电过程和电流脉冲形成。连续性方程控制着不同带电粒子的运动、产生和消散,用来计算电流脉冲不同阶段带电粒子的时空分布,同时采用泊松方程耦合来计算电场分布。控制方程如式(1)~式(5)所示。
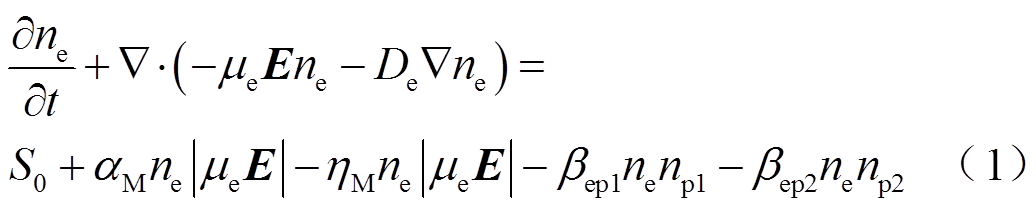
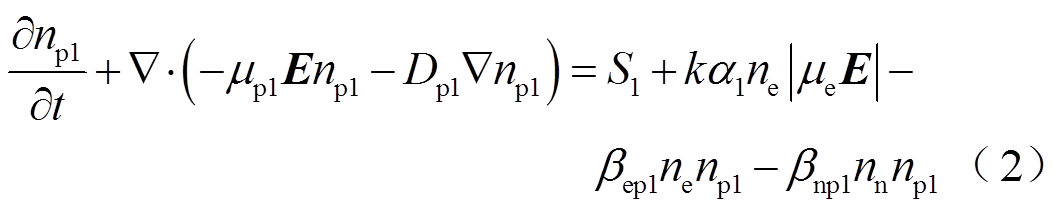
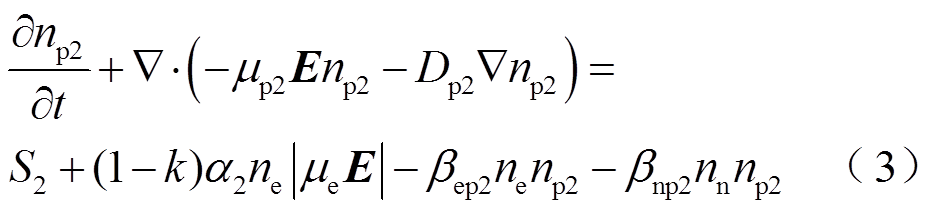
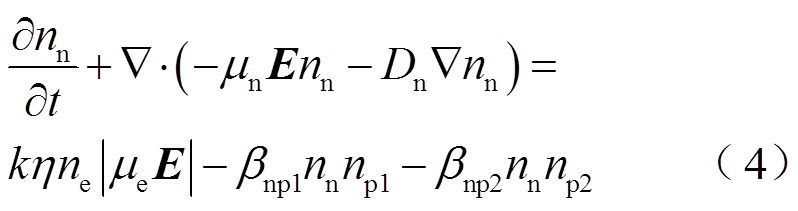
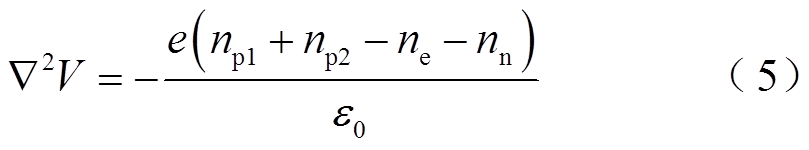
式中,αM、α1、α2分别为SF6/N2混合气体、纯SF6和纯N2的电离系数(m2);ηM、η分别为SF6/N2混合气体和纯SF6的附着系数(m2);k为混合气体中SF6体积分数;ne、np1、np2、nn,μe、μp1、μp2、μn和De、Dp1、Dp2、Dn分别为电子、SF6中正离子、N2中正离子和负离子的数密度(m-3)、迁移率(m2/V·s)和扩散系数(m2/s);βep1、βep2、βnp1、βnp2分别为电子与SF6中正离子、电子与N2中正离子、负离子与SF6中正离子、负离子与N2中正离子的复合系数(m3/s);t为时间(s),E为电场强度矢量(V/m);V为外施电压(kV);e为元电荷(C);ε0为真空介电常数(F/m);S0、S1、S2代表主要由光电离产生的带电粒子源项。
SF6和N2中的计算参数分别参考R. Morrow[18]和A. J. Davies等[19]的研究结果。SF6和N2的折合电离系数和折合附着系数分别为
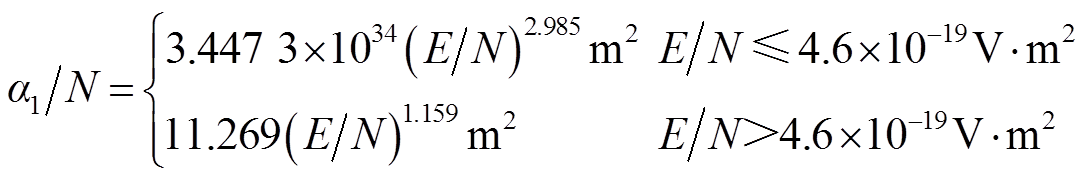 (6)
(6)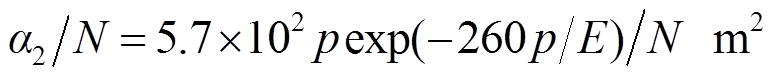 (7)
(7)
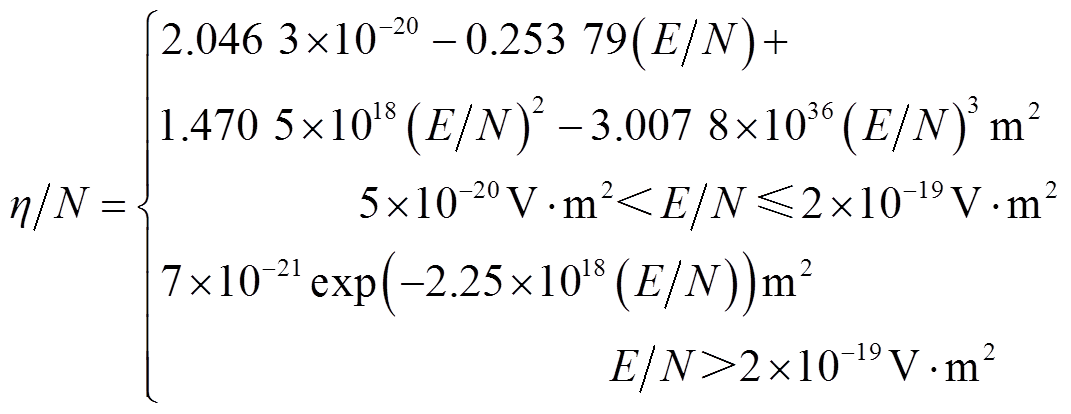 (8)
(8)
式中,E为电场强度(V/m);N为气体总数密度(m-3),p为气压(Torr, 1Torr=133.322Pa)。
由于SF6和N2的电子迁移速度和电子能量分布函数相近[20],可以认为两种气体之间相互作用较弱,因此SF6/N2混合气体的折合电离系数和折合附着系数可由式(9)计算得出[12,21]。
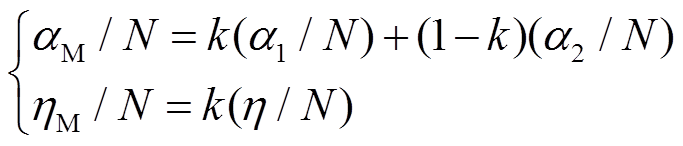 (9)
(9)电子迁移率和扩散系数分别为
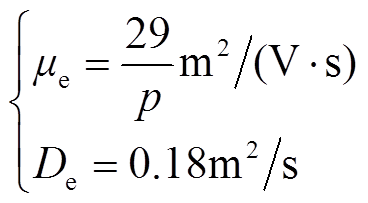 (10)
(10)
SF6和N2中正、负离子迁移率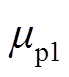 、
、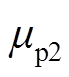 和
和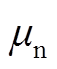 分别为
分别为
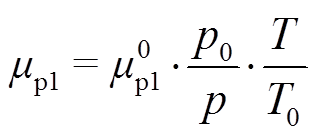 (11)
(11)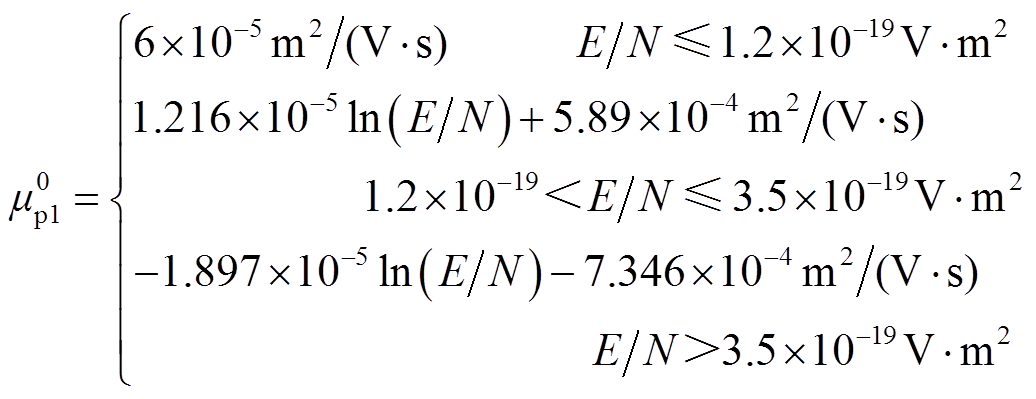 (12)
(12)
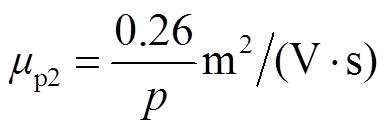 (13)
(13)
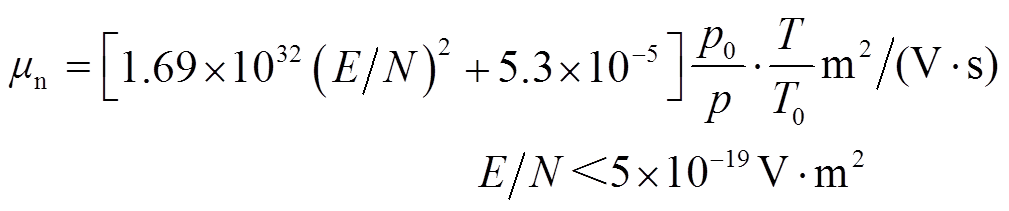 (14)
(14)式中,p、p0分别为设定气压、标准大气压(kPa);T、T0分别为气体温度、常温(K)。
正离子和负离子扩散系数由Einstein方程得到,仿真中设定离子温度为气体温度[22]。
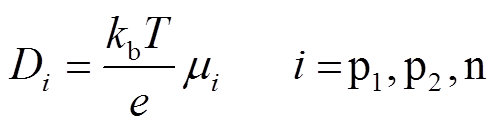 (15)
(15)式中,kb为玻耳兹曼常数(J/K)。
电子与正离子、正离子与负离子的复合系数分别为
 (16)
(16)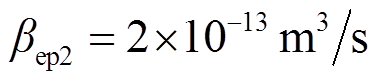 (17)
(17)
正离子撞击针电极产生二次电子,二次电子通量可由式(18)计算得出。
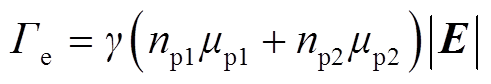 (18)
(18)式中,γ为二次电子发射系数,取值为0.01[17]。
在负电晕放电过程中,碰撞电离较弱区域需要光电离提供种子电子来引发新的电子崩,因此光电离在电晕发展中非常重要。目前关于SF6和SF6/N2混合气体中的光电离仿真模型并不成熟,且缺乏相关数据。在仅有的几篇报道中,有学者[23-24]通过设置电子和正离子初始数密度为常数项,使用背景电离代替光电离,并验证了该方法的合理性。但该方法仅能模拟一次流注电晕发展过程,即首个脉冲的产生与消散。还有学者[8,13]参考Zheleznyak空间光电离模型,但该模型计算繁琐且针对SF6/N2混合气体的参数并不完善。脉冲群的产生涉及电晕的多次放电,所以为了更好体现光电离在负电晕放电各阶段中的作用,本文采用在电子和正离子的连续性方程中增加常数项的方法替代背景电离常数项方法,认为每时刻都有确定数量的电子和正离子由光电离产生。参考已有报道中的常数范围,S0设置为10-10 mol/ (m3·s),S1和S2均设置为5×10-11 mol/(m3·s)。
负离子初始数密度设为0,正离子和电子的初始数密度服从高斯分布,即
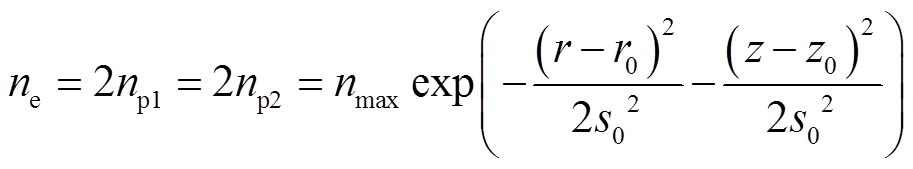 (19)
(19)式中,nmax为最大数密度,取值为1016 m-3;s0为50μm;(r0, z0)代表针尖坐标;r和z代表点(r0, z0)的圆柱坐标。
电晕电流采用N. Sato [25]提出的方法进行计算,计算式为
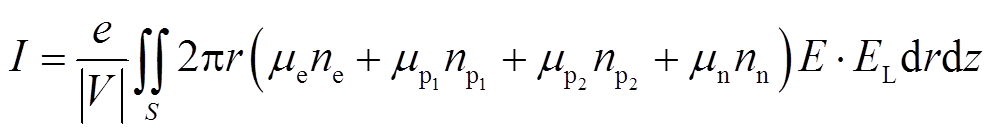 (20)
(20)式中,EL为拉普拉斯场(V/m);S为二维轴对称区域。
不同针电极曲率半径会改变电场分布,从而改变电场不均匀度,电场不均匀度一般使用电场不均匀系数f来表示。对于针-板模型,f可以由式(21)计算得出[26]。
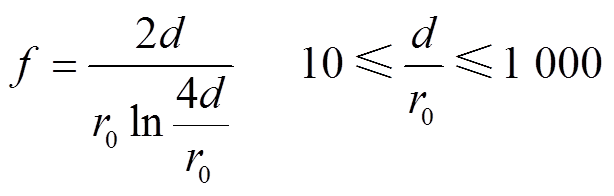 (21)
(21)当针-板间距为5mm时,给出了不同针电极曲率半径下计算得出的电场不均匀系数见表1。由表可以发现,随着针电极曲率半径的增大,电场不均匀系数减小,但均属于极不均匀电场。
表1 不同针电极曲率半径下的电场不均匀系数
Tab.1 Electric field non-uniformity coefficient under different needle tip radii

针电极曲率半径/μmf 5033.4 10018.9 20010.9 3007.9 5005.4
本文同时搭建了针-板模型电晕放电实验平台,如图2所示。针电极圆柱段直径2mm,板电极直径100mm,针-板间距0~30mm可调,针电极曲率半径与仿真条件一致,设置为50~500μm。针电极材料选用具有耐高温烧蚀的钨铜合金制成,板电极材料为不锈钢。针电极由高压直流电源提供负直流电压,中间串联阻值为2MΩ的限流电阻R1。板电极经阻值为75Ω的无感采样电阻接地,用于测量放电电流I2。针-板模型放置于密封腔体中,SF6/N2混合气体通过微量气体调节装置通入放电腔体,调节装置控制精度为0.1Pa。针电极电压U1由分压比为2 000:1的阻容分压器测量,采样电阻电压U2由低压探头测量,且电压信号均由数字示波器(Lecroy WaveSurfer 104MXs-B)存储,该示波器带宽1GHz,最高采样率10GS/s。示波器阻抗为1MΩ耦合,探头与示波器相匹配。放电电流I2=U2/R2,腔体侧壁设计有石英窗用于观察腔体内放电情况。
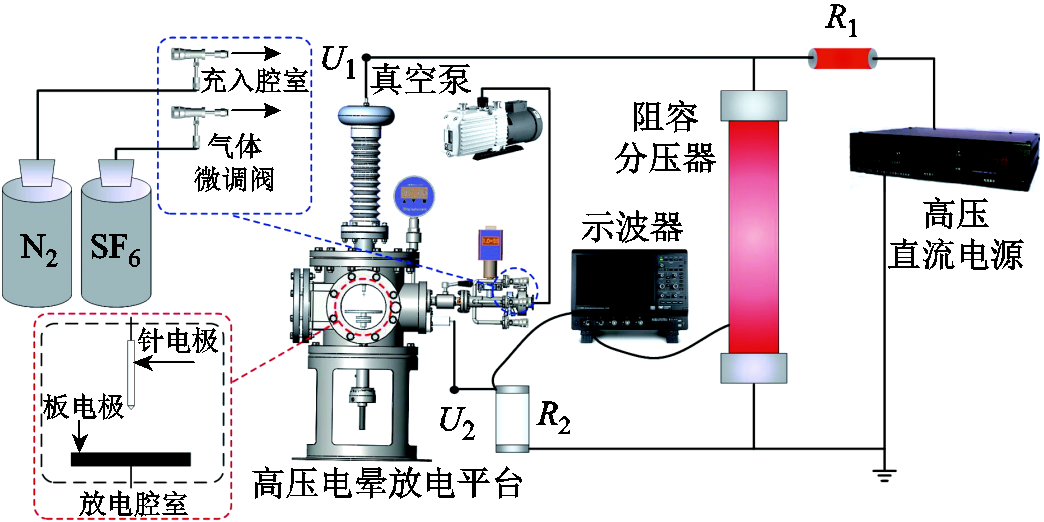
图2 实验平台示意图
Fig.2 Schematic diagram of the experimental platform
主要实验方法为:①利用砂纸对针电极尖端进行打磨处理,并通过电子显微镜对针电极曲率半径进行测量,确保满足实验要求;②放置针-板模型并调整间距至实验要求的5mm;③对放电腔体进行抽真空处理,通入N2纯气至0.2MPa,静置干燥12h,再次抽真空后通入SF6/N2混合气体至0.3MPa。根据Dalton分压定律,控制气体混合比等于控制单个气体分压[27],如式(22)所示。
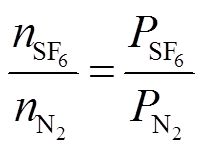 (22)
(22)式中,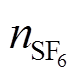 和
和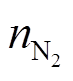 分别为纯SF6和纯N2的摩尔数;
分别为纯SF6和纯N2的摩尔数;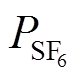 和
和 分别为两种气体组分的分压。因此,混合气体中SF6含量φ(SF6)可表示为
分别为两种气体组分的分压。因此,混合气体中SF6含量φ(SF6)可表示为
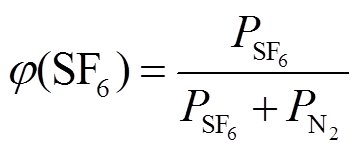 (23)
(23)为了提高气体混合比的准确度,应首先通入含量较少的气体组分,将两种气体充至实验所需压力后,静置24h以保证气体混合均匀。
图3给出了针电极曲率半径为100μm和500μm时,SF6/N2混合气体的电流脉冲波形。外施电压为仿真模型出现首个电流脉冲的起始电压,分别为5.7kV和17.5kV。实际研究结果中电压和电流均为负值,为方便表述,文中所有分析均采用绝对值。可以发现,虽然仿真结果的电流脉冲幅值和脉宽与实验结果存在一定差异,但电流脉冲波形和变化趋势相似,且仿真中不同针电极曲率半径下的脉冲幅值和脉宽对比更加明显,因此验证了仿真模型的有效性。需要注意的是,实验结果中的次峰叠加现象是由于电路中的行波变化所引起的,但并不会影响电流脉冲的变化趋势[28-29]。
负电晕放电的首个电流脉冲波形如图4所示,以针电极曲率半径100μm,外施电压5.7kV为例,根据负电晕电流脉冲的四个特征阶段,包括脉冲起始、脉冲峰值、脉冲下降沿半峰值和脉冲结束,给出了首个电流脉冲各阶段的带电粒子数密度和电场的变化过程。
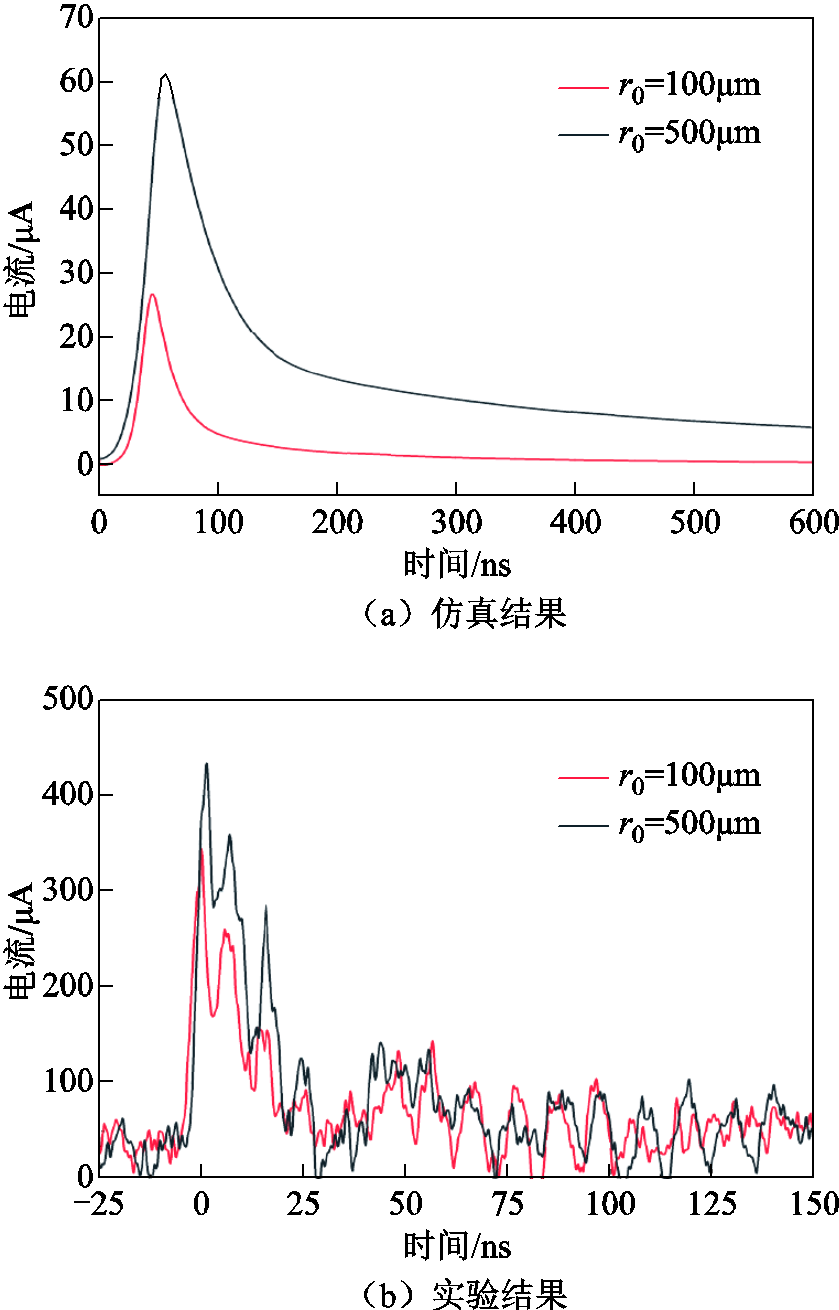
图3 不同针电极曲率半径下仿真和实验电流脉冲变化趋势比较
Fig.3 Comparison of simulated and experimental current pulse under different needle tip radii
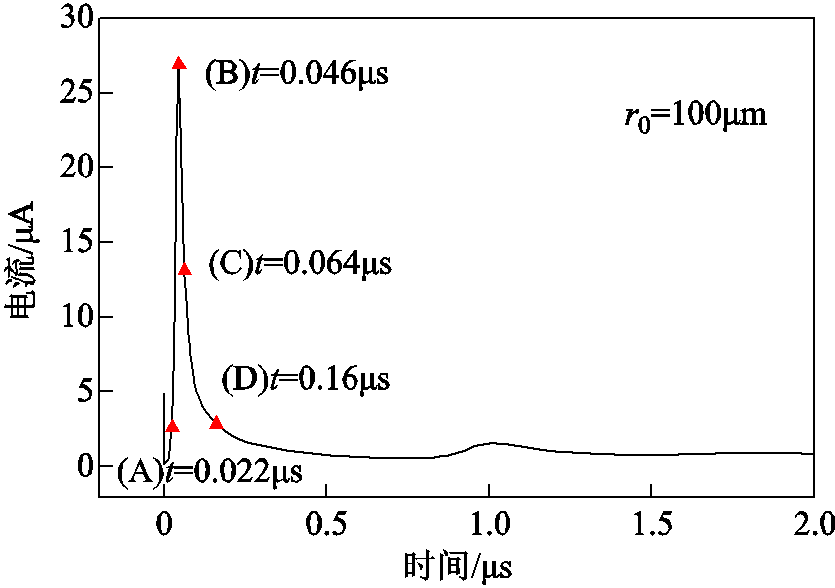
图4 负电晕放电的首个电流脉冲波形
Fig.4 First current pulse waveform of negative corona discharge
阶段A为脉冲起始阶段,如图5a所示,此时电子最大数密度为1.46×1016m-3,正离子最大数密度为1.58×1018m-3,负离子最大数密度为1.16×1018m-3,最大约化电场为523Td(1Td=10-21V·m2)。正离子向针电极移动,负离子和电子向板电极移动,并逐渐形成带电粒子云。空间电荷对拉布拉斯场影响较小,针尖电场变化不大,电离程度较强。
阶段B为脉冲峰值阶段,如图5b所示,带电粒子向针尖收聚,带电粒子最大数密度均增加了一个数量级。电子最大数密度为1.48×1017m-3,正离子最大数密度为4.61×1019m-3,负离子最大数密度为3.07×1019m-3。此时正离子云非常接近针电极表面,电离区域变窄,由于空间电荷的影响,最大约化电场增加至583Td,而正/负离子云之间的电场被逐渐抑制。正离子数密度与负离子相比增加较快,加强了正离子云与针尖之间区域电场,使得电离加剧,形成脉冲上升沿。

图5 电流脉冲特征阶段带电粒子数密度和电场的变化过程
Fig.5 Change process of number density of charged particles and reduced electric field in characteristic stages of current pulse
阶段C为脉冲下降沿半峰值阶段,如图5c所示,此时正离子云到达针电极表面,负离子云的电场削弱作用开始主导,最大约化电场降至459Td,电离减弱。针尖附近区域(阶段C约化电场分布中4.95mm到5mm区域)电场降至气体临界击穿场强以下,此区域电离停止,从而形成脉冲下降沿。随着电子数密度的减小,负离子数密度也会减小,且负离子云范围扩大。
在脉冲形成过程中,即从阶段A到阶段C,电子数密度远小于离子数密度,且正离子数密度大于负离子数密度。这是由于带电粒子最大数密度出现的位置是不同的,高场强区电离作用强,正离子数密度大;低场强区附着作用强,负离子数密度大。高场强区附着作用弱,电子数密度增量约等于正离子数密度增量,但在迁移作用下,正离子云向针电极移动,电子云远离针电极。由于正离子云两侧电场强度差异大,低电场强度下电子被大量附着形成负离子,因此形成了正离子云数密度最高,而负离子数密度也远大于电子数密度的现象。
阶段D为脉冲结束阶段,如图5d所示,此时负离子云远离针电极,电离停止区域电场逐渐恢复,放电进入下个电流脉冲起始阶段。
在脉冲阶段C处,正离子撞击针电极产生二次电子,由于针电极和负离子云的静电排斥,电子呈现远离针尖移动的趋势,并在针电极电场强度最大处由碰撞电离产生正离子,正离子云也呈现偏离针尖的趋势。但由于针电极曲率半径较小,电离停止区域较小,电子偏离趋势并不明显,下次放电仍然会从针尖处开始发展。
图6给出了针电极曲率半径为300μm和500μm时,脉冲阶段C和阶段D中电子和正离子数密度的变化过程。可以发现,随着电场不均匀系数的减小,电子和正离子偏离针尖的趋势逐渐明显。当针电极曲率半径为500μm时,由于针电极圆弧处电场分布均匀,而电离停止区域较大且电场并未完全恢复,所以下次放电会在偏离针尖处开始发展。
图7给出了不同针电极曲率半径下各脉冲结束时负离子数密度的空间分布。可以发现,每个电流脉冲对应一个负离子云的形成和迁移,随着电场不均匀系数的减小,曲率半径较大的针尖更利于带电粒子的偏移。与r0=100μm相比,当r0=300μm时,第二次放电形成的负离子云最大数密度位置已经偏离针尖。虽然电离停止区域有所增加,但高电场强度仍然集中在针尖附近,使得负离子云并未完全偏离针尖。当r0=500μm时,第二次放电会明显在偏离针尖处发展,而在电离停止区域的电场恢复后,第三次放电又会回移至针尖处开始发展。这是由于负离子云对针尖电场有较强的抑制作用,但偏离针尖处受其抑制作用较小,出现了偏离针尖处电场强度高于针尖电场强度的情况,因此放电会偏离针尖发展。而随着针尖电场强度的逐渐恢复,偏离针尖处电场强度减小,电离相对较弱,放电又会重新偏向针尖发展。因此,对于种子电子位于针尖的负电晕放电,随着电场不均匀系数的减小,电晕会有先偏离针尖发展,而后又向针尖回移的趋势。
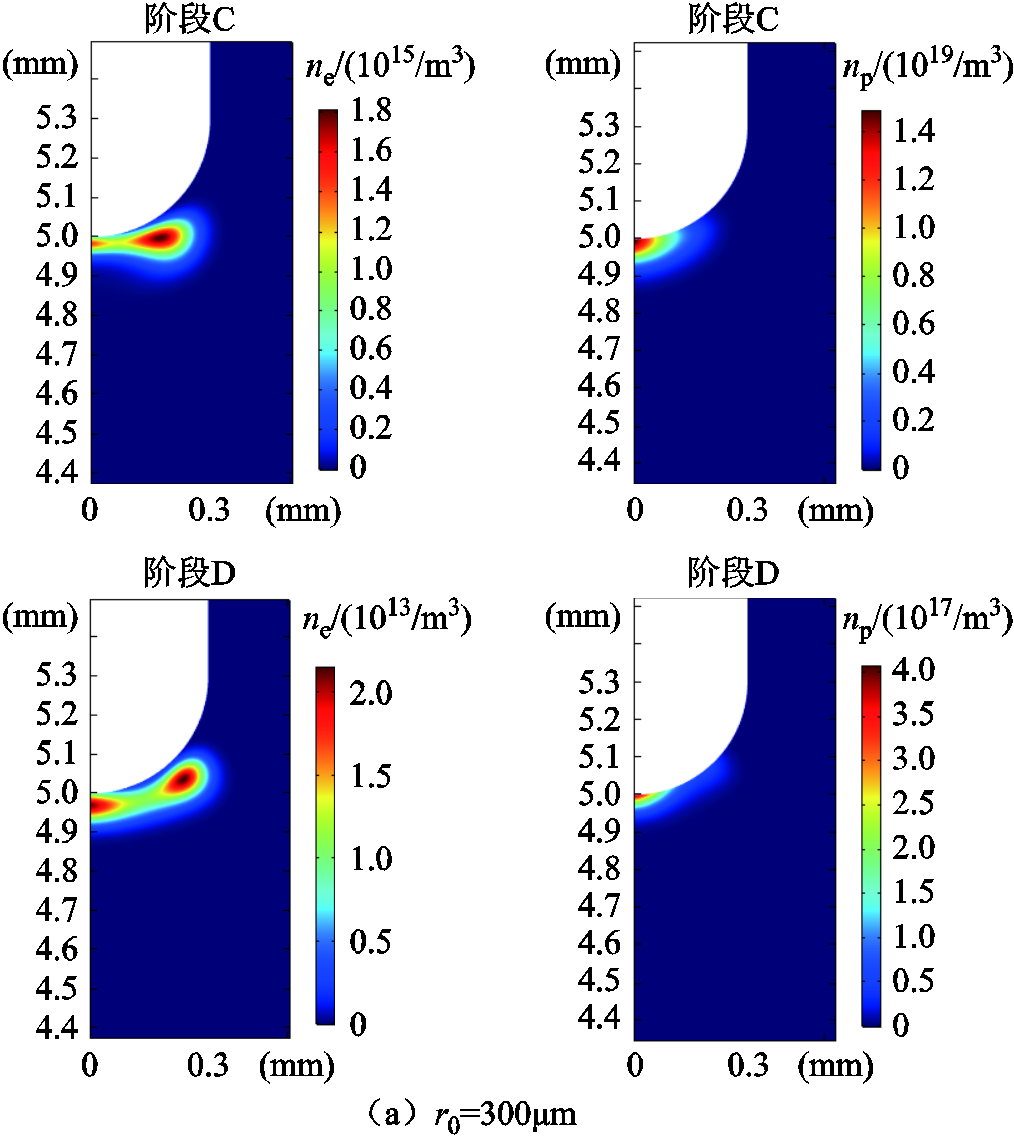
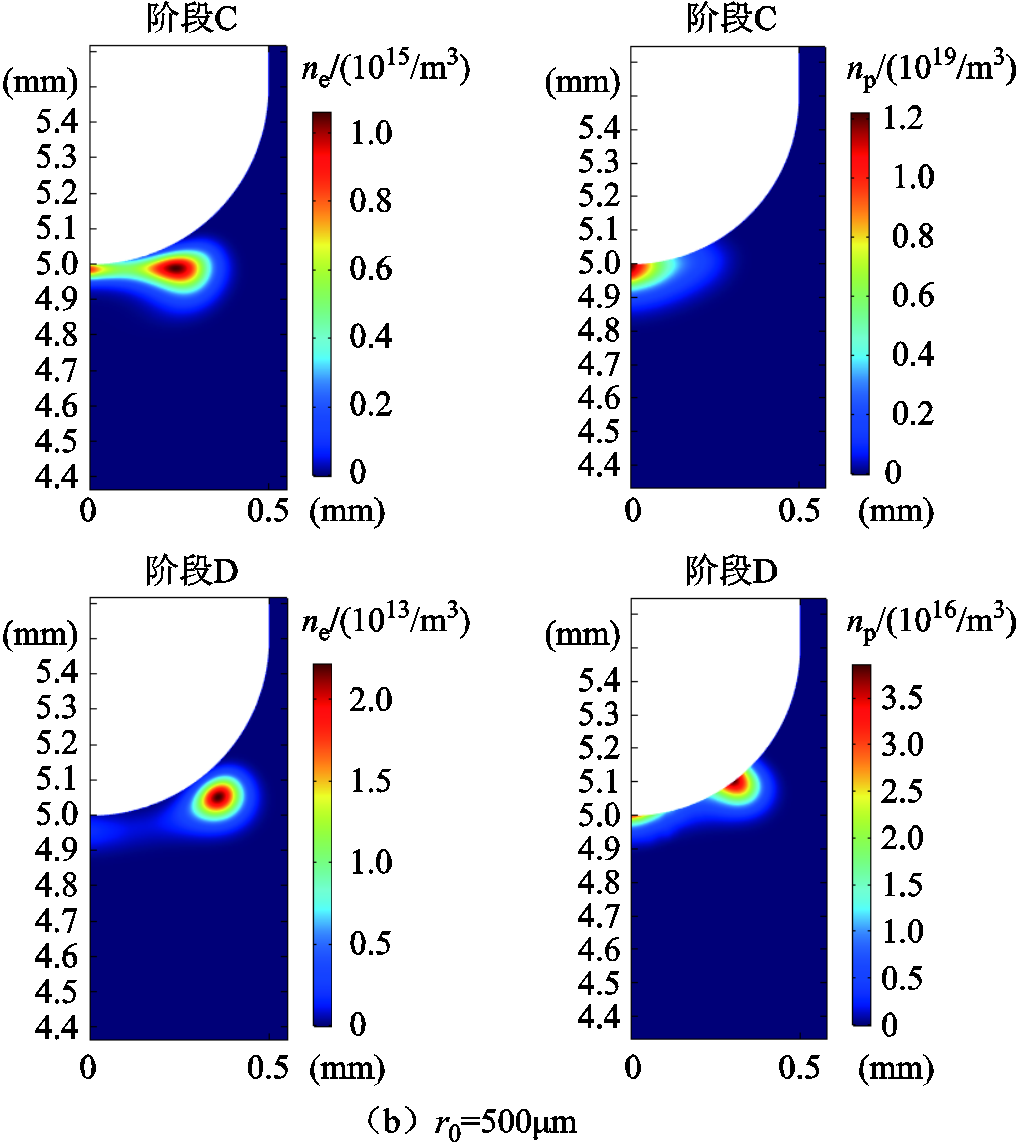
图6 不同针电极曲率半径下电流脉冲下降沿带电粒子数密度的变化过程
Fig.6 Change process of number density of charged particles in current pulse fall time under different needle tip radii
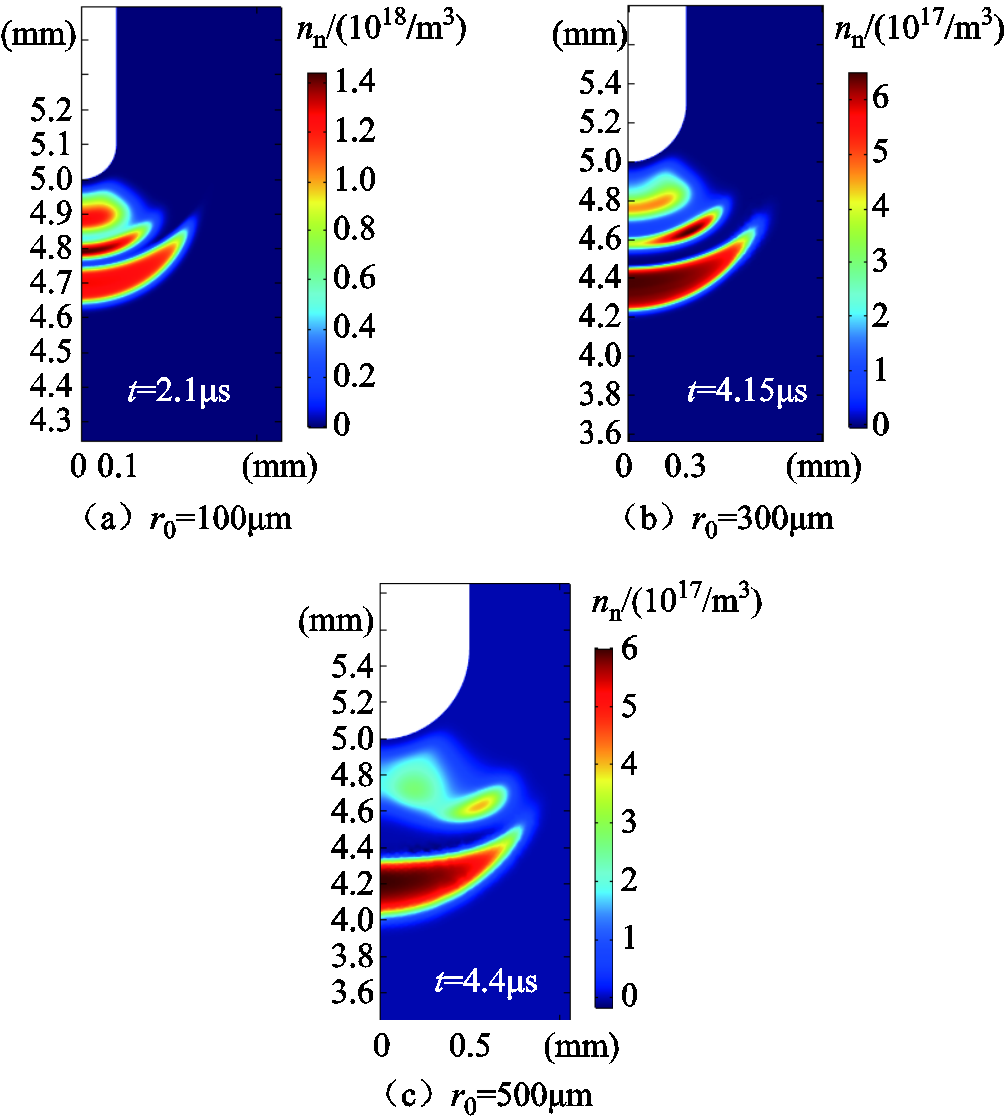
图7 各脉冲结束时负离子数密度的空间分布
Fig.7 Spatial distribution of the number density of negative ions at the end of each current pulse
图8给出了不同针电极曲率半径下负电晕电流波形,其中Ia表示初始脉冲幅值,虚线框内为第二个脉冲起始时间。仿真中所使用的外施电压均为该模型可以出现首个电流脉冲的起始电压,见表2。
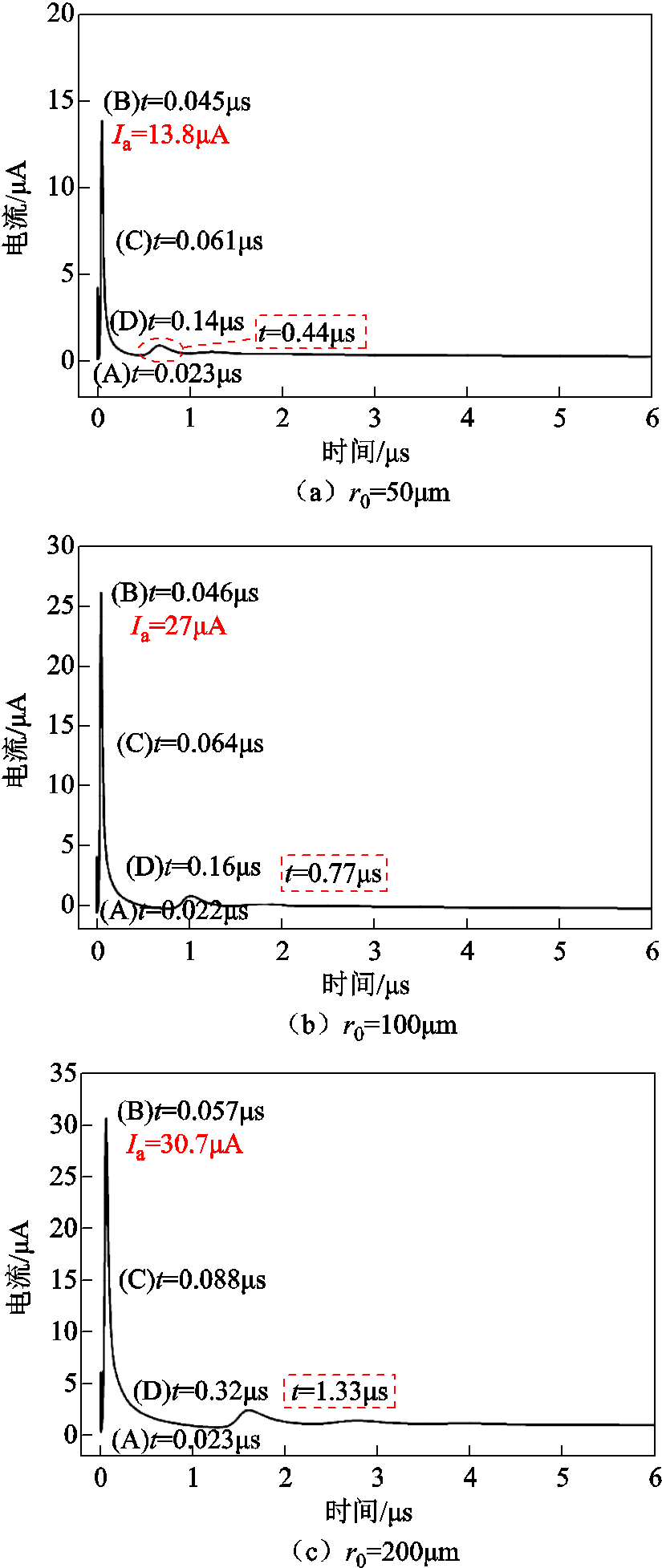
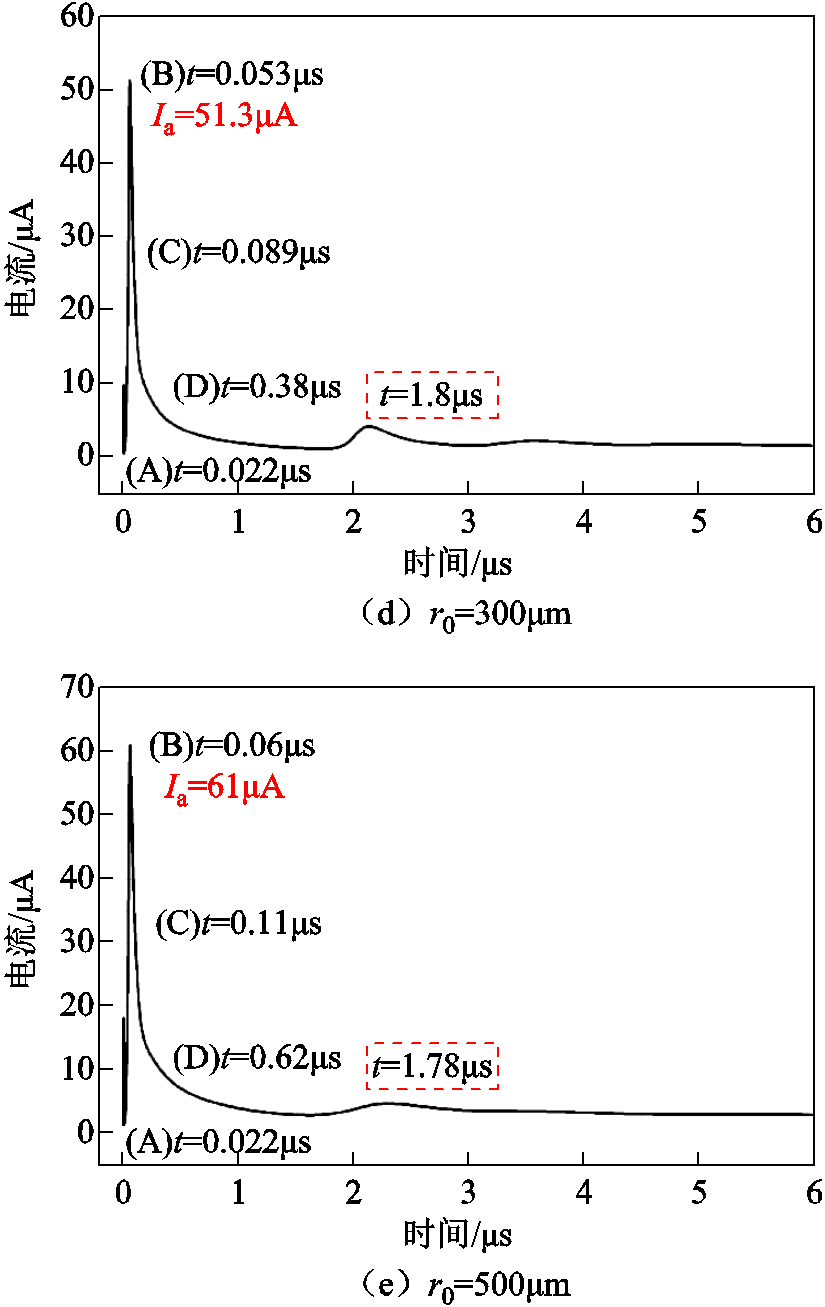
图8 不同针电极曲率半径下的负电晕电流波形
Fig.8 Current waveforms of negative corona under different needle tip radii
表2 不同针电极曲率半径下的仿真模型电压
Tab.2 The applied voltages of simulation model under different needle tip radii

针电极曲率半径/μm外施电压/kV 503.7 1005.7 2009.1 30012.2 50017.5
由图8和表2可以发现,随着电场不均匀系数减小,电流脉冲的幅值整体呈增大趋势,初始电流脉冲宽度更大,上升时间和下降时间更长。随着针电极曲率半径增大,针尖附近的电离区域增大,带电粒子的生成范围扩大,带电粒子数增加。但负离子数密度与小曲率半径时相比有所减小,因此脉冲阶段A中负离子云抑制作用减弱,使得电子碰撞电离更剧烈,产生了大量的电子和正离子,脉冲幅值更高。电离区域增大,使得有效电离距离(xTS)增大[30],相同气体环境中,电子迁移至电离边界时间增加,电流脉冲上升时间变长。脉冲阶段C中正离子云到达针电极表面后,负离子云对电场的削弱作用开始成为主导。虽然经过脉冲上升时间内的大量积聚,负离子数密度相对增加,但由于有效电离距离增大,负离子云距离针电极更远,削弱作用反而下降,所以电流脉冲下降时间更长,脉冲宽度更大。
随着电场不均匀系数减少,在首个脉冲结束时(阶段D),负离子云距离针尖更远,电场强度更小,不利于向板电极迁移。所以需要更多时间移除负离子云以恢复电场,使得相邻脉冲间隔更大,即脉冲重复率减小。而当r0=500μm时,由于正离子云和电子完全偏离针尖,摆脱了电离停止区域电场的影响,可以很快在高电场强度区域触发下一次放电,因此两次脉冲间隔时间略有减少。
图9给出了不同针电极曲率半径下初始脉冲幅值和相邻脉冲间隔的仿真和实验结果对比。由于仿真模型和实验测量得到的电晕起始电压存在差别,实验外施电压仍采用表2仿真模型电压,且在r0=50μm时选择实验电晕起始电压(4.5kV)作为外施电压。可以发现,仿真结果和实验结果的变化趋势一致,随着电场不均匀系数的减小,初始脉冲幅值和相邻脉冲间隔均呈现增加趋势。
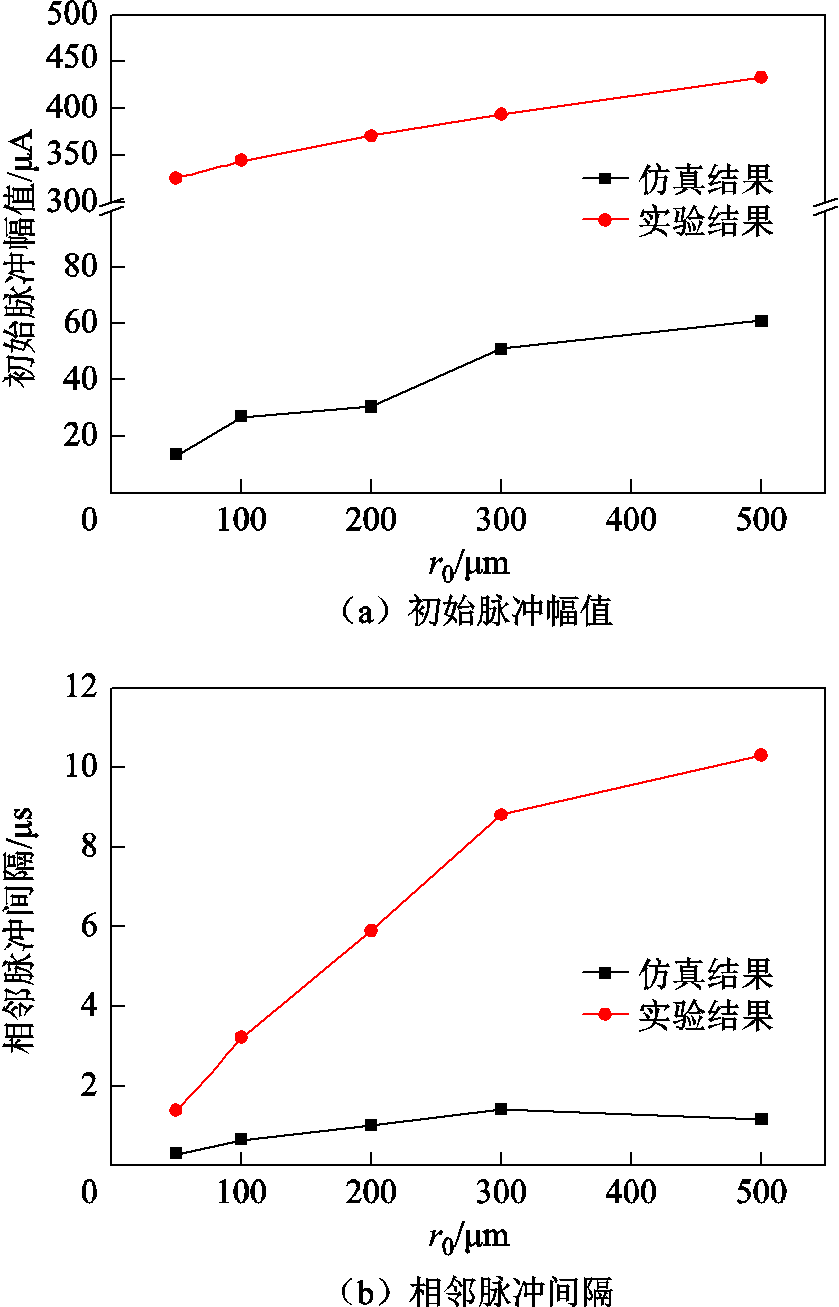
图9 不同针电极曲率半径下仿真和实验结果比较
Fig.9 Comparison of simulated and experimental results under different needle tip radii
本文建立了SF6/N2混合气体二维轴对称针-板几何模型,通过改变针电极曲率半径模拟了不同电场不均匀系数下的负直流电晕放电,并通过针-板模型电晕放电实验平台验证了仿真模型的有效性。研究了电流脉冲的形成机制,以及电场不均匀系数对带电粒子变化过程和电流脉冲特征参数的影响,具体结论如下:
1)SF6/N2混合气体负电晕电流脉冲形成过程中,电子数密度远小于离子数密度,且正离子数密度大于负离子数密度。
2)在负电晕放电过程中,每个电流脉冲对应一个负离子云的形成和迁移。随着电场不均匀系数减小,由于针电极和负离子云之间的静电排斥,负电晕会有先偏离针尖发展,而后又向针尖回移的趋势。
3)随着电场不均匀系数减小,电流脉冲幅值整体呈增大趋势,初始电流脉冲宽度增大,脉冲上升时间和下降时间增长,同时脉冲重复率减小。
参考文献
[1] 周朕蕊, 韩冬, 赵明月, 等. SF6替代气体分解特性的研究综述[J]. 电工技术学报, 2020, 35(23): 4998-5014. Zhou Zhenrui, Han Dong, Zhao Mingyue, et al. Review on decomposition characteristics of SF6 alternative gases[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4998-5014.
[2] 张晓星, 陈琪, 张季, 等. 高气压下环保型 C4F7N/CO2混合气体工频击穿特性[J]. 电工技术学报, 2019, 34(13): 2839-2845. Zhang Xiaoxing, Chen Qi, Zhang Ji, et al. Power frequency breakdown characteristics of environmental-friendly C4F7N/CO2 gas mixtures under high pressure conditions[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2839-2845.
[3] 刘溟, 邹建明, 邱睿, 等. SF6及SF6/N2中分解气体在气体绝缘传输管道内的扩散特性计算[J]. 电工技术学报, 2020, 35(11): 2478-2490. Liu Ming, Zou Jianming, Qiu Rui, et al. The computation of diffusion characteristics of decomposition gases in SF6 and SF6/N2 within gas insulated transmission lines[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2478-2490.
[4] 李康, 郭润睿, 张国强. 一种SF6替代气体——氟碳气体的故障分解气体产生规律及基于分解物气体的故障判据研究[J]. 电工技术学报, 2019, 34(12): 2649-2656. Li Kang, Guo Runrui, Zhang Guoqiang. Study on fault decomposition properties and fault diagnostic criterion of fluorocarbon gas—a substitute gas for SF6[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2649-2656.
[5] He Yanliang, Sun Anbang, Xue Jianyi, et al. Experimental study on pulse characteristics of negative corona discharge in SF6/N2 gas mixtures under DC voltages[J]. AIP Advances, 2020, 10(5): 055027.
[6] Lieberoth-Leden B, Pfeiffer W. Predischarge development in N2 and SF6 at high gas pressure[J]. IEEE Transactions on Electrical Insulation, 1989, 24(2): 285-296.
[7] 何寿杰, 张钊, 李庆, 等. 针板负直流电晕放电中的脉冲等离子体特性[J]. 高电压技术, 2018, 44(3): 870-875. He Shoujie, Zhang Zhao, Li Qing, et al. Characteristics of pulsing plasma in needle-plane corona discharge driven by negative direct power source[J]. High Voltage Engineering, 2018, 44(3): 870-875.
[8] 徐建源, 陈会利, 林莘, 等. 针−板电极下SF6的电晕放电特性分析[J]. 高电压技术, 2019, 45(1): 293-302. Xu Jianyuan, Chen Huili, Lin Xin, et al. Analysis of corona discharge characteristics of SF6 under pin-plate electrodes[J]. High Voltage Engineering, 2019, 45(1): 293-302.
[9] 臧奕茗, 钱勇, 刘伟, 等. C4F7N/CO2混合气体中尖端缺陷的流注放电仿真研究[J]. 电工技术学报, 2020, 35(1): 34-42. Zang Yiming, Qian Yong, Liu Wei, et al. Simulation study on streamer of tip defects in C4F7N/CO2 mixed gas[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 34-42.
[10] 梅丹华, 方志, 邵涛. 大气压低温等离子体特性与应用研究现状[J]. 中国电机工程学报, 2020, 40(4): 1339-1358. Mei Danhua, Fang Zhi, Shao Tao. Recent progress on characteristics and applications of atmospheric pressure low temperature plasmas [J]. Proceedings of the CSEE, 2020, 40(4): 1339-1358.
[11] Malik N H, Qureshi A H. Calculation of discharge inception voltages in SF6-N2 mixtures[J]. IEEE Transactions on Electrical Insulation, 1979, EI-14(2): 70-76.
[12] 邱毓昌, 冯允平. SF6/N2混合气体绝缘强度的计算[J]. 中国电机工程学报, 1993, 13(增刊1): 57-62. Qiu Yuchang, Feng Yunping. Calculation of dielectric strength of SF6/N2 gas mixtures[J]. Proceedings of the CSEE, 1993, 13(S1): 57-62.
[13] 汪沨, 李锰, 潘雄峰, 等. 基于FEM-FCT算法的SF6/N2混合气体中棒-板间隙电晕放电特性的仿真研究[J]. 电工技术学报, 2013, 28(9): 261-267. Wang Feng, Li Meng, Pan Xiongfeng, et al. Corona discharge simulations of rod-plate gap in SF6/N2 gas mixtures using FEM-FCT method[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 261-267.
[14] 陈会利, 徐建源, 李璐维, 等. 不均匀电场SF6/N2混合气体击穿特性的实验研究[J]. 高压电器, 2016, 52(12): 110-115. Chen Huili, Xu Jianyuan, Li Luwei, et al. Experimental study on breakdown characteristics of SF6/N2 mixtures in non-uniform electric field[J]. High Voltage Apparatus, 2016, 52(12): 110-115.
[15] 庞培川, 孙泽明, 张芊, 等. 直流电压作用下极不均匀电场中SF6/N2混合气体局部放电起始特性研究[J]. 西安交通大学学报, 2019, 53(4): 1-7. Pang Peichuan, Sun Zeming, Zhang Qian, et al. Study on partial discharge initial characteristics of extremely inhomogeneous electric field in SF6/N2 mixture under DC high voltage[J]. Journal of Xi’an Jiaotong University, 2019, 53(4): 1-7.
[16] Georghiou G E, Papadakis A P, Morrow R, et al. Numerical modelling of atmospheric pressure gas discharges leading to plasma production[J]. Journal of Physics D: Applied Physics, 2005, 38(20): R303-R328.
[17] Gao Qingqing, Niu Chunping, Adamiak Kazimierz, et al. Numerical simulation of negative point-plane corona discharge mechanism in SF6 gas[J]. Plasma Sources Science and Technology, 2018, 27(11): 115001.
[18] Morrow R. A survey of the electron and ion transport properties of SF6[J]. IEEE Transactions on Plasma Science, 1986, PS-14(3): 234-239.
[19] Davies A J, Davies C S, Evans C J. Computer simulation of rapidly developing gaseous discharges[J]. Proceedings of IEE, 1971, 118(6): 816-823.
[20] 李璐维, 林莘, 徐建源, 等. SF6/N2和SF6/CF4混合气体放电参数计算分析[J]. 高压电器, 2016, 52(12): 60-65. Li Luwei, Lin Xin, Xu Jianyuan, et al. Calculation of the discharging parameters of SF6/N2 and SF6/CF4 mixtures[J]. High Voltage Apparatus, 2016, 52(12): 60-65.
[21] Guo Can, Zhang Qiaogen, Ma Jingtan, et al. Negative synergistic effect of SF6/N2 gas mixtures in non-uniform electric field under lightning impulse[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(4): 1393-1402.
[22] Herrebout D, Bogaerts A, Yan M, et al. One-dimensional fluid model for an rf methane plasma of interest in deposition of diamond-like carbon layers[J]. Journal of Applied Physics, 2001, 90(2): 570-579.
[23] Dhali S K, Pal A K. Numerical simulation of streamers in SF6[J]. Journal of Applied Physics, 1988, 63(5): 1355-1362.
[24] Zeng F, Zhang M, Yang D, et al. Hybrid numerical simulation of decomposition of SF6 under negative DC partial discharge process[J]. Plasma Chemistry and Plasma Processing, 2019, 39(1): 205-226.
[25] Sato N. Discharge current induced by the motion of charged particles[J]. Journal of Physics D: Applied Physics, 1980, 13(1): L3-L6.
[26] 邱毓昌. GIS装置及其绝缘技术[M]. 北京: 水利电力出版社, 1994.
[27] 侯志强, 郭若琛, 李军浩. 直流电压下SF6/N2混合气体沿面局部放电特性[J]. 电工技术学报, 2020, 35(14): 3087-3096. Hou Zhiqiang, Guo Ruochen, Li Junhao. Partial discharge characteristics of the surface discharge in SF6/N2 of the mixed gas under DC voltage[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3087-3096.
[28] Reid A J, Judd M D. Ultra-wide bandwidth measurement of partial discharge current pulses in SF6[J]. Journal of Physics D: Applied Physics, 2012, 45(16): 165203.
[29] Reid A J, Judd M D, Stewart B G, et al. Partial discharge current pulses in SF6 and the effect of superposition of their radiometric measurement[J] Journal of Physics D: Applied Physics, 2006, 39(19): 4167-4177.
[30] He Yanliang, Sun Anbang, Zhang Xing, et al. Effect of trace SF6 on negative corona characteristics in SF6/N2 gas mixtures under DC voltages[J]. AIP Advances, 2020, 10(8): 085303.
Effect of Electric Field Non-Uniformity Coefficient on Current Pulse Characteristics of Negative DC Corona in SF6/N2 Gas Mixtures
Abstract In order to investigate the current pulse characteristics of negative DC corona in SF6/N2 gas mixtures, a two-dimensional axisymmetric needle-to-plane geometry model in SF6/N2 gas mixtures was established, and the negative DC corona discharge under different electric field non-uniformity coefficients was simulated. By coupling the continuity equations of positive ion, negative ion and electron in the discharge with Poisson equation, the formation mechanism of negative corona current pulse was studied. The effect of electric field non-uniformity coefficient on the change process of charged particles and current pulse characteristic parameters was analyzed. The validity of simulation model was verified by the needle-to-plane model corona discharge experimental platform. The simulation results show that during the formation of the current pulse, the electron number density is much smaller than the ion number density, and the positive ion number density is greater than the negative ion number density.Each current pulse corresponds to the formation and drift of a negative-ion cloud. With decreasing the electric field non-uniformity coefficient, the negative corona will deviate from the needle tip first and then move back to the needle tip due to the electrostatic repulsion between the needle electrode and the negative-ion cloud. The pulse amplitude shows an overall increasing trend, the initial pulse duration increases, the rise time and fall time of pulse increase, and the pulse-repetition rate decreases.
keywords:Negative DC corona, current pulse, electric field non-uniformity coefficient, SF6/N2 gas mixtures, needle-to-plane model
DOI:10.19595/j.cnki.1000-6753.tces.201633
中图分类号:TM851
何彦良 男,1992年生,博士研究生,研究方向为绝缘气体放电机理和高电压试验技术。 E-mail:ylhe2666@163.com
孙安邦 男,1984年生,博士,教授,博士生导师,研究方向为放电等离子体技术及其应用、低温等离子体数值仿真和电推进技术。E-mail:anbang.sun@xjtu.edu.cn(通信作者)
国家自然科学基金(51777164)和中央高校基本科研专项资金(xtr042019009, PY3A083)资助项目。
收稿日期 2020-12-11
改稿日期 2021-02-02
(编辑 郭丽军)