0 引言
MOSFET和IGBT等功率器件是实现电能变换与控制的关键器件，已被广泛应用于电力、交通、航空和航天等领域[1-3]。随着使用要求和制造工艺的不断提升，功率器件封装尺寸逐渐减小，但功率等级却日益增高，这导致器件面临着严重的热失效风险。为了准确评估器件的散热能力及寿命，需要有效获知器件在特定工作条件下的结温变化特性[4]。
一般情况下，器件结温可采用直接测量法、热敏电参数法和热网络模型等方法得到[5-7]。其中，直接测量法利用红外测温直接获取芯片温度，具有高精度和高分辨率的优势，但该方法需要打开器件封装，存在一定破坏性，难以在实际场合应用。热敏电参数法利用器件部分电参数与温度之间的映射关系推算结温，无需改变器件封装，且具有响应速度快的优势。但该方法对电参数测量电路的要求较高，目前仍处于发展阶段。热网络模型基于热电类比理论建立，利用热容和热阻构成的等效网络估计器件结温。在得到热网络参数后，热网络模型能够简单快速地实现结温估计，且其精度已在工程领域中被广泛接受，故已成为当前应用最广的结温获取方法[8-10]。
依据所需的边界温度不同，热网络模型可分为结-壳和结-环境两类[11]。结-壳热网络模型将器件壳温测量值作为结温估计的边界条件，重点关注结温与壳温之间的变化关系，适用于器件在线热管理和热保护。但该模型不能反映器件与环境之间的热交换过程，难以分析特定工况下的器件散热能力，也难以估计器件剩余工作寿命。结-环境热网络模型将环境温度作为解算的边界条件，反映了工作环境对器件壳温及结温的影响，是实现器件热安全评估和寿命预测的重要依据。
目前，结-环境热网络模型已经得到了广泛应用。文献[12]将该模型与PSpice和Saber等仿真软件相结合，建立了功率器件的热电联合仿真模型，为器件可靠性分析提供了基础。文献[13]在结-环境热网络模型基础上，对计及焊层疲劳影响的器件寿命进行了评估。文献[14-15]基于结-环境热网络模型，分析了风电变流器的热可靠性与寿命。此外，结-环境热网络模型还被用来评估自然冷却和强制冷却方式下的器件散热能力，有效地提升了器件工作的安全性[16]。
然而，当前结-环境热网络模型一般假设器件在稳定环境下工作，忽略了环境对流随机性对结温造成的影响。实际上，功率器件总是通过散热器或功率设备壳体与外界环境进行换热。由于工作环境空气流动的不确定性，功率设备不可避免地受到随机对流影响[17]。尤其对于采用自冷方式散热或在户外工作的功率设备，外界环境风速的随机变化会严重影响其内部功率器件的散热能力，进而引起器件结温的随机波动。为了向器件热安全分析和寿命预测方法提供更加真实可靠的结温变化数据，迫切要求对传统结-环境热网络模型加以改进，使其能够有效地描述结温在随机对流作用下的不确定性变化。
为此，本文在传统模型基础上，结合小波包变换和马尔可夫链方法，提出一种计及环境对流随机性的结-环境热网络模型，并以功率 MOSFET为对象进行了实验验证。结果表明，所提模型能够克服传统模型的不足，有效反映器件结温在随机对流作用下的变化规律。
1 传统结-环境热网络模型
1.1 模型原理
功率器件结-环境热网络模型由热阻和热容组成的等效网络表示，其典型结构如图1所示[11]。图1中，P为器件损耗，也称为热流量；Tj和Tc分别为器件结温和壳温；Th和Ta分别为散热器温度和环境温度； T1 ～ Tm−1、 C 1 ～ Cm 和 R1 ～ Rm分别为结-壳中各节点的温度、热容和热阻，m为网络节点数；Ch为散热器热容；Rch为壳与散热器之间导热材料的传导热阻；Rha为散热器与环境之间的对流热阻，表征了器件与环境之间的热交换能力。
图1 结-环境热网络模型的典型结构
Fig.1 Typical structure of junction-to-ambient thermal network model
由图1可见，结-环境热网络模型由结-壳热网络和壳-环境热网络两部分组成，可表示成微分方程组形式，即
其中，变量A、B和C分别为
将环境温度作为上述微分方程组求解时的边界条件，便可对器件结温进行估计。需要注意的是，对于IGBT功率模块而言，热网络模型中还应包括反并联二极管对应的热网络结构[18]。由于该热网络与器件本体热网络的结构形式完全相同，故不再赘述。
1.2 模型参数的确定
在结-环境热网络模型中，损耗P是重要的模型输入参数。一般情况下，损耗P主要包含器件通态损耗Pon、器件开关损耗Psw、体二极管或反并联二极管损耗 dP。上述损耗可由器件物理模型或查询数据手册等方法得到。为了便于使用，工程中通常将损耗拟合为器件工作电压V、电流I、频率f及结温Tj等参数的函数P(V, I, f, Tj)。限于篇幅，本文不对此展开介绍，有关损耗计算的方法和公式可详见文献[11, 19-21]。
热容 C 1 ～ Cm 和热阻 R1 ～ Rm等参数可通过器件的瞬态热阻抗曲线获得[11, 22]。一般情况下，器件厂家已经对这些热参数进行了测定，并在数据手册中提供。由于器件个体差异和老化程度影响，数据手册参数会存在一定误差，但其精度仍可满足大部分实际工程需要[19]。
热容Ch、传导热阻Rch和对流热阻Rha一般通过相应的定义计算，分别为
式中，ch和mh分别为散热器的定压比热容和质量；d c h、Ach和λch分别为壳与散热器之间导热材料的厚度、面积和导热系数；Aha和hha分别为散热器的对流散热面积和对流换热系数。
2 本文模型
2.1 模型原理
传统结-环境热网络模型通常假设功率器件在稳态环境中工作，即器件散热器与环境之间对流热阻Rha变化的不确定性被忽略。因此，传统模型无法准确反映随机对流作用下的器件结温变化规律。为此，本文提出了一种计及环境对流随机性的结-环境热网络模型，其结构如图2所示。
图2 本文模型结构
Fig.2 Structure of the proposed model
由图2可见，本文模型在传统模型的基础上，引入了对流热阻的样本获取及随机模拟两个环节。其基本思想是：首先利用器件历史损耗和温度数据，得到对流热阻样本的时间序列
，上标n为时间点；再利用小波包变换和马尔可夫链方法进行对流热阻的随机模拟，得到模拟序列
；随后将模拟序列
代入结-壳热网络中，以计及随机对流对器件温度变化造成的影响。由于多数工程中的器件电压和开关频率可预先得知，故最后只需在模型中指定器件工作电流和环境温度，便可模拟器件在当前随机对流环境和指定工况条件下的结温变化情况。
由于本文模型计及了环境对流热阻的动态变化，故可准确揭示对流随机性对结温造成的不确定性影响，有效地模拟随机对流环境下的结温波动现象，克服传统模型的不足。因此，本文模型能够为器件热安全性评估和寿命预测提供更加真实有效的数据支撑，有助于分析器件在当前随机对流环境和指定工况下的过热风险概率和老化程度。图3给出了本文模型在工程中使用的流程示意图。
图3 本文模型使用流程示意图
Fig.3 Flow chart of the proposed model
2.2 对流热阻样本的获取
当环境对流存在动态变化时，散热器的对流换热系数hha难以通过理论确定，故不宜通过式（7）计算对流热阻Rha。为了获取对流热阻样本，可先将式（1）在n时刻进行离散，并将其分离为
式中，Δt为离散步长；变量 D n 、 E n 、 F n 和 G n分别为
式（8）为结-壳热网络的离散表达式。当n时刻下的损耗 P n 和壳温
已知时，可通过式（8）求解n+1时刻下结-壳热网络内部各节点的温度。式（9）为壳-环境热网络的离散表达式，对其改写可得n时刻下的对流热阻表达式为
分析可见，只要已知n时刻下的器件损耗 P n、壳温
和环境温度
等历史数据，便可利用式（8）和式（14）得到对流热阻样本 
，并形成样本序列
。
2.3 对流热阻的随机模拟
受环境空气流速变化影响，发热器件的对流热阻并非简单随机变量，而是具有一定频域变化特性的复杂随机过程。为此，本文利用小波包变换和马尔可夫链方法实现对流热阻的随机模拟。其中，小波包变换用于分析对流热阻在不同频带内的变化特性，而马尔可夫链用于模拟各频带内对流热阻的随机变化。
小波包变换由小波变换发展而来，是对小波变换结果的进一步细分[23-24]，其基本原理是：通过多分辨率分析手段，将初始信号送入一系列频带划分不重叠的滤波器组中，从而获得信号在时频空间内的变化特征。小波包变换包含分解和重构两个算法，其分解算法及重构算法分别为
式中，
为原始信号的小波包分解结果；上标 j为小波包分解层数；下标l为分解结果所处子频带的序号；h和g分别为小波包分解的低通和高通滤波器，其取值由小波包基函数决定；h和g分别为h和g的对偶滤波器。
由小波包变换原理可知，若需获得原始信号在l子频带下的信号分量，应先将其他子频带下的分解结果设定为零，再将l子频带内的分解结果
重构回原始信号空间。通过此重构运算，便可获得对流热阻在l频带下的样本序列
。
马尔可夫链是一种随机过程描述方法，可模拟随机序列的变化情况[25-28]。依据马尔可夫链定义，随机序列 Y n在n+1时刻的状态只与其n时刻状态有关，与其他时刻状态无关。那么，随机过程 Y n 各状态之间的转移概率可由条件概率pij表示为
式中，si和sj分别为随机序列在n时刻和n+1时刻下的状态。
在总数为S的状态空间中，条件概率pij可组成状态转移概率矩阵pij，如式（19）所示。该矩阵表示 nY变化的随机特性，故利用其中的矩阵元素便可对随机过程进行模拟。
式中，
根据上述小波包变换和马尔可夫链方法原理，可得对流热阻的随机模拟流程，如图4所示。具体来看，对流热阻的随机模拟分为如下四个步骤：
图4 对流热阻的随机模拟流程
Fig.4 Flow diagram of convective thermal resistance random simulation
（1）通过式（15）～式（17），对流热阻样本序列
进行小波包变换，得到不同子频带下的对流热阻样本序列
，l∈[1,L]。其中，L为频带划分总数，由信号特征和系统计算能力综合确定。
（2）分别将每个子频带内对流热阻样本序列
划分为S个状态，并通过马尔可夫链构建样本序列
的状态转移概率矩阵pij,l。样本序列的状态总数S越大，状态转移概率统计越准确，但会增大计算量，故需依据系统计算能力综合确定。
（3）基于状态转移概率矩阵pij,l中的元素，对样本序列
进行随机模拟，得到各子频带下的对流热阻模拟序列
。
（4）将所有的子频带模拟序列
进行叠加，得到初始频带下的对流热阻模拟序列
，完成对流热阻的随机模拟。
3 实验平台设计
为了验证本文所提模型的有效性，设计了如图5所示的功率器件随机对流实验平台。该平台主要由实验电路、可控风扇、直流电源和 PC等设备单元构成。
图5 功率器件随机对流实验平台
Fig.5 Power device random thermal convection experimental set-up
实验平台中，实验电路是一个典型的单相全桥电路，由 4个 MOSFET Q1～Q4构成，实验电路拓扑如图6所示。MOSFET型号为IRFB4410PbF，且均装有型号为YA35、有效散热面积为56cm2的铝散热器。表1给出了厂家手册所提供的器件与散热器热参数。实验电路接有 0.5Ω 电阻和 0.1mH电感形成的阻感负载，并以200ms为周期进行换相。可控风扇由一台转速可控的小型直流电机驱动，用于产生随机对流环境。直流电源输出电压为16V，用于实验电路供电。PC用于存储和分析实验数据。
图6 实验电路拓扑
Fig6 Topology of the experimental circuit
表1 器件与散热器的热参数
Tab.1 Thermal parameters of power device and heat sink
热阻/(℃/W) 热容/(J/℃)模型参数 R1 R2 Rch C1 C2 Ch数值 0.274 0.338 0.015 0.001 0.012 6.69
需要说明的是，由于实验电路中功率器件的规格型号与散热方式均相同，故本文仅以器件Q1为对象开展模型的实验验证。即在后文的实验与分析中，有关器件温度数据均是指器件Q1的数据。
4 实验分析与验证
4.1 随机对流环境下的器件结温变化分析
在验证所提模型有效性之前，先分析器件结温在随机对流环境下的变化现象。为此，在户外微风环境中测量实际的随机风速，并以该随机风速为参考量，结合实验平台的风扇转速控制，使功率器件工作在模拟对流环境中。图7对风扇产生的实验环境风速与实际测量的自然环境风速进行了对比。由图7中数据可见，两者风速较为吻合，满量程误差最大仅为7.8%。这表明，实验平台风扇产生的风速有效地反映了实际风速的随机变化，能够用来模拟器件工作的随机对流环境。
图7 实验环境与自然环境风速对比
Fig.7 Comparison of wind speed between experimental environment and natural environment
对随机对流环境下的功率器件进行温升实验。温升过程中，实验电路的母线电流为 17.5A，环境温度为22℃。图8给出了器件壳温和结温在实验中的变化情况。其中，器件壳温通过传感器直接测量得到，而结温通过式（8）和壳温测量值估计得到。式（8）本质上是结-壳热网络模型的离散表达式。在壳温测量准确的前提下，这种结-壳热网络模型的估计精度已被广泛接受。因此，式（8）所得结果可以作为结温实验结果，也可以作为评价其他模型结果的基准。为观察因电路换相而引起的结温波动现象，图8中还给出了结温的部分局部放大结果。由图8可见，尽管器件工作电流和环境温度相对稳定，但在随机对流作用下，器件壳温仍然出现了随机波动。受此影响，器件结温除了存在因电路换相引起的高频波动外，还存在因对流随机性引起的低频波动。
图8 温升实验过程中的器件壳温和结温变化
Fig.8 Case temperature and junction temperature changes of power device during temperature rise experiment
为了进行定量分析，利用Welch方法[29-30]计算结温的功率谱密度，所得结果如图9所示。由于功率谱密度表征了随机过程在不同频段内的变化程度，故能够反映结温的变化规律。观察可见，在本文实验过程中，器件结温在5Hz附近频段存在剧烈波动。由换相周期可知，该频段的结温变化是由于电路换相引起。除去该频段后，器件结温波动程度随着频率的增大呈现减小趋势。但在环境对流随机特性的影响下，结温功率谱密度曲线并不光滑，存在明显噪声。上述数据表明，不同频段中的器件结温波动具有明显的不一致性。因此，为了准确反映结温变化规律，需要计及对流随机性对结温造成的影响。
图9 温升实验过程中的器件结温功率谱密度
Fig.9 Power spectral density of power device junction temperature during temperature rise experiment
4.2 本文模型的有效性验证
依据本文模型的原理，对其有效性进行验证。首先通过式（6）和式（8）计算对流热阻，并形成对流热阻样本序列
，对流热阻的样本序列如图10所示。可以发现，受环境对流影响，器件对流热阻也存在随机变化，且这种变化同样具有一定的频域特性。
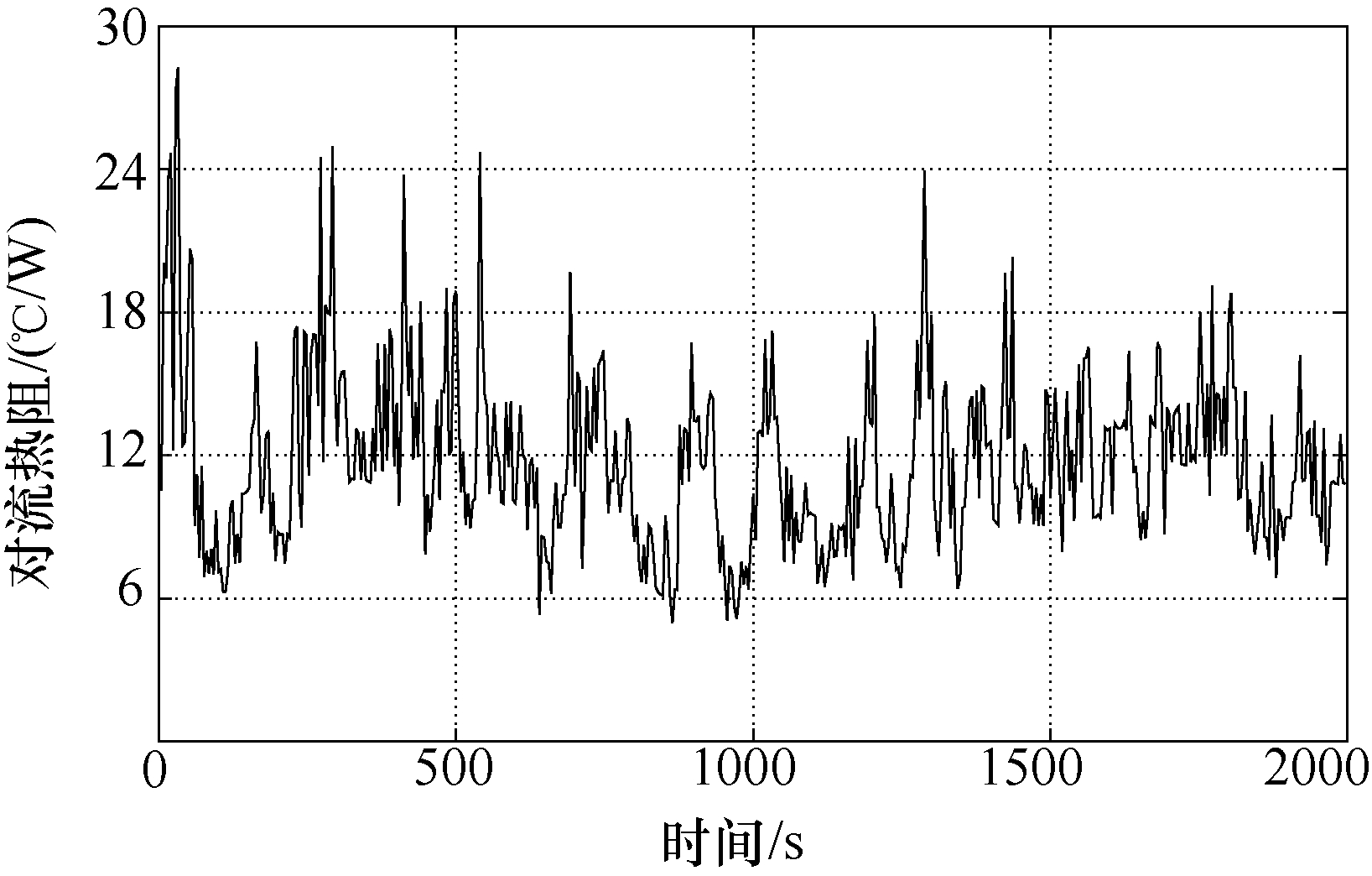
图10 对流热阻的样本序列
Fig.10 The sample sequence of convective thermal resistance
进行对流热阻的随机模拟。以db30小波为基函数，对样本序列
进行3层小
波包分解，并重构得到不同子频带l下的样本序列 ，不同子频带下的对流热阻样本序列如图11所示。由图中数据可见，对流热阻在不同频率下的时域变化特征并不同，其中，0～0.25Hz的低频段分量具有最高幅值。这表明，对流热阻的波动主要集中在该频段。
图11 不同子频带下的对流热阻样本序列
Fig.11 Sample sequences of convective thermal resistance in different sub-bands
将上述样本序列
划分为20个状态，并进行马尔可夫链统计，得到对流热阻的状态转移概率矩阵pij,1～pij,8，不同子频带下对流热阻样本序列的转移概率矩阵如图12所示。易发现，各状态转移概率矩阵元素之间存在较大差异，这也表明不同频带下的对流热阻变化规律并不相同。
图12 不同子频带下对流热阻样本序列的转移概率矩阵
Fig.12 Transition probability matrixes of convective thermal resistance sample sequences in different sub-bands
利用状态转移概率矩阵 pij,1～ pij,8，对不同频带下的对流热阻样本序列进行随机模拟。将不同子频带下的对流热阻模拟序列
进行叠加，得到初始频带下的模拟序列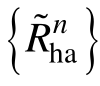
。随后，在电路母线电流为17.5A和环境温度为22℃条件下，利用所提模型得到一组器件结温模拟结果，本文模型和传统模型所得到的结温结果对比如图13所示。为了便于比较，图13还给出基于传统结-环境热网络模型所得的结温估计结果。由于传统模型未考虑环境对流的随机性，故其结温是利用对流热阻样本均值得到的。由图13中数据可见，传统模型所得结温估计结果波动较为平稳，这与图8所示的结温实验现象不符。而本文模型所得结温模拟结果呈现不确定波动，与结温实验结果相似。这表明，本文模型所得结果更加符合结温变化的实际现象。
图13 本文模型和传统模型所得到的结温结果对比
Fig.13 Comparison of junction temperature based on proposed model and traditional model
为定量分析本文模型所得随机结果，在相同条件下对器件结温波动进行 1 000次模拟，并计算所得结果的功率谱密度，本文模型所得结温结果的功率谱密度如图14所示。利用相关系数法[31]对图9和图14进行对比，可知两图中的功率谱密度相似程度高达99.63%。这表明，本文模型所得结温模拟结果与实验所得结温具有相似的随机变化规律。
图14 本文模型所得结温结果的功率谱密度
Fig.14 Power spectral density of power device junction temperature obtained by the proposed model
由于本文模型建立后，可以得到特定对流环境下的对流热阻随机变化规律和随机模拟结果。若将器件损耗与环境温度视为器件结-环境热网络中的自由参数，本文模型便可在随机对流环境中，对指定电流等级和环境温度下的器件结温随机变化进行模拟。为了对此进行验证，再从图10所示的对流热阻样本出发，依据本文模型原理，对不同母线电流和环境温度下的器件结温变化情况进行模拟。表2给出了结温模拟结果和相同条件下结温实验结果的功率谱密度相似度。由表中数据可见，结温模拟结果与实验结果的功率谱密度相似度均在98%以上。这表明，本文模型有效地克服了传统模型的不足，能够在随机对流环境中，对指定电流等级和环境温度下的器件结温随机变化现象进行描述。这对于提升器件热安全评估与寿命预测方法的准确度和可靠性具有重要意义。
表2 指定母线电流和环境温度下结温功率谱密度相似度
Tab.2 Similarity of power spectral density of junction temperature under the specified current and ambient temperature conditions
序号 母线电流/A 环境温度/℃ 功率谱密度相似度(%)1 7.5 18.4 98.86 2 10 21.8 99.36 3 12.5 23.3 99.60 4 15 26.8 99.63 5 20 27.5 99.42
5 结论
本文在功率器件的传统结-环境热网络模型基础上，结合对流热阻样本及其随机模拟方法，提出了一种计及环境对流随机性的结-环境热网络模型。设计了功率器件随机对流实验平台，对所提模型进行了验证。实验结果表明，本文模型有效地克服了传统模型的不足，能够在随机对流环境中，描述指定电流等级和环境温度下的器件结温随机变化现象，可为器件热安全评估与寿命预测方法提供更加真实有效的结温数据支撑。
未来还将开展两方面研究：①更加复杂的环境和工况下（如强迫对流和自然对流交替变化，日照、气温和负载随机波动等），进一步揭示器件结温变化的影响因素和随机规律；②结合滑窗和模型预测方法，不断对器件环境和工况随机特性进行预测、误差优化和滚动修正，自适应提升模型随机模拟结果精度，实现模型在工程中的在线应用。本文研究为上述工作的完成提供了良好基础。
[1]Dusmez S, Ali S H, Heydarzadeh M, et al.Aging precursor identification and lifetime estimation for thermally aged discrete package silicon power switches[J].IEEE Transactions on Industry Applications, 2017, 53(1): 251-260.
[2]Fleetwood D M, Winokur P S, Dodd P E.An overiview of radiation effects on electronics in the space telecommunications environment[J].Microelectronics Reliability, 2000, 40(1): 17-26.
[3]Ning Puqi, Li Lei, Wen Xuhui.A hybrid Si IGBT and SiC MOSFET module development[J].CES Transactions on Electrical Machines and Systems, 2017, 1(3):360-366.
[4]Xu Yang, Chen Hao, Sen Lü, et al.Thermal model for power converters based on thermal impedance[J].Journal of Power Electronics, 2013, 13(6): 1080-1089.
[5]陈明, 胡安, 唐勇, 等.绝缘栅双极型晶体管传热模型建模分析[J].高电压技术, 2011, 37(2):453-459.
Chen Ming, Hu An, Tang Yong, et al.Modeling analysis of IGBT thermal model[J].High Voltage Engineering, 2011, 37(2): 453-459.
[6]王莉娜, 邓洁, 杨军一, 等.Si和SiC功率器件结温提取技术现状及展望[J].电工技术学报, 2019,34(4): 703-716.
Wang Lina, Deng Jie, Yang Junyi, et al.Junction temperature extraction methods for Si and SiC power devices-a review and possible alternatives[J].Transactions of China Electrotechnical Society, 2019,34(4): 703-716.
[7]姚芳, 胡洋, 唐圣学, 等.风电变流器IGBT模块工作结温估算研究[J].电机与控制学报, 2018, 22(8):26-33.
Yao Fang, Hu Yang, Tang Shengxue, et al.Research on the junction temperature estimation of IGBT modules in wind power converters[J].ElectricMachines and Control, 2018, 22(8): 26-33.
[8]Ma Ke, Bahman A S, Beczkowski S, et al.Complete loss and thermal model of power semiconductors including device rating information[J].IEEE Transactions on Power Electronics, 2015, 30(5): 2556-2569.
[9]刘宾礼, 罗毅飞, 肖飞, 等.适用于器件级到系统级热仿真的IGBT传热模型[J].电工技术学报, 2017,32(13): 1-13.
Liu Binli, Luo Yifei, Xiao Fei, et al.IGBT thermal model for thermal simulation of device to system[J].Transactions of China Electrotechnical Society, 2017,32(13): 1-13.
[10]Zhang Jun, Du Xiong, Wu Yu, et al.Thermal parameter monitoring of IGBT module using case temperature[J].IEEE Transactions on Power Electronics, 2019, 8(34): 7942-7956.
[11]万萌, 应展烽, 张伟.分立型功率 MOSFET结温估计的非线性热网络模型和参数辨识方法[J].电工技术学报, 2019, 34(12): 2477-2488.
Wan Meng, Ying Zhanfeng, Zhang Wei.Nonlinear thermal network model and parameter identification method for junction temperature estimation of discrete power MOSFET[J].Transactions of China Electrotechnical Society, 2019, 34(12): 2477-2488.
[12]Luo Zhaohui, Ahn H, Elnokali M.A thermal model for insulated gate bipolar transistor module[J].IEEE Transactions on Power Electronics, 2004, 19(4): 902-907.
[13]汪波, 胡安, 唐勇.基于电热模型的IGBT结温预测与失效分析[J].电机与控制学报, 2012, 16(8):87-93.
Wang Bo, Hu An, Tang Yong.Junction temperature forecast and failure analysis of IGBT based on electrothermal model[J].Electric Machines and Control, 2012, 16(8): 87-93.
[14]Du Xiong, Li Gaoxian, Sun Pengju, et al.A hybrid modulation method for lifetime extension of power semiconductors in wind power converters[C]//2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, USA, 2015: 2565-2570.
[15]姚芳, 胡洋, 李静, 等.基于结温监测的风电 IGBT热安全性和寿命损耗研究[J].电工技术学报, 2018,33(9): 2024-2033.
Yao Fang, Hu Yang, Li Jing, et al.Study on thermal safety and lifetime consumption of IGBT in windpower converters based on junction temperature monitoring[J].Transactions of China Electrotechnical Society, 2018, 33(9): 2024-2033.
[16]Blinov A, Vinnikov D, Lehtla T.Cooling methods for high-power electronic systems[J].Scientific Journal of Riga Technical University Power Electrical Engineering, 2011, 29(1): 79-86.
[17]Shabny Y.Heat transfer: thermal management of electronics[M].Boca Raton: CRC Press, 2010.
[18]吴岩松, 罗皓泽, 李武华, 等.用于IGBT模块结温预测的热-电耦合模型研究[J].电工电能新技术,2014, 33(3): 13-17, 65.
Wu Yansong, Luo Haoze, Li Wuhua, et al.Researches on electrothermal model for junction temperature prediction in IGBT modules[J].Advanced Technology of Electrical Engineering and Energy, 2014,33(3): 13-17, 65.
[19]Lemmens J, Vanassche P, Driesen J.Optimal control of traction motor drives under electrothermal constraints[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(2): 249-263.
[20]Ciappa M, Fichtner W, Kojima T, et al.Extraction of accurate thermal compact models for fast electrothermal simulation of IGBT modules in hybrid electric vehicles[J].Microelectronics Reliability,2005, 45(9): 1694-1699.
[21]王希平, 李志刚, 姚芳.模块化多电平换流阀 IGBT器件功率损耗计算与结温探测[J].电工技术学报,2019, 34(8): 1636-1646.
Wang Xiping, Li Zhigang, Yao Fang.Power loss calculation and junction temperature detection of IGBT devices for modular multilevel valve[J].Transactions of China Electrotechnical Society, 2019,34(8): 1636-1646.
[22]万萌, 应展烽, 张旭东.基于功率器件壳温估计的逆变电路动态限流方法[J].电机与控制学报, 2020,24(5): 89-98, 106.
Wan Meng, Ying Zhanfeng, Zhang Xudong.A dynamic current limiting method of inverter circuit based on case temperature estimation of power devices[J].Electric Machines and Control, 2020,24(5): 89-98, 106.
[23]索超男, 张慧, 赵雄文.小波基在低压电力线信信道有色背景噪声建模中的应用研究[J].电力系统保护与控制, 2017, 45(4): 121-125.
Suo Chaonan, Zhang Hui, Zhao Xiongwen.Research on the application of wavelet basis functions on modeling of colored background noise for lowvoltage power line channels[J].Power System Protection and Control, 2017, 45(4): 121-125.
[24]王慧琴.小波分析与应用[M].北京: 北京邮电大学出版社, 2010.
[25]袁贝尔, 应展烽, 齐保军, 等.高压碳纤维复合芯导线输电线路热过载运行的风险评估方法[J].电力系统自动化, 2018, 42(1): 111-117.
Yuan Beier, Ying Zhanfeng, Qi Baojun, et al.Overheating risk assessment method for high voltage transmission line using aluminum conductor composite core[J].Automation of Electric Power Systems,2018, 42(1): 111-117.
[26]冯凯, 应展烽, 吴军基, 等.基于小波包变换和峰式马尔科夫链的风速短期预测[J].南京理工大学学报, 2014, 38(5): 639-643, 657.
Feng Kai, Ying Zhanfeng, Wu Junji, et al.Short-term wind speed forecast based on wavelet packet decomposition and peak-type Markov chain[J].Journal of Nanjing University of Science and Technology, 2014,38(5): 639-643, 657.
[27]任永峰, 薛宇, 云平平, 等.马尔可夫预测的多目标优化储能系统平抑风电场功率波动[J].电力系统自动化, 2020, 44(6): 67-76.
Ren Yongfeng, Xue Yu, Yun Pingping, et al.Multiobjective optimization of energy storage system with Markov prediction for power fluctuation suppression of wind farm[J].Automation of Electric Power Systems, 2020, 44(6): 67-76.
[28]朱晨曦, 张焰, 严正, 等.采用改进马尔科夫链蒙特卡洛法的风电功率序列建模[J].电工技术学报,2020, 35(3): 577-589.
Zhu Chenxi, Zhang Yan, Yan Zheng, et al.A wind power time series modeling method based on the improved Markov chain Monte Carlo method[J].Transactions of China Electrotechnical Society, 2020,35(3): 577-589.
[29]张玲华, 郑宝玉.随机信号处理[M].北京: 清华大学出版, 2003.
[30]马晓慧, 邹传云.数字超宽带信号的功率谱密度[J].电子与信息学报, 2007, 29(8): 1877-1881.
Ma Xiaohui, Zou Chuanyun.Power spectral density of digital ultra wide-band signals[J].Journal of Electronics and Information Technology, 2007, 29(8):1877-1881.
[31]关健, 郜峰利, 张弛, 等.间歇混沌合成 1/f噪声的相关特性分析[J].电子学报, 2016, 44(6): 1389-1393.
Guan Jian, Gao Fengli, Zhang Chi, et al.Analysis of characteristics of 1/f noise generated by inter mittency[J].Acta Electronica Sinica, 2016, 44(6): 1389-1393.