0 引言
与传统的两电平逆变器相比，多电平逆变器在提高功率等级和功率器件耐压等方面具有明显的优势，同时还具有传输效率高、传输功率大等优点[1]，逐渐成为中压大功率传动系统中首选拓扑结构[2]。级联H桥（Cascaded H-Bridge, CHB）[3-4]型逆变器由于具有传输效率高、传输功率大等优点，商业化价值较高[5-6]。
载波调制在CHB逆变器的控制方面应用普遍[7]，载波移相（Carrier Phase Shift, CPS）调制策略能够实现各H桥单元间功率均衡，但输出电压总谐波畸变率（Total Harmonic Distortion, THD）较高[8]，尤其是在低调制度时更为明显；同相层叠（In-Phase Disposition, IPD）正弦波脉宽调制（Sinusoidal Pulse Width Modulation, SPWM）策略输出电压的THD最小，但各功率分配不均衡[9-10]。虽然上述这几种调制方法各有特点，但当采用SPWM时，直流侧电压利用率都比较低[11]。
为了解决CPS-SPWM和IPD-SPWM策略下，直流电压利用率较低的问题，目前研究最多的是利用梯形波脉宽调制（Trapezoidal Pulse Width Modulation,TPWM）来替代正弦波进行控制的方法，在此基础上，文献[12-13]提出了一种 CPS-TPWM 技术，该技术利用梯形调制波的优点可以大幅度提高输出电压基波幅值，但文中没讨论在使用载波空间层叠（Carrier Disposition, CD）控制时对各级联单元输出功率进行均衡控制的问题。基于载波交叠（Carrier-Overlapping, CO）调制策略的基础，文献[14]引入了多电平逆变器具有多个控制自由度的概念，提出了一种优化的载波交叠PWM方法，利用向调制波中注入零序分量这个自由度，增加了直流电压的利用率，使调制度达到 1.15，使输出电压同时具有低调制度时良好的谐波性能和较高直流电压利用率的优点。但是该技术应用于CHB型逆变器时，与IPDPWM 一样不能实现级联单元间输出功率的均衡。文献[15]提出了线电压控制的三相 SPWM、调制波注入 3次谐波或零序分量、空间矢量调制（Space Vector Modulation, SVM）策略。这三种控制策略都能提高直流侧电压利用率，但三相SPWM和3次谐波或零序分量注入法只能用于三相系统，当 SVM技术应用于两个CHB逆变器级联以上时，会增加控制的复杂度。文献[16]提出了一种应用于CHB型逆变器型的优化均衡方法，该方法减少载波数量的同时将每个H桥单元的脉冲信号以1/4为单位进行周期循环，进而实现了各H单元的功率均衡。但在控制过程中过于复杂，并且输出电压uAN的THD较大。
本文以CHB七电平逆变器为研究对象，针对常规的多载波 PWM 策略直流侧电压利用率低以及CPS-PWM 策略在低调制度时谐波性能比较差的问题，本文以控制自由度组合提升输出电压基波幅值为基础，结合现有对传统CPS以及IPD调制策略中三角载波进行重构的分析，利用垂直偏移量循环调整载波排列方式，达到实现特定控制目标的研究[3, 17-19]，为此引入了一种改进型 PWM 技术，并通过仿真和实验进行了验证。
1 CHB 七电平拓扑及调制策略
1.1 逆变器拓扑
图1为CHB型七电平逆变器拓扑，该拓扑由三个H桥单元串联形成，每个H桥单元的直流侧电压相等，令各H桥单元的输出电压分别为uH1、uH2和uH3，输出相电压为 uAN。由 CHB逆变器的原理可知，逆变器的uAN由三个H桥单元输出电平合成得到，即
图1 CHB七电平逆变器拓扑
Fig.1 Topology of CHB seven level inverter
1.2 两种传统多载波PWM策略
图2为CPS-SPWM原理，图中，vm为调制波，载波vcri和vcri−具有一样的幅值与频率，并通过和正弦波的逻辑比较产生各H桥的输出电压。该策略能够使各H桥单元间功率均衡，但逆变器输出电压的THD较高，波形质量较差，同时当采用多载波正弦调制时，直流侧电压利用率较低。
图2 CPS-SPWM原理
Fig.2 CPS-SPWM schematic
图3为CPS-TPWM原理，vm为梯形调制波，该波形通过幅值为±UT截取三角波后获到，UC为三角波的幅值，则梯形波化率δ=UT/UC。因为逆变器的直流侧电压利用率及其谐波特性与δ值大小的选取有关，因此分析δ与各项指标的数学联系具有重要作用。
图3 CPS-TPWM原理
Fig.3 CPS-TPWM schematic
式（2）～式（4）分别体现了TPWM逆变器输出电压的THD、各低次谐波相对基波的幅值（ U n U1）以及直流电压利用率 U 1 ,m=1 Ed 与δ的关系。
式中，Ed为直流侧总电压，当调制比m=1时，基波幅值U1取最大值U1,m=1。输出电压THD、 U n/U1和 U 1, m=1/ Ed与δ的关系如图4所示，图4综合分析了δ值分别与其三者之间的数学联系，确定δ=0.4时为最优梯形调制波。TPWM在选取最佳梯形调制波的条件下，可使CHB多电平逆变器输出电压幅值升高，但其低次谐波相对较大，从而导致波形质量较差[20]。
图4 输出电压 THD、Un/U1和U1,m=1/Ed与δ 的关系
Fig.4 Relationship between THD, Un/U1 and U1,m=1/Ed of output voltage and δ
2 基于控制载波自由度的改进型CPS-PWM策略
理论上对于CHB多电平逆变器构成的方案中，要提高其直流电压侧电压利用率必须使其工作在PWM 过调制状态，但随之输出电压谐波含量就会增加。为了解决CPS-PWM策略下直流侧电压利用率较低，以及在低调制度时输出电压谐波性能较差的问题，本文仍延续现有CPS-PWM策略，以控制自由度组合提升输出电压基波幅值为基础，结合现有研究的三角载波重构为依据，提出一种改进型PWM策略。
2.1 改进型CPS-PWM载波重构原理及谐波分析
基于控制载波自由度的改进型CPS-PWM策略的载波自由度构造如图5所示，一般多载波 PWM策略包含三角载波、锯齿波等其他形状的自由度，该文对CPS-PWM策略中的三角波进行改进。如图5a可见，在一个载波周期 TC中，将三角形载波分割为12个载波段，其中，每个载波段都是由小等腰三角形的一个腰组成。由图5b可见，第1, 6, 7, 12个载波段用小等腰三角形的一个腰代替；第2, 3, 4,5, 8, 9, 10, 11个载波段用小等腰三角形代替，然后将新产生的1′, 2′, 3′等 12个载波段连接起来，保证载波变换前后载波周期相等，这样就构成了改进型CPS-PWM策略的一个周期的载波。12个阴影区域内的载波段构成基于控制载波自由度的改进型CPS-PWM策略中的一个重构载波周期，其余 5个重构载波与上述同理。
图5 载波自由度构造
Fig.5 Structure of carrier freedom degree
图6为改进型CPS-PWM策略原理，对比图2所示的CPS-SPWM原理可以看出，两个调制策略都具有相邻载波相差 60°、相同的载波幅值，且每个级联单元对应载波vcri和vcri−相差 180°的三角载波信号，并通过和正弦波的逻辑比较产生各H桥的输出电压。通过控制载波自由度的排列方式，各H桥单元虽然改变了输出的电压波形，但改进 CPSPWM实质与CPS-SPWM策略一样，也能实现CHB型逆变器中各级联单元间输出功率自均衡。
图6 改进型CPS-PWM策略原理
Fig.6 Schematic diagram of improved CPS-PWM strategy
根据前面分析，本文提出的改进型CPS-SPWM策略控制原理与CPS-SPWM策略下的完全相同，且重构后的载波周期与 CPS-SPWM 中三角载波周期完全一样。因此在这两种调制策略下，逆变器输出电压uAN的频谱分布基本相同。本文所提出的载波上下正负半波虽然有一定程度的不对称，对输出电压的THD有一些影响，但总体影响程度较小。
2.2 改进型CPS-PWM输出电压基波幅值分析
改进型CPS-PWM在CPS-SPWM策略基础上对载波进行了重构，因此当两种调制策略应用于CHB型逆变器时，输出电压特性必定也会有所改变，其直流电压利用率是否变化可做进一步的论证。由于直流电压利用率指的是逆变器输出的交流电压基波幅值与直流电压之比[12]，而直流侧电压是固定不变的，故将改进型 CPS-SPWM 输出电压基波幅值与CPS-SPWM进行比较，进一步判断两者直流电压利用率的变化。
CPS-SPWM输出电压基波表达式为
式中，m为调制度；sω为基波角频率。
由于CHB逆变器每一个H桥单元输出电压都相同。因此该文以一个 H桥单元为例来分析 CPSSPWM、改进型CPS-SPWM策略时输出电压基波幅值的变化情况，并假设在一个载波周期内，正弦调制波vm可以看作一个恒定值。
图7、图8分别为采用CPS-PWM和改进型CPSPWM 策略下，CHB逆变器各级联单元在调制度0＜ m ≤ 0.5内的输出电压。假设tH1+与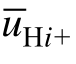
分别为级联H单元输出电压为Udc的时间和其载波周期平均值，以输出电压正半周期uH1+为例。
图7 0＜ m ≤ 0.5时CPS-SPWM的输出电压
Fig.7 Output voltage of CPS-SPWM when 0＜ m ≤ 0.5
图8 0＜ m ≤ 0.5时改进型CPS-PWM的输出电压
Fig.8 Output voltcage of improved CPS-PWM when 0＜ m ≤ 0.5
在CPS-SPWM技术下，有
此时，H1单元输出电压平均值u H 1+为
在改进型CPS-PWM方法下，有
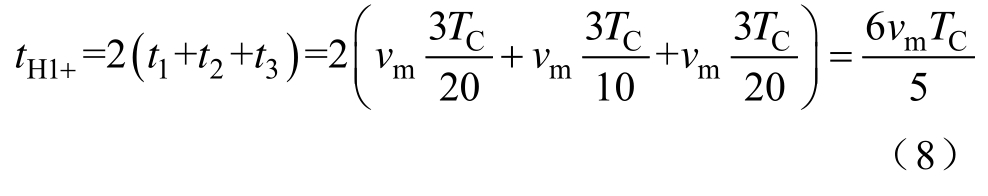
此时，H1单元输出电压平均值
为
图9、图10分别为采用CPS-SPWM和改进型CPS-PWM策略下，CHB逆变器各级联单元在调制度0.5＜m≤1内的输出电压。
图9 0.5＜m≤1时CPS-PWM的输出电压
Fig.9 Output voltage of CPS-PWM when 0.5＜m≤1
图10 0.5＜m≤1时改进CPS-PWM的输出电压
Fig.10 Output voltage of improved CPS-PWM when 0.5＜m≤1
在 CPS-SPWM 方法下，tH1+与
分别如式（6）、式（7）所示。
在改进型CPS-PWM方法下，有
此时，H1单元输出电压平均值
为
因此，CHB型七电平逆变器在CPS-SPWM方法下，输出电压载波周期平均值为
由式（9）和式（11）可知，在改进型CPS-PWM方法下，级联H单元输出电压载波周期平均值在整个调制度范围内为
因此，CHB型七电平逆变器在改进CPS-PWM方法下，输出电压载波周期平均值为
根据式（14）可知，在改进型CPS-PWM策略0＜ m ≤ 0.5范围内，输出电压基波幅值的线性增长率为18Udc/5，而在0.5＜m≤1范围内，输出电压基波幅值的线性增长率为12Udc/5。则在0＜m≤1范围内，输出电压基波幅值呈分段线性增长，在调制度0＜ m ≤ 0.5内的线性增长率大于0.5＜m≤1内的增长率。
对式（12）和式（14）进行比较可知，在调制度0＜ m ≤ 0.5范围内，CHB逆变器在改进型 CPSPWM下，输出电压基波幅值大于CPS-SPWM下的输出电压基波幅值，且前者的基波幅值线性增长速率大于后者；在调制度0.5＜m≤1范围内，改进型CPS-PWM 下的输出电压基波幅值也大于 CPSSPWM下的输出电压基波幅值，但前者的基波幅值线性增长率小于后者。因此，CHB型逆变器采用改进型CPS-PWM时输出电压的直流电压利用率大于采用CPS-SPWM时的值。在相同的条件下，其输出电压基波幅值越大，直流侧电压利用率越高；同理，负半周期亦如此。
2.3 改进型CPS-PWM功率均衡控制分析
（1）在改进CPS-PWM下，tHi+为在调制度0＜m≤ 0.5时，级联单元i在重构载波周期内输出电压为Udc的时间，由式（8）和式（9）可知，tH1+、tH2+和tH3+表示为
此时，各级联单元在重构载波周期内输出电压平均值
为
由于一相CHB逆变器中各H桥单元输出电流都相等，因此根据式（16）可得，各H桥单元输出平均功率
也都相等，即
（2）在改进CPS-PWM下，tHi+为在调制度0.5＜m≤ 1时，级联单元i在重构载波周期内输出电压为U d c的时间，由式（10）和式（11）可知，tH1+、tH2+和tH3+可表示为
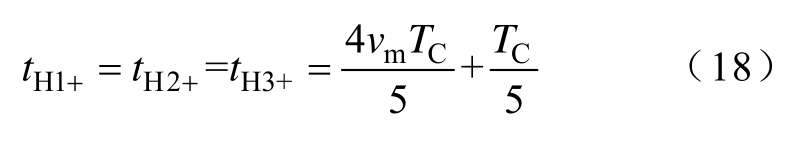
此时，各级联单元在重构载波周期内输出电压平均值
为
同理，由式（19）可得，在重构载波周期内各H桥单元输出平均功率
相等，如式（17）所示。
由上述可知，改进 CPS-PWM 技术可分别在0＜ m ≤ 0.5和0.5＜m≤1两个调制度范围内，使得各级联单元在一个重构载波周期内输出电压幅值都相等，从而保证各H桥单元输出平均功率相等。
3 仿真验证与分析
为了验证本文所提基于控制载波自由度的改进CPS-PWM策略的正确性，分别对CPS-SPWM策略、CPS-TPWM策略和改进型CPS-PWM策略进行了仿真验证，为了保证逆变器等效开关频率一致，改进型CPS-PWM、CPS-TPWM和CPS-PWM策略的载波频率均设置1 000Hz，仿真参数见表1。
表1 仿真参数
Tab.1 Simulation parameters
参 数 数 值E/V 50 R/Ω 10 L/H 0.002 f/Hz 50 m 0.9, 0.3载波比mf 20三角化率δ 0.4
图11为在载波频率为1 000Hz时，基于控制载波自由度的改进CPS-PWM策略下uH1、uH2、uH3和u A N的仿真波形。由图可以得出，各H桥单元输出电压uHi几乎完全相同，为三电平PWM波形，只存在相位之间微小的差异。
图11 改进CPS-PWM技术下逆变器输出仿真波形
Fig.11 Inverter output waveforms under improved CPS-PWM technology
图12、图13分别为调制度m为0.9、0.3时，逆变器在CPS-SPWM、CPS-TPWM和改进型CPSPWM策略下uAN的频谱分布。通过对比可见，三种策略下逆变器uAN频谱分布几乎完全相同，相电压u A N的最低次谐波群出现在6mf及其边带谐波处（见图中的6mf +1）。在低调制度m=0.3时，CHB七电平逆变器在改进CPS-PWM下输出电压的THD小于在CPS-SPWM下的THD，具有良好的谐波特性，并且基波分量在整个调制度周期内具有更高的幅值。而TPWM虽然可使CHB多电平逆变器输出电压幅值升高，但是CPS-TPWM下输出电压的THD大于在改进型CPS-PWM下输出电压的THD。在改进型CPS-PWM 方法中，虽然该调制策略控制下对逆变器输出电压THD总体的大小影响不大，但从快速傅里叶变换分析中观察各次谐波分布以及大小中发现，低次谐波含量的THD略增加，高次谐波含量的THD相应地会降低，因此总的THD大小变化不大。通过仿真进一步得出，本文所提出的载波上下正负半波虽然有一定程度的不对称，对输出电压的THD有一些影响，但总体影响程度较小。
图12 uAN的频谱仿真（m=0.9）
Fig.12 Spectrum simulation diagram of uAN (m=0.9)
图13 uAN频谱仿真（m=0.3）
Fig.13 Spectrum simulation diagram of uAN (m=0.3)
由图12、图13可知，由于改进CPS-PWM策略相电压的频谱与CPS-SPWM策略几乎相同，所以线电压频谱分布也几乎相同。
图14为CPS-SPWM、IPD-SPWM、CPS-TPWM和改进型CPS-PWM这四种策略时输出电压THD随m变化的曲线。除了本文已有的m=0.3, 0.9这两种情况，其他调制度下输出电压THD随m的变化曲线也通过Simulink仿真得出，根据图14可知，改进型CPS-PWM在0＜m ≤ 0.5时，输出电压THD小于IPDSPWM和CPS-SPWM策略；在0.5＜m≤1时，三种调制策略输出电压THD几乎一样，并且在 m ≥ 0.35∪m≤ 0.15时都低于 TPWM下输出电压 THD。通过比较可知，改进CPS-PWM技术可以改善输出电压在低调制度下的谐波性能。
图14 输出电压THD与m的关系曲线
Fig.14 Relation curves between THD and m of output voltage
由图15可知，在调制度0＜m≤1范围内，改进型CPS-PWM比IPD-SPWM和CPS-SPWM策略都具有更高的输出电压基波幅值，且在m=0.5时进行分段，其结果与理论分析几乎相同，同时在0＜m≤0.75时，改进型CPS-PWM略高于TPWM侧的输出电压基波幅值。经过仿真证明，在调制度 m=0.65时，CPS-SPWM和 IPD-SPWM输出电压基波幅值都为 97.5V，其直流电压利用率为 1。CPS-TPWM电压基波幅值为 116.2V，在最优值δ=0.4下，其直流电压利用率为1.191。而改进型CPS-PWM技术输出电压基波幅值为118.9V，其直流电压利用率最大约为1.219，显著地提高了直流电压利用率。
图15 输出电压基波幅值与m的关系曲线
Fig.15 Relation curves between output voltage fundamental amplitude and m
图16为基于控制载波自由度的改进型 CPSPWM策略在不同调制度下的平均功率对比。图中，P1、P2、P3为改进型CPS-PWM策略下各H桥的输出平均功率值。由图可见，各级联单元输出平均功率几乎完全相同。
图16 输出功率在不同调制度下的对比
Fig.16 Comparison of output power under different modulation systems
表2给出了三种调制策略在调制度m=0.3、m=0.6、m=0.9时，一个输出电压周期T内，级联单元i的开关次数。通过对比可知，采用改进型CPS-PWM策略时，逆变器的开关次数均大于 CPS-PWM 和IPD-PWM，这无疑增加了逆变器的开关损耗，同时也是改进型CPS-PWM技术的一个缺陷。由表2进一步可以看出，各H桥单元的开关数分布均匀。从等效开关频率定义 f a =pfm 可以计算出，fm为调制波频率，p为一个周期内开关产生的脉冲数，在1个周期内，所有开关管的等效开关频率均为2 000Hz，因此所有器件的开关损耗与工作应力相同，表明改进型CPS-PWM策略能有效地平衡开关器件的所有开关损耗。
表2 三种调制技术在不同调制度下级联单元的开关次数
Tab.2 Number of switching times of the cascade unit for three modulation techniques at different modulation degrees
开关次数调制策略 调制度单元1 单元2 单元3 逆变器0.3 20 20 20 60 0.6 20 20 20 60 CPS-SPWM 0.9 20 20 20 60 0.3 20 20 20 60 0.6 20 20 20 60 CPS-TPWM 0.9 20 20 20 60 0.3 40 40 40 120 0.6 40 40 40 120改进型CPS-PWM 0.9 40 40 40 120
4 实验结果
为了进一步验证基于控制载波自由度的改进CPS-PWM 策略的实际控制效果，搭建了级联七电平CHB型逆变器实验平台如图17所示，实验参数见表3。
图17 七电平CHB型逆变器实验平台
Fig.17 Seven-level CHB inverter experimental platform
表3 实验参数
Tab.3 Experimental parameters
参 数 数 值E/V 50 R/Ω 10 L/H 0.002 m 0.9, 0.3载波比mf 20三角化率δ 0.4
图18为CHB型七电平逆变器在本文所提出的调制策略下，各级联单元输出电压uH1、uH2、uH3和输出电压uAN的实验波形。
图18 逆变器输出电压实验波形
Fig.18 Experimental waveforms of inverter output voltage
图19、图20分别为m=0.9、m=0.3时，CHB型七电平逆变器采用 CPS-SPWM、CPS-TPWM 和改进型CPS-PWM策略时输出相电压的频谱。通过对比可知，三种调制技术下输出电压谐波分布相似，最低次谐波群均出现在 6mf及其边带谐波处，且在改进型CPS-PWM策略下输出电压的THD明显低于CPS-PWM策略下的THD。
图19 三种调制技术在调制度m=0.9时输出电压频谱
Fig.19 Three modulation techniques output voltage spectrum when modulation degree m=0.9
图20 三种调制技术在调制度m=0.3时输出电压频谱
Fig.20 Three modulation techniques output voltage spectrum when modulation degree m=0.3
改进型PWM下各H桥单元及各级联单元输出功率分别如图21和图22所示。由图21和图22可以直观地看出改进型CPS- PWM策略在不同调制度时功率的对比。
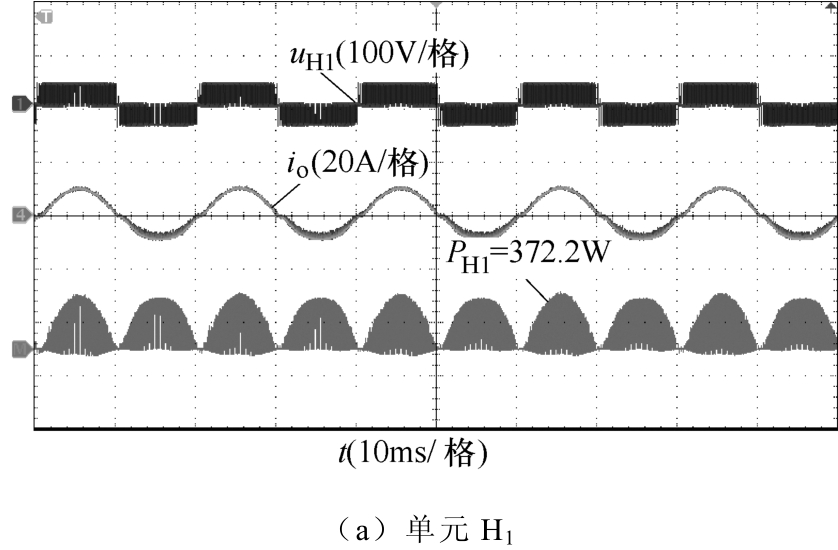
图21中，各H桥单元输出平均功率分别为PH1=372.2W、PH2=372.5W和PH3=371.9W。图22中，各H桥单元输出的平均功率分别为PH1=50.38W、PH2=50.17W和PH3=50.37W。显然，各H桥单元输出功率基本相等，因此改进型 CPS-PWM 策略保留了CPS-SPWM能实现各H桥单元间功率均衡的优点。
图21 改进型PWM下各H桥单元输出功率（m=0.9）
Fig.21 output power of each H-bridge unit under improved PWM (m=0.9)
图22 改进型PWM下各级联单元输出功率（m=0.3）
Fig.22 Output power of each H-bridge unit under improved PWM (m=0.3)
本文所提出改进型CPS-PWM策略的实验结果与仿真波形基本一致，因而验证了本文所提出调制策略的有效性和真实性。
5 结论
在对CPS-SPWM与CPS-TPWM策略分析研究的基础上，提出了一种改进型CPS-PWM策略，详细地分析了所提控制方法的控制原理，并给出改进型CPS-PWM策略输出电压基波幅值和功率均衡的分析，得出以下结论：
1）对于本文所提出的改进CPS-PWM策略，当m为低调制度时，逆变器输出电压的谐波性能优于CPS-SPWM策略，在0＜m≤1范围内，输出电压基波幅值高于CPS-SPWM，使直流电压利用率大于1，并且在0＜ m ≤ 0.75时，改进CPS-PWM略高于TPWM侧的输出电压基波幅值。
2）本文所提出的改进型CPS-PWM策略在实现各级联单元功率均衡的条件下，降低了输出电压总谐波畸变率（THD），有效地改善低调制度时的谐波性能。虽然本文所提出的调制方法，增加了开关次数与损耗，但能保证各单元开关损耗相同，开关管工作应力相同，相应地提高了系统的可靠性。
[1]叶满园, 聂宇.三相级联H桥光伏并网控制研究[J].华东交通大学学报, 2019, 36(2): 99-104.
Ye Manyuan, Nie Yu.Research on the control of three-phase cascaded H-bridge photovoltaic grid connection[J].Journal of East China Jiaotong University,2019, 36(2): 99-104.
[2]王要强, 周成龙, 李忠文, 等.单电源自均压九电平逆变器及其调制策略[J].电工技术学报, 2020,35(4): 818-826.
Wang Yaoqiang, Zhou Chenglong, Li Zhongwen, et al.Single-source self-voltage-balancing nine-level inverter and its modulation strategy[J].Transactions of China Electrotechnical Society, 2020, 35(4): 818-826.
[3]陈仲, 许亚明, 那显龙, 等.基于载波重构的级联逆变器功率均衡调制策略[J].电工技术学报, 2018,33(12): 2831-2840.
Chen Zhong, Xu Yaming, Na Xianlong, et al.Power balance modulation strategy based on carrier reconstruction for cascaded inverter[J].Transactions of China Electrotechnical Society, 2018, 33(12): 2831-2840.
[4]Liu Jiaomin, Sun Yuwei, Li Yonggang, et al.Theoretical harmonic analysis of cascaded H-bridge inverter under hybrid pulse width multilevel modulation[J].IET Power Electronics, 2016, 9(14): 2714-2722.
[5]Gao Zhigang, Lu Qi.A hybrid cascaded multilevel converter based on three-level cells for battery energy management applied in electric vehicles[J].IEEE Transactions on Power Electronics, 2018, 34(8):7326-7349.
[6]王付胜, 张德辉, 戴之强, 等.级联 H 桥光伏并网逆变器混合调制策略[J].电工技术学报, 2016,31(1): 137-145.
Wang Fusheng, Zhang Dehui, Dai Zhiqiang, et al.A hybrid control scheme of cascaded H-bridge inverters for grid-connection photovoltaic systems[J].Transactions of China Electrotechnical Society, 2016, 31(1):137-145.
[7]叶满园, 陈乐, 康力旋, 等.基于载波重构的混合多载波PWM技术[J].电机与控制学报, 2020, 24(10):60-68.
Ye Manyuan, Chen Le, Kang Lixuan, et al.Hybrid multi-carrier PWM technology based on carrier reconstruction[J].Electric Machines and Control,2020, 24(10): 60-68.
[8]Li Yufei, Wang Yue, Ben Q Li.Generalized theory of phase-shifted carrier PWM for cascaded H-bridge converters and modular multilevel converters[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 589-605.
[9]Sarkari, Fernandesb G.Modified hybrid multicarrier PWM technique for cascaded H-bridge multilevel inverter[C]//IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX,USA, 2014: 4318-4324.
[10]Venkataramanaiah Jammala, Suresh Yellasiri, Anup Kumar Panda.Development of a new hybrid multilevel inverter using modified carrier SPWM switching strategy[J].IEEE Transactions on Industrial Electronic, 2018, 33(10): 8192-8197.
[11]王立乔, 齐飞.级联型多电平变流器新型载波相移SPWM研究[J].中国电机工程学报, 2010, 30(3): 28-34.
Wang Liqiao, Qi Fei.Novel carrier phase-shifted SPWM for cascade multilevel converter[J].Proceedings of the CSEE, 2010, 30(3): 28-34.
[12]杨剑锋, 杨航, 赵恬.级联多电平逆变器 CPSTPWM 策略研究[J].南京理工大学学报, 2017,41(5): 596-601.
Yang Jianfeng, Yang Hang, Zhao Tian.Research on CPS-TPWM strategy for cascaded multilevel inverter[J].Journal of Nanjing University of Science and Technology, 2017, 41(5): 596-601.
[13]Ayob S M, Salam Z, Jusoh A.Trapezoidal PWM scheme for cascaded multilevel inverter[C]//2006 IEEE International Power and Energy Conference,Putra Jaya, Malaysia, 2006: 368-372.
[14]王鸿雁, 陈阿莲, 邓焰, 等.基于控制自由度组合的多电平逆变器载波 PWM控制方法[J].中国电机工程学报, 2004, 24(1): 131-135.
Wang Hongyan, Chen Alian, Deng Yan, et al.Multilevel inverter carrier-based PWM method based on control degrees of freedom combination[J].Proceedings of the CESS, 2004, 24(1): 131-135.
[15]杨向真, 丁明, 苏建徽, 等.准优化PWM技术在级联型多电平变流器中的应用[J].变频器世界, 2006(2):59-62.
Yang Xiangzhen, Ding Ming, Su Jianhui, et al.The application of quasi-optimization PWM technology in the cascaded multi-level converter[J].The World of Inverters, 2006(2): 59-62.
[16]叶满园, 康力璇, 陈乐, 等.级联多电平逆变器优化调制策略[J].高电压技术, 2019, 45(11): 3612-3619.
Ye Manyuan, Kang Lixuan, Chen Le, et al.Optimizes modulation strategy for cascaded multi-level inverter[J].High Voltage Engineering, 2019, 45(11): 3612-3619.
[17]Ye Manyuan, Chen Le, Kang Lixuang, et al.Hybrid multi-carrier PWM technique based on carrier reconstruction for cascaded H-bridge inverter[J].IEEE Access, 2019, 7: 53152-53162.
[18]陈仲, 那显龙, 许亚明, 等.基于控制自由度组合的级联H桥逆变器PD功率均衡控制方法[J].中国电机工程学报, 2017, 37(23): 6951-6961.
Chen Zhong, Na Xianlong, Xu Yaming et al.Power balance control method with phase disposition for cascaded H-bridge inverter based on control degrees of freedom combination[J].Proceedings of the CESS,2017, 37(23): 6951-6961.
[19]陈仲, 孙健博, 许亚明, 等.采用输出周期脉冲循环的级联H桥型逆变器功率均衡方法[J].电工技术学报, 2020, 35(4): 828-838.
Chen Zhong, Sun Jianbo, Xu Yaming, et al.Power balance method of cascaded H-bridge inverter based on pulse circulation in output period[J].Transactions of China Electrotechnical Society, 2020, 35(4): 828-838.
[20]Ye Manyuan, Ren Wei, Chen Le, et al.Research on power-balance control strategy of CHB multilevel inverter based on TPWM[J].IEEE Access, 2019, 7(1):157226-157240.