0 引言
近年来,不可逆电穿孔(Irreversible Electroration, IRE)肿瘤消融技术以其微创、非热等生物电学效应引起学者的广泛关注[1-6],其在脑[7-9]、肝脏[10-13]、胰腺[14]、前列腺[15-16]、肾脏[17]等多种器官局部肿瘤的成功消融,验证了其应用于临床治疗的安全性与有效性,表现出良好的发展前景。
准确的术前治疗计划是实现肿瘤安全有效消融的关键,也是进一步推进不可逆电穿孔肿瘤消融技术临床应用所需解决的关键难题之一[18-19]。所谓术前治疗计划,即根据组织电导率模型,结合患者肿瘤组织几何及电学特性,模拟计算脉冲电场作用下组织内部电场分布及肿瘤消融疗效,以确定最佳的治疗策略(包括电压、脉宽、重复频率、个数等脉冲参数及电极位置、暴露长度、施加顺序等电极参数)。可见,术前治疗计划的制定主要是基于数值模拟手段,其所应用的电导率模型的准确性与治疗是否过量或欠量直接相关[20]。
在早期研究中,为了降低治疗的复杂程度以及数值模拟的计算量,研究人员往往忽略脉冲作用下组织电导率发展的动态过程,考虑组织的电导率是不随脉冲电场强度、个数等因素变化的恒定值,即静态电导率模型[21]。然而,基于此静态电导率模型,忽略了变化的电导率对电场分布的影响,往往使得模拟值比实际消融面积偏小,即可能导致过量治疗,损伤周边正常组织[20]。随后,研究人员开始考虑脉冲电场作用下组织电导率分布的变化。2005年,D.Sel等基于静态电导率模型,考虑脉冲电场强度对电导率的影响,通过对实验数据进行拟合,提出随电场强度呈S形变化的动态电导率曲线,并通过实验电流与仿真电流、实验消融面积与仿真消融面积的良好匹配证明该曲线的合理性[22]。2010年,P.A.Garcia等采用二阶导数平滑曲线对电导率随电场强度的变化进行拟合,并考虑温度对电导率的影响,实现了随电场强度及温度变化的动态电导率模型的建立[23]。然而,从与脉冲作用无关的静态电导率模型到现如今发展较为成熟的随脉冲电场强度及温度变化的传统电导率模型,电导率均采用第一个脉冲作用下电压、电流数据进行求解,既忽略了脉冲个数的累积效应,也忽略脉冲期间组织特性的动态发展过程[24]。2014年,E.M.Dunki- Jacobs等在临床研究中发现,随着脉冲个数的增加,组织电穿孔程度及范围逐渐增加并趋于稳定[25];近期,本团队刘红梅等利用低压测量脉冲获取了马铃薯组织在不同电场强度、不同脉冲个数下电导率的变化,揭示了脉冲作用前后组织电特性变化规律,也证实了脉冲个数增加会导致组织电导率的增大,并建议目前的电导率模型应进一步考虑脉冲个数的影响[26]。因此,基于现有的传统电导率模型,进一步建立考虑脉冲数目对组织消融程度及范围有所影响的动态电导率模型,对进一步提升数值模型精确性具有重要意义。
本文基于已有研究成果,在建立随脉冲电场强度及温度变化的传统动态电导率模型的基础上,考虑脉冲个数对组织电导率的影响,建立电场、热场与脉冲数目的多因素动态电导率模型,并通过针电极模型下仿真电流与实验实测电流、仿真温升与实测温升相比较,验证本文所建立多因素动态电导率模型的合理性。通过本文多因素动态电导率模型的建立,有助于进一步理解组织电穿孔的动态发展过程,为后续的术前治疗计划的制定奠定基础。
1 材料与方法
马铃薯属于茄类植物组织,是评估趋势的合理模型,常用于脉冲作用下的阻抗分析、消融面积测定的研究,是研究不可逆电穿孔动态过程的常用组织[27]。因此,本文以马铃薯块茎组织作为实验对象,为避免不均匀电场引起电导率分布不均匀,采用平板电极施加脉冲。实验前,样本均处理成直径为15mm、厚度为5mm的圆柱体;实验时,两个半径为20mm的圆形金片电极以三明治形式,对马铃薯样品进行脉冲刺激,每组参数至少重复3次实验。
实验所使用的脉冲发生器由课题组自主研制,用于产生脉宽为 100μs,重复频率 1Hz的传统 IRE脉冲[29]。实验中,采用电流传感器(Pearson Electronics Inc.PaloAlto, USA)与高压探头(Teledyne LeCroy, PE5kV, USA)测量高压脉冲施加电压与响应电流,采用美国LumaSense Technologies公司生产的FOTLAB.KIT型光纤温度传感器测量组织中心位置的温度,并利用示波器(WavePro 760Zi-A,Teledyne LeCroy Inc., New York, USA)对实验中电压、电流及温度数据进行采集,采用频率500MHz。实验系统及电压波形如图1所示。

图1 实验系统及电压波形
Fig.1 Experimental system diagram and voltage waveform diagram
实验中,所施加的脉冲参数为脉冲脉宽100μs,脉冲场强从100~1 000V/cm,以100V/cm为梯度增加,脉冲施加个数均为90,重复频率均为1Hz。每一个实验样品的组织初始温度均保持为16~17℃,以减小组织间温度差异引起的初始电导率的显著不同。
实验中每组电压、电流数据均取自脉冲尾部500个采用点数据的平均值。每组数据至少重复测量3次,以尽量减小组织异质性带来的误差。
2 模型的建立
2.1 传统电导率模型的建立
随脉冲电场强度及温度变化的电导率模型已被广泛运用于数值模型的仿真拟合,根据文献[30],随脉冲电场强度及组织温度变化的电导率曲线为
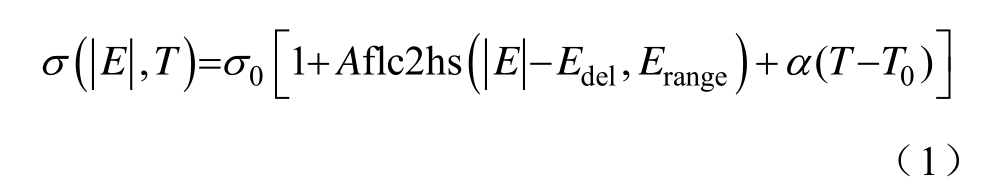
其中

式中,E为电场强度;σ 为电导率;σ0为初始电导率;T0为初始温度;T为组织温度;α为反映温度升高对电导率的影响系数,设置其值为 2%[31];A为电导率增长因子,用于描述电场作用下电导率的增加;Edel为电导率从初始电导率发展到稳定值这一变化区间的中间值,而Erange则表示整个过渡区间的变化范围的1/2;E0与E1分别为电导率开始变化与稳定对应的电场强度。flc2hs函数如图2所示。

图2 flc2hs函数
Fig.2 flc2hs function
在随电场强度及温度变化的电导率模型中,所测量的组织电导率主要由三部分组成:①脉冲未作用前的初始电导率σ0,表征组织固有介电特征;②脉冲作用过程中发生电穿孔引起的电导率的增加,主要与脉冲电场强度有关;③由脉冲作用产生焦耳热引起的电导率增加,主要与温度变化有关。
本文采用的传统脉冲的脉宽为 100μs,因此未考虑瞬态电容电流,脉冲脉宽尾部电压、电流数据均能达到稳定,则电导率可表示为
式中,ρ 为电阻率;L为组织厚度;S为样品面积;R为电阻;U为脉冲电压;I为组织负载电流。在低压脉冲作用下,电导率变化小,本文将低压25V时测量得到的平均电导率0.03S/m作为初始电导率[27]。
脉冲作用过程中,通过温度传感器实测温度变化。在电极电压为250V及500V脉冲作用下,实验组织温度变化如图3所示。在250V脉冲作用时,组织温度变化不明显,90个脉冲作用后温升在1℃左右,而在 500V电压作用时,温度随着脉冲个数逐渐增大且变化趋势明显,最大温升可达到 4℃左右。由此可知,在高电场强度脉冲作用下组织温升明显,对电导率影响也将更大,并且随脉冲个数增加,温度对电导率作用也将增大,由此在电导率模型中考虑温度的影响是必要的。

图3 实验组织温度变化
Fig.3 Experimental tissue temperature change
基于已有模型及实验参数,通过Matlab平台,采用最小二乘法对式(1)拟合,可得到不同脉冲个数作用下随电场强度及温度变化的电导率曲线。图4为消融效果与电导率曲线拟合。
不同脉冲数目下电导率拟合曲线与实验数据点拟合程度良好,脉冲个数N=1~90均建立随电场强度与温度的变化规律,各脉冲数目下的电导率曲线拟合度 R2均在 0.9以上。从图4c可知,随脉冲个数增加,引起电导率变化的电场强度降低,即脉冲数目的增加,将减小引起电导率变化所需的电场强度。


图4 消融效果与电导率曲线拟合
Fig.4 Ablation effect and conductivity curves fitting
当前广泛采用的传统电导率模型均是采用第一个脉冲作用时电压、电流数据进行电导率曲线的拟合,以此作为整个脉冲过程中组织的电导率特性。在本文中,传统电导率模型根据式(1),可得到该模型中的参数A=12.55,Edel=334.353,E0=92.014,即传统单因素模型可表示为
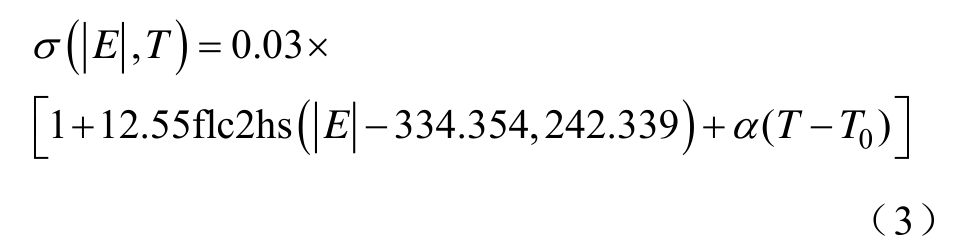
2.2 多因素动态电导率曲线
在建立随脉冲电场强度及温度变化的电导率曲线基础上,将脉冲数目的影响考虑其中。文中通过分别观测量化动态电导率模型中变量 A、Edel及 E0随脉冲数目的变化趋势,建立变量随脉冲数目的关系。
在对参数进行拟合时,需满足两个条件:①满足数据点随脉冲数目变化的趋势,与已有数据点相贴近;②在脉冲个数趋于0或无穷时,均满足理论要求。基于这两个条件,对于变量A的变化规律可进行拟合,即
参数A随脉冲个数变化的拟合曲线如图5所示。拟合度R2=0.933 2,由A的变化趋势可以看出,当脉冲数目N趋近于0时,A值趋近于0,电导率σ(E)=σ0,此时,未施加脉冲,组织未发生电穿孔。随着脉冲的施加,组织穿孔程度增加,电导率增加,且存在快速增加与平缓增加变化趋势,由此可看出,在脉冲个数较小时,引起的穿孔变化较大,随着个数增加,穿孔程度达到饱和,引起的电导率的变化趋于平稳状态。当个数N趋近于无穷时,已达到最大穿孔程度,电导率达到稳定状态,A(N)=15.158,此时电导率稳定在 16.158 4σ0。拟合函数规律与理论分析可紧密联系,证明该函数存在合理性。
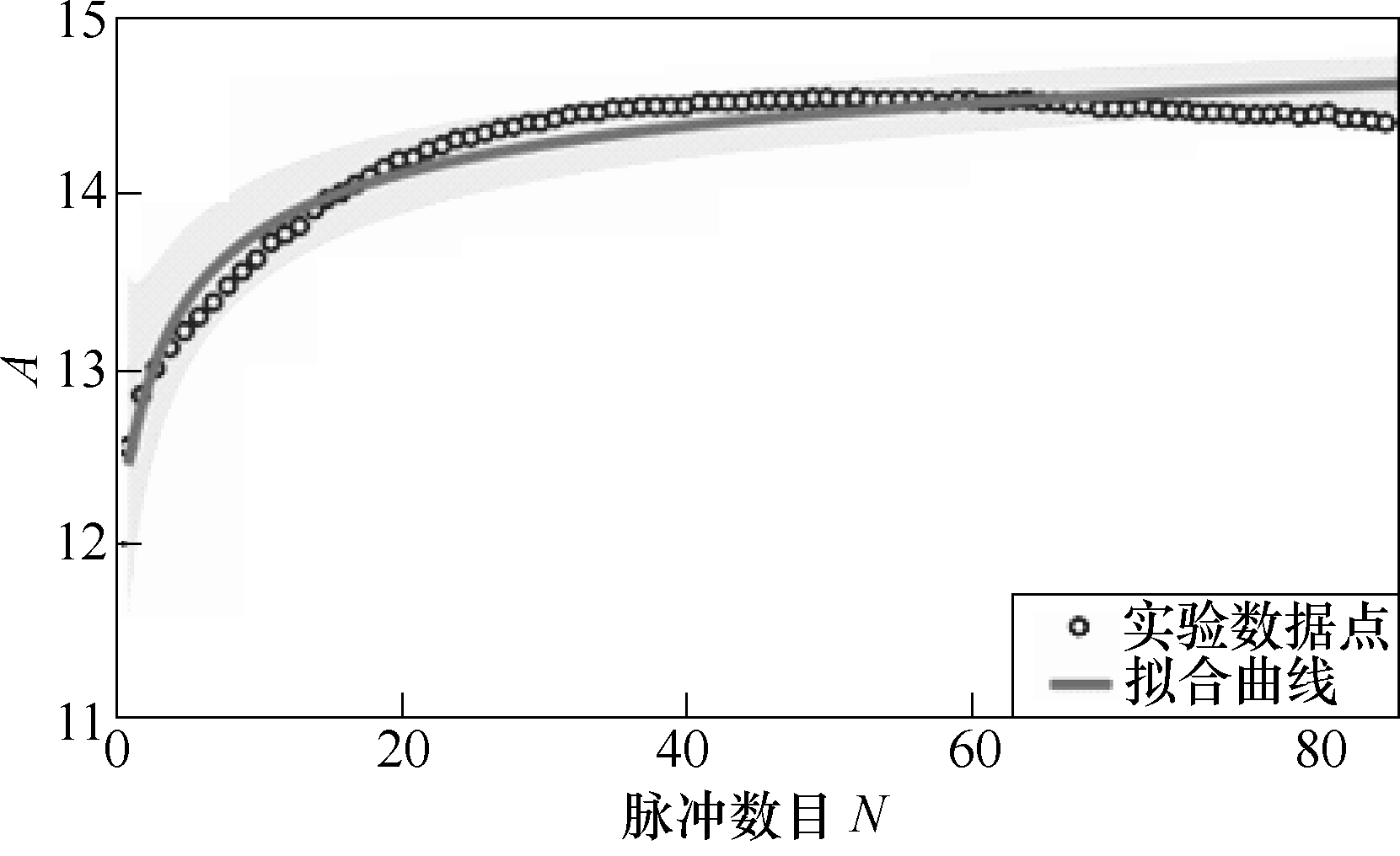
图5 参数A随脉冲个数变化的拟合曲线
Fig.5 The fitting curves of parameter A with the number of pulses
对于变量Edel可拟合为
参数Edel随脉冲个数变化的拟合曲线如图6所示。拟合度R2=0.997 2,由Edel变化趋势可以看出,当N趋近于0时,Edel(N)趋近于无穷,在未施加脉冲时电导率不发生变化;随着脉冲个数的增加,组织电导率变化更快,由此Edel值减小;当N趋近于无穷时,Edel(N)趋近于稳定值154.287。

图6 参数Edel随脉冲个数变化的拟合曲线
Fig.6 The fitting curves of the parameter Edel with the number of pulses
对于参数E0,可描述为
参数 E0随脉冲个数变化的拟合曲线如图7所示,拟合度R2=0.941。E0为电导率开始发生变化对应的最低电场强度,在未施加脉冲时,该值趋近于无穷,随着脉冲数目增加,引起电导率变化所需的电场强度降低,并逐渐趋近于0。
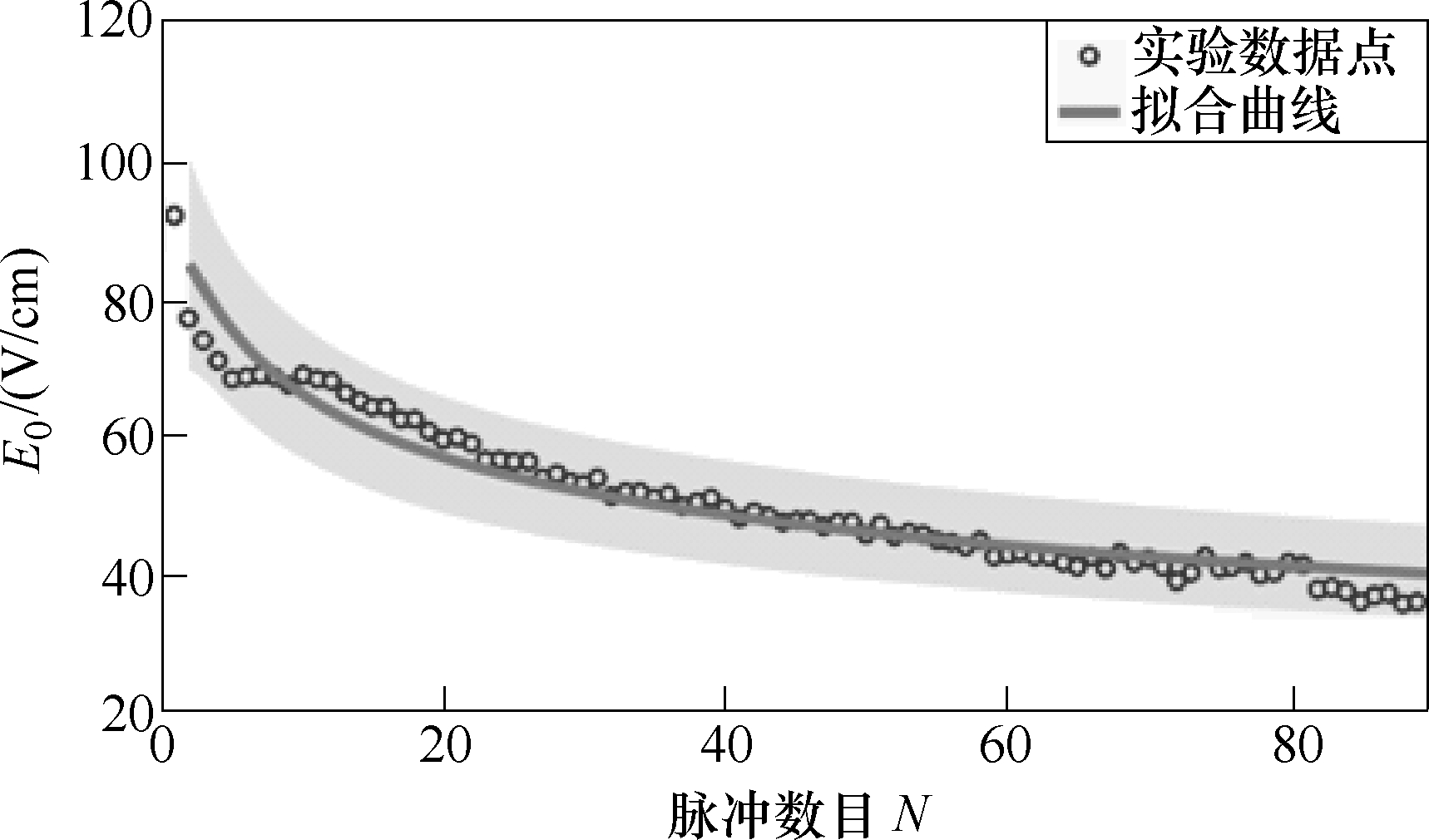
图7 参数E0随脉冲个数变化的拟合曲线
Fig.7 The fitting curves of the parameter E0 with the number of pulses
综上所述,结合式(4)~式(6)可得,随脉冲电场强度、温度及脉冲数目变化的多因素动态电导率模型为

其中
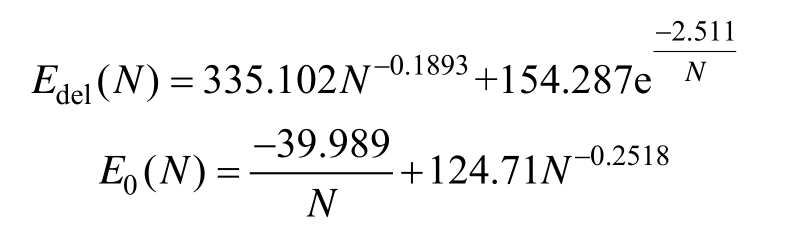
该电导率模型在原有考虑脉冲电场强度及温度影响的基础上加入脉冲数目,在温度为初始温度时,随电场强度及脉冲数目变化的电导率曲面如图8所示。

图8 随脉冲电场强度及个数变化的电导率曲面
Fig.8 Conductivity surface with pulse field strength and number
3 电导率模型的验证
为验证所建立的电导率模型的准确性,本文考虑针电极施加脉冲作用于组织诱导其消融的情境下,其对应的仿真模拟的响应电流与实验实测响应电流相比较来进行验证。实验中仍然采用马铃薯组织作为实验对象,并将其处理为半径 23mm、厚度5mm的圆柱体。电压分别为500V、700V、1 000V,脉宽为100μs的脉冲电场施加半径0.5mm、针间距10mm、暴露长度5mm的医用不锈钢针电极。实验电流通过图1所示的电流传感器进行采集。
为获取模拟电流值,本文借用COMSOL Multyphsics建立1∶1物理尺寸的有限元仿真模型,其几何模型如图9所示。

图9 针电极作用仿真几何模型
Fig.9 Needle electrode simulation model
采用电流模块及生物传热模块求解其在电场作用下的电热场分布,具体求解方程如下。
组织内的电场分布通过Laplace方程得到
式中,φ为电动势。
两电极电动势分别为
求解域外部边界条件设置为电绝缘。模型中组织电导率采用本文所建立的模型(见式(7)),针电极采用不锈钢介电特性。
对于组织内的传热,采用Pennes生物传热方程计算组织内部温升为
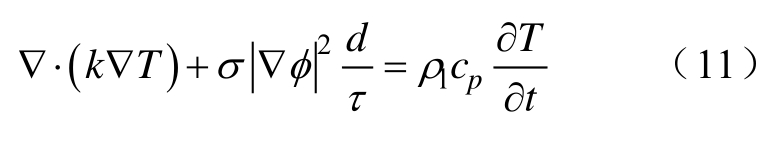
式中,k为组织热导率,k=0.570 2W/(m·K);T为组织温度;ρl 为组织密度,ρl=1 008kg/m3;cp为组织比热容,cp=3 161.36J/(kg·K)[1];此外,根据实测温度,传热模型中初始温度设置为16℃。![]() 为电流流过组织所产生的焦耳热,d为一个脉冲的高平时间,τ 为脉冲周期,由此将单个脉冲的焦耳热均分在一个脉冲周期上,简化计算,且对温升影响较小。
为电流流过组织所产生的焦耳热,d为一个脉冲的高平时间,τ 为脉冲周期,由此将单个脉冲的焦耳热均分在一个脉冲周期上,简化计算,且对温升影响较小。
仿真电流通过对针电极表面法向电流分量进行面积分来求取,即
式中,nJ为某一电极表面的法向电流密度;Is为计算得到的电流。
在不同电压等级及不同样品厚度条件下进行仿真与实验。不同电压等级样本在90个脉冲作用下的仿真电流与实验电流对比如图10所示。

图10 针电极实验电流与仿真电流对比
Fig.10 Comparison of experimental current and simulated current of needle electrode
仿真电流与实验电流在90个脉冲作用范围内的误差采用最大相对误差、最小相对误差及相对误差平均值来表述,其中相对误差及相对误差平均值分别为
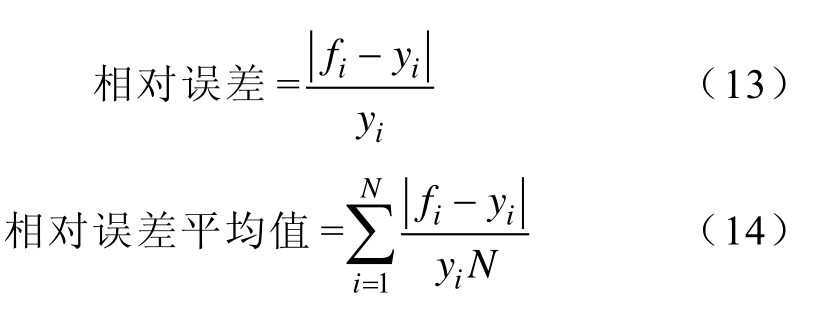
式中,fi为仿真电流值;yi为实测电流值;N为脉冲数目。由电流变化趋势及误差分析可看出,仿真电流与实验电流匹配良好,变化趋势相近,不同电压水平所得到的实验电流与仿真电流的相对误差平均值均在 4%以下,证明所建立的多因素电导率模型的合理性。实验值与仿真值的误差比较见表1。
表1 实验值与仿真值的误差比较
Tab.1 Comparison of experimental and simulated values
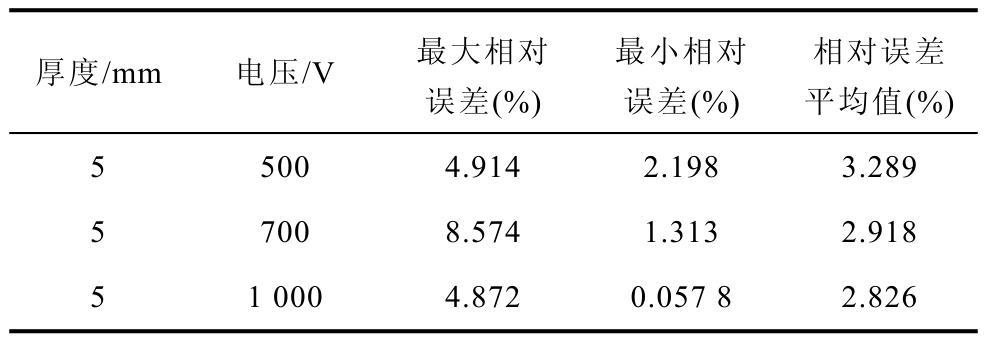
厚度/mm 电压/V 最大相对误差(%)最小相对误差(%)相对误差平均值(%)5 500 4.914 2.198 3.289 5 700 8.574 1.313 2.918 5 1 000 4.872 0.057 8 2.826
由于低压脉冲作用下温度变化不明显,难以将实验测量温升与仿真温升相结合,因此本文取高压1 000V脉冲作用下的中心点温度进行温升说明。90个脉冲作用后,实测温升平均值为4.46℃,而仿真温升为 4.35℃,与实测温度相差 2.45%,由此证明模型所考虑温度变化与实际脉冲作用过程中的温升作用相近,具有合理性。
4 讨论
4.1 实验及仿真模型中电导率的变化
Rodolfo等证明脉冲个数的累积引起组织电流的递增[33]。同样,根据本文实验数据也可直观观测出随着脉冲个数的变化,电流呈现增长趋势。图11为板电极电压为 250V(电场强度 500V/cm)时前20个脉冲作用下电压及电流的实验数据。可以看出,电压数据基本保持不变,而随着脉冲个数的增加,电流逐渐增加。从理论上进行分析,高压窄脉冲作用下细胞穿孔形成电流通路,在下一个脉冲作用前,组织在已有穿孔细胞上进一步形成穿孔或扩大孔径,由此电流通路进一步增加,电流增大,即电导率增加。因此将脉冲数目的累积通过电导率模型的方式进行描述是与实际组织变化相贴近的,本文所建立随脉冲电场强度、温度及脉冲数目变化的电导率模型为进一步描述脉冲作用下组织电导率动态变化过程提供模型基础,为后续动态消融效果的评估奠定仿真基础。
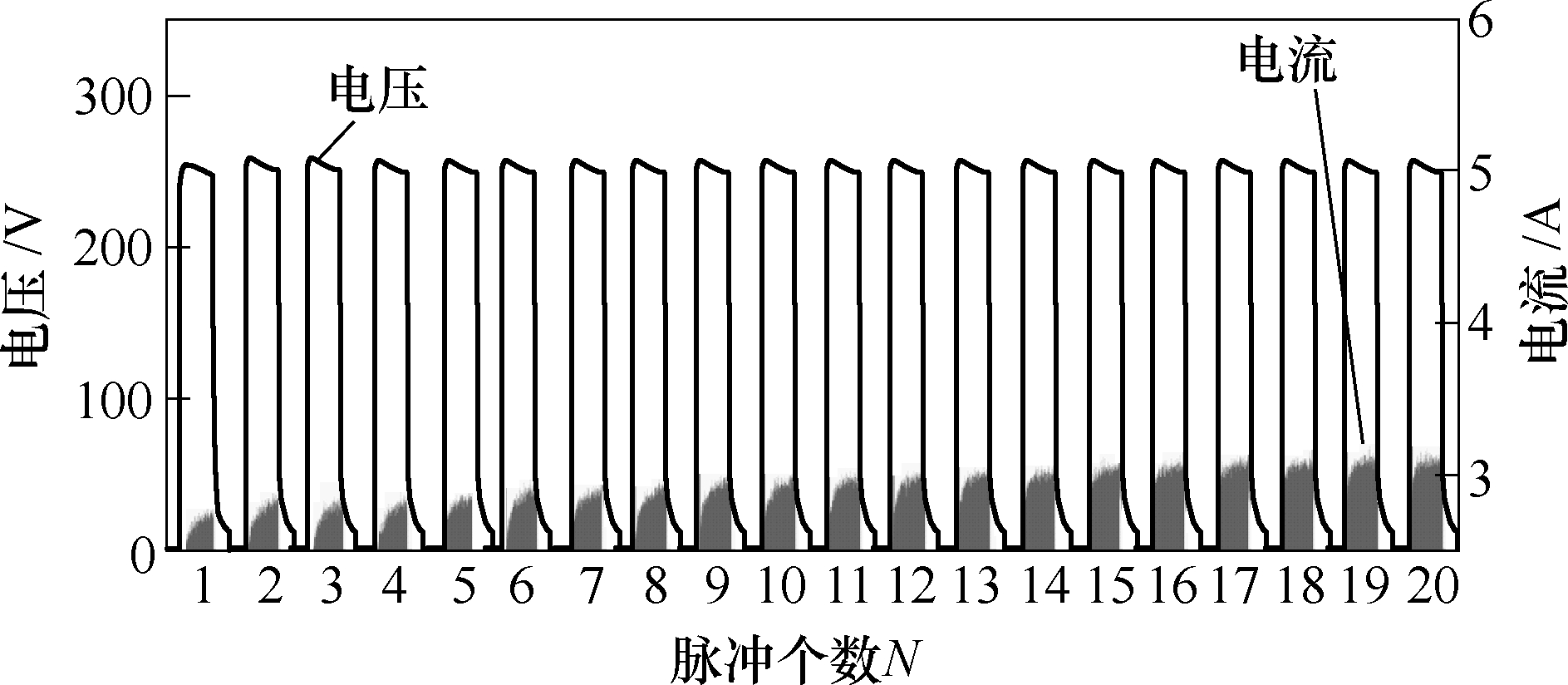
图11 电压250V时的实验电压与电流
Fig.11 Experimental voltage and current at 250V
本文所建立模型依据实验电压、电流,能够反映出组织电导率随脉冲个数增加的动态变化。在针电极电压为1 000V时,仿真模型中分别取脉冲个数N=1、N=30、N=60及N=90的电导率及温度分布如图12所示。可以看出,对于某一脉冲数目下的电导率而言,针电极附近高电场强度区域电导率最大,并随电场强度变化而变化;而对于不同个数下的电导率分布而言,同一位置处在电场强度作用下电导率随脉冲个数的增加而增强,且在高电场强度区域,随个数变化较为显著,而在低电场强度区域,电导率变化较小。由此可看出,仿真模型中电导率不仅随电场强度变化,且随脉冲施加个数的增加逐渐增强。同时,从温度分布可以看出,随着脉冲个数的增加,温升逐渐增加,体现温度随脉冲个数的积累。综上,多因素动态电导率模型能够体现随脉冲数目增加所带来的电导率的累积与温度的累积,与实际电导率及温度变化贴近。
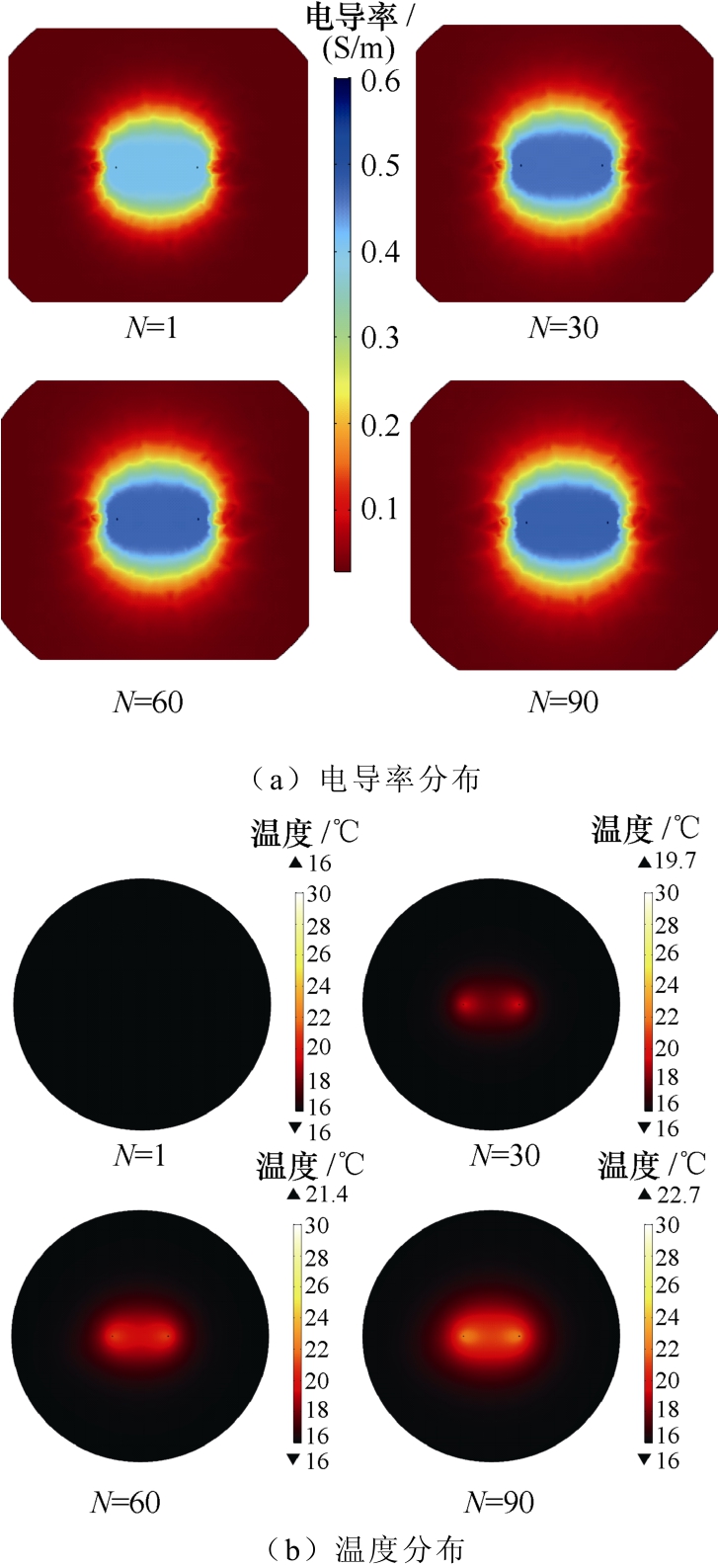
图12 脉冲个数为1、30、60及90时电导率及温度分布
Fig.12 Conductivity and temperature distribution when the number of pulses is 1, 30, 60 and 90
4.2 与传统电导率模型的差异
现在已有的传统模型考虑了脉冲电场强度及温度对电导率的影响,基于作用的第一个脉冲的电压、电流数据通过拟合的方式获得A、Edel及E0的参数,以此作为整个脉冲作用的电导率曲线。在针电极模型下,将本文建立的随脉冲电场强度、温度及脉冲数目变化的多因素电导率曲线与传统电导率模型进行对比如图13所示。由图13可以看出,在电压为500V、700V及1 000V时,传统模型下随着脉冲个数变化,电流保持恒定,各电压等级下,传统电导率模型 90个脉冲仿真电流与实验电流的误差分别为(16.399±5.608)%、(16.853±5.815)%及(16.171±4.549)%。本文建立多因素电导率模型仿真电流随脉冲数目的增加有逐渐增大趋势,且已证明与实验数据更为相近。由此可以看出,在传统电导率模型基础上,有所改进的多因素动态电导率模型实现了减小仿真电流与实验电流误差的优势,在传统模型基础上有所进步。

图13 多因素模型与传统模型仿真电流对比
Fig.13 Comparison of multi-factor model and traditional model simulation current
在电压等级为500V、700V及1 000V的针电极模型中,对两针电极中心点位置(见图8的P1)进行两种模型的温升分析,在三个电压等级作用下,多因素电导率模型在90个脉冲作用后的温升(500V、1.213℃;700V、2.618℃;1 000V、6.037℃)均高于传统电导率模型仿真温升(500V、1.213℃;700V、2.291℃;1 000V、4.821℃),由此可认为,在高压多脉冲治疗时,采用传统动态电导率模型进行术前治疗计划时,可能对组织剂量估算有所偏差,将造成不必要的组织损伤。本文所建立的多因素电导率模型在原有随脉冲电场强度及温度变化电导率模型基础上实现了时间维度的变化,且证明多因素动态电导率模型与实验结果更一致。由此认为,该模型可用于术前治疗计划中选取更为合理的脉冲数目,解决对形态、深度及大小等因素均不相同的肿瘤组织施加固定数目脉冲的问题,实现更为准确且优化的脉冲参数及电极参数的选择。为实现对各脉冲数目下治疗效果评估,接下来将探索在不同脉冲个数下的消融判别依据,通过多因素电导率模型与消融判据相结合,实现随脉冲数目变化的消融效果的仿真验证,建立完整的动态消融效果评估体系。
5 结论
本文通过金板电极施加高压脉冲作用下的组织电压、电流数据建立随脉冲电场强度、温度及脉冲数目变化的动态电导率模型,该模型在传统电导率模型基础上有所改进,进一步考虑脉冲数目动态变化,从一定程度上反映组织随脉冲数目的增加电穿孔程度逐渐增加直到稳定状态的动态阶段;并通过应用于针电极作用实现了仿真电流与实验电流的良好匹配,证明了本文建立的电导率模型的正确性。同时,通过与传统动态电导率模型的对比可看出,本文所建立多因素电导率模型通过将脉冲数目纳入模型考虑范围内,使得模型更加接近实际情况,与传统模型相比,与实验数据相差更小。因此,通过本文研究,为建立更加精确的术前治疗仿真模型建立了基础,对治疗计划的脉冲参数最优化选择具有重大意义,有利于实现精准治疗的目标。
[1]Chu K F, Dupuy D E.Thermal ablation of tumours:biological mechanisms and advances in therapy[J].Nature Reviews Cancer, 2014, 14(3): 199-208.
[2]姚陈果, 宁郡怡, 刘红梅, 等.微/纳秒脉冲电场靶向不同尺寸肿瘤细胞内外膜电穿孔效应研究[J].电工技术学报, 2020, 35(1): 115-124.
Yao Chenguo, Ning Junyi, Liu Hongmei, et al.Study on the effect of micro/nanosecond pulsed electric field on the electroporation of inner and outer membranes of tumor cells of different sizes[J].Transactions of China Electrotechnical Society, 2020,35(1): 115-124.
[3]姚陈果, 郑爽, 刘红梅, 等.面向临床多针消融肿瘤的不可逆电穿孔量效关系模型[J].电工技术学报,2020, 35(11): 2491-2498.
Yao Chenguo, Zheng Shuang, Liu Hongmei, et al.Irreversible electroporation dose-effect relationship model for clinical multi-needle ablation of tumors[J].Transactions of China Electrotechnical Society, 2020,35(11): 2491-2498.
[4]郭飞, 李成祥, 唐贤伦, 等.冲激辐射天线实现皮秒脉冲电场在人体大脑模型中聚焦的研究[J].电工技术学报, 2016, 31(3): 195-202.
Guo Fei, Li Chengxiang, Tang Xianlun, et al.Research on focusing of picosecond pulsed electric field in human brain model with impulse radiation antenna[J].Transactions of China Electrotechnical Society, 2016, 31(3): 195-202.
[5]米彦, 徐进, 刘宏亮, 等.基于网格传输网络模型的高频纳秒脉冲串作用下单细胞穿孔特性仿真[J].电工技术学报, 2018, 33(18): 4218-4229.
Mi Yan, Xu Jin, Liu Hongliang, et al.Simulation of single-cell perforation under high-frequency nanosecond pulse train based on grid transmission network model[J].Transactions of China Electrotechnical Society, 2018, 33(18): 4218-4229.
[6]刘红梅, 董守龙, 宁郡怡, 等.纳秒脉冲高频透膜效应优先杀伤化疗抗性肿瘤细胞的仿真与实验研究[J].电工技术学报, 2019, 34(22): 4839-4848.
Liu Hongmei, Dong Shoulong, Ning Junyi, et al.Simulation and experimental study of nanosecond pulse high-frequency transmembrane effect to preferentially kill chemotherapy-resistant tumor cells[J].Transactions of China Electrotechnical Society, 2019,34(22): 4839-4848.
[7]Rossmeisl J H, Garcia P A, Pancotto T E, et al.Safety and feasibility of the nanoknife system for irreversible electroporation ablative treatment of canine spontaneous intracranial gliomas[J].Journal of Neurosurgery, 2015, 123(4): 1008-1025.
[8]Rossmeisl J H, Garcia P A, Robertson J L, et al.Irreversible electroporation for the treatment of brain tumors: pre-clinical results in a canine model of spontaneous glioma[J].IFMBE Proceedings, 2015, 45:809-812.
[9]Garcia P A, Pancotto T, Rossmeisl J H, et al.Nonthermal irreversible electroporation (n-tire) and adjuvant fractionated radiotherapeutic multimodal therapy for intracranial malignant glioma in a canine patient[J].Technology in Cancer Research & Treatment, 2011, 10(1): 73-83.
[10]Vollherbst D, Fritz S, Zelzer S, et al.Specific ct 3d rendering of the treatment zone after irreversible electroporation (ire) in a pig liver model: The“chebyshev center concept” to define the maximum treatable tumor size[J].BMC Medical Imaging, 2014,14(1): 1-12.
[11]Siddiqui I A, Latouche E L, DeWitt M R, et al.Induction of rapid, reproducible hepatic ablations using next-generation, high frequency irreversible electroporation (h-fire) in vivo[J].International Hepato-Pancreato-Biliary Association, 2016, 18(9): 726-734.
[12]Campus G R.Irreversible electroporation: a new ablation modality-clinical implications[J].Technology in Cancer Research & Treatment, 2006, 6(1):37-48.
[13]Au J T, Kingham T P, Jun K, et al.Irreversible electroporation ablation of the liver can be detected with ultrasound b-mode and elastography[J].Surgery,2013, 153(6): 787-793.
[14]Bhutiani N, Doughtie C A, Martin R C G.Ultrasound validation of mathematically modeled irreversible electroporation ablation areas[J].Surgery, 2016,156(4): 1032-1040.
[15]Neal Ii R E, Smith R L, Kavnoudias H, et al.The effects of metallic implants on electroporation therapies: feasibility of irreversible electroporation for brachytherapy salvage[J].Cardiovascular and Interventional Radiology, 2013, 36(6): 1638-1645.
[16]Neal R E, Millar J L, Kavnoudias H, et al.In vivo characterization and numerical simulation of prostate properties for non-thermal irreversible electroporationablation[J].The Prostate, 2014, 74(5): 458-468.
[17]Neal I R, Garcia P, Kavnoudias H, et al.In vivo irreversible electroporation kidney ablation: experimentally correlated numerical models[J].IEEE Transactions on Biomedical Engineering, 2015, 62(2): 561-569.
[18]Selma C, Anze Z, Damijan M, et al.Numerical modeling and optimization of electric field distribution in subcutaneous tumor treated with electrochemotherapy using needle electrodes[J].IEEE Transactions on Plasma Science, 2008, 36(4): 1665-1672.
[19]Anže Ž, Selma Č, Damijan M, et al.Optimization of electrode position and electric pulse amplitude in electrochemotherapy[J].Radiology and Oncology,2008, 42(2): 93-101.
[20]José A B, Pintarelli G B, Afrânio de C A J, et al.Verification of electroporation models using the potato tuber as in vitro simulation[J].Journal of Medical and Biological Engineering, 2019, 39(2): 224-229.
[21]Rafael V, Davalos, Boris R, et al.Theoretical analysis of the thermal effects during in vivo tissue electroporation[J].Bioelectrochemistry, 2003, 61(1-2):99-107.
[22]Sel D, Cukjati D, Batiuskaite D, et al.Sequential finite element model of tissue electropermeabilization[J].IEEE Transactions on Biomedical Engineering, 2005, 52(5): 816-827.
[23]Garcia P A, Rossmeisl J H, Neal R E, et al.intracranial nonthermal irreversible electroporation:In vivo analysis[J].Journal of Membrane Biology,2010, 236(1): 127-136.
[24]Neal R E I, Garcia P A, Robertson J L, et al.Experimental characterization and numerical modeling of tissue electrical conductivity during pulsed electric fields for irreversible electroporation treatment planning[J].IEEE Transactions on Bio-medical Engineering, 2012, 59(4): 1076-1085.
[25]Dunki-Jacobs E M, Philips P, Martin R C G.Evaluation of resistance as a measure of successful tumor ablation during irreversible electroporation of the pancreas[J].Journal of the American College of Surgeons, 2014, 218(2): 179-187.
[26]刘红梅, 姚陈果, 董守龙, 等.基基于测量信号的不可逆电穿孔动态过程数值模拟及分析[J].电工技术学报, 2019, 34(18): 3722-3740.
Liu Hongmei, Yao Chenguo, Dong Shoulong, et al.Numerical simulation and analysis of irreversible electroporation dynamic process based on measurement signals[J].Transactions of China Electrotechnical Society, 2019, 34(18): 3722-3740.
[27]Ivorra A, Mir L M, Rubinsky B.Electric field redistribution due to conductivity changes during tissue electroporation: experiments with a simple vegetal model[J].International Federation for Medical and Biological Engineering Proceedings, 2009, 25(13):59-62.
[28]Hjouj M, Rubinsky B.Magnetic resonance imaging characteristics of nonthermal irreversible electroporation in vegetable tissue[J].Journal of Membrane Biology, 2010, 236(1): 137-146.
[29]王昌金.基于Marx和LTD拓扑的全固态复合模式脉冲源的研制[D].重庆: 重庆大学, 2018.
[30]Zhao Yajun, Bhonsle S, Dong Shoulong, et al.Characterization of conductivity changes during high-frequency irreversible electroporation for treatment planning[J].IEEE Transactions on Biomedical Engineering, 2018, 65(8): 1810-1819.
[31]Duck F A.Physical properties of tissues: a comprehensive reference book[M].UT, American: Academic Press, 2013.
[32]周智勇, 邸倩倩, 刘斌, 等.马铃薯热物性的测量[J].制冷与空调(四川), 2015(3): 306-309.
Zhou Zhiyong, Qiu Qianqian, Liu Bin, et al.Measurement of potato thermal properties[J].Refrigeration &Air Conditioning (Sichuan), 2015(3): 306-309.
[33]Weinert, Rodolfo, Pereira, et al.Inclusion of memory effects in a dynamic model of electroporation in biological tissues[J].Artificial Organs, 2019, 43(7):688-693.