0 引言
随着国家电网有限公司提出“三型两网”(“三型”即枢纽型、平台型和共享型,“两网”即坚强智能电网和泛在电力物联网)的战略目标以及南方电网公司提出的“透明电网”建设目标,越来越多的研究者开始投入到建设泛在电力物联网/“透明电网”的相关工作中。然而,目前的电力基础设施(如电力设备)最初并不是按照泛在电力物联网/“透明电网”的要求进行规划的(或者说不能满足建设泛在电力物联网/“透明电网”的要求):①所有相关设备与电力用户、电网企业、发电企业、电工装备企业等连接;②设备信息广泛交互和充分共享;③以数字化管理大幅提高装备制造的安全、质量、先进、效益效率水平;④通过智能传感器,让设备状态透明、运行状态透明;⑤设备具有自我感知能力。
高压断路器是电网中具有保护和控制功能的重要电力设备,在上述大背景下,对高压断路器的智能化和运行可靠性的要求越来越高,科学地评估高压断路器的运行状态,不仅能够为电力运维部门制定检修策略提供依据,也可以为制造企业提供改进方向。
对于高压断路器,常见的故障类型大致可以分为电气故障和机械故障两类[1-3]。其中,机械零部件故障是一种常见的机械故障,包括零部件异常磨损、异常变形、断裂等故障。零部件故障可能是由于加工工艺、装配等因素造成的,也可能是在其运行过程中(受到内外环境的综合作用)性能不断退化造成的。零部件故障会导致断路器动作性能不符合要求(如动作速度、动作时间不符合要求),严重时甚至会造成断路器开断、关合失败等事故。当机械零部件发生早期故障时,断路器仍可继续运行,但若不能及时发现而导致故障程度不断加剧,将会引起断路器机械传动异常,影响机械特性,最终破坏动触头的正常运动,进而引起开断、关合失败,甚至对电力系统造成影响。因此,有效判断断路器机械零部件的故障程度对提高断路器的可靠性具有重要的意义。
采用断路器分、合动作过程中产生的机械振动信号对断路器进行故障诊断一直是国内外研究的重 点与难点。自1988年M. L. Lai[4]等首次提出利用振动信号诊断断路器故障的优点及有效性以来,已经取得了一系列有价值的研究成果[5-13]。然而,目前的研究主要集中在对故障部位和故障类型的区分识别,而对故障严重程度的研究较少。实际上,断路器机械零部件故障是一个从轻微到严重的演变过程,准确识别故障演变过程对保证断路器安全运行有着重要的意义。文献[14]提出根据高压断路器的行程信号进行分闸弹簧故障程度诊断,通过从行程曲线中提取平均标准方差作为因变量、以弹簧预压缩变化量作为自变量构造拟合曲线函数,实现对分闸弹簧不同故障程度的判断。由于引起断路器行程信号变化的因素众多(弹簧仅是其中一个因素),且实际弹簧故障并不能完全等效为压缩量的改变,因此,这种拟合曲线方法的诊断精度有待进一步深入研究。文献[15]利用集合经验模态分解方法处理分合闸线圈电流信号,并求取能量矩相对熵作为故障程度评估指标,通过线性函数拟合不同故障程度下的熵值建立拟合曲线,从而对分闸衔铁行程不足、分闸线圈匝间短路故障的严重程度进行诊断。但该方法的不能较直观地描述线圈的故障程度、对判断线圈何时开始出现故障以及开始出现故障时的故障特征性质等有待进一步的研究。文献[16]通过求取断路器振动信号多尺度排列熵偏均值作为故障程度特征量,并对不同故障程度的特征量进行三次曲线拟合,通过拟合曲线的斜率判断故障程度。这种通过建立拟合曲线数学模型进行故障程度诊断的方法,对于不同型号断路器的鲁棒性有待进一步的深入研究。
基于上述情况,在文献[17]的研究基础上,本文提出了基于振动信号混沌吸引子形态特性的断路器机械零部件故障程度识别方法,能够有效地判断零部件的故障程度,克服了文献[17]研究的不足,研究结果有助于更加合理地安排检修计划。首先,针对现有信号分解方法——变分模态分解方法存在的不足进行了改进,提出了一种谱形态变分模态分解(Variational Mode Decomposition, VMD)方法,以对断路器振动信号进行参数自适应分解;其次,介绍了不同动力系统的吸引子特点,从中得出吸引子对系统状态的变化较敏感,并将其应用到断路器机械零部件故障程度的识别中;最后,对所提出的故障程度识别方法进行试验验证。研究表明,所提出的故障程度识别方法能够直观有效地反映断路器机械零部件故障严重程度。
1 谱形态变分模态分解(SSVMD)
经验模态分解类的信号分析方法所产生的模态混叠[18-19]等问题将导致所获信息失真,而变分模态分解可改善这些缺陷[20-22]。
VMD方法将原始信号x(t)分解为K个有限带宽的本征模态函数(Intrinsic Mode Function, IMF),IMF可表示为
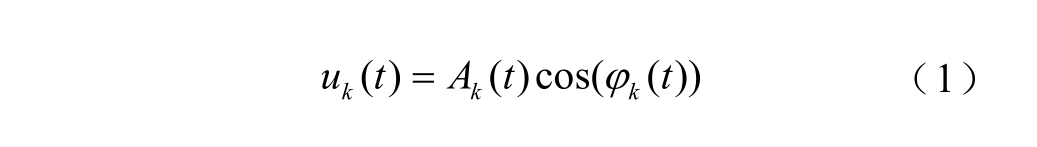
式中,Ak(t)和φk(t)分别为瞬时幅值和瞬时相位。
每个IMF分量uk(t)在中心频率ωk处集中,带宽可用高斯平滑偏移信号来估算,分解时对应的受约束变分模型为

式中,uk(t)满足
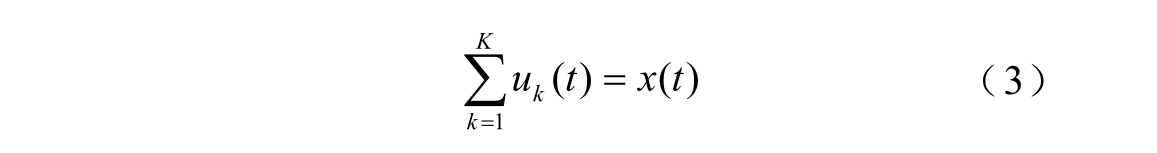
引入增广Lagrange求解上述最优解为
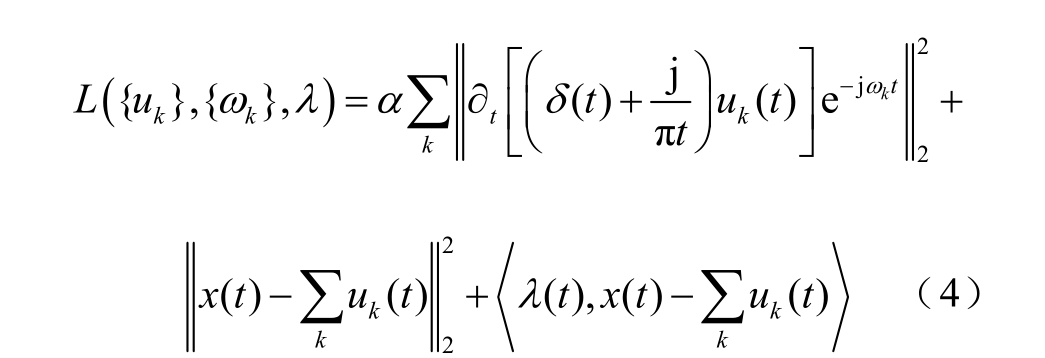
式中,λ为Lagrange算子;α为惩罚因子。
按照式(5)~式(7)分别在频域上更新![]() 、ωk和
、ωk和 ,即
,即

λ使用梯度下降法进行更新。
迭代停止条件为
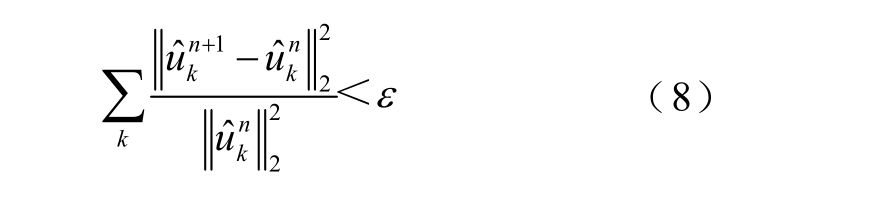
在VMD过程中,分解层数K需要预先设定,分解结果随K值的不同而不同,K值过大或过小均会影响分解结果的准确性。以图1a所示的由三种不同信号组成的信号为例,采用VMD将各个成分逐一分离出来,如果分解层数K设为3,那么分解结果是正确的,如图1b所示;如果分解层数K设为2,由图1c可知,分解误差比较大。

图1 分解层数K对VMD结果的影响
Fig.1 The influence of K on VMD results
目前对如何选取合理的K值的研究相对较少,没有形成统一的标准。特别是对于断路器振动信号,由于很难预知信号的组成成分(即多少个K值),加之断路器不同状态的振动信号、不同型号断路器的振动信号具有一定的差异性,使得根据经验选取合理的K值具有一定的难度和局限性。
鉴于此,本文提出一种基于IMF频谱(傅里叶谱)形态特点的K值选取方法,本文将该方法称为谱形态变分模态分解(Spectral Shape Based Variational Mode Decomposition, SSVMD)。
SSVMD方法通过分析IMF分量的频谱特点以确定最优K值,即如果IMF频谱具有多个波峰N_f_peak,则说明该IMF存在多个频率成分,意味着信号分解不彻底或不是最优的分解结果。SSVMD算法流程如图2所示,使用时只需事先指定一个最大阈值,算法根据IMF频谱形态特点自动确定最优K值,避免了人为选择K值造成对分解精度的影响。

图2 SSVMD算法流程
Fig.2 Flow chart of SSVMD algorithm
2 混沌吸引子
相空间(可理解为状态空间)给出了一种将数字转变成图形的方法,它把系统运动部分的每一实质信息都提取出来并绘制。在相空间中,动力系统在给定时刻的状态归结为一个点,这个点代表该时刻动力系统的状态。下一时刻,系统发生变化,这个点就做出相应的运动。于是,系统的演化就可以用这个运动的点表示出来。
例如,图3所示的无摩擦摆的相空间轨迹,摆的任一运动状态都可以在相空间中找到与之对应的点。摆系统两个变量(即位置和速度)的连续变化在相空间中画出相应的轨线,相空间的每一个点对应摆的一个运动状态,摆的往复运动使得相空间的轨迹一遍一遍地重复转下去。
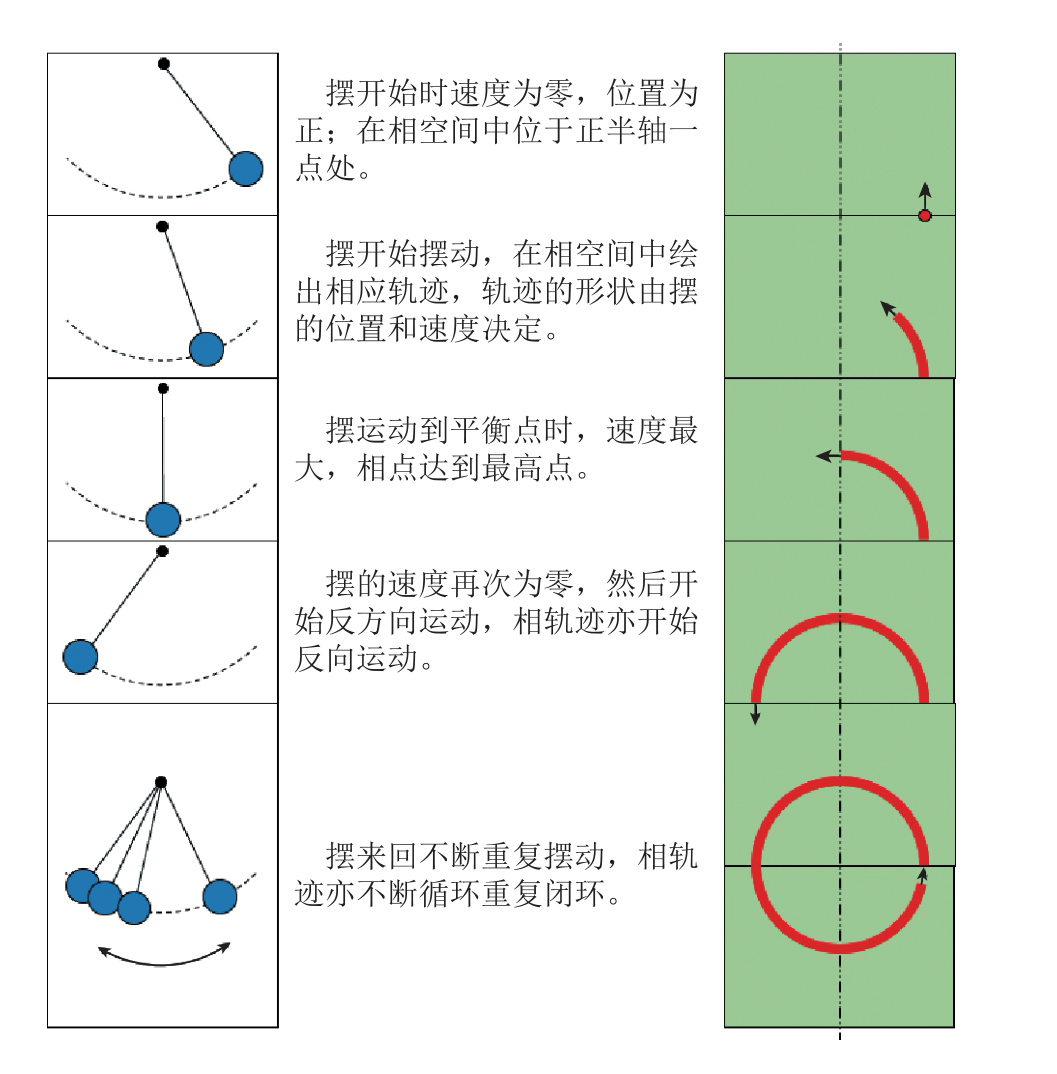
图3 在相空间中观察摆的运动(左:摆的运动,右:相空间轨迹)
Fig.3 Observe the motion of the pendulum in phase space (Left: pendulum motion, Right: phase space trajectory)
如果摆的能量不同或存在摩擦时,相空间轨迹的形状亦不同。例如,一个弱阻尼单摆振动的相空间轨迹如图4所示(图4中M为摆球质量,L为摆 线长度,C为阻尼系数),其相轨线为内缩螺旋线,表示摆的振幅随时间衰减到零的振荡过程。显然,相轨线的形状与阻尼的大小、摆线的长度、摆的质量等因素有关(即相轨线是单摆系统状态的反映)。图4称为点吸引子,表明吸引子的形状与系统的特征、运动状态等因素有关。

图4 阻尼单摆吸引子
Fig.4 Attractor of damped simple pendulum
简单吸引子(吸引子包括简单吸引子、混沌吸引子等)除了点吸引子外,还有极限环吸引子等。极限环吸引子具有一条吸引附近所有其他轨道的轨道,它表明系统从外界获得能量的同时也在消耗能量。Van der pol振子和Duffing振子是具有极限环吸引子的典型系统,图5所示为一Van der pol极限环吸引子(图5a)和Duffing极限环吸引子(图5b)。图5中,Van der pol参数:ε=1.0(非线性阻尼);Duffing参数:γ=0.25(控制阻尼度),α=0.1(控制韧度),β=1.0(控制动力的非线性度),δ=0.92(驱动力的振幅),ω=1.0(驱动力的角频率)。可以看出,这两个系统的极限环吸引子表现出完全不同的形态特征,表明动力学特性不同的系统的吸引子形态差异较大。

图5 Van der pol极限环和Duffing极限环
Fig.5 Van der pol limit cycle and Duffing limit cycle
随着系统参数的不断变化,耗散运动会出现混沌,简单吸引子就会变为混沌吸引子。混沌吸引子的相轨线被收缩到狭小的相空间内,在狭小的空间里随着系统的运动“纠缠不已”。图6a所示的混沌吸引子称为Lorentz吸引子,反映了对流模型中流体的流动状态:当流体在一个方向转动时,轨道处于左侧;当流体反向滚动时,轨道就进入另一侧。 又如图6b所示的从Lorentz吸引子中提取一种非对称结构的混沌吸引子,称为Rossler混沌吸引子。若Rossler系统的参数发生变化,则该系统的吸引子形状亦会发生相应的改变。

图6 Lorentz吸引子和Rossler吸引子
Fig.6 Lorentz attractor and Rossler attractor
由此得到启发:既然吸引子形态的变化能够反映动力系统状态的演变情况,那么能否通过分析断路器振动信号的吸引子形态去探究其机械状态的变化情况?特别是,由于动力系统的微小变化会导致吸引子形态发生显著的改变,那么是否可以利用吸引子的这种敏感性去分析断路器零部件早期故障阶段的微弱故障特征?
鉴于此,下面通过考察断路器振动信号的混沌吸引子形态特性来提取蕴含在振动信号中的断路器动力学信息,进而实现零部件故障程度诊断。
3 试验验证
文献[17]已通过试验证实了振动信号混沌吸引子对断路器状态变化的敏感性,不同故障类型的吸引子是不同的。
进一步,本文将以断路器零部件故障的不同严重程度(即从正常状态、早期故障至完全失效故障)为例,探究振动信号混沌吸引子对故障严重程度的敏感性及变化规律,据此希望能够实现对断路器零部件故障程度的有效诊断。
断路器零部件众多,其中一些零部件由于在断路器分、合闸过程中受到强烈的摩擦、冲击碰撞,导致发生故障的概率较高。图7所示为断路器典型的结构示意图,图中虚线右侧为断路器操动机构本体、左侧为连接灭弧室的传动机构,本文以操动机构中的分闸缓冲器和传动机构中的传动连杆连接轴销为研究对象(图中虚线框标记处),探究故障程度的诊断方法。选择这两个零部件作为研究对象的主要原因如下:
(1)分闸缓冲器直接影响断路器动触头反弹幅值的大小,继而对断路器电气性能和灭弧室机械寿命造成影响,严重时将会造成断路器开断失败[8]。目前一般通过测试断路器机械特性参数,通过反弹幅值等机械特性参数间接判断分闸缓冲器是否存在故障,这种方法效率较低且难于发现早期故障。鉴于此,本文对断路器分闸缓冲器的故障程度识别方法进行了试验研究。
(2)断路器零部件磨损,特别是零部件连接部位的磨损是不可避免的,对于某些受力复杂的连接部位,磨损更是严重。其中,断路器操动机构与传动机构之间的连接是磨损较为严重的部位(该处是操动机构将储能弹簧能量传递给动触头的交汇点,如图7所示),该部位一旦开始出现磨损,将会由于强烈的冲击碰撞,磨损急剧增加,最终导致连接轴销脱落,造成断路器分、合失败。因此,对断路器零部件的磨损情况进行监测识别尤为重要,特别是对某些关键零部件磨损状况的及时判断。鉴于此,本文以断路器传动连杆孔轴磨损为例,探究其磨损程度的识别方法。
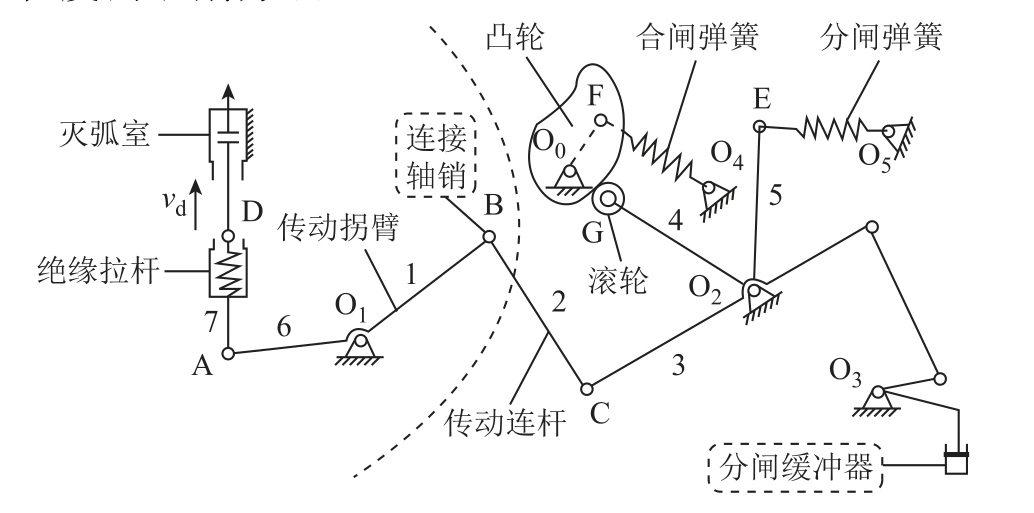
图7 断路器典型结构示意图
Fig.7 Typical structure of circuit breaker
下面通过两个试验分别进行说明,其中试验一针对的是分闸缓冲器故障程度诊断,试验二分析了传动连杆孔轴磨损程度的识别方法。
3.1 试验一
以西门子型号为3AE8174—2的真空断路器为研究对象,搭建试验平台,如图8所示。试验平台主要由真空断路器、振动信号采集装置及机械特性测试仪等组成。结合该断路器的结构特点,一方面考虑到后续现场测试的方便,另一方面为了能够较清晰地记录断路器的动作信息,本文将加速度传感器固定在操动机构顶部的侧面,具体如图8所示。加速度传感器(IEPE型)灵敏度为0.5mV/g(±10%)、最大量程为10 000g、频率响应范围为0.5~ 10 000Hz(±5%)。

图8 断路器零部件故障模拟试验平台
Fig.8 Test platform for circuit breaker component fault simulation
试验过程中采用外接控制电源的方式控制断路器分、合闸动作,外接控制电源为机械特性测试仪。采样率为100 kHz,采样时间为0.06 s。触发方式为阈值触发,即当振动幅值超过预先设定的触发阈值时开始记录并保存数据,触发阈值设为0.01g。
断路器实际运行过程中,分闸缓冲器由于密封老化、紧固件松动等原因导致其有效缓冲行程不断变小,直至缓冲性能完全失效。从功能上讲,分闸缓冲器发生故障的根本原因是其有效缓冲行程不能满足要求,使得断路器分闸机械特性值偏离厂家规定范围。因此,可以通过调节分闸缓冲器的有效缓冲行程来模拟分闸缓冲器故障的不同严重程度。
如前所述,由于分闸反弹幅值是断路器分闸动作的一个非常重要的机械特性指标,其大小直接影响灭弧室的机械寿命及开断的成败。因此,试验以分闸反弹幅值为主要参考依据来评判分闸缓冲器的性能(即故障程度)。
分闸缓冲器位置及缓冲行程调节方法如图9所示,通过调节x的大小改变分闸缓冲器的有效缓冲行程,将分闸缓冲器从正常状态、早期故障至完全失效故障划分为六个等级,对应表1中的分闸缓冲器状态编号1~6。表1中,分闸缓冲器状态编号1、2表示断路器分闸反弹幅值在规定的正常范围内(≤2mm),分闸缓冲器状态正常;状态编号3为分闸缓冲器开始出现异常的状态,此时的分闸反弹幅值已超出规定的上限值;状态编号4~6表示断路器分闸反弹幅值逐渐超出上限值,表明分闸缓冲器故障程度越来越严重。
表1 分闸缓冲器状态参数
Tab.1 State parameters of the opening damper

分闸缓冲器状态编号 1 2 3 4 5 6 距离x/mm 65.8 63.8 61.8 59.7 57.5 — 分闸缓冲器 状态 脱正常状态 开始出现 异常 故障程度 逐渐加剧 落 断路器状态 正常状态 分闸反弹幅值超标

图9 分闸缓冲器位置及缓冲行程调节方法
Fig.9 Position of the opening damper and its stroke adjusting method
图10例举了分闸缓冲器不同状态下的分闸振动信号,可以看到,从这些时域波形中很难辨别分闸缓冲器的状态。

图10 分闸缓冲器不同状态下的分闸振动信号
Fig.10 Opening vibration signals in different states of the opening damper
为了减小其他因素的干扰,提高分闸缓冲器故障特征提取的准确性,本文仅截取分闸缓冲器开始制动至分闸动作结束时段的振动信号进行分析。根据该型号断路器的分闸时间参数、分闸缓冲器制动时刻(在30~35ms之间开始制动),截取30ms之后的振动信号,然后对截取的主要包含缓冲制动信息的振动信号进行SSVMD处理,再对SSVMD的结果进行相空间重构,得到相应的混沌吸引子,最后根据混沌吸引子的形态特征判断分闸缓冲器故障程度。
图11为最后得到的结果,即分闸末期振动信号的模态分量(最后一个模态分量,IMF 8)混沌吸引子随分闸缓冲器状态变化的演变过程。图11a为分闸缓冲器正常状态时的混沌吸引子、图11b~图11e为分闸缓冲器开始出现故障至完全失效故障情况下的混沌吸引子,可以明显看出:
(1)缓冲器正常状态下的吸引子轨迹紧紧收缩在一起,表明缓冲器起到了有效的缓冲作用。
(2)当缓冲器开始出现异常时,如图11b所示,部分相轨迹开始试图逃离吸引域;随着缓冲器故障的不断加剧,逃离吸引域的相轨迹越来越多、吸引子形态不断增大(见图11c、图11d);最后,缓冲器完全失效,吸引子形态膨胀了起来,如图11e所示。
(3)可以以吸引子轨道的突然开始逃离吸引域为界限,如图11b所示,作为缓冲器开始出现故障的判据,此后若吸引子继续增大、膨胀,说明缓冲器故障程度继续加剧。

图11 分闸缓冲器不同状态下的模态分量混沌吸引子演化过程
Fig.11 Evolution of chaotic attractor of IMF component in different states of the opening damper
3.2 试验二
上述试验以12kV真空断路器为研究对象,探究并验证了利用振动信号模态分量混沌吸引子形态特性对断路器关键零部件——分闸缓冲器性能退化(即不同故障程度)进行评估的可行性。为了进一步验证该方法的有效性,本例以一252kV高压 SF6断路器为研究对象(型号为LW59—252/T4000—50),探究所提方法用于诊断高压断路器其他零部件故障程度的效果——操动机构传动连杆孔轴磨损程度诊断。
需要指出的是,本例故障,即传动连杆孔轴磨损致使连接轴销变形脱落,导致断路器合闸失败(操动机构与传动机构之间的连接轴销脱落导致操动机构动作而传动机构及以上部分未动作),非人为设置,而是在对该断路器开展其他试验时,如探究储能电机振动特征随负载(即合闸弹簧)变化情况多次分、合所致(传动连杆轴销脱落时计数器显示:398),具体将在下述讨论。
试验系统原理、断路器操动机构内部结构及加速度传感器固定位置如图12所示。试验过程中采用断路器机械特性测试仪给储能电机提供直流电源,并控制断路器分、合闸。采样率同实验一为100kHz,采样时间设为0.1s,信号触发方式为阈值触发,即当振动幅值超过预先设定的触发阈值(0.01g)时开始记录并保存数据。
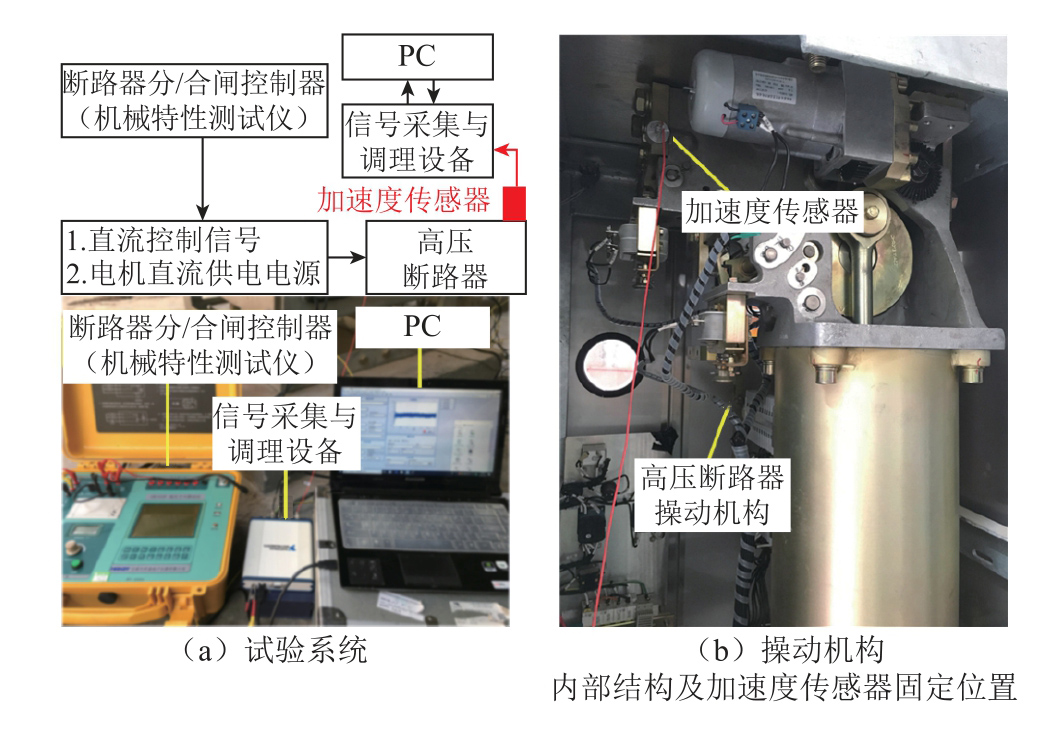
图12 试验系统及加速度传感器固定位置
Fig.12 Test system and position of the accelerometer
在试验过程中,随着断路器动作次数的增多,连接操动机构输出拐臂与传动机构传动拐臂(传动关系如图13所示)的传动连杆轴孔、连接轴销不断被磨损(为方便描述,下面将轴孔和轴销统称为孔轴),随着磨损程度的不断加剧,轴孔逐渐扩大、轴销不断变形,最终,在断路器动作了398次分合动作后轴销突然脱落,导致断路器合闸失败,如图14所示。

图13 操动机构与传动机构传动关系
Fig.13 Transmission relations between operating mechanism and transmission mechanism

图14 传动连杆及传动拐臂孔、连接轴销磨损导致轴销脱落故障
Fig.14 The shaft pin falls off due to severe wear of the connection
本例仍以分闸振动信号为例进行说明,图15给出了该断路器正常状态和传动连杆孔轴磨损不同程度的分闸振动信号,其中,图15a为断路器正常状态时的振动信号(开展本试验初次测试的振动信号);随着断路器操作次数的增多,孔轴磨损不断加剧,相应的振动信号如图15b所示;图15c为连接轴销突然脱落时的振动信号;图15d为轴销脱落后的振动信号,轴销脱落后,由于传动机构与操动机构脱离连接,导致操动机构动作而传动机构及以上部分(包括灭弧室动触头等零部件)未动作,断路器合闸失败。可以看到,各信号之间差异并不明显,很难直接判断孔轴是否出现磨损、磨损程度及轴销是否存在脱落的风险。
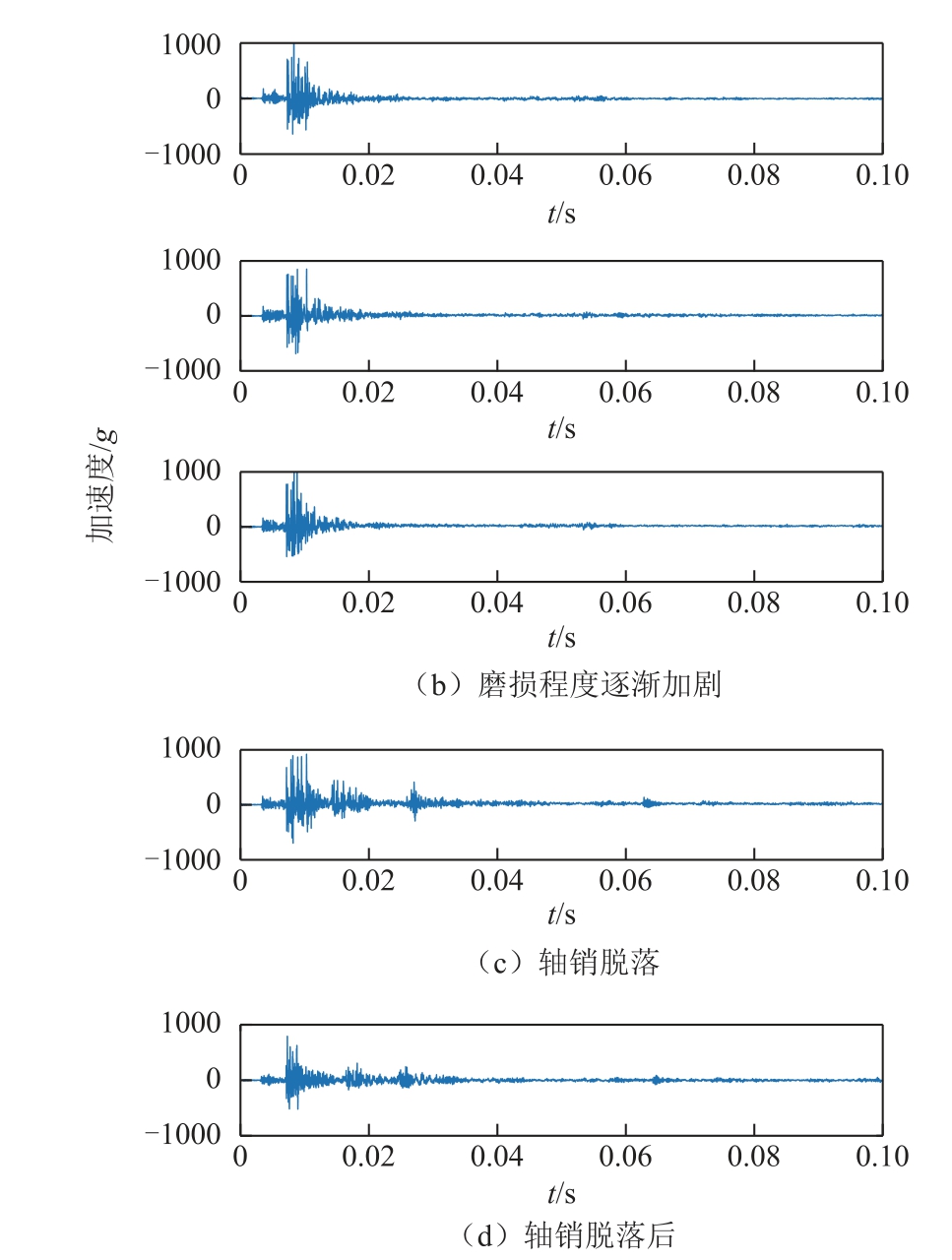
图15 正常状态和传动连杆孔轴磨损不同程度下的分闸振动信号
Fig.15 Opening vibration signals in normal state and different wear severity of the connection

在上述试验一中,由于分闸缓冲器仅在断路器动作末期起作用,因此截取了断路器动作末期的振动信号(即缓冲制动阶段的振动信号)进行分析。本例由于传动连杆孔轴磨损对断路器动作过程中的哪个阶段产生影响暂时未知,因此需要对断路器动作过程中各个阶段的振动信号进行分析。
断路器正常状态下的分闸振动信号分时分割处理如图16所示,小机械波1出现的时刻对应线圈铁心开始运动的时刻;机械波2是由于线圈铁心触发锁扣装置使得机构被解列而引起的;机构解列后,传动机构将能量传递给动触头快速向分闸位运动,这个阶段的设计理念是机构不存在阻碍,运动相对较顺畅、平稳,由于该阶段与机构解列阶段的界线不太明显,因此本文以机构解列后的第一个较明显的波谷作为机构解列阶段与传动阶段的分界线;机械波4是缓冲限位装置对机构传动链进行缓冲制动而引起的。由此,参考各振动事件的起始与结束时刻,将该断路器正常状态下的分闸振动信号分割成如图16所示的不同时段,即时段①为脱扣阶段、②为机构解列阶段、③为传动阶段、④为制动阶段。传动连杆孔轴磨损不同程度的分闸振动信号均以此为参考依据进行分时分割处理。

图16 断路器正常状态下的分闸振动信号分时分割处理
Fig.16 Division of opening vibration signal in normal state of circuit breaker
分别提取各阶段的振动信号进行SSVMD处理,然后进行吸引子重构,发现其中传动阶段振动信号(即阶段②)的模态分量(最后一个模态分量,IMF 6)混沌吸引子随孔轴的磨损程度表现出一定的规律性,如图17所示。可以明显看出:
(1)正常状态(孔轴不存在磨损)的混沌吸引子形态较规则,且轨迹收缩在一起,如图17a所示。
(2)当孔轴磨损时,吸引子形态明显伸展开来,形态变得不规则,如图17b所示。
(3)随着磨损的加剧,吸引子形态越来越复杂,这与磨损状态下机构连杆运动的不稳定性相一致,如图17c和图17d所示。

图17 传动连杆孔轴磨损不同程度的振动信号(传动阶段)模态分量混沌吸引子演化过程
Fig.17 Evolution of chaotic attractor of IMF component in different wear severity of the connection
(4)图17d是连接轴销脱落前一次的混沌吸引子,可以明显看出,该吸引子明显异于正常时的吸引子及其他磨损状态的吸引子,因此,可以以该吸引子的形态为界限,作为轴销脱落的预警判据。
(5)图17e是轴销脱落时的混沌吸引子,其形态达到最大、轨迹最为复杂。
(6)当轴销脱落后,如图17f所示,吸引子形态大小反而变小,形状复杂度降低,原因是传动拐臂及以上传动机构部分(包括绝缘拉杆、灭弧室动触头等)脱离了操动机构,操动机构动作而传动拐臂及以上部分未动作,使得机构动力学复杂度降低。
综合上述试验一与试验二,断路器振动信号经过本文所提方法进行处理后(主要流程为:振动信号分时分割→SSVMD提取模态分量→重构模态分量混沌吸引子),能够将蕴含在振动信号中的故障信息凸显出来,特别是对于零部件早期故障的微弱信息,能够以比较直观的方式呈现出来(即能直观反映故障程度的演变),有利于准确判断断路器零部件故障的严重程度,可为维修计划的合理安排提供一定的参考依据。
4 对比分析
针对断路器(机械零部件)故障程度识别的研究,国内外已有一些文献报道[5, 14-16, 23],这些方法与本文方法的优缺点对比如下。
文献[5]提出了利用振动信号的幅值和时间偏差来检测高压断路器是否出现异常,该文例举了一个实验室模拟合闸油缓冲器漏油故障的试验,通过改变油缓冲器油量的大小,获取相应的振动信号,并计算振动信号的幅值和时间偏差作为油缓冲器故障的预警指标。这种方法的优点是计算相对简单、对于发生较严重故障的预判可靠性较高,不足之处是需要根据具体型号断路器设定合理的预警阈值,以及由于断路器振动信号存在一定的分散性等原因,导致振动信号幅值和时间偏差并不一定随故障程度的加剧而严格线性变化(如表2中虚线方框所示),使得对故障程度的判断存在一定的误差。
表2 合闸油缓冲器不同故障程度下的振动信号幅值和时间偏差
Tab.2 Amplitude and time deviations as a function of the oil volume reduction in the closing oil damper

油体积减少量 /mL 振动信号幅值偏差/ms 振动信号时间偏差/ms 状态 0 7.4 1.3 -5 4.1 0.5 -10 12.7 1.5 -13 13.4 1.7 -16 15.3 2.0 正常 -19 17.2 2.5 -22 16.9 3.0 -25 16.7 2.9 报警
文献[23]采用样本间的欧氏距离评估万能式断路器的三相不同期程度。例如,以A相不同期为例,首先计算A相触头开距不同故障程度下的振动信号样本熵值(通过调节触头开距为2mm、3mm、4mm、5mm模拟不同期故障程度),如图18所示,然后选取3mm的触头开距作为参照,计算其他开距与该参照开距之间的样本间欧氏距离,通过欧氏距离的大 小判断不同期故障程度,A相不同期故障程度判定方法见表3。可以看出,该方法能够较好地量化断路器不同期故障程度,具有一定的实用性。该方法,对故障程度变化较大时较为有效[23],但对微小变化灵敏度有待进一步提高。
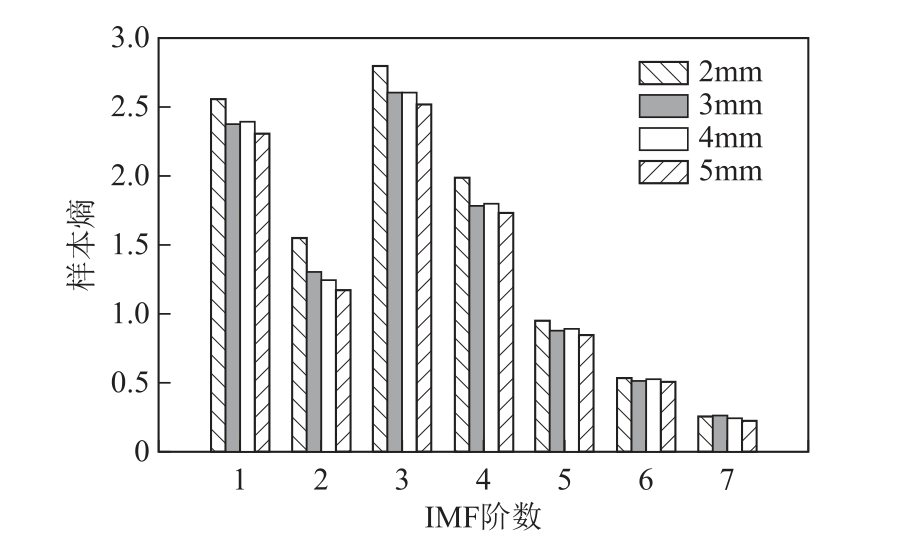
图18 A相不同期故障程度的特征对比
Fig.18 Feature contrast of A-phase non-synchronous fault degree
表3 A相不同期故障程度判定方法
Tab.3 Determination method for A-phase nonsynchronous fault degree
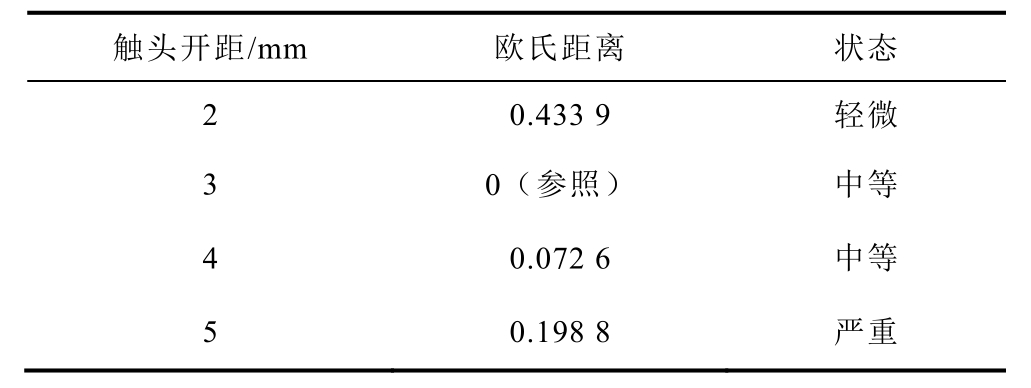
触头开距/mm 欧氏距离 状态 2 0.433 9 轻微 3 0(参照) 中等 4 0.072 6 中等 5 0.198 8 严重
文献[16]则利用振动信号的多尺度排列熵偏均值(Partial Mean of Multi-Scale Permutation Entropy, PMMPE)对低压万能式断路器分合闸故障程度进行评估。图19所示为断路器分合闸不同故障类型、不 同故障程度下的振动信号PMMPE拟合曲线[16],可以看出,随着故障程度的增大,PMMPE值呈现出较好的单调递减的趋势,因此参照该曲线,可以较方便地对分合闸故障程度进行评估。然而,对于某些不同的故障,PMMPE的区分度不是很明显,例如图19中的A/B/C三相不同期故障,曲线之间较为接近,区分性有待进一步的提高。
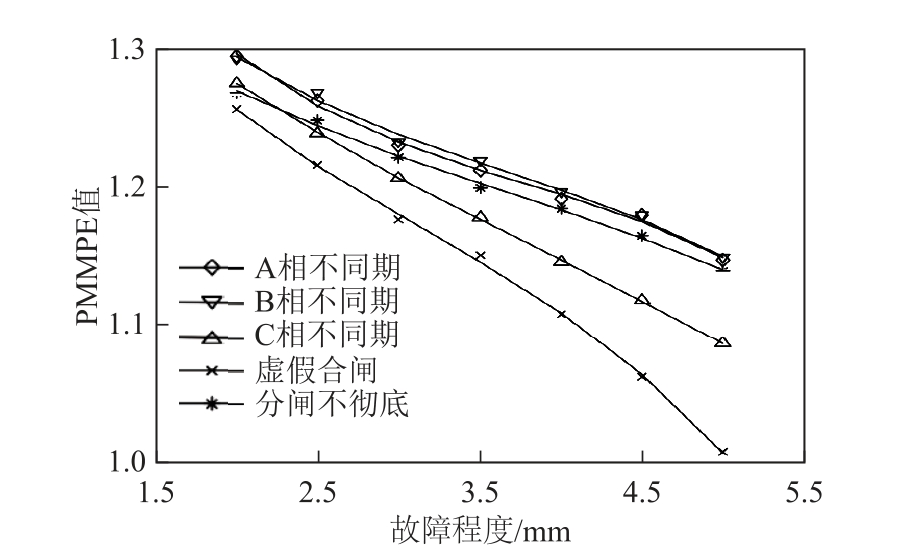
图19 不同故障模式下的PMMPE与故障程度特性曲线
Fig.19 Characteristic curves between PMMPE and fault degree in different working modes
除了上述利用振动信号对断路器(机械零部件)故障程度进行诊断外,还有利用触头行程信号[14]、线圈电流信号[15]实现故障程度诊断。这些方法与本文方法的优缺点对比总结见表4。
表4 断路器故障程度诊断方法对比
Tab.4 Comparison of diagnosis methods for CB fault severity

故障程度诊断方法 诊断对象 主要优点 存在不足 振动信号幅值和时间偏差[5] 振动信号样本熵及样本间欧氏距离[23] 振动信号多尺度排列熵偏均值(PMMPE)[16] 行程信号波动标准方差拟合函数[14]分合闸线圈电流信号集合经验模态分解(EEMD)能量矩相对熵[15] 振动信号混沌吸引子形态特性(本文方法) SF6高压断路器合闸油缓冲器 低压万能式断路器三相同期性 低压万能式断路器三相同期性、虚假合闸、分闸不彻底 SF6高压断路器分闸弹簧 低压万能式断路器分合闸线圈 12kV真空断路器分闸缓冲器,252kV SF6高压断路器传动连杆孔轴磨损 计算相对简单,对于发生较严重故障的预判可靠性较高,能够实现故障预警 能够较好地量化断路器不同期故障程度,具有一定的实用性 参照不同故障类型、不同故障程度振动信号的PMMPE拟合曲线,可以较方便地对三相不同期等分合闸故障程度进行评估 行程测试是目前检测断路器机械特性的常用手段,从行程信号中提取出来的标准偏差可以很好地反映断路器机械状态,进而能够较可靠地判断分闸弹簧故障程度 电流信号EEMD能量矩相对熵随故障程度的增大呈现出单调递增的变化,能够方便地对线圈故障程度进行定量评估 能够直观地表征断路器机械零部件的故障程度,且对早期故障敏感、对不同型号断路器的鲁棒性较好 需根据具体型号断路器选取合理的阈值,以及由于断路器振动信号的分散性等原因,导致振动信号幅值和时间偏差并不严格随故障程度的加剧而线性变化,使得对故障程度的判断存在一定的误差 该方法尚存在对微小变化不够灵敏,对故障程度变化较大时较为有效 对于某些故障的PMMPE区分性不明显,如A/B/C三相不同期故障,区分性能有待进一步提高 实际运行中的高压断路器分闸弹簧除了压缩量变化导致分闸故障外,弹簧疲劳也是引发故障的原因之一,结论对于弹簧疲劳失效是否适用,值得进一步深入研究 线圈不同故障类型的EEMD能量矩相对熵值在早期故障阶段存在交叉区(文献[15]图6),可能导致故障程度与故障类型之间的误判 需进一步研究能够有效量化故障严重程度的评价指标
5 结论
1)对断路器振动信号进行分时分割、特征模态提取以及重构混沌吸引子等处理后,可将断路器零部件早期故障的微弱故障特征显现出来。其中,①信号分时分割是以断路器正常状态时的振动信号为参考依据,结合断路器动作特点,将振动信号分割为脱扣、解列、传动及制动阶段,该方法有利于故障零部件的有效定位;②提出的SSVMD可以对振动信号进行参数自适应分解,该算法能够根据断路器振动信号自身特点,自动选择分解层数,避免目前VMD方法存在参数选择困难等不足。
2)断路器制动阶段的振动信号混沌吸引子能够有效反映分闸缓冲器的故障程度,可以以吸引子轨道突然开始逃离吸引域作为缓冲器开始出现故障的判据;而传动阶段的振动信号混沌吸引子能够有效反映传动连杆孔轴的磨损程度,轴销脱落前一次的混沌吸引子明显异于正常状态的吸引子,因此,可以以该吸引子的形态作为轴销脱落的预警判据。
3)通过对一台12kV真空断路器开展零部件故障程度模拟试验,以及通过分析一台252kV SF6高压断路器传动连杆孔轴磨损的演化过程,验证了所提方法的有效性和一定的普适性。所提方法能够有效识别断路器零部件的故障程度,特别是对于早期故障的微弱故障信息,能够以比较直观的方式呈现出来,有利于提高故障程度识别的准确性。
4)后续工作可根据断路器零部件不同故障程度的混沌吸引子形态特征,提出合适的量化形态特征的指标,以实现故障程度的定量评估。
[1]CIGRE Working Group A3.06. Final report of the 2004-2007 international enquiry on reliability of high voltage equipment, Part 2 - Reliability of high voltage SF6 circuit-breakers. CIGRE Technical Brochure 510, 2012.
[2]Razi-Kazemi A A, Vakilian M, Niayesh K, et al. Priority assessment of online monitoring investment for power system circuit breakers-part I: qualitativequantitative approach[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 928-938.
[3]Janssen A, Makareinis D, Solver C E. International surveys on circuit breaker reliability data for substation and system studies[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 808-814.
[4]Lai M L, Park S Y, Lin C C, et al. Mechanical failure detection of circuit breakers[J]. IEEE Transactions on Power Delivery, 1988, 3(4): 1724-1731.
[5]Landry M, Leonard F, Landry C, et al. An improved vibration analysis algorithm as a diagnostic tool for detecting mechanical anomalies on power circuit breakers[J]. IEEE Transactions on Power Delivery, 2008, 23(4): 1986-1994.
[6]万书亭, 豆龙江, 李聪, 等. 基于振动信号的高压断路器合闸特性参数在线检测方法研究[J]. 振动工程学报, 2019, 32(2): 359-367.
Wan Shuting, Dou Longjiang, Li Cong, et al. Study on on-line detection of high voltage circuit breaker closing characteristic parameters based on vibration signal[J]. Journal of Vibration Engineering, 2019, 32(2): 359-367.
[7]黄南天, 王斌, 蔡国伟, 等. 基于 Tsallis熵与层次化混合分类器的含未知故障断路器机械故障诊断[J]. 高电压技术, 2019, 45(5): 1518-1525.
Huang Nantian, Wang Bin, Cai Guowei, et al. Mechanical fault diagnosis containing unknown fault of high voltage circuit breaker based on Tsallis entropy and hybrid classifier[J]. High Voltage Engineering, 2019, 45(5): 1518-1525.
[8]杨秋玉, 阮江军, 黄道春, 等. 基于振动信号时频图像识别的高压断路器分闸缓冲器状态评估[J]. 电工技术学报, 2019, 34(19): 4048-4057.
Yang Qiuyu, Ruan Jiangjun, Huang Daochun, et al. Opening damper condition evaluation based on vibration time-frequency images for high-voltage circuit breakers[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4048-4057.
[9]Yang Qiuyu, Ruan Jiangjun, Zhuang Zhijian, et al. Chaotic analysis and feature extraction of vibration signals from power circuit breakers[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1124-1135.
[10]Yang Qiuyu, Ruan Jiangjun, Zhuang Zhijian, et al. Fault diagnosis of circuit breakers based on timefrequency and chaotic vibration analysis[J]. IET Generation, Transmission & Distribution, 2020, 14(7): 1214-1221.
[11]赵书涛, 马莉, 朱继鹏, 等. 基于CEEMDAN样本熵与FWA-SVM的高压断路器机械故障诊断[J]. 电力自动化设备, 2020, 40(3): 181-186.
Zhao Shutao, Ma Li, Zhu Jipeng, et al. Mechanical fault diagnosis of high voltage circuit breaker based on CEEMDAN sample entropy and FWA-SVM[J]. Electric Power Automation Equipment, 2020, 40(3): 181-186.
[12]杨秋玉, 阮江军, 张灿, 等. 基于定量递归分析的高压断路器机械缺陷辨识及应用[J]. 电工技术学报, 2020, 35(18): 3848-3859.
Yang Qiuyu, Ruan Jiangjun, Zhang Can, et al. Study and application of mechanical defect identification for high-voltage circuit breakers using recurrence quantification analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3848-3859.
[13]程序, 关永刚, 张文鹏, 等. 基于因子分析和支持向量机算法的高压断路器机械故障诊断方法[J]. 电工技术学报, 2014, 29(7): 209-215.
Cheng Xu, Guan Yonggang, Zhang Wenpeng, et al. Diagnosis method on the mechanical failure of high voltage circuit breakers based on factor analysis and SVM[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 209-215.
[14]李德阁, 武建文, 马速良, 等. 基于行程信息的断路器弹簧故障程度诊断[J]. 高压电器, 2018, 54(4): 20-27.
Li Dege, Wu Jianwen, Ma Suliang, et al. Fault degree diagnosis of circuit breaker spring based on travel signal[J]. High Voltage Apparatus, 2018, 54(4): 20-27.
[15]孙曙光, 张强, 杜太行, 等. 基于分合闸线圈电流的万能式断路器故障诊断[J]. 仪器仪表学报, 2018, 39(2): 130-140.
Sun Shuguang, Zhang Qiang, Du Taihang, et al. Fault diagnosis for conventional circuit breaker based on switching coil current[J]. Chinese Journal of Scientific Instrument, 2018, 39(2): 130-140.
[16]孙曙光, 张强, 杜太行, 等. 基于振动信号的低压万能式断路器分合闸故障程度评估方法的研究[J]. 中国电机工程学报, 2017, 37(18): 5473-5482, 5547.
Sun Shuguang, Zhang Qiang, Du Taihang, et al. Study of evaluation method for low voltage conventional circuit breaker switching fault degree based on vibration signal[J]. Proceedings of the CSEE, 2017, 37(18): 5473-5482, 5547.
[17]阮江军, 杨秋玉, 黄道春, 等. 高压断路器机械振动信号混沌吸引子形态特性[J]. 电力自动化设备, 2020, 40(3): 187-193.
Ruan Jiangjun, Yang Qiuyu, Huang Daochun, et al. Shape characteristic analysis of chaotic attractor for mechanical vibration signal of high-voltage circuit breaker[J]. Electric Power Automation Equipment, 2020, 40(3): 187-193.
[18]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings A, 1998, 454(1971): 903-995.
[19]任宜春, 翁璞. 基于改进Hilbert-Huang变换的结构损伤识别方法研究[J]. 振动与冲击, 2015, 34(18): 195-199.
Ren Yichun, Weng Pu. Structural damage detection based on improved Hilbert-Huang transform[J]. Journal of Vibration and Shock, 2015, 34(18): 195-199.
[20]Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[21]徐元博, 蔡宗琰, 胡永彪, 等. 强噪声背景下频率加权能量算子和变分模态分解在轴承故障提取中的应用[J]. 振动工程学报, 2018, 31(3): 513-522.
Xu Yuanbo, Cai Zongyan, Hu Yongbiao, et al. A frequency-weighted energy operator and variational mode decomposition for bearing fault detection[J]. Journal of Vibration Engineering, 2018, 31(3): 513-522.
[22]赵岩, 朱均超, 张宝峰, 等. 基于VMD与Hilbert谱的旋转机械碰摩故障诊断方法[J]. 振动、测试与诊断, 2018, 38(2): 381-425.
Zhao Yan, Zhu Yunchao, Zhang Baofeng, et al. Rubimpact fault diagnosis of rotating machinery based on VMD and Hilbert spectrum[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(2): 381-425.
[23]孙曙光, 于晗, 杜太行, 等. 基于振动信号样本熵和相关向量机的万能式断路器分合闸故障诊断[J]. 电工技术学报, 2017, 32(7): 20-30.
Sun Shuguang, Yu Han, Du Taihang, et al. Diagnosis on the switching fault of conventional circuit breaker based on vibration signal sample entropy and RVM[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 20-30.