0 引言
随着区域电网互联规模不断扩大、能源供应需求急剧增长,电力系统的运行日趋接近其极限,低频振荡已成为限制区域间功率传输能力、影响电网安全稳定运行的主要因素之一[1-2]。低频振荡特征参数的精准提取是预防和抑制电网低频振荡失稳的前提。传统基于电力系统微分代数模型的低频振荡分析方法虽然可准确求解出系统低频振荡的关键特征参数,但需构建详细、准确的电力系统动态模型,而在实际运行中很难随时间和运行条件变化来实时构建高精度的电力系统动态模型,因此该方法主要应用于电力系统的离线低频振荡分析。
广域量测系统(Wide Area Measurement System, WAMS)在电网广泛应用,为电力系统低频振荡分析提供了可靠的数据来源和全新的研究思路,使基于广域量测信息的低频振荡辨识方法得到了广泛关注[3-5]。该方法借助模式辨识的相关理论和技术,实时、准确分析电力系统广域量测信息中所隐含的电网动态信息,提取出反映系统低频振荡的关键特征参数,实现对电力系统动态稳定的快速评估[6-8]。
目前,基于广域量测信息的电力系统主导振荡模式辨识主要分为单通道辨识方法[9-15]和多通道辨识方法[16-21]。单通道辨识方法以单一量测通道获取的量测信息作为输入信号,来辨识系统的主导振荡模式,主要方法有快速傅里叶变换(Fast Fourier Transform, FFT)[9]、自回归滑动平均模型(Auto-Regressive Moving-Average, ARMA)[10]、Prony算法[11-12]、希尔伯特-黄变换(Hilbert-Huang Transform, HHT)[13-14]、连续小波变换(Continuous Wavelet Transform, CWT)[15]等。FFT是较早被用来辨识系统主导振荡模式的方法。文献[9]采用非线性最小二乘优化FFT的振荡模式辨识结果,提升FFT在含噪声环境下的辨识精度,但辨识结果仅能分析系统的主导振荡频率,无法辨识主导振荡模式的阻尼比。为此,文献[10]引入ARMA并借助谱估计方法追踪系统主导振荡模式的振荡频率和阻尼比,但该方法仅适用于分析类噪声信号。为从电力系统故障信号中实现振荡频率和阻尼比的高效辨识,文献[11]引入了Prony算法,但Prony算法的辨识结果易受量测噪声影响。为提高Prony算法的抗噪能力,文献[12]采用滑动窗技术滤除量测信号中的噪声,以提升Prony算法的鲁棒性,但该方法不适用于分析非线性、时变信号。为从非线性、时变广域量测信息中辨识出系统的主导振荡模式,文献[13]将经验模态分解(Empirical Mode Decomposition, EMD)与HHT相结合,从电力系统广域非线性、时变量测信号中捕捉到系统主导振荡频率的瞬变特性和阻尼比的时变特征,但辨识过程中易出现模式混叠和端点效应,严重影响辨识结果的精度。为此,文献[14]引入频率偏差法和端点延拓法以克服文献[13]中存在的模式混叠和端点效应,提升了主导振荡模式的辨识精度,但在辨识过程中产生的虚假振荡信息严重影响到主导振荡模式的筛选。为有效分离出虚假振荡模式,文献[15]基于小波相对能量实现了主导振荡模式与虚假振荡模式的有效分离。
上述单通道辨识方法虽然可有效地辨识系统的主导振荡模式,但受主导振荡模式可观性的影响,其辨识结果不能准确地反映系统的全局振荡特性。此外,单通道辨识方法需逐次分析单一通道量测信号的振荡特性,辨识效率较低,辨识结果不能给出表征发电机间动态振荡的主导振荡模态。而基于广域量测信息的多通道辨识方法充分考虑电力系统各量测通道间的关联性,从多通道量测信息中提取出表征系统动态振荡特性的主导振荡模态[16-17]。文献[18]采用随机子空间(Stochastic Subspace Identification, SSI)直接从多通道量测数据中提取振荡模式,并借助层次聚类解决了SSI模型定阶的难题,但计算过程中高维矩阵的处理导致该方法计算效率偏低。为此,文献[19]基于正交分解(Proper Orthogonal Decomposition, POD)实现高阶量测矩阵的快速降阶,进而提取出关键振荡信息的幅值和相位,但其辨识结果易遗失较为重要的动态振荡信息。为避免重要振荡信息的遗失,文献[20]引入库普曼模态分解(Koopman Mode Decomposition, KMD)提取系统的振荡信息来辨识振荡模态,但其计算过程较为复杂。为简化计算,文献[21]基于动态解耦(Dynamic Mode Decomposition, DMD)分析系统的振荡信息,利用振荡信息的时空耦合关系提取系统的主导振荡模式及模态,但该方法缺乏分离主导振荡模式信息和虚假振荡模式信息的有效手段,且动态稳定评估过程亟需进一步完善。
针对DMD在分离系统主导振荡模式信息与虚假振荡模式信息的不足,本文引入稀疏增强动态解耦(Sparsity Promoting Dynamic Mode Decomposition, SPDMD)筛选含系统关键振荡信息的主导振荡模式,进而实现主导振荡模式和模态的协同辨识。该方法借助DMD辨识系统振荡模式及模态,然后构建各振荡模式的最优振幅系数以分离由外施扰动或噪声引发的虚假振荡模式及模态;最后将所提方法应用到16机68节点测试系统和中国南方电网,对所提SPDMD算法进行分析、验证。
1 基于DMD的主导振荡模式及模态辨识
DMD最初是由巴黎综合理工大学的P J Schmid教授提出,用以解决流体力学中流体的流动特征提取问题[22-23]。该方法可实现高阶量测信息的快速降阶,显著提高辨识效率,且可有效避免模式混叠对计算精度的影响。基于DMD的主导振荡模式及模态辨识算法基本原理如下:
从广域量测系统的相量量测单元(Phasor Measurement Unit,PMU)中采集电力系统的广域量测信息,构建电力系统的广域量测信息矩阵X0为
式中,x1, x2,…, x N为各时间点所采集量测信息向量。
若量测信息xj+1可通过量测信息xj的线性映射A来表示,提取矩阵X0的前N-1个列向量和后N-1个列向量分别记为矩阵 X1=[x1 x2 … x N-1]和矩阵X2=[x2 x3 … x N],X1与X2的关系为
式中,A为可捕获量测信息内固有的动态变化特征的高阶复杂矩阵,其特征值和特征向量中包含系统的动态振荡信息;r为残差矩阵。
借助奇异值分解(Singular Value Decomposition,SVD)分解矩阵X1并忽略残差矩阵r,可得矩阵X2为
式中,U为左奇异向量矩阵,包含系统的空间振荡信息;Σ为奇异值矩阵;V为右奇异向量矩阵,矩阵ΣV*包含系统的时间振荡信息。U和V均为酉矩阵,满足U*U=V*V=I,I为单位矩阵。
由于矩阵A通常为高阶复杂矩阵,为简化计算,引入低阶矩阵F近似描述A的动态振荡特性,F为
将式(4)代入式(3),计算低阶状态矩阵F,并对其进行特征值分解得到
式中,Λ为振荡模式矩阵,Λ=diag(λ1 λ2 … λm);λi为振荡模式i对应的特征值;Y为特征向量矩阵,Y=[y1 y2 … ym],yi为λi的右特征向量;m为振荡模式数量。
进一步,由U、ΣV*、Λ和Y得到含系统动态振荡信息的广域量测矩阵X2的近似表达式为
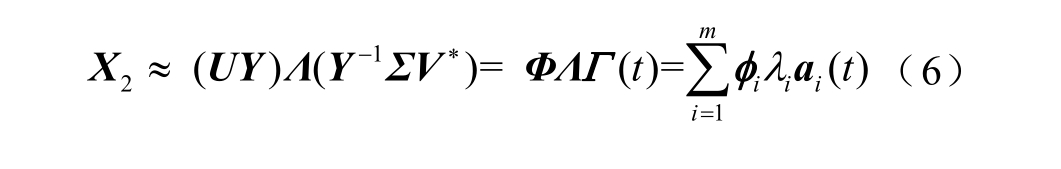
式中,Φ 为振荡模态,表征系统各发电机的相对振荡趋势,Φ=[φ1 φ2 … φ m];Γ(t)为与时间有关的振幅系数,表征振荡模态幅值随时间变化情况,Γ(t)= [ɑ1(t) ɑ2(t) … ɑm(t)]T。
由式(6)的振荡模式矩阵Λ,可得系统第i个振荡模式的振荡频率fi和阻尼比ζi为

受故障时间、故障类型及量测噪声的影响,所辨识的系统振荡模式中常伴有虚假振荡模式[24-25]。为有效辨识系统的主导振荡模式,本节通过式(8)计算各振荡模式的相对能量权重,再根据相对能量阈值分离系统的主导振荡模式。
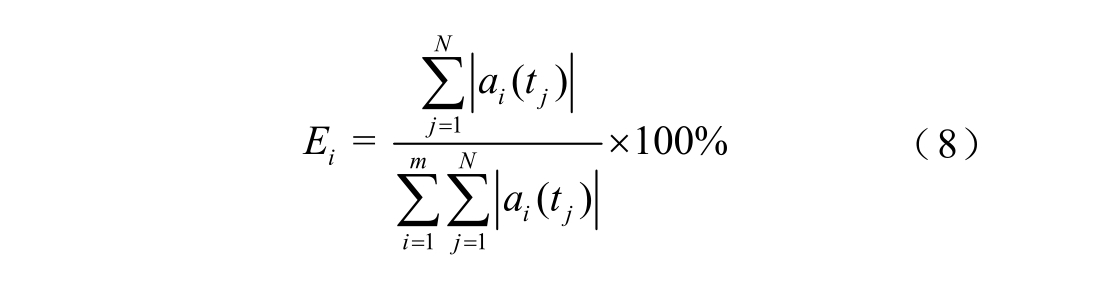
式中,Ei为振荡模式i的相对能量权重。相对能量阈值的合理选取可有效筛选系统的主导振荡模式。
DMD方法虽可在时空域内从电力系统的广域量测信息中辨识出系统的振荡模式和模态,并借助Γ(t)计算相对能量权重从振荡模式和模态中筛选主导振荡模式及模态,有效抑制模式混叠对振荡辨识结果的影响。但在采用式(8)所示的方法来分离主导振荡模式时,若主导振荡模式与虚假振荡模式间的相对能量权重较为接近,将无法有效地从所辨识的振荡模式中分离出电力系统的主导振荡模式。当主导振荡模式发生漏选情况时,遗失的主导振荡模式未经合理、有效的解决措施可能会导致系统发生失稳现象;当虚假振荡模式发生误选情况时,会为电力系统低频振荡分析带来不必要的麻烦,严重时可能会错失抑制低频振荡的最佳时机。上述两种情况均会对电网稳定产生严重威胁,故亟需一种简单、高效的方法实现主导振荡模式和虚假振荡模式的准确分离。
2 基于SPDMD的低频振荡特征参数提取
针对DMD方法从辨识的振荡模式中分离出系统主导振荡模式和虚假振荡模式的瓶颈,本节进一步引入SPDMD以分离主导振荡模式和虚假振荡模式,实现电力系统主导振荡模式及模态的协同辨识。
2.1 主导振荡模式及模态筛选
2.1.1 初始振幅系数建立
在DMD的辨识基础上,本节将式(6)中矩阵X2的量测信息在空间上进行快速解耦,构建高阶量测信息的低阶表达式,在保留系统关键振荡信息的基础上,利用低阶矩阵等效替换高阶矩阵,进而形成统一的标准来弥补DMD在主导振荡模式筛选中的不足。分解量测信息向量xj+1所构建的含初始振幅系数 αi的表达式为

式中,vj+1为假定与量测信息xj+1存在近似变化关系U的列向量; αi为由量测信息xj+1所分解该时刻振荡模态i的幅值;*为矩阵的复共轭转置。
根据式(9)提取矩阵X1含有的动态振荡信息,实现振荡模式辨识和振荡模态的协同辨识。
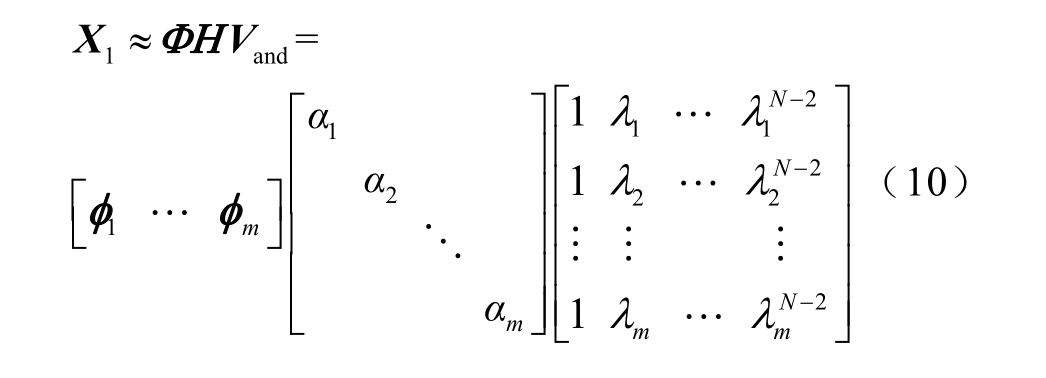
式中,H=diag(α1 α2 … αm)为初始振幅系数矩阵;Vand为含振荡模式信息的Vandermonde矩阵。
为获取更为准确的 αi以提取系统的关键振荡信息,本节采用F-范数将式(10)近似转换为优化问题,进而求解 αi[23]为
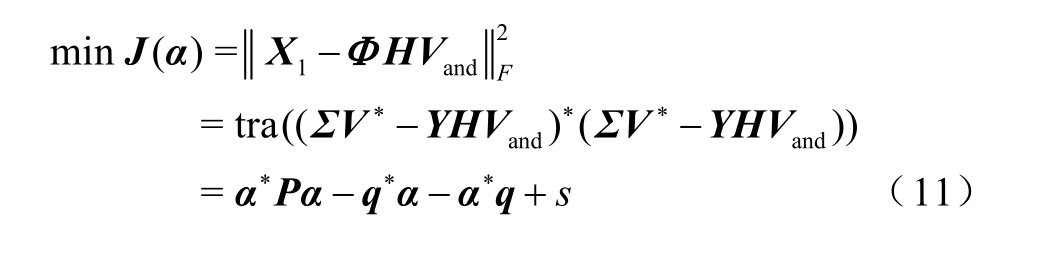
式中,P=(Y*Y)·[(VandVand*)*]T,·表示矩阵对应位置元素相乘;q=[diag(VandVΣ*Y)*]T;s=tra(Σ *Σ );tra表示矩阵主对角线上所有元素之和;α为 αi构成的向量,α=[α1 α2 … αm]T。
求解式(11),α可表示为
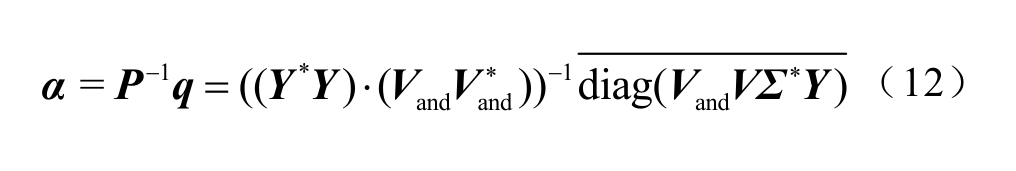
2.1.2 初始振幅系数优化
通过上述计算得到初始振幅系数α后,为使其可准确筛选含系统关键振荡信息的主导振荡模式,本节进一步引入具有稀疏性的罚函数,使含有系统关键振荡信息的主导振荡模式、模态与矩阵X1包含的动态振荡信息间的偏差达到最小,即采用主导振荡模式及模态实现对矩阵X1的分层描述。
式中,γ为正则化参数,其数值决定罚函数的稀疏性,其值越大表示稀疏性越高;pun(α)为正则化惩罚函数,常用的正则化惩罚函数为1-范数和2-范数。
为便于计算,采用1-范数将式(13)等效为
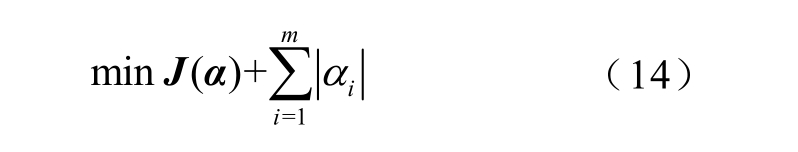
通过计算式(14)所示的多项式优化问题可求得α的最优解,进而有效分离出量测信息中含有的虚假振荡模式。为此,本节采用交替方向乘子法(Alternating Direction Multiplier Method,ADMM)求解式(14)以剔除系统中的虚假振荡信息,ADMM通过引入新变量等效替换部分原变量,在将式(14)中目标函数分为两部分的同时保证优化过程的可分解性,其主要过程如下:
1)采用变量βi替代αi,并引入等式约束。

根据ADMM原理可知:对于任意变量αi和βi,式(14)和式(15)是等价的。分别求解式(15)中αi和βi,可有效降低计算复杂程度。
2)引入式(15)的增广拉格朗日形式,计算α、β的最优解。

式中,β=[β1 β2 … βm]T;λ为拉格朗日乘子;ρ为惩罚参数,通常令ρ=1。
通过迭代计算α、β与λ。

式中,argmin为当目标函数Lρ达到最小值时α或β的值;k为迭代次数。
若α和β满足式(18),则迭代完成。

式中,rdual为对偶残差,等于每次迭代α与β的差值;rprim为原始残差,等于变量β迭代前后的差值。当式(18)满足相对停止阈值ε1、ε2时,βk+1即为α的迭代结果,令α=βk+1。
为使α内非零元素准确表征系统的关键振荡信息,根据式(11)引入约束条件
式中,E=[1 0 0 0 …; 0 0 1 0 …; 0 0 0 0 …; …];α=[0 α2 0 α4 …]T,α2和α4为任意实数。
进一步将式(19)转换为拉格朗日形式[23],即
式中,μ为拉格朗日乘子。
求解模型(19),当J(α)达到最小值时,α最优解为
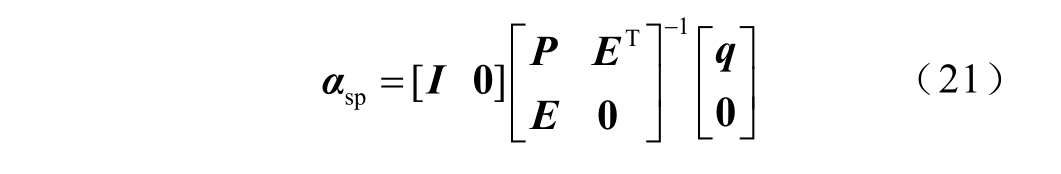
式中,αsp为最优振幅系数。
上述过程实现了αsp的准确构建,为主导振荡模式的筛选提供了依据。显然,由式(21)可知:引入ADMM和LM后,即实现了电力系统各振荡模式对应αsp的构建,进一步利用主导振荡模式所对应αsp不为0、虚假振荡模式所对应αsp为0这一特点,准确筛选出电力系统的主导振荡模式。αsp具备此特点的原因在于:式(2)将噪声等扰动信号保留在残差矩阵r中,使矩阵X2仅含关键振荡信息和由噪声激发的虚假振荡信息。进一步,由于α内元素可表征其所对应振荡信息的重要程度,当根据式(13)增强α的稀疏性时,其内部非零元素对应的振荡信息更为重要,因此,αsp内非零元素对应的振荡信息即为关键振荡信息,提取的振荡模式即为主导振荡模式。SPDMD时空解耦图如图1所示,SPDMD仅用有限个主导振荡模式、模态与αsp内非零元素的加权实现对系统量测信息的有效描述,即此时已通过αsp内0元素分离出系统的虚假振荡信息,量测信息中只有含关键振荡信息的主导振荡模式,最终根据式(10)中振荡模式与振荡模态的对应关系筛选出系统的主导振荡模态。

图1 SPDMD时空解耦图
Fig.1 Spatial-temporal decoupling by SPDMD
2.2 算法流程
综上所述,本文所提基于SPDMD的电力系统振荡模式与模态辨识方法整体流程如下:
(1)从PMU装置中采集电力系统的状态量测信息,对其进行标准化处理,然后构建如式(1)所示标准化的电力系统广域量测信息矩阵X0。
(2)根据式(2)分别提取标准化量测信息矩阵X0的前N-1列构建矩阵X1=[x1 x2 … x N-1]和后N-1列构建矩阵X2=[x2 x3 … xN],通过式(3)引入SVD分解矩阵X1获得矩阵U、Σ、V。
(3)根据式(5)利用矩阵X2以及分解X1所获子矩阵U、Σ、V计算矩阵F。
(4)采用特征值分解计算矩阵F的特征值矩阵Λ和特征向量矩阵Y,再根据式(6)中U、Σ、V、Λ和Y获取含系统动态振荡信息的矩阵X2。
(5)根据式(9)建立高阶量测信息的低阶表达形式,借助递推关系获得式(10)来辨识系统的振荡模式及模态,并通过式(12)计算初始振幅系数α。
(6)通过式(13)引入具有稀疏性的罚函数,采用ADMM和LM求解式(14)来优化α,进而获取最优振幅系数αsp。
(7)通过αsp中非零元素的位置来确定系统的主导振荡模式及模态,有效分离系统的虚假振荡信息。
3 算例分析
为验证所提基于SPDMD的主导振荡模式及模态协同辨识的准确性和有效性,本节分别以16机68节点测试系统和中国南方电网为例进行分析、验证。
3.1 16机68节点测试系统
16机68节点测试系统拓扑结构如图2所示,系统详细参数见文献[26]。该系统分为5个区域,发电机G1~G9位于区域1;发电机G10~G13位于区域2;发电机G14、G15、G16分别位于区域3、4、5。
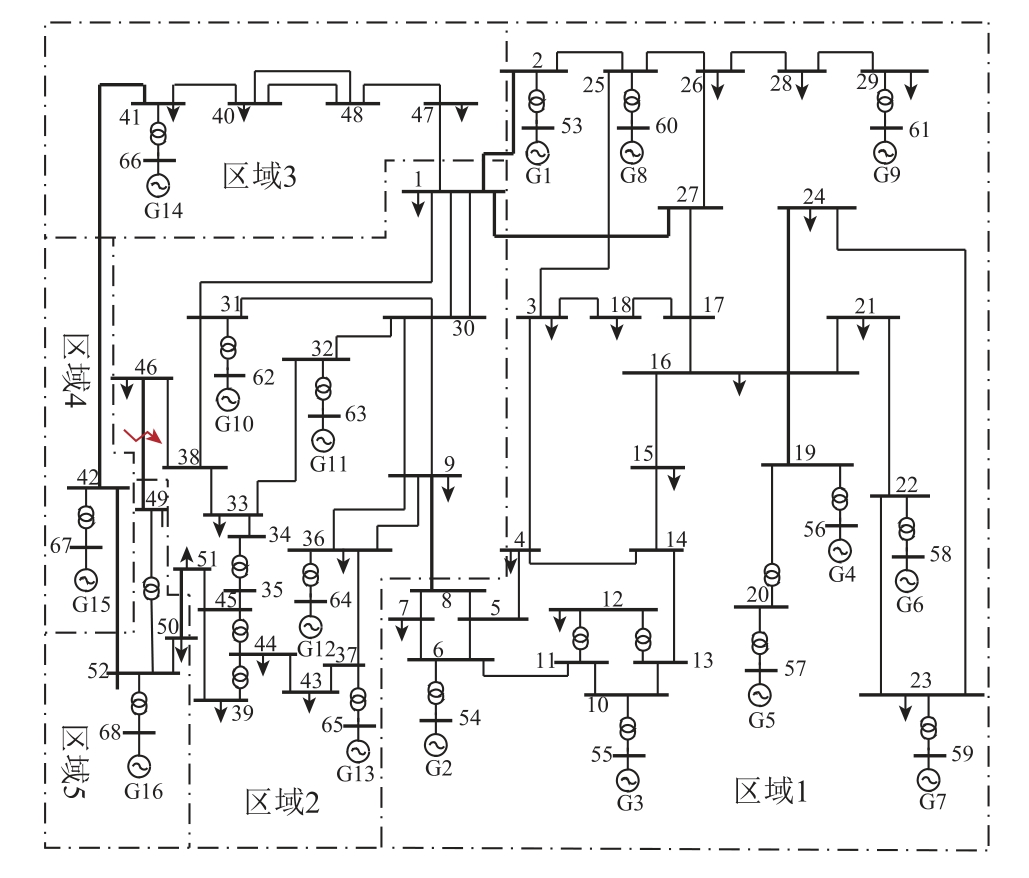
图2 16机68节点测试系统
Fig.2 16-machine 68-bu s test system
3.1.1 SPDMD准确性验证
以16机68节点测试系统的时域仿真数据模拟电网的广域量测数据,发电机G1为参考机,0.1s时在支路46-49近节点49侧设置三相短路故障,0.26s时节点49侧断路器跳开,0.28s时节点46侧断路器跳开,仿真持续至60s,采样频率为100Hz。故障期间,发电机相对转子角与角速度曲线分别如图3和图4所示,选取图3和图4中前30s的发电机转子角和角速度信息作为本文所提方法的输入,构建式(1)所示的广域量测信息矩阵X0。
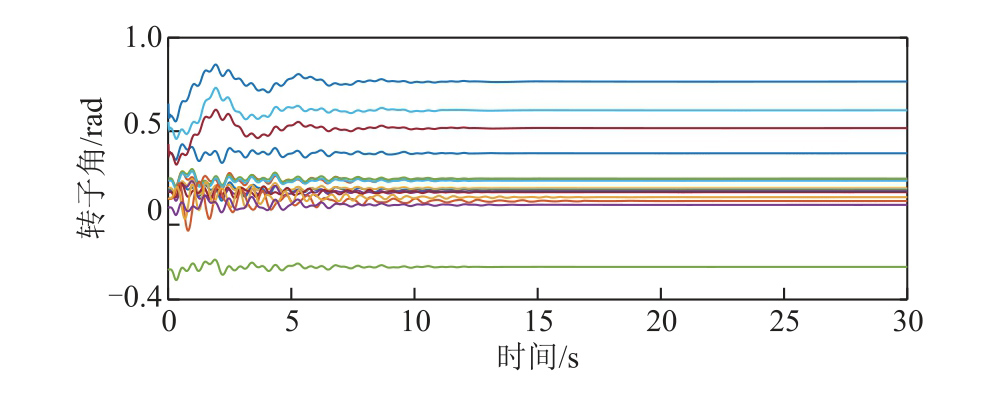
图3 16机68节点测试系统发电机转子角摇摆曲线
Fig.3 The oscillation curves of rotor angles in 16-machine 68-bus test system

图4 16机68节点测试系统发电机角速度摇摆曲线
Fig.4 The oscillation curves of rotor speeds in 16-machine 68-bus test system
由于输入的量测通道共30个,理论上振荡模式将以共轭对的方式出现,因此,振荡模式对应的αsp中含有15对元素,其中非零元素对应的振荡模式即为主导振荡模式,同理可筛选出主导振荡模态。
图5给出了基于SPDMD的αsp估计结果。由图5可知:本次故障下系统被激发出4组主导振荡模式,对应振荡频率分别为2.105 2Hz、1.640 0Hz、1.182 3Hz和0.240 7Hz,各主导振荡模式的最优振幅系数αsp分别为2.353 2、1.335 9、2.397 5和5.356 8。
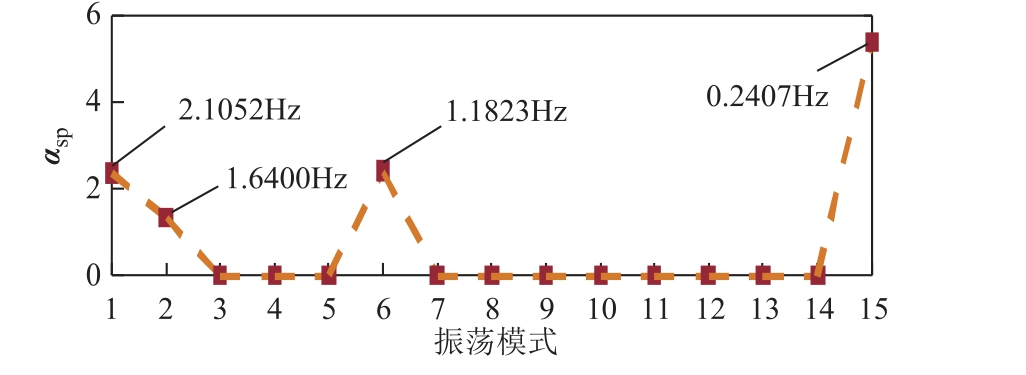
图5 SPDMD辨识各振荡模式的αsp
Fig.5 The αsp of each mode identified by SPDMD
图6进一步给出了采用FFT辨识的系统主导振荡频率。由图6可知:本次故障下FFT共辨识出4组主导振荡频率,分别为2.099 6Hz、1.599 1Hz、1.147 5Hz和0.268 6Hz。对比图5与图6中主导振荡频率的辨识结果可知:本文基于SPDMD所辨识的4组主导振荡频率与FFT的辨识结果基本一致,验证了所提SPDMD方法仅根据αsp中虚假振荡模式对应位置元素为0的特性,即可效分离出系统虚假振荡信息,实现主导振荡模式的有效筛选,避免因DMD相对能量阈值选择不合理而导致的主导振荡模式多选或漏选。

图6 FFT所辨识主导振荡模式
Fig.6 Dominant modes identified by FFT
SPDMD和特征值分析(Eigenvalue Analysis,EA) 主导振荡模式辨识结果对比见表1。表1表明,本文所提SPDMD主导振荡模式辨识结果与EA辨识结果一致,验证了所提SPDMD方法可准确辨识出系统的主导振荡模式。
表1 SPDMD与EA主导振荡模式辨识结果对比
Tab.1 The identified results comparison of dominant modes by SPDMD and EA
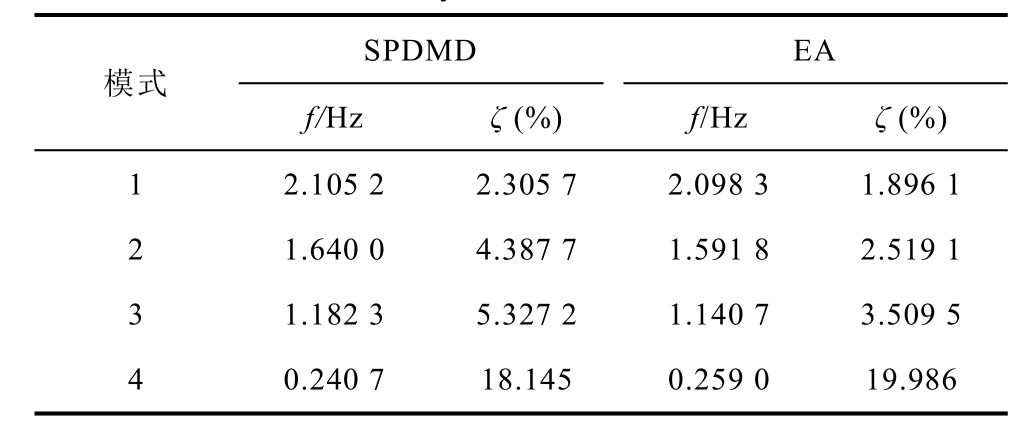
SPDMD EA 模式 f/Hz ζ (%) f/Hz ζ (%) 1 2.105 2 2.305 7 2.098 3 1.896 1 4.387 7 1.591 8 2.519 1 3 2 1.640 0 5.327 2 1.140 7 3.509 5 4 1.182 3 0.240 7 18.145 0.259 0 19.986
3.1.2 SPDMD与DMD主导振荡模式筛选结果对比
表2对比了SPDMD与DMD方法在分离主导振荡模式中的差异性。由表2可知:SPDMD根据各主导振荡模式的最优振幅系数αsp不为0而虚假振荡模式αsp均为0的特点,有效分离出4组主导振荡模式;而DMD计算得到的各振荡模式的能量权重均大于0,需设定合理的相对能量阈值才能分离出虚假振荡模式,若其相对能量阈值选取不合理则将严重影响主导振荡模式筛选结果。
表2 SPDMD与DMD的主导振荡模式筛选结果
Tab.2 The screening results of dominant modes by DMD and SPDMD

模式 f/Hz ζ(%) αsp(SPDMD) E(DMD) (%) 1 2.105 2 2.305 7 2.353 2 17.241 2 1.640 0 4.387 7 1.335 9 7.565 0 3 1.448 8 5.192 2 0 3.812 0 4 1.348 5 1.659 0 0 1.915 4 5 1.247 9 4.015 7 0 3.670 0 6 1.182 3 5.327 2 2.397 5 9.511 1 7 1.126 9 2.563 1 0 10.934 8 1.063 8 2.334 8 0 6.803 0 9 0.987 9 1.413 2 0 6.391 4 10 0.913 8 1.313 1 0 6.366 2 11 0.835 0 3.844 6 0 4.571 6 12 0.705 4 13.057 0 2.219 3 13 0.574 2 10.429 0 5.324 9 14 0.438 8 10.957 0 4.351 9 15 0.240 7 18.145 5.356 8 9.323 9
为进一步表明SPDMD筛选主导振荡模式的优势,表3分别对比了DMD相对能量阈值为6和9时,DMD的主导振荡模式筛选结果。显然,由表3可知:当DMD相对能量阈值为6时,共筛选出8组主导振荡模式,其中,模式4、5、6和7为虚假振荡模式;当DMD相对能量阈值为9时,虽筛选出4组振荡模式,但模式3为虚假振荡模式,且未辨识出振荡频率为1.640 0Hz的主导振荡模式。
表3 SPDMD与DMD筛选振荡模式对比
Tab.3 Comparison of selected modes of SPDMD and DMD

SPDMD DMD(r0=6) DMD(r0=9) 序 号f/Hz ζ(%) f/Hz ζ(%) f/Hz ζ(%) 1 2.105 2 2.305 7 2.105 2 2.305 7 2.105 2 2.305 7 2 1.640 0 4.387 7 1.640 0 4.387 7 1.182 3 5.327 2 3 1.182 3 5.327 2 1.182 3 5.327 2 1.126 9 2.563 1 4 0.240 7 18.145 1.126 9 2.563 1 0.240 7 18.145 5 — — 1.063 8 2.334 8 — — 6 — — 0.987 9 1.413 2 — — 7 — — 0.913 8 1.313 1 — — 8 — — 0.240 7 18.145 — —
上述分析表明:DMD可根据相对能量权重筛选主导振荡模式,但如果阈值选取得不合理,会产生主导振荡模式的遗漏或多选现象,严重影响主导振荡模式的辨识精度。而所提SPDMD有效避免采用相对能量阈值来筛选主导振荡模式的不足,实现了电力系统主导振荡模式的有效分离。
3.1.3 SPDMD与其他方法的辨识结果对比
为进一步验证所提方法提取系统低频振荡特征参数的优势,本节分别对比了SPDMD与POD、KMD、EA的主导振荡模式和模态辨识结果。
1)主导振荡模式辨识
表4对比了SPDMD、POD和KMD的主导振荡模式辨识结果,表5进一步以EA的辨识结果为基准,对比SPDMD与POD和KMD的辨识精度。由表4和表5的对比结果可知:POD能较为准确地辨识出系统主导振荡模式的振荡频率,但无法辨识主导振荡模式的阻尼比;KMD虽能有效辨识系统的振荡频率和阻尼比,但其辨识结果误差较大;而本文所提SPDMD辨识方法相对POD和KMD具有更高的辨识精度。
表4 主导振荡模式对比
Tab.4 The comparison of dominant modes

方法 模式1 模式2 模式3 模式4 f/Hz ζ(%) f(%) ζ(%) f/Hz ζ(%) f(%) ζ(%) SPDMD 2.11 2.31 1.64 4.39 1.18 5.33 0.24 18.1 POD 2.09 — 1.60 — 1.14 — 0.30 — KMD 2.10 3.40 1.62 3.21 1.17 4.27 0.37 8.98
表5 主导振荡模式误差分析
Tab.5 The error analysis of dominant modes

方法 模式1 模式2 模式3 模式4 Δf/Hz Δζ(%) Δf/Hz Δζ(%) Δf/Hz Δζ(%) Δf/Hz Δζ(%) SPDMD 0.01 0.41 0.05 1.87 0.04 1.82 0.02 1.84 POD 0.01 — 0.01 — 0.00 — 0.04 — KMD 0.00 1.50 0.03 0.69 0.03 0.76 0.11 11.0
2)主导振荡模态辨识
振荡模态可表征发电机在某一确定的主导振荡模式下的空间变化趋势,有助于运行调度人员分析和抑制电网低频振荡现象。根据式(10)中振荡模式与振荡模态的对应关系,本节基于SPDMD的主导振荡模态辨识结果如图7所示。
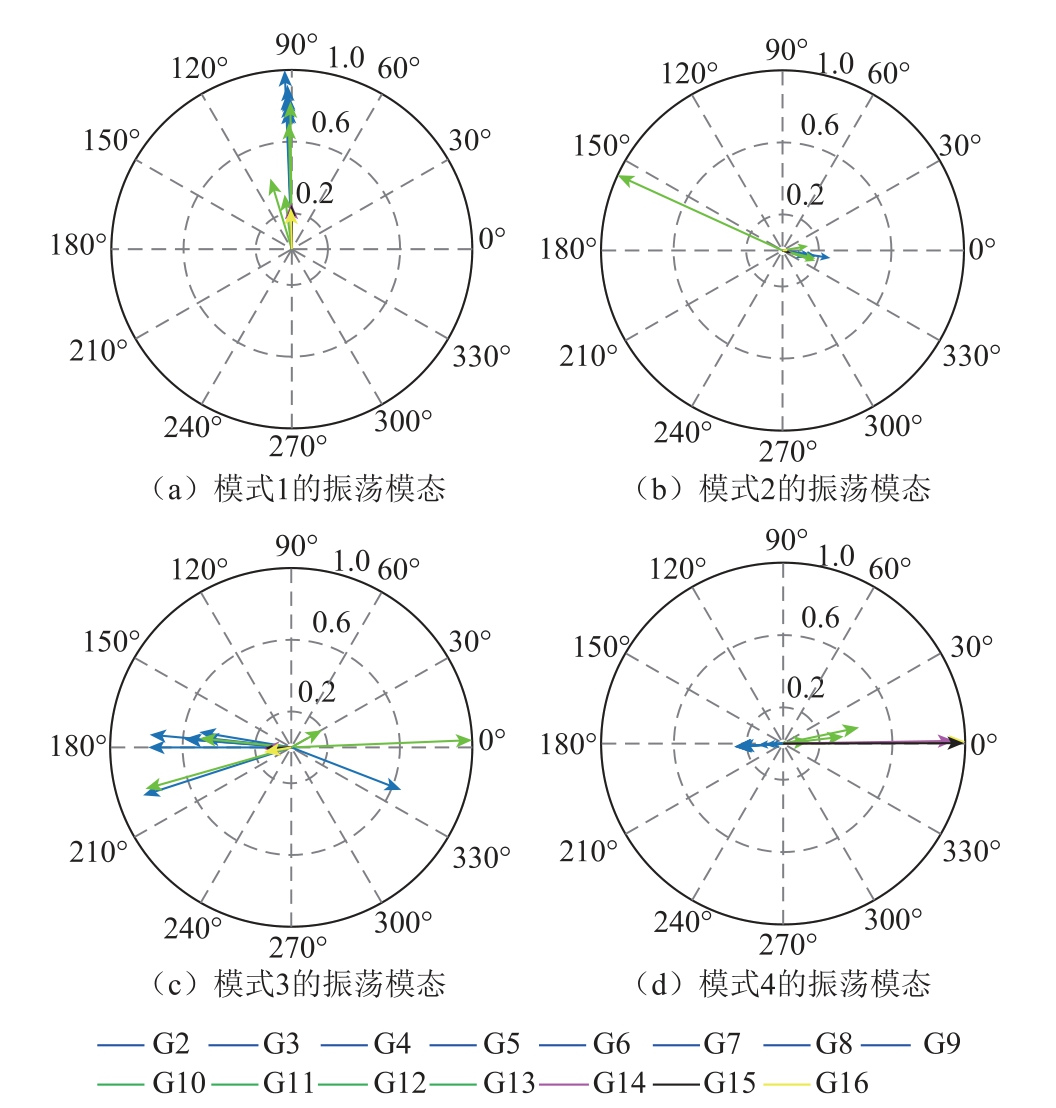
图7 SPDMD所辨识主导振荡模态
Fig.7 Dominant mode shapes identified by SPDMD
显然,由图7可知:主导振荡模式1主要表现 为位于区域1的发电机G1与系统中发电机G2~G16的相对振荡;主导振荡模式2主要表现为发电机G11相对区域内的其余发电机振荡;主导振荡模式3主要表现为位于区域1中的发电机G2~G7和G9与位于其他区域的发电机G12~G16同调,而与发电机G8、G10、G11相对振荡;主导振荡模式4主要表现为位于区域1的发电机G2~G9与区域2、3、4、5中的发电机G10~G16相对振荡。
图8~图10分别给出了采用POD、KMD和EA辨识出的系统主导振荡模态结果。
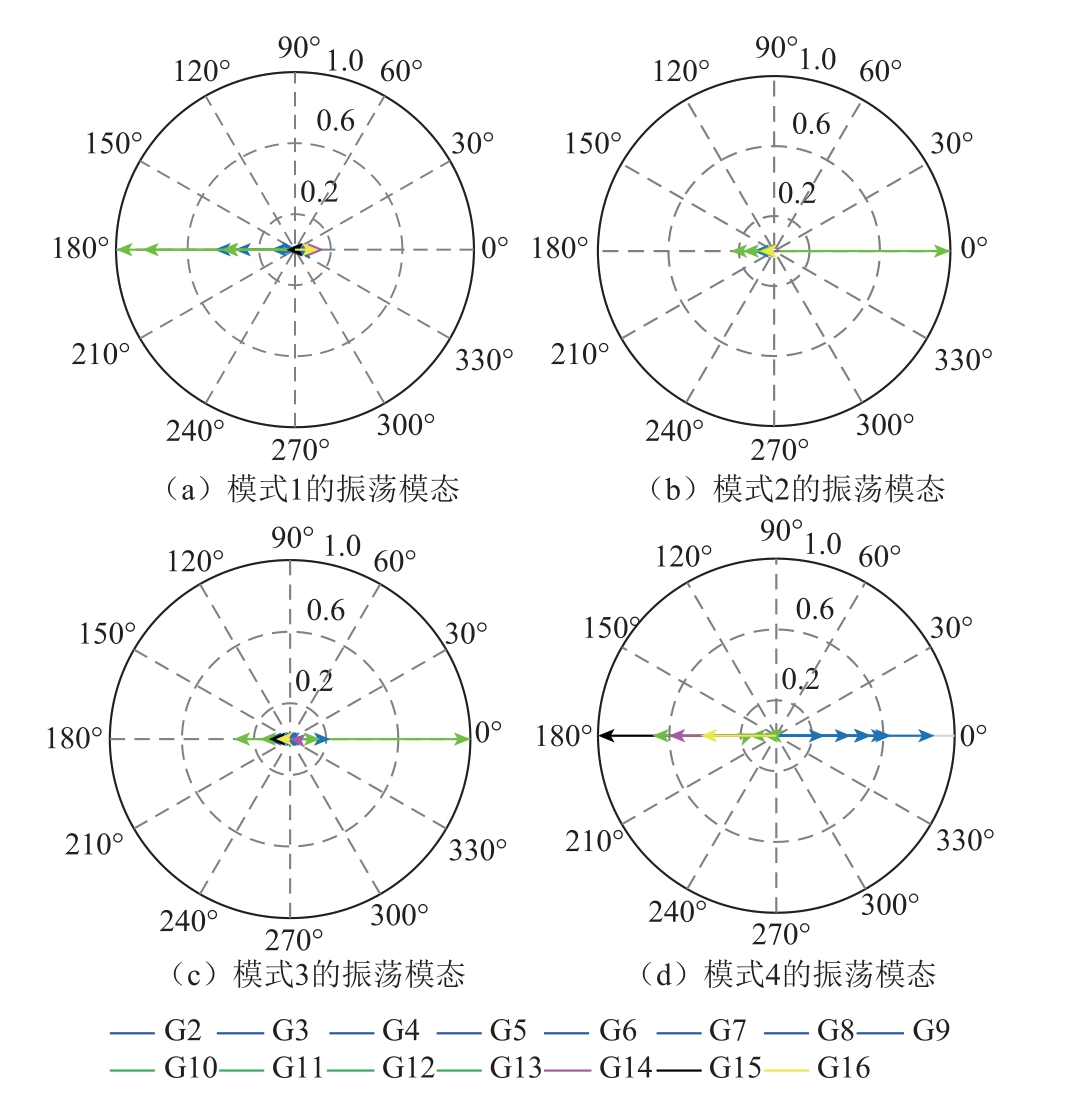
图8 POD所辨识主导振荡模态
Fig.8 Dominant mode shapes identified by POD
对比图7~图10的主导振荡模态辨识结果可知:虽然SPDMD、KMD和EA辨识的主导振荡模态在相位和幅值略有差别,但揭示的各主导振荡模 态下的相对振荡机群构成基本一致,而POD在主导振荡模式1和2下的振荡模态辨识结果与SPDMD、KMD和EA的辨识结果误差较大,如在主导振荡模式1中,POD辨识的振荡模态中发电机G5~G7、G14、G16同调,而与其余发电机发生相对振荡;在主导振荡模式2中,发电机G9、G11、G14同调。上述结果验证了SPDMD辨识系统主导振荡模态的准确性。

图9 KMD所辨识主导振荡模态
Fig.9 Dominant mode shapes identified by KMD

图10 EA所辨识振荡模态
Fig.10 Mode shapes identified by EA
3.2 中国南方电网算例
3.1节将所提方法应用到16机68节点测试系统中,验证了其在电力系统动态稳定协同评估的准确性和有效性。本节进一步将该方法应用到南方电网中,验证其在实际电力系统中应用的可行性。南方电网在某次故障下各变电站的PMU实测频率如图11所示,其中,LP位于云南;XR-Ⅰ和XR-Ⅱ位于贵州;SD、SZ和ZQ位于广东。

图11 中国南方电网PMU实测频率
Fig.11 PMU measured frequency in China Southern Power Grid
本节以该量测信号的20~60s数据作为所提方法的输入,各振荡模式的αsp计算结果如图12所示。

图12 PMU实测频率各振荡模式计算结果的αsp
Fig.12 The αsp of three dominant modes under PMU measured frequency
PMU实测频率的主导振荡模式筛选结果见表6。由表6可知:模式1和2为两组主导振荡模式,其αsp分别为1.025 5和0.362 8。其中,主导振荡模式1对应的振荡频率为0.408 2Hz,阻尼比为2.155 9%;主导振荡模式2对应的振荡频率为0.332 7Hz,阻尼比为3.479 8%。
表6 PMU实测频率的主导振荡模式筛选结果
Tab.6 The screening results of dominant modes by PMU measured frequency
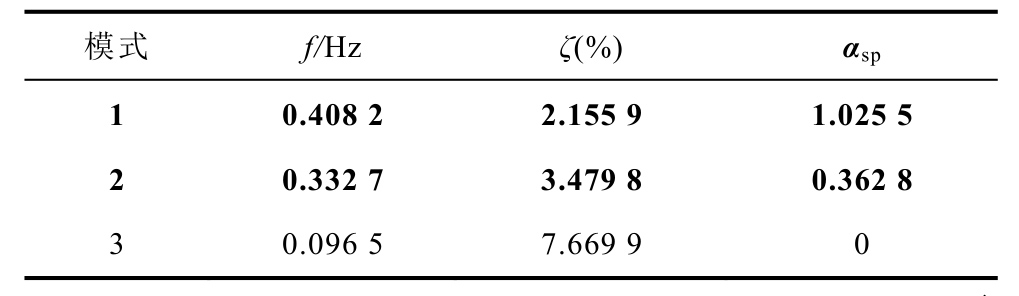
模式 f/Hz ζ(%) αsp 1 0.408 2 2.155 9 1.025 5 2 0.332 7 3.479 8 0.362 8 3 0.096 5 7.669 9 0
PMU实测频率所辨识主导振荡模态如图13所示。对比图13与参考文献[8]的辨识结果可知:主 导振荡模式1为南方电网的云贵振荡模式,即位于云南的LP与位于贵州和广东的XR-Ⅰ、XR-Ⅱ、SD、SZ、ZQ发生相对振荡;主导振荡模式2为南方电网的云广振荡模式,即位于广东的SD、SZ、ZQ与位于云南和贵州的LP、XR-Ⅰ、XR-Ⅱ发生相对振荡。

图13 PMU实测频率所辨识主导振荡模态
Fig.13 Dominant mode shapes identified by PMU measured frequency
由上述分析可知:本文所提SPDMD可从实际电网的广域量测信息中,有效辨识出系统主导振荡模式和振荡模态。验证了所提SPDMD应用于实际电网的有效性和可行性。
4 结论
本文提出一种基于SPDMD的电力系统振荡模式与模态的辨识方法,通过16机68节点测试系统和中国南方电网算例对所提SPDMD算法进行分析、验证,相关结论如下:
1)所提SPDMD算法通过辨识的最优振幅系数是否为0,实现了系统关键振荡信息与虚假振荡信息的有效分离,克服了DMD因相对能量阈值选取而无法有效分离系统主导振荡模式与虚假振荡模式的不足。
2)所提SPDMD算法完全不依赖电力系统动态模型,直接基于广域量测信息辨识电力系统主导振荡模式及模态,并根据辨识结果分析电网故障时各发电机间转子角的相对变化趋势,对抑制电力系统低频振荡具有一定的指导意义。
3)相比于基于广域量测信息的POD和KMD辨识算法,所提SPDMD算法具有更高的辨识精度。
4)中国南方电网的辨识结果证实所提SPDMD算法可应用于实际电网动态稳定的协同辨识,对基于广域量测信息的大电网动态稳定在线监测具有一定的应用参考价值。
[1]Jiang Tao, Jia Hongjie, Zhao Jinli, et al. Mode matching pursuit for estimating dominant modes in bulk power grid[J]. IET Generation, Transmission & Distribution, 2014, 8(10): 1677-1686.
[2]刘九良, 王彤, 朱劭璇, 等. 计及保护信息的电力系统暂态稳定裕度解析算法[J]. 电工技术学报, 2020, 35(3): 542-552.
Liu Jiuliang, Wang Tong, Zhu Shaoxuan, et al. An analytic method for power system transient stability margin considering protection information[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 542-552.
[3]马燕峰, 霍亚欣, 李鑫, 等. 考虑时滞影响的双馈风电场广域附加阻尼控制器设计[J]. 电工技术学报, 2020, 35(1): 158-166.
Ma Yanfeng, Huo Yaxin, Li Xin, et al. Design of wide area additional damping controller for doubly fed wind farms considering time delays[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 158-166.
[4]张小店, 王楷夫, 方连航, 等. 窄带模态分解算法在电力系统低频振荡特征参数辨识中的应用研究[J]. 电气技术, 2019, 20(4): 61-66, 71.
Zhang Xiaodian, Wang Kaifu, Fang Lianhang, et al. Applied study of narrow-band mode decomposition for identifying the parameters of low frequency oscillations in power systems[J]. Electrical Engineering, 2019, 20(4): 61-66, 71.
[5]薛安成, 王嘉伟. 基于非光滑分岔的单机水电系统超低频频率振荡机理分析[J]. 电工技术学报, 2020, 35(7): 1489-1497.
Xue Ancheng, Wang Jiawei. Mechanism analysis of ultra-low frequency oscillation of single hydropower system based on non-smooth bifurcation[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1489-1497.
[6]刘素贞, 魏建, 张闯, 等. 基于FPGA的超声信号自适应滤波与特征提取[J]. 电工技术学报, 2020, 35(13): 2870-2878.
Liu Suzhen, Wei Jian, Zhang Chuang, et al. Adaptive filtering and feature extraction of ultrasonic signal based on FPGA[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2870-2878.
[7]姜涛. 基于广域量测信息的电力大系统安全性分析与协调控制[D]. 天津: 天津大学, 2015.
[8]Jiang Tao, Mu Yunfei, Jia Hongjie, et al. A novel dominant mode estimation method for analyzing interarea oscillation in China Southern Power Grid[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2549-2560.
[9]Papadopoulos T A, Chrysochos A I, Kontis E O, et al. Measurement-based hybrid approach for ring-down analysis of power systems[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4435-4446.
[10]陈刚, 段晓, 张继红. 基于ARMA模型的低频振荡模式在线辨识技术研究[J]. 电网技术, 2010, 34(11): 48-54.
Chen Gang, Duan Xiao, Zhang Jihong. A new approach for online identification of low frequency oscillation modes based on auto-regressive movingaverage model[J]. Power System Technology, 2010, 34(11): 48-54.
[11]竺炜, 唐颖杰, 周有庆, 等. 基于改进Prony算法的电力系统低频振荡模式识别[J]. 电网技术, 2009, 33(5): 44-53.
Zhu Wei, Tang Yingjie, Zhou Youqing. Identification of power system low frequency oscillation mode based on improved Prony algorithm[J]. Power System Technology, 2009, 33(5): 44-53.
[12]张俊峰, 杨婷, 陈珉, 等. 基于Prony滑动平均窗算法的电力系统低频振荡特征分析[J]. 电力自动化设备, 2018, 38(10): 178-183.
Zhang Junfeng, Yang Ting, Chen Min, et al. Power system low-frequency oscillation characteristic analysis based on Prony moving average window algorithm[J]. Electric Power Automation Equipment, 2018, 38(10): 178-183.
[13]葛维春, 殷翔祥, 葛延峰, 等. 基于MEMD和HHT的电力系统低频振荡模式识别方法研究[J]. 电力系统保护与控制, 2020, 48(6): 124-135.
Ge Weichun, Yin Xiangxiang, Ge Yanfeng, et al. Estimating low frequency oscillation mode in power systems using multivariate empirical mode decomposition and Hilbert-Huang transform[J]. Power System Protection and Control, 2020, 48(6): 124-135.
[14]杨德昌, Rehtanz C, 李勇, 等. 基于改进希尔伯特-黄变换算法的电力系统低频振荡分析[J]. 中国电机工程学报, 2011, 31(10): 102-108.
Yang Dechang, Rehtanz C, Li Yong, et al. Researching on low frequency oscillation in power system based on improved HHT algorithm[J]. Proceedings of the CSEE, 2011, 31(10): 102-108.
[15]姜涛, 刘方正, 陈厚合, 等. 基于多通道快速傅里叶小波变换的电力系统主导振荡模式及模态协同辨识方法研究[J]. 电力自动化设备, 2019, 39(7): 125-132.
Jiang Tao, Liu Fangzheng, Chen Houhe, et al. Cooperated identification method of dominant oscillation modes and mode shapes for power system based on multi-channel fast Fourier transform based continuous wavelet transform[J]. Electric Power Automation Equipment, 2019, 39(7): 125-132.
[16]刘君, 肖辉, 曾林俊, 等. 基于RSSD和ICA算法的低频振荡模态参数辨识[J]. 电工技术学报, 2018, 33(21): 5051-5058.
Liu Jun, Xiao Hui, Zeng Linjun, et al. Parameter identification of low frequency oscillation based on RSSD and ICA algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5051-5058.
[17]Li Xue, Cui Hantao, Jiang Tao, et al. Multichannel continuous wavelet transform approach to estimate electromechanical oscillation modes,mode shapes and coherent groups from synchrophasors in bulk power grid[J]. International Journal of Electrical Power & Energy Systems, 2018, 96: 222-237.
[18]Jiang Tao, Yuan Haoyu, Jia Hongjie, et al. Stochastic subspace identification-based approach for tracking inter-area oscillatory modes in bulk power system utilising synchrophasor measurements[J]. IET Generation, Transmission & Distribution, 2015, 9(15): 2409-2418.
[19]Messina A R, Vittal V. Extraction of dynamic patterns from wide-area measurements using empirical orthogonal functions[J]. IEEE Transactions on Power Systems, 2007, 22(2): 682-692.
[20]Susuki Y, Mezić I. Nonlinear Koopman modes and coherency identification of coupled swing dynamics[J]. IEEE Transactions on Power Systems, 2011, 26(4): 1894-1904.
[21]Barocio E, Pal B C, Thornhill N F, et al. A dynamic mode decomposition framework for global power system oscillation analysis[J]. IEEE Transactions on Power Systems, 2015, 30(6): 2902-2912.
[22]Schmid P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanic, 2010, 656: 5-28.
[23]Mihailo R Jovanovi´c, Schmid P J, Nichols J W. Sparsity-promoting dynamic mode decomposition[J]. Physics of Fluids, 2014, 26(2): 024103-024124.
[24]苏安龙, 孙志鑫, 何晓洋, 等. 基于多元经验模式分解的电力系统低频振荡模式辨识[J]. 电力系统保护与控制, 2019, 47(22): 113-125.
Su Anlong, Sun Zhixin, He Xiaoyang, et al. Identification of low-frequency oscillation modes in power systems based on multiple empirical mode decomposition[J]. Power System Protection and Control, 2019, 47(22): 113-125.
[25]李雪, 姜涛, 陈厚合, 等. 基于图分割的电力系统同调机群辨识新方法[J]. 中国电机工程学报, 2019,39(23): 6815-6825.
Li Xue, Jiang Tao, Chen Houhe, et al. A graph cut approach for separating coherent groups of generators in bulk power grid using synchrophasors[J]. Proceedings of the CSEE, 2019, 39(23): 6815-6825.
[26]Rogers G. Power systems oscillations[M]. Norwell, MA: Kluwer, 2000.