0 引言
风电光伏发电等可再生能源集中式并网的规模日益增加，其出力的波动性将对接入系统的静态电压稳定性造成影响[1-2]。传统静态电压稳定性分析以确定性潮流方程或扩展潮流方程为基础[3]，忽略了可再生能源出力的波动性和负荷功率的时变性。确定性静态电压稳定性的评估结果已无法全面准确地反映系统电压的运行态势。
根据建模方式的不同，不确定性静态电压稳定性分析方法主要包括概率评估方法和区间评估方法。静态电压稳定性概率评估通常采用概率统计模型进行不确定量的建模，主要包括蒙特卡洛模拟法及改进方法[4-5]、点估计法[6]、半不变量法[7-8]、随机响应面法[9]和最大熵估计法[10-11]等。静态电压稳定性概率评估需要建立不确定量精确的概率分布模型，而实际应用中输入样本数据往往不足，导致所建立的概率分布模型精度不高，因而，多数研究中需假设输入不确定量服从某种概率分布，在一定程度上限制了静态电压稳定性概率评估方法的应用。
相比概率评估方法，静态电压稳定性区间评估方法仅需输入不确定量的边界信息，将不确定量波动范围的上、下边界描述为区间变量[12]，所需的统计信息较少，建模相对容易。文献[13]将可再生能源出力的波动范围上下界描述为区间输入变量，采用仿射算术[14]将含区间变量的连续潮流模型转换为仿射-线性优化模型求解。但基于极坐标系的连续潮流方程需要采用切比雪夫近似[15]对非线性三角函数估算，导致了区间扩张。文献[16]采用基于直角坐标系的连续潮流方程，结合仿射-线性优化方法求解静态电压稳定裕度区间，但仿射乘法运算将不可避免地引入新的噪声元，造成区间结果扩大。为此，文献[17]通过优化改进仿射乘法运算来避免仿射乘法的区间扩张效应。文献[18]通过建立风电场出力的概率区间分配模型，利用证据理论和双层规划方法求解静态电压失稳的概率区间。但上述静态电压稳定性区间评估方法仍存在如下两个主要问题：
1）常用仿射算术以一阶区间泰勒展开为基础构建[19]，导致其在求解静态电压稳定裕度的过程中抑制区间扩张效应的能力有限，需要研究新的评估方法以降低评估结果的保守性。
2）常用仿射算术借助噪声元的类同位素追踪功能[20]来定性分析各输入区间变量对系统输出区间变量的影响，目前尚未可量化评估各输入不确定量对静态电压稳定性影响重要程度的方法。
本文基于二阶区间泰勒展开的扩展仿射算术[21]提出了不确定性静态电压稳定性的全局灵敏分析方法。首先根据扩展仿射算术构建基于L指标的静态电压稳定性评估模型。然后利用基于解析化方差分解的全局灵敏度分析方法定量评估各输入区间变量对静态电压稳定性影响的重要性。通过IEEE标准测试系统中的多个仿真算例结果验证了本文所提方法的正确性和有效性。
1 基于扩展仿射算术的静态电压稳定性评估模型
1.1 扩展仿射算术
常用仿射算术将不确定量用仿射算子
表示，该算子由特定的仿射变量线性组合而成，即
式中，x0为标称运行点或期望运行值；
为由输入扰动源变动所引入的噪声元或仿射变量，
各元素的取值范围均为[-1 ,1]；系数 x1为一阶灵敏度系数向量，反映了仿射算子对噪声元的线性变化大小。 常用仿射算术也称为一阶仿射算术，由于忽略了非线性项（二阶项）对仿射算子
的影响，很容易在区间计算过程中造成区间结果扩张[22]。因此，本文引入二阶灵敏度系数，对常用的一阶仿射形式（1）进行扩展，得到二阶仿射形式，即
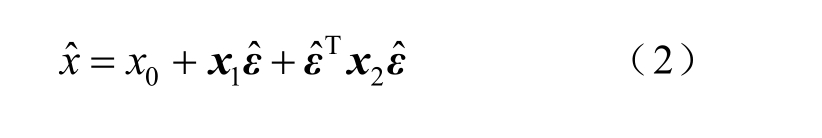
式中，系数 x2为二阶灵敏度系数矩阵，反映了仿射算子对噪声元
的非线性变化大小。
1.2 基于潮流解的静态电压稳定性L指标
评估静态电压稳定性的指标很多，主要包括灵敏度指标、奇异值指标、负荷裕度指标、L指标等。其中L指标物理概念清晰，计算速度快，被广泛应用于在线静态电压稳定性评估[23]。本文选取基于潮流解的L指标来评估不确定性静态电压稳定性。
基于潮流解的L指标是表征实际状态和稳定极限之间距离的量化指标，其值在0～1之间，用于描述电压解的存在性。该方法的基本思路为：首先将所有节点划分为发电机节点集合G（包括PV节点和平衡节点）、负荷节点集合D和网络联络节点集合K，按三类节点建立网络方程为
式中，U G和IG分别为发电机节点的电压和电流向量； U D和 ID为分别负荷节点的电压和电流向量；U K 为网络联络节点的电压向量；YG′G、YG′D、YG ′K、YD′G、YD′D、YD′K、YK′G、YK′D、YK ′K分别为相应节点的自导纳或互导纳子矩阵。
消去网络联络节点K后，式（3）可简化为
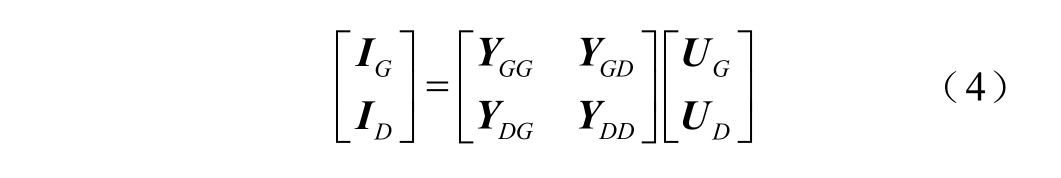
其中
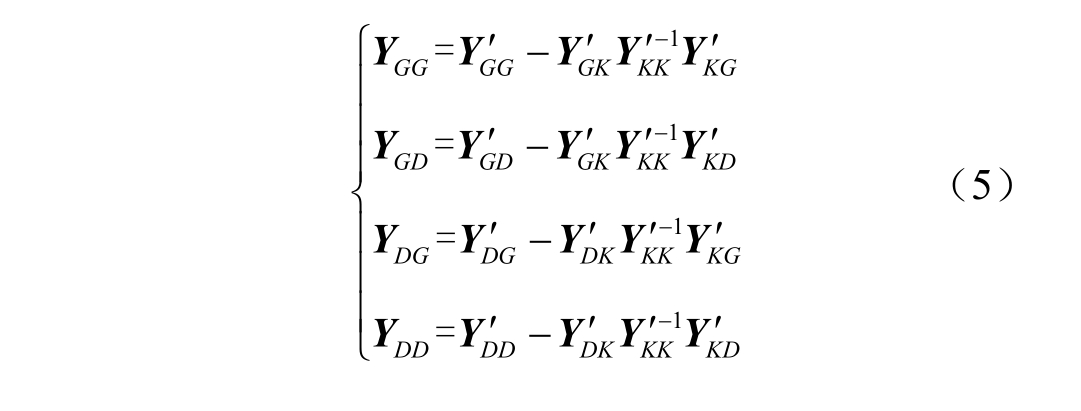
令 Z DD =
，式（4）可转换为
最后，求解负荷节点m (m∈D)，的静态电压稳定性指标为
式中，Fm k为负荷节点参与因子，是矩阵F =-Z DDYD G的m行k列。
系统的静态电压稳定性指标L定义为
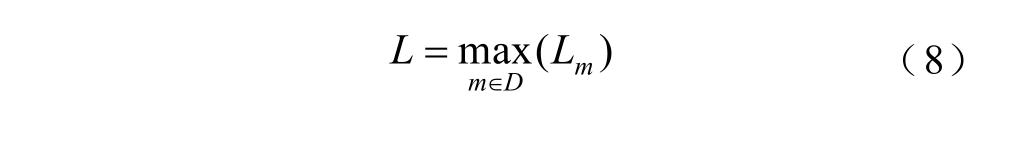
通过L值与1之间的临近程度来表征全系统电压发散程度[3]，当 L＜1 .0表示系统电压稳定，L =1.0表示系统电压稳定临界点，而 L＞1 .0则表示系统电压失稳。
1.3 基于L指标的静态电压稳定性区间评估模型
在1.2节静态电压稳定性L指标的基础上，本节利用扩展仿射算术建立基于L指标的静态电压稳定性区间评估模型。
定义
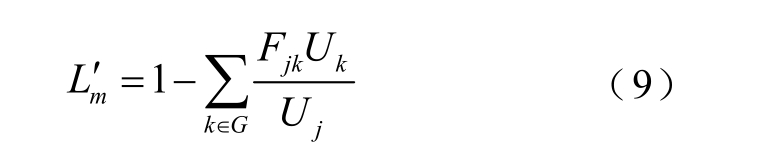
则式（7）可等效改写为
设直角坐标系下节点i电压为 U i=ei + j fi ，负荷节点参与因子为 F j k =G jk +j Bjk，则 
的实部
和虚部Im( L m′)分别为
式（11）中的待求变量为 ej、 fj、 ek、 fk。
随着节点注入有功功率和无功功率的随机波动，各节点电压也随之变化，进而静态电压稳定性L指标也将跟随变化。利用1.1节中的扩展仿射算术式（2）对节点注入功率扰动源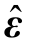
进行二阶区间泰勒展开，可得L指标的扩展仿射形式为
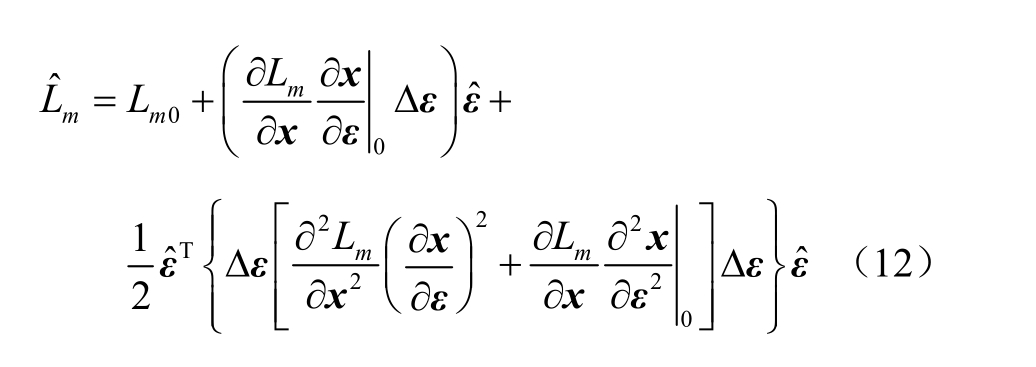
式中，Lm 0为标称运行点处的静态电压稳定性L指标值；
分别为节点电压待求变量x对输入功率扰动源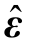的一阶、二阶灵敏度系数矩阵，其详细求解方法可参考文献[23]；下标0表示在期望运行点处取值；Δε为注入功率扰动源的区间半径；
分别为L指标对节点电压待求变量x的一阶、二阶灵敏度系数矩阵，其求解公式见附录式（A1）和式（A2）。
因此，可构造以式（12）为目标函数（最大值即为上边界，最小值即为下边界）、噪声元
为约束条件的二次规划模型，即静态电压稳定性L指标的扩展仿射优化模型。基于扩展仿射优化模型的静态电压稳定性评估方法通过二次规划方法压缩噪声元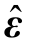范围，得到L指标的区间结果，进一步可以判断节点注入功率波动过程中系统是否失去静态电压稳定性。
从上述过程也可以看出：本文所提的扩展仿射方法是在确定性潮流基点的基础上进行区间泰勒展开逼近，即标称运行点处的解为基点，在输入波动区间范围内，先计算期望值处的L指标和相应的扩展仿射系数，利用区间泰勒展开就可以逼近L指标的区间范围。因此，即使在输入波动范围内会出现病态潮流无解的现象，只要期望点处的确定性潮流有解，扩展仿射方法都能获取L指标区间结果。
2 基于方差分解的静态电压稳定性全局灵敏度分析
通过静态电压稳定性扩展仿射评估模型可以真实地反映注入功率波动过程中L指标的区间范围，但无法辨识出输入扰动源对静态电压稳定性影响的重要性，只有对输入扰动源进行重要性排序，才更有利于全面评估系统电压的运行态势。通常采用灵敏度分析来量化输出响应中各输入量的影响程度，但常用灵敏度分析方法是在某个固定点附近，每次仅对一个变量进行微小变化，而保持其他变量不变，即建立于局部线性化模型的基础上，因此这类方法也被称为局部灵敏度分析方法[24]。
局部灵敏度分析由于不能反映输入变量波动对输出响应的影响，已不适用于对不确定性系统的分析。全局灵敏度分析（Global Sensitivity Analysis, GSA）[25-26]从输入变量的整个分布范围来定量衡量输入变量的不确定性对输出量（例如模型输出的方差或分布）的贡献程度。方差是用来度量不确定量和期望运行点之间的偏离程度，可以反映不确定量的波动程度。通过将输出响应的总方差分解得到各输入量的方差贡献，便能从输入变量的整个波动区间范围来量化输入变量的波动对模型输出响应的总方差贡献程度。因此，基于方差分解的全局灵敏度分析方法（Variance Based Global Sensitivity Analysis）受到了越来越多的关注，其中Sobol'法[27]应用最为广泛的。文献[28]基于Sobol'法全局灵敏度分析理论，构建了考虑源荷不确定性的孤岛微电网概率潮流全局灵敏度分析框架，并利用蒙特卡洛法求解了输入不确定性量的一阶全局灵敏度指标和总灵敏度指标。为了克服蒙特卡洛方法多次采样耗时的缺陷，文献[29]将概率潮流解用含随机变量的稀疏混沌多项式表示，建立了基于稀疏多项式混沌展开（sparse Polynomial Chaos Expansion, sPCE）的孤岛微电网潮流代理模型，只需少量的输入和输出样本就可以确定稀疏多项式系数，从而实现了全局灵敏度指标的快速高效求取。但文献[28-29]中均是基于独立变量的方差分解方法，并未考虑输入变量的相关性，文献[30]进一步利用sPCE提出了计及相关性的区域电-气联合系统全局灵敏度分析方法。
但sPCE是基于随机正交空间逼近理论，其逼近的精度决定了sPCE代理模型的准确性，它受输入样本空间大小和随机采样方法影响，因此，如何获取最优输入样本成为提高其准确度的关键点。与上述思路不同，本文在静态电压稳定性扩展仿射模型的基础上，提出考虑相关性的解析化方差分解方法，由于扩展仿射模型具有二阶显式表达，能快速、高效地将相关性方差和交叉贡献进行分解。
2.1 静态电压稳定性L指标的总方差计算
基于扩展仿射模型的静态电压稳定性评估模型式（12）可以统一改写为
式中，n为输入扰动源的维数；ai、bij分别为相应的一阶、二阶灵敏度系数。
可通过区间平移变换使得输入功率扰动源
处于标准区间[-1 ,1]，因此其期望运行处值，即期望值为0，而方差仍与输入扰动功率的方差相同。本文假设输入扰动源
的方差为
，且考虑
和
之间相关性，设其相关系数为 ρij。利用方差性质和协方差性质[31]，模型式（12）的输出方差为
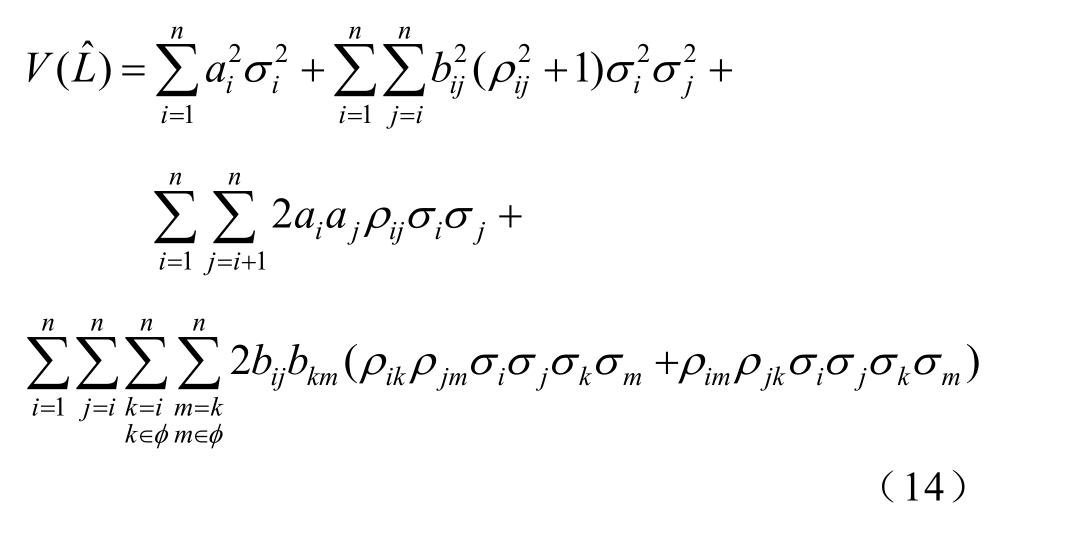
式中，
式
。通过式（14）即可解析化计算输出总方差。
2.2 L指标的总方差的新分解形式
通过对输出总方差式（14）的分解得到各输入扰动源的方差贡献量，就能清晰地辨识出各个扰动源对静态电压稳定性影响的重要程度。单个输入扰动源的总方差贡献分解框图如图1所示[32]。由于扰动源之间的相关性，单个输入扰动源的总方差贡献 
包括了总独立性贡献 
和总相关性贡献
，进一步总独立性贡献
又可细分为独立性主贡献 
和各阶独立性交叉贡献
…，总相关性方差贡献 
又可细分为各阶相关性贡献
…。
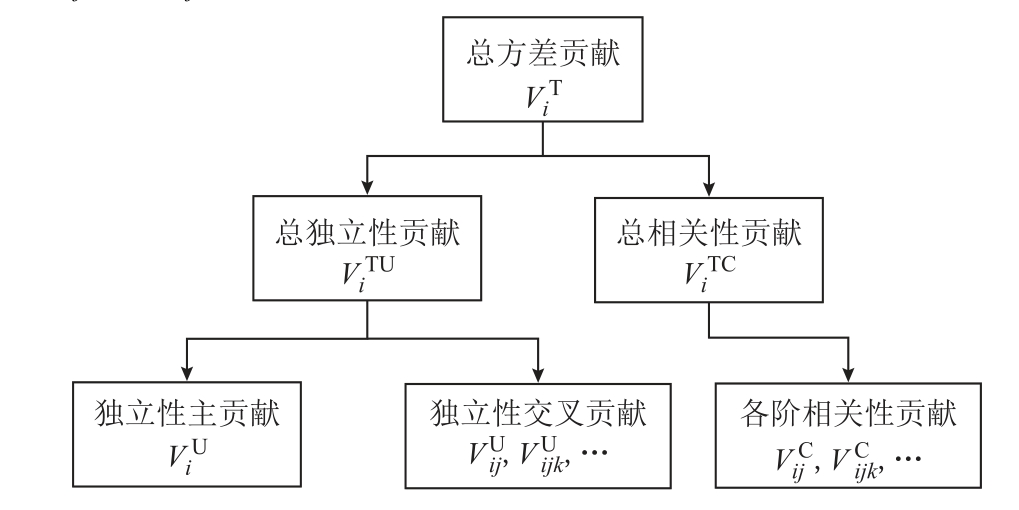
图1 总方差贡献新分解框图
Fig. 1 Novel decomposition framework of total variance contributions
2.3 基于新方差分解的全局灵敏度分析方法
基于方差分解的全局灵敏度分析是通过单个输入变量的方差贡献来反映各个输入不确定量的影响程度，将单个输入变量或者多个输入变量的方差贡献除以输出响应的总方差，即为全局灵敏度指标。通过比较输入扰动源的全局灵敏度指标大小便能清晰地辨识出对静态电压稳定性影响的主要因素和次要因素。本节在2.2节的基础上定义两类全局灵敏度指标：总灵敏度指标和主灵敏度指标。
1）总灵敏度指标 
式中，VU 、E U分别为不考虑
之间相关性的方差、期望运算；
为除
之外的所有噪声元。总灵敏度指标 
又可分解为总独立性灵敏度指标 
和总相关性灵敏度指标 
，即
2）主灵敏度指标 Si（或称为一阶独立性灵敏度指标）
为便于理解，以一个简单的含两个相关性输入变量的输出响应函数 
为例，说明上述全局灵敏度指标求解方法。设输入变量
均服从正态分布，
～ N(0,Σ)，其中协方差矩阵Σ为
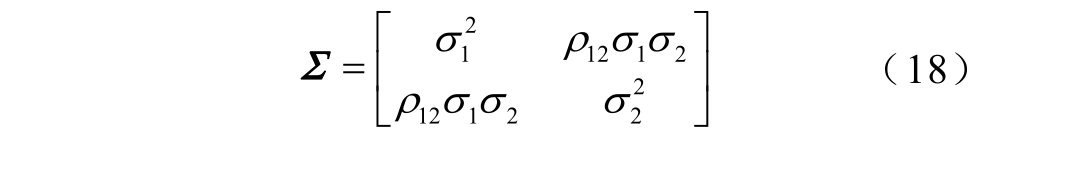
式中，
和 
分别为两个输入变量的方差； ρ12为两个输入变量之间的相关系数。则根据式（18）可求得输出响应函数的总方差为
根据图1得到输出响应总方差贡献分解结果见表1。
表1 输出总方差贡献分解结果
Tab.1 Decomposition of total output variance contributions
独立性 独立性主贡献 相关性交叉贡献 交叉贡献 σ12, σ2 2 σ12σ 22 2ρ12σ 1σ 2 +ρ12 2σ 12σ 22 σ12 + 2ρ12σ 1σ 2 + ρ12 2 σ 12σ 22 +σ 12σ 22,单个变量的总方差贡献 2ρ12σ 1σ 2 +σ 22 + ρ12 2 σ 12σ 22 +σ12σ 22单个变量总相关性方差贡献 2ρ12σ 1σ 2 + ρ1 22 σ 1 2σ 2 2 单个变量总独立性方差贡献 σ12 + σ 12σ 22，σ22 + σ 12σ 22
由表1可知：通过输入变量的总方差分解框架和计算公式，可以得出各个输入变量的独立性主贡献、独立性交互贡献、相关性交互贡献，也可以得到各个输入变量的总相关性方差贡献和总独立性方差贡献，这种分解形式有助于理清输入变量总方差的组成成分，追踪到关键环节。一旦获取了这种解析化的方差分解形式，可以很容易获得相应的全局灵敏度指标。当相关性系数 ρ12 = 0时，由相关性引起的相关性方差贡献为零，即单个变量的总方差贡献等于单个变量的总独立性方差贡献。因此，相关性系数为零时，本文所提出的全局灵敏度方差分解方法即退化为仅适用于独立型变量的Sobol'法。因此，本文所提出的基于方差分解的全局灵敏度分析方法具有更广泛的适用性。
3 算例测试与分析
3.1 有效性验证
首先采用含风电场的IEEE 30节点系统作为算例对象，以验证本文所提出的静态电压稳定性扩展评估模型的有效性。
含风电场的IEEE 30节点系统如图2所示，三个风电场依次接入节点5、8、13。设风电场采用恒电压控制方式，故可处理为PV节点。发电厂G1设置为平衡节点，设所有负荷节点和风电场节点注入功率为不确定性输入变量，同时考虑风电场节点之间输出有功功率之间的相关性。设不确定性输入变量的均值为期望值或标称运行点，标准差为相应均值的10%，三个风电场节点注入有功功率之间的相关性系数均为0.2。
图2 含风电场的IEEE 30节点系统
Fig.2 Diagram of IEEE 30-bus system with wind farms
为验证扩展仿射方法计算静态电压稳定性L指标的准确性，以蒙特卡洛方法多次抽样仿真得到的区间结果作为静态电压稳定性L指标的对比标准。蒙特卡洛模拟作为一种随机模拟技术，其模拟次数越多，计算结果越准确，但消耗计算时间也越多。测试中蒙特卡洛方法的抽样随机数在功率波动范围内服从均匀分布，在抽样次数超过1 800多次后，区间上、下边界的误差已经趋近于设置误差精度10-3，故本文采样2 000次作为其区间结果。分别采用扩展仿射方法（EAA）、仿射方法（AA）和蒙特卡洛方法（MC）三种方法求解各负荷节点L指标区间，并与确定性求解方法所得结果进行对比，结果如图3所示。
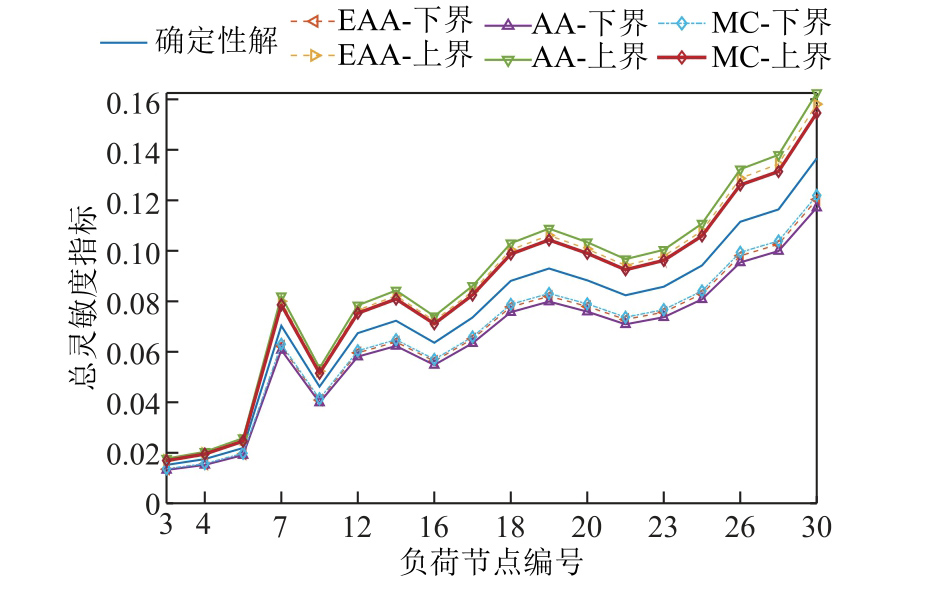
图3 IEEE 30节点系统各负荷节点L指标区间结果
Fig.3 Interval results of L index of each load node in IEEE 30 bus system
对比分析图3中各方法所得L指标的区间结果，可得出如下结论：
1）三类区间评估方法所得L指标区间均包含了确定性方法所得的L指标。
2）采用扩展仿射方法和仿射方法获得的L指标区间都严格包含了蒙特卡洛方法所得的区间，表明本文扩展仿射方法可严格获取L指标区间解集的上、下边界包络线，验证了本文所提出的静态电压稳定性扩展仿射评估模型的有效性。
3）以蒙特卡洛方法得到的结果作为“精确”的结果，可计算出扩展仿射方法和仿射方法计算得到的L指标平均估计误差精度分别为1.58%和4.17%。
可见，尽管两种方法均可得到准确的L指标区间结果，但基于扩展仿射方法的静态电压稳定性评估模型比基于仿射方法的评估模型获取的L指标区间结果更为精确。这是因为基于扩展仿射方法的静态电压稳定性评估模型实质上是对L指标进行二阶区间泰勒展开逼近，而仿射方法仅为一阶区间泰勒展开逼近，二阶项的计入使得扩展仿射方法获得较常用仿射方法更高的计算准确度。
进一步，可从图3中得出负荷节点30处的L指标最大，因此本节以负荷节点30处的L指标为例，对比分析输入变量不确定时负荷节点30处L指标的总灵敏度指标和主灵敏度指标。表2和表3分别 给出了不考虑相关性和考虑相关性且相关性系数为0.2时，部分输入不确定量对负荷节点30处的L指标的总灵敏度和主灵敏度。
表2 部分输入变量的总灵敏度指标和主灵敏度指标 (不考虑相关性)
Tab.2 Total sensitivity index and main sensitivity index of some input variables (without considering the correlation)
输入变量灵敏度指标 S (EAA)T(EAA)i S T(MC)i S (MC)i S i PW1 0.031 3 0.023 1 0.031 1 0.023 9 PW2 0.053 5 0.051 8 0.053 7 0.051 6 PW3 0.043 5 0.035 4 0.043 7 0.035 1 PL3 0.011 3 0.010 5 0.011 2 0.010 6 PL4 0.130 7 0.112 1 0.130 8 0.112 3 PL5 0.001 2 0.000 9 0.001 4 0.000 8 PL6 0.034 7 0.032 3 0.034 8 0.032 1 PL8 0.105 6 0.105 3 0.105 4 0.105 2 PL10 0.005 6 0.005 2 0.005 4 0.005 3 PL24 0.013 4 0.013 3 0.013 6 0.013 1 PL30 0.516 7 0.501 2 0.516 5 0.500 8 QL30 0.000 8 0.000 7 0.000 7 0.000 6
表3 部分输入变量的总灵敏度指标和主灵敏度指标 (考虑相关性且相关系数为0.2)
Tab.3 Total sensitivity index and main sensitivity index of some input variables(considering the correlation and The correlation coefficient is 0.2)
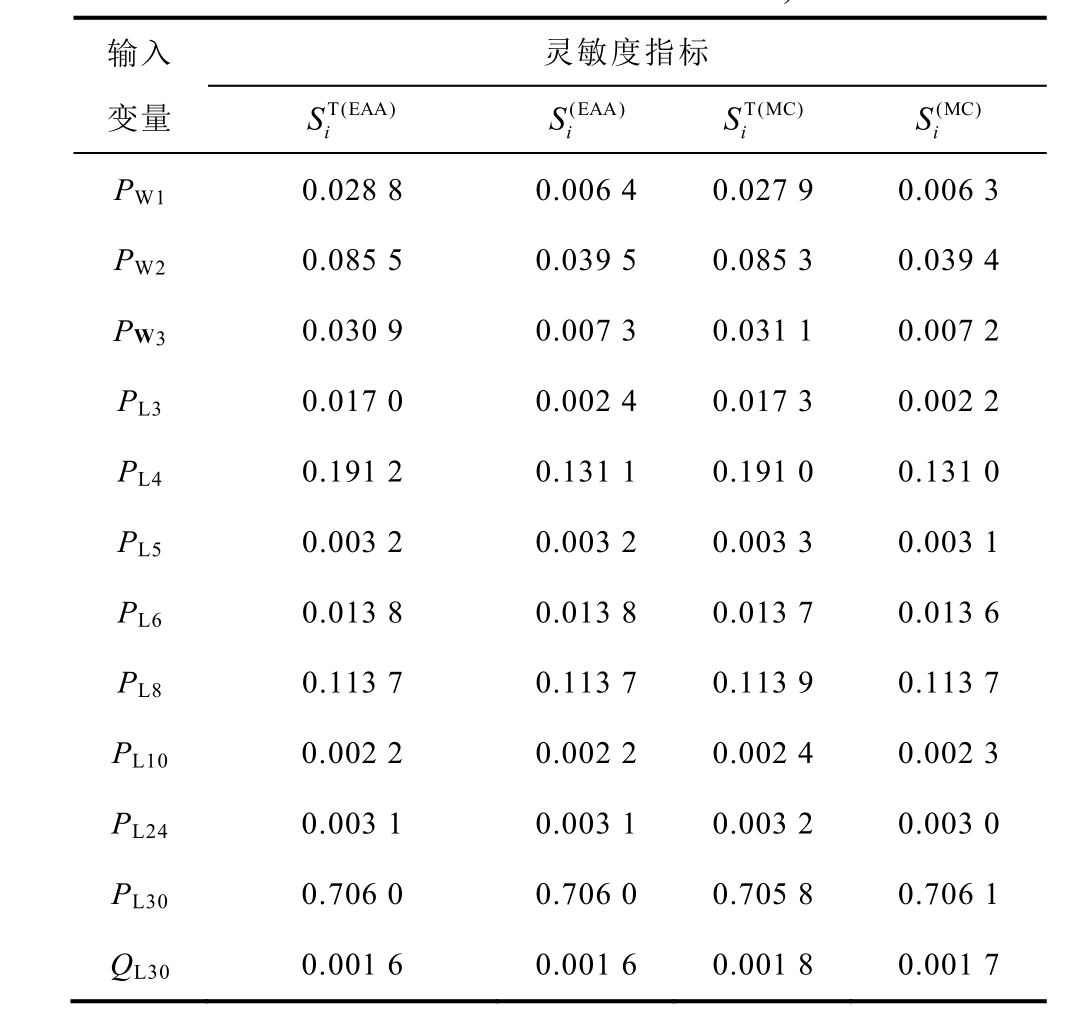
输入变量 灵敏度指标 S (EAA)T(EAA)i S T(MC)i S (MC)i S i PW1 0.028 8 0.006 4 0.027 9 0.006 3 PW2 0.085 5 0.039 5 0.085 3 0.039 4 PW3 0.030 9 0.007 3 0.031 1 0.007 2 PL3 0.017 0 0.002 4 0.017 3 0.002 2 PL4 0.191 2 0.131 1 0.191 0 0.131 0 PL5 0.003 2 0.003 2 0.003 3 0.003 1 PL6 0.013 8 0.013 8 0.013 7 0.013 6 PL8 0.113 7 0.113 7 0.113 9 0.113 7 PL10 0.002 2 0.002 2 0.002 4 0.002 3 PL24 0.003 1 0.003 1 0.003 2 0.003 0 PL30 0.706 0 0.706 0 0.705 8 0.706 1 QL30 0.001 6 0.001 6 0.001 8 0.001 7
在不考虑相关性时，与蒙特卡洛方法（即为经典的Sobol’法）所得结果进行对比分析可以发现，基于扩展仿射方法获得的总灵敏度指标与蒙特卡洛方法的最大相对误差小于14.29%，主灵敏度指标的最大相对误差小于6.8%。在考虑相关性时，与蒙特卡洛方法所得结果进行对比分析可以发现，基于扩展仿射方法获得的总灵敏度指标与蒙特卡洛方法的最大相对误差小于11.1%，主灵敏度指标的最大相对误差小于9.1%，从而验证了基于扩展仿射模型的全局灵敏度分析方法的有效性。
在不考虑相关性时，将表2全局灵敏度指标值由大到小排序，即为PL30＞PL8＞PL4＞PW2＞PW3＞PW1；而在在考虑相关性时，将表3全局灵敏度指标值由大到小排序，即为PL30＞PL4＞PL8＞PW2＞PW3＞PW1，可以看出考虑风电场输出功率的相关性对全局灵敏度度指标的影响。因此，在全局灵敏度分析各输入不确定量对L指标影响的重要性时需要计及相关性的影响。
表3表明1、2、3号风电场总灵敏度指标分别为0.028 8、0.085 5、0.030 9，即输出有功功率的不确定性对负荷节点30处的L指标影响最大是2号风电场，3号风电场居中，而1号风电场最小。此外，30号负荷节点的有功功率需求的不确定性对该节点的L指标贡献最大，达到0.706 0。
图4和图5进一步给出了所有负荷节点L指标的总灵敏度指标和主灵敏度指标。对比两图可知：主灵敏度指标和总灵敏度指标之间存在一定差异，这是因为主灵敏度指标仅考虑输入变量的一阶方差贡献，而总灵敏度指标反映了相应输入变量的总方差贡献，即包括了输入变量之间相互作用产生的一阶及高阶灵敏度。因此，主灵敏度指标和总灵敏度指标之间的差异性表明了输入变量之间相互作用的方差贡献。
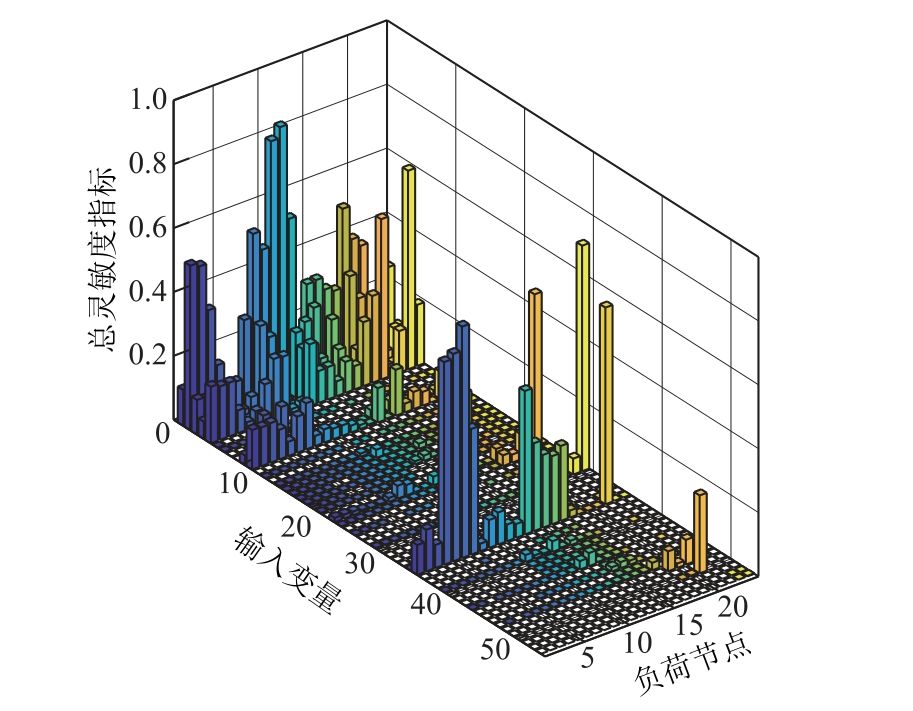
图4 所有负荷节点L指标的总灵敏度指标
Fig. 4 Total sensitivity index of L index of all load nodes
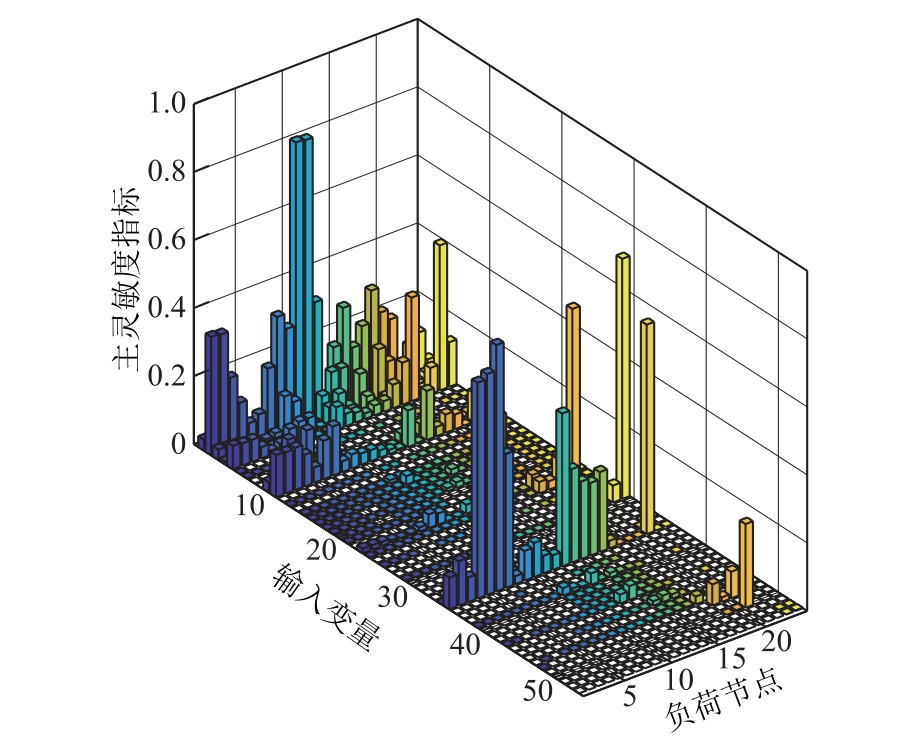
图5 所有负荷节点L指标的主灵敏度指标
Fig. 5 Main sensitivity index of L index of all load nodes
为验证扩展仿射方法应用于静态电压稳定性全局灵敏度分析的鲁棒性优于常用的仿射方法，本文将输入变量的标准差分别设为相应均值的10%、20%、40%、80%，计算得出输入变量PW1、PW2、PW3对负荷节点30处的L指标的总灵敏度指标和主灵敏度指标见表4。
表4 负荷节点30 L指标的总灵敏度指标和主灵敏度指标
Tab.4 Total sensitivity index and main sensitivity index of L index of 30 load node
总灵敏度指标 主灵敏度指标 输入变量 扩展 仿射方法 仿射 方法 扩展 仿射方法 仿射 方法 PW1 0.028 8 0.001 5 0.000 9 0.000 9 10% PW2 0.085 5 0.057 1 0.029 3 0.029 3 PW3 0.030 9 0.020 15 0.005 8 0.005 8 PW1 0.043 5 0.001 5 0.017 8 0.000 9 20% PW2 0.106 7 0.057 1 0.083 1 0.029 3 PW3 0.073 1 0.020 15 0.019 2 0.005 8 PW1 0.061 3 0.001 5 0.043 8 0.000 9 40% PW2 0.122 9 0.057 1 0.103 5 0.029 3 PW3 0.091 8 0.020 15 0.051 8 0.005 8 PW1 0.092 8 0.001 5 0.070 4 0.000 9 80% PW2 0.175 9 0.057 1 0.239 6 0.029 3 PW3 0.131 9 0.020 15 0.085 8 0.005 8
从表4中可以看出，由于传统仿射方法忽略了二阶项的影响，使得基于仿射模型的全局灵敏度分析方法得到的三个风电场输出功率变量的总灵敏度指标和主灵敏度指标随标准差的增大而保持不变，即总方差贡献与输入变量的标准差无关；而扩展仿射方法能清楚地揭示三个风电场输出功率变量PW1、PW2、PW3的总灵敏度指标和主灵敏度指标随输入变量标准差的增大而增大的变化趋势，这与式（14）给出的结果一致。因此，采用扩展仿射方法得到的总灵敏度指标和主灵敏度指标能更准确地揭示输入变量波动对L指标影响的变化规律。
3.2 相关性分析
以IEEE 30节点系统为例，设风电场的输出有功功率PW1、PW2、PW3之间存在相关性，图6给出了相关系数从-1到1变化时系统L指标的总灵敏度 指标的变化趋势。
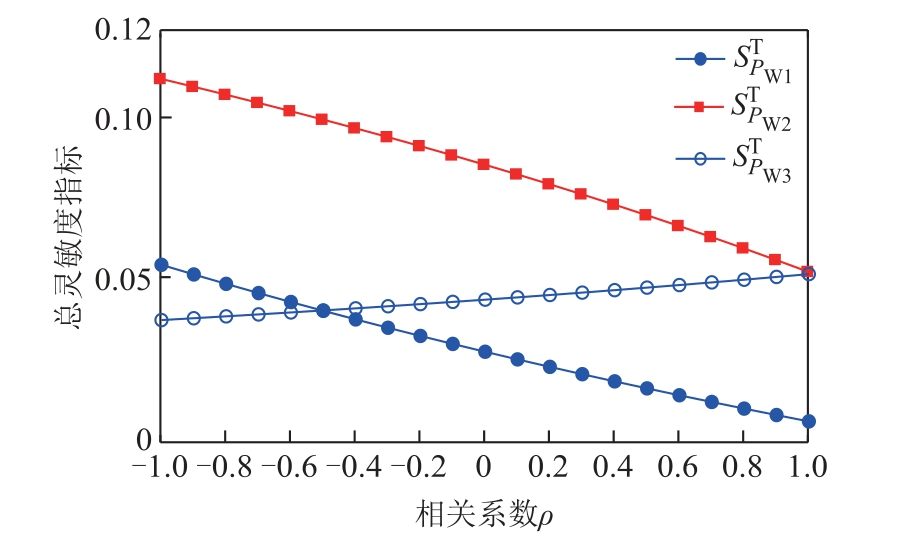
图6 系统L指标的总灵敏度指标随相关系数的变化曲线
Fig.6 Change curve of total sensitivity index of system L index with correlation coefficient
图6表明，风电场输出有功功率PW1和PW2的总灵敏度指标随着相关性系数的增加而下降，而风电场输出有功功率PW3的总灵敏度指标随着相关性系数的增加而缓慢增加。通过比较风电场输出有功功率PW1、PW2和PW3的总灵敏度指标变化曲线的斜率不难看出：相关性系数对风电场输出有功功率PW1和PW2的总灵敏度指标的影响明显大于风电场输出有功功率PW3。
3.3 计算效率比较
本文所提出的基于扩展仿射模型的静态电压稳定性全局灵敏度分析是一种解析式的方差分解方法，计算量小且计算效率高。在IEEE 30、IEEE 300和Case-2383算例系统中分别应用本文扩展仿射方法与蒙特卡洛方法，不同波动场景下两种方法的计算时间和平均误差统计于表5。其中的“平均误差”表示所有负荷节点的静态电压稳定性L指标的全局灵敏度指标相对误差的平均值；在IEEE 300和Case-2383中蒙特卡洛法分别模拟5 000次和10 000次。
表5 不同波动场景下计算时间和计算精度比较
Tab.5 Comparison of calculation time and accuracy in different fluctuation scenarios
扩展仿射方法 蒙特卡洛方法不同场景 算例系统 计算 时间/s 平均误差（%） 计算 时间/s IEEE 30 10.91 1.36 78.87 仅负荷波动10%区间 IEEE 300 85.07 2.43 595.39 Case-2383 804.86 5.19 6356.43仅发电机输出功率波动10%区间 IEEE 30 8.54 0.96 66.79 IEEE 300 64.82 1.85 545.39 Case-2383 782.72 4.28 6132.47发电机输出功率和负荷波动10%区间 IEEE 30 12.45 1.88 82.70 IEEE 300 96.33 3.28 630.06 Case-2383 835.09 6.25 6 618.74
表5中结果表明，由于基于扩展仿射模型的静态电压稳定性全局灵敏度分析方法具有解析化计算模式，相对于多次模拟采样的蒙特卡洛方法，其计算时间明显缩短，加速比可达到6～9。此外，与蒙特卡洛方法相比，基于扩展仿射模型的静态电压稳定性全局灵敏度分析方法具有很高的准确度，平均误差最大不超过6.25%；系统规模扩大时静态电压稳定性灵敏度指标的平均误差将有所增加。
4 结论
本文考虑新能源场站自身输出功率的波动性和场站间输出功率的相关性，利用扩展仿射方法构建系统静态电压稳定性评估的扩展仿射模型，可得到系统静态电压稳定性L指标的区间边界，同时能辨识出系统中的薄弱节点。进一步将基于解析化方差分解的全局灵敏度分析方法和静态电压稳定性评估的扩展仿射模型相结合，提出了基于扩展仿射模型的静态电压稳定性全局灵敏度分析方法。经在IEEE系统中的算例分析可得如下结论：
1）基于仿射方法和扩展仿射方法建立的静态电压稳定性评估模型均可获得准确的计算结果，但基于扩展仿射方法的静态电压稳定性评估模型比基于仿射方法的所得到的L指标区间更为精确。
2）与基于蒙特卡洛仿真的全局灵敏度分析方法相比，基于扩展仿射模型的静态电压稳定性全局灵敏度分析方法获得总灵敏度指标的最大相对误差小于11.1%，主灵敏度指标最大相对误差指标小于9.1%，且由于解析化计算方式而具有更高计算效率。
本文建立的基于L指标的静态电压稳定性全局灵敏度分析方法，计算简单且易于实现，适用于大规模风电并网后系统静态电压稳定性评估和静态电压稳定性在线快速扫描。下一步工作将考虑负荷的ZIP模型、发电机的无功限制等。
附 录
[1]朱泽安, 周修宁, 王旭, 等. 基于稳暂态联合仿真模拟的区域多可再生能源系统评估决策[J]. 电工技术学报, 2020, 35(13): 2780-2791.
Zhu Zean, Zhou Xiuning, Wang Xu, et al. Evaluation and decision-making of regional multi-renewable energy system based on steady-transient integrated simulation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2780-2791.
[2]余光正, 林涛, 汤波, 等. 计及谐波裕度-均衡度的分布式电源最大准入功率计算方法[J]. 电工技术学报, 2021, 36(9): 1857-1865.
Yu Guangzheng, Lin Tao, Tang Bo, et al. Calculation method of distributed generator maximum access power considering balance degree of harmonic margin[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1857-1865.
[3]汤涌. 电力系统电压稳定性分析[M]. 北京: 科学出版社, 2011.
[4]赵建伟, 李禹鹏, 杨增辉, 等. 基于拟蒙特卡罗模拟和核密度估计的概率静态电压稳定计算方法[J]. 电网技术, 2016, 40(12): 3833-3839.
Zhao Jianwei, Li Yupeng, Yang Zenghui, et al. Probabilistic static voltage stability calculation based on quasi-Monte Carlo and kernel density estimation [J]. Power System Technology, 2016, 40(12): 3833-3839.
[5]白杨, 王鹏, 韩肖清, 等. 基于负荷不确定性建模的静态电压稳定性风险评估[J]. 中国电机工程学报, 2016, 36(13): 3470-3478.
Bai Yang, Wang Peng, Han Xiaoqing, et al. Risk assessment of static voltage stability based on load uncertainty modeling[J]. Proceedings of the CSEE, 2016, 36(13): 3470-3478.
[6]王敏, 丁明. 考虑分布式电源的静态电压稳定概率评估[J]. 中国电机工程学报, 2010, 30(25): 17-22.
Wang Min, Ding Ming. Probabilistic evaluation of static voltage stability taking account of distributed generation [J]. Proceedings of the CSEE, 2010, 30(25): 17-22.
[7]Miao Shihong, Ran Xiaohong. Probabilistic evaluation for static voltage stability for unbalanced three-phase distribution system[J]. IET Generation, Transmission & Distribution, 2015, 9(14): 2050-2059.
[8]陈磊, 闵勇, 侯凯元. 考虑风电随机性的静态电压稳定概率评估[J]. 中国电机工程学报, 2016, 36(3): 674-680.
Chen Lei, Min Yong, Hou Kaiyuan. Probabilistic steady-state voltage stability assessment considering stochastic wind power[J]. Proceedings of the CSEE, 2016, 36(3): 674-680.
[9]鲍海波, 韦化. 考虑风电的电压稳定概率评估的随机响应面法[J]. 中国电机工程学报, 2012, 32(13): 77-85.
Bao Haibo, Wei Hua. A stochastic response surface method for probabilistic evaluation of the voltage stability considering wind power[J]. Proceedings of the CSEE, 2012, 32(13): 77-85.
[10]谢应昭, 卢继平. 基于多项式正态变换和最大熵估计的含风电系统电压稳定概率分析[J]. 电力自动化设备, 2015, 35(10): 66-73.
Xie Yingzhao, Lu Jiping. Probabilistic voltage stability analysis based on polynomial normal transformation and maximum entropy estimation for power system containing wind power[J]. Electric Power Automation Equipment, 2015, 35(10): 66-73.
[11]Kenari M, Sepasian M, Nazar M. Probabilistic voltage stability assessment of distribution networks with wind generation using combined cumulants and maximum entropy method[J]. International Journal of Electrical Power & Energy Systems, 2018, 95: 96-107.
[12]廖小兵, 刘开培, 李彧野, 等. 基于混合潮流方程的区间潮流计算方法[J]. 高电压技术, 2018, 44(10): 3417-3424.
Liao Xiaobing, Liu Kaipei, Li Yuye, et al. Interval power flow calculation method based on mixed power flow equations[J]. High Voltage Engineering, 2018, 44(10): 3417-3424.
[13]Muñoz J, Cañizares C, Bhattacharya K, et al. An affine arithmetic-based method for voltage stability assessment of power systems with intermittent generation sources[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4475-4487.
[14]de Figueiredo L H, Stolfi J. Affine arithmetic: concepts and applications[J]. Numerical Algorithms, 2004, 37(1-4): 147-158.
[15]杜萍静, 杨明, 曹良晶, 等. 含电压源换流器交直流系统的仿射潮流算法[J]. 电工技术学报, 2020, 35(5): 1106-1117.
Du Pingjing, Yang Ming, Cao Liangjing, et al. Affine power flow algorithm for AC/DC systems with voltage source converter[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1106-1117.
[16]卢苑, 林舜江, 刘明波, 等. 考虑风电场出力波动区间的电力系统静态电压稳定裕度计算[J]. 电力系统自动化, 2018, 42(8): 92-100.
Lu Yuan, Lin Shunjiang, Liu Mingbo, et al. Computation of static voltage stability margin for power system considering fluctuation interval of wind farm output[J]. Automation of Electric Power Systems, 2018, 42(8): 92-100.
[17]Adusumilli B S, Kumar B K. Modified affine arithmetic based continuation power flow analysis for voltage stability assessment under uncertainty[J]. IET Generation, Transmission & Distribution, 2018, 12(18): 4225-4232.
[18]鲍海波, 郭小璇, 韦化. 结合证据理论和双层规划的电压稳定不确定分析[J]. 电力系统自动化, 2018, 42(5): 120-126, 146.
Bao Haibo, Guo Xiaoxuan, Wei Hua, et al. Uncertainty analysis of voltage stability based on evidence theory[J]. Automation of Electric Power Systems, 2018, 42(5): 120-126, 146.
[19]Liao Xiaobing, Liu Kaipei, Niu Huanhuan, et al. An interval Taylor-based method for transient stability assessment of power systems with uncertainties[J]. International Journal of Electrical Power & Energy Systems, 2018, 98: 108-117.
[20]Wang Shouxiang, Han Liang, Wu Lei. Uncertainty tracing of distributed generations via complex affine arithmetic based unbalanced three-phase power flow[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3053-3062.
[21]廖小兵, 刘开培, 乐健, 等. 电力系统区间潮流计算方法综述[J]. 中国电机工程学报, 2019, 39(2): 447-458.
Liao Xiaobing, Liu Kaipei, Le Jian, et al. Review on interval power flow calculation methods in power system[J]. Proceedings of the CSEE, 2019, 39(2): 447-458.
[22]廖小兵, 刘开培, 张亚超, 等. 基于区间泰勒展开的不确定性潮流分析[J]. 电工技术学报, 2018, 33(4): 750-758.
Liao Xiaobing, Liu Kaipei, Zhang Yachao, et al. Uncertain power flow analysis based on interval Taylor expansion[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 750-758.
[23]姜涛, 李国庆, 贾宏杰, 等. 电压稳定在线监控的简化L指标及其灵敏度分析方法[J]. 电力系统自动化, 2012, 36(21): 13-18.
Jiang Tao, Li Guoqing, Jia Hongjie, et al. Simplified L-index and its sensitivity analysis method for on-line monitoring of voltage stability control voltage stability[J]. Automation of Electric Power Systems, 2012, 36(21): 13-18.
[24]Xu Xiaoyuan, Yan Zheng, Shahidehpour M, et al. Power system voltage stability evaluation considering renewable energy with correlated variabilities[J]. IEEE Transactions on Power Systems, 2018, 33(3): 3236-3245.
[25]Saltelli A. Global sensitivity analysis[M]. New York: John Wiley & Sons, 2008.
[26]Ni F, Nijhuis M, Nguyen P H, et al. Variance-based global sensitivity analysis for power systems[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1670-1682.
[27]Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1-3): 271-280.
[28]何琨, 严正, 徐潇源, 等. 基于Sobol’法的孤岛微电网潮流全局灵敏度分析[J]. 电力系统自动化, 2018, 42(14): 105-112.
He Kun, Yan Zheng, Xu Xiaoyuan, et al. Sobol’method based global sensitivity analysis of power flow in islanded microgrid[J]. Automation of Electric Power Systems, 2018, 42(14): 105-112.
[29]王晗, 严正, 徐潇源, 等. 基于稀疏多项式混沌展开的孤岛微电网全局灵敏度分析[J]. 电力系统自动化, 2019, 43(10): 64-77.
Wang Han, Yan Zheng, Xu Xiaoyuan, et al. Global sensitivity analysis for islanded microgrid based on sparse polynomial chaos expansion[J]. Automation of Electric Power Systems, 2019, 43(13): 64-77.
[30]胡潇云, 赵霞, 冯欣欣. 基于稀疏多项式混沌展开的区域电-气联合系统全局灵敏度分析[J]. 电工技术学报, 2020, 35(13): 2805-2816.
Hu Xiaoyun, Zhao Xia, Feng Xinxin, et al. Global sensitivity analysis for regional integrated electricity and gas system based on sparse polynomial chaos expansion[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2805-2816.
[31]Hao Wenrui, Lü Zhengzhou, Li Luyi. A new interpretation and validation of variance based importance measures for models with correlated inputs[J]. Computer Physics Communications, 2013, 184(5): 1401-1413.
[32]Zhang Kaichao, Lü Zhenzhou, Cheng Lei, et al. A new framework of variance based global sensitivity analysis for models with correlated inputs[J]. Structural Safety, 2015, 55: 1-9.