0 引言
直流系统中因为电缆接头松脱、接触不良、导线绝缘破裂等原因极易产生点接触直流故障电弧,其伴随着高热现象的持续产生会不断地对外界释放能量,这会使电极材料和绝缘层材料进行能量累积,当能量累积到一定程度时,会导致接触材料表面受热熔化,引发电极的烧蚀和绝缘层的熔滴,进而产生电缆火焰的蔓延现象[1],严重危害直流供配电系统的安全运行甚至引发电气火灾事故。通过导线热能累积诱发火灾的可能性与电弧故障热能的传递情况密切相关,因此,研究直流故障电弧的稳态传热特性,可为探究耐电弧烧蚀材料及直流防火电缆的研制提供理论依据,对于保障直流供配电系统的稳定可靠运行和提高电气火灾事故的预防能力具有重要意义。
电弧的发生是一个极复杂的多物理场耦合现象,涉及电磁学、传热学、流体力学、等离子学等多门学科。近年来,随着计算机技术的发展以及有限元分析软件的不断完善,基于计算机的数值仿真模拟技术已成为研究和分析工程热物理问题的高效手段[2-3],目前在接地电弧[4-5],交流电弧[6-8]、直流电弧[9-10]、电弧炉[11]、故障电弧神经网络模型[12]等领域都广泛存在电弧仿真的应用。在有关电弧热力学仿真中,使用较多的方法是基于磁流体动力学(Magneto-Hydrodynamics, MHD)的磁流体仿真[13],Huang Keyao等以继电器为研究对象,建立了高压直流继电器电弧触点打开过程的三维物理模型,研究了触电打开过程的燃弧行为并且观察到了弧根漂移的现象[14]。曹启纯等对不同磁场及银蒸气浓度下的直流继电器电弧进行三维仿真建模与实验验证,得到电弧弧根运动曲线[15]。翟国富等建立了小间隙低压金属重击穿放电微观的仿真模型模型,分析了弧柱放电区域温度的影响[16]。蒋原等建立了纵向磁场下中频真空电弧的仿真模型,并对电弧的重燃现象进行了分析[17]。王立军等对真空电弧在不同能流密度下的传热过程进行仿真分析,获得了电弧阳极沿轴向和径向的温度变化过程[18]。Rong Mingzhe等建立了封闭容器中交流故障电弧等离子体三维模型,并描述了电弧周围空气的温度与压力分布[19]。文献[20-22]建立了弓网电弧的二维物理模型,并在模型的基础上模拟了不同间隙、不同接触线廓型、不同廓型半径以及不同材料热导率的电弧温度分布情况,并且对电弧侵蚀接触线的温度和压力进行了研究。伍玉鑫等将电弧热源等效为高斯热源,研究 了大电流电弧作用下电接触材料的烧蚀过程及材料表面的烧蚀熔池随时间的变化规律[23-24]。付思等研究了真空开关导电触点传热过程与间隙击穿过程,模拟了触头分离瞬间蒸气电弧的形成[25]。钟昱铭等对铜蒸气下的直流电弧特性进行了温度仿真,并用光谱测试验证了模型的合理性[26]。Yang Fan等针对绝缘卡套中产生的短间隙电弧,提出使用椭球面热源和高斯热源分别等效弧柱和阴极表面的热效应,并与MHD模型作对比,验证等效模型的可行性[27]。付光晶建立了二维轴对称故障电弧模型,计算了直流故障电弧在0.18s时的温度分布和交流故障电弧半个周期内温度场的变化情况[28]。然而,由于电弧的放电行为呈现非稳态瞬时特性,其中交流放电时,电弧特征参量还会表现出周期性,因此相关研究更多集中在交流电弧瞬态模型分析上,关于直流故障电弧的研究极少,相关的研究也较少涉及电弧热源在不同工况条件下最高温度的变化规律和电弧热源对于电极的传热规律。
综上所述,针对直流故障电弧稳态时的传热特性,目前鲜有深入研究,对于直流故障电弧下电极材料的温度分布认识甚少。本文搭建了串联型直流故障电弧模拟的实验平台,基于该实验平台建立了直流故障电弧的数值模型,通过多物理场耦合模拟直流故障电弧传热特性,构建直流故障电弧的温度分布图像,并对在不同电路电压、电阻、电极间距下的直流故障电弧的传热规律进行研究与分析。
1 直流故障电弧实验电路与平台
本次模拟实验搭建了一套串联型直流故障电弧实验电路与实验平台,如图1所示。构成该电路的主要部分有直流电源、可调节电阻、电压表及电弧发生装置。在电路中引入霍尔电流传感器并与电流表相连,将电流表与电压表一起连接到示波器。故障电弧发生装置主要由碳——石墨材料为主的平头圆柱固定电极,以铜材料为主的尖端圆锥移动电极、绝缘夹、轴向调节装置、轴向滑动块和固定底座等构成。本次实验中所用到的供电电源为Sorensen SGI400/50直流电源,输出电压范围为0~400V,输出电流范围为0~50A,实验中选择电源恒压输出的方式。实验采用拉弧式电弧发生法,移动电极的拉断速度设置为0.5mm/s,当电极移动到相应设置的电极间距时,电极就停止移动,使电弧发生装置稳定产生电弧。本文模拟的实验是两电极全接触通电并拉开后电极间产生稳定放电电弧的状态,以此模拟实际直流电路系统中由于绝缘老化、导线破损和线路接触不良时产生的直流故障电弧。

图1 串联型直流故障电弧实验平台
Fig.1 The experimental platform of series DC fault arc
2 计算模型
2.1 几何模型及假设条件
将图1的两电极导体的正视图顺时针旋转90°,建立如图2所示的二维轴对称模型作为直流故障电弧的数值模型。图2a为总体计算模型,总体的计算区域长为100mm,宽为20mm。图2b为图2a中电极导体和电弧发生区域的放大部分,碳电极的半径为3mm,长度为50mm,铜电极的尖端长度为17mm,半径为1.5mm。剩下的区域为空气域。L为两电极 间距的长度,电弧发生区域在空气域中的两电极间距部分,图形关于r=0轴对称。数值模型中材料的各个物理特性参数见表1。

图2 直流故障电弧的仿真模型
Fig.2 The simulation model of DC fault arc
表1 数值模型中材料各物理特性参数
Tab.1 The physical property parameters of the material in the numerical model
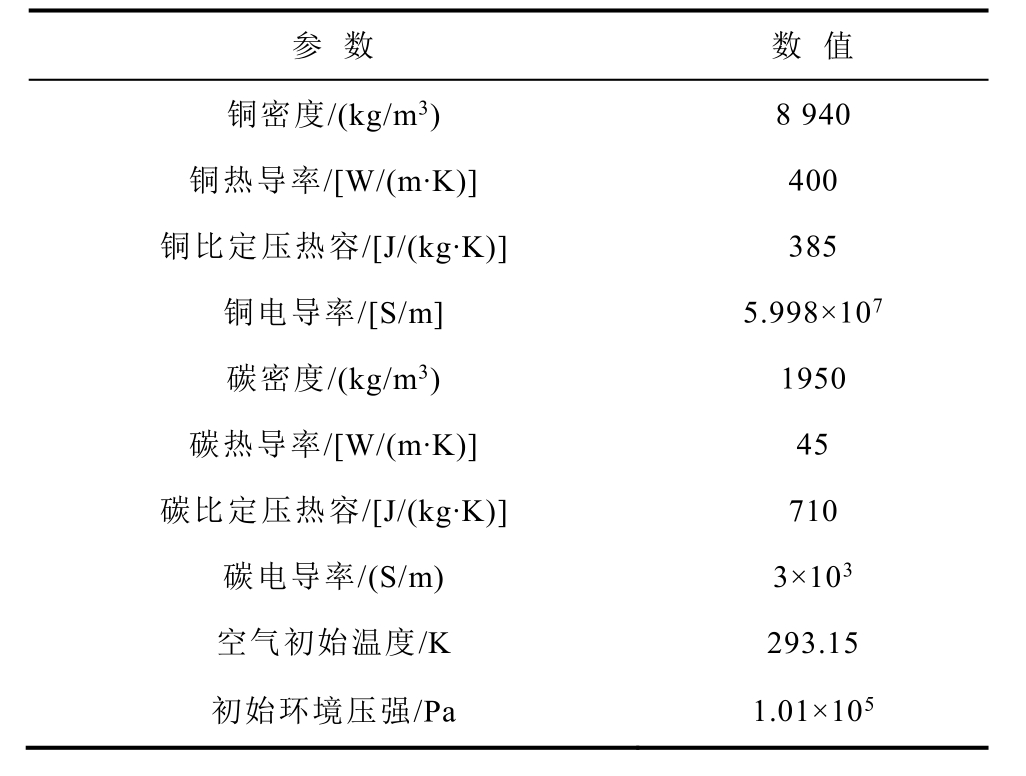
参 数 数 值 铜密度/(kg/m3) 8 940 铜热导率/[W/(m·K)]400 铜比定压热容/[J/(kg·K)]385 铜电导率/[S/m]5.998×107 碳密度/(kg/m3) 1950 碳热导率/[W/(m·K)]45 碳比定压热容/[J/(kg·K)]710 碳电导率/(S/m) 3×103 空气初始温度/K 293.15 初始环境压强/Pa 1.01×105
直流故障电弧的数值模拟是一个复杂的、涉及多物理场耦合的问题,为了简化计算并且使得数值模型计算时有较好的收敛性,降低模拟的复杂程度,在数值模型的构建过程中引入一些理想的假设条件:
(1)不考虑电弧产生的过程,数值计算从电弧的稳定燃烧开始。
(2)假设模拟求解的电弧产生的等离子为平衡等离子体,满足局部热力学平衡状态。
(3)假设电弧等离子体发生区域为轴对称发生区域,等离子的密度、电导率、热导率、比定压压热容、动力粘度系数仅为温度的函数。
(4)在数值模拟过程中,忽略电弧的产生对电极触头烧蚀及电极近极区鞘层的影响。
2.2 控制方程
综合以上的假设条件,将稳定燃烧的电弧对电极的热传导过程视为一个稳态传热过程。电弧在导体与空气中的热量传递过程可用传热方程组描述。电弧等离子体的产生是关于电场、磁场、热场、流场的相互耦合作用的一个多物理的复杂过程,电弧和电极材料的流体动力学方程组涉及能量守恒方程、动量守恒方程、质量守恒方程,而电磁场相关的方程包括电流连续性方程、麦克斯韦方程和欧姆定律,再由二维轴对称模型,电弧等离子体的控制方程可表示如下。
能量守恒方程

式中,ρ为密度;cp为比定压热容;T为温度;h为表面传热系数; rυ为径向速度; zυ为轴向速度;jr为径向电流密度;jz为轴向电流密度;σ为电导率;Qrad为总体积辐射系数;k为热导率;kB为玻耳兹曼常数;e为基本电荷。
径向动量守恒方程

轴向动量守恒方程

式中,P为等离子体压力;jrBθ和jzBθ为洛仑兹力;η为动力粘度系数。
质量守恒方程
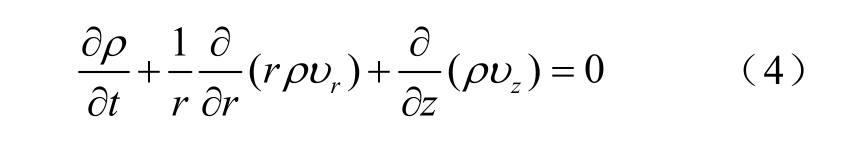
电流连续性方程
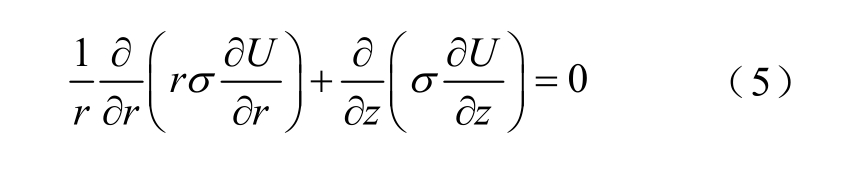
式中,U为电位。
麦克斯韦方程
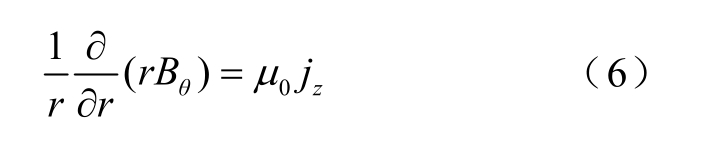
式中,μ0为真空磁导率。本文近似认为系统为准电中性,且由于感应电场远小于外加电场,因此采用近似处理得到式(6)的简化的麦克斯韦方程。
欧姆定律
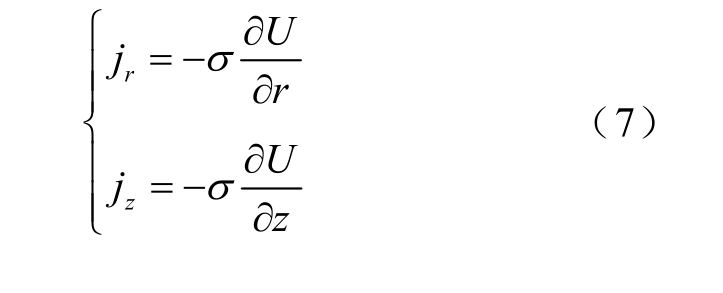
通过以上的物理场控制方程,可以求解电弧等离子体温度场、速度场、电场及磁场。计算仿真的结果与选取模型的材料参数(电导率、密度、热导率、总体积辐射系数、比定压热容、动力粘度系数)及计算模型边界条件的选取有关。通过控制材料域的边界条件,可以求出电弧等离子体对于周围材料特性的影响,最终求得整个仿真模型区域的物理场的分布。
2.3 边界条件
1)温度边界条件
电弧等离子体的能量主要以热传导的形式通过触头表面传导到两电极,以热对流为主要形式向空气域传递能量,因此,图2a的边界a、b、c设置为开放边界。图2b中,边界1、4、5设置为Neumann边界条件,边界2、3设置为开放边界。将空气与电极交界面处,即图2b的边界6、7设置为耦合边界条件。初始温度设置为293.15K。
2)电场边界条件
阴极为电子发射极,电弧产生时,大量的电子涌入弧隙中。本文忽略电弧的起弧过程,弧隙间的电场强度较小,不足以引起场致发射,阴极的表面发射以热发射为主。设电弧稳态燃烧时,电弧中的电流为I,将整个区域划分为N个单元,ji为界面单元面i上的电流密度。故单元界面i上阴极电流密度的表达式为

式中,W为阴极材料功函数;Ti、σi,N分别为阴极与电弧交界面第i个单元温度、电导率; KA为单元区域的面积。阳极的电场边界条件设置为恒定的零电位,作为电子的接收极。
3)磁场边界条件
计算区域的边界条件设置为磁绝缘,其中矢量磁位的各个方向分量设置为0。
4)流场边界条件
流场的边界条件设置为压力边界条件,压力大小为一个标准大气压(1.01325×105Pa)。此外,将模型中流场的初始速度设置为零,为了使流场和磁场更好地耦合,将磁场中的洛伦兹力大小作为流场的初始体积力大小,并代入流场方程中进行计算。
3 仿真结果与分析
考虑到回路中电流参数为因变量,且涉及电弧阻抗、电路热释放、路端电压等的耦合影响,故实验工况设计时选取了相对可控的电路电压和分压电阻作为回路边界条件。本文所建立的直流故障电弧数值模型引入了电源电压、电阻、电极间距三个变量,考虑电信和数据中心高压直流供电系统[29],选取具体数值见表2。求解了不同工况下直流故障电弧稳定燃烧时接触材料的温度分布和电弧发生区域的局部传热情况,并探究了在不同模拟条件下,直流故障电弧的最高温度及最高温度的变化规律。
表2 数值模拟条件
Tab.2 The conditions of numerical simulation

参 数 数 值 电源电压E/V 200, 250, 300, 350, 400 电阻R/Ω 20, 40, 60, 80, 100 电极间距L/mm 1, 1.5, 2, 2.5, 3, 3.5, 4
3.1 电弧最高温度变化的仿真分析
在完成了表2中不同工况下的直流故障电弧稳定燃烧时的温度分布模型计算后,提取电极间距为2mm、电路中电源电压为300V、电阻为40Ω的直流故障电弧模型并进行传热分析,仿真的三维结果图像如图3所示,整个直流故障电弧系统稳定燃弧的时候,该系统的最高温度位于电极间距的中心,电弧中心的最高温度为5 170.58K。电弧的温度呈现圆弧状向四周降低,部分热量通过热传导作用传递到两电极中,剩余大部分的热量散发到空气中,使得周围空气区域维持较高的温度。受制于两电极形状的不同和热对流作用的影响[30],电弧向铜电极尖端周围空气区域所传递的热量高于碳电极周围空气区域的热量,从而在直流电弧稳态燃烧时,使铜电 极尖端的周围高温区域范围多于碳电极平端的周围高温区域范围。

图3 直流电弧模型的三维温度场分布
Fig.3 Three-dimensional temperature distribution of DC arc model
在改变电路中电源电压、电阻和电极间距时,直流故障电弧系统的电弧最高温度会有一定的改变,此处,将对其直流故障电弧的最高温度和温度分布进行探讨。
1)恒定电极间距情况
将电阻作为变量,设置电极间距为4mm,控制电源电压在200~400V每隔50V的电压等级下作仿真模拟,提取计算结果的最高温度并相连,绘制电弧随电阻产生的最高温度变化规律如图4所示。可以看出,电阻在区间20 ~40Ω,电压变化导致电弧温度的变化幅度较为明显,而当电阻大于40Ω后,电压变化导致电弧最高温度的变化幅度不明显。当电压处于200V时,电弧最高温度随电阻值的升高而缓慢下降,下降幅度变化不大;当电源电压处于250~400V时,电弧最高温度在电阻20~40Ω区间的下降速度由大变小,温降速度于40Ω之后逐渐趋于平缓。

图4 电弧最高温度随电阻变化规律
Fig.4 Variation of maximum temperature of the arc with resistance
电弧温度和电弧电流的正相关关系及Fisher公式[31]为
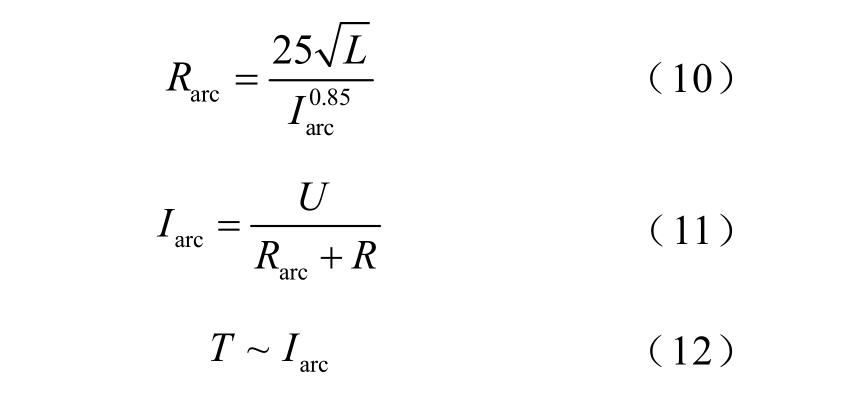
式中,Rarc为电弧阻抗;L为电极间距;Iarc为电弧电流;U为电路电压;R为电路电阻。式(12)表示T近似地正比于Iarc。当电极间距不变时,即ΔL=0,此时电极间距变化的影响可忽略,又因为电弧阻抗Rarc远小于电路电阻R,可得电弧电流在不同电压等级下与电路电阻的关系为

由式(12)、式(13)可得电弧最高温度T与电压和电阻关系为

即电阻增大导致电流减小,电弧最高温度T随R的变化呈反比例下降关系,该关系随着电压等级U的升高愈发明显。
2)恒定电压情况
将电极间距作为变量,为了模拟实际的电弧传热结果,在仿真前会考察在该间距下能否实际产生电弧。根据文献[32],电极间距选取为1~4mm,每隔0.5mm计算一次电弧的最高温度,提取模型计算结果的最高温度,并绘制电源电压200V时且不同电阻的工作条件下,电弧最高温度随电极间距变化规律如图5所示。

图5 电弧最高温度随电极间距变化规律
Fig.5 Variation of maximum temperature of the arc with electrode gap
可以看出,当电路电压不变时,即ΔU=0,此时电压变化的影响可忽略,根据式(10)、式(11),得

由电弧最高温度和电弧电流的正比关系,可得

电弧阻抗Rarc为电弧内部属性,电极间距和电弧最高温度的变化呈正相关,表现为以![]() 指数的分数指数形式上升,增长的速率较为稳定,但增长的幅度较小。相较而言,电极间距的变化对于电弧最高温度的影响远小于电阻等级的改变对于电弧最高温度的影响。
指数的分数指数形式上升,增长的速率较为稳定,但增长的幅度较小。相较而言,电极间距的变化对于电弧最高温度的影响远小于电阻等级的改变对于电弧最高温度的影响。
3)恒定电阻情况
将电源电压作为变量,电阻选择40Ω,在不同电极间距下完成模型的计算并提取最高温度,绘制电弧最高温度在不同电极间距下随电压变化规律如图6所示。可以看出,当电阻不变时,即ΔR=0,此时电路电阻变化的影响可忽略,根据式(10)、式(11)及电弧温度与电弧电流的关系可得
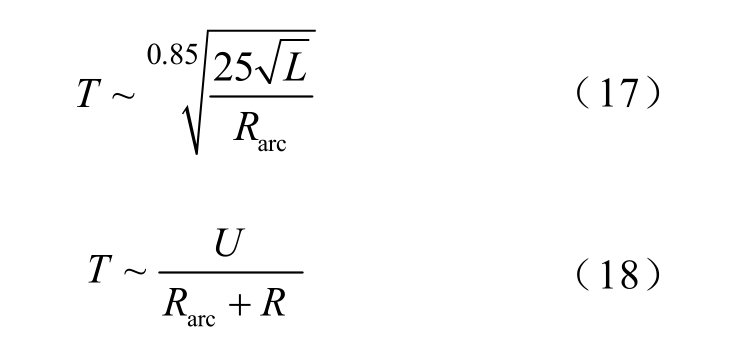

图6 电弧最高温度随电源电压变化规律
Fig.6 Variation of maximum temperature of the arc with supply voltage
可以看出,电弧最高温度随电压等级的增长而升高,且温度升高速率具有稳定性。电弧的最高温度在一定范围内呈线性增长,但随电压增加温度升高速率逐渐减小。相比于电极间距的变化对于电弧中心最高温度的影响,电路电压的变化对于电弧中心最高温度的影响效果更加明显。
综上可得,当电极间距不变时,电弧的最高温度变化随电阻增大表现出反比例下降的趋势;当电压不变时,电弧的最高温度变化随电极间距的增量变化表现为分数指数形式上升;当电阻不变时,电弧的最高温度随电路电源电压的增大在一定范围内呈现线性增长,但随电压增加趋势变缓。
3.2 稳定燃弧条件下电极的温度分布及变化
为了便于观察直流故障电弧稳定燃弧时电极的温度分布及变化,并分析电路中电压、电阻及电极间距的变化对于电极传热的影响,使用图2b的模型作为电弧对于电极传热的观察区域,通过控制变量的方式改变电路中电源电压、电阻及电极间距的大小,在仿真计算结果中提取二维剖面图并添加等温线。
设置电极间距为4mm、电路电压为200V,提取不同电阻下电弧对于电极传热的计算结果,如图7所示。

图7 不同电阻下的电弧电极温度场分布
Fig.7 Temperature distribution of arc electrode under different resistances
可以看出,在铜电极的尖端与碳电极端面的间隙部分,等温线分布较为密集,而在两电极内部的等温线分布较为松散。在电极导体内部,靠近电弧区域的部分温度较高,与电弧内部区域越远的导体部分温度越低。电阻较小的工况中的电极导体内的温度梯度的变化较为剧烈,随着电阻的增大,温度梯度趋于平缓。此外,由于铜电极的导热率高于碳电极,故在直流电弧稳定燃弧时,铜电极内部所保留的电弧热量会低于碳电极内部所保留的热量。
为了更好地研究电极内部的温度变化,以模型中铜电极底端作为起始点,碳电极的底端为终点,经过中轴线分别提取电极间距4mm、电路电压200V,不同电阻等级条件下模型中轴线上的温度数据,以模型轴线位置作为x轴,模型中点作为0点,负方向为铜棒方向,正方向为碳棒方向,绘制折线图如图8所示,从图中可得,轴线的中点附近由于是电极间距存在电弧,所以温度较高。由于电弧等离子的特性,电弧实际传热的效率不高,所以电弧到两电极位置的过渡区间温度显著性骤降,铜电极的最高温度只有电弧最高温度的17%~27%,碳电极最高温度只有电弧最高温度的41%~51%。电极导体内部的最高温度位于最靠近电弧的位置,越远离电弧处的电极导体位置温度越低。由于铜的导热系数高于碳,致使铜电极的散热更快,同一模型轴线上与中点位置相同距离的铜电极温度始终低于碳电极温度。此外,在图8中引入电弧最高温度点的参照线交于x轴,相交的位置并不位于x=0处,说明该模型中电弧的最高温度并不位于电极间距的中心。
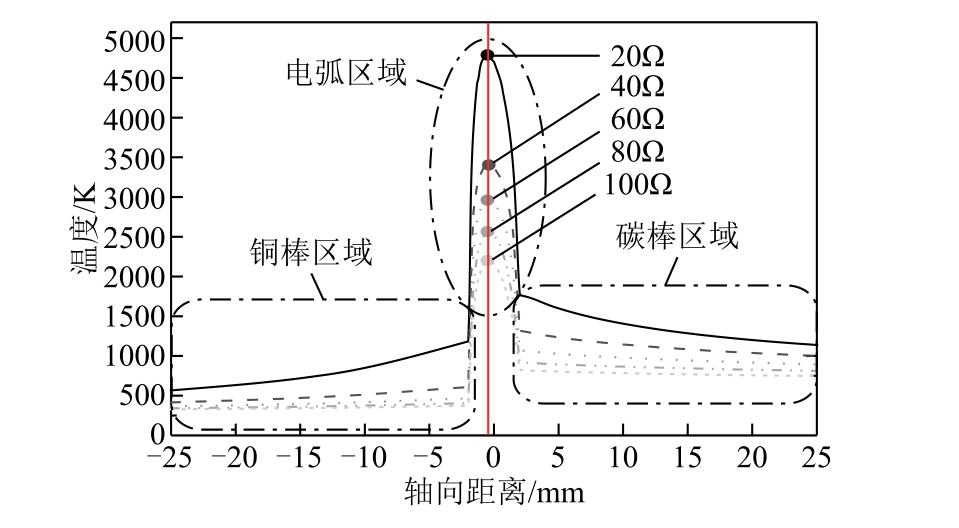
图8 电极轴向不同位置的温度变化情况
Fig.8 Temperature variation at different positions in axial direction of the electrode
电极间距4mm,电阻40Ω的温度结果如图9所示。电压增长会引起电弧温度上升,同时也会使靠近电弧处的电极导体内的温度梯度越明显。模型中轴线上温度数据如图10所示,以模型轴线的中点作为0点,负方向为铜棒方向,正方向为碳棒方向。可以看出当电压提高时,电弧内部能量会提高,电极导体所受电弧传导的热量也会增加,使得两电极靠近电弧处的导体最高温度也会提高。由于电极热传导,两电极靠近电弧处的温度下降速率会随着温度的提高而提高,电极导体的内部温度和温度下降速率会随着电极长度的延长而降低,最终在一定长度内稳定在某个数值范围。
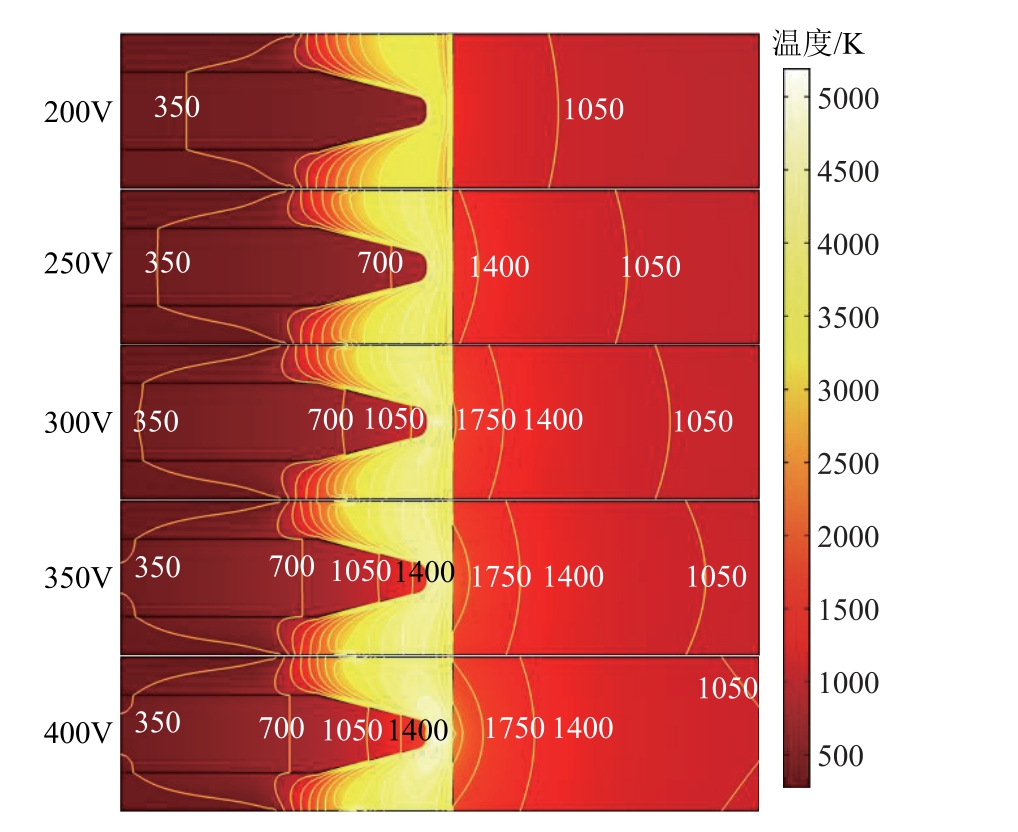
图9 不同电源电压下的电弧电极温度场分布
Fig.9 Temperature distribution of arc electrode under different supply voltage

图10 电极轴向不同位置的温度变化情况
Fig.10 Temperature variation at different positions in axial direction of the electrode
电源电压为200V、电阻40Ω的温度结果如图11所示。两电极导体的等温线变化随电极间距的增加而逐渐外扩,铜导体等温线的外扩程度没有碳导体明显。电极间距的增大使得电弧最高温度增大的同时也会将更多的热量传导到两电极导体上。

图11 不同间距下的电弧电极温度场分布
Fig.11 Temperature distribution of arc electrode under different electrode gap
以模型轴线的中点作为0点,负方向为铜棒方向,正方向为碳棒方向。温度变化曲线如图12所示。可以看出,随着电极间距增大,电弧最高温度有小范围的变化,但是对于电极上温度的变化更加不明显,将电极轴向范围放大至(-2mm, 2mm)处,在x=0处引入参照线,可以看出除了电极间距为1mm数据组的电弧最高温度位于电弧模型中心处,其余电弧模型的最高温度并不位于模型中心,即直流电弧的最高温度并不位于两电极间距中心,而是较为偏向铜电极位置,并且随着电极间距的增大,电弧最高温度位置会朝着铜电极的方向越远离电极间距中心位置。由图12b、图12c可以看出,在电极内部温度下降的速率近乎相同,电极间距由小变大对于电极内部温度变化规律影响甚微。

图12 电极轴向上不同位置的温度变化情况
Fig.12 Temperature variation at different positions in axial direction of the electrode
3.3 电弧温度的能量平衡分析
系统中能量变化与温度的变化有着直接的关系,因此可从功率输入和功率耗散的能量平衡角度分析电弧温度的变化规律。
提取仿真模型在不同工况下的电弧电流与电弧电压数值,分析其等效电弧功率的变化情况。采用图1的实验平台进行不同电源电压、电阻、电极间距下的直流故障电弧实验,实验工况具体参数见表3,以此验证不同工况下采集到的电弧电流和电弧电压数据,计算电弧等效功率并分析其变化规律。视等效电弧功率为理想电弧输入功率,同时在考虑电弧的功率耗散的情况下,揭示电弧最高温度变化规律。
表3 故障电弧实验的电路参数
Tab.3 The circuit parameters of fault arc experiment

参 数 数 值 电源电压E/V 200, 250, 300, 350, 400 电阻R/Ω 20, 40, 60, 80, 100 电极间距L/mm 1 , 2 , 3 , 4
将电阻作为变量,电极间距为4mm,同时控制电路的电源电压等级,提取电弧电流、电压、等效电弧功率的变化规律曲线,如图13所示,图中的线段表示仿真的规律曲线,几何图块表示的是相应电弧的电参数实验值。可以看出,实验值与仿真规律相符,由此验证数值方法的合理性。

图13 电弧电流、电压、等效功率随电阻的变化
Fig.13 Variation of current, voltage and equivalent power of the arc with resistance
由于电弧内部具有阻抗,因此当电路电源为恒压输出时,电路中的电流会因为电弧的出现而小幅度减少,但电弧的阻抗相比电路电阻而言较小,在许多工程问题上甚至可忽略,所以电弧电流与电阻基本满足反比例关系[33]。
在电弧电压的实验中,电弧的两端电压会随着电路电阻的增长而增大,变化范围在50V以内。提取仿真和实验的等效功率并绘制拟合曲线如图13c所示,可以看出,当电极间距不变时,等效电弧功率随电阻的变化趋势基本满足电弧电流随电阻的变化趋势,符合文献[9]的结论。当电源电压为200V时,等效电弧功率随电阻改变而变化的幅度在200W内,而当电源电压为400V时,等效功率随电阻改变而变化的幅度在400W内,并且电阻为20~40Ω时,等效电弧功率的变化幅度较大,而在40Ω之后趋于平缓。
将电极间距作为变量,电源电压为200V,同时控制电阻等级,提取仿真电弧电流、电压、等效电弧功率的变化规律曲线与实验数值,如图14所示。 可以看出,电弧电流会随着电极间距的增大出现小幅度的降低。当电极间距变化范围在1~4mm时,电极间距每增大1mm,电弧电流平均减少0.1~0.2A,而电弧的两端电压会随着电极间距的变化增大而增大。电弧电压对于电极间距变化的敏感程度远大于电弧电流。因此等效电弧功率也会出现随电极间距的增长而增大的规律,当电阻为20Ω时,等效电弧功率随电极间距的变化幅度在100W内,而在其他电阻条件下,功率的变化幅度在50W内。

图14 电弧电流、电压、等效功率随电极间距的变化
Fig.14 Variation of current, voltage and equivalent power of the arc with electrode gap
将电路电压作为变量,电阻选择为40Ω,同时控制电极间距等级,提取仿真电弧电流、电压,等效电弧功率的变化规律曲线与实验数值,如图15所示。可以看出,当电源电压变化范围处于200~400V时,电弧电流的变化会随着电源电压的增大而出现近似线性的增长,而电弧电压会随着电源电压的增大而减小,其减小的幅度也会根据电极间距的减小 而降低。通过计算其等效电弧功率,可以发现等效电弧功率随着电源电压的增加而增大,变化范围约为150W。

图15 电弧电流、电压、等效功率随电源电压的变化
Fig.15 Variation of current, voltage and equivalent power of the arc with supply voltage
综上可得,等效电弧功率受电阻变化的影响较大,受电源电压变化的影响次之,而受电极间距的影响较小;其变化规律与前文提到的电弧最高温度的变化规律相符。
通常而言,电弧的散热方式有三种形式:传导散热、对流散热、辐射散热。电弧的能量平衡方程为
式中,Pz为电弧的总散热功率;Pcd为传导散热功率;Pdl为对流散热功率;Pfs为辐射散热功率。
传导散热的功率可表示为

式中,λ为气体热导率;l为电弧长度;rh为电弧半径;Th为弧柱表面温度;T0为环境温度;r0为T0处的半径。
对流散热的功率可表示为
式中,h为表面传热系数,πdl为弧柱侧面积。
辐射散热的功率可表示为
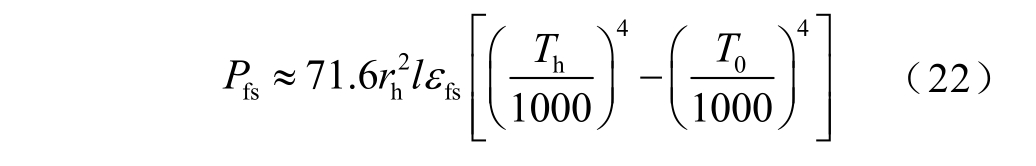
式中,![]() 为乘以经验系数的电弧体积项;εfs为弧柱发射率。
为乘以经验系数的电弧体积项;εfs为弧柱发射率。
在分析式(20)~式(22)时,可将电弧长度等效为电极间距L,而电弧半径rh的变化会随电极间距的增大而增大,但在本次实验中,电极间距的变化范围仅为1~4mm,因此电极间距的变化虽然可以小幅度地增大电弧的总散热功率,但是对电弧总散热功率起决定性影响的还是弧柱表面温度Th,其数值取决于电弧输入功率。当电弧持续产生并稳定燃烧时,弧柱的表面温度小于电弧中心的温度,所以电弧的总散热功率会小于电弧输入功率,最终的结果体现为温度的变化。又因为等效电弧功率的变化趋势与前文提到的电弧最高温度的变化趋势相符,故可证明仿真分析的电弧最高温度变化规律及电极温度分布的合理性。
4 结论
本文采用磁流体动力学建立了直流故障电弧稳态传热数值模型,探讨了不同电路电压、电阻、电极间距下的电弧最高温度变化规律及电弧热源对于电极内部温度传热规律,并进行了实验验证。可为直流电弧性电气火灾标准的制定提供理论依据,也为探索耐电弧阻燃电极材料的研制提供参考。本文研究所得结论:
1)铜电极尖端四周的空气具有比碳电极电弧侧更多的高温区域。但由于热导率高,使得铜内部在直流电弧稳定燃烧时保留的热量低于碳电极,所以稳态时铜导体内部温度在与中点相同距离的位置低于碳电极。
2)直流故障电弧最高温度会随着电路电源电压的增大在一定范围内呈现线性增长,但随电压增加温升速率逐渐减小,随电极间距的增大呈现为分数指数形式的上升规律。同时,电阻等级增大会引起电路中电流的减小,进一步造成电路输入功率的减少,使得电弧最高温度呈反比例下降,该趋势会随电压增大而越发明显。
3)虽然电弧发生区域拥有较高的温度,但是电弧传导到两侧电极处会发生温度的骤降,铜电极的最高温度只有电弧最高温度的 17%~27%,碳电极最高温度只有电弧最高温度的41% ~51%,两电极靠近电弧处的导体温度下降速率会随着电弧温度的提高而提高,但随着电极长度的延长,电极导体的内部温度和温度下降速率会降低。此外,电极间距变化对于电极内部温度变化和温度下降的速率影响不明显。
4)直流故障电弧的最高温度并不恒在电极间距中心。随着电极间距的增大,故障电弧的最高温度会随着向铜电极方向偏离电极间距中点。电弧最高温度之所以偏离电极间距中心,可能与铜电极和碳电极在靠近电弧侧的形状不一致有关,由于铜电极靠近电弧侧是尖端而碳电极是平端,所以稳态时电弧高温的区域会向相对于平端更无阻碍的尖端扩散,并随着电弧区域的增大越发明显。
[1]Huang Xinyuan, Nakamura Y. A review of fundamental combustion phenomena in wire fires[J]. Fire Technology, 2020, 56(1): 315-360.
[2]Zhu Gaojia, Liu Xiaoming, Li Longnv, et al. Coupled electromagnetic-thermal-fluidic analysis of permanent magnet synchronous machines with a modified model[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2):204-209.
[3]Wang Ning, Wang Huifang, Yang Shiyou. 3D eddy current and temperature field analysis of large hydrogenerators in leading phase operations[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 210-215.
[4]陈博博, 屈卫锋, 杨宏宇, 等. 小电流接地系统单相接地综合电弧模型与选线方法的研究[J]. 电力系统保护与控制, 2016, 44(16): 1-7.
Chen Bobo, Qu Weifeng, Yang Hongyu, et al. Research on single-phase grounding integrated arc model and line selection method for small current grounding system[J]. Power System Protection and Control, 2016, 44(16): 1-7.
[5]许晔, 郭谋发, 陈彬, 等. 配电网单相接地电弧建模及仿真分析研究[J]. 电力系统保护与控制, 2015, 43(7): 57-64.
Xu Ye, Guo Mufa, Chen Bin, et al. Modeling and simulation analysis of single-phase grounding arc in distribution networks[J]. Power System Protection and Control, 2015, 43(7): 57-64.
[6]高杨, 王莉, 张瑶佳, 等. 简化的Schavemaker交流电弧模型参数的计算方法研究[J]. 电力系统保护与控制, 2019, 47(8): 96-105.
Gao Yang, Wang Li, Zhang Yaojia, et al. Research on the calculation method of simplified Schavemaker AC arc model parameters[J]. Power System Protection and Control, 2019, 47(8): 96-105.
[7]李奎, 陈照, 张洋子, 等. 基于聚类分析和电磁辐射信号的电弧故障识别[J]. 电机与控制学报, 2018, 22(5): 94-101.
Li Kui, Chen Zhao, Zhang Yangzi, et al. Arc fault detection based on cluster analysis and electromagnetic radiation[J]. Electric Machines and Control, 2018, 22(5): 94-101.
[8]崔芮华, 王传宇, 王洋. VMD-ApEn在航空交流串联型电弧故障检测中的应用[J]. 电机与控制学报, 2020, 24(8): 141-149.
Cui Ruihua, Wang Chuanyu, Wang Yang. Application of VMD-ApEn in aviation AC series arc fault detection[J]. Electric Machines and Control, 2020, 24(8): 141-149.
[9]熊兰, 曾泽宇, 杨军, 等. 小电流直流故障电弧的数学模型及其特性[J].电工技术学报, 2019, 34(13): 2820-2829.
Xiong Lan, Zeng Zeyu, Yang Jun, et al. Mathematical model and characteristics of low-current DC fault arc[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2820-2829.
[10]赵铁军, 孟菁, 宋岳奇, 等. 组串式光伏系统直流串联电弧故障检测与保护策略[J]. 电力系统保护与控制, 2020, 48(20): 74-82.
Zhao Tiejun, Meng Jing, Song Yueqi, et al. Series arc detection and protection on the DC side of string-type PVs[J]. Power System Protection and Control, 2020, 48(20): 74-82.
[11]廖延涛, 胡骏, 张海龙, 等. 用于电能质量预测分析的交流电弧炉时变参数模型[J]. 电气技术, 2016, 17(3): 41-46.
Liao Yantao, Hu Jun, Zhang Hailong, et al. Timevarying parameter model of AC arc furnace for power quality prediction and analysis[J]. Electrical Engineering, 2016, 17(3): 41-46.
[12]陈烜, 冷继伟, 李海峰. 基于全相位谱和深度学习的串联故障电弧识别方法[J]. 电力系统保护与控制, 2020, 48(17): 1-8.
Chen Xuan, Leng Jiwei, Li Haifeng. Series fault arc recognition method based on an all-phase spectrum and deep learning[J]. Power System Protection and Control, 2020, 48(17): 1-8.
[13]荣命哲, 吴翊, 杨飞, 等. 开关电弧电流零区非平衡态等离子体仿真研究现状[J]. 电工技术学报, 2017, 32(2): 1-12, 23.
Rong Mingzhe, Wu Yi, Yang Fei, et al. Review on the simulation method of non-equilibrium arc plasma during current zero period in the circuit breaker[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 1-12, 23.
[14]Huang Keyao, Sun Hao, Niu Chunping, et al. Simulation of arcs for DC relay considering different impacts[J]. Plasma Science and Technology, 2019, 22(2): 21-30.
[15]曹启纯, 刘向军. 高压直流继电器电弧运动仿真分析与实验研究[J]. 电工技术学报, 2019, 34(22): 4699-4707.
Cao Qichun, Liu Xiangjun. Simulation analysis and experimental research on arc motion in high voltage DC relay[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4699-4707.
[16]翟国富, 薄凯, 李庆楠, 等. 直流电弧运动过程中重击穿现象及机理研究[J]. 电工技术学报, 2016, 31(11): 105-113.
Zhai Guofu, Bo Kai, Li Qingnan, et al. Research on the phenomenon and mechanism of rebreakdown during DC arc movement[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 105-113.
[17]蒋原, 李擎, 崔家瑞, 等. 纵向磁场下中频真空电弧的重燃现象分析[J]. 电工技术学报, 2020, 35(18): 3860-3868.
Jiang Yuan, Li Qing, Cui Jiarui, et al. Re-ignition of intermediate frequency vacuum arc at axial magnetic field[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3860-3868.
[18]王立军, 贾申利, 刘宇, 等. 纵磁下真空电弧阳极热过程的仿真[J]. 电工技术学报, 2011, 26(3): 65-73.
Wang Lijun, Jia Shenli, Liu Yu, et al. Simulation of anode thermal process in vacuum arc under axial magnetic field[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 65-73.
[19]Rong Mingzhe, Li Mei, Wu Yi, et al. 3-D MHD modeling of internal fault arc in a closed container[J]. IEEE Transactions on Power Delivery, 2017: 1220-1227.
[20]马云双, 高国强, 朱光亚. 高速列车弓网电弧温度场特性仿真研究[J]. 高电压技术, 2015, 41(11): 3597-3603.
Ma Yunshuang, Gao Guoqiang, Zhu Guangya. Simulation study on arc temperature field characteristics of high-speed train pantograph[J]. High Voltage Engineering, 2015, 41(11): 3597-3603.
[21]朱光亚, 吴广宁, 高国强, 等. 高速列车静态升降弓电弧的磁流体动力学仿真研究[J]. 高电压技术, 2016, 42(2): 642-649.
Zhu Guangya, Wu Guangning, Gao Guoqiang, et al. Magnetohydrodynamic simulation of static lifting bow arc of high-speed train[J]. High Voltage Engineering, 2016, 42(2): 642-649.
[22]许潘, 杨泽锋, 魏文赋, 等. 降弓电弧对接触线侵蚀的仿真研究[J]. 高电压技术, 2019, 45(11): 3529-3538.
Xu Pan, Yang Zefeng, Wei Wenfu, et al. Simulation study on erosion of contact line by downbow arc[J]. High Voltage Engineering, 2019, 45(11): 3529-3538.
[23]伍玉鑫, 王阳明, 杨泽锋, 等. 电弧作用下浸铜碳材料烧蚀过程的数值模拟[J]. 电工技术学报, 2019, 34(6): 1119-1126.
Wu Yuxin, Wang Yangming, Yang Zefeng, et al. Numerical simulation of the ablative process of copper carbon impregnated by electric arc[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1119-1126.
[24]伍玉鑫, 杨泽锋, 高国强, 等. 电弧作用下电接触材料的热烧蚀过程[J]. 高电压技术, 2019, 45(7): 2276-2283.
Wu Yuxin, Yang Zefeng, Gao Guoqiang, et al. Thermal ablation of electrically contacting materials under electric arc[J]. High Voltage Engineering, 2019, 45(7): 2276-2283.
[25]付思, 曹云东, 李静, 等. 触头分离瞬间真空金属蒸气电弧形成过程的仿真[J]. 电工技术学报, 2020, 35(13): 2922-2931.
Fu Si, Cao Yundong, Li Jinget al. Simulation researches on vacuum metal vapor arc formation at the initial moment of contact parting[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2922-2931.
[26]钟昱铭, 熊兰, 杨子康, 等. 计及铜蒸气介质的小电流直流电弧仿真与实验[J]. 电工技术学报, 2020, 35(13): 2913-2921.
Zhong Yuming, Xiong Lan, Yang Zikang. Numerical simulation and experiment of small current DC arc considering copper vapor medium[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2913-2921.
[27]Yang Fan, Liu Kai, Wang Shaohua, et al. A thermalstress field calculation method based on the equivalent heat source for the dielectric fitting under discharging[J]. Applied Thermal Engineering, 2018, 138: 183-196.
[28]付光晶. 基于COMSOL的故障电弧仿真研究[D]. 上海: 上海交通大学, 2018.
[29]刘希禹, 祁澎泳. 电信和数据中心高压直流供电系统的目标电压范围(260 VDC-400 VDC)[J]. 电源世界, 2014(7): 59-65.
Liu Xiyu, Qi Pengyong . Target voltage range of high voltage power feeding system for telecommunication and data center(260 VDC -400VDC) [J]. The World of Power Supply, 2014(7): 59-65.
[30]He Hailong, Wu Yi, Yang Zhuo, et al. Study of liquid metal fault current limiter for medium-voltage DC power systems[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2018, 8(8): 1391-1400.
[31]Fisher L E . Resistance of low-voltage AC arcs[J]. IEEE Transactions on Industry & General Applications, 2009, IGA-6(6): 607-616.
[32]Du Jianhua, Tu Ran, Zeng Yi, et al. An experimental study on the thermal characteristics and heating effect of arc-fault from Cu core in residential electrical wiring fires[J]. PLoS One, 2017, 12(8): e0182811.
[33]王其平. 电器电弧理论[M]. 北京: 机械工业出版社, 1991.