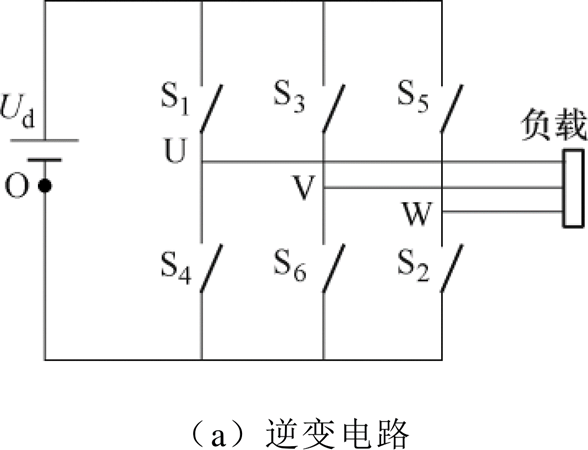
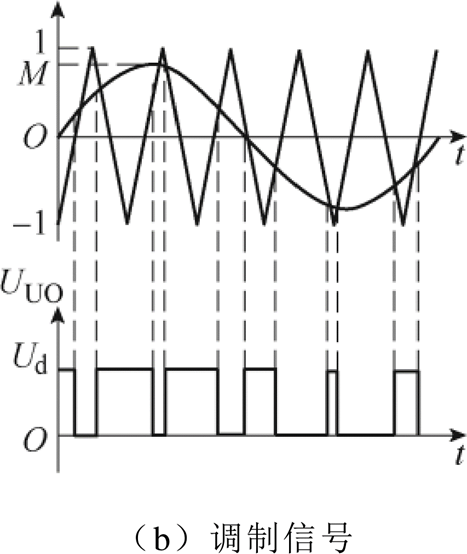
图1 逆变电路与调制信号示意图
Fig.1 Invert circuit and modulation signal
摘要 变频电机的振动噪声是影响电驱动产品应用的重要因素。为更准确掌握变频电机振动噪声激励，设计低噪声变频电机，该文建立变频电机振动噪声特性的一种分析模型，从变频机理出发，推导正弦脉宽调制（SPWM）变频器的输出谐波，再根据麦克斯韦定律计算分析变频激励下电机气隙的电磁激励力特性，并基于有限元法建立电磁-固-声多场耦合仿真计算模型，最后通过对比实测电机的声功率总结出变频谐波对变频电机振动噪声特性的影响。分析结果表明，电机振动噪声在低频部分的谐波由电机的调制频率产生，而变频器引入的高频谐波会使电机在开关频率附近辐射大量的噪声，因此，低噪声变频电机的设计必须消除或者削弱这些谐波。
关键词：变频电机 振动噪声 变频谐波 电磁-固-声耦合仿真
变频电机的振动噪声性能与电动汽车用户的乘车体验密切相关，受到电驱动产品相关行业的广泛关注。电磁噪声是电机噪声的主要成分，由气隙中的电磁径向力波作用到定子上产生[1]。变频驱动下的电磁径向力波会含有丰富的谐波[2]，使电机的振动噪声特性更加复杂[3-6]。因此，电机在变频激励下的电磁振动噪声特性受到了越来越多的重视。
针对变频电机的电磁振动噪声问题，可以通过理论计算和实验测试的方法研究振动噪声频谱。Y. Asano[7]解析计算电机的电磁径向力波，考虑了定子的槽参数，并分析了径向力的频率特性，发现同步电机中径向电磁力的幅值随定子绕组相数的增加呈减小的趋势。唐任远等[8]采用有限元法（Finite Element Method, FEM）计算变频供电时的气隙磁场，总结了气隙磁场主要谐波频率与开关频率的关系，并通过实验测试分析变频电机的噪声频谱。毛钰等[9]采用实验与解析法分析了电流谐波等因素对轮毂电机转矩波动的影响。A. Ruiz- Gonzalez等[10]通过对比实验研究发现，变频器的调制方式对电机的振动噪声有较大影响。A. C. Binojkumar等[11]以实验的方式研究了变频电机的辐射噪声特性，发现在高频时，电磁噪声比空气动力噪声与机械噪声更为突出。林福等[12]提出了带有谐波电流输入时电机噪声计算的半解析法用于快速分析电机振动噪声，并进行了实验验证。李文等[13]通过实验研究开关频率对变频电机振动的影响，发现增加开关频率可以减小电机的高频振动。Wang Chong等[14]通过实验测量了变频电机的声功率谱，发现变频谐波对噪声的影响随电机转速的增加而减小的趋势。
上述研究主要关注变频器的开关频率对电机振动噪声的影响，但鲜有电机调制频率对电机气隙磁场和振动噪声的研究报道。尽管实验测量电机振动噪声特性的结果准确性高，但是在样机方案不确定的电机优化降噪设计过程中，仅依赖实验测量会有很大的局限性。
为了更好地认识变频电机振动噪声激励，为低噪声变频电机设计提供技术支撑，本文建立了变频驱动下电机电磁振动噪声特性分析模型，从变频机理出发，计算出变频器的输出电压，然后对电信号进行二维傅里叶变换，进而计算出变频器输出电信号的谐波成分并通过仿真对变频器模型进行了模拟计算；再根据电机学理论，计算出变频电机气隙磁场径向磁感应强度的表达式，进而推导出变频激励下电机径向电磁力波的频率特性，接着采用电磁-固-声多场耦合仿真分析了电机在变频驱动时的电磁振动噪声规律。最后通过对某大型电机稳态运行下的振动噪声进行实际测量，验证了本文分析模型的准确性。
正弦脉宽调制（Sinusoidal Pulse Width Modu- lation, SPWM）是电机中使用较为成熟广泛的方法，被广泛地应用于各行业的驱动电机控制当中[15-17]，常见的三相SPWM变频方式的逆变电路如图1a所示。图中，U、V、W为电压的三相桥臂，而S1～S6为逆变电路的6个开关，同相的两个开关同一时刻只能打开1只，Ud为直流侧的电压源，一般由整流电路滤波后输出，通过控制6个开关的通断，可以在输出端得到交变电流，在SPWM中，开关的通断由一系列正弦排列的脉冲控制，输出的信号在经过滤波电路后，便可以得到近似正弦变化的电信号[18]。
图1 逆变电路与调制信号示意图
Fig.1 Invert circuit and modulation signal
控制U相开关的调制信号如图1b所示。开关信号由三角载波信号与调制波正弦信号共同控制，当三角波信号幅值大于正弦信号时，S1闭合，UO间电动势为0，否则S1断开，UO间电动势为Ud。单位幅值的三角载波信号ftr的数学模型[18]为
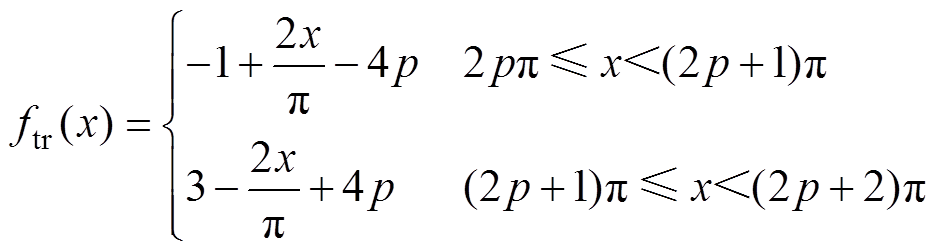
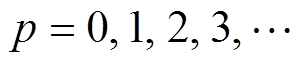（1）
为了保留调制波与载波的频率特性，方便后续对二者关系的讨论，此处对信号的横坐标进行了变量代换，其中，x=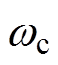
t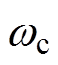，为载波频率，即开关频率，t为时间。
同理可以写出调制波信号fsin的数学表达式为
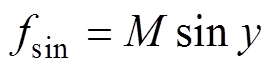（2）式中，M为调制波的幅值，也称为调制比；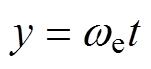
，
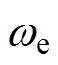为调制波的频率，即变频器期望输出的电信号频率[18]。
UO之间的电压可以表示为
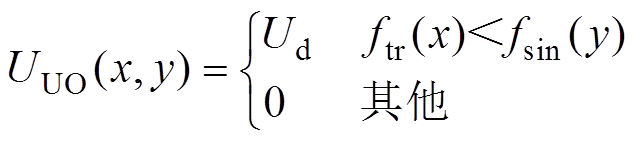（3）对电信号UUO进行二维傅里叶变换可以得到包含x、y的谐波分量，从而分析调制频率以及开关频率对变频输出的影响为
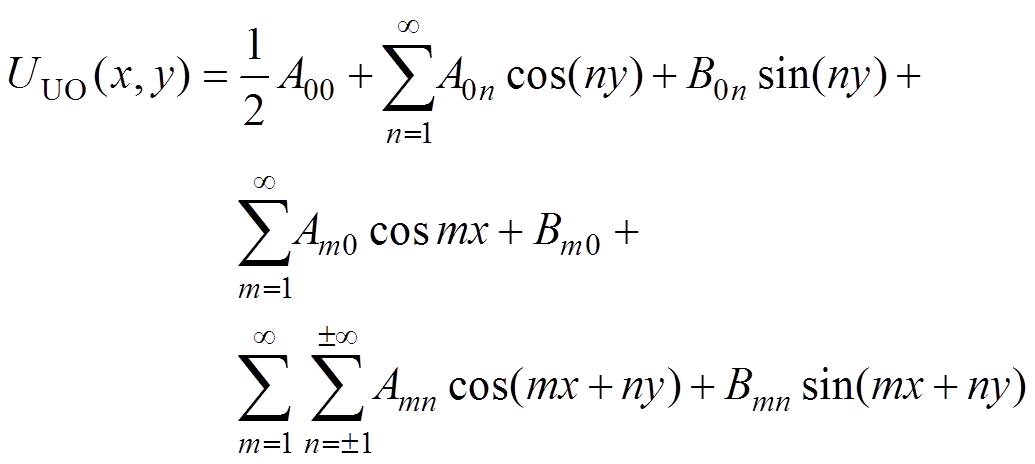（4）
式中，A、B分别为谐波系数，下标表示阶次；m为与调制频率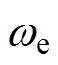有关的谐波阶次；n为和开关频率
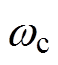有关的谐波阶次。令
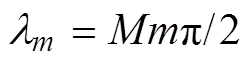，系数项可以通过积分求得，变频输出的相电压存在以下几种情况：
（1）直流分量。m=0, n=0。
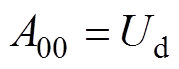（5）（2）与调制频率we有关的谐波项。m=0, n≠0。
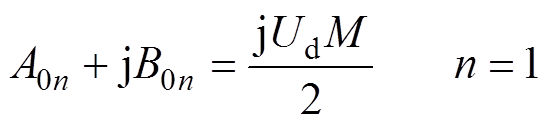（6）
（3）与开关频率wc有关的谐波项。m≠0。
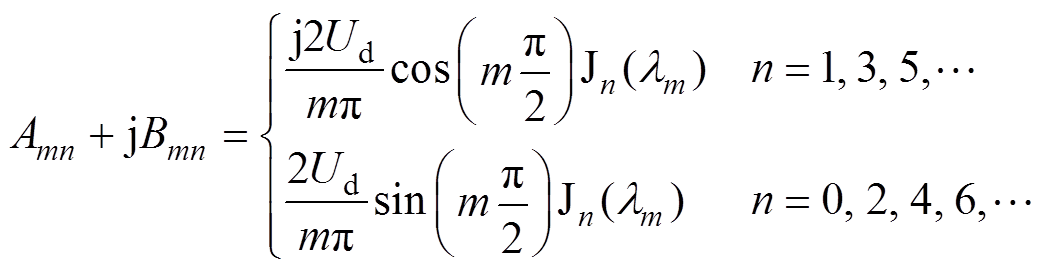（7）式中，Jn为n阶第一类贝塞尔函数。
从各谐波系数的表达式可以看出，变频输出的交流信号主要包含调制频率we的正弦信号，除此之外，由于变频调制的影响，在开关频率wc附近会产生大量的谐波。将调制波信号相位增加2p/3，代入式（4）中，即可得到V相电压UUO(x, y)，然后对两相电压做差，可以得到变频器的线电压UUV(x, y)。
由于V相电压的表达与本节前述分析相似，此处不再赘述，仅对输出线电压输出UUV(x, y)的频率特性进行陈述。输出信号主要包含两种类型的谐波：
（1）与调制频率we有关的谐波项。m=0, n≠0。
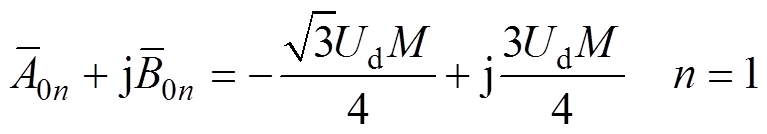（8）（2）与开关频率wc有关的谐波项。m≠0。
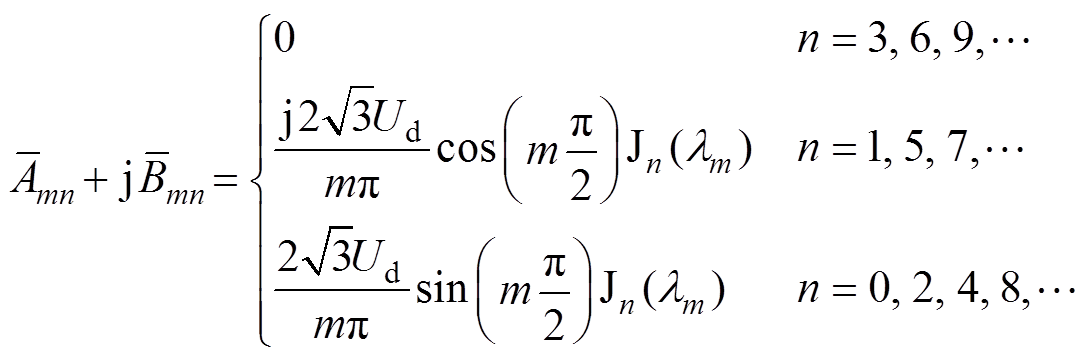（9）
可以看到，输出线电压幅值为相电压的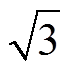
倍，且谐波特性与线电压基本一致，主要集中在开关频率附近。
本文建立SPWM模式变频器的逆变电路的模拟器，变频电路输出信号频谱如图2所示，并和解析结果进行对比。所仿真三相变频器的调制频率为28Hz，载波频率即开关频率设置为10kHz，外接滤波电感为5×10-4F，仿真结果如图2所示。所仿真变频器的输出信号的频率特性与解析模型的结果保持一致，相电压除了调制频率28Hz处的信号外，在开关频率10kHz以及附近会产生幅值较高的谐波信号，这些信号会导致变频电机既产生低频电磁力，又产生高频电磁力，进而辐射出以两个频段为主的电磁噪声。幅值上仿真结果会低于解析结果，这是因为在解析模型中，并未考虑外接滤波电路对输出信号的影响，滤波电路的耗能元件会使结果变低，同时也会在调制频率附近引入这些元器件的频率，但从图2中可以看出，这些频率的信号幅值可以忽略不计。
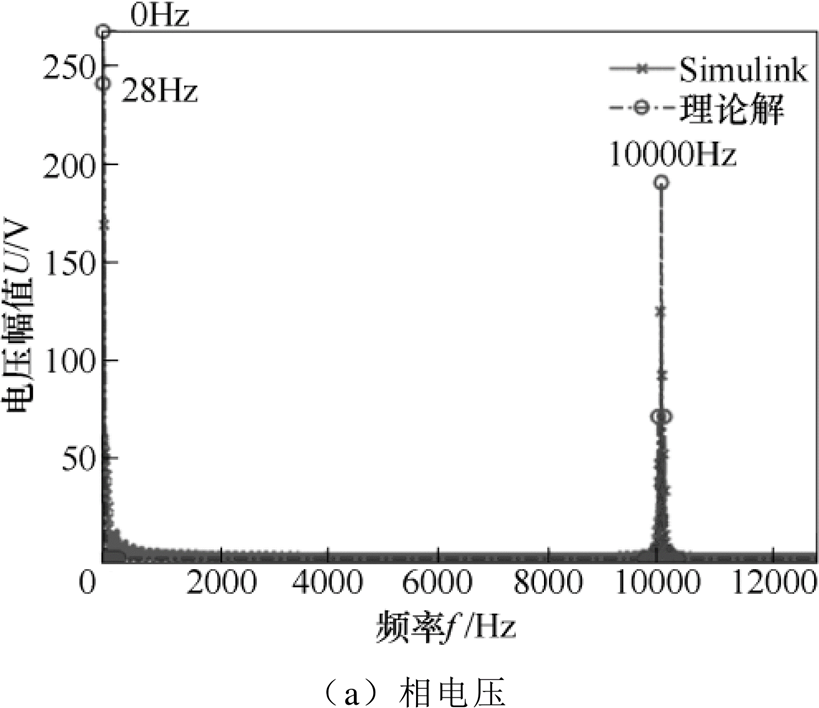
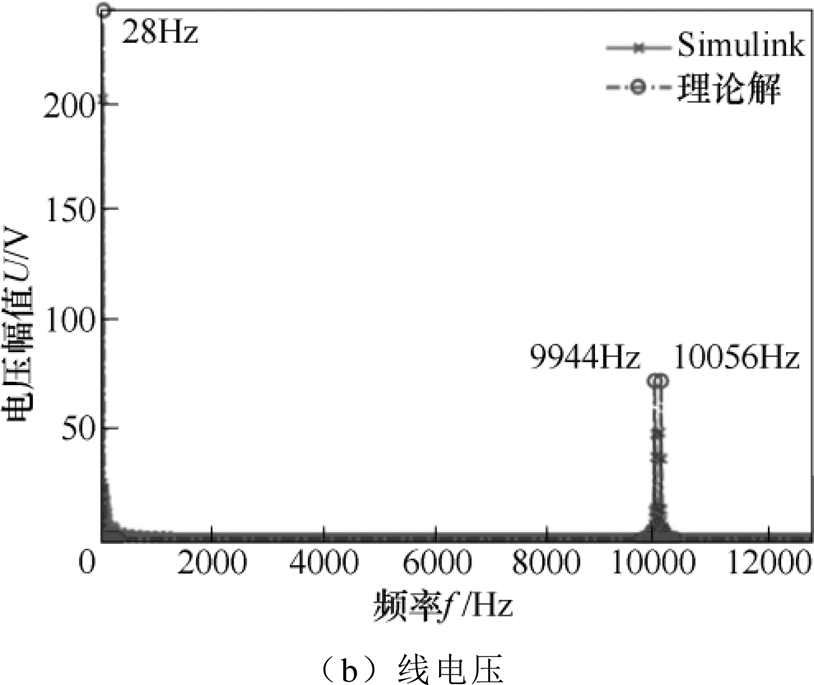
图2 变频电路输出信号频谱
Fig.2 Output spectrum of the simulation
电机气隙磁场主要由定子绕组电流感应出的磁场以及转子永磁体或绕组感应的电流合成。将定子沿母线方向展开，以旋转角q 作为横坐标，由电机学理论，气隙中的径向磁感应强度可以由气隙磁导Y与磁动势Fr的乘积表示[1]，有
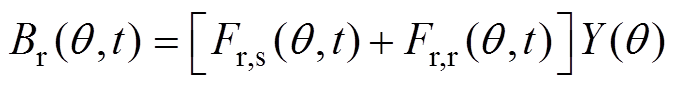（10）由定子三相绕组电流感应出的径向磁动势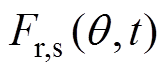
可由安培环路积分计算得到，并通过傅里叶级数展开成谐波形式为
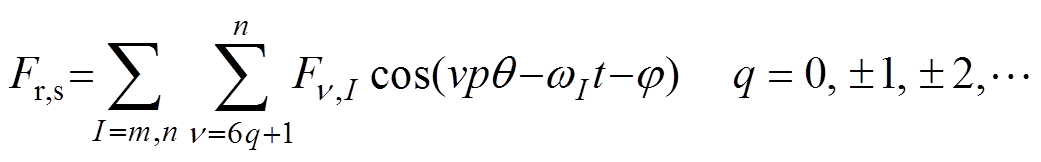（11）
式中，p为变频电机的极对数；v为磁动势的空间谐波阶数；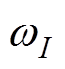
为定子绕组输入电流的频率，第1.2节中已经分析了变频器的输出信号，主要包含调制频率we与载波频率wc信号；
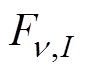为对应磁动势谐波的幅值，主要与绕组系数以及电流幅值有关；
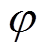为定转子磁动势的夹角。
由永磁体构成的转子产生的磁动势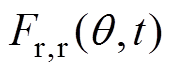
可以通过傅里叶级数展开[19]为
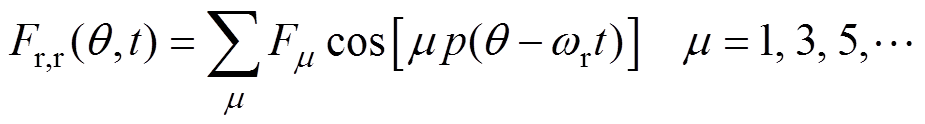（12）式中，m 为转子磁动势空间谐波的阶次；wr为电机转速，永磁电机的转速与定子绕组基波电流的关系为we=pwr。
电机气隙磁导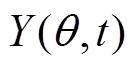
的近似解析表达式[1]为
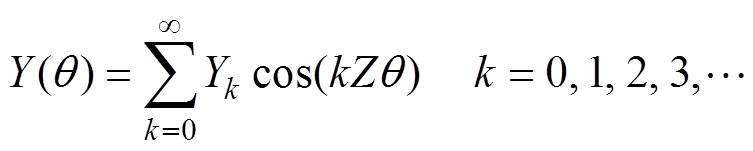（13）式中，Z为电机定子的槽数。
将式（11）～式（13）代入式（10）中，可以得到变频电机气隙的径向磁感应强度表达式为
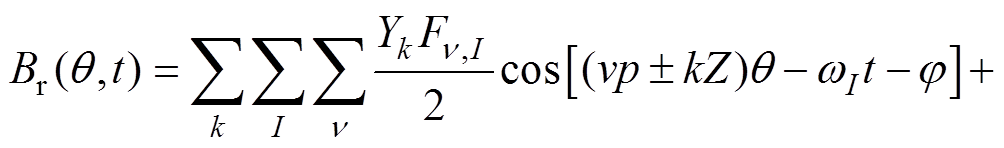
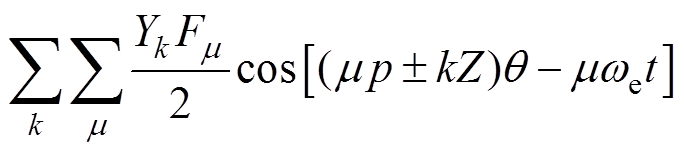（14）
从式（14）中可以看出，变频电机的气隙磁场空间谐波阶次主要为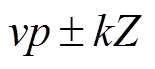
、
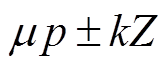阶，对于整数槽电机，槽数Z为电机极对数的偶数倍，而v、m 的取值均为奇数，因此气隙磁场空间谐波阶次
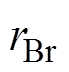可以表示为极对数p的奇数倍：
，
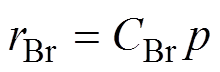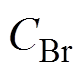= 1, 3, 5,…。时间谐波则主要包括m （m 为奇数）倍绕组电流频率，以及开关频率wc处的谐波。
根据麦克斯韦应力张量理论，电机气隙单位面积上的电磁激励力可用径向应力张量表示[12]为
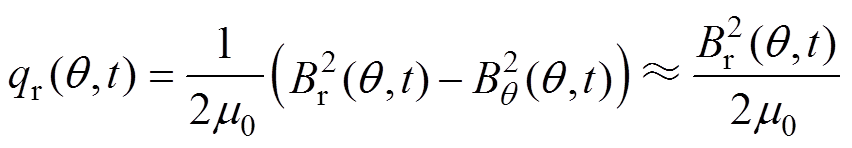（15）式中，m0为真空中的介电常数。由于气隙中磁感线的方向主要沿径向，切向磁感应强度可以忽略不 计[20]，因此可以认为，径向电磁激励力主要与径向磁感应强度有关。
将式（14）计算得到的变频电机气隙磁场代入式（15），可以得到变频电机电磁激励力的表达式为
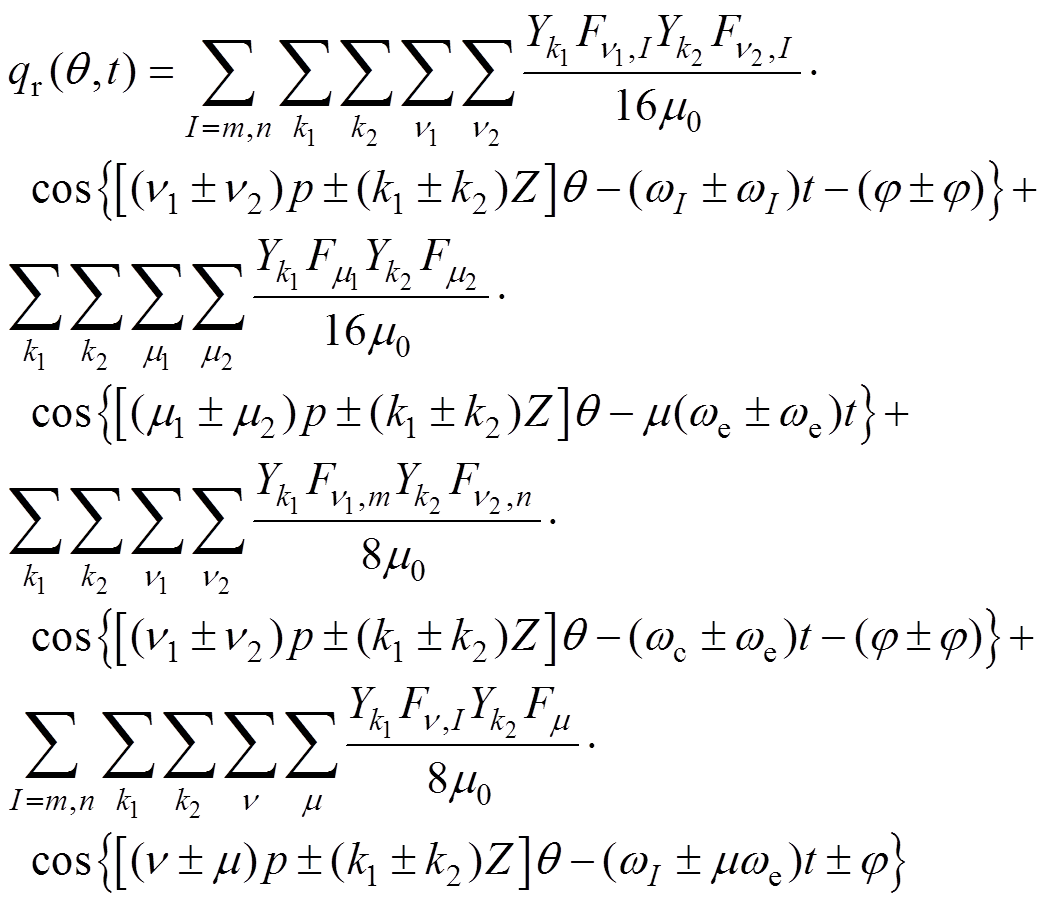（16）式中，正负号是由积化和差公式推导而来，与时间项t有关的频率分别为0, 2we, (m ±1)we, wc±we, wc±mwe, 2wc。由于m 为奇数，因此除直流分量外，低频部分的电磁力谐波频率主要为2倍输入电流基频的倍频，高频电磁力的频率则主要分布在开关频率wc两边，与开关频率相差奇数倍的电流基频。而从表达式中空间角度q 项的系数也可分析出电磁力的空间谐波阶次，由于v、m 均为奇数，同时整数槽电机中，槽数Z是极对数p的整数倍，因此电磁力的空间谐波阶次可以表示为极对数p的偶数倍，即rqr=Cqrp，Cqr=0, 2, 4,…。
变频电机作为一多自由度系统机械系统，其振动动力学模型可以用多自由度振动方程表示[12]为
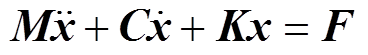（17）式中，M、C、K分别为变频电机结构的质量、阻尼以及刚度矩阵，由结构以及材料的机械特性决定；x为电机的多自由度位移向量，向量上的点表示对位移求导；F为电机受到的外力向量，在电磁振动中即为2.2节分析的电磁激励力。
通过式（17）求得电机表面的位移以及振速后，根据空气中波动方程可求解出变频电机在电磁激励力作用下辐射的噪声[11]，有
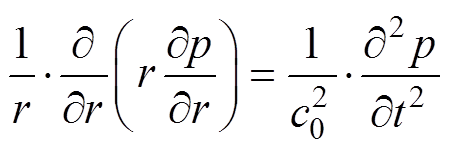（18）式中，r为柱坐标系，由于变频电机外形主体为圆柱形，因此用柱坐标系求解更为合适；p为声压；c0为空气中的声速。求解时需将变频电机表面的振动信号作为边界条件。
为验证变频激励下，前述电磁激励特性分析的正确性，同时研究调制频率和开关频率谐波对电机振动噪声的影响。以一台永磁同步电机为例，进行电磁-固-声多场耦合仿真，电机参数见表1。
本文建立的电机电磁有限元模型如图3所示。模型中的完美匹配层（Perfectly Matched Layer, PML）用于截断边界设置。电机对应的绕组电流调制频率为fe=pn/60=28Hz。首先进行时域的电磁场仿真，将频率为调制频率的正弦波电流和变频器开关频率10kHz的时间谐波电流输入到定子绕组中，计算气隙的磁场分布情况，进而计算气隙的电磁力。然后将时域电磁力信号进行傅里叶变换，施加到定子齿边界上，进行声-固耦合仿真。
表1 仿真电机参数
Tab.1 Parameters of the simulated motor
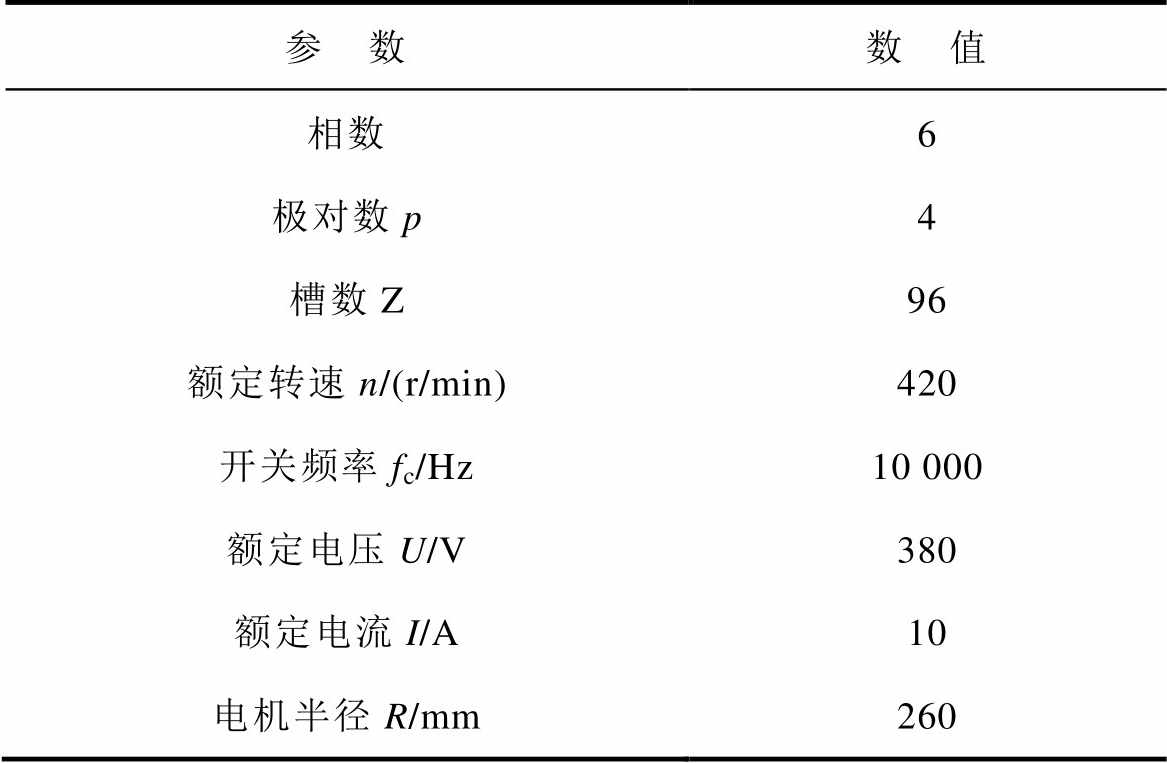
参 数数 值 相数6 极对数p4 槽数Z96 额定转速n/(r/min)420 开关频率fc/Hz10 000 额定电压U/V380 额定电流I/A10 电机半径R/mm260
图3 电磁-固-声多场耦合有限元模型
Fig.3 The electromagnetic-solid-acoustic coupling finite element model
电磁仿真得到的变频电机气隙磁场时域频谱与空间阶次谱如图4所示，傅里叶变换的频段为0～12 800Hz，频域分辨率为4Hz，阶次谱主要展示了气隙磁场前50阶的空间特性。
气隙磁场时间与空间谐波的仿真结果与2.1节推导一致，低频磁场主要包含调制频率fe=28Hz以及奇数倍的谐波信号，flow=Cf fe，Cf=1, 3, 5,…；高频磁场集中于开关频率fc=10kHz附近。磁场的空间阶次则为极对数4的奇数倍。
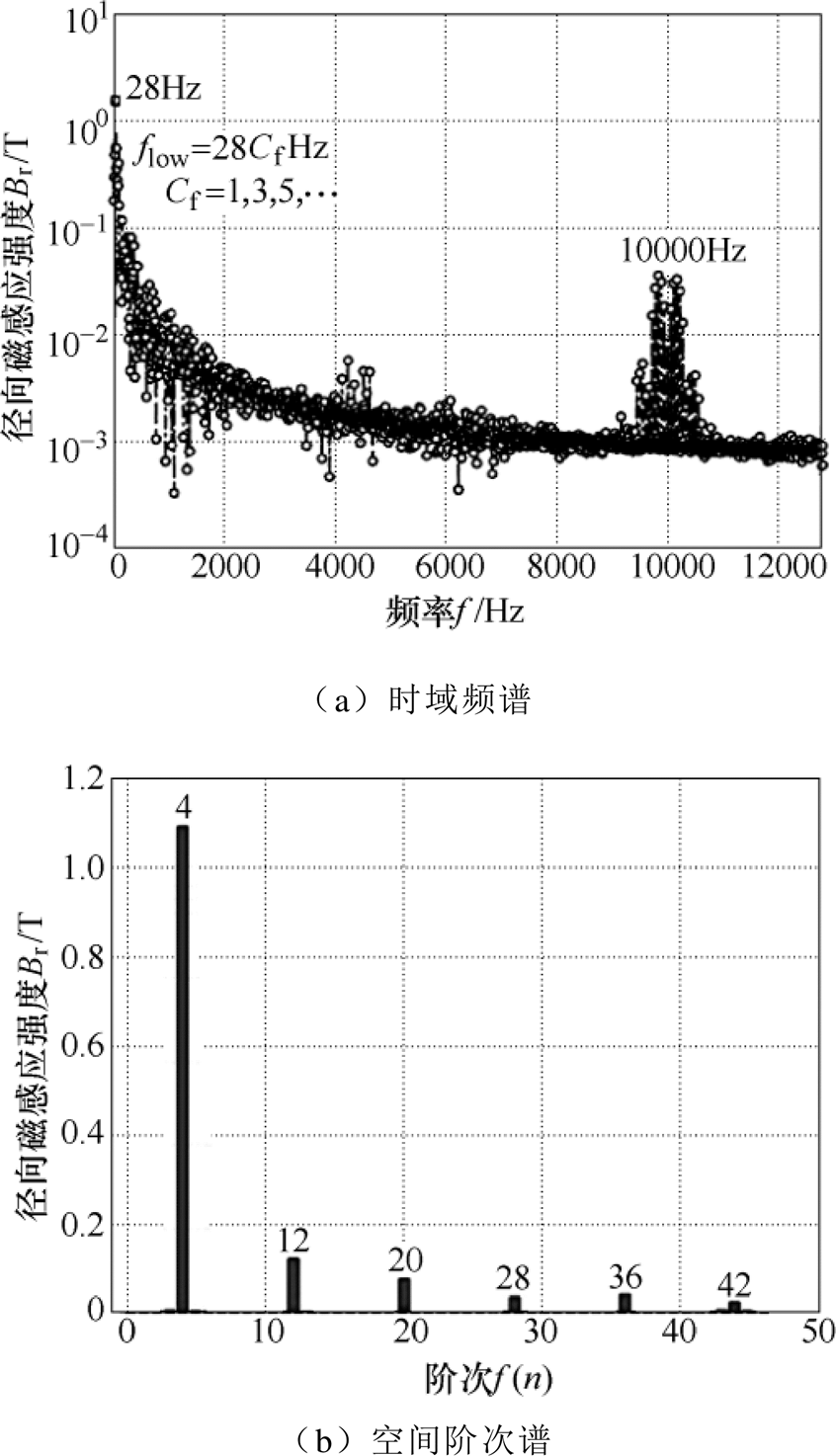
图4 变频电机径向气隙磁场频谱
Fig.4 Spectrum of the magnetic flux
变频电机径向电磁激励力仿真频谱如图5所示，由于频率为0的电磁力分量并不会使电机产生振动，因此不对其进行特别说明。除直流分量外，低频电磁力的频率主要为2倍调制频率56Hz的倍频，与2.2节变频电机的电磁力特性分析一致，高频部分的电磁力则与开关频率与调制频率有关，对应关系如2.2节推导fhigh=fc±m fe，m =1, 3, 5,…。电磁力的空间阶次则为电机极数8的整数倍，与2.2节的分析结果一致。
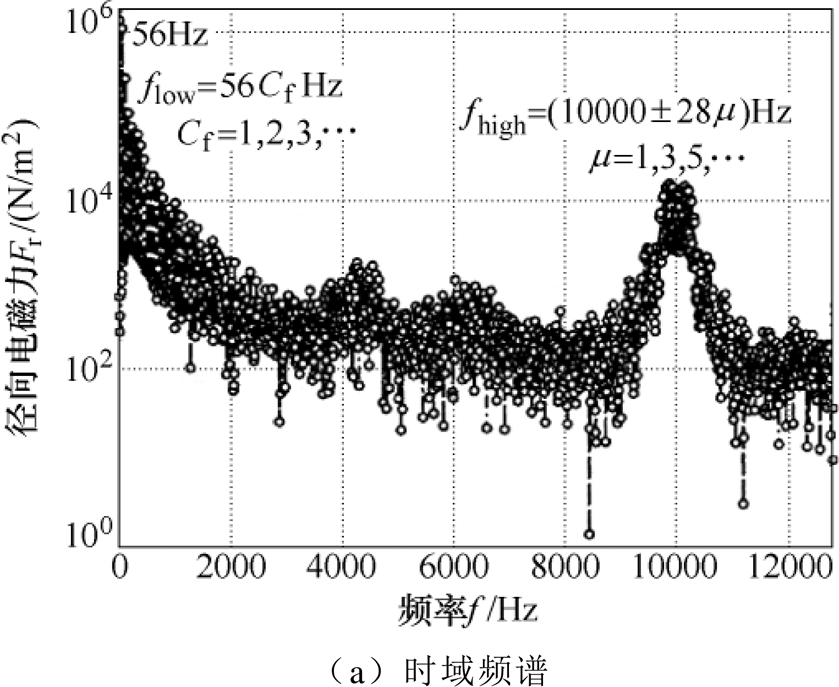
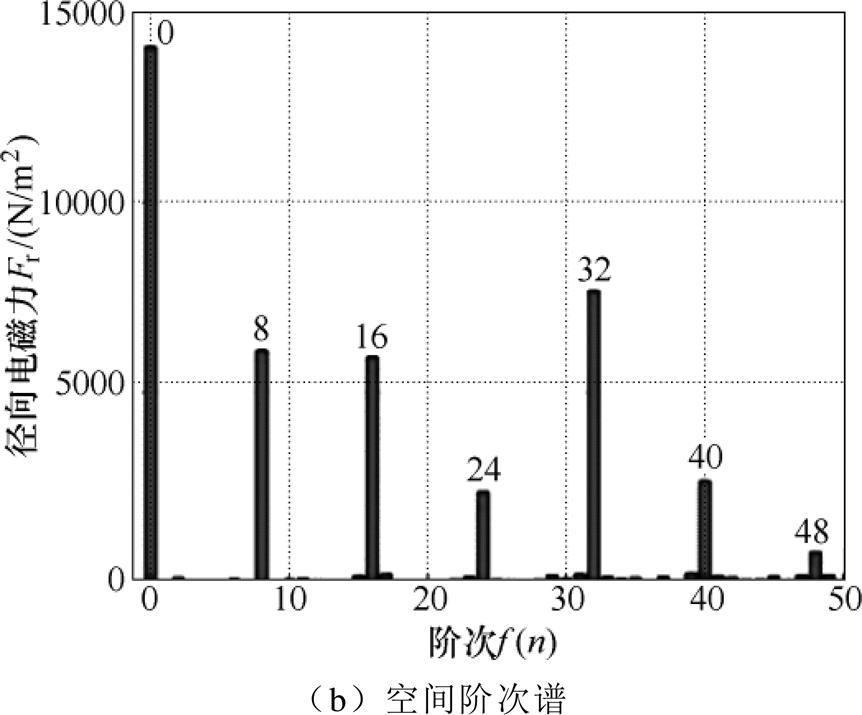
图5 变频电机径向电磁激励力仿真频谱
Fig.5 Spectrums of the electromagnetic force
将电磁仿真计算的电磁力进行傅里叶变换施加到定子齿上，通过声固耦合仿真计算变频电机辐射出的振动噪声，为了对比变频驱动对电机振动噪声信号产生的影响，对同一永磁电机仅输入调制频率电流信号进行仿真，作为对照，仿真得到的变频电机的振动频谱与辐射声功率级频谱如图6所示。
图6 变频电机振动位移响应与辐射噪声声功率级对比结果
Fig.6 The comparison of vibration response and radiated acoustic response
从声固耦合仿真的结果可以看出，振动噪声在低频部分与电磁激励力的频率特性一致，主要为2倍绕组调制电流频率56Hz的倍频。而在振动噪声的高频部分，变频谐波的存在会激励电机产生密集的高频电磁激励力。由于定子的刚度大，在高频处会有密集的模态分布，因此在变频激励下定子结构更容易与电磁力发生频率共振。
为了检验2.2节理论推导与有限元模型的准确性，测量了变频激励下永磁同步电机的响应。实验电机参数与仿真电机参数一致。本文基于声压法测量了该电机空载稳态运行下辐射的声功率。实测电机的控制器开关频率为10kHz，达到稳态的转速为420r/min。电机振动噪声测试现场如图7所示。
图7 电机振动噪声测试现场
Fig7 Test site of motor vibration and noise
本次噪声测试试验地点是半消实验室，图7中9个噪声测点离基准体（电机）表面的距离均为1m，按照矩形包络面布置。利用振动噪声测试系统测试的电机辐射空气噪声声功率级频谱如图8所示。为了确定变频电机辐射声功率谱的低频谐波和高频谐波的分布情况，将声功率频谱的低频部分放大，并截取开关频率附近的频谱，得到的结果如图9所示。
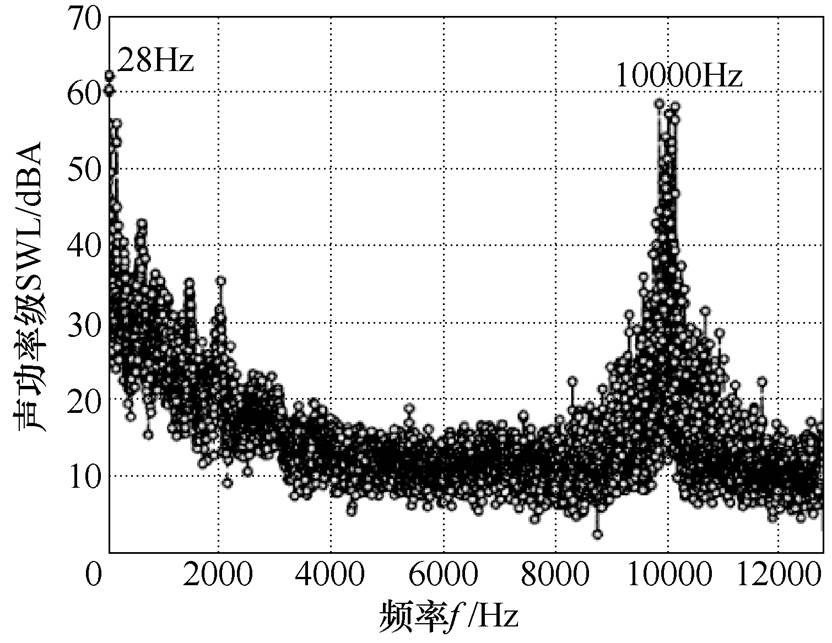
图8 实测变频电机辐射声功率级频谱
Fig8 Spectrum of measured noise power level
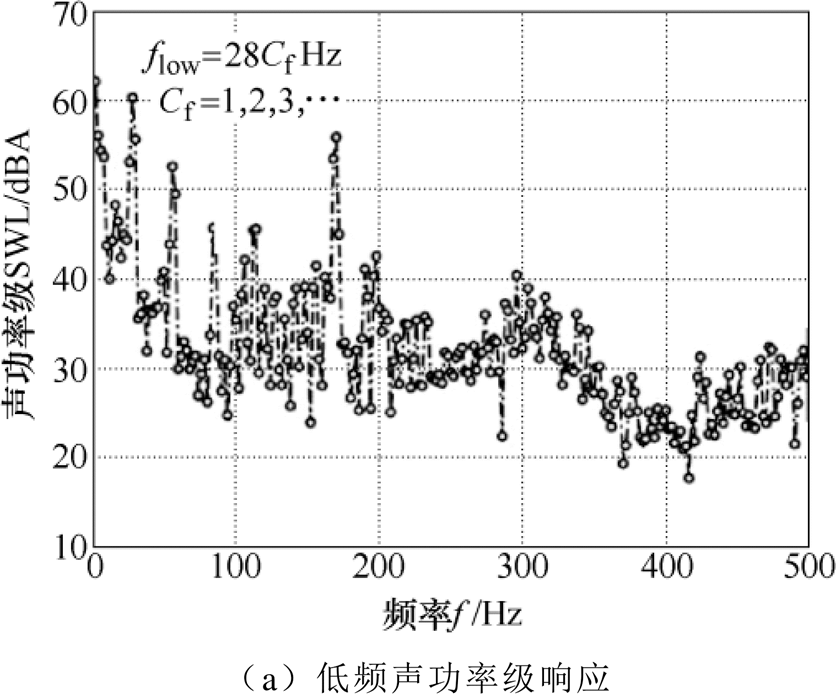
图9 电机辐射声功率局部频谱
Fig9 Partial spectrum of noise power level
由图9可知，电机辐射的噪声在低频部分包含以28Hz为基频的一系列谐波。而高频噪声则是集中在变频器开关频率及其倍频附近。但实验测得的声功率级幅值与仿真略有差异，本文认为原因在于，仿真没有考虑电机的机脚、端盖等结构的辐射噪声，因此仿真结果和实验结果有误差也是可以接受的。但是在噪声频率成分上与2.2节的理论和4.1节的仿真分析部分结果一致。说明本文提出的变频电机振动噪声分析模型可以有效地估计电机辐射噪声的频率成分。且从频谱上可以看到，高频噪声会成为变频电机噪声的主要成分。若能对变频产生的低频和高频谐波进行抑制，可使变频电机振动噪声性能得以提升。
本文对变频驱动下电机的电磁振动噪声特性进行了研究。从推导SPWM变频模型的输出谐波开始，到最后通过实验检验所提模型的准确性。得出了以下结论：
1）本文从变频器的输出信号谐波到变频电机的电磁振动噪声的频率特性建立了完整的模型，为变频电机的设计和振动噪声预报，提供了一种高效 手段。
2）变频器输出的信号主要包含调制频率fe信号以及开关频率fc附近的谐波信号，低频部分无谐波成分。
3）变频激励时，电机的电磁激励力频率主要为2倍调制频率2 fe的倍频，高频段则受调制频率与开关频率共同影响，主要电磁力频率分布为fc±k fe，k=1, 3, 5,…。
4）从多场仿真和实验测量结果看出，变频器输出谐波会使变频电机辐射出大量频率的噪声，使得电机更易发生频率共振，在设计时须予以重视。
参考文献
[1] 陈永校, 诸自强, 应善成. 电机噪声的分析和控制[M]. 杭州: 浙江大学出版社, 1987.
[2] 郑江, 代颖, 石坚. 车用永磁同步电机的电磁噪声特性[J]. 电工技术学报, 2016, 31(增刊1): 53-59.
Zheng Jiang, Dai Ying, Shi Jian. Electromagnetic noise characteristics of permanent magnet synchronous motor applied in electric vehicle[J]. Transactions of China Electrotechnical Society, 2016, 31(S1): 53-59.
[3] Wallace A K, Spee R, Martin L G. Current harmonics and acoustic noise in AC adjustable-speed drives[J]. IEEE Transactions on Industry Applications, 1990, 26(2): 267-273.
[4] Zhu Ziqiang, Howe D. Instantaneous magnetic field distribution in permanent magnet brushless DC motors. IV. magnetic field on load[J]. IEEE Transa- ctions on Magnetics, 1993, 29(1): 152-158.
[5] Lo W C, Chan C C, Zhu Z Q, et al. Acoustic noise radiated by PWM-controllel induction machine drives[J]. IEEE Transactions on Industrial Electro- nics, 2000, 47(4): 880-889.
[6] Le Besnerais J, Lanfranchi V, Hecquet M, et al. Characterization and reduction of audible magnetic noise due to PWM supply in induction machines[J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): 1288-1295.
[7] Asano Y, Honda Y, Murakami H, et al. Novel noise improvement technique for a PMSM with con- centrated winding[C]//Proceedings of the Power Conversion Conference-Osaka, Osaka, Japan, 2002: 460-465.
[8] 唐任远, 宋志环, 于慎波, 等. 变频器供电对永磁电机振动噪声源的影响研究[J]. 电机与控制学报, 2010, 14(3): 12-17.
Tang Renyuan, Song Zhihuan, Yu Shenbo, et al. Study on source of vibration and acoustic noise of permanent magnet machines by inverter[J]. Electric Machines and Control, 2010, 14(3): 12-17.
[9] 毛钰, 左曙光, 邓文哲, 等. 基于实测相电流的永磁同步电机转矩波动阶次来源分析及幅值预测[J].振动与冲击, 2018, 37(15): 239-245.
Mao Yu, Zuo Shuguang, Deng Wenzhe, et al. Order analysis and amplitude prediction of torque ripple in hub permanent magnet synchronous motors based on measured phase current[J]. Journal of Vibration & Shock, 2018, 37(15): 239-245.
[10] Ruiz-Gonzalez A, Vargas-Merino F, Perez-Hidalgo F, et al. Low switching PWM strategy to reduce acoustic noise radiated by inverter-fed induction motors[J]. IEEE International Symposium on Industrial Elec- tronics, Bari, 2010: 1353-1358.
[11] Binojkumar A C, Saritha B, Narayanan G. Acoustic noise characterization of space-vector modulated induction motor drives-an experimental approach[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3362-3371.
[12] 林福, 左曙光, 毛钰, 等. 考虑电流谐波的永磁同步电机电磁振动和噪声半解析模型[J]. 电工技术学报, 2017, 32(9): 24-31.
Lin Fu, Zuo Shuguang, Mao Yu, et al. Semi- analytical model of vibration and noise for permanent magnet synchronous motor considering current harmonics[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 24-31.
[13] 李文, 赵慧敏, 邓武. 变频器驱动异步电机振动频谱特征分析[J]. 电机与控制学报, 2012, 16(8): 67-73.
Li Wen, Zhao Huimin, Deng Wu. Analysis of vibration spectrum characteristics for asynchronous motor driven by inverter[J]. Electric Machines and Control, 2012,16(8): 67-73.
[14] Wang Chong, Astfalck A, Lai J C S. Sound power radiated from an inverter-driven induction motor: experimental investigation[J]. IEE Proceedings- Electric Power Applications, 2002, 149(1): 46-52.
[15] 陈娟, 何英杰, 王新宇, 等. 三电平空间矢量与载波调制策略统一理论的研究[J]. 中国电机工程学报, 2013, 33(9): 71-78.
Chen Juan, He Yingjie, Wang Xinyu, et al. Research of the unity theory between three-level space vector and carrier-based PWM modulation strategy[J]. Proceedings of the CSEE, 2013, 33(9): 71-78.
[16] 佟文明, 王云学, 贾建国, 等. 变频器供电内置式永磁同步电机转子损耗计算与试验[J]. 电工技术学报, 2018, 33(24): 5811-5820.
Tong Wenming, Wang Yunxue, Jia Jianguo, et al. Calculation and experimental research on the rotor loss of interior permanent magnet synchronous motors with converter supply[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5811- 5820.
[17] 刘国海, 宋成炎, 徐亮, 等. 基于SVPWM的五相永磁同步电机两相开路故障容错控制策略[J]. 电工技术学报, 2019, 34(1): 23-32.
Liu Guohai, Song Chengyan. Xu Liang, et al. SVPWM- based fault-tolerant control strategy under two-phase open-circuit fault of five-phase permanent-magnet synchronous motor[J]. Transactions of China Electro- technical Society, 2019, 34(1): 23-32.
[18] 刘松. 电力拖动自动控制系统[M]. 北京: 清华大学出版社, 2006.
[19] 肖士勇, 戈宝军, 陶大军, 等. 同步发电机定子绕组匝间短路时转子动态电磁力计算[J]. 电工技术学报, 2018, 33(13): 56-62.
Xiao Shiyong, Ge Baojun, Tao Dajun, et al. Calcu- lation of rotor dynamic electromagnetic force of synchronous generator under the stator winding interturn short circuit fault[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 56-62.
[20] Guo Xiaoqiang, Zhong Rui, Zhang Mingshu, et al. Improved model of radial vibration in switched reluctance motor including magnetic saturation[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2018, 2(4): 363- 370.
The Effect of Harmonics on Electromagnetic Vibration and Noise Characteristic in Inverter-Duty Motor
Abstract The vibration and noise characteristics of the inverter-duty motor are important factors affecting the application of electric products. In order to grasp the vibration and noise excitation of inverter-duty motor accurately and design low-noise inverter-duty motor, an analysis model of the vibration-noise characteristics of inverter-duty motor is established in this paper. The output of a SPWM converter is derived according to the modulation theory. Then the electromagnetic force in a motor is calculated based on Maxwell's Law and a coupled multi-physics FEM simulation model is built. Finally, by comparing the measured sound power of the motor, the results show that the harmonics of motor vibration noise in the low-frequency part are generated by the modulation frequency of the motor, and the high-frequency harmonics introduced by the inverter cause the motor to radiate a lot of noise near the switching frequency. Therefore, the design of low-noise inverter-duty motors needs to consider eliminating or weakening these harmonics.
keywords：Invert-duty motor, vibration and noise, harmonics of frequency, electromagnetic-solid- acoustic coupling simulation
中图分类号：TM344.6
DOI: 10.19595/j.cnki.1000-6753.tces.201272
国家自然科学基金资助项目（11874262）。
收稿日期 2020-09-19
改稿日期 2021-02-03
肖 阳 男，1982年生，高级工程师，研究方向为船舶电机。E-mail: 13971278912@139.com
蒋伟康 男，1961年生，教授，博士生导师，研究方向为噪声振动分析与控制。E-mail: wkjiang@sjtu.edu.cn（通信作者）
（编辑 崔文静）