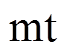 坐标系)下的交流异步电机数学模型,具体为
坐标系)下的交流异步电机数学模型,具体为摘要 为了提高交流异步电机在参数摄动和负载扰动下的位置跟踪控制性能,该文提出一种基于浸入与不变(I&I)理论的自适应控制方法。首先,通过构造非线性扩张状态观测器(NLESO)对系统的负载扰动进行动态观测,提高系统的跟踪控制精度;其次,基于I&I理论对系统的摄动参数设计自适应估计器,实现参数估计值渐近收敛到真实值;再次,基于I&I理论分别完成交流异步电机位置和磁链跟踪控制器的设计,实现对系统给定值的精确跟踪控制;最后,将该文所提方法与动态面控制(DSC)方法和I&I控制方法进行仿真及实验对比研究,结果验证了该文所提方法的有效性和可行性。
关键词:交流异步电机 自适应位置跟踪控制 浸入与不变理论 非线性扩张状态观测器
交流异步电机具有结构简单、体积小、运行成本低、可靠性高、维护方便等优点,在化工、纺织、冶金、建筑、农机、矿山等行业有着广泛应用,对我国的国民经济和人民生活有着密切联系和重要影响[1-3]。然而,交流异步电机具有多变量、非线性、强耦合等特征[4],且易受负载扰动和参数摄动等不确定因素的影响,给交流异步电机的分析和控制带来了一定的挑战。
为了实现交流异步电机在参数摄动和负载扰动下的位置跟踪控制,国内外许多学者进行了广泛而深入的研究。文献[5]通过对转子电阻等电机参数进行自适应估计,设计的复合自适应无源控制器有效提高了系统对参数摄动和负载扰动的鲁棒性;文献[6]基于严格正实理论设计的自适应控制器,实现了系统在未知电机参数和负载转矩下的位置跟踪控制;文献[7]基于广义预测理论设计的控制器,有效抑制了交流异步电机的稳态波动,提高了系统的抗干扰能力;文献[8]结合滑模增益自适应律和负载转矩观测器,设计的自适应滑模控制器有效增强了系统在负载扰动下的跟踪控制性能;文献[9]采用神经网络逼近系统的未知非线性函数,设计的自适应神经网络控制器有效提高了系统的跟踪控制精度;文献[10]利用模糊逻辑系统逼近系统的非线性项,设计的自适应模糊控制器有效抑制了参数摄动和负载扰动对系统性能的影响。
需要说明的是,文献[5-10]提出的控制方法虽然实现了交流异步电机在参数摄动和负载扰动下的位置跟踪控制,但也存在一些不足:一是控制器设计过程较复杂,如文献[6]中的坐标变换增加了控制器推导过程的复杂度;文献[7]中预测控制方法的在线计算量较大,可调参数较多;文献[9]综合了反步控制、神经网络和指令滤波器等方法,增加了控制器结构的复杂性,且不易验证其在实际系统中应用的可行性。二是自适应设计方法基于常规的确定等价原则,且无法与控制器设计分开进行,不便于系统控制参数的整定,如文献[5]将自适应与无源理论相结合;文献[6]将自适应与严格正实方法相结合;文献[8]将自适应与滑模控制相结合。由此,控制器设计过程的复杂性,以及自适应律设计对控制器的依赖,均在一定程度上限制了上述控制方法在实际系统中的应用。
与上述方法不同,A. Astolfi和R. Ortega于2003年提出的浸入与不变(Immersion and Invariance, I&I)理论[11]不但可以处理非线性系统的镇定问题,还可以解决非线性系统摄动参数的自适应估计问题,并且系统控制器设计和自适应估计器设计可以分开进行,这在一定程度上弥补了文献[5-10]的不足。针对非线性系统的镇定问题,基于I&I理论的控制器设计方法原则上不需要构造Lyapunov函数,而是选择稳定的低阶目标系统和浸入映射,通过设计控制律将被控对象浸入到目标系统中,使得被控系统的任何轨迹都是目标系统在该浸入映射下的像,从而确保了被控系统的全局渐近稳定性。另外,针对非线性系统摄动参数的自适应估计问题,基于I&I理论的自适应估计器设计方法将调节函数引入到参数估计误差流形面中,通过使流形面具有不变性和吸引性,来保证参数估计值渐近收敛到真实值。自I&I理论提出以来,国内外许多学者对其进行了深入研究,并将其应用到四旋翼飞行器[12-13]、小型无人直升机[14]、航天发动机[15]和高超声速飞行器[16]等系统中。此外,扩张状态观测器因其结构简单、参数易于整定等优点而被广泛应用,然而常规的线性扩张状态观测器(Linear Extended State Observer, LESO)易出现“初始尖峰”现象[17],而引入了类饱和非线性误差函数的非线性扩张状态观测器(Nonlinear Extended State Observer, NLESO),不仅可以削弱LESO存在的“初始尖峰”现象,还能够保证观测误差在有限时间内收敛。
基于上述分析,针对存在参数摄动和负载扰动的交流异步电机位置跟踪控制问题,本文提出一种基于I&I理论的自适应控制方法。相比于现有控制方法,本文所提方法具有结构简单、可调参数少、易于实现等优点。设计NLESO实现对系统负载扰动的动态观测,该方法不仅能加快扰动估计的收敛速度,而且能有效削弱LESO存在的“初始尖峰”现象。基于I&I理论分别设计定子电阻的自适应估计器以及位置、磁链控制器,以实现自适应估计器和控制器的分开设计,有利于各自控制参数的调整。将本文所提方法与动态面控制(Dynamic Surface Control, DSC)方法和I&I控制方法进行仿真及实验对比研究,以验证本文所提方法能够实现交流异步电机有效的位置跟踪控制,并具有较好的动、静态性能和抗干扰能力。
考虑到按转子磁链定向的矢量控制方法能够实现交流异步电机定子电流转矩分量和励磁分量的解耦,从而获得等效的直流电机模型,便于系统控制器的设计[18-19]。因此,本文采用按转子磁链定向同步旋转正交坐标系(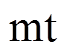 坐标系)下的交流异步电机数学模型,具体为
坐标系)下的交流异步电机数学模型,具体为
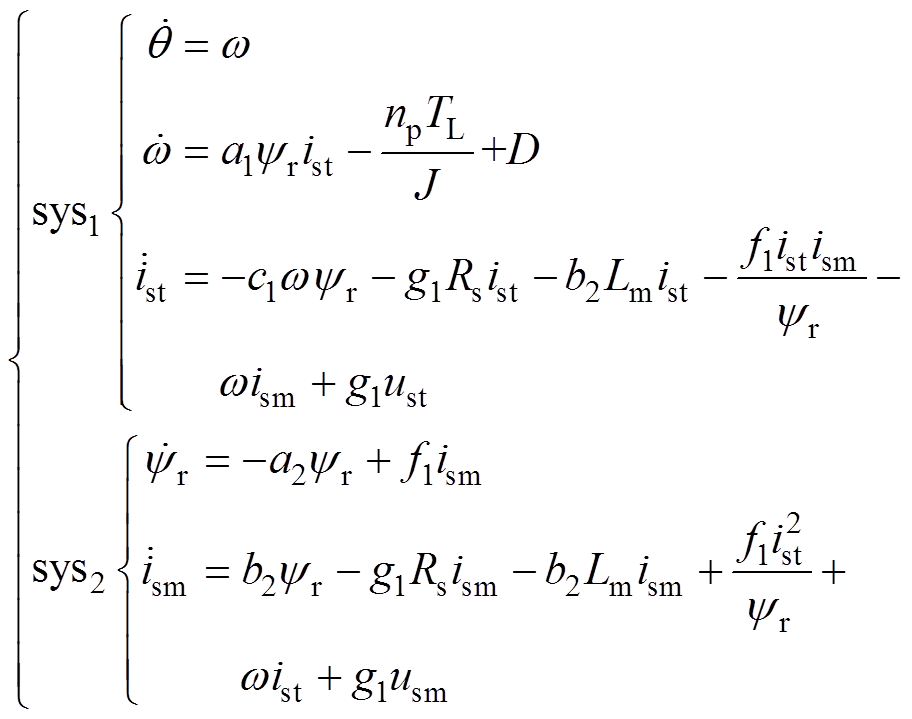 (1)
(1)式中,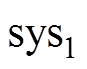 、
、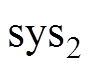 分别为交流异步电机的位置子系统和磁链子系统;
分别为交流异步电机的位置子系统和磁链子系统;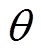 、
、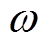 和
和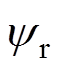 分别为转子位置、角速度和磁链;
分别为转子位置、角速度和磁链;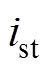 、
、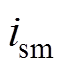 、
、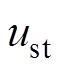 和
和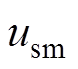 分别为沿
分别为沿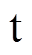 轴和
轴和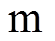 轴的定子电流分量和定子电压分量;
轴的定子电流分量和定子电压分量;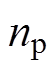 为磁极对数;
为磁极对数;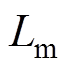 、
、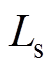 、
、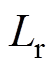 、
、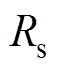 和
和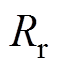 分别为互感、定、转子电感和定、转子电阻;
分别为互感、定、转子电感和定、转子电阻;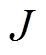 为转动惯量;
为转动惯量;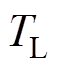 为负载转矩;
为负载转矩;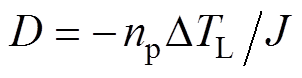 为负载扰动;其他模型参数:
为负载扰动;其他模型参数: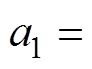
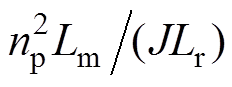 ,
,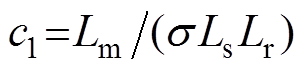 ,
,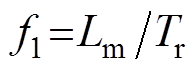 ,
,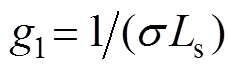 ,
,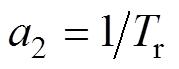 ,
,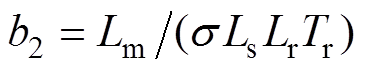 ;
;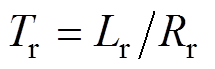 为转子电磁时间常数,
为转子电磁时间常数,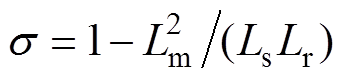 为漏磁系数。
为漏磁系数。
另外,考虑到交流异步电机的转子磁链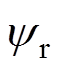 不可测,本文采用静止两相正交坐标系(
不可测,本文采用静止两相正交坐标系(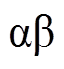 坐标系)下的电流模型来计算转子磁链,有
坐标系)下的电流模型来计算转子磁链,有
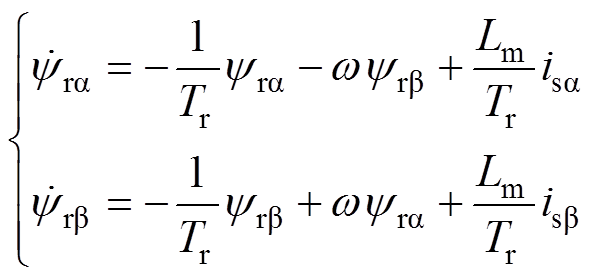 (2)
(2)式中,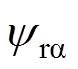 、
、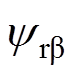 、
、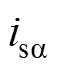 和
和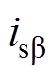 分别为沿
分别为沿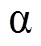 、
、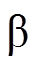 轴的转子磁链分量和定子电流分量。由式(2)采用直角坐标-极坐标变换可求得转子磁链矢量的幅值
轴的转子磁链分量和定子电流分量。由式(2)采用直角坐标-极坐标变换可求得转子磁链矢量的幅值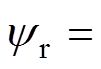
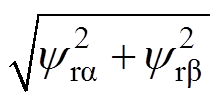 ,以及空间位置
,以及空间位置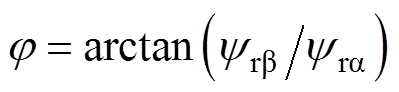 。
。
本文的控制目标是实现对交流异步电机转子位置给定值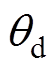 的跟踪控制,即
的跟踪控制,即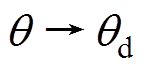 。然而由式(1)可以看出,
。然而由式(1)可以看出,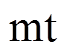 坐标系下的交流异步电机由位置子系统和磁链子系统组成,具有多变量、非线性、强耦合等特征,且受负载扰动
坐标系下的交流异步电机由位置子系统和磁链子系统组成,具有多变量、非线性、强耦合等特征,且受负载扰动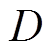 和摄动参数
和摄动参数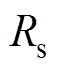 等不确定因素的影响。此外,为了实现交流异步电机精确的位置跟踪控制,需控制磁链
等不确定因素的影响。此外,为了实现交流异步电机精确的位置跟踪控制,需控制磁链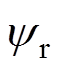 使之稳定在给定值
使之稳定在给定值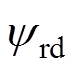 上(本文不考虑弱磁运行),即
上(本文不考虑弱磁运行),即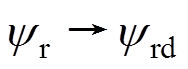 。因此,从控制理论的角度来看,交流异步电机模型式(1)的控制问题可归纳为:
。因此,从控制理论的角度来看,交流异步电机模型式(1)的控制问题可归纳为:
(1)设计干扰观测器,实现对系统模型中负载扰动的动态观测。
(2)设计参数自适应估计器,实现对系统模型中摄动参数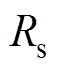 的自适应估计。
的自适应估计。
(3)分别设计交流异步电机位置和磁链控制器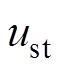 和
和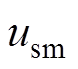 ,实现对交流异步电机精确的位置跟踪 控制。
,实现对交流异步电机精确的位置跟踪 控制。
定义1[20]:若S为状态空间中包含原点的一个区域,如果在某一特定时间后,保持在该区域内的系统的任何轨迹都最终收敛至原点,则称S为该系统的自稳定域(Self-Stable Region, SSR)。
引理1[21]:考虑系统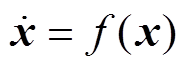 ,其中,
,其中,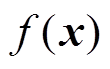 为位于原点的开邻域
为位于原点的开邻域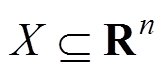 内的连续函数,并且满足
内的连续函数,并且满足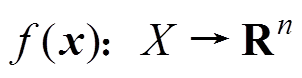 ,
,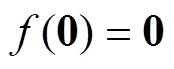 。若存在连续函数
。若存在连续函数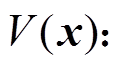
 ,使得下列条件成立:
,使得下列条件成立:
(1)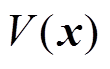 是正定的,即
是正定的,即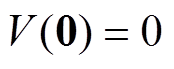 ,
,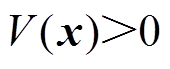 ,
,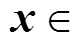
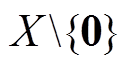 。
。
(2)存在正常数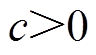 ,
,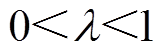 以及位于原点的一个开邻域
以及位于原点的一个开邻域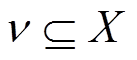 ,使得
,使得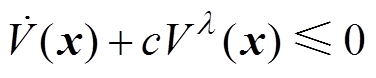 ,
,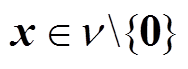 。
。
则原点是该系统的有限时间稳定平衡点,有
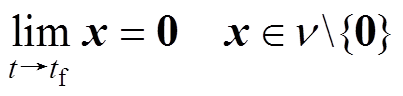 (3)
(3)并且设定时间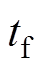 依赖于初始条件
依赖于初始条件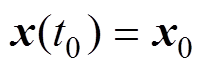 ,
,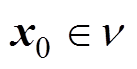 ,其表达式为
,其表达式为
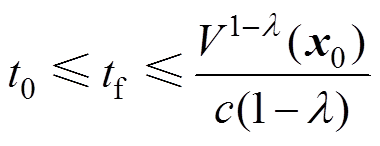 (4)
(4)
常规的LESO往往存在“初始尖峰”现象,使得系统的初始瞬态响应较差[17],而引入了类饱和非线性误差函数的NLESO可有效削弱此问题。故本节采用NLESO对系统模型式(1)中的负载扰动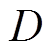 进行动态观测。
进行动态观测。
假设1: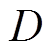 是有界的,即存在一个正常数
是有界的,即存在一个正常数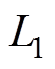 ,使得
,使得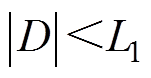 ;
;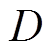 是连续可微的,且存在一个正常数
是连续可微的,且存在一个正常数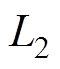 ,使得
,使得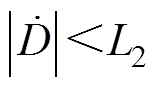 。
。
NLESO的构造形式具体为
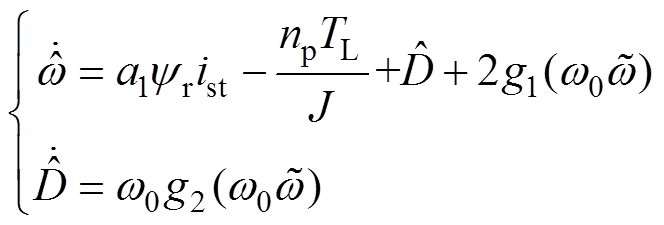 (5)
(5)式中,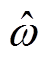 、
、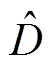 分别为角速度和负载扰动的观测值;
分别为角速度和负载扰动的观测值;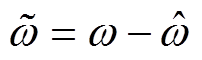 为角速度观测误差;
为角速度观测误差; 为NLESO的带宽;
为NLESO的带宽;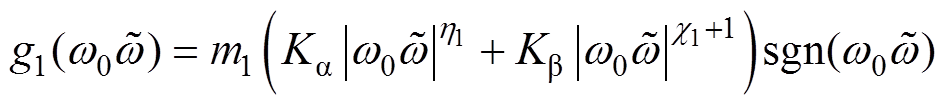 和
和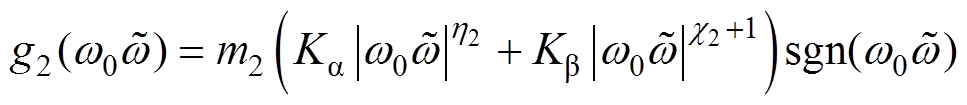 为构造的类饱和非线性误差函数,其中,
为构造的类饱和非线性误差函数,其中,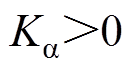 ,
,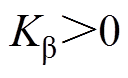 ,
,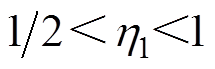 ,
,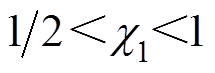 ,
,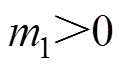 ,
,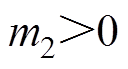 ,
,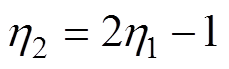 ,
,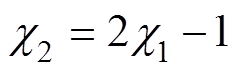 均为NLESO的参数。需要说明的是,
均为NLESO的参数。需要说明的是,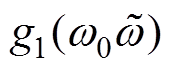 和
和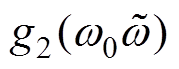 遵循“小误差,大增益;大误差,小增益”的原则,能有效减小NLESO在初始阶段较大的观测误差,进而削弱常规LESO存在的“初始尖峰”现象。
遵循“小误差,大增益;大误差,小增益”的原则,能有效减小NLESO在初始阶段较大的观测误差,进而削弱常规LESO存在的“初始尖峰”现象。
定理1:如果系统模型式(1)中的负载扰动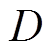 满足假设1,则所设计的NLESO式(5)是有限时间稳定的,即输出的观测值
满足假设1,则所设计的NLESO式(5)是有限时间稳定的,即输出的观测值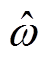 和
和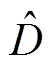 能在有限时间内收敛到真值
能在有限时间内收敛到真值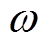 和
和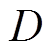 。
。
证明:所构造NLESO式(5)对负载扰动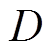 的观测误差为
的观测误差为
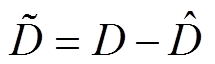 (6)
(6)进而将NLESO式(5)转化为误差形式,有
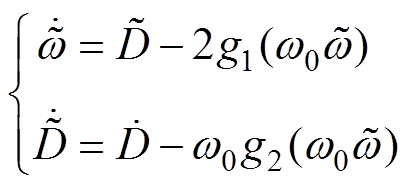 (7)
(7)
将构造的类饱和非线性误差函数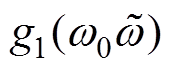 、
、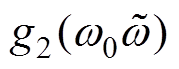 代入式(7),可得
代入式(7),可得
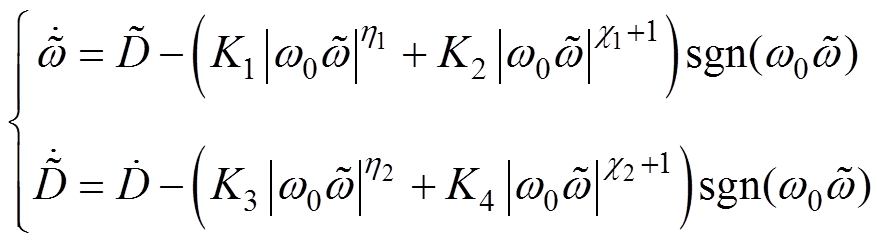 (8)
(8)其中
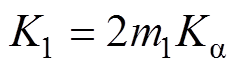
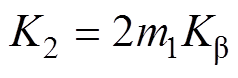
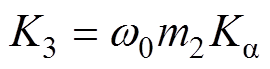
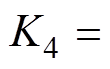
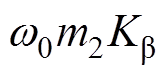
由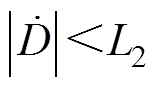 ,可将式(8)转化为
,可将式(8)转化为
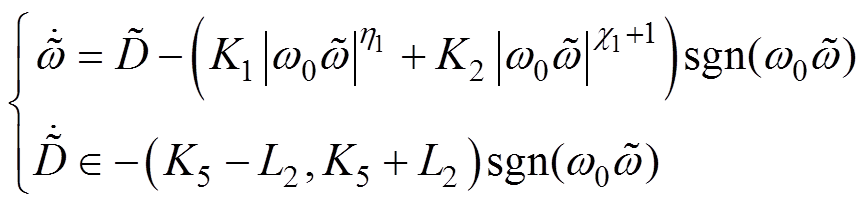 (9)
(9)
其中
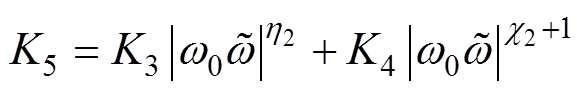
为便于所设计NLESO式(5)的稳定性分析,将式(9)进一步转化为
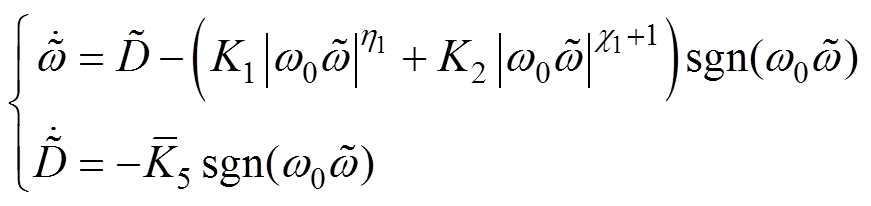 (10)
(10)
式中,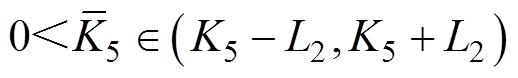 。
。
选择Lyapunov函数为
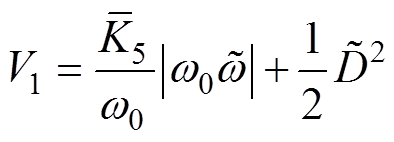 (11)
(11)对式(11)求导,并将式(10)代入可得
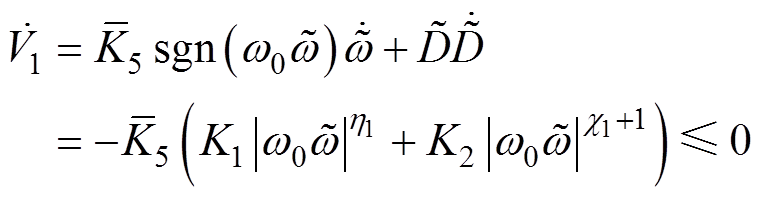 (12)
(12)
由LaSalle不变集原理可知,NLESO误差模型式(7)是全局渐近稳定的。
进一步地,基于SSR理论[20]证明NLESO式(5)的有限时间收敛性,具体如下:
令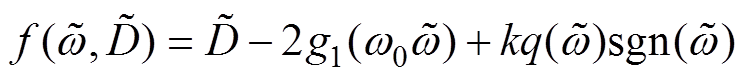 ,其中,
,其中,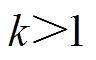 ,
,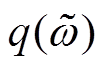 是一个正定连续函数;若
是一个正定连续函数;若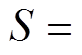
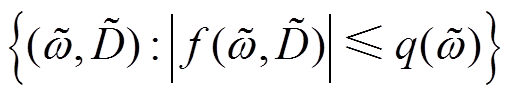 ,且存在
,且存在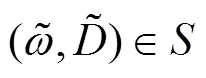 ,则将
,则将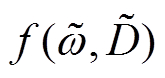 代入S,可有
代入S,可有
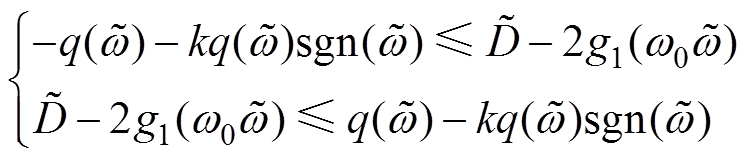 (13)
(13)选择Lyapunov函数为
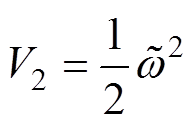 (14)
(14)
对式(14)求导,并将式(7)中的第一行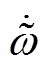 代入可得
代入可得
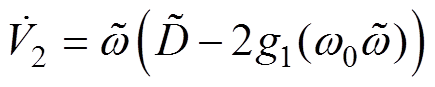 (15)
(15)进一步地,将式(13)中的第二行代入式(15)可得
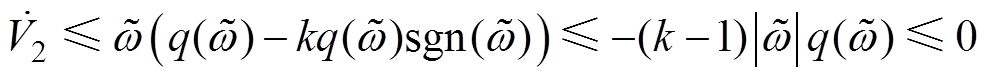 (16)
(16)
取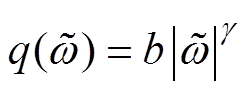 ,其中,
,其中,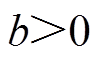 ,
,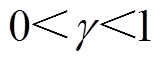 ,并代入式(16),有
,并代入式(16),有
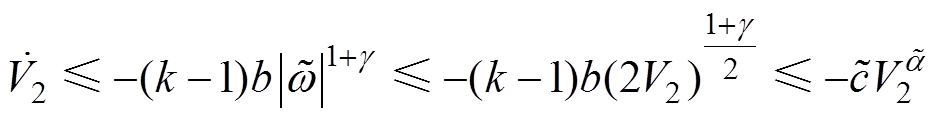 (17)
(17)式中,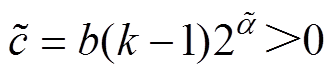 ;
;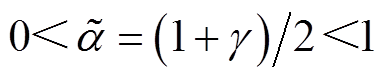 。
。
根据引理1可知,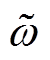 能在有限时间内收敛至平衡点;进一步地,根据式(13)可知,
能在有限时间内收敛至平衡点;进一步地,根据式(13)可知,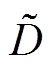 也能在有限时间内收敛至平衡点,即
也能在有限时间内收敛至平衡点,即
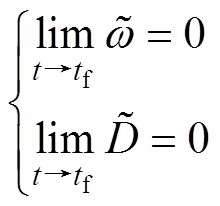 (18)
(18)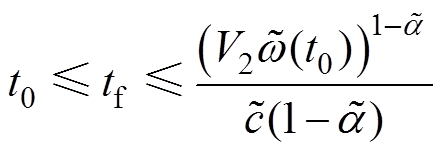 (19)
(19)
综合NLESO误差模型式(7)的全局渐近稳定性和有限时间收敛性,可知,NLESO误差模型式(7)是有限时间稳定的;进一步地,NLESO式(5)也是有限时间稳定的。
注1:为使观测曲线更加平滑,可将NLESO式(5)中的符号函数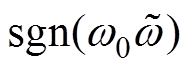 替换为
替换为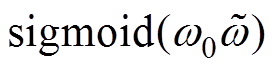 函数[22],有
函数[22],有
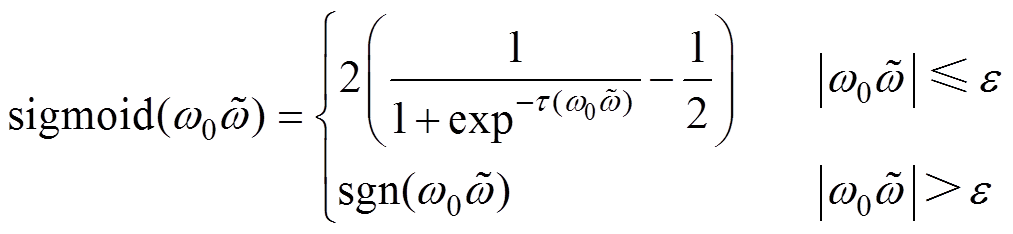 (20)
(20)式中,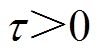 ;边界层常数
;边界层常数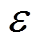 通常取较小的正数。
通常取较小的正数。
考虑到交流异步电机模型式(1)中的定子电阻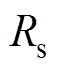 会随着电机温度升高而发生摄动,为抑制
会随着电机温度升高而发生摄动,为抑制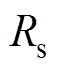 摄动对交流异步电机位置跟踪控制性能的影响,本节基于I&I理论设计
摄动对交流异步电机位置跟踪控制性能的影响,本节基于I&I理论设计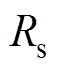 自适应估计器。
自适应估计器。
首先,给出参数估计误差为
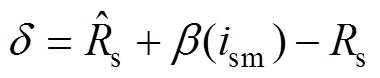 (21)
(21)式中,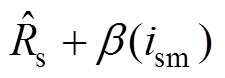 为
为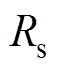 的估计值;
的估计值;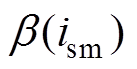 为待设计的调节函数。
为待设计的调节函数。
其次,构造参数估计误差流形面,有
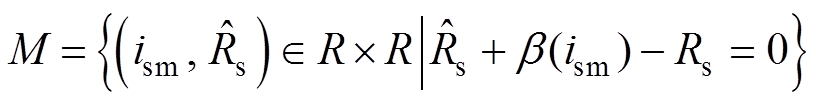 (22)
(22)本节通过设计合适的参数更新律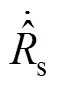 和调节函数
和调节函数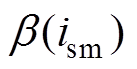 使流形面
使流形面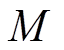 具有不变性和吸引性,进而保证
具有不变性和吸引性,进而保证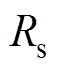 的估计值能够渐近收敛到真实值。
的估计值能够渐近收敛到真实值。
假设相对于自适应估计器的动态特性,定子电阻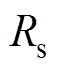 是慢时变的,即
是慢时变的,即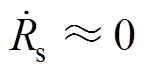 ,则结合系统模型式(1),对式(21)求导可得
,则结合系统模型式(1),对式(21)求导可得
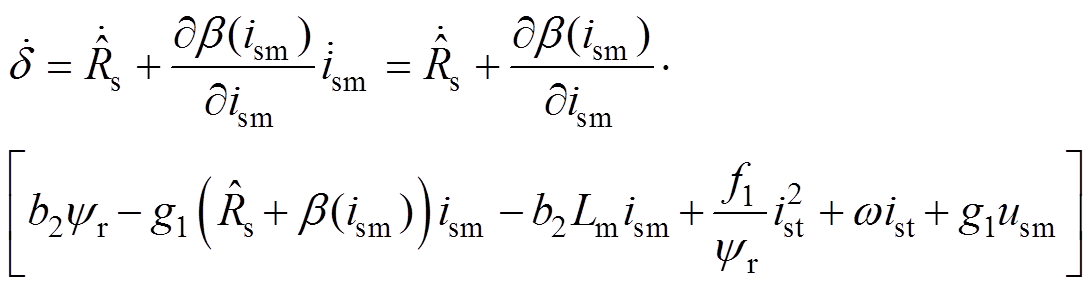 (23)
(23)根据式(23),可将参数更新律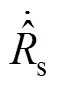 设计为
设计为
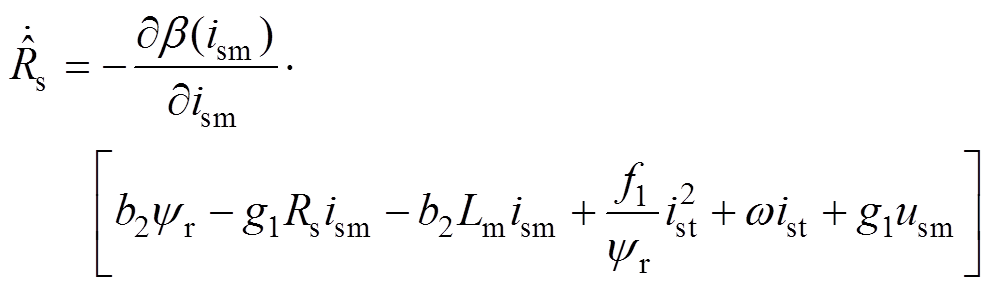 (24)
(24)
构造函数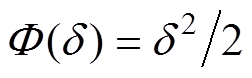 ,对其求导,并将式(23)和式(24)代入可得
,对其求导,并将式(23)和式(24)代入可得
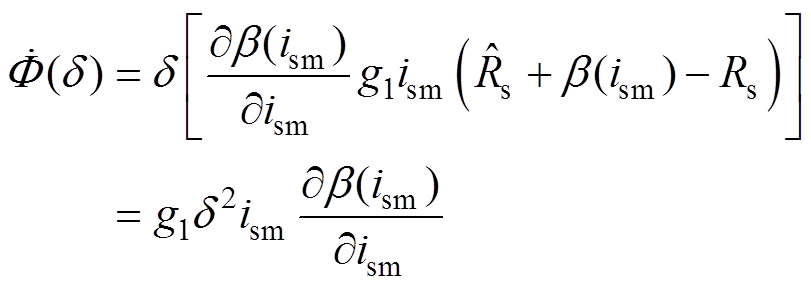 (25)
(25)选择调节函数为
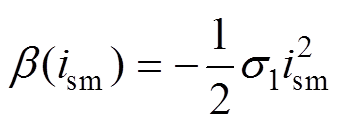 (26)
(26)
式中,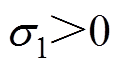 为可调参数。
为可调参数。
将式(26)代入式(25)可得
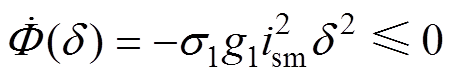 (27)
(27)由式(27)可知,参数估计误差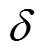 能渐近收敛至平衡点,且动态收敛过程可由参数
能渐近收敛至平衡点,且动态收敛过程可由参数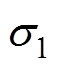 进行调节。
进行调节。
注2:基于I&I理论自适应方法的本质是通过设计参数更新律和调节函数,使参数估计误差流形面具有不变性和吸引性,进而保证参数估计值能渐近收敛到真实值。与常规基于确定等价原则的自适应方法不同,这里引入的调节函数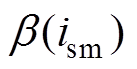 能将参数估计的动态调节过程由单一的积分作用转变为比例积分作用,从而有效提高估计参数动态调节过程的自由度和估计结果的准确性;此外,基于I&I理论的自适应估计器和控制器设计可以分开进行,便于各自控制参数的调整。
能将参数估计的动态调节过程由单一的积分作用转变为比例积分作用,从而有效提高估计参数动态调节过程的自由度和估计结果的准确性;此外,基于I&I理论的自适应估计器和控制器设计可以分开进行,便于各自控制参数的调整。
引理2[11]:考虑如下系统
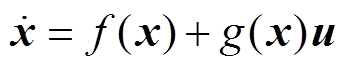 (28)
(28)式中,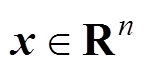 为系统状态;
为系统状态;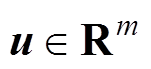 为控制输入;
为控制输入;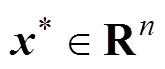 为系统的全局渐近稳定平衡点。令
为系统的全局渐近稳定平衡点。令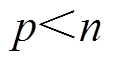 ,若存在映射
,若存在映射
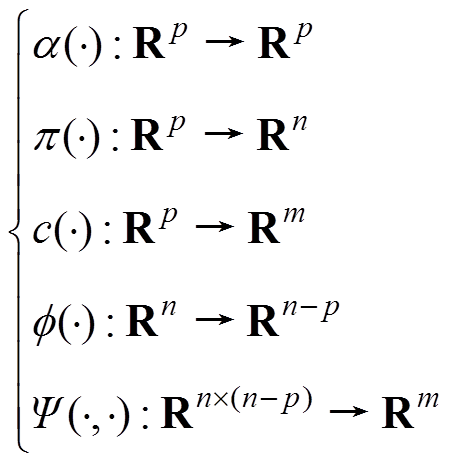 (29)
(29)
使得下列条件成立:
(1)目标系统
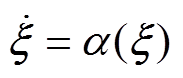 (30)
(30)式中,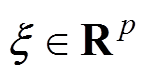 为目标系统状态量;
为目标系统状态量;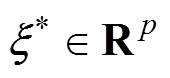 为系统的一个全局渐近稳定平衡点,且
为系统的一个全局渐近稳定平衡点,且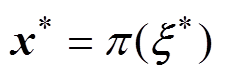 。
。
(2)浸入条件。对于所有的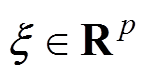 ,有
,有
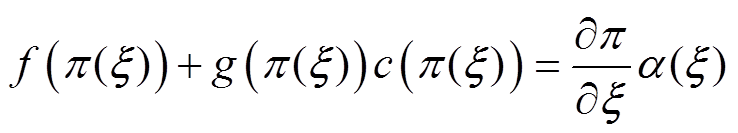 (31)
(31)(3)隐式流形。以下等式恒成立
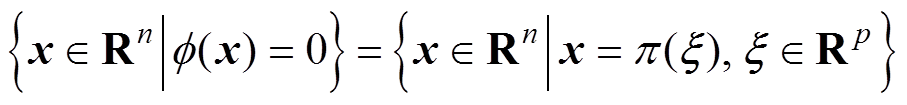 (32)
(32)
(4)流形吸引与轨迹有界。系统所有轨迹
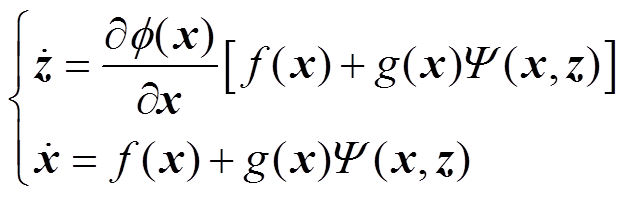 (33)
(33)是有界的并且满足
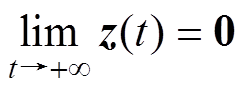 (34)
(34)
则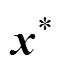 是闭环系统
是闭环系统
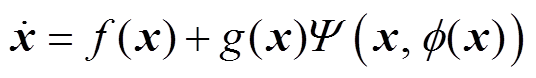 (35)
(35)的一个全局渐近稳定的平衡点。
为便于基于I&I理论设计交流异步电机位置和磁链跟踪控制器,需将交流异步电机模型式(1)转换为误差模型形式。首先,定义系统误差变量,有
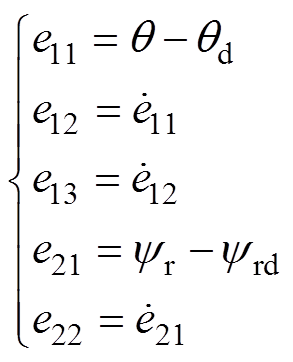 (36)
(36)式中,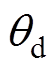 、
、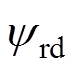 分别为交流异步电机位置和磁链的给定值。
分别为交流异步电机位置和磁链的给定值。
将交流异步电机模型式(1)中的负载扰动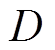 和定子电阻
和定子电阻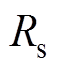 分别相应替换为NLESO式(5)的观测值
分别相应替换为NLESO式(5)的观测值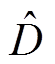 ,以及自适应估计器式(24)、式(26)的估计值
,以及自适应估计器式(24)、式(26)的估计值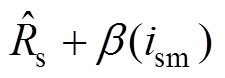 。进而可将交流异步电机模型式(1)转换为误差形式,有
。进而可将交流异步电机模型式(1)转换为误差形式,有
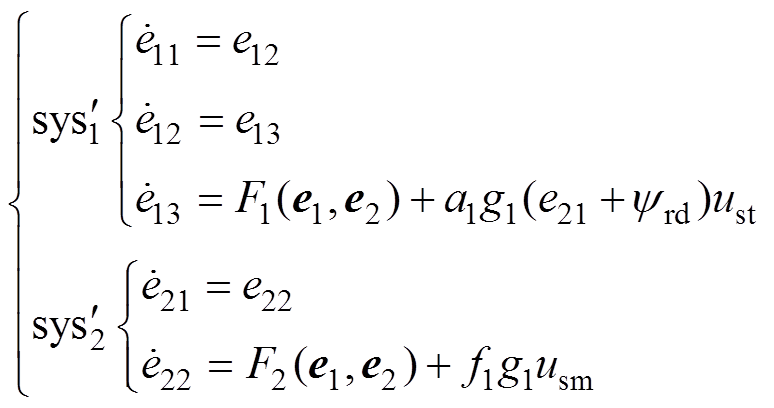 (37)
(37)其中
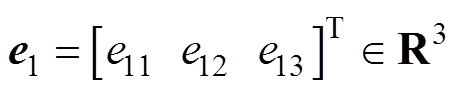
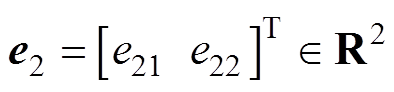
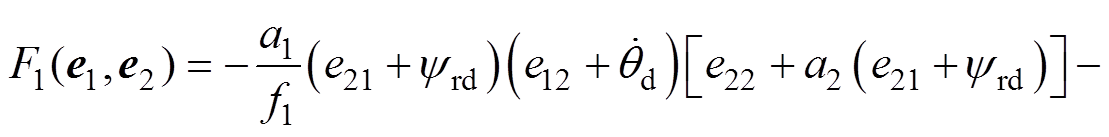
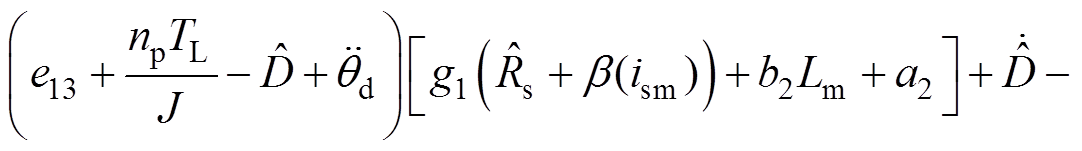
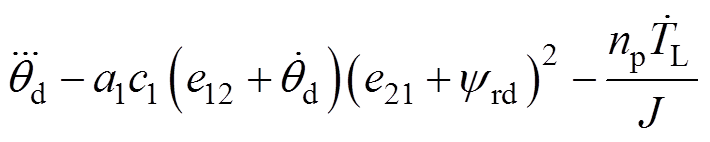
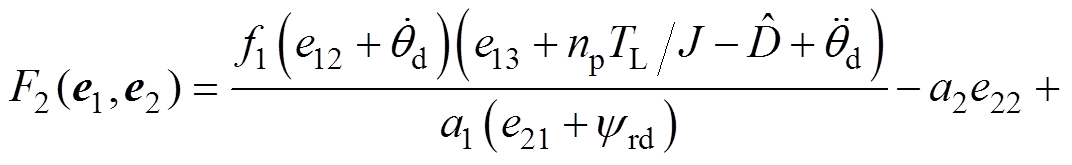
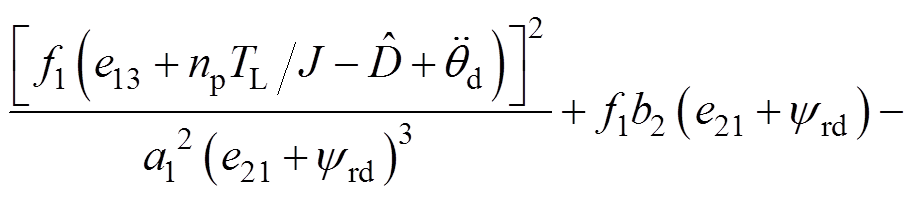
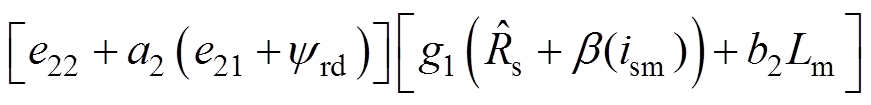
参照引理2,基于I&I理论的交流异步电机位置跟踪控制器 设计过程如下:
设计过程如下:
(1)目标系统。选择一个比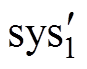 (见式(37))阶数低且稳定的二阶目标系统为
(见式(37))阶数低且稳定的二阶目标系统为
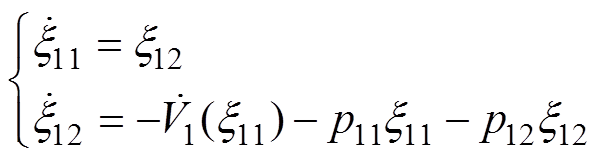 (38)
(38)式中,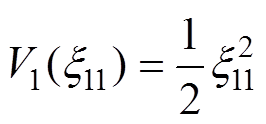 为非线性能量函数,且满足
为非线性能量函数,且满足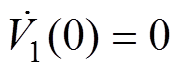 ,
,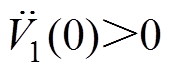 ;
;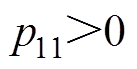 ,
,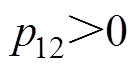 为阻尼系数。
为阻尼系数。
(2)浸入条件。考虑控制目标和目标系统动态,将映射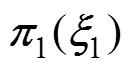 选择为
选择为
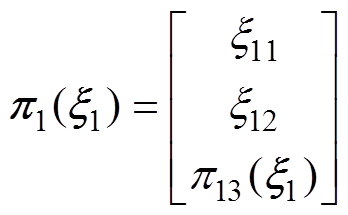 (39)
(39)式中,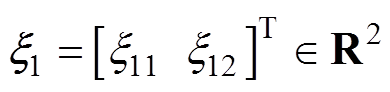 ;
;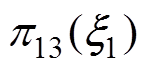 为待设计函数。
为待设计函数。
结合被控系统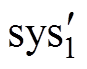 和目标系统(见式(38)),将浸入映射(见式(39))及其导数代入浸入条件(见式(31)),有
和目标系统(见式(38)),将浸入映射(见式(39))及其导数代入浸入条件(见式(31)),有
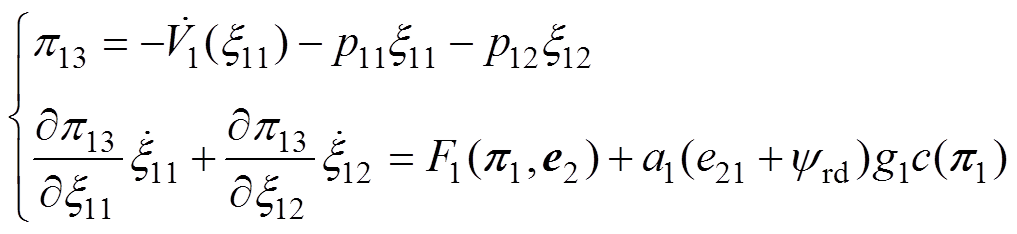 (40)
(40)由式(40)中的第一行可得
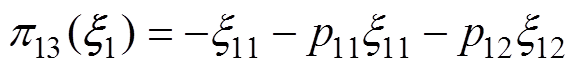 (41)
(41)
(3)隐式流形。流形面的隐式描述为
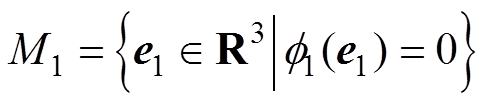 (42)
(42)其中
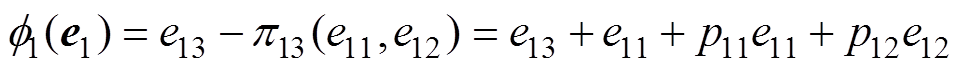
(4)流形吸引与轨迹有界。
定义偏流形坐标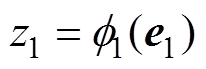 ,并对其求导可得
,并对其求导可得
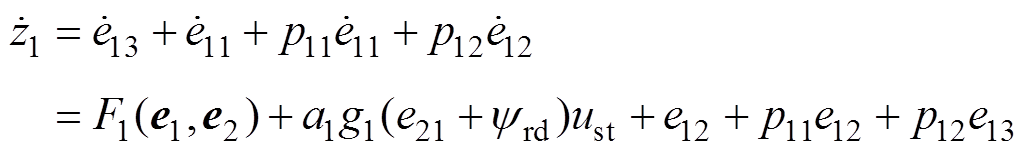 (43)
(43)为保证偏流形坐标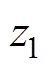 渐近收敛至平衡点,选择偏流形坐标
渐近收敛至平衡点,选择偏流形坐标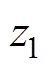 的动态行为满足
的动态行为满足
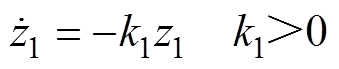 (44)
(44)
结合式(43)和式(44),交流异步电机的位置跟踪控制器 可设计为
可设计为
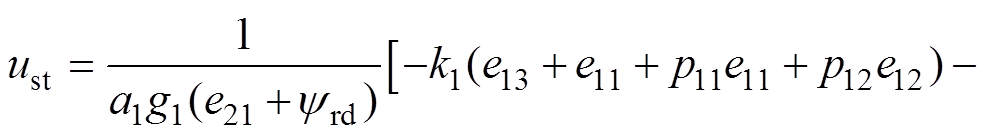
 (45)
(45)
同理,基于I&I理论的交流异步电机磁链跟踪控制器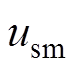 设计过程如下:
设计过程如下:
(1)目标系统。选择一个比 (见式(37))阶数低且稳定的一阶目标系统,有
(见式(37))阶数低且稳定的一阶目标系统,有
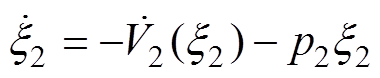 (46)
(46)式中,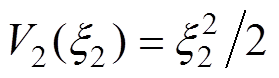 为非线性能量函数,且满足
为非线性能量函数,且满足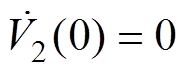 ,
,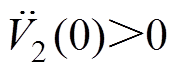 ;
;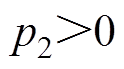 为阻尼系数。
为阻尼系数。
(2)浸入条件。考虑控制目标和目标系统动态,将映射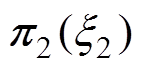 选择为
选择为
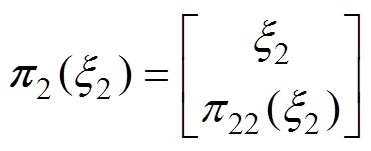 (47)
(47)式中,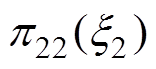 为待设计函数。
为待设计函数。
结合被控系统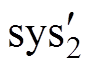 (见式(37))和目标系统(见式(46)),将浸入映射(见式(47))及其导数代入浸入条件(见式(31)),有
(见式(37))和目标系统(见式(46)),将浸入映射(见式(47))及其导数代入浸入条件(见式(31)),有
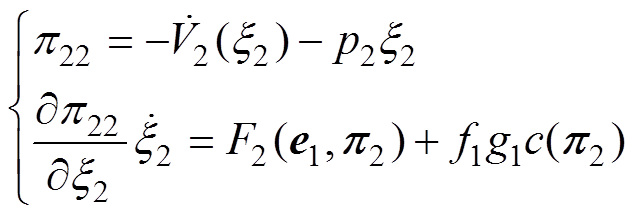 (48)
(48)由式(48)中的第一行可得
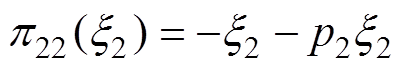 (49)
(49)
(3)隐式流形。流形面的隐式描述为
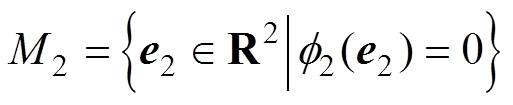 (50)
(50)其中
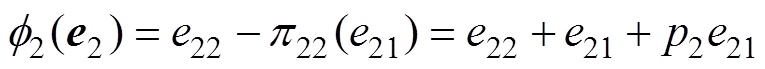
(4)流形吸引与轨迹有界。
定义偏流形坐标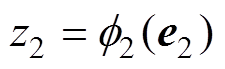 ,并对其求导可得
,并对其求导可得
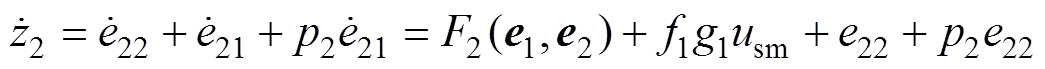 (51)
(51)为保证偏流形坐标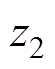 渐近收敛至平衡点,选择偏流形坐标
渐近收敛至平衡点,选择偏流形坐标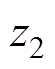 的动态行为满足
的动态行为满足
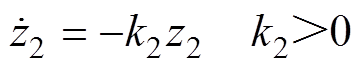 (52)
(52)
结合式(51)和式(52),交流异步电机的磁链跟踪控制器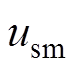 可设计为
可设计为
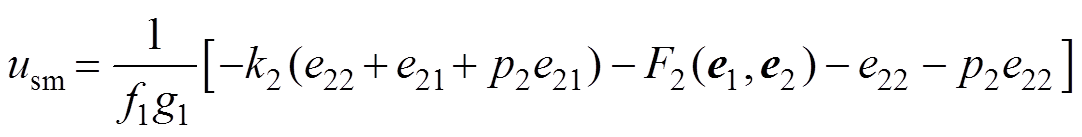 (53)
(53)综上,基于I&I理论的控制器设计方法,通过选择稳定的低阶目标系统(见式(38)和式(46)),以及浸入映射(见式(39)和式(47)),所设计的控制器(见式(45)和式(53))分别将被控系统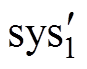 (见式(37))和
(见式(37))和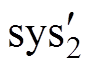 (见式(37))渐近地浸入目标系统中,使得被控系统的任何轨迹都是目标系统在浸入映射下的像,保证了被控系统的全局渐近稳定性。
(见式(37))渐近地浸入目标系统中,使得被控系统的任何轨迹都是目标系统在浸入映射下的像,保证了被控系统的全局渐近稳定性。
为了验证本文所提方法的有效性,在本节将本文所提方法与DSC方法和I&I控制方法进行仿真对比研究。交流异步电机参数见表1。
表1 交流异步电机参数
Tab.1 The parameters of AC asynchronous motor

参 数数 值 额定电压380 额定功率370 额定转速1 400 定子电阻10.98 转子电阻15 定子自感0.311 9 转子自感0.8 定转子互感0.297 磁极对数2 转动惯量0.008
假定交流异步电机的转子位置给定值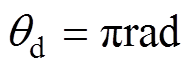 ,磁链给定值
,磁链给定值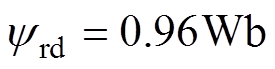 ;在整个仿真过程中,采用时变负载转矩
;在整个仿真过程中,采用时变负载转矩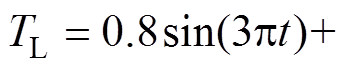
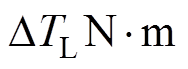 ,其中,
,其中,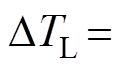
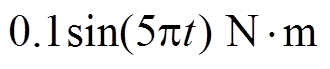 为扰动量;定子电阻
为扰动量;定子电阻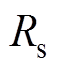 在
在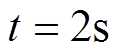 时发生
时发生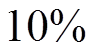 的摄动,变为
的摄动,变为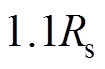 。
。
本文所提方法的主要控制参数取为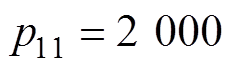 ,
,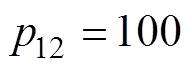 ,
,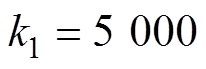 ,
, ,
,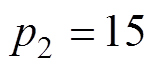 ,
,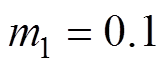 ,
,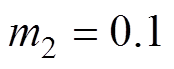 ,
,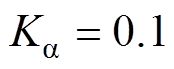 ,
,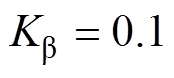 ,
,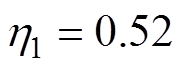 ,
,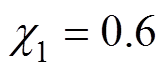 ,
,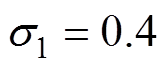 ,
,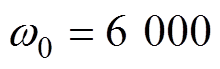 ,
,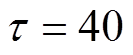 ,
,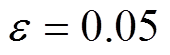 。
。
由于I&I控制方法与本文所提方法的区别在于,前者没有使用NLESO和I&I自适应估计器,因此,为便于对比分析,这里将I&I控制方法的控制参数与本文所提方法的相应参数选择一致。
DSC方法控制器具体设计[23]为

主要控制参数选取为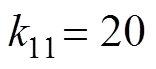 ,
,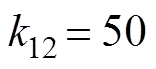 ,
,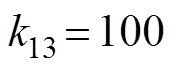 ,
,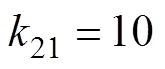 ,
,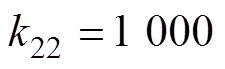 ;滤波时间常数
;滤波时间常数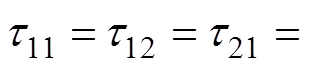
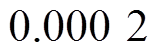 。
。
图1为交流异步电机跟踪控制仿真曲线。
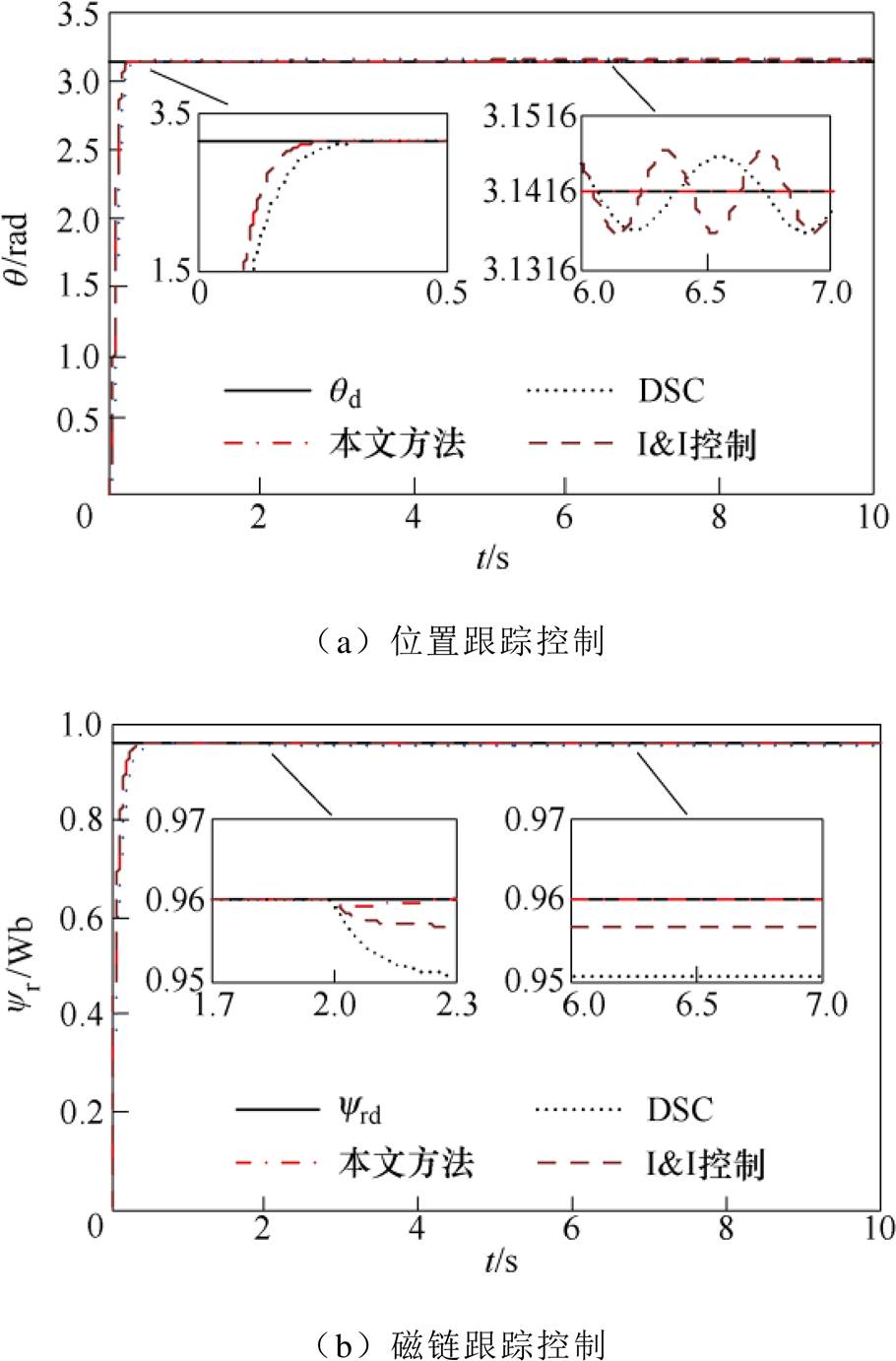
图1 交流异步电机跟踪控制仿真曲线
Fig.1 Tracking control simulation curves of AC asynchronous motor
从图1可以看出:①在DSC方法的作用下,系统输出变量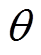 和
和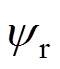 分别实现了对系统给定值
分别实现了对系统给定值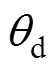 和
和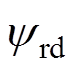 的跟踪控制,但系统的动态响应速度较慢、稳态精度较差;②在I&I控制方法的作用下,系统输出变量
的跟踪控制,但系统的动态响应速度较慢、稳态精度较差;②在I&I控制方法的作用下,系统输出变量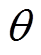 和
和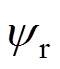 也分别实现了对系统给定值
也分别实现了对系统给定值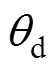 和
和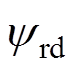 的跟踪控制,但系统的稳态精度较差、抗干扰能力较弱;③而在本文所提方法的作用下,系统输出变量
的跟踪控制,但系统的稳态精度较差、抗干扰能力较弱;③而在本文所提方法的作用下,系统输出变量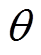 和
和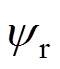 不仅分别实现了对系统给定值
不仅分别实现了对系统给定值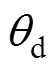 和
和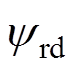 的跟踪控制,而且系统的动态响应速度较快、稳态精度较高、抗干扰能力较强。
的跟踪控制,而且系统的动态响应速度较快、稳态精度较高、抗干扰能力较强。
图2为NLESO的观测值及其观测误差曲线。可以看出,所设计的NLESO对系统的负载扰动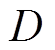 实现了有效的动态观测,即:①NLESO在
实现了有效的动态观测,即:①NLESO在 左右实现了对
左右实现了对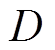 的观测估计,且不存在“初始尖峰”现象;②NLESO的观测误差稳定在
的观测估计,且不存在“初始尖峰”现象;②NLESO的观测误差稳定在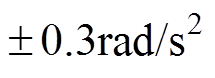 以内。
以内。
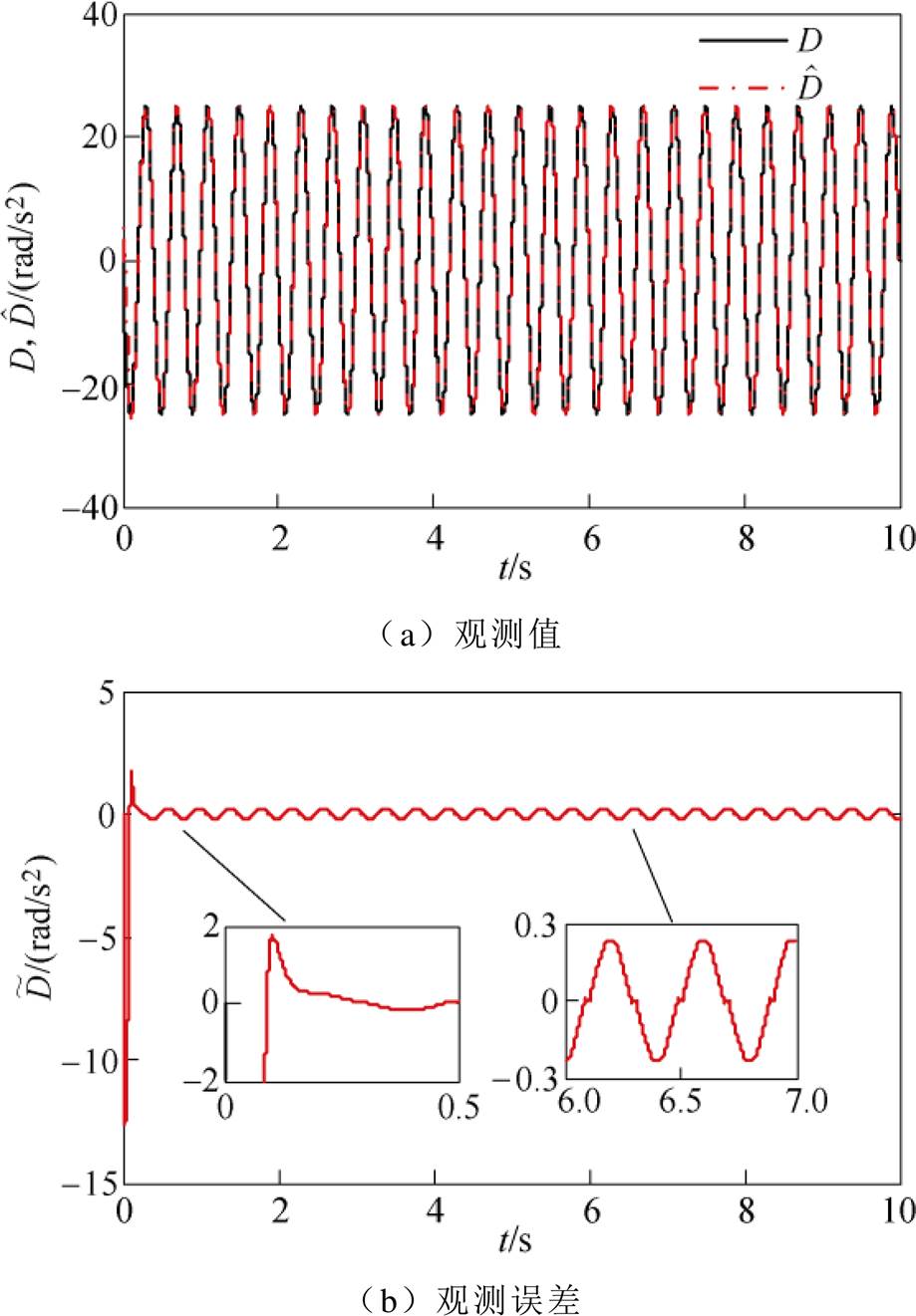
图2 NLESO的观测值及其观测误差曲线
Fig.2 Observation value and observation error curves of NLESO
图3为定子电阻Rs的估计值及其估计误差曲线。可以看出,所设计的I&I自适应估计器对Rs实现了有效的自适应估计,即:①I&I自适应估计器在 左右估计出Rs;②在
左右估计出Rs;②在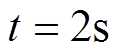 时刻,当Rs发生摄动变为1.1Rs后,I&I自适应估计器仍能较快重新估计出Rs,且估计误差
时刻,当Rs发生摄动变为1.1Rs后,I&I自适应估计器仍能较快重新估计出Rs,且估计误差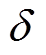 在稳态下接近理想零值。
在稳态下接近理想零值。
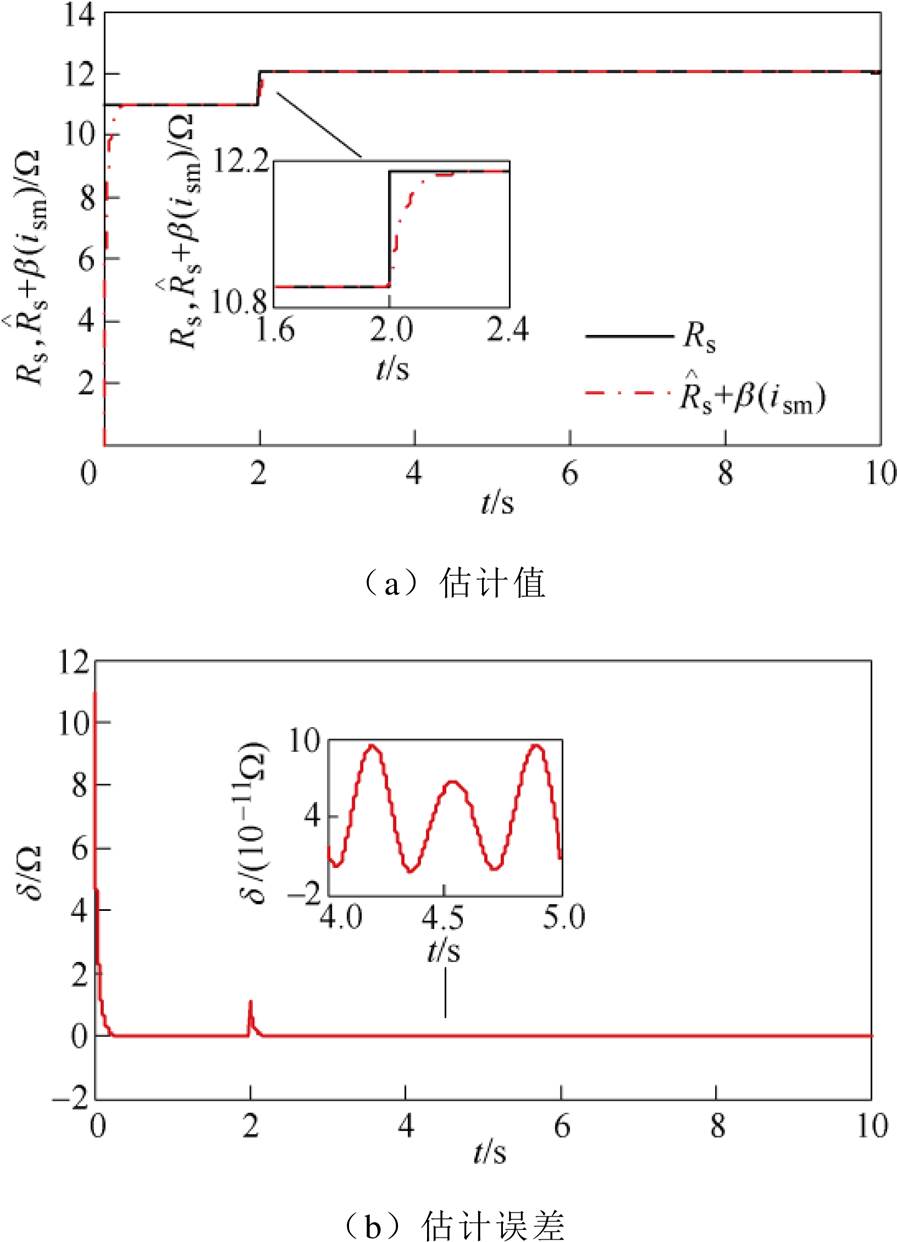
图3 定子电阻Rs的估计值及其估计误差曲线
Fig.3 Estimation value and estimation error curves of stator resistance Rs
基于如图4所示的dSPACE电机实验平台,将本文所提方法与DSC方法和I&I控制方法进行实验对比研究。

图4 dSPACE电机实验平台
Fig.4 dSPACE motor experiment platform
该实验平台硬件主要由DS1104板卡、I/O接口面板、功率驱动板、交流异步电机、增量编码器、负载驱动器、磁粉制动器、PC(装有ControlDesk实时监控软件)组成。其中,DS1104板卡是该实验平台的控制核心,其安装在PC的PCI槽口,并与I/O接口面板通过PHS总线相连;I/O接口面板提供了DS1104板卡与主电路间信号的输入输出接口;功率驱动板采用“交-直-交”变压变频方式驱动交流异步电机,开关频率为5 000Hz;交流异步电机(各项参数详见表1)两端通过联轴器分别与增量编码器和磁粉制动器联接;增量编码器(2 000线)的零位置信号,可通过将DS1104实时接口模块库中增量编码器接口模块子库下“DS1104ENC_POS_Cx”模块的初始位置选项设置为0得到;通过负载驱动器驱动磁粉制动器可以模拟电机不同的负载转矩;通过PC中的ControlDesk软件实时监测电机运行过程中的各项反馈数据。
在具体实验过程中,交流异步电机的磁链给定值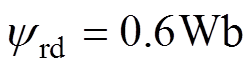 ,转子位置给定值分别采用如下四种形式:①阶跃信号:当
,转子位置给定值分别采用如下四种形式:①阶跃信号:当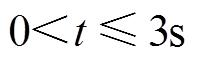 时,
时,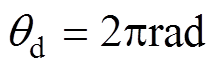 ,当
,当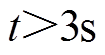 时,
时,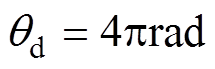 ;②正弦信号
;②正弦信号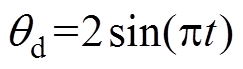
 ;③周期为
;③周期为 ,峰值为
,峰值为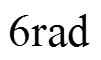 的三角波信号;④单方向时变信号
的三角波信号;④单方向时变信号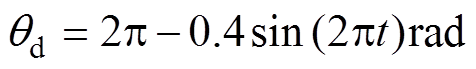 。另外,本文施加时变负载转矩
。另外,本文施加时变负载转矩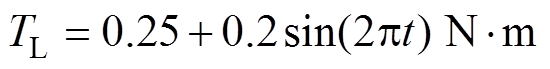 。交流异步电机位置跟踪控制框图如图5所示。
。交流异步电机位置跟踪控制框图如图5所示。
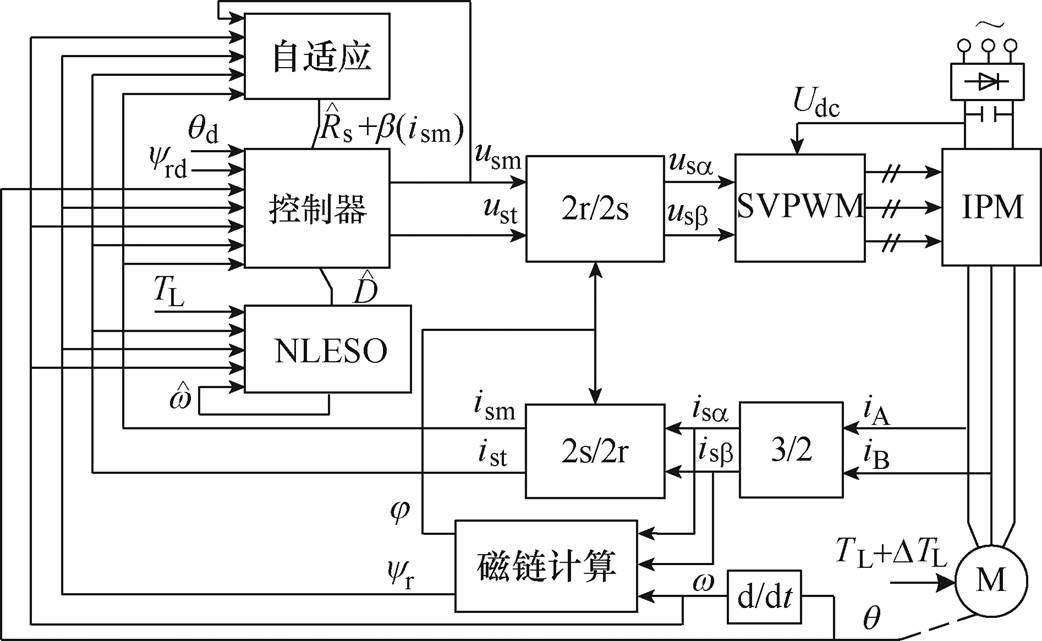
图5 交流异步电机位置跟踪控制框图
Fig.5 Position tracking control diagram of AC asynchronous motor
图6为交流异步电机位置跟踪控制实验曲线。从图6可以看出,所取得的实验结果与前面的仿真结果基本一致,具体:①在DSC方法的作用下,尽管交流异步电机实现了对不同转子位置给定值 的跟踪控制,但系统的动态响应速度较慢、稳态精度较差;②在I&I控制方法的作用下,交流异步电机也实现了对不同转子位置给定值
的跟踪控制,但系统的动态响应速度较慢、稳态精度较差;②在I&I控制方法的作用下,交流异步电机也实现了对不同转子位置给定值 的跟踪控制,但系统的稳态精度较差、鲁棒稳定性较弱;③而在本文所提方法的作用下,交流异步电机不仅实现了对不同转子位置给定值
的跟踪控制,但系统的稳态精度较差、鲁棒稳定性较弱;③而在本文所提方法的作用下,交流异步电机不仅实现了对不同转子位置给定值 的跟踪控制,而且系统的动态响应速度较快、稳态精度较高、鲁棒稳定性较强。
的跟踪控制,而且系统的动态响应速度较快、稳态精度较高、鲁棒稳定性较强。
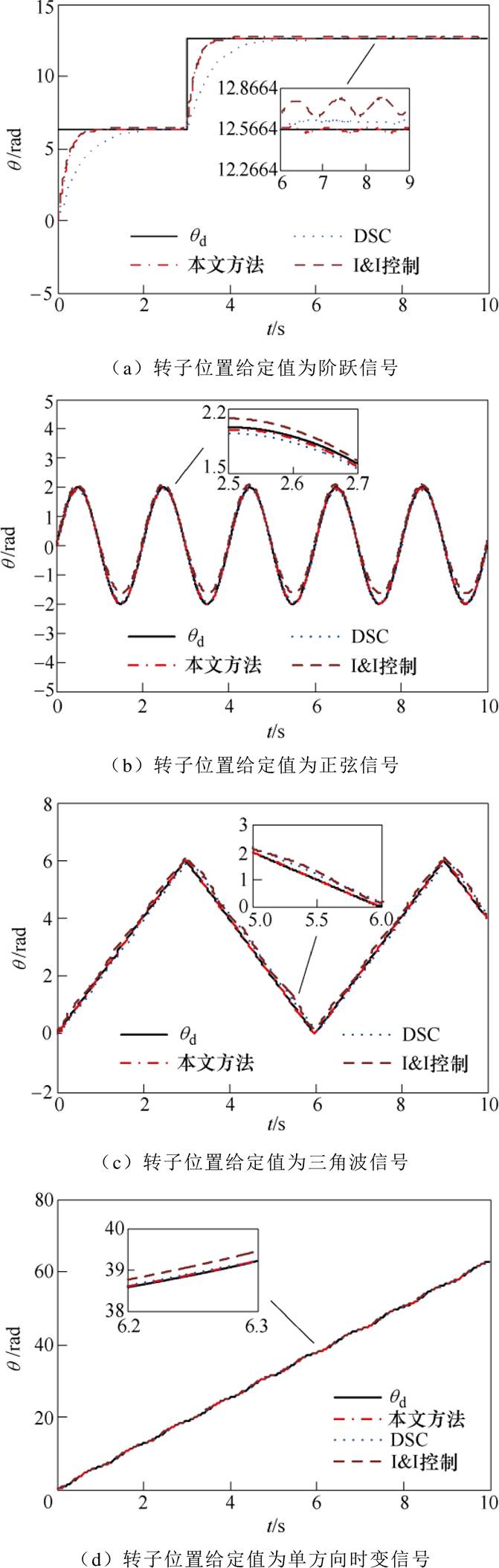
图6 交流异步电机位置跟踪控制实验曲线
Fig.6 Position tracking control experimental curves of AC asynchronous motor
图7为交流异步电机在参数失配(控制器中的 、
、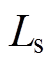 和
和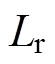 分别与实测值失配30%、5%和5%)情况下的位置跟踪控制实验曲线。则在图6分析的基础上,由图7可进一步看出:①在DSC方法的作用下,参数失配问题对交流异步电机转子位置跟踪精度的影响较其他两种控制方法更加明显;②在本文所提方法的作用下,交流异步电机对不同转子位置给定值
分别与实测值失配30%、5%和5%)情况下的位置跟踪控制实验曲线。则在图6分析的基础上,由图7可进一步看出:①在DSC方法的作用下,参数失配问题对交流异步电机转子位置跟踪精度的影响较其他两种控制方法更加明显;②在本文所提方法的作用下,交流异步电机对不同转子位置给定值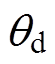 的跟踪性能受参数失配问题的影响较小,表现出较强的抗干扰性能。
的跟踪性能受参数失配问题的影响较小,表现出较强的抗干扰性能。
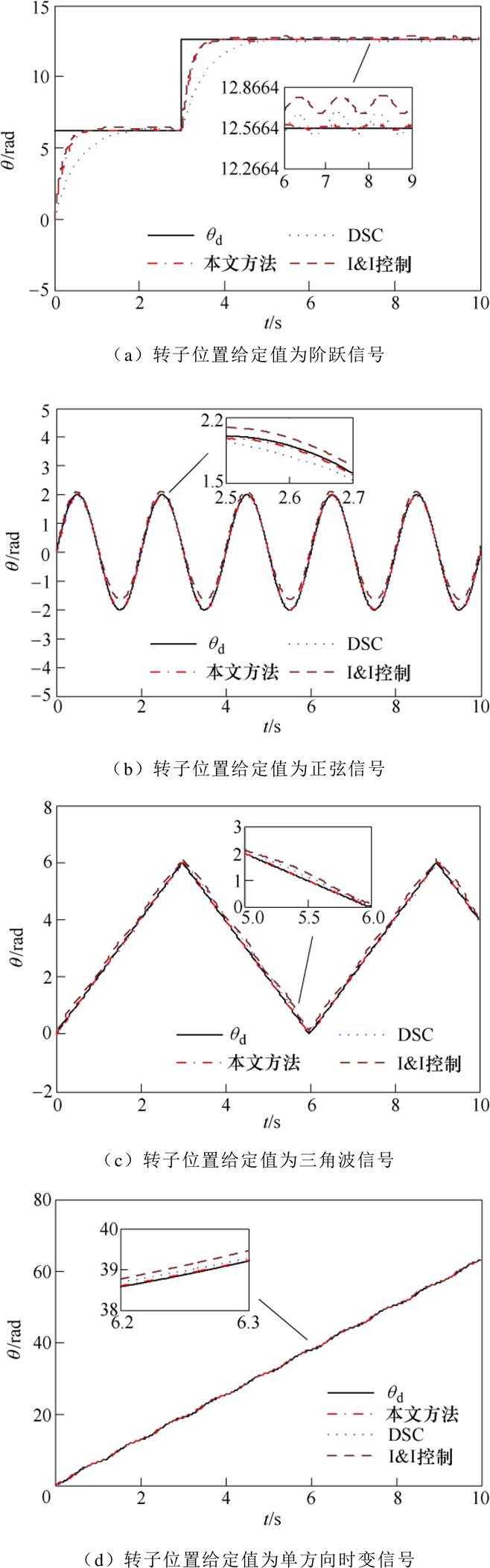
图7 参数失配下交流异步电机位置跟踪控制实验曲线
Fig.7 Position tracking control experimental curves of AC asynchronous motor under the parameter mismatches
针对存在参数摄动和负载扰动的交流异步电机位置跟踪控制问题,本文提出了一种基于I&I理论的自适应控制方法。通过将类饱和非线性误差函数引入到NLESO中,削弱了常规LESO存在的“初始尖峰”现象,同时理论分析表明,扰动估计的收敛速度也得到了进一步提升;考虑I&I理论能够同时处理系统镇定问题和摄动参数估计问题,基于I&I理论,首先将参数更新律和调节函数相结合,在保证参数估计误差流形面具有不变和吸引性的基础上,设计的定子电阻自适应估计器有效地提高了估计参数动态调节过程的自由度和估计结果的准确性,且理论分析表明,参数估计值能够以指数规律的形式收敛到真实值;进一步地,通过选择稳定的低阶目标系统和浸入映射,设计的位置和磁链控制器分别将被控对象渐近地浸入到目标系统中,保证了系统的全局渐近稳定性。最后的仿真和实验结果表明,本文所提控制方法具有动态响应速度快、稳态精度高、鲁棒性强的优点。
参考文献
[1] Reddy S, Loganathan U. Robust and high-dynamic- performance control of induction motor drive using transient vector estimator[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7529-7538.
[2] 陈闯, 王勃, 于泳, 等. 基于改进指数趋近律的感应电机滑模转速观测器研究[J]. 电工技术学报, 2020, 35(增刊1): 155-163.
Chen Chuang, Wang Bo, Yu Yong, et al. An improved exponential reaching law based-sliding mode observer for speed-sensorless induction motor drives[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 155-163.
[3] 刘和平, 刘庆, 张威, 等. 电动汽车用感应电机削弱振动和噪声的随机PWM控制策略[J]. 电工技术学报, 2019, 34(7): 1488-1495.
Liu Heping, Liu Qing, Zhang Wei, et al. Random PWM technique for acoustic noise and vibration reduction in induction motors used by electric vehicles[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1488-1495.
[4] 李杰, 詹榕, 宋文祥. 感应电机低采样频率的磁链观测器离散化模型研究[J]. 电工技术学报, 2019, 34(15): 3136-3146.
Li Jie, Zhan Rong, Song Wenxiang. Improved discrete observer model of induction motor at low sampling frequency[J]. Transactions of China Elec- trotechnical Society, 2019, 34(15): 3136-3146.
[5] Chen J. Passivity-based parameter estimation and composite adaptive position control of induction motors[J]. Transactions of the Canadian Society for Mechanical Engineering, 2013, 37(3): 559-569.
[6] Lee H T. Adaptive speed/position control of indu- ction motor based on SPR approach[J]. International Journal of Control, 2014, 87(11): 2209-2222.
[7] Silva W A, Junior A B, Torrico B C S, et al. Generalized predictive control robust for position control of induction motor using field-oriented con- trol[J]. Electrical Engineering, 2015, 97(3): 195-204.
[8] Barambones O, Alkorta P. Position control of the induction motor using an adaptive sliding-mode controller and observers[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6556-6565.
[9] Zhou Zhencheng, Yu Jinpeng, Yu Haisheng, et al. Neural network-based discrete-time command filtered adaptive position tracking control for induction motors via backstepping[J]. Neurocomputing, 2017, 260: 203-210.
[10] Han Yao, Yu Jinpeng, Zhao Lin, et al. Finite-time adaptive fuzzy control for induction motors with input saturation based on command filtering[J]. IET Control Theory and Applications, 2018, 12(15): 2148-2155.
[11] Astolfi A, Ortega R. Immersion and invariance: a new tool for stabilization and adaptive control of nonlinear systems[J]. IEEE Transactions on Auto- matic Control, 2003, 48(4): 590-606.
[12] 李晓静, 吴爱国, 张兆龙. 基于浸入和不变技术的非线性跟踪控制[J]. 控制理论与应用, 2019, 36(1): 73-78.
Li Xiaojing, Wu Aiguo, Zhang Zhaolong. Immersion and invariance modular nonlinear tracking control for an underactuated quadrotor[J]. Control Theory & Applications, 2019, 36(1): 73-78.
[13] Zou Yao, Meng Ziyang. Immersion and invariance- based adaptive controller for quadrotor systems[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(11): 2288-2297.
[14] 姜鑫燃, 鲜斌. 小型无人直升机浸入-不变集自适应控制[J]. 控制理论与应用, 2015, 32(10): 1378- 1383.
Jiang Xinran, Xian Bin. Immersion and invariance adaptive control for a miniature unmanned helico- pter[J]. Control Theory & Applications, 2015, 32(10): 1378-1383.
[15] Lou Z, Zhao Jun. Viable immersion and invariance control for a class of nonlinear systems and its application to aero-engines[J]. Journal of the Franklin Institute, 2019, 356(1): 42-57.
[16] Liu Zhen, Tan Xiangmin, Yuan Ruyi, et al. Immersion and invariance-based output feedback control of air- breathing hypersonic vehicles[J]. IEEE Transactions on Automation Science and Engineering, 2016, 13(1): 394-402.
[17] 孙佃升, 章跃进. 一种抑制初始微分峰值现象的改进型三阶时变参数扩张状态观测器[J]. 电机与控制学报, 2017, 21(9): 55-62.
Sun Diansheng, Zhang Yuejin. Improved third-order time-varying parameters nonlinear ESO restraining the derivative peaking phenomenon[J]. Electric Machines and Control, 2017, 21(9): 55-62.
[18] 王治国, 郑泽东, 李永东, 等. 三相异步电机电流多步预测控制方法[J]. 电工技术学报, 2018, 33(9): 1975-1984.
Wang Zhiguo, Zheng Zedong, Li Yongdong, et al. Predictive current control for three phase induction machine using multi-steps prediction horizon[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1975-1984.
[19] 杨淑英, 孙瑞, 曹朋朋, 等. 一种基于双复合滑模面滑模观测器的异步电机转子电阻辨识方案[J]. 电工技术学报, 2018, 33(15): 3596-3606.
Yang Shuying, Sun Rui, Cao Pengpeng, et al. Double compound manifold sliding mode observer based rotor resistance online updating scheme for induction motor[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3596-3606.
[20] Huang Yi, Han Jingqing. Analysis and design for the second order nonlinear continuous extended states observer[J]. Chinese Science Bulletin, 2000, 45(21): 1938-1944.
[21] Bhat S P, Bernstein D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751-766.
[22] 苟立峰, 王琛琛, 游小杰, 等. 基于积分滑模的感应电机无速度传感器带速重投控制策略[J]. 电工技术学报, 2018, 33(24): 5700-5710.
Gou Lifeng, Wang Chenchen, You Xiaojie, et al. A restart method based on integral sliding mode for speed sensorless controlled induction motor[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5700-5710.
[23] 刘乐, 蔺明浩, 李晓刚, 等. 基于模糊干扰观测器的电液伺服位置系统自适应反步控制[J]. 电机与控制学报, 2019, 23(12): 143-150, 158.
Liu Le, Lin Minghao, Li Xiaogang, et al. Adaptive backstepping control for the electro-hydraulic servo position system based on fuzzy disturbance obser- vers[J]. Electric Machines and Control, 2019, 23(12): 143-150, 158.
Immersion and Invariance Theory-Based Adaptive Position Tracking Control for Alternating Current Asynchronous Motor
Abstract In order to improve the position tracking control performance of alternating current (AC) asynchronous motor under parameter perturbation and load disturbance, an immersion and invariance (I&I) theory-based adaptive control method was proposed in this paper. Firstly, a nonlinear extended state observer (NLESO) was constructed to dynamically observe the load disturbance, which improved the tracking control accuracy of the system. Secondly, the I&I theory-based adaptive estimator was designed for the system perturbation parameter, and the parameter estimate was converged to the true value asymptotically. Thirdly, the position and flux tracking controllers of the AC asynchronous motor were designed respectively based on the I&I theory, which realized precise tracking control for the system given values. Finally, the proposed control method was compared with the dynamic surface control (DSC) method and the I&I control method by simulation and experiment. The results verify the effectiveness and feasibility of the proposed control method.
keywords:Alternating current asynchronous motor, adaptive position tracking control, immersion and invariance theory, nonlinear extended state observer
中图分类号:TM343+.2
DOI: 10.19595/j.cnki.1000-6753.tces.200384
国家自然科学基金(61803327, 61873226)和河北省自然科学基金(F2020203018,F2019203090)资助项目。
收稿日期 2020-04-18
改稿日期 2020-07-24
刘 乐 男,1985年生,博士,副教授,研究方向为复杂动态系统建模、分析与控制。E-mail: leliu@ysu.edu.cn(通信作者)
高 杰 男,1995年生,硕士研究生,研究方向为交流异步电机高性能位置/速度控制。E-mail: gj951012@163.com
(编辑 崔文静)