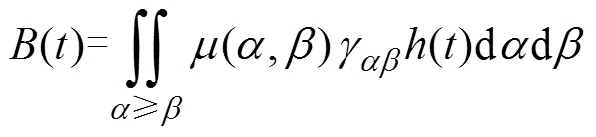（1）摘要 Preisach模型参数的快速辨识对实现考虑磁滞特性的电工装备有限元计算具有重要意义。该文结合显式Everett函数Preisach磁滞模型，提出一种基于改进速度可控粒子群算法的Preisach模型参数辨识方法，并对比分析全局优化算法在该问题应用的效率问题。首先，为了解决传统离散型Preisach模型因存储庞大Everett矩阵造成的计算效率低下问题，构建Everett函数的参数化显式表达式；其次，提出一种基于改进速度可控粒子群算法的Preisach模型参数辨识方法，并基于测量的硅钢片准静态磁滞回线，实现模型的参数辨识；最后，对比分析模拟退火算法、遗传算法与该文所提算法在模型迭代次数与计算时间、磁滞回线模拟准确度、参数辨识成功率三个方面的应用效率。结果表明，该文所提出的改进速度可控粒子群算法在Preisach模型辨识上同时兼具辨识精度高、收敛速度快、成功率高的特点。
关键词：磁滞模型 全局优化 电工磁材料 磁特性模拟
电工装备的精细电磁仿真离不开精准、高效的磁性材料磁滞模型。因此，建立精准、高效的磁滞模型对于新型电工装备的研发与节能降耗具有重要意义。目前，Preisach磁滞模型因其可以考虑磁化历史的影响以及易于数值实现等优点，成为了运用最广泛的一种磁滞模型[1-5]。充分考虑到Preisach模型的擦除特性与同余特性，并忽略Preisach模型的具体物理意义，Krasnoselskii提出了经典的Preisach模型（Classical Preisach Model, CPM）。由于经典的Preisach模型是一种输入速率无关的静态磁滞模型。I. Mayergoyz等随后提出一阶回转曲线法，该方法可以精确模拟铁磁材料的磁滞回线，但一阶回转曲线需通过实验测量或数值方法预测获得，辨识过程复杂，计算速度缓慢[6]；其后，G. Finocchio等采用洛伦兹函数替代分布函数的方法，建立起了磁场强度与磁通密度的导数关系式，但该方法的积分运算，计算过程复杂且仅能得到参数的近似解，模型辨识精度不高[7]；S. Hussain等采用离散单元法，实现了Preisach模型的快速、精确辨识，但其依赖于初始磁化状态，对不同磁通密度下的磁滞回线模拟精度不同，该问题有待进一步研究[8-9]。近年来，华北电力大学赵小军等提出基于定点谐波平衡有限元方法，可以通过修正的损耗函数来获得磁滞回线[10-11]；西安交通大学段娜娜等提出基于极限磁滞回线法的Preisach模型，能够根据极限磁滞回环模拟磁性材料的主磁滞回线与高阶回转曲线[12-14]；河北工业大学张长庚等，提出了逆Preisach模型，改进模型能够很好地解决经典模型对一阶回转曲线数据的依赖，同样仅需极限磁滞回线数据即可实现Preisach模型的辨识[15]。上述模型的改进，拓宽了Preisach模型的适用范围，简化了二重积分复杂耗时的计算工作，也避免了对一阶回转曲线数据的依赖，简化了经典Preisach模型的辨识过程。2016年，匈牙利学者Zsolt Szabó等，利用指数函数逼近拟合磁滞模型分布函数，提出基于封闭形式Everett函数的Preisach辨识方法，为Preisach模型的参数辨识问题提出了新的解决思路[16-18]。相较于传统的数值型Everett矩阵，该方法提出Everett函数的显式解析表达式，解决了传统方法需要在耦合有限元计算过程中大量存储离散型辨识数据的问题。但是，如何高效获取显式Everett函数的参数仍需要进一步研究。
本文将Preisach模型分布函数简化为两个相互独立的一维指数函数乘积的形式，得到指数形式的分布函数，并推导显式Everett函数的具体指数数学表达式，建立基于显式Everett函数的Preisach模型。其中，关键问题为寻找用数学函数逼近拟合Preisach模型分布函数的最优参数组合。同时，为得到更高效的辨识结果，需要结合一种高效优化算法来辨识参数。据此，本文提出一种基于改进速度可控粒子群算法的Preisach模型参数辨识方法，并通过与遗传算法以及模拟退火算法在模型迭代次数与计算时间、磁滞回线模拟准确度、参数辨识成功率三个方面进行对比，深入分析全局优化算法在模型参数辨识问题中应用的性能。结果表明，本文所提方法兼具辨识精度高、收敛速度快、成功率高的优点。
经典Preisach模型认为磁性材料是由一系列磁滞算子所组成[19-20]，铁磁材料的磁滞宏观表现即为这些磁滞算子磁特性的集体体现，经典Preisach模型认为磁滞回线的数学描述可表示为
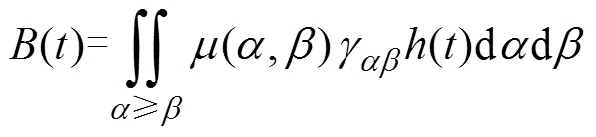（1）式中，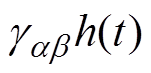
为正负翻转阈值
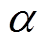和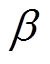
控制的单元磁滞算子，其值仅能为±1；
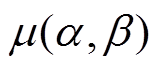为Preisach分布函数。
在ab平面上积分运算时，其Everett函数与分布函数关系式为
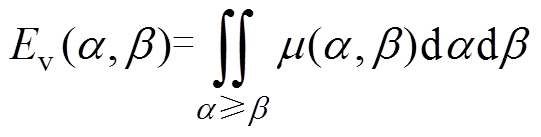（2）基于分布函数的对称性以及磁滞算子的矩形特性，开关值a、b 互相独立，Preisach模型分布函数可由两个相互独立的一维单值分布函数mi的乘积累加和进行近似[19]，有
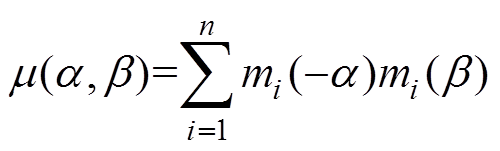（3）
式中，n为分布函数被分解的项数，由于不同材料的Preisach模型分布函数也不尽相同，应根据不同的应用场合建立不同的函数表达式，分解的项数越多，其准确度越高。
Preisach模型分布函数的单值函数分布近似为高斯分布，可采用高斯公式或洛伦兹公式进行近似。结合高斯函数分布与洛伦兹函数的构建形式，本文用指数函数来进行近似，有
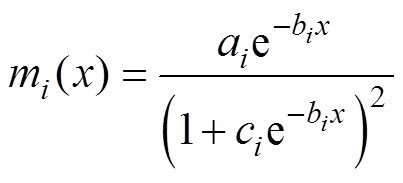（4）式中，ai、bi、ci为模型分布函数的参数，通过这三组参数的调整来保证分布函数的准确性。
Preisach模型分布函数假设的引入，使得Everett函数具有更加紧凑的单值数学函数形式，从而避免传统Everett函数的复杂积求解运算，大大提高了运算效率。显式Everett函数表达式可表示为
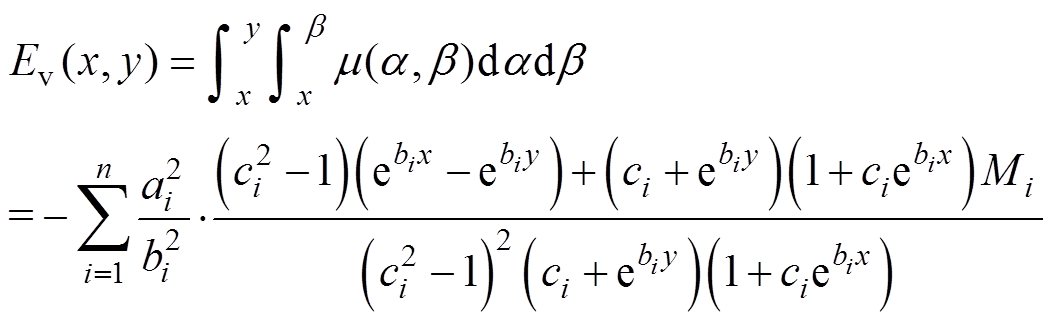（5）其中
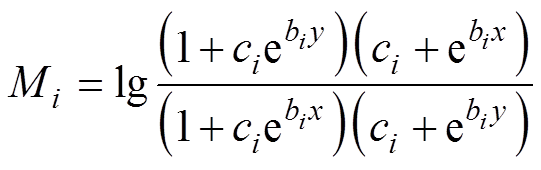
当ci=1时，显式Everett函数可进一步简化为
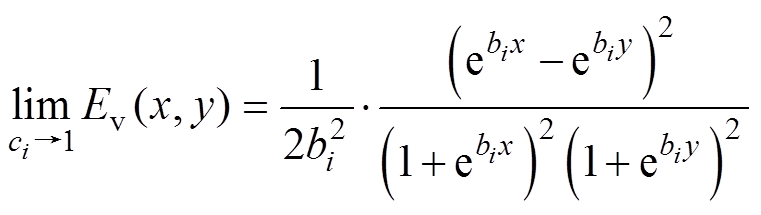（6）基于显式Everett函数的Preisach模型数学表达式可进一步定义为
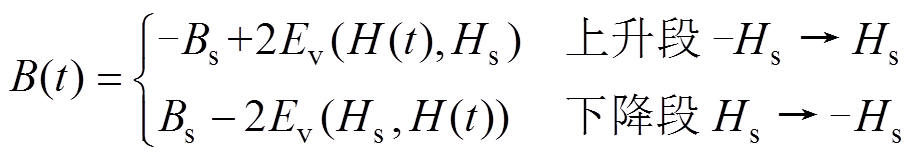（7）
式中，H(t)为t时刻的磁场强度；Hs为最大磁场强度；Bs为最大磁通密度，Bs的计算公式为
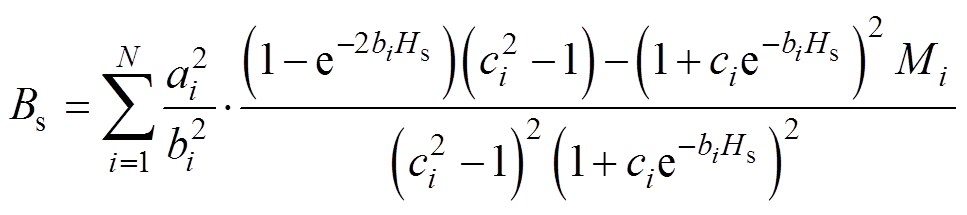（8）据此，基于显式Everett函数的Preisach模型，待辨识的参数仅有ai、bi、ci，与经典Preisach磁滞模型相比，具有更加简明的数学表达式。指数函数的求和运算，避免了使用复杂数学库来计算Everett函数的情况，从而提高了Preisach模型的计算效率，计算过程如图1所示。首先，加载实验测量得到的磁滞回线数据，以此作为验证模型有效性和准确性的基准；其次，读取模型参数，依据磁化历史，确定磁滞算子正负取值翻转阶梯线，根据参数的取值计算出Everett函数；最后，逐点分段计算上升支与下降支磁通密度值，更新磁化历史与阶梯线，直到整个周期所有N个采样点的磁通密度B计算完成，输出该材料的磁滞回线。
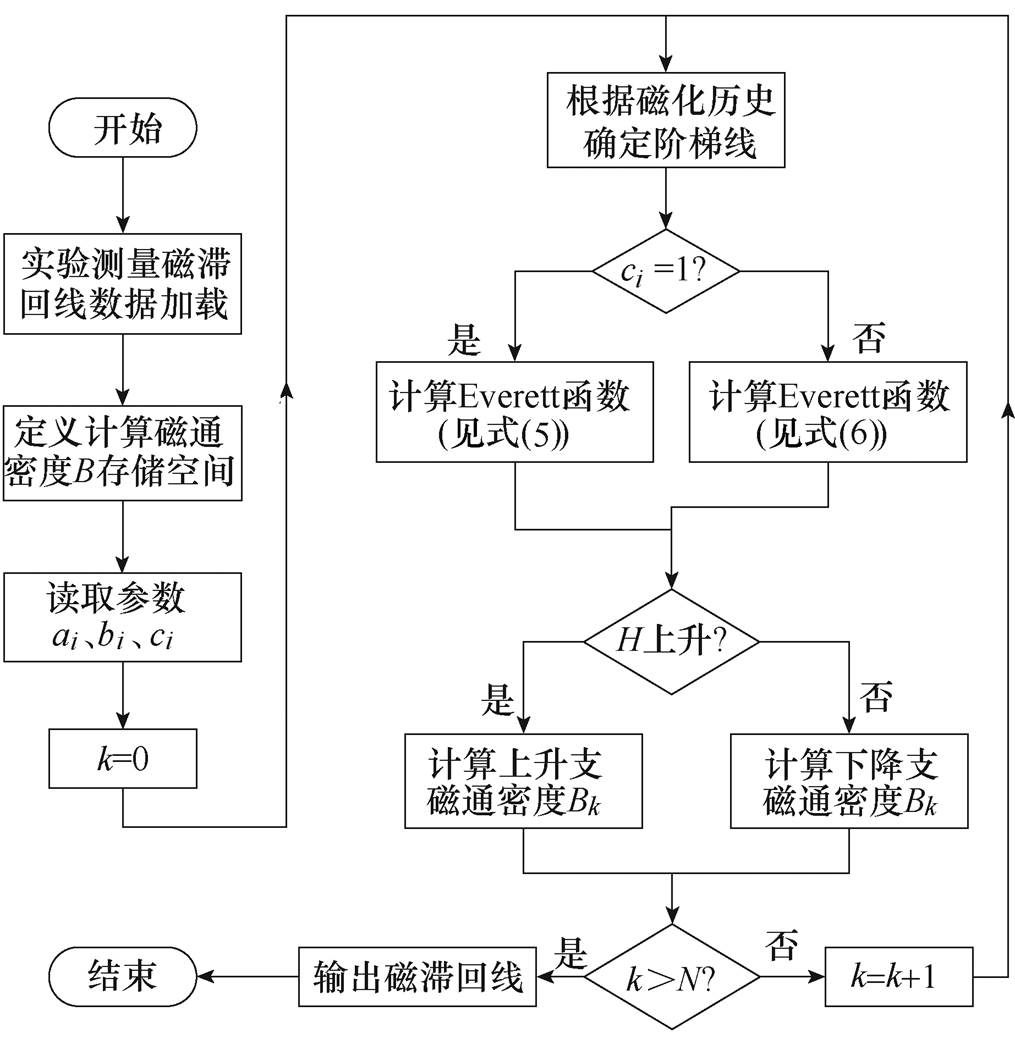
图1 Preisach模型计算过程
Fig.1 Calculation process of the Preisach model
Preisach模型本质上是一种输入速率无关的静态磁滞模型，本文在进行参数辨识时需要获取材料的准静态（f =5Hz）磁滞回线。为此，本文根据IEC 60404-2标准搭建了如图2所示的一维磁特性测量平台。该测量平台包括：基于NI PXI6115多功能数据采集系统、基于Labview嵌入式软件控制系统、AE7548功率放大器、爱泼斯坦（Epstein）方圈以及信号调理模块SR560。基于上述测量平台，在准静态（f =5Hz）条件下对B30P150硅钢片进行测试，得到B30P150型电工钢片在最大磁通密度分别为0.2T、1.0T、1.6T、1.8T时的静态磁滞回线，如图3所示。
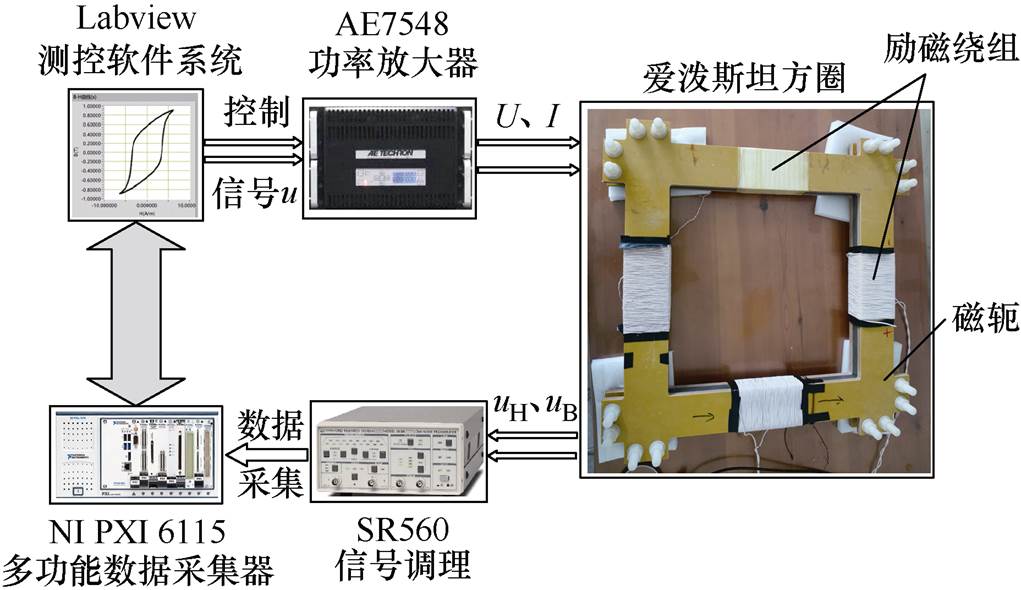
图2 磁特性测量系统
Fig.2 Magnetic properties measurement system
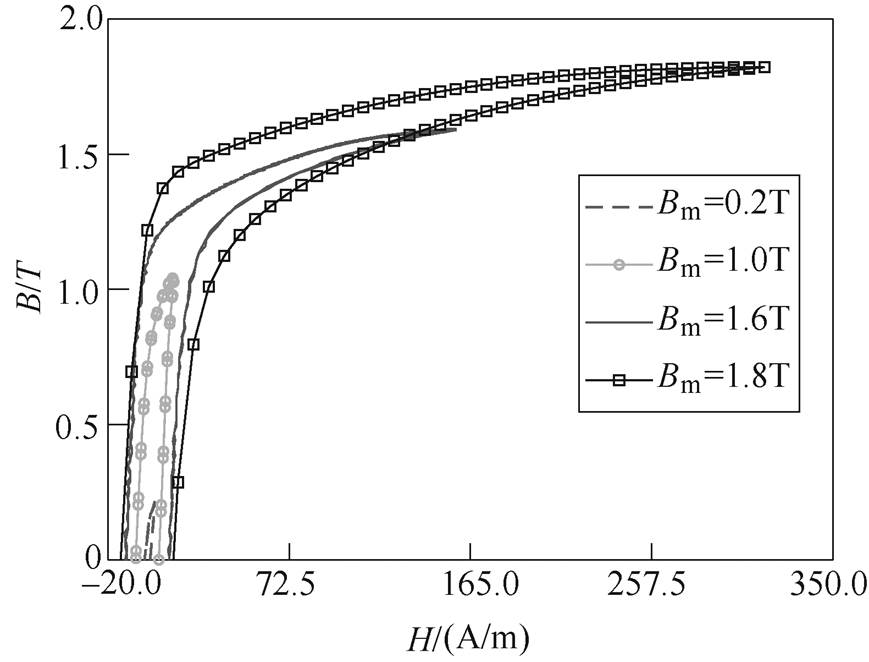
图3 B30P150硅钢片准静态磁滞回线
Fig.3 The quasi-static hysteresis loops of silicon steel B30P150
磁性材料的磁滞回线模拟是一个复杂的非线性多分支问题，在数值实现过程中的数学函数一般都是多参数的非线性组合，因此，在模型参数辨识过程中，需要借助全局优化算法构造寻求全局最优 解[21]。在全局优化问题中适应度函数（也称评价函数）的复杂度是优化算法复杂度的重要决定因素，因此，适应度函数在设计时应保证结果单值非负、计算的时间复杂度小。综合考虑模型参数优化问题，需以测量曲线数据为基准来检验模型的可靠性，故选择方均根误差作为适应度，有
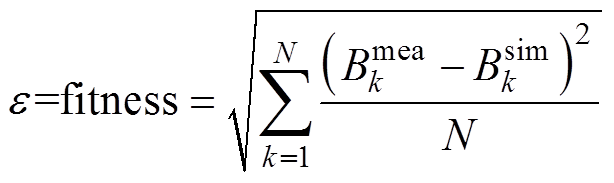（9）式中，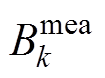
为一个周期内第k个磁通密度实验值；
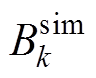为一个周期内第k个磁通密度计算值；N为采样个数。然而，若在Preisach模型的参数辨识过程中直接应用式（9），会造成适应度值太小、函数值太过接近、搜索过程中容易陷入局部最优等情况。为此，基于指数函数单调变化和增长率大的特点，本文将式（9）进行了非线性指数变换，使适应度修正值y有较大的区分度，实现高效的Preisach模型参数辨识且不陷入局部收敛，本文对比分析三种算法的辨识效果，评估侧重于迭代次数CPU计算时间、结果的准确性与可重复性。
遗传算法（Genetic Algorithms, GA）适用于具有多参数的优化辨识等复杂问题，但因其不依赖于初始种群的选择随机搜索机制，需要对目标函数进行多次评估以达到全局最小值，导致不能快速收敛。故在使用遗传算法辨识模型参数时，需要根据经验尽可能缩小搜索范围，以保证算法可以在较短的时间内找到最优解。遗传算法辨识Preisach磁滞模型参数流程如图4所示。
模拟退火（Simulated Annealing, SA）算法有着较好的收敛性和鲁棒性，且对目标函数以及约束函数没有限制，能较好地处理离散、连续和混合型等复杂非线性组合优化问题；但是在使用退火算法优化辨识参数时，需让初始温度足够高，降温速度足够慢，才更容易得到全局最优解。模拟退火算法辨识模型参数流程如图5所示。
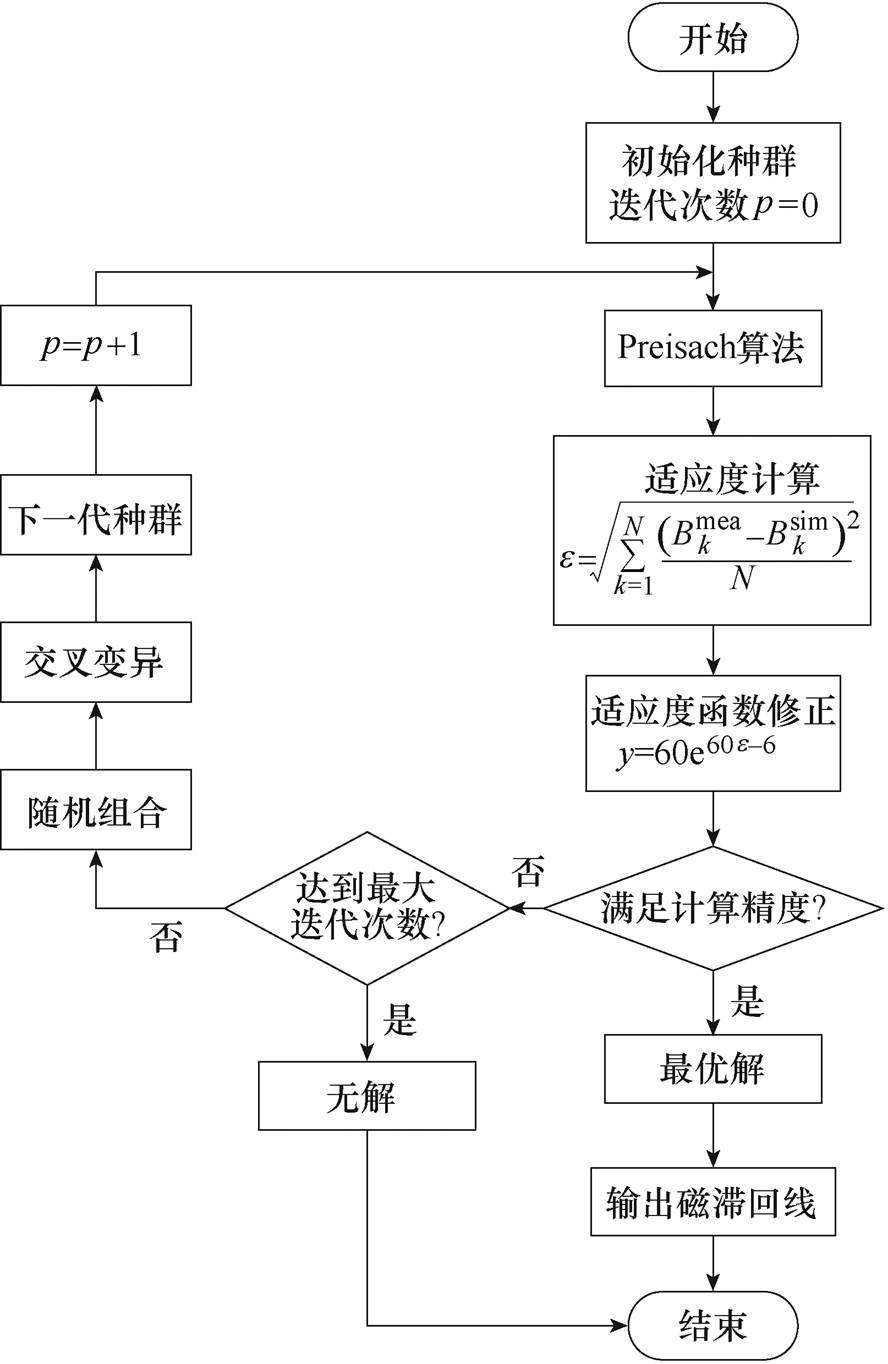
图4 GA辨识方法流程
Fig.4 The flowchart of GA method
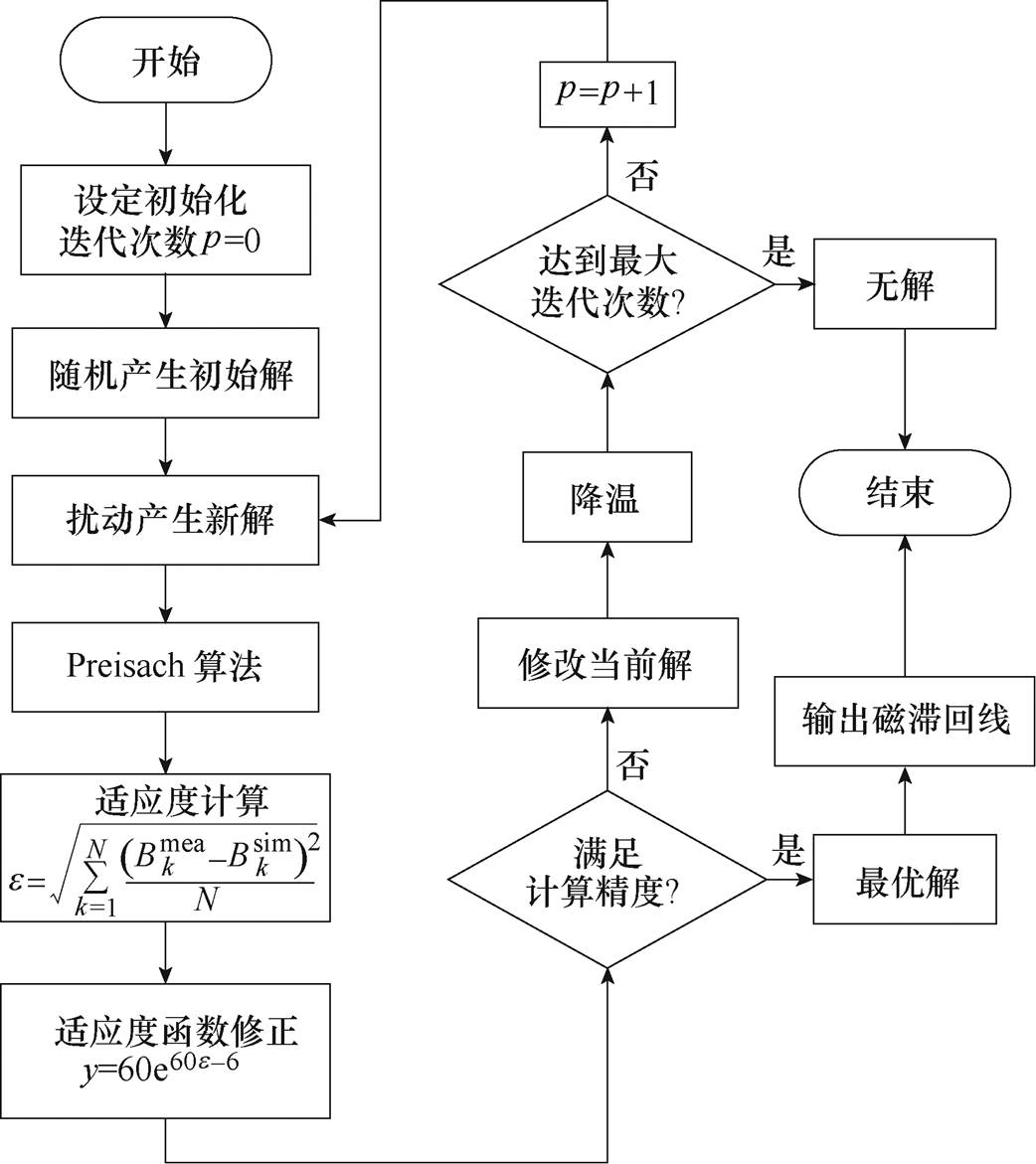
图5 SA辨识方法流程
Fig.5 The flowchart of SA method
针对传统粒子群算法高维复杂问题优化效果差、成功率低的问题，本课题组对传统粒子群算法进行了改进，提出了考虑粒子速度与边界关系的速度可控粒子群优化（Velocity-Controlled Particle Swarm Optimization, VCPSO）算法。在复杂非线性多分支问题中，传统粒子群算法因其速度无法调控，导致搜索效率低下、搜索精度不高、易陷入局部最优等问题。改进的速度可控粒子群算法对传统粒子群算法做了如下两项改进：①将传统粒子群算法的随机初始化粒子方法改为均匀初始化粒子方法；②通过统计更新后超出可行域粒子个数np与种群粒子个数ns的比值np/ns来判断粒子搜索状态是否需要调整：如果np/ns＜0.05，则通过改变惯性权重的衰减速度和最大速度限制值，增大粒子飞行速度；如果np/ns＞0.5，则调整惯性权重与最大限制速度，减小粒子速度；若0.05≤np/ns≤0.5，则保持先前搜索状态继续搜索。据此，达到对粒子搜索速度的自适应效果，实现粒子速度可控，提高搜索的成功率与收敛速度。
然而，由于速度可控粒子群算法以统计最新两代粒子前50%的优秀个体适应度平均值作为迭代终止条件，因此该方法不能直接应用于Preisach模型的参数辨识；同时，在优化过程中，当接近最优解时，由于其适应度值相近，变化不大。因此，传统算法的迭代终止条件易造成优化辨识精度不高、陷入局部最优。本文对速度可控粒子群算法进行了进一步改进，将速度可控粒子群算法的收敛迭代条件改为判断最新一代粒子群最优个体适应度是否满足精度要求，避免了算法在精度要求较高的参数辨识问题中易陷入局部最优的情况，参数辨识流程如图6所示。
首先，建立基于显式Everett函数的Preisach磁滞模型；其次，以实验值与计算值的方均根误差作为适应度函数。为了防止优化过程中适应度值区分度小的问题，本文根据指数函数快速增长的特性对传统的适应度函数进行了指数变换，得到适应度修正函数，并以修正函数对粒子做适应性评估；再次，合理设置速度可控粒子群初始参数，均匀初始化粒子群的位置信息，其中最大速度Vmax受到可行域范围[Xmin, Xmax]的约束，约束方程为：Vmax=k0(Xmax-Xmin)，k0的取值在0.1～1之间，且通常在每个参数维度都选择相同的设置取值；最后，根据上述搜索规则，更新粒子的速度、位置，完成辨识过程并输出待辨识模型分布函数的三组参数，绘制B30150型硅钢片的测量磁滞回线与仿真计算磁滞回线对比。
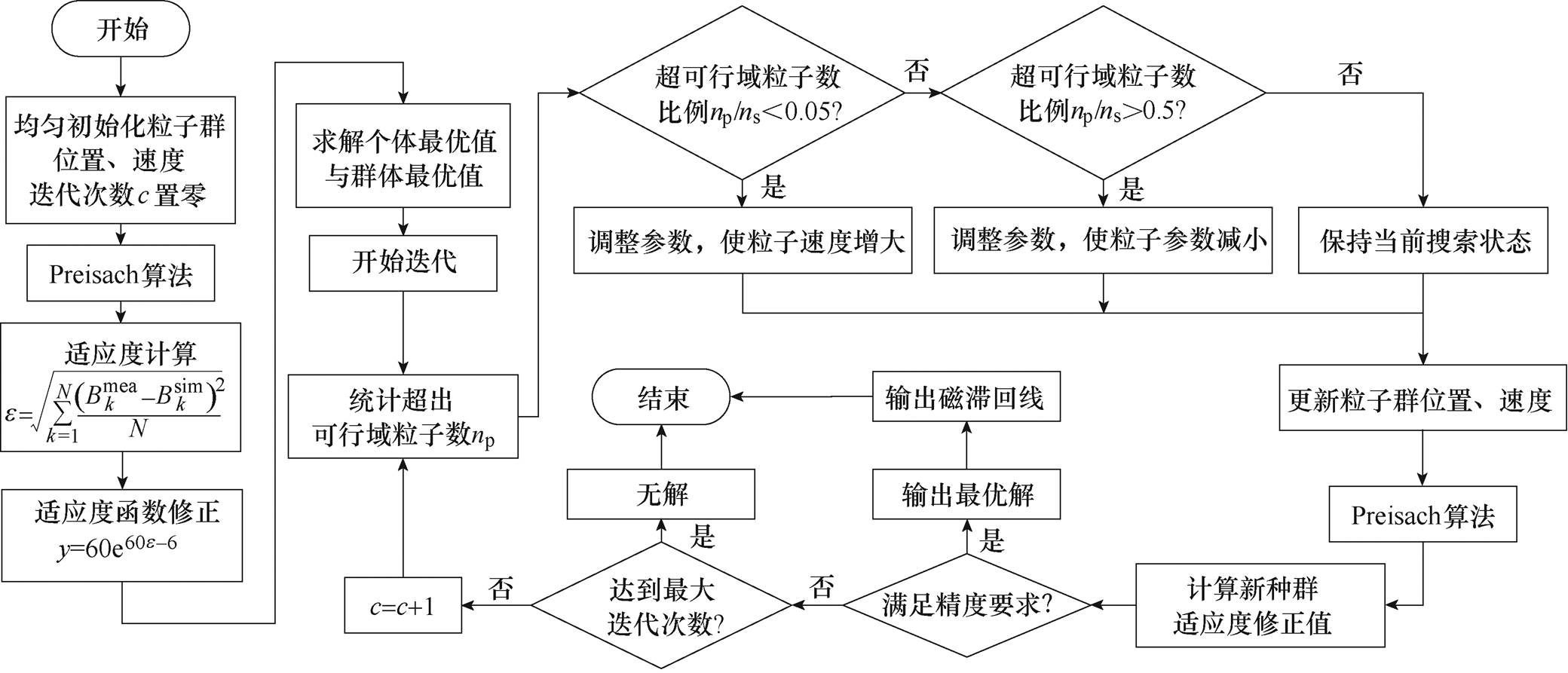
图6 改进VCPSO辨识方法流程
Fig.6 The flowchart of improved VCPSO method
本文运用遗传算法、模拟退火算法、改进速度可控粒子群算法三种全局智能优化算法分别完成了Preisach磁滞模型的参数辨识，分别计算得到B30P150硅钢片三种辨识方法相对应的磁滞回线，并对比辨识参数过程中三种优化算法所用的计算时间、迭代次数以及最终适应度函数修正值的最小值。通过对比分析仿真计算磁滞回线与实验测量的磁滞回线之间的方均根误差来验证模型的准确性与可靠性，评价三种算法在Preisach模型参数辨识过程中的优劣性。
图7～图9分别给出了三种优化算法仿真计算磁滞回线与测量得到的准静态磁滞回线对比。在辨识过程中，分布函数由3项一维指数函数累加和近似替代，即n=3，B30P150型硅钢片分布函数的参数辨识结果分别见表1～表3。对比分析遗传算法辨识法、模拟退火辨识法、速度可控粒子群算法辨识法三种方法的计算速度、辨识准确度，可以明显看出，在拟合效果上，速度可控粒子群优化算法辨识参数得到的磁滞回线与实验测量曲线具有最高的吻合度，能够较完美地拟合出B30P150硅钢片的磁滞回线。模拟退火算法辨识效果次之，遗传算法辨识效果最差，误差最大。但在不同精度要求下三种辨识方法均可以较好拟合B20P150硅钢片的磁滞回线，这也验证了该模型的有效性。
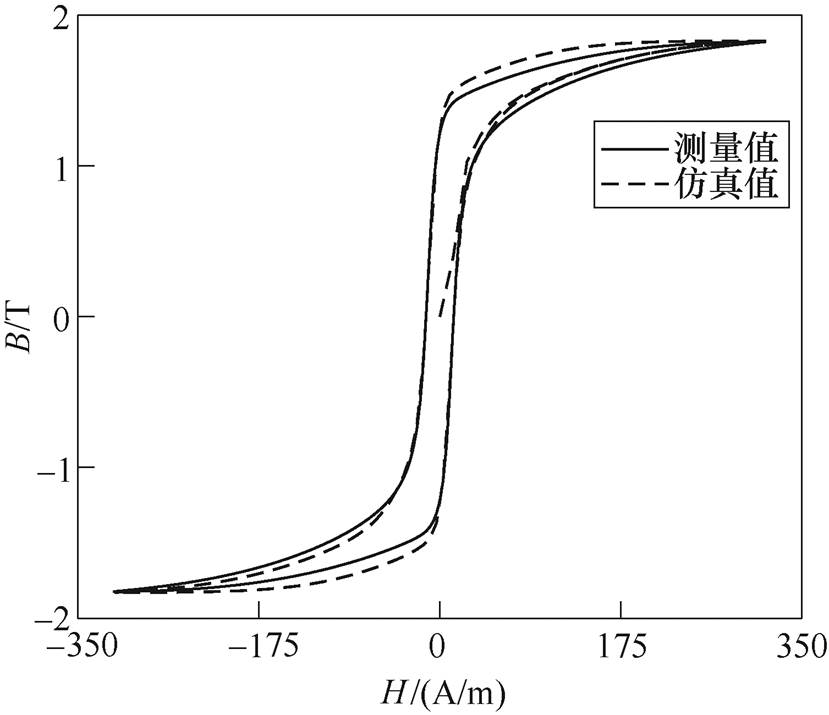
图7 遗传算法辨识
Fig.7 The identification approach of GA
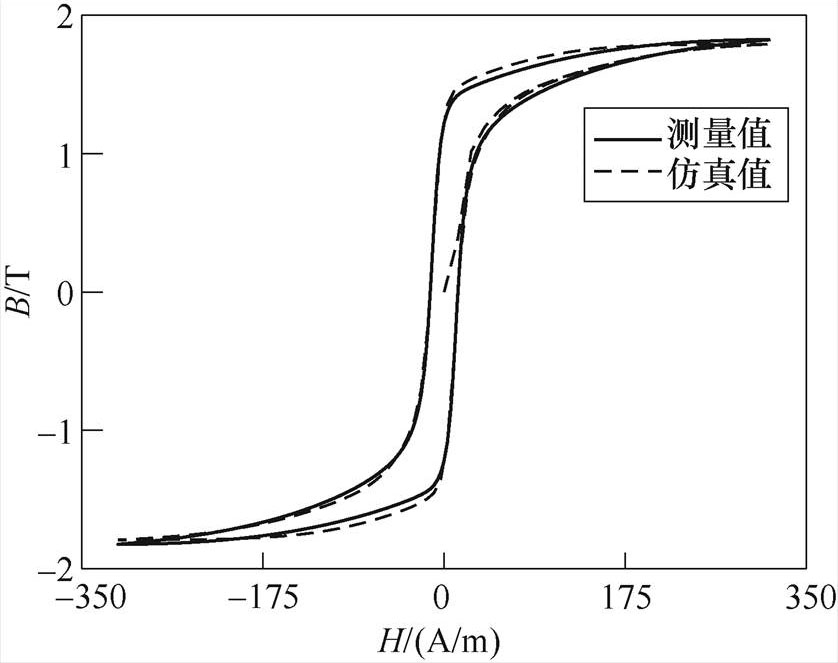
图8 模拟退火辨识
Fig.8 The identification approach of SA
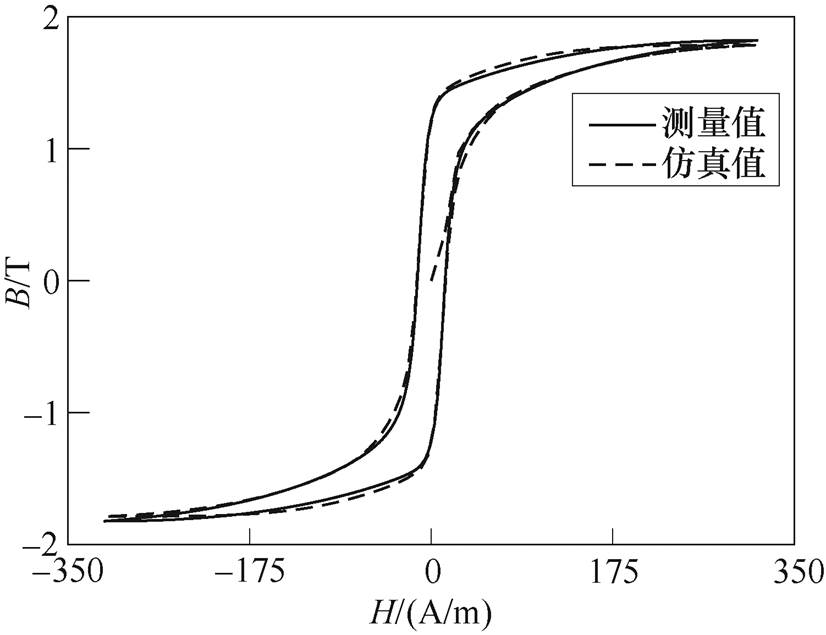
图9 速度可控粒子群优化辨识
Fig.9 The identification approach of VCPSO
表1 GA辨识方法在n=3时的分布函数参数
Tab.1 Parameters of distribution function at n=3 of GA
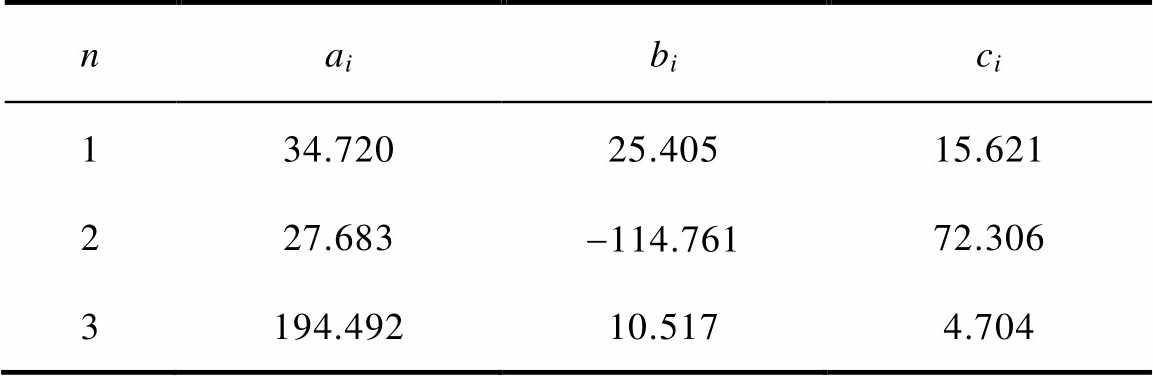
naibici 134.72025.40515.621 227.683-114.76172.306 3194.49210.5174.704
表2 SA辨识方法在n=3时的分布函数参数
Tab.2 Parameters of distribution function at n=3 of SA
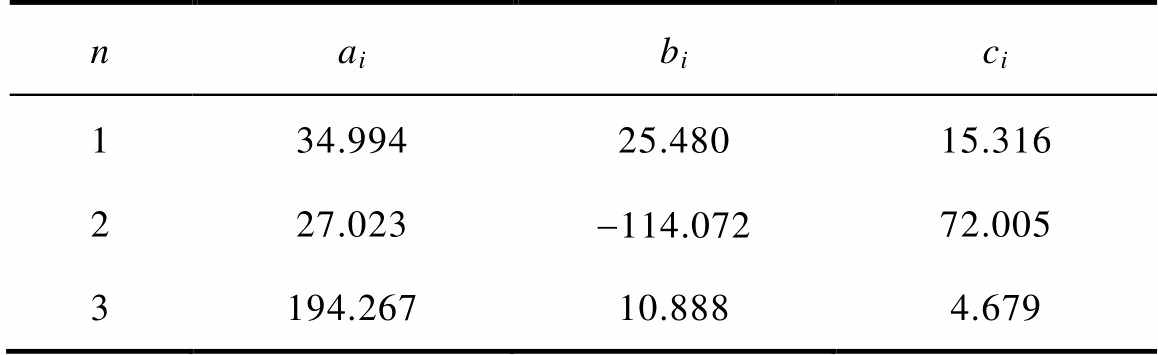
naibici 134.99425.48015.316 227.023-114.07272.005 3194.26710.8884.679
表3 VCPSO辨识方法在n=3时的分布函数参数
Tab.3 Parameters of distribution function at n=3 of VCPSO
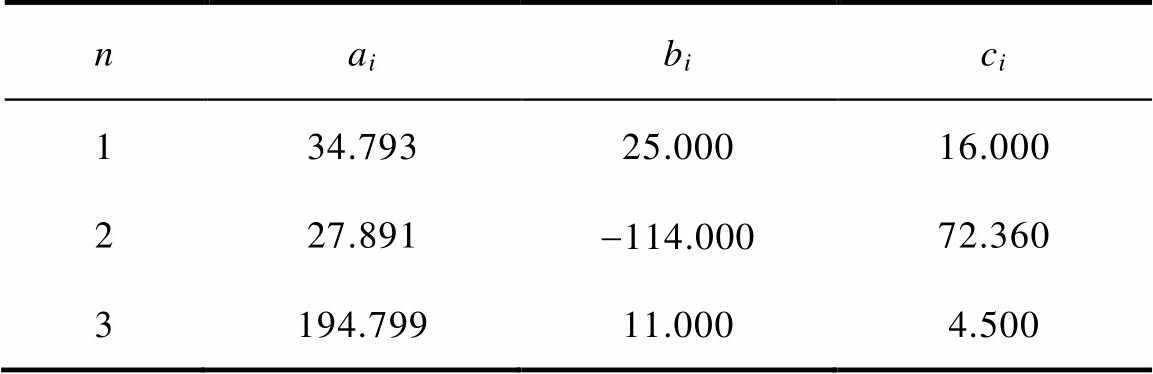
naibici 134.79325.00016.000 227.891-114.00072.360 3194.79911.0004.500
为了研究优化算法参数辨识过程中算法的计算效率与计算精度，利用三种优化算法对模型分别进行了参数辨识，过程如下：首先，设置相同的初始种群粒子数目、相等的最小允许误差值、相同参数的可行域（参数变量搜索范围）以及相同最大迭代次数；其次，优化算法提取Preisach模型分布函数参数，并分别输出三种方法适应度函数值与迭代次数的关系，如图10～图12所示；最后，记录三种优化算法在提取Preisach模型分布函数参数的过程所需要的计算时间。
图10～图12分别给出GA、SA算法与VCPSO算法在Preisach模型参数辨识问题中的收敛速度与最优适应度函数修正值。由于指数函数是单调函数，适应度函数在实际迭代过程中可由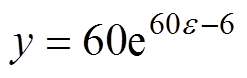
的修正值替代，加快收敛速度。适应度修正值y的最优值越小，算法的方均根误差越小，其精度越高；反之，精度越低。
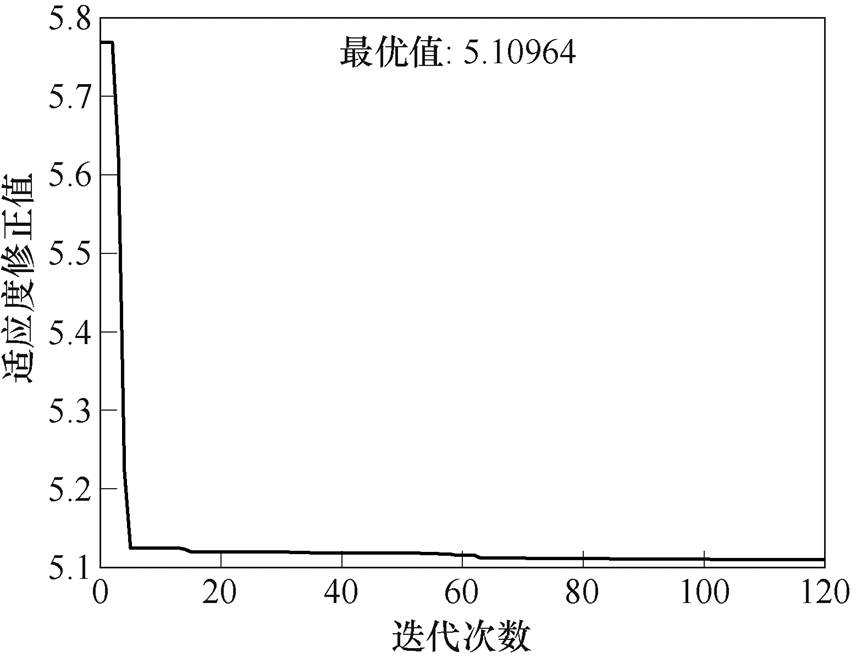
图10 GA辨识适应度随迭代次数变化
Fig.10 Fitness with the iterative number based on GA
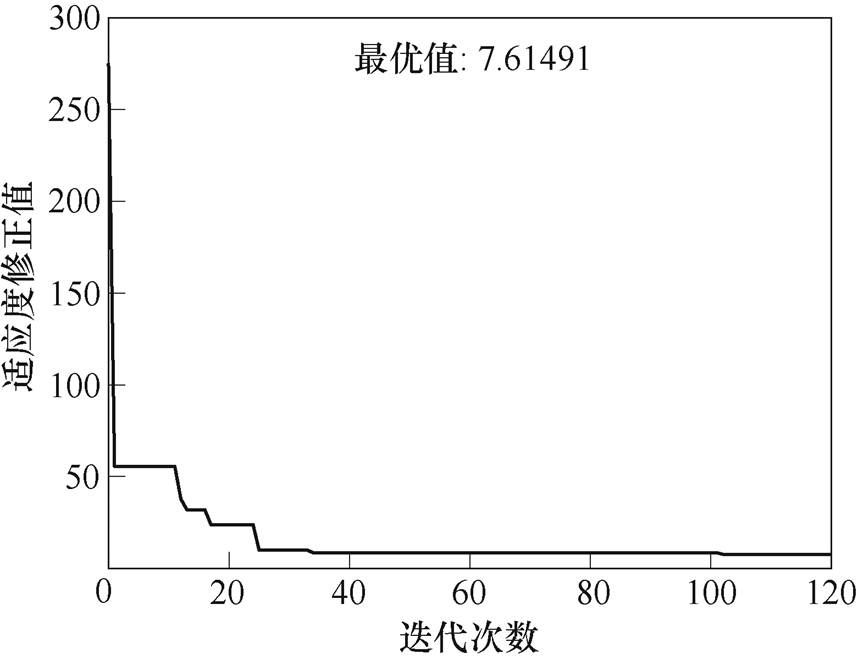
图11 SA辨识适应度随迭代次数变化
Fig.11 Fitness with the iterative number based on SA
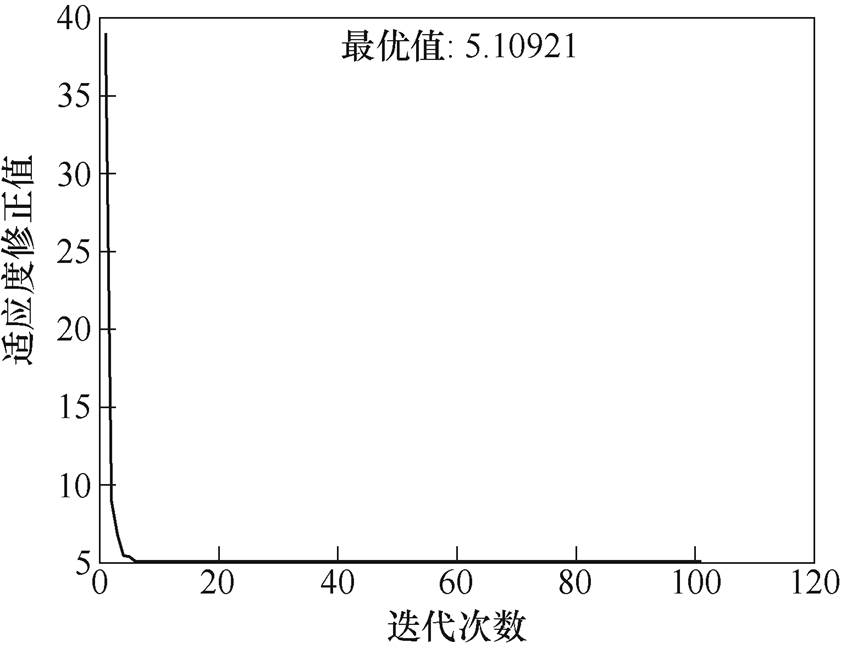
图12 VCPSO辨识适应度随迭代次数变化
Fig.12 Fitness with the iterative number based on VCPSO
从上述结果来看：收敛精度方面，遗传算法与速度可控粒子群算法精度较高，退火算法次之；迭代次数方面，速度可控粒子群算法收敛最快，退火算法次之，遗传算法迭代次数最多。
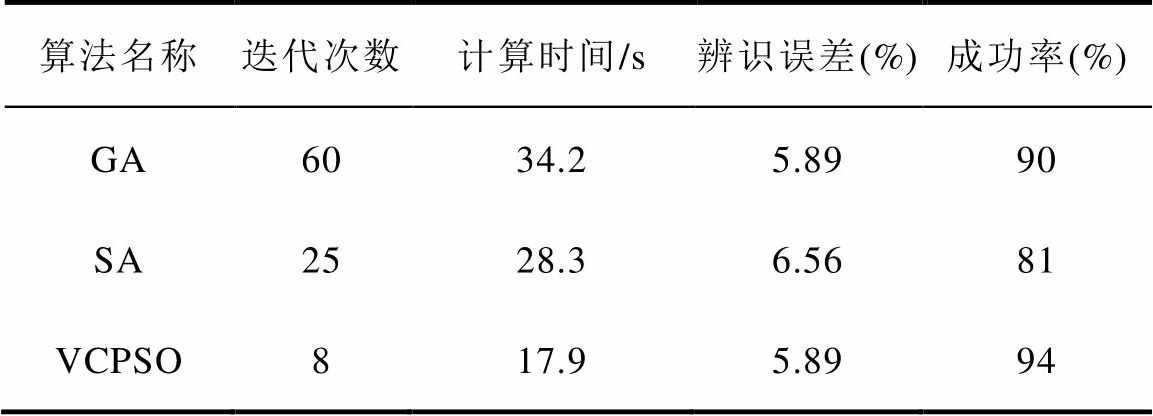
为了进一步测试三种优化算法在Preisach模型参数辨识过程中的可靠性。本文对三种算法进行了成功率测试，在测试过程中运行算法100次，统计成功找到最优解的次数。表4给出了三种算法在迭代次数、计算时间、辨识误差以及搜索成功率四个评价指标的对比。可以看出，速度可控粒子群算法具有最高的成功率以及最少的计算时间；通过适应度最优值计算出方均根误差的值，可以看出，遗传算法与速度可控粒子群算法精度较高，模拟退火算法精度稍低；总体来看，速度可控粒子群算法在辨识Preisach模型参数的问题上有着辨识精度高、计算速度快的优异性能。
表4 算法辨识优化结果对比
Tab.4 Comparison of algorithm results
算法名称迭代次数计算时间/s辨识误差(%)成功率(%) GA6034.25.8990 SA2528.36.5681 VCPSO817.95.8994
图13给出了利用由VCPSO算法对极限磁滞回线辨识得到的参数来模拟各个磁通密度Bm=1.0T、1.6T、1.8T下的磁滞回线。通过仿真值与实验数据对比发现：由本文所建立的模型在模拟最外层磁滞回线时得到了精确的结果，而在内部磁滞回线的模拟上存在一定的误差；计算方均根误差，得到内部磁滞回线的误差在10%以内。产生这种现象的主要原因为，在对Everett函数进行近似时，式（5）中n仅取了3项；当增加n的取值时，内部磁滞回线的模拟效果会得到明显改善，但会增加辨识参数，进而增加辨识难度和计算时间。考虑到计算效率，本文仅采取了3项指数函数来近似计算，亦可满足工程应用的精度要求。
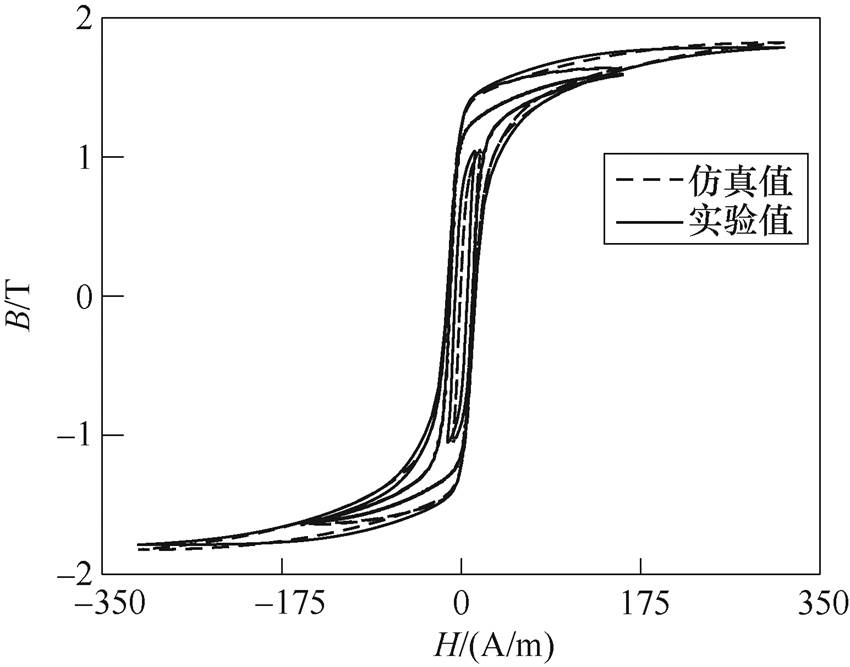
图13 内部磁滞回线模拟
Fig.13 Simulation of inner hysteresis loops
Preisach模型参数辨识的关键在于Preisach分布函数参数的确定。在利用数值函数近似代替分布函数的过程中，为保证模型的精度，采用的数值函数都是带有参数的基础数学函数的组合，具有效率高、速度快等优点。同时，针对不同磁性材料，需结合全局优化算法寻找当前应用场景下的磁滞模型最优参数解集。本文针对上述问题：首先，建立了基于显式Everett函数的Preisach模型，测量了B30P105型硅钢片准静态磁滞曲线；其次，分别实现了遗传算法、模拟退火算法、改进速度可控粒子群算法对Preisach模型参数优化辨识，并计算仿真得到B30P105型硅钢片磁滞回线；最后，以上述测量数据作为材料磁滞特性基准，对比三种方法，结论如下：
1）在模型计算与实验的磁滞回线吻合度方面，速度可控粒子群的计算误差最低、吻合度最高。
2）在计算时间、算法寻优迭代次数以及搜索成功率方面，三种优化算法在Preisach模型参数辨识问题上，都能满足参数优化设计任务，但是在综合考虑辨识速度与精度的情况下，本文所提出的改进速度可控粒子群算法兼具收敛速度快、辨识精度高、搜索成功率最高的优异性能。
3）本文所建立的显式Everett函数Preisach模型在模拟内部磁滞回线时，内部磁滞回线模拟的最大误差在10%以内，满足工程计算需求，对实现Preisach模型参数的快速辨识具有重要意义。为提高电工装备电磁性能有限元模拟计算效率提供了有力保障。
参考文献
[1] Bertotti G. Generalized Preisach model for thedescrip- tion of hysteresis and eddy current effects inmetallic ferromagnetic materials[J]. Journal of Applied Physics, 1991, 69(8): 4608-4610.
[2] 赵志刚, 马习纹, 姬俊安, 等. 铁心动态Energetic建模与验证[J]. 电工技术学报, 2020, 35(20): 4241- 4250.
Zhao Zhigang, Ma Xiwen, Ji Jun’an, et al. Dynamic Energetic modeling and verification of core under harmonic excitation[J] Transactions of China Elec- trotechnical Society, 2020, 35(20): 4241-4250.
[3] 李超, 徐启峰. 随温度变化的Preisach磁滞模型建模方法[J]. 电工技术学报, 2013, 28(12): 90-94.
Li Chao, Xu Qifeng. Modeling of temperature dependent hysteresis based on Preisach theory[J]. Transactions of China Electrotechnical Society, 2013, 28(12): 90-94.
[4] 刘任, 李琳, 王亚琦, 等. 基于随机性与确定性混合优化算法的Jiles-Atherton磁滞模型参数提取[J]. 电工技术学报, 2019, 34(11): 2260-2268.
Liu Ren, Li Lin, Wang Yaqi, et al. Parameter extraction for Jiles-Atherton hysteresis model based on the hybrid technique of stochastic and deter- ministic optimization algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2260- 2268.
[5] 贲彤, 陈龙, 闫荣格, 等. 考虑磁化及磁致伸缩特性各向异性的感应电机铁心电磁应力分析[J]. 电工技术学报, 2019, 34(1): 66-74.
Ben Tong, Chen Long, Yan Rongge, et al. Stress analysis of induction motor core considering aniso- tropic magnetic and magnetostrictive properties[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 66-74.
[6] Mayergoyz I. Mathematical model of hysteresis and their applications[M]. New York: Academic Press, 2003.
[7] Finocchio G, Carpentieri M, Cardelli E. Analytical solution of Everett integral using Lorentzian Preisach function approximation[J]. Journal of Magnetism and Magnetic Materials, 2006, 300(2): 451-470.
[8] Ferenc V, Edward D T. Minor loops in magnetization dependent Preisach models[J]. IEEE Transactions on Magnetics, 1992, 28(2): 1245-1248.
[9] Hussain S, Lowther D A. An efficient implementation of the classical Preisach model[C]//21st Conference on the Computation of Electromagnetic Fields, Daejeon, 2017:1-6.
[10] Zhao Xiaojun, Guan Dawei, Zhang Honggang, et al. Simulation of Preisach hysteresis model based on the first-order reversal curves[J]. International Journal of Applied Electromagnetics & Mechanics, 2017, 55(1-4): 1-9.
[11] 赵小军, 刘小娜, 肖帆, 等. 基于Preisach模型的取向硅钢片直流偏磁磁滞及损耗特性模拟[J]. 电工技术学报, 2020, 35(9): 1849-1857.
Zhao Xiaojun, Liu Xiaona, Xiao Fan, et al. Hysteretic and loss modeling of silicon steel sheet under the DC biased magnetization based on the Preisach model[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1849-1857.
[12] 段娜娜, 徐伟杰, 李永建, 等. 基于极限磁滞回线法的软磁复合材料磁特性模拟[J]. 电工技术学报, 2018, 33(20): 4739-4745.
Duan Nana, Xu Weijie, Li Yongjian, et al. Electro- magnetic property modeling of the soft magnetic composite material based on the limiting loop method[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4739-4745.
[13] 段娜娜, 徐伟杰, 李永建, 等. 一种考虑温度和压力影响的磁滞模型及其实验验证[J]. 电工技术学报, 2019, 34(13): 2686-2692.
Duan Nana, Xu Weijie, Li Yongjian, et al. A temperature and stress dependent hysteresis model with experiment validation[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2686-2692.
[14] Duan Nana, Xu Weijie, Wang Shuhong, et al. Hysteresis modeling of high-temperature super- conductor using simplified Preisach model[J]. IEEE Transactions on Magnetics, 2015, 51(3): 1-4.
[15] 张长庚, 杨庆新, 李永建. 电工软磁材料旋转磁滞损耗测量及建模[J]. 电工技术学报, 2017, 32(11): 208-216.
Zhang Changgeng, Yang Qingxin, Li Yongjian. Measurement and modeling of rotational hysteresis loss of electric soft magnetic material[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 208-216.
[16] Zsolt Szabó, János Füzi. Implementation and identi- fication of Preisach type hysteresis models with everett function in closed form[J]. Journal of Mag- netism & Magnetic Materials, 2016, 406: 251-258.
[17] Zsolt Szabó, Tugyi I, Gy Kádár, et al. Identification procedures for scalar Preisach model[J]. Physica B: Physics of Condensed Matter, 2004, 343(1/4): 142- 147.
[18] Zsolt Szabó. Preisach functions leading to closed form permeability[J]. Physica B: Condensed Matter, 2006, 372(1-2): 61-67.
[19] Stoleriu L, Andrei P, Stancu A. First order reversal curves identification procedures for vector models of hysteresis[J]. Journal of Applied Physics, 2008, 103(7): 07D923-07D926.
[20] Sjostrom M. Frequency analysis of classical Preisach model[J]. IEEE Transactions on Magnetics, 1999, 35(4): 2097-2103.
[21] Hergli K, Marouani H, Zidi M. Identification of Preisach hysteresis model parameters using genetic algorithms[J]. Journal of King Saud University Science, 2019, 31(4): 746-752.
Application and Performance Comparison of Global Optimization Algorithms in the Parameter Identification Problems of the Preisach Hysteresis Model
Abstract The rapid identification of the Preisach model parameters is of great significance to realize the finite element calculation of electrical equipment considering the hysteresis characteristics. Combined the explicit Everett function with the Preisach model, this paper proposes a parameter identification method based on an improved velocity-controlled particle swarm optimization algorithm, and compares the efficiency of the global optimization algorithm. Firstly, a parameterized explicit expression of the Everett function is constructed to solve the problem that low computational efficiency of the traditional discrete Preisach model as the storage of Everett matrix is huge. Secondly, a parameter identification method of the Preisach model based on the improved velocity-controlled particle swarm optimization algorithm is proposed. Based on the measured quasi-static hysteresis loops of silicon steel sheet, the parameters of the Preisach model are identified. Finally, the simulated annealing algorithm, genetic algorithm, and the algorithm proposed in this paper are compared and analyzed in terms of the iterations number and calculation time, the accuracy of hysteresis loop simulation, and the success rate of Parameter identification. The results show that the improved velocity-controlled particle swarm optimization algorithm proposed in this paper has high identification accuracy, fast convergence speed, and high success rate in identifying the Preisach model.
keywords：Hysteresis model, global optimization, electrical magnetic material, magnetic properties simulation
中图分类号：TM271
DOI: 10.19595/j.cnki.1000-6753.tces.201294
国家自然科学基金项目（52007102）、省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学）开放课题（EERIKF2019009）、湖北省自然科学基金项目（2020CFB212）、宜昌市应用基础研究项目（A19-302-03）和湖北省输电线路工程技术研究中心（三峡大学）开放基金课题（2019KXL10）资助。
收稿日期 2020-09-23
改稿日期 2021-01-03
陈 龙 男，1989年生，博士，讲师，硕士生导师，研究方向为磁性材料磁特性模拟、全局优化设计。E-mail: chenlong@ctgu.edu.cn
贲 彤 女，1991年生，博士，讲师，硕士生导师，研究方向为磁性材料磁特性、电磁场数值分析。E-mail: bentong@ctgu.edu.cn（通信作者）
（编辑 崔文静）