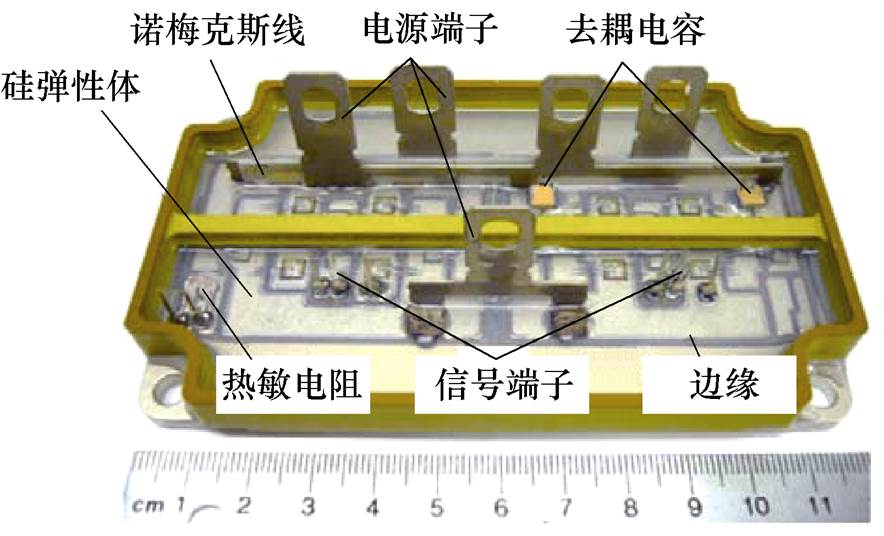
图1 有机硅弹性体灌封SiC MOSFET实物
Fig.1 Diagram of SiC MOSFET sealed by silicon elastomer
摘要 有机硅弹性体因具有良好的绝缘性与耐高温的特性,广泛应用于高频、高压、高温工况下的SiC器件中。在宽频率、宽温度范围内,有机硅弹性体材料的介电性能对SiC器件内部电场分布产生极大影响,因此该文采用频域介电谱分析方法获得了宽频(10-2~107Hz)、宽温度(20~280℃)范围内的有机硅弹性体介电特性数据,掌握有机硅弹性体在不同频率、温度条件下的介电弛豫过程,在此基础上,采用改进Cole-Cole模型对有机硅弹性体的弛豫特性进行分析,获得温度对有机硅弹性体介电响应过程与介电特征参数的影响规律。研究结果表明,随频率上升,复介电常数实部明显下降并趋于稳定,复介电常数虚部呈现先下降后上升到达峰值的趋势。在高温低频条件(160℃以上,100Hz以下)下,有机硅弹性体材料出现明显的低频弥散现象,280℃下观测到了电荷扩散过程的出现;不同温度下Cole-Cole模型特征参数中直流电导率sdc、弛豫强度De 与低频弥散强度x 与温度的关系满足Arrhenius方程规律;高频介电常数e∞随温度升高而降低,与温度近似呈线性变化;弛豫时间t 在高温下随温度上升具有明显指数型下降趋势,其机理可利用双势阱模型描述。该文获得的有机硅弹性体宽频、宽温度范围内的介电特性可以为SiC器件封装绝缘设计提供数据支撑。
关键词:SiC器件 宽频介电谱 有机硅弹性体 低频弥散 电荷扩散 Cole-Cole模型
高压大功率SiC器件是支撑电网新技术发展的基础。SiC材料相较于传统Si材料具有更高的耐压强度、更低的通态损耗、更高的饱和漂移速率、更高的热导率与更优的化学稳定性,使得其满足更高电压、更高开关频率、更高功率密度场合的需求。SiC器件更为复杂的工况因素对封装绝缘提出了更高的要求[1-2]。
有机硅弹性体材料具有良好的电气绝缘性能及耐超高温度的特性,且其固化后具有弹性与黏性,除可以满足SiC器件封装绝缘要求外,还可以为SiC器件内部应力均衡和粘接提供支撑;此外有机硅弹性体材料具有良好的阻燃性、防化学腐蚀性及一定程度的自愈性,可以满足器件长期运行的内部环境条件需求。因此,有机硅弹性体是高温、高压、高频工况下的SiC功率半导体器件封装绝缘材料的首选。
目前有机硅弹性体材料已经应用于众多SiC功率半导体器件的设计与实物封装中[3-4],图1展示了有机硅弹性体灌封SiC MOSFET实物[4],有机硅弹性体填充器件内部空间,使得器件各部分间具有良好的绝缘性与一定的抗振能力。
SiC器件正常运行频率为50Hz~500kHz[5],而SiC器件在导通和关断过程中,承受重复性方波电压,电压上升率升高,使得SiC器件承受的电压最高频率分量可达10MHz,同时SiC器件运行最高温度可达250~280℃[3-4]。绝缘材料在如此高的频率与温度范围内的介电特性会对重复性方波作用下SiC器件内部电场动态特性分布与绝缘性能产生重大影响。因此,需要对有机硅弹性体在宽频率、宽温度范围下的介电特性深入研究。

图1 有机硅弹性体灌封SiC MOSFET实物
Fig.1 Diagram of SiC MOSFET sealed by silicon elastomer
有机硅弹性体是一种特殊的硅凝胶,具有保持良好的固态形状的能力,其与普通硅凝胶的不同本质在于有机硅弹性体的交联度更大,包含非常少的自由液体混合物。针对功率器件封装用有机硅凝胶材料的介电特性及影响因素分析,国内外学者已经进行了部分研究。2006年法国国家科学研究中心和电介质材料实验室的M. T. Do等分析了高压功率半导体器件中绝缘封装用有机硅凝胶材料在20~160℃,10-4~103Hz范围内介质损耗的变化规律以及在不同时间的热老化作用下材料介电损耗的变化;并测得了在交流及直流电场下材料的介电强度,结果表明,两种情况下硅凝胶的介电强度都较高,且受温度影响小[6]。2014年弗吉尼亚工学院的Yao Yiying通过将有机硅弹性体悬涂在金属化的玻璃基板上,并在有机硅弹性体上方覆盖银电极的试验方式测量了不同频率下(1kHz与1MHz)的有机硅弹性体介电强度与相对电容率,结果表明,有机硅弹性体可以满足功率芯片封装的需求[3]。2014年法国的拉普拉斯实验室利用“三明治”电极结构测试了有机硅弹性体的介电特性,研究了在-150~300℃,10-1~106Hz范围内有机硅弹性体的介电特性变化,结果表明,在300℃以下时,有机硅弹性体的介电特性短期内基本稳定,但并未建立有机硅弹性体介电模型并对其介电特性进行描述[7]。可以看出,国内外缺乏对绝缘封装用有机硅弹性体在SiC器件运行所需宽频率、宽温度范围条件下的介电特性分析。
针对绝缘材料的介电特性的分析多采用介电弛豫模型来表征,而建立较为准确的宽频、宽温度范围的介电弛豫模型,对于考虑材料宽频介电特性影响的电场分布具有重要意义。常用的介电弛豫模型包括Debye模型、Cole-Cole模型、David-Cole模型、Havriliak-Negami模型和Dissado-Hill模型[8-16]。由于材料特性差异,难以用统一的介电弛豫模型来表征,需要结合材料自身的介电特性测量结果,选取合理的介电弛豫模型进行参数拟合,目前关于有机硅弹性体的介电弛豫模型还未见报道。
因此,本文面向高压SiC功率器件高温、高频运行工况需求,针对SiC器件封装常用的有机硅弹性体材料,测量了20~280℃、10-2~107Hz范围内的有机硅弹性体介电数据,利用改进Cole-Cole模型对有机硅弹性体介电弛豫过程进行表征,获得了温度对Cole-Cole模型的不同介电过程与介电特征参量影响规律。
本文测试有机硅弹性体为SiC器件用室温固化型双组份有机硅弹性体。有机硅弹性体制备平台[17]如图2所示,胶桶由空气压缩机提供动力,将液态的A、B组分注入点胶机,通过动态混合器将A、B两组分按1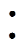 1比例混合,混合后利用控制器控制出胶量,将混合后的胶体装入模具中。
1比例混合,混合后利用控制器控制出胶量,将混合后的胶体装入模具中。

图2 有机硅弹性体制备平台
Fig.2 Silicon elastomer preparation platform
直接混合后的有机硅弹性体内部存在大量气泡,气泡是SiC器件封装绝缘的薄弱环节,因此需要对未固化的有机硅弹性体进行真空脱气处理[17]。本文引用文献[18]中关于气泡表面张力与黏性的关系和液体表面张力与黏性对气泡上升与变形的影响的相关理论,结合本课题组文献[17]中对有机硅凝胶多次泄压脱气过程的分析,同时由于相较普通硅凝胶,有机硅弹性体混合液黏度更大,内部气泡较难脱出;利用真空箱脱气时,因压强和温度的升高同样不利于气泡脱出等因素的影响,即采用常温下多次脱气、逐步排出气泡的方式,多次泄压过程解决了传统脱气过程脱气不完全的问题。脱气结束后,在80℃条件下固化1h可以得到良好的实验用有机硅弹性体实验样品,有机硅弹性体样品如图3所示,为透明状黏性固体,通过模具定型后,脱模可单独存放,状态不会发生改变,这一特性使得其在SiC器件中可以保持长久定型。

图3 有机硅弹性体样品
Fig.3 A sample of silicon elastomer
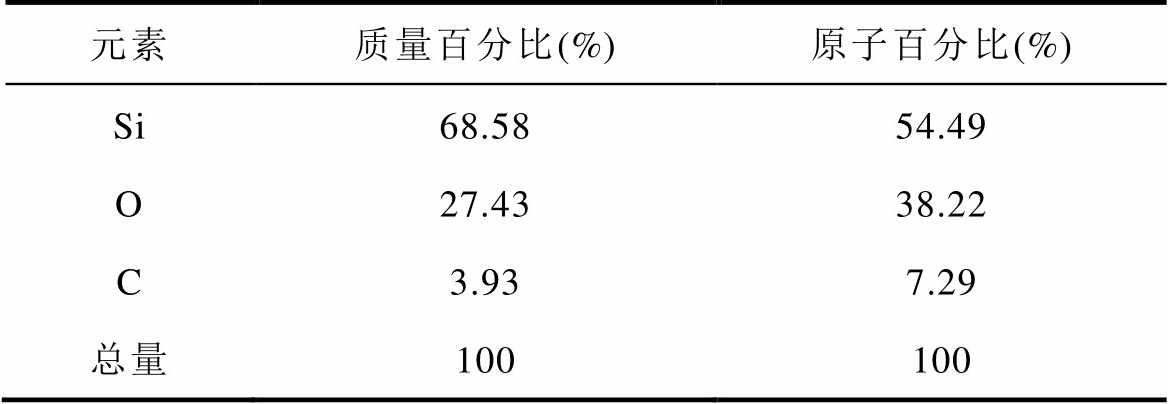
制备的试品经过扫描电镜(Scanning Electron Microscope, SEM)测试,测试结果如图4所示。有机硅弹性体在本文SEM测试中采用加速电压为15kV,从图4中可以看到,圈出部分为表面出现的不平整部分,尺寸为mm级,元素分析结果见表1,可以看出,制备出的试片杂质含量极少,表明制备的有机硅弹性体试片表面形貌良好,内部气泡与杂质颗粒较少,适合作为有机硅弹性体介电特性测量的实验样品。

图4 有机硅弹性体SEM测试结果
Fig.4 SEM test results of silicon elastomer
表1 有机硅弹性体元素含量
Tab.1 Element content of organic silicon elastomer
元素质量百分比(%)原子百分比(%) Si68.5854.49 O27.4338.22 C3.937.29 总量100100
有机硅弹性体试品经热重分析(Thermogravi- metric Analysis, TGA)测试,其测试曲线如图5所示,测试条件为:氮气环境、升温速率10℃/min。有机硅弹性体起始分解温度为280℃,280℃以下并无分解现象,结合文献[4]中有机硅弹性体在SiC器件高温测试中并无问题出现,说明有机硅弹性体可以满足SiC器件封装绝缘的温度需求。
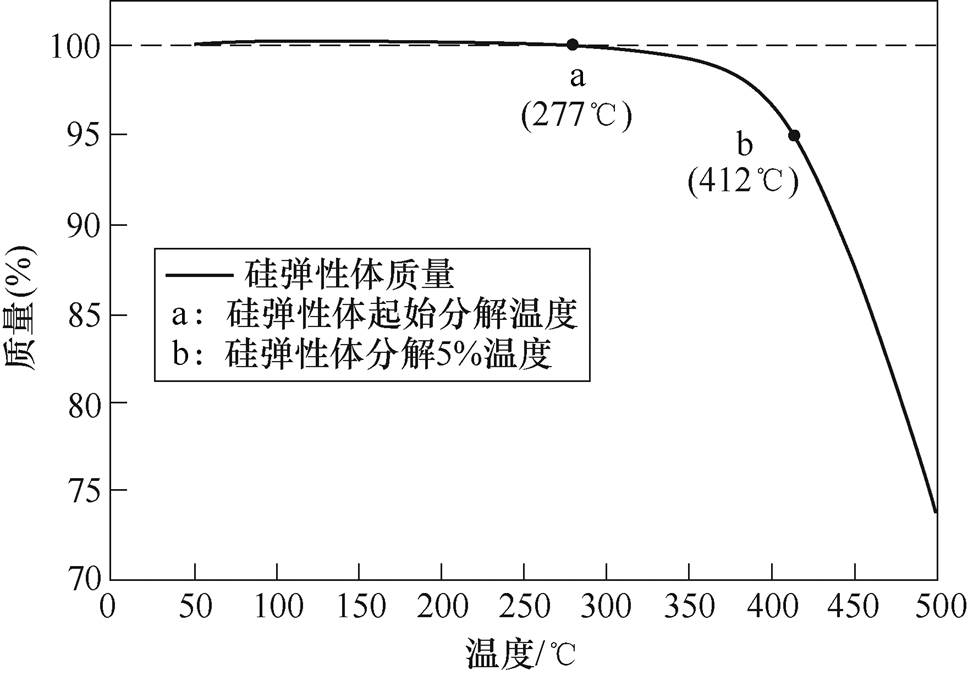
图5 有机硅弹性体的TGA测试曲线
Fig.5 TGA test curve of silicon elastomer
电介质的介电响应包括电导与极化两种基本的介电响应过程,两种过程分别对应自由载流子与束缚电荷的运动形式。在外电场作用下,电介质内部出现能量损耗与能量存储两种形式的能量转换,对应产生阻性电流与容性电流,因此容阻并联形式的电路常用于描述电介质材料的介电响应过程,电介质在外电场作用下的等效电路如图6所示。
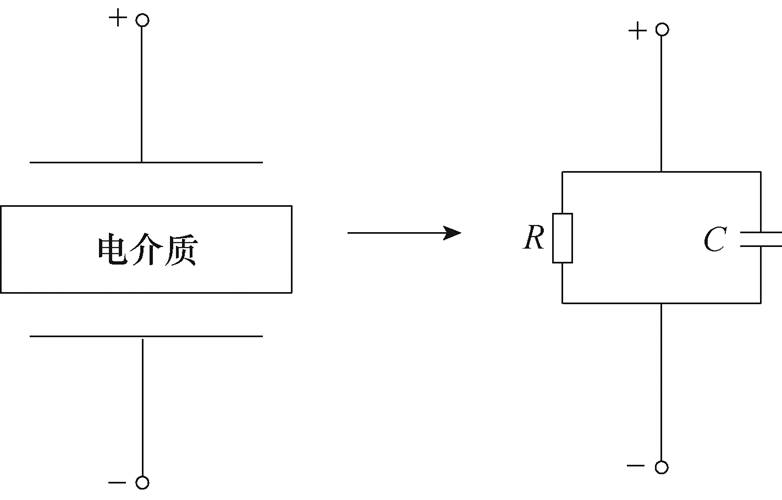
图6 电介质在外电场作用下的等效电路
Fig.6 The equivalent circuit of a dielectric under an external electric field
因此电介质内部电流可以定义为
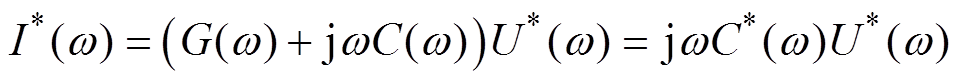 (1)
(1)式中,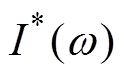 为电介质内部电流;
为电介质内部电流; 为图6中电阻的电导;
为图6中电阻的电导;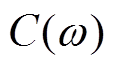 为图6中的电容;
为图6中的电容;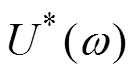 为电介质两端所加电压;
为电介质两端所加电压;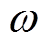 为外施电场角频率。
为外施电场角频率。
由此可以得到复电容C*与复相对介电常数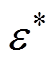 分别为
分别为
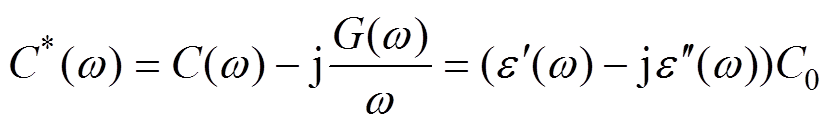 (2)
(2)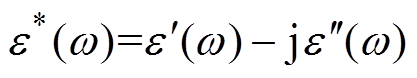 (3)
(3)
式中,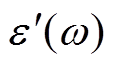 为复介电常数实部;
为复介电常数实部;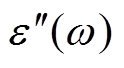 为复介电常数虚部。由式(2)和式(3)可见,复相对介电常数实部为极化强度大小,虚部为极化与电导过程的损耗。
为复介电常数虚部。由式(2)和式(3)可见,复相对介电常数实部为极化强度大小,虚部为极化与电导过程的损耗。
绝缘材料的介电特性测量主要包括时域方法与频域方法两大类[19]。本文采取频域方法中效果较好的频域介电谱(Frequency Domain dielectric Spectrum, FDS)方法,这种方法主要以材料的介电响应为基础,通过对试品在宽频率范围内施加激励,测得其介电常数等特征值。频域介电谱法因具有无损、不易受干扰等优点在绝缘材料特性测试中被广泛使 用[20-24]。由于研究使用的有机硅弹性体固化后具有良好的几何形状,因此可以使用平板电极进行测试。
因此,本文采取频域介电谱测试的方法,所用仪器为德国Novocontrol公司生产的宽频介电谱仪。针对SiC器件的实际应用工况,本文测量条件为:频率范围0.01Hz~10MHz,温度范围20~280℃(温度间隔为20℃),实验过程中,温度控制通过加热液氮使得测量用腔体内温度达到设定温度并保持,测量频率点数设置为80个。
不同温度下有机硅弹性体相对复介电常数的频域介电谱如图7所示。图7a和图7b分别给出了不同温度下的有机硅弹性体相对复介电常数的实部与虚部的测量结果。从测量图谱中可以看出,随频率升高,有机硅弹性体复介电常数实部下降并趋于稳定,复介电常数虚部呈现先下降后上升到达峰值的趋势;温度升高时,复介电常数实部稳定段下降,复介电常数虚部升高;特别地,当温度到达160℃时,复介电常数实部测量曲线在低频处出现了明显上升的趋势。为提取SiC器件封装所需有机硅弹性体介电数据,需要利用合适的介电模型对测试数据进行拟合。
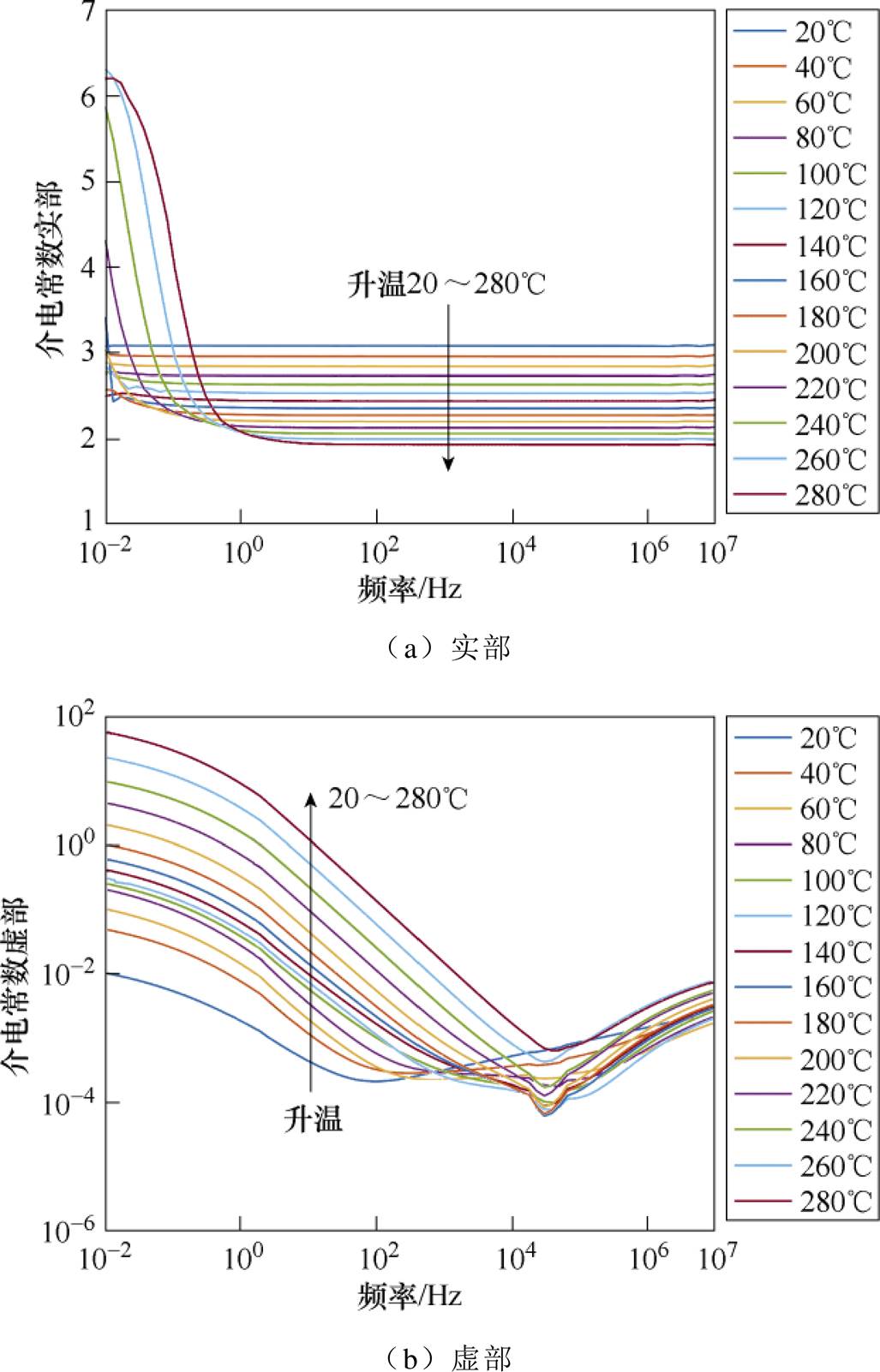
图7 不同温度下有机硅弹性体相对复介电常数的频域介电谱
Fig.7 Frequency domain dielectric spectroscopy of complex permittivity of silicone elastomer at different temperatures
Cole-Cole表征电介质复介电常数虚部与实部的关系,常用于判别介电弛豫行为偏离单一弛豫时间过程。图8给出了不同温度下有机硅弹性体复电模量的Cole-Cole,呈现单一的椭圆形,表明有机硅弹性体具有单一弛豫过程,但受电导等其他介电过程影响,脱离了Debye模型描述的标准半圆型[25]。温度升高,有机硅弹性体Cole-Cole占据面积增大,表明温度对有机硅弹性体介电过程有极大影响。结合本文介电谱测试结果,同时根据Cole-Cole呈现椭圆形较明显的特征,对文献[11]中给出的模型进行了改进,取拟合参数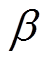 =1,同时引入参数
=1,同时引入参数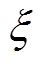 表征低频弥散强度,采用改进Cole-Cole模型对有机硅弹性体的介电弛豫特性进行拟合。
表征低频弥散强度,采用改进Cole-Cole模型对有机硅弹性体的介电弛豫特性进行拟合。
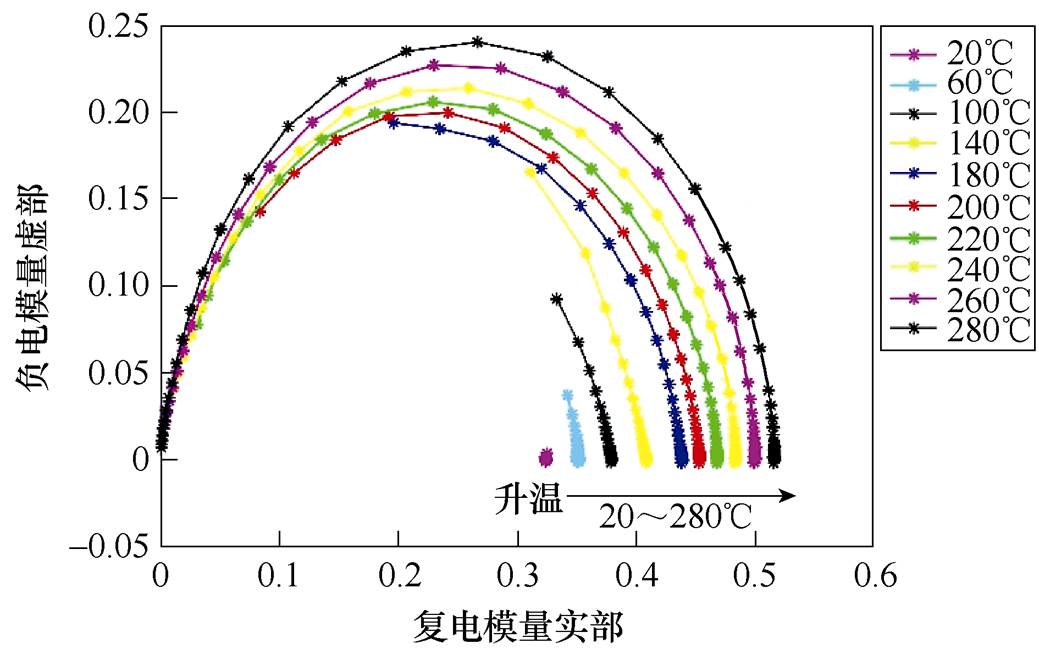
图8 不同温度下复电模量的Cole-Cole
Fig.8 Cole-Cole plots of complex electric modulus at different temperatures
结合图7分析,在有机硅弹性体复介电常数虚部低频处观测到明显的直流电导过程,高频处出现了明显的弛豫极化过程;复介电常数实部高频处有明显的高频介电稳定过程。但在测试温度160℃及以上时,复介电常数实部低频处出现了明显的反常上升的现象,部分文献中将图7a中低频处出现上升趋势归因于弛豫极化过程,但存在一定问题。
为进一步解释有机硅弹性体在高温低频处的反常现象,揭示有机硅弹性体完整的介电过程,确定改进Cole-Cole模型的表达形式,需要对电介质复介电常数实部与虚部关系进行进一步处理:结合式(2)分析,假设忽略电导损耗的影响,则复介电常数实部与虚部分别表征极化过程的强度与损耗的大小,由于此时复介电常数实部与虚部可由统一响应函数变换而来,因此二者之间满足Hilbert变换关系,这一关系被描述为Kramers-Kroning方程[26],即
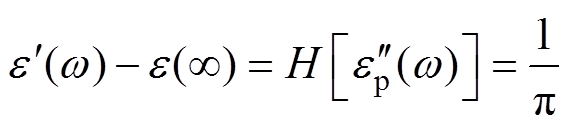

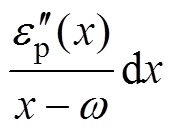 (4)
(4)式中,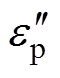 为忽略其他介电过程,仅表征弛豫极化过程引起的损耗强弱的复介电常数虚部;w 为外施电场角频率。
为忽略其他介电过程,仅表征弛豫极化过程引起的损耗强弱的复介电常数虚部;w 为外施电场角频率。
复介电常数实部与虚部关系如图9所示,表现为实部阶梯型下降段对应于虚部损耗峰出现,此时即为典型的弛豫极化过程,在图7b高频处可以观测到弛豫极化现象的出现,显然图7a中低频处的上升现象并不属于极化弛豫过程影响。
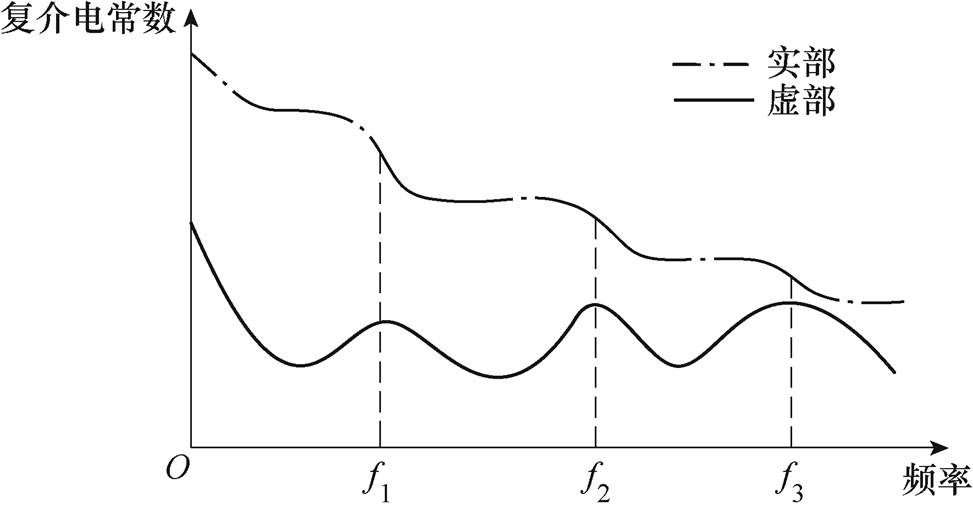
图9 复介电常数实部与虚部关系
Fig.9 The relationship between the real and imaginary parts of the complex dielectric constant
针对低频处这一现象,以A. K. Jonscher为代表的学者们提出了普适弛豫定律[8],该理论将电介质低频处复介电常数实部出现反常上升并未伴随弛豫峰出现的过程定义为低频弥散过程。
低频弥散过程的另一个特征为:在某一低频范围内,复介电常数虚部与实部在双对数坐标下相互平行,这一现象也称为CPA(constant phaseangle)现象。本文在160℃及以上测试的低频处测量结果符合此规律,因此确定在有机硅弹性体介电响应过程中出现了低频弥散这一介电响应过程,并需要在介电模型中加以考虑。
根据上述分析,在20~140℃时,复介电常数实部在测量频率范围内低频弥散过程的现象不明显。因此对于20~140℃测量范围,本文采取含有单一a 弛豫过程Cole-Cole模型对有机硅弹性体的相对复介电常数测量结果进行拟合,即
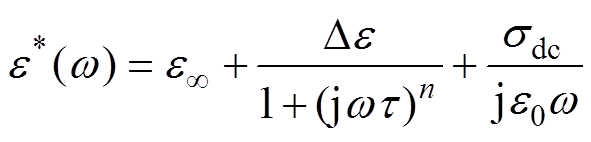 (5)
(5)式中,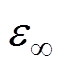 为高频介电常数;
为高频介电常数; 为弛豫极化强度;即静态介电常数es与无穷介电常数e∞ 的差值;e0为真空介电常数;t 为弛豫时间;n为弛豫参数;sdc为直流电导率。
为弛豫极化强度;即静态介电常数es与无穷介电常数e∞ 的差值;e0为真空介电常数;t 为弛豫时间;n为弛豫参数;sdc为直流电导率。
在测量温度160~280℃范围内,低频弥散过程已经可以被明显观测到,此时介电模型需要考虑低频弥散过程的影响,需添加一项来表征低频弥散过程,因此利用添加跳跃电导项的改进Cole-Cole模型进行拟合[11],即
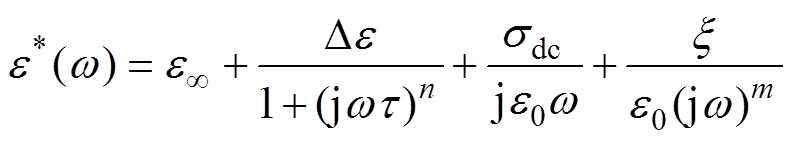 (6)
(6)式中,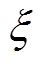 为低频弥散强度;m为低频弥散参数。低频弥散过程出现的物理本质在于电介质中,正、负电荷之间耦合作用不够强,导致电荷可以在有限制的通道上呈现自由跳跃的现象。因其图像形式为斜率固定的直线,类似电导过程,所以称之为跳跃电导项。
为低频弥散强度;m为低频弥散参数。低频弥散过程出现的物理本质在于电介质中,正、负电荷之间耦合作用不够强,导致电荷可以在有限制的通道上呈现自由跳跃的现象。因其图像形式为斜率固定的直线,类似电导过程,所以称之为跳跃电导项。
同时加以说明:图7b中,在测量最高温度280℃时,测量结果1Hz附近处出现了斜率变化的情况。这表明低频弥散过程达到了极限情况,在极高的温度与极低的频率下,电荷运动方式再次改变。文献[27]指出这一现象与电介质与电极接触处形成的偶电层有关,电荷扩散过程示意图如图10所示,这一过程称为电荷扩散过程。
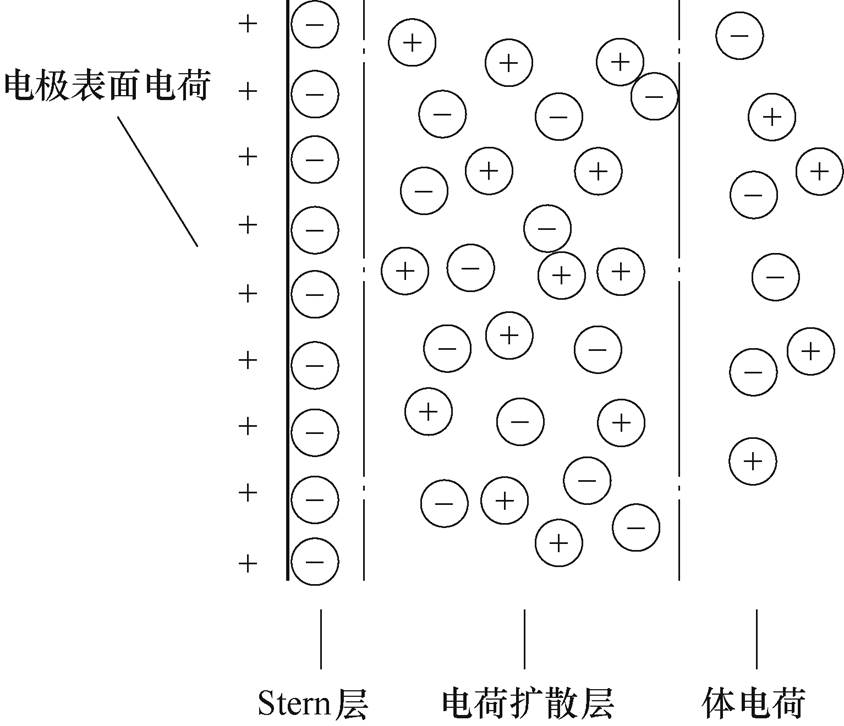
图10 电荷扩散过程示意图
Fig.10 Diagram of charge diffusion process
低频弥散过程与电荷扩散过程存在截止频率fc,因此,在考虑电荷扩散过程情况时,本文建议采用分段函数形式的Cole-Cole模型对电荷扩散现象进行描述:频率高于fc时表达式与式(6)相同,频率低于fc时在式(6)基础上添加电荷扩散过程修正项,修正项为
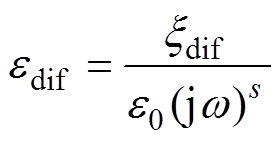 (7)
(7)式中,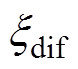 为电荷扩散强度,其表征参与电荷扩散过程电荷的浓度;s为电荷扩散过程特征参数,其与电荷扩散过程中电荷运动的分型维数以及电荷扩散运动过程指数有关[27-28]。一般取值范围为(1/3, 2/3)[29-30]。
为电荷扩散强度,其表征参与电荷扩散过程电荷的浓度;s为电荷扩散过程特征参数,其与电荷扩散过程中电荷运动的分型维数以及电荷扩散运动过程指数有关[27-28]。一般取值范围为(1/3, 2/3)[29-30]。
根据上述分析,可以总结出有机硅弹性体介电过程包括高频介电稳定过程、直流电导过程、弛豫极化过程、低频弥散过程与电荷扩散过程五部分。在本文测量范围内,电荷扩散过程现象并不明显,因此,本文忽略了电荷扩散过程,考虑其他四种介电过程,利用式(5)和式(6)给出的表达式进行分析。
根据式(6)给出的表达式,所需拟合特征参量为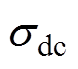 、
、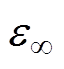 、
、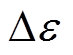 、
、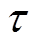 、n、
、n、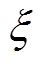 、m。采用先提取各参量初值,再基于最小二乘原理对选取的初值进行合理优化,从而获得各特征参量数值的算法。式(6)中复介电常数实部与虚部可分别表示为
、m。采用先提取各参量初值,再基于最小二乘原理对选取的初值进行合理优化,从而获得各特征参量数值的算法。式(6)中复介电常数实部与虚部可分别表示为
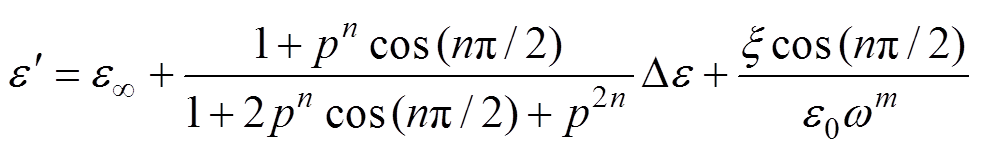 (8)
(8)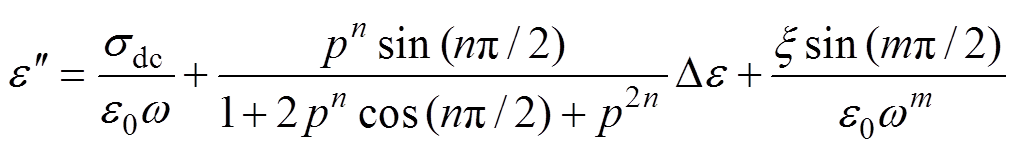 (9)
(9)
式中,p=wt。
直流电导率sdc仅影响介电常数虚部,在介电常数虚部低频段出现斜率为-1的部分,此时主要是直流电导的影响,忽略极化与低频弥散过程影响,得
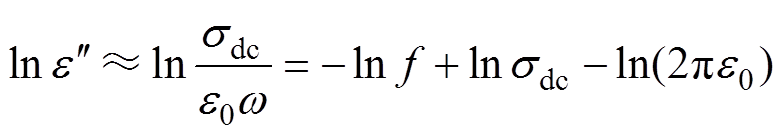 (10)
(10)式中,f为外施电压频率。设b为介电常数虚部低频段拟合的横截距,得到直流电导率sdc表达式为
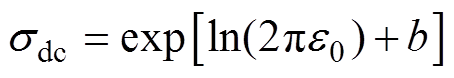 (11)
(11)
由式(6)可知,跳跃电导项的两个参数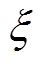 、m影响低频弥散过程。在相对介电常数实部低频处,高温(160℃及以上)情况下可以明显看到低频弥散现象的出现,此时有
、m影响低频弥散过程。在相对介电常数实部低频处,高温(160℃及以上)情况下可以明显看到低频弥散现象的出现,此时有
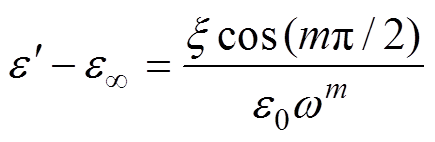 (12)
(12)两侧取对数得到
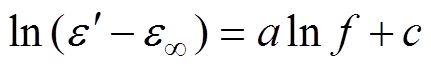 (13)
(13)
式中,a、c分别为双对数坐标下,去除高频介电常数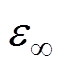 影响,高温低频下复相对介电常数实部与频率拟合一次函数的斜率与截距;
影响,高温低频下复相对介电常数实部与频率拟合一次函数的斜率与截距;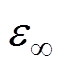 选取介电常数实部最小值。根据式(12)与式(13), m、
选取介电常数实部最小值。根据式(12)与式(13), m、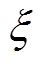 可分别表示为
可分别表示为
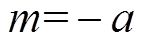 (14)
(14)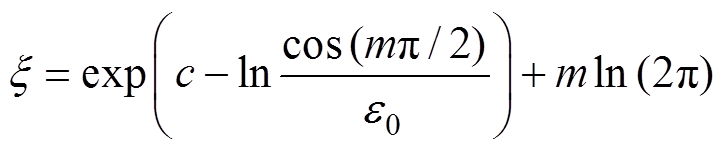 (15)
(15)
时间常数t 由弛豫峰所在位置决定,初值设置为峰值出现频率的倒数。n值取决于虚部高频处上升段斜率,虚部高频处弛豫现象起主要影响,此时忽略电导过程与低频弥散过程可以得到
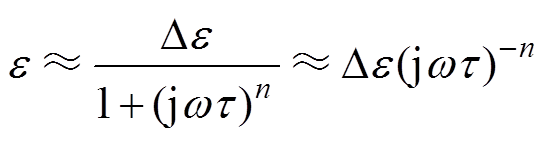 (16)
(16)利用三角形式表示为
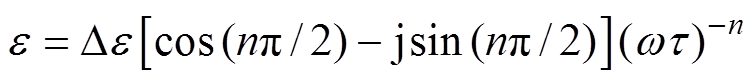 (17)
(17)
进一步地,可得
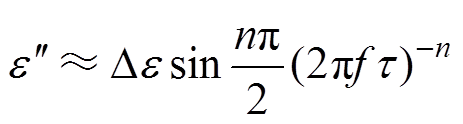 (18)
(18)式(18)两侧取对数,得到斜率绝对值即为n。
De 为静态介电常数与高频介电常数差值,为减小初值误差,本文选取介电常数虚部高频处最高频测量值,忽略电导过程与低频弥散过程,可以得到
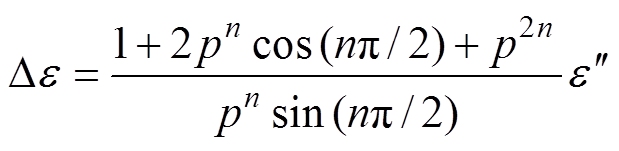 (19)
(19)电荷扩散过程参数初值的提取方式与低频弥散过程类似,截止频率fc选择复介电常数实部低频处的斜率改变处的频率数值。本文测量范围内电荷扩散过程影响微弱,因此忽略电荷扩散过程进行分析。
为了能够对测量结果进行准确拟合,防止出现局部误差过大影响拟合效果的问题,本文目标函数fv可以表示为
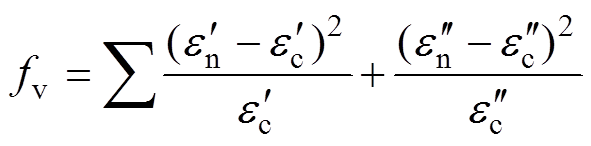 (20)
(20)式中,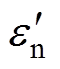 、
、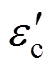 和
和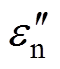 、
、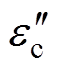 分别为复介电常数实部与虚部的计算值、实际值。优化目标是使目标函数达到最小值。约束条件防止出现数据不合理情况,限制电导率在一定范围内,即
分别为复介电常数实部与虚部的计算值、实际值。优化目标是使目标函数达到最小值。约束条件防止出现数据不合理情况,限制电导率在一定范围内,即
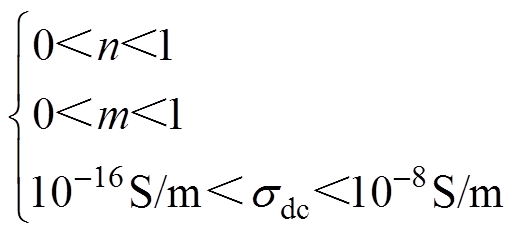 (21)
(21)
采用分温度区间拟合方式,对图7中的不同温度下的有机硅弹性体的介电特性测试结果进行了拟合,图11中给出了20℃和160℃下的测试和拟合对比结果,从图11中可以看出,本文提出的拟合方法及介电模型,可以很好地拟合实验结果。
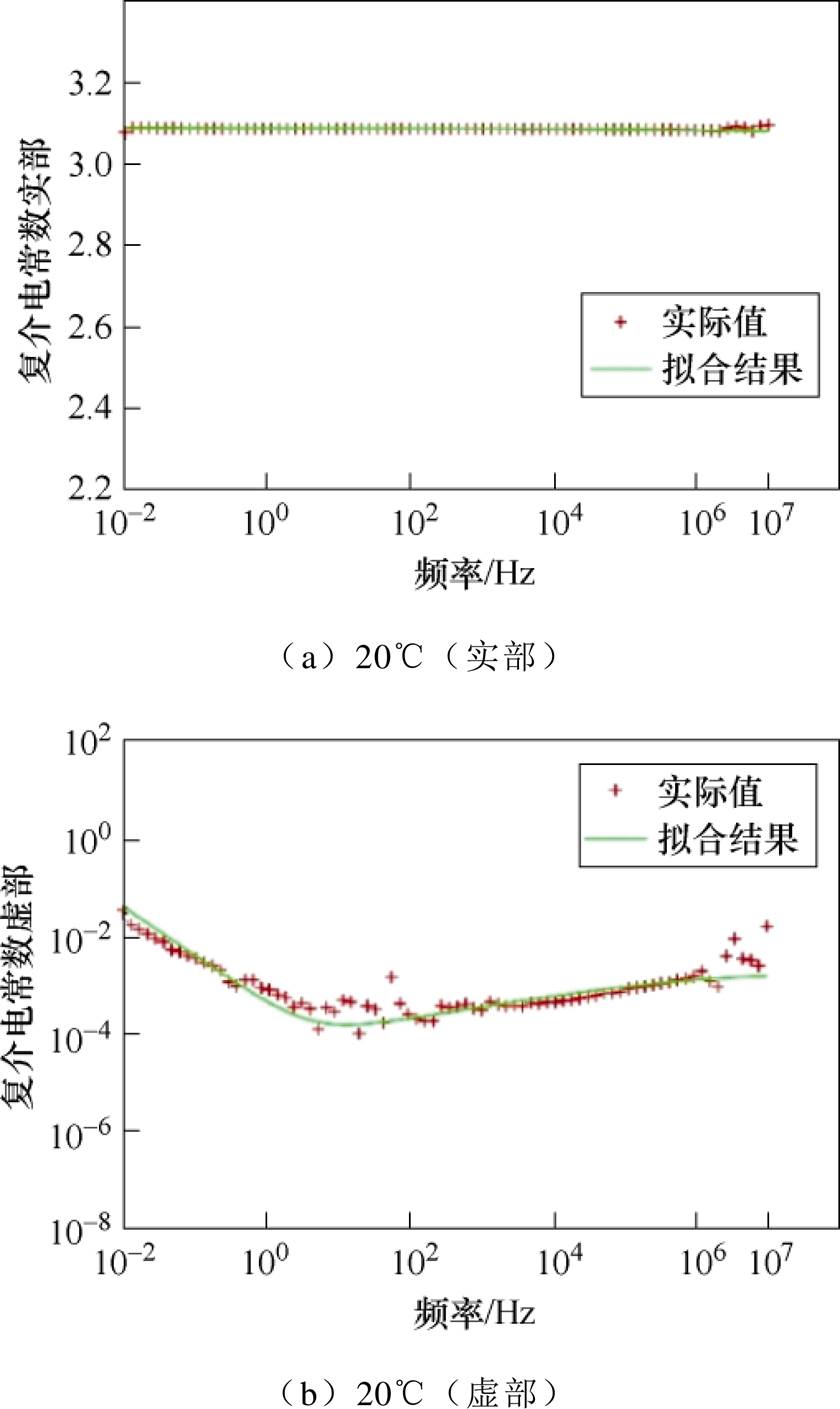
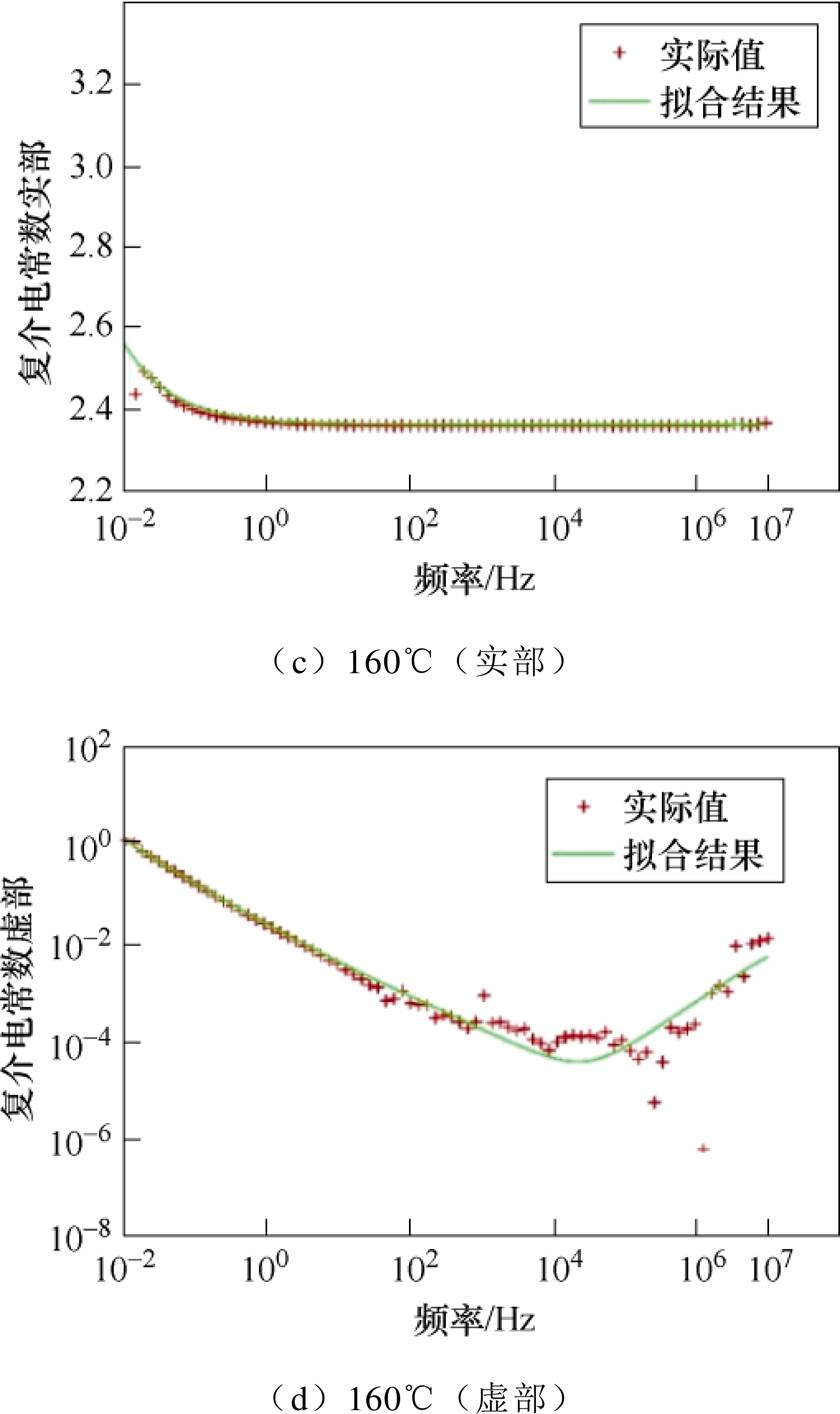
图11 20℃和160℃下有机硅弹性体介电谱拟合结果
Fig.11 Dielectric spectrum fitting results of silicone elastomer at 20℃and 160℃
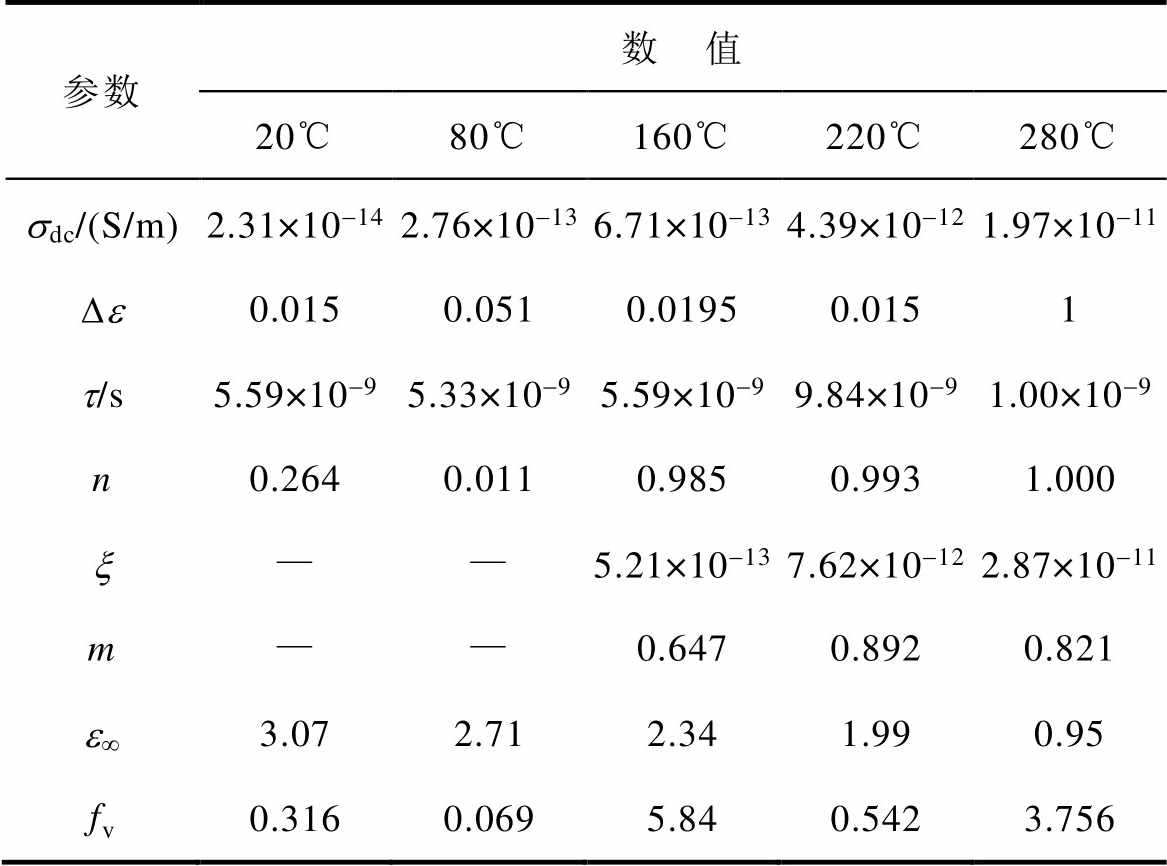
通过拟合得到不同温度下有机硅弹性介电特征参量见表2,随温度上升,直流电导率sdc、弛豫强度De、低频弥散强度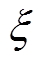 呈上升趋势;高频介电常数e∞与弛豫时间t 呈下降趋势,弛豫特征参量n与低频弥散特征参量m较为稳定。
呈上升趋势;高频介电常数e∞与弛豫时间t 呈下降趋势,弛豫特征参量n与低频弥散特征参量m较为稳定。
表2 不同温度下频域介电特征参量
Tab.2 Frequency domain dielectric characteristic parameters at different temperatures
参数数 值 20℃80℃160℃220℃280℃ sdc/(S/m)2.31×10-142.76×10-136.71×10-134.39×10-121.97×10-11 De0.0150.0510.01950.0151 t/s5.59×10-95.33×10-95.59×10-99.84×10-91.00×10-9 n0.2640.0110.9850.9931.000 x——5.21×10-137.62×10-122.87×10-11 m——0.6470.8920.821 e∞3.072.712.341.990.95 fv0.3160.0695.840.5423.756
直流电导过程仅与直流电导率sdc这一参数相关,电导率对SiC器件封装漏电流特性及绝缘寿命等方面起着决定性作用。提取到有机硅弹性体材料直流电导率与温度的拟合结果如图12所示,随着温度升高,有机硅弹性体直流电导率呈指数上升趋势。温度升高,使得有机硅弹性体中更多导电粒子被激活,导致材料电导率上升。
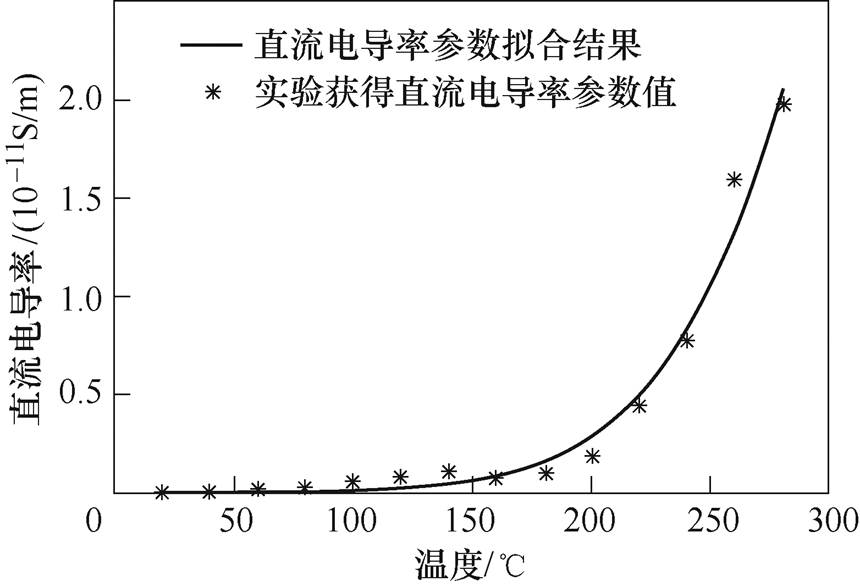
图12 直流电导率与温度的拟合曲线
Fig.12 Fitting curve of DC conductivity and temperature
一般来说,Arrhenius方程[31]可以描述自由电荷反应速率与温度之间的关系,本文采用Arrhenius方程实现对直流电导率参数与温度关系的拟合,具体为
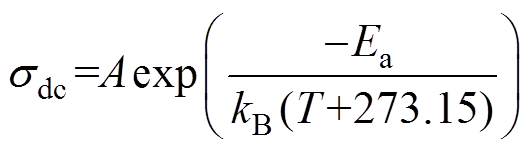 (22)
(22)式中,A为频率因数;Ea为直流电导率的热活化能;kB为Boltzmann常数,kB=1.380 650 5×10-23J/K;T为温度(℃)。
采用式(22)对图12中的直流电导数据进行拟合,频率因数A=2.74×10-6,所得有机硅弹性体热活化能Ea=0.562eV,拟合获得拟合优度为0.98。
高频介电稳定过程仅与高频介电常数e∞这一参数相关。图13给出了高频介电常数随温度变化的拟合结果,从图中可以看出,随着温度的增加,高频介电常数线性减小。高频介电常数只影响复相对介电常数实部,并且与频率无关,是仅与温度相关的反映有机硅弹性体材料储存电荷能力的参数。本文采用一次函数来对高频介电常数与温度的关系进行拟合,具体如式(23)所示,拟合优度为0.91。
 (23)
(23)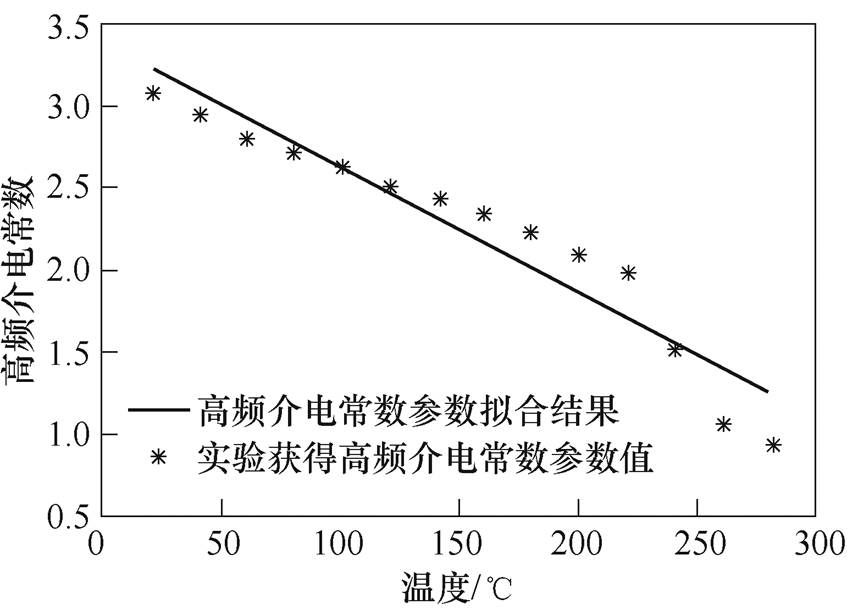
图13 高频介电常数与温度的拟合曲线
Fig.13 Fitting curve of high frequency dielectric constant with temperature
弛豫极化过程与弛豫强度De、弛豫时间t 和弛豫特征参数n三个参数相关。2.3节已经介绍了各参数对弛豫过程影响。弛豫强度与温度的拟合关系如图14所示,从图14可以看出,采用Arrhenius方程可以达到很好的拟合效果,拟合结果如式(24)所示。拟合优度为0.93,所得热活化能为0.520eV。弛豫强度随温度上升而迅速增强,说明随着温度升高,载流子运动更加剧烈,使得电介质内部的极化强度增强,这与大部分固体电介质弛豫强度随温度的变化规律相吻合。
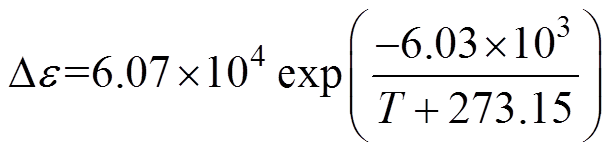 (24)
(24)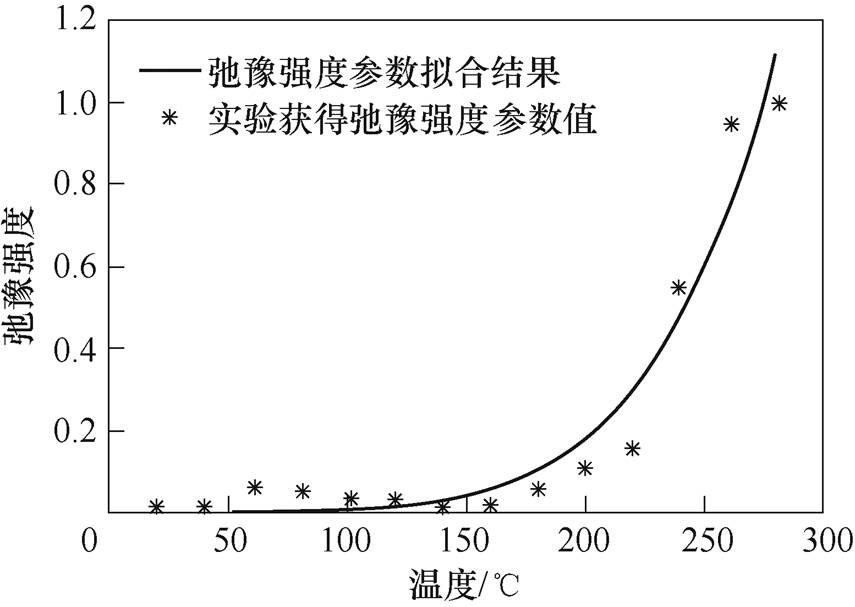
图14 弛豫强度与温度的拟合曲线
Fig.14 Fitting curve of relaxtion intensity with temperature
弛豫时间参数t随着温度升高,低温(160℃以下)处弛豫时间变化并不明显,本文推荐弛豫时间采用5~6ns的固定值。而在高温(160℃及以上)处,弛豫时间随温度呈明显下降趋势,弛豫时间与温度的拟合关系如图15所示。弛豫过程这一现象可利用双势阱模型进行解释。
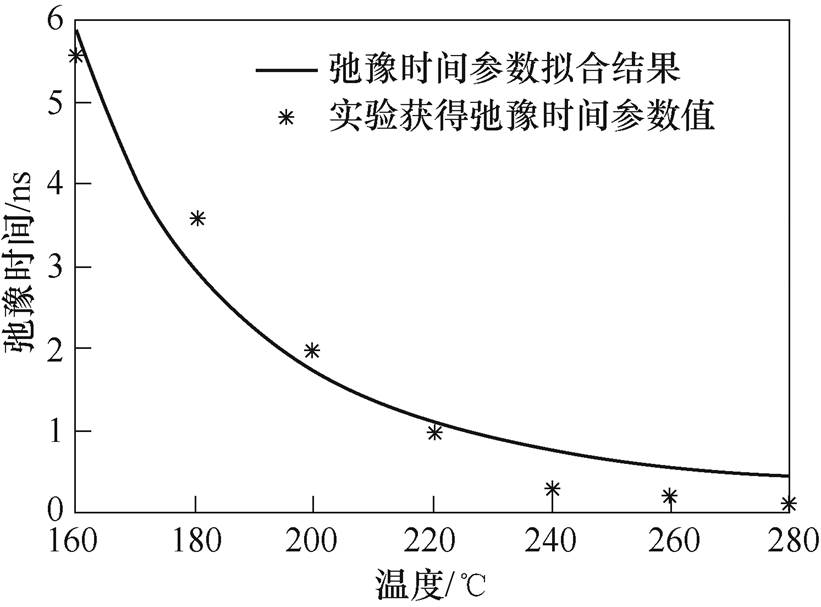
图15 弛豫时间与温度的拟合曲线
Fig.15 Fitting curve of relaxtion time with temperature
弛豫型极化过程本质上是有机硅弹性体内部带电粒子在电场作用下穿越势垒运动的过程,双势阱模型示意图如图16所示,纵坐标h表示势能值,横坐标x表示位置。势能曲线存在相距L的A、B两个势能极小值点,A、B之间存在一定的势垒高度H,在无电场作用下,A、B势垒深度一致,表现为有机硅弹性体内部带电粒子仅存在热运动;在外电场E作用下,在A处带电荷量为q的粒子的势能可能将比B处带电荷量为q的粒子的势能高2DH(DH= qLE/2),使得有机硅弹性体内部带电粒子从A处运动至B处的概率增加,在宏观上表现为带电粒子由A向B运动,这一现象即为弛豫极化过程。由Boltzmann分布定律可知,粒子占据能级的概率与该能级的简并度和Boltzmann因子成正比,表示为
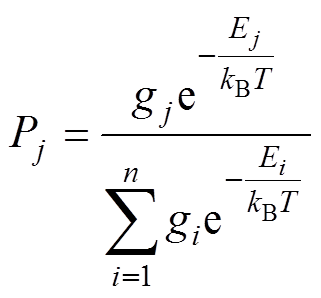 (25)
(25)式中,Pj为粒子占据j能级的概率;gi为能级简并度;Ej为j量子态的能量。
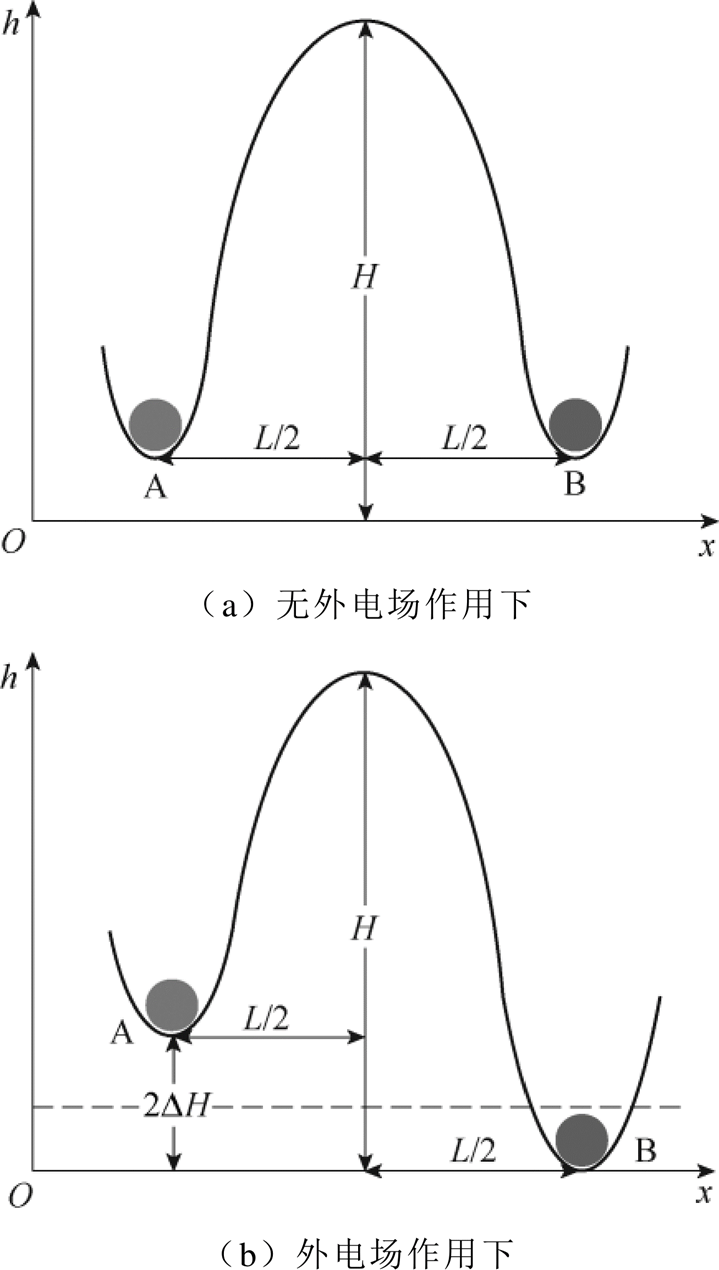
图16 双势阱模型示意图
Fig.16 Schematic diagram of double well model
本文中粒子穿越势垒概率可表示为
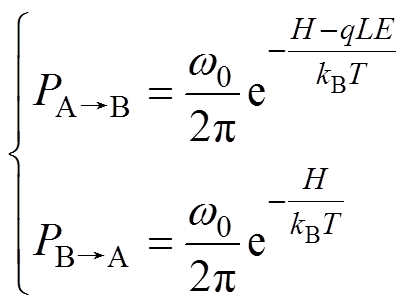 (26)
(26)当qLE kBT时,近似有
kBT时,近似有
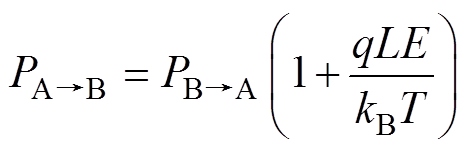 (27)
(27)
设A与B位置粒子数分别为NA和NB,有
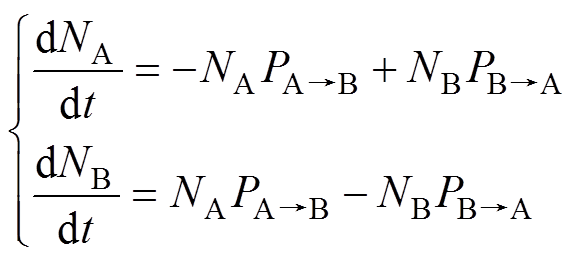 (28)
(28)由式(28)可得
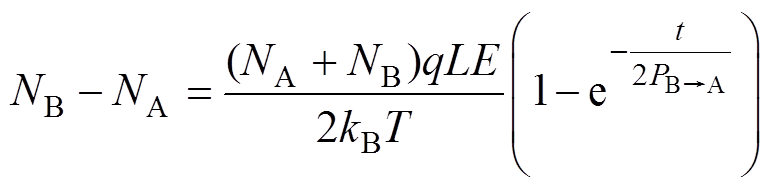 (29)
(29)
式中,A与B位置粒子之和为常数。因此获得弛豫极化过程时间常数表达式为
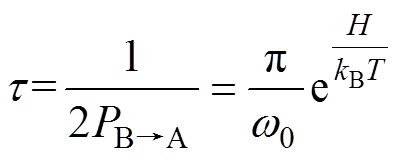 (30)
(30)式中,ω0为粒子在势阱中的固有角频率。可以看出,弛豫时间t 与温度T之间存在指数下降关系,温度与弛豫时间的拟合关系如图15所示,表达式为
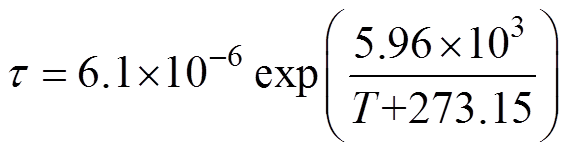 (31)
(31)
拟合优度为0.95,得到势垒高度H=0.514eV。
弛豫特征参数n为人为添加的修正系数,拟合数值上较为稳定,建议在本文测量频率范围内,160℃以下情况取0.2,160℃以上取1。
低频弥散过程与低频弥散强度x 和低频弥散特征值m相关。其中低频弥散特征值m在本文测量范围内变化不大,可以取0.8为通用值,而温度T与低频弥散强度x 的关系如图17所示,符合Arrhenius方程规律,式(32)给出了低频弥散强度与温度的拟合结果,拟合优度为0.95,拟合得到的热活化能为0.53eV。
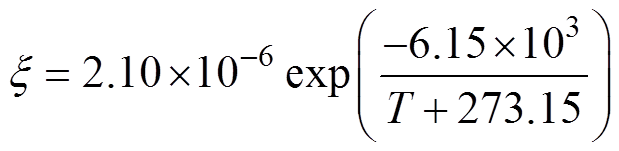 (32)
(32)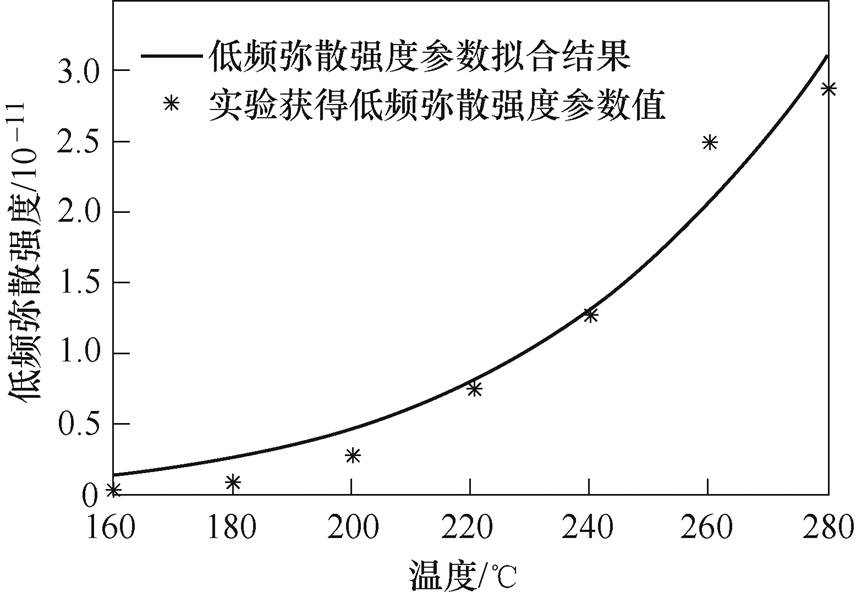
图17 温度与低频弥散强度的拟合曲线
Fig.17 Fitting curve of low frequency dispersion strength with temperature
从提取到的数据可得到结论:在高温(160℃以上)下,低频弥散过程在低频率(100Hz以下)范围内对复介电常数实部起着主导作用;此时相对于直流电导过程,低频弥散过程对低频处复介电常数虚部的影响更大,因此在高温条件下,低频弥散过程在材料低频介电响应过程中起主要作用。
出现低频弥散现象原因在于:低频处,电荷运动时间显著增加,运动自由度增大,不同于高频时电荷可以沿着某些限制的路径,通过跳跃的形式进行运动,由于此时电荷运动脱离原有路径,频率越低,使得电荷移动距离越长,宏观表现出极化过程随着频率降低而增强,呈现明显的弥散现象;温度升高使得电荷运动加剧,增强了低频弥散过程的强度。
本文针对有机硅弹性体在SiC器件应用工况下的介电特性展开研究,测量并获得了宽频、宽温度范围内有机硅弹性体的介电特性数据,分析了有机硅弹性体介电响应特性,揭示了温度及频率对有机硅弹性体介电响应过程的影响规律,本文结论如下:
1)在实验室内制备了适用于SiC器件封装用的有机硅弹性体,分析了其热特性与形貌特征,为有机硅弹性体介电特性测试提供了试品。采用频域介电谱测试方法,测量获得了宽频(10-2~107Hz)、宽温度(20~280℃)范围内的有机硅弹性体介电特性数据,发现了有机硅弹性体介电响应过程中出现低频弥散过程与电荷扩散过程,揭示了高温低频条件(大于160℃,小于1Hz)下,低频弥散过程相比于直流电导过程占据材料介电响应主要影响地位。
2)揭示了有机硅弹性体介电响应包括高频介电稳定过程、直流电导过程、介电弛豫过程、低频弥散过程与电荷扩散过程,根据测试结果,给出了不同温度范围内包含上述介电过程的改进Cole-Cole模型表达式,建立了优化目标函数,实现了模型各参数的有效提取。
3)获得了不同温度下Cole-Cole模型介电特征参数,揭示了温度对材料介电过程产生影响的原因,发现了直流电导率sdc、弛豫强度De 与低频弥散强度x 与温度变化规律符合Arrhenius方程规律,所得热活化能分别为0.562eV、0.52eV和0.53eV。高频介电常数e∞与温度呈现近似一次函数关系。弛豫时间t随温度变化规律可利用双势阱模型解释,且与温度变化均满足指数型规律,得到势垒高度为0.514eV。
参考文献
[1] Fu Pengyu, Zhao Zhibin, Li Xuebao, et al. Partial discharge measurement and analysis in PPIs[J]. IET Power Electronics, 2018, 12(1): 138-146.
[2] Fu Pengyu, Zhao Zhibin, Cui Xiang, et al. Partial discharge measurement and analysis in high voltage IGBT modules under DC voltage[J]. CSEE Journal of Power and Energy Systems, 2018, 4(4): 513-523.
[3] Yao Yiying. Thermal stability of Al2O3/silicone composites as high-temperature encapsulants[D]. Blacksburg: Virginia Tech, 2014.
[4] Chen Zheng, Yao Yiying, Zhang Wenli, et al. Deve- lopment of a 1200V 120A SiC MOSFET module for high-temperature and high frequency applications[C]// Wide Bandgap Power Device & Applications, Columbus, 2013: 52-59.
[5] zuhide Ino K A, Mineo, Miura, et al. SiC power device evolution opening a new era in power electronics[C]//2019 IEEE International Conference on Electronic Device and Solid-State Circuits (EDSSC), Xi’an, 2019: 1-3.
[6] Do M T, Auge J L, Lesaint O. Dielectric losses and breakdown in silicone gel[C]//Electrical Insulation and Dielectric Phenomena, 2006 IEEE Conference on Electrical Insulation & Dielectric Phenomena, Kansas, 2006: 541-544.
[7] Locatelli M L, Khazaka R, Diaham S, et al. Evalu- ation of encapsulation materials for high-temperature power device packaging[J]. IEEE Transactions on Power Electronics, 2014, 29(5): 2281-2288.
[8] Jonscher A K. Dielectric relaxation in solids[J]. Journal of Physics D: Applied Physics, 1999, 32(14): 57-70.
[9] Debye P J William. Polar molecules[M]. New York: Chemical Catalog Company, 1929.
[10] Cole K S, Cole R H. Dispersion and absorption in dielectrics I. alternating current characteristics[J]. The Journal of Chemical Physics, 1941, 9(4): 341-351.
[11] Enis Tuncer, Stanislaw M G. Electrical properties of filled silicone rubber[J]. Journal of Physics Con- densed Matter, 2000, 12(8): 1873-1897.
[12] Davidson D W, Cole R H. Dielectric relaxation in glycerol, propylene glycol, and n-propanol[J]. The Journal of Chemical Physics, 1951, 19(12): 1484- 1490.
[13] Havriliak S, Negami S. A complex plane analysis of α-dispersions in some polymer systems[J]. Journal of Polymer Science Part C: Polymer Symposia, 1966, 14(1): 99-117.
[14] Dissado L A, Hill R M. Anomalous low-frequency dispersion, near direct current conductivity in dis- ordered low-dimensional materials[J]. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics, 1984, 80(3): 291-319.
[15] Dissado L A, Hill R M. A cluster approach to the structure of imperfect materials and their relaxation spectroscopy[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1983, 390(1798): 131-180.
[16] Hill R M. Characterisation of dielectric loss in solids and liquids[J]. Nature, 1978, 275(5676): 96-99.
[17] 顼佳宇, 李学宝, 崔翔. 高压大功率IGBT器件封装用有机硅凝胶的制备及耐电特性研究[J]. 电工技术学报, 2021, 36(2): 352-361.
Xu Jiayu, Li Xuebao, Cui Xiang. Research on preparation process and breakdown properties of silicone gel used for the encapsulation of IGBT power modules[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 352-361.
[18] 张淑君. 气泡动力学特性的三维数值模拟研究[D]. 南京: 河海大学, 2006.
[19] 王政平, 任维赫. 材料复介电常数测量方法研究进展[J]. 光学与光电技术, 2011, 9(1): 93-96.
Wang Zhengping, Ren Weihe. Progress in the measurement of complex dielectric constants of materials[J]. Optics & Optoelectronic Technology, 2011, 9(1): 93-96.
[20] Vu T A T, Augé J L, Lesaint O. Partial discharges and light emission from ceramic substrates embedded in liquids and gels[C]//2011 IEEE International Con- ference on Dielectric Liquids, Trondheim, 2011: 1-4.
[21] 杨丽君, 高思航, 高竣, 等. 油纸绝缘频域介电谱的修正Cole-Cole模型特征参量提取及水分含量评估方法[J]. 电工技术学报, 2016, 31(10): 26-33.
Yang Lijun, Gao Sihang, Gao Jun, et al. Characteri- stic parameters extracted from modified Cole-Cole model and moisture content assessment methods study on frequency-domain dielectric spectroscopy of oil-paper insulation[J]. Transactions of China Electro- technical Society, 2016, 31(10): 26-33.
[22] 杨国清, 黎洋, 王德意, 等. 超支化聚酯改性纳米SiO2/环氧树脂的介电特性[J]. 电工技术学报, 2019, 34(5): 1106-1115.
Yang Guoqing, Li Yang, Wang Deyi, et al. Dielectric properties of nano-SiO2/epoxy resin modified by hyperbranched polyester[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1106-1115.
[23] 林朝明, 叶荣. 油浸式变压器绝缘诊断方法的研究进展[J]. 电气技术, 2019, 20(12): 1-6.
Lin Chaoming, Ye Rong. Research progress of insulation diagnosis method for oil-immersed trans- former[J]. Electrical Engineering, 2019, 20(12): 1-6.
[24] 李长云, 郝爱东. 机-热协同老化对纤维素绝缘纸频域介电谱特性的影响[J]. 电工技术学报, 2019, 34(17): 3705-3712.
Li Changyun, Hao Aidong. Effect of mechanical thermal synergistic aging on frequency domain dielectric spectrum characteristics of cellulose insu- lating paper[J]. Transactions of China Electro- technical Society, 2019, 34(17): 3705-3712.
[25] Debye P. Polar molecules[M]. New York: Dover Publications Inc, 1929.
[26] Lucarini V, Peiponen K E, Saarinen J J, et al. Kramers-Krong relations in optical materials research[M]. New York: Springer, 2005.
[27] Hill R M, Pickup C. Barrier effects in dispersive media[J]. Journal of Materials Science, 1985, 20(12): 4431-4444.
[28] Niklasson G A. Fractal aspects of the dielectric response of charge carriers in disordered materials[J]. Journal of Applied Physics, 1987, 62(7): R1-R14.
[29] Shapiro B, Abrahams E. Scaling for the frequency- dependent conductivity in disordered electronic systems[J]. Physical Review B, 1981, 24(8): 4889- 4891.
[30] Dissado L A. A fractal interpretation of the dielectric response of animal tissues[J]. Physics in Medicine and Biology, 1990, 35(11): 1487-1503.
[31] Singh B K, Kumar B. Impedance analysis and high temperature conduction mechanism of flux grown Pb(Zn1/3Nb2/3)0.91Ti0.09O3 single crystal[J]. Crystal Research & Technology, 2010, 45(10): 1003-1011.
Analysis of High Temperature Wide Band Dielectric Properties of Organic Silicone Elastomer for High Voltage SiC Device Packaging
Abstract Because of their good insulation and high temperature resistance, organic silicone elastomers are widely used in SiC devices under high frequency, high pressure and high temperature working conditions. In a wide range of frequency and temperature, the dielectric properties of silicone elastomer materials have a great impact on the electric field distribution in SiC devices. Therefore, the dielectric properties of organic silicone elastomers with wide broadband (10-2~107Hz) range and wide temperature (20~280℃) range were obtained by frequency-domain dielectric spectrum analysis in this paper. The dielectric process of silicon elastomers at different frequencies and temperatures was revealed, the method of distinguishing low-frequency dispersion process from relaxation polarization process was improved, and an improved Cole-Cole model was introduced. Finally, the influence of temperature on the dielectric response process and dielectric characteristic parameters of organic silicone elastomers was obtained. The results show that with the increase of frequency, the real part of the complex dielectric constant decreases and tends to be stable, while the imaginary part of the complex dielectric constant decreases first and then rises to the peak value. Temperature and frequency have great influence on the dielectric properties of the organic silicone elastomer. Under the condition of high temperature and low frequency, the organic silicone elastomer material has obvious phenomena of low frequency dispersion and charge diffusion. The characteristic parameters of Cole-Cole model at different temperatures are extracted. The relationship of the DC conductivity sdc, the relaxation intensity De and the low frequency dispersion strength x with temperature satisfies the Arrhenius equation law. The high frequency dielectric constant e∞ shows an approximate first-order function relationship with temperature and decreases with the increase of temperature; the relaxation time t decreases with the increase of temperature at high temperature, and its mechanism can be revealed by the double well model. The characteristic parameters obtained in this paper provide data support for insulating design of SiC device package.
keywords:SiC device, broadband dielectric spectrum, organic silicon elastomer, low frequency dispersion, charge diffusion, Cole-Cole model
中图分类号:TM211
DOI: 10.19595/j.cnki.1000-6753.tces.201088
国家自然科学基金与国家智能电网联合基金资助项目(U1766219)。
收稿日期 2020-08-30
改稿日期 2020-11-27
李学宝 男,1988年生,博士,副教授,研究方向为电力系统的电磁环境和电磁兼容、高压设备绝缘问题。E-mail: lxb08357@ncepu.edu.cn(通信作者)
刘东明 男,1996年生,硕士研究生,研究方向为高压大功率电力电子器件封装技术、电力系统电磁环境与电磁兼容。E-mail: 18810527119@163.com
(编辑 陈 诚)