图1 功率模块截面热量流向示意图
Fig.1 Schematic of heat flow in power module section
摘要 碳化硅（SiC）MOSFET具有耐压高、开关速度快、导通损耗低等优点，将越来越广泛地应用于高效、高功率密度场合。在这些应用场合中，SiC MOSFET面临着严峻的可靠性考验，而结温的在线准确提取是实现器件寿命预测和可靠性评估的重要基础。该文提出一种基于功率模块内置负温度系数（NTC）温度传感器的器件结温在线提取方法。首先建立考虑多芯片热耦合效应的内置温度传感器至功率芯片的热网络模型，并建立SiC MOSFET的损耗快速计算方法；通过有限元仿真提取热网络模型的阻抗参数，并验证该热网络参数在不同边界条件下的稳定性。仿真和实验结果表明，所提出的结温在线估计方法能够准确地获得器件的动态结温，且热网络模型参数不受环境温度、散热条件等边界条件变化的影响，适用于实际任务剖面下的结温监测与寿命 预测。
关键词：负温度系数温度传感器 SiC MOSFET 热网络模型 芯片温度
碳化硅（Silicon Carbide, SiC）MOSFET作为典型的宽禁带半导体器件，具有高开关速度、低导通损耗和高热导率等优点，可以减小电感、电容和散热器等元器件的体积，大幅提升系统的功率密度，非常适用于高效、高功率密度需求场合[1]，近年来已逐步应用于电气化交通领域[2-3]。随着SiC器件的推广应用，其健康管理和可靠性评估也越来越受到学术界和工业界的关注[4]。由电力电子系统可靠性调研报告可知，电力电子变流器中约有34%的失效是由功率器件引起[5]，其中由热应力引起的器件失效占比高达55%[6]。根据试验统计数据和失效机理分析，功率器件在失效前所经历的温度循环周期主要由结温摆幅ΔTj、最高结温Tj.max和平均结温Tj.ave等因素决定[7]，而SiC功率模块具有功率密度高、封装紧凑和耐高温等特点，其运行结温更高且结温波动更大。因此，器件结温的精准在线提取是其寿命预测、健康管理和可靠性评估的基础[8]。
目前，功率器件结温提取方法主要有光学测量法、物理接触法、热网络模型法和热敏电参数法四类[9]。其中，热敏电参数法和热网络模型法能够满足非侵入、可在线集成的要求。热敏电参数法是通过测量对结温敏感性强的外部电气参数来逆向预估芯片的温度，被认为是极具应用前景的结温检测方法[9]。然而，现阶段的热敏电参数法也还存在相应的缺陷，如影响器件正常的运行[10-11]、测量参数灵敏度过低、极易受到干扰[12-14]等，应用于复杂工况时会受到很大的限制，且目前的研究也主要聚焦于热敏电参数的温度特性和离线校正，较少涉及实际工况下结温的在线测量和SiC器件的结温提取研究[9, 15]。热网络模型法[16-18]是基于器件的实时损耗与瞬态热阻抗网络模型，通过实时计算或离线查表估算芯片结温及其变化趋势，优点是无需外部测量电路，在获得准确而稳定的热网络模型参数和损耗计算值的条件下，易于准确地在线提取器件结温。然而，传统的包含功率模块外部条件的热网络模型具有很大的局限性：以模块基板温度为参考点时，需要在模块基板开槽埋设热电偶，热电偶的埋设位置也会对最终模块内部芯片热状态估计结果造成很大影响[19]；以环境温度为参考点时，则需要获得导热硅脂和散热器的热阻抗，而导热硅脂的老化会导致硅脂层的热阻抗发生较大的变化，冷却风扇故障或液冷循环系统故障时散热器的热阻抗也会发生大幅的变化，导致温度估计结果产生较大误差[15]。
现有功率模块基本都内置有负温度系数（Negative Temperature Coefficient, NTC）温度传感器，但NTC传感器并不能直接准确地反映器件结温，通常只用于模块的内部温度监测和过载过温保护[20]。目前仅有极少量文献[21-23]研究了基于NTC温度传感器实现器件的动态结温提取。文献[21-22]采用实验测试的方法获取IGBT模块的热网络参数，但忽略了二极管的热阻抗及芯片之间的热耦合效应，而且缺乏不同边界条件下的有效性验证。文献[23]建立了以NTC热敏电阻为参考的简化IGBT热网络模型，得到芯片估计温度用于逆变器热优化控制，但其研究侧重点为逆变器的热优化控制，并未详细讨论热建模过程和散热条件边界条件对热网络模型的影响。
鉴于此，本文提出了一种基于功率模块内置温度传感器的功率模块结温在线提取方法。该方法以功率模块内置NTC传感器作为温度参考点，建立考虑热耦合效应的内置NTC传感器至功率芯片的新型热网络模型。该热网络模型对模块外部导热硅脂老化和散热器热阻变化不敏感，结合准确的损耗在线计算可以实现器件结温的准确在线提取。本文通过有限元仿真提取热网络模型参数，结合NTC传感器和SiC MOSFET的实时损耗计算实现对SiC MOSFET功率模块内部芯片结温的在线提取。最后通过实验和有限元仿真验证了所提方法的可行性和有效性。
功率模块内置NTC温度传感器并不是安装在功率芯片表面且测量响应速度慢，因此NTC传感器并不能准确反映芯片的温度，本文通过研究NTC温度与芯片结温之间的相关性，基于传热原理构建以NTC传感器为温度参考点的新型热网络模型，不包含参数易发生变化的底部物理层的热网络，简化了传统热网络模型。
功率模块截面热量流向示意图如图1所示。功率芯片产生的热量经过直接覆铜陶瓷基板（Direct Bonded Copper, DBC）层和导热基板传递到散热器，一部分热量通过DBC和基板传递到NTC，在芯片和NTC之间产生热耦合。图2为功率模块中NTC至单个功率芯片的等效热模型，其不仅包括传统热网络模型中芯片至环境的热阻抗，同时也包含芯片至NTC传感器的热阻抗。
图1 功率模块截面热量流向示意图
Fig.1 Schematic of heat flow in power module section
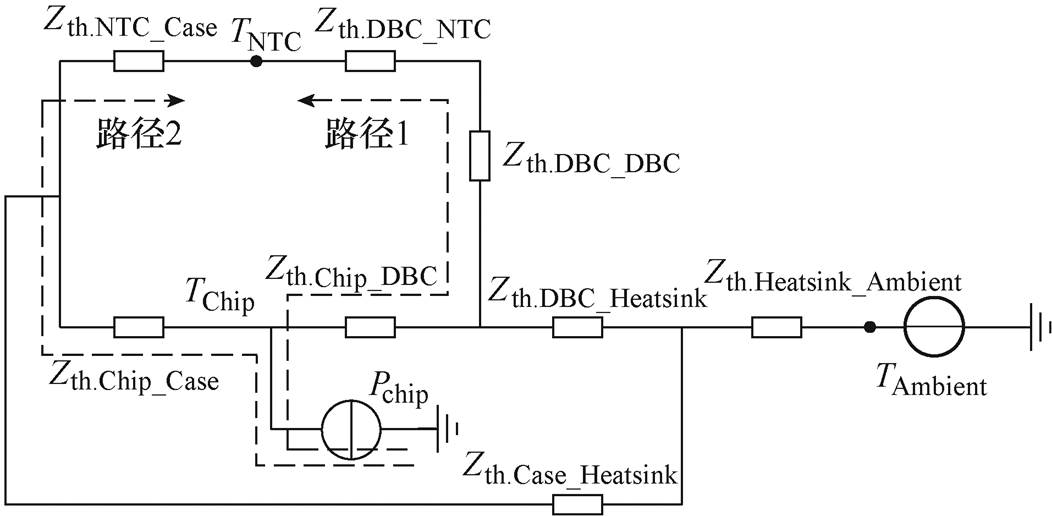
图2 包含NTC功率模块的等效热模型
Fig.2 Equivalent thermal model with NTC power module
由图2可知，芯片产生的热量传递到NTC有两条路径，路径1为芯片—DBC—NTC，路径2为芯片—DBC—基板—DBC—NTC。由于芯片与NTC之间通过基板交换的热量很小，并且芯片与NTC的热容相对于铜基板的热容可以忽略不计[24]，因此可忽略传递路径2，从而得到如图3所示的简化等效热模型。考虑到实际功率模块中DBC（陶瓷-铜键合基板）平面大小及其热容，DBC层的热阻抗Zth.DBC-DBC要比芯片至DBC热阻抗Zth.Chip_DBC和DBC至NTC热阻抗Zth.DBC_NTC大得多，DBC至环境的热阻抗Zth.DBC_Ambient包含焊料层、基板、导热硅脂和散热器的所有热阻抗，Zth.DBC_Ambient的值比Zth.DBC-DBC大得多。因此，NTC传感器至芯片的热阻抗Zth.j-NTC对外部导热硅脂和散热器热阻抗变化不敏感，Zth.DBC-DBC参数也只与DBC几何形状以及NTC传感器相对于芯片的距离有关，不易受其他因素的影响。
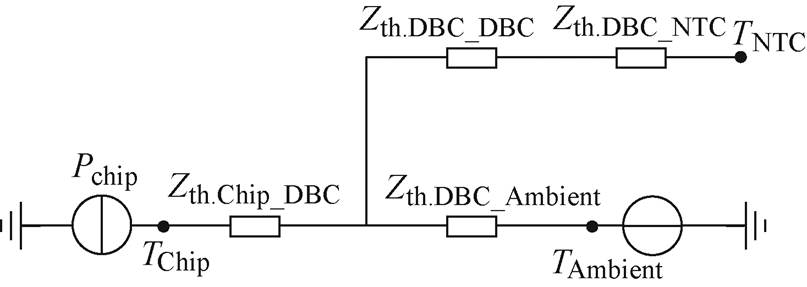
图3 简化后的等效热模型
Fig.3 Simplified equivalent thermal model
功率模块的多物理层热模型可以使用Foster热网络模型来描述[24]，芯片m至温度参考点之间的自热阻抗曲线可以定义为
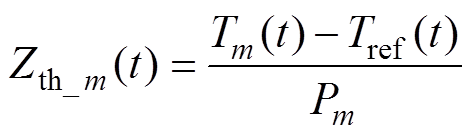（1）式中，Tm(t)和Tref(t)分别为芯片m与参考点随时间变化的温度；Pm为芯片m产生的功率损耗。
在Foster热网络模型中，热阻热容参数值都由热阻抗曲线拟合而来，一般可采用多阶指数曲线拟合获得两者之间的热阻抗参数，即
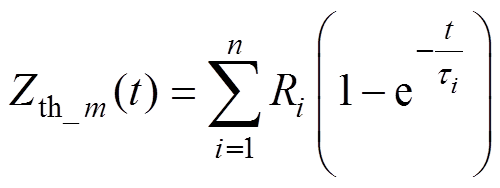（2）式中，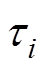
=RiCi，Ri、Ci分别为各阶热阻和热容。
任何产生功率损耗的芯片在散热过程中都会对其周围芯片造成影响，而当热量由功率损耗较小的芯片向较大的散热器传递时，这种热量横向传导、热流路径相互叠加的影响也更加明显，使得周围所有芯片的温度升高，这种现象也被称作交叉热耦合现象，如图4所示。文献[25]表明，当模块处于逆变工作状态时，功率芯片热阻抗比单独工作时要高约10%。
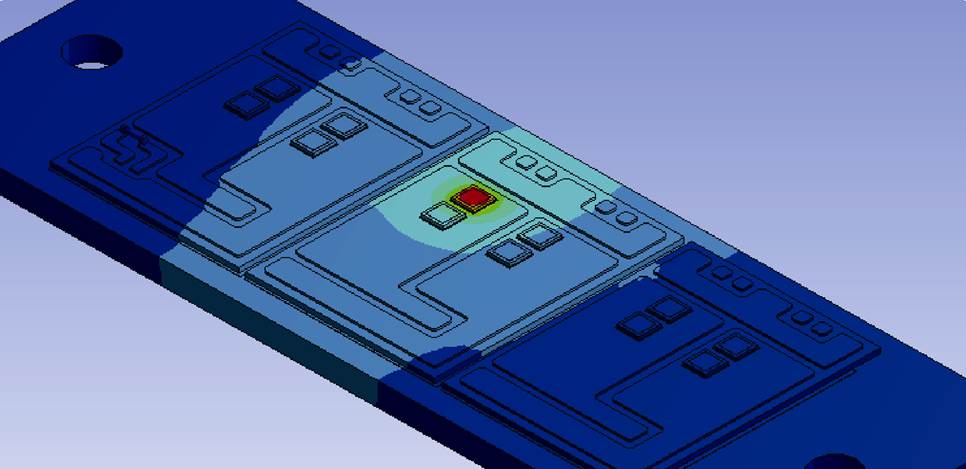
图4 芯片之间交叉热耦合现象
Fig.4 Cross thermal coupling between chips
因此，为了保证热网络模型的准确性，还需考虑热耦合现象。当对芯片n施加损耗时，温度参考点和芯片m之间的耦合热阻抗定义为
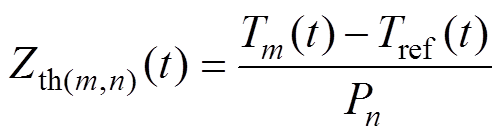（3）式中，Pn为芯片n施加的功率损耗。
因此，对于多芯片热源模型，以NTC为参考点时，热网络模型中的耦合热阻抗网络矩阵和自热阻抗矩阵可分别表示为
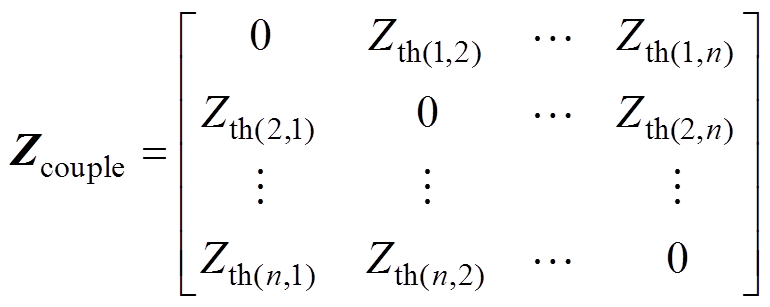（4）
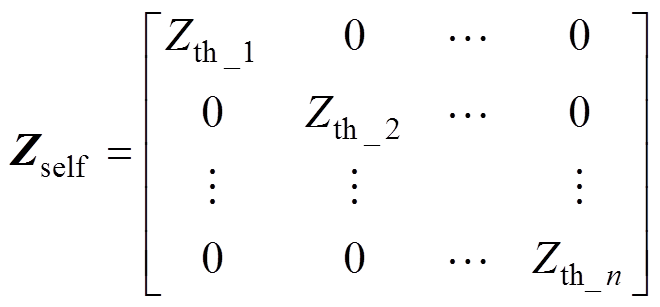（5）
根据叠加原理可得计及热耦合影响时的芯片结温计算表达式为
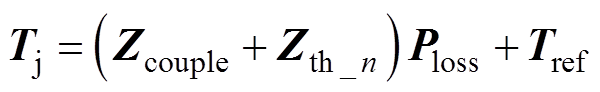（6）式中，Tj、Ploss、Tref分别为功率模块中各芯片结温、各芯片功率损耗和参考点温度，均为n×1向量。将热阻抗矩阵式（4）、式（5）中的Zth按实际采样时间离散化之后，可得到用于结温在线提取的离散化热网络。
综上所述，当参考点为功率模块内部的NTC时，耦合热阻抗网络模型结构如图5所示，热耦合的叠加点都设置在热阻抗值较大的Zth.DBC-DBC端。
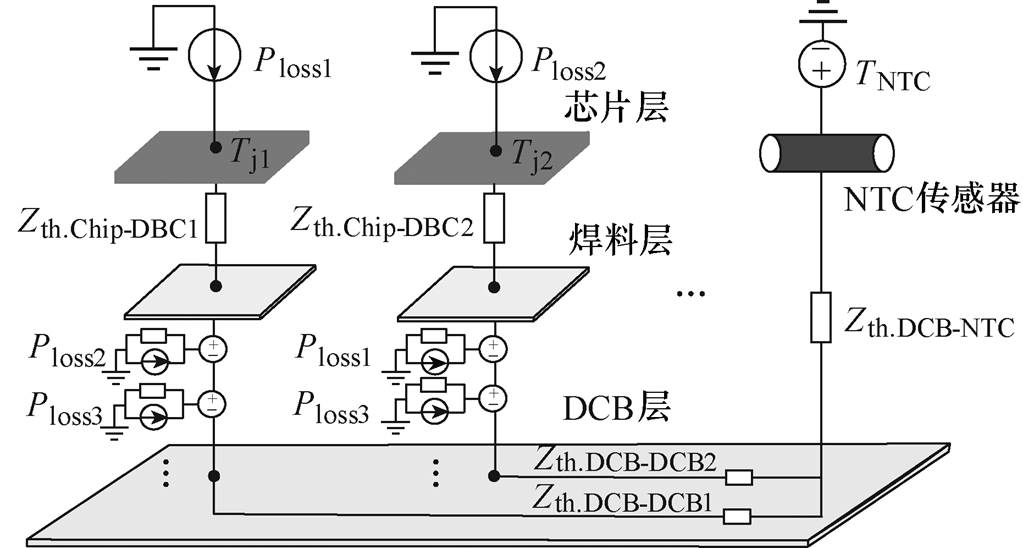
图5 基于NTC的耦合热网络模型
Fig.5 Coupled thermal network model based on NTC
由式（6）可知，在获得热阻抗矩阵参数并完成离散化之后，只要实时采样NTC传感器的温度并根据电压、电流和结温采样值计算器件的损耗，就能获得模块内各芯片的实时结温。SiC MOSFET工作状态如图6所示。图6中，S1为SiC MOSFET，VD1为SiC肖特基势垒二极管（Schottky-Barrier Diode, SBD）。
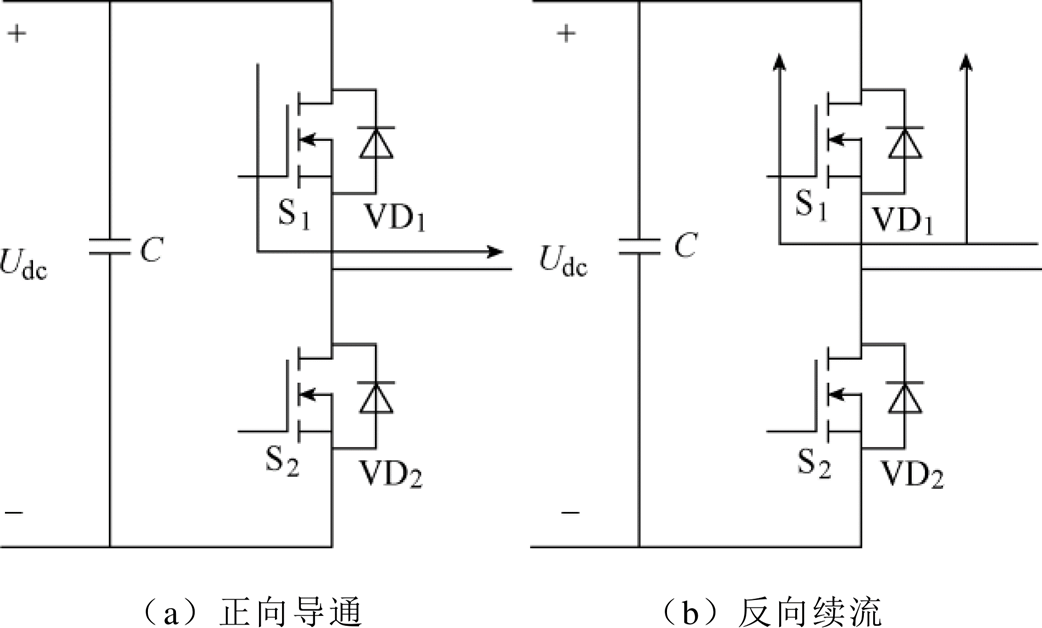
图6 SiC MOSFET工作状态
Fig.6 Operation modes of SiC MOSFET
SiC MOSFET具有双向导通特性，即当栅源极电压大于开启电压时，无论漏源极电压Vds是正值还是负值，沟道均可以导通。因此，在传统三相逆变系统应用中，SiC MOSFET自身会参与反向续流，导致其损耗特性不同于IGBT。本文SiC MOSFET功率模块的应用场合为电机驱动逆变器，其损耗分析以A相桥臂为例。
当A相电流由逆变器流向电机负载时，电流流经上桥臂S1，S1处于正向导通状态，反并联的二极管VD1处于反向截止状态。当A相电流由电机流向逆变器时，上桥臂将处于反向续流阶段，由于S1为开通状态，而VD1的导通需要一定的正向电压，续流初期的电流将全部从S1流过，该阶段为S1的单独续流阶段；当续流电流流经S1所产生的导通压降达到VD1的开通阈值电压VTH-VD后，S1与VD1以并联的形式共同续流，流经S1和VD1的续流电流由其各自导通电阻决定。综上所述，在逆变器工作过程中流经S1和VD1的电流可表示为
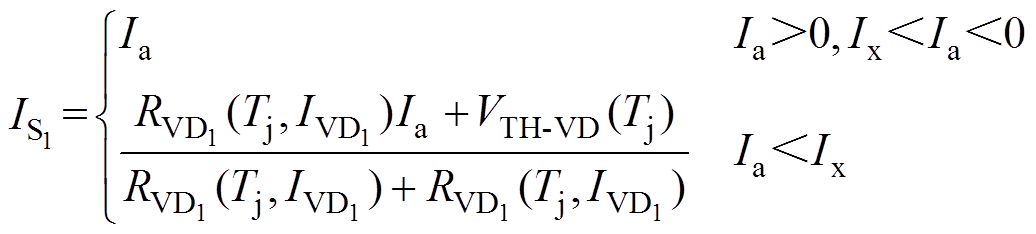（7）
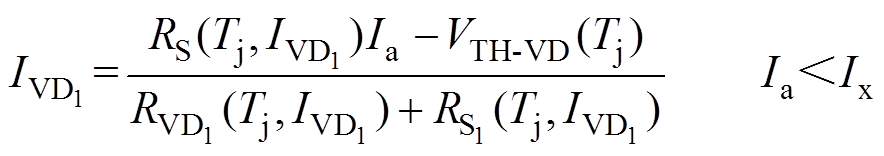（8）
式中，Ia为逆变器A相线电流；Ix=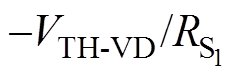
；
、
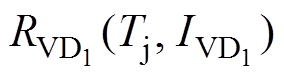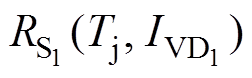分别为VD1与S1的导通电阻，阻值与芯片自身的结温及流过芯片的电流相关；VTH-VD(Tj)为VD1的开通阈值电压。A相桥臂S1和VD1的电流波形如图7所示。
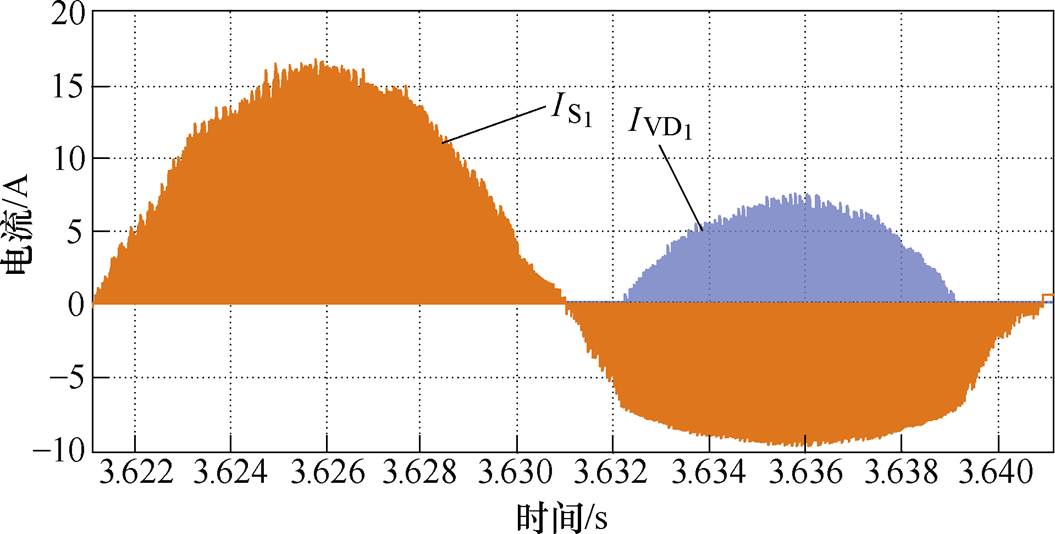
图7 A相桥臂S1和VD1的电流波形
Fig.7 The current waveforms of S1 and VD1 in phase A
1.3.1 SiC MOSFET导通损耗计算
当S1导通时，S1的导通压降VDS可表示为
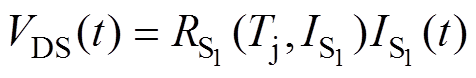（9）因此，S1导通期间任意两时间点的导通损耗可表示为
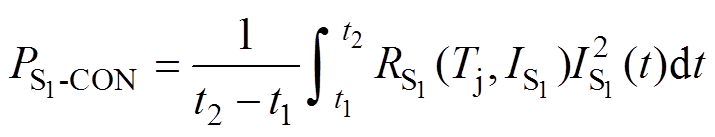（10）
当开关频率较高时，为了减小损耗在线计算的资源占用，可将损耗计算的计算周期设为N个开关周期，采样首尾两个开关周期的负载电流和占空比，将采样首尾周期负载电流的平均值作为N个开关周期内的电流值，首尾两个开关周期的占空比平均值作为整个阶段的占空比。因此，单个开关周期内的导通损耗计算简化为
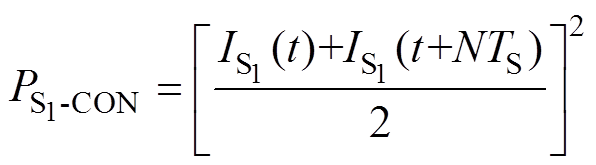
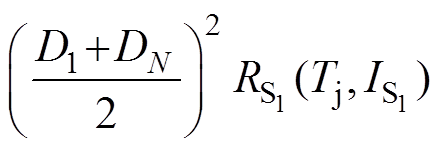（11）式中，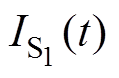
、
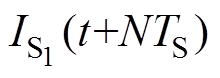分别为首、尾周期采样的流经S1的电流；TS为开关周期；D1与DN分别为第一个和最后一个开关周期的占空比；
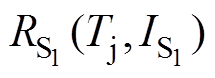可由SiC器件数据手册构建的二维表线性插值计算得到。
1.3.2 SiC MOSFET开关损耗计算
SiC MOSFET的开关过程的实际波形是包含尖峰和振荡过程的不规则波形，其开关损耗难以进行精确的理论计算。在本文中，只采样计算S1在N个开关周期中首尾两个开关周期的开关损耗，将N个开关周期内的S1平均开关损耗表示为
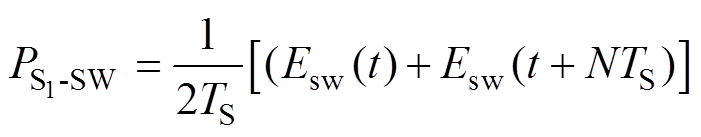（12）式中，Esw(t)、Esw(t+NTS)分别为首、尾两个采样开关周期内器件开通损耗Eon、关断损耗Eoff之和。考虑到Eon和Eoff受到器件漏极电流ID、器件结温Tj、直流侧电压UDC以及栅极驱动电阻Rg的影响，其中UDC、Rg一般为固定值，本文根据器件数据手册中给出的不同条件下的Eon、Eoff曲线线性插值构建Eon、Eoff关于ID、Tj的二维查询表，根据采样得到的ID、Tj计算相应的开关损耗。
1.3.3 SiC SBD 损耗计算
SiC SBD不存在开关损耗和反向恢复损耗，只在其参与续流期间产生导通损耗，VD1的前向导通电压VSBD可近似认为是流过电流的线性函数，即
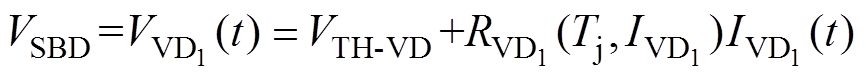（13）因此，在两任意时刻内VD1的导通损耗计算表示为
（14）
与S1导通损耗分析同理，得到VD1的导通损耗计算表达式为
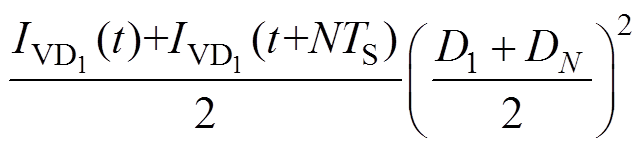（15）
式中，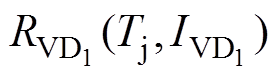
可由数据手册中的反并联二极管特性曲线构建的二维表线性插值计算得到；VTH-VD的变化很小，可认为是一个恒定值。
为获得以NTC传感器为温度参考点时各芯片的自热阻抗和耦合热阻抗，本文采用Ansys暂态有限元法（Finite Element Method, FEM）仿真提取热网络模型参数，相应流程如图8所示。
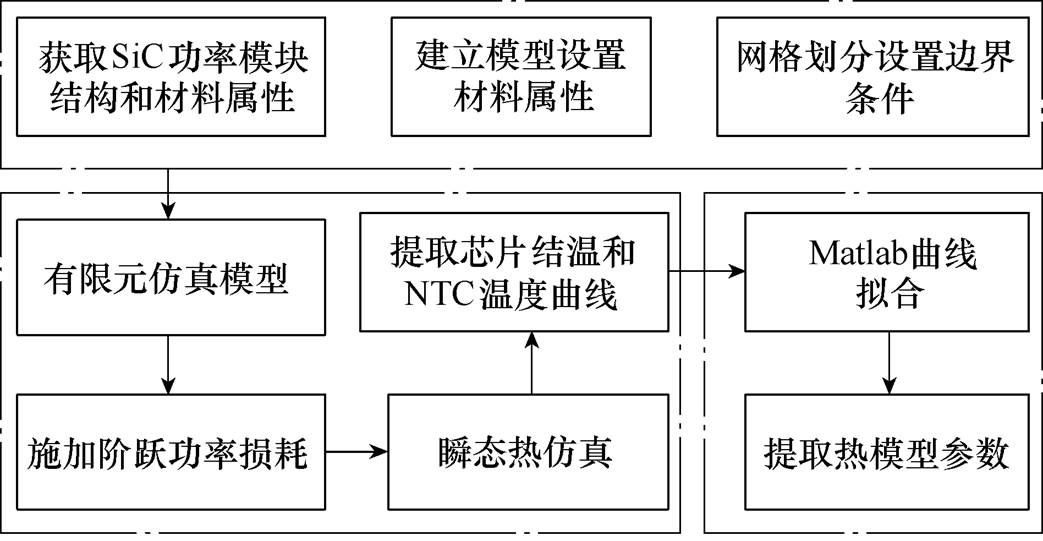
图8 FEM仿真提取热阻抗参数流程
Fig.8 FEM simulation process for extracting thermal impedance parameters
本文的研究对象为CREE CCS020M12CM2三相全桥SiC MOSFET功率模块，其内部包含了6个SiC MOSFET芯片、6个SiC SBD和一个NTC热敏电阻，CREE CCS020M12CM2三相全桥模块内部结构如图9所示。
图9 CREE CCS020M12CM2三相全桥模块内部结构
Fig.9 Intrenal structure of the CREE CCS020M12CM2
模块结构及材料参数如图10所示。模块的结构和各层材料参数如图10a所示，A相结构及尺寸如图10b所示。由文献[25-26]可知，键合线、模块引脚及环氧树脂外壳对模块内芯片的散热影响很小，可将模型简化，模块3D有限元仿真模型如图11所示。
图10 模块结构及材料参数
Fig.10 Structure and material parameters of the module
在设置仿真环境时，本文将功率模块基板的底面与侧面设置为模块自然对流散热形式，而芯片表面与DBC上铜层在实际中由于覆盖了灌封硅凝胶，故认为芯片热量全部从模块基板流失，其他表面视为绝热，暂态热仿真参数见表1。
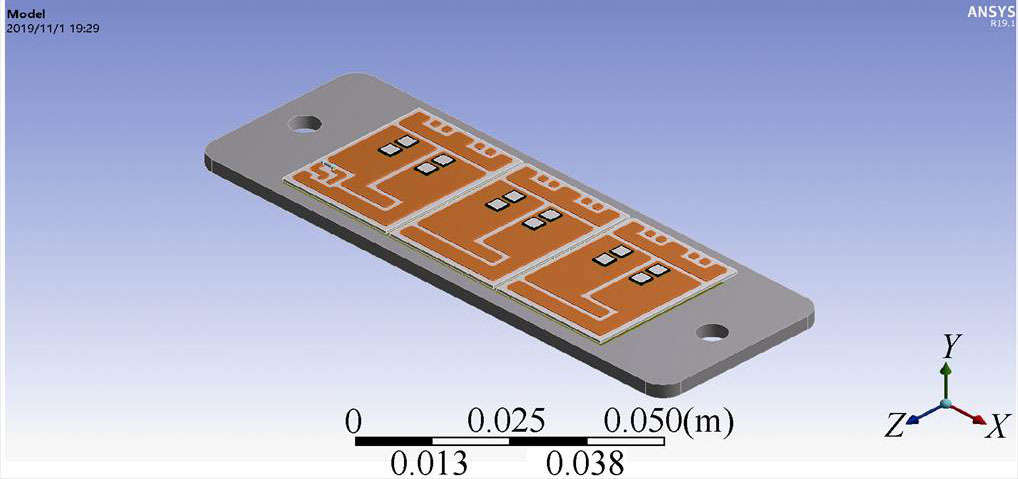
图11 模块3D有限元仿真模型
Fig.11 3D finite element simulation model of the module
表1 暂态热仿真参数
Tab.1 Parameters for transient thermal simulation
参 数数 值 功率损耗/W20 基板传热系数/[W/(m2·K)]50 仿真步长/s1×10-4 初始/环境温度/℃25 网格数目10 964
热阻抗参数的提取采用热响应拟合法，分别在每个芯片上独立地施加阶跃功率损耗作为激励，由有限元仿真获得目标芯片的温度响应曲线，再计算暂态阻抗曲线，热响应曲线获取流程如图12所示。
图12 热响应曲线获取流程
Fig.12 Extracting process of dynamic thermal response curves
2.2.1 FEM法提取热阻抗参数的准确性验证
为验证所建立的有限元仿真模型的准确性，本文首先提取功率模块的结-壳热阻抗曲线，并与功率模块数据手册中的结-壳热阻抗曲线进行对比。当两者误差过大时，对有限元模型进行修正，修正方法包括调整材料参数、微调几何尺寸或者提高网格划分的质量。
图13所示为FEM仿真得到结壳热阻抗曲线与数据手册热阻抗曲线的对比。可以看出，两者在整个时间范围都较为接近，在暂态值部分FEM高于数据手册，稳态值部分FEM略小于数据手册，但最大误差都保持在5%以内，可以认为所建立的模型和参数准确性符合要求。
图13 FEM仿真与数据手册热阻抗对比
Fig.13 Comparison of FEM simulation results and transient thermal resistance from datasheet
2.2.2 考虑热耦合效应的热阻抗参数提取
图14为对A相SiC MOSFET芯片M1施加20W功率损耗后的温度分布，芯片之间的热耦合现象会随着芯片之间距离的增加而快速减弱。当以NTC温度为参考时，通过仿真得到的耦合热阻抗大小与芯片距离之间的关系如图15所示。耦合热阻抗大小随芯片间距的增加呈指数减小，且当两芯片间距大于10mm时，其热耦合影响可忽略不计。此外，鉴于三相逆变应用的对称性，为简化热网络，本文只对包含NTC热敏电阻的A相桥臂进行研究。
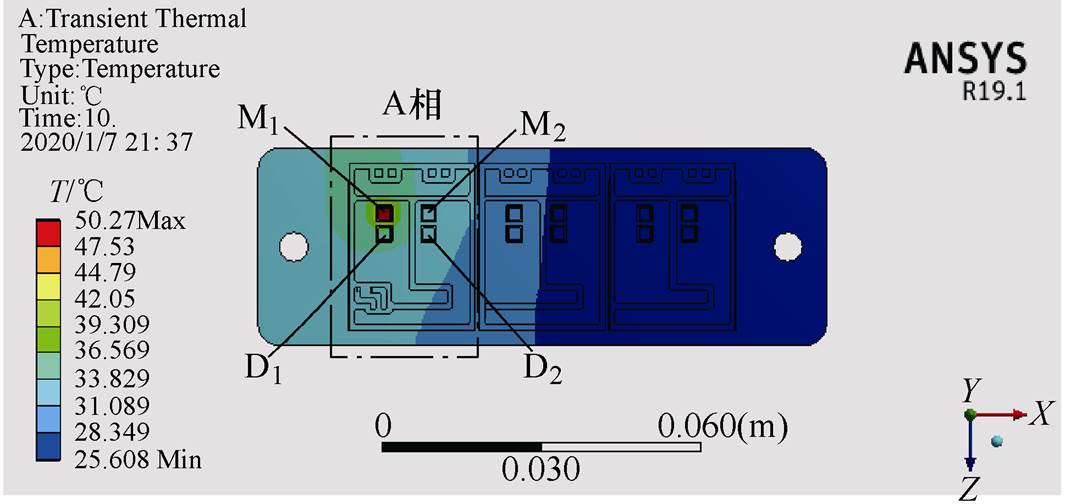
图14 模块温度分布
Fig.14 Temperature distribution of the module
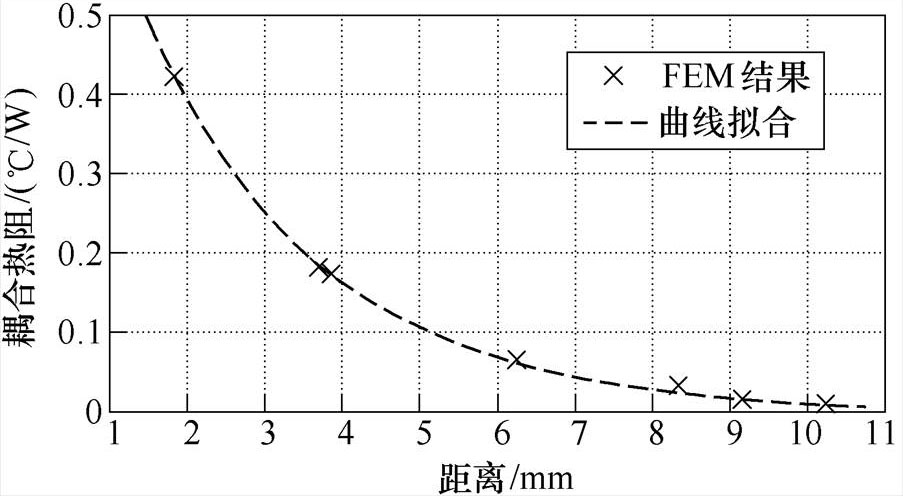
图15 耦合热阻抗与芯片间距的关系
Fig.15 The relationship between coupled thermal impedance and chip spacing
对A相各芯片单独施加阶跃损耗，按图12步骤提取的以NTC为参考点的SiC MOSFET芯片M1与SiC SBD芯片D1的自热阻抗曲线如图16所示。
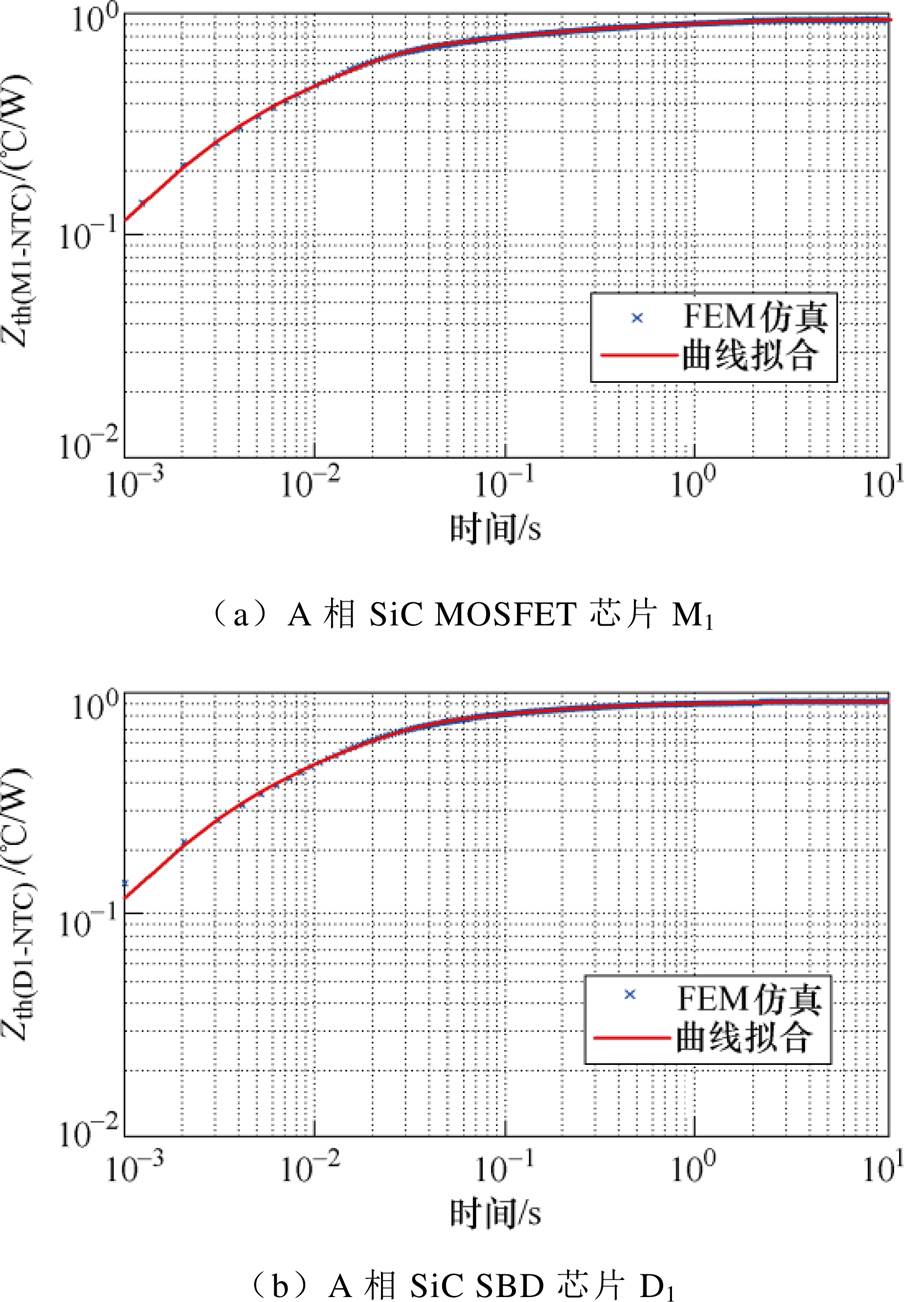
图16 暂态自热阻抗及其拟合曲线
Fig.16 Transient self-heating impedance and fitted curves
芯片的自热阻抗和耦合热阻抗曲线分别使用四阶、一阶RC热网络来拟合，得到的热阻抗参数见表2和表3，进而可构建出1.2节中的考虑热耦合效应的热网络模型。
2.2.3 边界条件对热模型的影响
功率模块工作时，其芯片温度不仅与功率损耗有关，还与散热条件、环境温度等边界条件有关。对于散热条件的变化，可设置不同的表面传热系数（Heat Transfer Coefficient, HTC）值来表征散热系统的冷却能力[19]，本文在有限元仿真中将功率模块基板设置为不同的HTC（5～10 000W/(m2·K)）以模拟不同条件的自然空气冷却和水冷散热方式。此外，为讨论环境温度对热阻抗的影响，FEM仿真的环境温度设置为25～100℃，提取的芯片M1至NTC的热阻抗曲线如图17所示。
表2 A相芯片热阻抗参数
Tab.2 Parameters of thermal impedance for phase A
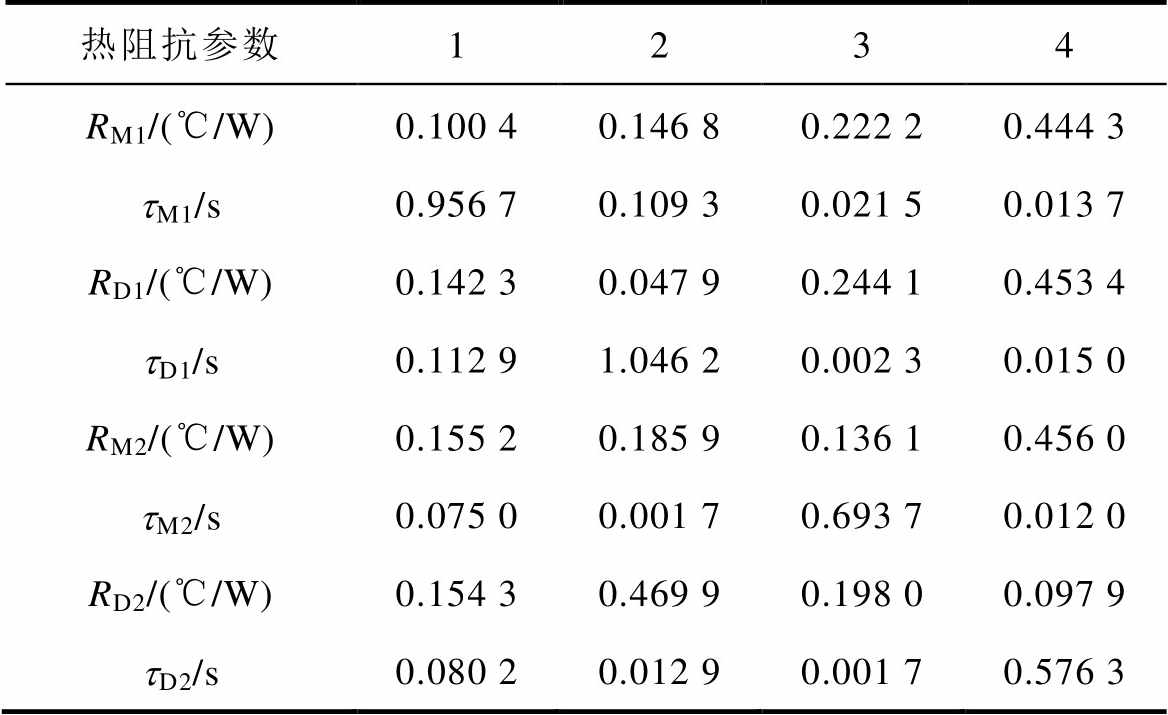
热阻抗参数1234 RM1/(℃/W)0.100 40.146 80.222 20.444 3 tM1/s0.956 70.109 30.021 50.013 7 RD1/(℃/W)0.142 30.047 90.244 10.453 4 tD1/s0.112 91.046 20.002 30.015 0 RM2/(℃/W)0.155 20.185 90.136 10.456 0 tM2/s0.075 00.001 70.693 70.012 0 RD2/(℃/W)0.154 30.469 90.198 00.097 9 tD2/s0.080 20.012 90.001 70.576 3
表3 A相芯片耦合热阻抗参数
Tab.3 Coupled thermal impedance of phase A
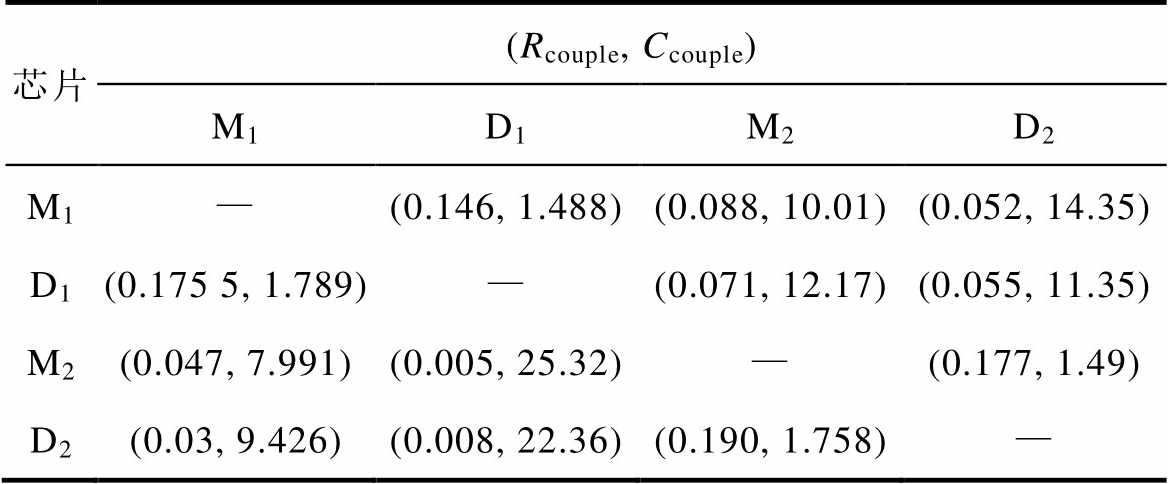
芯片(Rcouple, Ccouple) M1D1M2D2 M1—(0.146, 1.488)(0.088, 10.01)(0.052, 14.35) D1(0.175 5, 1.789)—(0.071, 12.17)(0.055, 11.35) M2(0.047, 7.991)(0.005, 25.32)—(0.177, 1.49) D2(0.03, 9.426)(0.008, 22.36)(0.190, 1.758)—
由图17可知，在不同散热条件下，芯片M1至NTC的暂态热阻抗几乎不变，稳态热阻在传热系数为10 000W/(m2·K) 时只减小了0.043℃/W，变化率仅为4.7%；在不同环境温度下，芯片M1至NTC的热阻抗会随着温度上升而有所增加，但最大差值仅为0.031 9℃/W，变化率也仅为3.5%。上述结果表明，本文所提出的新型热网络模型受功率模块的散热条件和模块所处的环境温度影响很小，热阻抗参数稳定，更适用于长时间在线估计功率模块内部芯片结温。
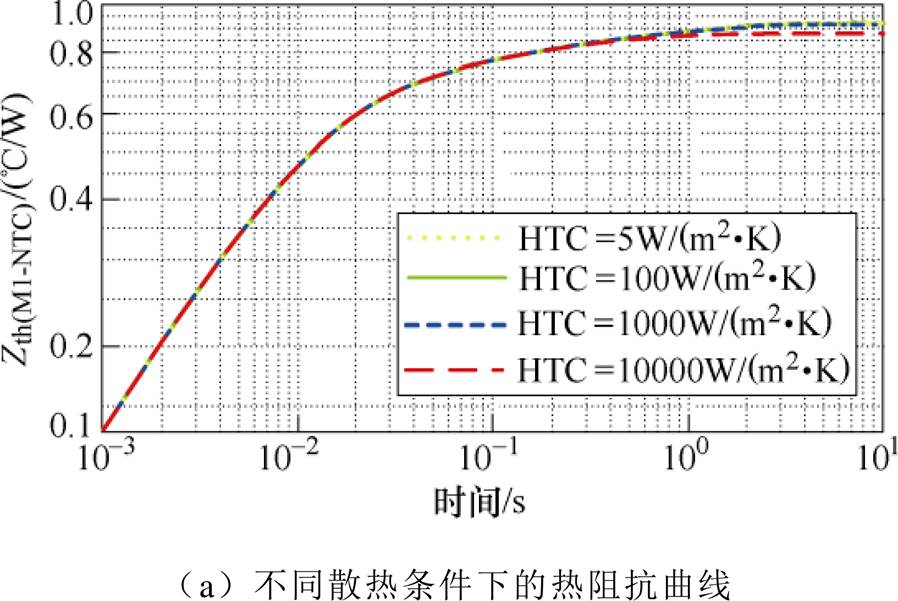
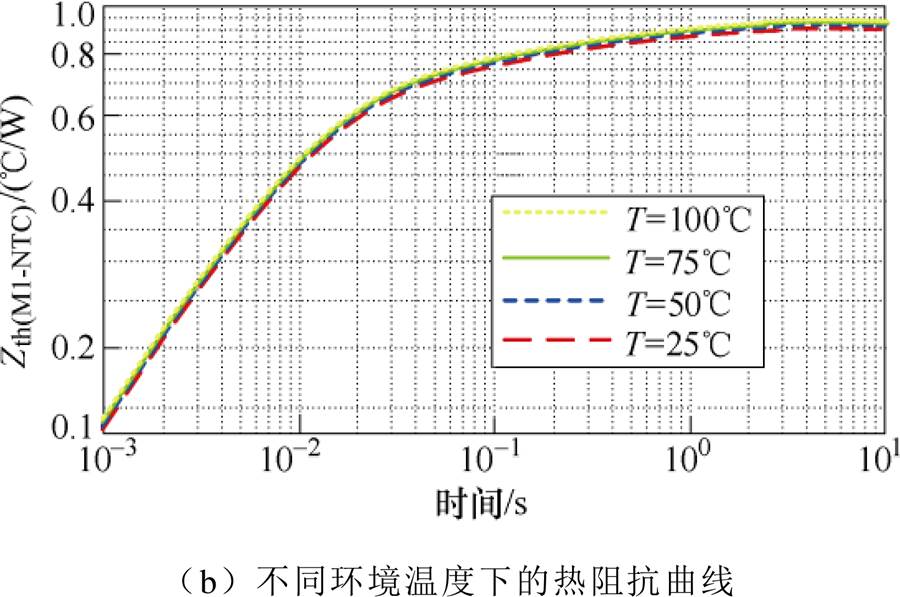
图17 不同边界条件下芯片M1至NTC的热阻抗曲线
Fig.17 Thermal resistance curves under different boundary conditions
本文采用红外测量和有限元仿真两种方法对所提结温估算方法的可行性和准确性进行验证。结温观测实验平台如图18所示。图18a为所搭建的实验平台，主要参数见表4。为了能够使用红外热成像仪准确地测量芯片结温，先打开功率模块封装，使用化学溶剂（Adrox 2312）溶解去除功率模块内部的灌封硅凝胶，再对功率模块均匀喷涂黑色耐高温绝缘漆（MOTIP 04031）。图18b为SiC逆变器及处理后的便于红外测温的SiC功率模块。
本文采用TI TMS320F28379 DSP作为实验平台控制芯片，在电机控制程序中集成了基于NTC传感器采样温度的结温在线估算功能。为了减少DSP的计算量，控制程序中的损耗计算和结温估计模块的采样计算周期设置为10个开关周期，每次结温计算结果通过CAN转USB通信上传至计算机，将此结温数据与红外热成像观测数据以及FEM仿真数据对比便可验证所提结温估算方法的可行性和准确性。
图18 结温观测实验平台
Fig.18 Experimental setup for junction temperature observation
表4 逆变器和负载电机主要参数
Tab.4 Main parameters of the inverter and motor
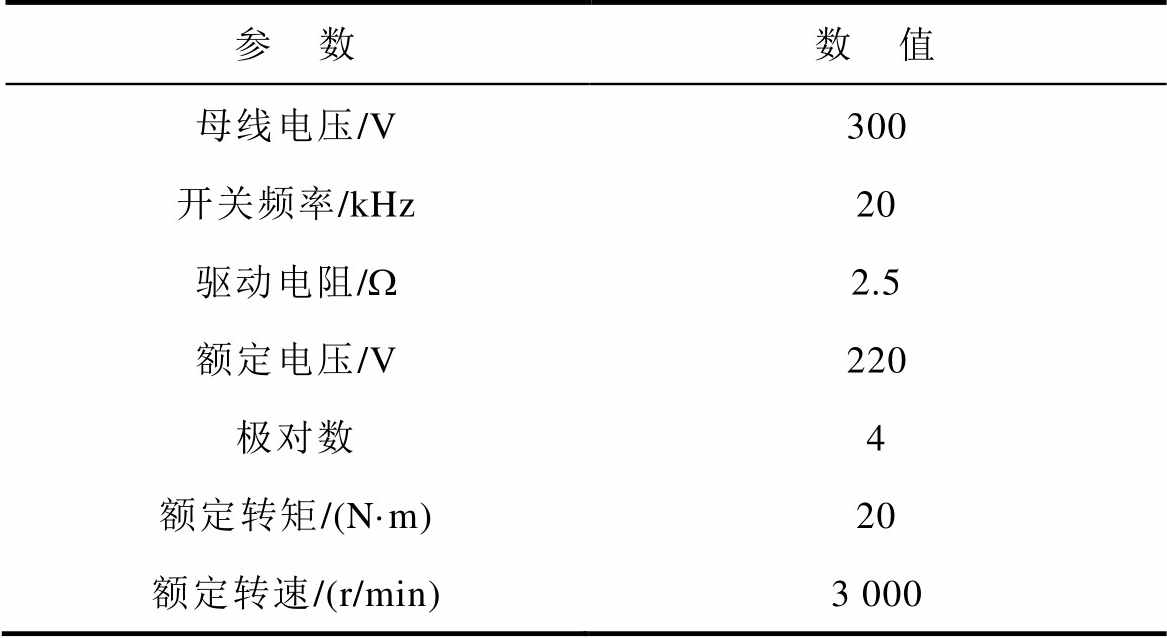
参 数数 值 母线电压/V300 开关频率/kHz20 驱动电阻/W2.5 额定电压/V220 极对数4 额定转矩/(N·m)20 额定转速/(r/min)3 000
本文采用红外热成像仪对功率模块A相芯片M1、D1和NTC传感器温度进行观测，结温红外定点观测设置如图19所示。
图20和图21为不同工况下的红外观测结果和在线计算结果。对比可知，在150r/min、10N·m的低频高转矩工况下，稳态时M1结温的计算值和红外测量值的平均值非常接近，约为45℃，在线计算结温为42～49℃，红外测量的结温为43～47℃。A相二极管VD1和NTC传感器温度的计算值和测量值也很接近。在750r/min、5N·m工况下，芯片结温的波动值较小，在线计算结温为35～37℃，红外测量值的波动只有1℃左右。
图19 结温红外定点观测设置
Fig.19 Infrared fixed-point setting for junction temperature observation
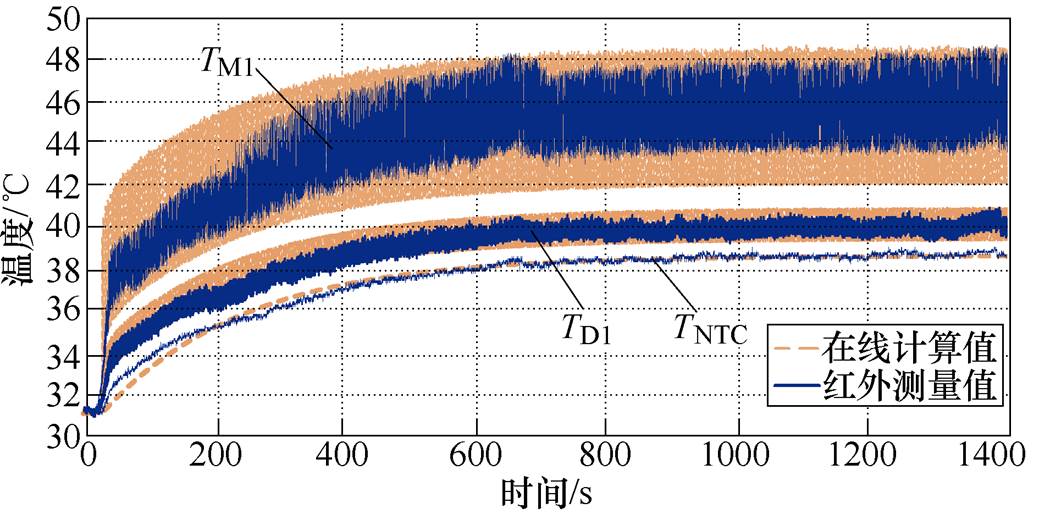
图20 150r/min，10N·m工况曲线对比
Fig.20 Junction temperature curves under 150r/min, 10N·m
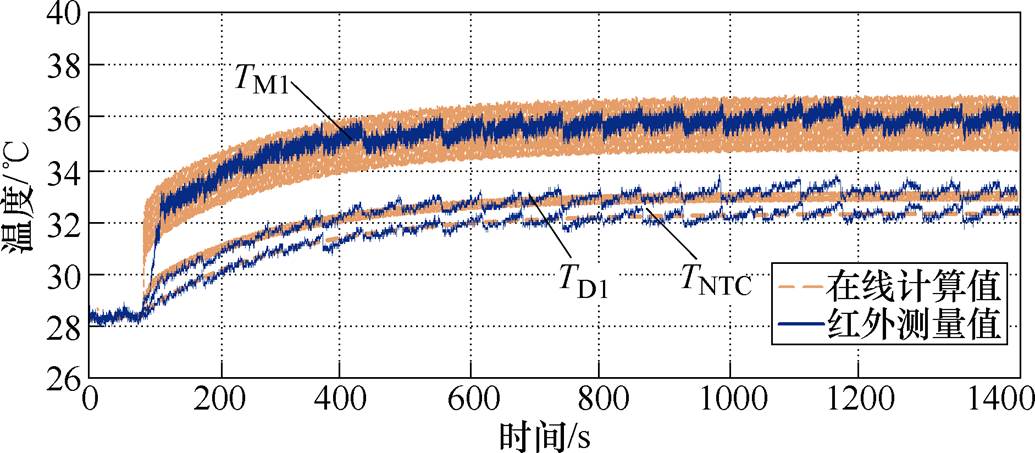
图21 750r/min，5N·m工况结温曲线对比
Fig.21 Junction temperature curves under 750r/min, 5N·m
需要说明的是，本实验使用的红外热成像仪为Fotric 326Pro，其最高有效刷新频率为16Hz，其在电机电流频率超过16Hz（对应电机转速约500r/min）时观测结温波动范围会有较大失真，但平均结温是准确的。鉴于此，可认为本文所提结温在线提取方法可行，并具有较高的准确度。
本文还采用有限元仿真模拟器件的特殊运行工况，将FEM仿真得到的NTC温度值作为参考输入到本文构建的以NTC为参考点的新型热网络模型中，验证所提结温计算方法在散热条件突变工况和波动损耗条件下结温提取的准确性。
3.2.1 恒定大功率损耗、散热条件突变工况
为了验证在散热条件突变工况下的器件结温提取效果，在FEM仿真过程中将功率模块的基板表面传热，系数在120s的仿真时间内设置为三段：0～50s，5 000W/(m2·K)；55～80s，50W/(m2·K)；80～120s，2 000W/(m2·K)。A相芯片M1和M2的发热功率设置为恒定50W，D1和D2的发热功率设置为恒定5W，模拟系统在重载运行条件下水冷散热系统突发故障情况，恒定大功率损耗、散热条件突变工况的结温如图22所示。
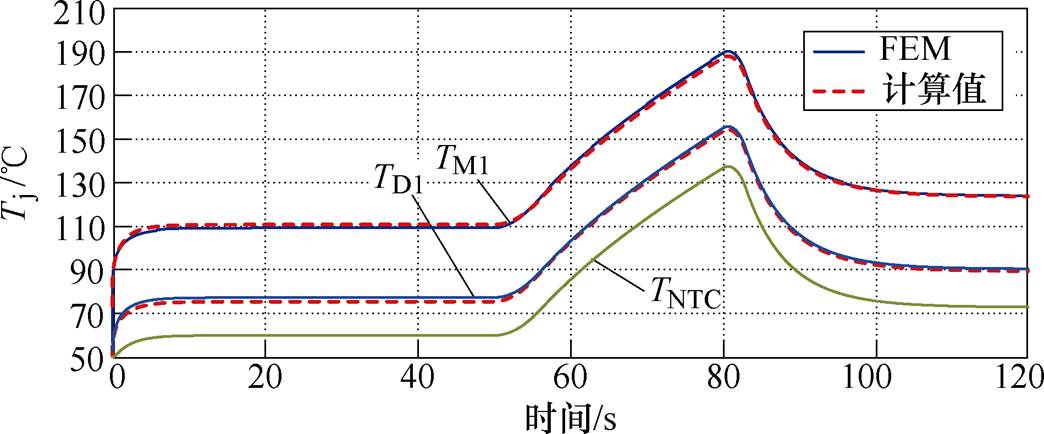
图22 恒定大功率损耗、散热条件突变工况的结温
Fig.22 Junction temperatures under constant high power loss and sudden changing in cooling conditions
由图22可知，在0～50s内，散热条件良好情况下（表面传热系数：5 000W/(m2·K)，即强迫水冷），A相芯片温度在5s内达到稳态值，这一阶段结温的仿真值和计算值几乎重合；在55～80s内，表面传热系数突然大幅下降（可等效为水冷系统突然失效），芯片温度快速上升，本文方法的计算值与有限元仿真结果非常吻合，误差在5℃以内。
3.2.2 波动损耗工况
对于功率器件而言，结温波动ΔTj的快速准确提取对于器件寿命预测和优化非常重要。为了进一步验证所提结温估计方法的有效性，本文针对电机运行于重载和高温环境工况进行分析，具体的工况条件见表5，结果如图23～图25所示。
表5 运行工况
Tab.5 Working conditions
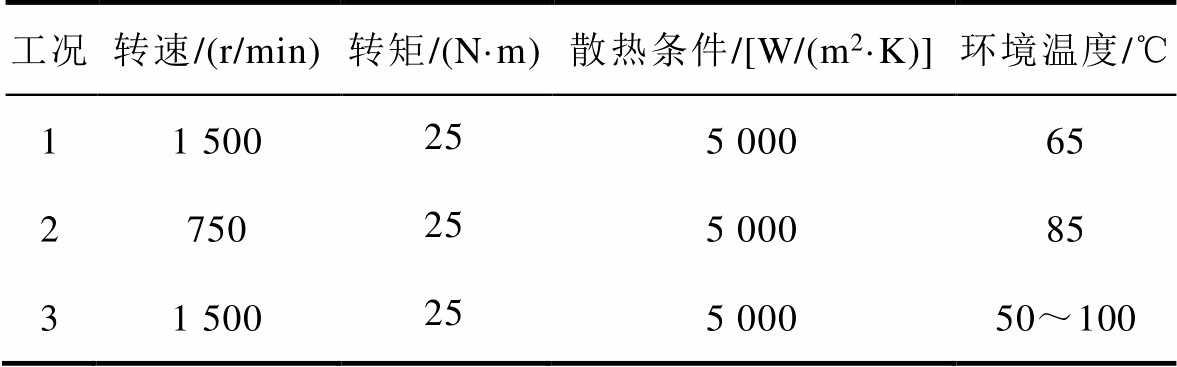
工况转速/(r/min)转矩/(N·m)散热条件/[W/(m2·K)]环境温度/℃ 11 500255 00065 2750 255 00085 31 500255 00050～100
图23和图24为相同输出转矩、不同转速（即不同逆变器交流输出频率）和环境温度下的器件结温，图25为模拟恶劣运行条件下（重载且环境温度在短时间内大幅上升，2～2.5s内由50℃上升到100℃）的器件结温。由三种工况下的对比结果可知，所提出的结温计算方法在重载及散热环境恶劣等条件下均能够快速准确地获取器件的动态结温，误差在5℃以内。
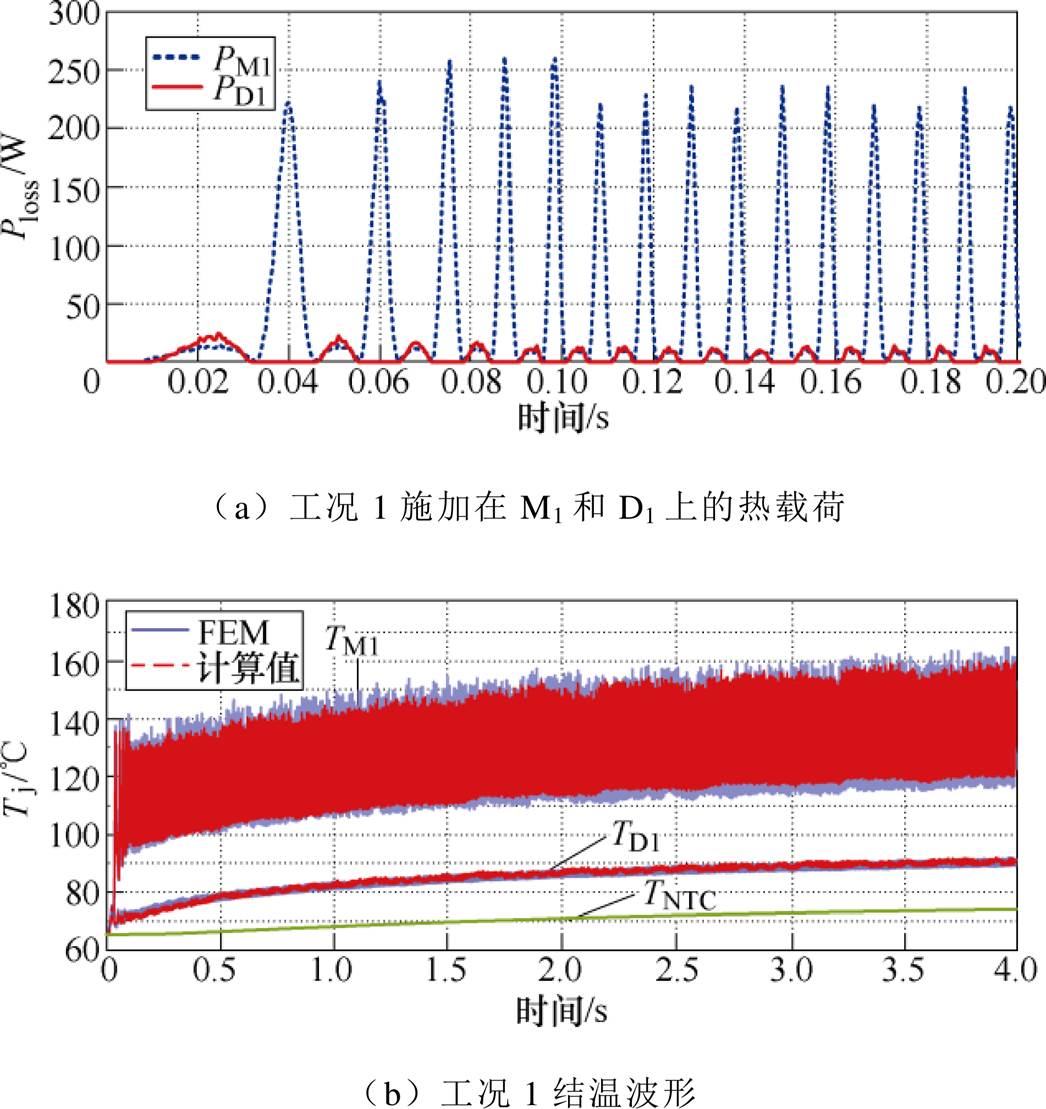
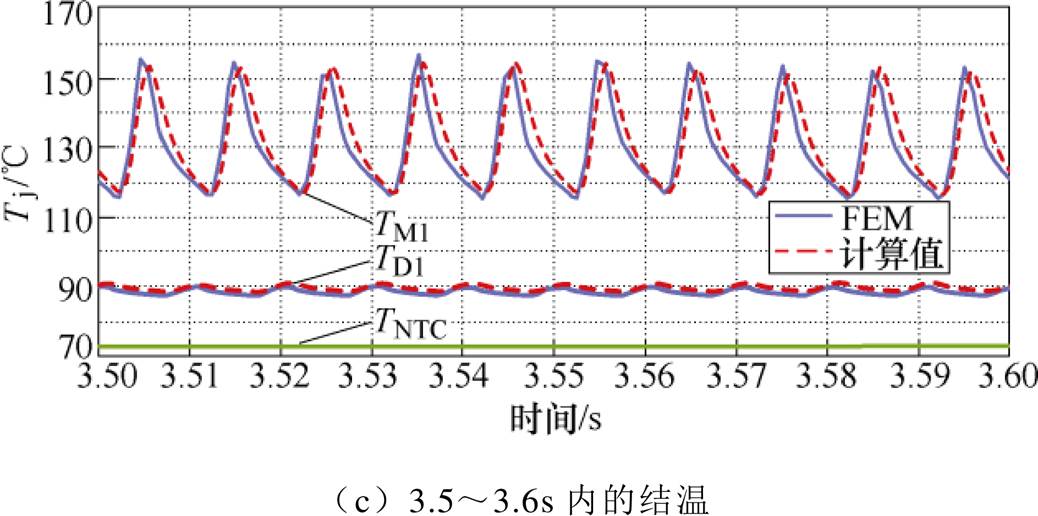
图23 工况1的损耗与结温对比结果
Fig.23 Power loss and comparison results of junction temperature under working condition 1
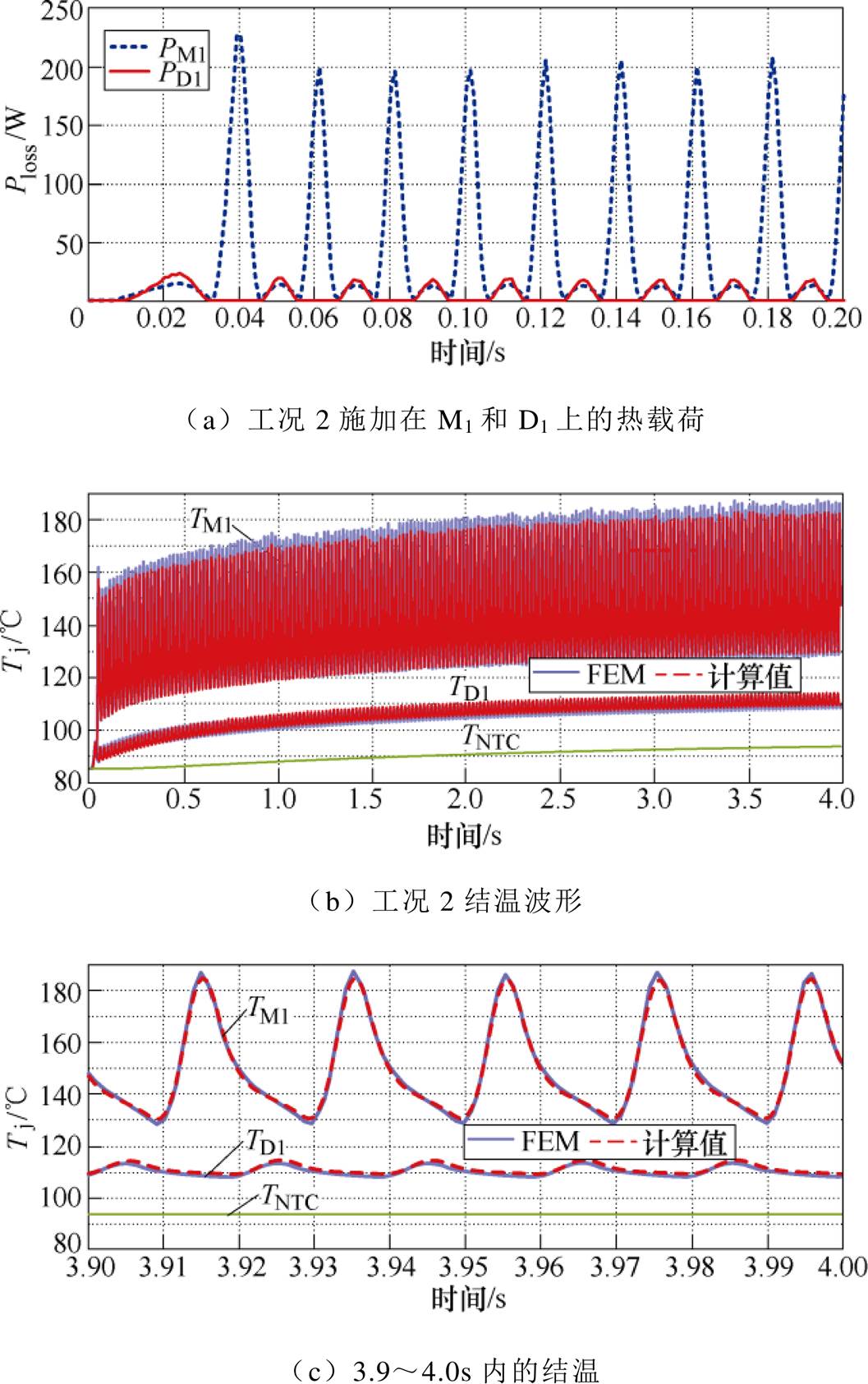
图24 工况2的损耗与结温对比结果
Fig.24 Power loss and comparison results of junction temperature under working condition 2
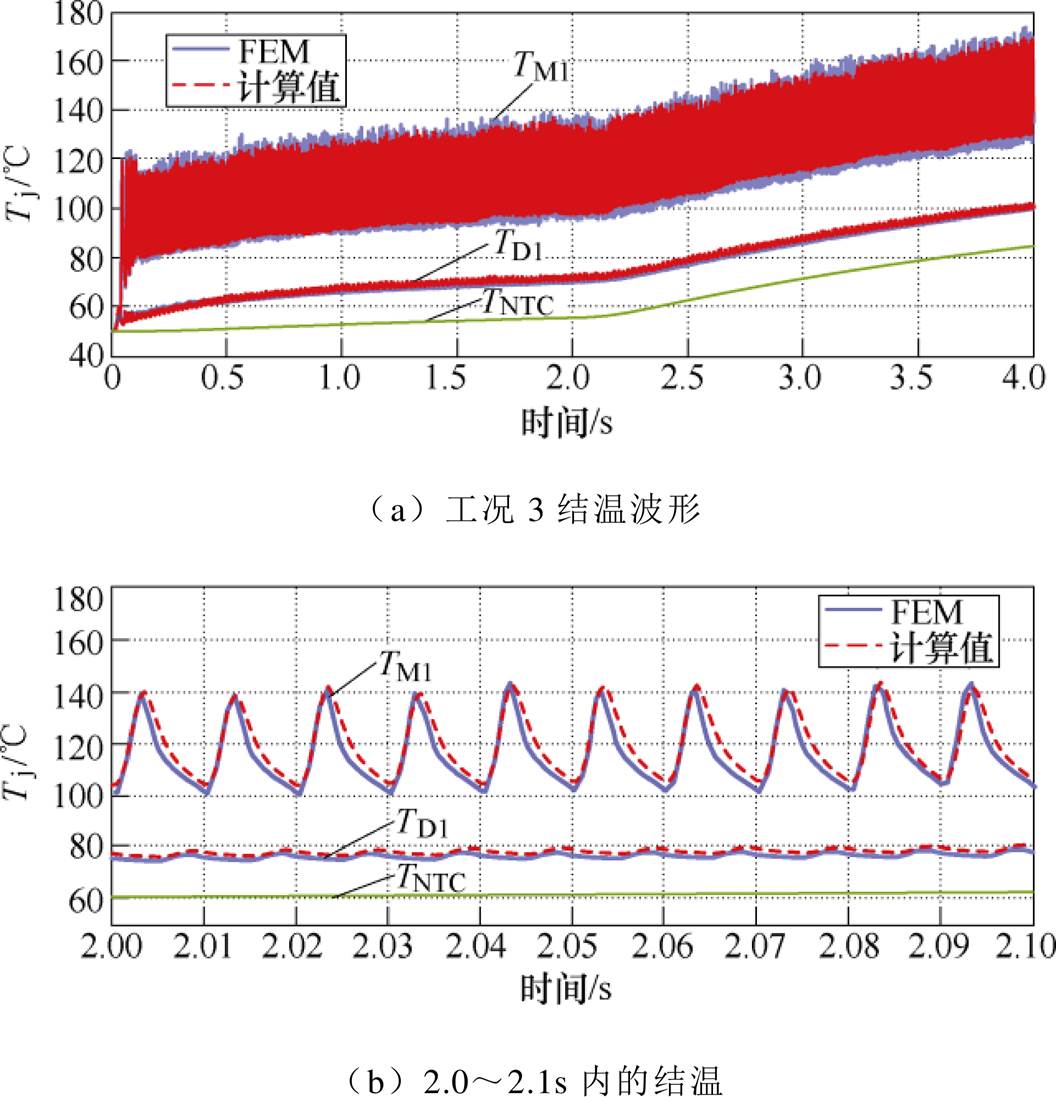
图25 工况3结温对比结果
Fig.25 Comparison results of junction temperature under working condition 3
本文提出了一种基于内置温度传感器的功率模块结温在线提取方法。首先建立了考虑热耦合效应的内置NTC传感器至功率芯片的热网络模型，并给出了SiC功率模块应用于电机驱动时的损耗快速计算方法；然后通过有限元仿真提取热网络模型参数，结合NTC传感器和SiC MOSFET的实时损耗计算实现了对SiC MOSFET功率模块内部芯片结温的在线提取。仿真与实验对比结果验证了所提结温估算方法的可行性和有效性。该方法具有以下优点：
1）易于在线集成、结温估算准确。不需要增加额外测量电路，损耗计算和结温估计方法易于集成到控制程序中，结温平均值和波动值估算准确。
2）热网络参数稳定。新型热网络模型参数对环境温度、散热器工作条件等变化不敏感，非常适用于变换器中功率模块的长时间结温监测，并可在此基础上实施热优化控制。
在实际中应用本文所提方法时，需要对不同的功率模块进行复杂的三维建模和有限元分析以获得新型热网络参数，该方法比较繁琐复杂。因此，通用、准确、流程化的热网络参数提取方法是本文进一步研究的重点，更加准确而实用的损耗建模也有待进一步的深入研究。
参考文献
[1] Hamada K, Nagao M, Ajioka M, et al. SiC-emerging power device technology for next-generation electri- cally powered environmentally friendly vehicles[J]. IEEE Transactions on Electronic Devices, 2015, 62(2): 278-285.
[2] 王学梅. 宽禁带碳化硅功率器件在电动汽车中的研究与应用[J]. 中国电机工程学报, 2014, 34(3): 371- 379.
Wang Xuemei. Researches and applications of wide bandgap SiC power devices in electric vehicles[J]. Proceedings of the CSEE, 2014, 34(3): 371-379.
[3] 赵炫, 蒋栋, 刘自程, 等. SiC功率器件在轨道交通行业中的应用[J]. 机车电传动, 2020(1): 38-44.
Zhao Xuan, Jiang Dong, Liu Zicheng, et al. Appli- cation of silicon carbide power devices in rail transit[J]. Electric Drive for Locomotive, 2020(1): 38-44.
[4] 任磊, 韦徵, 龚春英, 等. 电力电子电路功率器件故障特征参数提取技术综述[J]. 中国电机工程学报, 2015, 35(12): 3089-3101.
Ren Lei, Wei Zheng, Gong Chunying, et al. Fault feature extraction techniques for power devices in power electronic converters: a review[J]. Proceedings of the CSEE, 2015, 35(12): 3089-3101.
[5] Yang Shaoyong, Bryant A, Mawby P, et al. An industry based survey of reliability in power electronic converters[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1441-1451.
[6] Wang Huai, Liserre M, Blaabjerg F. Toward reliable power electronics: challenges, design tools, and opportunities[J]. IEEE Industrial Electronics Magazine, 2013, 7(2): 17-26.
[7] 王学梅, 张波, 吴海平. 基于失效物理的功率器件疲劳失效机理[J]. 电工技术学报, 2019, 34(4): 717-727.
Wang Xuemei, Zhang Bo, Wu Haiping. A review of fatigue mechanism of power devices based on physics-of-failure[J]. Transactions of China Electro- technical Society, 2019, 34(4): 717-727.
[8] 周雒维, 王博, 张益, 等. 非平稳工况下功率半导体器件结温管理技术综述[J]. 中国电机工程学报, 2018, 38(8): 2394-2407, 2549.
Zhou Luowei, Wang Bo, Zhang Yi, et al. Review on junction temperature management of power semi- conductor devices under power fluctuation condition[J]. Proceedings of the CSEE, 2018, 38(8): 2394-2407, 2549.
[9] 任磊, 沈茜, 龚春英. 电力电子电路中功率晶体管结温在线测量技术研究现状[J]. 电工技术学报, 2018, 33(8): 1750-1761.
Ren Lei, Shen Qian, Gong Chunying. Current junction temperature online measurement techniques of power transistors in power electronic converters[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(8): 1750-1761.
[10] Khatir Z, Dupont L, Ibrahim A. Investigations on junction temperature estimation based on junction voltage measurements[J]. Microelectronics Reliability, 2010, 50(9-11): 1506-1510.
[11] Xu Zhuxian, Xu Fan, Wang Fei. Junction temperature measurement of IGBTs using short-circuit current as temperature-sensitive electrical parameter for converter prototype evaluation[J]. IEEE Transactions on Indu- strial Electronics, 2015, 62(6): 3419-3429.
[12] Chen H, Pickert V, Atkinson D J, et al. On-line monitoring of the mosfet device junction temperature by computation of the threshold voltage[C]// Proceedings of the 3rd IET International Conference on Power Electronics, Machines and Drives, The Contarf Castle, Dublin, 2006: 440-444.
[13] 方化潮, 郑利兵, 王春雷, 等. IGBT 模块栅极电压米勒平台时延与结温的关系[J]. 电工技术学报, 2016, 31(18): 134-141.
Fang Huachao, Zheng Libing, Wang Chunlei, et al. The relationship between junction temperature and time delay of gate voltage miller plateau of IGBT module[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 134-141.
[14] 孙鹏飞, 罗皓泽, 董玉斐, 等. 基于关断延迟时间的大功率IGBT模块结温提取方法研究[J]. 中国电机工程学报, 2015, 35(13): 3366-3372.
Sun Pengfei, Luo Haoze, Dong Yufei, et al. Junction temperature extraction of high power IGBT module based on turn-off delay time[J]. Proceedings of the CSEE, 2015, 35(13): 3366-3372.
[15] 王莉娜, 邓洁, 杨军一, 等. Si和SiC功率器件结温提取技术现状及展望[J]. 电工技术学报, 2019, 34(4): 703-716.
Wang Lina, Deng Jie, Yang Junyi, et al. Junction temperature extraction methods for Si and SiC power devices-a review and possible alternatives[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(4): 703-716.
[16] 魏克新, 杜明星. 基于集总参数法的IGBT模块温度预测模型[J]. 电工技术学报, 2011, 26(12): 79-84.
Wei Kexin, Du Mingxing. Temperature prediction model of IGBT modules based on lumped parameters method[J]. Transactions of China Electrotechnical Society, 2011, 26(12): 79-84.
[17] 万萌, 应展烽, 张伟. 分立型功率MOSFET结温估计的非线性热网络模型和参数辨识方法[J]. 电工技术学报, 2019, 34(12): 2477-2488.
Wan Meng, Ying Zhanfeng, Zhang Wei. Nonlinear thermal network model and parameter identification method for junction temperature estimation of discrete power MOSFET[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2477-2488.
[18] 李辉, 胡姚刚, 刘盛权, 等. 计及焊层疲劳影响的风电变流器IGBT模块热分析及改进热网络模型[J]. 电工技术学报, 2017, 32(13): 80-87.
Li Hui, Hu Yaogang, Liu Shengquan, et al. Thermal analysis and improved thermal network model of IGBT module for wind power converter considering solder fatigue effects[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 80-87.
[19] Wintrich A, Nicolai U, Werner T, et al. Application manual power semiconductors[M]. Nuremberg: SEMIKRON International GmbH, 2011.
[20] Wang Ke, Liao Yongjun, Song Gaosheng. Over- temperature protection for IGBT modules[C]// International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 2014: 1-7.
[21] Zhou Yu, Shi Wei, Tang Junsong, et al. Dynamic junction temperature estimation via built-in negative thermal coefficient (NTC) thermistor in high power IGBT modules[C]//IEEE Applied Power Electronics Conference and Exposition Tampa, FL, USA, 2017: 772-775.
[22] Ma Xin, Zhao Jia, Yang Yong. A new transient thermal impedance model for estimating the dynamic junction temperature of IGBT modules[C]//Inter- national Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 2018: 1-5.
[23] Calzo G Lo, Lidozzi A, Solero L, et al. Thermal regulation as control reference in electric drives[C]// 15th International Power Electronics and Motion Control Conference, Novi Sad, Serbia, 2012: 1-7.
[24] 盛永和, 罗纳德P. 柯利诺. 电力电子模块设计与制造[M]. 北京: 机械工业出版社, 2011.
[25] Morgan A J, Xu Y, Hopkins D C, et al. Decom- position and electro-physical model creation of the CREE 1200V, 50A 3-Ph SiC module[C]//2016 IEEE Applied Power Electronics Conference and Exposition, Long Beach, CA, USA, 2016: 2141-2146.
[26] Ayadi M, Ammous A, Ounejjar Y, et al. Thermal interaction of semiconductor devices in multi-chip modules[C]//IEEE International Conference on Systems, Man and Cybernetics, Yasmine Hammamet, Tunisia, 2002: 6-16.
Online Junction Temperature Extraction for SiC Module Based on Built-in Temperature Sensor
Abstract Silicon carbide (SiC) MOSFET has the advantages of high switching speed and low loss, which will be more and more widely used in high efficiency and high power density applications. In these applications, SiC MOSFETs are facing severe reliability tests, and the online accurate extraction of junction temperature is essential for lifetime prediction and health assessment. This paper proposed an online junction temperature extraction method for power module based on built-in negative temperature coefficient (NTC) temperature sensor. First, the thermal network model between the built-in NTC sensor and the power chips considering the thermal coupling effect was established, and a fast loss calculation method for SiC MOSFET was proposed. Then, the thermal network parameters were extracted by finite element simulation, and the stability of thermal network parameters under different boundary conditions was verified. Simulation and experimental results show that the proposed method can accurately obtain the dynamic junction temperature, and the thermal network model parameters are not affected by changes in boundary conditions such as ambient temperature and heat dissipation conditions. It is suitable for junction temperature monitoring and lifetime prediction under real mission profiles.
keywords：Negative temperature coefficient temperature sensor, SiC MOSFET, thermal network model, chip temperature
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.201442
国家自然科学基金项目（51977065）和天水大型电气传动系统与装备技术国家重点实验室开放资金项目（SKLLDJ022019003）资助。
收稿日期 2020-10-30
改稿日期 2021-02-03
刘 平 男，1983年生，博士，副教授，研究方向为电动车辆高性能电力电子变换与电机驱动控制。E-mail: pingliu@hnu.edu.cn（通信作者）
李海鹏 男，1995年生，硕士研究生，研究方向为宽禁带半导体器件驱动与可靠性。E-mail: 2099325157@qq.com
（编辑 陈 诚）