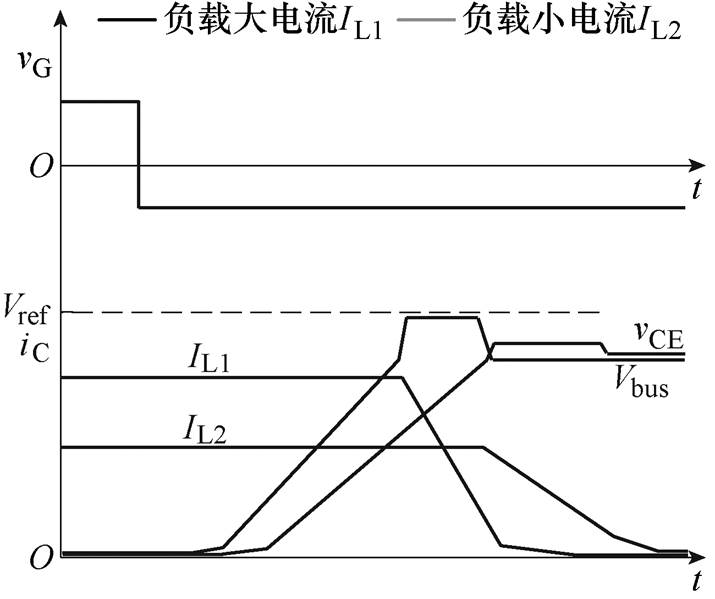
图1 CGD方法不同负载电流IL下的关断瞬态示意图
Fig.1 Diagram of turn off under different IL with CGD
摘要 常规驱动(CGD)对绝缘栅双极型晶体管(IGBT)开关特性的控制优化程度有限。当换流条件改变时,CGD方法也无法保证器件开关特性可以保持在最优状况,即缺乏自调节能力。学术界相应地提出主动栅极驱动(AGD)方法来实现对开关特性的自调节控制。但在实施自调节控制时,会遇到自调节控制稳定性、控制精度等方面的问题。该文在之前工作的基础上开展后续深入研究,针对这些问题,从理论上提出自调节控制时的3个关键设计点,并分别进行了实验验证,为AGD方法实施自调节控制提供了指导。该文综述已有驱动对IGBT关断峰值电压控制的缺陷,提出一种端电压峰值采样电路。将该采样电路与自调节控制结合,通过实验验证了直接控制端电压峰值的准确性,为更安全、更低损耗地关断IGBT打下了坚实基础。
关键词:IGBT 开关特性 自调节控制 主动栅极驱动 开通延迟 关断端电压峰值
功率半导体器件绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)自20世纪80年代诞生之后就获得了广泛运用[1-4]。因此,对IGBT的电气性能进行优化就显得很有意义。IGBT断、通态电气性能基本是由器件本体性质决定,而其开关瞬态电气特性可以通过外部电路进行更大程度的控制与优化。文献[5]对改善IGBT开关特性的主要方法作了详细归纳与分析,说明了从驱动侧对IGBT开关瞬态过程施加控制具备更显著的优势,即有可控性高、无需改变主电路且不会影响器件通态电流大小等优点。
最常用的IGBT驱动就是常规驱动(Conventional Gate Drive, CGD)方法,但它对开关特性的控制和优化能力有限[5],这里以关断瞬态为例。CGD方法不同负载电流IL下的关断瞬态示意图如图1所示,图中,Vref为预设的端电压上限,vG为驱动电压,iC为IGBT管电流,vCE为端电压,Vbus为母线电压,IL为负载电流。端电压峰值随着负载电流IL增大而增大。因而在选取驱动电阻时,需要使最大端电压峰值(IL最大时)不能超过一定的值(见图1中的Vref),这将造成端电压峰值在IL较小的情况下可能明显小于预设的上限值Vref,即绝对值|diC/dt|很低,器件关断瞬态的管电流下降阶段的损耗大。可见,当IGBT换流条件不同时(如负载电流IL、换流回路杂散电感LS不同),驱动器应当自动调节驱动量,使得开关特性始终保持或接近最优化。文献[6]将驱动方法的这种自动调节能力称作“自调节”控制能力(Self- Regulating Capability, SRC),并提出一种新的数字驱动方法,即自调节电压源型驱动(Self-Regulating Voltage-Source Drive, SRVSD)方法。如文献[6]所介绍的,SRVSD方法可以自调节地准确控制开关时长和开关损耗等特性。其中对于开关损耗的控制,除了可以降低变换器损耗,还可以用于抑制器件结温,从而提高器件寿命[7-8]。

图1 CGD方法不同负载电流IL下的关断瞬态示意图
Fig.1 Diagram of turn off under different IL with CGD
为了提高驱动方法对IGBT开关特性的控制能力,学术界和工业界在IGBT诞生后的40年里提出了大量的主动栅极驱动(Active Gate Drive, AGD)[2-3, 5-6, 9-22]。这里将这些AGD驱动方法按照是否需要反馈划分为开环[9-15]和闭环[2, 6, 16-22]两类,并考察它们是否具有自调节控制能力。
开环型驱动方法[9-15]一般只能依靠固定的驱动方式,如采用优化的驱动电压、驱动电路波形来改善开关行为。由于没有反馈采样回路,该类驱动方法多数时候无法随着工况的改变而做出相应驱动量的调整,即一般无法实现自调节控制。
闭环驱动方法[2, 6, 16-22]有反馈电路,多数闭环驱动方法可以判断IGBT处于开关瞬态的具体阶段,因而很多具有自调节控制能力。文献[2]提出的闭环驱动方法,通过直接采样diC/dt和dvCE/dt,可以对它们施加精确的控制。文献[2]有实现自调节控制的潜力,但由于它的参考值是硬件上给定的电位,所以需要增加其他元件才能实现。文献[19-20]提出的驱动方法,都能够在线改变控制参考值,从而灵活地调节开关行为,实现自调节控制。但是这两种AGD方法都存在无法控制的开关特性,如文献[19]的AGD方法无法控制开通瞬态dvCE/dt和关断瞬态diC/dt。相较而言,文献[6]提出的SRVSD方法可以实现开关瞬态各阶段的自调节控制。如文献[6]所分析的,SRVSD通过特定的通信协议和一根光纤,可同时接收开关信号和换流工况或控制目标值,从而方便地施加自调节控制。表1列出了这几个高性能闭环驱动的元器件数量和成本,包括现场可编程门阵列(Field Programmable Gate Array, FPGA)、模数转换器(Analog-to-Digital Converter, ADC)和数模转换器(Digital-to-Analog Converter, DAC)。从表1可知,SRVSD方法的元器件数量相对较少,成本更低。
表1 各驱动方法关键元器件数量比较
Tab.1 Counts of critical components in different AGDs

驱动方法文献[2]文献[19]文献[20]SRVSD 元件数量1个FPGA3个运放4个开关1个FPGA3个ADC1个DAC1个电流源1个FPGA3个运放1个DAC2个比较器1个开关1个FPGA1个运放1个DAC2个比较器 单片价格/$—>136—73.1
本文是文献[6]的后续深入研究,主要有:
(1)SRVSD方法对开关特性施加自调节控制时,怎样对驱动电压限幅来保证器件正常开关,自调节控制的稳定性及比例-积分(Proportional- Integral, PI)参数的整定方法,自调节控制主要误差来源及控制准确性。这部分工作从理论分析和实验两方面进行。
(2)提出了一种对关断瞬态端电压峰值的精确采样方式,并进行端电压峰值的自调节控制实验 验证。
图2为SRVSD方法控制时基本换流单元器件开关瞬态波形示意图,图中,S1~S4分别为开通延迟、diC/dt、dvCE/dt和稳态阶段,S5~S8分别为关断延迟、dvCE/dt、diC/dt和稳态阶段,在SRVSD方法控制时,vG为IGBT的驱动电压,VEE、VCC分别为通态驱动电压和断态驱动电压,vCE为端电压,IL、Vbus分别为负载电流和母线电压,irr、vos分别为开通瞬态管电流过冲和关断瞬态端电压过冲,vknee为器件拐点电压,itail为拖尾电流。
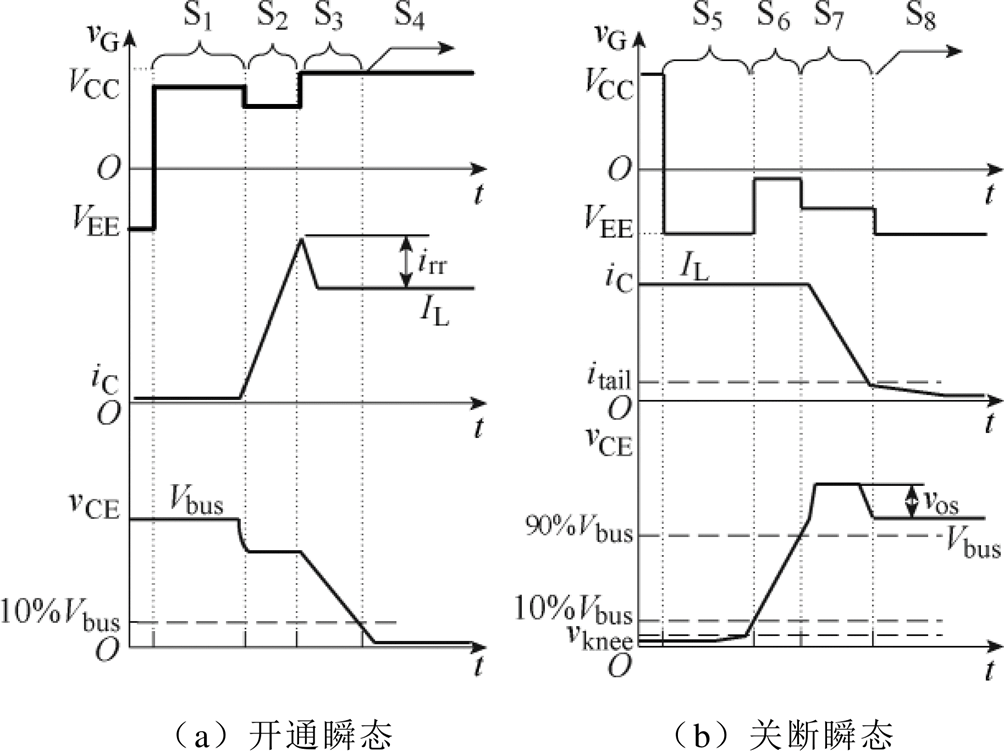
图2 SRVSD方法控制时基本换流单元器件开关瞬态波形示意图
Fig.2 Diagram of switching behavior in the basic commutation cell with the control of SRVSD method
如文献[6]所述,SRVSD方法的基本原理是将硬开关的开通、关断瞬态各划分为四个阶段,然后施加不同的驱动电压以达到调节开关行为的目的。SRVSD通过一个DAC产生不同驱动电压,这里将DAC数字输入量记作CODE,那么驱动电压vG为
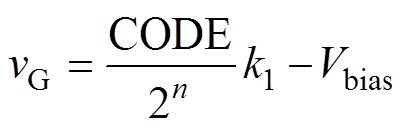 (1)
(1)式中,n为DAC位数;CODE可调范围为(0, 2n-1);k1、Vbias分别为相应的系数和偏置电压。
这里将文献[6]推得的开关时长计算式,重新写作如式(2)~式(7)所示,以表征各开关阶段时长与驱动电压的关系,其中按照文献[6]的标记,TSx、vGSx分别为Sx阶段的时长和驱动电压;Rgon、Rgoff分别为开通和关断驱动电阻;Vth、Vml分别为阈值电压和米勒电平;gm为跨导;Cies、CgcL分别为栅极输入总寄生电容和高端电压时的米勒电容;DvCE为S2阶段vCE跌落值。
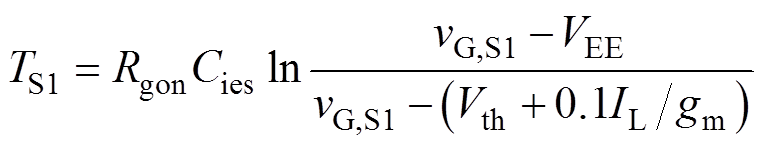 (2)
(2)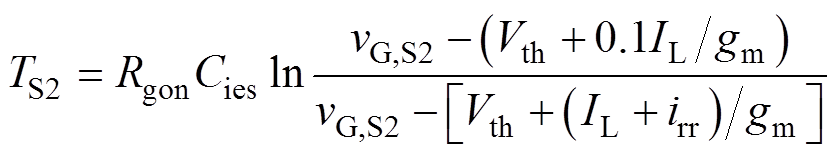 (3)
(3)
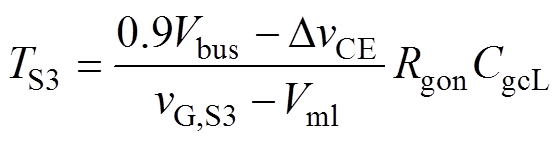 (4)
(4)
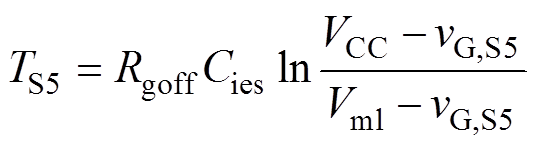 (5)
(5)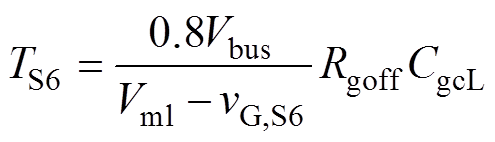 (6)
(6)
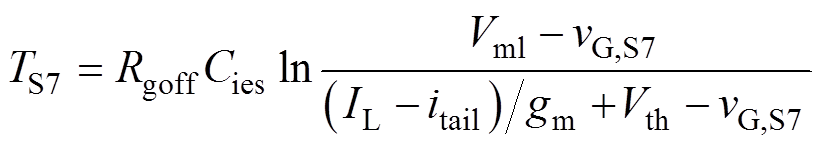 (7)
(7)
此处给出vCE过冲vos为
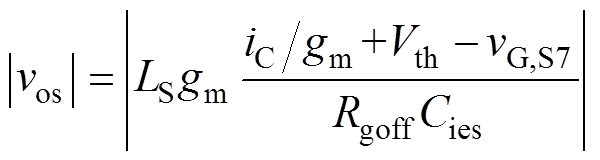 (8)
(8)SRVSD方法实现自调节控制的基本方式是:在每个开关瞬态根据驱动器上的反馈采样回路,实时获取开关特性量,将其与参考值比较后,通过比例-积分调节器(Proportional-Integral Regulator, PIR)产生下一个开关瞬态的DAC数字输入量,从而产生相应的驱动电压,最终在几个脉冲内将开关特性控制到目标值。
为了方便下文的讨论,以开通延迟TS1为例,简要介绍自调节控制的控制策略。
第i个开通瞬态之前,FPGA对S1阶段的计数器清零。当FSM(Main)识别出S1阶段时,则对其计时。将计数值NS1,i与参考值NS1,ref作差,得到第i个S1时长误差eS1,i,即
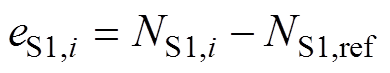 (9)
(9)在开关信号的下降沿,对下一个开通瞬态的值Preg,i+1、Ireg,i+1进行锁存,得出
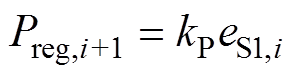 (10)
(10)
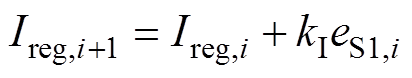 (11)
(11)式中,kP、kI分别为PI调节器的比例、积分系数。
在锁存比例、积分分量Preg和Ireg后,通过组合逻辑计算出下一个S1阶段DAC输入量,即CODEi+1表示为
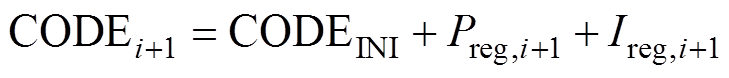 (12)
(12)式中,CODEINI为初始的DAC输入量,决定了第一个开通瞬态S1阶段的驱动电压。
在第4节研究IGBT端电压峰值自调节控制前,需要先对SRVSD方法实现自调节控制时,在驱动电压限幅、控制稳定性、控制精度等问题上作理论分析。
2.2.1 各阶段对驱动电压限幅的理论研究
根据式(2)~式(7),为了使IGBT正常工作,各个阶段驱动电压都需要保持在一定范围,如式(13)~式(18)所示。可以根据式(1),将式(13)~式(18)给出的上、下限转换为DAC数字量CODE的上、下限,从而对式(12)的计算结果限幅。
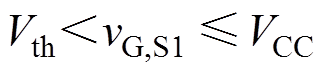 (13)
(13)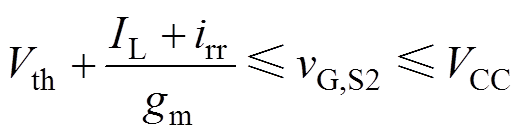 (14)
(14)
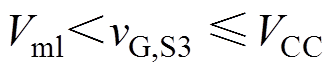 (15)
(15)
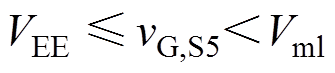 (16)
(16)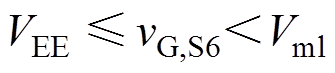 (17)
(17)
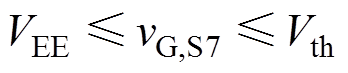 (18)
(18)
这里以式(15)为例对驱动电压限幅原则进行说明。S3为开通瞬态端电压下降阶段,此时栅极电压维持在米勒电平Vml,栅极电流全部流向米勒电容Cgc,因此驱动电压vG,S3总是大于Vml。在第3节中会展示实验中遇到的vG,S7过小引发的器件故障。
2.2.2 自调节控制稳定性及PI参数整定方法研究
由上文分析,SRVSD方法依靠PI调节器,对各开关特性施加自调节控制。本文提出一种高效的PI参数整定方法,采用的是理论计算与手动调试相结合的方式。
一般地,希望PI参数kP、kI尽可能大,因为较大的kP、kI可以使受控对象快速达到目标值。但是kP、kI也不能太大,否则会导致控制量饱和,以及控制变量出现较大的过冲或振荡。这里提出的理论计算方法就是为了获得kP、kI的上限值,而手动调试就是从该上限值开始往更小值进行调试,一般可以迅速找到使得控制稳定的较大的kP、kI。下面以TS1为例,说明理论计算PI参数上限值的方法。
这里假设在第一个有效开通脉冲时,S1阶段的驱动电压vG,S1=VCC,由于施加的初始vG,S1是最大值,因此式(9)中初始计数值NS1,1最小。那么在TS1的控制效果较好时(快速达到目标值,且过冲、振荡小),可以认为初始的负值误差eS1,1是绝对值最大的误差。根据2.1节介绍的控制策略,可根据式(10)~式(12),用eS1,1计算得出第2个开通瞬态S1阶段的Preg,2、Ireg,2,进而计算出CODE2。由于eS1,1、Preg,2、Ireg,2为负值,因此如式(13)所示,CODE2对应的驱动电压应大于Vth。由式(9)~式(13),经过简单的计算可以得到如式(19)所示的PI参数上限值,其中CODE(vG=VCC)和CODE(vG= Vth)为分别使得驱动电压等于VCC和Vth的DAC数字输入量。
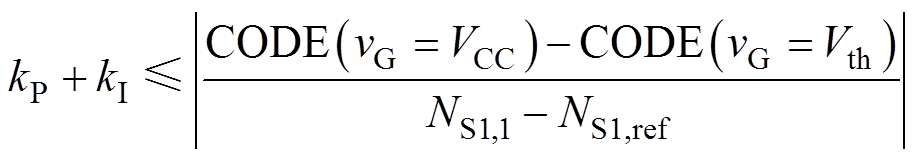 (19)
(19)控制稳定性及PI参数整定过程将在第3节中进行实验验证。
2.2.3 DAC分辨率对控制精度影响的理论分析
根据式(1),由于DAC只能输出特定电平,相应地,SRVSD方法也只能产生分立的驱动电压值。分立的驱动电压只能产生特定的开关行为,于是对开关特性施加自调节控制,就会不可避免地产生误差。且根据式(1),DAC的分辨率(位数)越高,那么SRVSD方法可产生的驱动电平也越多,分辨率也更高。
这里以TS1为例,从理论上推导由于驱动电压分立所导致的TS1最大相对误差的表达式。
SRVSD方法分立驱动电压引起TS1控制误差的计算示意图如图3所示,横坐标表示驱动电压,vG,H、vG,L分别为vG,S1的上、下限。假设v1、v2为SRVSD输出的两个相邻驱动电压值,v2-v1为驱动电压分辨率,且v1、v2分别产生了开通延迟T1、T2。这里认为目标时长Tref落在T2、T1之间,那么在自调节控制下,驱动电压将会在v1、v2切换,实际TS1相应地会在T2、T1之间切换。据此,可以通过式(20)得出TS1在参考值Tref下最大相对误差。从图3和式(20)可以看到,DAC位数越高,则vG分辨率越高,T1、T2就会跟Tref更接近,相对误差也会降低。
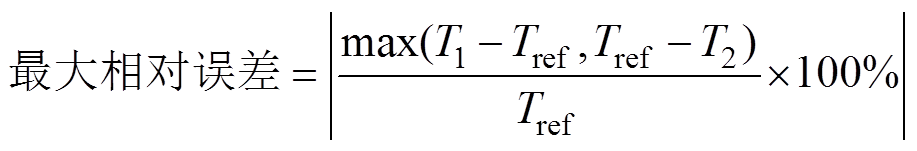 (20)
(20)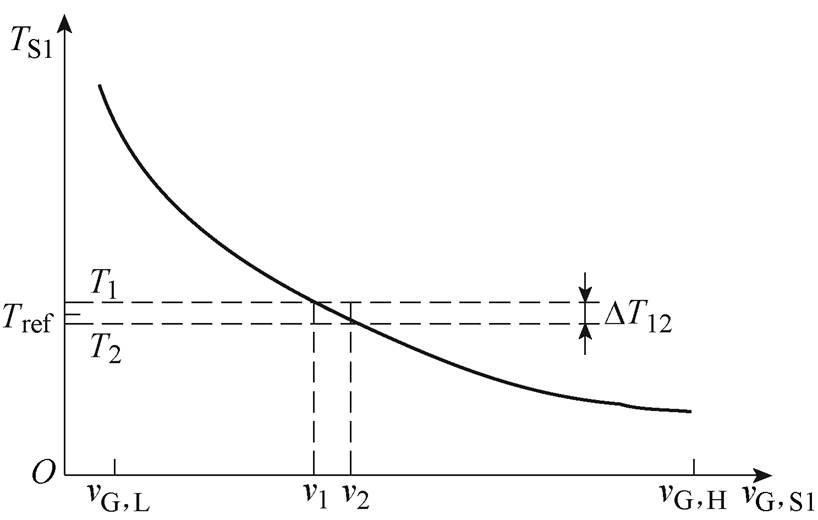
图3 SRVSD方法分立驱动电压引起TS1控制误差的计算示意图
Fig.3 Diagram for the calculation of TS1 control error due to discrete drive voltages with the SRVSD method
这里可以计算出使用不同分辨率(不同位数)DAC时,不同TS1参考值下的相对误差。将Infineon的IGBT模块FF1400R12IP4的驱动参数以及各DAC分辨率下所有驱动电压值代入式(2)和式(20),可以计算得到各TS1下的相对误差,SRVSD方法在不同DAC分辨率下TS1控制相对误差计算结果如图4所示。可以看到,DAC分辨率越高,控制误差会明显降低。图4的结果可以作为SRVSD方法控制精度的参考。下文中会对不同DAC分辨率下的TS1控制精度作实验比较。
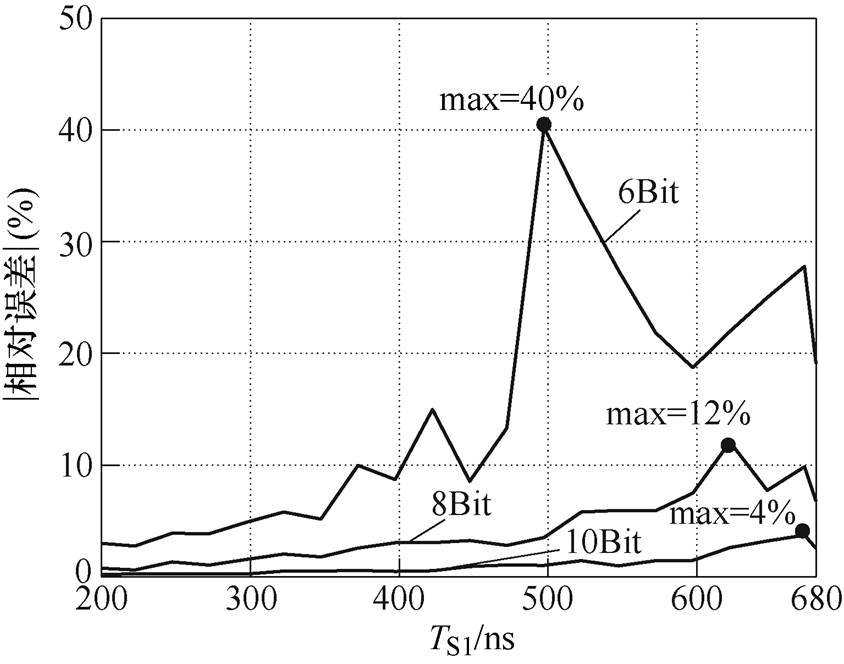
图4 SRVSD方法不同DAC分辨率下TS1控制相对误差计算结果
Fig.4 Calculation results for the control error of TS1 control under different DAC resolutions with the SRVSD
本节先对第2节理论分析的关键设计点的必要性进行实验验证,然后以开通延迟为例,说明SRVSD方法的自调节控制能力。
3.1.1 各阶段对驱动电压限幅必要性的实验验证
SRVSD方法下由于vG,S3过小引起器件失效全过程实验波形如图5所示,图5中,没有对vG,S3进行限幅,而在自调节控制实验时vG,S3取值过小,导致器件过热损坏。所用器件是Infineon的1 200V/300A IGBT模块FF300R12ME4。图5中,vSTATE为FPGA输出的表示器件当前状态的标志位,在S3、S4、S8阶段,vSTATE分别为1、0、1。下面分析图5中器件出现非正常开关动作到最终完全失控损坏的过程。
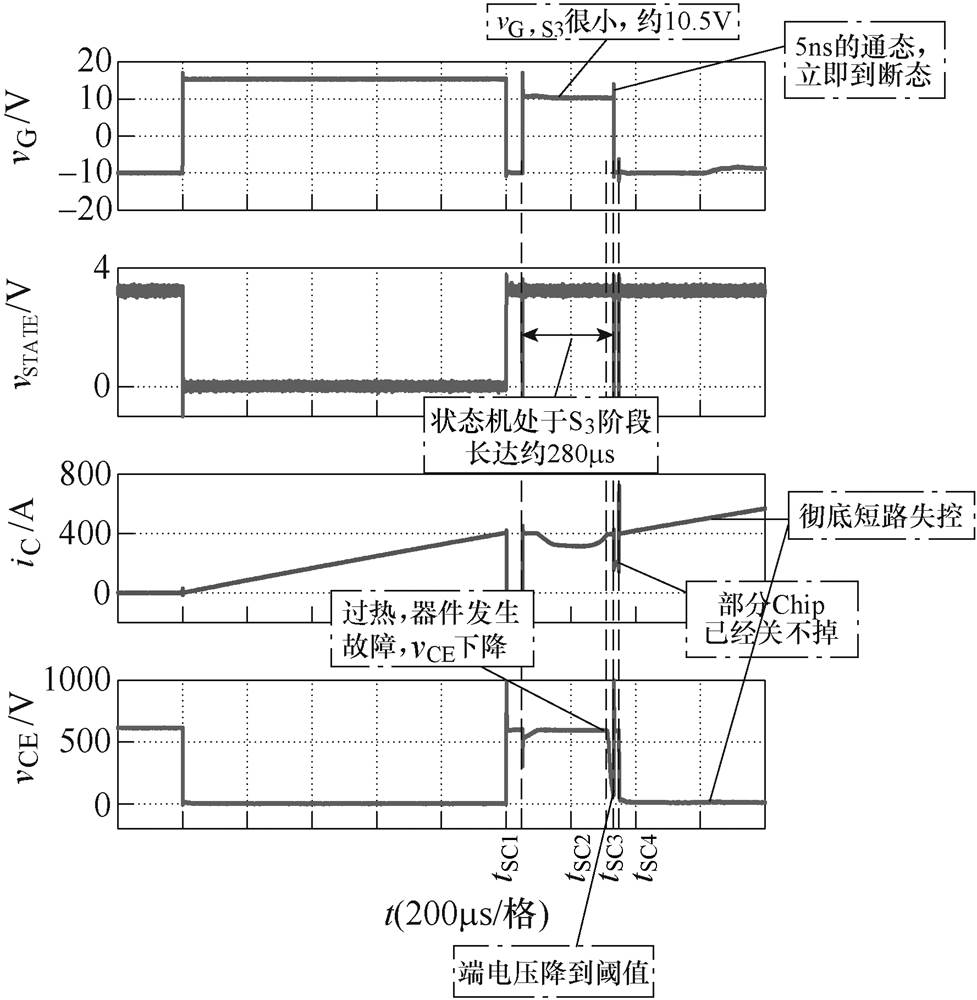
图5 SRVSD方法下由于vG,S3过小引起器件失效全过程实验波形
Fig.5 Experimental waveforms for the destruction of IGBT due to low vG,S3 level with the SRVSD methods
tSC1~tSC2:tSC1时刻器件已经从S2切换至S3,可以看到管电流为400A,明显大于器件的额定电流,因此S3阶段vgi=Vml应该较大。但是vG,S3=10.5V较小,使得tSC1~tSC2之间vCE几乎没有下降。这段时间IGBT承受600V母线电压和400A负载电流,功耗很大。这段时间持续了280ms左右,在高电压和大电流下,器件内部会产生大量的热,最终在tSC2时刻开始发生故障。
tSC2~tSC3:tSC2时刻开始,器件发生短路故障,vCE迅速下降。由于开通管vCE下降,换流的二极管端电压开始承压,iC=IL轻微上升。当vCE下降至10%Vbus时,状态机从S3切换至通态阶段S4。
tSC3时刻附近:状态机到通态S4阶段后,此时开关指令已经关断,S4阶段持续了一个工作时钟后迅速切换至断态S8。相应地,从图5可以看到,tSC3附近驱动电压上升后又突然下降至VEE。主器件开始关断,端电压迅速上升到母线电压Vbus,对二极管正向恢复续流。与正常的关断行为不同,tSC3时刻后,由于器件已经损坏,无法完全关断,iC仍然维持在200A左右。
tSC3之后:这段时间器件仍处在高电压和大电流下,于是在tSC4时刻发生彻底短路损坏。从tSC4时刻开始,器件短路,两端电阻几乎为0,vCE迅速下降,栅极对器件彻底失去控制。tSC4之后,iC=IL在母线电压充电下继续增大。iC持续增大,器件内部的键合线最终断开,彻底断路损坏。
SRVSD方法下vG,S3过小引起器件失效照片如图6所示,可以看到,开通主管(下管)损坏,而上管没有明显损坏。

图6 SRVSD方法下vG,S3过小引起器件失效照片
Fig.6 Photo for the breakdown IGBT due to low vG,S3 with the SRVSD method
从本节的实验结果和分析可以看到,对SRVSD方法在开关各阶段的驱动电压进行限幅是必要的,否则器件可能无法正常地完成开关动作。图6正是在实验中对驱动电压限幅不合适时,发生器件故障和损坏的情况。在实际设计中,为了确保器件和装置的安全,还可以同时采取一些其他保护措施,如设置一个时长上限阈值,对S1~S3、S5~S7各阶段计时,当某一阶段时间达到阈值时,就立刻关断器件。
3.1.2 控制稳定性即PI参数整定过程的实验验证
本节仍然用FF300R12ME4作为开关器件,以TS1的自调节控制为例,用实验验证2.2.2节中PI整定方法。TS1自调节控制时PI参数整定实验数据如图7所示。
首先,kP、kI的上限值可由式(19)计算得出。其中驱动电压等于VCC,Vth时各自对应的CODE可由式(1)计算得出,相差242。对开关时长计数的时钟频率为100MHz,第一个S1阶段施加vG,S1=VCC产生了250ns的开通延迟,NS1,1=25。S1时长参考值TS1,ref =380ns,对应的NS1,ref =38。将这些量代入式(19)可得
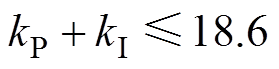 (21)
(21)这里从该上限值开始,逐步以减小的趋势进行手动调试。先取kP=3.6,kI=15,这组参数达到了式(21)中的上限,实验结果如图7a所示,可以看到,vG,S1和TS1在每次自调节后都存在严重的振荡。将PI参数适当降低至kP=1.5, kI=13,实验结果如图7b所示,可以看到,TS1经过一个周期就达到了与目标值大致误差为5%的数值,之后也一直是稳定的。如图7c、图7d所示,将PI参数进一步降低,时长的控制都是稳定的,但是响应速度进一步降低,需要经过更多的周期才能达到目标值。
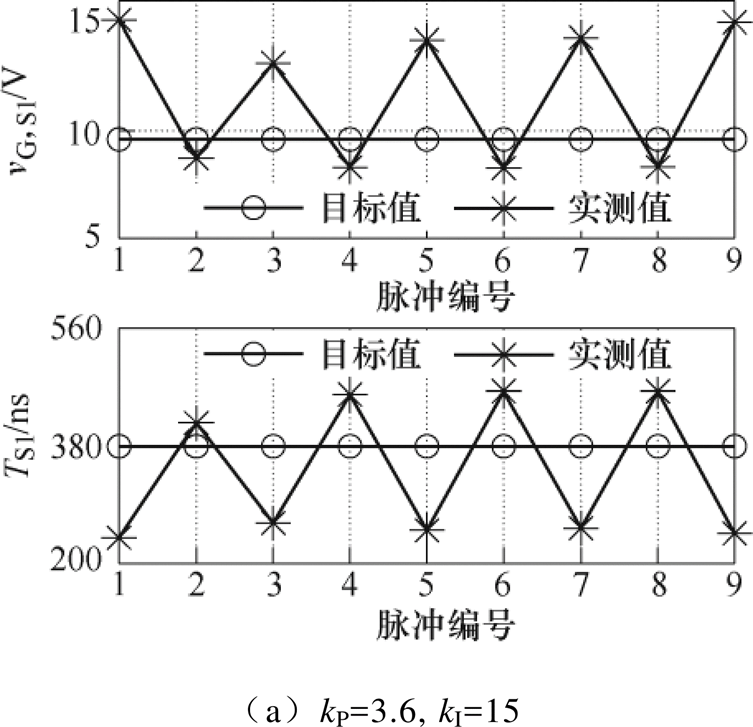

图7 TS1自调节控制时PI参数整定实验数据
Fig.7 Experimental datas of the PI tuning process with TS1 self-regulating control
这一部分的实验对2.2.2节中关于开关时长自调节控制的稳定性分析和PI参数整定方法进行了验证,可以看到,所提的整定方法可以帮助迅速找到尽可能大的合适PI参数。提出的PI参数整定方法也适用于其他数字型闭环驱动器。
3.1.3 DAC分辨率对控制精度影响的实验验证
这里以TS1为例,根据2.2.3节的理论分析,就不同DAC分辨率对自调节控制精度的影响作实验比较。
在考虑了驱动电压限幅和控制稳定性的情况下,得到了6位和10位DAC时的控制实验数据,TS1自调节控制精度实验数据如图8所示。TS1参考值为460ns,从图8a可见,6位DAC时控制是稳定的,但是由于分辨率较低,最终TS1只能围绕着参考值上下浮动,而与其总是存在着超过10%的误差。相较而言,从图8b可以看到,10位DAC控制时稳定,且最终的误差不超过0.1%。
该实验结果验证了2.2.3节中关于DAC分辨率越高,控制精度越高的理论分析与计算。
本节以开通瞬态时长为例,在不同负载电流下,用实验验证SRVSD方法对开关特性的自调节控制能力,实验所用器件为FF1400R12IP4。
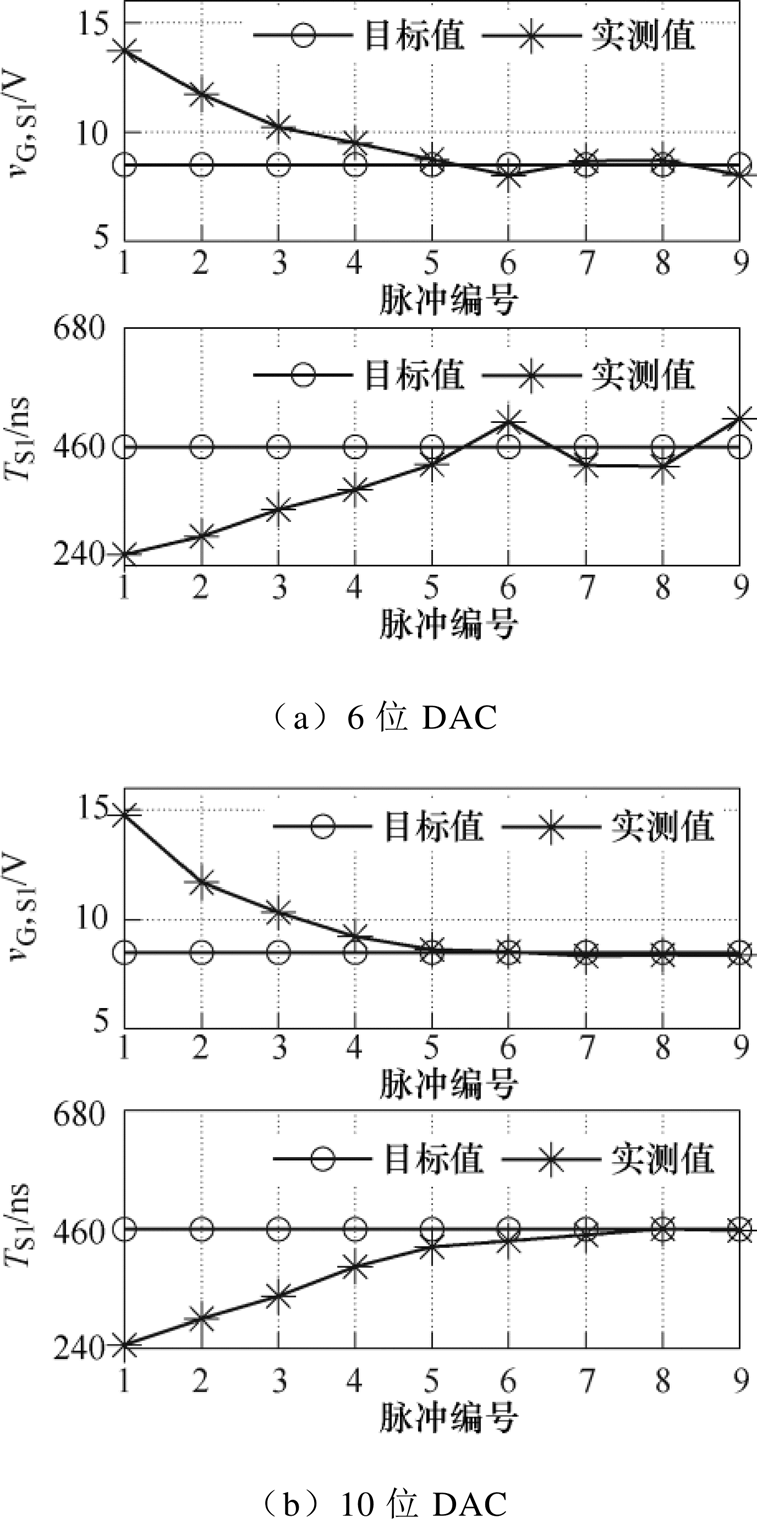
图8 TS1自调节控制精度实验数据
Fig.8 Experimental datas of control accuracy of different DAC resolutions with TS1 self-regulating control
在满足上文关键设计点的基础上,对开通瞬态各阶段的目标值设置为:负载电流为400A(TS1,ref, TS2,ref, TS3,ref)=(600ns, 200ns, 500ns),600A(TS1,ref, TS2,ref, TS3,ref)=(600ns, 300ns, 500ns),800A(TS1,ref, TS2,ref, TS3,ref)=(600ns, 400ns, 500ns)。在各负载电流下作连续脉冲实验,初始脉冲开通瞬态各阶段驱动电压都是VCC,图9给出了TS1、TS3在各负载电流下,在自调节控制下各开通瞬态的数据。从图9可见,SRVSD方法可以在不同负载电流下,准确、稳定地通过控制驱动电压来实现相同的参考开关特性。SRVSD方法具有自调节控制能力,在换流条件改变时,也可最大限度实现或接近目标特性。
图10给出了在图9中控制达到稳态时不同负载电流的开通波形,可以看到,开通延迟总是相同的。由于TS1与负载电流成正比,因此各IL下S2阶段的diC/dt和端电压跌落值DvCE都相同。因为TS3、DvCE、Vbus是相同的,因此各负载电流下dvCE/dt也保持一致。
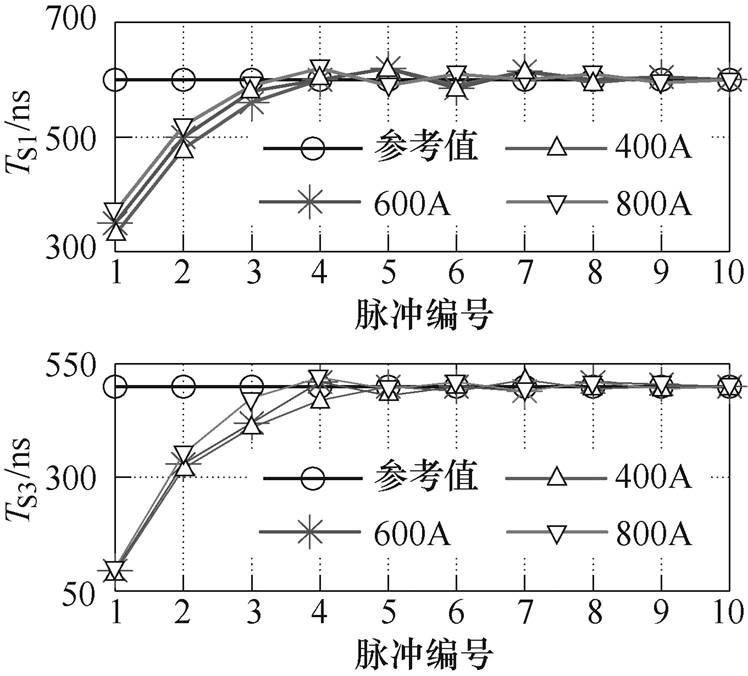
图9 不同负载电流下TS1、TS3自调节控制实验数据
Fig.9 Experimental datas for self-regulating control of TS1, TS3 under different load currents
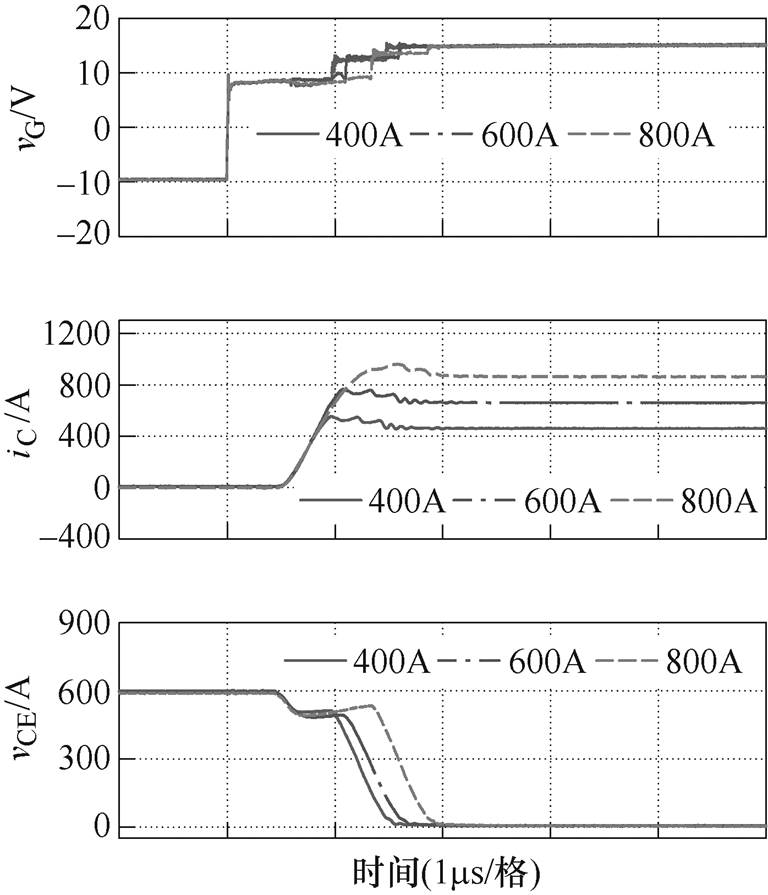
图10 不同负载电流下控制达到稳态时实验波形
Fig.10 Stable experimental waveforms of self-regulating control under different load currents
如图2b所示,IGBT的关断瞬态端电压峰值vCE,PK可以表示为
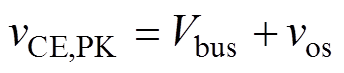 (22)
(22)如果vCE,PK过大,器件可能会发生击穿损坏。一般地,CGD方法选择足够大的关断驱动电阻值Rgoff使得最大负载电流IL下,vCE,PK处在预设上限值(见图1中的Vref)。在这个Rgoff下,当IL更小时,vCE,PK会更低,保证了器件安全关断。但是更低的vCE,PK就意味着iC下降速度更慢,而选用较大的Rgoff也会使得S5阶段栅极放电变慢,S6阶段vCE上升变缓,这些都会导致关断延迟和损耗增大。
此外,还有一些学者提出了对vCE,PK进行抑制或控制的措施。文献[20]提出的过电压保护电路,不影响主动栅极驱动方法对关断延迟、关断损耗的改善。该过电压保护电路,将采样得到的vos经过运算放大器输出一个控制量,再经电流源向栅极注入额外电流,从而减缓S7阶段iC下降速度。但是控制减缓后的iC下降速度,仍然会使vCE,PK超过设置的参考值,这一点可以从文献[20]中给出的实验波形中看到。因为在文献[20]给出的过电压抑制波形中,在vCE过冲时,额外注入的栅极电流始终存在。
文献[22]提出一种AGD方法,通过在S6、S7阶段施加较大关断驱动电阻值Rgoff来抑制vCE,PK。文献[22]的AGD方法,可以在一定程度上对vCE,PK起到抑制作用,但是当换流条件(负载电流IL、换流回路杂散电感LS等)改变时,该方法无法对IGBT的端电压尖峰进行准确控制。
为了保证IGBT安全、低损耗关断,这里提出一种直接精确控制IGBT关断瞬态端电压峰值的思路。用较小的驱动电阻Rgoff,缩短S5、S6阶段,从而获得低关断延迟和损耗。同时对vCE,PK进行直接采样,将采样值与参考值比较,二者的误差经过PI调节器的计算,获得下一个关断瞬态的vG,S7,最终达到准确控制关断瞬态iC下降速度的目的。在这样的控制下,各负载电流下vCE,PK都不超过预设上限Vref,并在较宽范围的IL下,vCE,PK可以达到Vref。这有助于缩短S7阶段时长,从而降低关断损耗。具体实施时,为防止刚开始端电压峰值超过Vref,可以在初始的S7阶段施加较高的vG,S7,然后通过SRVSD方法的自调节控制,将vCE,PK调整到尽可能接近Vref的水平。
为了实现关断瞬态端电压峰值的自调节控制,需要对端电压峰值进行直接和准确的采样。这里提出了一种对峰值电压进行采样和数字化的方法,其原理如图11所示。
图11分为两部分,前级用于端电压分压以及vCE,PK采样。前级输出的峰值量vsmp,PK与vCE,PK的关系为
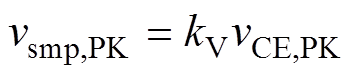 (23)
(23)式中,kV为端电压分压比,这里取为1/223。由式(23)可见,采样到vsmp,PK后,就可以推出vCE,PK。图11前级电路中VD2用于vCE从峰值跌落后,保持OP1运放工作在负反馈的单位增益状态,加速OP1响应;SW1用于断开前对电容C保存的峰值进行复位;在前级输出稳定后,后级断开SW2从而实现RPK、CPK串联电路零状态充电,当CPK达到vsmp,PK时比较器输出会有上升沿。FPGA读取CPK充电时长TPK,i,就可以根据参数VD、RPK、CPK推算出vsmp,PK。
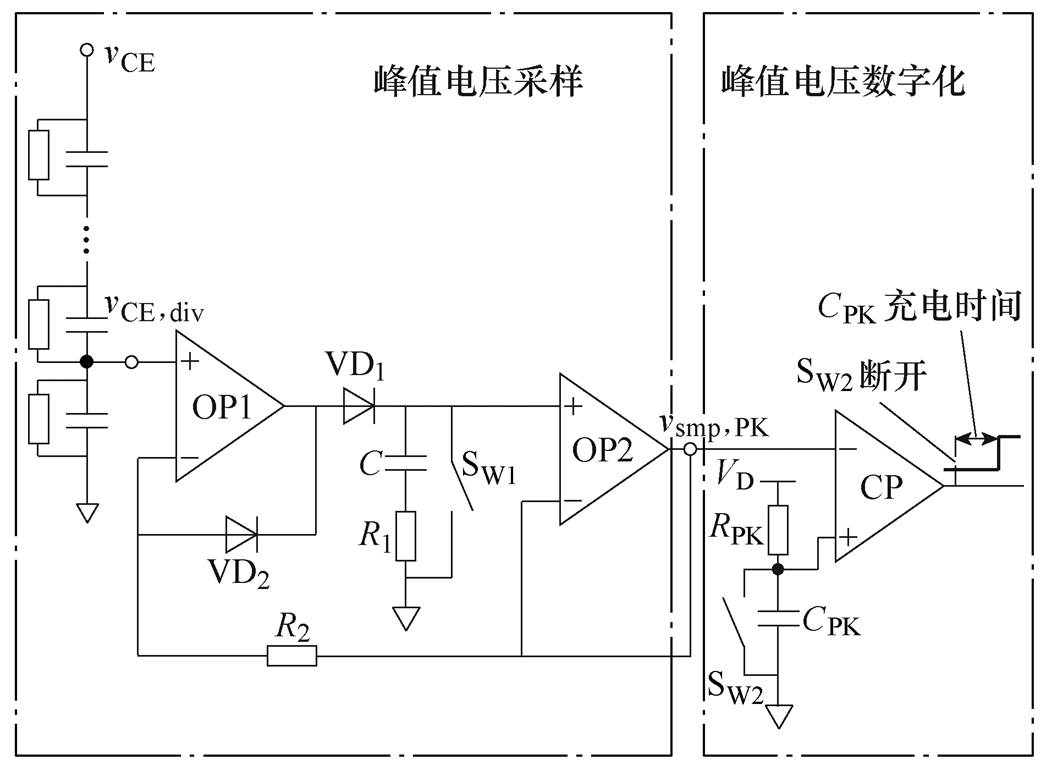
图11 端电压峰值采样电路原理
Fig.11 Circuit diagram of vCE peak values sampling
只需要FPGA的两个引脚(控制SW2,读比较器OP输出),后级电路即可完成对vCE,PK的数字化,比直接用ADC占用更少的资源。由于只需要在一个开关周期内完成对vsmp,PK的数字化,因此这里的开关SW2和比较器CP可以不用高速器件,而采用通用器件以降低驱动器成本。SW2和CP的总延迟Tdly可以在vsmp,PK=0V时离线测得,而在实际计算vsmp,PK时将该延迟减去即可,于是有
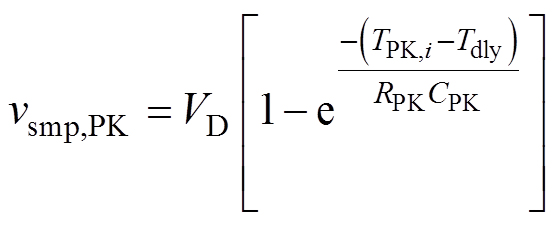 (24)
(24)图12所示为关断瞬态端电压峰值采样的控制时序。可以看到,图11中的CPK在VPWM上升沿之后进行复位,然后等到VPWM下降沿Td之后,输出vsmp,PK稳定后进行零状态充电。FPGA从CPK开始充电时启动计时,当CPK充电达到vsmp,PK时结束计时。在实际工作时,可以在FPGA中存一个查找表,在每个关断瞬态测得CPK充电时间TPK,i后,就可以用线性插值方便地求得vCE,PK的数值。
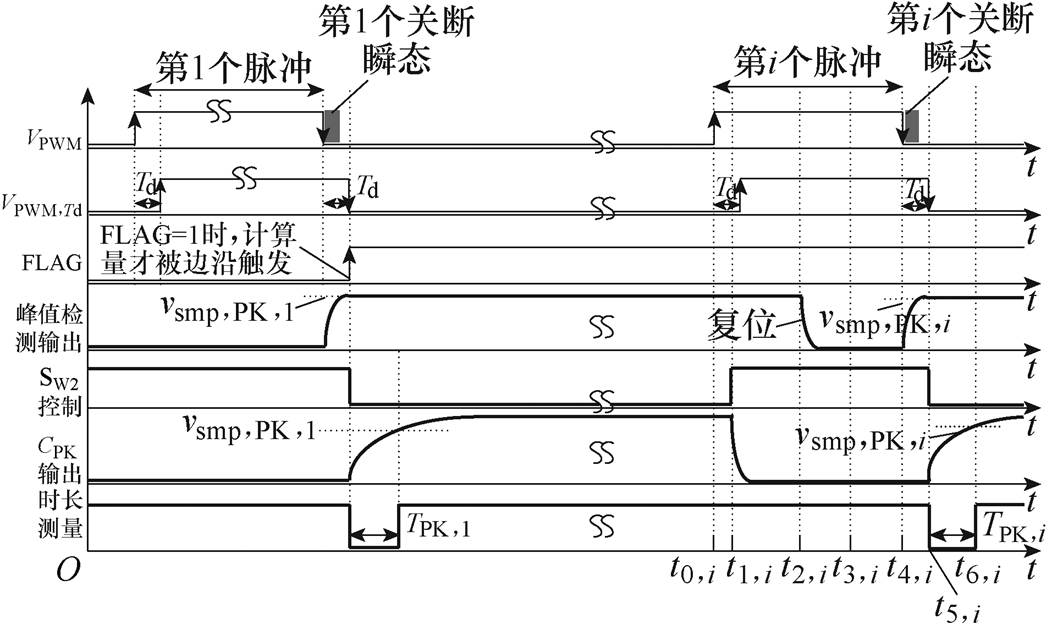
图12 端电压峰值采样电路控制时序
Fig.12 Sequential chart for sampling of vCE peak values
本节先通过实验验证图11所示电路对vCE,PK采样的准确性,然后给出在不同的换流回路杂散电感LS下,验证SRVSD方法对vCE,PK控制的实验效果。本节实验对象是FF300R12ME4模块。
4.3.1 对峰值电压检测准确性的实验验证
图13给出了SRVSD驱动板PCB照片,标识了驱动电压产生电路,iC、vCE反馈电路,vCE,PK检测电路和FPGA连接端。
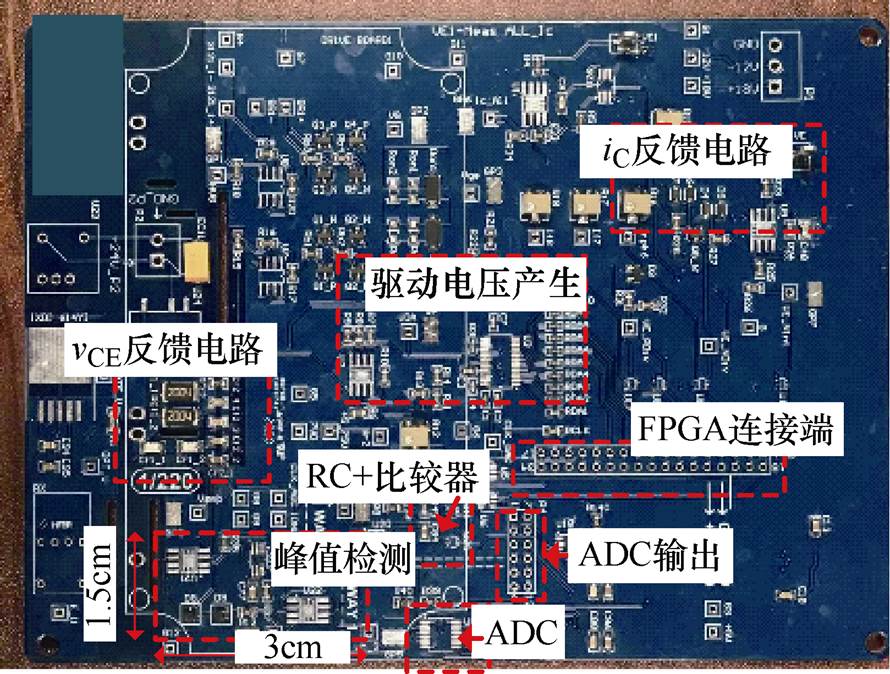
图13 SRVSD驱动板PCB照片
Fig.13 Photo of the SRVSD drive board
根据4.2节的分析,先测得了采样回路延迟(包括开关SW2延迟、比较器延迟)为120ns。
端电压峰值采样实验波形如图14所示,测试了vCE,PK的采样精度。可以看到,vsmp,PK=+2.89V与测得的vCE分压后的峰值为+2.872V基本相同,即图11中前级的峰值电压采样电路准确性很高。接着考察对该峰值进行数字化的准确性。注意到直接测得的CPK充电时长1 050ns,减去延迟的120ns,可知实际的CPK充电时长为930ns。将该充电时长与参数(VD, RPK, CPK)=(5V, 5kW, 220pF)代入式(24)获得SRVSD方法采样所得端电压峰值的分压结果,该值与图14中真实的+2.872V的误差为0.6%,该精度可以接受。
4.3.2 对端电压峰值自调节控制的实验验证
这里控制vCE,PK的目标值为Vref =900V,负载电流在200A左右,驱动电阻值为Rgoff =4W。这里在层叠母排上预留了接口,可以串入铜排(杂散电感约60nH)以改变换流回路杂散电感LS。这里在接入和不接入铜排的两种情况下,分别测试CGD和SRVSD驱动下关断瞬态vCE,PK的大小。注意在SRVSD方法对vCE,PK施加自调节控制时,满足了2.2节列出的关键设计点。
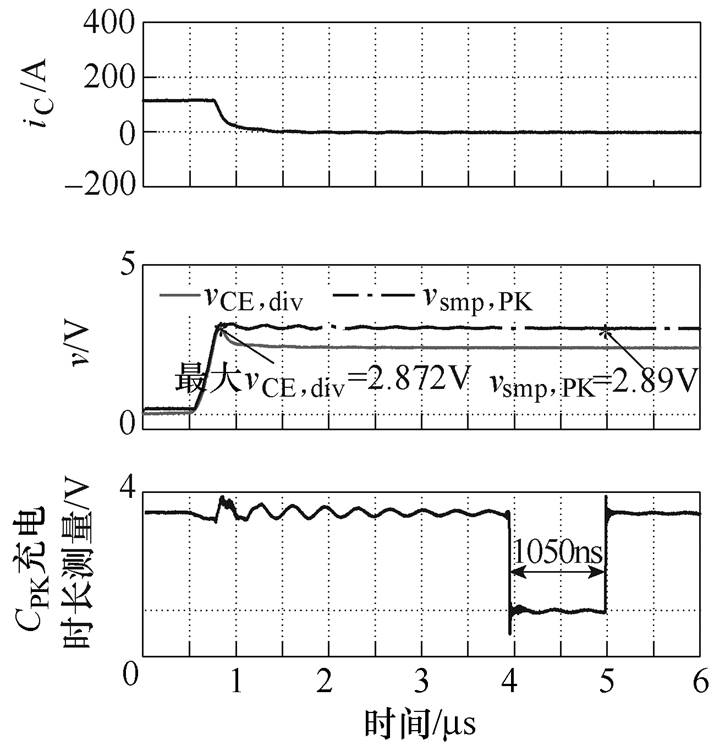
图14 端电压峰值采样实验波形
Fig.14 Experimental waveforms for the sampling of vCE peak values
图15是LS较小时,600V/200A下,CGD和SRVSD方法对vCE,PK自调节控制的关断瞬态实验波形对比。根据图15a,CGD方法下,从第1个到第10个关断瞬态,端电压峰值vCE,PK随着负载电流的增大而增大。由于LS较小,在负载电流最大的第10个关断瞬态施加vG,S7=VEE也只产生峰值vCE,PK= 885V<900V。
在图15b中,如4.1节最后一段所述,SRVSD方法在对vCE,PK施加自调节控制时,可以在初始的S7阶段施加较高的驱动电压,确保初始的关断电压峰值低于Vref,这里取初始vG,S7=-1V。第1个关断瞬态vCE,PK=730V,远低于Vref。如图15b所示,在自调节控制下,为了加快管电流下降速度使vCE,PK尽量接近Vref,第2个关断瞬态vG,S7几乎降低到VEE的水平,而此时端电压峰值仍然比Vref小。此后由于LS很小,vCE,PK始终低于Vref,则vG,S7一直保持VEE不变。
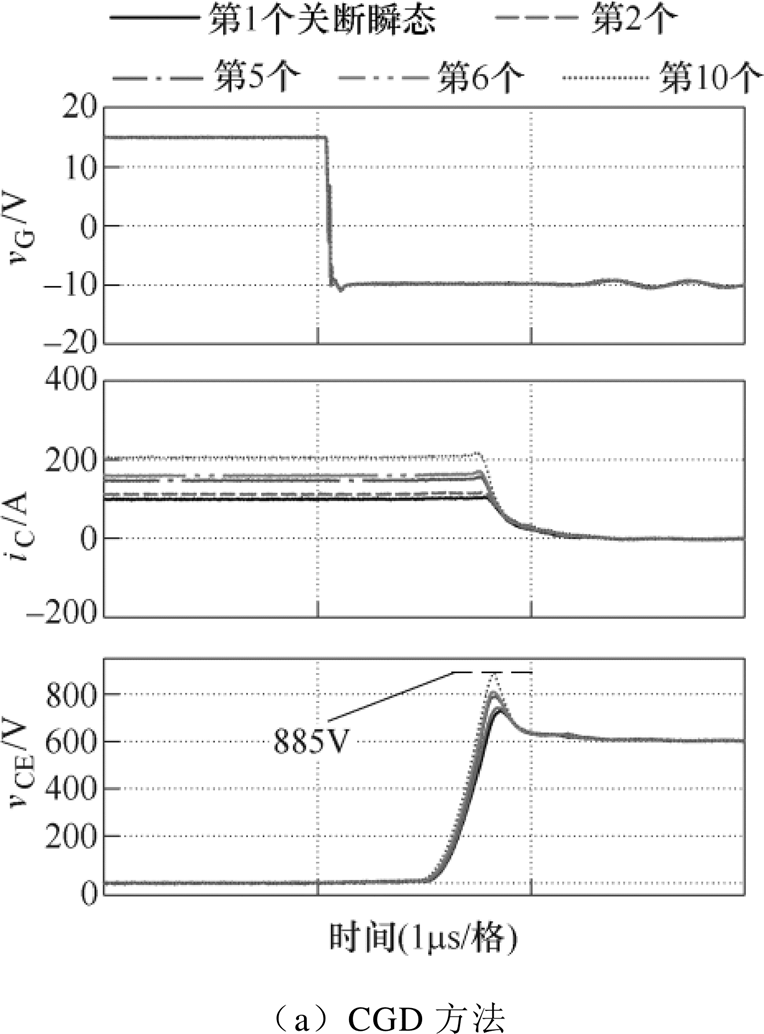
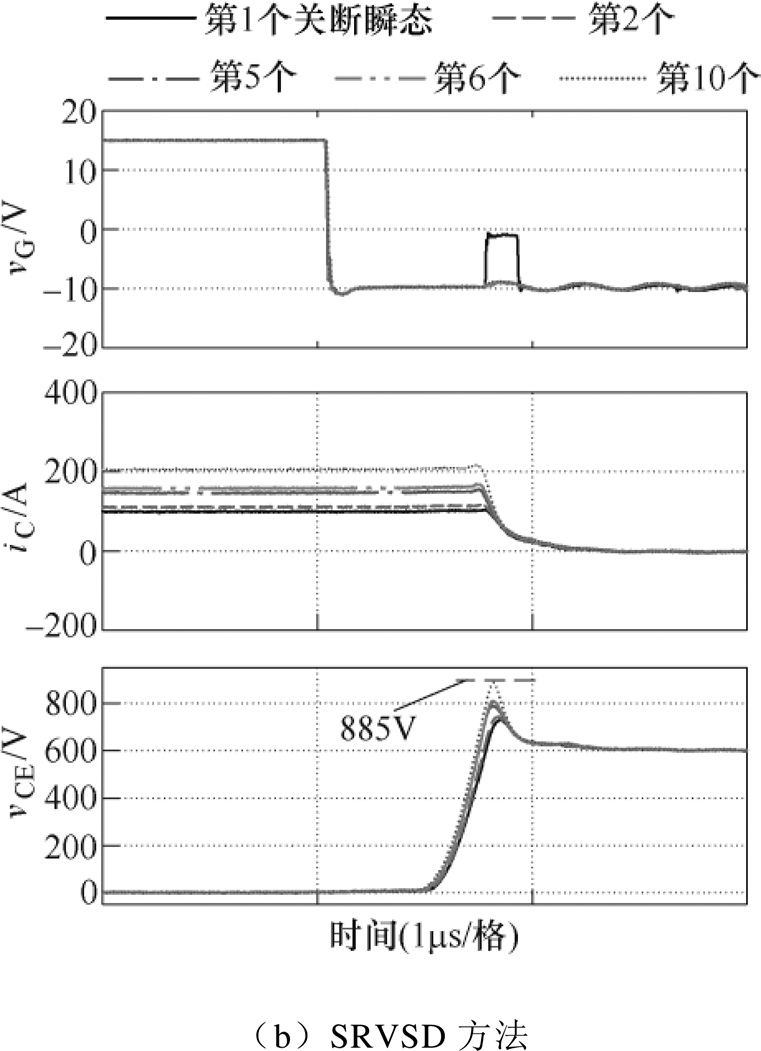
图15 LS较小时,600V/200A下CGD和SRVSD方法端电压峰值自调节控制各关断瞬态的实验波形对比
Fig.15 Experimental turn-off waveforms comparison between CGD and the SRVSD with self-regulating control for vCE peak values under 600V/200A and smaller LS
接入铜排后,在较大LS下,关断瞬态实验波形如图16所示。从图16a可见,在使用CGD方法时,由于LS较大且没有对vCE,PK的控制,当负载电流增大到第10个关断脉冲时,vCE,PK达到了940V,已经超过预设的Vref=900V限制。
在图16b中,SRVSD方法在初始的S7阶段,仍然施加较高的-1V驱动电压。当检测到vCE,PK远小于Vref时,在SRVSD的自调节控制下,降低了第2个vG,S7以加速iC下降,vG,S7降低的趋势一直持续到第6个关断瞬态。此后由于负载电流增大,为了使得vCE,PK不大于且尽可能靠近Vref,SRVSD将调节vG,S7不断增大。注意到,在第10个关断瞬态时,vG,S7已经达到+3V,这样将CGD下940V的端电压峰值控制到了目标值Vref附近。
图15b和图16b中,vG,S5=vG,S6保持在最低的VEE以获得最小的关断延迟和损耗。
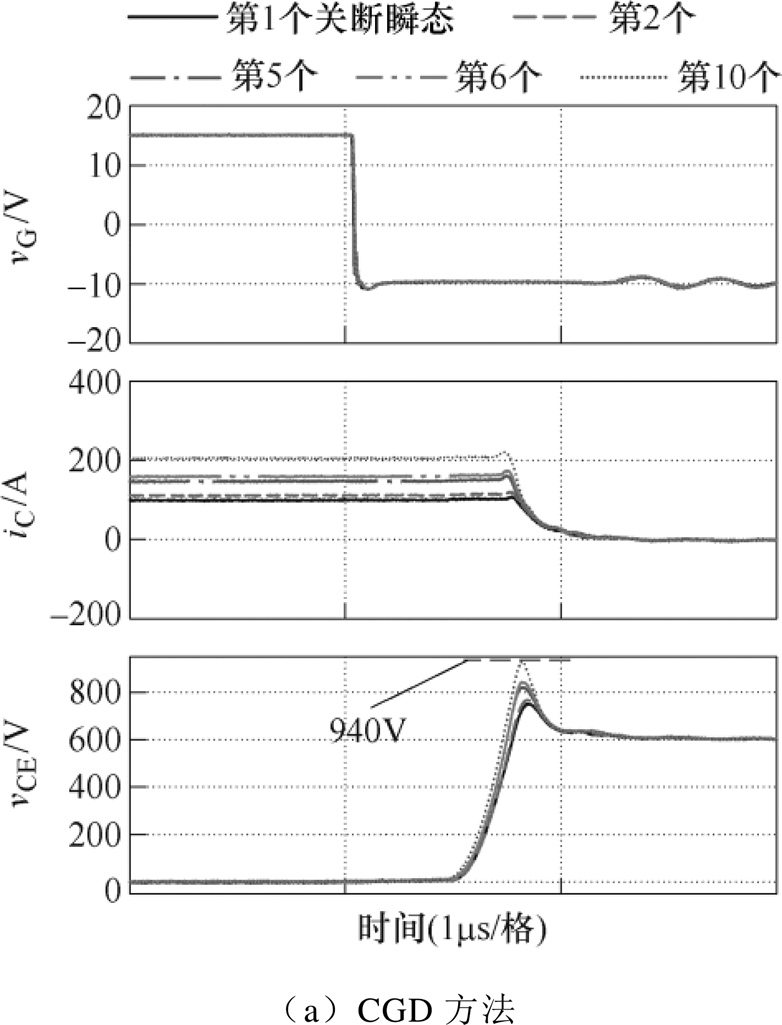
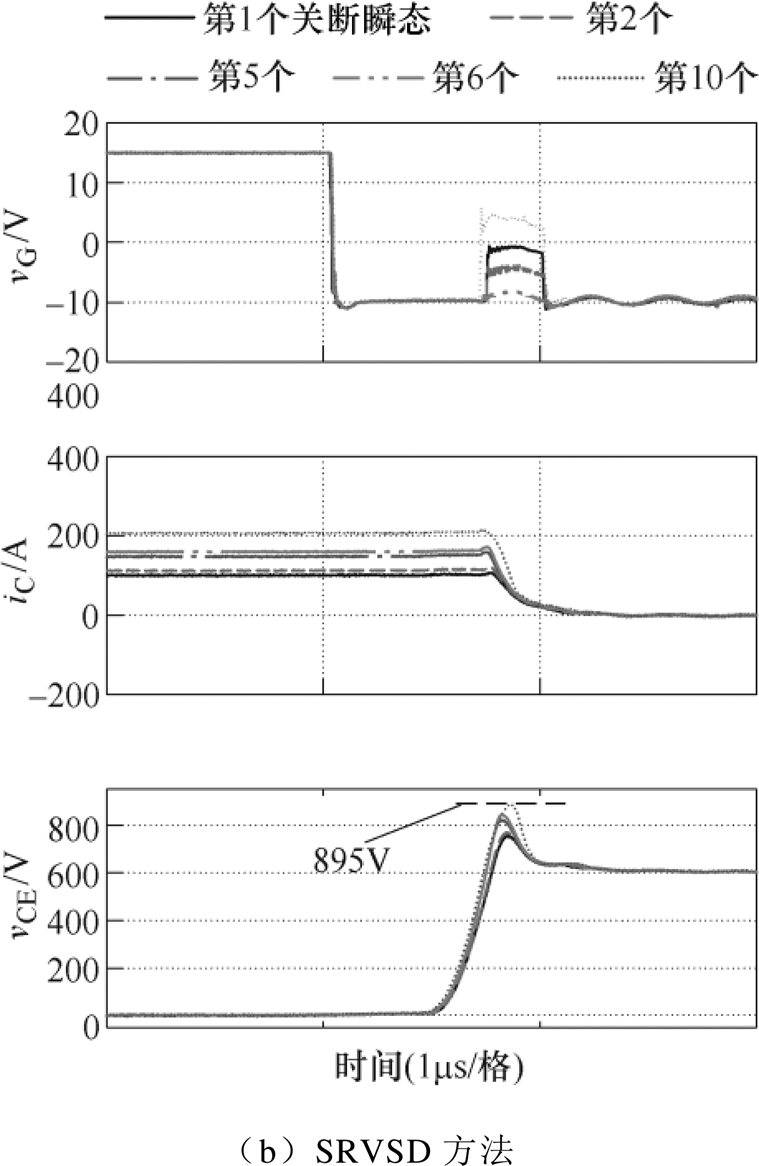
图16 LS较大时,600V/200A下CGD和 SRVSD方法端电压峰值自调节控制各关断瞬态的实验波形对比
Fig.16 Experimental turn-off waveforms comparison between CGD and the SRVSD with self-regulating control for vCE peak values under 600V/200A and larger LS
4.3.3 小结
第4节介绍了SRVSD实现端电压峰值自调节控制的方法,包括峰值采样方法、控制策略。最后在不同换流条件下(不同LS值)通过实验验证了峰值控制的准确性与有效性,其中当峰值vCE,PK小于目标值Vref时,为了降低损耗,SRVSD会降低vG,S7以加快关断瞬态iC下降速度;当IL增大时,SRVSD又会及时地增大vG,S7以减缓iC下降速度,保证vCE.PK基本等于Vref。
相对于CGD方法,在峰值电压自调节控制下,SRVSD方法可以采用更低的驱动电阻值Rgoff,使得vCE,PK始终不超过Vref,且在更宽的负载电流范围内达到Vref,这样可以显著降低S7阶段的损耗。同时,更小的Rgoff可以帮助SRVSD方法获得更小的关断延迟和更快的vCE上升速度,后者也带来了更低的关断损耗。
本文主要完成了关于数字主动驱动SRVSD方法自调节控制能力的后续深入研究,突出了SRVSD方法在实现自调节控制时的一些关键设计点:开关瞬态各阶段驱动电压限幅,自调节控制稳定性及PI参数整定方法,自调节控制精度。本文对这些关键点逐一做了理论分析、计算和实验验证,这些研究不仅为SRVSD方法的实际工程应用提供良好的理论基础,提出的PI整定方法和控制精度分析方法,同样也可以指导其他数字型闭环驱动方法的控制参数整定和控制精度分析。在此分析基础上,SRVSD方法适用于各种容量的IGBT器件。
本文第4节提出了一种对关断瞬态端电压峰值精确采样的方法。在不同换流回路杂散电感LS下,用实验验证了vCE,PK采样和自调节控制的效果。控制实验的同时与CGD方法作了比较,证明了SRVSD方法准确控制vCE,PK的能力。如4.3.3节总结的,通过对vCE,PK的自调节控制,SRVSD方法可以在更低的驱动电阻值Rgoff下获得与CGD方法相同的关断瞬态端电压峰值vCE,PK的同时,实现更低的关断延迟和损耗。同时,对vCE,PK施加自调节控制,可以省去CGD方法下调试驱动电阻的步骤。
SRVSD方法的自调节控制能力,增强了驱动方法的适应性,可以在不同的换流条件下,最大限度实现开关特性的优化。
参考文献
[1] Baliga B J. Fundamental of power semiconductor devices[M]. 北京: 科学出版社, 2012.
[2] Lobsiger Yanick. Closed-loop IGBT gate drive and current balancing concepts[D]. Swiss Confederation: ETH Zurich, 2014.
[3] 杨媛, 文阳, 李国玉. 大功率IGBT模块及驱动电路综述[J]. 高电压技术, 2018, 44(10): 3207-3220.
Yang Yuan, Wen Yang, Li Guoyu. Review on high- power IGBT module and drive circuit[J]. High Voltage Engineering, 2018, 44(10): 3207-3220.
[4] 罗旭, 王学梅, 吴海平. 基于多目标优化的电动汽车变流器IGBT及开关频率的选择[J]. 电工技术学报, 2020, 35(10): 2181-2193.
Luo Xu, Wang Xuemei, Wu Haiping. Selections of IGBTs and switching frequency of the electric vehicle converter based on multi-objective optimization[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2181-2193.
[5] 朱义诚, 赵争鸣, 施博辰, 等. 绝缘栅型功率开关器件栅极主动控制技术综述[J]. 高电压技术, 2019, 45(7): 2080-2092.
Zhu Yicheng, Zhao Zhengming, Shi Bochen, et al. Review of active gate control methods for insulated- gate power switching devices[J]. High Voltage Engin- eering, 2019, 45(7): 2080-2092.
[6] Ling Yatao, Zhao Zhengming, Zhu Yicheng. A self- regulating gate driver for high-power IGBTs[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3450-3461.
[7] 李辉, 胡玉, 王坤, 等. 考虑杂散电感影响的风电变流器IGBT功率模块动态结温计算及热分布[J]. 电工技术学报, 2019, 34(20): 4242-4250.
Li Hui, Hu Yu, Wang Kun, et al. Thermal distribution and dynamic junction temperature calculation of IGBT power modules for wind turbine converters considering the influence of stray inductances[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4242-4250.
[8] 孙林, 孙鹏菊, 罗全明, 等. 基于状态反馈线性化的IGBT外部热管理[J]. 电工技术学报, 2020, 35(24): 1-10.
Sun Lin, Sun Pengju, Luo Quanming, et al. External thermal management of IGBT based on state feedback linearization[J]. Transactions of China Electrotech- nical Society, 2020, 35(24): 1-10.
[9] 焦明亮, 李云, 朱世武, 等. IGBT门极驱动技术现状和发展趋势[J]. 大功率变流技术, 2015(2): 18-23.
Jiao Mingliang, Li Yun, Zhu Shiwu, et al. Status and trend of IGBT gate drive technology[J]. High Power Converter Technology, 2015(2): 18-23.
[10] Lee H, Lee Y, Suh B. An improved gate control scheme for snubberless operation of high power IGBTs[C]//IEEE Industry Applications Conference, Thirty-Second IAS Annual Meeting, New Orleans, LA, USA, 1997: 975-982.
[11] Grbovic Petar. An IGBT gate driver for feed-forward control of turn-on losses and reverse recovery current[J]. IEEE Transactions on Power Electronics, 2008, 23(2): 643-652.
[12] Miyazaka K, Abe S. General-purpose clocked gate driver IC with programmable 63-level drivability to optimize overshoot and energy loss in switching by a simulated annealing algorithm[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 2350-2357.
[13] Berry J P. MOSFET operating under hard switching mode: voltage and current gradients control[C]// Proceedings of Symposium on Materials and Devices Power Electron, Firenze, Italy, 1991: 130-134.
[14] Dulau L, Pontarollo S. A new gate driver integrated circuit for IGBT devices with advanced protections[J]. IEEE Transactions on Power Electronics, 2006, 21(1): 38-44.
[15] 胡亮灯, 肖明恺, 楼徐杰. 中高压大功率IGBT数字有源门极开环分级驱动技术[J]. 电工技术学报, 2018, 33(10): 2365-2375.
Hu Liangdeng, Xiao Mingkai, Lou Xujie. Open-loop hierarchy control technology of high-power IGBT digital active gate drive[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2365-2375.
[16] Shu Lu, Zhang Junming. Active current source IGBT gate drive with closed-loop di/dt and dv/dt control[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3787-3796.
[17] Velander E, Kruse L. An IGBT turn-on concept offering low losses under motor drive dv/dt con- straints based on diode current adaption[J]. IEEE Transactions on Power Electronics, 2021, 33(2): 1143-1153.
[18] 宁红英, 孙旭霞, 杨媛. 一种基于diC/dt反馈控制的大功率IGBT驱动保护方法[J]. 电工技术学报, 2015, 30(5): 33-41.
Ning Hongying, Sun Xuxia, Yang Yuan. A high- power IGBT drive protection method based on diC/dt feedback control[J]. Transactions of China Electro- technical Society, 2015, 30(5): 33-41.
[19] Dang Lan, Kuhn Harald. Digital adaptive driving strategies for high-voltage IGBTs[J]. IEEE Transa- ctions on Industry Applications, 2013, 49(4): 1628- 1636.
[20] Zhang Fan, Yang Xu, Yu Ren, et al. Advanced active gate drive for switching performance improvement and overvoltage protection of high-power IGBTs[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 3802-3815.
[21] Idir Nadir, Bausiere Robert, Franchaud J Jean. Active gate voltage control of turn-on di/dt and turn-off dv/dt in insulated gate transistors[J]. IEEE Transactions on Power Electronics, 2006, 21(4): 849-855.
[22] Kim Jin-Hong, Park Dong-Hyun, Kim Jeong-Bin, et al. An active gate drive circuit for high power inverter system to reduce turn-off spike voltage of IGBT[C]// IEEE International Conference on Power Electronics, Daegu, South Korea, 2007: 127-131.
Self-Regulating Control of IGBT Switching Characteristics with Active Gate Drive
Abstract The widely used conventional gate drive (CGD) has limited effects as to the control and optimization of switching characteristics of insulated gate bipolar transistors (IGBTs). Besides, when the switching conditions change, CGD cannot keep the device characteristics in an optimal state, i.e., it lacks self-regulating ability. Numerous active gate drive (AGD) methods have been developed to realize the self-regulating control. However, problems such as control stability and control accuracy will occur when applying this control. In this paper, to solve these problems, three key design points regarding the self-regulating control are proposed and verified by experiments, which provides a reference for AGD methods to achieve self-regulating control. This paper summarizes the control of IGBT turn-off peak voltage and proposes a novel circuit for precise sensing of IGBT collector-emitter peak voltage. It is shown that by combining the peak sensing circuit and self-regulating control, the peak voltage can be regulated with high accuracy, laying a solid foundation for safe and low-loss turn off for power semiconductors.
keywords:IGBT, switching characteristics, self-regulating control, active gate drive, turn-on delay, turn-off voltage peak
中图分类号:TM315
DOI: 10.19595/j.cnki.1000-6753.tces.210102
国家自然科学基金委员会—中国国家铁路集团有限公司高速铁路基础研究联合基金资助项目(U2034201)。
收稿日期 2021-01-19
改稿日期 2021-03-04
凌亚涛 男,1992年生,博士研究生,研究方向为IGBT和SiC MOSFET主动栅极驱动、PWM变换器控制和电力电子仿真算法。E-mail: 1546517440@qq.com
赵争鸣 男,1959年生,教授,博士生导师,主要研究方向为大容量电力电子变换系统、光伏发电、电机控制和无线电能传输等。E-mail: zhaozm@tsinghua.edu.cn(通信作者)
(编辑 陈 诚)