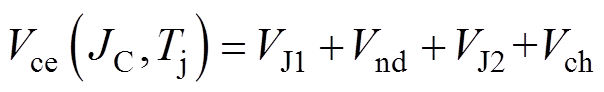（1）式中，VJ1为J1结压降；Vnd为n--漂移区压降；VJ2为J2结压降；Vch为沟道压降；Tj为器件温度；JC为流过IGBT的集电极电流密度。
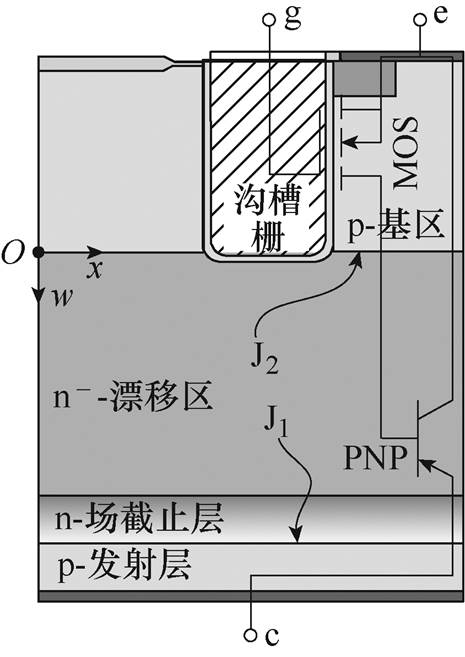
图1 IGBT结构示意图与等效电路
Fig.1 Schematic diagram and equivalent circuit of IGBT
摘要 绝缘栅双极型晶体管（IGBT）功率模块在新能源汽车动力总成系统中应用广泛。高功率密度和极限工况运行的应用需求对IGBT模块的热可靠性设计提出严峻挑战。受芯片导通压降温变效应的影响，芯片表面电流密度呈现不均匀分布，导致传统的热建模方法无法准确地描述功率模块温度场分布，这给芯片过电流工况下的强健性评估带来困难。该文将功率模块连续域三维温度场模型与芯片有源区离散化一维电学模型进行联合，提出一种热-电场路耦合的功率模块三维温度场解析建模方法，实现片上温度场的准确描述，误差小于4.0%。进一步地，研究芯片的电流分布规律，发现正温度特性下电流集中在IGBT有源区边缘，这种非均匀分布特征对片上温度峰值有抑制作用，能有效提升功率模块的过电流能力。最后以型号SEMiX603GB12E4p模块为例，针对提出的解析建模方法进行了验证，仿真与实验结果均表明，该模型能够准确表征不同电流水平下IGBT模块的热特性，验证了该模型算法的准确性和有效性。
关键词：功率模块 温变效应 场路耦合 三维温度场 过电流能力
功率模块在新能源汽车动力总成系统中应用广泛[1-4]。高功率密度和高集成化趋势加剧了芯片表面温度梯度[5]，而元胞电学参数具有温变效应[6]，导致芯片形成电流密度不均匀分布特征。因汽车低速大转矩、重载定子堵转、起步加速等极端工况下半导体芯片过电流运行[7]，元胞电流分配不均更加严重，为功率模块安全运行带来隐患。因此，对功率模块片上电致温度场的建模与分析尤为迫切。
针对功率模块芯片温度的建模，热网络模型法通过将热传递近似为一维过程，建立Foster或Cauer型RC热网络[8-11]，具有计算速度快的显著特点。然而，热网络模型通常只能描述一个位置节点信息。文献[11]将芯片分为九块区域分别建立四层Foster型热网络，增加了片上温度监测点数量，可实现对芯片表面温度梯度的粗略评估。
为了实现芯片表面温度梯度的准确建模，国内外学者利用数值模型法对不同工况下芯片的热-电场路耦合问题做了大量工作[12-15]。文献[12]用单元胞模型表征整个芯片的电学特性，用有限元软件COMSOL和PSpice研究了绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）模块短路工况下芯片与键合线的温度梯度。文献[13]用有限元软件Ansys内置thermal-electric模块研究了MOSFET体二极管导通下的功率循环寿命。文献[14]用Ansys和PSpice联合仿真研究了IGBT芯片多元胞阈值电压不一致对短路能力的影响。文献[15]用有限元和PSpice联合仿真验证了电击穿下芯片多元胞的热-电耦合模型。然而有限元法需要求解微元的偏微分方程，计算量大；同时在解决功率具有温度依赖性的非线性问题时存在收敛性问题[16]，限制了其在热-电耦合问题研究中的应用。
为了提高计算效率和避免迭代算法不收敛，傅里叶解析法被引入用于实现芯片电致温度场的快速精准描述[17-20]。傅里叶解析法通过求解偏微分方程，将待求函数展开为傅里叶级数，由边界条件确定系数，可实现功率模块连续性三维温度场的提取。该方法只通过数学解析运算，具有运行时间短、无收敛问题、分析效率高等优点。文献[17]将傅里叶解析法发展为适用功率模块多层多芯片封装结构，提高了傅里叶解析模型的通用性，并用红外热成像仪验证了模型的准确性。文献[18]建立了晶闸管结构的傅里叶解析模型，得到各层材料热阻抗的时域传热学表达式，进而分析了晶闸管瞬态温度响应。文献[19]建立了压接式功率模块的傅里叶解析模型，验证了多个子模块耦合下热模型的准确性。文献[20]将傅里叶法拓展至瞬态傅里叶解析模型，并用有限元验证了模型的准确性。然而，上述傅里叶解析方法均未考虑芯片的温变特征，导致无法应用于功率模块热-电耦合问题的研究。
本文以型号SEMiX603GB12E4p模块为典型案例，将基于傅里叶解析法的功率模块三维温度场模型与芯片有源区电学物理模型联合，提出一种热-电场路耦合的模块温度场解析建模方法，可实现片上温度场的准确描述，有助于揭示芯片多元胞电流分布特点对片上温度峰值和模块输出功率的作用规律。
IGBT芯片的截面[21]如图1所示，图中，n--漂移区与p-发射区和p-基区之间的PN结分别记为J1和J2。IGBT的通态饱和压降由四部分组成，可表示为
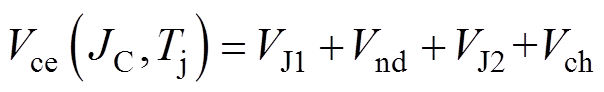（1）式中，VJ1为J1结压降；Vnd为n--漂移区压降；VJ2为J2结压降；Vch为沟道压降；Tj为器件温度；JC为流过IGBT的集电极电流密度。
图1 IGBT结构示意图与等效电路
Fig.1 Schematic diagram and equivalent circuit of IGBT
IGBT器件n--漂移区在大电流工况下空穴和电子浓度分布近似相等，在此基础上，VJ1、VJ2、Vch和Vnd分别表示[21]为
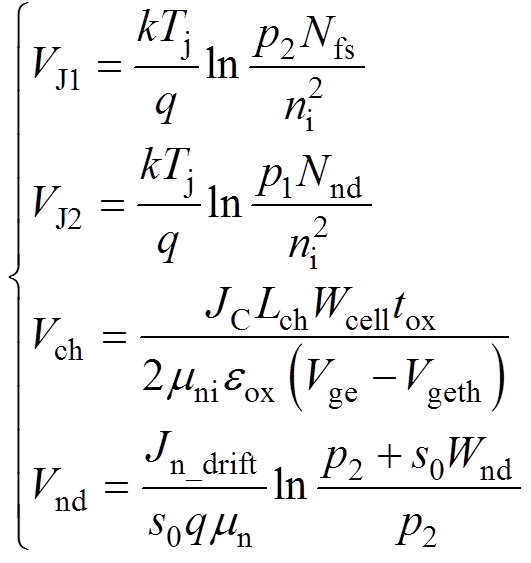（2）其中
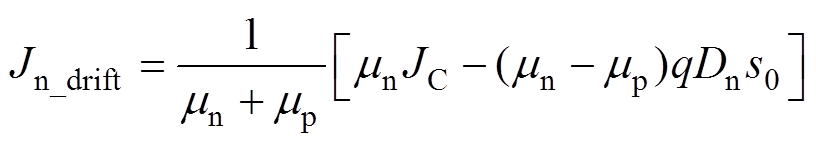
式中，p1为w=0附近的载流子浓度；p2为w=Wnd处的载流子浓度；k为玻耳兹曼常数；q为电荷系数；Nfs和Nnd分别为n-场截止层和n--漂移区的掺杂浓度；ni为本征载流子浓度；Lch为沟道长度；Wcell为元胞节距；tox为氧化物厚度；mni为沟道中的电子迁移率；eox为栅极氧化层的介电常数；Vge为IGBT栅极电压；Vgeth为栅极阈值电压；Jn_drift为n--漂移区中的电子漂移电流密度；s0为n--漂移区载流子浓度分布的近似斜率绝对值，s0≈(p1-p2)/Wnd；mn和mp分别为电子和空穴的迁移率；Dn为电子的扩散系数。
由式（2）可知，芯片导通压降由结温与流经电流直接影响，同时也受器件的温度敏感参数间接影响，主要包括沟道电子迁移率mni、漂移区载流子迁移率mn(mp)、栅极阈值电压Vgeth。以赛米控IGBT模块SEMiX603GB12E4p芯片为例，以上关系可表示为
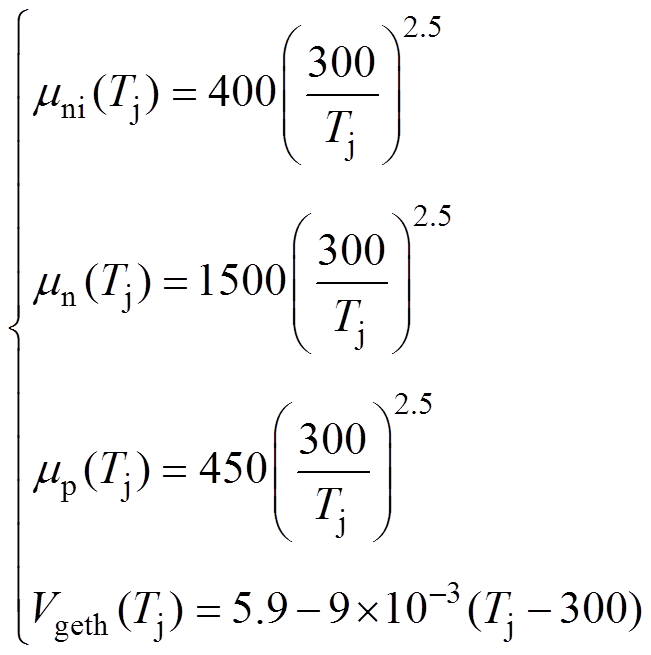（3）SEMiX603GB12E4p所用芯片掺杂特性及几何尺寸见表1。图2为模块SEMiX603GB12E4p所采用芯片在Vge=15V下的导通压降模型与实验结果的对比，所建物理模型与实验结果一致，可作为研究芯片导通压降温变特性的基础。芯片正向导通压降受温度的影响与注入电流等级有关，当芯片电流大于59.1A时，正向导通压降随温度升高而增大，为正温度特性区，当芯片电流小于59.1A则相反，为负温度特性区。
表1 SEMiX603GB12E4p芯片掺杂特性及几何尺寸
Tab.1 Doping characteristics and geometric dimensions of SEMiX603GB12E4p
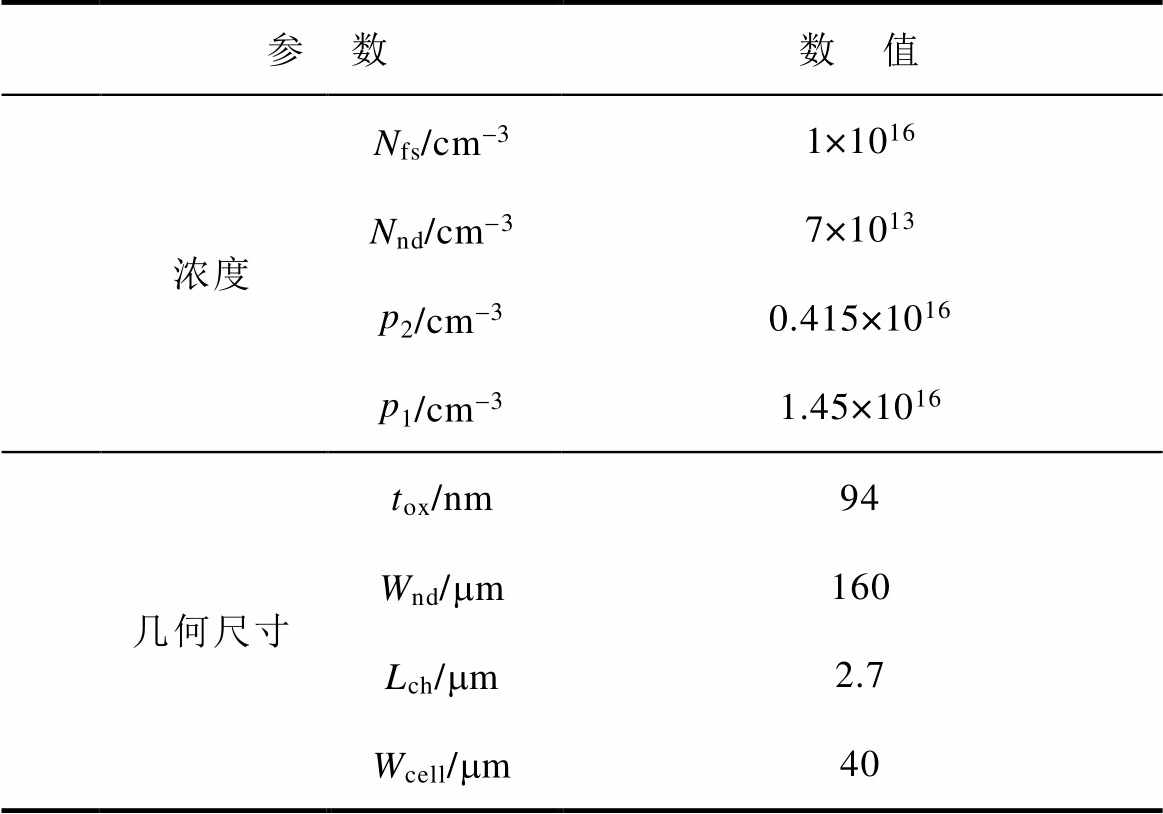
参 数数 值 浓度Nfs/cm-31×1016 Nnd/cm-37×1013 p2/cm-30.415×1016 p1/cm-31.45×1016 几何尺寸tox/nm94 Wnd/mm160 Lch/mm2.7 Wcell/mm40
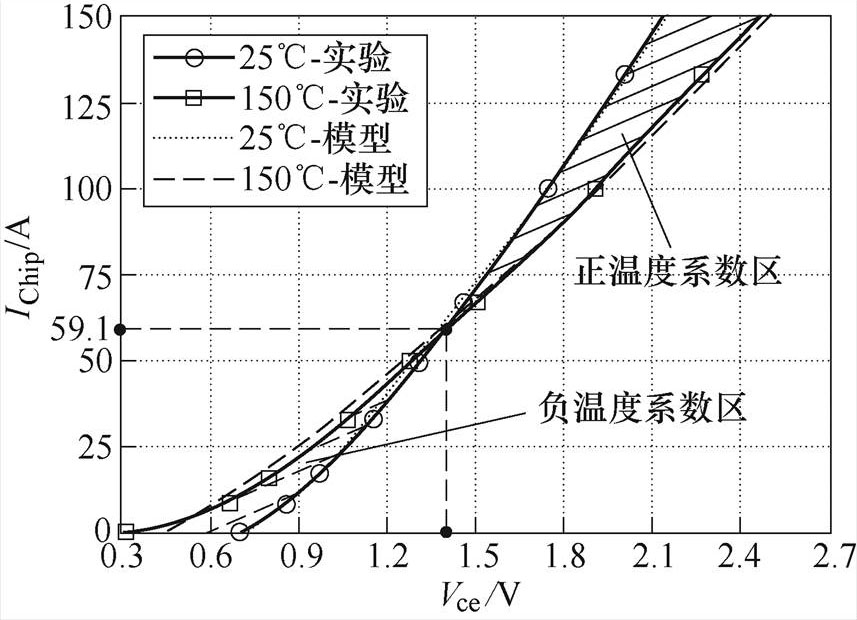
图2 SEMiX603GB12E4p芯片导通模型与实验对比
Fig.2 Comparison between model and experimental values of semiconductor conduction drop
典型多层封装材料的IGBT功率器件几何结构与边界条件示意图如图3所示。自上至下结构依次为芯片、芯片焊料、直接覆铜陶瓷衬底（Direct Bond Copper, DBC）、DBC焊料、基板，热导率及厚度依次为kc(tc)、kcs(tcs)、k1(t1)、k2(t2)、k3(t3)、k4(t4)及k5(t5)。以DBC左下角为坐标系原点，DBC长度方向为x轴正方向，宽度方向为y轴正方向，厚度方向为z轴正方向，DBC长、宽分别为LDBC、WDBC，芯片长、宽分别为LChip、WChip，芯片中心Oc位于坐标(Xc, Yc)。Tj(x, y)为芯片表面温度分布函数，TCu(x, y)为DBC上铜层表面温度分布函数。F 为芯片的热损耗体密度（W/mm3），Tf为冷却液温度，h为对流换热系数（W/(mm2·℃)），功率器件的四个侧壁及上表面均为绝热条件。
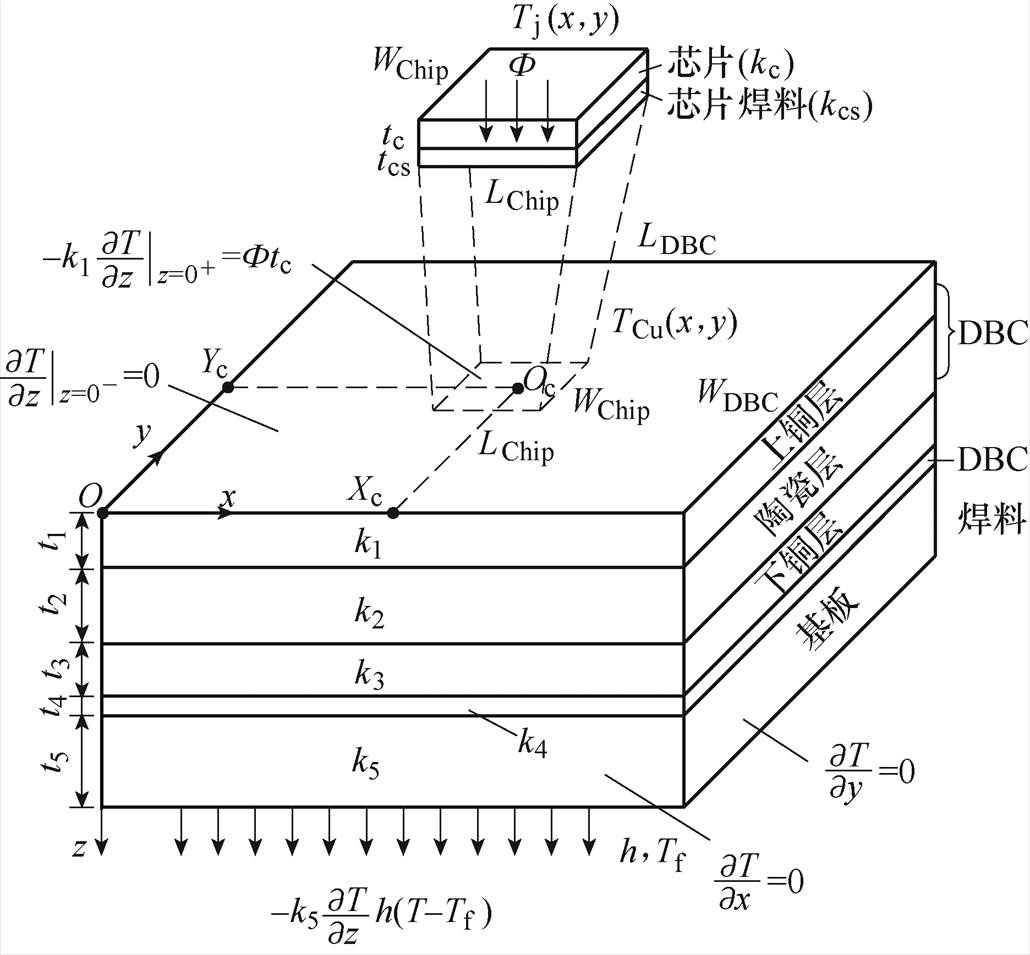
图3 多层结构IGBT功率器件几何结构与边界条件
Fig.3 Boundary condition and geometry structure of multi-layer IGBT power module
根据传热学理论，对于各向同性、有内热源且与周围介质有热交换物体，稳态下满足拉普拉斯导热微分方程，即
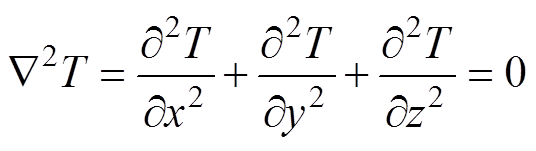（4）散热器表面与流体发生对流换热时，根据能量守恒原理，单位时间内流体介质与散热器的换热量等于散热器内部向其表面传导的热量。上述边界条件可列写数学表达式为
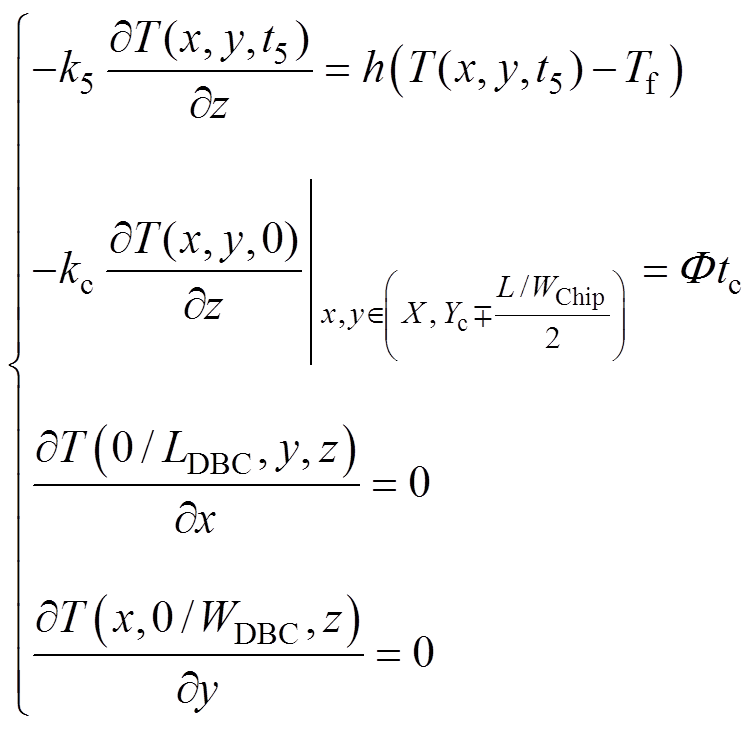（5）
采用变量分离法，求解式（4）中二阶偏微分方程特征值，结合式（5）边界条件求解待定系数。
DBC上铜层表面温度在某一芯片位置坐标（Xc, Yc）下的分布函数为
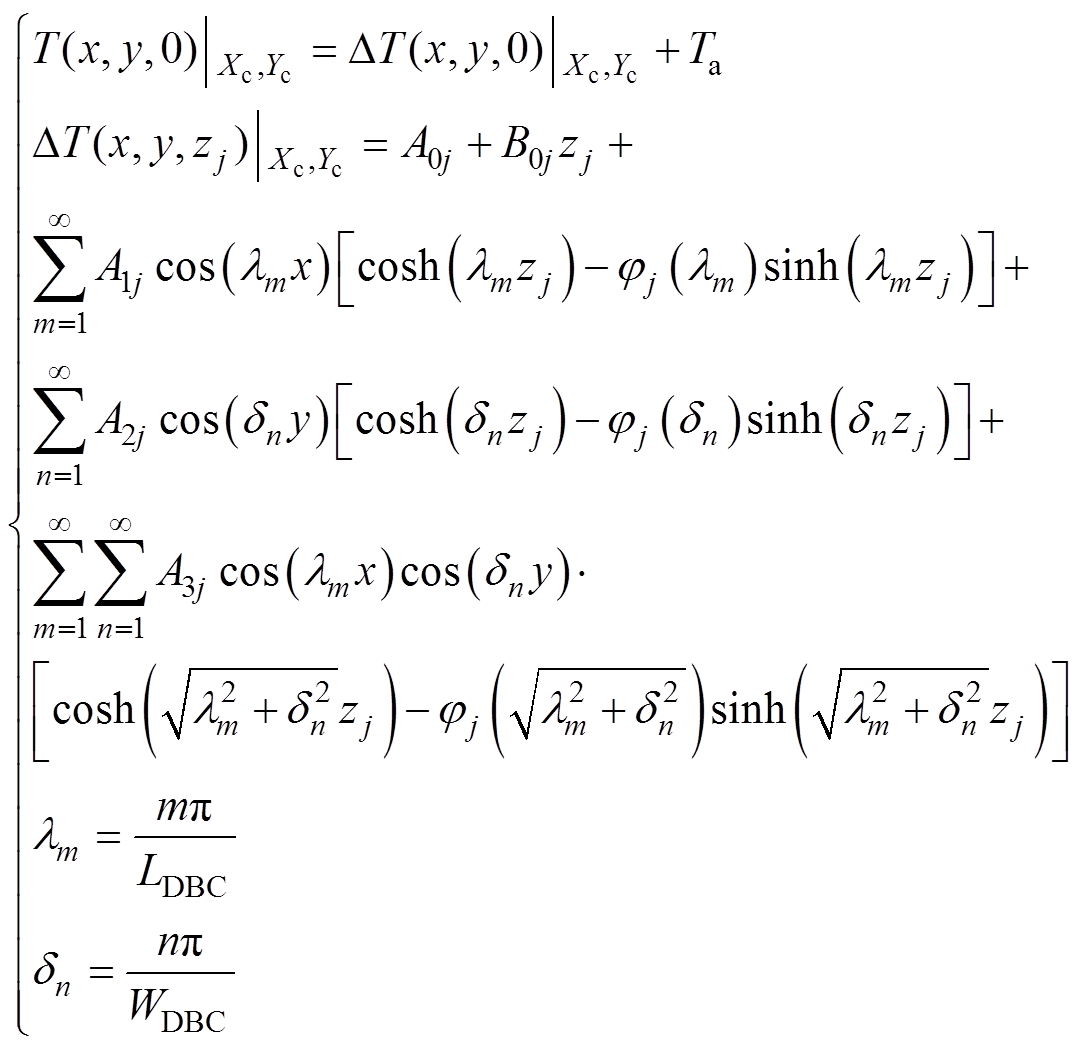（6）式中，j=1,…,5。
具体求解过程及相关系数求解公式参见附录。芯片传热采用具有内热源的一维导热模型，芯片焊料采用无内热源的一维导热模型[22]为
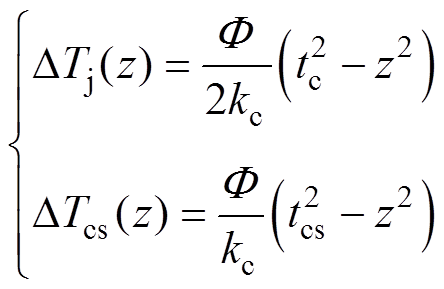（7）式中，F 为热损耗体密度，F =(IcVce)/(LcWctc)，Vce为导通压降；Ic为流经芯片电流，Lc、Wc分别为芯片长度、宽度。
联立式（6）和式（7），可得芯片表面温度分布函数Tj(x, y)为
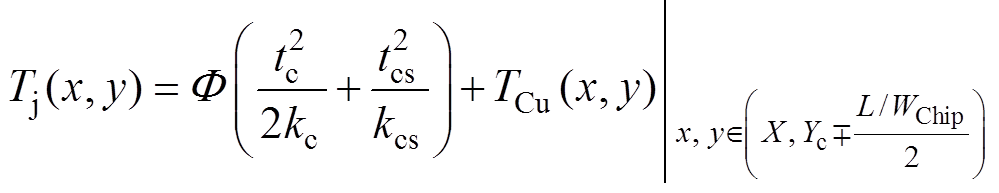（8）三维温度场及场路耦合计算流程如图4所示，输入功率模块的材料参数、边界条件、尺寸参数与IGBT芯片位置，根据输入参数和式（A9）递归计算函数j1，再结合式（A10）计算傅里叶级数系数。根据坐标变量z判断当前计算的封装层数j，从而选择式（6）中对应的zj计算得到芯片以下结构的三维热阻函数
。进一步判断（x, y），当（x, y）位于IGBT芯片范围内时，结合式（7）得到芯片及芯片焊料的三维热阻函数。根据热损耗功率P和环境温度Ta，最终得到封装内所有位置温度信息。
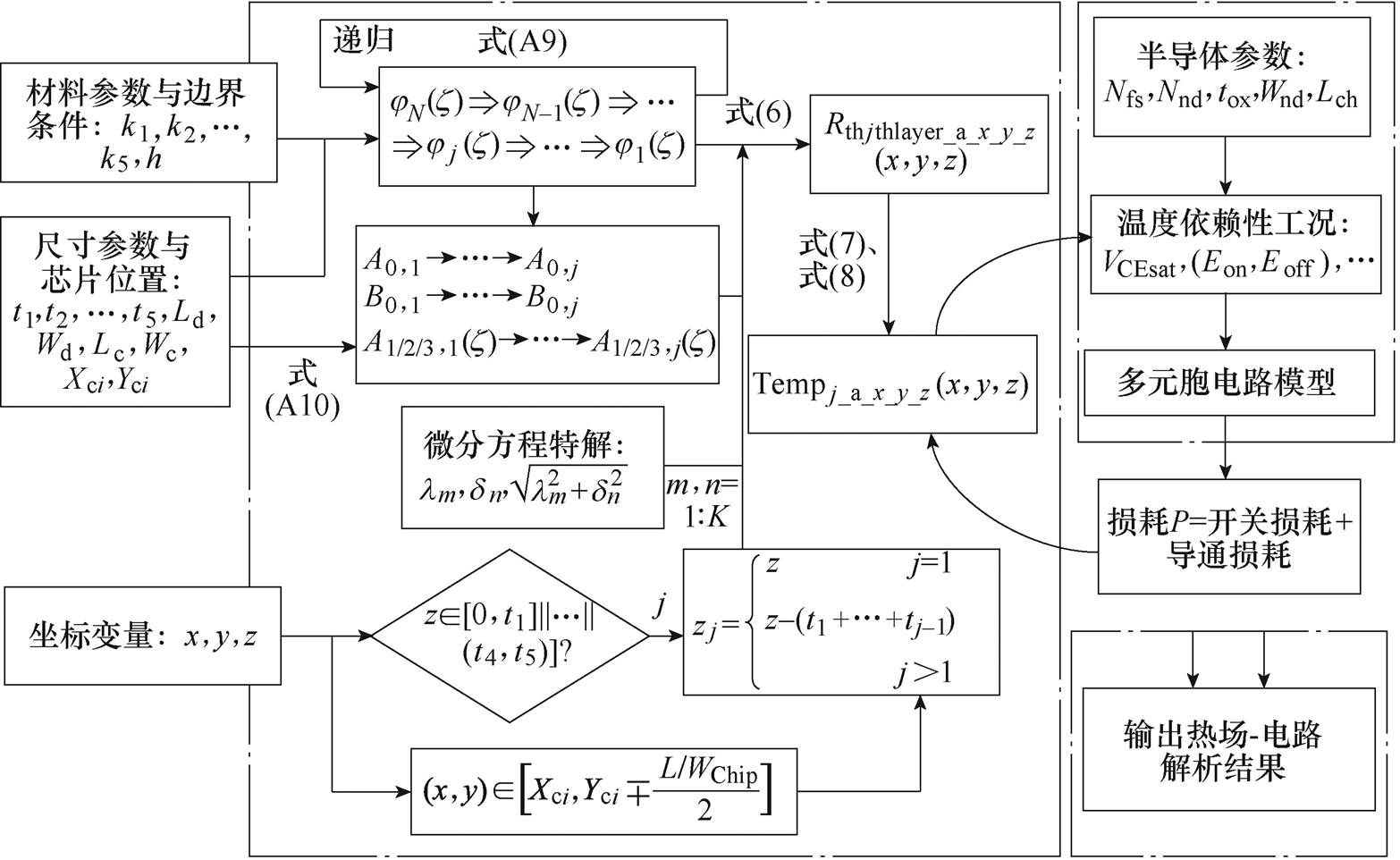
图4 三维温度场及场路耦合计算流程
Fig.4 Process of 3-D temperature field and field-circuit coupling
计及芯片压降温变效应时，由于芯片表面温度场的分布特征，芯片的电流密度也具有分布性特征，因此将芯片有源区划分为多元胞结构，其示意图如图5所示。芯片厚度为120mm，远小于功率模块的厚度，因此芯片内电流可近似为面电流，使用二维离散方法。将芯片划分为N（N=NlNw）个尺寸参数为DlDwtc元胞[23]，总共流经电流为Ic，各元胞电流依次为I1, I2,…, IN，形成的正向导通压降Vce。
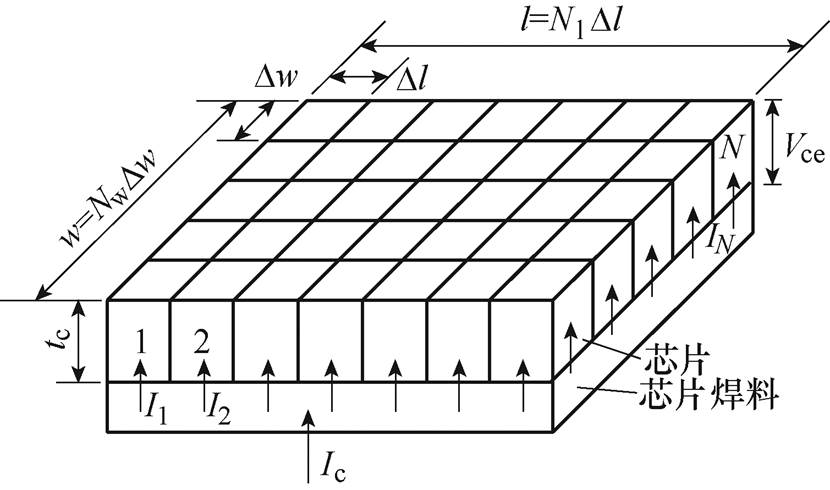
图5 芯片有源区多元胞结构示意图
Fig.5 Schematic diagram of multicellular chip structure
由1.2节可知，IGBT芯片在注入直流电流Ic后，芯片整体基于初始温度Ta形成初始正向导通电压降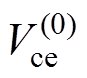
，因此产生的热损耗P(0)在芯片表面形成温度场分布
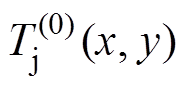，此过程为不计及芯片导通压降温变效应的热过程。
在此温度场分布基础上，芯片各元胞（Xci, Yci）基于本地温度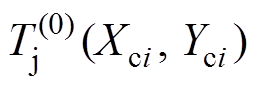
形成新的芯片导通压降
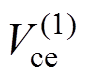，由此各元胞产生的本地热损耗P(1)(Xci, Yci)形成的温升场分布
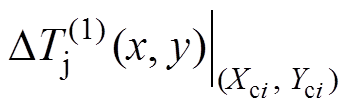线性叠加，形成新的温度场分布
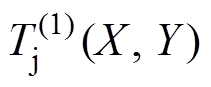及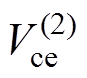
。以此过程迭代，直至第k次迭代后
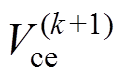不再变化，此时
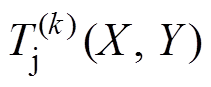即为计及芯片导通压降温变效应的热过程形成的最终芯片温度场分布。多元胞电-热创新迭代流程如图6所示。上述迭代过程涉及的数学表达式[24]为
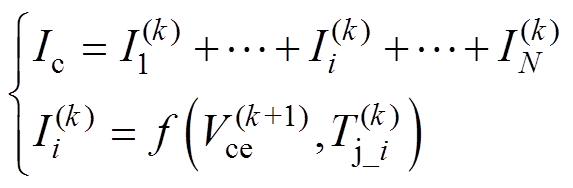（9）式中，f函数来自1.1节式（2）；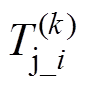
为元胞i的温度。
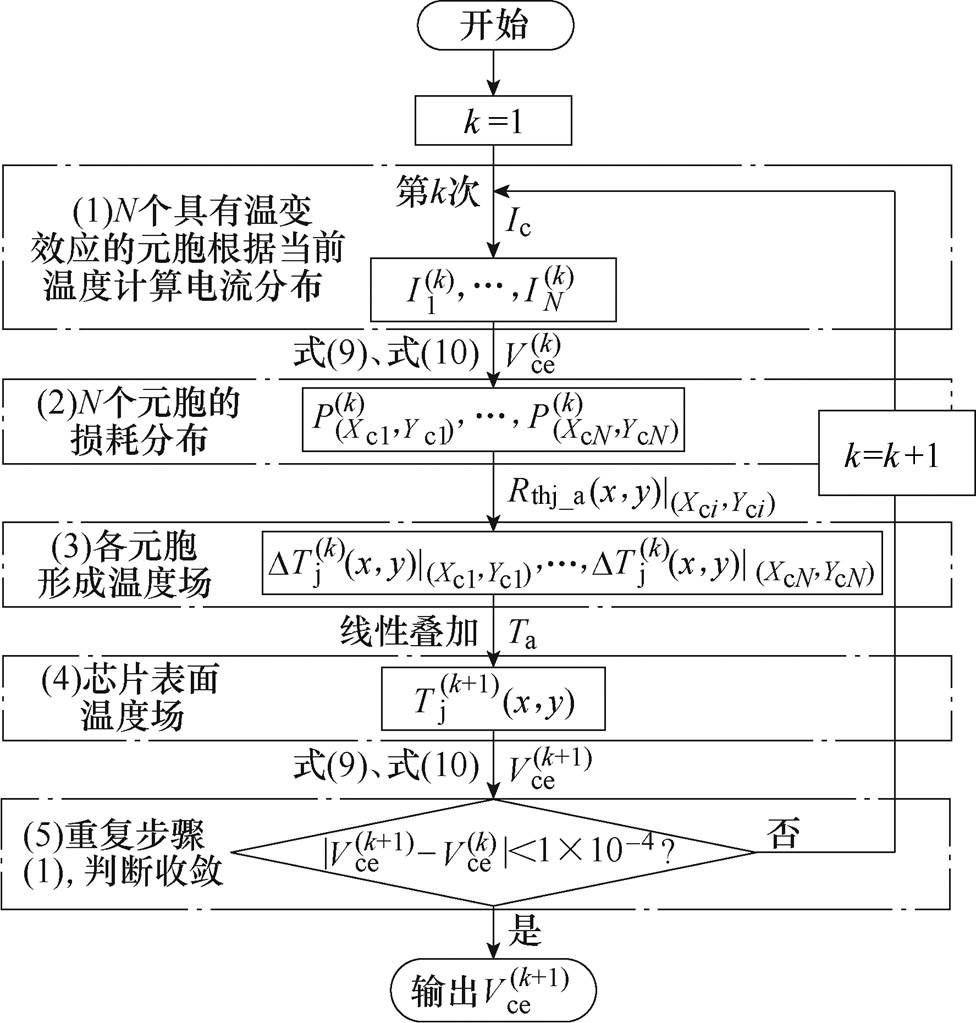
图6 多元胞电-热创新迭代流程
Fig.6 Iteration process of multicellular field-circuit coupling
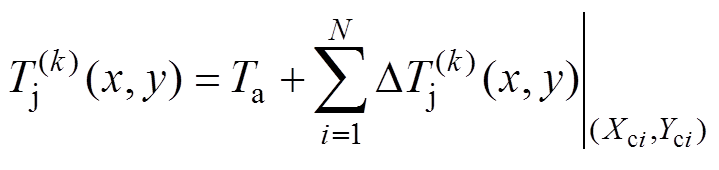（10）以单个芯片为例，由图2已知待研究芯片正/负温度系数分界电流为59.1A，图7为芯片在不同电流下元胞电流密度分布。当电流为20A（负温度系数区）时，各元胞电流往芯片中间聚拢；当电流为150A（正温度系数区）时，各元胞电流呈外扩“趋肤效应”分布特征。
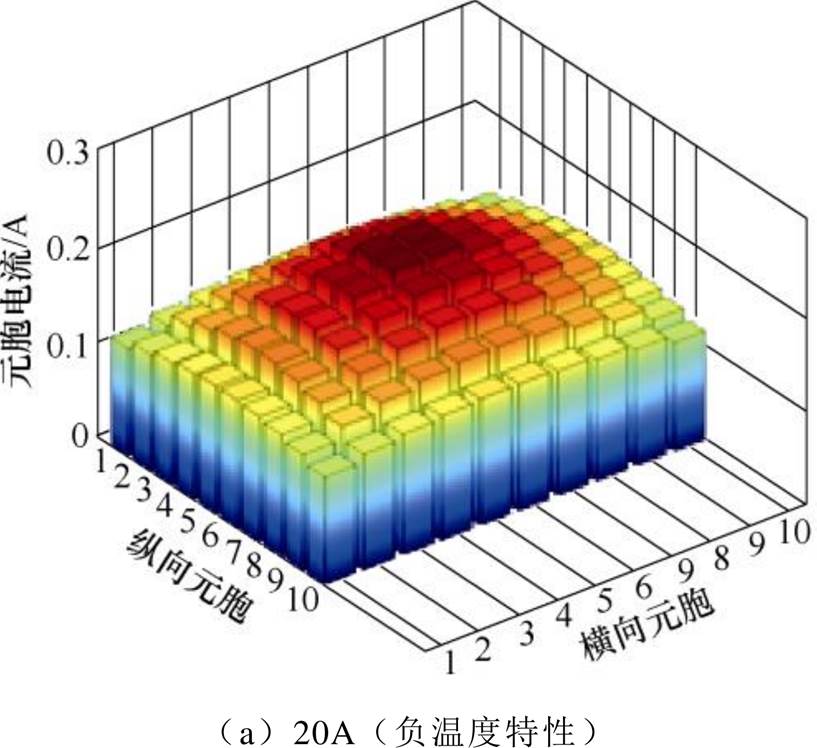
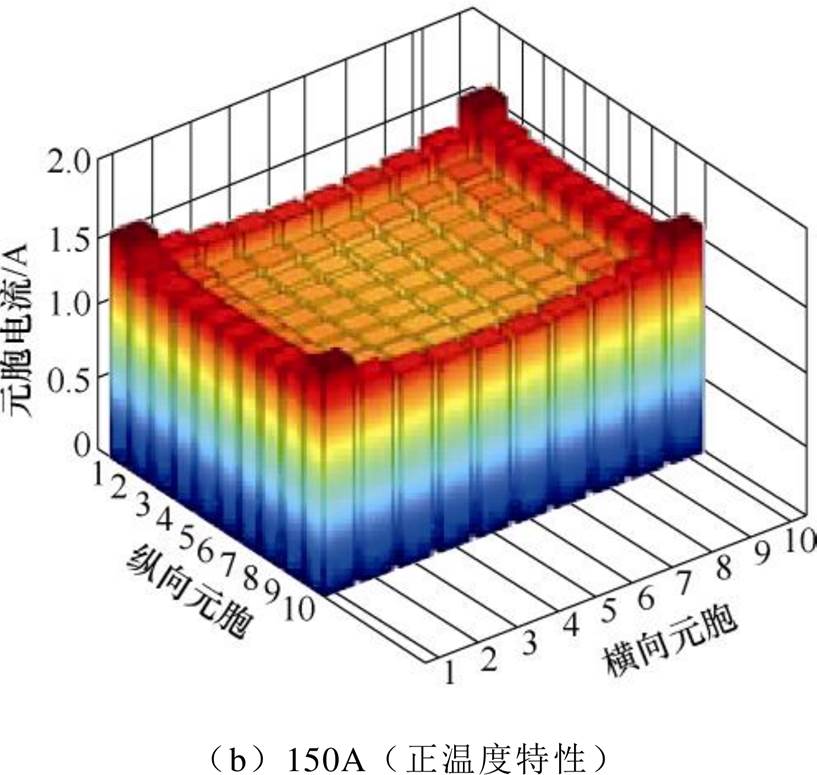
图7 不同温度特性下元胞电流分布
Fig.7 Current density distribution under different semiconductor temperature effect
芯片表面在1、2路径上横轴方向各位置热阻如图8a所示。芯片正温度特性下表面热阻峰值（0.177K/W）相较负温度特性下热阻峰值（0.191K/W）降低了7.9%，说明芯片热阻峰值与芯片所运行温度特性区相关。在正温度特性区，电流分布不均衡度及热阻峰值随功率变化趋势如图8b所示。随着功率增加，电流分布不均衡度由14.77%增加至32.92%，引起热阻峰值减小3.0%。进一步说明了元胞电流密度“趋肤”分布对片上温度峰值的抑制作用。
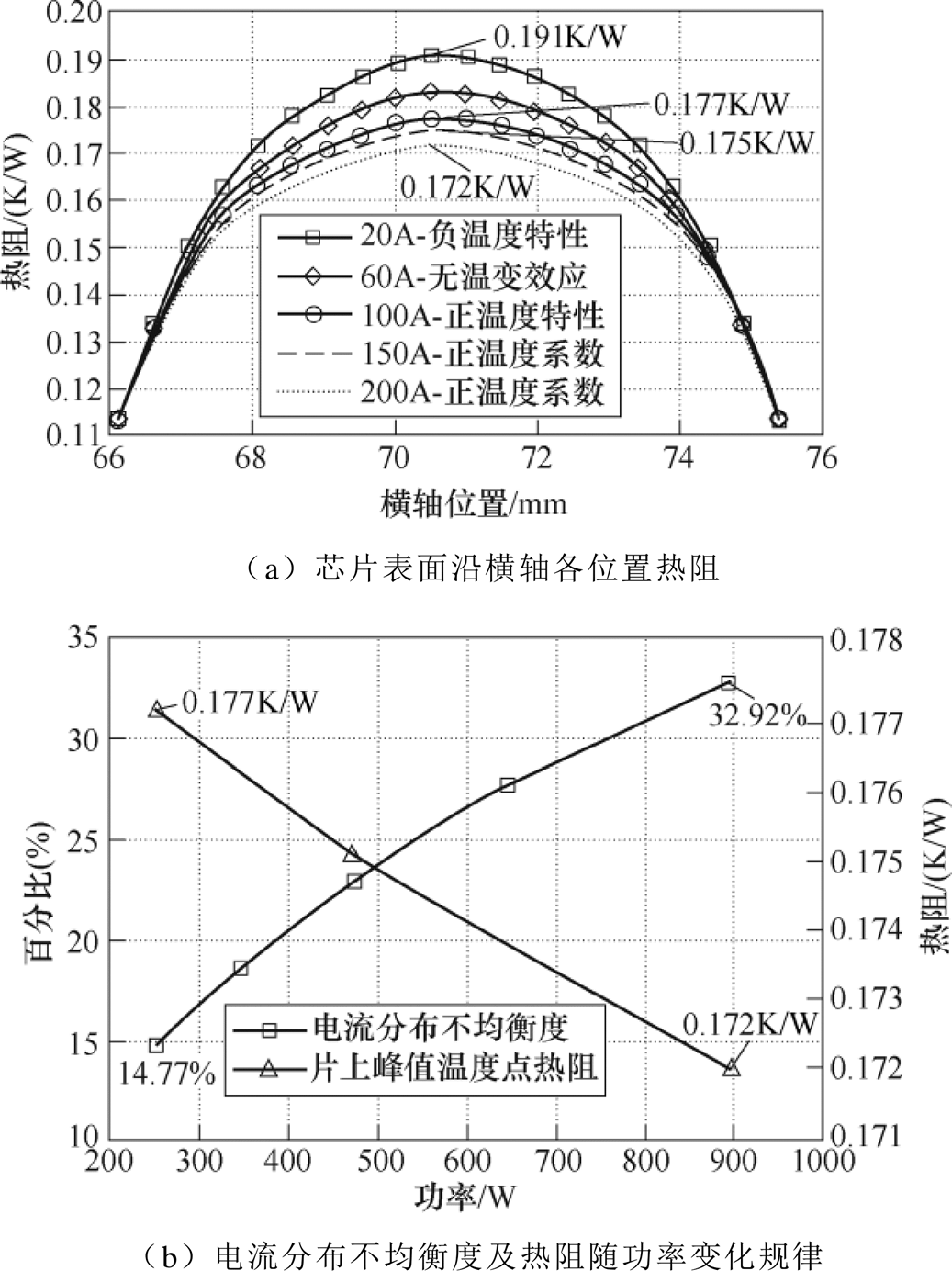
图8 正温度特性下元胞电流分布对热阻影响
Fig.8 Influence of current non-uniform on thermal resistance under positive temperature characteristics
选择赛米控型号为SEMiX603GB12E4p功率模块作为研究对象，其结构如图9所示，该模块为单相上下桥臂结构，一个桥臂由三个IGBT芯片并联组成，每个芯片有源区尺寸（长×宽×高）为9.7mm× 14.5mm×120mm，由四块分立的金属层覆盖，门极区位于芯片一侧，有源区以外为绝缘终端结构。键合线对热仿真结果影响很小[25]，本文不予考虑。一个桥臂的DBC表面尺寸为48.8mm×47mm。基板背面安装在水冷板上，可认为基板背面保持为冷却液温度Ta=22℃。图中，路径1、2用于验证x轴方向温度谱，路径3、4用于验证y轴方向温度谱，路径5、6用于验证z轴方向温度谱。厚度参数、材料特性、芯片坐标见表2。
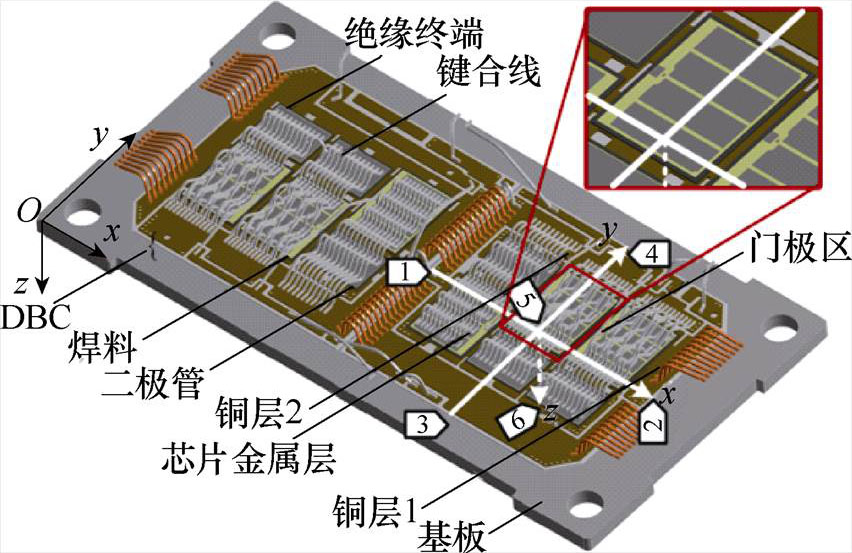
图9 IGBT功率模块SEMiX603GB12E4p结构
Fig.9 Structure of power module SEMiX603GB12E4p
表2 功率模块结构参数、材料参数及芯片位置
Tab.2 Structure, material parameters and chip position
参 数数 值 kc/[W/(m·℃)]98.9 kcs, k4/[W/(m·℃)]55 k1, k3, k5/[W/(m·℃)]380 k2/[W/(m·℃)]24 tc/mm0.12 tcs/mm0.12 t1, t3, t4/mm0.3 t2/mm0.32 t5/mm3 LChip(有源区)/mm9.7 WChip(有源区)/mm14.5 LDBC/mm118.6 WDBC/mm58.6 (Xc1, Yc1)/mm(70.7, 24.0) (Xc2, Yc2)/mm(84.5, 34.2) (Xc3, Yc3)/mm(97.5, 34.2)
在以表2参数作为基准案例的基础上，选取不同的芯片导通压降温变敏感度和芯片尺寸做进一步对比，来研究芯片结构与材料参数对所提方法结果与有限元结果重合度的影响。
为便于描述芯片导通压降温变敏感性，定义该芯片某一电流（如IChip=150A）下的等效电阻率表达式为
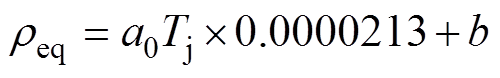（11）式中，a0为所定义等效电阻率温变敏感度；b为电阻率表达式截距，b=0.016 3W·m。
研究材料参数与芯片结构对所提方法结果与有限元结果重合度影响的典型案例见表3。有限元结果与所提方法结果对比如图10所示。图10a中，路径经过芯片区间代表芯片表面温度，未经过芯片区间代表铜层或陶瓷表面温度。图10b～图10d为有限元仿真结果与所提出模型结果对比，可见芯片面积与芯片导通压降温变敏感度对所提方法结果与有限元结果重合度的影响不显著。x轴路径最大误差位于芯片绝缘终端区域，为3.1%；y轴路径最大误差位于芯片金属层区域，为3.6%；z轴路径下整体趋势一致性最好，最大误差为1.1%。由文献[26]可知，SiC较硅材料具有更高的导通温敏性，是硅材料的7～8倍，另外碳化硅芯片面积为硅芯片面积的1/2～3/5，因此说明该方法也适用于基于碳化硅芯片封装功率模块的热建模。
表3 研究材料参数与芯片结构对所提方法结果与有限元结果重合度影响的典型案例
Tab.3 Typical cases for studying the influence of material parameters and chip structure
案例a0芯片尺寸/(mm×mm) 一19.7×14.5 二79.7×14.5 三19.7×7.25
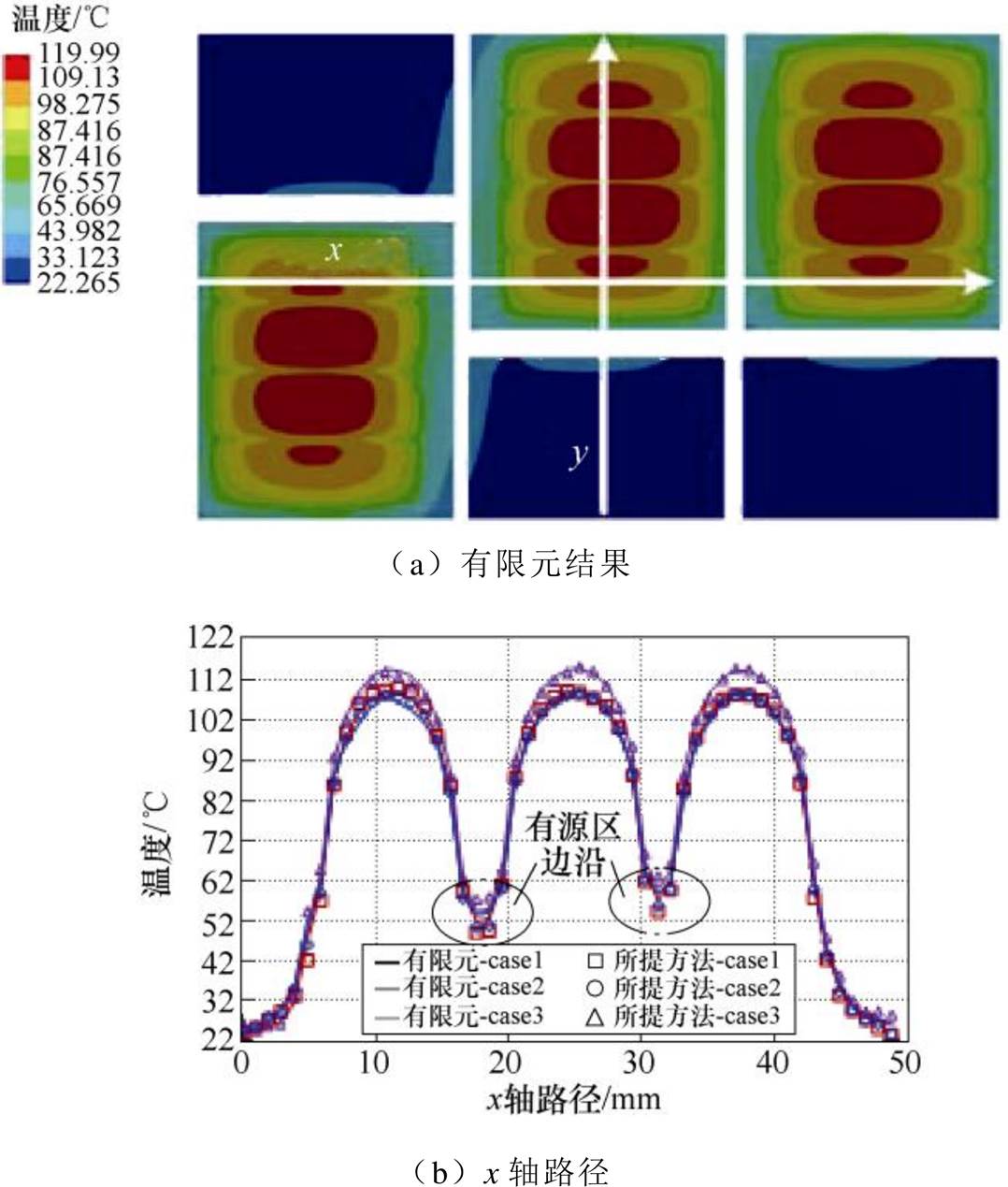
图10 有限元结果与所提方法结果对比
Fig.10 Comparison between FEM and proposed model
实验装置与电气原理如图11所示。为进一步验证所提方法的有效性，搭建如图11a所示实验装置，将功率模块安装在散热冷板上，散热冷板内液油通过Julabo PRESTO A80控制稳定，制冷功率最高达1.2kW。采用型号为Fluke Ti450热成像仪对功率模块上表面进行测量，采用光纤测温仪Opsens 15S0208和光纤探头OTG-F-10监测功率模块壳温以确保恒定，电压表测量模块信号端子两端电压以提取集-射极电压。电气原理如图11b所示，驱动电压源提供+15V门极电压使IGBT处于完全导通状态，功率电流源提供直流大电流用于加热模块。改变不同电流后，经热成像仪观察温度稳定后记录热成像温度图谱与IGBT压降值。多次测量后，上桥臂的热成像图谱结果如图12所示。
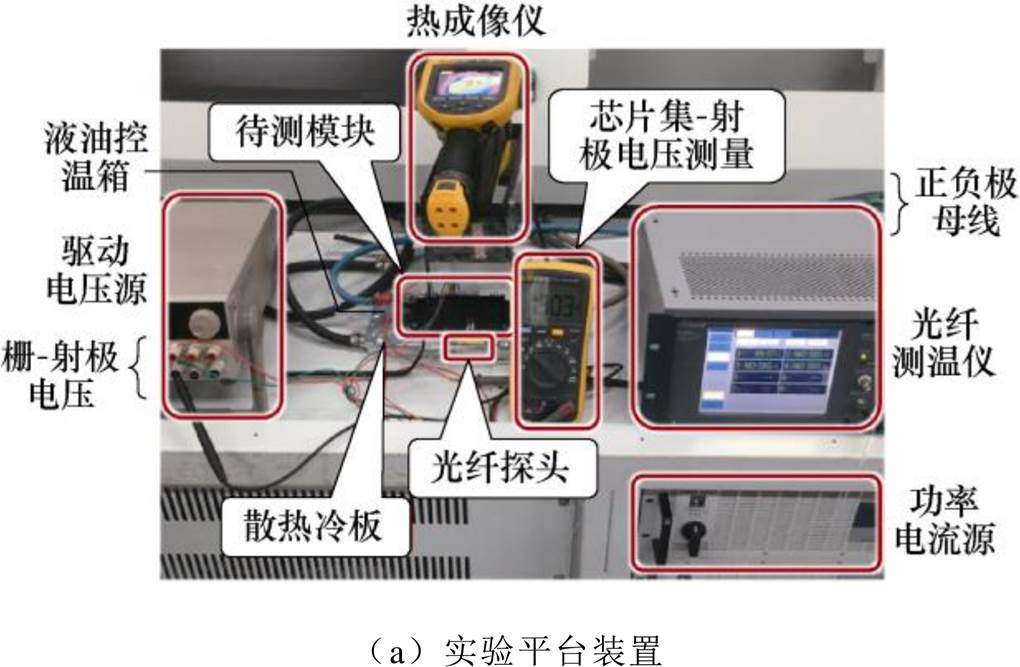
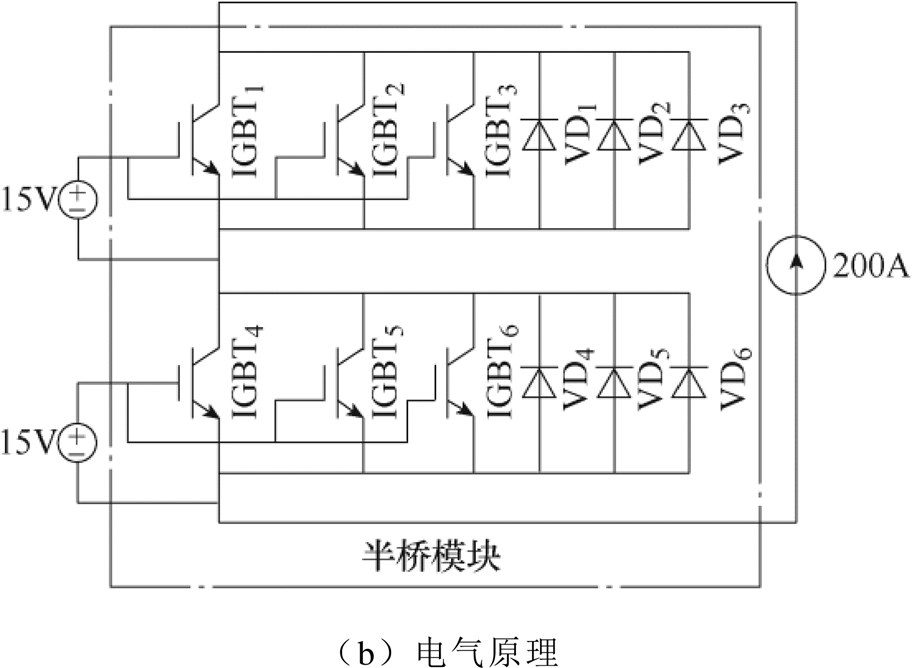
图11 实验装置与电气原理
Fig.11 Experimental setup and electrical schematic diagram
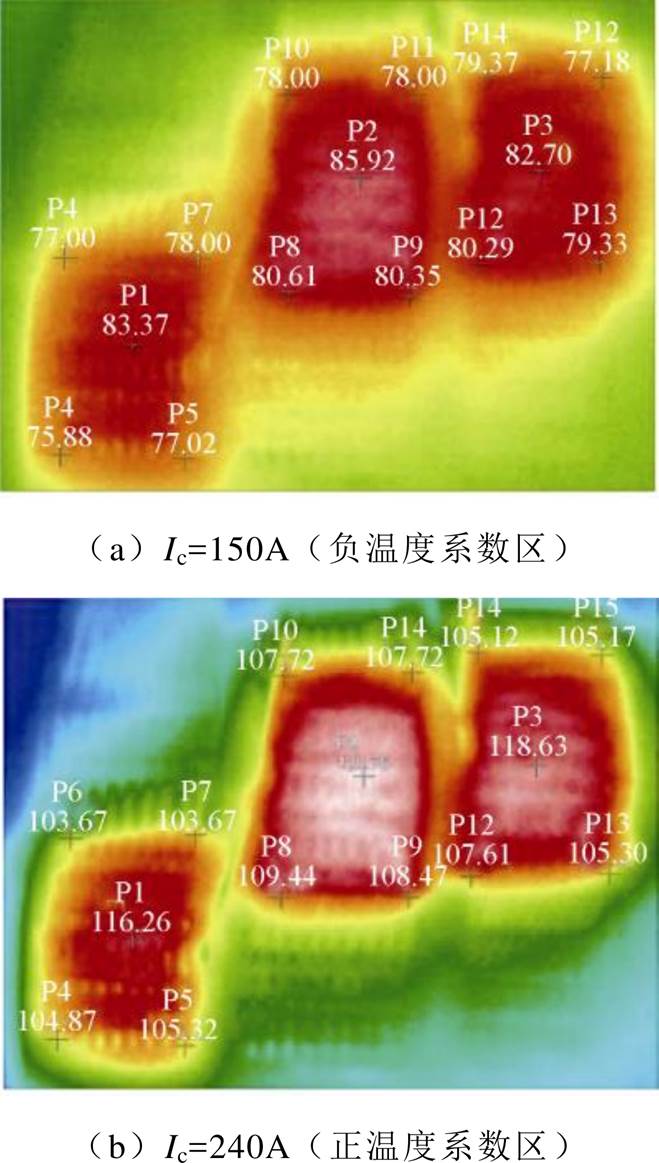
图12 实验结果
Fig.12 Experimental results
测温点P1～P15位置见图12，P1、P2、P3分别位于三个芯片中心，其余测温点分别位于各芯片边缘。各位置坐标代入所提解析模型中得出相应温度，并与实验结果对比。实验结果与所提出模型结果对比见表4。所有测温点的结果误差不超过4.0%，验证了所提建模方法的准确性与有效性。
上桥臂测温点P1、P2、P3所得的热阻结果如图13所示。此时芯片运行在正温度特性区（大于177.3A），可见每个芯片的热阻峰值均随着功率增加而减小，依次减小了15.2%、15.6%、17.7%。
图13 热阻实验结果与模型结果分析
Fig.13 Experimental and modelling thermal resistance
表4 实验与模型结果对比
Tab.4 Comparison between experiment and model
Ic/A温度/℃误差(%) 实验模型 160（负温度系数区）83.3784.981.93 85.9283.59-2.71 82.7082.66-0.05 75.8874.79-1.44 77.0274.80-2.88 76.0075.16-1.11 78.6475.57-3.90 80.6179.77-1.04 80.3580.450.12 78.9079.200.38 78.6080.722.70 80.2980.410.15 79.3378.59-0.93 79.3780.831.84 77.1878.932.27 240（正温度系数区）116.26118.311.76 120.75118.58-1.80 118.63117.93-0.59 104.87102.11-2.63 105.82103.62-2.08 103.67101.92-1.69 107.70103.78-3.64 109.44108.29-1.05 108.41109.110.65 109.16110.681.39 107.72109.811.94 107.61108.330.67 105.30103.42-1.79 108.22109.541.22 105.47108.552.92
为验证所提出解析模型法的计算效率，与Ansys Workbench 18.0软件内置Thermal-Electric模块的计算用时进行对比。软件在同一计算机上运行，CPU型号为Intel Xeon E5-1630 v3，运行内存32GB。微元数量和计算用时对比见表5。可见本文方法仅需对芯片有源区域进行离散化，无离散耗时。随着划分精度的提高，所提出方法结果误差随之减小，当芯片划分精度为0.88mm（11×11矩阵）时已实现网格无关性，此时微元数量仅为有限元法微元数量的0.22%，计算速度提高约96%。结果表明，本文方法在分析芯片温度场时可有效控制微元数量，并提高计算效率，较传统方法具有明显优势。
表5 有限元法与所提方法的微元数量、计算用时对比（a0=1, b=0.016 3W·m）
Tab.5 Comparison of filaments quantity and elapsed time between FEM and proposed method (a0=1, b=0.016 3W·m)
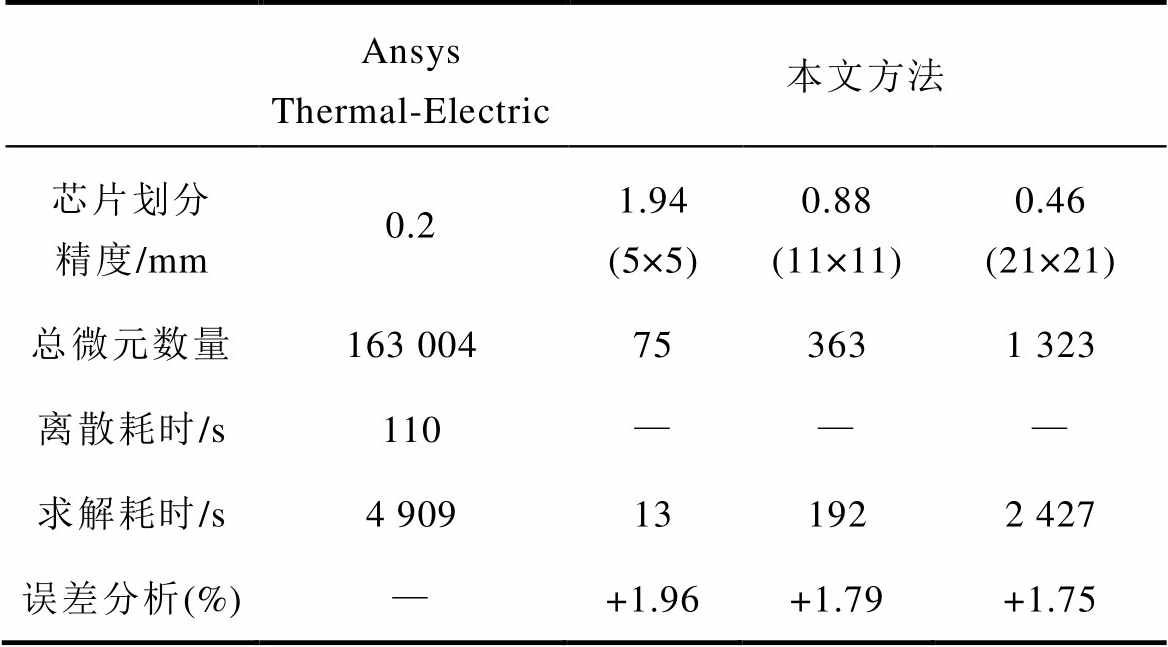
Ansys Thermal-Electric本文方法 芯片划分精度/mm0.21.94 (5×5)0.88 (11×11)0.46 (21×21) 总微元数量163 004753631 323 离散耗时/s110——— 求解耗时/s4 909131922 427 误差分析(%)—+1.96+1.79+1.75
为验证所提出解析模型法的收敛度，选取不同芯片导通温变敏感度a0下有限元法与所提方法的收敛误差、迭代次数与求解耗时进行对比，收敛度对比结果见表6。由表6可见，随着a0增加，有限元法的迭代次数增加约97%，求解耗时增加约90%，当a0=8时，有限元法不能收敛。而所提方法随着a0增加，迭代次数没有显著增加，未出现不收敛情形，求解耗时仅增加约33%，且所得结果误差没有显著提高。结果表明，本文方法可有效解决传统方法迭代算法不收敛的局限性，对不同芯片导通温变敏感度有较强适应性。
表6 有限元法与所提方法在不同芯片导通温变敏感度下的收敛度对比
Tab.6 Comparison of convergence influenced by the semiconductor temperature effect
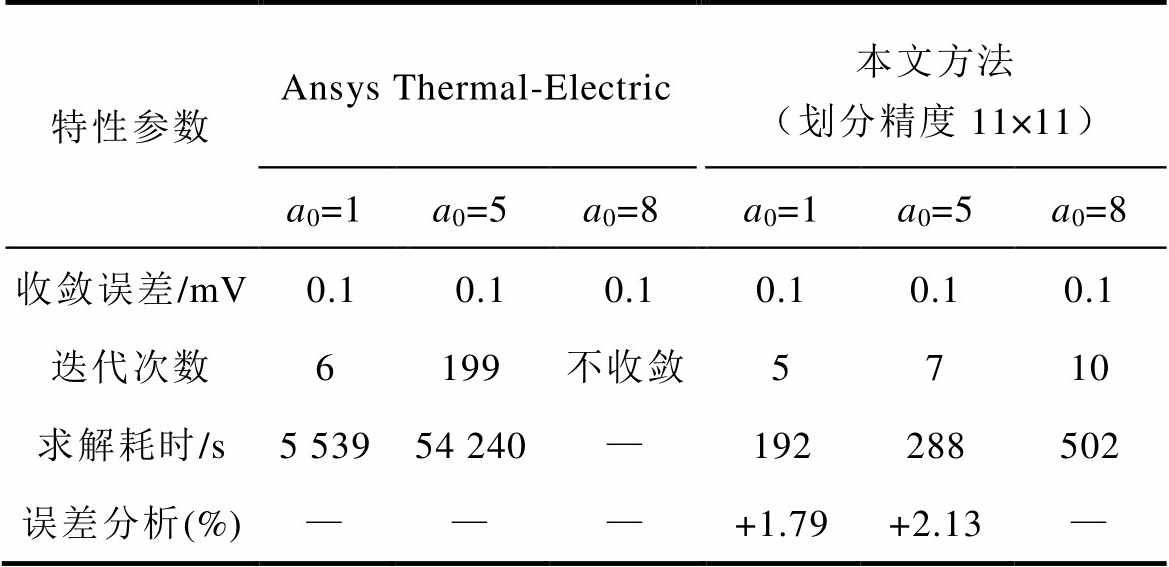
特性参数Ansys Thermal-Electric本文方法（划分精度11×11） a0=1a0=5a0=8a0=1a0=5a0=8 收敛误差/mV0.10.10.10.10.10.1 迭代次数6199不收敛5710 求解耗时/s5 53954 240—192288502 误差分析(%)———+1.79+2.13—
针对IGBT芯片在真实工况运行条件下表现的电流密度分布不均问题，提出了一种基于IGBT芯片导通压降温变效应的功率模块三维分布温度场建模方法，根据IGBT芯片在不同电流下表现的正/负温度特性，结合多芯片多层封装结构下的傅里叶级数解析热模型，通过对IGBT芯片有源区进行多元胞划分，实现了IGBT芯片各元胞的电-热耦合仿真，揭示了不同电流密度分布特点对芯片表面温度场形成的规律。最后通过稳态过电流实验对所提出模型进行了验证，实验结果表明，测试结果与建模方法结果误差不超过4.0%，且验证了IGBT芯片表面电流密度不均对温度场的影响，为极端工况下器件功率评估与可靠性分析提供新方法。
对式（4）中的变量进行分离，令
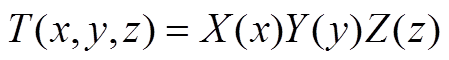（A1）得到的常微分方程为
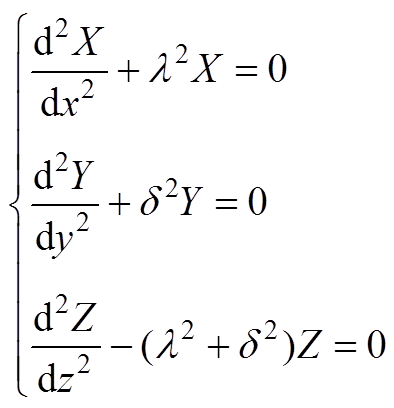（A2）
求解式（A2）可得
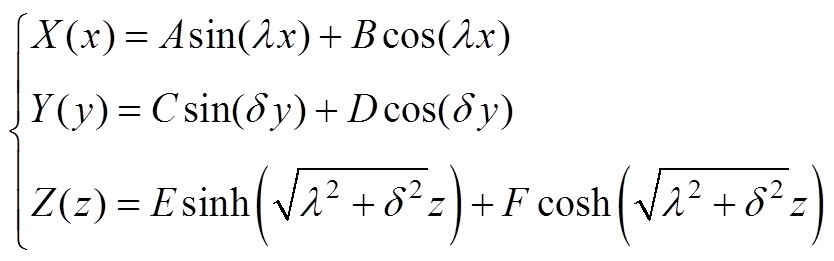（A3）式中，A、B、C、D、E、F为待定系数。
将式（A3）代入式（5）可得
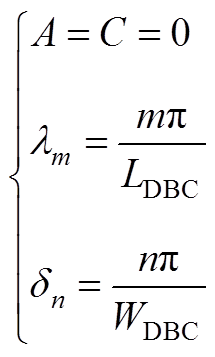（A4）式中，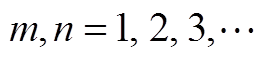
。
因此，式（A3）可写为
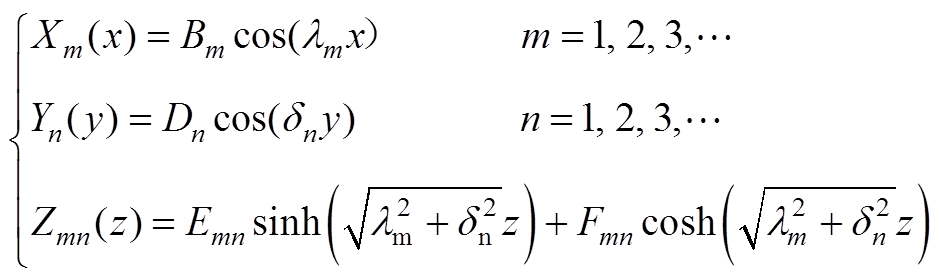（A5）对于m, n=0，定义函数形式为
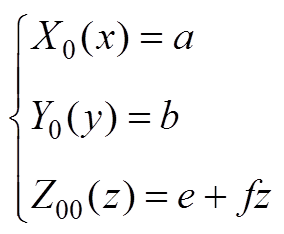（A6）
将式（A4）～式（A6）代入式（A1），得
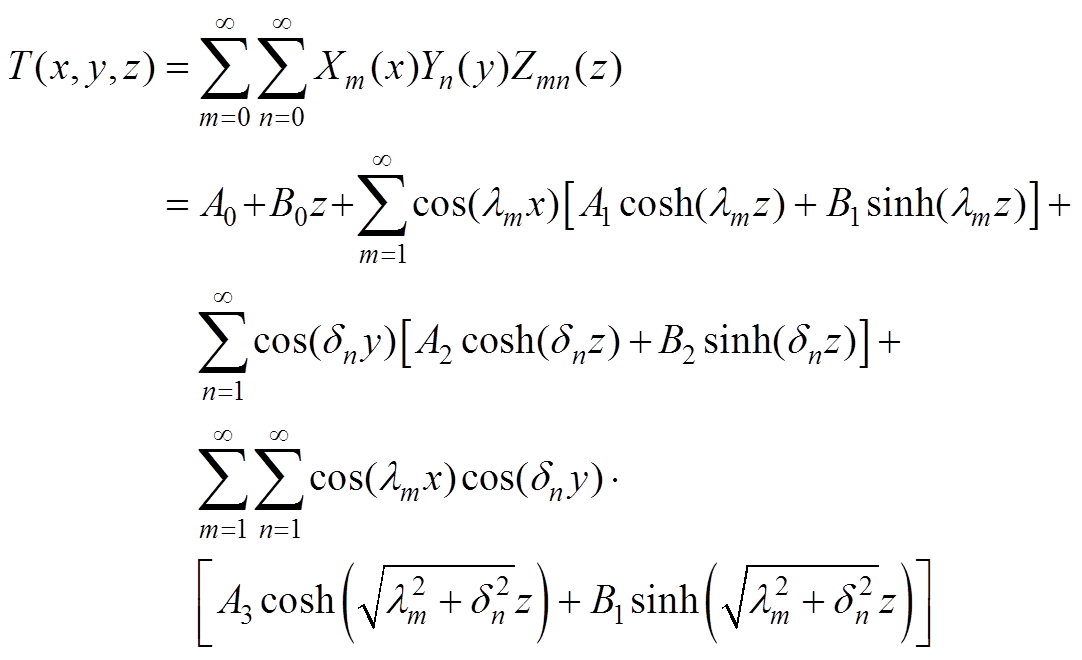（A7）对铜层上表面温度进行求解，即z=0。利用边界条件式（6）对剩余系数A1、A2、A3进行求解得
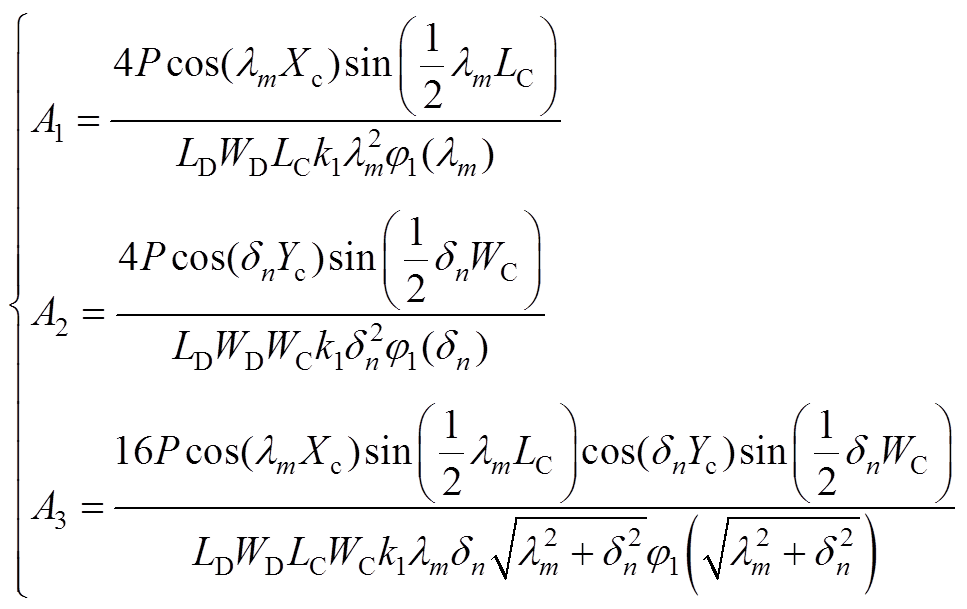（A8）
式中，扩散函数j1为DBC上铜层的扩散函数，表示层与层间热扩散关系，j1函数表达式可由基板层jN逐层递归所得，其过程为
（A9）其中
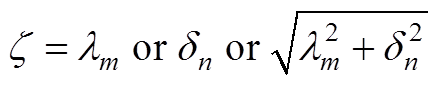
每层系数A的求解过程表示为
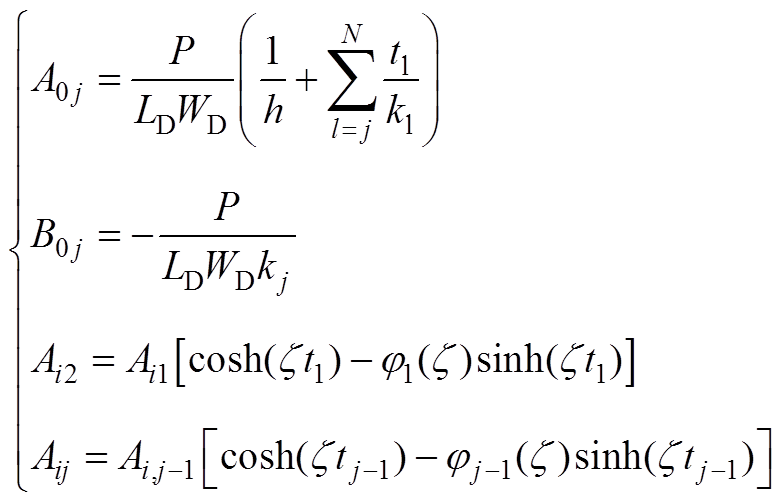（A10）参考文献
[1] 曾正, 欧开鸿, 吴义伯, 等. 车用双面散热功率模块的热-力协同设计[J]. 电工技术学报, 2020, 35(14): 3050-3064.
Zeng Zheng, Ou Kaihong, Wu Yibo, et al. Thermo- mechanical co-design of double sided cooling power module for electric vehicle application[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(14): 3050-3064.
[2] 唐勇, 汪波, 陈明, 等. 高温下的IGBT可靠性与在线评估[J]. 电工技术学报, 2014, 29(6): 17-23.
Tang Yong, Wang Bo, Chen Ming, et al. Reliability and on-line evaluation of IGBT modules under high temperature[J]. Transactions of China Electro- technical Society, 2014, 29(6): 17-23.
[3] 罗皓泽, 高洪艺, 朱春林, 等. 电动汽车IGBT芯片技术综述和展望[J]. 中国电机工程学报, 2020, 40(18): 5718-5730.
Luo Haoze, Gao Hongyi, Zhu Chunlin, et al. Review and prospect of IGBT chip technologies for electric vehicles[J]. Proceedings of the CSEE, 2020, 40(18): 5718-5730.
[4] 姚芳, 胡洋, 李铮, 等. 基于结温监测的风电IGBT热安全性和寿命损耗研究[J]. 电工技术学报, 2018, 33(9): 2024-2033.
Yao Fang, Hu Yang, Li Zheng, et al. Study on thermal safety and lifetime consumption of IGBT in wind power converters based on junction temperature monitoring[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2024-2033.
[5] Baker N, Dupont L, Munk-Nielsen S, et al. IR camera validation of IGBT junction temperature measurement via peak gate current[J]. IEEE Transactions on Power Electronics, 2017, 32(4): 3099-3111.
[6] Du B, Hudgins J L, Santi E, et al. Transient electro- thermal simulation of power semiconductor devices[J]. IEEE Transactions on Power Electronics, 2010, 25(1): 237-248.
[7] 袁登科, 徐延东, 李秀涛. 永磁同步电动机变频调速系统及其控制[M]. 北京: 机械工业出版社, 2015.
[8] 李辉, 胡玉, 王坤, 等. 考虑杂散电感影响的风电变流器IGBT功率模块动态结温计算及热分布[J]. 电工技术学报, 2019, 34(20): 4242-4250.
Li Hui, Hu Yu, Wang Kun, et al. Thermal distribution and dynamic junction temperature calculation of IGBT power modules for wind turbine converters considering the influence of stray inductances[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4242-4250.
[9] 马铭遥, 郭伟生, 严雪松, 等. 用于电动汽车功率模块热分析的紧凑型热网络模型[J]. 中国电机工程学报, 2020, 40(18): 5796-5805.
Ma Mingyao, Guo Weisheng, Yan Xuesong, et al. Compact thermal network model for thermal analysis of power modules in electric vehicle[J]. Proceedings of the CSEE, 2020, 40(18): 5796-5805.
[10] 刘宾礼, 罗毅飞, 肖飞, 等. 基于传热动力学作用特征的IGBT结温预测数学模型[J]. 电工技术学报, 2017, 32(12): 79-87.
Liu Binli, Luo Yifei, Xiao Fei, et al. Junction temperature prediction mathematical model of IGBT based on the characteristics of thermal dynamics[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 79-87.
[11] Bahman A S, Ma K, Blaabjerg F. A lumped thermal model including thermal coupling and thermal boundary conditions for high-power IGBT modules[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2518-2530.
[12] 贾英杰，肖飞，罗毅飞，等. 基于场路耦合的大功率IGBT多速率电热联合仿真方法[J]. 电工技术学报, 2020, 35(9): 1952-1961.
Jia Yingjie, Xiao Fei, Luo Yifei, et al. Multi-rate electro-thermal simulation method for high power IGBT based on field-circuit coupling[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1952- 1961.
[13] Schwabe C, Seidel P, Lutz J. Power cycling capability of silicon low-voltage MOSFETs under different operation conditions[C]//31st International Symposium on Power Semiconductor Devices and ICs (ISPSD), Shanghai, 2019: 495-498.
[14] Wu Rui, Iannuzzo F, Wang Huai, et al. Fast and accurate Icepak-PSpice co-simulation of IGBTs under short-circuit with an advanced PSpice model[C]//IET International Conference on Power Electronics, Machines and Drives, Manchester, UK, 2014: 1-5.
[15] Riccio M, Falco G D, Maresca L, et al. 3D electro- thermal simulations of wide area power devices operating in avalanche condition[J]. Microelectronics Reliability, 2012, 52(9): 2385-2390.
[16] 郑利兵, 韩立, 刘钧, 等. 基于三维热电耦合有限元模型的IGBT失效形式温度特性研究[J]. 电工技术学报, 2011, 26(7): 242-246.
Zheng Libing, Han Li, Liu Jun, et al. Investigation of the temperature character of IGBT failure mode based on 3D thermal-electro coupling FEM[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 242- 246.
[17] Choudhury K R, Rogers D. Steady-state thermal modeling of a power module: an N-layer Fourier approach[J]. IEEE Transactions on Power Electronics, 2018, 34(2): 1500-1508.
[18] 熊诗成, 鲁军勇, 郑宇锋, 等. 基于各层材料传热特性的晶闸管结温计算等效电路模型[J]. 中国电机工程学报, 2018, 38(4): 1157-1164.
Xiong Shicheng, Lu Junyong, Zheng Yufeng, et al. Equivalent circuit model based on the heat transfer characteristics of each layer for pulsed power thyristor junction temperature calculation[J]. Pro- ceedings of the CSEE, 2018, 38(4): 1157-1164.
[19] Zhang Yiming, Deng Erping, Zhao Zhibin, et al. A physical thermal network model of press pack IGBTs considering spreading and coupling effects[J]. IEEE Transactions on Components, Packaging and Manufa- cturing Technology, 2020, 10(10): 1674-1683.
[20] Wang Kangjia, Pan Zhongliang. An analytical model for steady-state and transient temperature fields in 3-D integrated circuits[J]. IEEE Transactions on Components, Packaging and Manufacturing Tech- nology, 2016, 6(7): 1-14.
[21] 陈玉香. 大容量沟槽栅——场截止型IGBT本征关断特性和短路强健性研究[D]. 杭州: 浙江大学, 2019.
[22] 陶文铨. 传热学[M]. 5版. 北京: 高等教育出版社, 2019.
[23] Andrea I, Giovanni B, Paolo S. New developments of THERMOS3, a tool for 3D electrothermal simulation of smart power MOSFETs[J]. Microelectronics Reliability, 2007, 47(1): 1696-1700.
[24] 贾英杰, 罗毅飞, 肖飞, 等. 一种符合欧姆定律的IGBT等效电阻模型[J]. 电工技术学报, 2020, 35(2): 310-317.
Jia Yingjie, Luo Yifei, Xiao Fei, et al. An equivalent electrical resistance model of IGBT suitable for Ohm’s law[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 310-317.
[25] Chen Jie, Deng Erping, Xie Luhong, et al. Investigations on averaging mechanisms of virtual junction temperature determined by VCE(T) method for IGBTs[J]. IEEE Transactions on Electronic Devices, 2020, 67(3): 1106-1112.
[26] Akbari M, Bahman A S, Reigosa P D, et al. Thermal modeling of wire-bonded power modules considering non-uniform temperature and electric current inter- actions[J]. Microelectronics Reliability, 2018, 88(3): 1135-1140.
Analytical 3D Temperature Field Model for Power Module Considering Temperature Effect of Semiconductor Voltage Drop
Abstract Insulated gate bipolar transistor power modules are widely used in EV powertrain systems. The thermal design is challenged by the demands of high power density and extreme operating conditions. Due to the temperature effect of semiconductor voltage drop, the chip current presents a non-uniform distribution. Therefore, the traditional thermal model cannot accurately describe the temperature field, which brings difficulties to the robustness design under overcurrent conditions. In this paper, combined with a continuous 3-D temperature field model and a multicellular 1-D electrical model, a field-circuit coupling based 3-D temperature field is proposed to achieve accurate description of the semiconductor temperature. The error is less than 4.0%. Furthermore, it is found that the multicellular current is concentrated on the edge of the IGBT active region. The non-uniform effect can suppress the peak temperature and can effectively improve the overcurrent capability. Finally, the proposed analytical model is verified by the SEMiX603GB12E4p module. The FEM and experimental results show that the model can describe the temperature effect at different current levels, and its accuracy and effectiveness are verified.
keywords：Power module, temperature effect, field-circuit coupling, 3D temperature field, over- current capabilit
中图分类号：TN46
DOI: 10.19595/j.cnki.1000-6753.tces.201440
国家自然科学基金杰出青年科学基金项目（51925702）、国家自然科学基金面上项目（51677166）、上汽基金会项目“电机控制器IGBT寿命模型研究”（1924）和中央高校基本科研业务费专项资金项目（K20200097）资助。
收稿日期 2020-11-01
改稿日期 2020-12-22
陈 宇 男，1993年生，博士研究生，研究方向为功率器件可靠性技术。E-mail: yu.chen@zju.edu.cn
罗皓泽 男，1986年生，特聘研究员，研究方向为功率器件可靠性技术。E-mail: haozeluo@zju.edu.cn（通信作者）
（编辑 陈 诚）