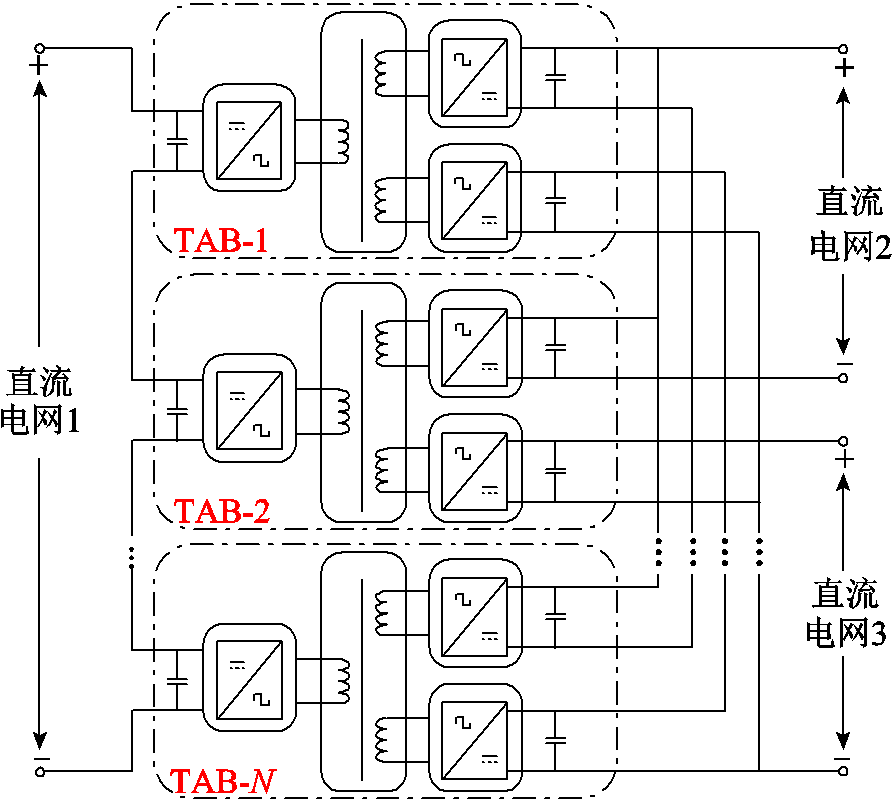
图1 模块化组合的TAB变换器
Fig.1 Modular combination of TAB converters
摘要 传统单移相（SPS）控制策略下三有源桥（TAB）变换器控制简单，但内部存在较大回流功率，增加了变换器的电流有效值和损耗。采用多重移相（MPS）控制策略虽然能提高控制灵活度、降低回流功率，但其分析过程复杂、移相角选取思路不明确。针对上述问题，该文提出一种MPS控制策略下TAB变换器的简化分析模型和优化控制策略。首先建立TAB变换器的傅里叶级数等效模型，推导MPS控制策略下TAB变换器的统一表达形式，并提出TAB变换器的简化分析模型，降低了MPS控制策略下TAB变换器的分析和计算难度；然后结合简化分析模型，提出一种基于无功功率的TAB变换器优化控制策略，能有效减小TAB变换器的电流有效值，降低控制器的设计难度；最后通过仿真和实验验证了所提控制策略的有效性。
关键词：三有源桥变换器 多重移相 傅里叶级数模型 无功功率 电流有效值 优化控制策略
直流变压器用于实现直流电网中的能量交换，是直流电网中的关键设备[1-2]。对于含多条不同电压等级母线的直流电网，需要配备具有多向潮流能力的多端口直流电压器，以满足不同电压等级直流母线之间的能量交换和分布式能源的接入[3-7]。现有研究中，多端口直流变压器拓扑按能量耦合形式，可以分为电耦合型和磁耦合型[8-11]。电耦合型多端口直流变压器本质上是多台两端口直流变压器的并联运行，各部分相对独立，但由于是多机并联运行，不利于能量的统一调度和控制。磁耦合型多端口直流变压器采用集中设计方案，通常借助多绕组变压器实现能量的汇聚与转移，具备良好的电气隔离特性，各端口能量统一调度分配，潮流特性灵活，是未来直流变压器研究的重要方向。
三有源桥（Triple Active Bridge, TAB）变换器由两端口双有源桥（Dual Active Bridge, DAB）变换器扩展而来，隶属于磁耦合型多端口直流变压器行列，可以通过模块化组合方式用于连接不同电压等级的直流电网，如图1所示。TAB变换器保留了DAB变换器功率密度大、潮流方向灵活、具备电气隔离等优点，能满足直流电网高电压大功率的需求，同时适用于光伏、储能等分布式能源的接入，得到了国内外学者的广泛关注。目前，针对TAB变换器的研究主要集中在端口功率解耦控制、器件软开关等方面[12-17]，而对TAB变换器回流功率、电流有效值优化等效率方面问题的研究较少。
图1 模块化组合的TAB变换器
Fig.1 Modular combination of TAB converters
TAB变换器一般采用单移相（Single Phase Shift, SPS）控制策略，SPS控制策略简单方便，易于实现，但SPS控制策略自由度低，无法对电感电流进行灵活控制。在位于同一桥臂的开关管交替导通时刻，有部分功率流回了输入侧，产生了回流功率。回流功率的存在，增大了电流有效值，从而增加了变换器的损耗，降低了变换器的运行效率[18-20]。对于两端口DAB变换器，通常使用多移相（Multi Phase Shift, MPS）控制策略对变换器的回流功率、电流有效值等物理量进行优化，但TAB变换器由于端口数量增多，使用MPS控制策略时控制自由度骤增，采用传统的电路模态分析方法对MPS控制策略下的TAB变换器进行分析，难度大、计算复杂。
针对上述问题，本文开展了TAB变换器简化分析模型及优化控制策略的研究。首先分析了SPS控制策略和MPS控制策略下TAB变换器的工作特性，然后借助多绕组变压器等效电路，建立TAB变换器的傅里叶级数等效模型，推导MPS控制策略下TAB变换器的统一表达形式，根据分析结果对傅里叶级数进行了合理简化并提出了简化分析模型。在此基础上，结合简化模型中无功功率与电路模态分析中回流功率的对应关系，提出了基于无功功率的TAB变换器优化控制策略。最后，通过仿真和实验验证了所提出控制策略的有效性。
TAB变换器由三个H桥模块通过三绕组变压器连接而成，拓扑结构如图2所示。TAB变换器的三个端口均为双向端口，根据输入输出端口数量可以将TAB变换器的工作模式分为单输入双输出模式和双输入单输出模式。两种工作模式在分析方法上具有一定的相似性，在本文中仅讨论单输入双输出工作模式。图2中，L1、L2、L3为三个端口包含漏感的辅助电感，C1、C2、C3为三个端口的滤波电容，三绕组高频变压器电压比为N1:N2:N3。
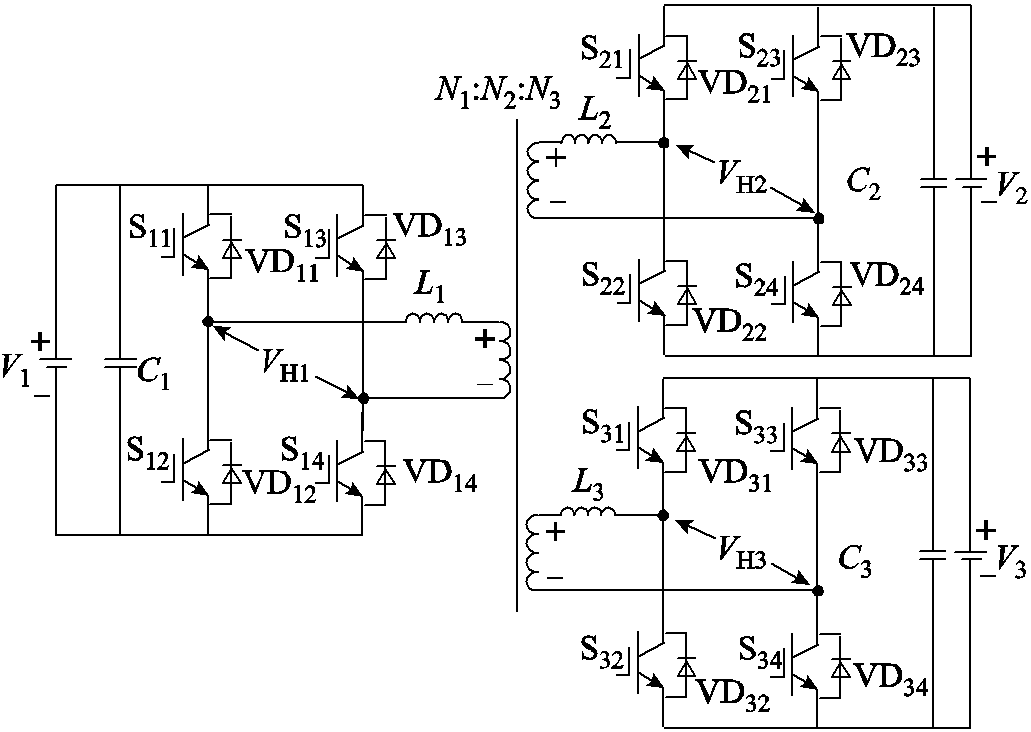
图2 TAB变换器的拓扑结构
Fig.2 Topology of TAB converter
在SPS控制策略下，通过控制TAB变换器各端口输出至变压器侧方波电压VHi(i=1, 2, 3)之间的移相角来调节各端口的输出功率。SPS控制策略下TAB变换器各开关器件导通信号及各端口方波电压和电流波形如图3a所示。从图3 a中可以看到，SPS控制策略下各H桥位于对角线的开关器件在一个周期内同时导通和关断，位于同一桥臂的开关器件在一个周期内交替导通。在SPS控制策略下，变换器共有两个控制自由度，VH1、VH2之间的移相角β12和VH1、VH3之间的移相角β13，对于每一个固定工作点，仅存在唯一的β12和β13组合。
SPS控制策略下，结合电感电流过零点和开关器件导通顺序，一个周期内TAB变换器可以分为12个工作模态。在前后半个周期内，TAB变换器的工作模态具有对称性。为节省篇幅，本文省去了具体的模态分析过程，表1中给出了SPS控制策略下前半个周期内TAB变换器各端口的电流表达式。表1中，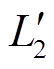
、
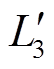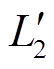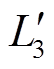为端口2、3输出电压V2、V3折算至端口1侧的值，移相占空比dij=βij/π(i,j=1,2,3, i≠j)，fs为变换器的开关频率，和为端口2、3的辅助电感折算至端口1侧的等效电感，等效电感M为
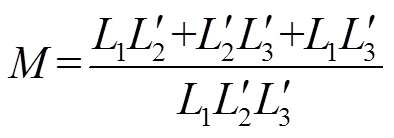（1）表1 SPS控制策略下TAB变换器各端口电感电流表达式
Tab.1 Current expression of TAB converter’s each port under SPS control strategy
时段各端口电感电流表达式端口 t0～t11 2 3 t1～t21 2 3 t2～t31 2 3
由于SPS控制策略无法对变换器的各工作模态和电感电流灵活控制，因此在SPS控制策略下TAB变换器内部存在较大回流功率，如图3a中阴影区域所示。回流功率产生的原因是由于SPS控制策略无法在开关器件交替导通时，为电感电流提供续流通道，因而使得部分功率经反并联二极管流回功率输入端口。通过增加控制自由度，在器件交替导通时刻为电感电流续流提供卸能通道，可以消除功率回流模态，从而减小回流功率。
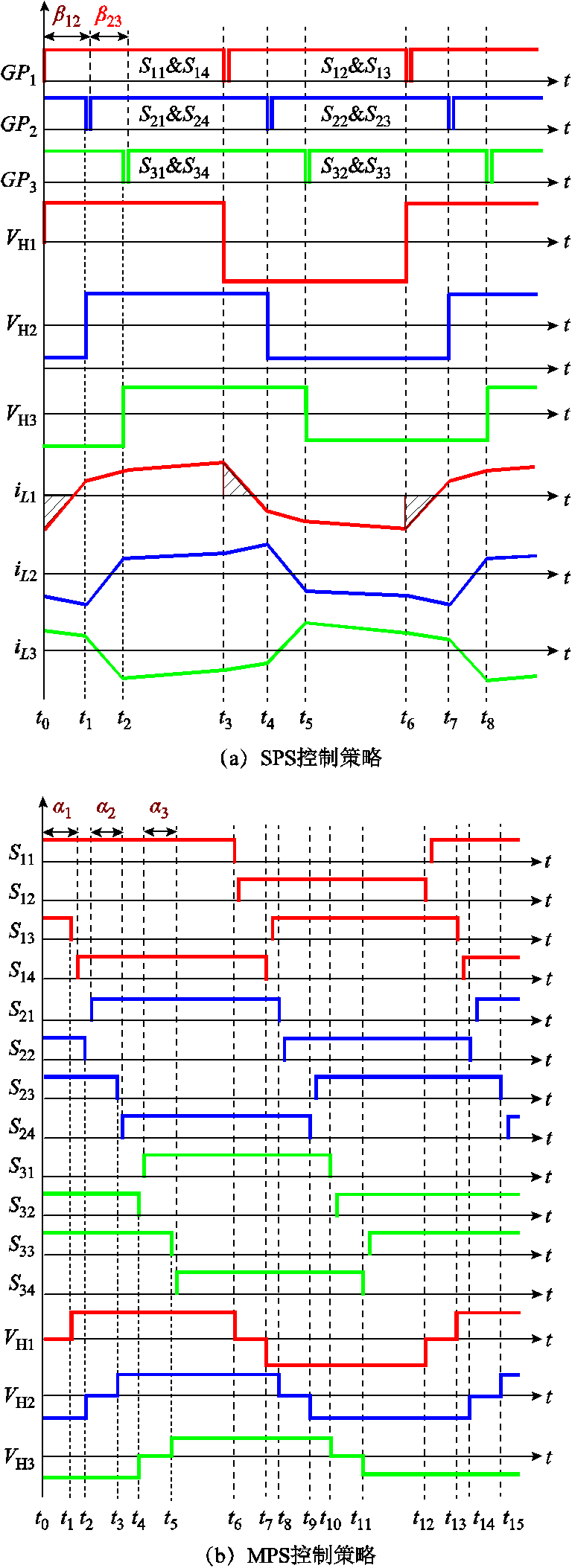
图3 TAB变换器各端口导通信号和电压方波
Fig.3 Turn-on signal and square wave voltage of TAB converter
MPS控制策略下，在TAB变换器各端口内加入控制自由度αi（在本文中，定义控制自由度αi为各端口的内移相角，其中i为端口编号，i=1,2,3）。各端口加入内移相角后在电路模态上体现为，SPS控制策略下各端口位于对角线位置同时导通的开关管之间加入了移相角度αi，如图3b所示。
MPS控制策略的实质是在SPS控制策略对各端口输出至变压器侧方波电压VHi移相的基础上，增加了对VHi占空比的控制。在电路模态上表现为，当器件交替导通时，通过位于上桥臂（或下桥臂）的两个开关器件为电感续流电流提供卸能通道，使得电流不流回功率输入端口，从而阻止了回流功率的产生。
在MPS控制策略下，TAB变换器各端口的内移相角α1、α2、α3存在多种取值和组合方式，全部分类情况多达几十种。此外，从表1中可以看到，在仅包含两个控制自由度的SPS控制策略下，TAB变换器各模态中各端口电感电流表达式非常繁琐，随着控制自由度的增加，表1中的表达式将会变得更加复杂。因此，采用传统的模态分析方法难以对MPS控制策略下全部内移相角组合进行分析和计算。基于此，本文对TAB变换器各端口方波电压VHi进行傅里叶分解，结合多绕组变压器的等效电路，建立了TAB变换器的傅里叶级数等效模型，避免了由于控制自由度的增加带来的分析和计算难度。
在MPS控制策略下，TAB变换器各端口输出至变压器侧的方波电压VHi如图4所示。在图4中，由于加入了内移相角，各端口方波电压VHi占空比变为di=(π-αi)/π。为了简化计算，将端口1的方波电压VH1向左平移了α1/2，使得端口1的方波电压为奇函数[21-22]。由于方波电压具有周期性，因此简化计算对TAB变换器的相关电气量无影响。
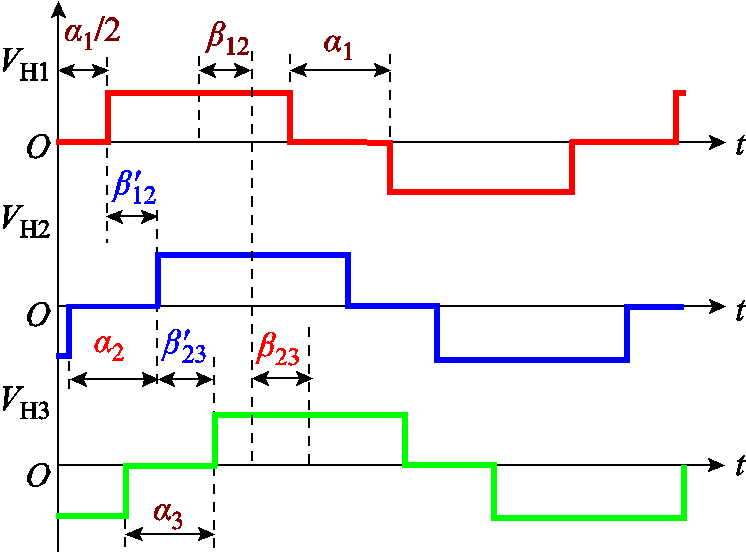
图4 MPS控制下TAB变换器各端口方波电压
Fig.4 Square wave voltage of TAB converter’s each port under MPS control
在此定义MPS控制策略下外移相角βij为各端口方波电压VHi中点之间的相位差，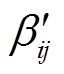
为SPS控制策略下各端口输出至变压器侧方波电压上升沿之间的相位差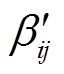，和βij之间的数学关系为
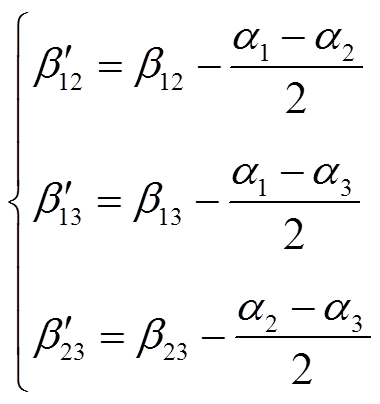（2）对图4中各端口方波电压做傅里叶分解，可以得到
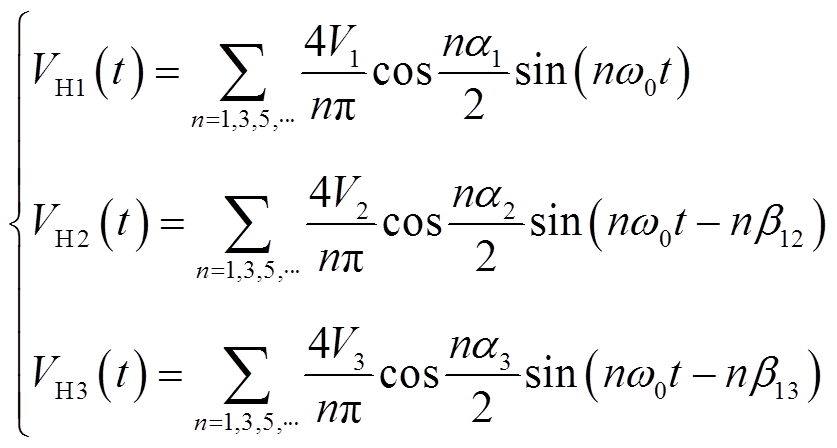（3）式中，角频率ω0=2πfs。将端口2、3折算至端口1侧，可以将TAB变换器简化为如图5所示的△和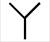
形等效电路[23]。由于励磁电感Lm相较于端口的辅助电感较大，在图5b中略去了励磁支路，V0为三绕组变压器
形等效电路中的中性点。
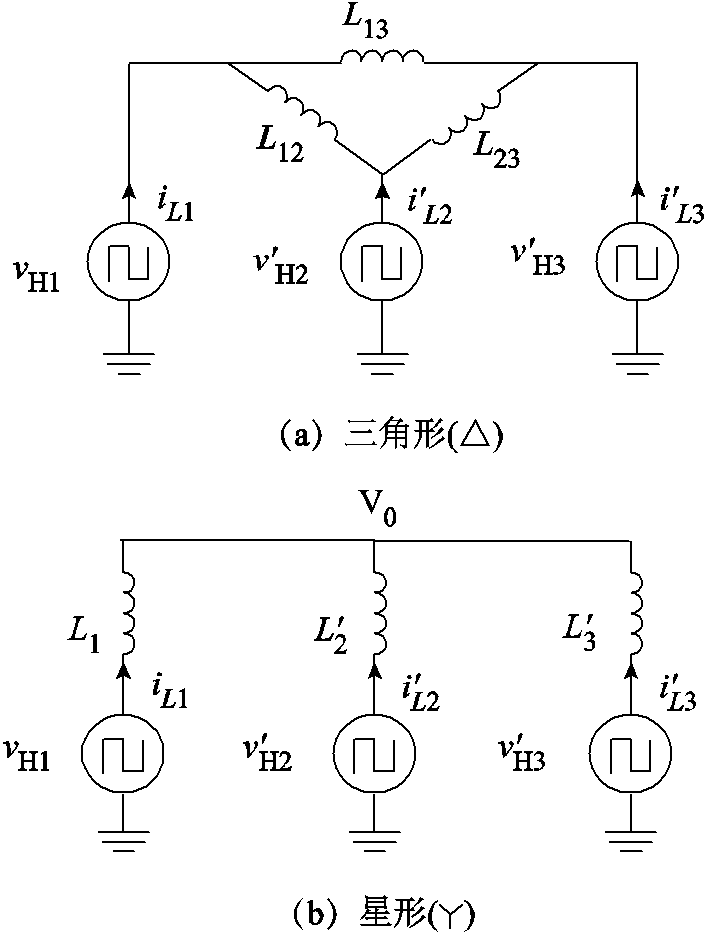
图5 TAB变换器等效电路
Fig.5 TAB converter’s equivalent circuit diagram
根据KVL，可以求得中性点V0处的电压为
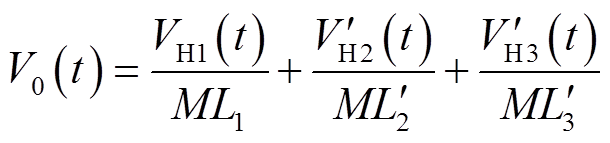（4）式中，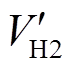
、
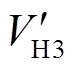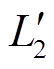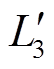为端口2、3方波电压VH2、VH3折算至端口1侧的值。结合式（3）、式（4）可以得到电感L1、和上的电流表达式为
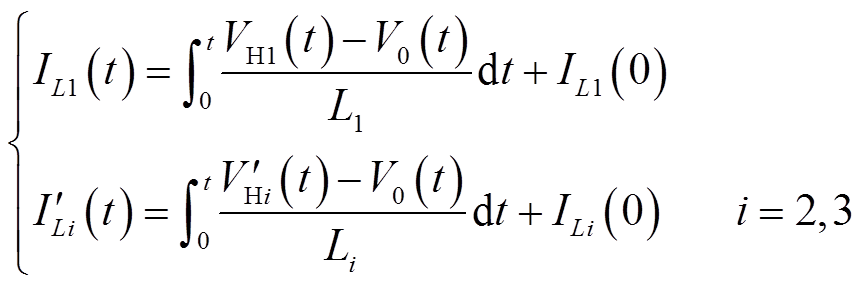（5）根据伏秒平衡原则，电感电流在前后半个周期内具有对称性，可以得到
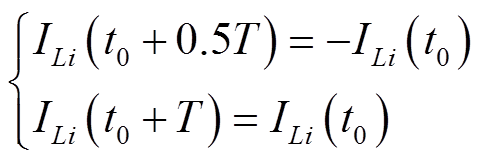（6）联立式（4）～式（6），整理后得到一个周期内电感L1、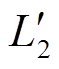
和
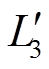上的电流表达式为
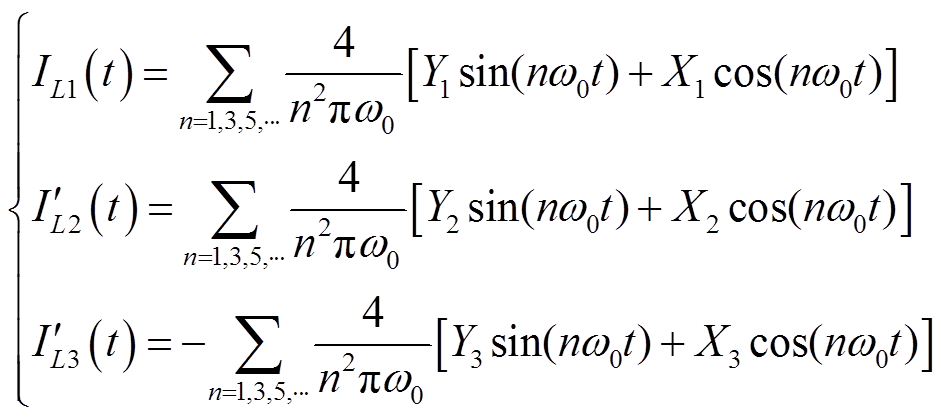（7）式中，电感电流均以流入变压器为正方向；X1、X2、X3、Y1、Y2、Y3为系数，具体表达式如附录中式（A1）所示。
在一个周期内，TAB变换器各端口向外发出的有功功率可以分为基波有功功率、同频次电压和电流发出的有功功率、不同频次电压和电流发出的有功功率[24]。由于三角函数的正交性，不同频次电压和电流积分后结果为0，因此傅里叶级数模型下TAB变换器的有功功率仅由基波有功功率和同频高次电压和电流产生的有功功率两部分组成。式（8）给出了TAB变换器各端口有功功率的计算表达式。
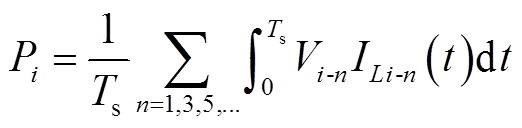（8）式中，Ts为开关周期，Vi-n和ILi-n分别为端口i的n次电压和电流。将式（3）、式（7）代入式（8）中，整理后可以得到TAB变换器各端口有功功率表达式，如式（9）所示。其中，Lij为端口ij之间的等效电感，如附录中式（A2）所示，各端口的有功功率以向变压器侧输出功率为正方向。
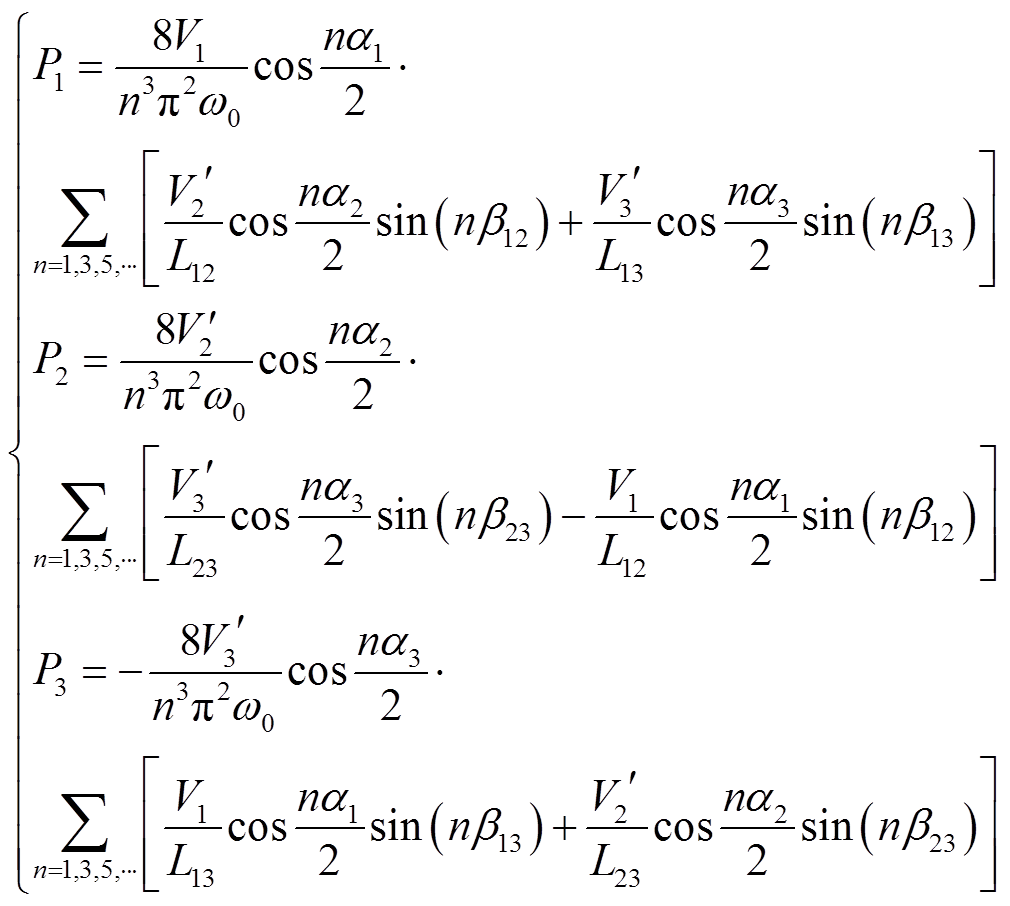（9）在一个周期内，TAB变换器发出的无功功率可分为由基波电压电流产生的基波无功功率、同频高次电压和电流产生的高频无功功率两部分，式（10）给出了TAB变换器各端口无功功率的计算表达式。
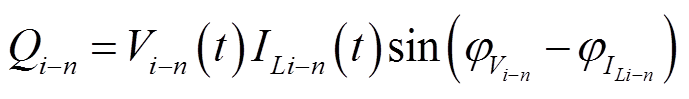（10）式中，
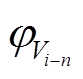和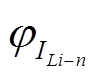
分别为端口i的n次电压和电流的相角。
将式（3）、式（7）代入到式（10）中，整理后可以得到TAB变换器在傅里叶级数模型下各端口无功功率表达式为
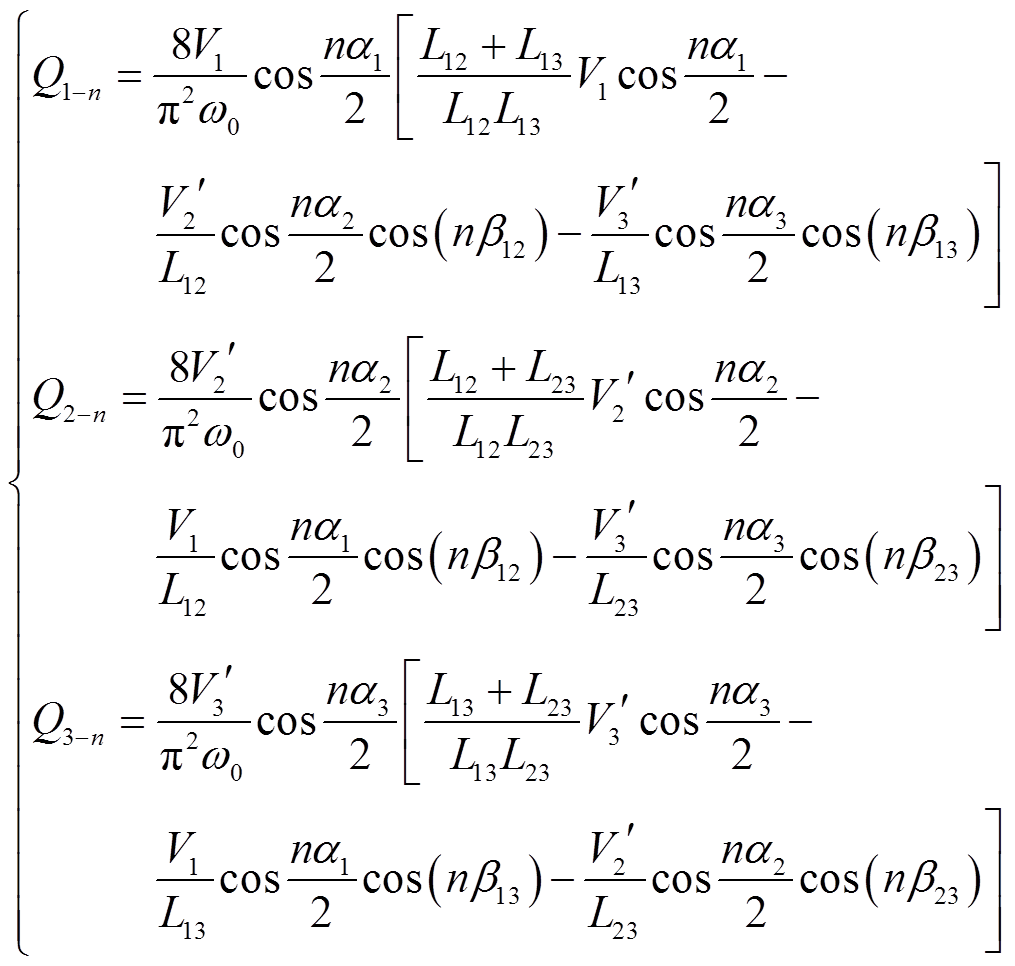（11）式中，Qi-n为端口i的n次无功功率，各端口无功功率的正方向与有功功率方向一致。
结合式（9）可以得到全功率范围内TAB变换器各端口基波有功功率、各高频次有功功率和总有功功率的示意图，如图6所示。从图6中可以看到，基波有功功率在全功率范围内与总有功功率大小接近、变化趋势相同。当β12=β13=π/2时，TAB变换器位于最大功率工作点，各端口基波有功功率和总有功功率误差约为3.2%，各端口3次有功功率约为基波功率的3.7%，各端口5次有功功率约为基波功率的0.8%。在全功率范围内，基波有功功率相对于其他频次有功功率较大，在总功率中占绝大部分。
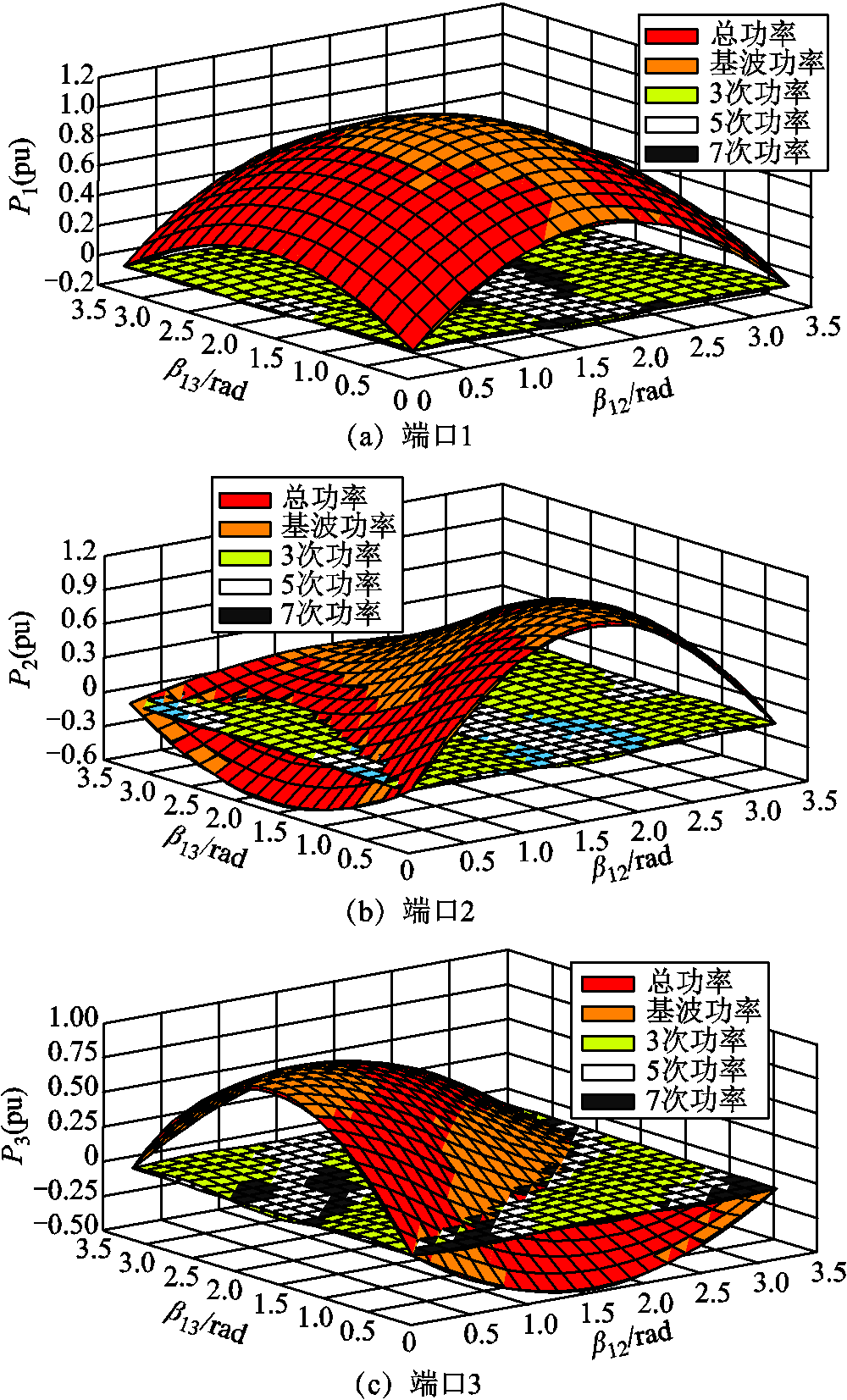
图6 TAB变换器各端口各频次有功功率
Fig.6 Active power of TAB converter’s each port at each frequency
结合式（11）可以得到全功率范围内TAB变换器各端口基波无功功率、各高频次无功功率的示意图，如图7所示。从图7中可以看到，基波无功功率在全功率范围内相对于其他高频次无功功率较大，7次以上高频次无功功率由于数值太小，基本可以忽略。当β12=β13=π/2时，TAB变换器位于最大功率工作点，各端口3次无功功率约为基波功率的3.7%，各端口5次无功功率约为基波功率的0.79%，各端口7次无功功率约为基波功率的0.29%。
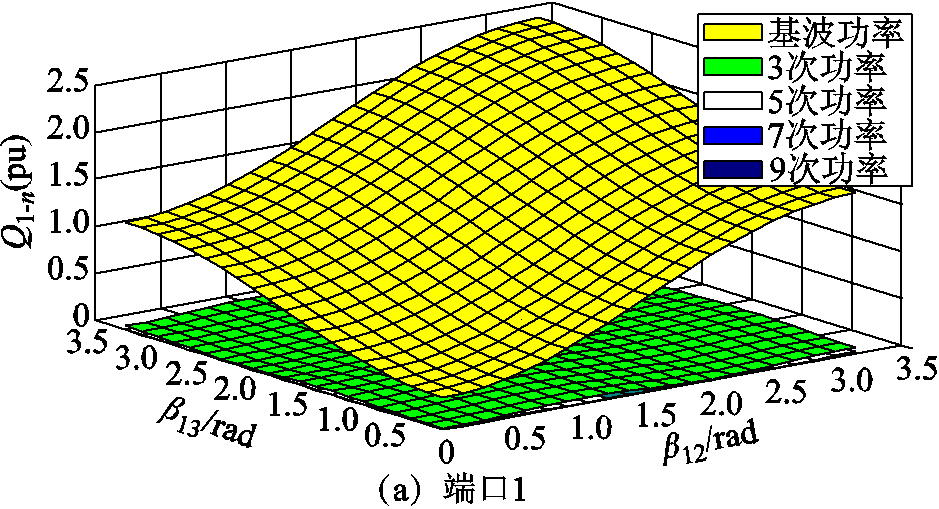
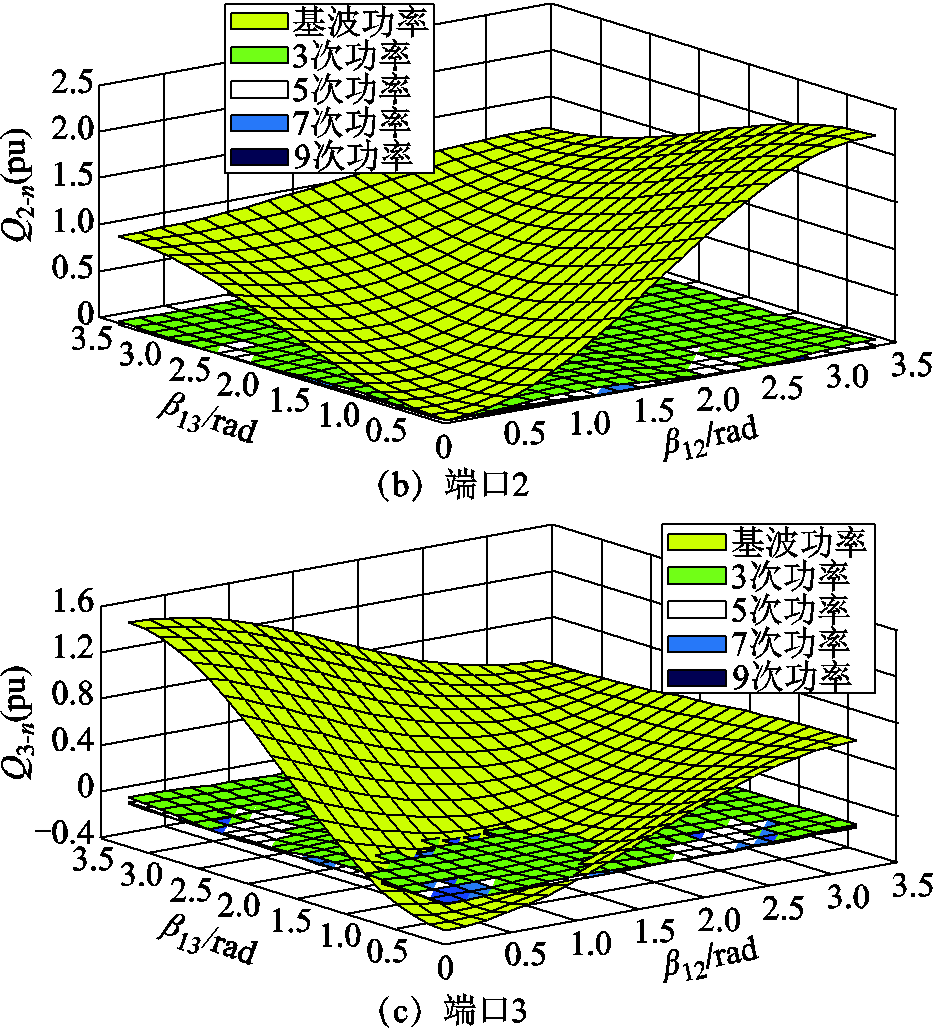
图7 TAB变换器各端口各频次无功功率
Fig.7 Reactive power of TAB converter’s each port at each frequency
通过上述分析可以发现，TAB变换器基波模型与实际模型中各电气量大小相近、变化趋势相同，误差在可接受范围内。一般场合下，可以采用基波模型对TAB变换器进行简化，在保持精度的同时，能减少计算和分析的复杂程度，TAB变换器基波简化分析模型如图8所示。
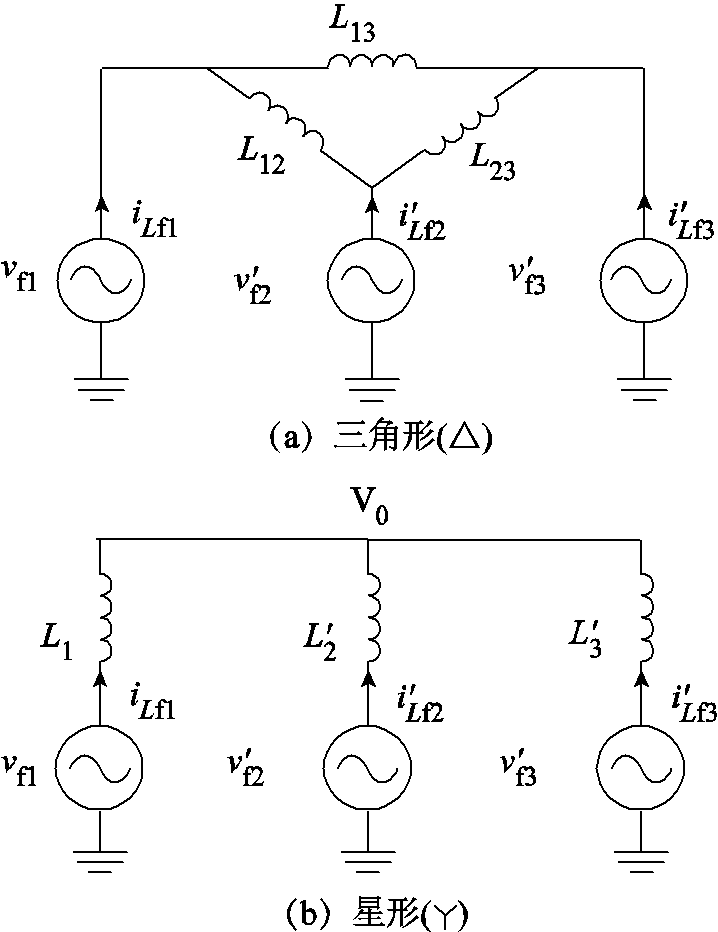
图8 基波简化分析模型
Fig.8 Fundamental simplified analysis model
TAB变换器的损耗主要分为通态损耗、开关损耗和变压器损耗，其中通态损耗与电流有效值成正相关性，开关损耗与开关频率成正相关性。本文研究的TAB变换器应用于中低压直流配电网中，通常工作在高压大功率场合，开关频率相较小功率场合较低，此时TAB变换器的总损耗中通态损耗占绝大部分，因此在此工况下应当优先优化通态损耗。根据电流有效值与通态损耗的正相关性，可以通过降低电流有效值实现对通态损耗的优化。
对图3a中的回流功率进行分析不难发现，对于流回输入侧的回流功率，输入侧需要传递大小相等的正向功率以抵消回流功率的影响，因此回流功率的存在增加了变换器的电流有效值。对TAB变换器的回流功率直接进行优化，需要考虑不同工况和模态下的多种情况，分析和计算过程复杂。考虑回流功率与无功功率的相似性，可以通过对简化模型中的无功功率进行优化，从而实现对电流有效值的优化。
从图5和图8中可以看到，TAB变换器各端口通过控制电感电流实现对端口功率的控制。由于电感的存在，各端口基波电压和基波电流之间存在较大相位差。因此，各端口在传输有功功率的同时，也产生了较大无功功率。无功功率在变换器内部流动，并不消耗有功，但无功功率的存在使得各端口电流有效值增大，从而增加了变换器的损耗。
由于TAB变换器端口数量增加，各端口电流、功率等电气量不再保持一定的线性关系，因此单独对一个端口的无功功率进行优化可能会导致其他端口的无功功率增加，对于整个变换器而言，总的优化效果并没有得到提升。因此，本文将图8中各端口的基波无功功率相加，对基波无功功率之和进行优化。取n=1，结合式（11）整理后可以得到各端口基波无功功率之和Qft见式（12）。
从式（12）中可以看到，基波无功功率由电压匹配部分Vicos(αi/2)-Vjcos(αj/2)和电压耦合部分2ViVjcos(αi/2)cos(αj/2)(1-cosβij)两部分组成。电压匹配部分与变换器的实际工况及设计参数相关，当Vicos(αi/2)-Vjcos(αj/2)=0时，TAB变换器工作在端口电压匹配模式。Vicos(αi/2)-Vjcos(αj/2)之差越大，变换器端口电压不匹配度越高。电压耦合部分随移相角的变化而变化，当TAB变换器输出功率和耦合功率增大时，电压耦合部分也增大。本文选择对电
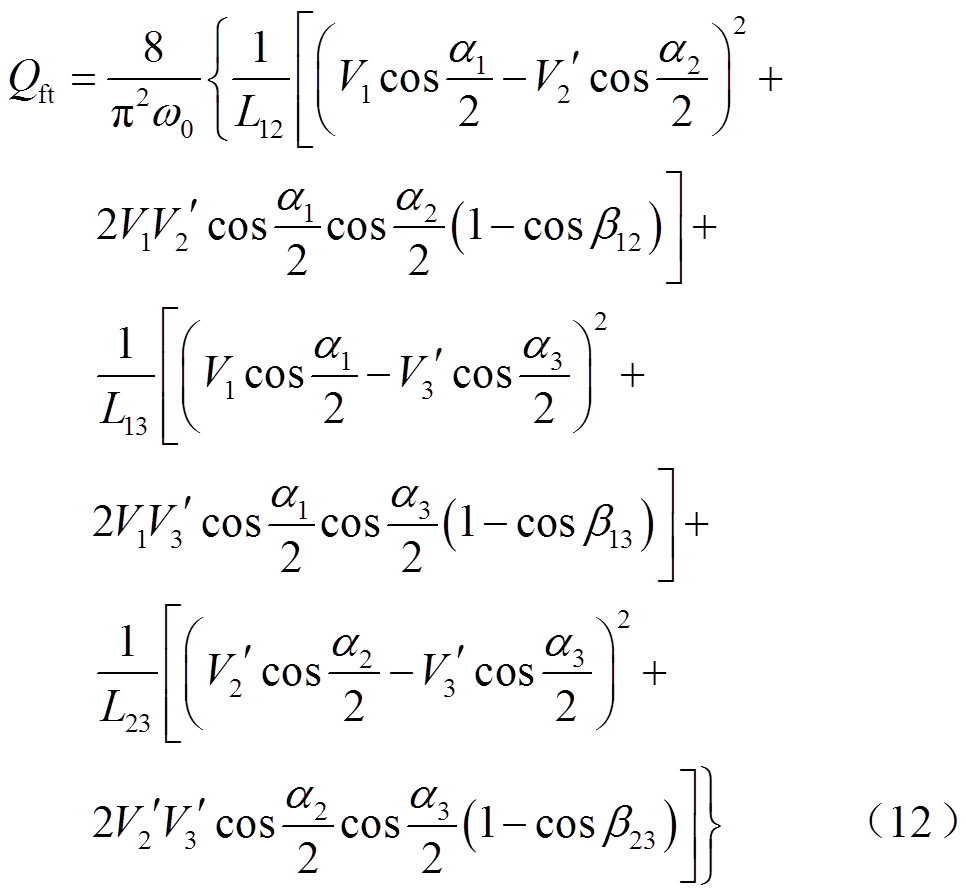
压匹配部分进行优化，通过选择合适的内移相角组合，保证在任意工况下TAB变换器各端口实现电压匹配。为保持电压匹配部分为0，各端口的内移相角应满足
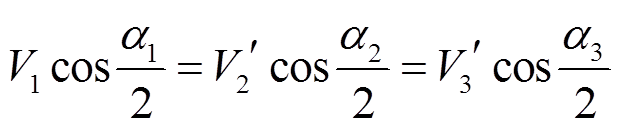（13）本文中端口1为功率输入端口，端口2、3为功率输出端口，假设电压折算至一次侧后有V1＞V2′＞V3′。对于任意两个端口，当传输功率一定时，端口电压占空比越小，端口方波电压之间的移相角越大。为了取得较小的βij，使得基波无功功率中电压耦合部分足够小，应当调节等效电压最小端口（本例中为端口3）方波电压的占空比至最大。在此令α3=0，由式（13）可以得到
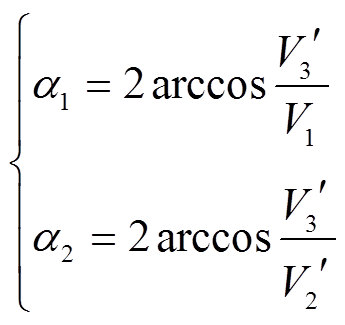（14）根据式（14），本文设计了TAB变换器的优化移相控制（Optimized Phase Shift, OPS）策略。由于TAB变换器的端口之间存在功率耦合，为提高变换器动态性能，因此需要对耦合端口进行功率解耦。针对解耦环节，本文选取较为常用的逆矩阵解耦方式，TAB变换器OPS策略框图如图9所示。
图9中，TAB变换器整体采用电压电流双闭环的控制策略。首先，检测端口2、3的输出电压，与参考值比较后，将误差电压传递至电压PI控制器，电压PI控制器的输出作为端口2、3的电流参考值，与端口2、3的电流实际值比较后，经电流PI控制器后得到解耦前的外移相角，经解耦环节消除耦合量后得到最终的外移相角控制信号。与此同时，对端口2、3的电压进行实时检测，通过优化控制环节后得到各端口的内移相角αi，与外移相角信号βij一起送入PWM信号发生器中，产生驱动信号。
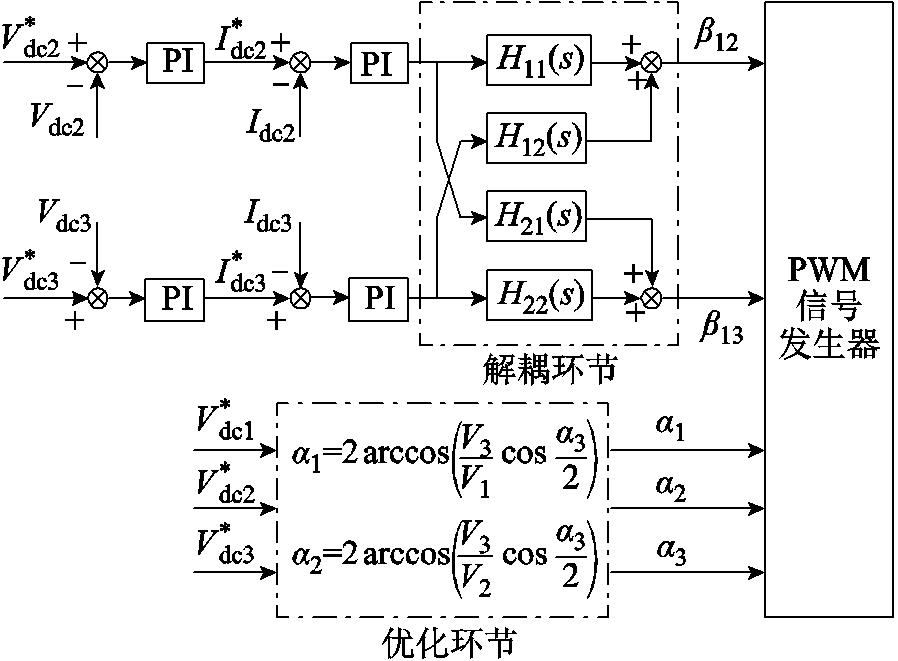
图9 TAB变换器OPS策略框图
Fig.9 OPS strategy block diagram of TAB converter
为了验证本文所提出控制策略的有效性，在Matlab/Simulink中搭建了TAB变换器的等效模型和相应的控制环节，仿真中的参数见表2。
表2 仿真参数
Tab.2 Simulation parameters
参数数值 端口2电压/V750 端口3电压/V400 开关频率/Hz5 000 变压器电压比4.8:3:1.6 端口1电感/mH0.4 端口2电感/mH0.15 端口3电感/mH0.12
图10和图11中给出了TAB变换器在端口1输入电压分别为1 500V和2 000V时，采用SPS控制策略和OPS控制策略下端口1方波电压VH1和电感电流iL1的波形，端口2、3电感电流波形如附录中附图1和附图2所示。在图10和图11中，以端口1在最大输入功率P1max时的电感电流有效值和端口1输入电压作为电压电流的基准值，对方波电压和电感电流进行了标幺化。
从图10和图11中可以看到，采用OPS控制策略下端口1电感电流的峰值均小于SPS控制下各端口电感电流峰值。图10a和图11a中，点画线框中电压和电流所围成的面积为SPS控制策略下端口1产生的回流功率。从图10b、图11b中可以看到，采用OPS控制策略时，端口1没有回流功率产生。
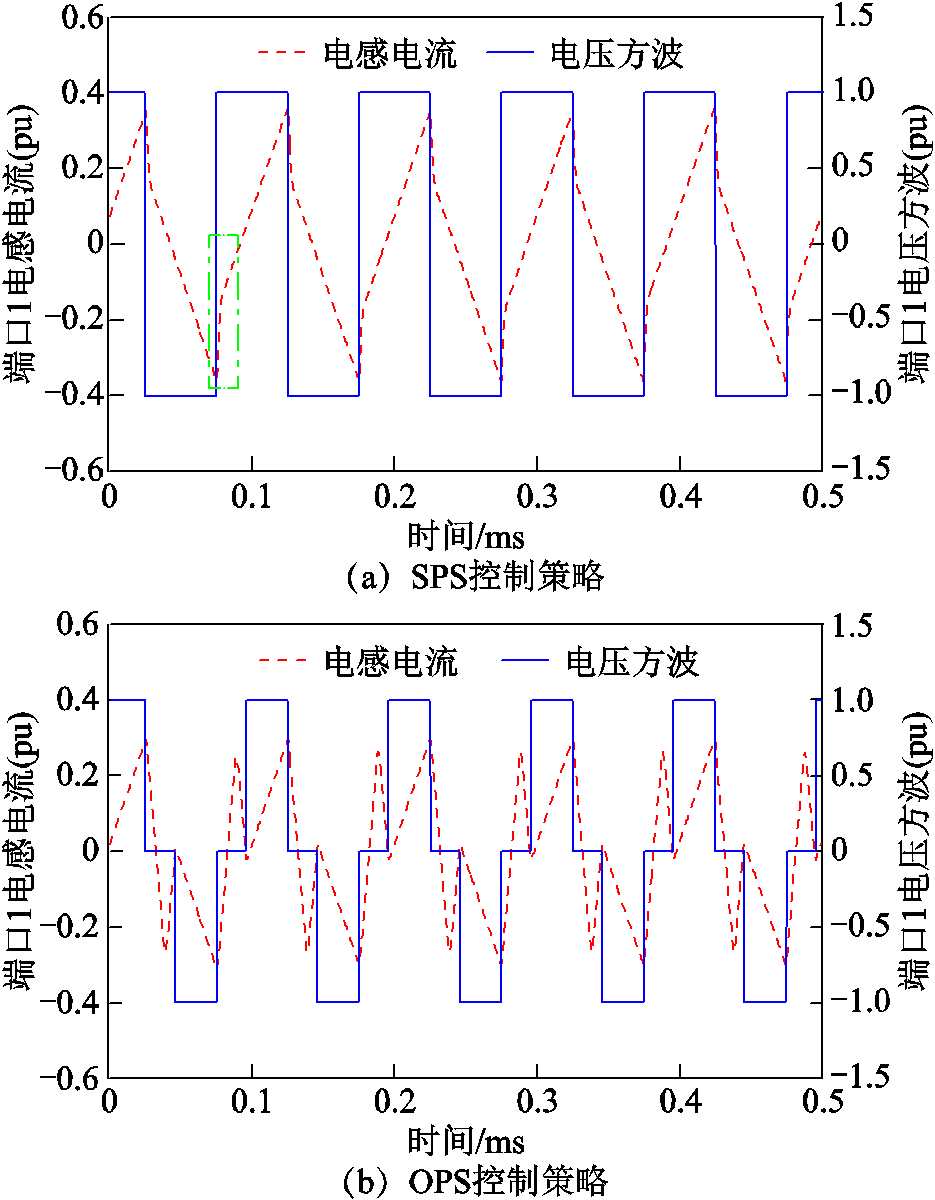
图10 V1=1 500V, P1=0.15(pu)时端口1方波电压和电感电流
Fig.10 Square wave voltage and inductor current of Port 1 when V1 = 1 500V, P1 = 0.15(pu)
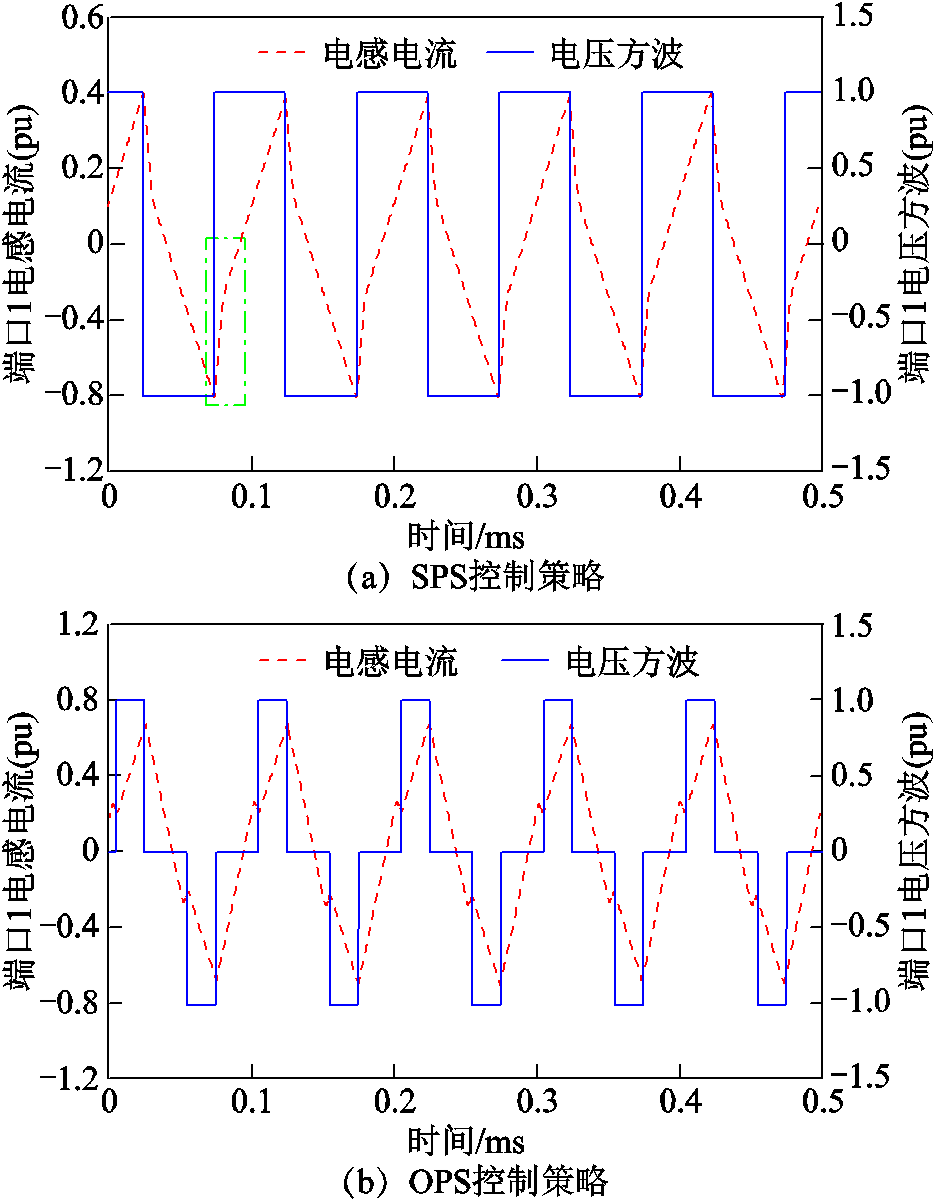
图11 V1=2 000V, P1=0.4(pu)时端口1方波电压和电感电流
Fig.11 Square wave voltage and inductor current of Port 1 when V1 = 2 000V, P1 = 0.4(pu)
电流有效值引起的损耗与电流有效值的二次方成正比。为验证对变换器整体优化的效果，本文将各端口电流有效值二次方相加，并选取端口1在最大功率输出时的端口电流有效值二次方为电流基准值，对各端口电流有效值的二次方和进行标幺化。在图10工况下，采用OPS控制策略下各端口电流有效值（标幺值）二次方和为0.094，采用SPS控制策略下各端口电流有效值（标幺值）为0.109；在图11所示工况下，采用OPS控制策略下各端口电流有效值（标幺值）二次方和为0.711，采用SPS控制策略下各端口电流有效值二次方和为0.830。
在图12和图13中，以端口1最大输出功率P1max为功率基准值，对各端口的基波无功功率进行了标幺化。图12和图13给出了端口1输入电压分别为1 500V和2 000V时，采用SPS控制策略和OPS控制策略下各端口基波无功功率之和、端口电流有效值二次方和随变换器输入功率变化的示意图。
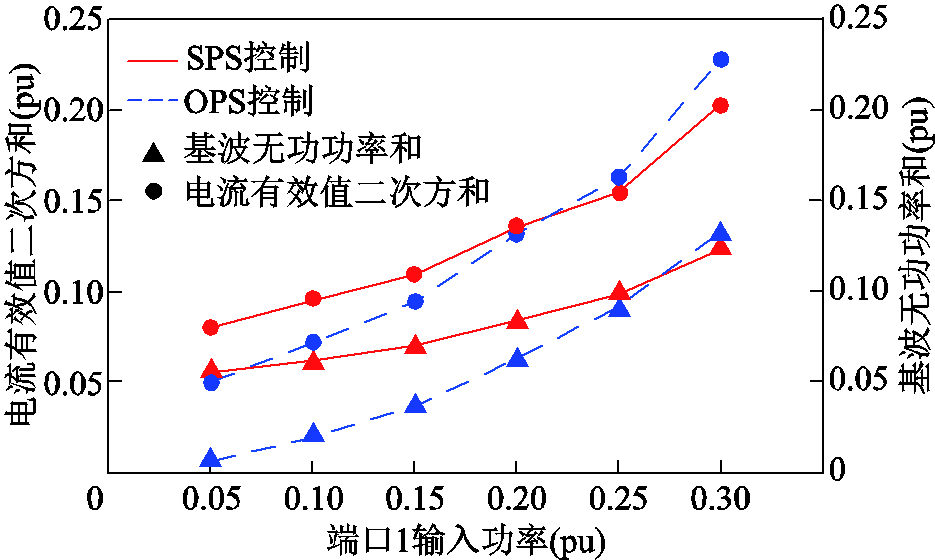
图12 V1=1 500V时TAB变换器的电流有效值二次方和与基波无功功率
Fig.12 Sum of current square and fundamental reactive power of TAB converter when V1=1 500V
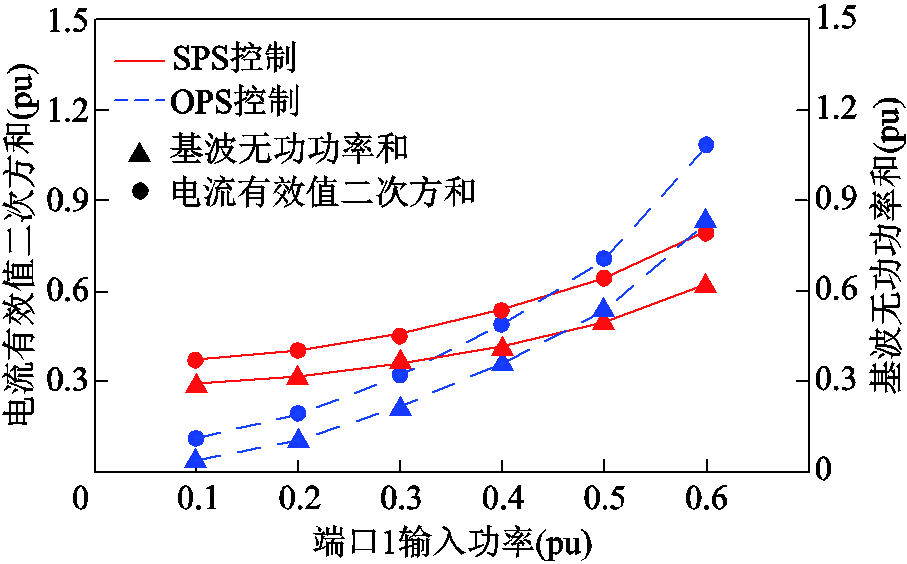
图13 V1=2 000V时TAB变换器的电流有效值二次方和与基波无功功率
Fig.13 Sum of current square and fundamental reactive power of TAB converter when V1=2 000V
从图12和图13中可以看到，基波无功功率之和与电流有效值二次方和保持相同的变化趋势，证明了基波无功功率之和与电流有效值的正相关性。在中低功率段，采用OPS控制策略相比于SPS控制策略有较小的端口电流有效值二次方和。在高功率段，随着外移相角βij增大，电压耦合部分在基波无功功率之和中占据了主要部分，由于SPS控制策略具有较小的外移相角βij，从而具有较小的电压耦合部分，因此在高功率段SPS控制策略具有较小的端口电流有效值二次方和。对比图12和图13可以发现，端口电压不匹配度越大，在基波无功功率之和中，电压匹配部分所占比例也越大，本文提出的控制策略的优化范围也越大。
为验证仿真结果的正确性，在实验室搭建了一台5kW的TAB变换器样机，表3给出了样机的部分参数。
表3 TAB变换器样机参数
Tab.3 TAB converter prototype parameters
参数数值 端口2电压/V100 端口3电压/V60 开关频率/Hz5 000 变压器电压比26:15:9 端口1电感/μH80 端口2电感/mH40 端口3电感/mH30
图14～图17中给出了TAB变换器在端口1输入电压分别为220V和290V时，采用SPS控制策略和OPS控制策略下端口1方波电压VH1和电感电流iL1的波形，端口2、3方波电压和电感电流波形如附图3～附图6所示。
从图14～图17中可以看到，OPS控制策略下，端口1的电感电流峰值均小于SPS控制策略。在SPS控制策略下，端口1中存在较大回流功率，而在OPS控制策略下，端口1中不存在回流功率。
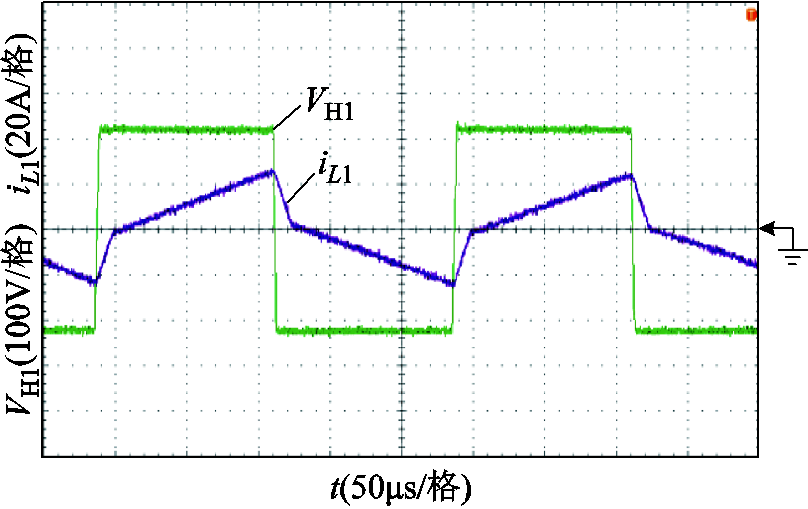
图14 V1=220V、P1=0.15(pu)时SPS控制策略下端口1方波电压和电感电流
Fig.14 Square wave voltage and inductor current of Port 1 under SPS control strategy when V1=220V, P1=0.15(pu)
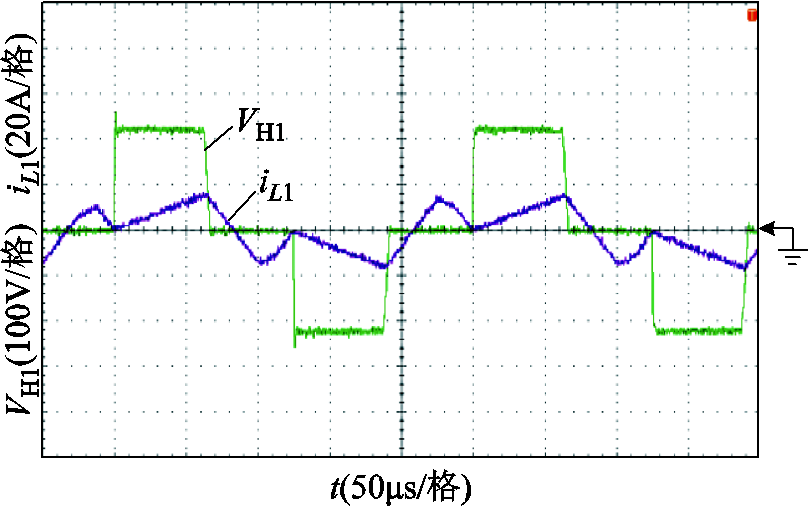
图15 V1=220V、P1=0.15(pu)时OPS控制策略下端口1方波电压和电感电流
Fig.15 Square wave voltage and inductor current of Port 1 under OPS control strategy when V1 =220V, P1=0.15(pu)
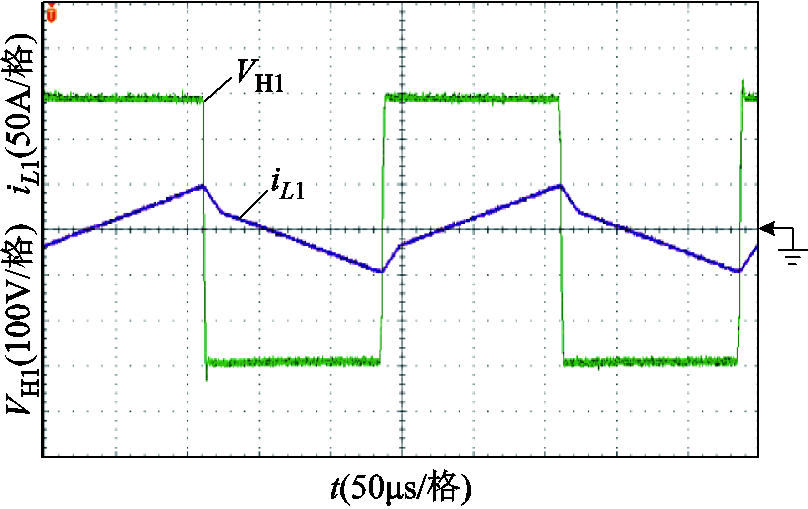
图16 V1=290V、P1=0.3(pu)时SPS控制策略下端口1方波电压和电感电流
Fig.16 Square wave voltage and inductor current of Port 1 under SPS control strategy when V1 = 290V, P1 = 0.3(pu)
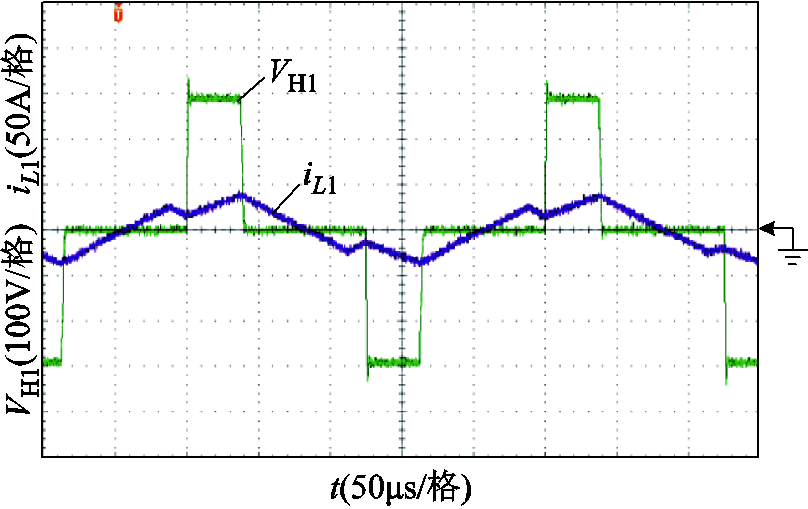
图17 V1=290V、P1=0.3(pu)时OPS控制策略下端口1方波电压和电感电流
Fig.17 Square wave voltage and inductor current of Port 1 under OPS control strategy when V1 = 290V, P1 = 0.3(pu)
与仿真中的分析类似，将各端口的电流有效值二次方和标幺化后相加。当V1=220V、P1=0.15(pu)时，SPS控制策略下各端口电流有效值二次方和为0.136，OPS控制策略下各端口电流有效值二次方和为0.127；当V1=290V、P1=0.3(pu)时，SPS控制策略下各端口电流有效值二次方和为0.512，OPS控制策略下各端口电流有效值二次方和为0.385。
图18和图19给出了输入电压V1分别为220V和290V时，TAB变换器各端口电流有效值二次方和随变换器输入功率变化的示意图。
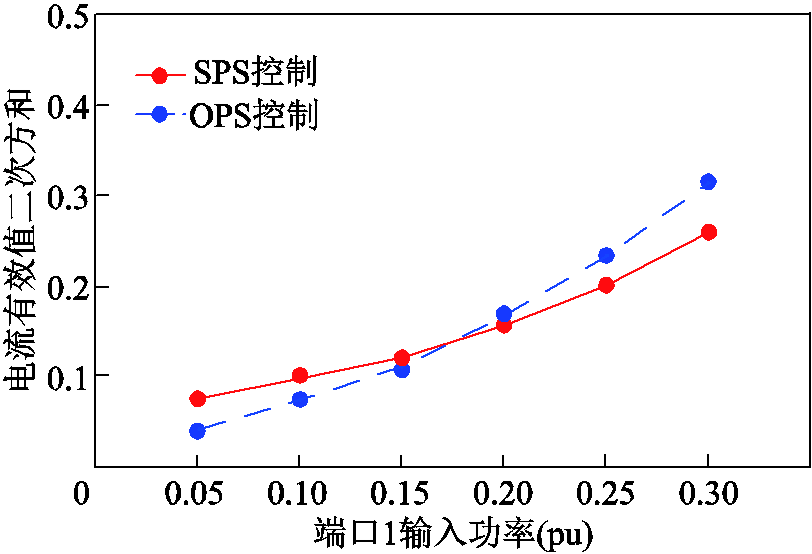
图18 V1=220V时TAB变换器的电流有效值二次方和
Fig.18 Sum of current square of TAB converter when V1=220V
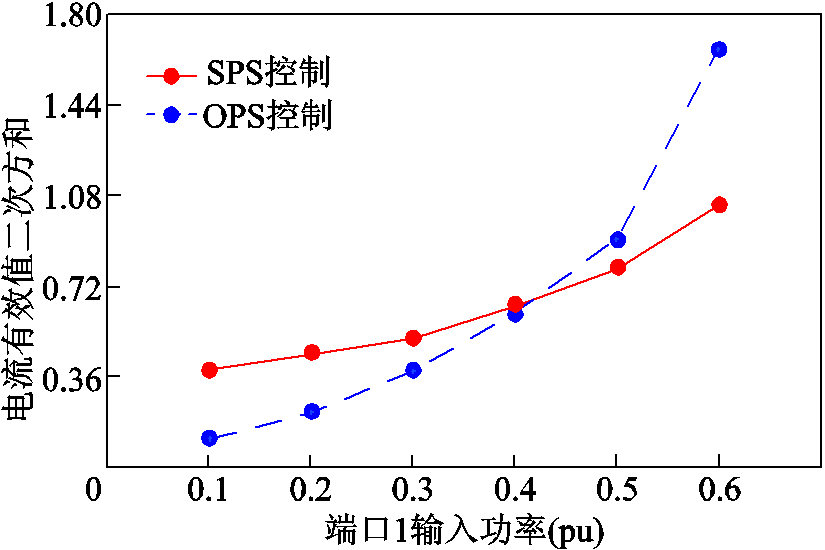
图19 V1=290V时TAB变换器的电流有效值二次方和
Fig.19 Sum of current square of TAB converter when V1=290V
从图18和图19中可以看到，在中低功率段，OPS控制策略相较于SPS控制策略有较小的端口电流有效值二次方和。在高功率段，电压耦合部分在基波无功功率之和中占据主要部分，由于SPS控制策略具有较小的外移相角βij，从而具有较小的电压耦合部分，因此在高功率段SPS控制策略具有较小的端口电流有效值二次方和。对比图18和图19可以看到，当端口电压不匹配度越大时，在基波无功功率之和中，电压匹配部分占比也越大，本文提出的控制策略的优化范围也越大。
针对MPS控制策略下TAB变换器分析复杂、移相角选取困难等问题，本文开展了基于多重移相的TAB变换器简化模型和优化控制策略的研究。建立了TAB变换器的傅里叶级数等效模型，推导了MPS控制策略下TAB变换器的统一表达形式，结合基波模型与实际模型之间的误差分析，提出了简化分析模型。在此基础上，根据简化模型中无功功率与电路模态分析中回流功率的对应关系，提出了基于无功功率的TAB变换器优化控制策略。仿真和实验结果表明，所提出的优化控制策略能在中低功率段减小TAB变换器的基波无功功率之和，能减小变换器各端口电流有效值的二次方和。当TAB变换器输入输出电压不匹配程度越大时，本文所提出优化控制策略的优化空间也越大。
式（7）中，系数X1、X2、X3、Y1、Y2、Y3的表达式如式（A1）所示。
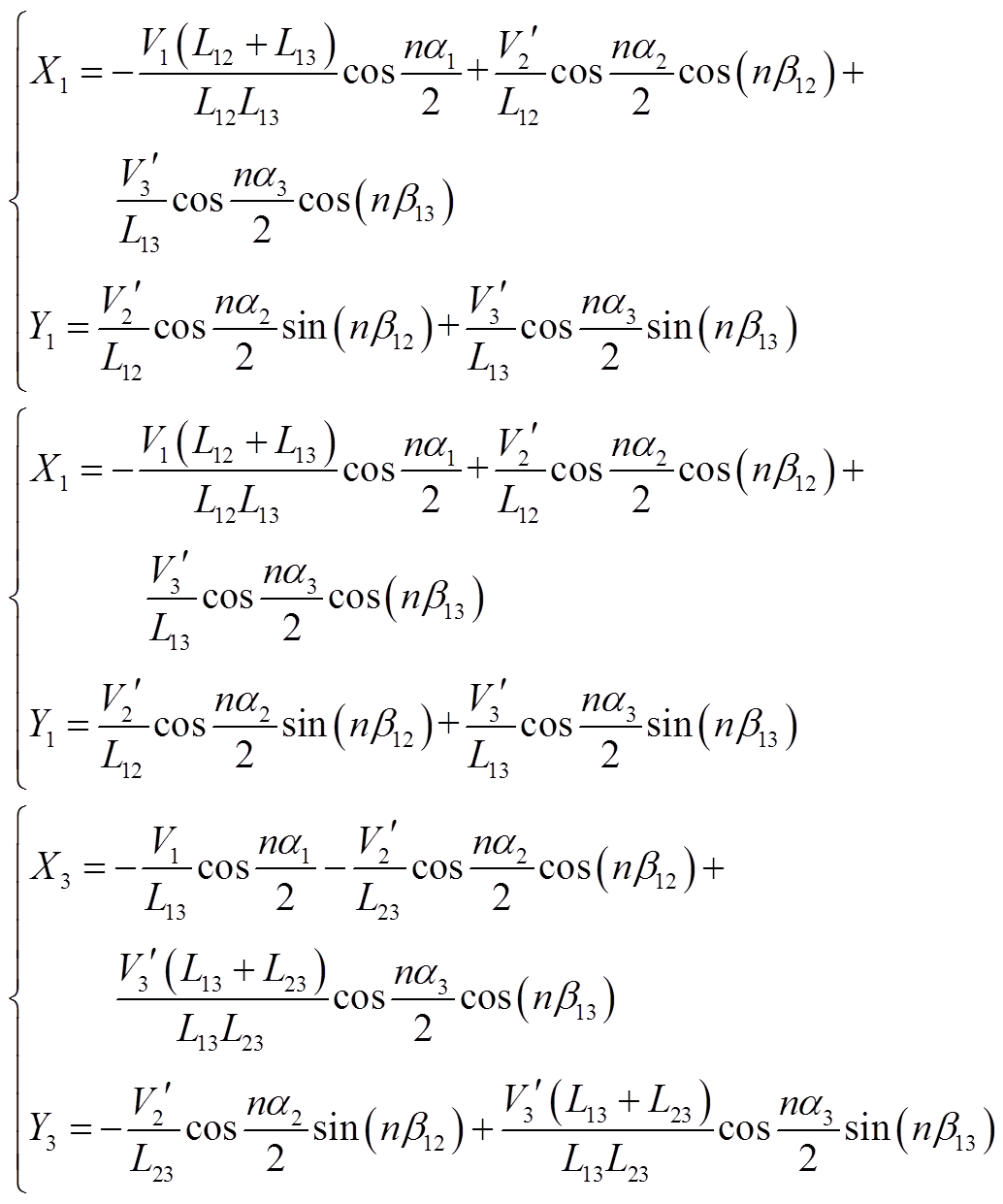（A1）式（10）中，端口ij之间的等效电感Lij表达式为
（A2）端口1输入电压为1 500 V和2 000 V时，采用SPS控制策略和OPS控制策略下端口2、3电感电流仿真波形如附图1、附图2所示。
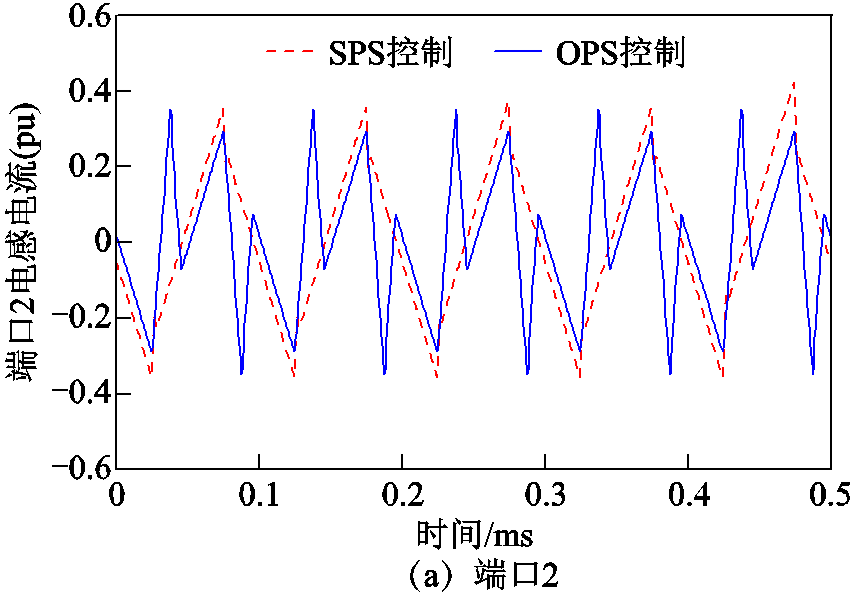
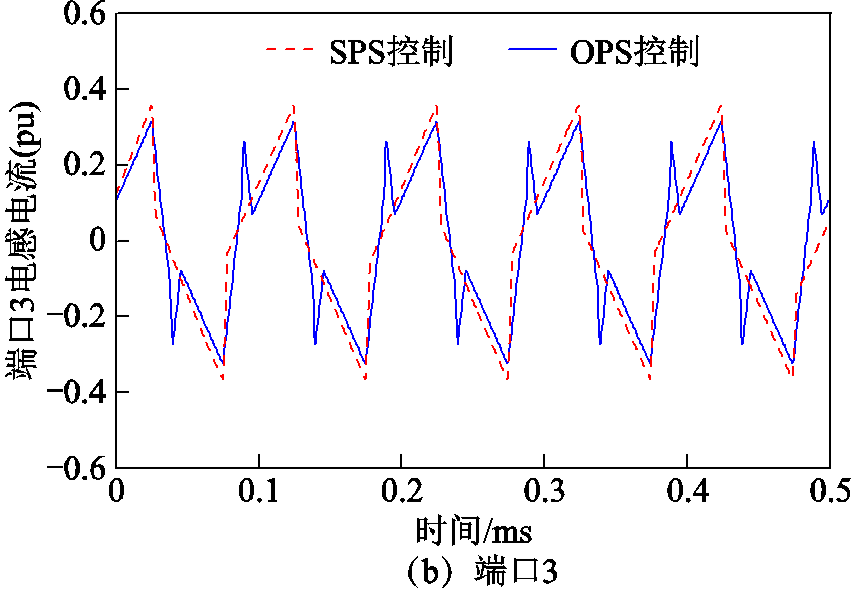
附图1 V1=1 500V、P1=0.15(pu)时各端口电感电流
App.Fig.1 Inductance current of each port when V1 = 1 500V, P1 = 0.15(pu)
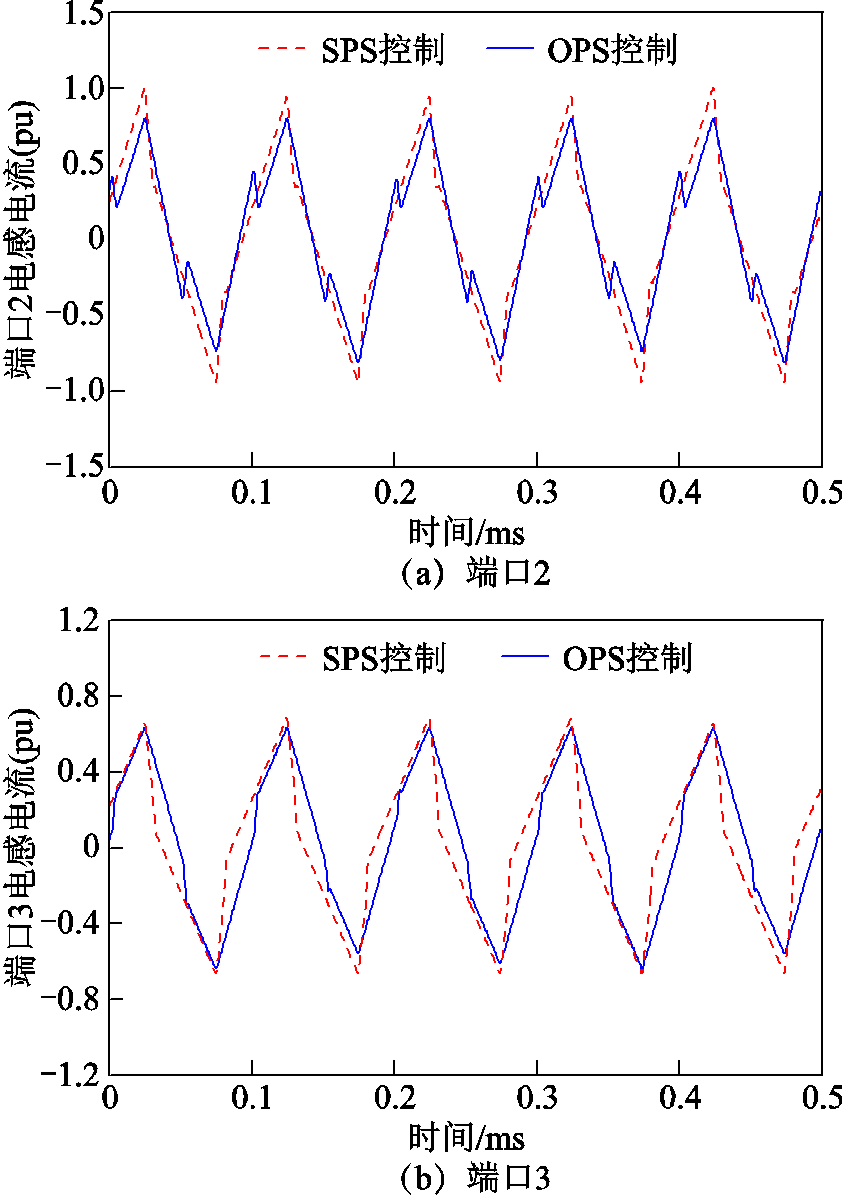
附图2 V1=2 000V、P1=0.4(pu)时各端口电感电流
App.Fig.2 Inductance current of each port when V1 = 2 000 V, P1 = 0.4(pu)
端口1输入电压为220V和290V时，采用SPS控制策略和OPS控制策略下端口2、3方波电压和电感电流波形如附图3～附图6所示。
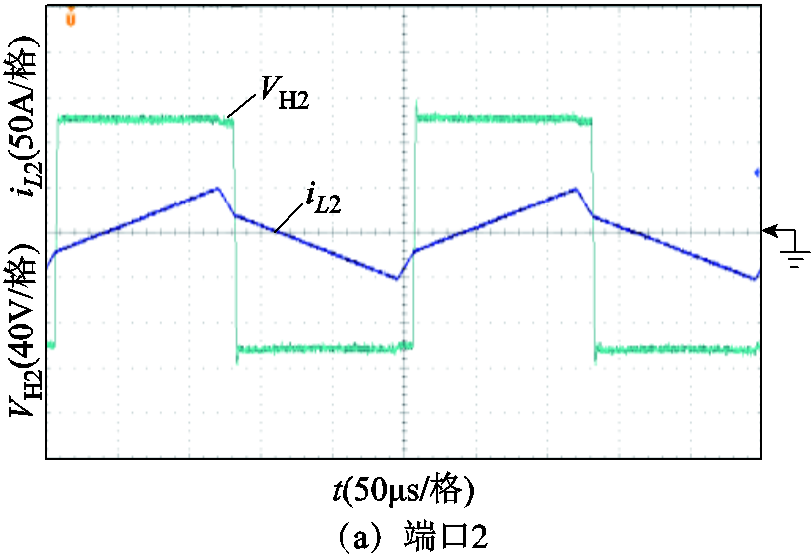
附图3 V1=220V、P1=0.15(pu)时SPS控制策略下各端口方波电压和电感电流
App.Fig.3 Square wave voltage and inductor current of TAB converter’s each port under SPS control strategy when V1 = 220V, P1 = 0.15(pu)
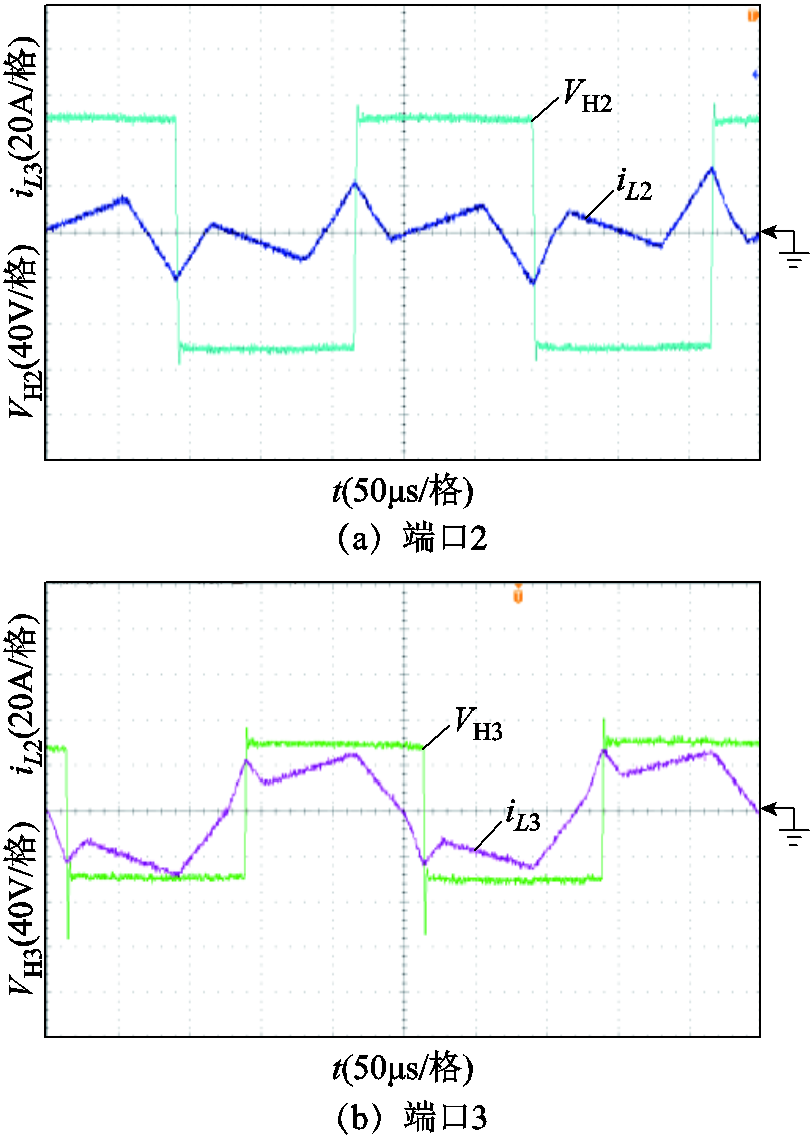
附图4 V1=220V、P1=0.15(pu)时OPS控制策略下各端口方波电压和电感电流
App.Fig.4 Square wave voltage and inductor current of TAB converter’s each port under OPS control strategy when V1 = 220V, P1 = 0.15(pu)
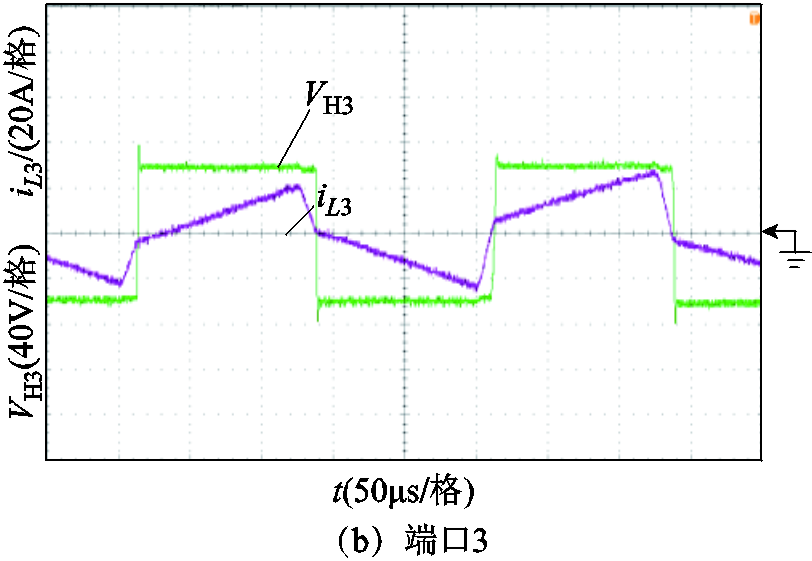
附图5 V1=290V、P1=0.3(pu)时SPS控制策略下各端口方波电压和电感电流
App.Fig.5 Square wave voltage and inductor current of TAB converter’s each port under SPS control strategy when V1 = 290V, P1 = 0.3(pu)
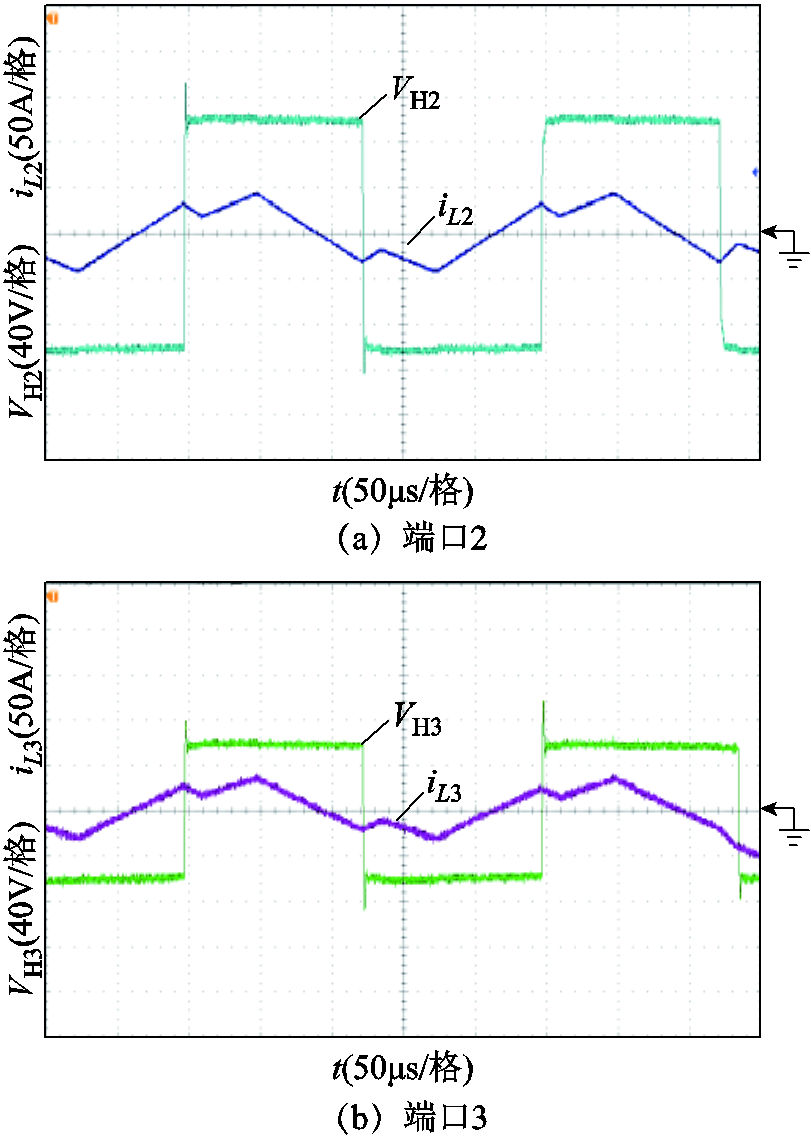
附图6 V1=290V、P1=0.3(pu)时OPS控制策略下各端口方波电压和电感电流
App.Fig.6 Square wave voltage and inductor current of TAB converter’s each port under OPS control strategy when V1=290V, P1=0.3(pu)
参考文献
[1]宋强, 赵彪, 刘文华, 等. 智能直流配电网研究综述[J]. 中国电机工程学报, 2013, 33(25): 9-19.Song Qiang, Zhao Biao, Liu Wenhua, et al. An overview of research on smart DC distribution power network[J]. Proceedings of the CSEE, 2013, 33(25): 9-19.
[2]赵彪, 赵宇明, 王一振, 等. 基于柔性中压直流配电的能源互联网系统[J]. 中国电机工程学报, 2015, 35(19): 4843-4851. Zhao Biao, Zhao Yuming, Wang Yizhen, et al. Energy internet based on flexible medium-voltage DC distribution[J]. Proceedings of the CSEE, 2015, 35(19): 4843-4851.
[3]李周, 李亚洲, 陆于平, 等. 多端柔性直流电网主动功率平衡协调控制策略[J]. 电力系统自动化, 2019, 43(17): 117-124. Li Zhou, Li Yazhou, Lu Yuping, et al. Active power balance oriented coordinating control strategy for VSC-MTDC system[J]. Automation of Electric Power Systems, 2019, 43(17): 117-124.
[4]Zhang Xing, Wang Mingda, Zhao Tao, et al. Topological comparison and analysis of medium-voltage and high-power direct-linked PV inverter[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 327-334.
[5]Huang A Q, Crow M L, Heydt G T, et al. The future renewable electric energy delivery and management (FREEDM) system: the energy internet[J]. Proceedings of the IEEE, 2011, 99(1): 133-148.
[6]马骏超, 江全元, 余鹏, 等. 直流配电网能量优化控制技术综述[J]. 电力系统自动化, 2013, 37(24): 89-96. Ma Junchao, Jiang Quanyuan, Yu Peng, et al. Survey on energe optimized control technology in DC distribution network[J]. Automation of Electric Power Systems, 2013, 37(24): 89-96.
[7]吴济东, 汪可友, 黄鑫, 等. 孤立直流微电网多DC-DC变换器分布式协调控制策略[J]. 电力系统保护与控制, 2020, 48(11): 76-83. Wu Jidong, Wang Keyou, Huang Xin, et al. Distributed coordinated control scheme of parallel DC-DC converters in isolated DC microgrids[J]. Power System Protection and Control, 2020, 48(11): 76-83.
[8]Wu Hongfei, Lei Zhu, Fan Yang. Three-port-converter-based single-phase bidirectional AC–DC converter with reduced power processing stages and improved overall efficiency[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10021-10026.
[9]Wang Zhan, Li Hui. An integrated three-port bidirectional DC–DC converter for PV application on a DC distribution system[J]. IEEE Transactions on Power Electronics, 2012, 28(10): 4612-4624.
[10]Fan Haifeng, Li Hui. High-frequency transformer isolated bidirectional DC–DC converter modules with high efficiency over wide load range for 20 kVA solid-state transformer[J]. IEEE Transactions on Power Electronics, 2011, 26(12): 3599-3608.
[11]李微, 周雪松, 马幼捷, 等. 三端口直流微网母线电压控制器及多目标控制[J]. 电工技术学报, 2019, 34(1): 92-102. Li Wei, Zhou Xuesong, Ma Youjie, et al. Three-port DC microgrid bus voltage controller and multi-objective control[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 92-102.
[12]Bhattacharjee A K, Kutkut N, Batarseh, I. Review of multiport converters for solar and energy storage integration[J]. IEEE Transactions on Power Electronics, 2018, 34(2): 1431-1445.
[13]余雪萍, 涂春鸣, 肖凡, 等. 三端口隔离DC-DC变换器的暂态直流偏置机理及抑制策略[J]. 电工技术学报, 2020, 35(9): 1962-1972. Yu Xueping, Tu Chunming, Xiao Fan, et al. Transient DC bias mechanism and suppression strategy of the three-port isolated DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1962-1972.
[14]Irfan M S, Ahmed A, Park J H. Power-decoupling of a multiport isolated converter for an electrolytic-capacitorless multilevel inverter[J]. IEEE Transactions on Power Electronics, 2017, 33(8): 6656-6671.
[15]年珩, 叶余桦. 三端口隔离双向DC-DC变换器模型预测控制技术[J]. 电工技术学报, 2020, 35(16): 3478-3488. Nian Heng, Ye Yuhua. Model predictive control of three-port isolated bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3478-3488.
[16]刘飞龙, 张涵, 孙孝峰, 等. 双有源桥四绕组变压器双向DC-DC变换器[J]. 电工技术学报, 2019, 34(20): 4272-4282. Liu Feilong, Zhang Han, Sun Xiaofeng, et al. Improved dual active bridge bidirectional DC-DC converter with four-winding transformer structure[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4272-4282.
[17]曾进辉, 孙志峰, 雷敏, 等. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J].电工技术学报, 2019, 34(12): 2507-2518. Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Global current stress analysis and optimal control strategy of dual-active full bridge converter based on dual phase shift control[J]. Transactions of China Electrote-chnical Society, 2019, 34(12): 2507-2518.
[18]魏腾飞, 王晓兰, 李晓晓. 双向直流隔离变换器功率回流的分析及消除[J]. 电机与控制学报, 2019, 23(11): 100-108. Wei Tengfei, Wang Xiaolan, Li Xiaoxiao. Analysis and elimination backflow power in bidirectional DC-DC isolation converter[J]. Electric Machines and Control, 2019, 23(11): 100-108.
[19]杨超, 许海平, 张祖之, 等. PWM与移相结合控制下的混合三电平隔离型双向DC-DC最小回流功率控制研究[J]. 电工技术学报, 2019, 34(15): 3186-3197. Yang Chao, Xu Haiping, Zhang Zuzhi, et al. Minimum backflow power control of the hybrid three level isolated bi-directional DC-DC converters based on PWM-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3186-3197.
[20]李婧, 袁立强, 谷庆, 等. 一种基于损耗模型的双有源桥DC-DC变换器效率优化方法[J]. 电工技术学报, 2017, 32(14): 66-76. Li Jing, Yuan Liqiang, Gu Qing, et al. An efficiency optimization method in dual active bridge DC-DC converter based on loss model[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 66-76.
[21]Zhao Biao, Song Qiang, Liu Wenhua, et al. Universal high-frequency-link characterization and practical fundamental-optimal strategy for dual-active-bridge DC-DC converter under PWM plus phase-shift control [J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6488-6494.
[22]沙广林. 电力电子变压器中双有源桥DC-DC变换器的研究[D]. 北京: 中国矿业大学, 2016.
[23]王政, 储凯, 张兵, 等. 移相占空比控制的三端口双向直流变换器[J]. 电机与控制学报, 2015, 19(7): 81-87. Wang Zheng, Chu Kai, Zhang Bing, et al. Three-port bidirectional DC-DC converter with duty cycle and phase-shifting control[J]. Electric Machines & Control, 2015, 19(7): 81-87.
[24]赵彪, 宋强. 双主动全桥DC-DC变换器的理论和应用技术[M]. 北京: 科学出版社, 2017.
Simplified Analysis Model and Optimal Control Strategy of Triple Active Bridge Converter
Abstract Under the traditional single-phase-shift (SPS) strategy, there is a large backflow power in the triple-active-bridge (TAB) converter, the backflow power increases the RMS current and the loss of the converter. Multi-phase-shift (MPS) strategy can improve the control flexibility and reduce the backflow power, but the analysis process and the phase shift angle selection method are extremely complicated. To solve this problem, this paper proposed a simplified analysis model based on multiple phase shifts and an optimized control strategy. Firstly, this paper established the equivalent Fourier series model of TAB converter, derived the unified expression form of TAB converter under MPS control strategy, and proposed a simplified analysis model of TAB converter, which reduces the difficulty of analysis and calculation of TAB converter. On this basis, an optimized control strategy based on reactive power is proposed, which can reduce the RMS current and the loss of TAB converter. Finally, simulation and experiment verified the effectiveness of the proposed control strategy.
keywords：Triple active bridge (TAB) converter, multi-phase-shift, Fourier series model, reactive power, current root-mean-square, optimal control strategy
中图分类号：TM46
DOI：10.19595/j.cnki.1000-6753.tces.191800
国家重点研发计划（2018YFB0904100）和国家电网公司科技项目（SGHB0000KXJS1800685）资助。
收稿日期 2019-12-23
改稿日期 2020-12-24
刘 贝 男，1991年生，博士研究生，研究方向为多端口直流变压器。E-mail：beiliu@hnu.edu.cn
肖 凡 男，1988年生，博士，研究方向为电力电子技术在电力系统中的应用。E-mail：woliaokk123@126.com（通信作者）
（编辑 郭丽军）