
图1 所选取的电力电子变换单元物理模型
Fig.1 The selected physical model of the power electronics transformation unit
摘要 随着半导体器件功率等级提高、开关速度加快,开关过程引起的电磁干扰(EMI)问题也日渐突出。与传统的EMI问题不同,电力电子系统的EMI问题由功率半导体器件的开关瞬态过程引起,其本质上是一个能量瞬变问题而非信号传输问题,变换形式为脉冲型而非连续型波形,传输载体和路径本质上是空间电磁场而非仅是电路电压电流。这三个特点决定了传统上从信号传播、正弦周期量变换和集总参数等效电路的角度研究EMI的方法难以揭示电力电子系统EMI问题的本质特点和规律。为此,该文从能量脉冲和电磁场瞬变过程的角度,对电磁场和载流子场耦合作用下的电力电子系统中的电磁脉冲进行建模分析。建立了面向电力电子系统EMI机理研究的三维电磁场数值模型,解算了微纳秒级开关瞬态过程中功率器件内部和空间中电磁场的分布及变化情况,并从数值计算和原理分析角度验证了所建三维电磁场数值模型的正确性。该文为电力电子系统EMI机理研究提供了有效的数值分析基础。
关键词:电磁干扰 开关过程 电磁脉冲 三维建模
电力电子技术的高速发展对功率半导体器件的功率等级、开关频率和响应速度的要求越来越高。在这样的要求下,以碳化硅(SiC)和氮化镓(GaN)为代表的宽禁带功率半导体器件由于具有更好的开关特性,成为研究和应用中的热点[1-4]。但是,宽禁带半导体器件更快的开关速度,会引起空间电磁场更加剧烈的变化,由此产生的负面影响之一就是更加严重的电磁干扰(Electromagnetic Interference, EMI)[2-3,5]。
EMI问题有三个要素:干扰源、传播路径和敏感元部件。本文聚焦于电力电子开关过程中的EMI问题,此时干扰源主要为电力电子开关过程中的瞬变电磁脉冲;传播路径主要为沿导线传导、近场耦合和远场辐射三种,并依据传播途径的不同将EMI分为传导、近场耦合、远场辐射三种[6]。敏感元部件主要为电路中的电容、电感,控制信号回路,以及附近其他弱电装置等。由于电力电子装置中存在较大的di/dt、dv/dt,驱动控制回路与电磁能量回路距离近[7]等因素,导致电力电子装置中EMI问题突出,经常带来异常脉冲[8-10]、装置损坏[11-12]等严重的后果。
在研究EMI方面研究人员已经做了很多工作。在传导和近场耦合EMI方面,主要集中于EMI的建模和抑制方法研究[7,13],多利用高频下的等效电路模型进行建模[14-15],使用傅里叶分析的方法在频域上进行研究[16-18]。所使用的EMI抑制方法,也多为立足于电路分析的无源滤波器[19-20]、有源滤波器[21]、为噪声电流提供通路的电路拓扑设计[22]及副边谐振技术[23]等。
在辐射EMI方面的研究还较少,目前工作多集中于研究辐射EMI的建模、预测方法,建模时多利用带杂散参数的电路模型、天线模型等。如文献[24]使用基于传输线的电路模型对印制电路板(Printed Circuit Board, PCB)上的电流进行计算,并基于此预测近场磁场的大小及分布情况。文献[25]通过测量仪器,扫描得到PCB附近磁场的分布情况,再根据环形电流偶极子理论,将发射源等效建模为特定大小的环形电流,从而对辐射磁场的强度进行预测。文献[26-27]通过对近场磁场的扫描测量,利用等效源建构的思想对辐射EMI进行建模,在文献[26]中使用该磁场得到PCB上的电流分布,再利用电流计算远场辐射的大小;文献[27]利用近场磁场得到惠更斯表面的电场分布,在此基础上对远场的电磁干扰进行预测。文献[28-29]对电缆线上的共模(Common Mode, CM)电流导致的辐射EMI进行研究,其中,文献[28]利用PCB与电缆之间的寄生电容模型解释共模电流的形成,并利用电压驱动的辐射模型进行建模;文献[29]则提出了一种更精确的确定等效天线模型参数的方法。
总的来说,现有的研究侧重于EMI的建模、预测和抑制,使用的研究方法多为等效电路模型、等效偶极子辐射模型及频域分析等。
与传统电气设备的EMI问题不同,电力电子系统的EMI问题根源是功率半导体器件的开关瞬态过程,其本质上是一个电磁能量瞬变问题,变换形式为脉冲型,传输载体和路径对近场耦合和远场辐射EMI来说是空间电磁场,对传导EMI来说可以认为是沿电路导体的电压电流,但其物理本质也是电磁。这三个特点决定了传统上从信号传播、正弦周期量变换和集总参数等效电路角度研究EMI的方法难以揭示电力电子系统EMI问题的本质特点和规律。
因此,本文从能量脉冲和电磁场瞬变过程的角度,对电磁场和载流子场耦合作用下的电力电子系统电磁脉冲进行建模分析,为开关瞬态过程EMI机理的研究建立三维电磁场数值模型。
该建模过程有三个难点:①由开关瞬态情形的特殊性决定了模型方程的复杂性;②模型的强非线性;③瞬态变化的快速性。本文针对这三个难点问题,建立了有效的三维电磁场数值模型,解算了微纳秒级开关瞬态过程中功率器件内部和空间中电磁场的分布和变化情况,并从数值计算和原理分析两个角度验证了所建模型的正确性,为电力电子系统EMI机理研究提供了有效的数值分析基础。
首先选取合适的建模对象。电力电子系统是以成对互锁开关为基本单元工作的,选择如图1所示的基本变换电路,其中包含一个以SiC MOSFET和二极管组成的基本变换单元、无源器件和负载等必要的组成部分。为了降低模型复杂度、便于对关键现象进行观察和分析,没有在电路中添加其他复杂结构。

图1 所选取的电力电子变换单元物理模型
Fig.1 The selected physical model of the power electronics transformation unit
建模对象的实物图如图1a所示,对应的电路图和PCB示意图分别如图1b和图1c所示。基于前面所述原则,在从实物抽象至电路和PCB模型时,省略了一些非必要元件。同时,由于需研究的现象来源于功率回路,故在数值模型中控制回路的作用用简单的电路信号表示。
从图1b的电路图中可看到,在MOSFET闭合时,电源通过MOSFET向负载供电,二极管处于关断状态。MOSFET断开时,由于负载的感性效应,电流无法突变,产生反向电动势,使得二极管导通,负载通过二极管回路续流。PCB上焊盘与电路元件的对应关系已在图1c中标出。
为完整体现电力电子开关过程的电磁脉冲物理本质,本文建立了电磁场与载流子场的耦合模型,并使用场路混合的解算方法进行精细求解。该模型分为四个部分:空间电磁场、导体中的电磁场、半导体中的载流子场及连接模块电路的电流、电压。模型各部分划分及建模方法见表1。下面分别介绍每个部分的建模方式及整个模型的空间范围。
表1 模型各部分划分及建模方式
Tab.1 The division and modeling method of each part

需建模部分建模方式 空间电磁场麦克斯韦方程组 导体中的电磁场麦克斯韦方程组(面电流) 半导体中的载流子场载流子输运方程组 连接模块电路的电流电压电路模型
对空间电磁场部分,由于电力电子系统的高电压、大电流及它们快速的变化,需同时考虑静生因素和感生因素,因此使用完整的电磁场方程、即麦克斯韦方程组进行建模。
导体中的电磁场也应使用麦克斯韦方程组建模,但在导体中起主要作用的是电流而非电位移,故需将高斯定律方程换成电流连续性方程。需要说明的是,这里由于导体(铜片)本身厚度极薄,在厚度方向上的感生电场会导致其内部电子移动,很快就会使电子聚集在两侧,并形成一个反向的库仑电场,与原来的感生电场相抵消。由于电子运动速度很快,可认为该方向上没有电流,故可将铜片中电流的部分建模设成没有厚度的面电流。
半导体中的载流子场需使用载流子输运方程组进行建模,以体现其中载流子的运动特性。
其余的电路连接模块用电路模型表示,起到提供合适电路关系的作用即可。数值模型各部分间耦合关系如图2所示。
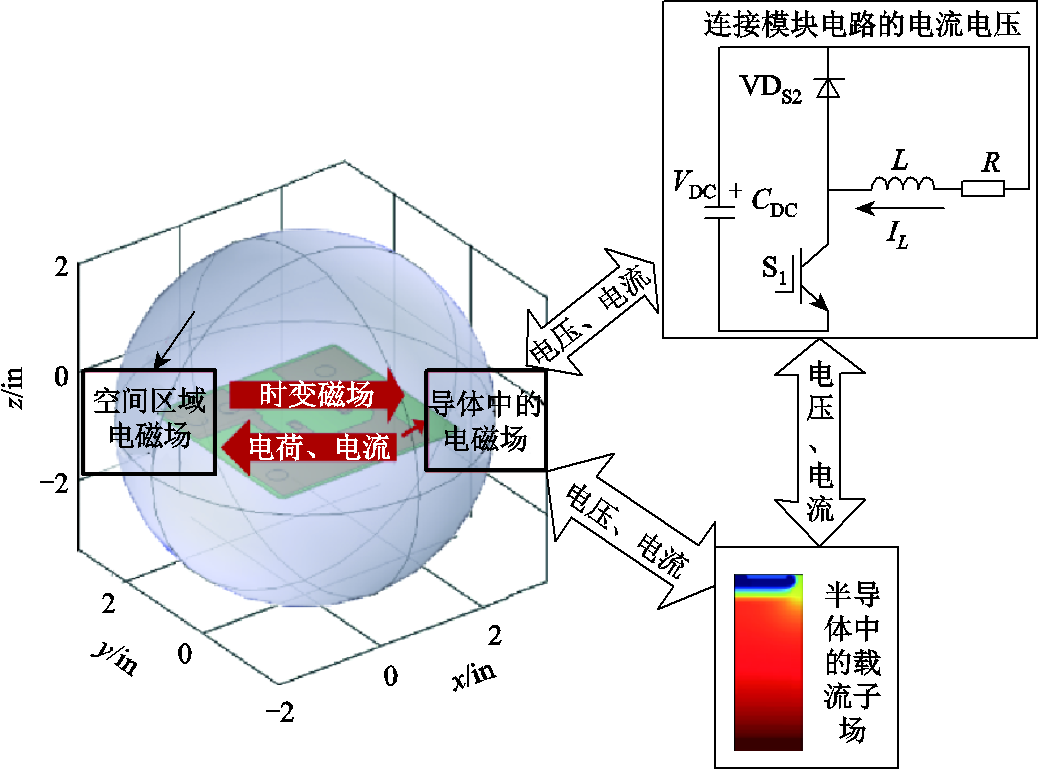
图2 数值模型耦合关系示意图
Fig.2 Schematic diagram of numerical model coupling relationship
模型的空间范围如图3所示。将略长于板子对角线的一个长度记为一倍直径,以五倍直径的球体作为仿真的区域,PCB的中心位于球心处,此时既可观察到近场的电磁耦合现象,又可观察到远场的电磁辐射现象。图示中最外侧区域为无限元域,起到模拟无限远处边界条件的作用。
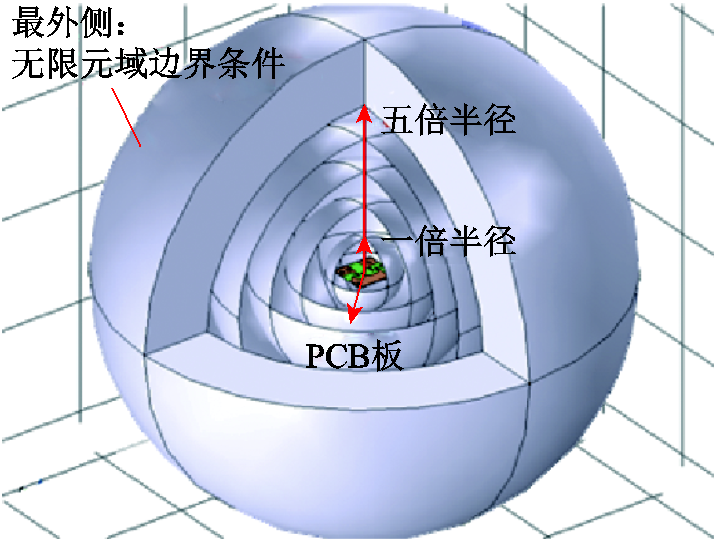
图3 模型作用空间范围示意图
Fig.3 Schematic diagram of the spatial scope of the model
在每个部分建模时,都需要明确场域方程、交界面条件和边界条件。对空间区域电磁场来说,场域方程为麦克斯韦方程组,即
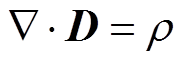 (1)
(1)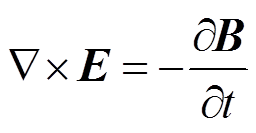 (2)
(2)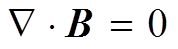 (3)
(3)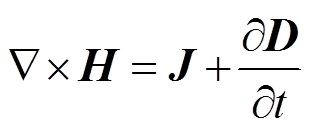 (4)
(4)式中,E为电场强度;B为磁通量密度;D为电位移矢量;H为磁场强度;J为电流密度;ρ为电荷密度;t为时间。式(1)为高斯定律,式(2)为电磁感应定律,式(3)为磁场连续性定理,式(4)为麦克斯韦-安培定律。电磁场本构关系为
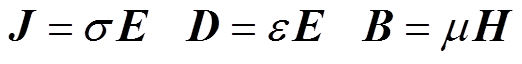 (5)
(5)式中,σ为电导率;ε为介电常数;μ为磁导率。
从数值建模的便利性角度考虑,使用磁矢势A和电势V作为自变量,并选取高斯标定 ⋅A=0。磁矢势A和电势V的定义为
⋅A=0。磁矢势A和电势V的定义为
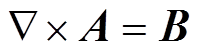 (6)
(6)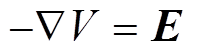 (7)
(7)此时,原电场和磁场可表示为
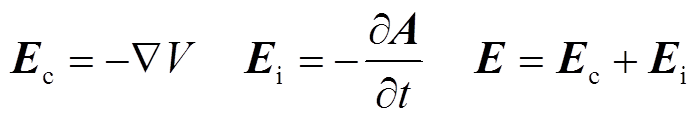 (8)
(8)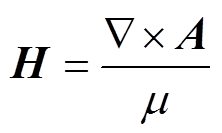 (9)
(9)式中,Ec为库仑电场,以电压(电荷)为源;Ei为感生电场,以变化的磁场为源。在高斯标定下,库仑电场和感生电场可分别被V和A表示。
此时,原麦克斯韦方程组中式(2)、式(3)被直接满足,式(1)、式(4)可写为
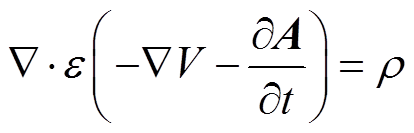 (10)
(10)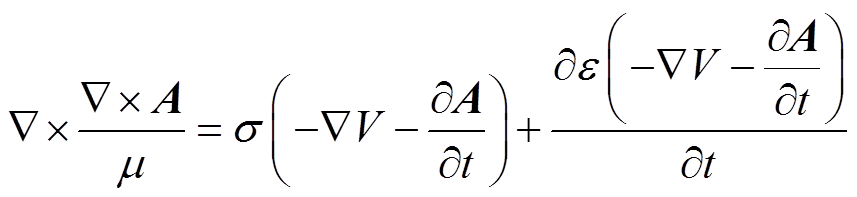 (11)
(11)在空间中,没有自由电荷;由于空气的电导率σ很小,也几乎没有漏电流,故式(10)、式(11)可写为
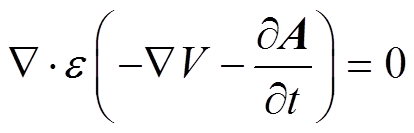 (12)
(12)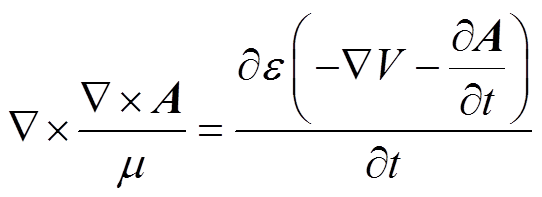 (13)
(13)式(12)、式(13)即为空间区域的场域方程。
接下来明确交界面条件及边界条件。根据前面的分析,PCB上的铜片被建模成一个没有厚度的面,需给定在这个面上的交界面条件,即
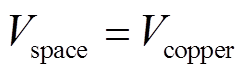 (14)
(14)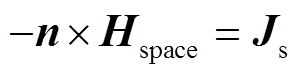 (15)
(15)式中,下标space表示空间区域;下标copper表示导体(铜);Js为导体中的面电流密度;n为垂直于表面向外的单位矢量。可看出,此处的交界面条件也相当于是给定了电磁场的一部分源。
最后,需给定在最外侧边界的边界条件。此处使用“无限元域”方法,用以模拟无穷远处的边界条件,如图3所示。
使用与空间部分相同的自变量和标定方式,可将麦克斯韦方程组写为
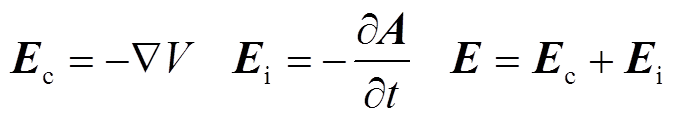 (16)
(16)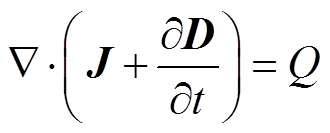 (17)
(17)式中,Q为外部电流密度。由于电磁场本构关系不变,为式(5),且在导体中起主要作用的本构关系是J=σE而非D=εE,故采用式(17)所示的电流连续性定理而非高斯定律对导体中电磁场进行建模。需要说明的是,此处没有采用求解磁场H的麦克斯韦-安培定律方程,是由于空间中已对其进行了解算,而导体作为空间中的一个面,其上的磁场强度、磁矢势等也已被计算完毕,不需要再单独列方程进行解算。
该部分的边界条件作如下处理:焊盘是与外部电路相连接的位置,故此处应给定边界条件为
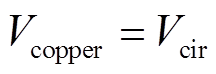 (18)
(18)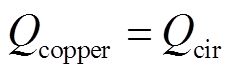 (19)
(19)式中,Vcir为由电路给出的电压;Qcir为由电路带来的外部电流密度。
在导体区域的其他边界,需满足绝缘边界条件,即
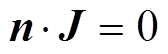 (20)
(20)在对载流子场进行建模时,使用经典的载流子输运方程组,即
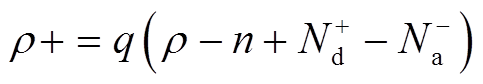 (21)
(21)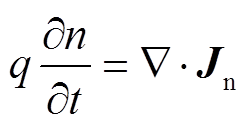 (22)
(22)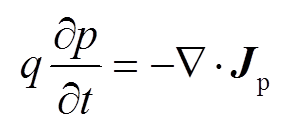 (23)
(23)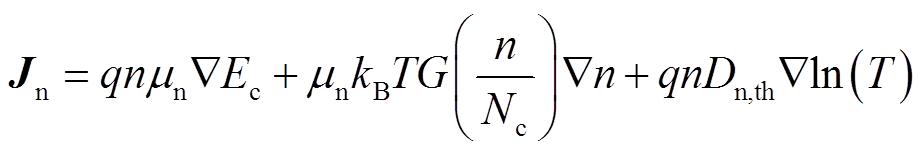 (24)
(24)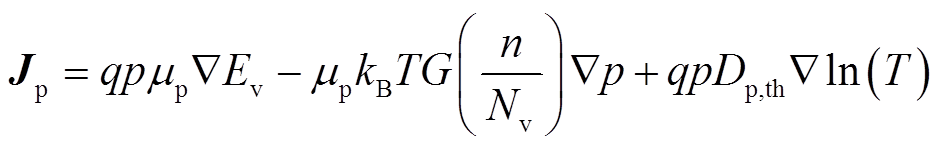 (25)
(25)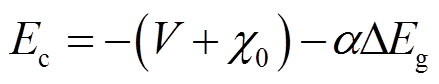 (26)
(26)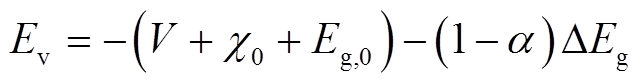 (27)
(27)式中,p、n、V分别为正电荷载流子浓度、负电荷载流子浓度和电势。
式(21)为电荷方程,q为单个电荷的电量,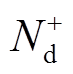 为施者离子浓度,
为施者离子浓度,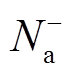 为受者离子浓度。
为受者离子浓度。
式(22)和式(23)为电流连续性方程,Jn、Jp分别为负电荷、正电荷电流密度,两方程表示对负电荷和正电荷分别满足。
式(24)和式(25)为电流密度和载流子浓度、电场强度的关系。以式(24)为例,等号右侧第一项表示漂移电流,其中Ec为导带的能级,表达式如式(26)所示,作梯度运算后为电场,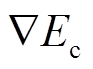 前系数为漂移系数;第二项表示扩散电流,其中
前系数为漂移系数;第二项表示扩散电流,其中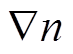 前的系数为扩散系数。式(25)同理,其中Ev为价带的能级。在用于计算Ec和Ev的式(26)、式(27)中,等号右侧除电势V外为均为常数。
前的系数为扩散系数。式(25)同理,其中Ev为价带的能级。在用于计算Ec和Ev的式(26)、式(27)中,等号右侧除电势V外为均为常数。
这样对半导体部分建模的好处是,由于其内部结构完全按照实际情况建模,且对电压、电场、载流子分布情况等作了详细的解算,故而可以完整地体现半导体开关器件的行为对整体的影响,其中也包含着对EMI影响较大的分布电容效应等。
电路连接模块指的是电路中除半导体器件外的其他元器件,如二极管、负载、电源,以及将它们与PCB相连接的导线。此部分依据图1b所示的电路,使用传统电路模型进行搭建即可。电路连接模块与PCB上铜中的导体场需进行耦合连接,保证PCB上的铜导体是电路中的一部分。电压电流方程为
 (28)
(28)式中,Vdc为母线电压;L为电感;i为电流;R为电阻;Vmos为MOS管上的电压;VD为二级管上的电压。
该数值模型采用多物理场仿真软件COMSOL搭建并解算。依据前述分析,由于该电磁脉冲模型复杂的耦合关系、强非线性和瞬态变化的快速性,使得模型解算非常困难。下面首先介绍解算中面临的主要问题及其解决方案,然后进行解算结果的正确性检验。验证从以下两个角度展开:从数值计算角度,通过改变解算设置、建模方式后对比结果的一致性进行验证;从原理角度,通过分析仿真结果的合理性说明所建数值模型本身的正确性。最后,从EMI角度对仿真结果的分析,包括对瞬变电磁场的直观描述,表示可据此对电力电子开关过程产生的EMI进行定量分析。
3.1.1 网格划分
有限元数值方法通过网格对空间进行离散,有限元网格必须足够细化才能在较高精度下解析场的空间变化,但带来的问题是解算时间的加长、内存占用的提升。因此,理想情况下,对于物理量空间变化率较大的区域,应使用小网格;而在其他区域使用大网格。
依据以上原则,在实际解算时,对半导体区域根据掺杂浓度的大小进行网格划分。在沟道、高掺杂浓度区使用小单元网格,在低掺杂浓度区使用较大单元网格。
在PCB及空间区域中,由于PCB上的焊盘处电势梯度大,导体的拐角处电流方向迅速变化,磁场梯度大,故这些部位应使用小单元网格;PCB上其他部分及靠近PCB的空间区域,由于距板近,物理量在空间中变化快,故使用较小单元,而远离PCB的空间使用大单元。PCB和空间区域的网格划分情况如图4所示,从图4a中可看到PCB上焊盘和导体拐角处网格较小、较密,其余部位网格相对稀疏;图4b中内部球为包围PCB的最小的一倍半径球体,外侧为二倍半径球体,可以看到内部网格与外部网格相比更密。

图4 网络划分示意图
Fig.4 Schematic diagram of finite element meshing
这样的网格划分下,既解决了收敛问题和精度问题,又保证模型能在合理时间内解算完毕。
3.1.2 由简到繁的解算
由于该电磁脉冲模型是由多个部分组成的,存在多场耦合、多物理规律混杂且相互影响的特点,如直接使用完整耦合的方程组进行瞬态求解,非常不易收敛。因此需采取由简到繁的思想,即先对简单情况求解,在此基础上加一些条件,过渡到完整的情况。具体体现为两个过渡方法:方法一是由稳态解向瞬态解的过渡;方法二是由各部分独立的解向全耦合解的过渡。解算过程示意图如图5所示,其中过程①~③对应方法一,过程②对应方法二。
应用方法一时,需要首先了解瞬态求解的原理:从给定的初始值开始,向后移动一定的步长,寻找下一组解,以此类推完成整个时域上的解算。默认的初始值为零初值,但在本模型中,这样的初值与实际的初始情况差距较大,向后无法找到可收敛的解。故需先对稳态情况求解,以此为瞬态求解时的初值,方能得到瞬态解。
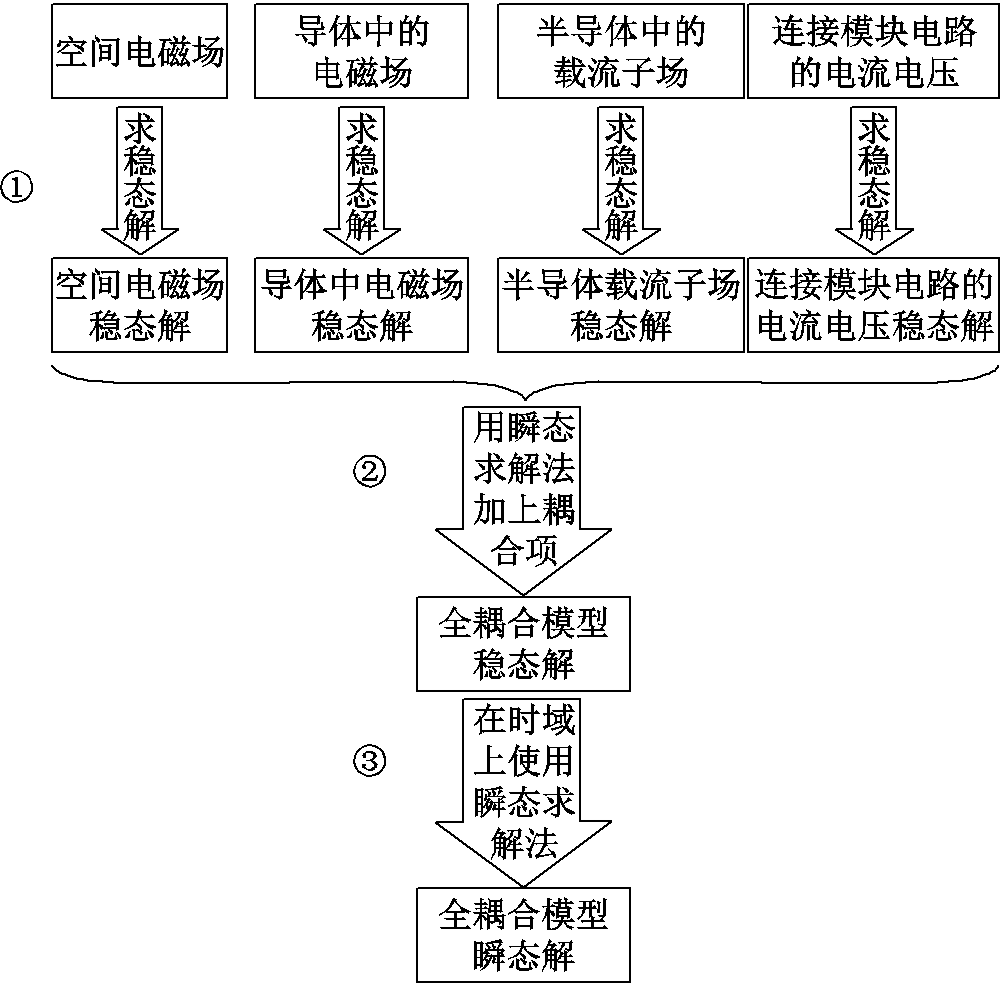
图5 解算过程示意图
Fig.5 Schematic diagram of solving process
应用方法二时,需注意到,虽然整体模型由于存在不同部分间的耦合而难以收敛,但若单独对每个部分进行解算,都有较好的收敛性,且不同部分之间仅通过边界条件、交界面条件相互耦合,如式(14)和式(15)所体现的铜中导体场与空间电磁场的耦合项。因此,可先对每个部分分别解算,再运用一次瞬态求解,利用斜坡函数缓慢加上各个耦合项,完成由独立解到耦合解的过渡。
得到解算结果后,应对其进行正确性检验,确保结果合理可信。由于模型耦合关系复杂、解算过程中有诸多困难,因此有必要对建模和解算过程进行检验,确保其在数值计算角度的正确性。
首先,在同一个模型的基础上,对网格剖分和瞬态解算的步长设置等作改变,观察解算结果是否发生变化。若在改变某设置时,解算结果几乎不发生变化,则说明该设置已经达到了较好的程度,结果对该设置的进一步改善已不敏感,进而说明该解算方式的正确性。
在网格剖分设置上,保持3.1节所述网格的划分方式,分别对不同空间区域的小单元、较小单元、大单元网格部分进行加密操作;在研究的步长设置上,也采用了不同的设置,分别限制开关动作后仿真的最大步长为0.3ns、0.03ns、0.003ns等。通过比较不同设置下的解算结果,发现所采用的网格剖分、0.03ns的步长设置已经可以满足研究需求。
其次,利用相同软件,使用不同的建模方式,再次对同一情形进行仿真。在基本方程和关系保持不变的情况下,改变在求解时物理量在软件中的耦合途径,将此方案记为方案二,原方案记为方案一。取空间中一点,对电场、磁场大小随时间的变化曲线进行比较,结果如图6所示。
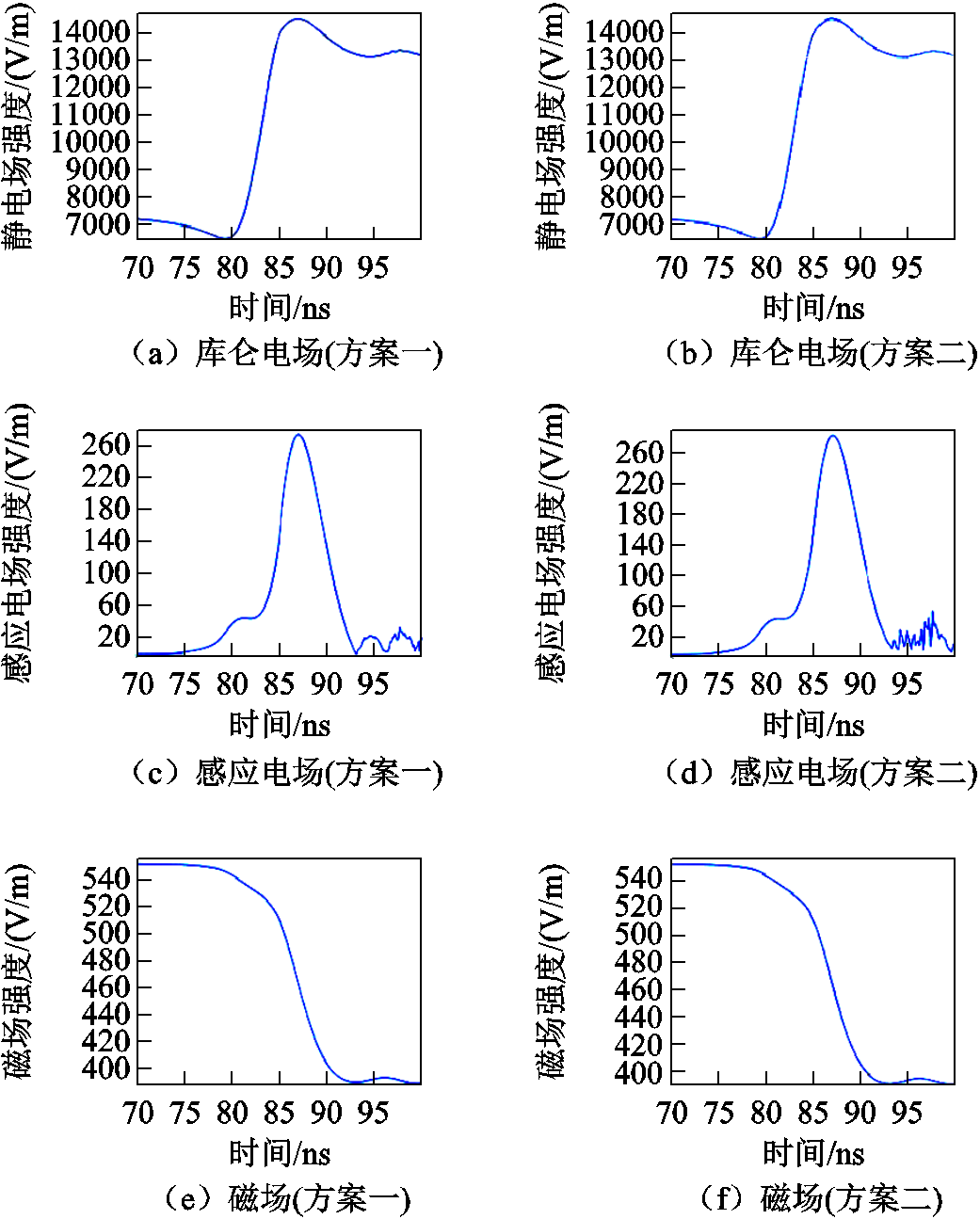
图6 两种建模方式结果的对比图
Fig.6 Comparison between two modeling methods
从图6中可看出:两曲线吻合程度很高,可以进一步说明该数值模型在数值计算方面的正确性,即在模型搭建、解算设置等方面是无误的。
3.3.1 仿真结果的可视化表示
接下来通过原理分析,验证仿真结果与理论的契合度,从而进一步验证所建数值模型及其解算的正确性。首先将解算结果进行合理的可视化表示。将开关过程MOSFET两端的电压和电流及空间中的电场、磁场、电磁能量等作为可视化对象,分别对一平面上场量的大小、该场量的源量(如电压、电流密度等)进行刻画,以清晰直观地展现空间电磁场的分布、变化情况,以及电磁能量的分布状况。在近场区域和全空间区域分别作图,以便同时对近场和远场的情况进行观察分析。选取的可视化对象及方式总结见表2。
表2 可视化对象及方式
Tab.2 Visualization objects and methods

位置可视化对象可视化方式 近场区域库仑电场一平面上的库仑电场强度 PCB上导体铜表面的电势 感应电场一平面上的感应电场强度 一平面上的感应电场旋度源强度 磁场一平面上的磁场强度 PCB上导体铜中的传导电流密度 一平面上的位移电流密度 能量一平面上的电磁场能量密度 全空间感应电场一平面上的感应电场强度 磁场一平面上的磁场强度 能量远场区域一点处能量密度随时间变化的曲线
对每种情况,分别作其在稳态时、以及开关断开后的瞬态时的图像。可视化后的结果如图7~图12所示。
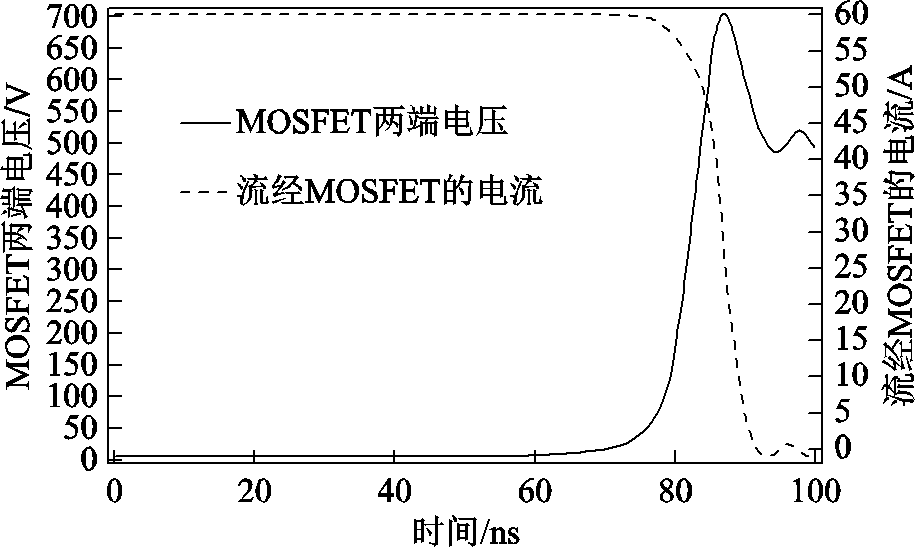
图7 MOSFET两端电压电流曲线
Fig.7 The curve over time of drain-to-source voltage of MOSFET and current current through it
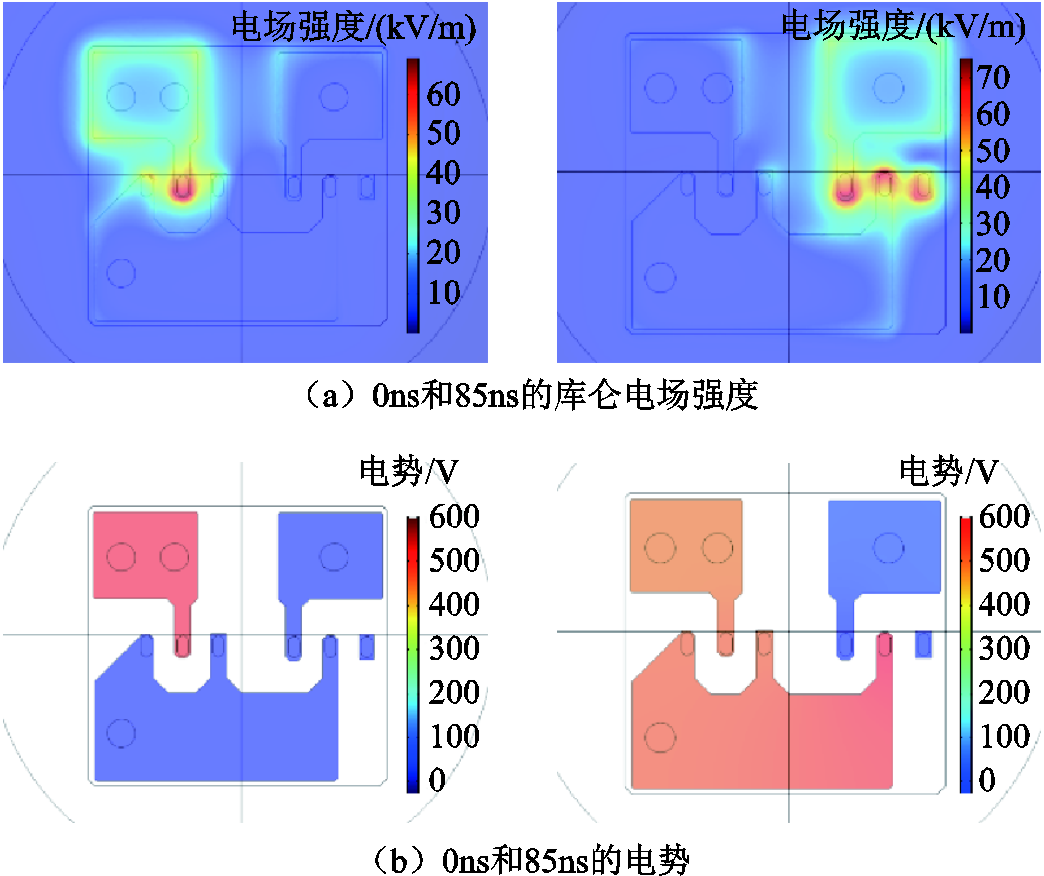
图8 近场区域库仑电场及其源的分布
Fig.8 Distribution of coulomb electric field and its source near PCB
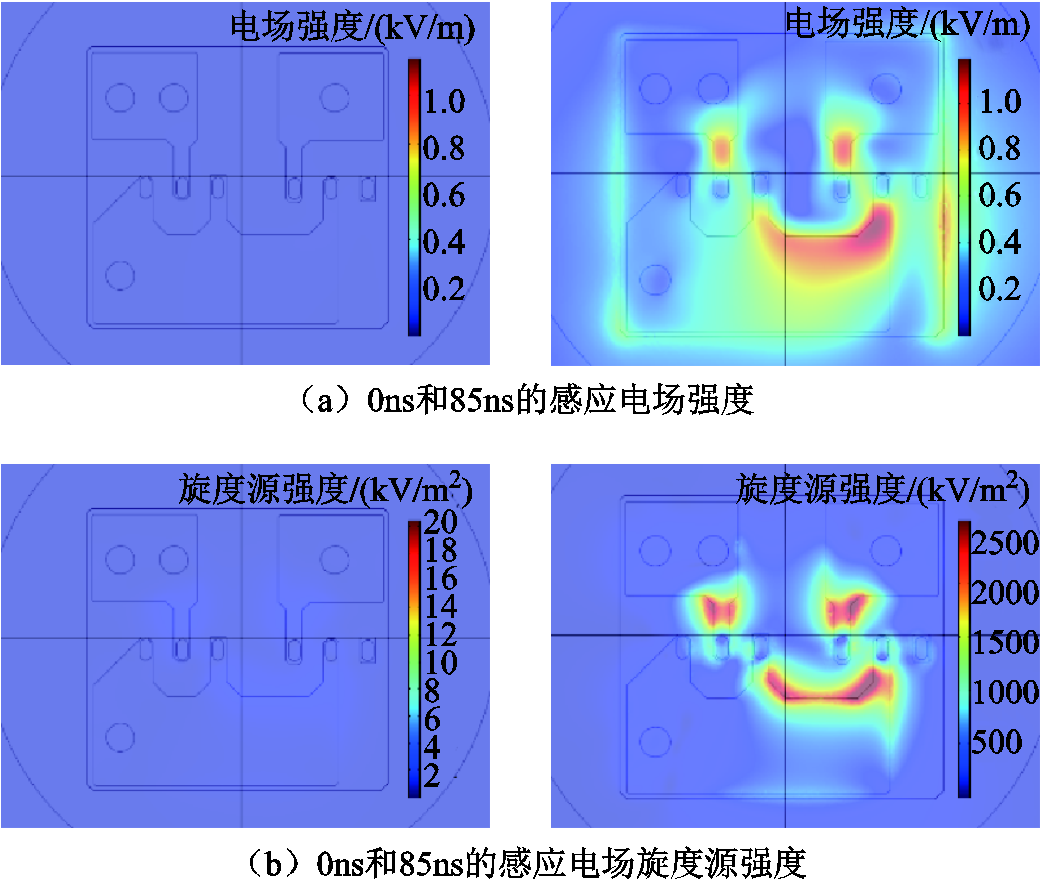
图9 近场区域感应电场及其源的分布
Fig.9 Distribution of induced electric field and its source near PCB
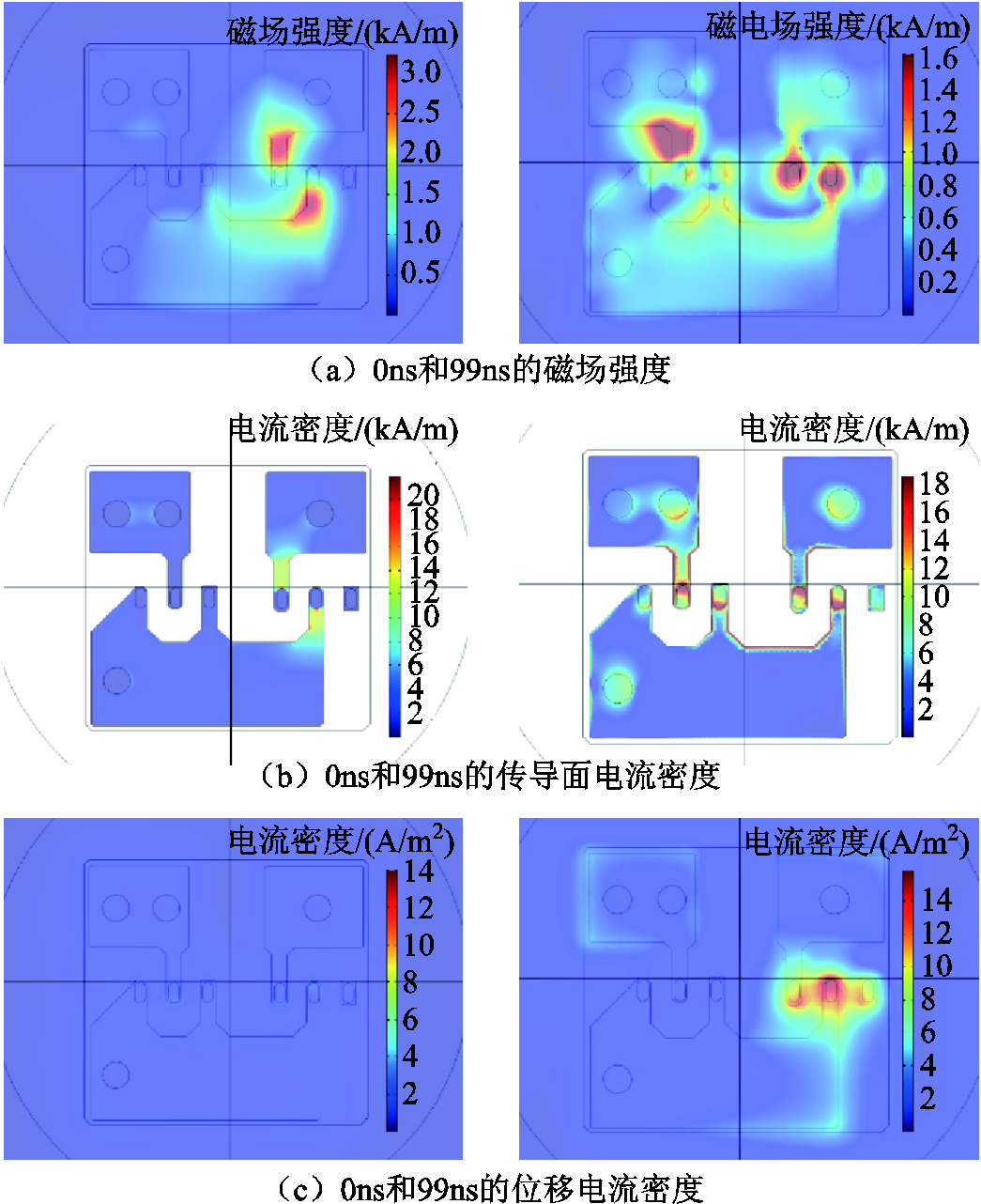
图10 近场区域磁场及其源的分布
Fig.10 Distribution of magnetic field and its source near PCB
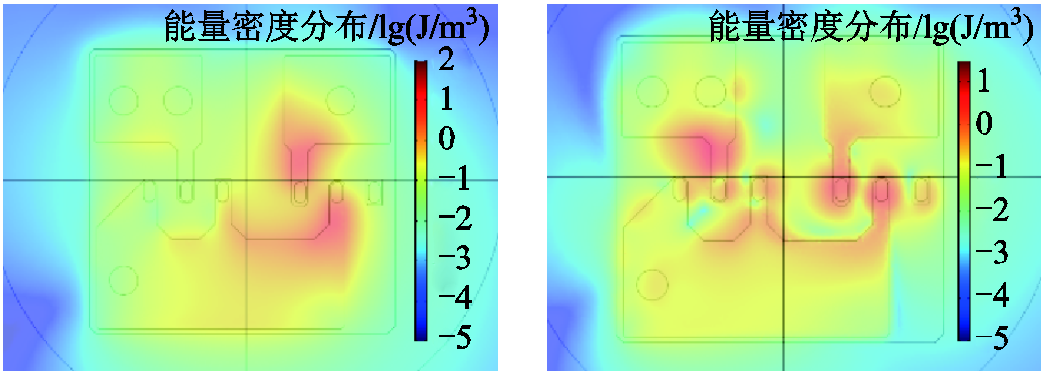
图11 近场区域0ns和99ns的能量密度分布
Fig.11 Distribution of electromagnetic energy density near PCB at 0ns and 99ns
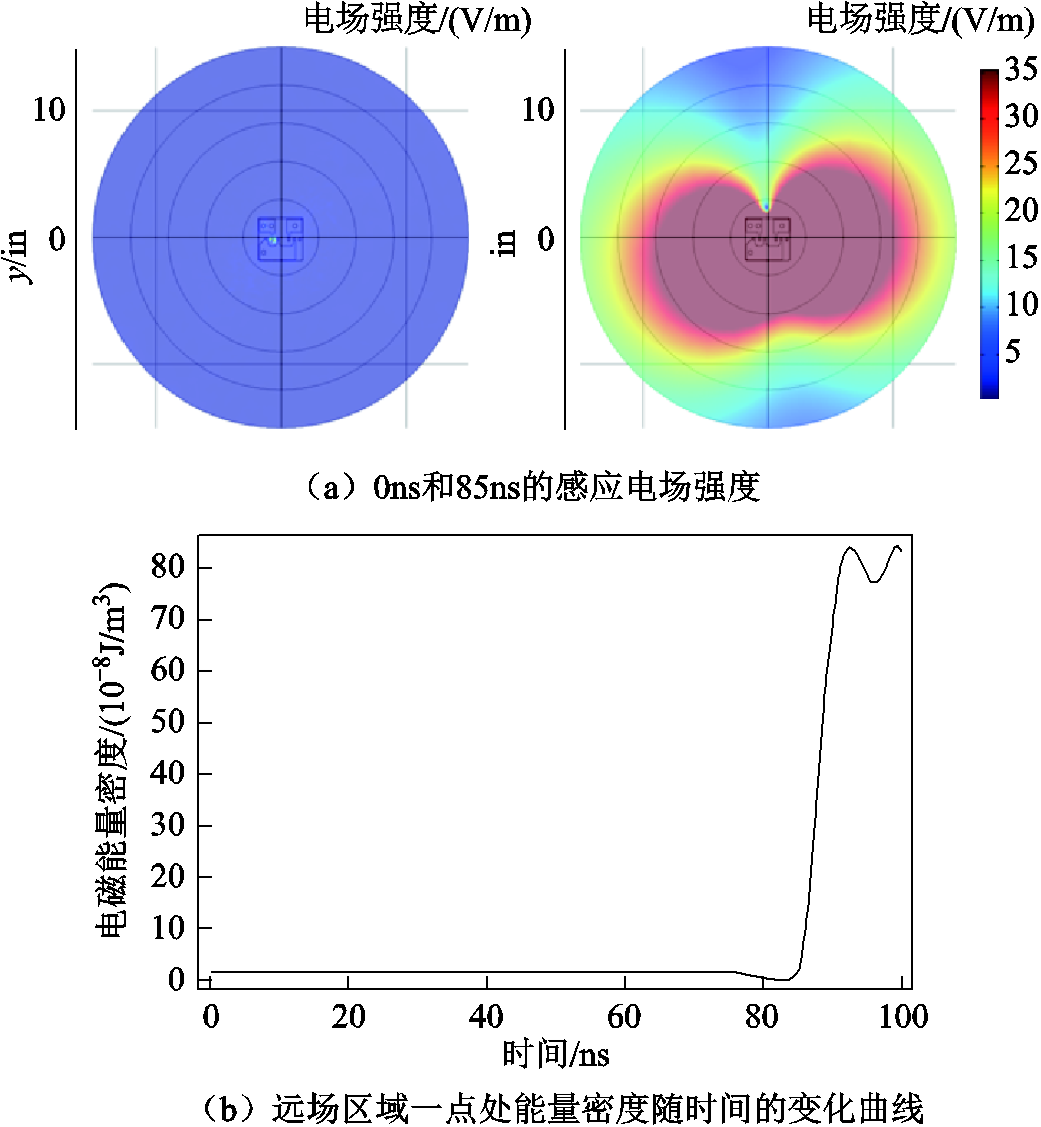
图12 全空间电场、磁场、能量密度分布或变化情况
Fig.12 Distribution or variation curve of electric field, magnetic field and electromagnetic energy density in the whole simulation space
3.3.2 近场区域的结果分析
首先对近场区域的结果进行分析。从图8中可以看到,空间中库仑电场的大小(图8a)与电路中电压的分布情况(图8b)有较强相关性。开关动作前的稳态,MOSFET导通,左上区域导体的电势为500V,右上区域和下方区域的导体电势为0V。故二极管的正负极之间及左上区域导体的周围位置电场强度大。开关断开后,二极管导通,下方导体电势逐渐变为500V。此时MOSFET各引脚间及右上区域导体的周围处电场强度大。
从图9中可以看到感生电场的大小(图9a)与空间中磁场对时间的变化率,即感应电场旋度源(图9b)有较强相关性。稳态时,磁场几乎不随时间变化,感应电场强度很小。开关断开后,从图7可知85ns左右电流变化较快,此时在二极管和MOSFET处B的时间偏导较大,进而产生了较大的感应电场。
对图10进行分析可见,空间磁场的大小(图10a)与导体中传导电流分布情况(图10b)有较强的相关性。稳态时,MOSFET处的电流密度最大,故此处的磁场强度最大。开关断开后,MOSFET逐渐关断,电流通过二极管流动,故二极管处的电流密度变大,相应的磁场强度变大;此时由于导体中感生电流的存在,导致MOSFET处也有一定的电流密度和磁场强度。在空间磁场的影响因素中,图10c所示的空间中位移电流由于较其他因素而言大小较小,不起主要作用。
空间电磁场能量密度由u=0.5(DE+BH)得到,经比较可知DE BH。从图11中可以看到,在稳态时能量主要集中在MOS管处,开关动作后在二极管和MOS处都有较大电磁能量,这与上述磁场的分布相吻合。
BH。从图11中可以看到,在稳态时能量主要集中在MOS管处,开关动作后在二极管和MOS处都有较大电磁能量,这与上述磁场的分布相吻合。
3.3.3 全空间的结果分析
接下来分析全空间的结果,从图12a、图12b中,可以看到感应电场和磁场在稳态时都仅在PCB附近的值较大,在开关动作后的瞬态时在仿真空间范围内都较大,有向外辐射的趋势。图12c为空间中离PCB较远处一点(位于三倍半径到四倍半径之间)的电磁能量密度随时间变化的曲线,从中可见在开关动作后此处能量呈脉冲式增加,且有随着电压波动而波动的趋势,与前述的电压电流的变化情况相吻合。
从3.3.2节和3.3.3节的分析中可以看到,电场、磁场、能量密度的大小及分布均与它们的源相吻合,且均与图7中显示的电压电流变化曲线相吻合。从原理角度分析得到仿真结果的合理性,也可以进一步证明该数值模型及其解算的正确性。
3.4.1 电磁场中的现象规律
电磁场是EMI传播的直接途径和物理本质,因此通过对电磁场的观察和分析,可得到与EMI相关的现象和规律。
近场耦合EMI可分为电场耦合和磁场耦合两种。在电路理论中,分别体现为能量通过寄生电容和寄生电感的传输,在电磁场理论中则对应感生电场和感生磁场的效应,场越大,说明磁场、电场变化越剧烈,则EMI干扰源越强,越易建立耦合路径。图9和图10c清晰地展示了它们的分布情况。从图中可看出,开关动作后的瞬态过程中,在二极管和半导体器件及它们之间的一段导体区域处感应电场较大,磁场随时间变化剧烈;在半导体器件处感应磁场大,电场随时间变化剧烈。归纳得到电磁场的变化遵循如下规律:在时间上,与电压电流的变化基本同步;在空间上,与物理量本身大小和PCB上布线情况相关,一般来说,在物理量本身值较大的区域,其时间偏导也相对较大;在导体尺寸较小或两导体相距很近的区域,电磁场时间偏导也较大。
而远场辐射EMI则是由电磁波的传输引起的。从图7可以看到,在开关动作后,以开关瞬态时快速变化的电磁脉冲为源,感生电场、磁场及电磁能量的向外传播对应于辐射EMI的现象。
3.4.2 研究展望
以上仅是从该数值模型及其解算中得到的对EMI现象的初步分析和探索,但以其在模型搭建上的完整性和本质性特点,该数值模型及其解算将为研究电力电子系统EMI问题奠定可行的分析基础。
首先,在EMI预测方面,数值解算方法避免了硬件实验中由于测量探头分辨率、尺寸,以及示波器精度的限制带来的对波形、量值测量的影响,可以方便准确地对各个位置、各个时间的物理量进行测量,包括与EMI直接相关的电场、磁场,以及电路中某点的电压电流等,直接为EMI预测提供参考;其次,由于可获得数据的完整性以及仿真平台的便利性,有望在数值解算中通过更多的测量、对照实验,结合理论分析,形成一套更准确通用的用以计算EMI的数学模型;再次,该数值仿真结果对微纳秒级时间尺度内,电磁场、电路及载流子场的行为作了完整的表征,包括强度、场线分布及它们的变化特点等,未来可基于此进行深入分析,形成一套适用于电力电子开关瞬态过程的、从能量脉冲和电磁场角度对EMI进行表征的可视化机理模型。
本文的主要意义在于实现了面向电力电子系统EMI研究的耦合场数值模型的搭建、解算和验证,为研究EMI提供数值实验平台,出于实现意义、降低难度的考虑,本文忽略了一些因素,如对负载、门极回路、电缆等更精细的建模,故而无法考虑到它们的寄生参数对EMI的影响。一方面,本文意在研究EMI的共性问题,故将一对互锁开关作为主要的研究对象,忽略次要因素,具有其合理性;但另一方面,这些分布参数对EMI会产生影响,直接忽略会导致仿真结果与实际情况有所出入,使得模型具有局限性。因此,未来应完善模型的各处参数,使模型更准确。
本文面向电力电子系统EMI机理的研究,依据对电力电子系统开关瞬态过程EMI的认识,从能量脉冲和电磁场瞬变过程的角度,搭建三维电磁场数值分析模型,以电磁场和载流子场耦合作用下的电磁脉冲为建模对象,以有限元法为解算方法,得到微纳秒级时间尺度的开关瞬态过程中空间电磁场的分布及变化情况,并从数值模型和原理分析两个角度验证了该数值解算的正确性,为从电力电子系统的物理本质出发对EMI进行机理研究提供了有效的工具。
本文以包含碳化硅MOSFET和二极管的互锁开关、电容和负载的电路为例,给出了从物理模型向数值模型的转换、对电磁脉冲的建模、解算结果的可视化表征、分析及正确性验证的全过程,并从电磁场角度初步观察提炼了EMI现象,从正确性和应用价值方面证明了该数值解算的有效性。与传统电路理论相比,本数值解算方法建立了电路、电磁场与载流子场的耦合作用下的三维模型,不仅考虑了更全面的物理因素,而且能更直观、本质地刻画EMI现象,有利于对EMI产生、传播及影响电路的机理进行深层次的研究。
本文在利用该数值模型研究EMI方面仅做了初步探索,未来将基于该模型继续深化研究,提炼总结电力电子开关瞬态过程EMI的机理,形成数学和物理层面的表征方法,更好地从理论层面为面向实际应用的工作提供指导。
参考文献
[1]Millan J, Godignon P, Perpina X, et al. A survey of wide bandgap power semiconductor devices[J]. IEEE Transactions on Power Electronics, 2014, 29(5): 2155-2163.
[2]刘佳斌, 肖曦, 梅红伟. 基于GaN-HEMT器件的双有源桥DC-DC变换器的软开关分析[J]. 电工技术学报, 2019, 34(增刊2): 534-542. Liu Jiabin, Xiao Xi, Mei Hongwei. Soft switching analysis of dual active bridge DC-DC converter based on GaN-HEMT device[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 534-542.
[3]Josifovic I, Popovic-gerber J, Ferreira J A. Improving SiC JFET switching behavior under influence of circuit parasitics[J]. IEEE Transactions on Power Electronics, 2012, 27(8): 3843-3854.
[4]钱照明, 盛况. 大功率半导体器件的发展与展望[J]. 大功率变流技术, 2010(1): 1-9. Qian Zhaoming, Sheng Kuang. Development and perspective of high power semiconductor device[J]. High Power Converter Technology, 2010(1): 1-9.
[5]李建轩, 赵治华, 张向明, 等. 电磁发射系统逆变装置的高频干扰电流测量[J]. 电工技术学报, 2018, 33(24): 5805-5810. Li Jianxuan, Zhao Zhihua, Zhang Xiangming, et al. Measurement technology of high frequency interference current of the electric energy conversion device in the electromagnetic launch system[J]. Transaction of China Electrotechnical Society, 2018, 33(24): 5805-5810.
[6]Zhang B, Wang S. A survey of EMI research in power electronics systems with wide-bandgap semiconductor devices[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 626-643.
[7]钱照明, 陈恒林. 电力电子装置电磁兼容研究最新进展[J]. 电工技术学报, 2007, 22(7): 1-11. Qian Zhaoming, Chen Henglin. State of art of electromagnetic compatibility research on power electronic equipment[J]. Transaction of China Electrotechnical Society, 2007, 22(7): 1-11.
[8]Wang Kangping, Yang Xu, Wang Laili, et al. Instability analysis and oscillation suppression of enhancement-mode GaN devices in half-bridge circuits[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1585-1596.
[9]Umetani K, Matsumoto R, Hiraki E. Prevention of oscillatory false triggering of GaN-FETs by balancing gate-drain capacitance and common-source inductance[J]. IEEE Transactions on Industry Applications, 2019, 55(1): 610-619.
[10]Lemmon A, Mazzola M, Gafford J, et al. Instability in half-bridge circuits switched with wide band-gap transistors[J]. IEEE Transactions on Power Electronics, 2014, 29(5): 2380-2392.
[11]Zhang Lei, Yuan Xibo, Wu Xiaojie, et al. Performance evaluation of high-power SiC MOSFET modules in comparison to Si IGBT modules[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1181-1196.
[12]赵争鸣, 施博辰, 朱义诚. 对电力电子学的再认识——历史、现状及发展[J]. 电工技术学报, 2017, 32(12): 5-15. Zhao Zhengming, Shi Bochen, Zhu Yicheng. Reconsideration on power electronics: the past, present and future[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 5-15.
[13]Mainali K, Oruganti R. Conducted EMI mitigation techniques for switch-mode power converters: a survey[J]. IEEE Transactions on Power Electronics, 2010, 25(9): 2344-2356.
[14]Zhu H B, Lai J S, Hefner A R, et al. Analysis of Conducted EMI emissions from PWM inverter based on empirical models and comparative experiments[C]// 30th Annual IEEE Power Electronics Specialists Conference, Charleston, SC, USA, 1999: 861-867.
[15]Wang S, Kong P, Lee Fred C. Common mode noise reduction for boost converters using general balance technique[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1410-1416.
[16]Huang X D, Pepa E, Lai J-S, et al. Three-phase inverter differential mode EMI modeling and prediction in frequency domain[C]//38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, 2003: 2048-2055.
[17]Liu Q, Shen W, Wang F, et al. Experimental evaluation of IGBTs for characterizing and modeling conducted EMI emission in PWM inverters[C]//IEEE 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 2003: 1951-1956.
[18]曹勇, 杨飞, 李春晖, 等. 不同耦合系数下的交错并联电流连续模式Boost功率因数校正变换器的传导电磁干扰[J]. 电工技术学报, 2019, 34(10): 2176-2186. Cao Yong, Yang Fei, Li Chunhui, et al. Conducted electromagnetic interference of interleaved continuous current mode Boost power factor correction converter with different coupling coefficients[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2176-2186.
[19]江师齐, 刘艺涛, 银杉, 等. 基于噪声源阻抗提取的单相逆变器电磁干扰滤波器的设计[J]. 电工技术学报, 2019, 34(17): 3552-3562. Jiang Shiqi, Liu Yitao, Yin Shan, et al. Electromagnetic interference filter design of single-phase inverter based on the noise source impedance extraction[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3552-3562.
[20]Shen W, Wang F, Boroyevich D, et al. Optimizing EMI filter design for motor drives considering filter component high-frequency characteristics and noise source impedance[C]//Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 2004: 669-674.
[21]Poon N K, Liu J C P, Tse C K, et al. Techniques for input ripple current cancellation: classification and implementation[J]. IEEE Transactions on Power Electronics, 2000, 15(6): 1144-1152.
[22]Zumel P, Garcia O, Cobos J A, et al. EMI reduction by interleaving of power converters[C]//Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 2004: 688-694.
[23]陈强, 陈章勇, 陈勇. 基于副边谐振技术的单端反激式变换器EMI分析[J]. 电工技术学报, 2019, 34(4): 728-737. Chen Qiang, Chen Zhangyong, Chen Yong. Electromagnetic interference analysis of single-ended fly-back converter based on secondary-resonance-technology[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 728-737.
[24]Antonini G, Cnstina S, Orlandi A. EMC characterization of SMPS devices: Circuit adiated emissions[J]. IEEE Transactions on Electromagnetic Compatibility, 1996, 38(3): 300-309.
[25]Aouine O, Labarre Cé, Costa F. Measurement and modeling of the magnetic near field radiated by a buck chopper[J]. IEEE Transactions on Electromagnetic Compatibility, 2008, 50(2): 445-449.
[26]Hernando M M, Fernandez A, Arias M, et al. EMI radiated noise measurement system using the source reconstruction technique[J]. IEEE Transactions on Industrial Electronics, 2008, 55(9): 3258-3265.
[27]Gao Xu, Fan Jun, Zhang Yaojiang, et al. Far-field prediction using only magnetic near-field scanning for EMI test[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(6): 1335-1343.
[28] Chen Henglin, Wang Tao, Feng Linmin, et al. Determining far-field EMI from near-field coupling of a power converter[J]. IEEE Transactions on Power Electronics, 2014, 29(10): 5257-5264.
[29] Zhang Yingjie, Wang Shuo, Chu Yongbin. Predicting far-field radiation with the emission models of power converters[C]//2017 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI), Washington, DC, USA, 2017: 797-802.
Numerical Modeling and Analysis of Electromagnetic Interference in Power Electronics Systems
Abstract With the increase of power level and switching speed of semiconductor devices, electromagnetic interference (EMI) caused by switching process is becoming more and more serious. Different from traditional EMI problems, the EMI problem of power electronics systems which mainly caused by the transient switching process of power semiconductor device, is intrinsically about energy conversion rather than signal propagation, implemented by pulse rather than continuous wave, and essentially carried by electromagnetic radiation in space rather than voltage and current in circuit. These three characteristics determine that it is difficult to reveal the essential features and rules of EMI problem of power electronics systems by using traditional method of signal propagation, sinusoidal periodic waveform analysis and equivalent circuit modeling. Based on this understanding, from the perspective of energy pulse and electromagnetic filed transient process, this paper models and analyzes the electromagnetic pulse under the coupling effect of electromagnetic field and carrier field. A three-dimensional numerical model for EMI mechanism research is built, and the distribution and variation of electromagnetic field both in power device and space during the nanosecond switching transients are computed. The correctness of this numerical model is verified both in numerical calculation’s and principle’s aspect. This work will provide an effective numerical analysis basis for EMI mechanism research of power electronics systems.
keywords:Electromagnetic interference(EMI), switching process, electromagnetic pulse, 3-D modeling
中图分类号:TM46
DOI:10.19595/j.cnki.1000-6753.tces.200555
国家自然科学基金重大项目资助(51490680, 51490683)。
收稿日期 2020-05-28
改稿日期 2020-08-11
贾圣钰 女,1997年生,博士研究生,研究方向为功率开关器件瞬态建模。E-mail:jia_shengyu@163.com
赵争鸣 男,1959年生,教授,博士生导师,研究方向为大容量电力电子变换系统、光伏发电、电机控制、无线电能传输等。E-mail:zhaozm@tsinghua.edu.cn(通信作者)
(编辑 赫蕾)