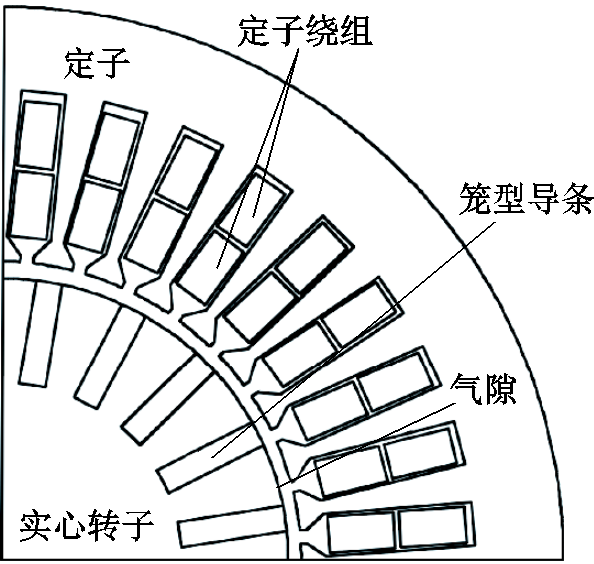
图1 笼型实心转子感应电机横截面示意图
Fig.1 Cross section of cage solid-rotor induction machine
摘要 笼型实心转子感应电机实心体与导条感应电流相互耦合,尤其是两极电机起动时,实心体涡流对导条电流分布产生很大影响,使导条电流密度由槽口至槽底呈现先减小后增大的不对称U型分布。传统计算方法会导致转子参数计算误差较大,严重影响电机设计的准确性。该文建立考虑磁场饱和效应的二维多层电磁场解析模型,求解两极笼型实心转子感应电机起动工况下的磁场分布。在此基础上,计及转子铁心轭部感应电流影响,建立转子导条电流解析计算模型,并求解电机在起动运行时笼型导条电流密度的分布。最后,通过与有限元仿真结果对比,验证不同电压下起动时,所求解的导条电流密度分布规律的准确性。结果表明所提出的计算方法适用于包括两极电机在内的各种极数笼型实心转子感应电机,为该类电机起动参数及性能的准确计算提供了参考。
关键词:笼型实心转子 解析计算 起动 电流密度分布
实心转子感应电机的转子采用导电导磁材料制成,具有机械强度高、起动性能好等优点[1]。为了改善电机在高速运行时功率因数和效率等性能指标,通常在转子侧加装笼型导条,制成笼型实心转子[2-3]。笼型感应电机高转差运行时,特别是电机起动时,转子笼型导条内感应电流的频率与定子供电电源频率相同,由于存在趋肤效应,使得导条截面上电流密度分布呈现由槽口向槽底逐渐减小的趋势[4]。趋肤效应会使电机交流电阻大于直流电阻,同时还会影响导条的槽漏抗。对于笼型实心转子感应电机,导条内的电流分布还会影响实心体与笼型导条间互漏抗的计算[5-6]。因此为了精确计算电机起动性能,必须精确计算电机起动时笼型导条内的电流分布。
由于笼型实心转子感应电机转子结构较为复杂,实心体与笼型导条间电磁场相互耦合,涡流分布复杂,特别是在电机起动时,电磁场分布尤为复杂。针对感应电机起动时转子侧感应电流的趋肤效应问题,国内外学者展开了大量研究工作,并很好地解决了感应电机起动时趋肤效应对电机运行性能的影响,主要包括修正系数法、电磁场解析法及有限元仿真分析。修正系数法是引入修正系数,用修正系数与导条的直流阻抗的乘积来计及趋肤效应对电机起动运行时转子侧交流阻抗参数的影响[7];电磁场解析计算法是对转子侧磁路进行简化,忽略铁心饱和的影响,同时对导条进行分层处理,通过磁路法分别计算各层导条的阻抗参数及导条各层之间的互漏感参数,进而求得导条电流的分布规律[8-9];最为准确的方法是采用有限元仿真,能够有效避免解析计算时采取的一系列简化引入的误差,精确计算导条电流的分布规律[10-11],但是有限元仿真无法像解析计算一样给出解析公式,所以不能较为明显地揭示现象的物理规律以及电机参数与运行特性之间的关系。文献[12]中发现,运用电磁场解析法求解两极笼型实心转子电机起动特性时,由于传统计算方法没有考虑实心体感应涡流对转子导条的电流密度分布的影响,无法精确计算两极笼型实心转子感应电机起动时导条电流的分布规律,导致计算所得起动转矩与起动电流与有限元仿真结果存在较大误差。
为了解决两极笼型实心转子感应电机起动特性解析计算时,由于转子实心体磁场饱和效应及实心体感应涡流对笼型导条电流分布的影响,本文提出一种改进的转子导条电流解析计算方法。该方法考虑了电机起动时的趋肤效应、转子齿部及轭部的饱和效应及实心体轭部感应电流对笼型导条电流分布的影响,能够准确计算两极笼型实心转子感应电机起动时,笼型导条电流密度由导条槽口向槽底先减小后增大的不对称U型分布规律,并通过有限元仿真结果表明解析算法在不同起动电压下笼型导条电流分布计算的准确性,为笼型实心转子感应电机起动时电机参数及性能的计算提供参考。
一台2/6极变极笼型实心转子感应电机的横截面示意图如图1所示。通过有限元仿真,可以得到不同极数和不同转子材料情况下稳态堵转运行的导条电流密度分布情况。

图1 笼型实心转子感应电机横截面示意图
Fig.1 Cross section of cage solid-rotor induction machine
图2a给出的是叠片转子感应电机在定子绕组两极接法下起动时,转子导条内电流密度的分布,以及导条辅助线上电流密度的变化曲线。可以看出,常规笼型转子感应电机在起动瞬间,由于趋肤效应,导条电流趋于转子表面分布,电流密度由槽口至槽底呈现递减趋势[13]。图2b和图2c分别为笼型实心转子感应电机在六极和两极接法下起动时,转子导条内电流密度的分布,以及导条辅助线上电流密度的变化曲线。可以看出,笼型实心转子感应电机在六极接法下起动时,导条内部电流密度分布与叠片转子电机非常相似。然而,笼型实心转子感应电机在两极接法下起动时,导条内部电流分布明显不同,导条电流密度由槽口至槽底先减小后增大,呈现不对称U型分布,如图2c所示。
考虑改变转子导条的尺寸和形状,如图3所示,对于导条采用梯形槽和圆形槽的情况,有限元仿真结果显示,导条电流密度同样呈现不对称U型分布。
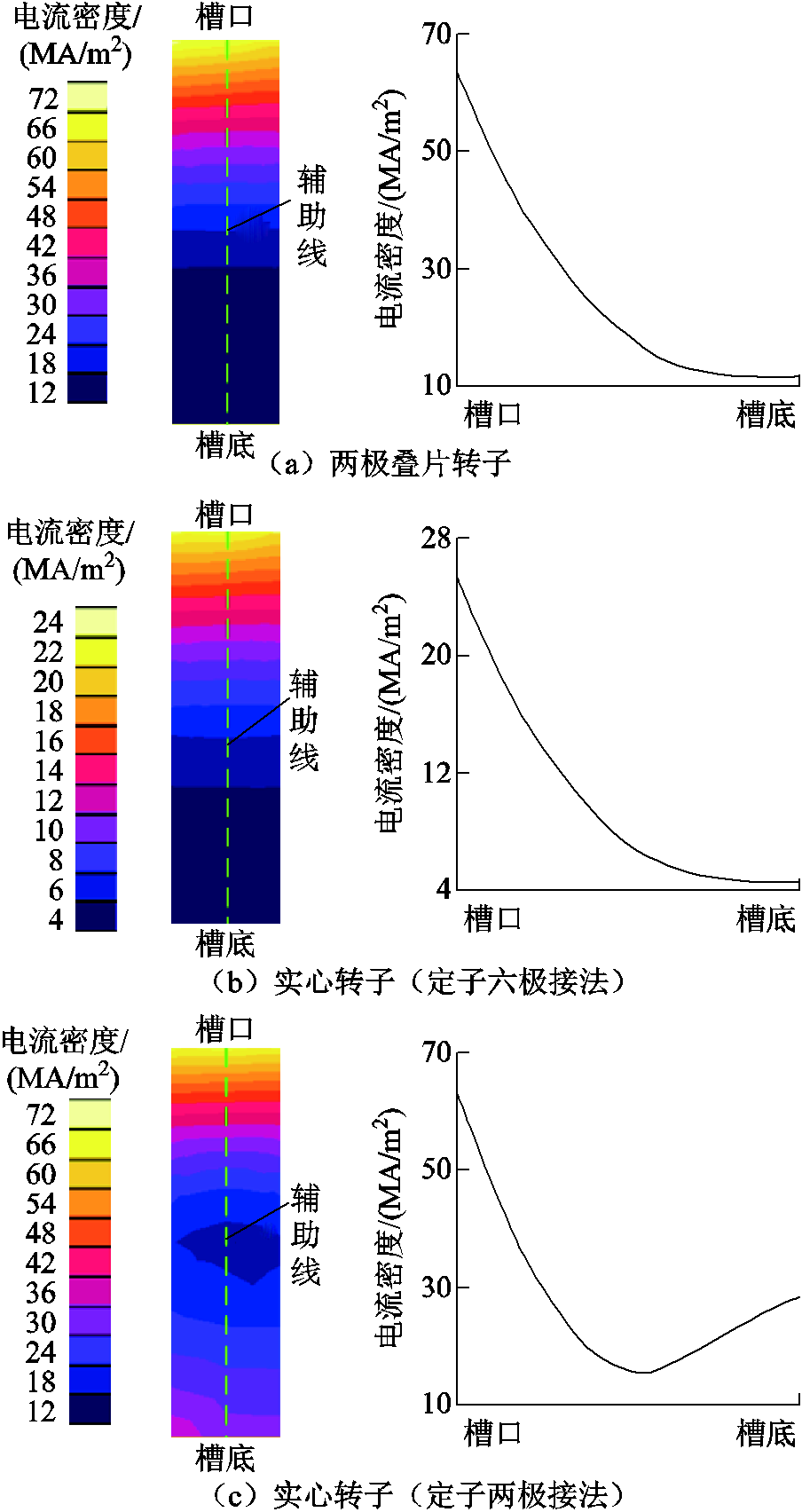
图2 不同转子结构的感应电机导条电流密度分布
Fig.2 The starting current density distributuion of the rotor bar with different rotor structures
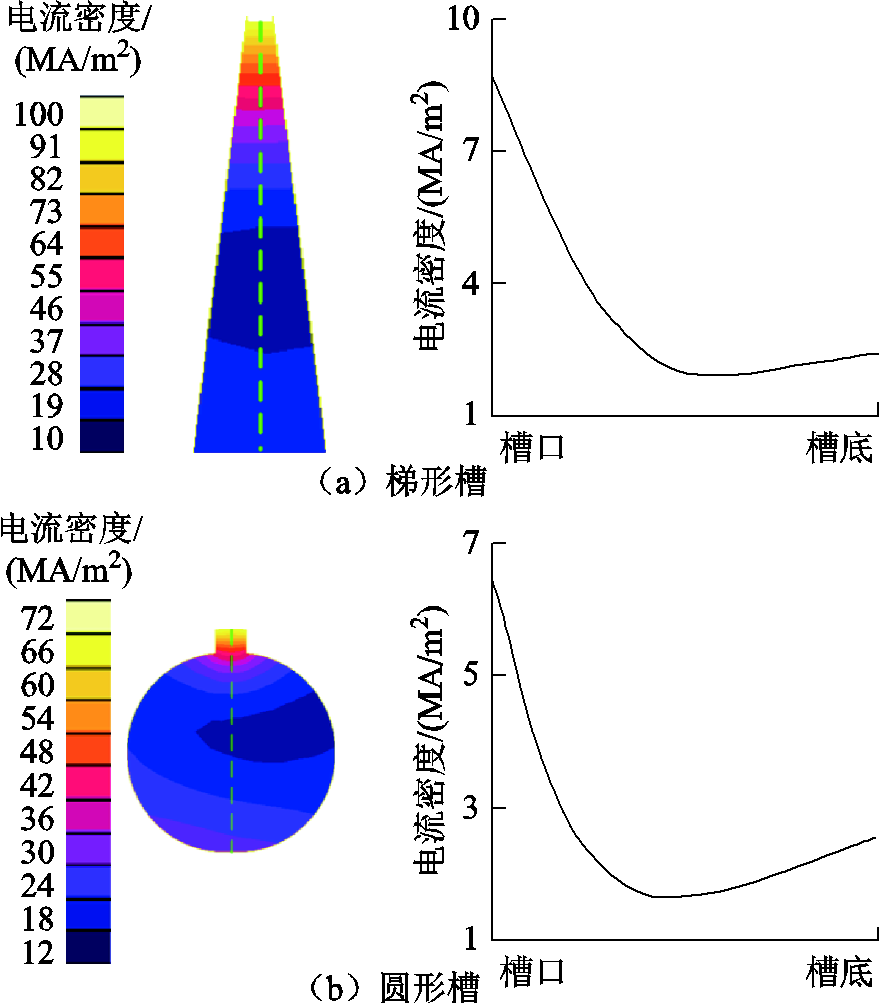
图3 不同转子槽型的导条电流密度分布
Fig.3 The starting current density distributuion of the rotor bar with different bar structure
为了探究两极笼型实心转子电机起动时笼型导条电流呈现不对称U型分布的原因,通过有限元仿真,对比定子绕组两极与六极接法情况下电机在起动时转子铁心的磁场分布与感应电流密度分布的特点。首先,在不同极对数笼型实心转子感应电机定子侧施加幅值与频率相同的三相电压起动,转子实心体磁感应强度和电流密度分布云图如图4所示。可以看出,在六极情况下,转子实心体的感应电流主要分布在外表面,齿顶部位的磁场最强,而铁心内部磁场很小。然而,在两极情况下,转子齿部和轭部磁感应强度都很大,且均存在比较大的感应电流。

图4 不同极对数笼型实心转子感应电机起动时实心转子的磁感应强度和电流密度分布云图
Fig.4 The starting current density and magnetic flux density distributuion of the rotor with different pole-pairs
为了进一步验证实心体齿部与轭部感应电流对笼型导条感应电流分布的影响,分别将转子齿部与轭部设置为不同导电性质的材料,进行有限元仿真分析。
首先将转子齿部设置为导磁不导电材料,而轭部仍然为导磁导电材料,观察实心体轭部感应电流对电机起动时笼型导条电流分布的影响;然后再将转子轭部设置为导磁不导电材料,而将齿部设置为导磁导电材料,观察实心体齿部感应电流对电机起动时笼型导条电流分布的影响,对应的有限元仿真结果如图5所示。可以看出,当转子轭部铁心材料导电而齿部不导电时,导条电流密度随槽深呈不对称U型分布;反之,则与常规感应电机的情况一致。也就是说,笼型导条槽底部位电流密度增大的主要原因是由于转子轭部存在较大的感应电流。
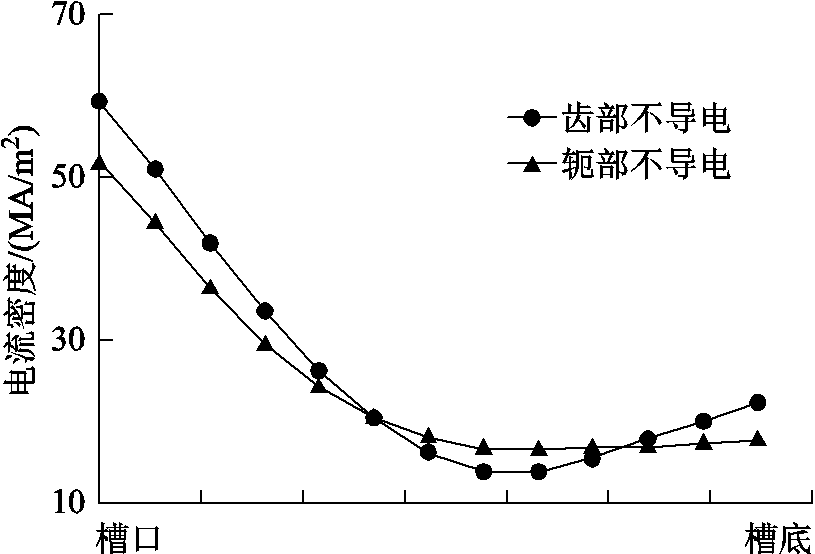
图5 笼型导条起动电流密度分布曲线
Fig.5 The starting current density distributuion curves of the rotor bar
为了精确计算笼型导条内电流密度的分布,需要对导条周围的电路与磁路进行分析计算,以考虑转子实心体齿部与轭部的饱和程度、轭部磁场透入深度及实心体感应电流对导条电流分布的影响。
由于笼型实心转子电机的转子铁心采用导磁导电的特种钢材料制成,转子涡流分布复杂,各支路电流产生的磁场相互耦合,加大了电机解析计算的复杂性。针对实心体转子感应电机电磁场解析计算,文献[14]提出复合转子感应电机二维多层电磁场解析计算模型,建立电机计算程序;文献[15-16]分别采用二维多层电磁场理论推导了开槽实心转子感应电机与笼型实心转子屏蔽感应电机转子侧磁场的解析解并进行实验验证。本文结合前人的研究,根据两极实心转子感应电机起动运行的特点,提出改进的二维多层电磁场解析计算模型,对电机转子侧电磁场进行解析计算。
图6为两极笼型实心转子感应电机起动时实心转子的相对磁导率云图,磁导率越低意味着饱和程度越高。可以看出,此时转子齿部磁导率分布不均匀,齿顶严重饱和,转子轭部透磁区域也出现明显的饱和现象。所以,为了在计算导条电流分布时,考虑转子实心体的磁场饱和效应和感应电流的影响,将电机转子侧按照各个部位磁导率与电阻率的不同,划分为气隙、转子齿槽区域、转子实心体轭部透磁区域与非透磁区域四部分,如图7所示。转子轭部非透磁区设置为平行磁场边界条件,未在模型中画出。然后将转子齿槽区进行进一步细分,本文将其近似等效为三个磁导率不同的区域,以考虑起动时实心体齿部磁导率的不均匀分布。

图6 起动时实心转子的相对磁导率云图
Fig.6 The relative permeability distribution of the solid-rotor when the motor start
具体电机电磁场解析计算模型如图7所示,其中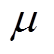 和
和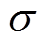 分别表示各个区域的相对磁导率和电导率,下标t代表实心体,下标b代表笼型导条。
分别表示各个区域的相对磁导率和电导率,下标t代表实心体,下标b代表笼型导条。 为考虑了端环电阻折算以后的笼型导条电导率[12]。
为考虑了端环电阻折算以后的笼型导条电导率[12]。
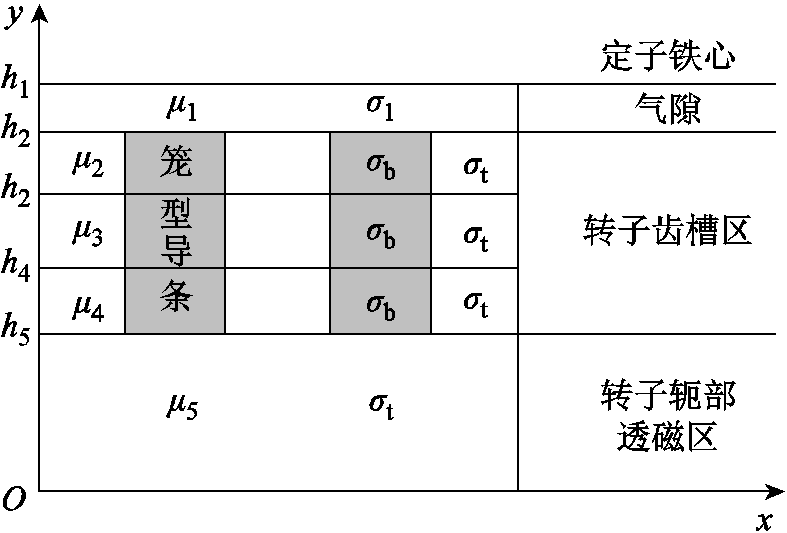
图7 电机二维多层电磁场解析计算模型
Fig.7 2D-multilayer electromagnetic analytical model of the motor
对模型做如下假设:①模型求解域中电磁场量均为正弦量;②通过修正系数来修正定转子展开成平面后所忽略的曲率效应;③定子侧铁心等效为磁导率无穷大的不导电面域;④矢量磁位只有z轴方向的分量,定转子的端部效应通过端部系数修正;⑤忽略导磁材料的磁滞效应。
根据上述模型建立复数矢量磁位方程,并且根据各层间的交界面上的矢量磁位与切向磁场强度的连续性等边界条件,结合实心体感应电机设计方法的流程,可以求解各层媒质中的矢量磁位、磁感应密度、电场强度及相对磁导率等[16-17]。计算公式为
 (1)
(1)式中,s为转差率;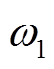 为定子角频率;
为定子角频率;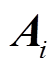 为各个区域的矢量磁位;
为各个区域的矢量磁位;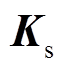 为等效的定子内表面面电流密度。
为等效的定子内表面面电流密度。
转子轭部磁场的透入深度D的计算公式为
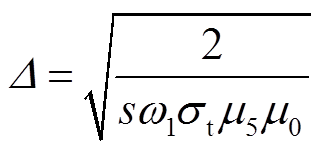 (2)
(2)对比笼型导条底部与实心体轭部导磁区域感应电流的相位,所取电流区域如图8所示。在导条底部取中心处一点的电流密度值,等效近似为槽底区域电流密度的平均值,在轭部对应位置也取相同个数的点,各个位置电流相位如图9所示。从图9中可以看出,轭部感应电流与导条底部电流相位差接近180°。
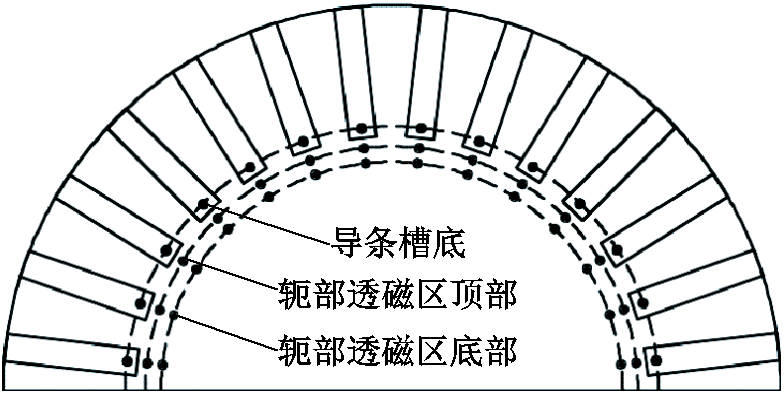
图8 电流的相位所取的参考点
Fig.8 The reference point of the phase of the current
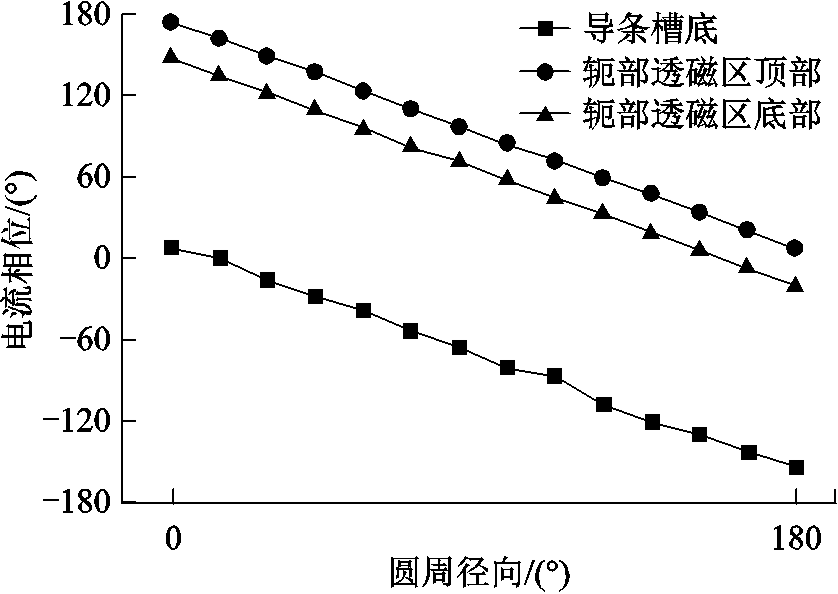
图9 不同区域电流的相位分布
Fig.9 The current phase of different regions
对于相邻的带电导电体,当两导体通入相反相位的交流电流,两者磁场相互作用,导体内部电流受到临近效应的影响,作用结果类似于趋肤效应,使得导体交界面电流密度增大[18]。所以两极电机起动时,由于磁力线发生强烈扭曲,导致转子轭部感应大量与导条底部电流相位相反的涡流,二者感应电流产生的磁场相互作用,使得导条底部电流密度增大。
根据上文分析,忽略实心体齿部感应电流对笼型导条电流分布的影响,仅考虑位于导条正下方的实心体轭部透磁区域的感应电流对导条电流分布的影响,这是因为在同一极下,某一导条两侧的齿部区域感应电流方向相同,因此齿部感应电流在此导条中产生的磁场方向相反,相互抵消,所以可以近似忽略其影响来简化计算。图10为解析计算模型,将笼型导条分为n层,假设每层电流分布均匀,转子实心体齿部则分为三层,齿部与轭部的相对磁导率以及轭部透入深度通过2.1节解析计算方法可以求得。
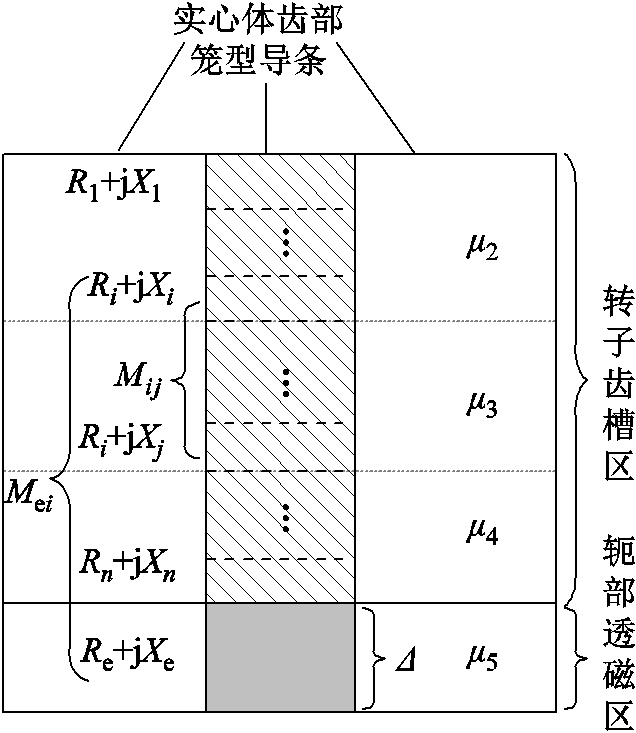
图10 导条电流密度分布解析计算模型
Fig.10 Analytical model of the current density distribution of the rotor bar
对模型做如下假设:①导条每层电阻率均取相同工作温度75℃下的电阻率;②为了简化计算,近似认为磁力线与导条的中心线垂直或平行,且经由实心体的磁通路径紧贴导条与实心体的交界面。
根据上述模型,通过磁路法计算笼型导条各层之间电阻、漏感及互漏感矩阵,并且通过计算转子轭部透磁区域的自感及其与导条的互感,来考虑轭部导电区域对笼型导条导电区域电流分布的影响,最后通过矩阵运算得出笼型导条电流的分布规律。
对于笼型导条,各层的电阻为
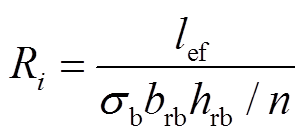 (3)
(3)式中,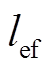 为实心铁心轴向长度。
为实心铁心轴向长度。
各层自漏抗可分为两部分,以i层为例;第一部分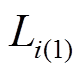 是i层电流产生的磁场穿过i层自身与部分电流交链所产生的漏抗,如图11中的1回路;第二部分
是i层电流产生的磁场穿过i层自身与部分电流交链所产生的漏抗,如图11中的1回路;第二部分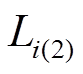 是i层电流产生的磁场穿过i层上方与i层所有电流交链所产生的漏抗,如图11的2回路所示[12]。以下给出自漏抗的推导,以i层电流底
是i层电流产生的磁场穿过i层上方与i层所有电流交链所产生的漏抗,如图11的2回路所示[12]。以下给出自漏抗的推导,以i层电流底
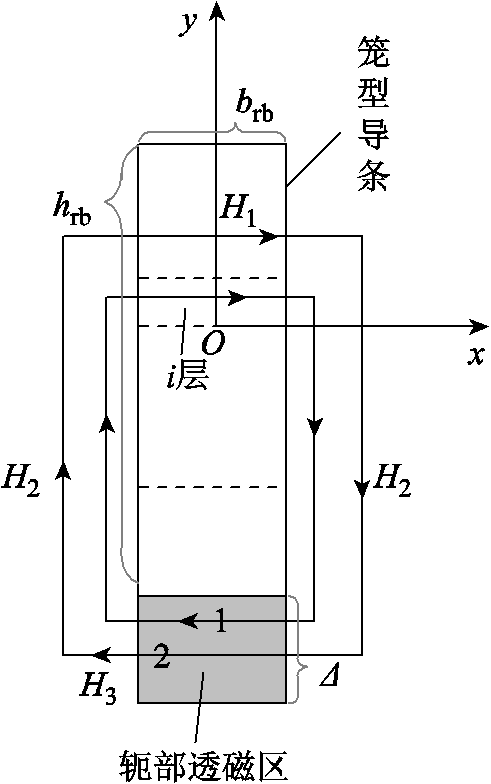
图11 自漏感的计算模型
Fig.11 The calculation model of the self leakage inductance
部中心为坐标轴原点。
根据安培环路定理及电感的计算公式可得
 (4)
(4)式中,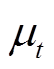 为齿部相对磁导率,根据磁路经过的路径的不同取值为
为齿部相对磁导率,根据磁路经过的路径的不同取值为 。对于
。对于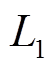 ,
,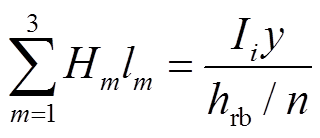 ;对于
;对于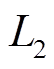 ,
,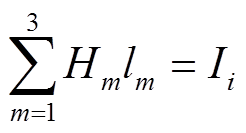 。
。
令
 (5)
(5)则
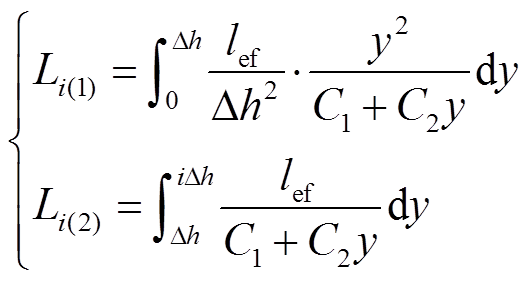 (6)
(6)可得
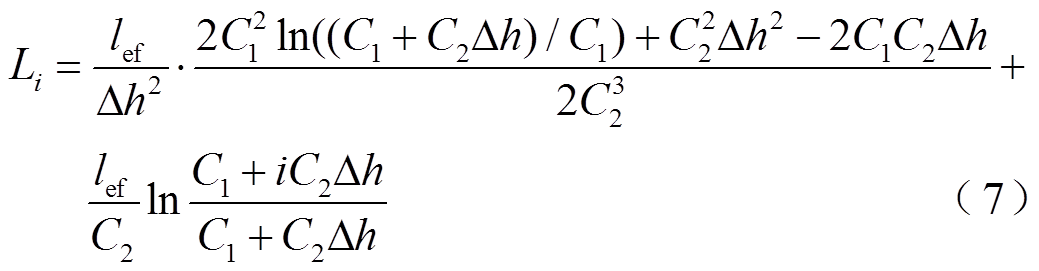
同理可得轭部的自漏感与电阻,此处不再推导。
各层间的互漏感也包含两部分,以第i层与第j层为例,其中i层电流位于j层电流上方,即i<j。第一部分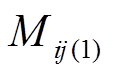 是第j层电流产生的磁场穿过第i层与第i层部分电流交链产生的互漏感,如图12的回路1,第二部分
是第j层电流产生的磁场穿过第i层与第i层部分电流交链产生的互漏感,如图12的回路1,第二部分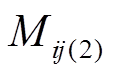 是与穿过第i层上方与第i层全电流交链所产生的互漏感,如图12的回路2 [12]。这里假设第n层电流相角为
是与穿过第i层上方与第i层全电流交链所产生的互漏感,如图12的回路2 [12]。这里假设第n层电流相角为 ,互漏感的计算方法如下。
,互漏感的计算方法如下。
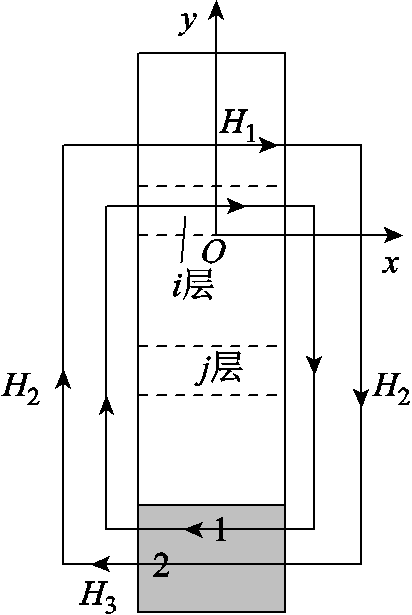
图12 互漏感的计算模型
Fig.12 The calculation model of the mutual leakage inductance
根据安培环路定理可得
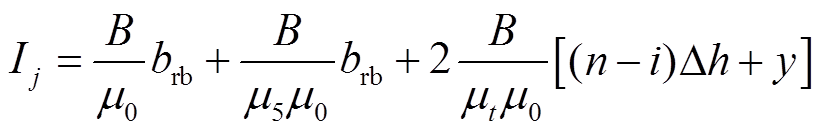 (8)
(8)第一部分互漏感对应的第i层的磁通为
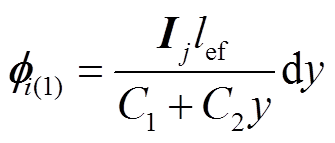 (9)
(9)其中
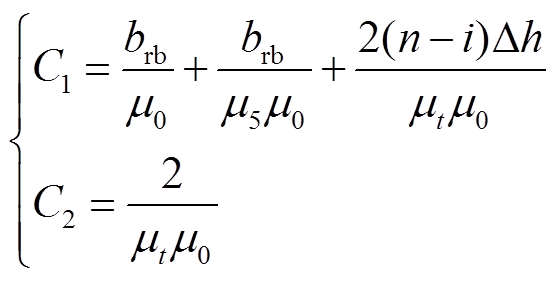 (10)
(10)所以该磁通与第i层部分电流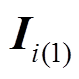 交链的互感磁能为
交链的互感磁能为
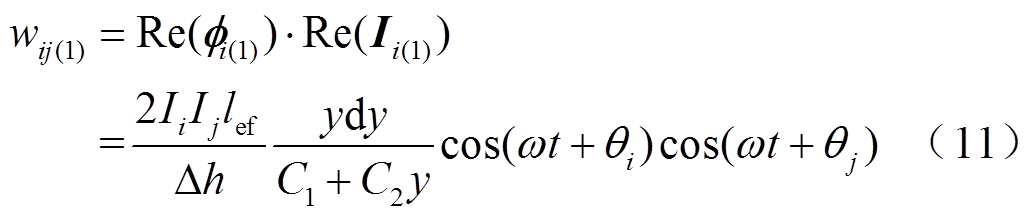
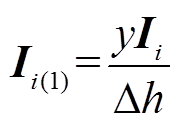 (12)
(12)一个周期内两者对应的互感磁能平均值为
 (13)
(13)所以根据能量法,由总互感磁可以求出第一部分互漏感为
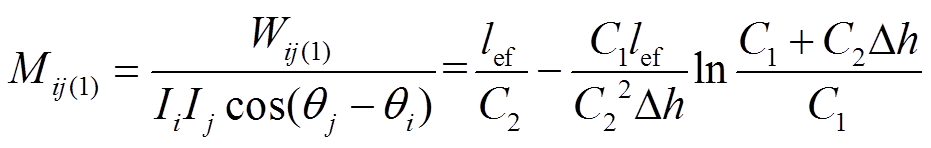 (14)
(14)同理可得第二部分互漏感为
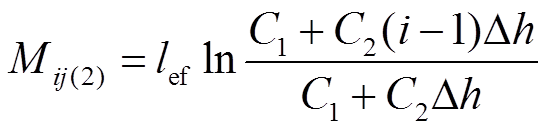 (15)
(15)轭部与导条第i层间的互漏感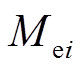 也可通过上述方法计算。
也可通过上述方法计算。
由此可得到n+1阶的阻抗矩阵Z为
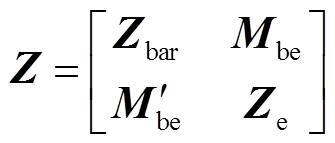 (16)
(16)其中
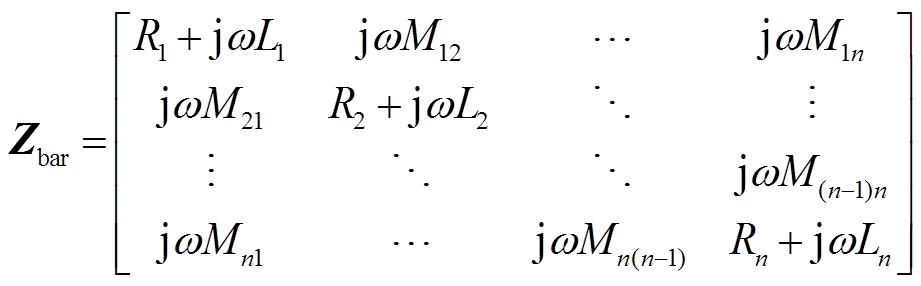 (17)
(17)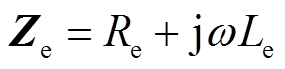 (18)
(18)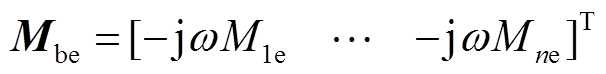 (19)
(19)最后通过求解式(20)的矩阵方程得到电流矩阵,电流矩阵前n行即是笼型导条电流密度的分布规律。
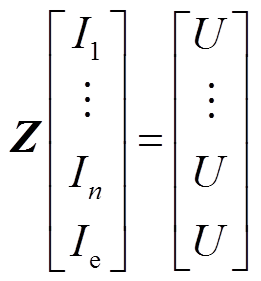 (20)
(20)本文提出的解析计算方法在计算笼型导条电流密度分布时,考虑了电机起动时转子实心体齿部与轭部的磁场饱和现象及转子轭部感应涡流对笼型导条电流分布的影响;而传统的计算方法[9,12]在计算导条各层自漏抗和互漏抗时,忽略了磁路在转子实心体处齿部与轭部的磁压降,并且没有考虑实心体轭部感应涡流的影响。
根据2.3节笼型导条电流密度分布解析计算方法中的公式,结合2.1节二维多层电磁场解析计算模型所求得的实心体齿部相对磁导率 与轭部透磁区域的相对磁导率
与轭部透磁区域的相对磁导率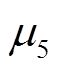 ,以及轭部透磁区域的深度
,以及轭部透磁区域的深度 ,可以通过解析计算求得笼型导条电流密度的分布规律。表1给出本文所研究的电机在定子绕组两极接法下起动时,转子侧各层区域的关键参数值。
,可以通过解析计算求得笼型导条电流密度的分布规律。表1给出本文所研究的电机在定子绕组两极接法下起动时,转子侧各层区域的关键参数值。
表1 电机转子侧各区域关键参数
Tab.1 The key parameters of the rotor side regions of the motor
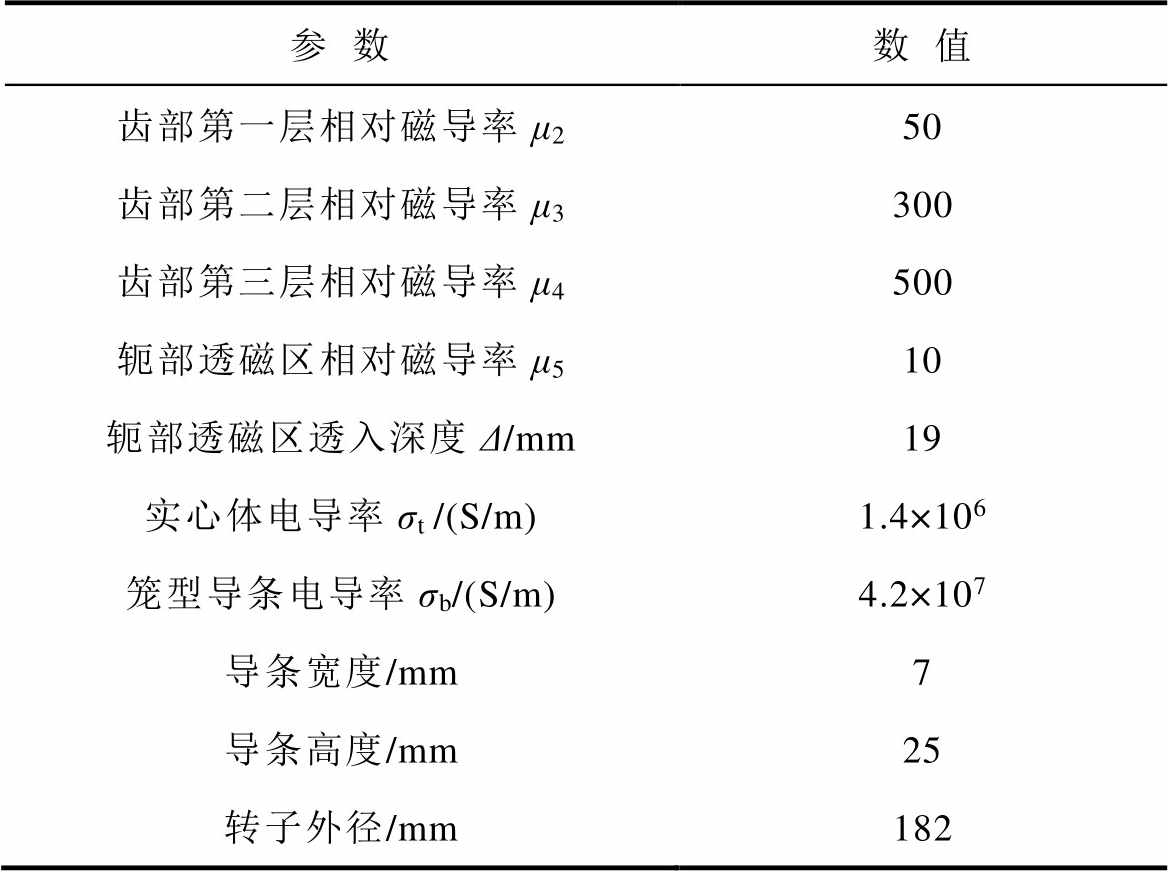
参数数值 齿部第一层相对磁导率μ250 齿部第二层相对磁导率μ3300 齿部第三层相对磁导率μ4500 轭部透磁区相对磁导率μ510 轭部透磁区透入深度Δ/mm19 实心体电导率σt/(S/m)1.4×106 笼型导条电导率σb/(S/m)4.2×107 导条宽度/mm7 导条高度/mm25 转子外径/mm182
将新的解析计算方法推导的笼型导条电流密度分布与有限元仿真结果及传统解析计算方法的结果对比,电机定子侧三相交流相电压有效值为220V,频率是50Hz。三者对比结果如图13所示。三者均取有限元仿真结果的最小电流密度值作为基准值。可以看出,传统解析计算方法在求解电机定子绕组两极接法起动下笼型导条电流密度的分布规律时,误差较大且变化规律与有限元结果相去甚远。而采用本文所提出的解析计算方法则可以较为精确地求解导条电流分布,其结果与有限元仿真结果平均误差为12.4%,而传统计算方法误差高达39.7%,并且无法精确计算电流密度的分布规律。
本文在电机电磁场解析计算时,将转子齿部按
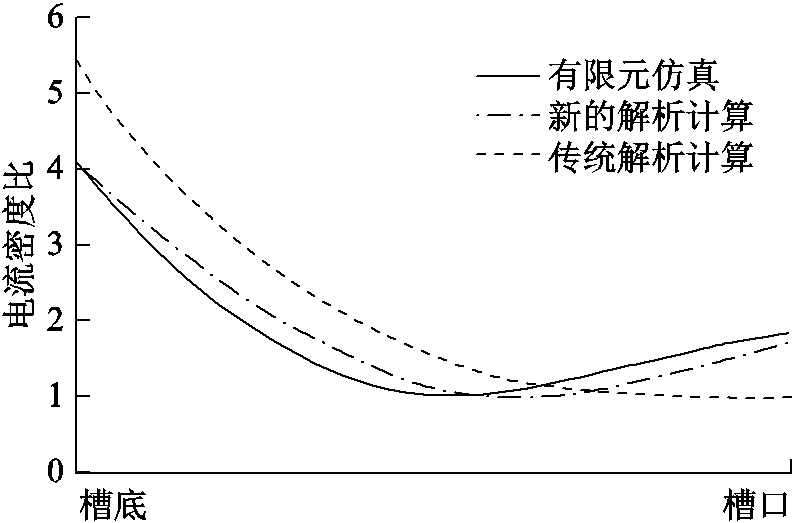
图13 解析计算与有限元仿真分析所得导条电流密度对比图
Fig.13 The comparison of the starting current density distributuion of the rotor bar between the analytical method and finite element analysis
照磁场饱和程度的不同分为三层区域,下面对比转子齿部不分层及齿部分为五层时,笼型导条电流密度分布规律的计算精度,结果如图14所示。当齿部不考虑分层时,导条电流分布计算结果与有限元仿真结果平均误差为13.64%;进一步将齿部细分为五层时,平均误差减小到12.32%。
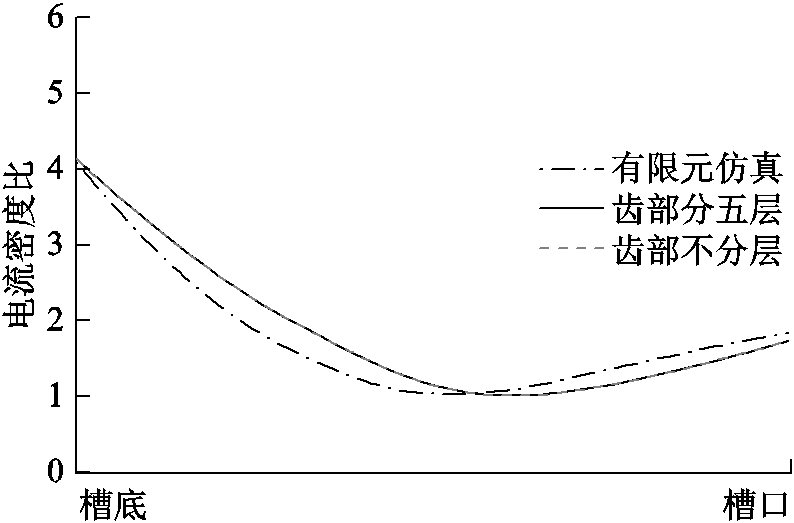
图14 齿部不同分层数的解析计算结果对比图
Fig.14 The comparison of analytical calculation results with different layer in rotor teeth
本文提出的解析计算方法与传统方法的最大不同之处在于考虑了转子实心体轭部透磁区域的感应涡流对笼型导条电流分布的影响。图15给出齿部分为三层,不考虑轭部感应涡流影响时,笼型导条电流密度分布规律的计算精度。
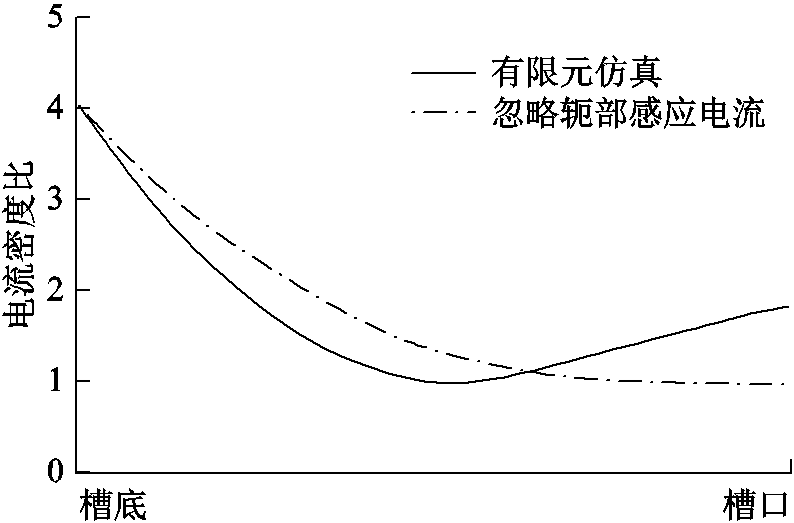
图15 忽略轭部感应电流的解析计算与有限元仿真所得电流密度对比图
Fig.15 The comparison of the current density distributuion between the finite element analysis and analytical method neglecting the induced current in rotor yoke
从上述计算结果可见,为求解笼型实心转子感应电机定子绕组两极接法起动时笼型导条电流密度的分布规律,最重要的是要考虑实心体轭部透磁区域产生的感应涡流对笼型导条电流分布的影响。如果忽略轭部感应涡流的影响,则无法精确计算导条电流密度由槽口至槽底呈现先减小后增大的不对称U型分布规律。而通过对实心体齿部进行分层来考虑磁场的饱和效应则可以提高计算精度。传统方法并没有考虑轭部感应涡流的影响,因而无法准确计算电机在两极起动时笼型导条电流密度的分布规律。
为了验证计算模型的通用性,对比两极笼型实心转子感应电机降压起动时,笼型导条电流的分布情况,电机定子侧三相交流相电压有效值为80V,频率是50Hz,结果如图16所示,平均误差为7.53%,对于传统解析计算方法,误差则是25.9%。而对于六极的情况,解析计算结果与有限元仿真分析结果如图17所示,平均误差仅为0.39%,而传统计算方法的误差为1.16%。可见,本文的方法在计算非两极电机起动下笼型导条电流密度的分布规律时的精度略有提高。
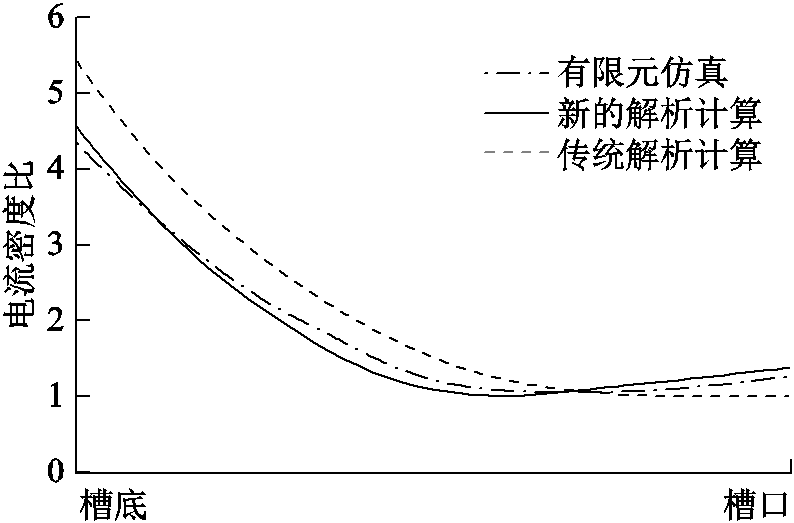
图16 降压起动时导条电流密度对比
Fig.16 The comparison of the reduced voltage starting current density distributuion of the rotor bar
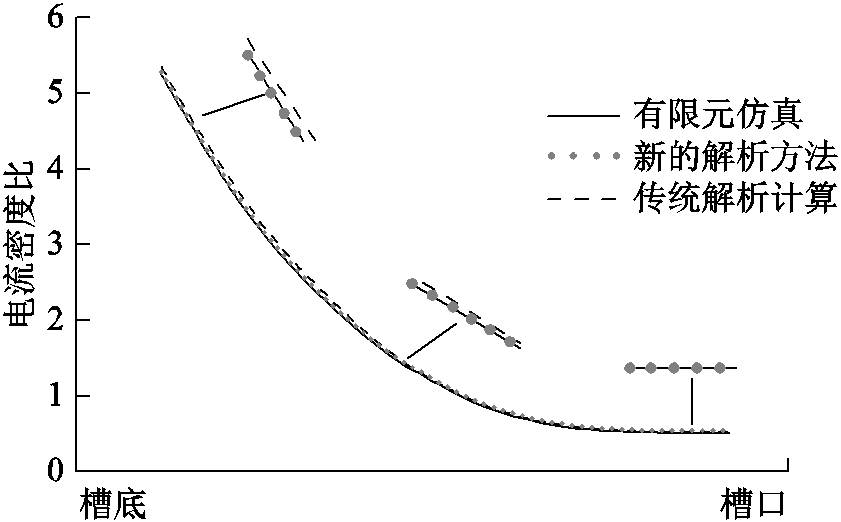
图17 六极电机导条的起动电流分布对比
Fig.17 The comparison of the starting current density distributuion of the rotor bar of six poles motor
综上所述,传统的解析计算方法在计算非两极笼型实心转子感应电机起动时,笼型导条电流密度的分布精度很高,但是无法准确计算两极的情况。对于两极电机,本文所提出的解析计算方法则能够较为精确地计算电流密度分布,解析计算结果与有限元仿真结果相比,导条电流密度分布整体右移。由2.2节和2.3节解析模型的简化与电感系数的推导可以看出,由于对磁路做出简化导致磁路路径减小,导条自感与互感计算值偏大。由矩阵计算可以看出自感增大会导致导条电流密度曲线整体右移,互感增大会导致曲线整体下移。
其他产生误差的原因还包括:即使考虑了转子实心体齿部与轭部的饱和效应,仍然是对磁路进行了简化,认为每一层的相对磁导率是均匀的,两极电机在起动时转子齿部与轭部的磁场饱和现象非常明显,所以转子表面到轭部磁路的磁导率差异很大,如图6所示;在考虑轭部电流对笼型导条电流的影响时,为了简化计算,将轭部电流近似看成与槽底导条电流反相,而实际情况如图9所示,并非完全反相;还有一个原因是忽略了转子实心体齿槽区域感应电流对导条电流分布的影响,从而引入了误差。
本文结合笼型实心转子感应电机在定子绕组两极接法下起动运行时磁场分布的特点,建立了考虑电机起动时转子实心体局部磁场饱和效应、实心体轭部感应电流对笼型导条感应电流的影响的解析计算模型,较为精确地计算笼型实心转子感应电机在起动时的导条电流密度分布。所建立的解析模型适用于不同极对数的笼型实心转子感应电机在不同电压下起动时笼型导条电流密度分布的计算,特别是解决了传统的计算方法无法精确计算笼型实心转子感应电机在定子绕组两极接法下起动时笼型导条电流密度的分布规律的问题,显著提高了计算精度。对于电机在非两极起动时,计算的准确度略有提高。
参考文献
[1]崔旭, 司纪凯, 封海潮, 等. 大小极环形绕组实心转子感应电机工作机理及电磁特性分析[J]. 电工技术学报, 2019, 34(9): 1850-1856. Cui Xu, Si Jikai, Feng Haichao, et al. Operating principle and electromagnetic characteristic analysis for large-small pole solid-rotor induction motor with toroidal windings[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1850-1856.
[2]李伟力, 曹君慈, 丁树业, 等. 复合笼型转子感应电动机起动性能的数值计算[J]. 电工技术学报, 2004, 19(7): 26-31. Li Weili, Cao Junci, Ding Shuye, et al. Numerical calculation of starting performance of the induction motor with compound cage rotor[J]. Transactions of China Electrotechnical Society, 2004, 19(7): 26-31.
[3]凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(一): 等效电路及其参数分析[J]. 电工技术学报, 2018, 33(15): 3518-3526. Ling Zaixun, Zhou Libing, Zhang Yi, et al. Parameters determination and electromagnetic field analysis of canned solid-rotor induction motor (1): an overview of motor'sequivalent circuit and its parameter analysis methods[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3518-3526.
[4]Bir O, Bohm P, Preis K, et al. Edge finite element analysis of transient skin effect problems[J]. IEEE Transactions on Magnetics, 2000, 36(4): 835-839.
[5]Yang Rui, Zhou Libing, Wang Jin, et al, et al. Performance calculation for a canned solid-rotor induction motor with squirrel-cage[C]//International Conference on Electrical Machines and Systems,Sydney, 2017: 1-5
[6]凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(三): 实用等效电路及其参数的推导[J]. 电工技术学报, 2018, 33(19): 4496-4507.
Ling Zaixun, Zhou Libing, Zhang Yi, et al. Parameters determination and electromagnetic field analysis of canned solid-rotor induction motor(3): practical equivalent circuit and its parameter analysis[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4496-4507.
[7]陈世坤. 电机设计[M]. 北京: 机械工业出版社, 1990.
[8]Boglietti A , Cavagnino A , Lazzari M. Computational algorithms for induction motor equivalent circuit parameter determination—part II: skin effect and magnetizing characteristics[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 3734-3740.
[9]吴新振, 王祥珩. 异步电机双笼转子导条趋肤效应的计算[J]. 中国电机工程学报, 2003, 23(3): 116-120. Wu Xinzhen, Wang Xiangheng. Calculation of skin effect for double-cage rotor bar of the induction machine[J]. Proceedings of the CSEE, 2003, 23(3): 116-120.
[10]Yang Tong, Zhou Libing, Wei Jiang. Calculation of eddy current losses in a solid-rotor cage induction motor by finite element analysis[C]//International Conference on Electrical Machines and Systems, Wuhan, 2008: 3656-3659.
[11]严登俊, 刘瑞芳, 李伟. 有限公式法二维涡流场计算技术及其在电机趋肤效应计算中的应用[J]. 中国电机工程学报, 2008, 28(9): 133-138. Yan Dengjun, Liu Ruifang, Li Wei. Finite formulation computation technology for 2D eddy current field and application for skin effect in squirrel cage motor[J]. Proceedings of the CSEE, 2008, 28(9): 133-138.
[12]杨瑞. 笼型实心转子屏蔽电机起动参数及特性计算[D]. 武汉: 华中科技大学, 2018.
[13]黄加明. 深槽式双笼型异步电动机启动性能改善的机理研究[J]. 电气传动自动化, 2016, 38(2): 38-40. Huang Jiaming. Research on the mechanism of improving the startup performance to the deep grooves on double cage asynchronous motors[J]. Electric Drive Automation, 2016, 38(2): 38-40.
[14]唐孝镐, 宁玉泉, 傅丰礼. 实心转子异步电机及其应用[M]. 北京: 机械工业出版社, 1991
[15]黄子果, 王善铭, 孙宇光, 等. 开槽实心转子电机的等效电路参数计算与性能分析[J]. 中国电机工程学报, 2017, 37(4): 1208-1215. Huang Ziguo, Wang Shanming, Sun Yuguang, et al. Equivalent-circuit parameter calculations and performance analysis of slit solid rotor asynchronous machines[J]. Proceedings of the CSEE, 2017, 37(4): 1208-1215.
[16]凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(二): 二维多层电磁场模型及其解析计算[J]. 电工技术学报, 2018, 33(17): 4016-4028. Ling Zaixun, Zhou Libing, Zhang Yi, et al. Parameters determination and electromagnetic field analysis of canned solid-rotor induction motor(2): 2D-multilayer electromagnetic model and its analytical calculation[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4016-4028.
[17]凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(四): 等效电路参数有限元计算法及验证[J]. 电工技术学报, 2018, 33(21): 4987-4997. Ling Zaixun, Zhou Libing, Zhang Yi, et al. Parameters determination and electromagnetic field analysis of canned solid-rotor induction motor (4): equivalent parameters calculation by finite element method and its verificatio[J]. Transactions of China electrote-chnical Society, 2018, 33(21): 4987-4997.
[18]张国权, 徐月朗. 开关电源中线圈的邻近效应研究[J]. 中国高新技术企业, 2010(4): 911. Zhang Guoquan, Xu Yuelang. Research on proximity effect of coil in switching power supply[J]. China Hi-Tech Enterprises, 2010(4): 9-11.
Analytical Calculation of Rotor Bar Current Distribution in Starting Condition of Cage Solid-Rotor Machine Considering the Effect of Eddy Current in Solid-Rotor
Abstract The induced current of solid-rotor and rotor bar of cage solid-rotor induction machine coupled with each other. Especially during the start-up process of two-pole machine, the current density of rotor bar shows an asymmetric U-shaped distribution due to the current of solid-rotor, decreasing first and then increasing from the top to the bottom of the slot. The traditional calculation method leads to large calculation error, affecting the accuracy of machine design. In this paper, a two-dimensional multilayer electromagnetic field analysis model that considered the effects of magnetic field saturation is established to solve the magnetic field distribution under starting condition. On this basis, considering the influence of the induced current of the rotor core yoke, an analytical calculation model was established to solve the current density distribution of rotor bar during the starting operation. Finally, by comparing with the finite element simulation, the accuracy of the calculation of the current density distribution was verified when the machine was started at different voltages. The proposed analytical calculation method is applicable to cage solid-rotor induction machines with different pole-pairs and provides a reference for accurate calculation of starting parameters and performance of the machine.
keywords:Cage solid-rotor, analytical calculation, start-up, current density distribution
中图分类号:TM32
DOI:10.19595/j.cnki.1000-6753.tces.200147
国家重点研发计划资助项目(2018YFB0606001)。
收稿日期 2020-02-17
改稿日期 2020-06-18
郑印钊 男,1994年生,硕士,研究方向为电机设计与电机电磁场计算。E-mail:yzzheng@hust.edu.cn
王 晋 男,1979年生,副教授,研究方向为大型与特种电机。E-mail:jinwang@hust.edu.cn(通信作者)
(编辑 赫蕾)