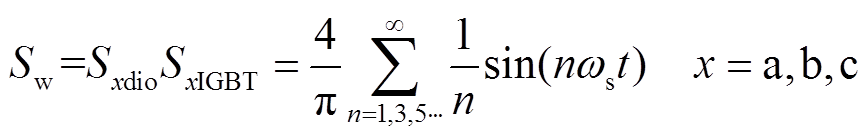 (1)
(1)式中,ωs为高频方波信号的角频率。
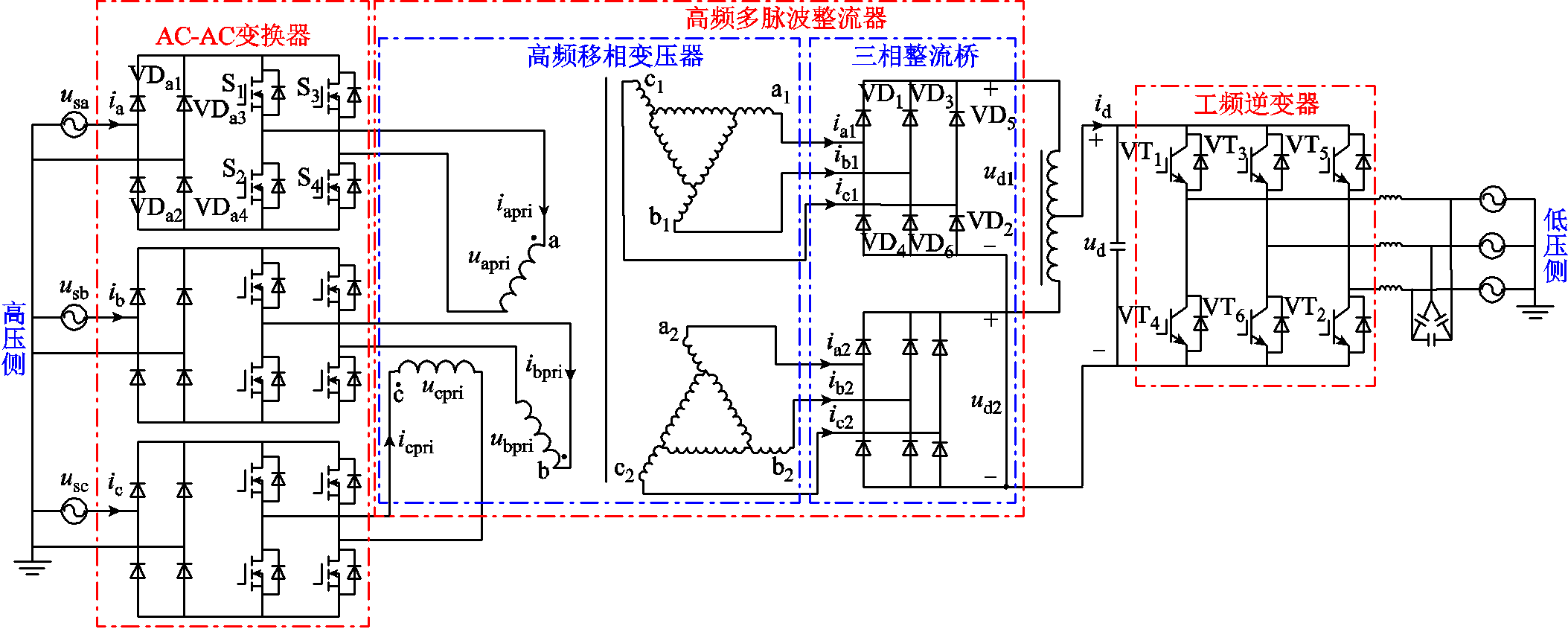
图1 基于固态变压器的移动变电站拓扑
Fig.1 Mobile substation topology based on solid state transformer
摘要 为减小移动变电站中主变压器的体积和质量,提高移动变电站的高压侧电能质量,提出一种用于移动变电站的固态变压器拓扑。所提出的固态变压器由AC-AC变换器、高频多脉波整流器、工频逆变器三部分组成,该文首先分析了AC-AC变换器的工作原理,并从降低开关损耗的角度出发,设计其控制策略;然后从磁路和电路对称的角度出发,设计用于高频多脉波整流器的移相变压器,并应用开关函数法计算固态变压器的输入电流和输出电压;最后设计固态变压器中AC-AC变换器的控制和驱动电路,搭建了移动变电站的缩比仿真和实验平台。仿真和实验结果表明,使用固态变压器代替传统的工频主变压器后,主变压器体积减小了三分之二,其体积和质量得到显著降低;使用所设计的三相五芯柱变压器作为移相变压器后,固态变压器的输入电流总谐波畸变率(THD)值由22%降到了16%,有效提高了移动变电站的电能质量。
关键词:移动变电站 固态变压器 AC-AC变换器 高频多脉波整流器 移相变压器
移动变电站具有容量配置和选址灵活、快速移动性、结构紧凑、可快速并网等优点,能够有效弥补地区性、时段性的电力供应不足,在事故抢修、自然灾害救援、变电站负荷转供、铁路牵引等场合得到了越来越广泛的应用[1-2]。主变压器容量大(功率密度低)及大量一次设备和二次设备导致的移动变电站整体体积大(超宽、超重、超高)等不足一直影响着移动变电站的现场投运[3-4]。
现有移动变电站包括主变压器模块、自动控制保护模块、中压配电模块及运输车辆等[2]。考虑运输和安装方便性的要求,移动变电站各组成部分要尽可能小型化、模块化,尤其是主变压器的小型化。主变压器工作在工频状态,在大功率场合,其铁心体积大,是导致移动变电站整体体积大的主要原因。在保证容量的前提下,主变压器的小型化和紧凑化设计可以减轻其质量和压缩其占用的空间[3]。近年来,有学者提出了使用自耦变压器代替传统的隔离型主变,自耦变压器各绕组之间交互连接,通过磁耦合传递的功率仅占负载功率的一小部分,这会显著降低变压器的体积和容量[5-6]。但是,自耦变压器的输入与输出端之间没有电气隔离,当其应用于输出与输入电压等级差别比较大的场合时,会存在安全问题。另一方面,传统主变压器功能单一,仅有电压等级变换和电气隔离功能。为实现电能质量管理,移动变电站需配备电能质量控制装置,如交流侧无功补偿及谐波抑制装置,这也增加了移动变电站的体积和质量[7]。
固态变压器集成了电力电子变换器和高频变压器,不仅具有传统交流变压器的电压等级变换和电气隔离功能,同时具有交流侧无功补偿及谐波抑制、可再生能源/储能设备直接接入、端口间故障隔离等功能[9-14]。与集成了工频变压器及电能质量治理功能的传统移动变电站相比,固态变压器在效率、成本、功率密度和电能质量管理等方面具有明显优势,特别适用于移动变电站[14]。现有三相高频隔离变压器与电力电子变换器相结合组成固态变压器时,由于磁路和电路结构不对称,导致固态变压器输入电能质量较低。为此,本文提出一种应用于移动变电站的固态变压器拓扑,该拓扑由AC-AC变换器、高频多脉波整流器和工频逆变器三部分组成。所提出的固态变压器使用高频多脉波整流器中的移相变压器作为主变压器,有效降低了主变压器的体积和质量;移相变压器使用三相五芯柱铁心,保证了磁路的对称;移相变压器的二次绕组结构使用延边三角形联结,保证了电路的对称;AC-AC变换器使用方波控制,有效降低了开关损耗。上述研究有效提高了固态变压器的综合性能。
图1所示为基于固态变压器的移动变电站的主电路拓扑。图1中,固态变压器由AC-AC变换器、高频多脉波整流器、工频逆变器三部分组成。与传统的隔离型主变压器相比,图1中高频多脉波整流器所用的移相变压器工作于高频状态,所需铁心材料少,其体积和质量大幅降低;该移相变压器采用三相五芯柱形式,二次绕组为延边三角形联结,有效解决了三芯柱移相变压器绕组结构不对称和磁路不平衡的问题;同时,AC-AC变换器中的H桥使用SiC MOSFET,能够有效提高AC-AC变换器的效率。
图1中,AC-AC变换器由单相二极管整流桥和H桥组成,可实现低频交流电到高频交流电的频率变换;当输入电压较高时,AC-AC变换器可采用级联形式。在频率变换过程中,使用等占空比的高频方波信号对H桥进行控制,将网侧工频电压切分为高频电压,使用方波控制有利于降低H桥的开关损耗。图2所示为AC-AC变换器的开关函数波形。图2中,Sadio为单相二极管整流桥的开关函数,SaIGBT为H桥的开关函数,Sw为AC-AC变换器的开关函数。
根据图2,可得AC-AC变换器开关函数为
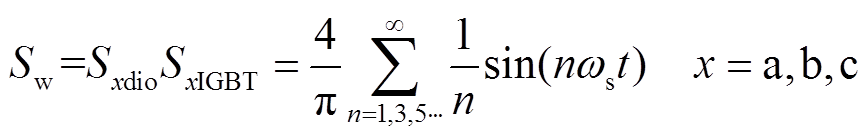 (1)
(1)式中,ωs为高频方波信号的角频率。

图1 基于固态变压器的移动变电站拓扑
Fig.1 Mobile substation topology based on solid state transformer
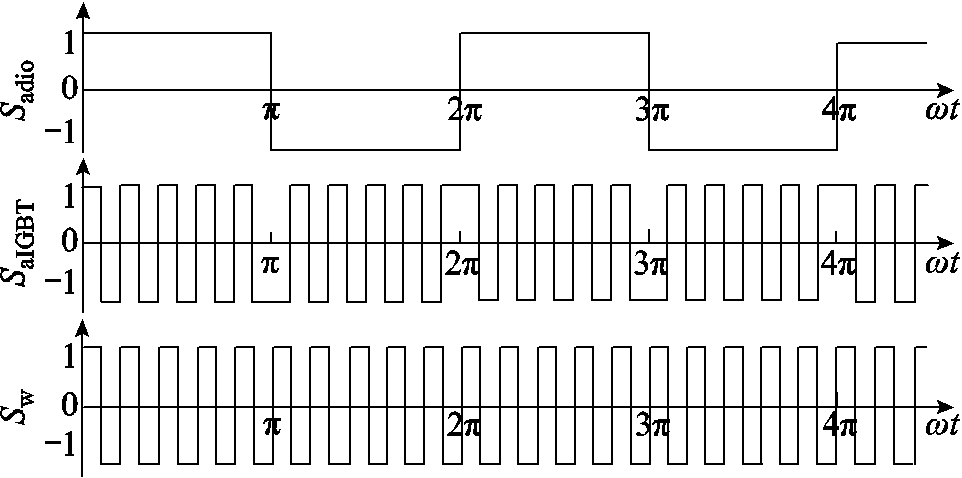
图2 AC-AC变换器各部分的开关函数波形
Fig.2 Switching function of the AC-AC converter
图1中,高频多脉波整流器由三相五芯柱移相变压器和两组三相整流桥组成,其功能是将AC-AC变换器输出的高频交流电进行整流。三相五芯柱移相变压器的主要功能有三个:提供电气隔离;升降压;对AC-AC变换器的输出电压进行移相,输出两组存在30o相位差的三相电压。图3所示为三相五芯柱移相变压器的绕组结构及其相量图。三相五芯柱移相变压器带有两个旁轭芯柱,可为零序磁通提供流通通道,从而减少电路中的零序电流。
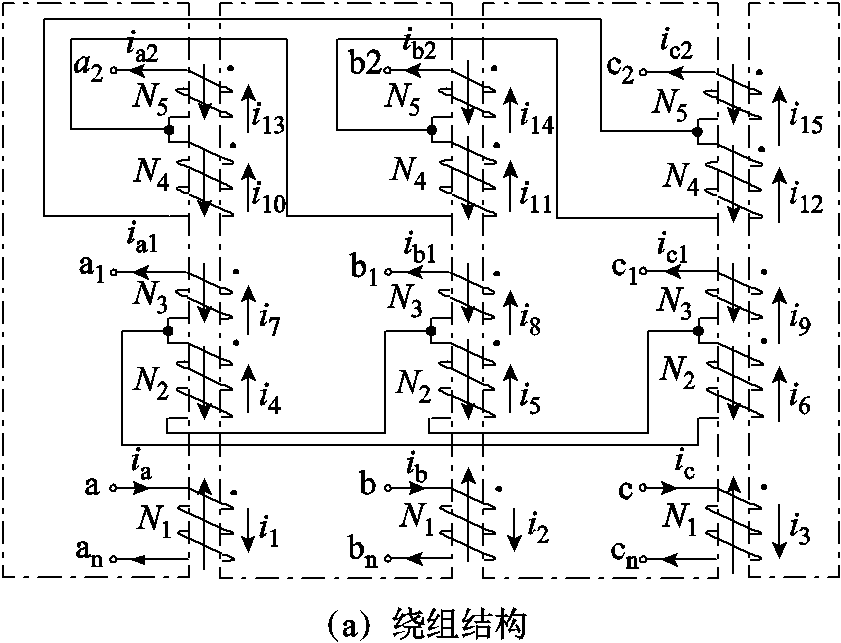
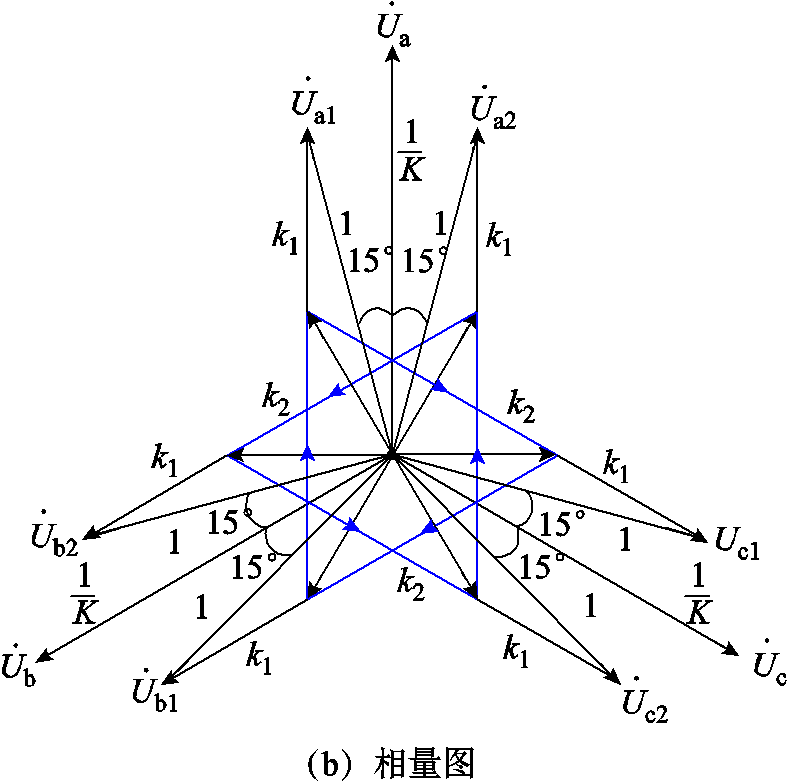
图3 三相五芯柱移相变压器的绕组结构及其相量图
Fig.3 Winding configuration phase diagram of the three-phase five core limb transformer
为便于分析,假设图3b中二次侧输出电压的幅值为单位1,延边绕组的电压幅值为k1,二次侧三角形绕组的线电压幅值为k2。
为使移相变压器输出的两组三相电压存在30°的相位差,k1和k2应为
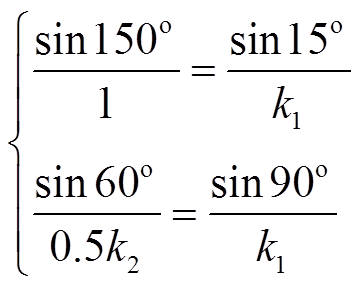 (2)
(2)由式(2)可得
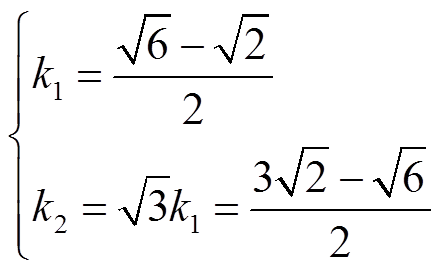 (3)
(3)结合图3a,移相变压器的电压比K与其绕组的匝数关系应为
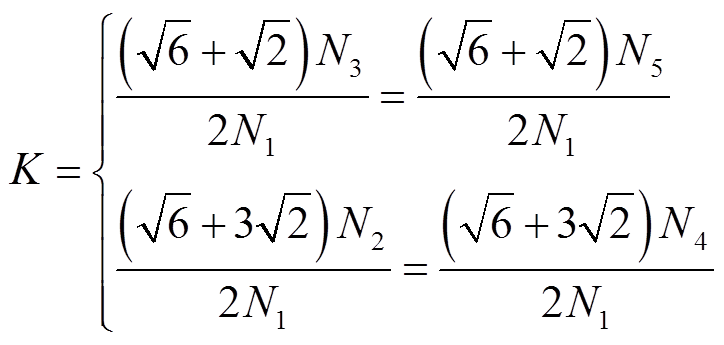 (4)
(4)由式(2)和式(4)可知,根据整流器对移相变压器移相角的要求,可计算出k1和k2的大小;依据整流器对移相变压器升降压的要求,可确定电压比K。
图3中,根据KCL和安匝平衡原理,可得
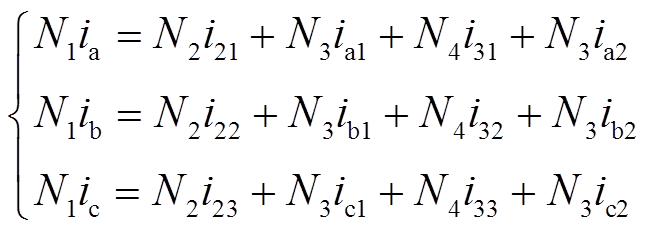 (5)
(5)式中,ia、ib、ic为三相五芯柱移相变压器的一次绕组电流;i21、i22、i23、ia1、ib1、ic1、i31、i32、i33、ia2、ib2、ic2为各二次绕组电流。
可以证明,ia、ib、ic与固态变压器的输入电流相等,限于篇幅问题,此处不再证明。
式(5)中,各绕组电流为
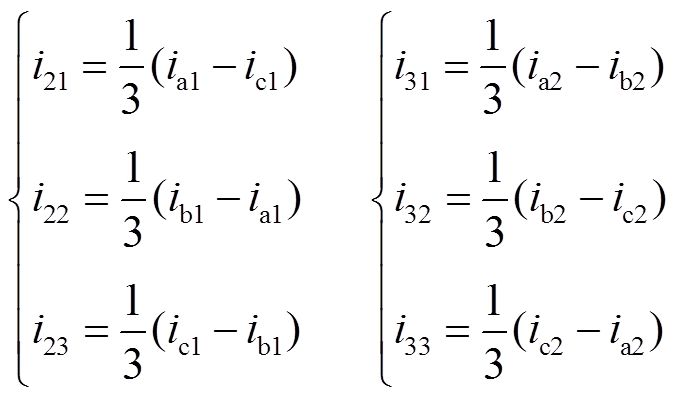 (6)
(6)根据开关函数的定义,可得高频移相变压器的六相输出电流为
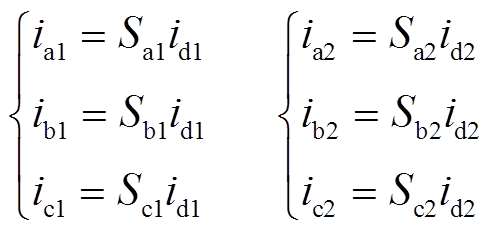 (7)
(7)式中,Sa1、Sb1、Sc1、Sa2、Sb2、Sc2分别为两组三相整流桥各相的开关函数。
假设工频逆变器的输入电流恒定,为Id,则两个三相整流桥的输出电流为
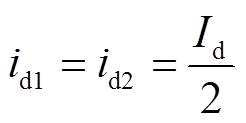 (8)
(8)将式(6)、式(7)代入式(5),可得整流器的输入电流为
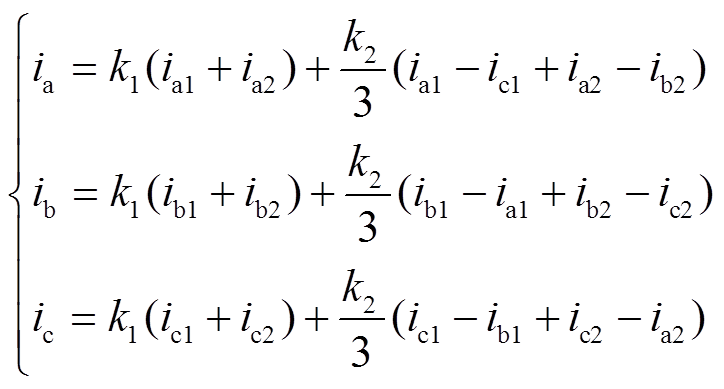 (9)
(9)根据式(8)及两组三相整流桥各相的开关函数,可计算固态变压器输入电流的Fourier级数表达式。以a相为例,其Fourier级数为
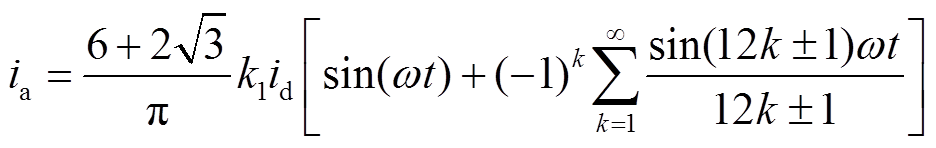
k=1, 2, 3, … (10)
根据式(10),在Matlab中可绘制输入电流的波形,如图4所示。由图4可知,固态变压器的输入电流为12阶梯波,与12脉波整流器相同,这表明固态变压器输入端的AC-AC仅起到提高三相五芯柱移相变压器输入电压频率的目的,而对固态变压器的输入电流没有影响。
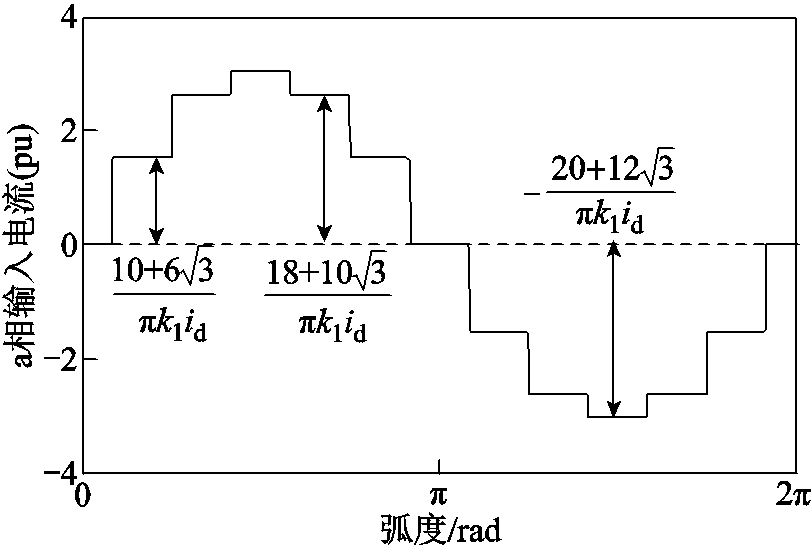
图4 固态变压器的a相输入电流
Fig.4 Input current of the solid state transformer
假设固态变压器的三相输入电压为
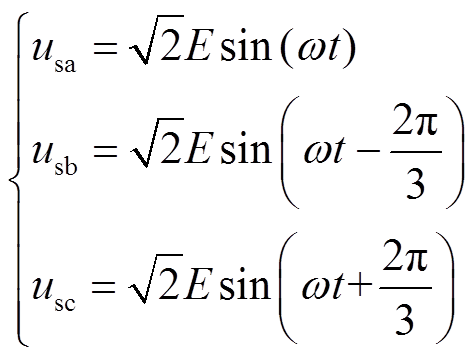 (11)
(11)式中,E为输入相电压的有效值;ω为三相交流电源的角频率。
根据图1、图3和式(1)、式(5),可得移相变压器二次绕组的输出电压为
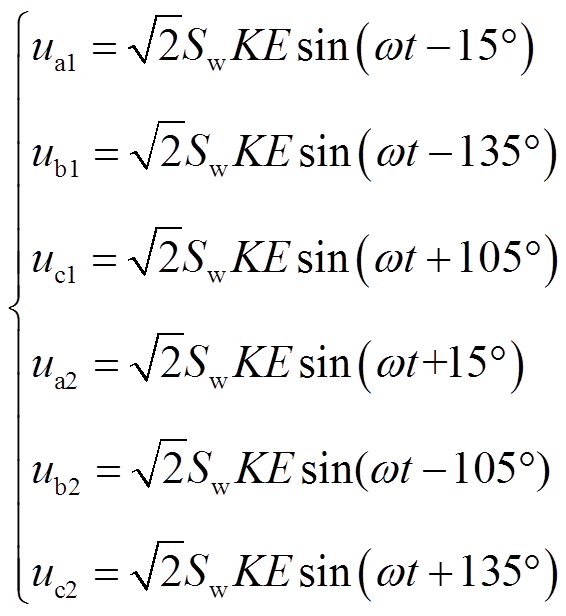 (12)
(12)根据调制理论,两个二极管整流桥的输出电压为
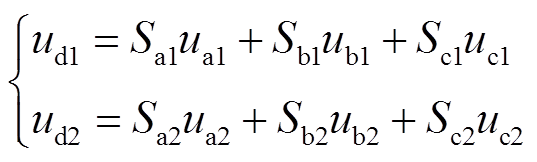 (13)
(13)式中,ud1、ud2为两个整流桥的输出电压。
将式(12)代入式(13),可得
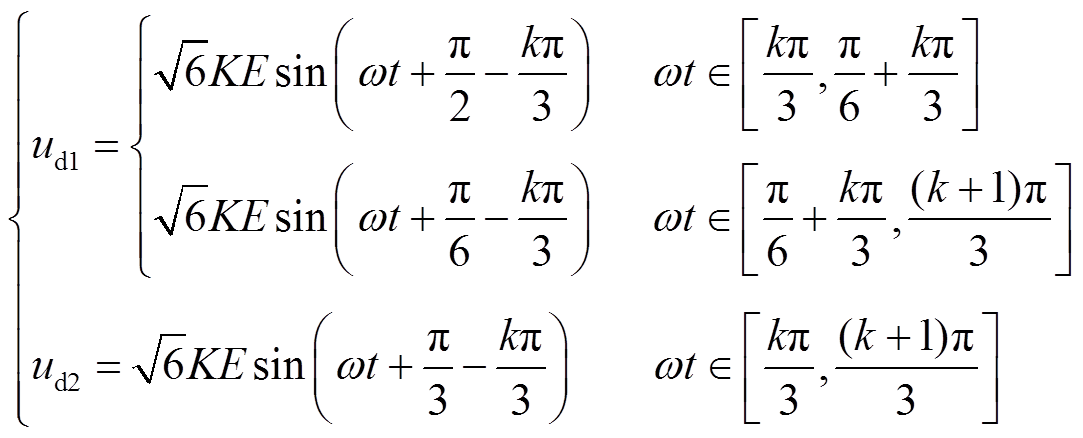 (14)
(14)式中,k=1, 2, 3…。
根据KVL,高频多脉波整流器的输出电压为
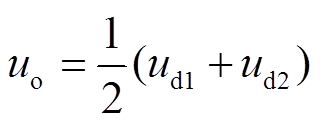 (15)
(15)将式(14)代入式(15),可得高频多脉波整流器的输出电压为
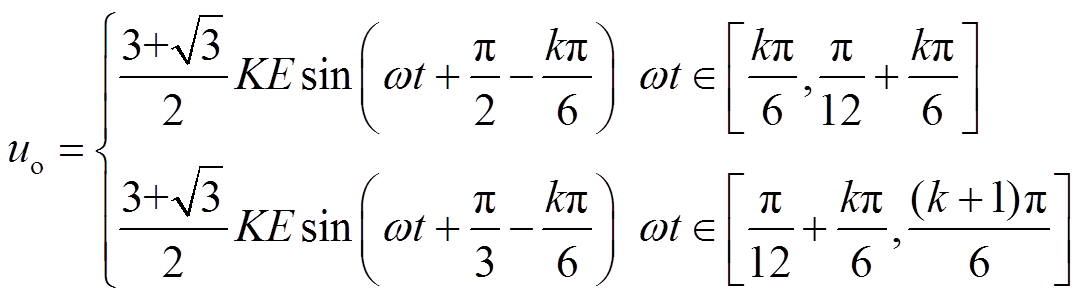 (16)
(16)根据式(16),在Matlab中绘制输出电压的波形,如图5所示。由图5可知,在一个电源周期内,高频多脉波整流器的输出电压含有12个波头,与传统工频12脉波整流器相同。
AC-AC变换器由单相二极管整流桥和H桥组成,经过单相不控整流和固定占空比控制的全桥逆变后将50Hz的低频交流电转换为500Hz的高频交流电,产生了式(1)中以开关函数Sw表示的高频电压谐波,高频电压谐波经移相变压器为两组三相整流桥供电,AC-AC变换器的开关函数与后级三相二极管整流桥的开关函数相乘后,消去了高频方波函数Sw,从而使图5中高频多脉波整流器的输出电压与工频多脉波整流器相同。根据以上分析可知,AC-AC变换器与移相变压器共同作用产生了高频谐波信号,而这些高频谐波信号与后级三相整流桥产生的谐波信号相互抵消,整流器中只剩下由三相整流桥二极管非线性所产生的12k±1次谐波。
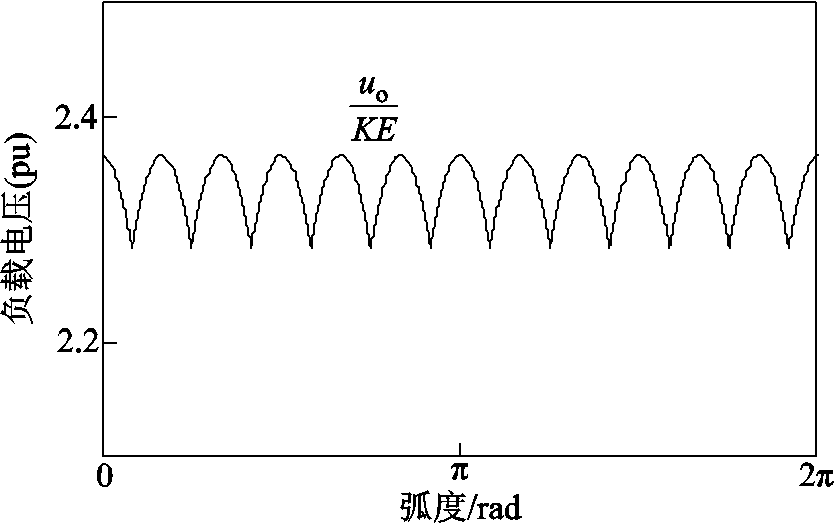
图5 高频多脉波整流器的输出电压
Fig.5 Output voltage of the high-frequency multi-pulse rectifier
AC-AC变换器的控制部分由电压相位采样电路、控制信号生成电路和驱动电路组成。
为精确控制AC-AC变换器中开关器件的通断,需采样移动变电站的输入电压相位。本文中,采样电路由单相同步变压器DTB3515和同向电压跟随器构成,如图6所示。
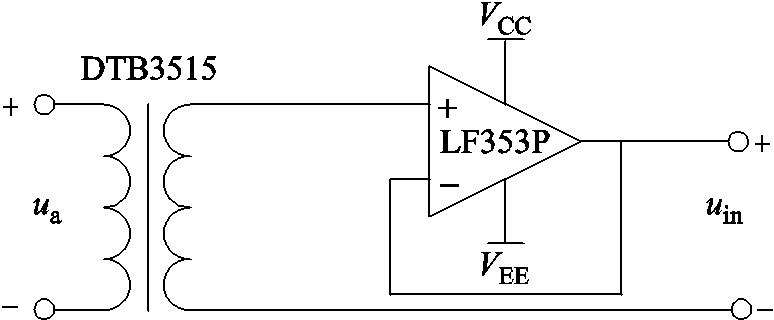
图6 电压相位采样电路
Fig.6 Sampling circuit of the input voltage phase
图6中,DTB3515检测输入电压,并隔离强、弱电信号;同向电压跟随器使用LF353P运算放大器,其可隔离同步电压信号和控制器。若主电路发生短路,LF353P将首先被击穿,输出直流信号给控制器,避免过电流信号对控制器输入端口的冲击,提高了采样电路的容错率。图7所示为电压采样波形,ua的有效值为120V,采样电压uin为6V。
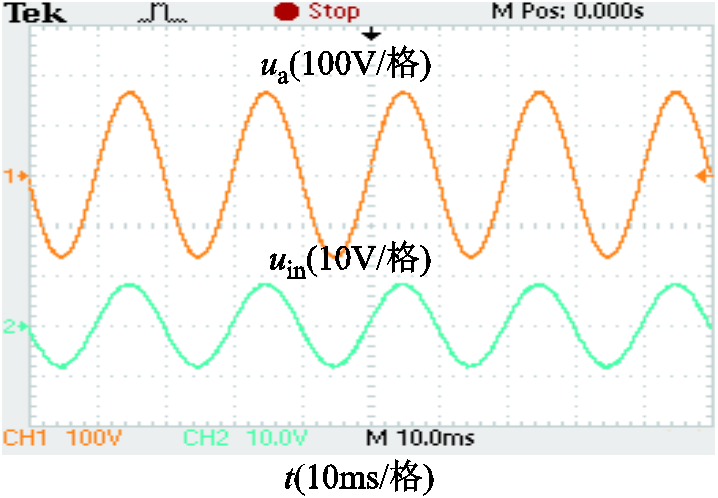
图7 电压相位采样波形
Fig.7 Sampled waveform of the input voltage phase
由图2可得
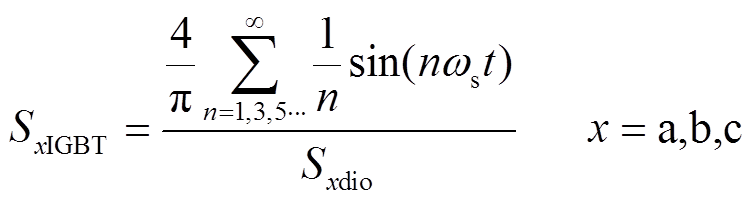 (17)
(17)根据图3和式(17),可绘制各相AC-AC变换器中H桥的开关函数,如图8所示。图8中,SaIGBT、SbIGBT、ScIGBT分别为a、b、c相AC-AC变换器中H桥的开关函数。由图8可知,当S=1时,VT1和VT4导通;当S=-1时,VT2和VT3导通。
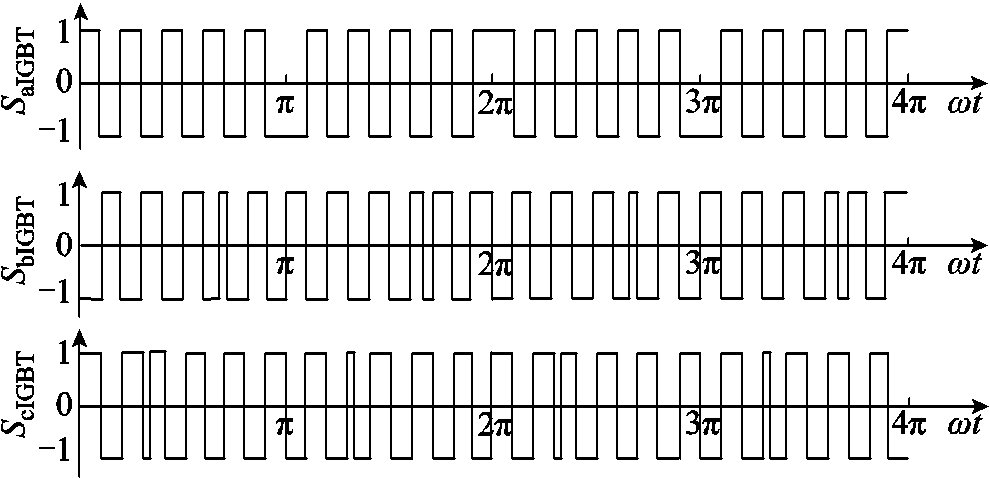
图8 H桥的开关函数
Fig.8 Switching function of the H bridge
根据图8所示的H桥的开关函数,可以得到控制算法的Simulink模型,如图9所示。图9中,控制器通过单相锁相环获取采样电压信号的相位信息,经查表模块完成方波信号的生成功能。
为降低实现难度,本文中控制信号由NI公司的快速控制原型(Rapid Prototype Control,RCP)实现。该算法模型首先在Matlab中编译为C语言底层代码,然后下载至MT RCP硬件控制器中,该控制器与实物硬件构成闭环,完成控制算法的实时运行。MT RCP硬件控制器的CPU结合FPGA的架构,K7-160T FPGA芯片的IO延迟低至ns级,可满足控制需求。电压相位采样电路将幅值和相位信息送入控制器,经CPU运算,可生成相应的控制信号。图10所示为控制器输出的AC-AC变换器的a相控制信号波形。
图1中,H桥的开关器件端电压等于二极管整流桥的输出电压,其峰值为高频多脉波整流器输入电压的峰值,电流峰值为输入电流的峰值。在本节中,假设高频多脉波整流器的输入电压峰值为170V,电流最大值为5A,工作频率为500Hz。考虑到开关器件开通和关断期间的过电压和过电流,本文选取英飞凌公司的IHW30N60T(600V, 30A)作为H桥的开关管。为正常驱动IHW30N60T,选取落木源公司的TX-KA103大功率IGBT驱动器作为驱动电路的主体。图11所示为驱动模块的电路。
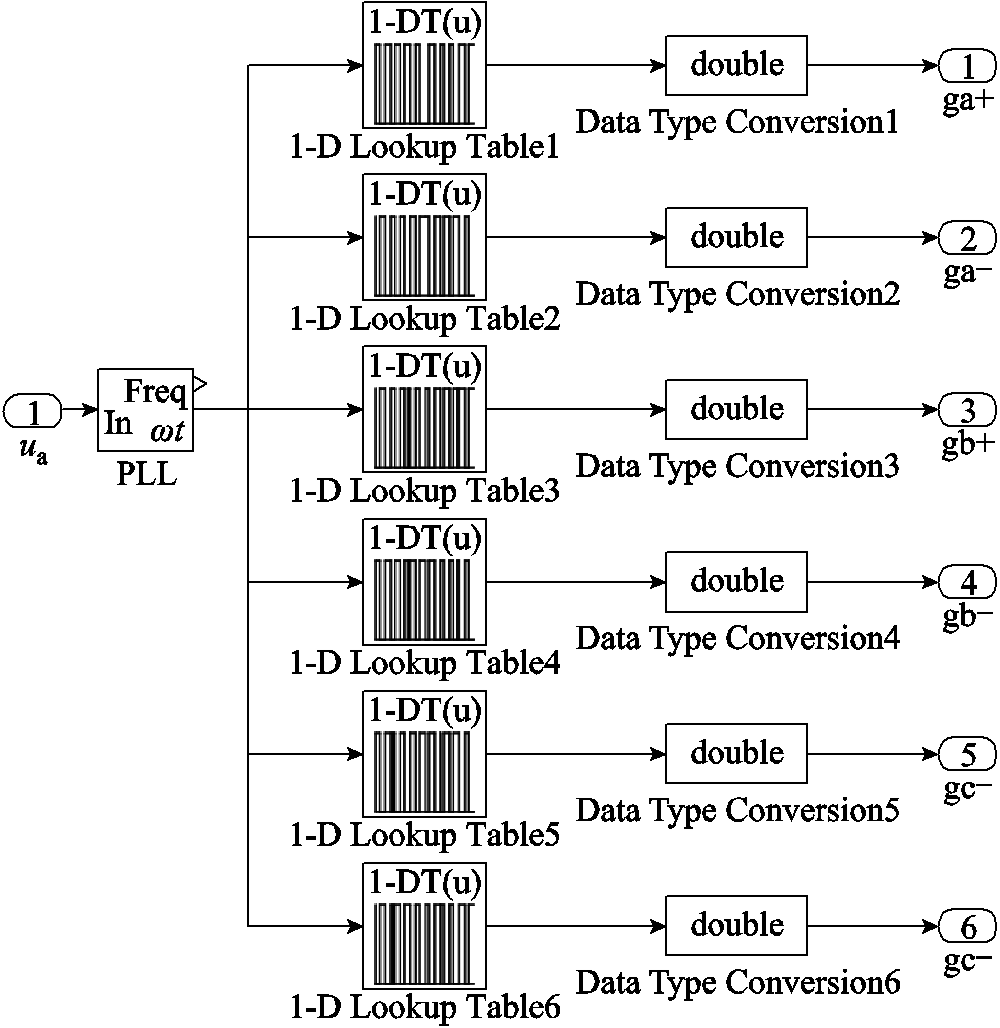
图9 控制算法的Simulink模型
Fig.9 Simulink model of the control method
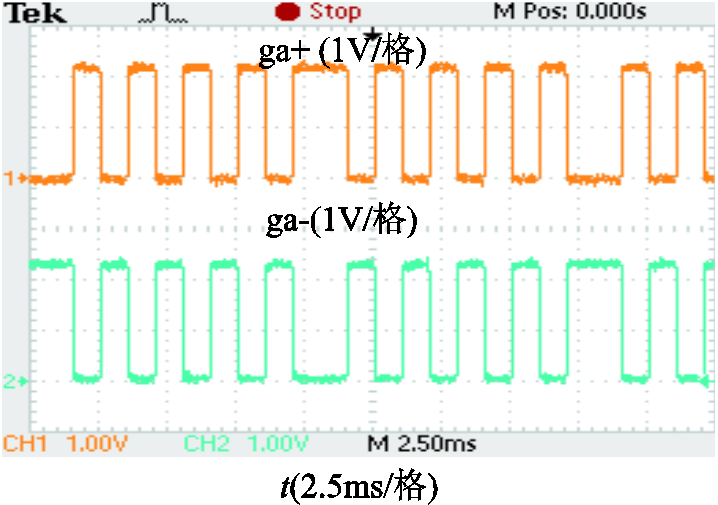
图10 AC-AC变换器的a相控制信号
Fig.10 Control signal of phase a in the AC-AC converter
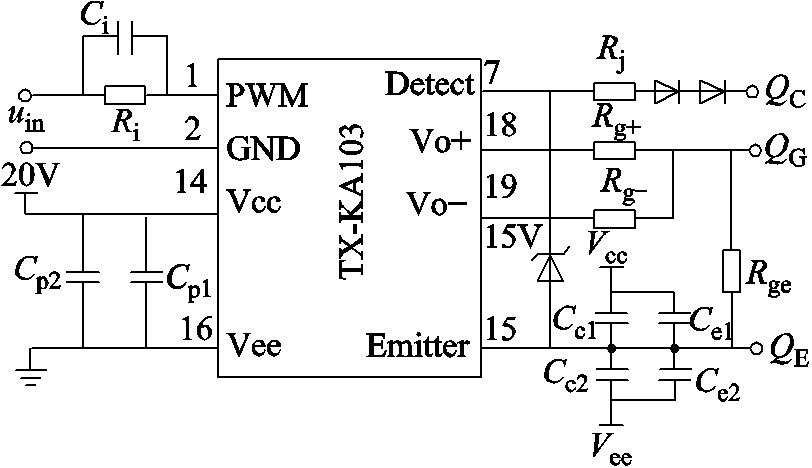
图11 驱动电路
Fig.11 Drive circuit
图12所示为驱动电路的输出波形。由图12可知,驱动电路可准确跟踪控制信号,稳定输出+15V和-8V的驱动信号。
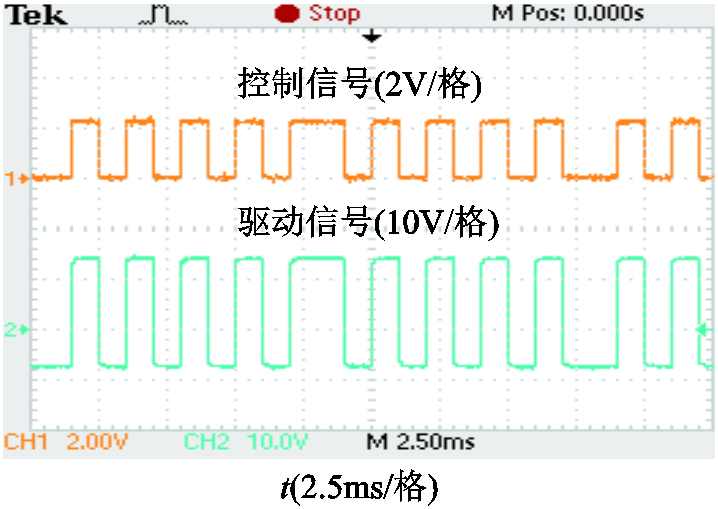
图12 AC-AC变换器的驱动信号
Fig.12 Driving signal of the AC-AC converter
为了验证上述理论分析的正确性和有效性,本文设计了移动变电站的缩比实验平台,并进行了相应的仿真和实验验证。仿真和实验条件如下:①固态变压器的容量为1.6kV·A;②固态变压器的控制由Modeling Tech公司的StarSim RCP(Rapid Control Prototype)控制器实现;③AC-AC变换器输出电压的频率为500Hz,即三相五芯柱移相变压器的输入电压频率为500Hz;④移动变电站的输入相电压有效值为120V;⑤工频逆变器使用阻性负载代替,阻值为25Ω。同时,为便于对比,本文设计了使用Y/Y/D三相三芯柱移相变压器的固态变压器。
图13所示为三相五芯柱移相变压器和工频变压器的体积和质量。根据1.6kV×A的缩比固态变压器分析计算,三相五柱变压器的体积、质量均为工频变压器的1/3左右。
从结构形式上来说,随着电压等级和容量的增加,移动变电站需拆分为开关、变电、配电三部分,分别安装于三个不同的车载平台上,即三车装载;在某些对电能质量要求比较严格的场合,还需要无功补偿车。三车装载虽然增加了移动变电站容量和功能配置的灵活性与机动性,但是无法从根本上降低主变压器的质量和高度,反而降低了响应速度,增大了移动变电站的占地面积。固态变压器还具有无功补偿/谐波抑制、故障隔离等功能,即使用固态变压器后,可以不再使用移动变电站中原有的电能质量治理设备和与继电保护相关的一次、二次设备,主变压器体积与质量的降低也极大地节省了空间,因此,基于电力电子变压器的新型移动变电站可将高压开关、变电、配电三部分集中到一个车载平台上;相比于传统的三车装载移动变电站,基于电力电子变压器的新型移动变电站只需一车装载,其体积与占地面积均降低了2/3左右,显著提高了移动变电站的灵活性与响应速度。

图13 三相五芯柱移相变压器和工频变压器的实物图
Fig.13 Power frequency and five-limb core transformers
图14和图15分别为使用三相五芯柱移相变压器和三相三芯柱移相变压器时的固态变压器输入电流及其质量分析图。对比图14和图15可知,使用三相五芯柱移相变压器时,三相输入电流波形较为对称,输入电流THD值为16%左右;使用三相三芯柱移相变压器时,输入电流THD值为22%左右。这表明三相五芯柱移相变压器的电路和磁路的对称性更好,提高了电能品质。
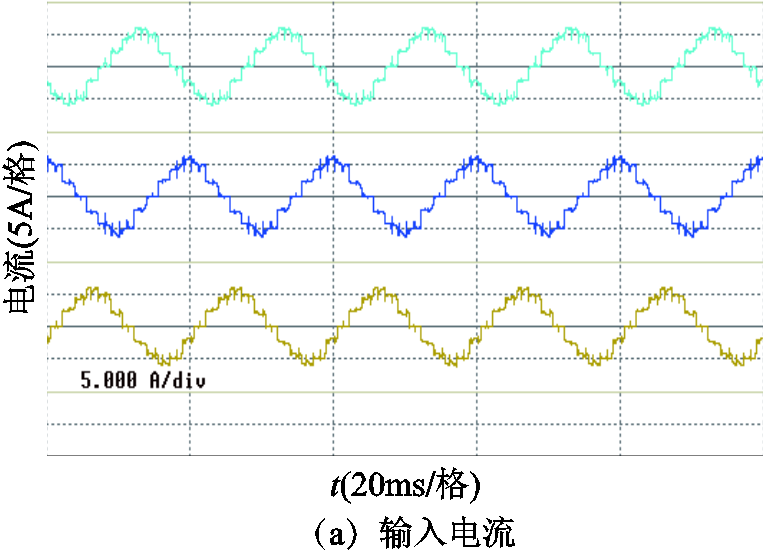
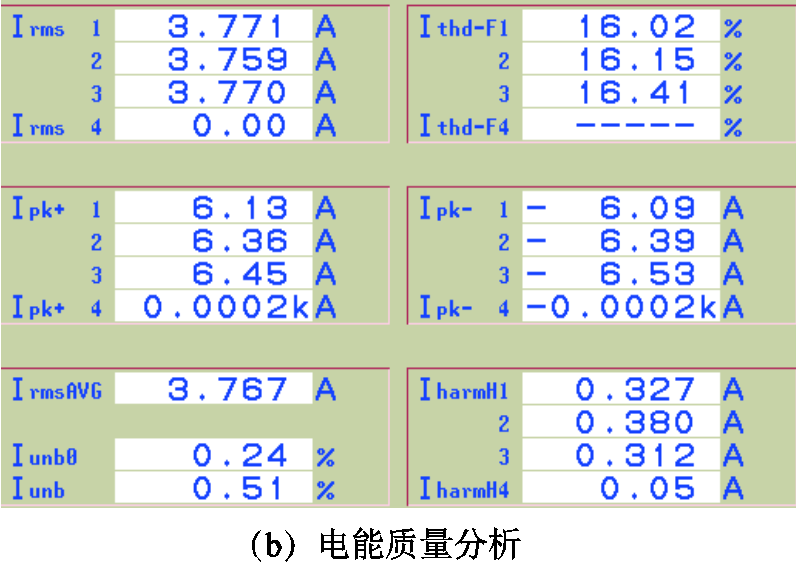
图14 使用三相五芯柱移相变压器时的固态变压器输入电流及其电能质量分析
Fig.14 Input current and its power quality of the solid state transformer using three-phase five-limb core transformers
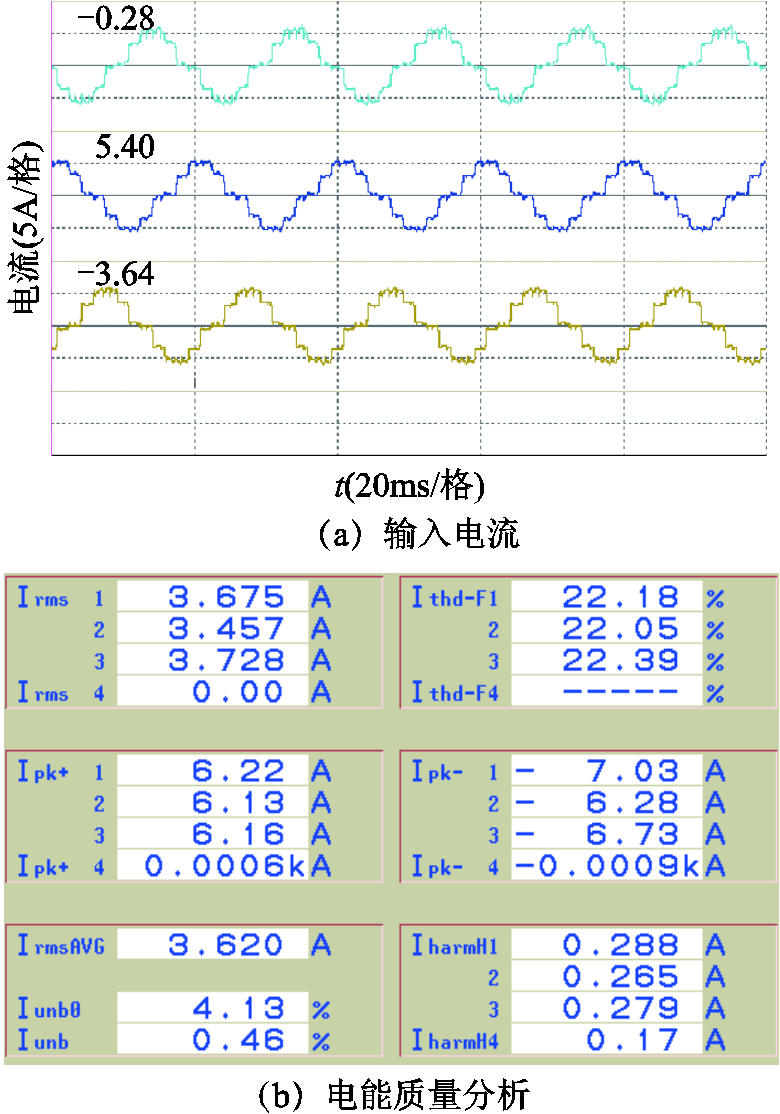
图15 使用三相三芯柱移相变压器时的固态变压器输入电流及其电能质量分析
Fig.15 Input current and its power quality of the solid state transformer using three-phase three-limb core transformers
图16所示为高频多脉波整流器的输出电压和电流。在一个电源周期内,输出电压和电流含有12个波头,实验过程中,由于固态变压器的开关作用,输出电压和电流中含有较多毛刺。
图17所示为固态变压器的效率实测图。由图17可知,该固态变压器的实测效率为94.9%。使用SiC器件后,功率开关器件的损耗会有所降低,使固态变压器具有较高的效率。若移相变压器使用性能更优的铁心材料,如非晶硅或者铁氧体,其效率还会有所提高。
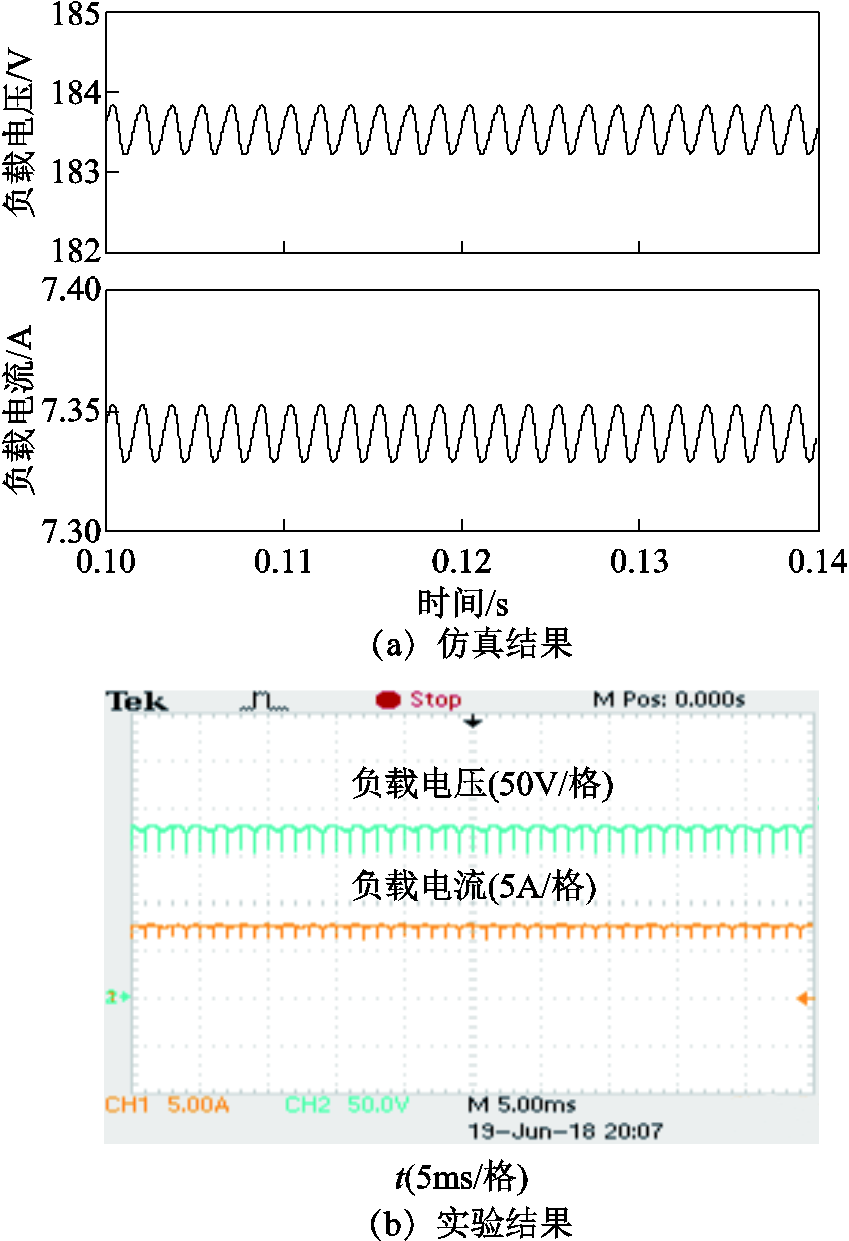
图16 高频多脉波整流器的输出电压和和电流
Fig.16 Output current and voltage of the high-frequency multi-pulse rectifier
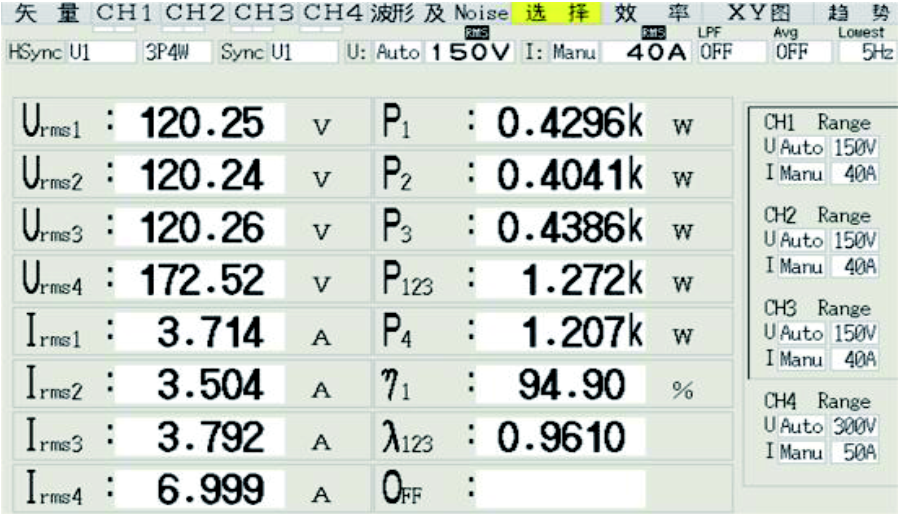
图17 固态变压器的效率实测图
Fig.17 Efficiencydiagram of the solid state transformer
本文提出了一种应用于移动变电站的固态变压器拓扑,使用该拓扑,可显著降低主变压器的体积和质量,并可以提高移动变电站的输入侧电能质量。所提出的固态变压器包含AC-AC变换器、高频多脉波整流器、工频逆变器等三部分组成。为提高固态变压器的输入电能质量,高频多脉波整流器使用三相五芯柱隔离变压器作为移相变压器,有效提高了变压器的磁路对称性;该变压器的二次绕组采用延边三角形联结,有效提高了变压器的电路对称性。同时,为提高固态变压器的能量变换效率,AC-AC变换器中功率开关器件使用了SiC MOSFET。实验结果表明,使用三相五芯柱移相变压器后,固态变压器的输入电流THD值由22%降到了16%,能量变换效率达到了94.9%。
由于实验条件所限,本文所设计的固态变压器容量较小,仅进行了功能性测试,后续工作中需设计大容量的固态变压器,并对级联形式的AC-AC变换器的控制策略、高频多脉波整流器中的高频变压器等进行优化设计。
参考文献
[1]刘满君, 程林, 黄道姗, 等. 基于运行可靠性理论的高可靠性供电路径搜索方法[J]. 电工技术学报, 2019, 34(14): 3004-3011. Liu Manjun, Cheng Lin, Huang Daoshan, et al. The high reliability supply path searching method based on the operational reliability theory[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3004-3011.
[2]汤振鹏, 刘泽庭, 胡中, 等. 移动变电站技术进展综述[J]. 电网技术, 2019, 43 (9): 3415-3423. Tang Zhenpeng, Liu Zeting, Hu Zhong, et al. Overview on technology progress in mobile substation[J]. Power System Technology, 2019, 43(9): 3415-3423.
[3]Lopez-Roldan J, Devriendt C, Enns J, et al. How to achieve a rapid development of mobile substation and to guarantee its integrity during transport[J]. IEEE Transactions on Power Delivery, 2008, 23(1): 196-202.
[4]Devriendt C, Guillaume P, Lopez-Roldan J. Structural dynamics of a mobile substation during transport[J]. Engineering Structures, 2007, 29(11): 3377-3389.
[5]孟凡刚, 骆霁嵘, 高蕾, 等. 基于相分量法的星形自耦变压器的全解耦模型[J]. 电机与控制学报, 2017, 21(1): 14-21. Meng Fangang, Luo Jirong, Gao Lei, et al. Decoupled model of star-connected autotransformer based on phase-coordinate method[J]. Electric Machines and Control, 2017, 21(1): 14-21.
[6]赵亮亮, 陈超英. 电力系统暂态仿真中自耦变压器模型的研究[J]. 电力系统及其自动化学报, 2004, 16(1): 83-88. Zhao Liangliang, Chen Chaoying. Study of model of three-phases autotransformer in electric system transient simulation[J]. Proceedings of the CSV-EPSA, 2004, 16(1):83-88.
[7]李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274-1289. Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer technologies[J]. Proceedings of the CSEE, 2018, 38(5): 1274-1289.
[8]孟凡刚, 满忠诚, 高蕾, 等. 基于电力电子移相变压器的12脉波整流技术[J]. 电工技术学报, 2019, 34(18): 3865-3872. Meng Fangang, Man Zhongcheng, Gao Lei, et al. 12-pulse rectification technology based on power electronic phase-shifting transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3865-3872.
[9]张雪垠, 徐永海, 肖湘宁. 适用于中高压配电网的高功率密度谐振型级联 H 桥固态变压器[J]. 电工技术学报, 2018, 33(2): 310-321. Zhang Xueyin, Xu Yonghai, Xiao Xiangning. A high power density resonance cascaded H-bridge solid-state transformer for medium and high voltage distribution network[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 310-321.
[10]Xu She, Huang A Q, Rolando Burgos. Review of solid-state transformer technologies and their application in power distribution systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2013, 1(3): 186-198.
[11]Huang A Q. Medium-voltage solid-state transformer: technology for a smarter and resilient grid[J]. IEEE Industrial Electronics Magazine, 2016, 10(3): 29-42.
[12]杨斌, 赵剑锋, 季振东, 等. 混合变压器技术研究综述[J]. 电力自动化设备, 2020, 40 (2): 205-213. Yang Bin, Zhao Jianfeng, Ji Zhendong, et al. Overview of hybrid transformer technologies[J]. Electric Power Automation Equipment, 2020, 40(2): 205-213.
[13]Jonas E Huber, Johann W Kolar. Applicability of solid-state transformers in today’s and future distribution grids[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 317-326
[14]Krishna Mainali, Awneesh Tripathi, Sachin Madhusoodhanan, et al. A transformerless intelligent power substation: a three-phase SST enabled by a 15-kV SiC IGBT[J]. IEEE Power Electronics Magazine, 2015, 2(3): 31-43.
Abstract In order to reduce the volume and weight of the main transformer, and to improve the input power quality of mobile substation, this paper proposes a solid state transformer topology used in the mobile substation. The proposed mobile substation comprises a AC-AC converter, high-frequency multi-pulse rectifier, and a line-frequency inverter. The operating principle of the AC-AC converter is analyzed, and its control strategy is designed from reducing its switching losses. The phase-shifting transformer used in the high-frequency multi-pulse rectifier is designed from the symmetry of magnetic and electric circuit, and the input current and output voltage of the solid state transformer are also calculated based on the switching function. The control and drive circuit of the AC-AC converter is designed, and the scaling simulation and experimental platform is also setup. The simulation and experimental results show that volume of the main transformer reduced to 1/3 of that of the line frequency transformer under the same kV·A rating; after using the phase-shifting transformer, the THD of the input line current decreases from 22% to 16%.
keywords:Mobile substation, solid state transformer, AC-AC converter, high-frequency multi-pulse rectifier, phase-shifting transformer
10.19595/j.cnki.1000-6753.tces. L90004
中图分类号:TM933
国家自然科学基金资助项目(51777042)。
收稿日期 2020-04-09
改稿日期 2020-12-26
高美金 女,1980年生,硕士,高级工程师,研究方向为移动变电站设计与经济运行。E-mail:550650305@qq.com
孟凡刚 男,1982年生,博士,教授,博士生导师,研究方向为电能变换与电能质量控制。E-mail:motor@tju.edu.cn(通信作者)
(编辑 郭丽军)