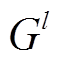 计算公式为
计算公式为摘要 准确预测光伏发电功率对电网调度具有十分重要的意义。该文提出一种基于灰色关联分析和GeoMAN模型的光伏发电功率短期预测方法。首先,利用灰色关联分析对某地区多光伏电站进行空间相关性分析,选取与待预测光伏电站高度相关的周边电站;然后,基于GeoMAN模型动态提取待预测光伏电站的时空特征和外部气象因素,GeoMAN模型采用编解码结构,利用编码器动态提取待预测光伏电站的站内特征和与周边相关电站的站间空间特征,利用解码器提取输入变量的时间特性,并融合晴空指数和数值天气预报动态输出光伏发电预测功率;最后,采用实际光伏电站进行案例分析,结果表明该文所提出的预测方法与传统LSTM模型相比,实现了更高精度的光伏发电功率短期预测。
关键词:光伏功率短期预测 灰色关联分析 GeoMAN模型 时空相关性 注意力机制
光伏发电受到太阳辐射周期、地理环境及各种气象因素变化的影响,对其进行准确的建模和特性分析是一个多影响因素的数学难题[1]。准确的预测光伏发电功率可以使电力调度部门及时调整调度计划,提高电网运行的经济性和稳定性,促进新能源消纳[2]。
光伏发电是一个连续不断的过程,光伏发电数据作为一个典型的时间序列,不仅是非线性的,而且具有时间相关性[3]。光伏发电功率每时刻的变化不仅取决于当前时刻,还取决于过去时刻。文献[4]提出基于多维时间序列的光伏发电功率预测方法,采用相关性分析对不同时间尺度的光伏功率序列进行分析,然后利用支持向量回归方法建立光伏功率预测模型。但在天气类型突变的情况下,模型的预测精度不高。文献[5]建立了基于差分整合移动平均自回归模型(Autoregressive Integrated Moving Average Model, ARIMA)与支持向量机的分布式光伏功率预测模型,并在不同天气类型下进行案例分析,但由于缺乏对空间特征的提取,模型精度有待进一步提升。
每个光伏电站具有独特的地理空间位置,光伏发电功率具有空间相关性[6]。对于临近地区的多个光伏电站而言,由于地理位置条件相近,且在相似的天气、气温等气象条件作用下,光伏电站输出功率呈现一定程度的相似性[7]。针对光伏电站时空相关性的研究,文献[8]提出一种深度时空特征提取的光伏发电功率预测模型,针对邻近区域的光伏电站进行图建模,使用长短期记忆(Long Short-Term Memory, LSTM)模型进行时间特征提取,使用图卷积原理提取电站的空间特征。但是由于分布式光伏电站具有强空间性[9],图机器学习还应该结合地理方位和云层运动,以达到更加精准的预测效果。文献[10]利用聚类方法对大规模区域光伏电站进行分块形成群光伏电站,然后进一步筛选群光伏电站中与待预测电站具有空间相关性的光伏电站,建立自回归滑动平均模型(Auto-Regression and Moving Average, ARMA)实现对光伏发电功率的预测。模型具有一定的预测能力,但随着预测时长的增加预测精度下降。
现有工作大多依赖光伏电站气象装置量测的气象数据或者数值天气预报(Numerical Weather Prediction, NWP)中的气象数据,仅采用某些针对性特征进行功率预测,缺乏对多源数据信息的有效利用。本文结合电站实测数据和NWP数据,基于灰色关联分析和GeoMAN(Geo-sensory Multi-level Attention Networks)模型,提出一种动态时空特征提取和外部气象因素融合的光伏发电功率短期预测方法。采用灰色关联分析对所有电站进行相关性分析,选取与待预测光伏电站高度相关的周边电站。然后基于待预测光伏电站和周边相关电站的信息,利用GeoMAN模型实现对光伏发电功率的短期预测。GeoMAN模型采用编解码器架构[11],编码器包含站内特征注意力机制,站间空间注意力机制和LSTM,以提取待预测光伏电站的站内局部特征和与周边相关电站的站间空间特征。解码器包含时间注意力机制和LSTM,从而预测光伏发电功率。外部气象模块融合了晴空指数和NWP数据,进一步提升光伏发电功率预测精度。以某地区真实光伏电站的数据进行案例分析,验证了所述方法的有效性。
本文采用灰色关联分析[12]选取与待预测光伏电站相关的周边电站。待预测光伏电站与第l个光伏电站间的关联度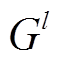 计算公式为
计算公式为
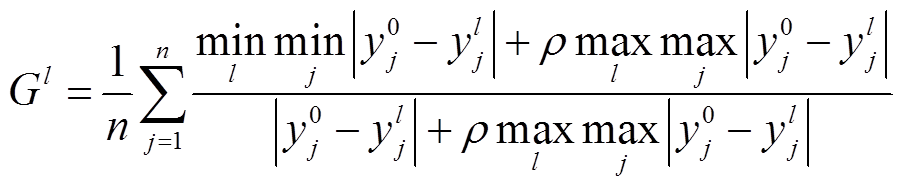 (1)
(1)式中,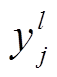 为第l个光伏电站的第j个功率;
为第l个光伏电站的第j个功率;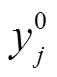 为待预测光伏电站的第j个功率,
为待预测光伏电站的第j个功率,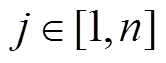 ,n为光伏电站输入功率序列长度;
,n为光伏电站输入功率序列长度;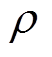 为常数,通常取0.5;关联度
为常数,通常取0.5;关联度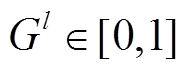 ;
;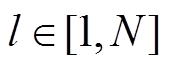 ,N为某地区除待预测光伏电站外所有电站的数量。
,N为某地区除待预测光伏电站外所有电站的数量。
利用式(1)计算某地区所有电站与待预测光伏电站之间的关联度,选取关联度较高的光伏电站作为与待预测光伏电站高度相关的周边电站,用于GeoMAN模型提取待预测光伏电站的空间特征。
GeoMAN模型是Liang Yuxuan[13]等于2018年提出的地理空间传感器参数预测模型。GeoMAN模型能够提取输入变量的时空相关性并融合影响传感器参数的外部因素,从而更准确地预测传感器参数。图1为GeoMAN模型应用于光伏发电功率预测的框架。GeoMAN模型编码器中的站内特征注意力机制对待预测光伏电站的局部特征进行提取,站间空间注意力机制利用相似度向量赋予相关电站不同的空间特征权重,编码器中的LSTM[14]对站内特征注意力机制和站间空间注意力机制的输出向量进行编码。解码器中的时间注意力机制自适应地提取相关时间间隔的数据特征,LSTM对编码器输出的特征向量进行解码,并融合晴空指数和NWP实现对光伏发电功率的预测。

图1 GeoMAN功率预测模型框架
Fig.1 GeoMAN power forecasting model framework
1.2.1 待预测光伏电站的站内特征注意力机制
每个光伏电站的局部特征与功率之间具有复杂的相关性,随着时间和气象的变化,局部特征每时刻对功率的影响各不相同[15]。采用GeoMAN模型的站内特征注意力机制动态捕捉待预测光伏电站站内特征与预测功率之间的相关性。待预测光伏电站的站内特征注意力机制为
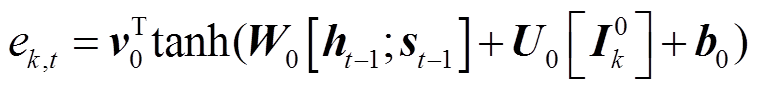 (2)
(2)式中,![]() 为拼接符;
为拼接符;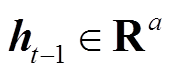 和
和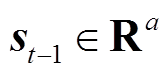 是t-1时刻的隐藏状态和细胞状态,分别构成编码器LSTM的长、短期记忆,其中a为LSTM隐藏神经元数量;
是t-1时刻的隐藏状态和细胞状态,分别构成编码器LSTM的长、短期记忆,其中a为LSTM隐藏神经元数量;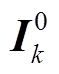 为待预测光伏电站站内的第k个时间序列,
为待预测光伏电站站内的第k个时间序列, ,其中
,其中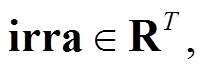
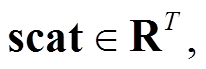
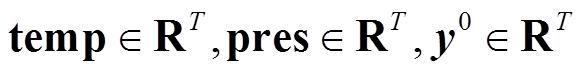 为待预测光伏电站的五个特征,分别为总辐照度、散射辐照度、环境温度、气压和历史功率;T为模型输入历史时间序列长度;
为待预测光伏电站的五个特征,分别为总辐照度、散射辐照度、环境温度、气压和历史功率;T为模型输入历史时间序列长度;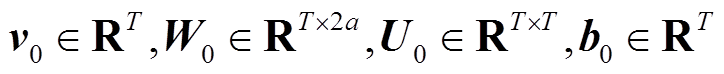 为可学习参数,在训练过程中通过反向传播算法确定参数值。
为可学习参数,在训练过程中通过反向传播算法确定参数值。
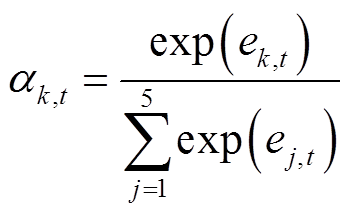 (3)
(3)式中,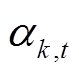 为t时刻第k个特征的注意权值,则第t时刻的站内特征注意力机制输出向量为
为t时刻第k个特征的注意权值,则第t时刻的站内特征注意力机制输出向量为
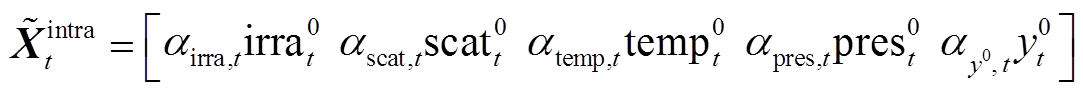 (4)
(4)1.2.2 待预测光伏电站与相关电站的站间空间注意力机制
站间空间注意力机制捕捉待预测光伏电站与相关电站的空间相关性,根据相关程度的不同赋予相关电站不同的注意力机制权重。待预测光伏电站与第l个电站的站间空间注意力机制为
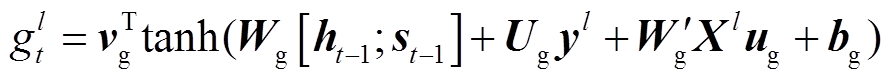 (5)
(5)式中,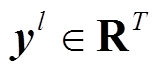 为第l个光伏电站的历史功率序列,
为第l个光伏电站的历史功率序列,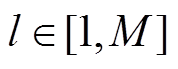 ,M为与待预测光伏电站高度相关的电站个数;
,M为与待预测光伏电站高度相关的电站个数;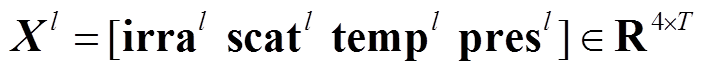 为第l个光伏电站的特征序列;
为第l个光伏电站的特征序列;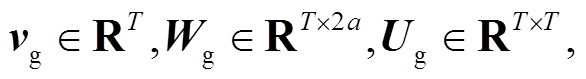
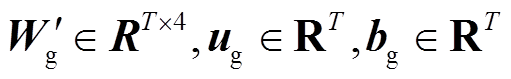 为可学习参数。
为可学习参数。
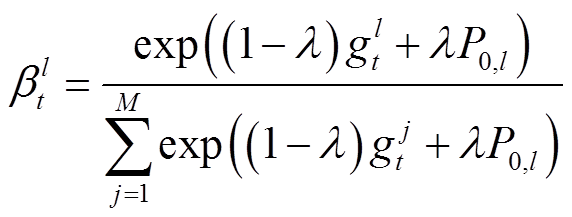 (6)
(6)式中,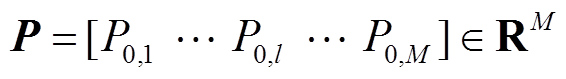 为相似度向量,
为相似度向量,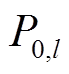 为待预测光伏电站与第l个电站之间的灰色关联系数;
为待预测光伏电站与第l个电站之间的灰色关联系数;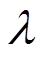 为可调参数;
为可调参数;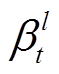 为t时刻第l个电站的注意权值,则第t时刻的站间空间注意力机制输出向量为
为t时刻第l个电站的注意权值,则第t时刻的站间空间注意力机制输出向量为
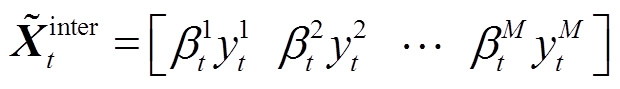 (7)
(7)1.2.3 编码器中的LSTM
GeoMAN模型中编码器包括站内特征注意力机制、站间空间注意力机制和LSTM。编码器中的LSTM用于提取待预测光伏电站的站内特性和空间特性并进行编码。LSTM的输入为由站内特征注意力机制输出向量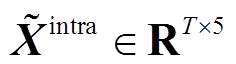 和站间空间注意力机制输出向量
和站间空间注意力机制输出向量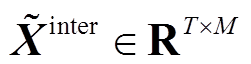 组成的拼接向量
组成的拼接向量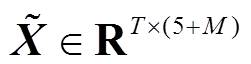 ,即
,即
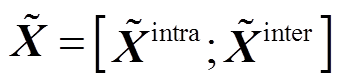 (8)
(8)编码器中LSTM的输出为历史T时刻待预测光伏电站的特征提取隐藏向量,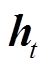 为编码器t时刻输出的特征提取隐藏向量,
为编码器t时刻输出的特征提取隐藏向量,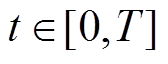 。
。
1.2.4 提取时序特征的时间注意力机制
每个时刻的隐藏向量对输出功率的影响不尽相同,时间注意力机制自适应地选择相关的时间间隔进行功率预测,每个历史时刻隐藏状态的注意力权重计算公式为
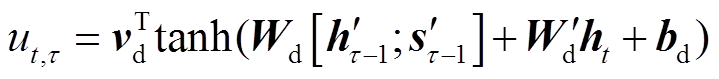 (9)
(9)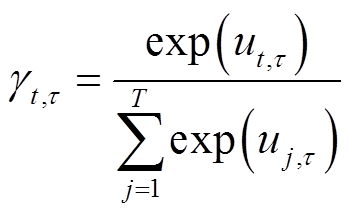 (10)
(10)式中,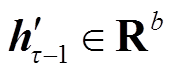 和
和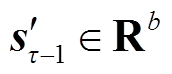 为
为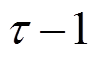 时刻解码器中LSTM的隐藏状态和细胞状态;
时刻解码器中LSTM的隐藏状态和细胞状态;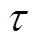 为输出预测时刻;
为输出预测时刻;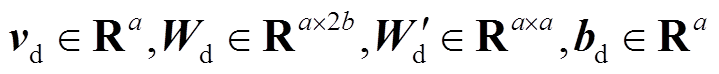 为可学习参数。
为可学习参数。![]() 时刻时间注意力机制的输出向量为
时刻时间注意力机制的输出向量为
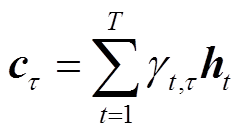 (11)
(11)1.2.5 外部气象因素融合模块
太阳辐射量、地面温度和天气类型等外部因素都在影响光伏发电功率[16-17]。GeoMAN模型的外部因素模块融合待预测光伏电站的6维预测特征,分别为晴空指数和NWP数据中的预测总辐照度、预测直射辐照度、预测地面百叶箱气温、预测地面百叶箱相对湿度及地面10m风速,则t时刻外部气象因素融合向量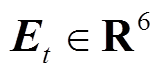 。
。
1.2.6 解码器中的LSTM
GeoMAN模型中解码器包括时间注意力机制和LSTM。解码器中的LSTM用于预测未来τ时刻的光伏发电功率。LSTM的输入为由时间注意力机制输出向量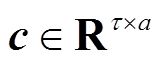 ,外部气象因素融合向量
,外部气象因素融合向量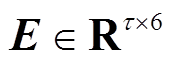 和解码器前一时刻的隐藏向量
和解码器前一时刻的隐藏向量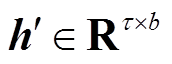 组成的拼接向量
组成的拼接向量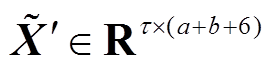 。
。
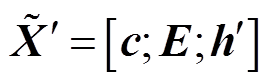 (12)
(12)解码器中LSTM的输出为未来![]() 时刻待预测光伏电站的预测功率。
时刻待预测光伏电站的预测功率。
图2为基于灰色关联分析和GeoMAN模型的光伏发电功率预测流程。图中灰色关联分析用于选择与待预测光伏电站高度相关的周边电站,去除其他电站的干扰,使得GeoMAN模型能更高效地提取待预测光伏电站的空间特征,降低模型复杂度。
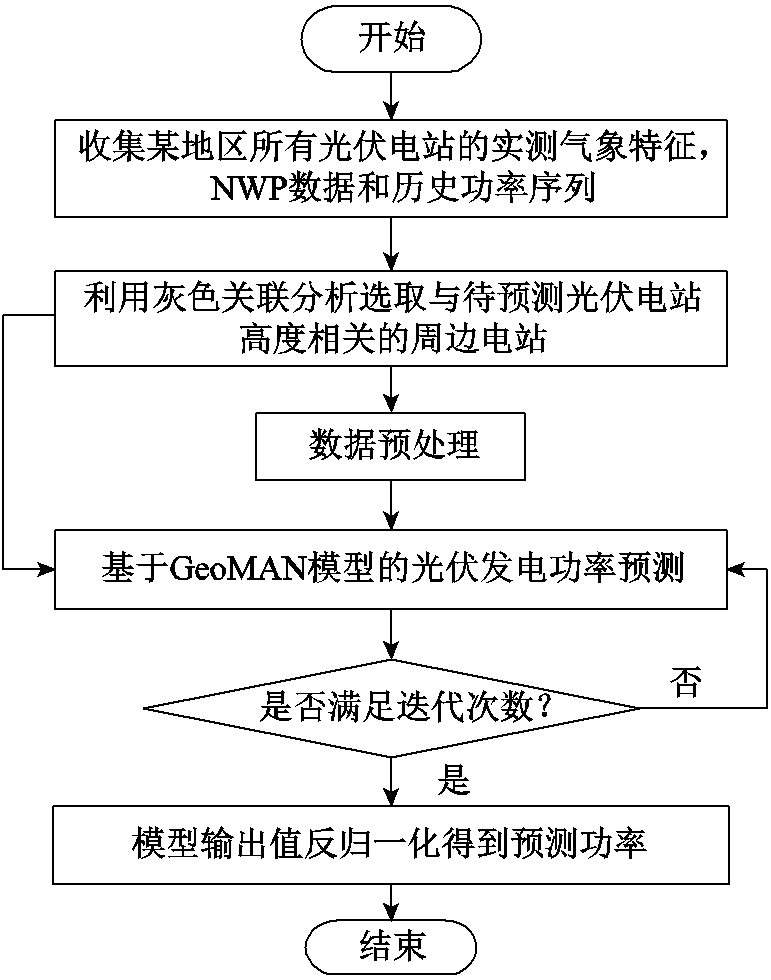
图2 基于灰色关联分析和GeoMAN模型的光伏发电功率短期预测流程
Fig.2 Short-term photovoltaic power forecasting flow chart based on grey relational analysis and GeoMAN model
数据预处理包括去除夜间无功率数据和归一化。由于光伏发电功率较集中,去除夜间19:30至次日5:15的无功率数据有助于降低模型复杂度。Z-score标准归一化公式为
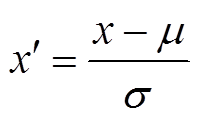 (13)
(13)式中,![]() 为序列的均值;
为序列的均值;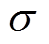 为标准差。
为标准差。
将预处理后的数据按比例6:2:2划分为训练集、验证集和测试集。训练集和验证集用于训练GeoMAN模型,Adam优化器用于更新模型参数,以使实际功率与预测功率间的方均根误差(Mean Square Error, MSE)损失最小。训练后的GeoMAN模型对测试集进行预测,反归一化后动态输出待预测光伏电站未来![]() 时刻的预测功率。与传统方法无法高效提取历史气象数据的时间和空间特征相比,GeoMAN模型采用了编解码结构,两个LSTM的深层网络结构通过非线性变换将输入向量映射到高维,可以更加全面地提取光伏电站时间和空间上的特性,从而更准确地预测光伏发电功率。
时刻的预测功率。与传统方法无法高效提取历史气象数据的时间和空间特征相比,GeoMAN模型采用了编解码结构,两个LSTM的深层网络结构通过非线性变换将输入向量映射到高维,可以更加全面地提取光伏电站时间和空间上的特性,从而更准确地预测光伏发电功率。
本文所有数据均来源于某地区多个实际光伏电站,其中每个光伏电站的数据集包含2018年7月1日~2019年6月13日逐15min的实测气象数据,数值天气预报数据和光伏发电功率。基于Tensorflow建立光伏发电功率短期预测模型,分别利用本文提出方法和传统LSTM模型对测试集进行功率预测,验证本文所述方法的可行性。
利用式(13)将所有光伏电站的功率进行归一化,然后利用式(1)计算待预测光伏电站和周边其他光伏电站的灰色关联度,待预测光伏电站与其中五个光伏电站的灰色关联度结果见表1。
表1 灰色关联分析结果
Tab.1 Results of Grey Relational Analysis

待预测光伏电站序号与待预测光伏电站的关联度 01 10.921 582 20.898 685 30.912 694 40.918 176 50.920 216
由表1可知,1号和5号光伏电站与待预测光伏电站的灰色关联度最高,因此选择1号和5号光伏电站作为待预测光伏电站的相关电站,用于GeoMAN模型提取待预测光伏电站的空间特征。表1中灰色关联系数是GeoMAN模型提取空间相关性的相似度向量。
基于灰色关联分析和GeoMAN模型的光伏发电功率短期预测方法的输入为待预测光伏电站和周边相关电站历史T=58个时刻即历史一天的实测总辐照度、实测散射辐照度、环境温度、气压和功率,外部因素模块输入待预测光伏电站未来τ=58个时刻即未来一天的晴空指数、预测总辐照度、预测直射辐照度、预测地面百叶箱气温、预测地面百叶箱相对湿度和地面10m风速。模型输出待预测光伏电站未来一天的预测功率。GeoMAN的编解码器中两个LSTM均采用单层网络结构,隐藏层神经元个数为128,模型采用Adam优化器、MSE损失函数和Relu激活函数等参数,其他自由参数由模型在训练过程中自动选择。传统LSTM对比模型的输入输出与GeoMAN模型相同,由于GeoMAN模型采用两个单层LSTM,为保持结构相似,对比LSTM模型中采用双层LSTM结构,其内部参数与GeoMAN模型保持一致。
根据天气预报网的天气类型,分别选取2019年5月26日雨天、6月2日阴天和6月11日晴天三种天气类型对GeoMAN模型和LSTM模型进行对比实验。图3为GeoMAN模型和LSTM模型的预测功率与实际发电功率在不同天气类型下的对比图。
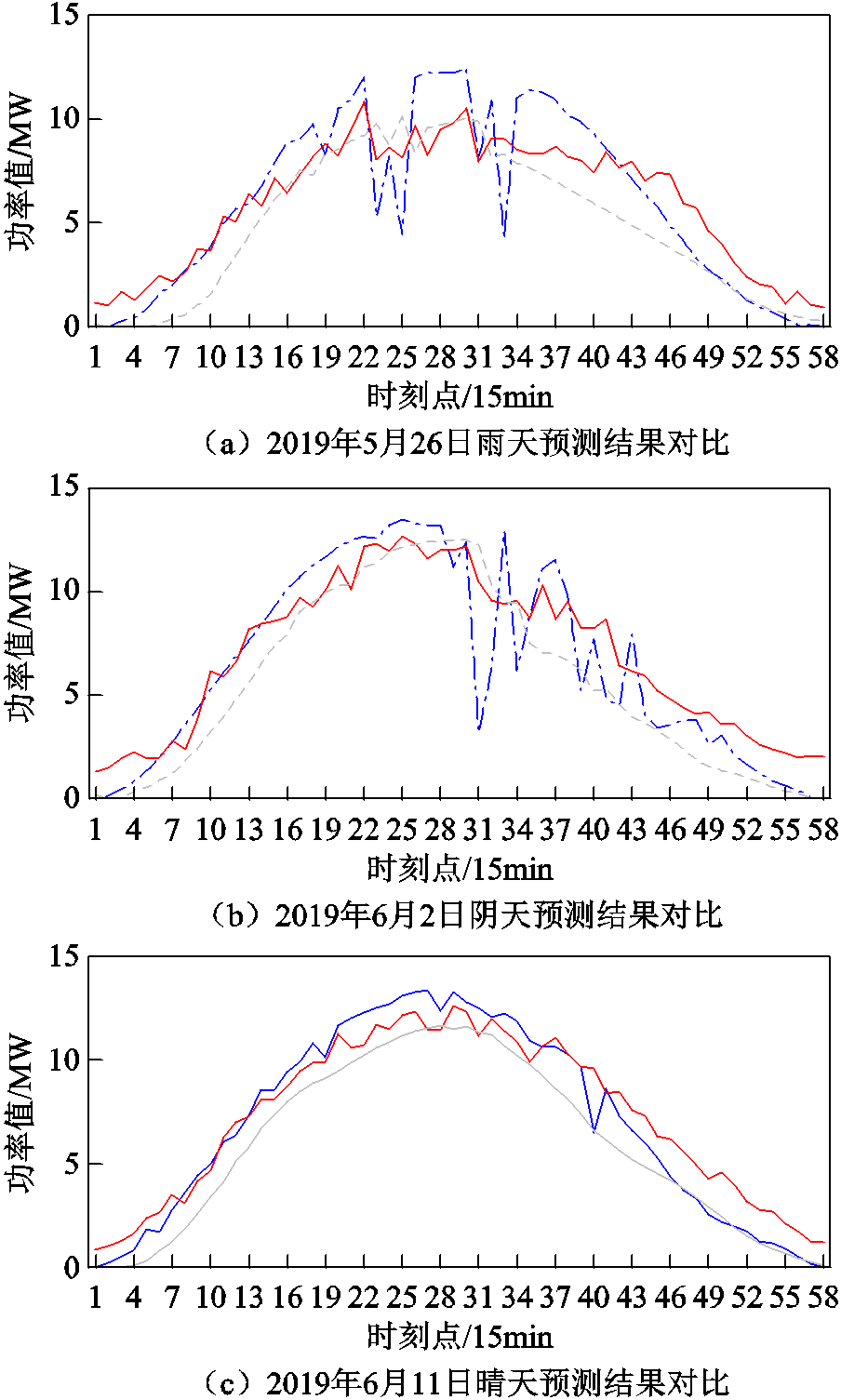
图3 不同天气类型下GeoMAN模型和LSTM模型的预测结果对比图
Fig.3 Comparison of forecasting results between GeoMAN model and LSTM model under different weather types
方均根误差(RMSE)和平均绝对误差(MAE)[20]用于评估预测模型的准确性,公式为
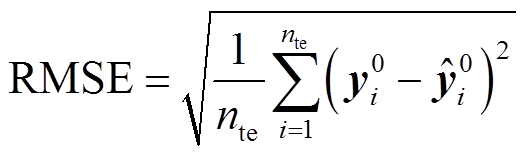 (14)
(14)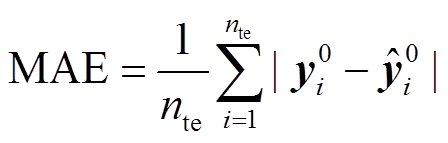 (15)
(15)式中,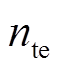 为测试集样本个数;
为测试集样本个数;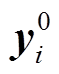 为待预测光伏电站的实际功率值;
为待预测光伏电站的实际功率值;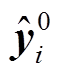 为预测功率值。
为预测功率值。
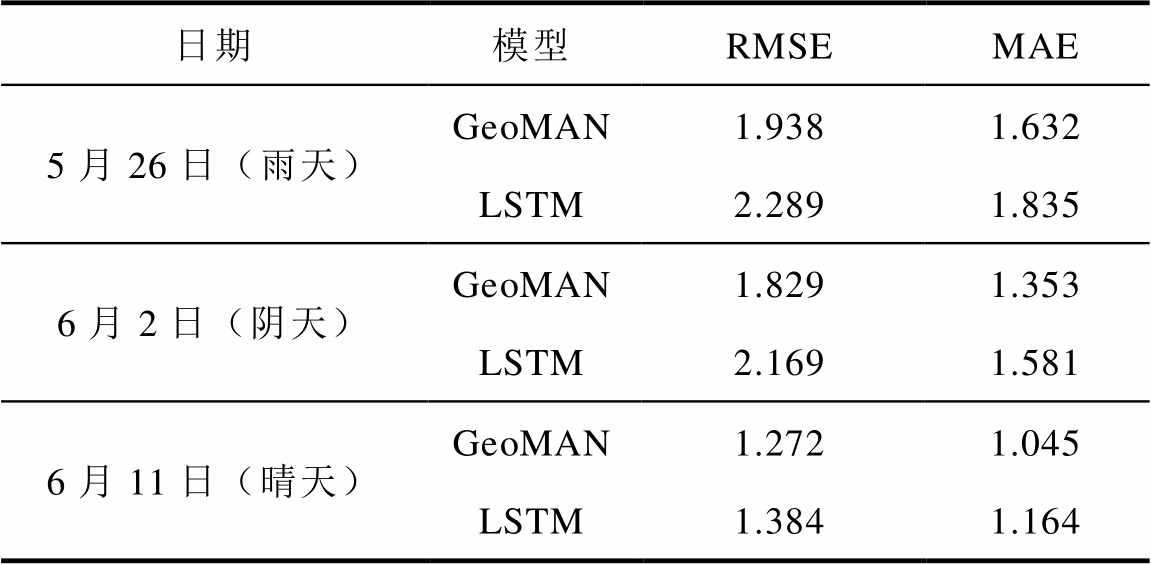
表2 不同天气类型下GeoMAN模型和LSTM模型的预测结果对比
Tab.2 Comparison of forecasting results between GeoMAN model and LSTM model under different weather types
日期模型RMSEMAE 5月26日(雨天)GeoMAN1.9381.632 LSTM2.2891.835 6月2日(阴天)GeoMAN1.8291.353 LSTM2.1691.581 6月11日(晴天)GeoMAN1.2721.045 LSTM1.3841.164
由图3和表2可知,在雨天、阴天和晴天三种天气类型下,GeoMAN模型的预测结果均优于LSTM模型的预测结果,GeoMAN模型的RMSE和MAE误差指标均小于LSTM模型。晴天时,GeoMAN模型和LSTM模型的预测精度最高,两模型间的误差最小,雨天和阴天的预测精度差于晴天的预测精度。这是因为晴天时功率曲线较平滑,更易于准确地预测功率。雨天和阴天时功率波动性最大,模型很难动态感知功率曲线一天的变化。但总体而言,LSTM模型只捕捉了待预测光伏电站的时序特征和外部因素特征,对于每个特征每个时刻赋予相同的权重,无法高效提取输入数据间的关联特性和每个输入数据自身的时序特征。GeoMAN模型使用两层注意力机制赋予输入数据不同的权重,不仅提取了输入数据自身的时序特征,还捕捉了待预测光伏电站的空间特性。编解码器中的两个LSTM根据注意力机制的输出更好地学习模型内部参数,从而更加准确地预测光伏发电功率。
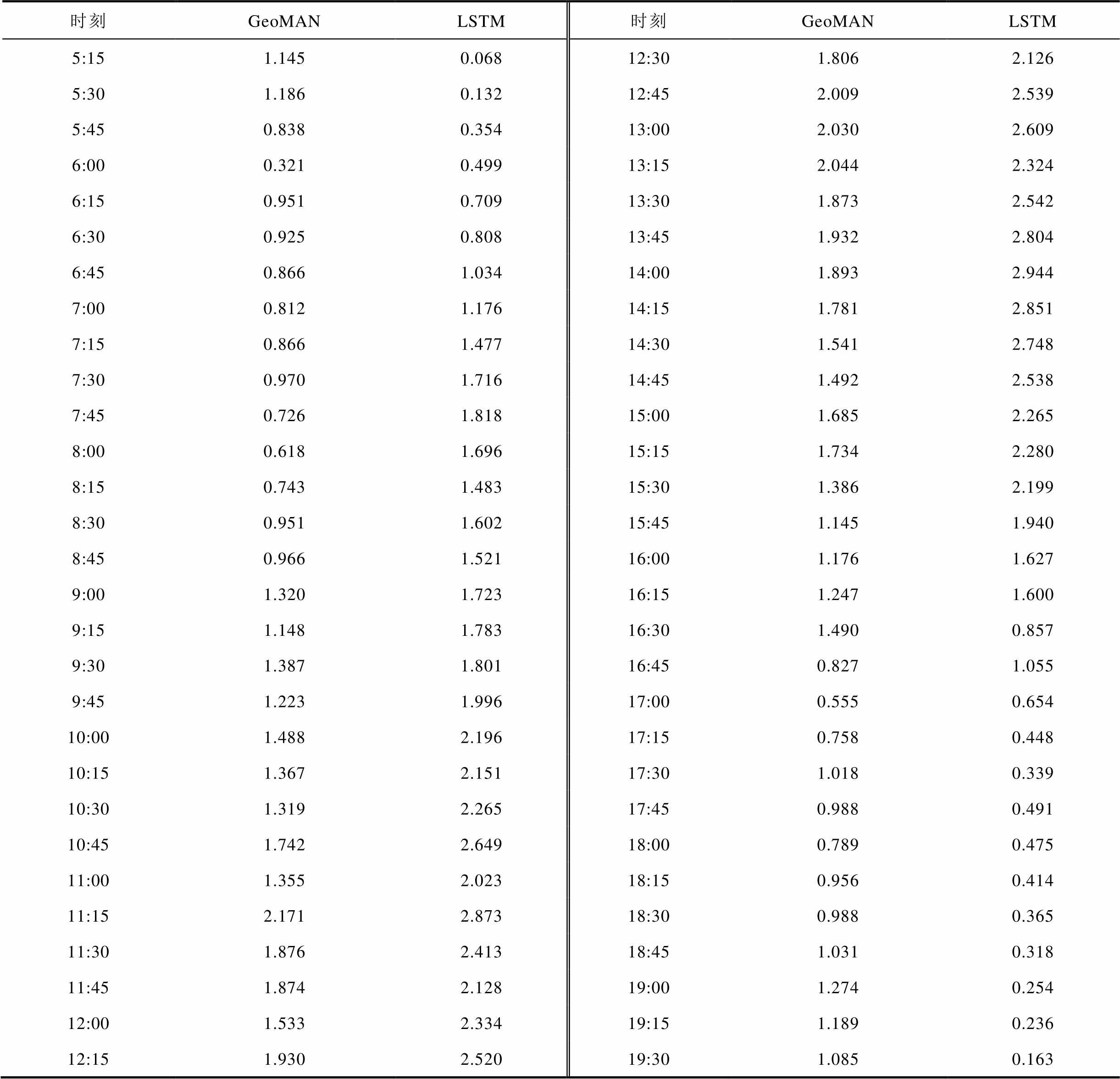
2019年5月10日~2019年6月13日的数据为测试集,分别利用GeoMAN模型和LSTM模型对测试集进行功率预测。GeoMAN模型和LSTM模型每15min预测功率的绝对值见表3。除每天早晚时刻LSTM模型预测误差小于GeoMAN模型预测误差外,6:45~17:00共42个时刻点的GeoMAN模型误差均小于LSTM模型,因此GeoMAN模型对光伏功率曲线的起止点预测效果欠佳,但是对光伏功率曲线的坡度和峰值预测较准确。GeoMAN模型和LSTM模型在测试集上整体预测结果见表4,基于灰色关联分析和GeoMAN模型的光伏发电功率预测精度优于LSTM模型。与LSTM模型相比,GeoMAN模型预测误差指标RMSE降低15.3%,MAE降低17.8%,说明GeoMAN模型应用于光伏发电功率预测的可行性和高效性。
表3 GeoMAN模型和LSTM模型的每15min预测结果对比
Tab.3 Comparison of forecasting results between GeoMAN model and LSTM model every 15 minutes
时刻GeoMANLSTM时刻GeoMANLSTM 5:151.1450.06812:301.8062.126 5:301.1860.13212:452.0092.539 5:450.8380.35413:002.0302.609 6:000.3210.49913:152.0442.324 6:150.9510.70913:301.8732.542 6:300.9250.80813:451.9322.804 6:450.8661.03414:001.8932.944 7:000.8121.17614:151.7812.851 7:150.8661.47714:301.5412.748 7:300.9701.71614:451.4922.538 7:450.7261.81815:001.6852.265 8:000.6181.69615:151.7342.280 8:150.7431.48315:301.3862.199 8:300.9511.60215:451.1451.940 8:450.9661.52116:001.1761.627 9:001.3201.72316:151.2471.600 9:151.1481.78316:301.4900.857 9:301.3871.80116:450.8271.055 9:451.2231.99617:000.5550.654 10:001.4882.19617:150.7580.448 10:151.3672.15117:301.0180.339 10:301.3192.26517:450.9880.491 10:451.7422.64918:000.7890.475 11:001.3552.02318:150.9560.414 11:152.1712.87318:300.9880.365 11:301.8762.41318:451.0310.318 11:451.8742.12819:001.2740.254 12:001.5332.33419:151.1890.236 12:151.9302.52019:301.0850.163
表4 GeoMAN模型和LSTM模型的测试集预测结果对比
Tab.4 Comparison of forecasting results between GeoMAN model and LSTM model on test set

模型RMSEMAE GeoMAN1.7871.330 LSTM2.0611.568
综上,LSTM模型可以预测出光伏发电功率的大致趋势,预测曲线较平滑且波动性不强,而在实际光伏发电中,功率受到各种外部因素的影响而呈现较剧烈的波动性。因此LSTM模型预测功率与实际功率间的误差较大。GeoMAN模型的预测功率波动性更强,更贴近于实际发电功率。因此本文基于灰色关联分析和GeoMAN模型提出的一种动态时空特征提取和外部气象因素融合的光伏发电功率短期预测方法能有效提升光伏发电功率预测精度。
本文充分考虑了光伏发电功率的时空相关性和影响光伏发电的外部气象因素,提出基于灰色关联分析和GeoMAN模型的光伏发电功率短期预测方法。利用灰色关联分析选取与待预测光伏电站关联度较高的周边电站,为提取待预测光伏电站的空间特征提供依据。基于GeoMAN的功率预测模型中设置了站内特征注意力机制,站间空间注意力机制和时间注意力机制,充分挖掘了待预测光伏电站的动态时空特征。模型还融合了多源外部气象因素模块,进一步提升光伏发电功率的预测精度。算例分析结果表明,本文所述模型较LSTM模型具有更高的精度,说明基于灰色关联分析和GeoMAN的光伏发电功率短期预测模型应用于光伏发电功率预测的可行性和高效性,可以满足短期实时调度需求。
参考文献
[1]赖昌伟, 黎静华, 陈博, 等. 光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1201-1217. Lai Changwei, Li Jinghua, Chen Bo, et al. Review of photovoltaic power output prediction technology[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1201-1217.
[2]张雨曼, 刘学智, 严正, 等. 光伏-储能-热电联产综合能源系统分解协调优化运行研究[J]. 电工技术学报, 2020, 35(11): 2372-2386. Zhang Yuman, Liu Xuezhi, Yan Zheng, et al. Decomposition-coordination based optimization for PV-BESS-CHP integrated energy systems[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2372-2386.
[3]He Hui, Hu Ran, Zhang Yaning, et al. A power forecasting approach for PV plant based on irradiance index and LSTM[C]//Proceedings of the 37th Chinese Control Conference, Wuhan, China, 2018: 9404-9409.
[4]黄磊, 舒杰, 姜桂秀, 等. 基于多维时间序列局部支持向量回归的微网光伏发电预测[J]. 电力系统自动化, 2014, 38(5): 19-24. Huang Lei, Shu Jie, Jiang Guixiu, et al. Photovoltaic generation forecast based on multidimensional time-series and local support vector regression in microgrids[J]. Automation of Electric Power Systems, 2014, 38(5): 19-24.
[5]赵滨滨, 王莹, 王彬, 等. 基于ARIMA时间序列的分布式光伏系统输出功率预测方法研究[J]. 可再生能源, 2019, 37(6): 820-823. Zhao Binbin, Wang Ying, Wang Bin, et al. Research on output power forecast method of distributed photovoltaic system based on ARIMA time series[J]. Renewable Energy, 2019, 37(6): 820-823.
[6]焦田利, 章坚民, 李熊, 等. 基于空间相关性的大规模分布式用户光伏空间分群方法[J]. 电力系统自动化, 2019, 43(21): 97-105, 162. Jiao Tianli, Zhang Jianmin, Li Xiong, et al. Spatial clustering method for large-scale distributed user photovoltaics based on spatial correlation[J]. Automation of Electric Power Systems, 2019, 43(21): 97-105, 162.
[7]于若英, 陈宁, 苗淼, 等. 考虑天气和空间相关性的光伏电站输出功率修复方法[J]. 电网技术, 2017, 41(7): 2229-2236. Yu Reying, Chen Ning, Miao Miao, et al. A repair method for PV power station output data considering weather and spatial correlations[J]. Power System Technology, 2017, 41(7): 2229-2236.
[8]阚博文, 刘广一, Khodayar Mahdi, 等. 基于图机器学习的分布式光伏发电预测[J]. 供用电, 2019, 36(11): 20-27. Kan Bowen, Liu Guangyi, Khodayar M, et al. Distributed photovoltaic generation prediction based on graph machine learning[J]. Distribution & Utilization, 2019, 36(11): 20-27.
[9]王晶, 黄越辉, 李驰, 等. 考虑空间相关性和天气类型划分的多光伏电站时间序列建模方法[J]. 电网技术, 2020, 44(4): 1376-1384. Wang Jing, Huang Yuehui, Li Chi, et al. Time series modeling method for multi-photovoltaic power stations considering spatial correlation and weather type classification[J]. Power System Technology, 2020, 44(4): 1376-1384.
[10]焦田利. 基于时空关系的广域分布式光伏发电群出力预测关键模型研究[D]. 杭州: 杭州电子科技大学, 2019.
[11]路宽, 赵岩, 王昕, 等. 一种基于编码解码长短期记忆网络的短期风电功率预测方法: 中国, CN108711847B[P]. 2019-06-04.
[12]钟建林, 何友, 王红星. 基于多频小波分析和D-S推理的电路故障诊断[J]. 电工技术学报, 2010, 25(8): 180-184, 192. Zhong Jianlin, He You, Wang Hongxing. Circuit fault diagnosis based on multi-frequency wavelet analysis and D-S reasoning[J]. Transactions of China Electrotechnical Society, 2010, 25(8): 180-184, 192.
[13]Liang Yuxuan, Ke Songyu, Zhang Junbo, et al. GeoMAN: multi-level attention networks for Geo-sensory time series prediction[C]//Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, 2018: 3428-3434.
[14]李冬辉, 尹海燕, 郑博文, 等. 改进的LSTM方法在冷水机组传感器故障检测中的应用[J]. 电工技术学报, 2019, 34(11): 2324-2332. Li Donghui, Yin Haiyan, Zheng Bowen, et al. Application of improved LSTM method in sensor fault detection of the chiller[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2324-2332.
[15]朱文立, 张利, 杨明, 等. 考虑日周期性影响的光伏功率爬坡事件非精确概率预测[J]. 电力系统自动化, 2019, 43(20): 31-40. Zhu Wenli, Zhang Li, Yang Ming, et al. Imprecise probabilistic prediction of photovoltaic power ramp event considering daily periodic effect[J]. Automation of Electric Power Systems, 2019, 43(20): 31-40.
[16]谢恩哲. 考虑气象要素的光伏预测模型研究[D]. 哈尔滨: 哈尔滨理工大学, 2015.
[17]吉锌格, 李慧, 刘思嘉, 等. 基于MIE-LSTM的短期光伏功率预测[J]. 电力系统保护与控制, 2020, 48(7): 50-57. Ji Xinge, Li Hui, Liu Sijia, et al. Short-term photovoltaic power forecasting based on MIE-LSTM[J]. Power System Protection and Control, 2020, 48(7): 50-57.
[18]王晨, 寇鹏. 基于卷积神经网络和简单循环单元集成模型的风电场内多风机风速预测[J]. 电工技术学报, 2020, 35(13): 2723-2735. Wang Chen, Kou Peng. Wind speed forecasts of multiple wind turbines in a wind farm based on integration model built by convolutional neural network and simple recurrent unit[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2723-2735.
Short-Term Photovoltaic Power Forecast Based on Grey Relational Analysis and GeoMAN Model
Abstract Accurate forecast of photovoltaic (PV) power is important for power system dispatch. A new short-term PV power forecasting method is proposed based on grey relational analysis and GeoMAN model. Firstly, grey relational analysis is utilized to analyze spatial correlation among multiple PV stations. And several surrounding PV stations highly related with the target PV station are selected. Then, GeoMAN model is established for dynamically extracting the spatiotemporal feature and external meteorological factors. GeoMAN model adopts encoder and decoder structure. The encoder is utilized to dynamically extract the intra-station feature of the target station and the inter-station spatial feature with the related stations. The decoder is utilized to extract the time feature of input variables. Clearness index and numerical weather prediction (NWP) are finally integrated for short-term PV power forecast. A case study is conducted using data collected from practical PV stations. Study results indicate that the proposed method can achieve higher accuracy compared with long short-term memory (LSTM) model.
Keywords:Short-term PV power forecast, grey relational analysis, GeoMAN model, spatiotemporal correlation, attentional mechanism
中图分类号:TM615
DOI:10.19595/j.cnki.1000-6753.tces.200538
国家电网河北电力有限公司科技项目资助(kj2019-077)。
收稿日期 2020-05-25
改稿日期 2020-08-22
时 珉 男,1976年生,本科,高级工程师,研究方向为电力系统运行与控制、可再生能源发电系统。E-mail:shimin9999@126.com
王 珏 男,1981年生,博士,研究生导师,研究方向为人工智能算法与应用软件、高性能计算。E-mail:wangjue@cnic.cn(通信作者)
(编辑 赫蕾)