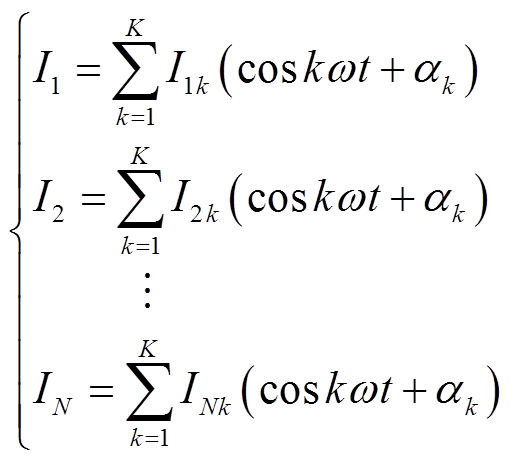（1）摘要 为了实现对电力系统负荷的高效监测，提出了针对其暂态与稳态工作状况的非侵入式监测方法。对于准确获得任意稳态时刻的负荷工作状态的问题，提出了基于自筛选的优化遗传算法（AOGA）的稳态监测模型，将电力参数模型转换为有功分量模型及无功分量模型，以此建立双目标函数，解决了由于高谐波电流影响小、求解参数少引起监测误差的问题。优化遗传算法构造了自筛选程序，将适应度相同的结果先做筛选，再利用欧氏距离对功率进行判别，解决了传统遗传算法（GA）进行负荷监测时由于适应度相同引起误判的缺陷。当负荷进行投切时，为了准确获得投切类型，该文建立了基于功率-时间（P-T）的暂态监测Matlab-Simulink模型，首先利用离散傅里叶分解的方法提取暂态发生前后功率的变化量，通过对比功率匹配度对动作负荷进行识别；在功率监测的基础上，以负荷的谐波含有率为负荷特征进行谐波特征判别，进一步提高了暂态负荷监测的精度。
关键词：非侵入式 自筛选优化遗传算法 双目标函数 P-T模型 谐波特征
随着我国经济社会和科技的快速发展，智能电网已经成为电力系统未来的发展方向，对电力系统负荷进行高效监测是实现电网智能化的重要组成部分。目前的电力监测手段是在每个负荷上装设独立的监测装置，通过对每个负荷的单独监测实现对其运行状态的判定，耗费了大量的人力、物力、财力[1-4]。对于上述问题，提出了一种非侵入式的负荷监测方式，即不需要进入用户用电系统的内部，只需要在电力入口处装设监测设备，通过监测入口处的总电压及总电流等电气量，并将其进行分解就可以得到电力系统内部每个负荷的运行状态[5-6]。通过这种方式，不仅可以很好地保护用户的用电隐私，也可节省大量的监测设备，减少分析与处理数据的工作，同时又可以实现对系统中每类负荷运行状态的监测。
非侵入式负荷状态监测对电力系统总端处监测到的负荷数据进行分解与识别，分析系统内每类或每个负荷的运行状态，可以更为准确地了解整个电力系统的负荷组成，每种负荷的用电分配量以及用电时间，进而合理地规范负荷用电量以及安排负荷的运行时间。非侵入式负荷分解技术不仅可以使电力部门实时了解用户的用电情况，以便于规划合理的计价系统，同时也能够给用户提供有效的用电建议，因此对非侵入式负荷分解技术进行优化改进是非常必要的[7-10]。从工作状态的角度，现有的非侵入式的负荷状态监测主要分为暂态监测和稳态监测两大类。暂态监测主要是为了获知负荷投切的工作时间，以便于获得负荷的工作规律[8-9]；稳态监测主要是为了获知任意稳态时刻下的负荷工作状态，以便于合理分配电量[11-12]。
目前对电力系统非侵入式状态监测的方法有，Srinivasan等引用神经网络[13-14]，根据负荷稳态电流的相关特征对负荷工作状态进行分解。Najmeddine等，结合对电压和电流的相关属性量分析以及功率的大小确定负荷投切状态[15-16]。随后，提出了V-I轨迹曲线的方法。通过V-I曲线反映待测范围内所有的用电负荷，通过归一化处理使负荷特征数据统一，Marchiori等利用贝叶斯判别通过对用电设备加入贝叶斯分类器，但由于需要的参数多，进而使结果不准确[17-18]。许仪勋等将负荷稳定工作时电流的基波谐波作为负荷特征，利用改进的鸡群算法进行求解，但存在无非识别重叠工作负荷的不足[19-20]。王志超等将稳态时的电流参数作为负荷特征，利用决策树的方法进行识别，可以准确地识别出特征差异较大的负荷，但是对于相似度高的负荷，无法准确识别[21]。
基于上述分析，本文分别从稳态和暂态的角度入手，对不同状态下的电气特征，针对性地进行建模分析。对于稳态监测，建立基于自筛选的优化遗传算法（Automatic screening Optimized Genetic Algorithm, AOGA），解决了由于高谐波电流影响小、求解数据量少引起监测误差的问题，以及传统遗传算法（Genetic Algorithm, GA）中因适应度相同引起的误判的问题。通过与传统GA算法的对比，AOGA算法不仅收敛速度快，而且准确率高，具有一定的先进性。对于暂态监测，建立了基于功率-时间（P-T）的暂态监测模型，通过监测功率的变化以及暂态发生时的持续时间，确定暂态发生的时刻。利用功率的变化量进行识别，以确定发生暂态的负荷类型。为了使暂态监测的误差更小，本文在此基础上利用谐波含有率做了进一步的识别，解决了因功率接近引起误判的问题，提高了暂态监测精度。
为了得知某一时刻下的负荷工作状况，本文对稳态电流信号进行分解，将端口总电流进行傅里叶分解，分别构造有功分量模型和无功分量模型。利用AOGA算法对其进行监测识别，将最优结果记录并筛选，再利用欧氏距离进行功率判别提高精度。
由基尔霍夫电流定律可得，总端处的电流可由各支路的电流相叠加而成，本文将总端电流以及负荷库中的电流信息作为负荷特征，将N种负荷进行傅里叶分解，建立方程组为
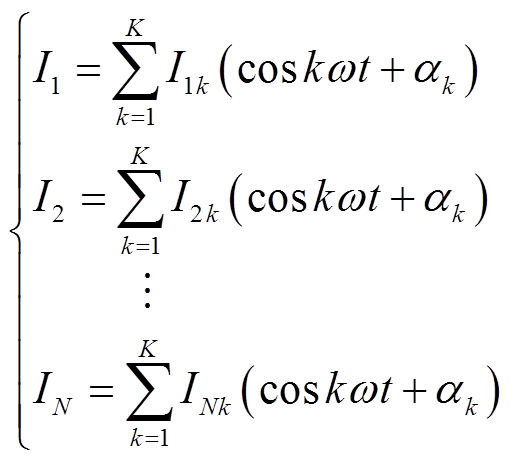（1）将总电流i进行快速傅里叶（Fast Fourier Transfer, FFT）展开得
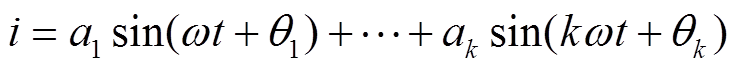（2）经过FFT算法对电流i进行傅里叶分解，由基尔霍夫电流定律可得N种负荷电流形成的总电流It在t时刻的表达式为
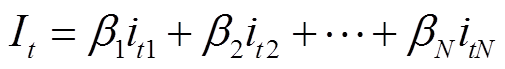（3）式中，itn为各负荷的电流，n=1,2,
,N；βn为各负荷的工作状态，当βn=1时，表示负荷处于工作状态，当βn=0时，表示负荷处于未工作状态。用矩阵可表示为
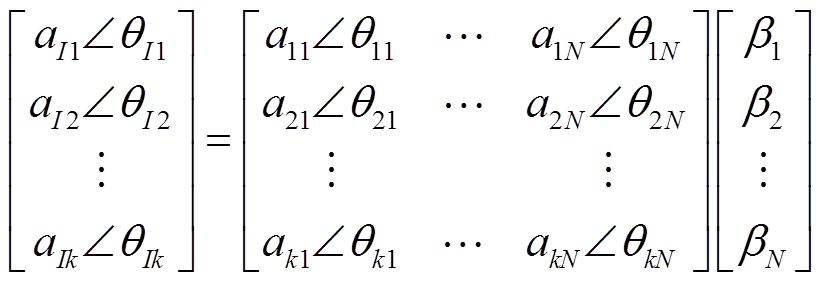（4）式中，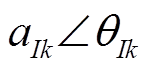
为总电流It的第k次谐波的幅值与角度；
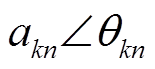为第n个负荷第k次谐波的幅值与角度。
由于式（4）模型参数求解复杂，精度偏低，本文将负荷特征转换为有功分量与无功分量特征。得到，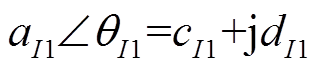
。转换后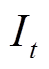
的有功分量与无功分量的表达式为
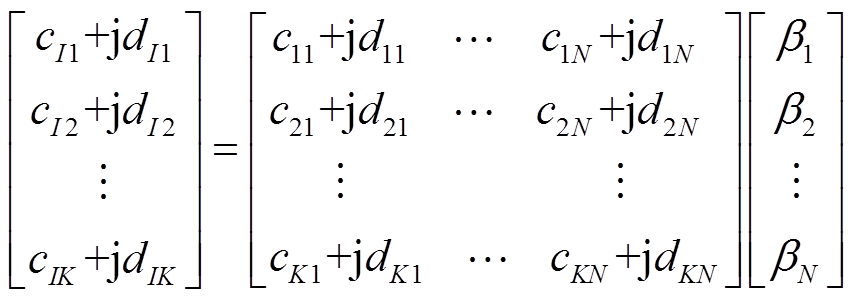（5）式中，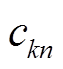
为第n种负荷第k次谐波的有功分量；
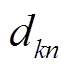为第n中负荷第k次谐波的无功分量。以式（5）为基础建立双目标函数模型，得到
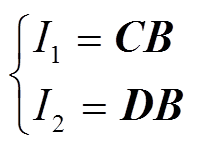（6）式（6）第一式为有功分量运算的表达形式，第二式为无功分量运算的表达形式。C为有功分量负荷信息的系数矩阵；D为无功分量负荷信息的系数矩阵；B为待求解矩阵，反映负荷的工作状态，且
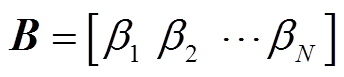（7）
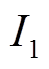与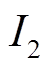
分别表示总电流的有功分量与无功分量。建立误差函数
（8）第一式为有功误差函数，第二式为无功误差函数。求解目标为匹配准确度最大，在模型中表现为误差函数值最小，以此建立综合目标函数为
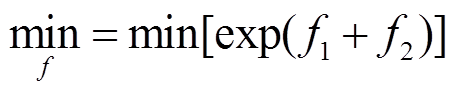（9）1.2.1 目标函数的建立
根据负荷匹配准确度最大化的目标，建立AOGA算法适应度为
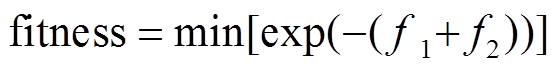（10）1.2.2 AOGA算法模型的建立
传统的遗传算法主要包括种群的设定、生成初始种群、种群的复制得到新种群、新种群交叉、新种群的变异、适应度以及目标函数的计算、结果储存等过程。传统遗传算法具有初始种群生成时的随机性大，每一个子代之间交叉变异的局限性大、无法将优秀子代的特征保留等不足，本文提出了AOGA算法模型。具体过程如下：
（1）设置种群大小。
（2）设置染色体编码长度，染色体长度等于负荷库中总电气数目。
（3）进行轮盘复制，以优质染色体扩大种群数目。
（4）保留每次迭代产生的优秀子代，将优秀子代作为下一次循环的初始种群，此方法不仅提高了筛选速度，而且大大提高了负荷的匹配程度。
（5）对目标函数进行寻最优匹配。
（6）针对当适应度相同时，可能会存在不同负荷工作的情况，本文增加了自筛选算法，再通过其他负荷特征做进一步的筛选识别，减小了传统负荷分解由于信息重合引起的误差，提高了负荷识别的准确性。稳态负荷监测流程如图1所示。
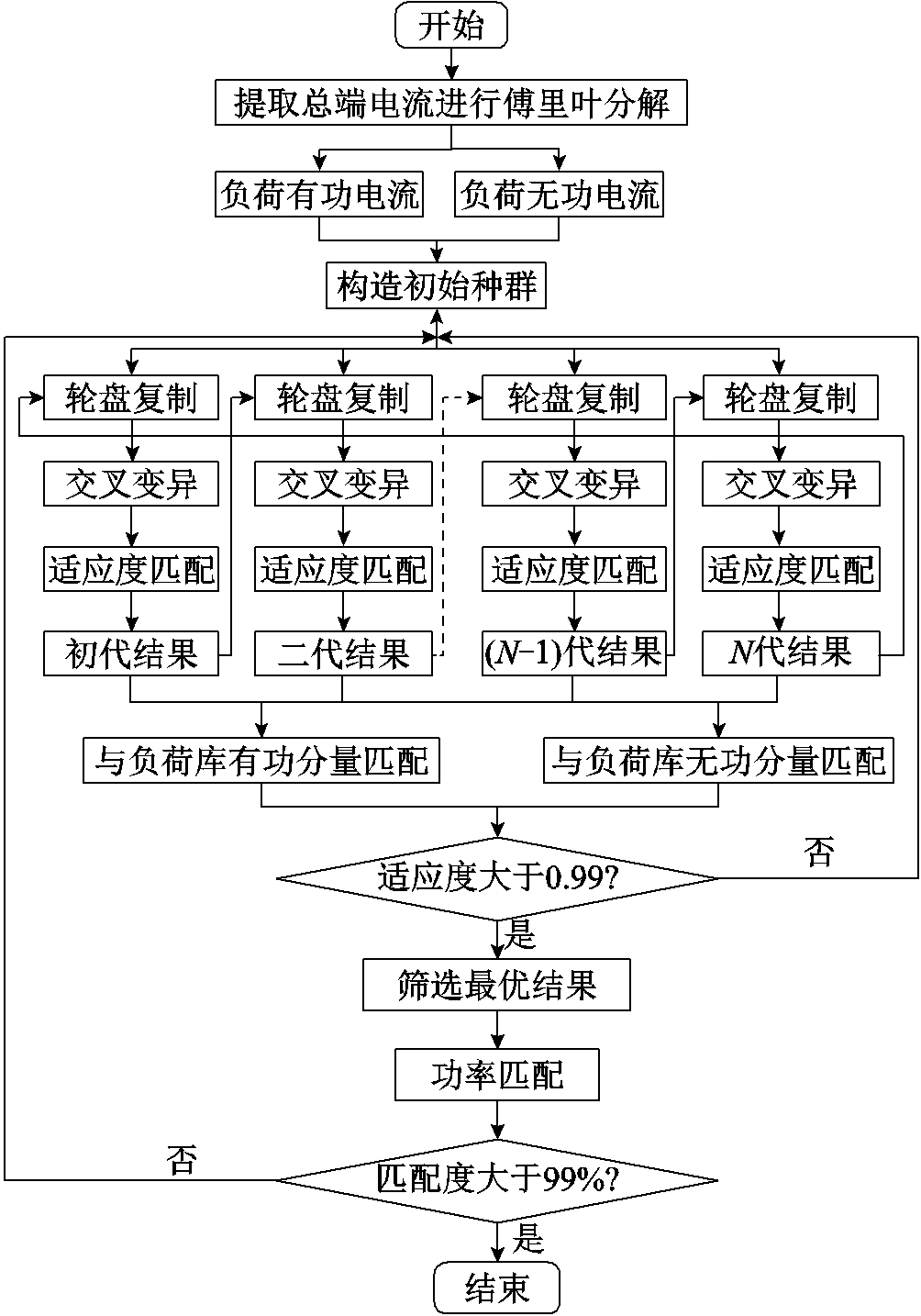
图1 稳态负荷监测流程
Fig.1 Flow chart of steady-state negative monitoring
当电力系统中的负荷从一个状态变化为另一个状态时，引起特征量发生明显变化的过程称为暂态过程[22]。如果可以得知各类负荷的投切时间，用电系统便可以针对某一时刻精准分配供电量，降低用电成本，节约资源。本文首先对暂态过程进行了监测，识别出暂态过程发生的时刻，再提取暂态发生前后负荷的有功功率，得到初步识别的结果，由于有功功率存在相似性，进一步利用不同投切下的谐波含量差作为判别依据，得到更为精确的判别结果。
对暂态过程的准确监测是进行暂态识别的前提，当系统中发生暂态过程时，一般会伴随着明显的电气量的变化，例如有功功率及电流幅值等的暂态监测数据，如图2和图3所示。
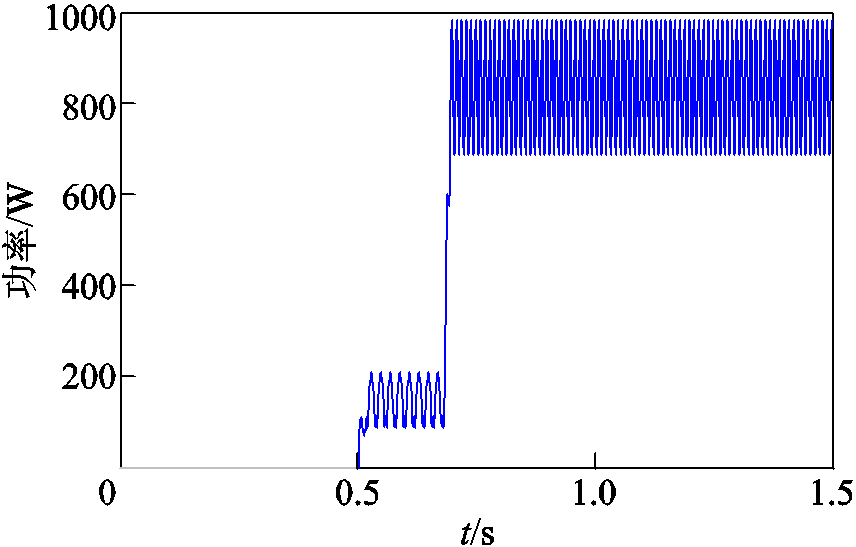
图2 功率暂态监测
Fig.2 Transient monitoring of power
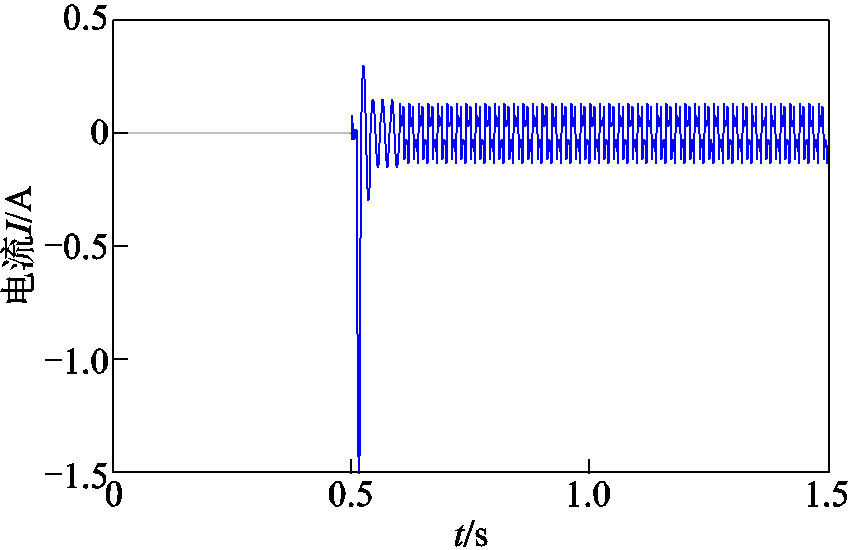
图3 电流暂态监测
Fig.3 Transient monitoring of current
由图2和图3可知对于同一种负荷，功率的突变结果（＞200W）比电流的突变结果（＜2A）明显，因此以功率的突变点为基准进行监测较为准确。
两个相邻的周期中功率的变化量为
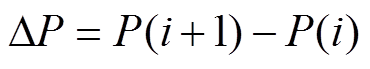（11）暂态过程开始的判据为
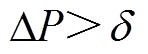（12）式中，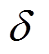
为功率判定阈值，一般采用小于负荷库中最小功率的值，本文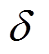值取10W。
在负荷进行投切时，负荷特征会发生明显的变化，为了减小噪声误差，本文利用暂态维持时间与暂态监测时间的比值为判据，提高判断的准确率。暂态过程确定的判据为
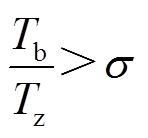（13）式中，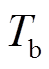
为暂态持续时间；
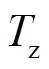为监测时间；
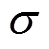为暂态时间的判定阈值，本文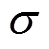取0.1s。
当式（12）与式（13）的限定条件同时成立时，判定暂态发生。在得知暂态发生时间的基础上，再对投切负荷的类型加以识别。暂态判定流程如图4所示。
图4 暂态判定流程
Fig.4 Flow chart of transient judgment
通过2.1节的判定，得知负荷的投切时刻。为了对发生投切的负荷种类进行判别，本节首先根据常用的电器名牌数据建立了功率负荷库，见表1。
表1 功率负荷库
Tab.1 Load statistics of power
负荷功率/W 取暖器1 834.8 计算机46.032 8 节能灯15.4
（续）
负荷功率/W 吹风机1 072.447 2 空调2 376 洗碗机1 351.46 微波炉1 604.57 风扇45.738 台式计算机84.238 电水壶2 464.396 电热器867.922 取暖器1 380.632
依据有功功率是瞬时功率在一个周期中取平均值的定义，利用离散的傅里叶展开的方法，提取有功功率，即
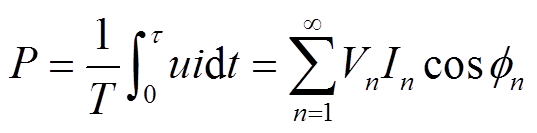（14）为了确定发生投切的负荷类型，建立了基于P-T模型的Simulink仿真如图5所示。
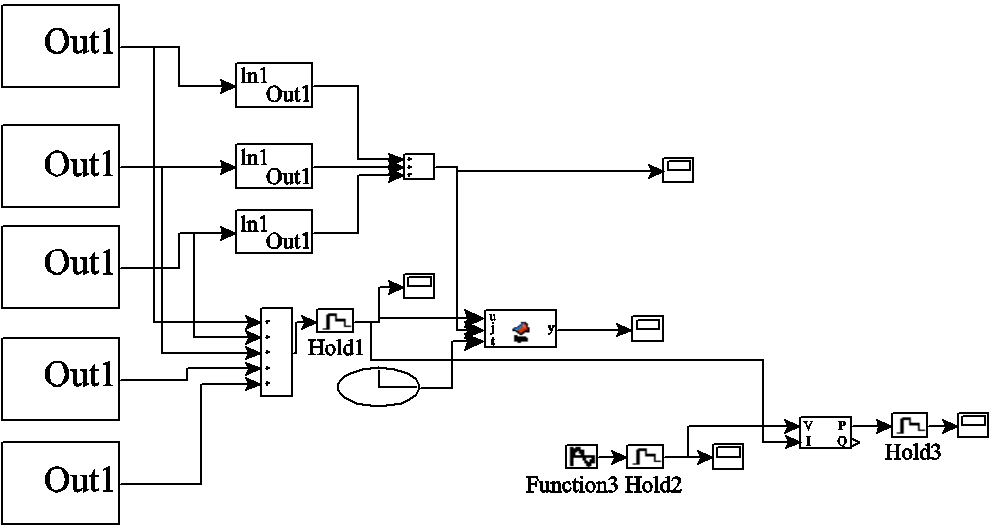
图5 基于P-T模型的Simulink仿真平台
Fig.5 Simulink simulated platform based on P-T model
此处暂时以六种负荷进行识别，若有需要可在此基础上增加负荷。建立功率模型后，利用式（11）求出暂态点前后的稳态功率差。在确定暂态发生时间的基础上，将得到的每个暂态点处的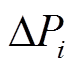
与建立好的负荷库中的各类电器的功率进行做差比较，当|ΔPi-Pi|＜λ时，可记为第i种负荷在工作，
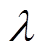为功率判定的阈值，本文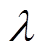的取值为1W。
由于部分负荷的功率极其相似，采用功率判别会产生误差，本文在功率判别的基础上引入了谐波特征作为第二判别依据。在过去研究中，多利用谐波幅值作为识别判定的特征量，而由于实际生活中部分谐波幅值与基波差别过大，此时谐波特征将不能做为判别依据，因此，本文提出以谐波含有率作为负荷特征提高判别的准确度。
谐波含有率的定义为
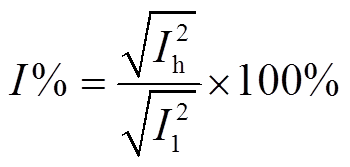（15）进行稳态分析时，本文选取了21种负荷进行工作状态识别。首先通过傅里叶分解，建立有功电流与无功电流的负荷库，此处展示负荷库中部分负荷的傅里叶变换结果，如图6所示。
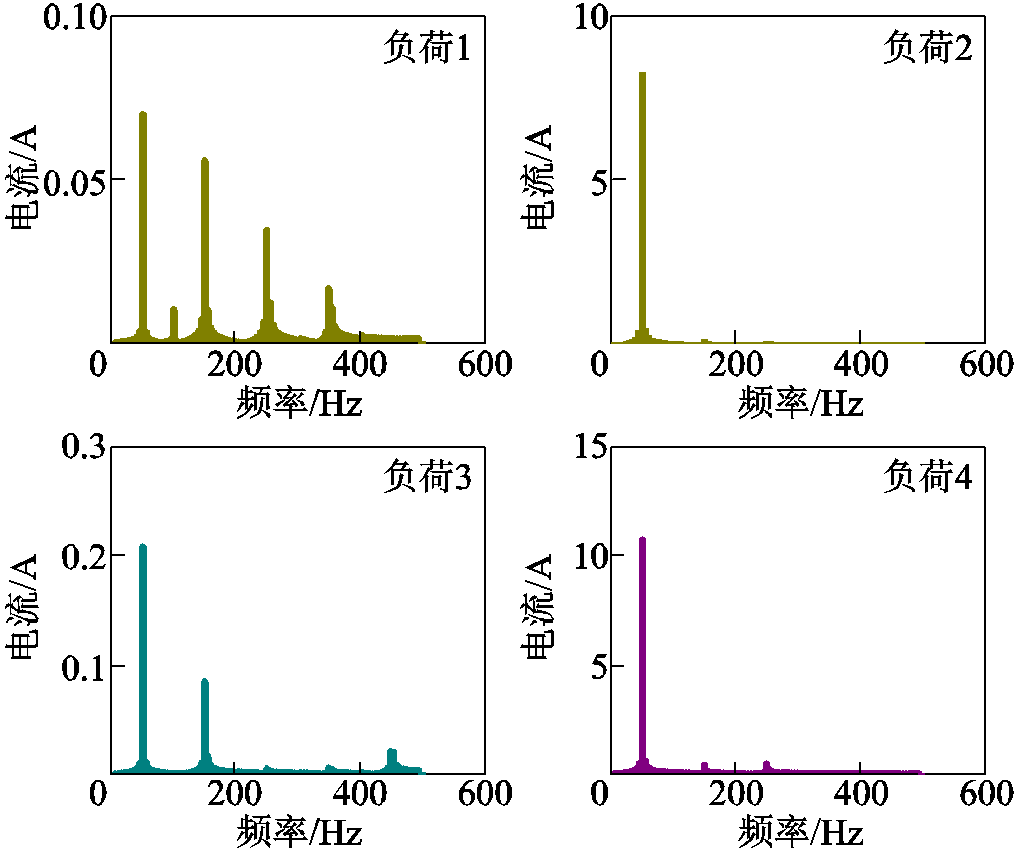
图6 负荷1～4的傅里叶变换
Fig.6 Fourier transform of load 1～4
提取总端电流，利用傅里叶分解得到电流的各次谐波信息，谐波次数越高信息量总越多，识别准确度越高。但是当谐波次数越高，电流值降低越快，当数值小到一定程度时谐波在判别过程中几乎不起作用。为了提高识别准确度，本文提取了总端电流的10次谐波，将其分解成有功分量和无功分量，使得负荷匹配参数增加一倍，即解决了高次谐波电流幅值过小的问题，又增加了匹配参数。对总电流的有功和无功分量见表2和表3。
表2 总电流有功分量
Tab.2 Active component of total current
谐波次数谐波幅值/A谐波次数谐波幅值/A 132.208 1460.018 61 20.071 9170.255 18 30.617 7380.004 86 40.035 3690.102 72 50.500 33100.156 95
表3 总电流无功分量
Tab.3 Reactive component of total current
谐波次数谐波幅值/A谐波次数谐波幅值/A 119.205 860.012 35 20.043 6370.133 24 30.399 1780.002 07 4-0.005 3190.075 19 5-0.089 41100.015 69
由式（7）的待求矩阵B可知，负荷仅有工作和未工作两种状态，因此，在AOGA算法的参数设定中采用0-1二进制编码。AOGA算法参数设定如下：
（1）提取总端电流参数，作为待分解参量。
（2）导入负荷库。
（3）设置自变量数目，在AOGA算法模型中，自变量数目以及染色体编码长度均为电气量数目，此数目可因负荷库的大小改变，本文为21。
（4）初始化种群，即随机生成设置初始种群的大小，本文设置为100。
（5）进行轮盘复制，扩大种群数目，在此基础上进行染色体的交叉变异和基因突变。本文设定交叉概率为0.8，突变概率为0.09。
（6）计算每次迭代的适应度大小，将适应度大于0.8的种群保留，作为初始种群，进入下一次迭代循环，本文设定的算法迭代次数为250次。
（7）每次迭代结果与前一次迭代结果进行对比，将适应度大的迭代结果保留。迭代过程中适应度最大的种群作为每次循环的最优种群保留。
（8）AOGA算法设定遗传循环次数为10次，对比每次循环结果，自动筛选适应度大于0.99的种群，保留适应度最优的循环次数，作为AOGA算法的最终计算结果。
AOGA算法的运算结果见表4。
表4 AOGA算法负荷识别结果
Tab.4 Results of load identification based on AOGA
循环次数适应度负荷最优工作组合 80.999 897110001011000011000000 90.999 897110001011000011000000
AOGA算法将适应度大于0.99的运算结果均筛选出来，与传统的遗传算法相比，降低了运算误差，提高了负荷识别的准确度。AOGA进化过程和运行结果如图7和图8所示。
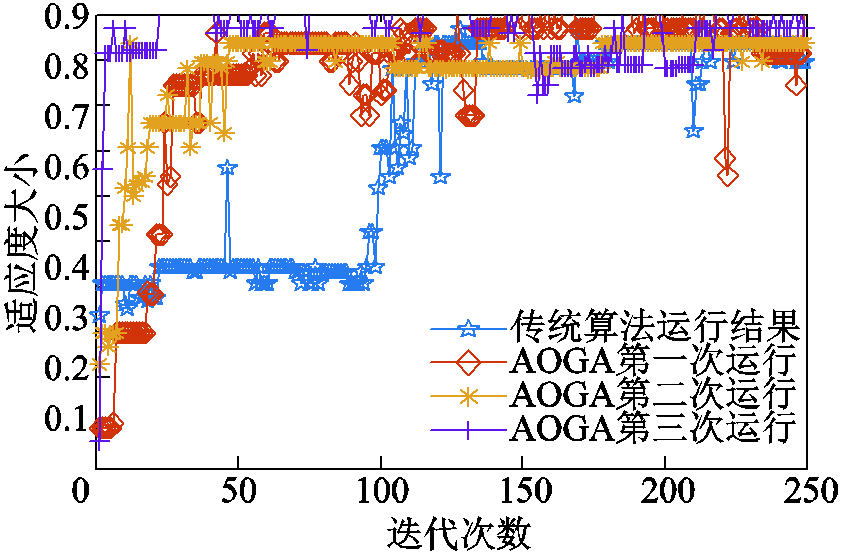
图7 AOGA进化过程
Fig.7 Evolutionary process diagrams of AOGA
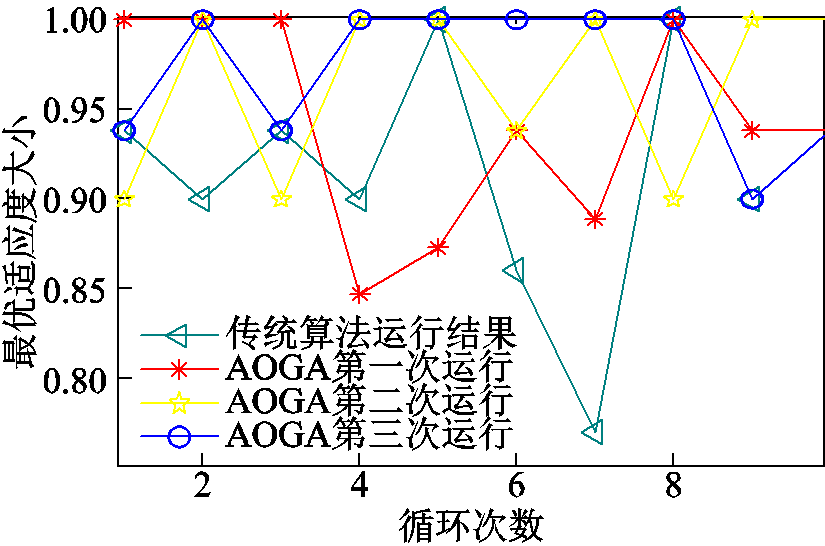
图8 AOGA运行结果
Fig.8 Operation results AOGA
图7可以看出，AOGA算法相对于传统的GA算法适应度收敛速度快，计算准确度提高。增加运行次数收敛速度加快，体现了每次保留最优结果作为初始种群的优越性。并且，AOGA在运行3次结果趋于一致，体现了算法的稳定性。
图8可以看出，AOGA算法相对于传统的GA算法适应度明显提高，即计算误差明显减小。
传统GA算法进行负荷识别时，引起识别误差的原因主要有以下两种：
（1）工作负荷不同，但是误差叠加后结果相同，使得识别结果不准确。
（2）出现式（16）的情况。
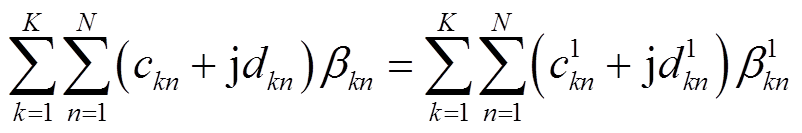（16）式中，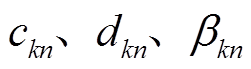
为实际工作的负荷参数；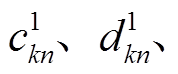
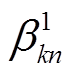为另一组负荷参数。
针对以上问题，AOGA算法做了一步的改进，自动筛选出适应度达到最优的所有结果，见表5。
由AOGA的运行结果可知，当解的大小相同时，可能出现不同的工作状态，例如，表5中的第3、5、7次分解结果与第6、8、9次的分解结果并不相同。为了找到最优解，计算每组筛选结果的功率大小，并与负荷库中的功率进行对比。本文利用式（17）的欧式距离，得到距离最小的解为最优解，并作为AOGA算法的最终监测识别结果。
表5 AOGA算法负荷识别结果
Tab.5 Results of load identification based on AOGA
次数适应度负荷最优工作组合 30.999 897010001011000011000001 50.999 897010001011000011000001 60.999 897110001011000011000000 70.999 897010001011000011000001 80.999 897110001011000011000000 90.999 897110001011000011000000
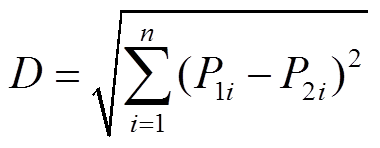（17）在AOGA运行结果的基础上，引入欧式距离对负荷工作状态进行进一步识别，结果见表6。
表6 引入欧式距离识别结果
Tab.6 Recognition results by introducing Euclidean distance
次数适应度负荷最优工作组合 30.999 897010001011000011000001 50.999 897010001011000011000001 70.999 897010001011000011000001
由AOGA的运行结果可知，实际负荷工作状态为第3、5、7次计算出来的工作状态。因此，利用功率欧式距离的筛选可以解决传统GA算法在负荷识别中产生的误差，提高了负荷识别精度。
本文以六种负荷的投切做暂态的结果评估，首先对负荷进行编号，见表7。
表7 负荷编号
Tab.7 Load number of the load
编号负荷编号负荷 1取暖器4吹风机1 2日光灯5空调 3节能灯6吹风机2
负荷投切的仿真运行结果如图9所示。针对图9展示的负荷投切仿真过程，通过提取到的暂态数据，利用暂态负荷识别算法，得到每个暂态发生的时间以及暂态点功率的变化情况如图10所示，识别结果见表8。
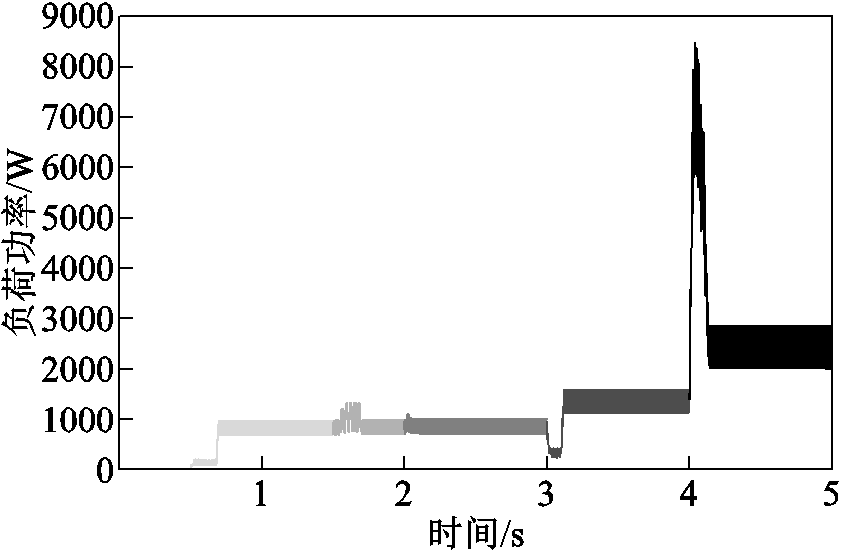
图9 负荷投切P-T仿真运行图
Fig.9 P-T simulation diagram of load switching
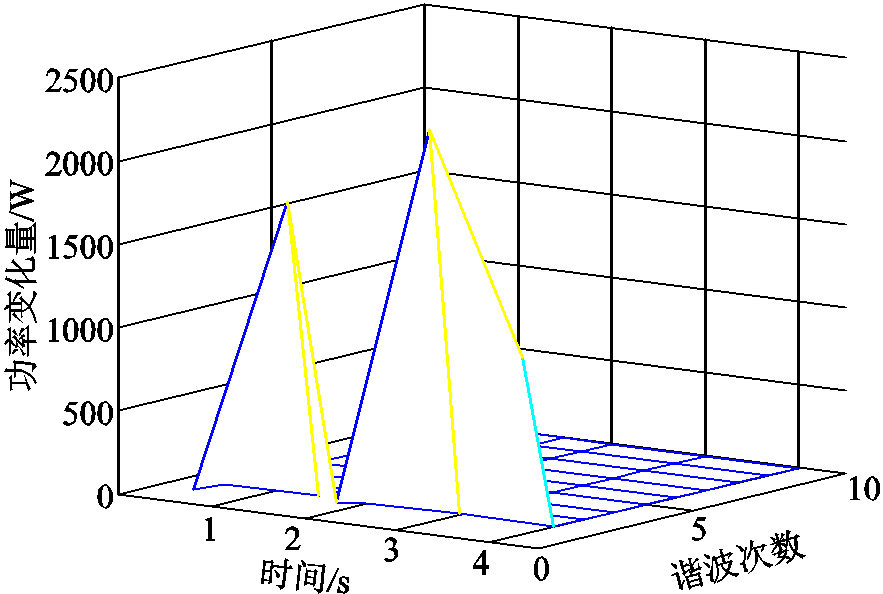
图10 暂态发生时间以及功率变化
Fig.10 Transient time and power change
表8 负荷投切结果判别
Tab.8 Judgment of load switching results
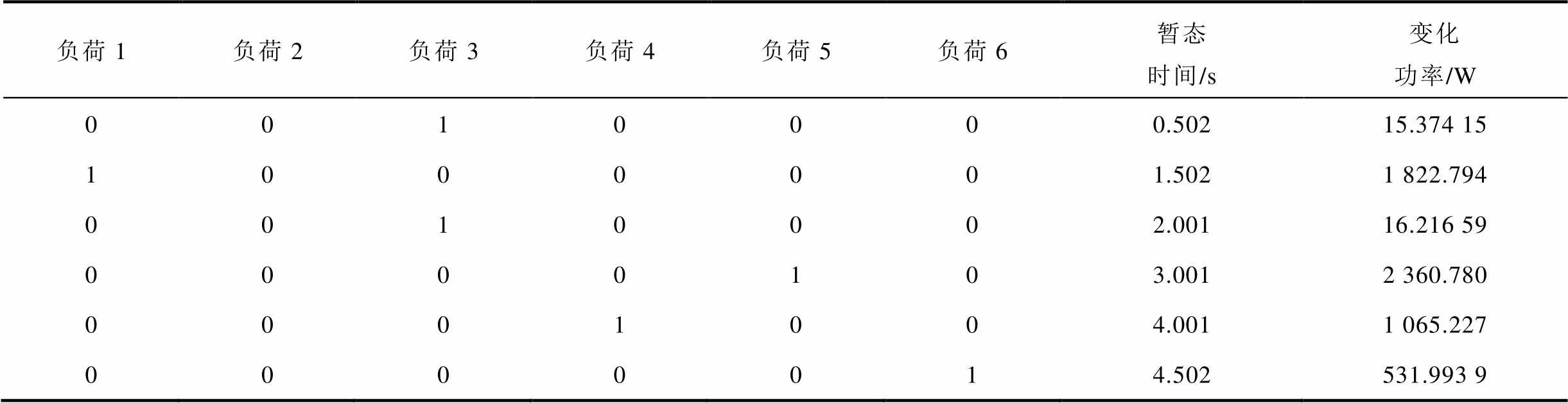
负荷1负荷2负荷3负荷4负荷5负荷6暂态时间/s变化功率/W 0010000.50215.374 15 1000001.5021 822.794 0010002.00116.216 59 0000103.0012 360.780 0001004.0011 065.227 0000014.502531.993 9
表8中，负荷所在列为1时，表明负荷工作。根据功率进行负荷判别时的结果为：负荷5（吹风机1）在3.001s的时候开始工作，功率变化大小为2 360.780W；负荷4（空调）在4.001s的时候开始工作，功率变化大小为1 065.227W，其余负荷以此类推。与图7的仿真结果相比，负荷投切类型判断均正确。
对于负荷投切时间，负荷1、负荷2、负荷6的时间均延迟0.02s，负荷3、负荷4、负荷5的判别时间均延迟0.01s。由此可见，当负荷在非整数秒进行投切时，识别延迟0.02s；在整数秒投切时，识别延迟0.01s。
由图8可以看出，功率识别时可以确定暂态发生的时间，但是对于发生投切的负荷类型的识别存在误差，即2s时应该是负荷2发生投切而误判成负荷3发生投切。这是由于仅利用功率进行判别时，基波的影响作用相比，谐波的作用几乎为零，当基波的功率非常接近时，可能会造成判别失误。本文设定的功率判定阈值为1W，因而当两种负荷的功率差小于1W时，就可能引起误判。因此为了提高判别精度，本文引入谐波含有率作为判据，由式（15）可得，不同负荷谐波含有率如图11所示。
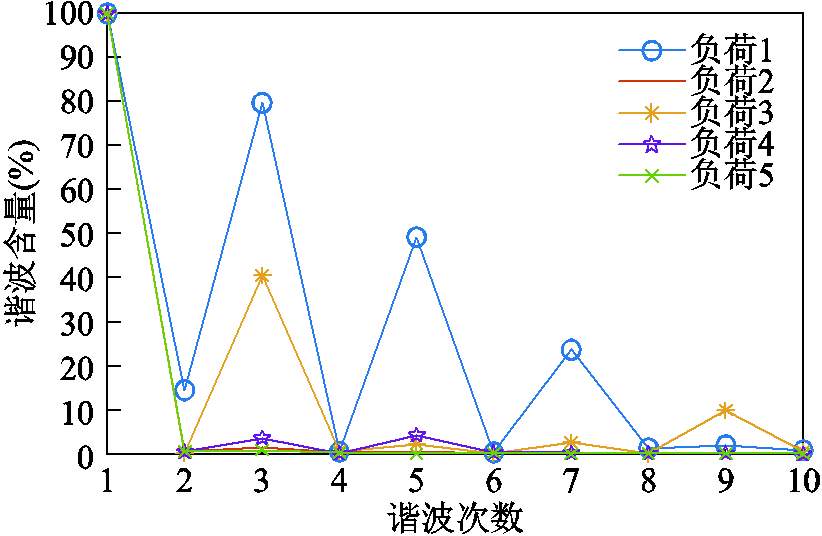
图11 各负荷谐波含有率
Fig.11 Harmonic content of each load
由图11可以看出，不同负荷之间的谐波含有率的差异较大，将其作为负荷判断的一种依据，可以提高负荷识别的准确率。
针对图9展示的负荷投切仿真过程，提取暂态数据，利用谐波含有率进一步分析，得到每个暂态发生的时间以及暂态点谐波含有率的变化情况如图12所示，判别结果如图13所示。
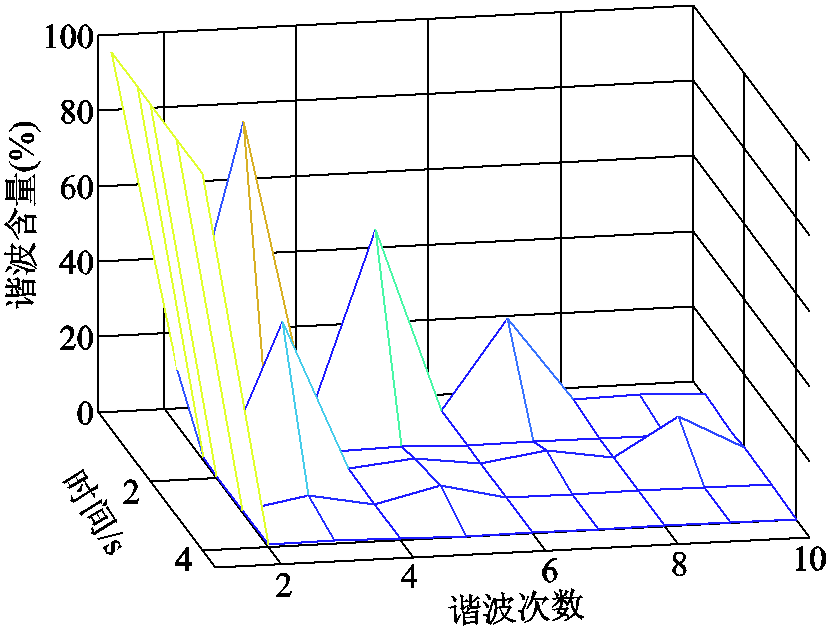
图12 暂态发生时间以及谐波含有率的变化
Fig.12 The change of transient time and harmonic content
以电流的谐波含有率（图12）与功率（图10）在负荷进行投切时的负荷特征做对比，谐波含有率在二次判别时各次谐波的影响较为明显，并且准确识别出了负荷2在2s时发生投切的工作状态，使负荷类型的判别更为准确。
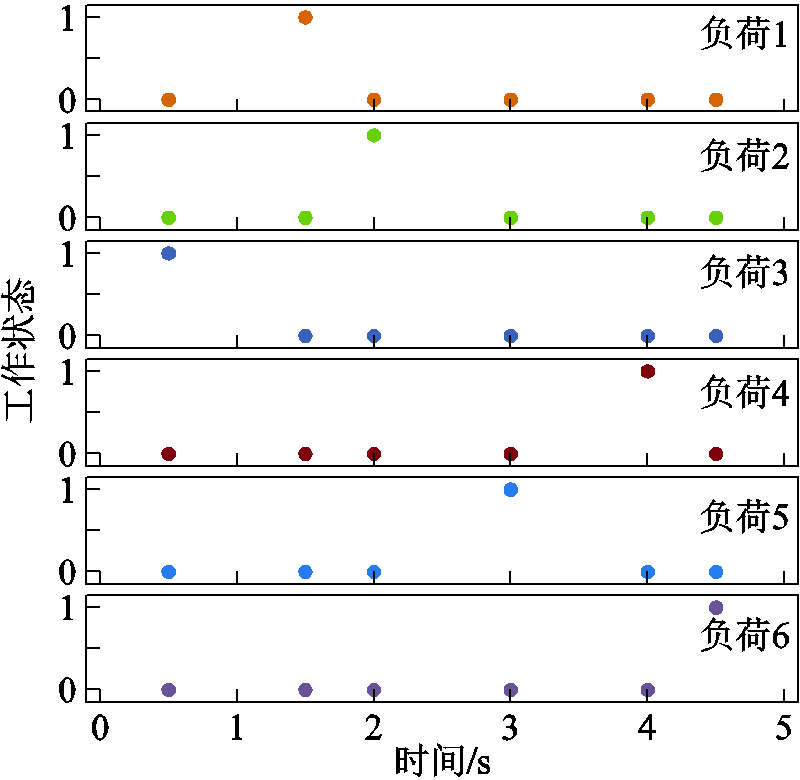
图13 谐波含有率暂态判别结果
Fig.13 Transient distinguish results of harmonic content
图13为通过谐波含有率的方式得到的判别结果，可知负荷1在1.5s的时候发生了投切，负荷2在2s的时候发生了投切，负荷3在0.5s的时候发生了投切，以此类推。图中，工作状态“1”表示工作；“0”表示不工作。
上述结果表示，在功率判别的基础上增加谐波判别不仅提高了识别准确度，而且消除了功率判别时的0.02s以及0.01s的误差，提高了判别精度。
本文通过傅里叶分解建立了负荷特征库，稳态监测过程中，通过将电气参数分解为有功分量与无功分量，以此构建双目标函数，解决了由于高谐波电流影响小、求解参数少引起监测误差的问题。利用AOGA算法进行求解，将适应度相同的结果先做筛选再利用欧氏距离对功率进行判别，解决了传统GA算法进行负荷监测时由于适应度相同引起误判的不足，加快了运算速度，提高了监测精度。
暂态检测过程中，建立了基于P-T的暂态监测Matlab-Simulink模型，通过监测功率的变化以及暂态发生时的持续时间，确定暂态发生的时刻。利用功率的变化量进行识别，在此基础上再通过谐波含有率做进一步的识别；解决了功率识别时因功率接近引起误判的问题，提高了暂态监测精度。
综上所述本文分别从电力系统稳态和暂态的角度对负荷的工作状态进行了监测，加快了运算速度，改善了传统监测方法的不足，提高了监测精度，具有一定的先进性。但还存在一些问题需要做进一步的研究：
1）对于稳态部分：针对优化遗传算法后续可能存在的误差处理，仅提出了一种采用功率进行进一步识别的方法，还需对加入功率是否会存在误差做进一步的探究。
2）对于暂态部分，仅考虑了负荷投切引起的暂态过程，未考虑由于系统故障引起的暂态过程，后续应对此过程进行探究。
参考文献
[1]孙毅. 基于遗传优化的非侵入式家居负荷分解方法[J].电网技术, 2016, 40(12): 3912-3917. Sun Yi. Anon-intrusive household load monitoring method based on genetic optimization[J]. Power System Technology, 2016, 40(12): 3912-3917.
[2]刘世成. 基于大数据的非侵入式负荷分解技术研究[J]. 电力信息与通信技术, 2016,14(12): 9-14. Liu Shicheng. Research on non intrusive load decomposition technology based on big data[J]. Electric Power Information and Communication Technology, 2016, 14(12): 9-14
[3]Martins J F, Lopes R, Lima C, et al. A novel nonintrusive load monitoring system based on the S-transform[C]//2012 13th IEEE International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 2012: 973-978.
[4]Remscrim Z, Paris J, Leeb S B, et al. FPGA-based spectral envelope preprocessor for power monitoring and control[C]//Applied Power Electronics Conference and Exposition(APEC), Palm Springs, CA, USA, 2010: 2194-2201.
[5]张虹, 侯宁, 葛得初. 供需互动分布式发电系统收益-风险组合优化建模及其可靠性分析[J]. 电工技术学报, 2020, 35(3): 623-635. Zhang Hong, Hou Ning, Ge Dechu. Modeling and reliability analysis of benefit-risk portfolio optimization for supply and demand interactive distributed generation system[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 623-635.
[6]刘博, 非侵入式电力负荷监测与分解技术[D]. 天津: 天津大学, 2013.
[7]张义志, 王小君, 和敬涵, 等. 考虑供热系统建模的综合能源系统最优能流计算方法[J]. 电工技术学报, 2019, 34(3): 562-570. Zhang Yizhi,Wang Xiaojun, He Jinghan, et al. The optimal energy flow calculation method of comprehensive energy system considering heating system modeling[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 562-570.
[8]王毅, 张宁, 康重庆, 等. 电力用户行为模型: 基本概念与研究框架[J]. 电工技术学报, 2019, 34(10): 2056-2068. Wang Yi, Zhang Ning, Kang Chongqing, et al. Electrical consumer behavior model: basic concept and research framework[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2056-2068.
[9]曹敏, 魏龄, 邹京希, 等. 基于暂态过程的非侵人式负荷监测研究[J]. 水电能源科学, 2018, 36(8): 177-180. Cao Min, Wei Ling, Zou Jingxi, et al. Research on non-intrusive load monitoring based on transient state process[J]. Water Resources and Power, 2018, 46(5): 97-103.
[10]李刚, 于长海, 王天军, 等. 居民负荷设备的非侵入式识别方法研究[J]. 电力信息与通信技术, 2017, 15(5): 54-60. Li Gang, Yu Changhai, Wang Tianjun, et al. Non-intrusive identification method for residential appliances[J]. Electric Power Information and Communication Technology, 2017, 15(5): 54-60.
[11]方红伟, 宋如楠, 冯郁竹, 等. 基于差分进化的波浪能转换装置阵列优化[J].电工技术学报, 2019, 34(12): 2597-2605. Fang Hongwei, Song Runan, Feng Yuzhu, et al. Array optimization of wave energy converters by differential evolution algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2597-2605.
[12]姜涛, 王长江, 陈厚合, 等. 基于正则化投影孪生支持向量机的电力系统暂态稳定评估. 电力系统自动化, 2019, 43(1): 141-148. Jiang Tao, Wang Changjiang, Chen Houhe, et al. Transient stability assessment of power system based on projection twin support vector machine with regularization[J]. Automation of Electric Power Systems, 2019, 43(1): 141-148.
[13]Srinivasan D, Ng W S, Liew A C. Neural-network-based signature recognition for harmonic source identification[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 398-405.
[14]Jian Liang, Simon K K N, Gail K, et al. Load signature study—Part I: basic concept, structure, and methodology[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 551-560.
[15]Najmeddine H, Drissi K E K, Pasquier C, et al. State of art on load monitoring methods[C]//2008 IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 2008: 1256-1258.
[16]Du Yi, Du Liang, Lu Bin, et al. A review of identification and monitoring methods for electric loads in commercial and residential buildings[C]// IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 2010: 4527-4533.
[17]Marchiori A, Hakkarinen D, Han Q, et al. Circuit-level load monitoring for household energy management[J]. IEEE Pervasive Computing, 2011, 10(1): 40-48.
[18]He Dawei, Du Liang, Yang Yi, et al. Frontend electronic circuit topology analysis for model-driven classification and monitoring of appliance loads in smart buildings[J]. IEEE Transactions on Smart Grid, 2012, 3(4): 2286-2293.
[19]许仪勋, 李旺, 李东东, 等. 基于改进鸡群算法的非侵入式家电负荷分解[J]. 电力系统保护与控制, 2016, 44(13): 27-32. Xu Yixun, Li Wang, Li Dongdong, et al. Disaggregation for non-invasive domestic appliances based on the improved chicken swarm optimization algorithm[J]. Power System Protection and Control, 2016, 44(13): 27-32.
[20]韩佶, 苗世洪, 李超, 等. 计及相关性的电-气-热综合能源系统概率最优能量流[J]. 电工技术学报, 2019, 34(5): 1055-1067. Han Ji, Miao Shihong, Li Chao, et al. Probabilistic optimal energy flow of electricity-gas-heat integrated energy system considering correlation[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1055-1067.
[21]王志超. 住宅用电负荷的非侵入式监测方法研究[D].重庆: 重庆大学, 2015.
[22]牛卢璐, 贾宏杰. 一种适用于非侵入式负荷监测的暂态事件检测算法[J]. 电力系统自动化, 2011, 35(9): 30-35. Niu Lulu, Jia Hongjie. Transient event detection algorithm for non-intrusive load monitoring[J]. Automation of Electric Power Aystems, 2011, 35(9): 30-35.
Research on Non-Invasive Load Monitoring Method in Power System
Abstract In order to monitor the power system load efficiently, this paper proposes a non-invasive monitoring method for its transient and steady-state working conditions. In order to accurately obtain the load working state at any steady-state time, an automatic screening optimized genetic algorithm (AOGA) is proposed, steady-state monitoring model, which transforms the power parameter model into active component model and reactive power component model, establishes double objective function, and solves the problem of monitoring error caused by small influence of high harmonic current and less solving parameters. The AOGA algorithm constructs a self screening program, which filters the results with the same fitness first, and then uses Euclidean distance to judge the power, which solves the defect of misjudgment caused by the same fitness in traditional genetic algorithm (GA). When the load is switched on and off, in order to obtain the switching type accurately, this paper establishes a power-time(P-T) based on power time, In the Matlab/Simulink model of transient monitoring, the discrete Fourier decomposition method is used to extract the power change before and after the transient occurrence, and the action load is identified by comparing the power matching degree; on the basis of power monitoring, the harmonic characteristics are identified by taking the harmonic content of the load as the load characteristics, which further improves the accuracy of the transient load monitoring.
keywords：Non-invasive, automatic screening optimized genetic algorithm, double objective function, P-T mode, harmonic characteristics
中图分类号：TM762
DOI：10.19595/j.cnki.1000-6753.tces.200622
收稿日期 2020-06-09
改稿日期 2020-07-20
雷怡琴 女，1996年生，硕士研究生，研究方向为电力电子与电气传动，电磁环境及防护技术。E-mail：786790332@qq.com
叶志浩 男，1975年生，教授，博士生导师，研究方向为电力系统分析设计与保护。E-mail：yxyx928@126.com（通信作者）
（编辑 郭丽军）