基于容量增量曲线峰值区间特征参数的锂离子电池健康状态估算
杨胜杰1 罗冰洋1 王 菁1 康健强2 朱国荣1
(1. 武汉理工大学电力电子技术研究所 武汉 430070 2. 武汉理工大学现代汽车零部件技术湖北省重点实验室 武汉 430070)
摘要 当前,学术界广泛采用容量增量(IC)曲线上的特征参数(FPs)估算锂离子电池的健康状态(SOH)。该方法通常利用整个IC峰区域的FPs实现SOH估算,而不同IC峰区域下的FPs对SOH估算有较大差异。为了提高电池SOH估算的准确性,该文采用锂离子电池在IC曲线的峰值区间(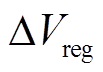 ,通常为峰下的部分荷电状态区间)提取FPs的SOH估算方法,基于高斯过程(GP)回归建立SOH估算模型。通过三个峰值区间下的SOH估算结果,发现SOH对不同
,通常为峰下的部分荷电状态区间)提取FPs的SOH估算方法,基于高斯过程(GP)回归建立SOH估算模型。通过三个峰值区间下的SOH估算结果,发现SOH对不同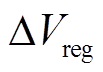 的FPs敏感程度不同。该文进一步利用NASA提供的5号、6号、7号和18号电池数据,对11组峰值区间
的FPs敏感程度不同。该文进一步利用NASA提供的5号、6号、7号和18号电池数据,对11组峰值区间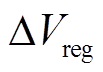 在[23.1%, 100%]内的SOH估算结果进行分析,结果表明,6号、7号和18号电池的峰值区间
在[23.1%, 100%]内的SOH估算结果进行分析,结果表明,6号、7号和18号电池的峰值区间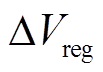 分别选取[53.4%, 88.1%]、[50.4%, 92.3%]和[42.3%, 100%]时,其估算的方均根误差小于2%,这说明SOH对上述峰值区间范围更敏感。利用该文的方法量化SOH对峰值特征参数的敏感区间,在敏感区间内的SOH估算有较高的准确性。
分别选取[53.4%, 88.1%]、[50.4%, 92.3%]和[42.3%, 100%]时,其估算的方均根误差小于2%,这说明SOH对上述峰值区间范围更敏感。利用该文的方法量化SOH对峰值特征参数的敏感区间,在敏感区间内的SOH估算有较高的准确性。
关键词:锂离子电池 峰值区间 电池健康状态 容量增量
0 引言
锂离子电池广泛应用于电子产品、电动汽车和储能系统中。与其他充电电池相比,它们具有能量密度高、使用寿命长、安全性能好等优势。在应用过程中,如果存在过度充电、过度放电、局部过热等情况,锂离子电池将加速老化[1-2]。过度老化的电池不仅可用的容量大幅减少而且也存在安全隐患,因此,需要对电池健康状态(State of Health, SOH)进行评估。
国内外关于SOH估算方法可分为两类:电化学机理分析法和数据驱动法。电化学机理分析法旨在深入研究电化学机理,建立电池衰退的数学模型[3]。数据驱动法将锂离子电池的外部特性映射为电池容量损失来建立电池老化模型。通过从充放电数据中提取出能够表征电池SOH的特征参数(Feature Parameters, FPs),建立FPs与SOH之间的定量关系。数据驱动法主要包括自适应状态估算方法、神经网络法、支持向量机法和贝叶斯方法等[4-8]。Guo Zhen等[9]利用等效电路模型辨识出的参数推导充电过程中恒流部分的传递函数来估算电池SOH。Yang Qingxia和Xu Jun等[10]提出一种基于区间容量的SOH估算方法,利用不同电压区间的容量变化对电池SOH进行估算,结果表明在电压区间为3.95~4.15V时估算的SOH误差范围在-0.03%~ 0.015%。Yang Duo等[11]从充电曲线中提取四个特征参数,结合改进的高斯回归模型进行SOH估算,其估算结果的方均根值均低于0.04。孙冬等[12]提出基于多模型数据融合技术的电池SOH估算方法,SOH估算误差在5%以内,能够有效提高SOH估算精度和可靠性。孙丙香等[13]研究SOC区间的累积容量衰退率和累积内阻衰退率的相关性,得到的相关性模型拟合度在95%以上,并验证了在不同温度下该模型的适用性。上述方法在不考虑电池内部电化学特性情况下,需要大量的电池实验数据和繁琐的数据处理工作,并且提取的特征参数易受数据波动的影响,进而影响SOH的估算精度[14]。
为了提高SOH的估算精度,有研究发现,电池的衰退与电池在充放电过程的端电压变化密切相关[15-19]。利用端电压对容量的导数提出了锂离子电池容量增量(Incremental Capacity, IC)分析法,这种求导分析方法既能辨识电池老化机制,也可用于电池SOH估算[15]。Li Yi等[16]通过电池静态充电曲线提取IC曲线的峰值位置、峰谷位置特征参数,定量它们与SOH的关系,估算的最大误差为2.5%。这种方法既能满足估算精度,又能减少计算复杂度,为应用于电池管理系统(Battery Management System, BMS)提供理论基础。Tang Xiaopeng等[17]选取IC曲线峰值左右两侧的固定电压间隔,获得固定电压间隔下的放电区域容量,从而建立区域容量与SOH的线性函数。利用美国宇航局的5号、6号、7号和34号电池进行验证,结果表明四个电池的SOH估算误差均低于2.5%。Bian Xiaolei等[18]利用峰值函数积分得到容量模型,所提出的容量模型能够准确地拟合IC曲线的峰值参数,Li Xue等[19]为了将容量模型应用于SOH估算,文中提出了learning-unrequired和learning-required两种估算模型,learning-required模型性能更加稳定且估算误差更小。
上述研究中利用IC曲线进行SOH估算时,只利用一组峰FPs进行SOH估算,未讨论不同IC峰区域下的FPs对估算结果的敏感程度。针对以上问题,本文采用一种考虑峰值区间的锂离子电池SOH估算方法,采用三组峰FPs和基于高斯过程(Gaussian Process, GP)回归模型估算SOH。结果发现,三元锂和磷酸铁锂电池分别选择峰值区间为16.7%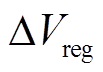 和52.6%
和52.6%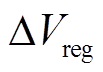 时,能够以较少的电池数据获得较高的估算精度,所采用的峰值区间FPs能够准确地预测电池的健康状态,而且能够适用不同类型电池。此外,关联度最高的四个FPs的估算精度要高于只有峰面积下的SOH估算精度。最后,通过NASA电池5号、6号、7号和18号数据验证SOH对峰值区间的敏感性,量化峰值区间对估算方均根误差的影响。通过这种方法,能够找到电池SOH敏感程度更高的峰值区间范围,从而实现利用有限的电池数据量得到较高精度的SOH。
时,能够以较少的电池数据获得较高的估算精度,所采用的峰值区间FPs能够准确地预测电池的健康状态,而且能够适用不同类型电池。此外,关联度最高的四个FPs的估算精度要高于只有峰面积下的SOH估算精度。最后,通过NASA电池5号、6号、7号和18号数据验证SOH对峰值区间的敏感性,量化峰值区间对估算方均根误差的影响。通过这种方法,能够找到电池SOH敏感程度更高的峰值区间范围,从而实现利用有限的电池数据量得到较高精度的SOH。
1 容量增量分析法
1.1 容量增量原理
容量增量(IC)曲线的原理为将电池在恒流充电或放电工况下的端电压-容量(V-Q)曲线求一阶导数得到端电压-容量变化率(V-dQ/dV)曲线。V-dQ/dV曲线描述了电池在单位电压下充入或放出的电量大小。以电池恒流放电工况为例,当电池的端电压曲线出现电压平台时,在电压平台持续的时间内,电池放出的电量线性增加而电池端电压变化很小,即表现在IC曲线为一个dQ/dV峰,电池电压平台越平坦,dQ/dV峰值越大[20]。求解IC曲线一阶导数,首先需要对V-Q曲线进行函数拟合,这不可避免地引入了拟合误差。因此本文采用一种简单实用绘制IC曲线的方法。以固定电压区间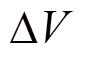 代替dV,
代替dV, 为对应
为对应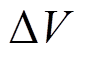 区间下的容量变化,当
区间下的容量变化,当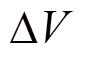 趋近于0时,近似有
趋近于0时,近似有
不同电池选择的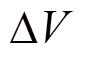 不同,这取决于IC曲线所含测量噪声的严重程度。当IC曲线用来分析电池电化学行为时,电池应在较低电流倍率下(通常在0.05C下)充放电,因为一些峰值较小的IC峰通常在较大电流倍率下无法辨识。而估算SOH时,电流倍率为电池循环的实验倍率[17]。
不同,这取决于IC曲线所含测量噪声的严重程度。当IC曲线用来分析电池电化学行为时,电池应在较低电流倍率下(通常在0.05C下)充放电,因为一些峰值较小的IC峰通常在较大电流倍率下无法辨识。而估算SOH时,电流倍率为电池循环的实验倍率[17]。
常用的电池SOH定义方法有两种:一种是基于电池内阻的方法[21],即
式中,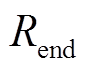 为电池终止寿命时的内阻;
为电池终止寿命时的内阻;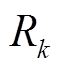 为第k次循环的内阻;
为第k次循环的内阻;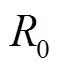 为新电池的内阻。另一种定义为电池当前最大充电/放电容量与额定容量之比[21-22],其表达式为
为新电池的内阻。另一种定义为电池当前最大充电/放电容量与额定容量之比[21-22],其表达式为
式中,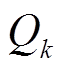 为第k次循环的充电或放电容量;
为第k次循环的充电或放电容量;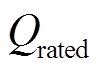 为电池出厂标定的额定容量。本文采用式(3)定义SOH的方法进行后续研究。
为电池出厂标定的额定容量。本文采用式(3)定义SOH的方法进行后续研究。
1.2 锂离子电池IC曲线
锂离子电池内部可以等效为一个高度非线性系统,因电池在使用过程中受环境温度、电流倍率、充放电深度等影响,较难分析其非线性特征变化规律,因此不同使用条件下的IC曲线差异也较大。图1为磷酸铁锂电池在不同温度、不同倍率和不同电压区间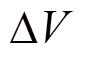 的IC曲线。图1a为不同温度下锂离子电池的IC变化曲线,可以看出,随着温度的升高,IC曲线朝电压增大方向偏移,并且峰高度随温度增加而增高,表明在温度较高的情况下,电池放电容量较低温下变多。图1b为不同倍率下锂离子电池的IC变化曲线,随着电流倍率增加,IC曲线整体向低电压方向移动,且电池峰宽度增加而峰高度减小,3号和4号峰在大于0.5C倍率时被2号峰吸收。图1c为不同
的IC曲线。图1a为不同温度下锂离子电池的IC变化曲线,可以看出,随着温度的升高,IC曲线朝电压增大方向偏移,并且峰高度随温度增加而增高,表明在温度较高的情况下,电池放电容量较低温下变多。图1b为不同倍率下锂离子电池的IC变化曲线,随着电流倍率增加,IC曲线整体向低电压方向移动,且电池峰宽度增加而峰高度减小,3号和4号峰在大于0.5C倍率时被2号峰吸收。图1c为不同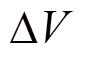 的IC变化,可以看到,各峰高度随
的IC变化,可以看到,各峰高度随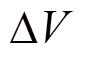 增加而减小,峰位置基本不变。当
增加而减小,峰位置基本不变。当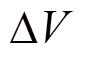 选取过大时,IC曲线峰值较低,无法真实反映电池在对应峰位上的相变结构,当
选取过大时,IC曲线峰值较低,无法真实反映电池在对应峰位上的相变结构,当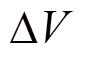 选取过小时,IC曲线的噪声也会随着增大。
选取过小时,IC曲线的噪声也会随着增大。
1.3 电池循环老化实验
本文实验采用的两款电池参数见表1。
表1 电池参数
Tab.1 The parameters of batteries

电池类型额定容量/(A·h)额定电压/V 三元锂电池(1号、2号)243.7 磷酸铁锂电池(3号、4号)3.23.3
本文对这四个电池进行循环寿命实验,三元锂电池采用12A(0.5C)电流进行了1 800次循环老化,磷酸铁锂电池以3.2A(1C)电流进行了350次循环工况。四个电池都放置于25℃的恒温箱内。实验参数见表2。
表2 实验参数
Tab.2 The parameters of experiments

电池类型循环次数/次截止电压/V循环倍率 三元锂电池(1号、2号)1 800上限:4.2下限:2.512A(0.5C) 磷酸铁锂电池(3号、4号)350上限:3.75下限:23.2A(1C)
1号、2号电池经过1 800次循环后容量从初始的24.05A·h、23.769A·h衰减到19.246A·h、19.531A·h,而3号、4号电池经过350次循环容量分别从3.197A·h、3.19A·h衰减至2.666A·h、2.613A·h。
1.4 IC曲线提取
在1.1节中介绍了IC曲线原理及绘制IC曲线的简便方法,本节利用这种简便方法绘制IC曲线。三元锂电池选取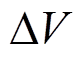 =3mV,磷酸铁锂电池选取
=3mV,磷酸铁锂电池选取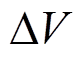 =0.5mV,两种电池的IC曲线随循环次数变化结果如图2所示。
=0.5mV,两种电池的IC曲线随循环次数变化结果如图2所示。
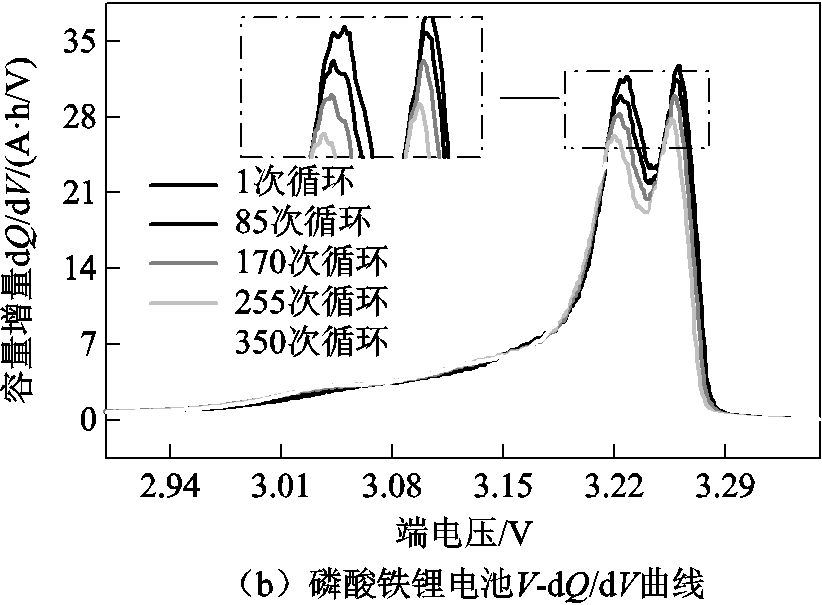
IC曲线的峰个数对应电池放电曲线的电压平台个数,每个电压平台是电池正负极电化学反应叠加的结果。从图2a中可以看到,三元锂电池的IC曲线只出现了一个峰,并且峰值位置随循环次数增加向电压减小方向移动,峰值高度也逐渐减少。图2b也呈现出与图2a相似的变化,但磷酸铁锂电池的IC曲线有两个峰值。从局部放大图看到,右侧峰峰顶比左侧峰顶平滑,且右侧峰高度大于左侧峰高度。
2 IC曲线的峰值区间特征参数
从IC峰中可以提取出多个特征参数,包括峰高度、峰位置、峰面积、峰宽度和峰的左右斜率等。通过这些参数的变化,可以分析电池老化机理,从而对电池的健康状态进行管理。
2.1 峰值区间特征参数
常用的IC曲线提取特征参数方法是利用峰顶与峰谷之间包络的面积来获得。这种定义方式忽略了峰曲线中的变化,理想的IC曲线为平滑的双曲线,而实际的IC曲线并不是理想的双曲线。通过定义峰值区间(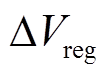 )的方式,可以找到不同
)的方式,可以找到不同 下FPs与SOH的多组关系。峰值区间即以峰顶所在位置为中心,在峰的左右两侧各选取
下FPs与SOH的多组关系。峰值区间即以峰顶所在位置为中心,在峰的左右两侧各选取 /2的端电压范围作为该峰的区域。通过固定峰宽度的方式来提取其他IC特征参数。
/2的端电压范围作为该峰的区域。通过固定峰宽度的方式来提取其他IC特征参数。 定义的峰左右两侧的端电压为
定义的峰左右两侧的端电压为
式中, 为峰值电压;
为峰值电压;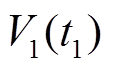 为
为 在
在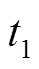 时刻左侧端电压;
时刻左侧端电压; 为
为 在
在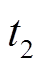 时刻右侧端电压。
时刻右侧端电压。
以 定义的峰面积、放电时间、峰左右斜率分别为
定义的峰面积、放电时间、峰左右斜率分别为
式中, 为峰面积;
为峰面积;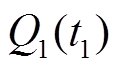 和
和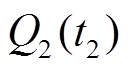 分别为峰左、右侧端电压的放电容量;
分别为峰左、右侧端电压的放电容量;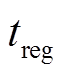 为峰值区间的放电时间;
为峰值区间的放电时间; 和
和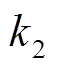 分别峰的左斜率和右斜率;
分别峰的左斜率和右斜率;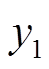 和
和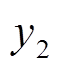 分别为峰左、右侧端电压对应的dQ/dV值;
分别为峰左、右侧端电压对应的dQ/dV值;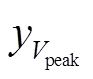 为峰高度。
为峰高度。
以三元锂电池的IC曲线为例,不同 下的IC曲线特征参数如图3所示。
下的IC曲线特征参数如图3所示。
图3中三元锂电池的IC峰值区间 为500mV。点画线和虚线分别表示两组FPs(
为500mV。点画线和虚线分别表示两组FPs(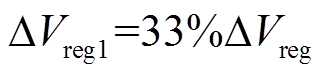 和
和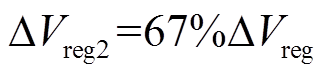 ),各组FPs的数学关系取决于
),各组FPs的数学关系取决于 的大小。
的大小。
IC曲线FPs包括①峰高度、①峰面积、①峰位置及①峰左右斜率,除此之外,还有①峰放电时间共六个参数。而磷酸铁锂电池的IC峰有两个,相应的FPs有12个。若将所提取的FPs全部用于SOH估算模型的输入,估算结果并不会达到最好效果。因此需要分析FPs与SOH的关联程度,关联程度越高,则认为这个特征参数对SOH的影响越大。
2.2 特征参数关联性分析
两个序列间随时间或不同变量而变化的关联性大小称为关联度。灰色关联度分析能够实现动态系统特征量的变化趋势,因此可用于IC曲线特征参数与SOH的关联分析。灰色关联度分析的步骤如下:
1)确定参考序列Y={y(k)|k=1,2, ,n},其中n是序列长度,y(k)=SOH(k);比较序列Xi={xi(k)},其中i代表序列数量。在本文中,xi为峰值区间下的特征参数。
,n},其中n是序列长度,y(k)=SOH(k);比较序列Xi={xi(k)},其中i代表序列数量。在本文中,xi为峰值区间下的特征参数。
2)将比较序列Xi归一化。
3)计算关联系数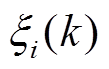 。
。
式中,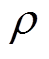 为关联系数,
为关联系数, ,通常取值为0.5。
,通常取值为0.5。
4)计算关联度ri。
本文首先对三元锂电池的FPs关联度进行分析,依次选取8.3% 、16.7%
、16.7% 、33.3%
、33.3% 三个峰值区间,结果见表3。
三个峰值区间,结果见表3。
表3 2号电池FPs与SOH的关联度
Tab.3 The relational degree between FPs and SOH of No.2 battery

FPs8.3%16.7%33.3% ①峰高度0.6940.6940.729 ①峰位置0.5620.5810.598 ①峰放电时间0.6390.6590.722 ①峰面积0.6390.6580.722 ①峰左斜率0.6870.7350.882 ①峰右斜率0.6730.6150.561
从表3中可以看到,当峰值区间为8.3% 时,关联度前四个排序为:①峰高度>①峰左斜率>①峰右斜率>①峰面积(①峰放电时间);当峰值区间为16.7%
时,关联度前四个排序为:①峰高度>①峰左斜率>①峰右斜率>①峰面积(①峰放电时间);当峰值区间为16.7% 或33.3%
或33.3% 时,关联度排序为:①峰左斜率>①峰高度>①峰面积(①峰放电时间)>①峰位置。可见,选取的
时,关联度排序为:①峰左斜率>①峰高度>①峰面积(①峰放电时间)>①峰位置。可见,选取的 不同,FPs的关联度排序发生变化,即各个FPs对SOH的影响程度随
不同,FPs的关联度排序发生变化,即各个FPs对SOH的影响程度随 变化。此外,①峰面积为峰区域容量,当
变化。此外,①峰面积为峰区域容量,当 增大时,峰面积(峰区域容量)也增大,而SOH是根据式(3)定义的,当
增大时,峰面积(峰区域容量)也增大,而SOH是根据式(3)定义的,当 趋近于电池端电压的最大值,即峰区域容量为电池放电容量时,电池SOH接近于实际值。
趋近于电池端电压的最大值,即峰区域容量为电池放电容量时,电池SOH接近于实际值。
在图2b中,将IC曲线的左侧峰和右侧峰分别定义为Ⅰ号峰和Ⅱ号峰。磷酸铁锂电池的Ⅱ号IC峰值区间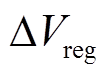 为38mV。利用灰色关联分析方法对磷酸铁锂电池的IC曲线FPs进行分析,依次选取36.8%
为38mV。利用灰色关联分析方法对磷酸铁锂电池的IC曲线FPs进行分析,依次选取36.8% 、52.6%
、52.6% 、63.2%
、63.2% 三个峰值区间。表4给出了磷酸铁锂电池特征参数与SOH的关联度。
三个峰值区间。表4给出了磷酸铁锂电池特征参数与SOH的关联度。
表4 4号电池FPs与SOH的关联度
Tab.4 The relational degree between FPs and SOH of No.4 battery

FPs36.8%52.6%63.2% Ⅰ峰高度0.6830.6830.683 Ⅰ峰位置0.6240.6240.624 Ⅰ峰放电时间0.7230.7060.642 Ⅰ峰面积0.7220.7050.641
(续)

FPs36.8%52.6%63.2% Ⅰ峰左斜率0.6280.7480.583 Ⅰ峰右斜率0.4650.3550.368 Ⅱ峰高度0.8310.8310.831 Ⅱ峰位置0.6710.6710.671 Ⅱ峰放电时间0.8210.8210.821 Ⅱ峰面积0.8210.8210.821 Ⅱ峰左斜率0.1390.1390.139 Ⅱ峰右斜率0.6850.6850.685
从表4中可以看到,由于Ⅰ号峰峰顶不平滑,提取出的FPs与SOH的关联度相较于Ⅱ号峰峰低。关联度前四个排序为:Ⅱ号峰高度>Ⅱ号峰面积(Ⅱ号峰放电时间)>Ⅱ号峰右斜率,Ⅱ号峰每个 的FPs关联度都相同,这说明每组FPs随电池老化的偏移量完全相同。因此将IC曲线中的Ⅱ号峰关联度最高的四个FPs作为后续锂离子电池SOH估算模型的输入变量。
的FPs关联度都相同,这说明每组FPs随电池老化的偏移量完全相同。因此将IC曲线中的Ⅱ号峰关联度最高的四个FPs作为后续锂离子电池SOH估算模型的输入变量。
2.3 高斯过程回归模型
本文采用高斯过程回归模型,通过建立训练数据中特征参数与SOH的关系,对测试数据的SOH值进行估算,并给出置信区间。
高斯过程可看作是有限个随机变量服从高斯分布的集合。对于输入集合的每个数据点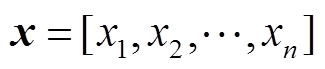 ,其函数f(x)的概率分布服从高斯分布:
,其函数f(x)的概率分布服从高斯分布: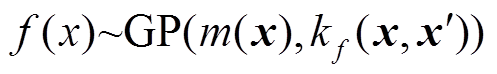 ,所以f(x)的性质由它的均值
,所以f(x)的性质由它的均值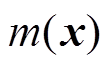 和协方差函数
和协方差函数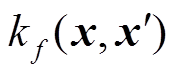 决定[23-24],其方程分别为
决定[23-24],其方程分别为
协方差函数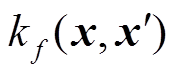 的选取取决于实际应用,文中选取Mattern核函数,其一般形式为
的选取取决于实际应用,文中选取Mattern核函数,其一般形式为
回归问题可以表述为函数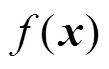 的输出值受到噪声的影响,观测序列y是
的输出值受到噪声的影响,观测序列y是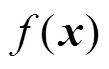 的输出序列和噪声大小的和,其表达式为
的输出序列和噪声大小的和,其表达式为
式中,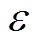 为噪声且服从高斯分布,即
为噪声且服从高斯分布,即
观测值的先验分布满足
式中,y为观测序列;x为输入集合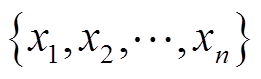 ;
;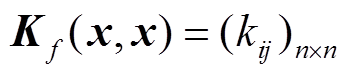 ,
, ;I为n维单位矩阵;
;I为n维单位矩阵;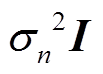 为噪声协方差矩阵。
为噪声协方差矩阵。
在式(12)中,核函数由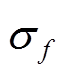 和λ两个参数决定,噪声方差
和λ两个参数决定,噪声方差 也是未知的。将未知参数
也是未知的。将未知参数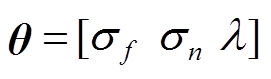 称为超参数。超参数可以用极大似然法确定[23],这里不再赘述。核函数形式和超参数确定后,高斯过程回归的模型便确定了。通过计算后验分布
称为超参数。超参数可以用极大似然法确定[23],这里不再赘述。核函数形式和超参数确定后,高斯过程回归的模型便确定了。通过计算后验分布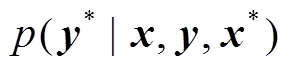 ,高斯过程回归模型可以预测测试样本。对于一个新的数据集
,高斯过程回归模型可以预测测试样本。对于一个新的数据集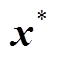 ,估算值
,估算值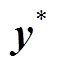 也服从高斯分布。则观测值y和估算值
也服从高斯分布。则观测值y和估算值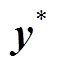 的联合高斯分布为
的联合高斯分布为
根据先验分布可推导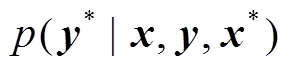 也服从高斯分布,即
也服从高斯分布,即
其中
式中,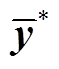 为
为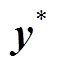 的均值;
的均值;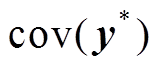 为测试数据的方差矩阵,反映了估算值的可靠性。
为测试数据的方差矩阵,反映了估算值的可靠性。
当建立了基于训练数据( ,
, )的回归模型后,在新数据集
)的回归模型后,在新数据集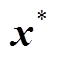 下,预测均值
下,预测均值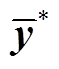 和预测方差
和预测方差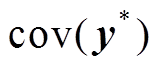 已经给出,则预测值的95%的置信区间为
已经给出,则预测值的95%的置信区间为
3 SOH估算与误差分析
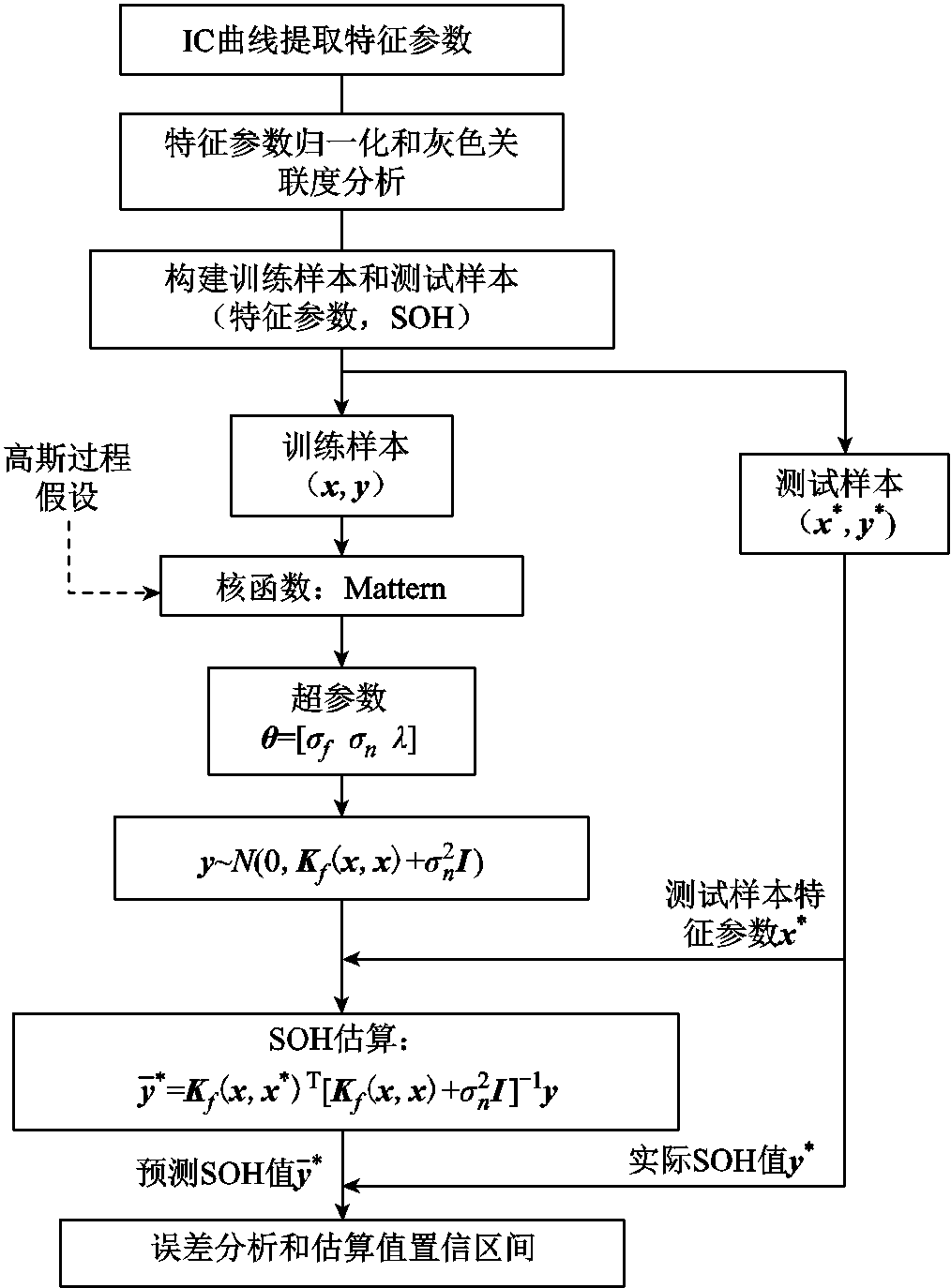
高斯过程回归模型的SOH估算流程如图4所示。
3.1 三元锂电池SOH估算
本文选择2号、4号电池的FPs和SOH分别作为三元锂电池和磷酸铁锂电池的训练数据,而1号、3号电池的FPs和SOH作为相应的测试数据。2号电池选择8.3% 、16.7%
、16.7% 、33.3%
、33.3% 三个峰值区间的FPs,4号电池取36.8%
三个峰值区间的FPs,4号电池取36.8% 、52.6%
、52.6% 、63.2%
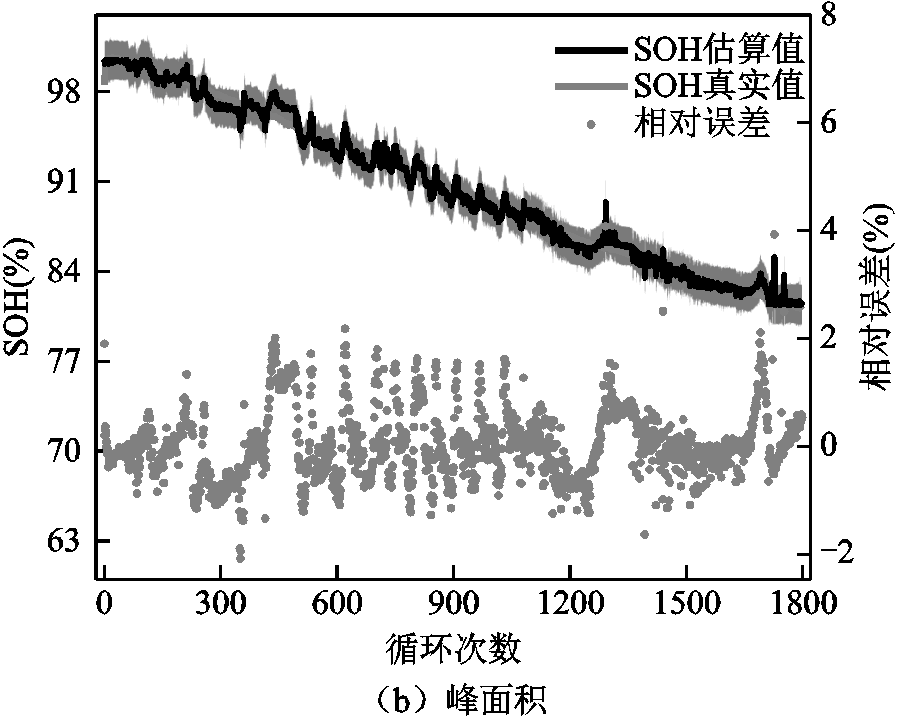
、63.2% ,为了比较不同FPs的SOH估算能力,分别选择关联度最高的四个FPs和峰面积作为训练数据的输入。图5为1号电池SOH估算结果和误差,图5a为考虑四个FPs的估算结果,图5b为峰面积下的估算结果。由于三个峰值区间下的估算结果图差异不大,这里给出16.7%
,为了比较不同FPs的SOH估算能力,分别选择关联度最高的四个FPs和峰面积作为训练数据的输入。图5为1号电池SOH估算结果和误差,图5a为考虑四个FPs的估算结果,图5b为峰面积下的估算结果。由于三个峰值区间下的估算结果图差异不大,这里给出16.7% 的情形。
的情形。
图5中的深灰色区域是估算结果的95%置信区间,置信区间宽度越窄,表明估算结果的可靠性更高。从图5a估算结果曲线来看,估算值能较好地跟随真实值,并且95%的置信区间的宽度较窄,表明该情况下的估算结果具有较高的可靠性。从误差曲线分析,估算的整体相对误差落在±3%内。从图5b中看出,估算结果曲线与图5a大体相似。为了区分四个FPs和峰面积下的估算结果差异,表5和表6分别给出了1号电池三个峰值区间在四个FPs和峰面积下的误差统计结果。
表5 考虑四个FPs下1号电池SOH误差统计结果
Tab.5 The SOH error statistical results of No.1 battery under four FPs

峰值区间相对误差最大值(%)绝对值最大误差方均根误差(%)平均绝对误差 8.3%4.850.039 70.630.004 8 16.7%3.820.032 80.54 0.004 1 33.3%2.240.019 20.470.003 6
表6 考虑峰面积下1号电池SOH误差统计结果
Tab.6 The SOH error statistical results of No.1 battery under the peak area

峰值区间相对误差最大值(%)绝对值最大误差方均根误差(%)平均绝对误差 8.3%5.390.04410.710.005 4 16.7%4.110.03960.630.004 8 33.3%2.650.02160.480.003 7
表5中定义了四个误差参数,分别为相对误差最大值、表6中绝对值最大误差、方均根误差(Root Mean Squared Error,RMSE)和平均绝对误差。方均根误差反映估算值和真实值之间的离散程度,方均根误差越小,表明估算曲线越接近于真实曲线。平均绝对误差代表实际电池的SOH与估算SOH绝对差值的平均值。当峰值区间为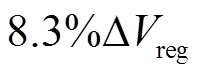 时,误差值最大,而峰值区间为
时,误差值最大,而峰值区间为 时,整体误差最小。
时,整体误差最小。
对比表5中的各项误差数据,在相同峰值区间下,考虑峰面积下的估算误差都高于考虑四个FPs的误差,这说明考虑四个FPs的估算效果要优于峰面积下的估算。尽管峰值区间增加,相应的误差都在减小,但所需的电池数据更多,实际应用时电池通常不是长时间处于工作状态,所以获取的数据量也是有限的。选取的峰值区间较小时,估算误差较大,不能满足实际要求。因此,选择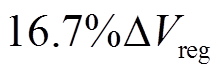 下的四个关联度最高的FPs来估算SOH能得到最优的结果。
下的四个关联度最高的FPs来估算SOH能得到最优的结果。
3.2 磷酸铁锂电池SOH估算
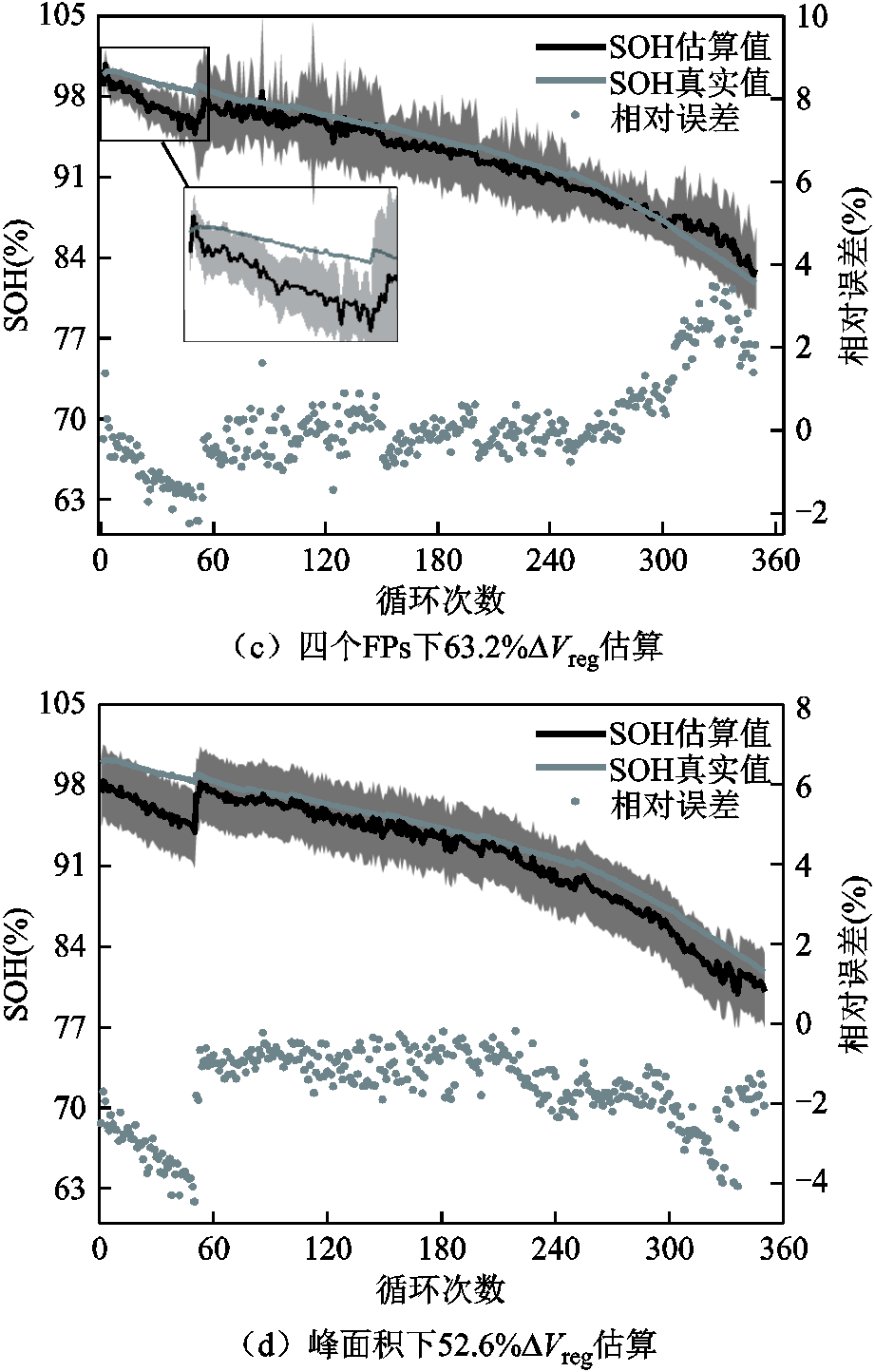
图6为3号电池SOH估算结果和误差。图6a、图6b和图6c分别为四个FPs下三个峰值区间的估算结果和误差,图6d为峰面积下峰值区间为52.6%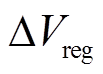 的估算结果和误差。
的估算结果和误差。
从图6b中可以看出,测试样本的真实SOH与估算值具有较好的一致性,其相对误差较小。而图6a的估算结果波动较大,其对应的相对误差也存在一定的波动。同时,图6c的估算结果与实际相差较为明显,在大约前50次循环时,估算偏差最大。SOH真实值落在95%置信区间之外,并且95%置信区间宽度较宽,这表明估算的不确定性较大。从图6d中看到,估算的SOH整体低于真实值,在前50次循环时,估算的相对误差较大。表7和表8分别给出了各种情形下的具体误差。
表7 考虑四个FPs下3号电池SOH误差统计结果
Tab.7 The SOH error statistical results of No.3 battery under four FPs

峰值区间相对误差最大值(%)绝对值最大误差方均根误差(%)平均绝对误差 36.8%3.60.030 90.440.001 6 52.6%1.560.019 20.240.000 8 63.2%3.620.035 60.560.002 1
表8 考虑峰面积下3号电池SOH误差统计结果
Tab.8 The SOH error statistical results of No.3 battery under the peak area

峰值区间相对误差最大值(%)绝对值最大误差方均根误差(%)平均绝对误差 36.8%3.140.0310.480.001 6 52.6%4.460.043 80.790.003 63.2%4.30.042 80.770.002 7
从表7的量化指标中可以看出,当峰值区间为 时,相对误差最大值不超过2%,且方均根误差为0.24%,误差值低于另外两种情况,同时平均绝对误差为0.000 8,表明估算的SOH接近于真实值。此外,不同峰值区间下的估算误差也有较大差别,这说明不同峰值区间提取的IC曲线FPs有较大差别,进而影响SOH估算精度。
时,相对误差最大值不超过2%,且方均根误差为0.24%,误差值低于另外两种情况,同时平均绝对误差为0.000 8,表明估算的SOH接近于真实值。此外,不同峰值区间下的估算误差也有较大差别,这说明不同峰值区间提取的IC曲线FPs有较大差别,进而影响SOH估算精度。
对比表7的统计误差,除了峰值区间为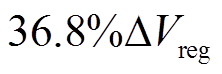 情况下,表8中以峰面积估算的SOH误差值小幅增加,其他情形下的误差结果都明显增加,其中
情况下,表8中以峰面积估算的SOH误差值小幅增加,其他情形下的误差结果都明显增加,其中 误差增加幅度最大,其平均绝对误差从0.000 8增大至0.003。整体来看,考虑峰面积下的3号电池SOH误差比采用四个FPs下的误差要大。不同峰值区间下的估算结果变化规律不明显,但考虑四个FPs,峰值区间为
误差增加幅度最大,其平均绝对误差从0.000 8增大至0.003。整体来看,考虑峰面积下的3号电池SOH误差比采用四个FPs下的误差要大。不同峰值区间下的估算结果变化规律不明显,但考虑四个FPs,峰值区间为 时的误差最小,在估算SOH时,能够获得较高的精度。
时的误差最小,在估算SOH时,能够获得较高的精度。
3.3 NASA数据集验证
3.1节和3.2节讨论了三个峰值区间下不同FPs作为模型输入的SOH估算结果,结果发现,SOH估算精度与峰值区间和IC峰FPs紧密相关。为了进一步验证这一结论,本节利用美国国家宇航局(NASA)公开的5号、6号、7号和18号电池数据进行IC处理。提取11个峰值区间的IC特征参数并进行高斯过程回归模型的SOH估算,这11个峰值区间依次为23.1%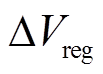 、30.8%
、30.8%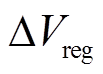 、38.5%
、38.5%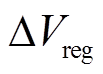 、46.2%
、46.2%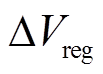 、53.9%
、53.9%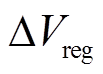 、61.5%
、61.5%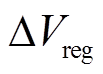 、69.2%
、69.2%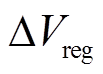 、76.9%
、76.9%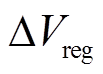 、84.6%
、84.6%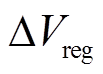 、92.3%
、92.3%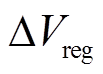 、100%
、100%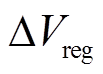 ,其中
,其中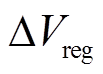 为130mV。以5号电池的FPs作为高斯过程回归模型的训练数据,6号、7号和18号作为测试数据。对提取到的11组峰FPs进行SOH估算。考虑四个最高关联度的FPs下,峰值区间为61.5%
为130mV。以5号电池的FPs作为高斯过程回归模型的训练数据,6号、7号和18号作为测试数据。对提取到的11组峰FPs进行SOH估算。考虑四个最高关联度的FPs下,峰值区间为61.5%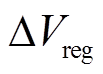 的6号、7号和18号电池的SOH估算结果如图7所示。
的6号、7号和18号电池的SOH估算结果如图7所示。
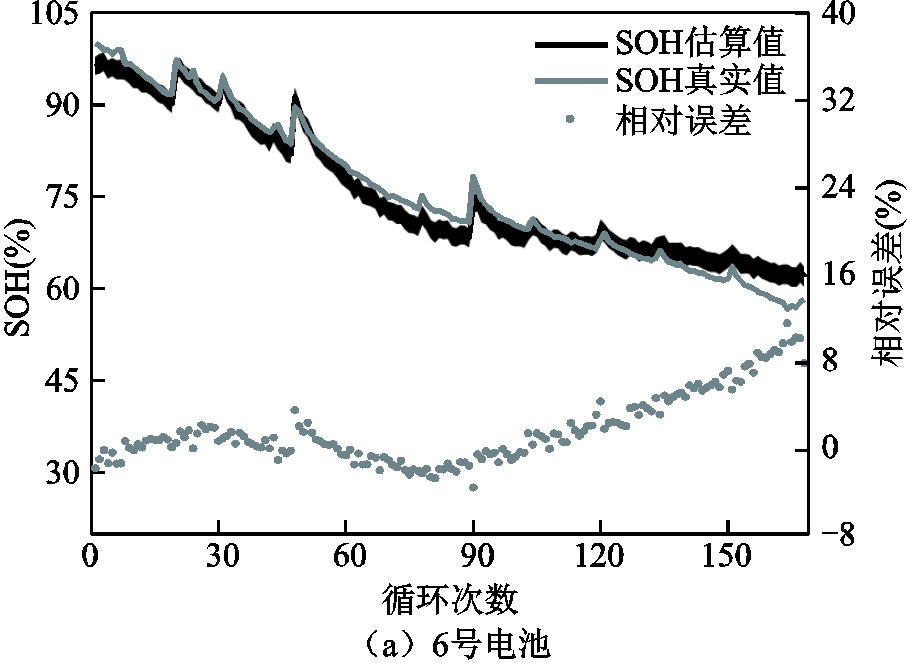
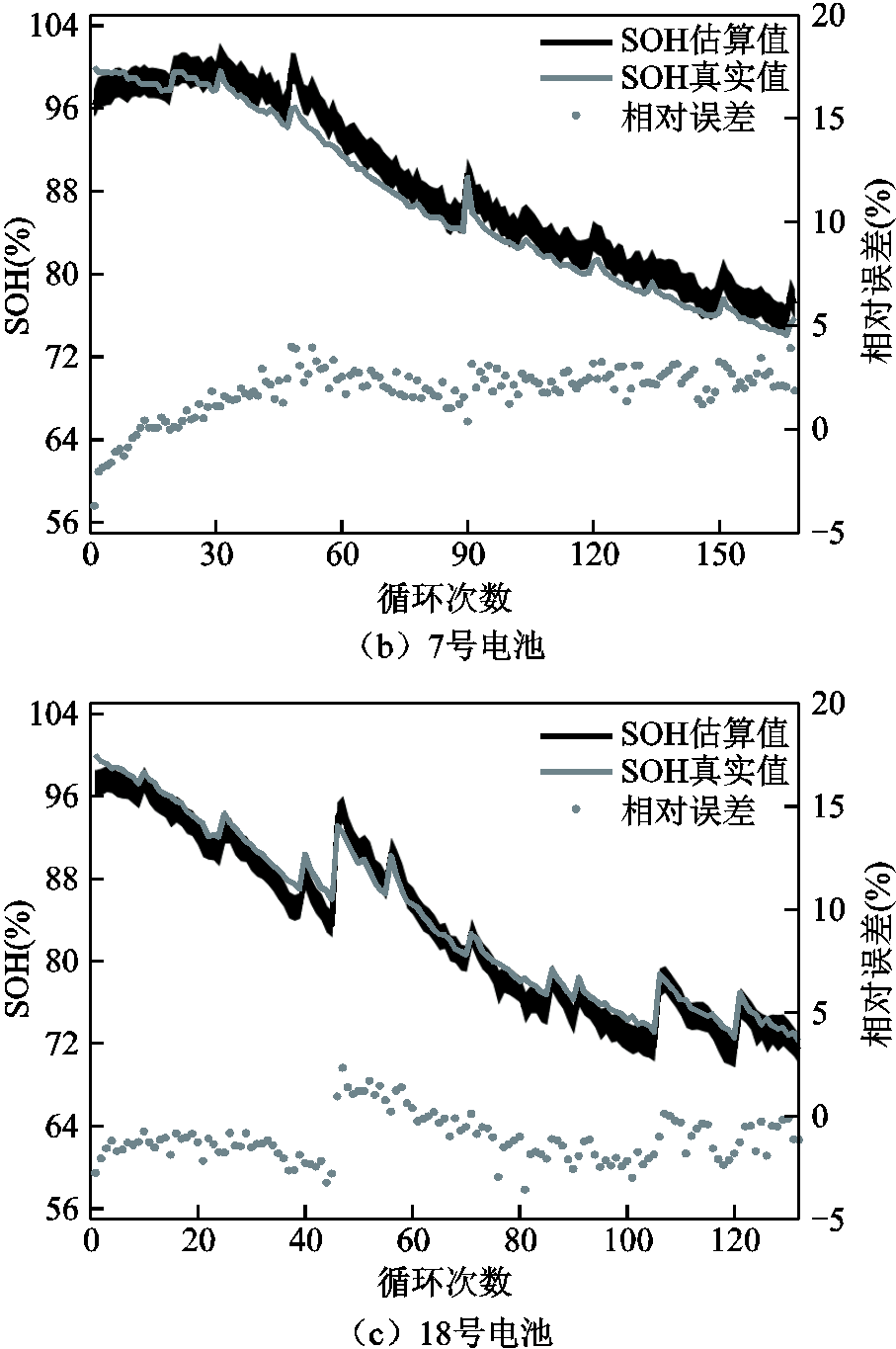
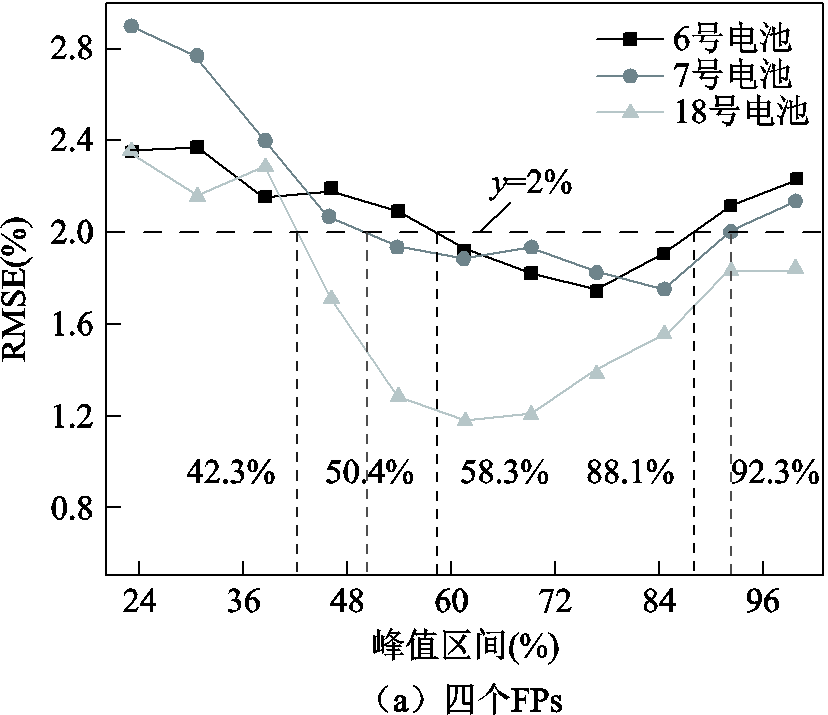
从图7a中可以看出,6号电池在循环次数小于120次之前,相对误差稳定在±3%以内,这说明模型估算的SOH较为准确;当循环次数大于120次之后,即SOH降低至70%之后,其相对误差值逐渐增大到11%,这表明,SOH模型对低SOH值下的估算精度较差。图7b中,7号电池的估算值整体高于真实值,相对误差在3%以内波动。图7c为18号电池的估算结果,其估算结果跟真实值较为吻合。为了对11组估算结果进行分析,图8给出了6号、7号和18号电池的RMSE误差曲线。
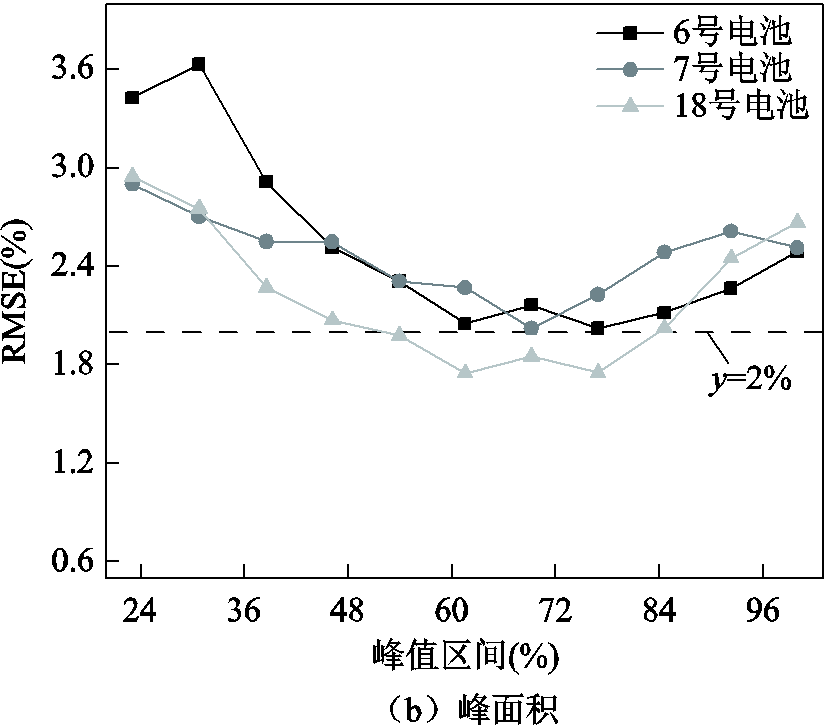
图8a为考虑四个FPs下的RMSE曲线,图中虚线为设定的y=2%误差线,通过设定RMSE误差线来确定电池SOH对峰值区间的敏感范围。从图8a看出,6号、7号和18号电池的峰值区间分别选取[53.4%,88.1%]、[50.4%,92.3%]和[42.3%,100%]时,其对应的RMSE低于2%。图8b为峰面积下的各峰值区间的SOH估算RMSE曲线,对比图8a,各个峰值区间下的RMSE均大于四个FPs下的RMSE,6号和7号电池的RMSE均在y=2%误差线之上。从以上分析,利用NASA电池数据验证了电池SOH对峰值区间的敏感性,并通过11组估算结果量化了电池SOH对峰值区间的敏感范围。
4 结论
本文针对三元锂电池和磷酸铁锂两种电池的SOH估算展开研究。
1)给出了峰值区间下IC曲线FPs的定义方法,提取三个不同峰值区间下的FPs。
2)将与SOH关联度最高的四个FPs和峰面积分别作为训练集,共六组训练数据,利用六组训练数据分别进行高斯过程回归模型的SOH估算。
3)关联度最高的四个FPs情况下,三元锂电池选择峰值区间为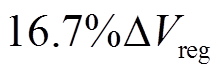 和磷酸铁锂电池选择峰值区间为
和磷酸铁锂电池选择峰值区间为 时,能够获得最优的估算效果,其方均根误差分别为0.54%和0.24%,所选取的峰值区间能满足电池SOH估算高精度的要求。
时,能够获得最优的估算效果,其方均根误差分别为0.54%和0.24%,所选取的峰值区间能满足电池SOH估算高精度的要求。
此外,利用NASA提供的5号、6号、7号和18号电池数据验证峰值区间对SOH估算的影响,找到了电池SOH对IC峰区域的敏感区间。
参考文献
[1]姚芳, 田家益, 黄凯. 锂电池组健康状态计算方法综述[J]. 电源技术, 2018, 42(1): 135-138.Yao Fang, Tian Jiayi, Huang Kai. Review of state of health calculation method for lithium battery[J]. Chinese Journal of Power Sources, 2018, 42(1): 135-138.
[2]李建林, 李雅欣, 吕超, 等. 退役动力电池梯次利用关键技术及现状分析[J]. 电力系统自动化, 2020, 44(13): 172-183. Li Jianlin, Li Yaxin, Lü Chao, et al. Key technology and research status of cascaded utilization in decommissioned power battery[J]. Automation of Electric Power Systems, 2020, 44(13): 172-183.
[3]Jin X, Vora A, Hoshing V, et al. Physically-based reduced-order capacity loss model for graphite anodes in lithium-ion battery cells[J]. Journal of Power Sources, 2017, 342: 750-761.
[4]李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J].电工技术学报, 2020, 35(19): 4106-4119. Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106-4119.
[5]颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J].电工技术学报, 2019, 34(18): 3937-3948. Yan Xiangwu, Deng Haoran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3937-3948.
[6]Wu Ji, Wang Yujie, Zhang Xu, et al. A novel state of health estimation method of lithium-ion battery using group method of data handling[J]. Journal of Power Sources, 2016, 327: 457-464.
[7]Dong Hancheng, Jin Xiaoning, Lou Yangbing, et al. Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector regression-particle filter[J]. Journal of Power Sources, 2014, 271: 114-123.
[8]张江帆. 基于高斯过程回归模型的锂电池数据处理[D]. 北京: 北京交通大学, 2017.
[9]Guo Zhen, Qiu Xinping, Hou Guangdong, et al. State of health estimation for lithium ion batteries based on charging curves[J]. Journal of Power Sources, 2014, 249: 457-462.
[10]Yang Qingxia, Xu Jun, Cao Binggang, et al. State-of-health estimation of lithium-ion battery based on interval capacity[J]. Energy Procedia, 2017, 105: 2342-2347.
[11]Yang Duo, Zhang Xu, Pan Rui, et al. A novel gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve[J]. Journal of Power Sources, 2018, 384: 387-395.
[12]孙冬, 许爽. 梯次利用锂电池健康状态预测[J]. 电工技术学报, 2018, 33(9): 2121-2129. Sun Dong, Xu Shuang. State of health prediction of second-use lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2121-2129.
[13]孙丙香, 刘佳, 韩智强, 等. 不同区间衰退路径下锂离子电池的性能相关性及温度适用性分析[J]. 电工技术学报, 2020, 35(9): 2063-2073. Sun Bingxiang, Liu Jia, Han Zhiqiang, et al. Performance correlation and temperature applicability of Li-ion batteries under different range degradation paths[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2063-2073.
[14]李晓宇, 徐佳宁, 胡泽徽, 等. 磷酸铁锂电池梯次利用健康特征参数提取方法[J]. 电工技术学报, 2018, 33(1): 9-16. Li Xiaoyu, Xu Jianing, Hu Zehui, et al. The health parameter estimation method for LiFePO4 battery echelon use[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 9-16.
[15]Berecibar M, Garmendia M, Gandiaga I, et al. State of health estimation algorithm of LiFePO4 battery packs based on differential voltage curves for battery management system application[J]. Energy, 2016, 103: 784-796.
[16]Li Yi, Abdel-Monem M, Gopalakrishnan R, et al. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter[J]. Journal of Power Sources, 2018, 373: 40-53.
[17]Tang Xiaopeng, Zou Changfu, Yao Ke, et al. A fast estimation algorithm for lithium-ion battery state of health[J]. Journal of Power Sources, 2018, 396: 453-458.
[18]Bian Xiaolei, Liu Longcheng, Yan Jinying. A model for state-of-health estimation of lithium ion batteries based on charging profiles[J]. Energy, 2019, 177: 57-65.
[19]Li Xue, Jiang Jiuchun, Wang Leyi, et al. A capacity model based on charging process for state of health estimation of lithium ion batteries[J]. Applied Energy, 2016, 177: 537-543.
[20]张昊. 基于IC曲线特征参数的锂离子电池SOH估计及DSP实现[D]. 北京: 北京交通大学, 2018.
[21]郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J]. 电工技术学报, 2019, 34(19): 3968-3978. Guo Yongfang, Huang Kai, Li Zhigang. Fast state of health prediction of lithium-ion battery based on terminal voltage drop during rest for short time[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3968-3978.
[22]杨刘倩, 詹昌辉, 卢雪梅. 电动汽车锂电池健康状态估算方法研究[J]. 电源技术, 2016, 40(4): 823-825, 853. Yang Liuqian, Zhan Changhui, Lu Xuemei. Research on estimation method of healthy status for EV lithium battery[J]. Chinese Journal of Power Sources, 2016, 40(4): 823-825, 853.
[23]Richardson R R, Osborne M A, Howey D A. Battery health prediction under generalized conditions using a gaussian process transition model[J]. Journal of Energy Storage, 2019, 23: 320-328.
[24]Richardson R R, Birkl C R, Osborne M A, et al. Gaussian process regression for in-situ capacity estimation of lithium-ion batteries[J]. IEEE Transactions on Industrial Informatics, 2018, 15(1): 127-138.
State of Health Estimation for Lithium-Ion Batteries Based on Peak Region Feature Parameters of Incremental Capacity Curve
Yang Shengjie1 Luo Bingyang1 Wang Jing1 Kang Jianqiang2 Zhu Guorong1
(1. Power Electronics Technology Research Institute Wuhan University of Technology Wuhan 430070 China 2. Hubei Key Laboratory of Advanced Technology for Automotive Components Wuhan University of Technology Wuhan 430070 China)
Abstract At present, researchers have widely used feature parameters (FPs) of incremental capacity (IC) curve to estimate the state of health (SOH) of lithium ion batteries. The FPs are commonly extracted from a whole peak in the IC curve. The method fails to consider the effect of the FPs extracted from different ranges of the peak on the accuracy of estimated SOH. In order to provide an accurate SOH estimation, we select the FPs from the peak region(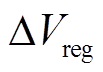 , a state of charge range of a peak). Then SOH estimation is achieved by setting up the relationship between the SOH and the FPs based on Gaussian process (GP) regression. Results show that the accuracy of SOH estimation is sensitive to the different FPs, according to the estimated SOH under the three
, a state of charge range of a peak). Then SOH estimation is achieved by setting up the relationship between the SOH and the FPs based on Gaussian process (GP) regression. Results show that the accuracy of SOH estimation is sensitive to the different FPs, according to the estimated SOH under the three 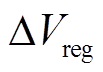 . Furthermore, the comparison of the eleven
. Furthermore, the comparison of the eleven 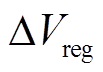 ofFPs that the data come from the NASA No.5, 6, 7 and 18 batteries between 23.1% and 100% is studied. It is found that the estimated SOH root mean square error is less than 2% when the
ofFPs that the data come from the NASA No.5, 6, 7 and 18 batteries between 23.1% and 100% is studied. It is found that the estimated SOH root mean square error is less than 2% when the 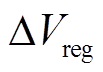 of No.6,7 and 18 batteries are in the regions of [53.4%, 88.1%], [50.4%, 92.3%] and [42.3%, 100%], respectively. It is indicated that that SOH estimation is more sensitive to the above peak region. This method gives an approach to achieve the high precision of SOH estimation because we prove that the SOH estimation is sensitive to
of No.6,7 and 18 batteries are in the regions of [53.4%, 88.1%], [50.4%, 92.3%] and [42.3%, 100%], respectively. It is indicated that that SOH estimation is more sensitive to the above peak region. This method gives an approach to achieve the high precision of SOH estimation because we prove that the SOH estimation is sensitive to 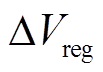 .
.
keywords:Lithium-ion battery, peak region, state of health, incremental capacity analysis
中图分类号:TM912
DOI:10.19595/j.cnki.1000-6753.tces.L90355
国家自然科学基金资助项目(51777146, 51977163)。
收稿日期 2020-07-10
改稿日期 2021-02-07
作者简介
杨胜杰 男,1996年生,硕士研究生,研究方向为电动汽车动力电池管理系统。E-mail:yangsj_77@whut.edu.cn
康健强 男,1976年生,副教授,硕士生导师,研究方向为动力及储能电池应用技术。E-mail:kjqiang@whut.edu.cn(通信作者)
(编辑 赫蕾)
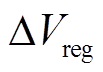 ,通常为峰下的部分荷电状态区间)提取FPs的SOH估算方法,基于高斯过程(GP)回归建立SOH估算模型。通过三个峰值区间下的SOH估算结果,发现SOH对不同
,通常为峰下的部分荷电状态区间)提取FPs的SOH估算方法,基于高斯过程(GP)回归建立SOH估算模型。通过三个峰值区间下的SOH估算结果,发现SOH对不同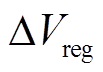 的FPs敏感程度不同。该文进一步利用NASA提供的5号、6号、7号和18号电池数据,对11组峰值区间
的FPs敏感程度不同。该文进一步利用NASA提供的5号、6号、7号和18号电池数据,对11组峰值区间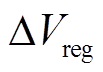 在[23.1%, 100%]内的SOH估算结果进行分析,结果表明,6号、7号和18号电池的峰值区间
在[23.1%, 100%]内的SOH估算结果进行分析,结果表明,6号、7号和18号电池的峰值区间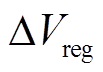 分别选取[53.4%, 88.1%]、[50.4%, 92.3%]和[42.3%, 100%]时,其估算的方均根误差小于2%,这说明SOH对上述峰值区间范围更敏感。利用该文的方法量化SOH对峰值特征参数的敏感区间,在敏感区间内的SOH估算有较高的准确性。
分别选取[53.4%, 88.1%]、[50.4%, 92.3%]和[42.3%, 100%]时,其估算的方均根误差小于2%,这说明SOH对上述峰值区间范围更敏感。利用该文的方法量化SOH对峰值特征参数的敏感区间,在敏感区间内的SOH估算有较高的准确性。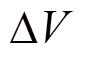 代替dV,
代替dV,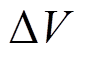 区间下的容量变化,当
区间下的容量变化,当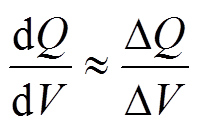 (1)
(1)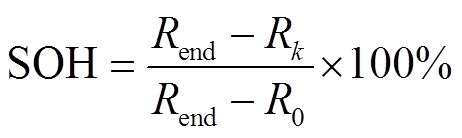 (2)
(2)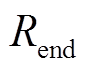 为电池终止寿命时的内阻;
为电池终止寿命时的内阻;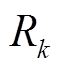 为第k次循环的内阻;
为第k次循环的内阻;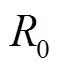 为新电池的内阻。另一种定义为电池当前最大充电/放电容量与额定容量之比
为新电池的内阻。另一种定义为电池当前最大充电/放电容量与额定容量之比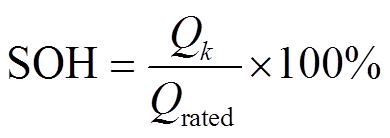 (3)
(3)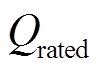 为电池出厂标定的额定容量。本文采用式(3)定义SOH的方法进行后续研究。
为电池出厂标定的额定容量。本文采用式(3)定义SOH的方法进行后续研究。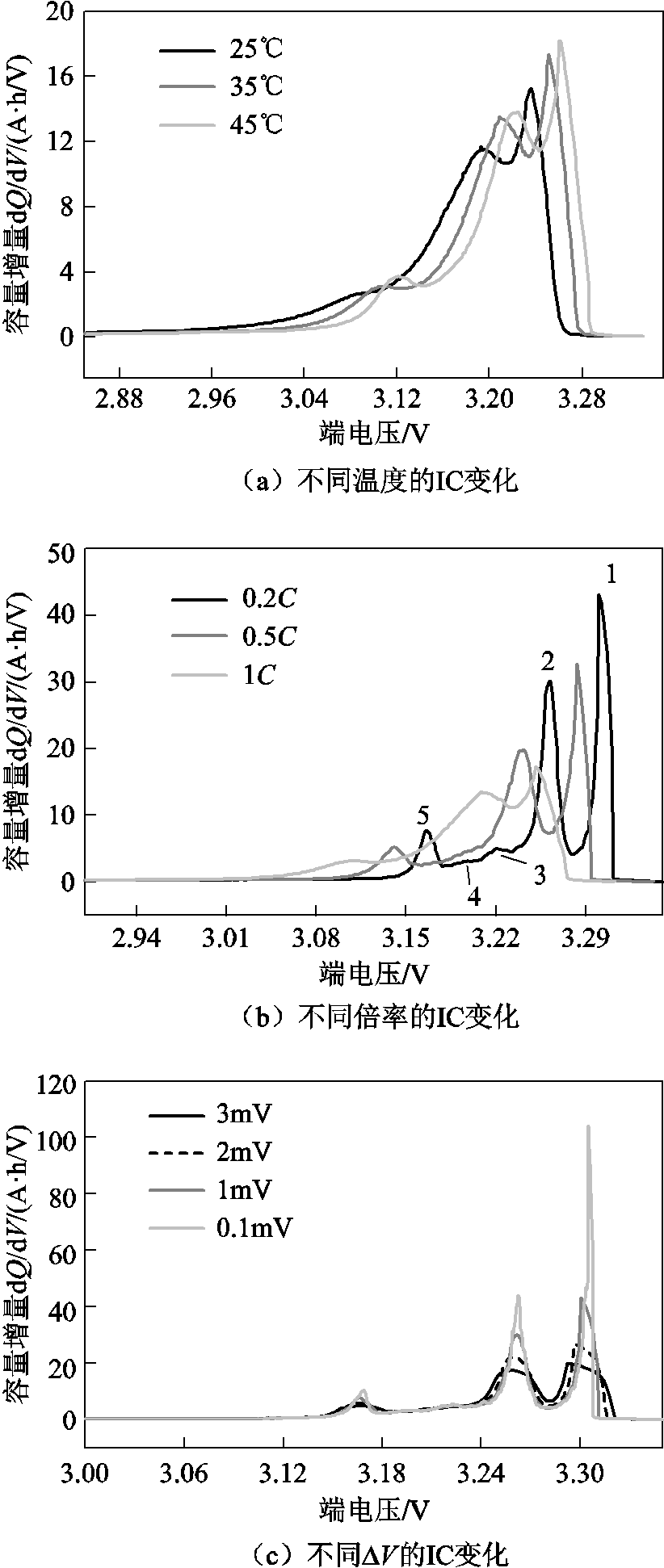


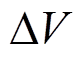 =3mV,磷酸铁锂电池选取
=3mV,磷酸铁锂电池选取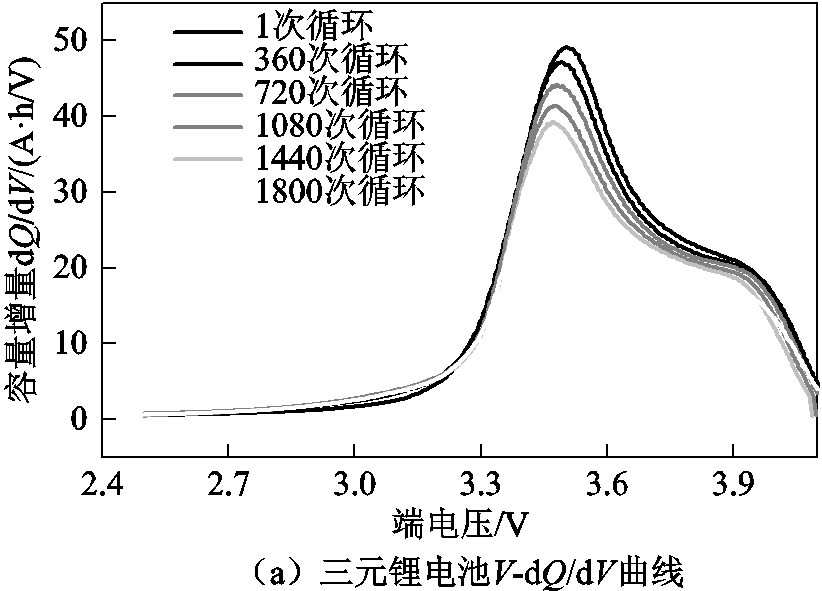
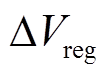 )的方式,可以找到不同
)的方式,可以找到不同 下FPs与SOH的多组关系。峰值区间即以峰顶所在位置为中心,在峰的左右两侧各选取
下FPs与SOH的多组关系。峰值区间即以峰顶所在位置为中心,在峰的左右两侧各选取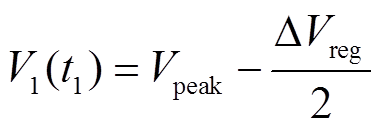 (4)
(4)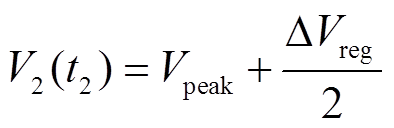 (5)
(5) 为峰值电压;
为峰值电压;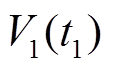 为
为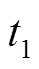 时刻左侧端电压;
时刻左侧端电压; 为
为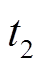 时刻右侧端电压。
时刻右侧端电压。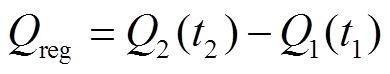 (6)
(6)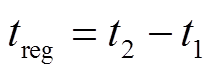 (7)
(7)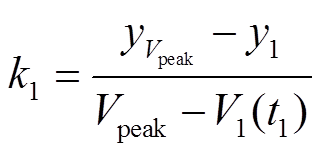 (8)
(8)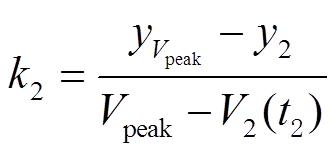 (9)
(9) 为峰面积;
为峰面积;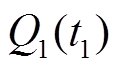 和
和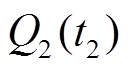 分别为峰左、右侧端电压的放电容量;
分别为峰左、右侧端电压的放电容量;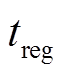 为峰值区间的放电时间;
为峰值区间的放电时间; 和
和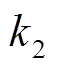 分别峰的左斜率和右斜率;
分别峰的左斜率和右斜率;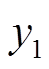 和
和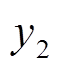 分别为峰左、右侧端电压对应的dQ/dV值;
分别为峰左、右侧端电压对应的dQ/dV值;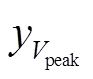 为峰高度。
为峰高度。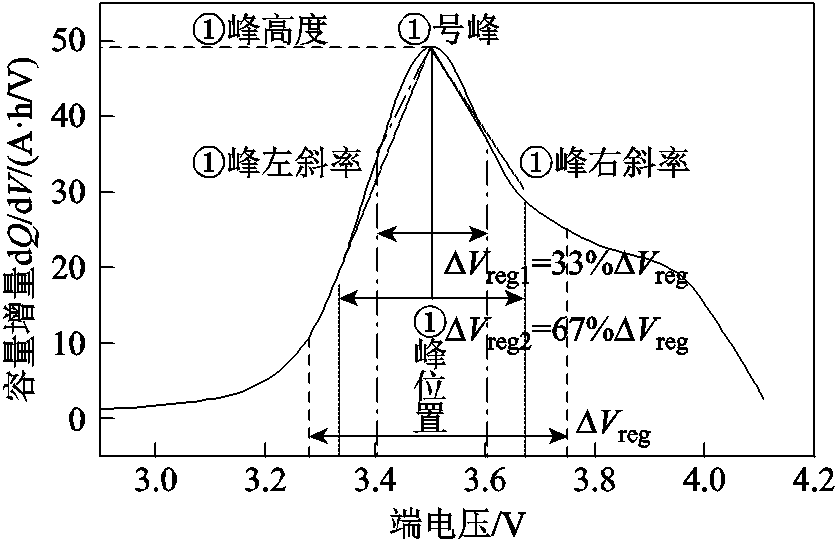
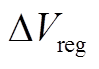 的IC曲线特征参数
的IC曲线特征参数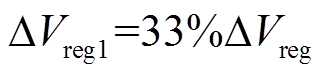 和
和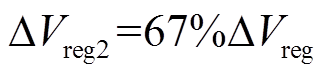 ),各组FPs的数学关系取决于
),各组FPs的数学关系取决于 ,n},其中n是序列长度,y(k)=SOH(k);比较序列X
,n},其中n是序列长度,y(k)=SOH(k);比较序列X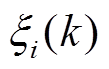 。
。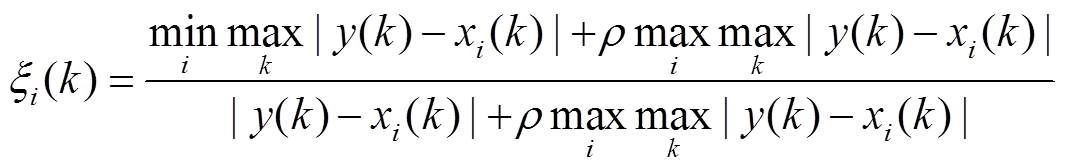
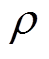 为关联系数,
为关联系数, ,通常取值为0.5。
,通常取值为0.5。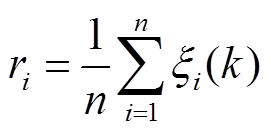



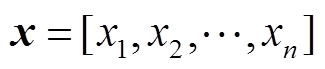 ,其函数f(x)的概率分布服从高斯分布:
,其函数f(x)的概率分布服从高斯分布: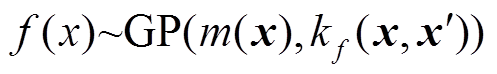 ,所以f(x)的性质由它的均值
,所以f(x)的性质由它的均值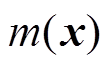 和协方差函数
和协方差函数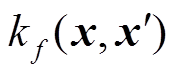 决定
决定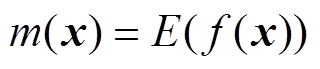 (10)
(10)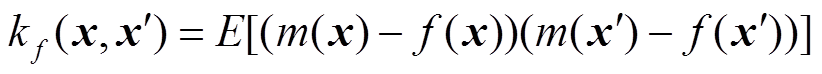 (11)
(11)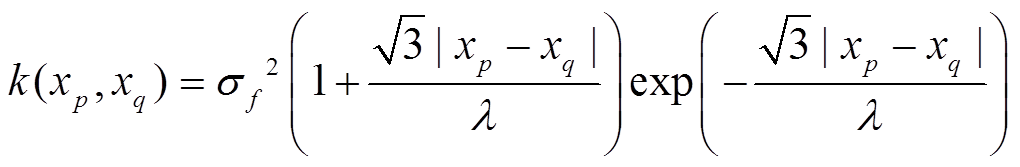 (12)
(12)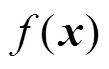 的输出值受到噪声的影响,观测序列y是
的输出值受到噪声的影响,观测序列y是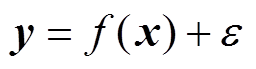 (13)
(13)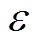 为噪声且服从高斯分布,即
为噪声且服从高斯分布,即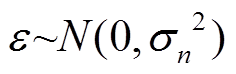 (14)
(14)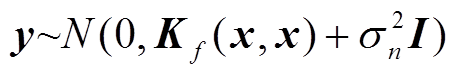 (15)
(15)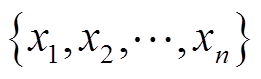 ;
;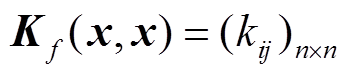 ,
, ;I为n维单位矩阵;
;I为n维单位矩阵;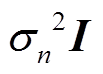 为噪声协方差矩阵。
为噪声协方差矩阵。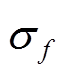 和λ两个参数决定,噪声方差
和λ两个参数决定,噪声方差 也是未知的。将未知参数
也是未知的。将未知参数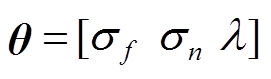 称为超参数。超参数可以用极大似然法确定
称为超参数。超参数可以用极大似然法确定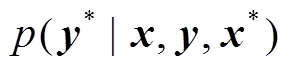 ,高斯过程回归模型可以预测测试样本。对于一个新的数据集
,高斯过程回归模型可以预测测试样本。对于一个新的数据集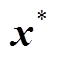 ,估算值
,估算值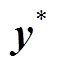 也服从高斯分布。则观测值y和估算值
也服从高斯分布。则观测值y和估算值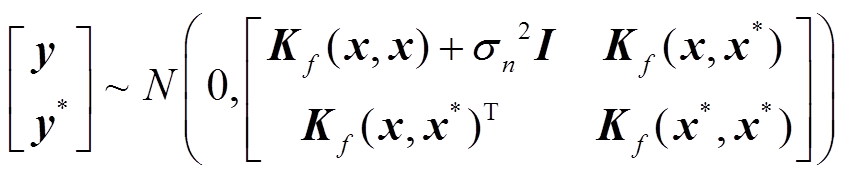 (16)
(16)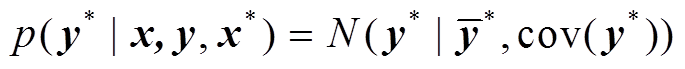 (17)
(17)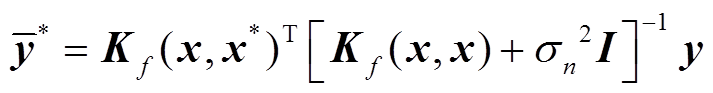 (18)
(18)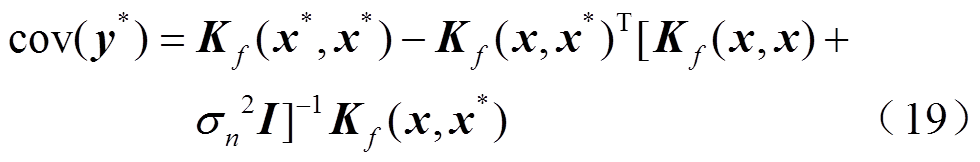
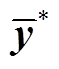 为
为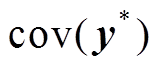 为测试数据的方差矩阵,反映了估算值的可靠性。
为测试数据的方差矩阵,反映了估算值的可靠性。 ,
, )的回归模型后,在新数据集
)的回归模型后,在新数据集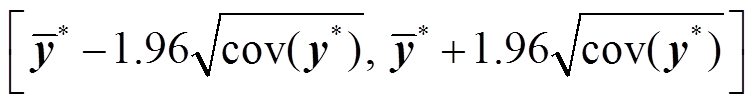 (20)
(20)

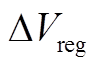 下1号电池SOH估算结果和误差
下1号电池SOH估算结果和误差

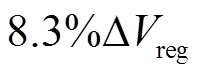 时,误差值最大,而峰值区间为
时,误差值最大,而峰值区间为 时,整体误差最小。
时,整体误差最小。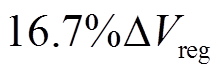 下的四个关联度最高的FPs来估算SOH能得到最优的结果。
下的四个关联度最高的FPs来估算SOH能得到最优的结果。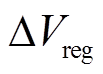 的估算结果和误差。
的估算结果和误差。


 时,相对误差最大值不超过2%,且方均根误差为0.24%,误差值低于另外两种情况,同时平均绝对误差为0.000 8,表明估算的SOH接近于真实值。此外,不同峰值区间下的估算误差也有较大差别,这说明不同峰值区间提取的IC曲线FPs有较大差别,进而影响SOH估算精度。
时,相对误差最大值不超过2%,且方均根误差为0.24%,误差值低于另外两种情况,同时平均绝对误差为0.000 8,表明估算的SOH接近于真实值。此外,不同峰值区间下的估算误差也有较大差别,这说明不同峰值区间提取的IC曲线FPs有较大差别,进而影响SOH估算精度。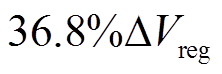 情况下,表8中以峰面积估算的SOH误差值小幅增加,其他情形下的误差结果都明显增加,其中
情况下,表8中以峰面积估算的SOH误差值小幅增加,其他情形下的误差结果都明显增加,其中