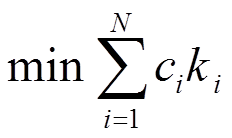（1）摘要 配电网受到极端扰动后可靠故障定位是提升配电网供电可靠性的重要手段。在极端扰动中，配电网中发生复故障的概率增大，主要体现在故障重数多、故障类型多、高阻接地等特征。文章提出一种考虑复故障的有源配电网故障定位方法。基于μPMU优化配置下的区域划分，形成各个监测域。通过搜索算法确定可疑监测域，并启动故障定位算法，利用不平衡电流分量幅值比较的故障区段检测判据定位故障。通过PSCAD/EMTDC和Matlab，验证了该方法不受故障位置和故障类型的影响，适用于多重、多类型故障等复杂场景，且有较高的抗过渡电阻能力。
关键词：复故障 可疑监测域 不平衡电流分量 故障定位 广域相量测量
随着极端扰动造成的大规模停电事故日益频繁，在极端扰动下，配电网发生复故障的比例大大增加。学术界和工业界逐渐开始重点关注到与负荷直接相关的配电网对极端扰动的应对能力[1-2]。作为直接服务于用户的关键环节，配电网能否可靠定位故障，对全网及时恢复供电具有重要意义。
现代配电网结构复杂，分支线路众多且分布式电源不断广泛接入，导致线路故障区段的定位比较困难，现在主要依靠馈线终端单元（Feeder Terminal Unit, FTU）等配电网自动化设备进行故障定位[3]，但仅适用于分布式发电（Distributed Generation, DG）渗透率小于25%的配电网[4]。其他主要方法还包括基于电气量信息和系统参数的故障分析法、应用领域不断扩大的人工智能算法以及输电网常用的行波法等。故障分析法包括受过渡电阻、线路分支等因素影响的单端量法和对同步时钟要求较高[5]的两端量法。人工智能算法包括遗传算法、蚁群算法、蝙蝠算法等，容错性较高[6]，但随着电网拓扑结构的不断变化及极端天气造成的复杂故障，算法运行随之变得复杂。广泛应用于结构相对简单的输电线路的行波法也难以适应于配电网，且对双重及双重以上故障等复故障情形缺乏普适性。
专家学者对于电力系统发生复故障，特别是两重以上故障的故障定位问题研究较少，大部分为FTU获取电流信息，再结合人工智能算法进行优化。文献[7]阐述了“故障确信度”的概念，基于此，提出一种利用广域信息的多重故障辨识方法，先求出不相邻线路两重可疑线路组合，再利用确信度的概念准确定位故障线路。文献[8]利用PMU获取线路电流，排序各线路电流实际值与估计值的残差，再根据电压故障分量计算出线路故障点位置。文献[9]构建了计及漏报和误报下的配电网区段定位完全解析模型，利用矛盾假设、模型分层等因素进行降维，单一、双重、三重故障情形下可以定位故障区段。文献[10]依据风电机组加入配电网的新情景，对传统的开关函数和适应度函数进行改进，提出基于粒子群算法和遗传算法的混合算法，可判断出一重、两重及三重故障下的故障区段，出现“未成熟收敛”的概率降低。文献[11]针对现有诊断方法在多重多相故障时存在耗时长、准确率不高、容错能力低的情况，提出一种模型分层诊断方法，适应于小概率的大范围短路故障。文献[12]提出了一种含光伏的配电网故障区段定位方法，目标函数为多个，利用多目标粒子群优化算法进行优化，通过仿真验证了该故障定位方法既适用于单一故障，也适应于多重故障，且对信息畸变具有较好的容错性。文献[7-12]没有考虑断线故障的情形，且人工智能算法难以适用于含有多重短路、断线等极端、复杂的故障。
本文提出一种考虑复故障的中压有源配电网故障定位方法。基于微型相量测量单元（Micro Phasor Measurement Unit, μPMU）的优化配置，以配置μPMU的节点为区域边界的划分原则，进行监测域划分，形成两种类型的监测域。通过搜索算法中启动判据确定含有故障的监测域，即可疑监测域。若为第一类监测域，则直接确定故障；若为第二类监测域，则启动故障定位算法，采用基于不平衡电流分量幅值比较的故障区段检测判据进行故障定位。通过设置不同故障场景对所提出的方法进行仿真验证该方法原理简单，对复故障、多类型故障等复杂场景具有良好的适应性，不受故障类型、故障位置的影响，有一定的抗高阻能力。
本文基于μPMU优化配置，提出监测域划分方法。利用各监测域相量信息，确定可疑监测域，并启动故障定位算法定位故障区段，减少计算量，提高故障定位的实时性，同时减小复故障分析的复杂度。
配电网线路分支线路众多，考虑经济性、数据处理量，目前在全网各节点均配置配电网相量测量单元[13]并不现实，考虑到电网正常运行时应完全可观，需要对μPMU优化配置。电力系统可观性是指系统中量测装置的数量和分布情况足够来求解系统的当前状态[14]，当发生单一故障时，各节点依然通过配置μPMU节点的电气量间接计算保持可观性。
本文在0-1整数规划算法的基础上，根据节点可观性建立优化配置模型，构建节点关联矩阵并进行分析，从而求解中压有源配电网模型中μPMU配置位置。因10kV中压配电网中零注入节点极少，对配置μPMU数量影响不大，便不予考虑。以最少配置μPMU数量为目标函数，以系统各节点电压全部可观作为约束条件，如式（1）、式（2）所示。
目标函数为
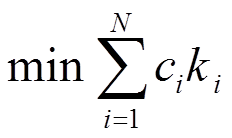（1）约束条件为
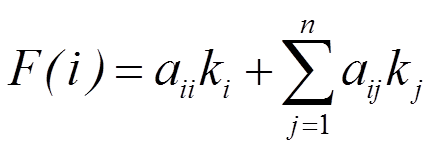≥1（2）
式中，i、j为节点；ci为ki的权重系数，表征在节点i安装量测装置的费用，取ci=1；ki为配电网第i个节点的量测装置配置情况。
（3）矩阵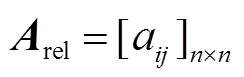
为节点关联矩阵，表示节点间连接关系。若aij=1，表示节点i、j相连接；反之，aij=0，则表示节点i、j不相连。对于对角线元素，规定为1，即
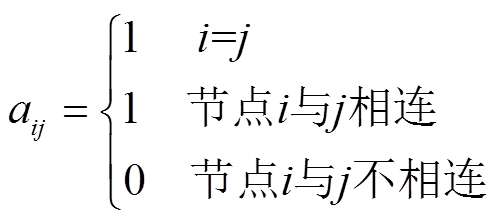（4）在节点关联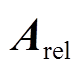矩阵
中，行矩阵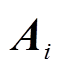
表示节点i与其他节点的连接关系，节点i相连接的节点总数越大，则该节点关键度越大，配置优先级越高，数值越大。特别指出，将电源节点设为优先级最高的节点。
优先级高的节点i配置μPMU后，其相邻节点可观测，将相连节点的配置系数设置为0。若节点的配置优先级一致，则按照序号顺序依次配置，将全网遍历一遍，直到Arel中所有节点完全可观。
根据优化配置结果，将10kV有源配电网拓扑结构划分为多个双端无分支区域，称之为监测域（Monitoring Area, MA），其划分原则为：MA的两端边界节点必须配置μPMU，这样可以保证边界节点直接量测可观，正常运行情况下监测域内节点全部可观。
基于上述划分原则，MA可分为两种类型，如图1所示。
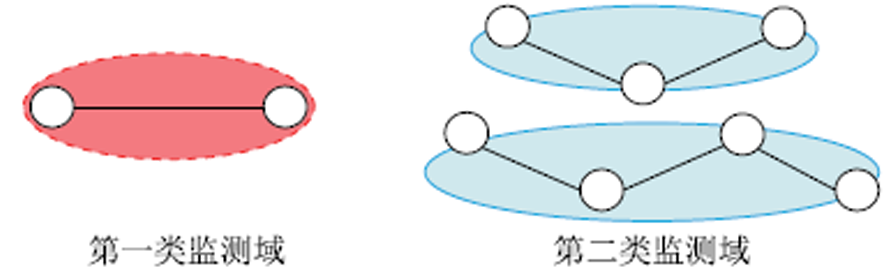
图1 监测域类型
Fig.1 Monitoring area type
第一种记为MA1(a,b)，即仅包含两个节点a和b，以及节点间连线形成一个监测域。第二种记为MA2(a,b,c)或MA2(a,b,c,d)。MA2(a,b,c)即节点a，b和c，以及节点间连线形成一个监测域。同理，另一种记为MA2(a,b,c,d)。以上两种类型的监测域是划分的基本区域单元。
按照修正的有源IEEE 33节点配电网模型，采取上述μPMU优化配置流程，基于μPMU优化配置结果，以配置μPMU节点作为监测域的边界节点，形成两类监测域，如图2所示。某节点处带有配置符号，表示该节点直接量测可观，其余为间接可观节点。各监测域的类型、节点、线路区段序号见表1。
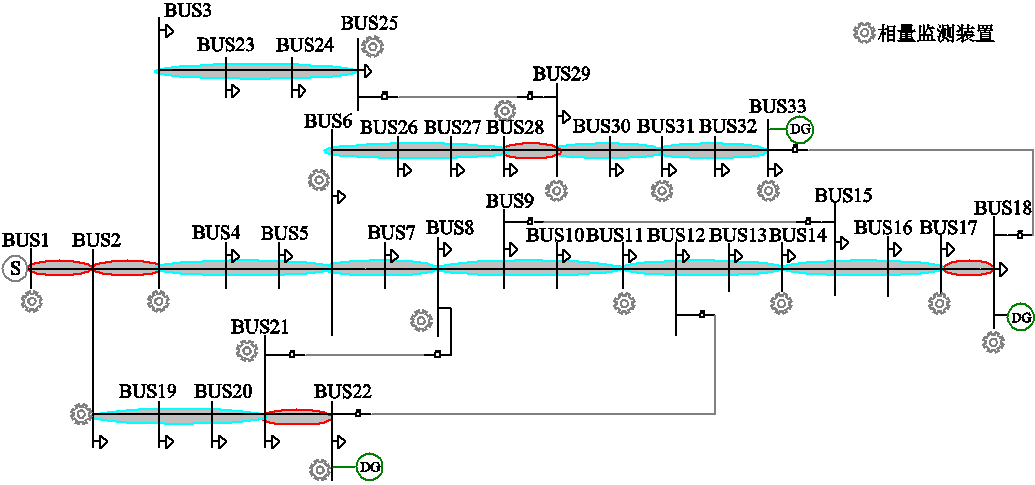
图2 基于μPMU配置的监测域划分
Fig.2 MA partitioning based on μPMU configuration
表1 各监测域分布情况
Tab.1 Distribution of monitoring areas
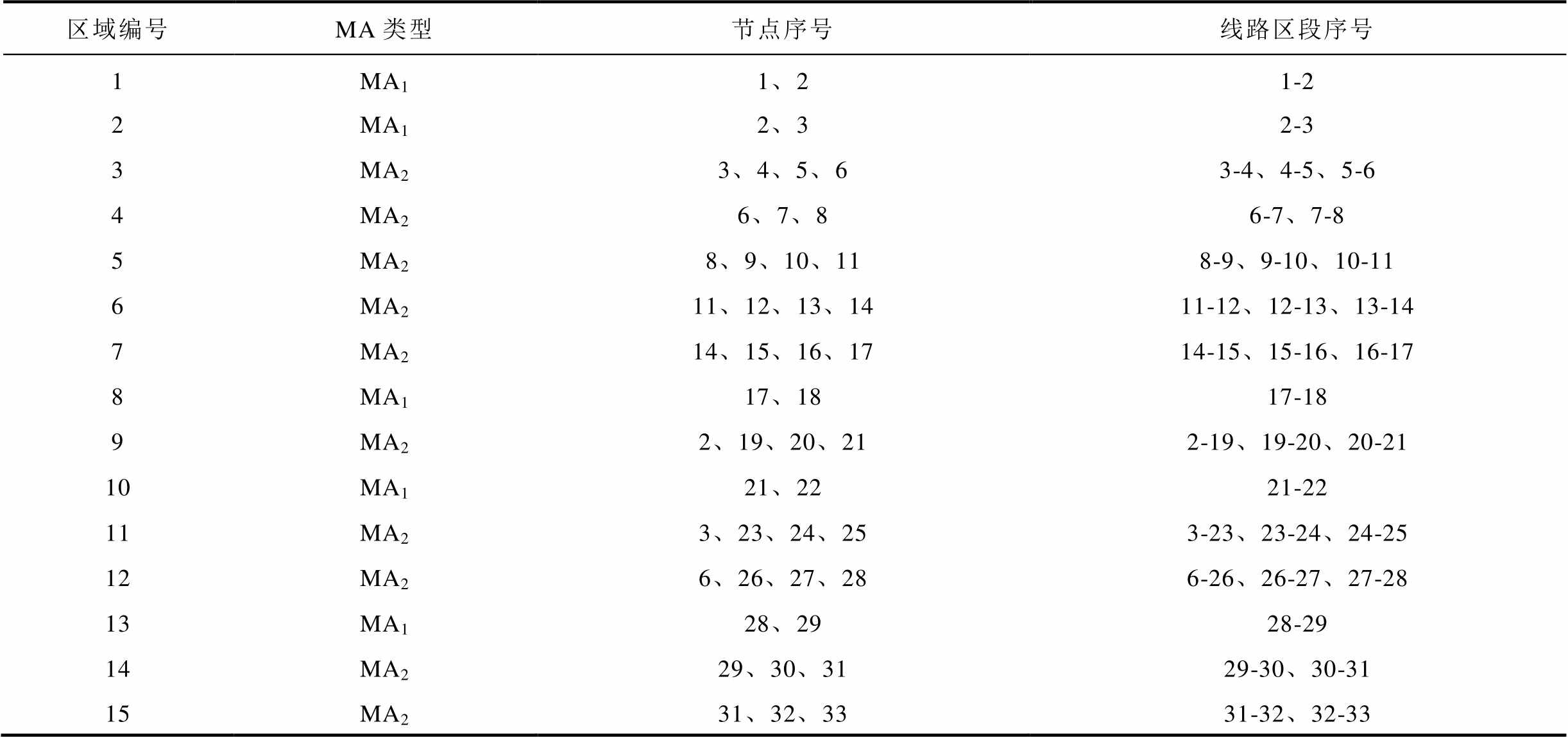
区域编号MA类型节点序号线路区段序号 1MA11、21-2 2MA12、32-3 3MA23、4、5、63-4、4-5、5-6 4MA26、7、86-7、7-8 5MA28、9、10、118-9、9-10、10-11 6MA211、12、13、1411-12、12-13、13-14 7MA214、15、16、1714-15、15-16、16-17 8MA117、1817-18 9MA22、19、20、212-19、19-20、20-21 10MA121、2221-22 11MA23、23、24、253-23、23-24、24-25 12MA26、26、27、286-26、26-27、27-28 13MA128、2928-29 14MA229、30、3129-30、30-31 15MA231、32、3331-32、32-33
若某个监测域两端的节点为分别为m、n，定义系统内电流的参考正方向为由母线指向线路，节点m、n处的节点电流相位分别为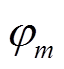
、
。
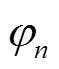根据短路、断线故障的差异，在全网各监测域内同时计算、搜索。对于短路故障，采集监测域两端的突变点前后各三个周波的三相电流数据，然后对其进行快速傅里叶变换（Fast Fourier Transform, FFT）求取正序电流相位，最后得到相位差，即
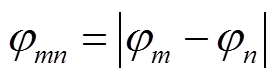（5）式中，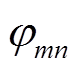
为监测域两端的相位差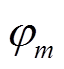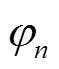；、分别为监测域两端同一时刻的正序电流相位。对于理想情况而言，全系统阻抗角相同，两侧电动势相位相同，系统正常运行或区外故障时，
=180°。实际上，含有分布式电源的主动配电网中，系统正常运行或区外故障时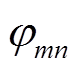，的值不一定为180°。发生区内故障时，监测域两端相位差会发生改变，以此作为短路故障启动判据，即
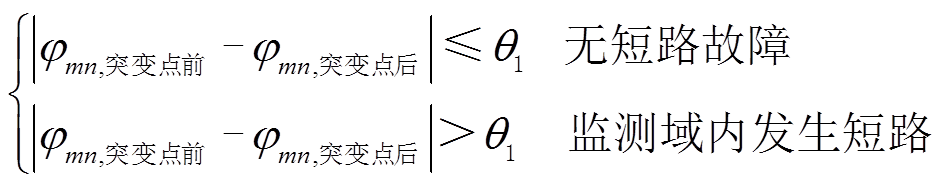（6）式中，θ1为短路故障定位启动的门槛值。考虑到线路参数、CT测量及监测装置等均会产生误差[15]，从而导致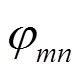
的测量值与实际值存在一定的偏差。考虑一定裕度，设置可靠系数krel=1.1～1.2，θ1取2.2°～2.5°，可以正确识别监测域内短路故障，且正常区域不会被误判。
对于断线故障，检测每一个监测域两端的支路是否存在一相或多相电流幅值突变为0。对于断相故障，相电流会突变为0；正常情况下，相电流不会突变为0。断线故障启动判据为
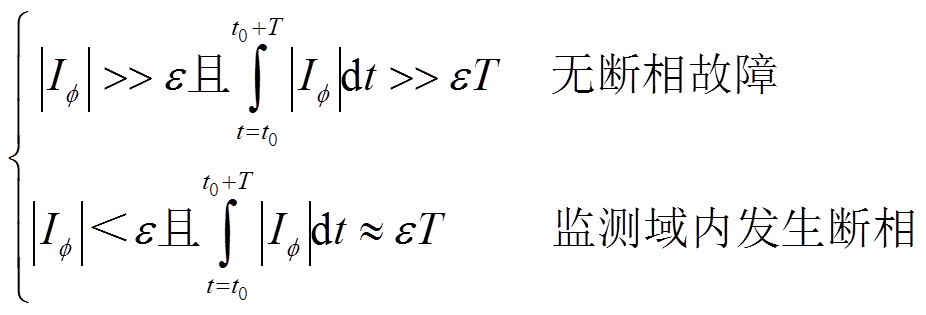（7）式中，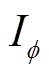
为相电流；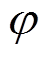
为相电流的相别；t0为突变时刻；T为电流周波时间；ε为断线故障定位启动值。考虑到线路参数、CT测量及监测装置等均会产生误差[15]，考虑一定裕度，设置可靠系数krel=1.1～1.2，ε取10-3～10-2kA，可以正确识别监测域内断线故障，且正常区域不会被误判。
监测域若满足上述任意一个启动判据，便认定为可疑监测域。判断该监测域类别，若为第一类监测域，则直接判定出故障区段；若为第二类监测域，则启动故障定位算法，利用不平衡电流分量幅值比较的故障区段检测判据定位故障。
本文不平衡电流分量（Unbalance Current, UC）是指节点注入电流量测值与计算值之差[16]。节点注入电流的计算值为故障时刻节点电压相量与配电网节点导纳矩阵的乘积。
选取故障发生时刻3个周波后的正序分量进行离散傅里叶变换（Discrete Fourier Transform, DFT）。本文首先对短路、断线下节点导纳矩阵维度进行分析，再对系统发生复杂故障情形节点导纳矩阵元素进行分析。
当中压有源配电网某区段发生短路故障时，系统的正序拓扑结构均会增加一个故障节点。其节点电压方程也随之发生变化，相量维度增加，变为n+1维。
断线故障分为三相断线和非全相断线。三相断线故障，相当于在电网中去掉一条线路，正序节点导纳矩阵维数不变，仍为n维非全相断线，会导致原配电网正序导纳矩阵中增加2个节点，变为n+2维。
下面以双重故障为例，分析配电网发生多重复杂故障后节点导纳矩阵元素的变化。
3.2.1 不相连线路发生双重故障
假设某中压有源配电网由n个节点和b条支路组成，根据节点间连接关系，得到正常运行时节点导纳矩阵为
（8）不相邻线路发生复故障，假设节点i、j间连线上发生了故障f1，节点w、v间连线上也发生了故障f2，由3.1节可知，新增了故障节点（三相断线除外），配电网节点导纳矩阵维度发生变化，如式（9）所示。
（9）假设两处均发生短路故障，分析节点导纳矩阵中三类元素的变化：①第一类为与故障点不相邻的节点，因为系统的结构参数均没有发生变化，此类节点的自导纳与互导纳均无变化，即与故障前相同；②第二类为新增的故障节点×、
，其自导纳和与相连节点的互导纳为矩阵新增元素；③第三类为与故障点直接相邻的节点i、j、w、v，因为新增故障节点，i、j、w、v的自导纳和彼此的互导纳也会发生变化，与故障前不相同。
删去节点导纳矩阵中故障点所在行、列后为
（10）修改后的节点导纳矩阵与故障前节点导纳矩阵维度一样，不同的矩阵元素只有第三类元素，即Yii、Yij、Yjj、Yji、Yww、Yvv、Ywv、Yvw。
3.2.2 相连线路发生双重故障
假设n节点配电网中节点i、j、k是相连节点，根据节点间连接关系，得到正常运行时节点导纳矩阵为
（11）相邻线路发生复故障，假设节点i、j间连线上发生了故障f1，节点j、k间连线上也发生了故障f2，由3.1节可知，新增了故障节点（三相断线除外），配电网节点导纳矩阵维度发生变化，如式（12）所示。
（12）将故障节点所在的行和列删去，得到修改后的节点导纳矩阵为
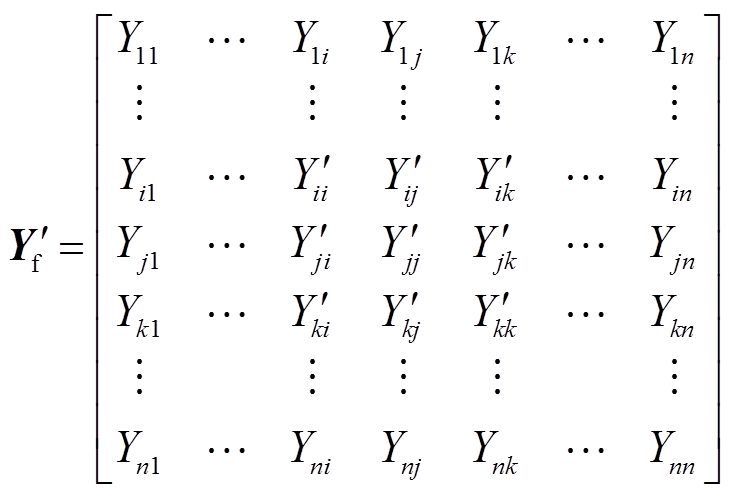（13）修改后的节点导纳矩阵与故障前节点导纳矩阵维度相同，不同的矩阵元素也只有第三类元素，即Yii、Yij、Yik、Yjj、Yji、Yjk、Yki、Yki、Ykk。
由3.2节可知，比较系统正常运行时和故障时修正的节点导纳矩阵，与故障相连节点的自导纳、互导纳元素均发生了变化，利用节点注入电流计算公式计算故障后的节点注入电流，如式（14）所示。
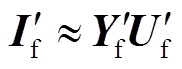（14）将正常运行时的正序节点导纳矩阵近似代替故障时修正的节点导纳矩阵，得到不平衡电流分量为
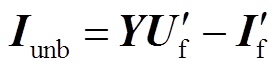（15）式中，Y为故障前的系统正序节点导纳矩阵；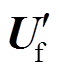
为故障时各节点电压；
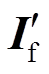为故障后各节点注入电流测量值列向量。对于系统主电源和系统拓扑结构末端配置DG的节点，其节点注入电流为μPMU量测值；对于在系统拓扑结构中间的DG，假定节点注入电流为μPMU量测值；对于其他没有配置电源的负荷节点，将其节点注入电流假定为0。
对于系统金属性短路或过渡电阻较小时，设置检测故障区段的门槛值，比较各节点不平衡电流分量的幅值，就能确定故障区段。考虑线路参数、量测等误差[15]，并考虑一定裕度，设置可靠系数krel=1.2，门槛值取为0.09kA，经过有源配电网故障定位方法测试平台验证，可以适用于各类中压有源配电网的故障定位，即与故障相连的节点的不平衡电流分量幅值会均超过0.09kA。若过渡电阻较大（超过10Ω），存在各节点的不平衡电流分量幅值小于门槛值的可能，需对不平衡电流分量进行均一化处理，即将幅值最小的不平衡电流分量作为参考值Iref，各节点的修正不平衡电流分量矩阵
为
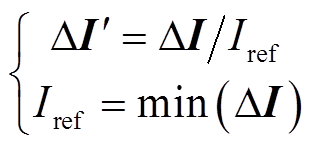（16）若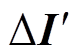
中元素数值超过门槛值δ（本文δ取4.5），则对应节点为与故障相连的节点，该取值可以保证系统发生过渡电阻较大的短路故障时正确定位故障区段。
考虑复故障的中压有源配电网故障定位方法流程如图3所示。
图3 故障区段定位流程
Fig.3 The flow chart for fault section location
按照故障重数与可疑监测域个数的组合，分为四种情形：①单一故障；②单一监测域内发生复故障；③多个监测域内发生单一故障；④多个监测域内发生复故障。常见故障场景如图4所示。
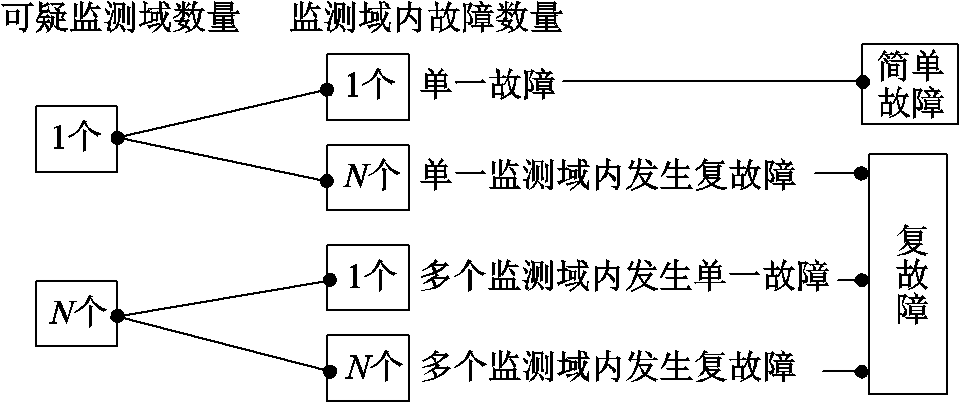
图4 常见故障场景
Fig.4 Common fault scenarios
在全网进行μPMU部分配置的前提下，若配电网同一监测域只发生一个故障，系统各节点依然保证可观。
当配电网发生两重及以上复杂故障场景时，分析该故障定位对复故障的适应性。同一监测域内发生多重复杂故障会造成监测域内部分节点失去可观性，如图5所示。在不平衡电流分量的幅值计算中，除了与故障点相连节点的导纳矩阵元素发生改变，不可观节点的电压幅值也会因发生故障而明显变化。本文选取故障前三个周波的节点电压幅值代替故障后不可观的节点电压，由此也会导致不平衡电流分量产生。综上所述，不平衡电流分量产生的原因为系统拓扑结构变化和节点电压不可观。本文算法准确率定义为某一故障场景下实际故障区段占定位方法所检测区段的比例。
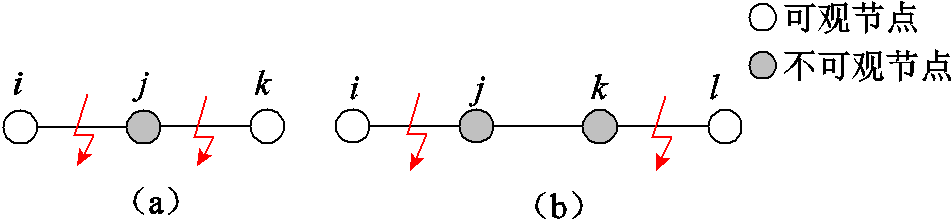
图5 复故障情形分析
Fig.5 Complex fault situation analysis
图5a中的监测域包含3个节点i、j、k，形成的节点导纳矩阵为
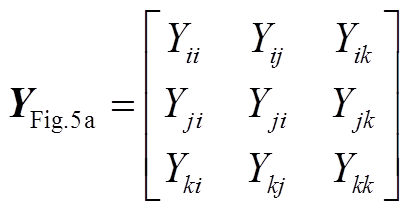（17）发生双重故障后，线路i-j、j-k的参数已经发生改变。中间节点j因没有配置μPMU，通过正常运行情况下的线路参数间接计算得到电压值并非真实值而失去可观性。故障时电压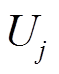
用故障前电压
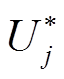代替，如式（18），将所得结果代入式（15），节点j也会产生不平衡电流分量。
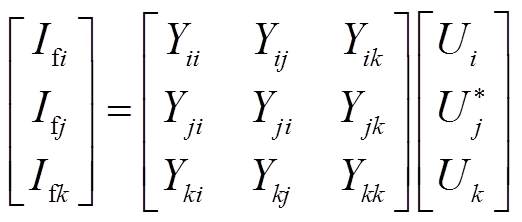（18）与故障相连的节点为i、j、k，不可观节点为j。因此，产生不平衡电流分量的节点同为i、j、k，不平衡电流分量所在的节点为故障线路的两端，即定位的区段为i-j、j-k，共两个，可疑监测域中真实的故障区段也为i-j、j-k，即该场景下故障区段准确率为100%。
图5b中的监测域包含4个节点i、j、k、l，形成的节点导纳矩阵为
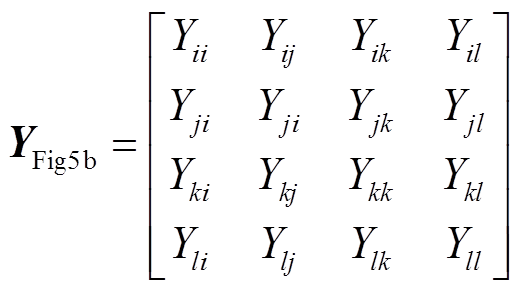（19）发生双重故障后，线路i-j、k-l的参数已经发生改变。中间节点j、k因没有配置μPMU，通过正常运行情况下的线路参数间接计算得到电压值并非真实值而失去可观性。故障时电压Uj、Uk分别用故障前电压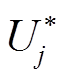
、
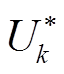代替，如式（20），将所得结果代入式（15），节点j、k也会产生不平衡电流分量。
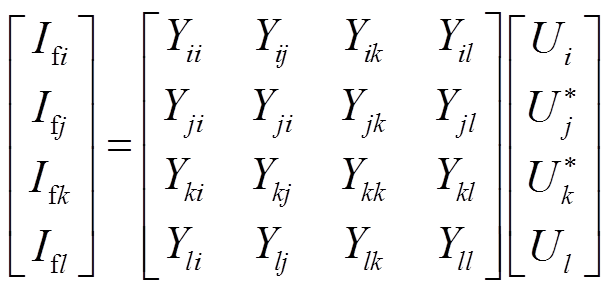（20）与故障相连的节点为i、j与k、l，不可观节点为j、k。因此，产生不平衡电流分量的节点为i、j、k、l，不平衡电流分量所在的节点为故障线路的两端，即定位的区段为i-j、j-k和k-l，共三个，但可疑监测域中真实故障区段为i-j、k-l，即该场景下故障区段准确率为66.7%。该方法对各种复故障适应性分析见表1、表2。
表1 两重复故障适应性分析
Tab.1 Double fault adaptability analysis
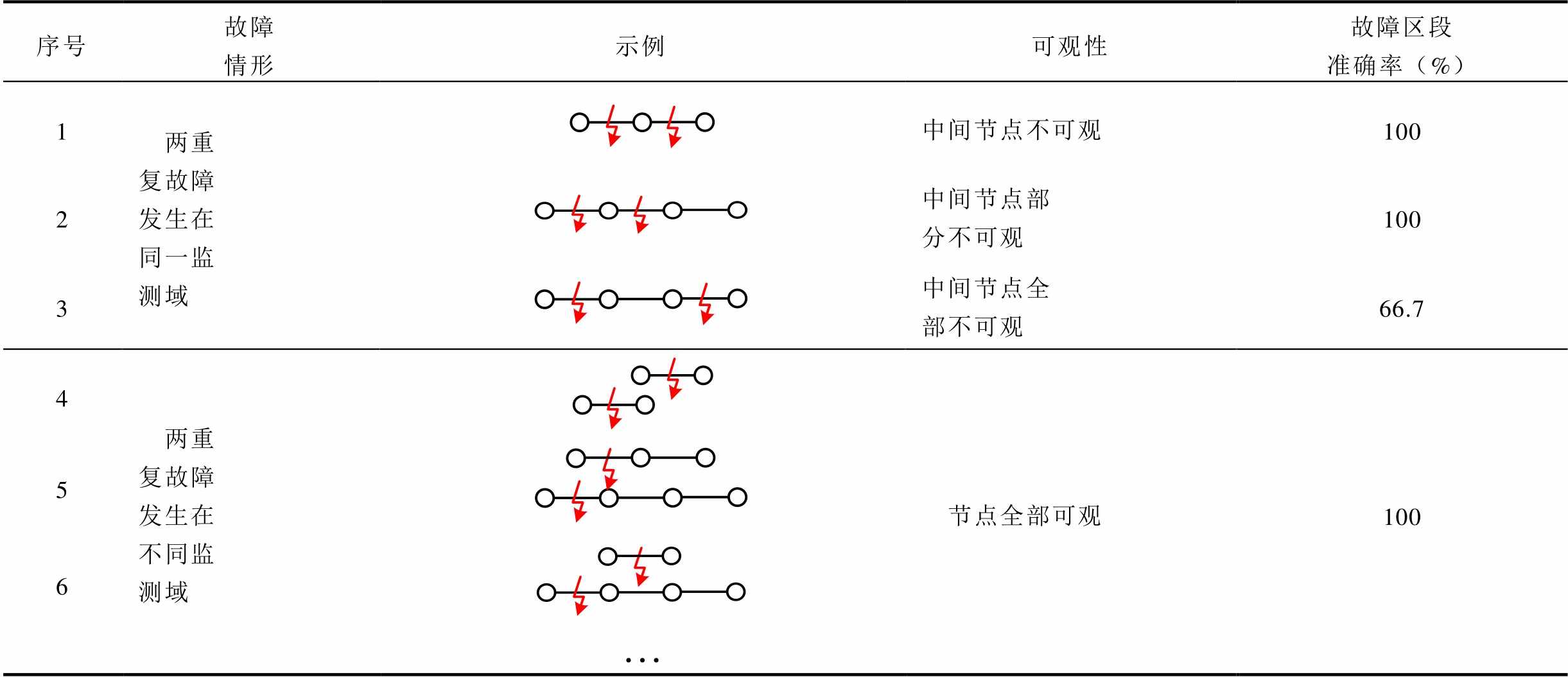
序号故障情形示例可观性故障区段准确率（%） 1两重复故障发生在同一监测域中间节点不可观100 2中间节点部分不可观100 3中间节点全部不可观66.7 4两重复故障发生在不同监测域节点全部可观100 5 6
由表1、表2可知，该定位方法在绝大多数复故障情景下故障区段定位准确率为100%，即实际故障区段与检测判据所定位的区段完全一致；但在极少数复故障场景下，中间节点全部不可观，故障区段定位准确率为66.7%或75%，实际故障区段少于检测判据所定位的区段，即误判可疑监测域内的正常区段。
表2 两重以上复故障适应性分析
Tab.2 Double or more fault adaptability analysis
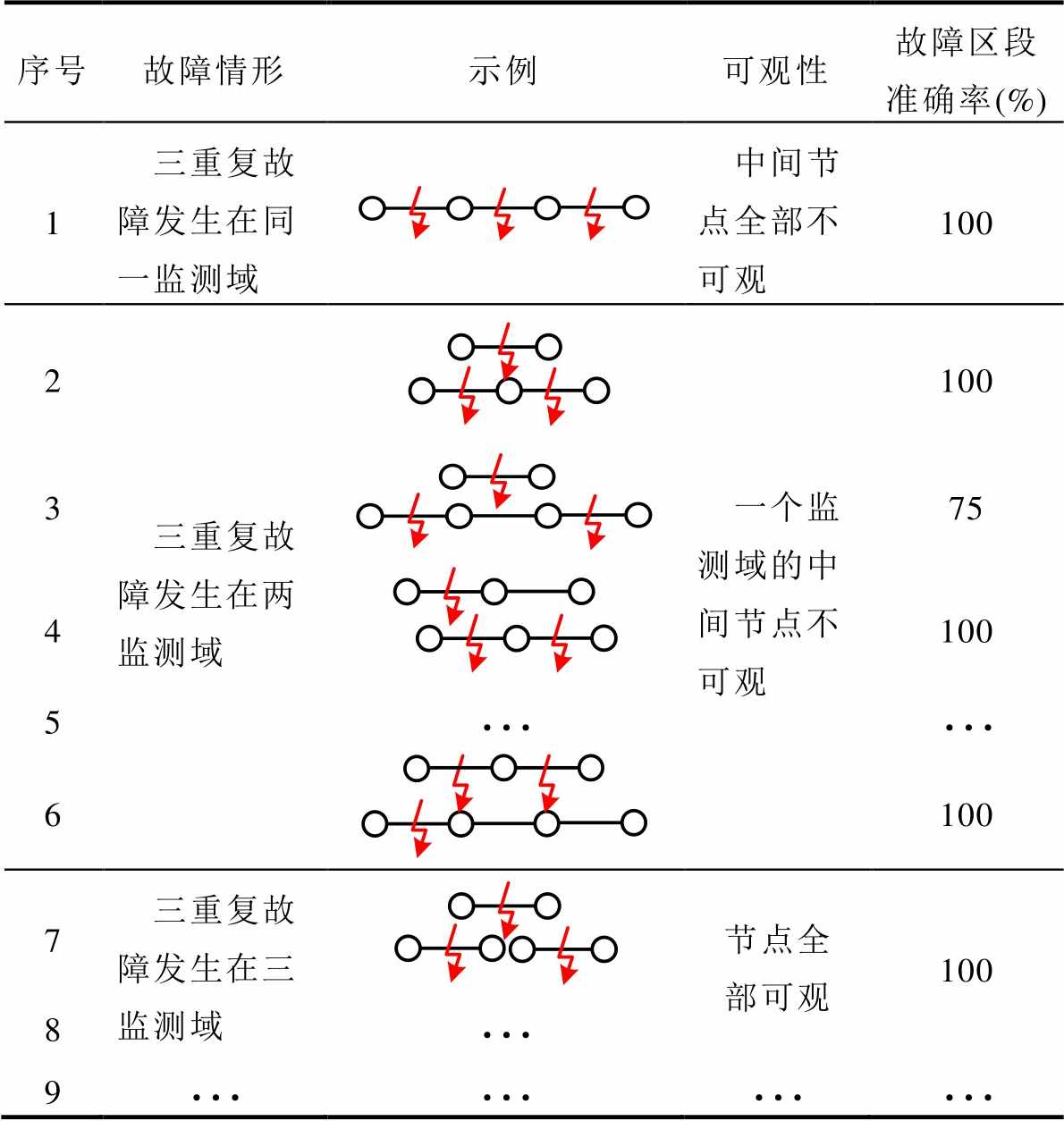
序号故障情形示例可观性故障区段准确率(%) 1三重复故障发生在同一监测域中间节点全部不可观100 2三重复故障发生在两监测域一个监测域的中间节点不可观100 375 4100 5 6100 7三重复故障发生在三监测域节点全部可观100 8 9
本文搭建如图2所示的有源IEEE33节点PSCAD配电网模型，系统为闭环结构，开环运行，基准电压为10kV，基准功率为10MW，额定负荷容量为4MW，负荷波动取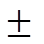
10%，三个逆变型DG的有功输出均为1MW，额定状态下DG的渗透率[17]为75%。按照同一故障区段发生复故障、不同区段发生复故障和高阻接地故障进行仿真分析，并对该方法的性能进行分析。
在同一个区段16-17上内设置复故障，对故障定位方法进行验证，过渡电阻Rf=0，复故障发生位置如图6所示。经过PSCAD/EMTDC仿真和Matlab编程实现，得到同一故障区段发生复故障定位结果见表3。
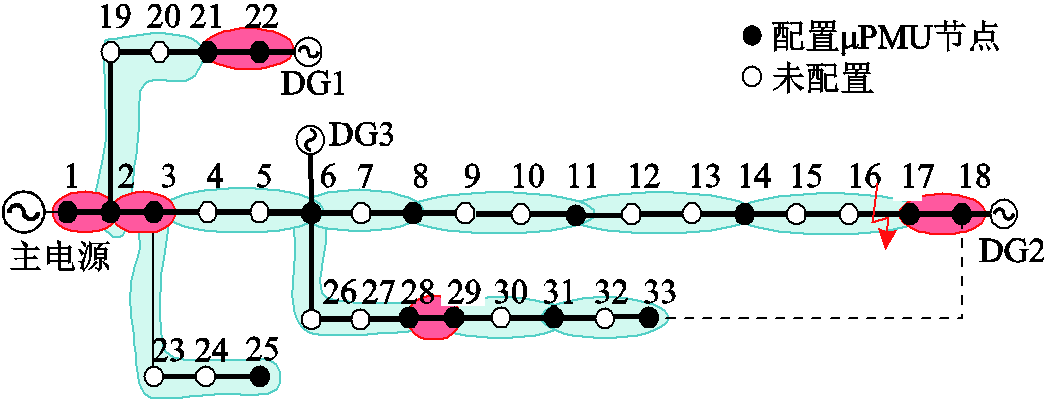
图6 同一故障区段复故障发生位置
Fig. 6 Combination fault locations in the same fault section
表3 同一故障区段发生复故障定位
Tab.3 Fault location where combination fault occurs in the same fault section
故障情形故障位置监测域相位差/(°)或电流变化/kA 不平衡电流幅值能否确定可疑监测域能否定位故障区段 AG1AG216-17：183.48→61.71能能 ABG1 ABC216-17：183.38→42.43能能 A相断线与B相断线16-17I16-17,AB=0能能 AB断线与两相短路16-17：192.17→243.15I16-17,AB=0能能
由表3可以看出，该故障定位方法适用于同一故障区段发生复故障的场景，可以准确定位故障区段。当复故障发生在同一故障区段，本文假定合并处理，即按照各故障区段仅发生一个故障处理。
在各个不相连线路或相邻线路上分别设置各个故障类型的复故障，位置如图7所示。为保证准确检测故障区段，本文设定不平衡电流幅值门槛值，通过PSCAD/EMTDC仿真和Matlab编程实现，复故障的故障区段判定结果见表4。
图7 不同区段复故障发生位置
Fig.7 The locations of combination faults in different sections
表4中，系统发生故障后，可疑监测域的相量值满足式（6）或式（7），其他监测域未发生故障，其正序电流相位差变化小于阈值或线路相电流正常。通过搜索算法，确定可疑监测域，并启动故障定位算法。最后通过式（14）计算监测域内各节点的不平衡电流分量幅值，与故障相连节点的不平衡电流分量幅值大于设定的门槛值，正常节点的不平衡电流分量幅值约为0。其中算例3-6、9-10发生复故障的区段分别在两个监测域，各监测域内的节点全部可观，利用基于不平衡电流分量幅值的故障区段定位方法可以准确定位故障区段；算例1-2、7-8发生复故障的区段全部处于同一监测域，导致部分节点不可观，用故障前节点电压代替，通过基于不平衡电流分量幅值的故障区段检测判据也可以正确定位故障区段，但算例1、7中正常区段9-10被误判为故障区段。
表4 复故障的故障区段判定
Tab.4 Fault section determination of combination faults
算例故障类型故障位置真实故障区段监测域相位差/(°)或幅值变化/kA不平衡电流幅值/kA疑似故障区段 1AG18-9、 10-11Δφ区域5： 182.62→213.64ΔI节点8=0.12ΔI节点9=0.13ΔI节点10=0.14ΔI节点11=0.138-9、 9-10、 10-11 2AG4 8-9、 9-10Δφ区域5： 182.69→214.30ΔI节点8=0.14ΔI节点9=0.17ΔI节点10=0.14 8-9、 9-10 3ABG2 13-14、 16-17Δφ区域6： 181.63→217.07Δφ区域7： 192.33→199.29ΔI节点13=0.26ΔI节点14=0.25ΔI节点16=0.31ΔI节点17=0.36 13-14、 16-17 4ABG5 13-14、 14-15Δφ区域6： 181.55→216.82Δφ区域7： 192.29→204.12ΔI节点13=0.25ΔI节点14=0.29ΔI节点15=0.27 13-14、 14-15 5AB3 21-22、30-31Δφ区域10： 180.10→260.56Δφ区域14： 181.47→205.29ΔI节点21=0.47ΔI节点22=0.44ΔI节点30=0.32ΔI节点31=0.31 21-22、30-31 6AB6 20-21、 21-22Δφ区域9： 190.30→185.50Δφ区域10： 180.11→228.89ΔI节点20=0.58ΔI节点21=0.60ΔI节点22=0.16 20-21、 21-22 7ABC1 8-9、 10-11Δφ区域5： 182.63→202.89ΔI节点8=0.86ΔI节点9=0.87ΔI节点10=0.75ΔI节点11=0.738-9、 9-10、 10-11 8ABC4 8-9、9-10Δφ区域5： 182.69→203.25ΔI节点8=1.73ΔI节点9=0.63ΔI节点10=0.38 8-9、 9-10 9A相断线3 21-22、 30-31I21-22, A=0I30-31, A=0ΔI节点21=21.1ΔI节点22=25.6ΔI节点30=2.01ΔI节点31=2.04 21-22、 30-31 10A相断线5 13-14、14-15I13-14, A=0I14-15, A=0ΔI节点13=3.06ΔI节点14=10.8ΔI节点15=8.89 13-14、 14-15
5.1节和5.2节的算例都为系统发生金属性短路的情形，过渡电阻Rf=0。分别选取表4中不同的故障位置，分析不同过渡电阻对定位结果的影响。据统计，在过渡电阻小于3kΩ的接地故障中，过渡电阻小于140Ω的比例为85%[18]。通过PACAD/EMTDC和Matlab分别对过渡电阻Rf为10Ω、100Ω、150Ω、500Ω和1 000Ω的算例进行验证，得到各区域的相位差变化与可疑监测域内不平衡电流分量幅值仿真结果见表5、表6。
表5 线路发生各类接地短路复故障各区域相位差变化
Tab.5 Change in phase difference in MA under combination fault
故障位置过渡电阻/Ω三相短路下相位差变化/(°)两相接地短路下相位差变化/(°)单相接地短路下相位差变化/(°) 210Δφ区域6：181.5→187.1Δφ区域7：192.2→212.8Δφ区域6：181.5→186.3Δφ区域7：192.2→207.5Δφ区域6：181.5→185.6Δφ区域7：192.2→199.0 100Δφ区域6：181.5→185.3Δφ区域7：192.2→199.3Δφ区域6：181.5→184.7Δφ区域7：192.2→214.2Δφ区域6：181.5→184.5Δφ区域7：192.2→205.9 150Δφ区域6：181.5→184.8Δφ区域7：192.2→217.5Δφ区域6：181.5→184.9Δφ区域7：192.2→211.6Δφ区域6：181.5→184.4Δφ区域7：192.2→203.8 500Δφ区域6：181.5→184.8Δφ区域7：192.2→205.7Δφ区域6：181.5→184.2Δφ区域7：192.2→202.1Δφ区域6：181.5→184.1Δφ区域7：192.2→197.5 1000Δφ区域6：181.5→184.4Δφ区域7：192.2→200.5Δφ区域6：181.5→184.2Δφ区域7：192.2→200.4Δφ区域6：181.5→184.0Δφ区域7：192.15→197.5 610Δφ区域9：180.1→177.4Δφ区域10：180.1→200.3Δφ区域9：180.1→177.4Δφ区域10：180.1→200.4Δφ区域9：180.1→177.4Δφ区域10：180.1→200.4 100Δφ区域9：180.1→177.4Δφ区域10：180.1→200.5Δφ区域9：180.1→177.4Δφ区域10：180.1→200.4Δφ区域9：180.1→177.4Δφ区域10：180.1→200.3 150Δφ区域9：180.1→177.4Δφ区域10：180.1→200.5Δφ区域9：180.1→177.4Δφ区域10：180.1→200.4°Δφ区域9：180.1→177.4Δφ区域10：180.1°→200.4 500Δφ区域9：180.1→177.4Δφ区域10：180.1→200.5Δφ区域9：180.1→177.4Δφ区域10：180.1→200.4°Δφ区域9：180.1→177.4Δφ区域10：180.1→200.4 1000Δφ区域9：180.1→177.4Δφ区域10：180.1→200.4Δφ区域9：180.1→177.4Δφ区域10：180.1→200.4Δφ区域9：180.1→177.4Δφ区域10：180.1→200.4
表6 复故障可疑监测域的各节点不平衡电流分量幅值
Tab.6 The UC in MA under calculation fault
故障位置过渡电阻/Ω可疑监测域内不平衡电流分量幅值ΔI/kA(修正值ΔI′) 三相短路两相接地短路单相接地短路 210ΔI节点13= 0.12ΔI节点14=0.12ΔI节点16= 0.11ΔI节点17=0.11ΔI节点13= 0.11ΔI节点14=0.11ΔI节点16=0.10ΔI节点17=0.10ΔI′节点13=13.70ΔI′节点14=13.90ΔI′节点16=11.23ΔI′节点17=11.26 100ΔI′节点13=10.74ΔI′节点14=10.93ΔI′节点16= 9.93ΔI′节点17=9.63ΔI′节点13=9.20ΔI′节点14=9.30ΔI′节点16=8.43 ΔI′节点17=8.17ΔI′节点13= 6.14ΔI′节点14=6.14ΔI′节点16= 6.13ΔI′节点17=6.12 150ΔI′节点13=5.19 ΔI′节点14=6.84ΔI′节点16=6.93 ΔI′节点17=6.61ΔI′节点13=5.45ΔI′节点14=5.71ΔI′节点16= 7.13ΔI′节点17=5.13ΔI′节点13=12.6ΔI′节点14=14.1ΔI′节点16=4.89ΔI′节点17=4.56 500ΔI′节点13=4.65ΔI´节点14=4.42ΔI′节点16= 5.21ΔI′节点17=5.08ΔI′节点13=4.95 ΔI′节点14=6.00ΔI′节点16= 6.11ΔI′节点17=4.68— 610ΔI节点20= 2.90ΔI节点21=2.85ΔI节点22=2.13ΔI节点20=2.40ΔI节点21=2.35ΔI节点22=1.31ΔI节点20= 0.62ΔI节点21=0.63ΔI节点22=0.18 100ΔI′节点20= 25.03ΔI´节点21=31.18ΔI´节点22=17.45ΔI节点20=0.29ΔI节点21=0.31ΔI节点22=0.12ΔI′节点20=25.02ΔI´节点21=31.08ΔI′节点22=10.87 150ΔI节点20=0.18ΔI节点21=0.20ΔI节点22=0.16ΔI节点20= 0.17ΔI节点21=0.19ΔI节点22=0.11ΔI′节点20=17.47ΔI′节点21=28.52ΔI′节点22=40.49 500ΔI′节点20=5.28 ΔI´节点21=6.21ΔI′节点22=5.99ΔI′节点20=4.98ΔI′节点21=5.76ΔI′节点22=5.86—
表5验证了本文可疑监测域搜索算法在过渡电阻1kΩ的情况下仍能准确识别可疑监测域，并启动故障定位算法。表6验证了基于不平衡电流分量的故障定位算法在过渡电阻在150～500Ω以内可以准确定位故障区段。其中，对于单相接地短路故障，抗过渡电阻能力可达150Ω；对于两相接地短路与三相短路故障，可达500Ω。综上所述，该方法抗高阻能力较强。
本文选取了标准遗传算法[19]（Standard Genetic Algorithm, SGA）、基于FTU过流信息的矩阵算法[20]与所提方法进行对比。限于篇幅，以区段L13-14、L16-17发生单相接地短路故障、两相接地短路、两相短路、三相短路为例，考虑不同DG渗透率水平，分别为20%、50%、70%，分别进行测试，结果如图8所示。
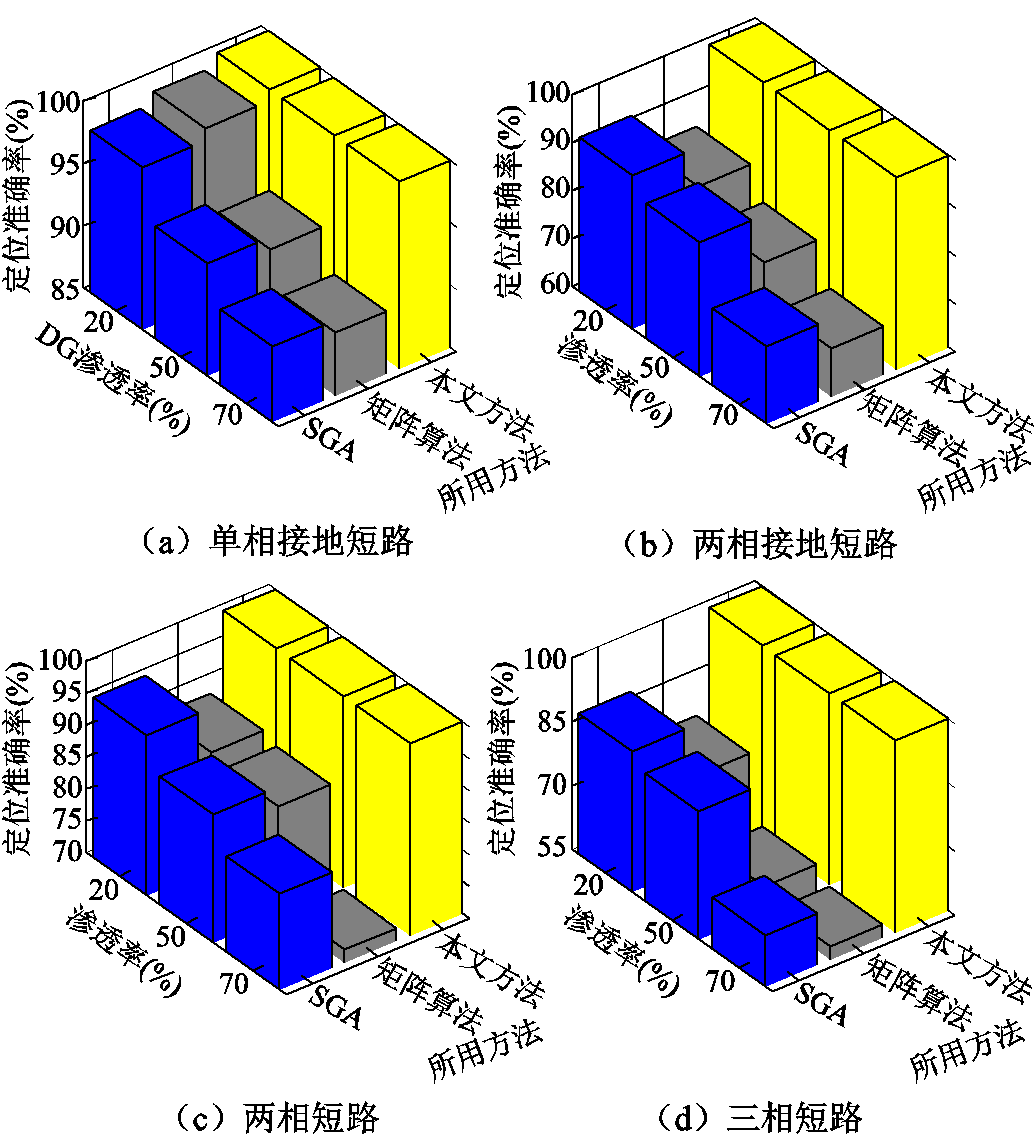
图8 各方法性能对比及分析
Fig.8 Comparison and analysis with classical methods
由图8可以看出，电力系统发生复故障后，当配电网DG渗透率较小（20%）时，三种故障定位方法的准确度相差不大。随着DG渗透率的不断提高，本文所提故障定位方法的准确性依然很高，而基于FTU过电流信息的矩阵算法和基于标准遗传算法的智能优化算法因不适用于含DG的配电网而准确率下降，验证了本文算法适用于DG高渗透率的配电网复故障区段定位，可靠性高。
选取可靠性相对较高的标准遗传算法与本文定位方法就仿真计算时间进行分析。限于篇幅，以系统发生单相接地短路复故障为例，在不同规模节点的配电网中分别使用标准遗传算法和本文采用的故障定位算法进行比较，各运算10次，取平均耗时得到如图9所示的结果。
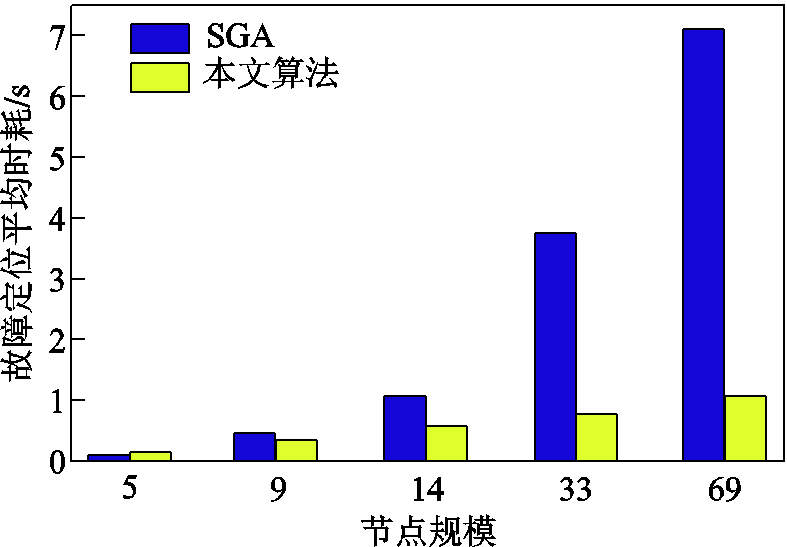
图9 两种方法计算速度对比及分析
Fig.9 Comparison and analysis of calculation speed
由图9可以看出，在节点数量较少时，本文所提算法与遗传算法耗时相近。随着节点规模的不断扩大，在9节点及其更大规模的系统中，耗时与遗传算法相比更少。在中、大型规模的配电网中本文故障定位方法优势更加明显。
利用有源配电网故障定位方法测试平台对所提方法的性能进行测试。该平台适用于实际10kV配电网馈线故障数据、数值模拟，通过设置不同故障位置、故障类型、过渡电阻、DG渗透率，验证了该方法适用于各类中压有源配电网不同场景下的故障定位，测试结果见表7。
表7 测试平台批量验证结果
Tab.7 Test platform batch verification results
参数设置 故障类型单相接地短路、两相接地短路、两相短路、三相短路 过渡电阻0、50、100、150 故障位置10-11、13-14、16-17、21-22、30-31 DG渗透率(%)0～75随机 方法诊断率(%)100
本文提出的考虑复故障的中压有源配电网故障定位方法，基于μPMU优化配置结果对配电网进行区域划分，形成两种类型的监测域。根据搜索算法，可以快速确定可疑监测域，并启动故障定位算法。基于PSCAD/EMTDC和Matlab的仿真结果表明，可以得出以下结论：
1）对于发生复故障等复杂场景，可能会导致监测域内部分节点不可观，本文采用故障前电压代替，绝大多数场景算法可完全适应，并准确定位故障区段。
2）本文可疑监测域搜索算法，可快速确定可疑监测域，并启动故障定位算法，降低了故障定位的运算维度，极大提高了定位的效率，且抗过渡电阻能力在1kΩ以内。
3）本文方法采用不平衡电流分量幅值比较的检测判据，可适用于短路、断线等多类型，两重及以上等复故障，准确判断有源配电网的故障区段，且抗过渡电阻能力在150～500Ω之间。
该方法目前主要针对中压有源配电网在极端、复杂条件下的故障定位，对于MA2(a,b,c,d)监测域内两端区段故障，导致中间节点不可观，从而误判b-c正常区段，后续研究中可利用广域相量信息结合故障指示器等多源信息来进行综合定位。
参考文献
[1]许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019, 34(16): 3416-3429. Xu Yin, He Jinghan, Wang Ying, et al. A review on distribution system restoration for resilience enhancement[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3416-3429.
[2]李振坤, 王法顺, 郭维一, 等. 极端天气下智能配电网的弹性评估[J]. 电力系统自动化, 2020, 44(9): 60-71. Li Zhenkun, Wang Fashun, Guo Weiyi, et al. Resilience assessment of intelligent distribution networks in extreme weather[J]. Automation of Electric Power Systems, 2020, 44(9): 60-71.
[3]张艳霞, 尹佳鑫, 蒙高鹏, 等. 基于错误逻辑区域检测的配电网容错故障定位[J]. 电机与控制学报, 2017, 21(11): 1-8. Zhang Yanxia, Yin Jiaxin, Meng Gaopeng, et al. False-tolerant fault location method for distribution networks based on wrong-logic region detecting[J]. Electrical Machines and Control, 2017, 21(11): 1-8.
[4]王宾, 孙华东, 张道农. 配电网信息共享与同步相量测量应用技术评述[J]. 中国电机工程学报, 2015, 35(增刊1): 1-7. Wang Bin, Sun Huadong, Zhang Daonong. Technical review on sharing and synchronous phasor measurement in distribution network[J]. Proceedings of the CSEE, 2015, 35(S1): 1-7.
[5]谢李为, 李勇, 罗隆福, 等. 基于距离矩阵与分支系数的配电网故障定位方法[J]. 中国电机工程学报, 2020, 40(7): 2180-2191, 2397. Xie Liwei, Li Yong, Luo Longfu, et al. Based on distance matrix and branch coefficient distribution network fault location method[J]. Proceedings of the CSEE, 2020, 40(7): 2180-2191, 2397.
[6]王秋杰, 金涛, 谭洪, 等. 基于分层模型和智能校验算法的配电网故障定位技术[J]. 电工技术学报, 2018, 33(22): 5327-5337. Wang Qiujie, Jin Tao, Tan Hong, et al. The technology on fault location of distribution network based on hierarchical model and intelligent checking algorithm [J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5327-5337.
[7]马静, 许冬, 王桐, 等. 基于故障确信度的广域多重故障识别新算法[J]. 电网技术, 2012, 36(12): 88-93. Ma Jing, Xu Dong, Wang Tong, et al. A new wide-area multiple fault identification algorithm based on fault certainty[J]. Power System Technology, 2012, 36(12): 88-93.
[8]王晨, 童晓阳, 王睿晗. 有限相量测量单元下最小二乘估计的广域后备保护算法[J]. 电力系统自动化, 2015, 39(20): 124-129. Wang Chen, Tong Xiaoyang, Wang Ruihan. Wide-area backup protection algorithm for least squares estimation under finite phasor measurement unit[J]. Automation of Electric Power Systems, 2015, 39(20): 124-129.
[9]王秋杰, 金涛, 申涛, 等. 利用多因素降维的配电网区段定位完全解析模型[J]. 电工技术学报, 2019, 34(14): 3012-3024. Wang Qiujie, Jin Tao, Shen Tao, et al. A complete analytical model for location of distribution network segment with multi-factor dimensionality reduction[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3012-3024.
[10]金涛, 李鸿南, 刘对. 基于BPSOGA的含风电机组的配电线路故障区段定位[J]. 电力自动化设备, 2016, 36(6): 27-33. Jin Tao, Li Hongnan, Liu Dui. Fault location of distribution line with wind turbine based on BPSOGA [J]. Electric Power Automation Equipment, 2016, 36(6): 27-33.
[11]王秋杰, 金涛, 梅李鹏, 等. 基于模型分层的配电网故障诊断方法[J]. 电力自动化设备, 2020, 40(1): 73-79. Wang Qiujie, Jin Tao, Mei Lipeng, et al. Fault diagnosis method of distribution network based on model layer[J]. Electric Power Automation Equipment, 2020, 40(1): 73-79.
[12]吴凡, 赵晋泉, 朱斌, 等. 基于MOPSO的含分布式光伏配电网故障区段定位[J]. 电力系统保护与控制, 2018, 46(6): 46-53. Wu Fan, Zhao Jinquan, Zhu Bin, et al. Fault location of distributed photovoltaic power distribution network based on MOPSO[J]. Power System Protection and Control, 2008, 46 (6): 46-53.
[13]陶维青, 窦开明, 方陈, 等. 配电网相量数据接入方式比较及技术分析[J]. 电网技术, 2019, 43(3): 784-792. Tao Weiqing, Dou Kaiming, Fang Chen, et al. Comparison and technical analysis of phasor data access modes in distribution network[J]. Power System Technology, 2019, 43(3): 784-792.
[14]邱璐, 陈丽华, 臧天磊, 等. 基于可观性量测和梯度投影算法的谐波源定位[J]. 电网技术, 2016, 40(2): 649-655. Qiu Lu, Chen Lihua, Zang Tianlei, et al. Harmonic sources location method based on observability measurement and gradient projection algorithm[J]. Power System Technology, 2016, 40(2): 649-655.
[15]罗深增, 李银红, 游昊, 等. 基于同步相量测量单元的串联补偿线路自适应故障定位算法[J]. 电工技术学报, 2017, 32(5): 143-151. Luo Shenzeng, Li Yinhong, You hao, et al. An adaptive fault location algorithm based on PMU measurement for series compensated transmission lines[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 143-151.
[16]Jiang Quanyuan, Li Xingpeng, Wang Bo, et al. PMU-based fault location using voltage measurements in large transmission networks[J]. IEEE Transactions on Power Delivery, 2012, 27(3): 1644-1652.
[17]赵波, 王财胜, 周金辉, 等. 主动配电网现状与未来发展[J]. 电力系统自动化, 2014, 38(18): 125-135. Zhao Bo, Wang Caisheng, Zhou Jinhui, et al. Present and future development trend of active distribution network[J]. Automation of Electric Power Systems, 2014, 38(18): 125-135.
[18]徐丙垠, 薛永端, 冯光, 等. 配电网接地故障保护若干问题的探讨[J]. 电力系统自动化, 2019, 43(20): 1-7. Xu Bingyin, Xue Yongduan, Feng Guang, et al. Discussion on several problems of earthing fault protection in distribution network[J]. Automation of Electric Power Systems, 2019, 43(20): 1-7.
[19]刘鹏程, 李新利. 基于多种群遗传算法的含分布式电源的配电网故障区段定位算法[J]. 电力系统保护与控制, 2016, 44(2): 36-41. Liu Pengcheng, Li Xinli. Fault section location ofdistribution network containing distributed generation based on the multiple-population genetic algorithm[J]. Power System Protection and Control, 2016, 44(2): 36-41.
[20]黄佳乐, 杨冠鲁. 配电网故障区间定位的改进矩阵算法[J]. 电力系统保护与控制, 2014, 42(11): 41-45. Huang Jiale, Yang Guanlu. Modified matrix algorithm for fault location of distribution network[J]. Power System Protection and Control, 2014, 42(11): 41-45.
Fault Location Method for Active Distribution Networks Considering Combination Faults
Abstract Reliable fault location is an important means to improve the power supply reliability of distribution networks after extreme disturbance. In extreme disturbance, the probability of combination fault in distribution networks increases, mainly reflected in the features of high fault multiplicity, multiple fault types and high resistance grounding. In this paper, a fault location method for active distribution networks considering combination faults is proposed. Through the area division based on optimal μPMU configuration, each monitoring area is formed. The suspicious monitoring area is determined by the search algorithm criterion, and the fault location algorithm is started. The fault section detection criterion comparing the amplitude of the unbalanced current component is used to locate the fault. Through PSCAD/EMTDC and Matlab, it is verified that this method is not affected by fault location and fault type, and is suitable for complex scenarios such as combination and multi-type faults. Moreover, it has high resistance against transition resistance.
keywords：Combination faults, suspicious monitoring area, unbalanced current component, fault location, wide area phasor information
中图分类号：TM77
DOI:10.19595/j.cnki.1000-6753.tces.200487
国家电网有限公司总部科技项目资助（基于综合能源系统的智能配电网弹性技术与应用基础研究52060019001H）。
收稿日期 2020-05-14
改稿日期 2020-09-15
张健磊 男，1996年生，硕士研究生，研究方向为电力系统继电保护、故障定位。E-mail：zhangjianlei@mail.sdu.edu.cn
高湛军 男，1974年生，副教授，硕士生导师，研究方向为电力系统继电保护、故障诊断。E-mail：jacob-gao@sdu.edu.cn（通信作者）
（编辑 赫蕾）