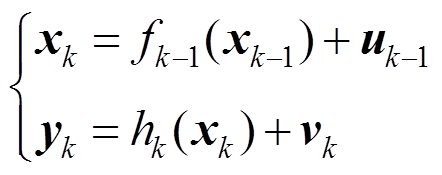 (1)
(1)摘要 配电网中各类噪声对相量测量产生较大影响,研究在高噪声环境下能够可靠检测并能快速跟踪电力信号突变的同步相量测量算法,对保证电网的稳定性与可靠性具有重要意义。提出基于量测量误差协方差次优估计的自适应强跟踪无迹卡尔曼滤波(SEMEC-ASTUKF)的同步相量测量算法。首先根据递归最小二乘法提出一种自适应常值噪声统计估计器提高量测噪声协方差估计精度;然后根据电力信号突变后特征,构建突变检测算法和渐消因子次优估计算法,改善强跟踪无迹卡尔曼滤波(STUKF)算法在高噪声环境下对突变检测能力弱和跟踪突变慢的缺陷。利用实测信号对算法性能进行验证,结果表明,SEMEC-ASTUKF算法具有更高的测量精度,对突变具有更好的检测灵敏度和更高的跟踪速度。
关键词:高噪声 强跟踪无迹卡尔曼滤波 常值噪声统计估计器 渐消因子
同步相量测量单元(Phasor Measurement Unit, PMU)作为实现广域测量系统(Wide Area Measurement System, WAMS)的基础和核心[1-2],其测量算法至关重要。受非线性负荷及设备[3]、部分负荷[4]、采样过程[5-6]及大量分布式电源和电动汽车[7]投入的影响,配电网电力信号中存在大量的谐波、间谐波及随机噪声,同时大负荷投切等因素往往导致配电网部分节点相量发生突变[8]。配电网信号的高噪声及强瞬变的特性对同步相量测量算法产生了很大影响,研究能够在高噪声条件下具有高测量精度并能快速跟踪突变的同步相量测量算法对保证电力系统的可靠性与稳定性具有重要意义。
目前国内外的同步相量测量算法大致可分为频域类算法和估计类算法两类。频域类算法是指以离散傅里叶变换算法及其改进算法为基础的同步相量测量算法[9-11],这类算法可有效屏蔽谐波对相量测量的影响,但对含有较多间谐波及噪声的信号作用有限,为了保证测量精度需增大时间窗长,无法同时兼顾测量精度和实时性。为此,国内外部分学者提出了估计类算法,这类算法有非线性回归法[12]、粒子滤波法[13]及卡尔曼滤波法[14-16]等,卡尔曼滤波算法因其高实时性和高测量精度被广泛关注。近年来,基于强跟踪卡尔曼[17]、无迹卡尔曼滤波[18-19]算法的同步相量测量算法被相继提出。为进一步提高无迹卡尔曼滤波算法跟踪突变的能力,文献[20]提出了一种自适应采样强跟踪比例无迹卡尔曼滤波(Adaptive Sampling Strong Tracking Scaled Unscented Kalman Filter, ASST-SUKF)算法,该方法提出了一种集中引入渐消因子的方法,增强算法实时性的同时提高了算法对突变的跟踪速度。强跟踪无迹卡尔曼滤波(Strong Tracking Unscented Kalman Filter, STUKF)算法[21]采用嵌入弱化因子的方法对残差序列协方差的估计误差进行屏蔽,但同时也弱化了算法检测和跟踪突变的能力。为增强算法检测和跟踪突变的能力,需要一种新的方法估计渐消因子。
针对上述问题,本文提出一种量测量误差协方差次优估计的自适应强跟踪无迹卡尔曼滤波(Adaptive Strong Tracking Unscented Kalman Filter based on Suboptimal Estimate of Measurement Error Covariance, SEMEC-ASTUKF)算法。首先提出一种自适应常值噪声统计估计器,精确估计量测噪声协方差,在此基础上提出了一种系统状态判定算法及渐消因子次优估计算法对渐消因子进行估计,在保证算法的测量精度前提下,提高算法跟踪突变的能力。最后利用实测数据验证了所提算法的有效性。
考虑非线性高斯系统
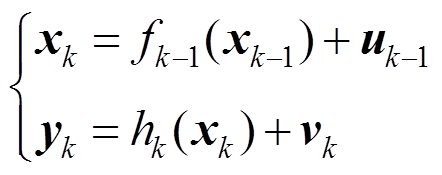 (1)
(1)式中,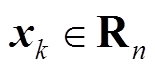 和
和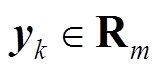 分别为k时刻下n维状态变量与m维量测量;
分别为k时刻下n维状态变量与m维量测量; 和
和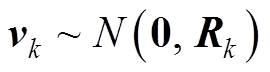 分别为系统过程噪声和量测噪声,
分别为系统过程噪声和量测噪声,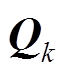 与
与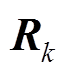 分别为
分别为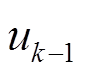 与
与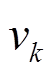 的协方差阵;
的协方差阵;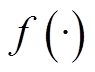 为非线性状态转移函数;
为非线性状态转移函数;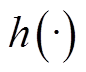 为非线性量测函数。
为非线性量测函数。
假设k-1时刻状态变量服从期望为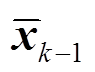 、协方差阵为
、协方差阵为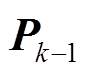 的正态分布:
的正态分布: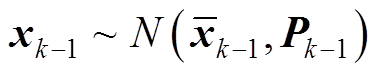 ,按照对称采样策略选取2n+1个Sigma点为
,按照对称采样策略选取2n+1个Sigma点为
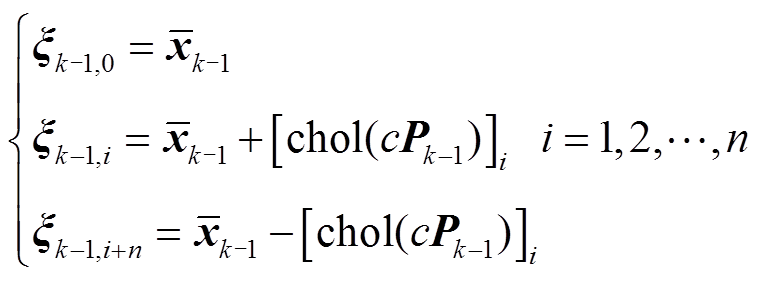 (2)
(2)式中,c=n+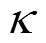 ,
, 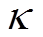 为一个比例系数;三阶系统中一般取0;
为一个比例系数;三阶系统中一般取0;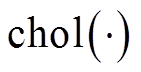 为矩阵的Choleshy分解;
为矩阵的Choleshy分解;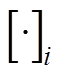 代表括号内矩阵的第i列。
代表括号内矩阵的第i列。
对应于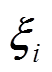 (i=0,1,
(i=0,1, ,2n)的权值为
,2n)的权值为
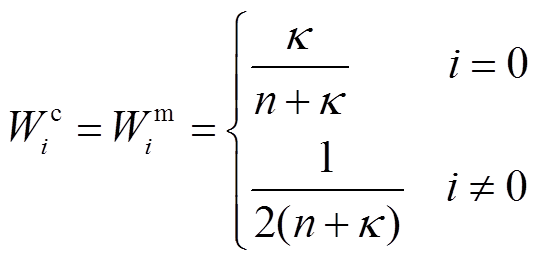 (3)
(3)式中,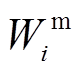 为一阶统计特性权系数;
为一阶统计特性权系数;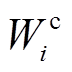 为二阶统计特性权系数。
为二阶统计特性权系数。
计算未引入渐消因子时的状态预测协方差阵、自协方差阵和互协方差阵为
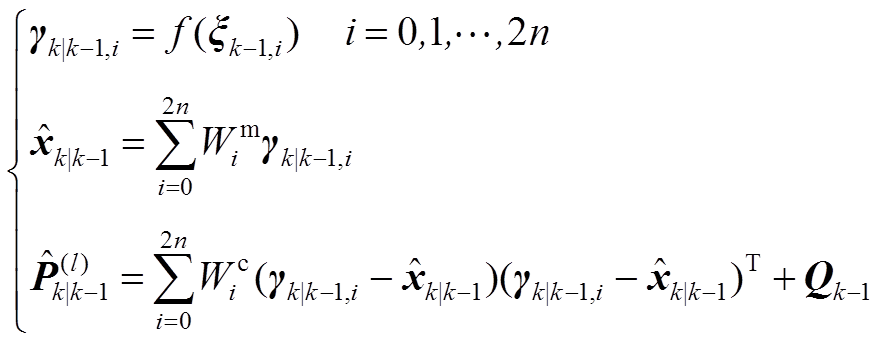 (4)
(4)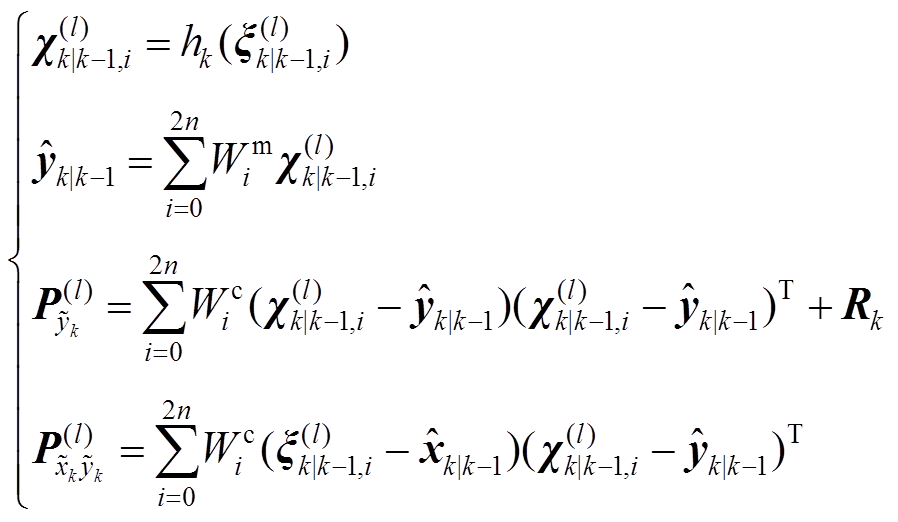 (5)
(5)式中,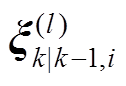 为由
为由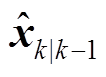 和
和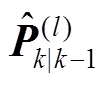 所构造的Sigma采样点。
所构造的Sigma采样点。
根据得到的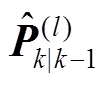 、
、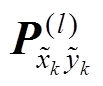 与
与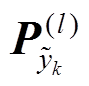 ,计算渐消因子为
,计算渐消因子为
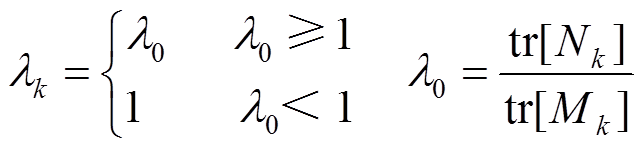 (6)
(6)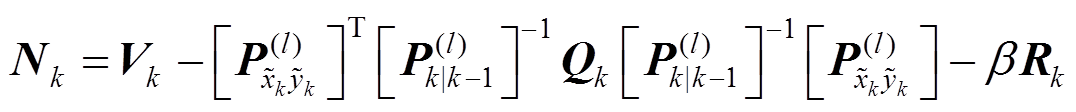 (7)
(7)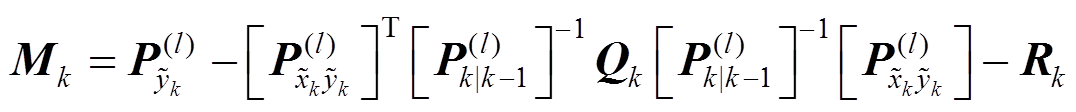 (8)
(8)式中,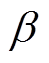 为弱化因子,
为弱化因子,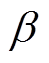 ≥1;tr[·]为矩阵的迹。
≥1;tr[·]为矩阵的迹。
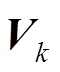 为残差序列的协方差阵,其估算式为
为残差序列的协方差阵,其估算式为
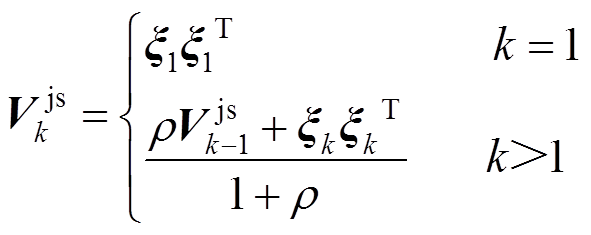 (9)
(9)式中,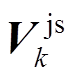 为
为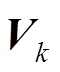 的估计值;
的估计值;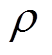 为遗忘因子,0<
为遗忘因子,0<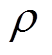 ≤1,本文取
≤1,本文取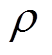 =0.95;
=0.95;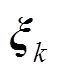 为k时刻的残差序列。
为k时刻的残差序列。
在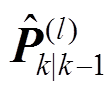 中引入渐消因子,重新计算
中引入渐消因子,重新计算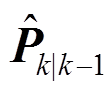 为
为
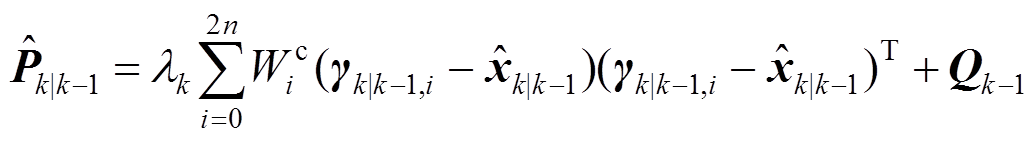 (10)
(10)按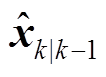 和
和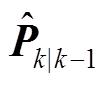 重新采样后,计算量测量均值、自协方差阵和互协方差阵为
重新采样后,计算量测量均值、自协方差阵和互协方差阵为
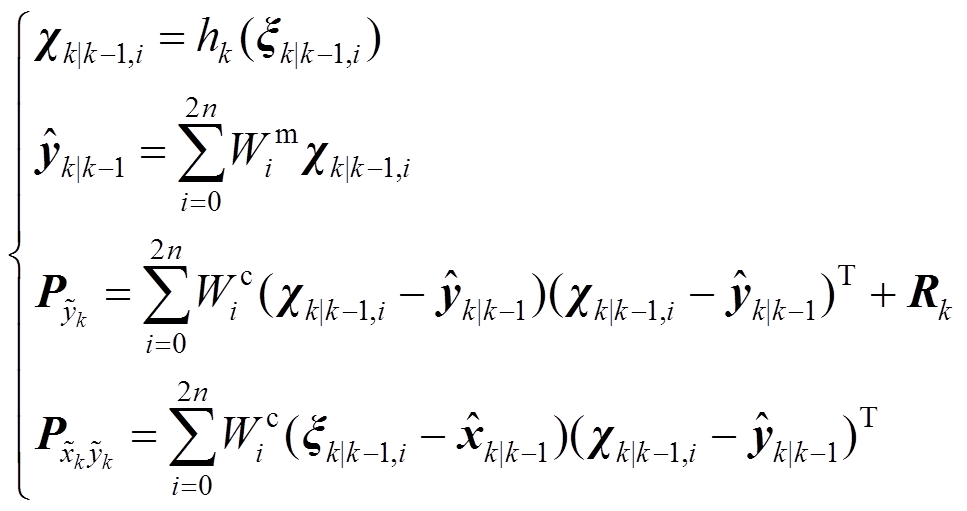 (11)
(11)获得新的量测值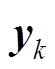 后,进行滤波更新为
后,进行滤波更新为
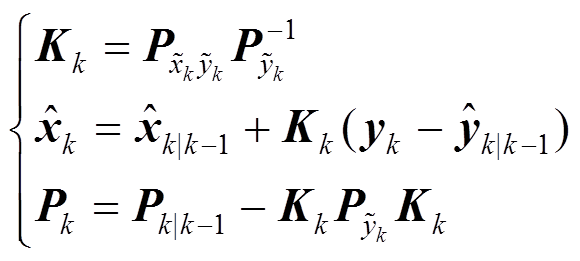 (12)
(12)电力信号在k时刻采样值可表示为
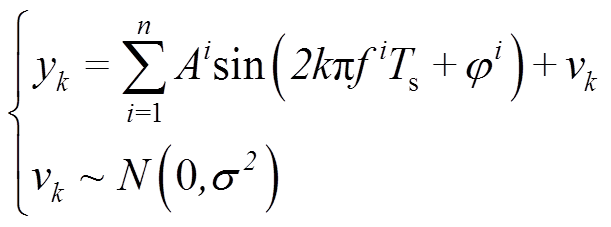 (13)
(13)式中,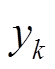 为信号的瞬时采样值;
为信号的瞬时采样值;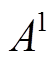 、
、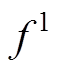 、
、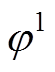 分别为基波信号的幅值、频率和初相角;
分别为基波信号的幅值、频率和初相角;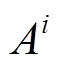 、
、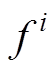 、
、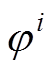 (i≠1)分别为第i种谐波或间谐波的幅值、频率和初相角;k为采样次数;Ts为采样间隔;
(i≠1)分别为第i种谐波或间谐波的幅值、频率和初相角;k为采样次数;Ts为采样间隔;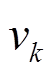 为与信号相互独立的高斯白噪声,其均值为0、方差为σ2。
为与信号相互独立的高斯白噪声,其均值为0、方差为σ2。
采样时刻较长时,谐波、间谐波与基波相关性很弱,故可将其纳入噪声中滤除,于是本文只将基波相量参数纳入状态变量,定义电力信号的状态变量为
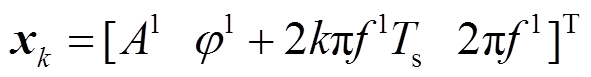 (14)
(14)易知,系统的状态转移方程为
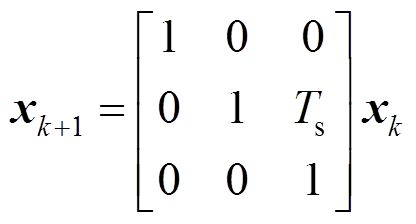 (15)
(15)系统的观测方程为
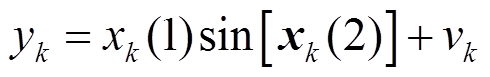 (16)
(16)由式(14)可知,迭代k次时的基波参量可按式(17)~式(19)计算,则有
幅值为
 (17)
(17)频率为
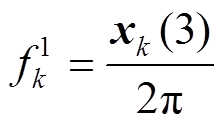 (18)
(18)初相角为
 (19)
(19)由式(6)~式(8)可知,渐消因子计算准确的前提是量测噪声协方差阵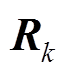 准确,
准确,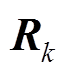 实际未知,需在线估算。
实际未知,需在线估算。
为估计量测噪声协方差阵和方便说明,定义如下变量。
量测量误差协方差为
 (20)
(20)第k个采样点时量测量均方差为
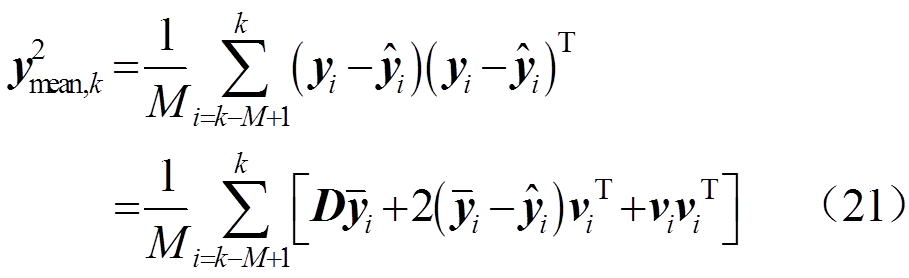
辅助说明变量为
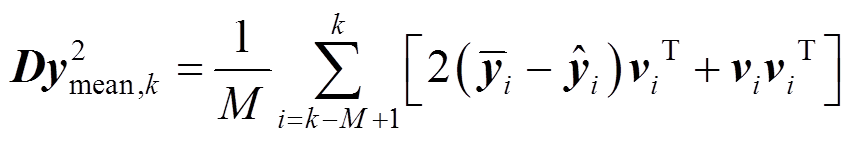 (22)
(22)式中,M为计算均方差值的时间窗长;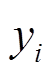 、
、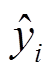 、
、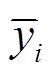 分别为第i个采样点量测量的采样值、估计值及期望值。
分别为第i个采样点量测量的采样值、估计值及期望值。
计算易知,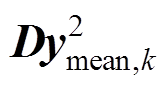 为期望为R、协方差近似为2(RTR)/M的随机变量,根据递推最小二乘法原理,可构建估计量测噪声协方差阵R的修正方程为
为期望为R、协方差近似为2(RTR)/M的随机变量,根据递推最小二乘法原理,可构建估计量测噪声协方差阵R的修正方程为
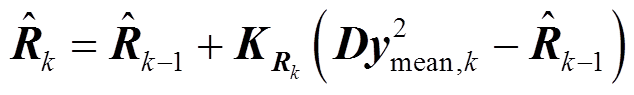 (23)
(23)式中,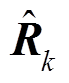 为第k个采样点时R的估计值;
为第k个采样点时R的估计值;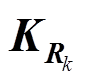 为第k个采样点时的修正增益矩阵。
为第k个采样点时的修正增益矩阵。
对比式(21)和式(22),易知
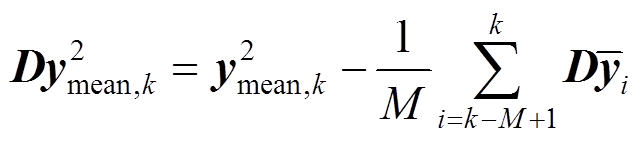 (24)
(24)又
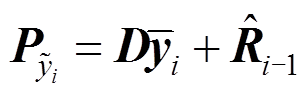 (25)
(25)式中,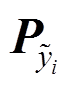 为第i个采样点的量测量自协方差阵估计值。
为第i个采样点的量测量自协方差阵估计值。
得到
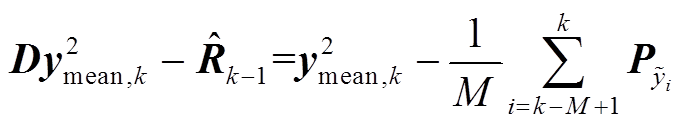 (26)
(26)改变修正方程式(23)为
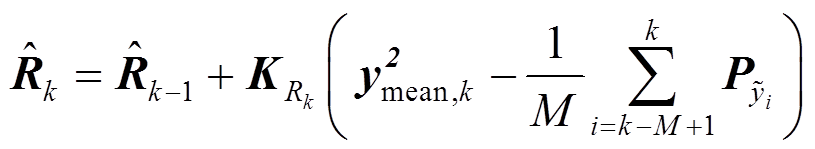 (27)
(27)根据递推最小二乘法原理,量测噪声协方差阵增益矩阵及状态变量误差协方差矩阵更新式为
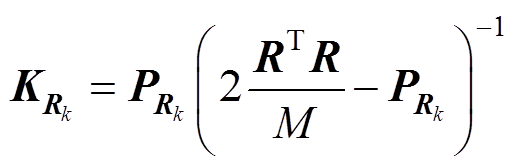 (28)
(28)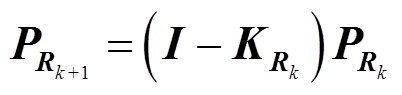 (29)
(29)式中,I为单位矩阵。
2.2.1 基于量测量误差协方差的渐消因子次优估计
由于系统惯性,一般短时内大系统中频率变化非常小,即突变前后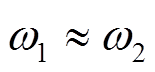 ,忽略突变前估计误差,突变后量测量误差协方差的真实值可近似认为是突变前后差值相量模值的二次方,即
,忽略突变前估计误差,突变后量测量误差协方差的真实值可近似认为是突变前后差值相量模值的二次方,即
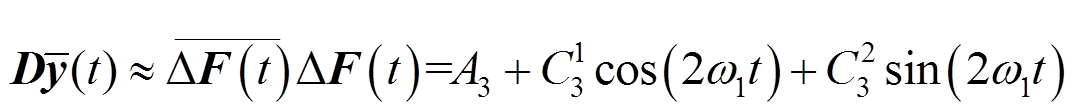 (30)
(30)其中
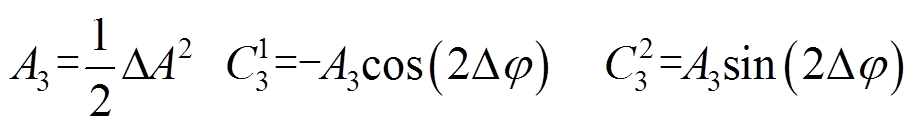 (31)
(31)式中,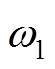 为突变前的角速度估计值;
为突变前的角速度估计值;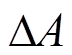 为突变前后差值相量的幅值;
为突变前后差值相量的幅值;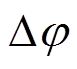 为突变前后差值相量的初相位。
为突变前后差值相量的初相位。
任意时刻的残差序列均满足关系为
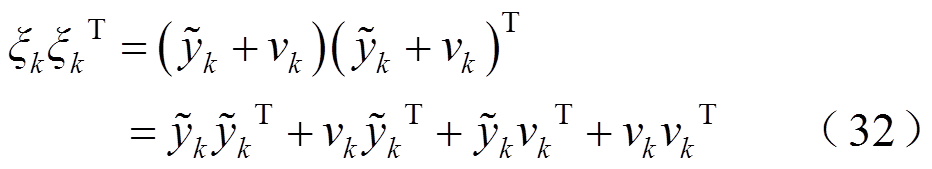
其中
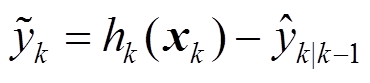 (33)
(33)则第i个采样点的残差与其转置的乘积实质上是期望为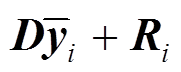 的随机变量,为
的随机变量,为
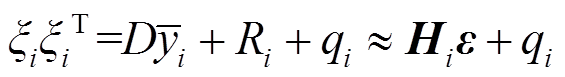 (34)
(34)其中
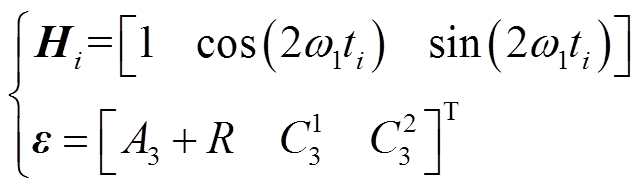 (35)
(35)式中,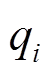 为期望为0的随机变量。
为期望为0的随机变量。
截取突变后时间窗长N,可根据最小二乘法对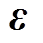 进行估计,得到为
进行估计,得到为
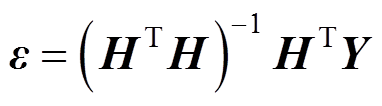 (36)
(36)其中
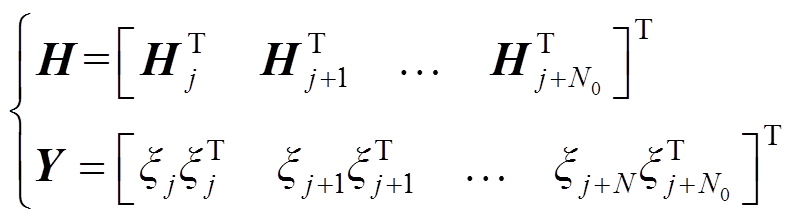 (37)
(37)式中,j为检测到突变的时刻;Y为检测到突变时间窗长N0内的残差与其转置乘积的序列。
得到突变后任意k时刻的量测量误差协方差的次优估计值为
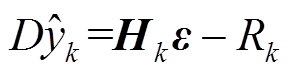 (38)
(38)根据式(38)及式(6)~式(8)可得到渐消因子为
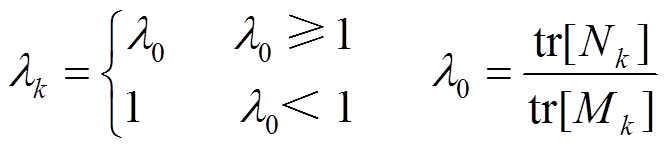 (39)
(39)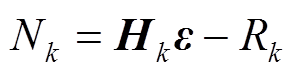 (40)
(40)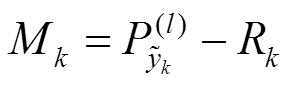 (41)
(41)其中
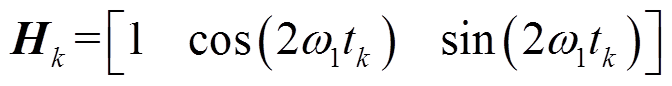 (42)
(42)2.2.2 系统状态判定算法
为便于说明,本文将算法收敛后状态变量未发生变化时的状态称为稳定状态,将状态变量突变后算法收敛前的状态称为突变状态。
当算法收敛后,量测量真实值与估计值之间差值很小可忽略,根据式(32)可知,收敛后在稳定状态时为
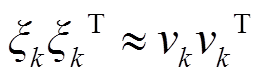 (43)
(43)为判定系统状态构建判定变量为
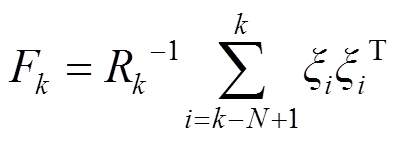 (44)
(44)式中,N为时间窗长度。
由式(43)可知,收敛后稳定状态时为
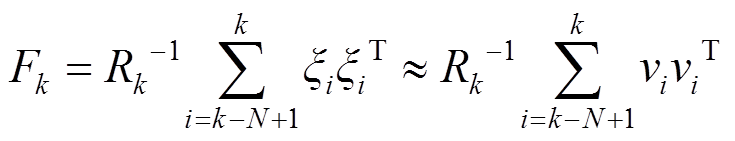 (45)
(45)稳定时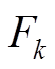 近似服从自由度为N的卡方分布,有
近似服从自由度为N的卡方分布,有
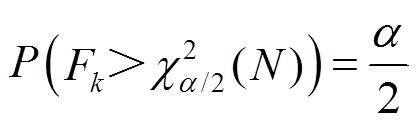 (46)
(46)式中,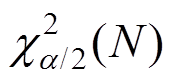 为卡方分布的上分位点。
为卡方分布的上分位点。
当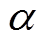 很小时,可认为
很小时,可认为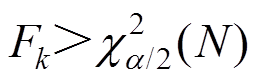 是小概率事件,几乎不可能发生。突变状态时为
是小概率事件,几乎不可能发生。突变状态时为
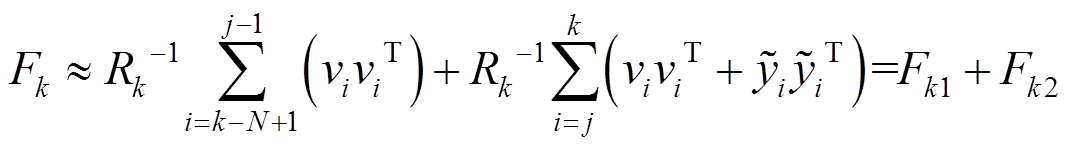 (47)
(47)其中
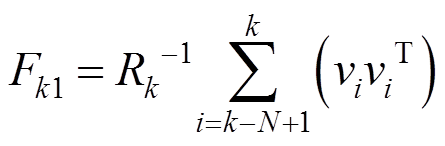 (48)
(48) (49)
(49)式中,j为状态变量突变时刻。
此时,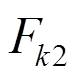 值较大,
值较大,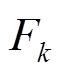 大概率大于
大概率大于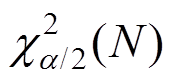 ,根据此差异即可区分系统状态。
,根据此差异即可区分系统状态。
2.2.3 基于SEMEC-ASTUKF的同步相量测量算法流程
基于以上理论,本文构建基于SEMEC-ASTUKF的同步相量测量算法如下:
(1)设定状态变量初始值、状态变量初始误差协方差矩阵及量测噪声协方差阵,选取时间窗长及适当的卡方分布上分位点,设置系统判定状态为稳定状态。
(2)按式(3)计算权值。
(3)按式(2)选取Sigma点,按式(4)、式(5)进行未引入渐消因子时的状态预测和量测更新。
(4)按式(21)计算量测量均方差,按式(28)计算增益矩阵后,按式(27)和式(29)更新量测噪声协方差的估计值及其误差协方差阵。
(5)构建时间窗,根据式(44)计算判定变量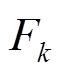 。
。
(6)系统状态为稳定状态时,判断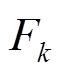 小于上分位点是否成立,若成立,保持系统判定状态不变,直接按式(12)进行滤波更新,反之则判定为突变状态。
小于上分位点是否成立,若成立,保持系统判定状态不变,直接按式(12)进行滤波更新,反之则判定为突变状态。
(7)系统状态为突变状态时,从检测到突变的时刻开始,等待N0个采样点不进行滤波更新,而后按式(36)计算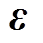 ,按式(39)计算渐消因子,按式(10)、重新进行引入渐消因子后的状态预测和量测更新,并恢复滤波更新,算法重新收敛后转换系统状态为稳定状态。
,按式(39)计算渐消因子,按式(10)、重新进行引入渐消因子后的状态预测和量测更新,并恢复滤波更新,算法重新收敛后转换系统状态为稳定状态。
(8)完成滤波更新后,按式(17)~式(19)计算相量参数,随着不断获得新的采样点,重复式(3)~式(8)。
算法流程如图1所示。
使用河北省电力科学研究院的福禄克三相电能功率标准源6130A产生突变的实验信号,并利用横河高精度示波器DL850E采样获取实际的信号数据,实验设备如图2所示。
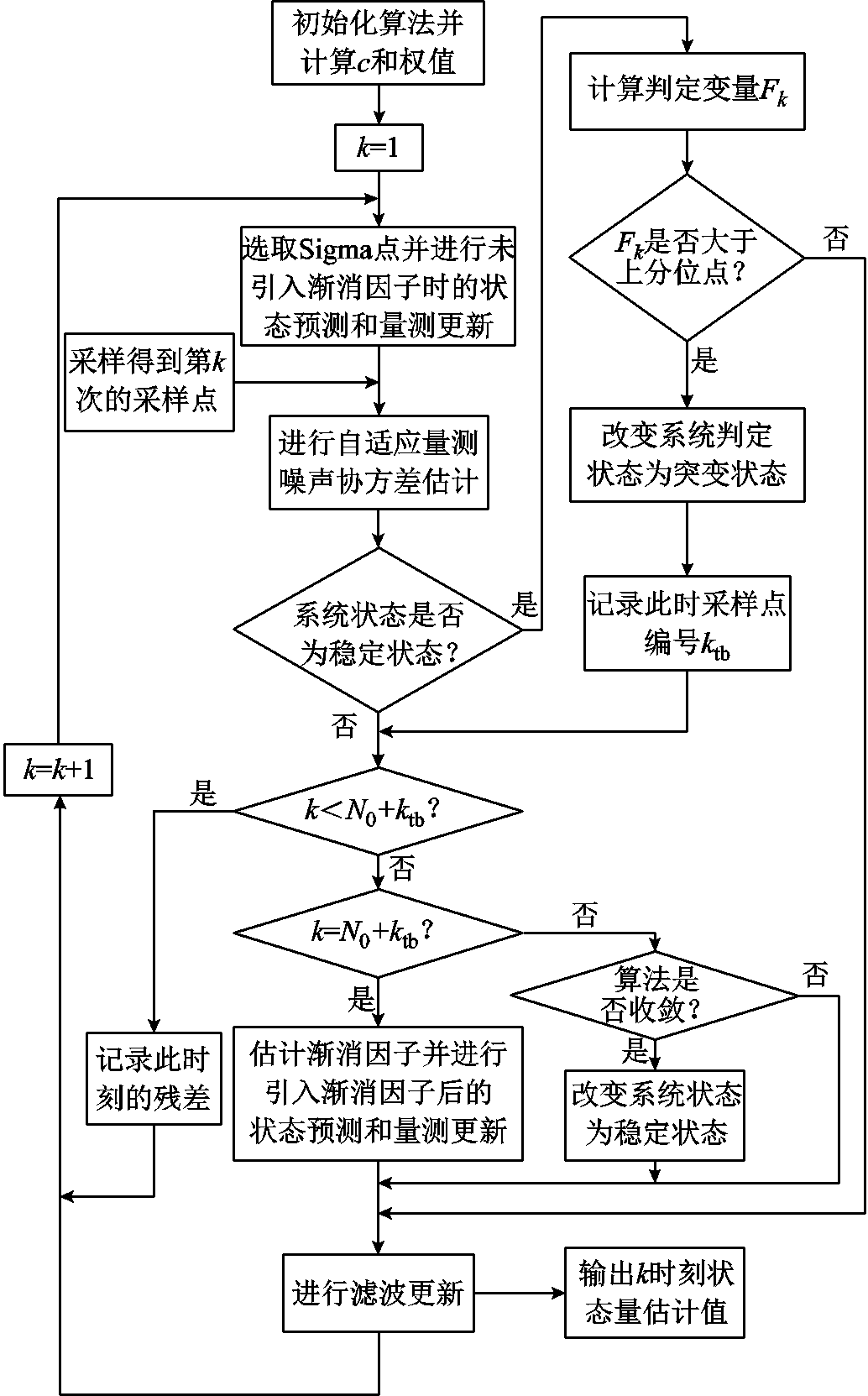
图1 SEMEC-ASTUKF同步相量测量算法流程
Fig.1 Process of synchronous phasor measurement algorithm based on SEMEC-ASTUKF

图2 三相电能功率标准源实物图
Fig.2 Standard source for three-phase electric energy
采用戴尔便携式计算机(windows10系统、CPU型号为i5-8550U)作为实验平台,对算法性能进行验证。实测采样得到三组信号,信号通式为
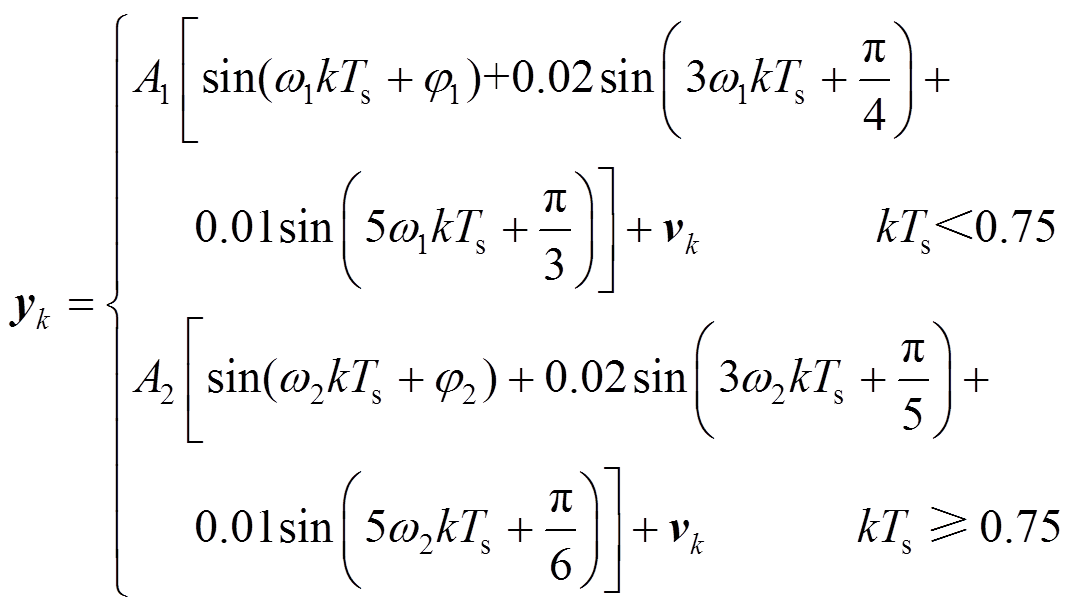 (50)
(50)式中,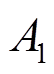 、
、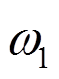 、
、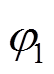 和
和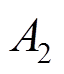 、
、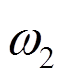 、
、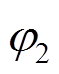 分别突变前后相量的幅值、角速度及初相位,
分别突变前后相量的幅值、角速度及初相位,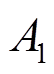 、
、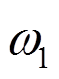 、
、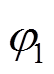 分别为1.042、100.6π和π/4;采样时间间隔Ts为1/9600s,总采样时间为4s;
分别为1.042、100.6π和π/4;采样时间间隔Ts为1/9600s,总采样时间为4s;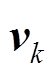 为高斯白噪声,SNR为30dB。
为高斯白噪声,SNR为30dB。
为表现算法在不同突变条件下的性能,本文设置了三组突变实验,实验相量参数见表1。
表1 各组突变实验相量参数
Tab.1 Phasor parameters of mutation experiment

实验编号 10.942100.6ππ/4 21.042100.6ππ/5 31.142100.602π3π/10
为体现算法性能,本文选取了文献[9]的基于扩展卡尔曼滤波的AMDFT算法和文献[20]的ASST-SUKF算法参与对比,算法参数设置如下:AMDFT算法选取时间窗长为192个采样点;SEMEC-ASTUKF算法选取时间窗长度N为960个采样点,上分位点选为1 200,时间窗长N0设置为192个采样点;ASST-SUKF算法弱化因子设置为20。
为描述量测噪声误差协方差估计精度,定义噪声估计相对误差为
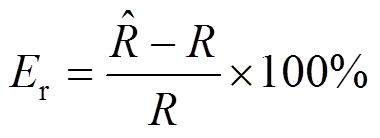 (51)
(51)式中, 和
和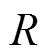 分别为量测噪声协方差的估计值与实际值。
分别为量测噪声协方差的估计值与实际值。
为验证本文所提自适应噪声统计估计器性能,选取文献[21]所提常值噪声统计估计器参与对比,得到各采样时刻噪声估计相对误差如图3所示。
由图3可看出标准常值噪声统计估计器在初始阶段估计出负值,实际中常造成算法发散。本文所提自适应常值噪声统计估计器稳定收敛且快于标准常值噪声统计估计器,收敛后其相对误差稳定在5%以内,估计精度高于标准常值噪声统计估计器。
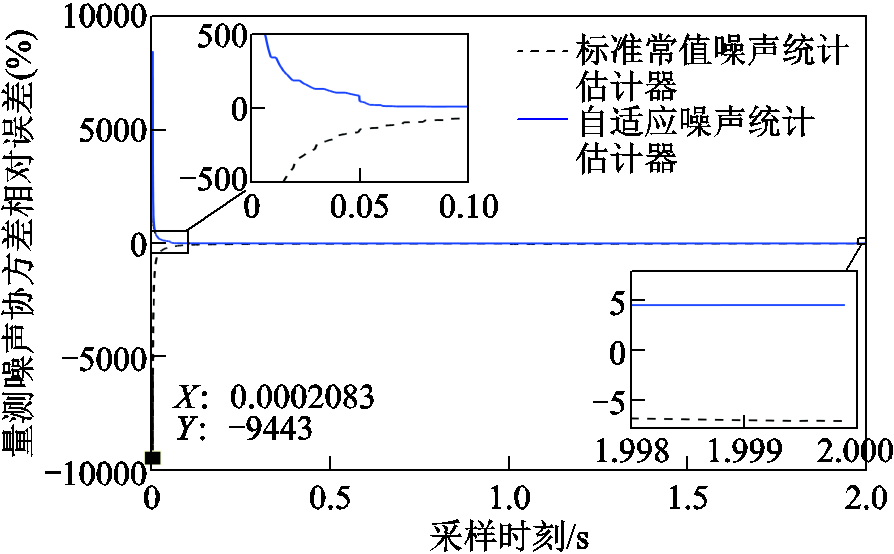
图3 量测噪声协方差估计相对误差对比图
Fig.3 Comparison of estimated relative errors of measurement noise covariance
本小节对比三种算法的实时性,测量表1实验3信号,得到收敛后算法计算用时对比见表2。
表2 算法计算用时对比
Tab.2 Comparison of the time algorithm use to calculates

算法平均用时/s最大用时/s AMDFT20.7×10-558.9×10-5 ASST-SUKF8.21×10-5222×10-5 SEMEC-ASTUKF9.30×10-5140×10-5
由表2可知,AMDFT所需计算时间最长,约为其他两种算法的两倍。由于添加了均方差计算,SEMEC-ASTUKF算法比ASST-SUKF算法计算时间长,但未突变时计算时间增幅不大,约增长了13.3%,且实时性明显优于AMDFT算法。
实验记录ASST-SUKF和SEMEC-ASTUKF算法检测各实验突变结果对比见表3。
表3 突变检测性能对比
Tab.3 Comparison of mutation detection performance
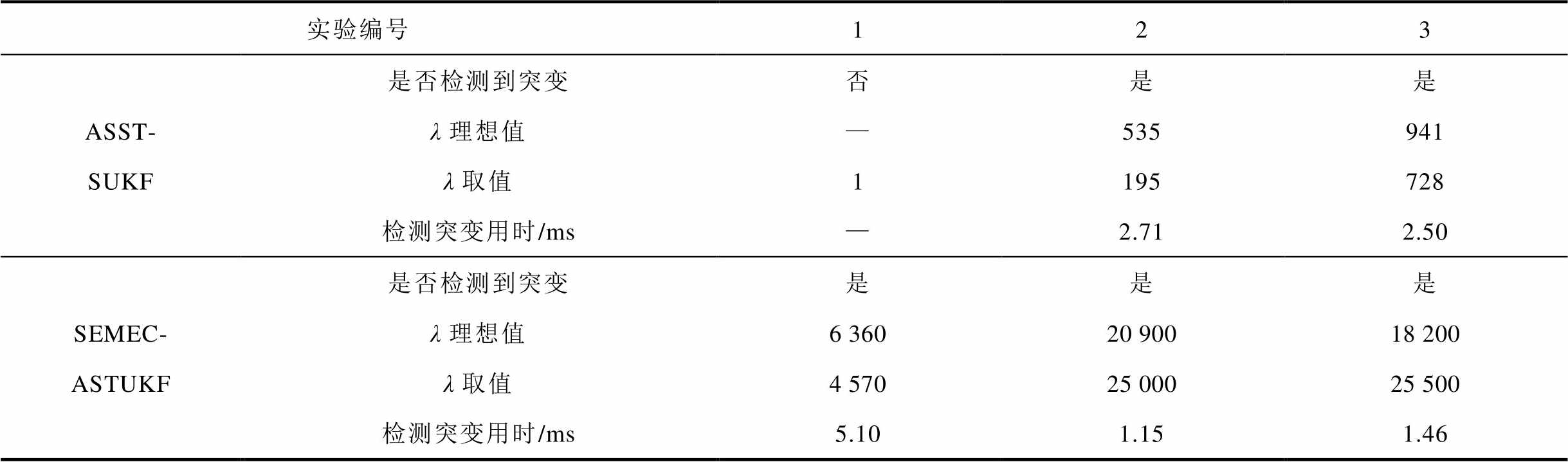
实验编号123 ASST-SUKF是否检测到突变否是是 λ理想值—535941 λ取值1195728 检测突变用时/ms—2.712.50 SEMEC-ASTUKF是否检测到突变是是是 λ理想值6 36020 90018 200 λ取值4 57025 00025 500 检测突变用时/ms5.101.151.46
由表3可知,由于ASST-SUKF算法的弱化因子掩盖了一定的突变信息,该算法在实验1未检测到突变,且实验2和3检测突变所需时间较长。改进后的SEMEC-ASTUKF能够较准确地估计量测量误差协方差,三组实验均能可靠地检测到突变,且λ取值更接近其理想值,由于保留了较多的突变信息,其检测到突变所需时间更短。
同步相量测量算法测量精度要求[22]见表4。
表4 基波相量准确度要求
Tab.4 Fundamental phasor accuracy’s requirements

幅值测量误差极限频率测量误差极限相角测量误差极限 0.2%0.002Hz0.2°
为评价算法的测量精度,设置如下评价标准。
第i种相量参数的均方根误差(RMSE)为
 (52)
(52)第k个采样点第i种相量参数的绝对误差为
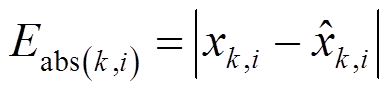 (53)
(53)第i种相量参数的最大绝对误差为
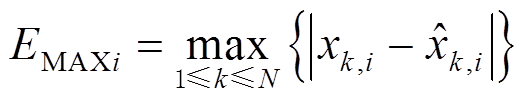 (54)
(54)式中,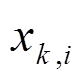 和
和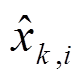 分别为第k个采样点对应时刻相量第i种参数的真实值及估计值;N为计算均方根误差的采样点总个数。
分别为第k个采样点对应时刻相量第i种参数的真实值及估计值;N为计算均方根误差的采样点总个数。
利用表1三组实验对各算法测试,得到信号3.9~4s的相量测量精度对比结果见表5~表7。
表5 实验1估计精度对比
Tab.5 Comparison of estimation accuracy in experiment 1
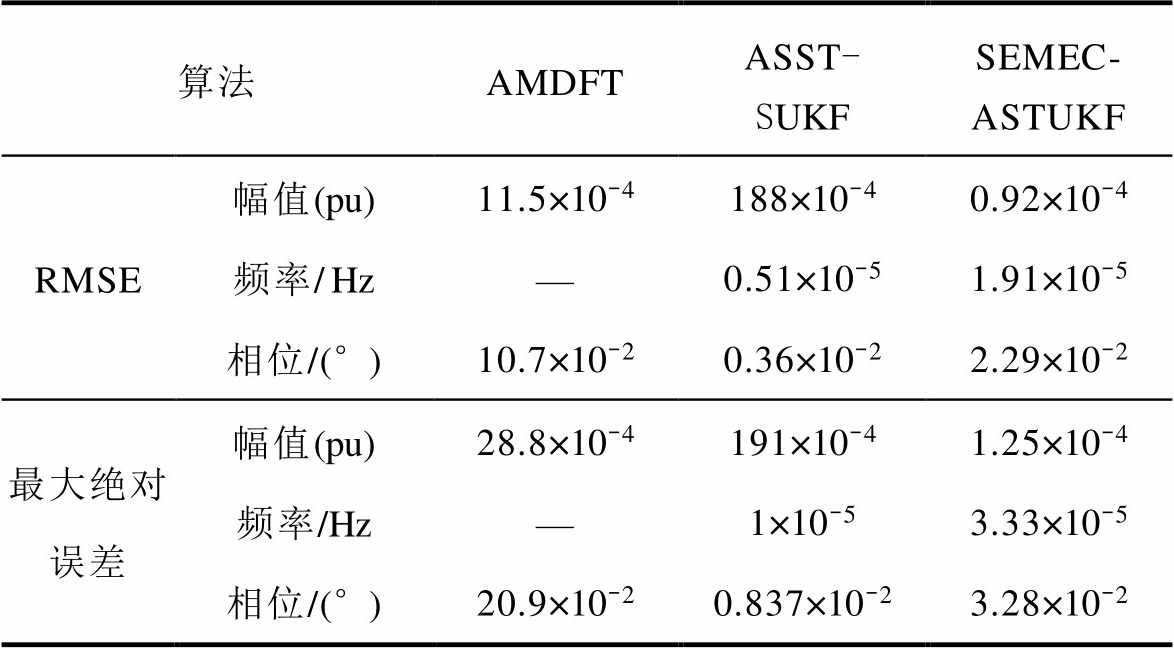
算法AMDFTASST-SUKFSEMEC-ASTUKF RMSE幅值(pu)11.5×10-4188×10-40.92×10-4 频率/Hz—0.51×10-51.91×10-5 相位/(°)10.7×10-20.36×10-22.29×10-2 最大绝对误差幅值(pu)28.8×10-4191×10-41.25×10-4 频率/Hz—1×10-53.33×10-5 相位/(°)20.9×10-20.837×10-23.28×10-2
表6 实验2估计精度对比
Tab.6 Comparison of estimation accuracy in experiment 2

算法AMDFTASST-SUKFSEMEC-ASTUKF RMSE幅值(pu)26.7×10-41.03×10-40.873×10-4 频率/Hz—7.75×10-51.43×10-5 相位/(°)9.99×10-28.74×10-20.53×10-2 最大绝对误差幅值(pu)49.8×10-41.41×10-41.28×10-4 频率/Hz—9×10-52.46×10-5 相位/(°)17.4×10-29.57×10-21.09×10-2
表7 实验3估计精度对比
Tab.7 Comparison of estimation accuracy in experiment 3
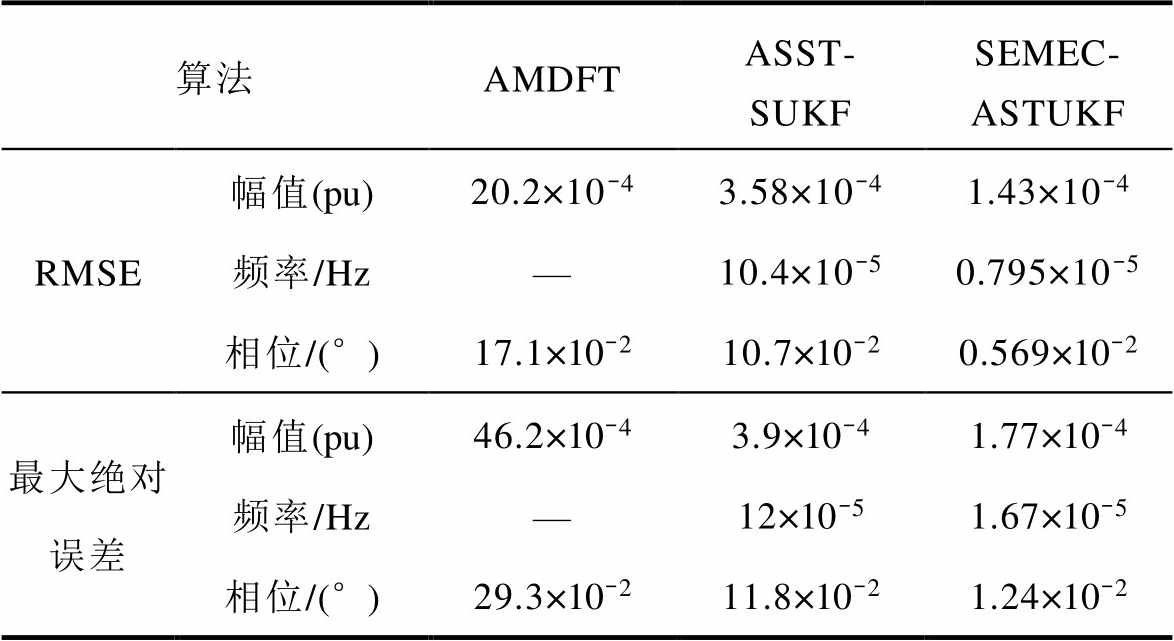
算法AMDFTASST-SUKFSEMEC-ASTUKF RMSE幅值(pu)20.2×10-43.58×10-41.43×10-4 频率/Hz—10.4×10-50.795×10-5 相位/(°)17.1×10-210.7×10-20.569×10-2 最大绝对误差幅值(pu)46.2×10-43.9×10-41.77×10-4 频率/Hz—12×10-51.67×10-5 相位/(°)29.3×10-211.8×10-21.24×10-2
由表5~表7可知,实验1中,由于ASST-SUKF算法未检测到突变,幅值长时间测量不准,无法满足精度要求。实验1~实验3中,由于SEMEC-ASTUKF算法均可靠地检测到了突变,且渐消因子取值接近理想值,收敛后其测量误差很小且高于AMDFT算法和ASST-SUKF算法。
实验3中相量参数估计绝对误差如图4~图6。由图4~图6可知,由于SEMEC-ASTUKF算法返回了较为理想的渐消因子,虽然等待了一周波未对突变进行跟踪,但跟踪突变速度仍高于AMDFT算法和ASST-SUKF算法,能够以更快的速度达到规范的精度要求。SEMEC-ASTUKF算法收敛后测量精度高于AMDFT算法和ASST-SUKF算法,AMDFT算法存在受噪声影响部分点的测量误差不能满足规范要求的问题。
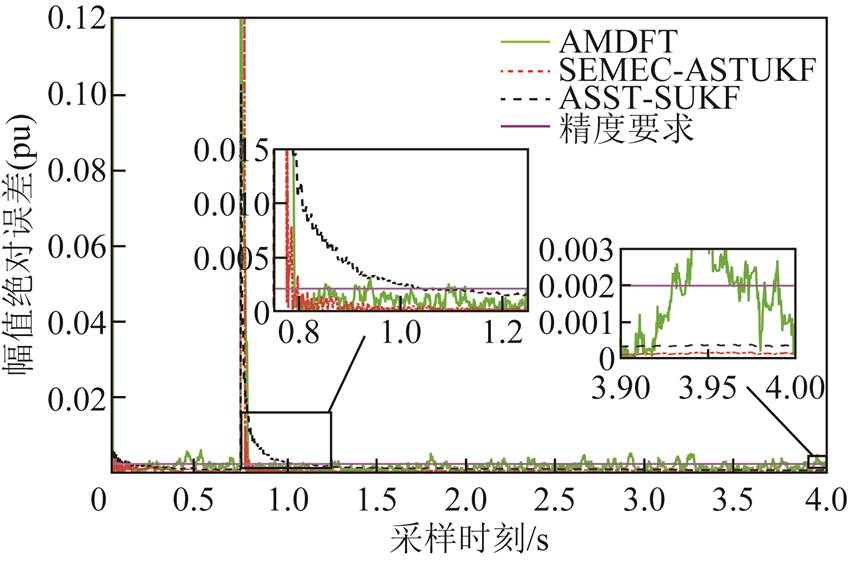
图4 实验3各算法幅值绝对误差
Fig.4 Amplitude absolute error in experiment 3
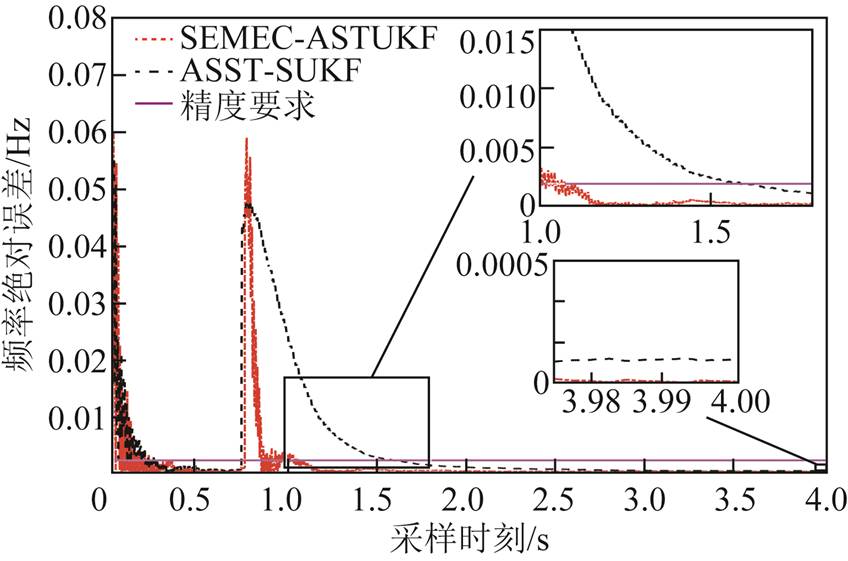
图5 实验3各算法频率绝对误差
Fig.5 Frequency absolute error of in experiment 3
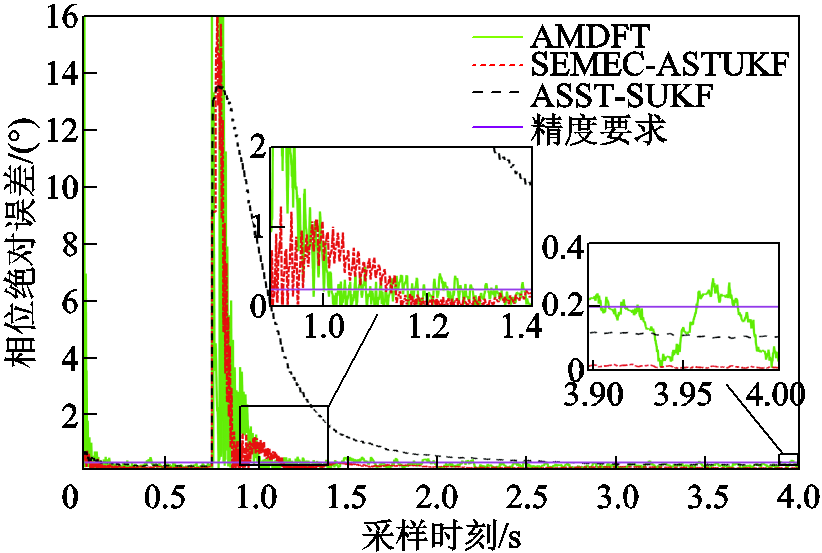
图6 实验3各算法相位绝对误差
Fig.6 Phase absolute error in experiment 3
本文针对STUKF算法在高噪声环境下检测突变能力弱、跟踪突变较慢的缺陷,提出了基于SEMEC-ASTUKF的同步相量测量算法。
1)基于递归最小二乘法理论构建了自适应噪声统计估计器,该估计器具有更稳定的估计性能和更快的收敛速度,且收敛后具有更高的估计精度。
2)基于卡方分布理论提出了一种突变判定方法,并根据电力信号突变后特征构建了新的渐消因子次优估计算法。该方法在高噪声环境下对突变具有更高的检测灵敏度,对渐消因子的估计精度更高。
3)对含有谐波和随机噪声的多种突变实测信号进行相量估计。实验结果表明,SEMEC-ASTUKF对高含量的谐波和随机噪声具有较优的屏蔽效果,测量精度更高;对各种突变状况均能可靠跟踪,且具有更高的跟踪速度。
参考文献
[1]刘友波, 刘俊勇, Gareth Taylor, 等. 面向同步相量轨迹簇规则的电力系统暂态稳定实时评估[J]. 中国电机工程学报, 2011, 31(16): 32-39. Liu Youbo, Liu Junyong, Taylor G, et al. Rule-based combined algorithm for power system real-time transient stability assessment using synchronized phasor trajectory clusters[J]. Proceedings of the CSEE, 2011, 31(16): 32-39.
[2]鞠平, 郑世宇, 徐群, 等. 广域测量系统研究综述[J]. 电力自动化设备, 2004(7): 37-40, 49. Ju Ping, Zheng Shiyu, Xu Qun, et al. Survey of wide area measurement system[J]. Electric Power Automation Equipment, 2004(7): 37-40, 49.
[3]李俊堂. 有源电力滤波器谐波电流预测与控制方法研究[D]. 长沙: 长沙理工大学, 2009.
[4]刘海涛, 张保会, 谭伦农. 低压电网信道容量的研究[J].电力系统自动化, 2004, 28(4): 40-44. Liu Haitao, Zhang Baohui, Tan Lunnong. Reasearch on the channel capacity in a low voltage network channel[J]. Automation of Electric Power Systems, 2004, 28(4): 40-44.
[5]胡蓓, 肖浩, 李建光, 等. 光纤电流互感器的噪声分析与信噪比优化设计[J]. 高电压技术, 2017, 43(2): 654-660. Hu Bei, Xiao Hao, Li Jianguang, et al. Noise analysis and SNR optimization design of fiber optical current transformers[J]. High Voltage Engineering, 2017, 43(2): 654-660.
[6]Cárdenas-Olaya A C, Rubiola E, Friedt J M, et al. Noise characterization of analog to digital converters for amplitude and phase noise measurements.[J]. The Review of Scientific Instruments, 2017, 88(6): 287-291
[7]原凯, 宋毅, 李敬如, 等. 分布式电源与电动汽车接入的谐波特征研究[J]. 中国电机工程学报, 2018, 38(增刊1): 53-57. Yuan Kai, Song Yi, Li Jingru, et al. Harmonic characteris-tics of distributed generation and electric vehicle supplying access to the grid[J]. Proceedings of the CSEE, 2018, 38(S1): 53-57.
[8]王晶, 陈学允. UPFC对动态电能质量影响的分析研究[J].电工技术学报, 2004, 19(1):44-48. Wang Jing, Chen Xueyun. Study of the impacts of UPFC on dynamic power quality[J]. Transactions of China Electrotechnical Society, 2004, 19(1): 44-48.
[9]王科, 陈丽华, 麦瑞坤, 等. 基于扩展卡尔曼滤波频率跟踪的DFT同步相量测量算法[J]. 电网技术, 2014, 38(9): 2519-2524. Wang Ke, Chen Lihua, Mai Ruikun, et al. An improved discrete Fourier transformation based synchronous phasor measurement algorithm using frequency tracking founded on extended Kalman filter[J]. Power System Technology, 2014, 38(9): 2519-2524.
[10]邝昊云, 温和. 基于泰勒-傅里叶变换的电压闪变测量方法[J]. 电工技术学报, 2020, 35(22): 4798-4806. Kuang Haoyun, Wen He. Voltage flicker measurement based on Taylor-Fourier transform[J]. Journal of Electrical Technology, 2020, 35(22): 4798-4806.
[11]肖勇, 赵伟, 黄松岭. 基于离散傅里叶级数的非同步采样下谐波功率测量算法[J]. 电工技术学报, 2018, 33(7): 1570-1578. Xiao Yong, Zhao Wei, Huang Songling. Harmonic power measurement algorithm based on discrete fourier series in asynchronous sampling[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1570-1578.
[12]王璐. 适用于PMU校准器的相量测量方法研究及应用[D]. 北京: 华北电力大学(北京), 2017.
[13]孙国强, 王晗雯, 卫志农, 等.基于无迹粒子滤波算法的发电机动态状态估计[J].电力系统自动化, 2017, 41(14): 133-139. Sun Guoqiang, Wang Hanwen, Wei Zhinong, et al. Dynamic state estimation for generators based on unscented particle filtering algorithm[J]. Automation of Electric Power Systems, 2017, 41(14): 133-139.
[14]Wu Pengfei, Shi Zhangsong, Yan Penghao. Improved EKF-SLAM algorithm of unmanned helicopter autonomous landing on ship[C]//2018 37th Chinese Control Conference, Wuhan, 2018: 5287-5292.
[15]Kung Y S, Risfendra. Model Sim/Simulink co-simulation of a sensorless control for PMSM drives based on I-F startup and EKF[C]//2016 International Conference on Applied System Innovation, Okinawa, 2016: 1-4.
[16]李扬, 李京, 陈亮, 等. 复杂噪声条件下基于抗差容积卡尔曼滤波的发电机动态状态估计[J]. 电工技术学报, 2019, 34(17): 3651-3660. Li Yang, Li Jing, Chen Liang, et al. Dynamic state estimation of synchronous machines based on robust cubature Kalman filter under complex measurement noise conditions[J]. Transactions of China Electrote-chnical Society, 2019, 34(17): 3651-3660.
[17]刘洁波, 黄纯, 江亚群, 等. 基于强跟踪泰勒-卡尔曼滤波器的动态相量估计算法[J]. 电工技术学报, 2018, 33(2): 433-441. Liu Jiebo, Huang Chun, Jiang Yaqun, et al. Dynamic phasor estimator based on strong tracking Taylor-Kalman filter[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 433-441.
[18]龙嘉川, 王先培, 赵宇, 等. 自适应无迹卡尔曼平滑算法及其在电力系统中的应用[J]. 中国电机工程学报, 2015, 35(23): 6048-6056. Long Jiachuan, Wang Xianpei, Zhao Yu, et al. Adaptive unscented Kalman smoothing algorithm and its application in power system[J]. Proceedings of the CSEE, 2015, 35(23): 6048-6056.
[19]赵洪山, 田甜. 基于自适应无迹卡尔曼滤波的电力系统动态状态估计[J]. 电网技术, 2014, 38(1): 188-192. Zhao Hongshan, Tian Tian. Dynamic state estimation for power system based on an adaptive unscented Kalman filter[J]. Power System Technology, 2014, 38(1): 188-192.
[20]牛胜锁, 王康乐, 梁志瑞. 基于改进强跟踪无迹卡尔曼滤波的电力系统同步相量估计方法[J]. 电网技术, 2019, 43(9): 3218-3225.Niu Shengsuo, Wang Kangle, Liang Zhirui. Synchronous phasor estimation method for power system based on modified strong tracking unscented Kalman filter[J]. Power System Technology, 2019, 43(9): 3218-3225.
[21]赵琳. 非线性系统滤波理论[M]. 北京: 国防工业出版社, 2012.
[22]国家调度电力通信中心. Q/GDW 1131—2014电力系统实时动态监测系统技术规范[S]. 北京: 国家电网公司, 2015.
An Algorithm for Tracking Synchronous Phasor of Power Signals Based on Improved Strong Tracking Unscented Kalman Filter
Abstract All kinds of noises in the distribution network have a great impact on phasor measurement, so it is of great significance to study the synchronous phasor measurement algorithm which can reliably detect and quickly track the sudden change of power signal in the high noise environment to ensure the stability and reliability of the power network. An algorithm, adaptive strong tracking unscented Kalman filter based on suboptimal estimate of measurement error covariance (SEMEC-ASTUKF),for synchronous phasor measurement was proposed. An adaptive constant noise statistical estimator was proposed to improve the estimation accuracy of measured noise covariance.Based on the characteristics of power signal after mutation, the mutation detection algorithm and the fading factor sub-optimal estimation algorithm were constructed to improve the strong tracking unscented filter (STUKF) algorithm's weak of mutation detection ability and slow mutation tracking under high noise environment. The results show that the SEMEC-ASTUKF algorithm has higher measurement accuracy, better detection sensitivity and tracking speed for mutation.
keywords:Strongnoise, strong tracking unscented Kalman filter, adaptive constant noise statistical estimator, fading factor
中图分类号:TM712
DOI:10.19595/j.cnki.1000-6753.tces.L90028
国家重点研发计划资助项目(2017YFB0902901)。
收稿日期 2020-05-19
改稿日期 2020-09-20
牛胜锁 男,1980年生,博士,讲师,研究方向为广域测量技术与电能质量检测分析。E-mail:niushengsuo@163.com
王春鑫 男,1994年生,硕士研究生,研究方向为配电网电力信号参数估计。E-mail:m13731216508@163.com(通信作者)
(编辑 郭丽军)