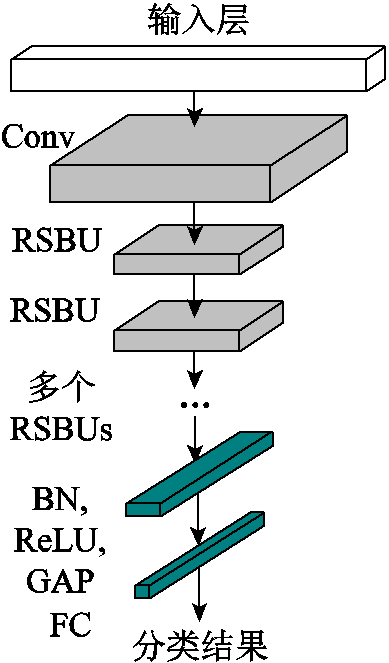
图1 深度残差网络结构
Fig.1 Deep residual network structure diagram
摘要 针对电力系统暂态稳定评估中,电力系统同步相量测量装置(PMU)量测数据在采集和传输过程可能存在噪声问题,以及由于暂态稳定与失稳样本不平衡,导致基于数据驱动的暂态稳定评估模型训练的倾向性和误判后果严重问题,提出基于改进深度残差收缩网络(IDRSN)的电力系统暂态稳定评估方法。首先将底层量测电气量构建成特征图形式作为模型输入,利用模型深层结构建立输入与稳定结果之间的映射关系。面对噪声问题,模型通过注意力机制,采用软阈值函数自动学习噪声阈值,减小噪声及无关特征干扰;并通过焦点损失函数(FL),引入权重系数修正模型训练的倾向性,利用调制因子重点关注误分类样本,提高模型训练效率和评估性能。通过新英格兰10机39节点系统进行仿真分析,所提模型能够有效减小不同程度的噪声干扰,在不平衡数据集上修正模型训练偏向性,以减少误分类样本,在不同PMU配置方案下,均取得较好评估效果。
关键词:电力系统 暂态稳定评估 深度学习 深度残差收缩网络 焦点损失函数
电力系统暂态稳定是指系统受到大扰动之后能否保持同步稳定的能力[1]。随着智能电网建设不断发展,新能源、高压直流输电的不断加入,使得电力系统结构及其动态特性更加复杂[2],相应地增加了面对故障时对系统进行稳定分析与控制的难度。因此,快速、准确地掌握暂态态势,实现电力系统暂态评估,具有重要意义。
传统电力系统暂态稳定分析方法主要有时域仿真法和直接法[3-5]。时域仿真法,模型构建较为精细,计算结果准确,但是耗时长,随着电网规模增大,计算速度受到制约,难以在线应用;直接法,计算速度快,但是所用简化模型,使得结果偏保守。
随着同步相量量测技术的不断发展,广域测量信息系统(Wide Area Measurement System, WAMS)不断完善,为电网运行监测提供大量实时数据,机器学习算法利用其稳态及暂态期间的数据与稳定结果,构造输入特征与输出之间的映射关系,无需对系统建模,就能实现暂态稳定评估,从而受到研究人员广泛关注,相应研究工作主要包括人工神经网络[6-9](Artificial Neural Network, ANN)、支持向量机[10-15](Support Vector Machine, SVM)、决策树[16-17](Decision Tree, DT)和集成学习[18-22](Ensemble Learning, EL)等机器学习算法,传统机器学习算法对相量测量装置(Phasor Measurement Unit, PMU)采集到的生数据,特征提取能力弱,需要依靠人工提取特征,耗时耗力,且难免存在人工提取的特征不能完全表征系统特性的问题。
近年来,深度学习发展迅速,理论算法应用方面进步显著,其善于从原始数据中挖掘隐藏规律,被广泛应用于图像识别、视觉计算和自然语言处理等多个领域,在电力系统负荷识别[23]、状态检测[24]和暂态稳定评估等多个方向也是热点研究[25],其中暂态稳定评估常用方法有深度置信网络[26-28]、卷积神经网络[29-32]、自动编码器[33-35]和生成对抗网络[36]等,其中卷积神经网络利用卷积运算能够有效提取数据集特征,备受关注,被广泛应用于各个领域。
电力系统本身是一个高维非线性的系统,若要对其量测数据挖掘本质规律,需要构造较深层次的神经网络,随着电网规模的不断扩大,所需要的深度学习评估模型也不断加深,较深层次的神经网络会出现训练困难;PMU装置传输信息时可能存在部分噪声,影响模型判断能力;电力系统中失稳样本数量少于稳定样本数量,数据集存在天然不平衡,模型训练会有偏向性,若不加控制措施,模型训练会偏向稳定样本,更容易判定为稳定,若失稳样本误判为稳定,系统将会失去稳定,甚至解列,造成巨大的损失。本文结合电力系统暂态稳定评估的特点,提出基于改进深度残差收缩网络的电力系统暂态稳定评估方法。采用深度残差收缩网络能够巧妙地减轻深层网络训练负担,在残差单元中引入收缩模块克服噪声干扰,利用焦点损失函数,解决电力系统暂态稳定与失稳数据集不平衡情况,并为误分类样本设置更多关注,以减少误分类情况。最后通过仿真验证所提方法在暂态稳定评估方面的有效性。
深度残差收缩网络[37](Deep Residual Shrinkage Networks,DRSN)是2019年发表在国际期刊IEEE Transactions on Industrial Informatics上的一种人工智能方法。从本质上讲,深度残差收缩网络为解决故障诊断噪声问题,将注意力机制和软阈值函数引入深度残差网络[38],在深度残差网络的内部实现了自动软阈值化,自适应地在特征学习的过程中消除冗余信息,提高有用特征的学习效果。本文所提模型将焦点损失函数(Focal Loss, FL)[39]引入DRSN中,改善数据不平衡引起的训练问题,关注误分类样本,最终形成改进深度残差收缩网络(Improved Deep Residual Shrinkage Networks, IDRSN)。
深度残差收缩网络是深度残差网络的变体,深度残差网络ResNet[38]是由何凯明团队2015年提出的一种改进型卷积神经网络,其通过引入恒等路径,降低模型训练难度,解决神经网络深层结构容易出现的梯度消失或爆炸问题。卷积网络层与层之间存在交叉熵损失梯度,在恒等路径的作用下,深层结构能够链接距离输入层“更近”、“更早”的神经网络层,使梯度参数有效传递与更新,网络参数的训练难度大幅降低,从而容易训练出效果好的深度学习模型。
深度残差收缩网络,整体结构包括输入层,卷积层[40](Convolutional layer, Conv),多个残差收缩单元(Residual Shrinkage Building Units,RSBUs)、批标准化层[41](Batch Normalization, BN)、激活函数(Rectifier Linear Unit,ReLU)、全局平均池化层(Global Average Pooling,GAP)和输出全连接层(Fully Connected layer,FC),如图1所示,

图1 深度残差网络结构
Fig.1 Deep residual network structure diagram
卷积层Conv,是卷积网络不同于传统全连接神经网络的关键元素。卷积层极大地减少了所需训练的参数量。通过卷积运算代替矩阵乘法,卷积层内核所需参数比全连接网络的变换矩阵更少,从而降低模型过拟合风险,卷积层的运算可表示为
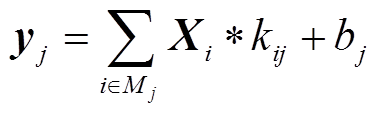 (1)
(1)式中,Xi为特征图X第i个通道的输入;yj为特征图的第j个通道的输出;kij为卷积核;bj为偏置;Mj为用于计算输出特征图的第j通道的集合。
批标准化层BN,在机器学习理论中,规范化是数据预处理的一个步骤,其目的在于尽可能地缩小样本数据及各维度特征的差异。传统数据预处理只能保证输入层数据具有较好的规范化特性,经过权值、偏置、激活函数一系列计算之后,无法保证隐藏层数据的规范化。批标准化层BN是在隐藏层之前对数据进行批标准化处理,保证隐藏层获取规范化数据,加速网络优化。BN算法实现步骤:①计算该批次数据的均值、方差;②用方差做分母,对批数据进行正态分布处理;③取值范围限制在(0,1)。
激活函数ReLU,每个神经元计算最后步骤都是通过激活函数转换权值和偏置的计算结果,其输入输出都是一个实数。激活函数能够将神经元的输出值限定在一定范围内,不至于出现无限大,并且使神经元具有非线性计算能力,从而使神经网络能够处理非线性问题。传统的激活函数sigmoid容易出现梯度消失问题。针对以上问题,本文采用ReLU函数,表达式为
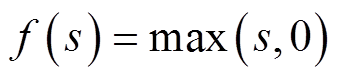 (2)
(2)在变量s≤0时,导数固定为0;s>0,导数固定为1,解决激活函数容易出现梯度消失的问题。
全局平均池化层GAP,在全连接输出层之前,是计算每个特征通道平均值的运算,其作用在于进行特征压缩,提取主要特征,减少权重个数,简化网络计算复杂度,防止模型过拟合,有一定的抗干扰能力。
输出全连接层FC,通过sigmoid函数将前一层传递来的数据x,转换成概率,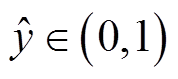 用于分类,
用于分类,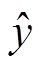 默认阈值为0.5,小于0.5标签为0,否则标签为1。
默认阈值为0.5,小于0.5标签为0,否则标签为1。
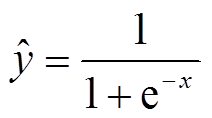 (3)
(3)残差收缩单元是在残差单元基础上,将软阈值函数引入层与层链接的路径中,并利用注意力机制自动确定阈值,从而达到自动提取重要特征的效果。
1.2.1 软阈值函数(soft thresholding)
软阈值函数在信号去噪领域应用广泛,运作机制为:卷积神经网络自动进行滤波器学习,将原始数据映射到另一空间,进行软阈值化处理,软阈值化是将阈值区间[-τ,τ]内的特征置为0,让距0较远的特征x向0进行收缩。软阈值函数及其导数如图2所示,软阈值公式为
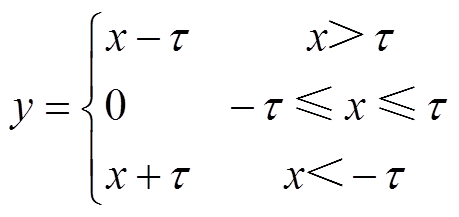 (4)
(4)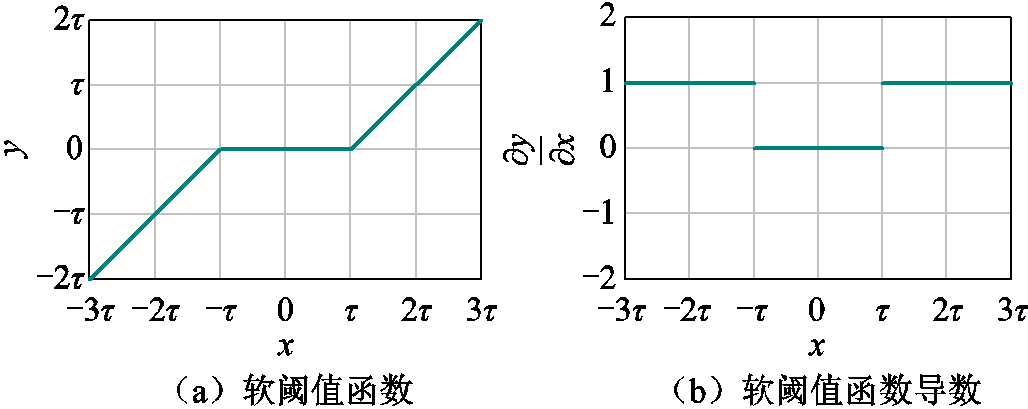
图2 软阈值函数及其导数
Fig.2 Soft threshold function and its derivative graph
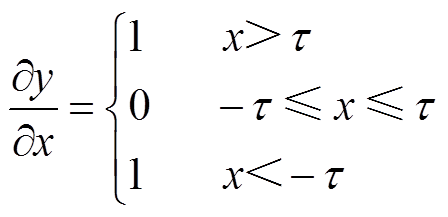 (5)
(5)因为τ是可以通过自动学习得到的参数,所以软阈值化,可以将任意区间的特征置为零,能够灵活删除某个取值范围的特征,更好地表征非线性映射。
1.2.2 注意力机制
在深度残差收缩网络中,样本具有不同的阈值,这是一种注意力机制:从所有输入信息中找到需要重点关注的部分,并且从中挖掘重要特征,剔除不重要甚至无关的特征。虽然通过恒等路径,高层特征中会存在不重要特征,但是通过模块的深度堆叠,不重要特征所占比重会逐渐降低,直至消失。
残差收缩单元,根据通道间阈值是否共享,分为阈值独立型残差收缩单元(Residual Shrinkage Building Unit with Channel-Wise thresholds, RSBU-CW)和阈值共享型残差收缩单元(Residual Shrinkage Building Unit with Channel-Shared thresholds, RSBU-CS)。深度残差收缩单元如图3所示,其中C和W分别表示特征图的通道数和宽度。残差单元嵌入含有软阈值处理的非线性变换层,能够有效避免噪声干扰,而且能够利用模型深层结构自动学习阈值取值,无需专家利用专业知识针对噪声专门设计阈值。
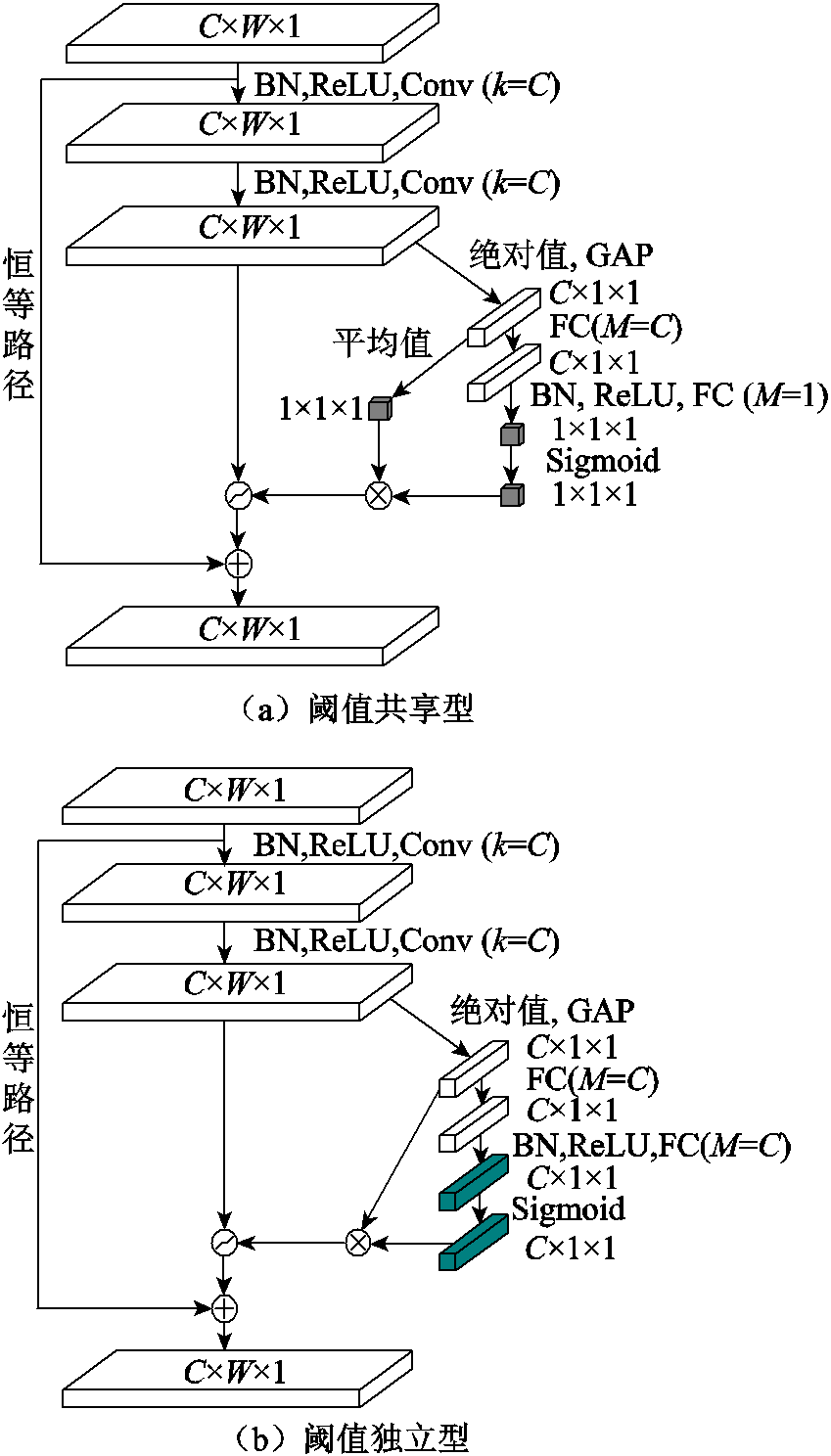
图3 深度残差收缩单元
Fig.3 Deep residual shrinkage unit
RSBU-CW每个通道都具有独立的阈值,特征图通过绝对值和全局平均池化降为一个一维向量,传递给一个两层的全连接网络,全连接网络第二层神经元个数等于输入特征图通道个数,其输入被缩放到(0,1)之间,缩放参数为
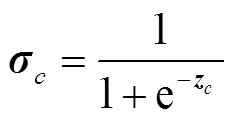 (6)
(6)式中,zc为第c层神经元的特征;σc为第c层的缩放参数,阈值被定义为
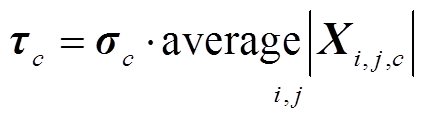 (7)
(7)式中,τc为特征图第c通道的阈值;i、j、c分别为特征图X的宽度、高度和通道。σc乘|X|用以获取阈值,阈值为正且不能过大,若阈值大于特征图最大绝对值,软阈值输出将会置零。
RSBU-CS所有通道共用一组阈值,所以式(6)、式(7)中的σc和τc不分通道计算,记为σ和τ。
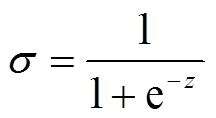 (8)
(8)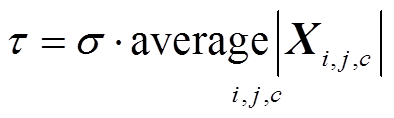 (9)
(9)为解决暂态稳定数据集不平衡以及稳定误分类后果严重问题,将焦点损失函数FL引入深度残差收缩网络中,表达式为
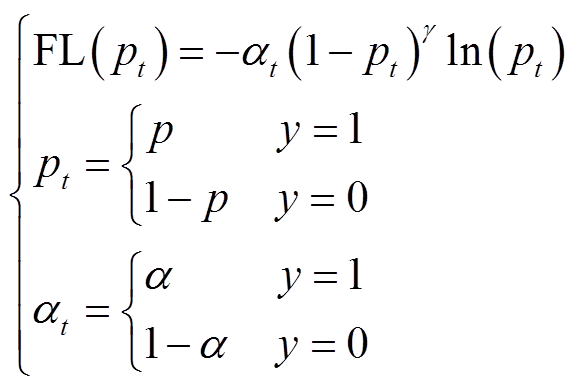 (10)
(10)式中,p为模型预测的样本标签概率,p∈[0,1];y为样本实际标签;t为类别。大量的稳定样本使模型训练时,具有偏向稳定的判定倾向。神经网络训练的关键步骤就是计算损失函数值和更新梯度。因为稳定样本数量较多,自然会导致模型更加关注稳定样本的训练情况,为了改善这种数据数量上导致的不平衡,训练时加入α参数,调节类别权重,即为失稳样本占总样本的比重,α∈[0,1],在损失函数中设置不平衡权重,改善模型训练倾向稳定问题。
若仅设置类别训练权重,只能改善模型训练的倾向性问题,但是不能关注到模型误分类的样本,这些样本对训练模型来说比较困难。考虑到实际电力系统暂态稳定评估错误将会带来严重后果,失稳误判为稳定,紧急控制措施不能启动,将会造成系统失稳,甚至解列;稳定判定为失稳,系统将会启动一定控制装置,虽然能够增加一定的安全裕度,但是会复杂化运行维护工作。在此,引入(1-pt)γ作为调制因子,解决大量易分类正确样本可能导致的损失函数值下降缓慢,无法收敛至最优的问题,增加对误分类样本的关注,减少误分类样本个数,从而提高分类准确度。当调制因子指数γ=0时,损失函数即为带训练权重的普通二分类交叉熵损失函数,只解决模型训练的倾向性问题;γ>0,调制因子发挥作用,重点关注误分类情况。γ越大,对误分类样本的关注越多。
本文旨在训练一种端对端的评估模型,将电力系统中PMU装置直接采集到的电气量作为模型输入,并结合三段式特征选择原则,将全系统各节点,故障前t0,故障瞬间tf和故障切除时刻tc的电压幅值U和相角θ作为模型特征量输入,构造出三维数据分布,如图4所示,与图结构的长度、宽度和通道类似,有利于卷积模块提取特征。
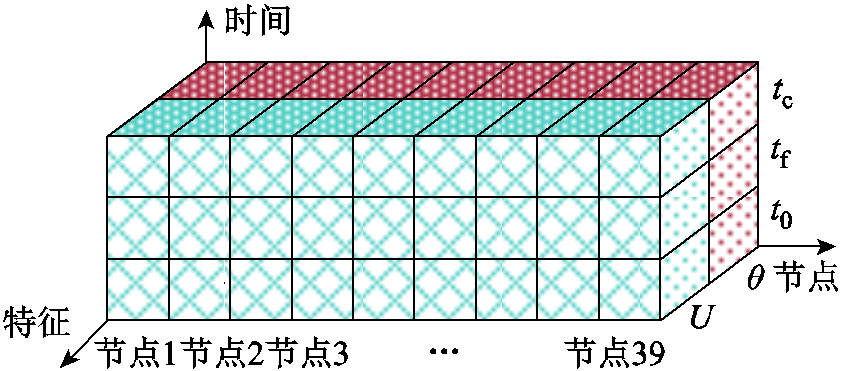
图4 输入特征图
Fig.4 Input feature map
模型输出为功角稳定结果,稳定判据μ为
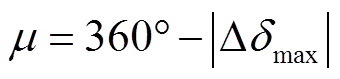 (11)
(11)式中,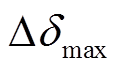 为仿真期间任意两个发电机的最大相对功角差。μ>0,表示系统稳定,标签为0;μ<0,系统失稳,标签为1。
为仿真期间任意两个发电机的最大相对功角差。μ>0,表示系统稳定,标签为0;μ<0,系统失稳,标签为1。
电力系统暂态稳定评估是二分类问题,而且样本集存在不平衡和误判代价不同现象。本文兼顾模型分类精度、不平衡样本集和误判代价不同三个方面,选择准确率ACC、G-mean值,f1失稳评估综合指标以及综合分类指标(Comprehensive Assessment Index, CAI)作为评估指标。表1为暂态稳定分类的混淆矩阵。
表1 混淆矩阵
Tab.1 Confusion matrix

评估真实 稳定失稳 稳定 失稳
 (12)
(12)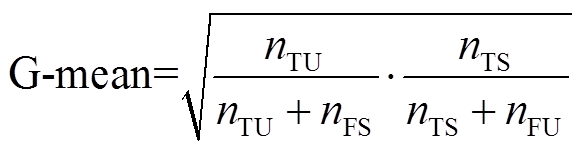 (13)
(13)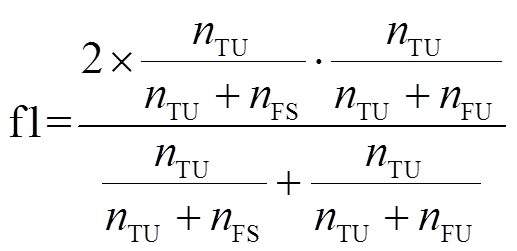 (14)
(14)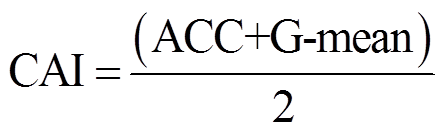 (15)
(15)式中,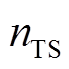 为正确评估为稳定的样本数;
为正确评估为稳定的样本数;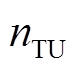 为正确评估为失稳的样本数;
为正确评估为失稳的样本数;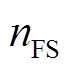 为错误预测为稳定的样本数;
为错误预测为稳定的样本数;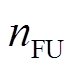 错误预测为失稳的样本数;ACC为评估总准确率;G-mean值是稳定判准率和失稳判准率的几何平均值,是不平衡数据集上评估模型的重要指标;f1指标是针对失稳样本判准率和查全率的调和平均,是重点关注失稳样本的重要指标;综合评价指标CAI,为ACC和G-mean值的加权平均,综合考虑不平衡数据集下的分类效果。
错误预测为失稳的样本数;ACC为评估总准确率;G-mean值是稳定判准率和失稳判准率的几何平均值,是不平衡数据集上评估模型的重要指标;f1指标是针对失稳样本判准率和查全率的调和平均,是重点关注失稳样本的重要指标;综合评价指标CAI,为ACC和G-mean值的加权平均,综合考虑不平衡数据集下的分类效果。
根据电力系统所提取数据的特征,本文所设计的IDRSN模型总体结构包括卷积层Conv、残差收缩单元RSBUs、批标准化BN、激活函数ReLU、全局池化层GAP和全连接输出层FC。残差收缩单元包括1个RSBU-CW,2个RSBU-CS。其中,RSBU-CW采用不同阈值收缩不同通道噪声相关的特征,相比RSBU-CS只有一组阈值,RSBU-CW更加准确灵活,但是所需参数量大;而RSBU-CS,减少了神经网络需要训练的参数个数,大大降低了训练负担,本文兼顾准确性和训练情况,在总模型中组合两种类型的残差收缩单元。本文暂态评估流程分为离线训练模型和在线评估,如图5所示。
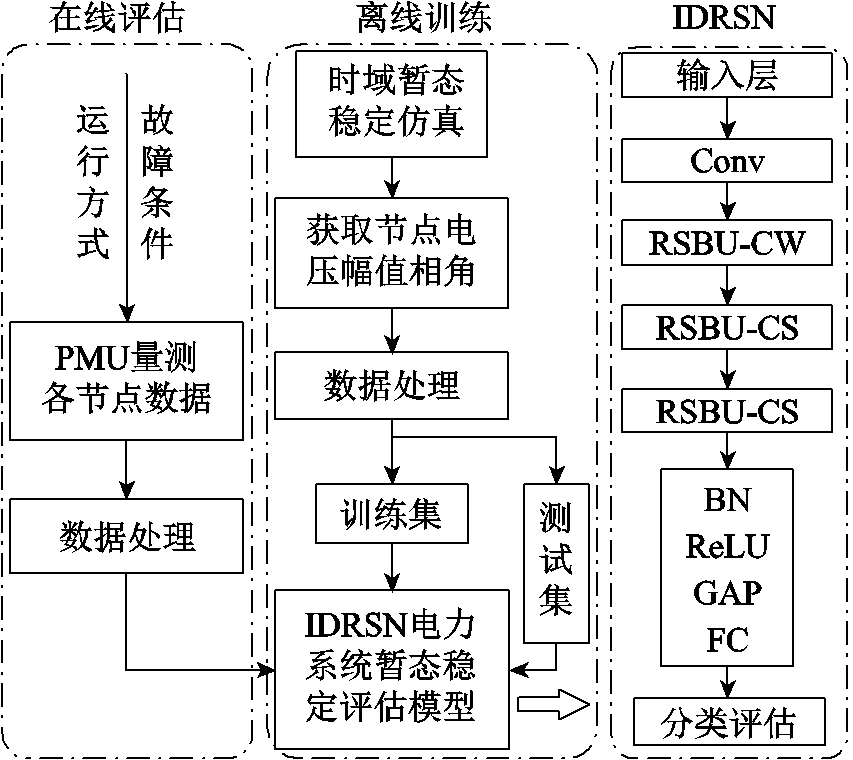
图5 暂态稳定评估流程
Fig.5 Evaluation flow chart
离线训练,通过时域仿真获取系统各节点在t0、tf、tc时刻电压幅值和相角,处理成2.1节中样本集构成,并进行标准化处理;将全数据集分为训练集和测试集,进行模型训练和测试。在线评估,是通过将PMU量测各节点数据,进行数据处理,然后传递给IDRSN暂态评估模型,进行稳定分类。
本文算例采用新英格兰39节点标准系统,如图6,此系统含10台发电机,39个节点,46条线路,系统电压为345kV,基准功率为100MW。采用电力系统仿真软件PSD-BPA搭建仿真模型,发电机采用五阶模型,负荷模型采用恒阻抗模型。负荷水平在0.8~1.2之间变化,为保证系统节点电压在合理范围,以及潮流收敛,随机改变发电机出力,故障设置为最严重的三相短路,故障持续时间分别为0.1s、0.14s、0.18s、0.2s,生成N-1线路故障集,去除电压失稳样本,共生成4 551个样本,其中有2 744个稳定样本,1 807个失稳样本。
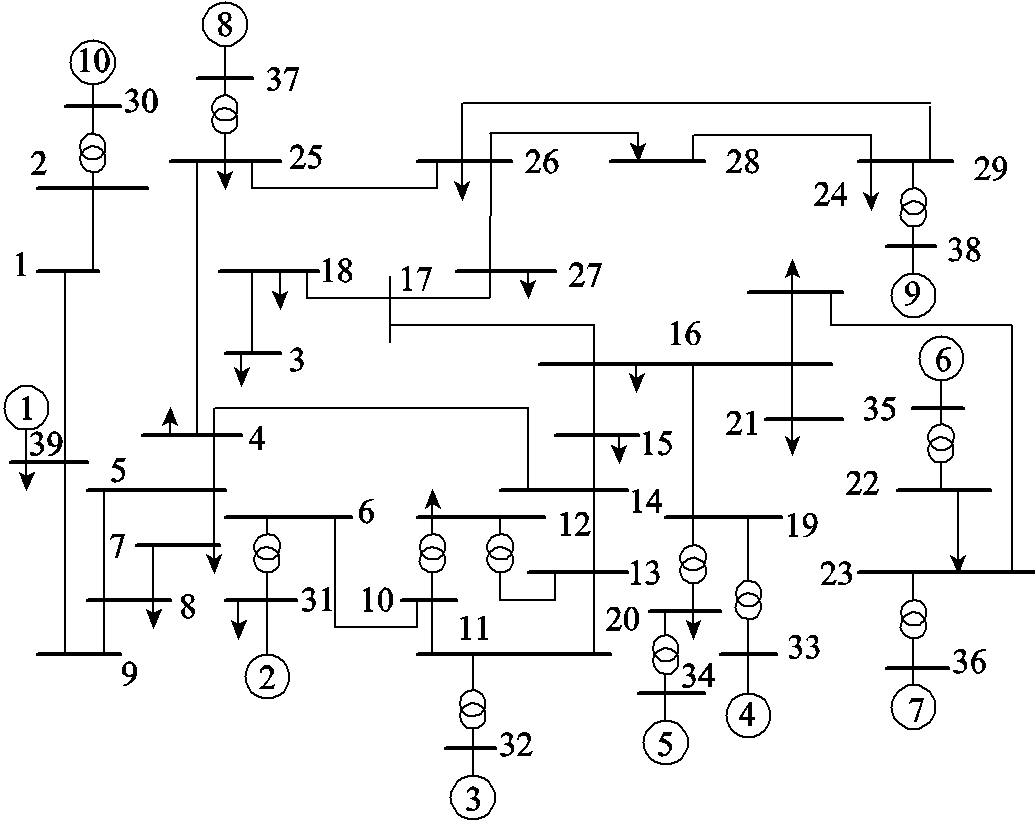
图6 新英格兰10机39节点模型
Fig.6 New England 10 machine 39 bus model diagram
仿真验证本文所提模型,并与逻辑回归(Logistic Regression, LR)、支持向量机(SVM),K近邻(K-Nearest Neighbor, KNN)、多层感知机(Multilayer Perceptron, MLP)、决策树DT、随机森林(Random Forest, RF)、深度残差网络(Deep Residual Network,DRN)以及深度残差收缩网络DRSN进行比较。本文所提改进深度残差收缩网络IDRSN模型采用Adam学习算法自适应调整学习率,采用L1和L2结合正则化训练,L1和L2正则项系数分别设置为0.08和0.000 5。采用焦点损失函数,引入两个超参数α和γ。α为失稳样本数量与总数据集数量比值,γ为调制因子指数。文献[39]中,经过大量数据集训练验证了当γ=2时,模型训练效果最好,经本文数据验证,取γ=2。由式(10)可知,当γ=0时,损失函数即为带训练权重的普通二分类交叉熵损失函数,训练情况对比如图7所示。
图7 模型训练损失值对比
Fig.7 Comparison of model training loss
由图7可以看出,在训练集和测试集上,加了调制因子的焦点损失函数比普通交叉熵损失函数下降得更快,训练过程也更加平稳。采用焦点损失函数的模型,训练集与测试集损失值同步下降,且差距较小,而普通交叉熵损失函数训练过程中,训练集和测试集损失值差距较大,说明本文模型采用焦点损失函数防止模型过拟合,从而使模型泛化能力更好。以下仿真讨论均采用γ=2作为超参数。
LR采用lbfgs求解器,加入L2惩罚项,正则化系数设置为0.4;SVM采用径向基核函数,c=1,γ=0.006;MLP激活函数为Relu,训练方法采用Adam自适应调整学习率,DT采用CART(classification and regression trees)算法,最大树深度设置为7,RF基分类器与DT相同,最大深度设置为6,DRN模型学习率、正则化和网络基本结构与所提模型保持一致,采用交叉熵损失函数,DRSN模型结构与IDRSN保持一致,采用交叉熵损失函数。仿真硬件为Intel Core i5-6200 CPU,4GB RAM 64位PC,GPU为NVIDIA Tesla P4。原始数据集取80%做训练集,20%做测试集,各模型评估性能指标见表2。
表2 各模型评估性能指标
Tab.2 Evaluation performance indicators of each model
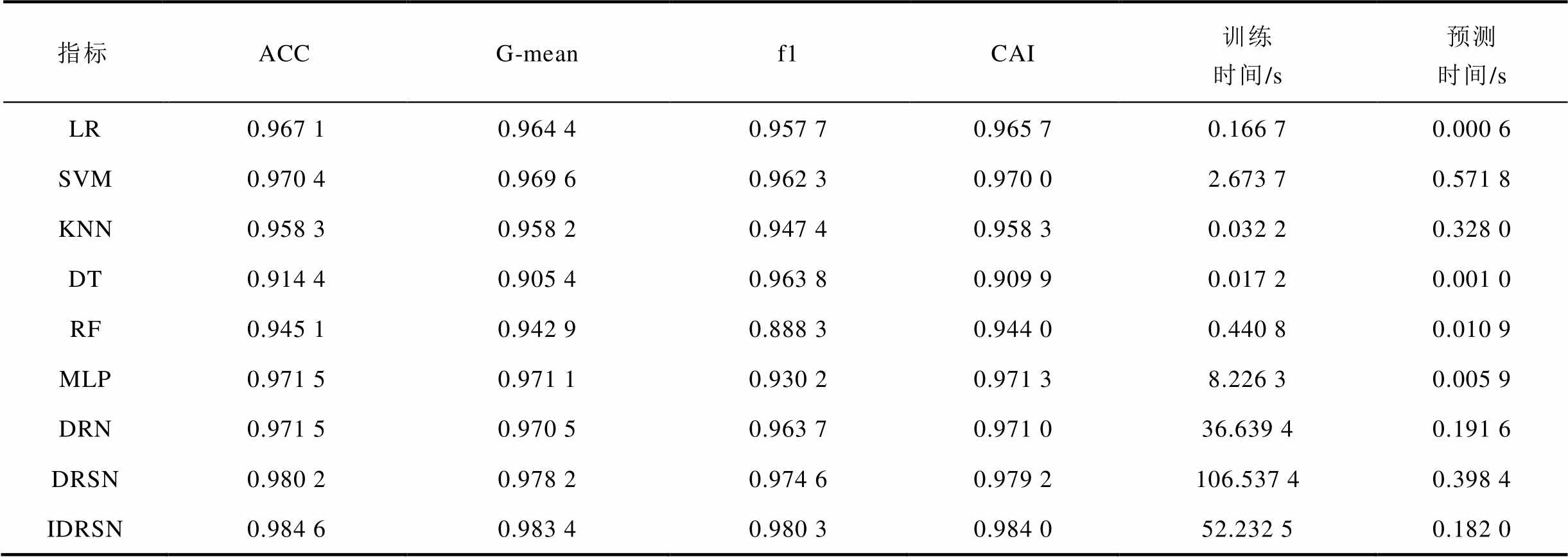
指标ACCG-meanf1CAI训练时间/s预测时间/s LR0.967 10.964 40.957 70.965 70.166 70.000 6 SVM0.970 40.969 60.962 30.970 02.673 70.571 8 KNN0.958 30.958 20.947 40.958 30.032 20.328 0 DT0.914 40.905 40.963 80.909 90.017 20.001 0 RF0.945 10.942 90.888 30.944 00.440 80.010 9 MLP0.971 50.971 10.930 20.971 38.226 30.005 9 DRN0.971 50.970 50.963 70.971 036.639 40.191 6 DRSN0.980 20.978 20.974 60.979 2106.537 40.398 4 IDRSN0.984 60.983 40.980 30.984 052.232 50.182 0
从表2可以看出,LR、SVM、MLP、KNN表现较好,准确率分别达到了0.970 4、0.971 5、0.967 1和0.958 3;DT表现较差,比IDRSN准确率低了0.070 2,RF是DT的集成,效果比DT好,但是也只有0.945 1;DRN与IDRSN层次结构相同,准确率达到0.971 5,DRSN仅在损失函数上与所提模型不同,由于原始数据集的不平衡,所以模型表现略逊色于IDRSN,所提模型是残差收缩模块和焦点损失函数的应用改进模型,使评估准确率进一步提高,达到0.984 6。
从数据不平衡和代价不平衡角度看G-mean值和f1指标,所提模型G-mean值高于其他模型,说明本文模型能够较好地克服数据不平衡导致的训练倾向性问题;由于稳定样本多于失稳样本,浅层机器学习算法失稳判准综合f1指标往往偏小,但是失稳误判为稳定的后果较为严重,该评估倾向不利于系统安全运行;从综合指标CAI来看,IDRSN比其他算法表现优秀。
从训练时间及预测时间来看,深度学习模型由于其深层架构,参数精细且较多,较浅层机器学习模型具有较长的训练时间,但是模型表现优秀,IDRSN经过损失函数改进,专注于误分类样本,比DRSN模型训练高效,评估指标提升的同时,时间大大缩减,所提模型预测时间平均单个样本耗时0.2ms,基本能够符合暂态稳定评估的时长要求。
PMU装置在实际量测数据时,可能存在因外部设备损坏或者故障造成噪声污染、数据缺失等现象。根据 IEEE C37.118标准[42],PMU相量量测误差应小于1%,按照信噪比(Signal-to-Noise Ratio, SNR)计算公式
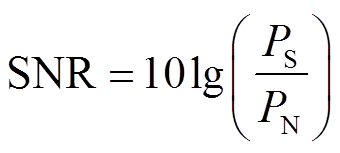 (16)
(16)式中,PS和PN分别为信号和噪声的有效功率,含有1%的噪声折算为信噪比等于20dB。为测试模型的抗噪能力,将原始数据集中加入不同水平,服从标准正态分布的高斯白噪声,信噪比为60dB、50dB、40dB、30dB、20dB、15dB,模拟噪声污染,综合指标CAI见表3。
表3 不同噪声条件下各模型CAI
Tab.3 CAI of each model under different noise conditions

噪声/dB无605040302015 LR0.965 70.974 50.965 50.957 70.936 60.863 80.832 6 SVM0.970 00.970 00.969 00.969 00.963 80.925 20.304 1 KNN0.958 30.958 30.957 30.958 00.958 00.955 20.936 4 DT0.909 90.890 00.908 40.849 80.870 10.790 10.797 1 RF0.944 00.941 20.934 00.916 60.926 60.904 80.871 8 MLP0.971 30.963 80.921 00.944 00.914 40.866 10.831 0 DRN0.971 00.969 20.966 70.961 00.964 50.948 00.922 7 DRSN0.979 20.976 80.977 70.974 50.975 00.971 20.957 5 IDRSN0.984 00.981 00.980 70.975 50.975 70.971 70.969 2
由表3可以看出,随着噪声增大,相比于DRN的综合指标下降4.83%,所提模型IDRSN和DRSN只下降了1.48%和2.17%,幅度和程度均比较小,得益于模型中残差收缩模块的抗噪能力,所以始终能保持较好的评估性能;LR、SVM、KNN、DT属于简单机器学习算法,学习能力有限,噪声增加的同时评估效果下降严重,分别下降13.31%、66.59%、2.19%、11.28%,尤其是SVM在无噪声和噪声较小的时候,仍能保持较高的分类水平,在噪声较大的时候,模型抗噪能力弱的缺点就凸显出来;RF集成多棵决策树,评估效果比单一决策树好,CAI下降了7.22%;而MLP下降幅度较大,达到14.03%,说明模型抗噪能力弱。
在噪声为15dB时,各算法综合指标下降最多,采用t-SNE可视化技术,将IDRSN的残差收缩模块的输出情况展示在(V1,V2)二维空间,噪声条件下各层输出数据分布如图8所示。
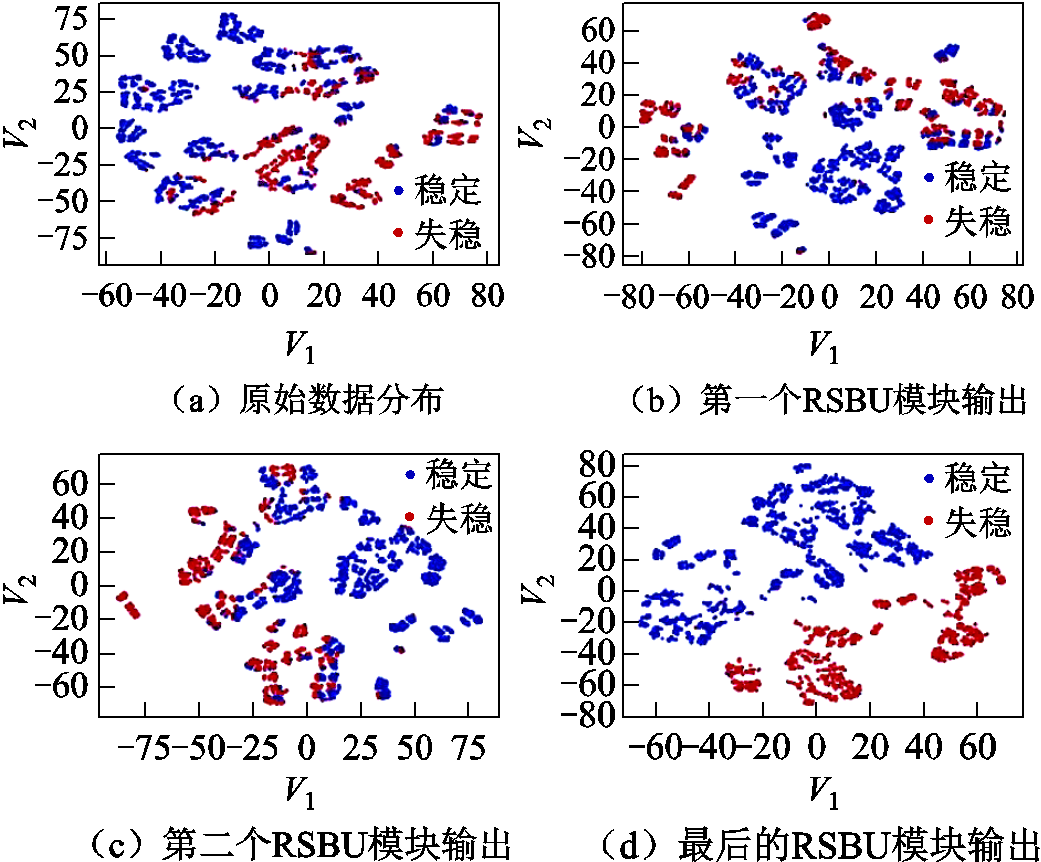
图8 噪声条件下各层输出数据分布
Fig.8 Distribution of output data of each layer under noise conditions
由图8a~图8d变化可以看出,每经过一层残差收缩模块之后,数据分布逐渐改善,在经过最后一层残差收缩模块后,数据分布明显,说明模型在高噪声条件下,仍能对特征进行有效提取,实现分类评估有效性,模型具有良好的鲁棒性。
在实际电网运行中,暂态失稳情况远远少于稳定情况,因此数据集两种样本的比例呈现不平衡状况。为验证模型对不平衡样本的评估能力,在原数据集稳定与不稳定样本中随机抽取比例为1800:1 800,2 100:1 500,2 400:1 200,2 700:900,准确率ACC,数据不平衡综合评估指标G-mean,失稳判准综合指标f1和综合评价指标CAI,具体表现如图9所示。
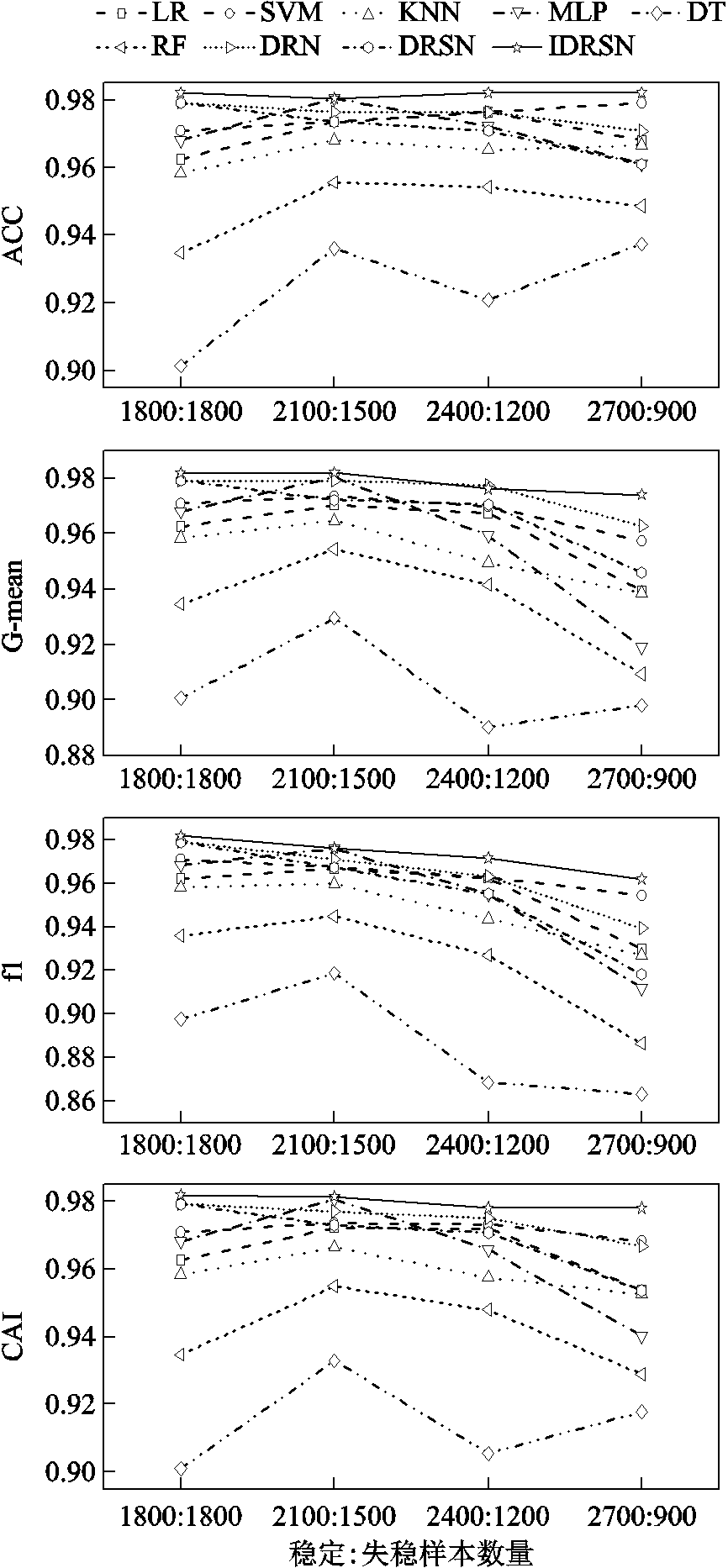
图9 不平衡条件下模型评估指标
Fig.9 Model evaluation indicators under imbalanced conditions
由图9可以看出,从ACC指标来看,随着稳定样本逐渐增多,机器学习算法LR、SVM、KNN、DT、DF逐渐上升,神经网络MLP、DRN和DRSN的训练受数据分布不平衡影响,表现出下降的分类准确度。本文所提模型IDRSN虽然以神经网络为基础,但是针对不平衡样本集做出改进,所以ACC一直保持较高水平,且波动较小。在不平衡数据集上,单一地看ACC指标对系统安全运行往往没有太大意义,所以需要分析不平衡相关指标以及对系统安全运行影响较大的失稳判准指标。从G-means指标来看,不平衡加剧整体呈现下降趋势,MLP、DT、RF受影响较大,波动程度较大,LR、SVM、KNN、DRN、DRSN次之,本文所提模型下降幅度明显小于其他模型。从综合指标CAI来看,随着样本不平衡程度的加大,综合指标有所下降,在样本平衡时,各模型的分类性能较好。从f1指标来看,随着失稳样本逐渐减小,各模型训练时更偏向稳定样本(多数样本),失稳误分类率有所提高,所以各类模型失稳判准综合指标均呈现下降趋势。相比于DRSN模型随着数据不平衡程度加剧,各项指标下降程度较大,模型泛化能力较弱,难以较好地适应暂态稳定问题中存在的数据不平衡问题。本文模型通过为失稳样本自适应设置权重,并引入调制因子,关注误分类样本进行训练,减小了下降程度,使得指标总体保持较高水平。
在电力系统暂态评估过程中,需要有全系统节点实时数据,因此需要大量的同步相量量测装置(PMU),保证全系统的可观性,但是PMU装置昂贵,大量安装经济性较差,因此PMU的安装位置和安装个数是影响模型评估的重要影响因素。本文采用轻型梯度提升机(Light Gradient Boosting Machine, LGBM)[43],对各节点特征重要程度排序,并在特征重要程度大的节点位置安装PMU,配置方案见表4,模型评估结果如图10所示。
表4 PMU配置方案
Tab.4 PMU configuration scheme
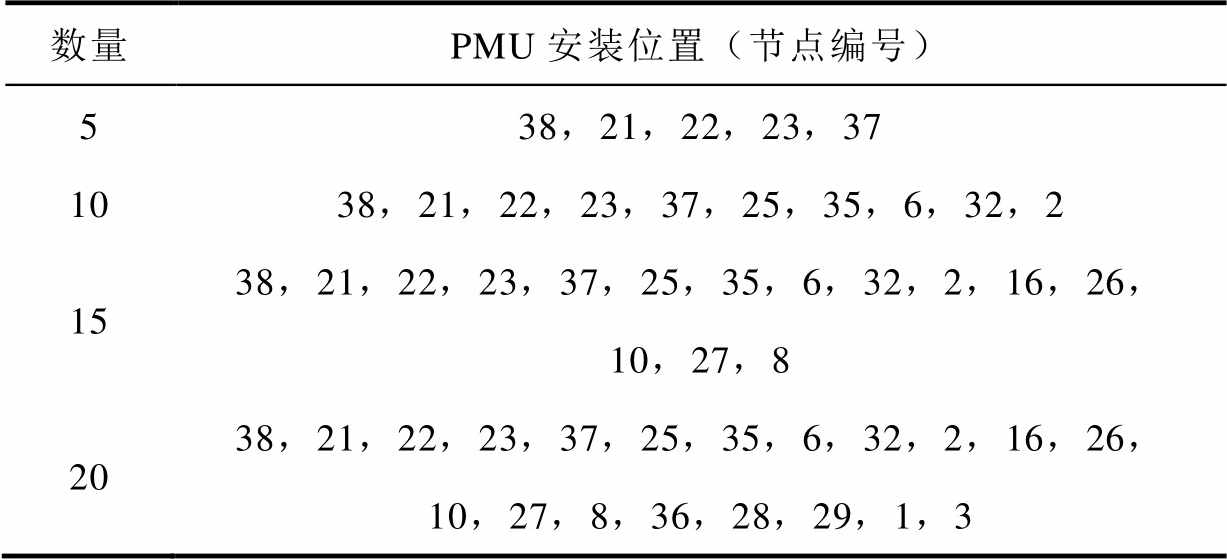
数量PMU安装位置(节点编号) 538,21,22,23,37 1038,21,22,23,37,25,35,6,32,2 1538,21,22,23,37,25,35,6,32,2,16,26,10,27,8 2038,21,22,23,37,25,35,6,32,2,16,26,10,27,8,36,28,29,1,3
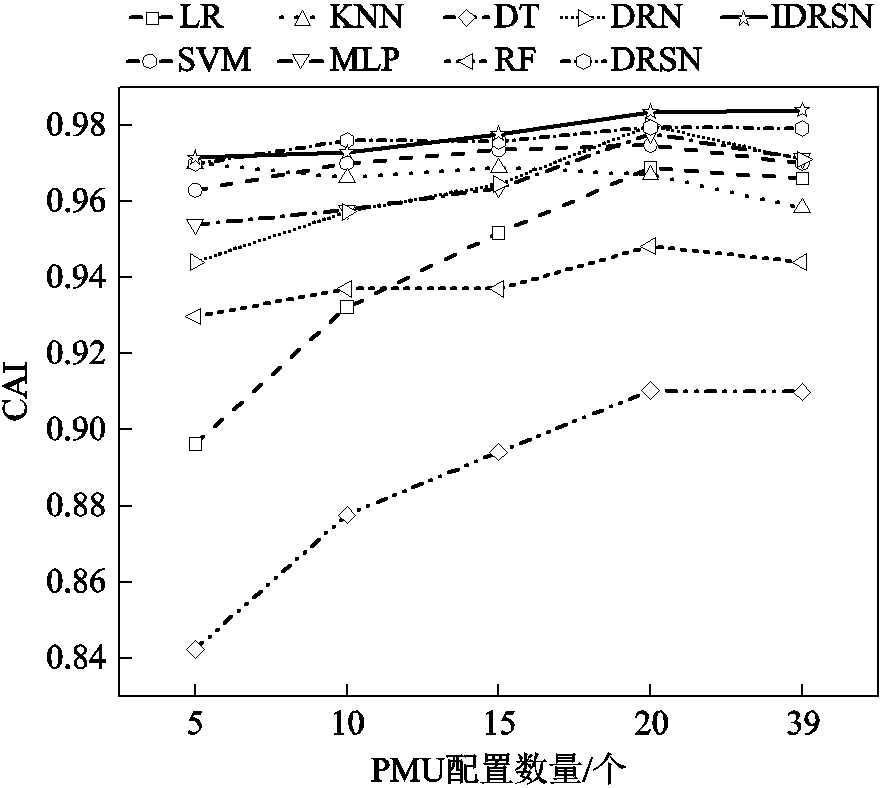
图10 不同PMU配置方案下的模型评估对比
Fig.10 Comparison of model evaluation under different PMU configuration schemes
在不同的PMU配置方案下,可以看出随着PMU安装数量的减少,所有模型的综合指标CAI均有一定下降,其中,本文所提模型的CAI指标下降最少,仅为1.25%,说明模型较其他评估模型,具有较好的泛化能力,能从有限数据中挖掘深层信息,达到较好的评估效果。在PMU安装数量达到20个后,IDRSN和DRSN评估参数没有明显上升,其他模型效果略有下降,说明之后的信息存在冗余,得益于残差收缩网络中的注意力机制,能够找到全部节点信息中的关键节点信息,剔除不重要节点信息的影响,并且挖掘其与稳定结果之间的关系,从而得到较好的稳定判别结果。
本文提出基于改进深度残差收缩网络的电力系统暂态稳定评估方法。构建暂态过程全阶段的特征图信息作为模型输入,稳定结果作为输出,进行模型训练,并在新英格兰10机39节点系统进行仿真验证,所得结论如下:
1)相比于传统浅层机器学习算法LR、SVM、KNN、MLP、DT、RF以及同层次结构的深度学习算法DRN、DRSN、IDRSN算法直接面向底层电气量测数据,能够更加有效地挖掘数据隐藏信息,进行特征提取,并在分类性能评估指标上表现优秀。
2)数据采集传输过程中可能存在噪声干扰,噪声越大,数据质量下降越严重,严重影响分类效果。IDRSN得益于其结构中的软阈值函数模块和注意力机制,能够自动设置阈值,从而减小甚至消除噪声对模型效果的影响,在不同大小的噪声数据中均能够保持较好的评估性能。
3)暂态稳定问题是一种不平衡数据集分类问题,IDSRN引入焦点损失函数FL,在对不平衡数据集设置权重系数的同时,引入调制因子,重点关注误分类样本,改善模型训练具有倾向于稳定样本的现象,提高训练效率,减少误分类情况。
4)所提方法在系统PMU配置有限时,仍能保持较好的分类性能,泛化能力较好;在出现信息冗余时,也能够对信息进行有效挖掘,减小冗余信息对模型的影响,具有较好的鲁棒性。
参考文献
[1]汤奕, 崔晗, 李峰, 等. 人工智能在电力系统暂态问题中的应用综述[J]. 中国电机工程学报, 2019, 39(1): 4-15, 317. Tang Yi, Cui Han, Li Feng, et al. Review on artificial intelligence in power system transient stability analysis[J]. Proceedings of the CSEE, 2019, 39 (1): 4-15, 317.
[2]蒋海峰, 张曼, 赵斌炎, 等. 基于改进Hilbert-Huang变换的电网故障诊断[J]. 电工技术学报, 2019, 34(增刊1): 336-342, 351. Jiang Haifeng, Zhang Man, Zhao Binyan, et al. Fault diagnosis of power grid based on improved Hilbert-Huang transform[J]. Transactions of China Electrote-chnical Society, 2019, 34(S1): 336-342, 351.
[3]倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[4]闵勇, 陈磊, 姜齐荣. 电力系统稳定分析[M]. 北京:清华大学出版社, 2016.
[5]陈厚合, 王长江, 姜涛, 等. 基于端口能量的含VSC-HVDC的交直流混合系统暂态稳定评估[J]. 电工技术学报, 2018, 33(3): 498-511. Chen Houhe, Wang Changjiang, Jiang Tao, et al. Transient stability assessment in hybrid AC/DC systems with VSC-HVDC via port energy[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 498-511.
[6]刘艳芳, 顾雪平. 一种用于半监督BP算法的实用结束判据及其应用[J]. 电力系统自动化, 2003, 27(14): 41-44. Liu Yanfang, Gu Xueping. A useful ending-criterion of semi-supervised BP algorithm and its application[J]. Automation of Electric Power Systems, 2003, 27(14): 41-44.
[7]Almasri A N, Kadir M Z, Hizam H, et al. A novel implementation for generator rotor angle stability prediction using an adaptive artificial neural network application for dynamic security assessment[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2516-2525.
[8]顾雪平, 李扬, 吴献吉. 基于局部学习机和细菌群体趋药性算法的电力系统暂态稳定评估[J]. 电工技术学报, 2013, 28(10): 277-285. Gu Xueping, Li Yang, Wu Xianji. Transient stability assessment of power systems based on local learning machine and bacterial colony chemotaxis algorithm[J]. Transactions of China Electrotechnical Society, 2013, 28 (10): 277-285.
[9]卢锦玲, 於慧敏. 极限学习机和遗传算法在暂态稳定评估特征选择中的应用[J]. 电力系统及其自动化学报, 2016, 28(12): 107-112. Lu Jinling, Yu Huimin. Application of extreme learning machine and genetic algorithm to feature selection of transient stability assessment[J]. Proceedings of the CSU-EPSA, 2016, 28 (12): 107-112.
[10]Gomez F, Rajapakse A D, Annakkage U D, et al. Support vector machine-based algorithm for post-fault transient stability status prediction using synchronized measurements[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1474-1483.
[11]霍思敏, 王科, 陈震海, 等. 基于轨迹输入特征支持向量机的湖南电网暂态稳定在线识别[J]. 电力系统保护与控制, 2012, 40(18): 19-23, 29. Huo Simin, Wang Ke, Chen Zhenhai, et al. Hunan power grid transient stability online detection based on support vector machine with trajectory input features[J]. Power System Protection and Control, 2012, 40 (18): 19-23, 29.
[12]邵雅宁, 唐飞, 刘涤尘, 等. 一种适用于WAMS量测数据的系统暂态功角稳定评估方法[J]. 电力系统保护与控制, 2015, 43(6): 33-39. Shao Yaning, Tang Fei, Liu Dichen, et al. An approach of transient angle stability assessment in power system for WAMS measured data[J]. Power System Protection and Control, 2015, 43 (6): 33-39.
[13]Wang Bo, Fang Biwu, Wang Yajun, et al. Power system transient stability assessment based on big data and the core vector machine[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2561-2570.
[14]陈厚合, 王长江, 姜涛, 等. 基于投影能量函数和Pin-SVM的电力系统暂态稳定评估[J]. 电工技术学报, 2017, 32(11): 71-80. Chen Houhe, Wang Changjiang, Jiang Tao, et al. Transient stability assessment in bulk power grid using projection energy function and support vector machine with Pinball loss[J]. Transactions of China Electrotechnical Society, 2017, 32 (11): 71-80.
[15]田芳, 周孝信, 于之虹. 基于支持向量机综合分类模型和关键样本集的电力系统暂态稳定评估[J]. 电力系统保护与控制, 2017, 45(22): 6-13. Tian Fang, Zhou Xiaoxin, Yu Zhihong. Power system transient stability assessment based on comprehensive SVM classification model and key sample set[J]. Power System Protection and Control, 2017, 45 (22): 6-13.
[16]Amraee T, Ranjbar S. Transient instability prediction using decision tree technique[J]. IEEE Transactions on Power Systems, 2013, 28(3): 3028-3037.
[17]石访, 张林林, 胡熊伟, 等. 基于多属性决策树的电网暂态稳定规则提取方法[J]. 电工技术学报, 2019, 34(11): 122-132. Shi Fang, Zhang Linlin, Hu Xiongwei, et al. Power system transient stability rules extraction based on multi-attribute decision tree[J]. Transactions of China Electrotechnical Society, 2019, 34 (11): 122-132.
[18]He Miao, Zhang Junshan, Vittal V. Robust online dynamic security assessment using adaptive ensemble decision-tree learning[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4089-4098.
[19]Chen Minghua, Liu Qunying, Chen Shuheng, et al. XGBoost-based algorithm interpretation and application on post-fault transient stability status prediction of power system[J]. IEEE Access, 2019: 13149-13158.
[20]张晨宇, 王慧芳, 叶晓君. 基于XGBoost算法的电力系统暂态稳定评估[J]. 电力自动化设备, 2019, 39(3): 83-89, 95. Zhang Chenyu, Wang Huifang, Ye Xiaojun. Transient stability assessment of power system based on XGBoost algorithm[J]. Electric Power Automation Equipment, 2019, 39 (3): 83-89, 95.
[21]周挺, 杨军, 周强明, 等. 基于改进LightGBM的电力系统暂态稳定评估方法[J]. 电网技术, 2019, 43(6): 81-90. Zhou Ting, Yang Jun, Zhou Qiangming, et al. Power system transient stability assessment based on modified LightGBM[J]. Power System Technology, 2019, 43 (6): 81-90.
[22]李兵洋, 肖健梅, 王锡淮. 融合邻域粗糙约简与深度森林的电力系统暂态稳定评估[J]. 电工技术学报, 2020, 35(15): 3245-3257. Li Bingyang, Xiao Jianmei, Wang Xihuai. Power system transient stability assessment based on hybrid neighborhood rough reduction and deep forest[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3245-3257.
[23]徐春华, 陈克绪, 马建, 等. 基于深度置信网络的电力负荷识别[J]. 电工技术学报, 2019, 34(19): 4135-4142. Xu Chunhua, Chen Kexu, Ma Jian, et al. Recognition of power loads based on deep belief network[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4135-4142.
[24]张倩, 王建平, 李帷韬. 基于反馈机制的卷积神经网络绝缘子状态检测方法[J]. 电工技术学报, 2019, 34(16): 3311-3321. Zhang Qian, Wang Jianping, Li Weitao. Insulator state detection of convolutional neural networks based on feedback mechanism[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3311-3321.
[25]周念成, 廖建权, 王强钢, 等. 深度学习在智能电网中的应用现状分析与展望[J]. 电力系统自动化, 2019, 43(4): 180-197. Zhou Niancheng, Liao Jianquan, Wang Qianggang, et al. Analysis and prospect of deep learning application in smart grid[J]. Automation of Electric Power Systems, 2019, 43 (4): 180-197.
[26]胡伟, 郑乐, 闵勇, 等. 基于深度学习的电力系统故障后暂态稳定评估研究[J]. 电网技术, 2017, 41(10): 3140-3146. Hu Wei, Zheng Le, Min Yong, et al. Research on power system transient stability assessment based on deep learning of big data technique[J]. Power Grid Technology, 2017, 41 (10): 3140-3146.
[27]朱乔木, 党杰, 陈金富, 等. 基于深度置信网络的电力系统暂态稳定评估方法[J]. 中国电机工程学报, 2018, 38(3): 735-743. Zhu Qiaomu, Dang Jie, Chen Jinfu, et al. A method for power system transient stability assessment based on deep belief networks[J]. Proceedings of the CSEE, 2018, 38 (3): 735-743.
[28]李宝琴, 吴俊勇, 邵美阳, 等. 基于集成深度置信网络的精细化电力系统暂态稳定评估[J]. 电力系统自动化, 2020, 44(6):17-28. Li Baoqin, Wu Junyong, Shao Meiyang, et al. Refined transient stability evaluation for power system based on ensemble deep belief network[J]. Automation of Electric Power Systems, 2020, 44(6):17-28.
[29]杨维全, 朱元振, 刘玉田. 基于卷积神经网络的暂态电压稳定快速评估[J]. 电力系统自动化, 2019, 43(22): 46-52, 139. Yang Weiquan, Zhu Yuanzhen, Liu Yutian. Fast assessment of transient voltage stability based on convolutional neural network[J]. Automation of Electric Power Systems, 2019, 43(22): 46-52, 139.
[30]高昆仑, 杨帅, 刘思言, 等. 基于一维卷积神经网络的电力系统暂态稳定评估[J]. 电力系统自动化, 2019, 43(12): 30-38. Gao Kunlun, Yang Shuai, Liu Siyan, et al. Transient stability assessment for power system based on one-dimensional convolutional neural network[J]. Automation of Electric Power Systems, 2019, 43 (12): 30-38.
[31]Yan Rong, Geng Guangchao, Jiang Quanyuan, et al. Fast transient stability batch assessment using cascaded convolutional neural networks[J]. IEEE Transactions on Power Systems, 2019, 34(4): 2802-2813.
[32]Shi Zhongtuo, Yao Wei, Zeng Lingkang, et al. Convolutional neural network-based power system transient stability assessment and instability mode prediction[J]. Applied Energy, 2020, 263: 114586.
[33]Zhu Qiaomu, Chen Jinfu, Zhu Lin, et al. A deep end-to-end model for transient stability assessment with PMU data[J]. IEEE Access, 2018, 6: 65474-65487.
[34]朱乔木, 陈金富, 李弘毅, 等. 基于堆叠自动编码器的电力系统暂态稳定评估[J]. 中国电机工程学报, 2018, 38(10): 2937-2946, 3144. Zhu Qiaomu, Chen Jinfu, Li Hongyi, et al. Transient stability assessment based on stacked autoencoder[J]. Proceedings of the CSEE, 2018, 38 (10): 2937-2946, 3144.
[35]王怀远, 陈启凡. 基于代价敏感堆叠变分自动编码器的暂态稳定评估方法[J]. 中国电机工程学报, 2020, 40(7): 2213-2220, 2400. Wang Huaiyuan, Chen Qifan. A transient stability assessment method based on cost-sensitive stacked variational auto-encoder[J]. Proceedings of the CSEE, 2020, 40 (7): 2213-2220, 2400.
[36]谭本东, 杨军, 赖秋频, 等. 基于改进CGAN的电力系统暂态稳定评估样本增强方法[J]. 电力系统自动化, 2019, 43(1): 203-214. Tan Bendong, Yang Jun, Lai Qiupin, et al. Data augment method for power system transient stability assessment based on improved conditional generative adversarial network[J]. Automation of Electric Power Systems, 2019, 43(1): 203-214.
[37]Zhao Minghang, Zhong Shisheng, Fu Xuyun, et al. Deep residual shrinkage networks for fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2019, 16(7): 4681-4690.
[38]He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Deep residual learning for image recognition[C]// IEEE Conference on Computer Vision & Pattern Recognition. IEEE Computer Society, Las Vegas, USA, 2016: 770-778.
[39]Lin Tsungyi, Goyal P, Girshick R, et al. Focal loss for dense object detection[C]//2017 IEEE International Conference on Computer Vision (ICCV), 2017, Venice, Italy, 2999-3007.
[40]Shelhamer E, Long J, Darrell T, et al. Fully convolutional networks for semantic segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(4): 640-651.
[41]Ioffe S, Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift[C]//international conference on machine learning, Lile, France, 2015: 448-456.
[42]Martin K E, Hamai D, Adamiak M, et al. Exploring the IEEE Standard C37. 118–2005 synchrophasors for power systems[J]. IEEE Transactions on Power Delivery, 2008, 23(4): 1805-1811.
[43]Ke Guolin, Meng Qi, Finley T W, et al. LightGBM: a highly efficient gradient boosting decision tree[C]//Advances in Neural Information Processing Systems, Long Beach, USA, 2017: 3147-3155.
Power System Transient Stability Assessment Based on Improved Deep Residual Shrinkage Network
Abstract In power system transient stability assessment, the measurement data of power system synchronous phasor measurement unit (PMU) may exist noise problems during acquisition and transmission process, and the transient stability and instability samples are imbalanced, resulting in the tendency of data-driven transient stability assessment model training and serious misjudgment problems. This paper proposes a power system transient stability assessment method based on improved deep residual shrinkage networks (IDRSN). First, the bottom-level measured electrical quantity is constructed as a feature map as the input of model, and the deep structure of model is used to establish the mapping relationship between the input and the stable result. Faced with noise problems, the model uses the attention mechanism to automatically learn the noise threshold through a soft threshold function to reduce noise and irrelevant feature interference; and through focus loss function (FL), the weight coefficient is introduced to correct the tendency of model training. Modulation factors is used to focus on misclassified samples to improve model training efficiency and evaluation performance. Through the simulation verification of the New England 10-machine 39-node system, the proposed model can effectively reduce the noise interference of different degrees, correct the bias of the model training on the imbalanced data set, and reduce the misclassified samples. Under different PMU configuration schemes, all are obtained better evaluation effect.
keywords:Power system, transient stability assessment, deep learning, deep residual shrinkage network, focal loss
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.200437
收稿日期 2020-05-05
改稿日期 2020-08-05
卢锦玲 女,1971年生,博士,副教授,研究方向为电力系统运行、分析与控制等。E-mail:lujinling@126. com
郭鲁豫 女,1996年生,硕士研究生,研究方向为电力系统运行、分析。E-mail:guoluyu111@126. com(通信作者)
(编辑 赫蕾)