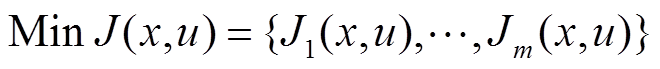 (1)
(1)摘要 随着综合能源系统的提出,电网和天然气网之间联系越来越紧密。为了保证电-气互联系统的安全、经济运行,需要对其进行联合规划研究。首先根据系统具有大规模、多维、非凸、非线性等特性,提出一种电-气能源互联系统的多目标优化调度模型;其次,针对多目标求解算法中种群收敛性和分布性冲突不断加剧的现象,提出一种加强非支配解占优关系的多目标差分进化算法;最后,以IEEE 30节点电力系统和比利时20节点天然气系统为例,说明了所提算法能够对所考虑的目标函数产生分布良好的帕累托最优前沿,而且可以在高维目标求解中得到一组较好的优化解,以此满足不同工况下系统的运行要求。
关键词:最优潮流 综合能源系统 多目标优化 加强非支配解占优关系 差分进化
最优潮流(Optimal Power Flow, OPF)问题是一个大规模、多维、非凸、非线性、有约束的优化问题[1-2]。目前大部分OPF问题的研究都是基于以化石燃料燃烧为主的传统电网进行的,但随着一次能源的不断减少和环境污染问题的不断加重,寻找一种清洁的能源代替传统的能源是非常必要的[3-4]。由于天然气具有燃烧完全、燃烧热值高、碳排放量低、有害物质排放少等优点,而且我国天然气储量丰富,所以使用天然气发电的比例越来越高。根据《电力发展“十三五”规划》,全国气电将新增投产5万MW,2020年达到1.1亿kW,因此,天然气发电将成为电网和气网联系的主要纽带[5-6]。随着综合能源系统[6](Inter grated Energy System, IES)的提出,不同能源之间相互连接,潮流运行分析不只限于传统电网,对气网等多能源进行综合潮流分析也是一个非常有意义的研究课题。
由于IES涉及煤炭、石油、天然气、电能等多种能源,包含许多设备,所以系统整体的运行情况会变得非常复杂,需要从能效、经济、环境、安全等多个方面进行综合优化,从而需要建立多目标的优化策略来满足不同工况的需求。为了应对新能源注入电网的不确定性,文献[7]将区间算法引入潮流运算中。文献[8]提出了一种适用于电-气-热互联系统的扩展N-R潮流分析算法,并提出了将压缩机与气网分离的建模方法。文献[9]建立了电、气、热潮流的统一求解模型,文献[10]在文献[9]基础上,提出了电-气-热多能流系统的分布式顺序求解算法,并对IES的不同耦合情况分别进行了分析。但以上文献只是基于当前运行状态对IES进行统一的潮流分析,并没有从优化的角度构建潮流模型。文献[11]对IES进行了统一优化,同时考虑不确定能源注入时的影响。文献[12-13]将碳交易机制引入电-气互联IES中,分析了不同碳交易价格、天然气价格时系统的运行状况。文献[14]重点考虑了环境影响下的气-电IES的运行模式,并利用内点法对综合系统进行优化。文献[15]将㶲效率引入了IES中,并利用凸松弛方法将系统模型转换成凸优化问题进行OPF分析。虽然文献[11-15]对能源系统进行了优化,但它们只是考虑了系统运行的经济性、安全性等方面,不能满足现代电力市场对综合能源系统运行的需求。尽管存在一些传统的优化算法,如非线性规划法、二次规划法、内点法等,但这些算法主要是对单一目标进行优化时才能得到较理想的优化解,显然这已经不能满足多目标优化时的需求。
近年来启发式优化算法,如粒子群优化算法(Particle Swarm Optimization, PSO)、多目标遗传算法(Non Dominated Sorting Genetic Algorithm-II, NSGA-II)和多目标差分进化算法(Multi-Objective Differential Evolution, MODE)[16-19]等被广泛应用于最优潮流优化问题。与经典优化算法不同的是,它们克服了系统模型中非凸、非线性的缺点,利用强大的搜索能力,在复杂的约束环境下寻找到一组优化解。文献[20-22]基于权重因子方法将多目标转换成单目标进行优化,但对复杂的IES来说,很难找到一组合适的权重因子。文献[23-25]基于Pareto占优关系进行快速非支配排序对目标函数进行优化,而这种优化方法只适用于2~3个目标的多目标优化问题。然而,在优化IES时,随着目标函数的增加,基于Pareto支配关系的多目标优化算法的寻优能力会变得非常差,很难找到一组均衡收敛性和分布性的优化解集[26]。
综上所述,本文针对目前电-气互联系统最优潮流求解中存在的问题,提出了基于加强非支配关系的多目标差分进化算法,解决了高维目标寻优时Pareto占优关系变弱的问题,同时在种群进化过程中加入了优势个体寻优操作,克服了由于进化而使优势个体寻优能力变弱的现象,进一步提高了本文算法的寻优能力。最后利用IEEE 30节点电力系统和比利时20节点天然气系统进行仿真,证明了所提算法的优越性。
最优潮流是在满足系统中等式约束和不等式约束的前提下,通过调整系统中可利用的手段实现预定目标最优的系统稳定运行状态[27]。在IES潮流优化时,所求解的这些目标函数往往是相互抑制的,并且很难找到一个最优解满足这些目标。因此,只能将潮流优化问题转换为多目标优化问题。最优潮流问题是一个典型的非线性、非凸的多目标规划问题,可以表示为
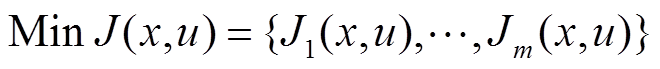 (1)
(1)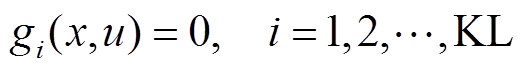 (2)
(2)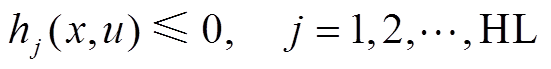 (3)
(3)式中,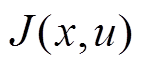 为目标函数,一共有
为目标函数,一共有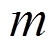 个目标函数;
个目标函数;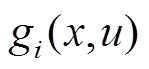 =0和
=0和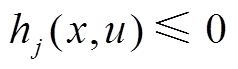 分别为第
分别为第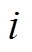 个等式约束和第
个等式约束和第![]() 个不等式约束,其中
个不等式约束,其中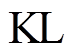 和
和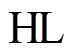 分别为等式约束和不等式约束的个数;
分别为等式约束和不等式约束的个数;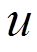 为控制变量,其包括发电机的有功功率
为控制变量,其包括发电机的有功功率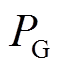 、发电机端电压幅值
、发电机端电压幅值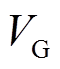 、并联无功补偿器
、并联无功补偿器![]() 、线路的变压器电压比
、线路的变压器电压比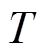 、气网管道平衡节点压强
、气网管道平衡节点压强 、压缩机的压缩比
、压缩机的压缩比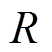 和气源点天然气流量
和气源点天然气流量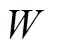 ;
;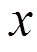 为状态变量,其包括松弛节点处发电机的有功功率
为状态变量,其包括松弛节点处发电机的有功功率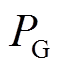 、发电机无功功率
、发电机无功功率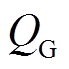 、
、![]() 节点处的电压幅值
节点处的电压幅值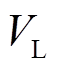 、线路传输功率
、线路传输功率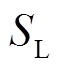 、气网管道中除平衡节点的节点压强
、气网管道中除平衡节点的节点压强 和平衡节点的天然气流量
和平衡节点的天然气流量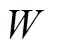 。所以,
。所以,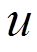 和
和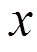 可以表示为
可以表示为
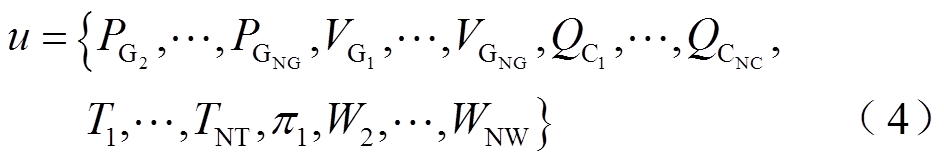
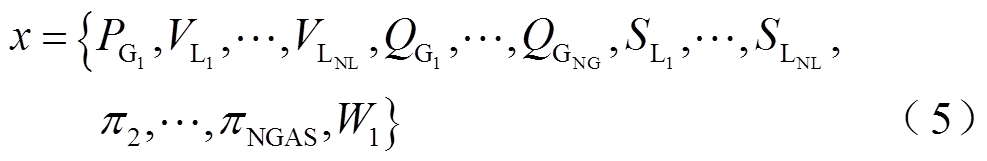
式中,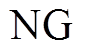 为发电机的数量;
为发电机的数量;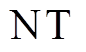 为变压器的数量;
为变压器的数量;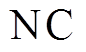 为并联无功补偿器的数量;
为并联无功补偿器的数量;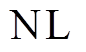 为线路的数量;
为线路的数量;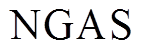 为天然气的节点数量;
为天然气的节点数量;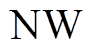 为天然气网气源点的数量。
为天然气网气源点的数量。
以燃料费用最小作为第一个目标函数,即
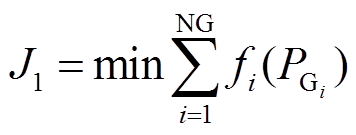 (6)
(6)其中,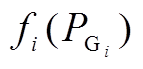 可表示为
可表示为
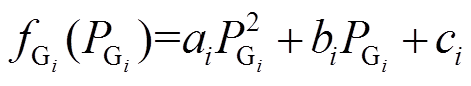 (7)
(7)式中,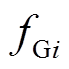 为第
为第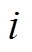 台发电机关于有功功率
台发电机关于有功功率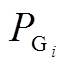 的费用函数;
的费用函数;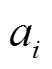 、
、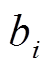 和
和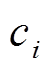 为第
为第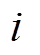 台发电机的燃料费用系数。
台发电机的燃料费用系数。
考虑到煤炭燃烧产生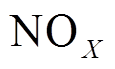 和
和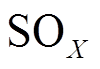 等污染物对环境的影响,因此,将污染物排放量作为第二个目标函数,即
等污染物对环境的影响,因此,将污染物排放量作为第二个目标函数,即
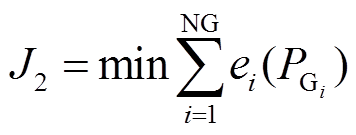 (8)
(8)其中,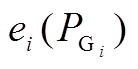 可表示为
可表示为
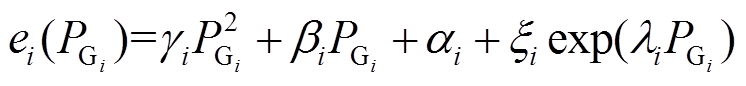 (9)
(9)式中,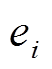 为第
为第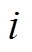 台发电机所排放的废气量;
台发电机所排放的废气量;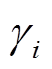 、
、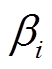 、
、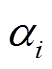 、
、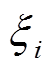 和
和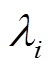 为第
为第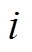 台发电机所排废气量的拟合系数。
台发电机所排废气量的拟合系数。
减少线路的功率损耗可以提高一次能源的利用效率,同时也是降低环境污染的一个有效措施。所以,将线路间的有功损耗作为第三个目标函数,即
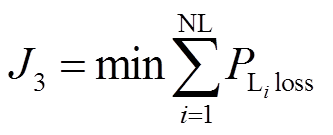 (10)
(10)式中,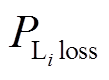 为
为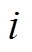 条线路的有功损耗,可表示为
条线路的有功损耗,可表示为
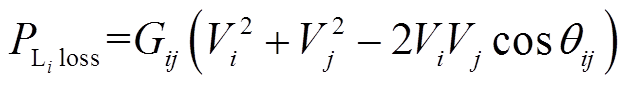 (11)
(11)电压偏差也是电力系统中电压质量的一种衡量指标,为了提高电力系统的稳定性、降低系统崩溃的发生率,将电压波动作为第四个目标函数,即所有节点与标幺值的累计偏差为
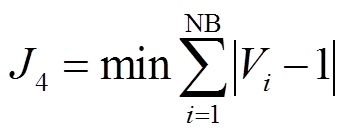 (12)
(12)在求天然气系统最优潮流目标函数时,以消耗天然气总成本最少为目标,即
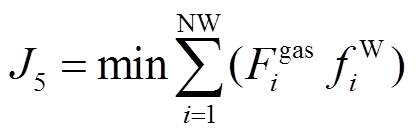 (13)
(13)式中,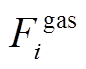 为气源点天然气的价格;
为气源点天然气的价格;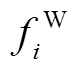 为节点
为节点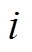 输入的天然气量。
输入的天然气量。
在天然气运输过程中,管道内的气体压力会因为气体与管道内壁摩擦而使压力减小,因此需要向管道内不断地注入压力,使气体到达负荷侧[28-29]。本文采用燃气压缩机为管道补偿压力损失,并选用燃气压缩机的气体消耗量作为其中的一个目标函数,即
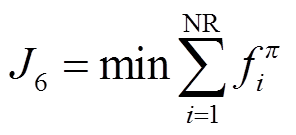 (14)
(14)式中,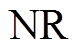 为燃气压缩机的数量;
为燃气压缩机的数量;![]() 为第
为第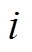 台燃气压缩机消耗的天然气流量,其表达式为
台燃气压缩机消耗的天然气流量,其表达式为
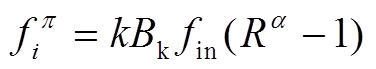 (15)
(15)式中,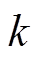 为能量效率转换常数;
为能量效率转换常数;![]() 为压缩机的入口流量;
为压缩机的入口流量;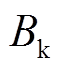 为与压缩机效率、温度、天然气热值有关的常数;
为与压缩机效率、温度、天然气热值有关的常数;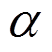 为与压缩机相关的多变指数;
为与压缩机相关的多变指数;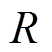 为压缩机的压缩比[12]。
为压缩机的压缩比[12]。
1.2.1 等式约束条件
等式约束包括电网中节点功率平衡方程和气网节点天然气流量平衡方程,即
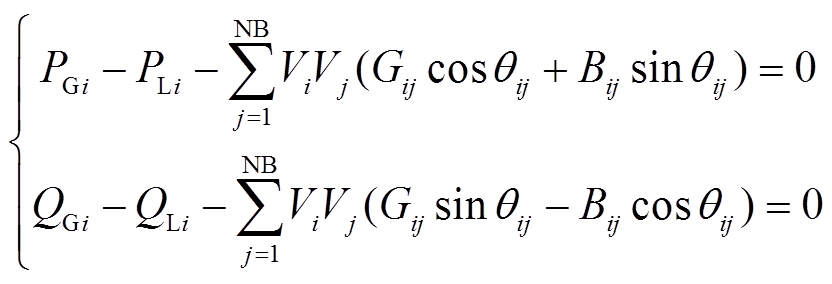 (16)
(16)式中,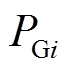 、
、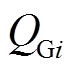 分别为第
分别为第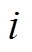 条母线上发电机发出的有功功率和无功功率;
条母线上发电机发出的有功功率和无功功率;![]() 和
和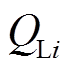 分别为第
分别为第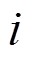 条母线上的有功负荷和无功负荷;
条母线上的有功负荷和无功负荷;![]() 、
、![]() 和
和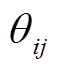 分别为节点
分别为节点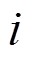 和
和![]() 之间线路的电导、电纳和两个节点的相位差;
之间线路的电导、电纳和两个节点的相位差;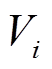 为节点
为节点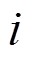 的电压幅值。节点流量平衡方程为
的电压幅值。节点流量平衡方程为
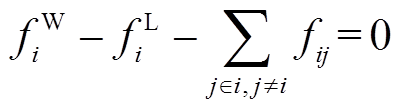 (17)
(17)式中,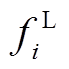 为节点
为节点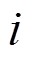 消耗的天然气量;
消耗的天然气量;![]() 为天然气系统节点
为天然气系统节点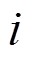 和
和![]() 的天然气传输量,其计算式为
的天然气传输量,其计算式为
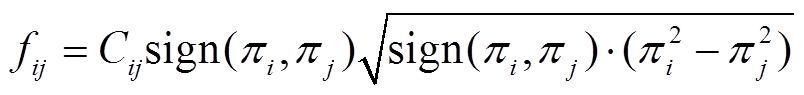 (18)
(18)式中,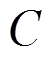 为管道系数;
为管道系数;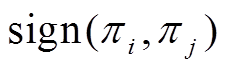 为气体流动的方向,当
为气体流动的方向,当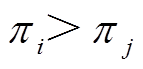 时取+1,否则取-1,具体参数请见文献[10]。
时取+1,否则取-1,具体参数请见文献[10]。
若节点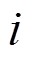 和节点
和节点![]() 之间有
之间有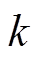 条输气管道,那么它的等效管道常数为
条输气管道,那么它的等效管道常数为
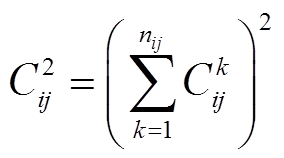 (19)
(19)1.2.2 不等式约束条件
不等式约束包括发电机输出功率约束、节点电压约束和支路功率约束、天然气管道压强约束、气源点输出天然气流量约束等,即
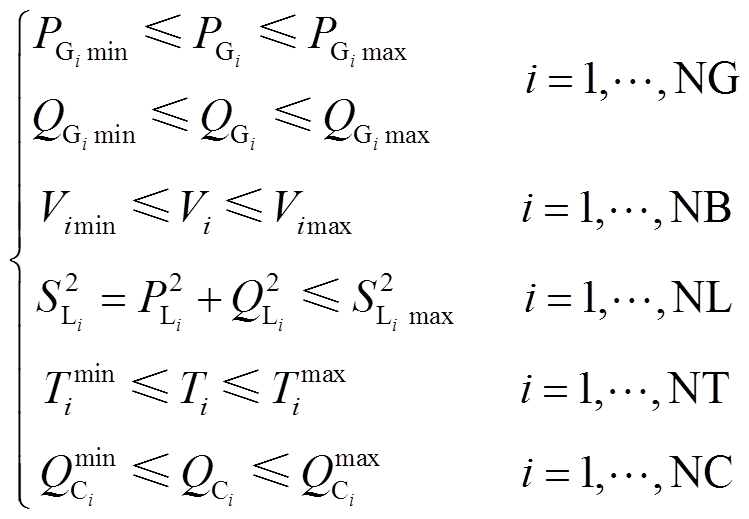 (20)
(20)式中,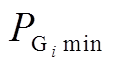 和
和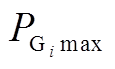 分别为第
分别为第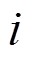 台发电机所发有功功率的下、上限;
台发电机所发有功功率的下、上限;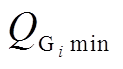 和
和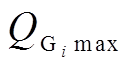 分别为第
分别为第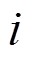 台发电机所发无功功率的下、上限;
台发电机所发无功功率的下、上限;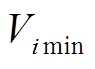 和
和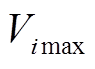 分别为节点
分别为节点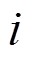 电压幅值的下、上限;
电压幅值的下、上限;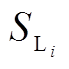 为第
为第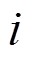 条线路的视在功率;
条线路的视在功率;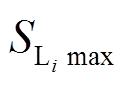 为第
为第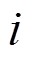 条线路的功率传输极限;
条线路的功率传输极限;![]() 为第
为第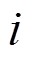 个变压器的电压比;
个变压器的电压比;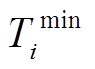 和
和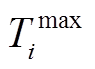 为
为![]() 的下、上限;
的下、上限;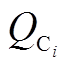 为第
为第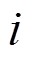 个无功功率补偿器的补偿值;
个无功功率补偿器的补偿值;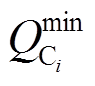 和
和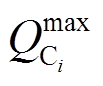 分别为其补偿值的下、上限。
分别为其补偿值的下、上限。
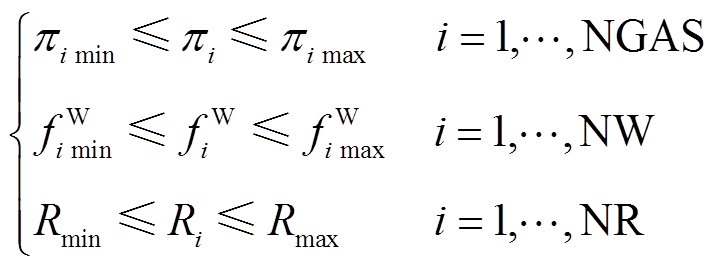 (21)
(21)式中,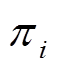 为天然气节点
为天然气节点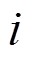 的管道压强;
的管道压强;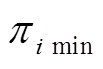 和
和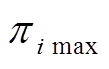 分别为节点
分别为节点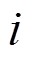 的管道压强的下、上限;
的管道压强的下、上限;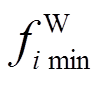 和
和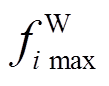 分别为节点
分别为节点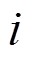 所提供天然气量的下、上限;
所提供天然气量的下、上限;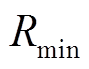 和
和 分别为压缩机压缩比的下、上限。
分别为压缩机压缩比的下、上限。
多目标差分进化算法是在遗传算法(Genetic Algorithm, GA)等进化思想的基础上提出来的一种用于求解多维空间中目标的优化算法。本节针对多目标求解算法中种群收敛性和分布性冲突不断加剧的现象,提出了一种强化非支配解占优关系的多目标差分进化算法。与原来的进化算法相比,如:NSGAII,增加了寻优操作;而且根据Pareto最优解集的思想,重新定义了非支配占优的关系。通过每一次进化得到一组非劣解,经过迭代最终得到一组优化解集,然后根据决策者对不同的运行工况做出选择。
2.1.1 参数向量的初始化
差分进化是在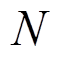 维连续空间中找出最优解的一种优化算法,它从一个随机初始化的实值函数向量开始。设它的种群个体为
维连续空间中找出最优解的一种优化算法,它从一个随机初始化的实值函数向量开始。设它的种群个体为 ,进化次数为
,进化次数为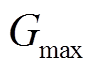 ,向量空间为
,向量空间为
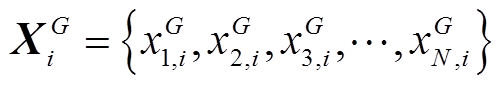 (22)
(22)其中,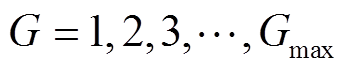 ;
;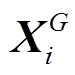 的范围为
的范围为
![]()
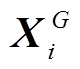
![]()
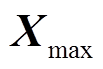 ,
,
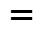
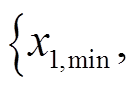


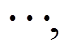
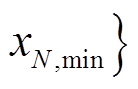 ,
,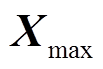
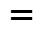
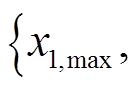
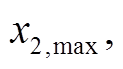
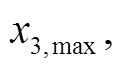
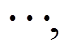
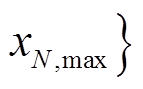 。
。
为了更好地寻找到适应度值,避免陷入局部最优,初始向量应该包括整个搜索空间,即
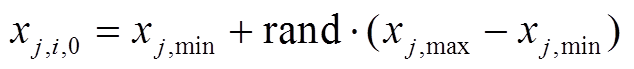 (23)
(23)式中,![]() ;
;![]() 。
。
2.1.2 变异、交叉操作
随着目标函数的增加,约束条件之间相互抑制,会使进化速度变慢,需要加快其进化的速度、避免陷入局部最优。因此,从上一代种群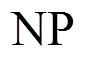 中随机选取四个个体
中随机选取四个个体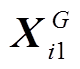 、
、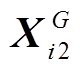 、
、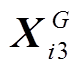 和
和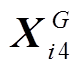 ,并通过变异和交叉,得到一个新的个体
,并通过变异和交叉,得到一个新的个体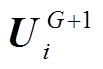 。
。
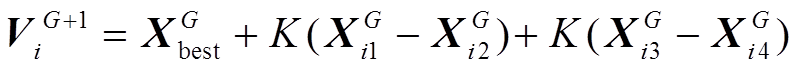 (24)
(24) (25)
(25)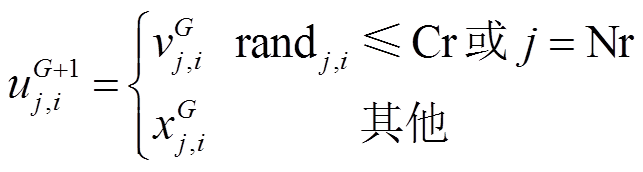 (26)
(26)式中,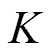 为种群变异率;
为种群变异率;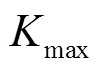 和
和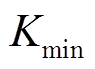 分别为最大变异率和最小变异率;
分别为最大变异率和最小变异率;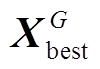 为非支配排序中的第一层随机个体;
为非支配排序中的第一层随机个体;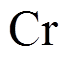 为交叉概率;
为交叉概率;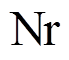 则确保一定会有新的基因注入新种群,以此来使群体不断处于进化的状态,
则确保一定会有新的基因注入新种群,以此来使群体不断处于进化的状态,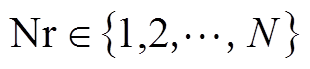 。
。
2.1.3 寻优操作
虽然变异、交叉操作能够保证个体的多样性,但是它往往只能达到最优解的附近。为了弥补这一缺点,需对优势个体进行进一步寻优操作,即
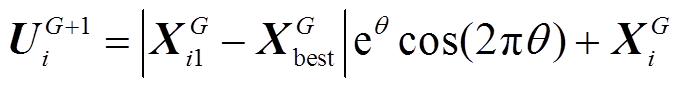 (27)
(27)式中,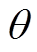 为寻优因子,随机选取,其取值范围为
为寻优因子,随机选取,其取值范围为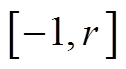 ,
,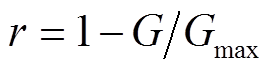 。随着迭代次数的增加,优化的值落在最优解的附近,因此,使搜索范围由大变小,搜索密集性提高。
。随着迭代次数的增加,优化的值落在最优解的附近,因此,使搜索范围由大变小,搜索密集性提高。
2.1.4 选择操作
为使下一代的群体具有更好的适应度值,利用式(28)进行个体的选择。
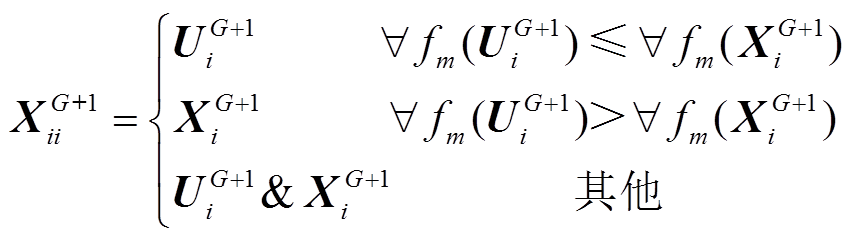 (28)
(28)2.2.1 基于Pareto的多目标选择
设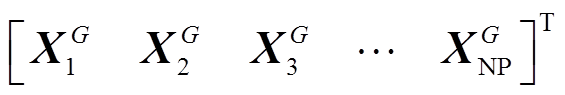 为第
为第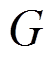 代种群个体,
代种群个体,![]() 是其适应度值,
是其适应度值,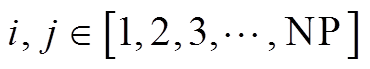 。具体操作如下:
。具体操作如下:
1)设每个个体的被支配个数为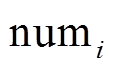 ,并令其等于0,设支配解的集合为
,并令其等于0,设支配解的集合为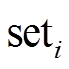 ,并令其为空集合。
,并令其为空集合。
2)从![]() =1开始,直到
=1开始,直到![]() ,对于个体
,对于个体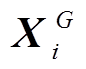 ,若任意
,若任意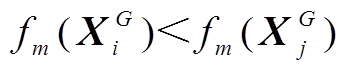 ,则
,则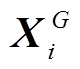 对于
对于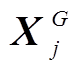 具有支配性,并将
具有支配性,并将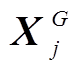 放入集合
放入集合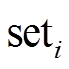 中;若任意
中;若任意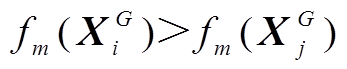 ,则使
,则使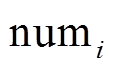
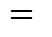
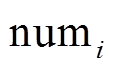 +1;若为其他情况,则进入下一循环。
+1;若为其他情况,则进入下一循环。
3)若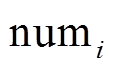 =0,则说明
=0,则说明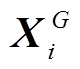 具有非支配性,并将
具有非支配性,并将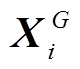 标记为1。
标记为1。
4)根据步骤2)和步骤3),将剩下的个体重新进行非支配排序,并将非支配解进行标记。
对种群个体进行非支配排序后,种群被分为N层,并对每一层的所有个体按照适应度值进行排序。在每一层中,种群个体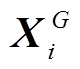 的拥挤度为
的拥挤度为
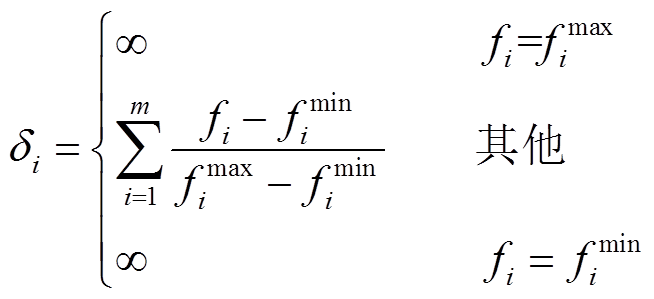 (29)
(29)式中,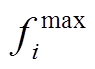 和
和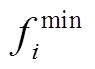 分别为当前层的最大和最小适应度值。
分别为当前层的最大和最小适应度值。
2.2.2 基于加强非支配关系的多目标选择
目前,大部分的多目标优化算法仅限于处理二维或者三维的多目标优化问题,如NSGA-II、NSGA-III[24]等,而在处理高维多目标时,非支配排序的能力被削弱。本文为了加强非支配解的占优关系,对2.2.1节中步骤2)进行了改进,根据几何夹角之间的关系,提出基于加强非支配占优关系的多目标选择方法,认为只要满足式(30),就认为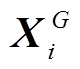 对
对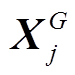 具有支配性。
具有支配性。
 (30)
(30)式中,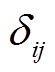 为第G代种群中个体i和j之间的夹角,即
为第G代种群中个体i和j之间的夹角,即
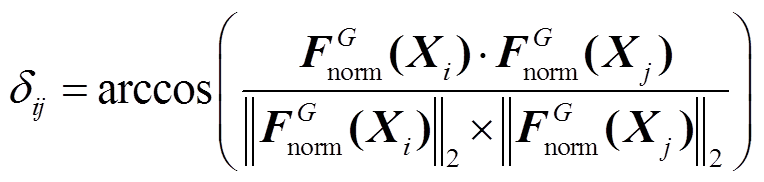 (31)
(31)式中,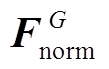 (
(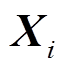 )为各个适应度值的标幺值;
)为各个适应度值的标幺值;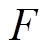 (
(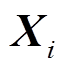 )为
)为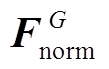 (
(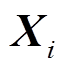 )的1范数;
)的1范数;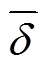 为个体间最大与最小夹角和的一半,即
为个体间最大与最小夹角和的一半,即
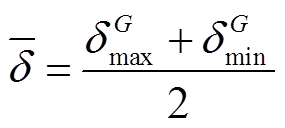 (32)
(32)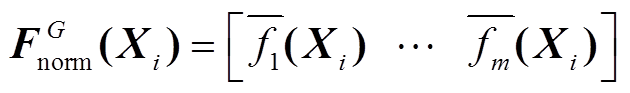 (33)
(33)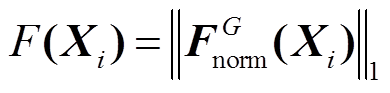 (34)
(34)根据式(30),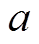 对
对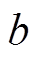 具有非支配性,如果
具有非支配性,如果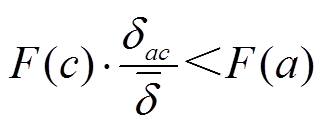 ,则c对a具有非支配性;如果
,则c对a具有非支配性;如果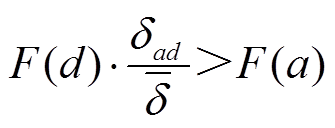 ,则a对d具有非支配性。
,则a对d具有非支配性。
基于几何夹角的非支配占优关系如图1所示。
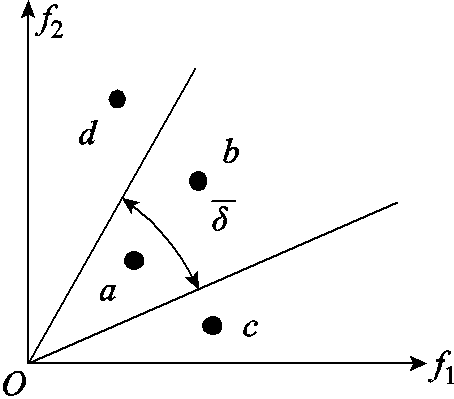
图1 基于几何夹角的非支配占优关系图
Fig.1 A dominant relationship of non-dominant solution nondominant diagram based on geometric angle
随着目标函数的增加,利用传统的拥挤度控制方法已经不能满足解向量在高维解空间中的均匀分布。因此,引入基于偏角的种群拥挤度控制策略[30],使种群均匀分散在可行域内,即
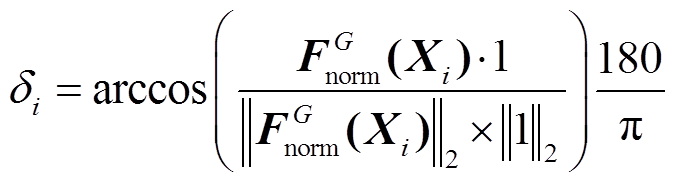 (35)
(35)本文所考虑的电-气互联系统是一种含有多种类型约束条件的非凸、非线性的多目标优化模型。利用强化多目标差分进化算法(S-MODE),最终可以得到一组优化解。
电-气互联系统多目标最优潮流求解策略流程如图2所示。
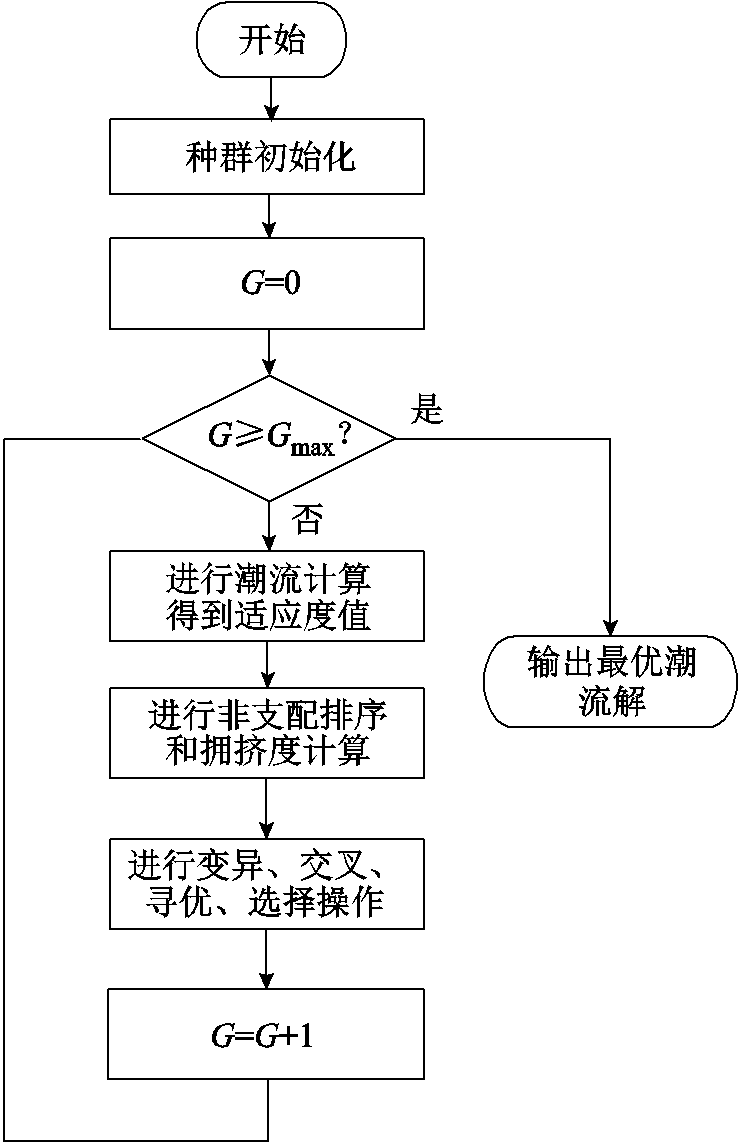
图2 电-气互联系统多目标最优潮流求解策略流程
Fig.2 Flow chart of multi-objective optimal power flow solution strategy forintegrated electricity and gas systems
S-MODE算法的最优潮流计算流程如下:
1)确定算法各项初始参数,如电力系统、天然气网的网络参数、进化次数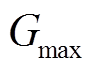 、种群数
、种群数 和约束参数等,对种群进行初始化并令
和约束参数等,对种群进行初始化并令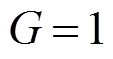 。
。
2)根据牛顿-拉弗逊法,对初始化后的个体进行潮流计算,得到适应度值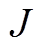 ,其中迭代精度需要满足
,其中迭代精度需要满足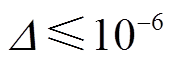 。
。
3)根据式(30)~式(35)对种群进行强化非支配排序和拥挤度计算。
4)根据式(27)对第一层的个体进行寻优操作,对其他层的个体进行变异、交叉操作得到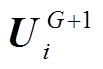 ,并利用步骤2)得到新个体的适应度值,然后根据式(28)得到新的子代种群
,并利用步骤2)得到新个体的适应度值,然后根据式(28)得到新的子代种群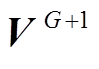 。
。
5)对新的子代种群进行强化非支配排序和拥挤度计算,然后利用竞标赛法筛选出 个优势个体。
个优势个体。
6)判断进化次数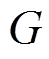 是否大于
是否大于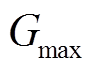 ,若是,则退出循环;否则返回步骤3)。
,若是,则退出循环;否则返回步骤3)。
为了验证加强非支配解占优关系的多目标差分算法在电-气互联系统潮流的有效性,本文利用IEEE 30节点电力系统、比利时20节点天然气系统,通过燃气轮机耦合成一个电-气互联的能源系统。IEEE 30节点电力系统如图3所示。IEEE 30节点系统中包括6台发电机、41条支路、4个变压器和9个并联无功补偿器,总的装机容量为435MW,总负荷为283.4MW,其他参数详见文献[31]。比利时天然气20节点系统中包括6个气源点、2台压缩机、23条天然气通道,其他参数详见文献[12]和附录。
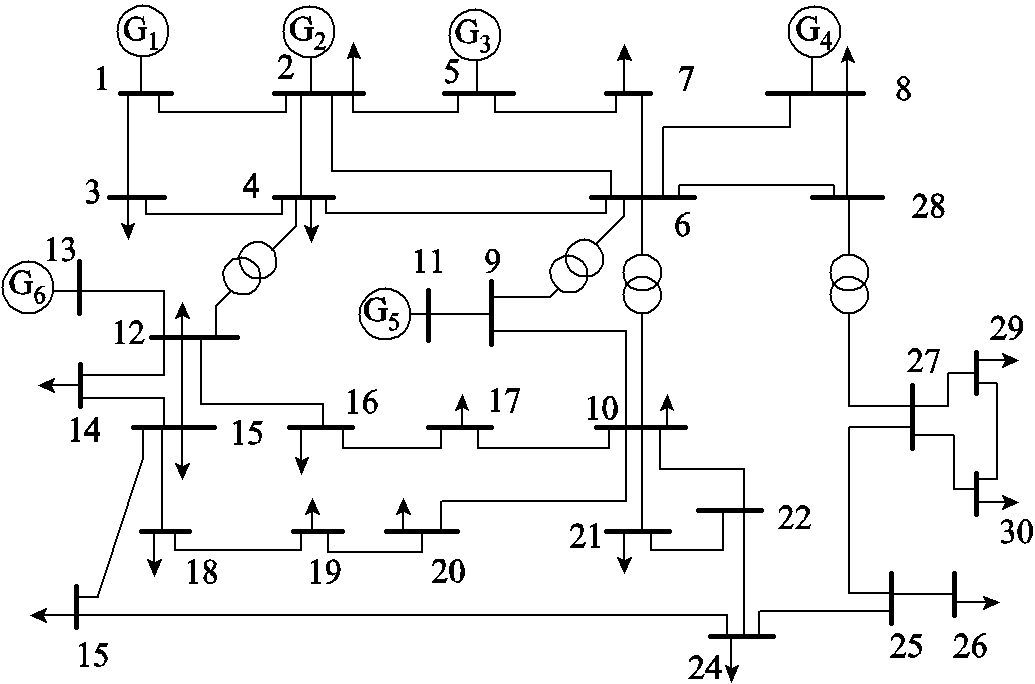
图3 IEEE 30节点电力系统
Fig.3 Topology diagram of IEEE 30-bus system
4.2.1 低维目标时的最优潮流
根据文献[26],小于或等于3个目标函数的优化算法为低维目标优化算法,大于3个目标函数的优化算法为高维目标优化算法。
首先,为了验证S-MODE算法在低维目标寻优中的优越性,基于传统电网,利用NSGA-II算法、PSO算法、GA算法和文献[24]中的算法与其进行对比,其中目标函数为燃料费用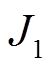 和污染物排放量
和污染物排放量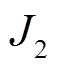 ,所有算法搜索个体
,所有算法搜索个体 均设为50,迭代次数
均设为50,迭代次数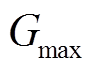 设为100。
设为100。
从图4可以看出,本文算法的Pareto前沿解集优于其他三种算法,即在不同运行模式下,能够保证在污染物排放量最低的时候,燃料费用也是最少的。这说明S-MODE算法在多目标寻优过程中更容易找到良好的折中解。具体IEEE 30节点电力系统不同算法结果对比见表1。
表1 IEEE 30节点电力系统不同算法结果对比
Tab.1 Comparison solutions for different algorithms of IEEE 30-bus system
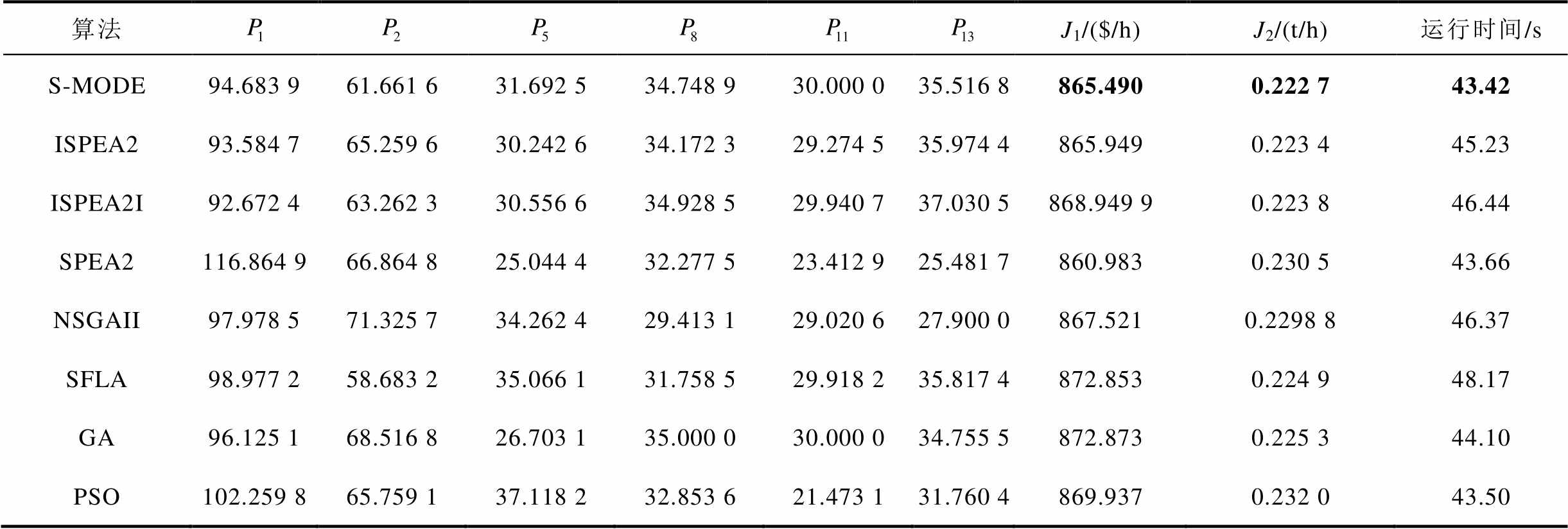
算法J1/($/h)J2/(t/h)运行时间/s S-MODE94.683 961.661 631.692 534.748 930.000 035.516 8865.4900.222 743.42 ISPEA293.584 765.259 630.242 634.172 329.274 535.974 4865.9490.223 445.23 ISPEA2I92.672 463.262 330.556 634.928 529.940 737.030 5868.949 90.223 846.44 SPEA2116.864 966.864 825.044 432.277 523.412 925.481 7860.9830.230 543.66 NSGAII97.978 571.325 734.262 429.413 129.020 627.900 0867.5210.2298 846.37 SFLA98.977 258.683 235.066 131.758 529.918 235.817 4872.8530.224 948.17 GA96.125 168.516 826.703 135.000 030.000 034.755 5872.8730.225 344.10 PSO102.259 865.759 137.118 232.853 621.473 131.760 4869.9370.232 043.50
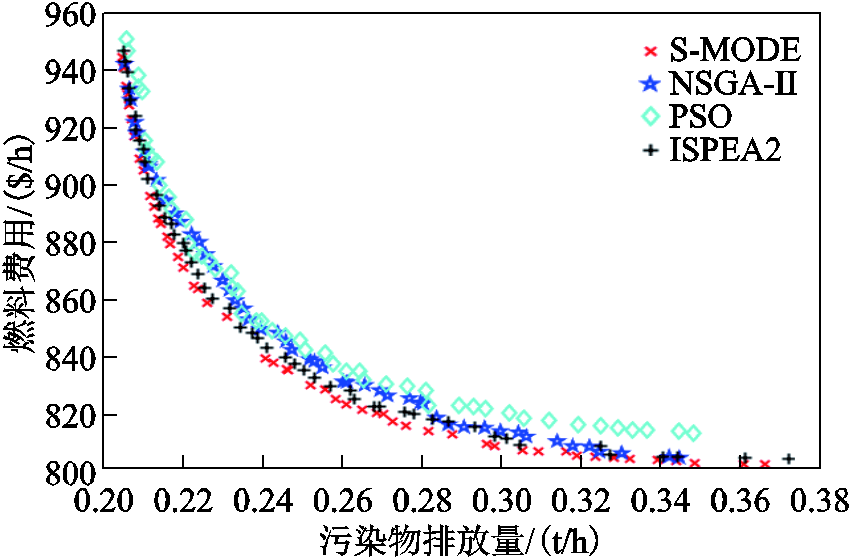
图4 IEEE 30节点电力系统不同算法对比
Fig.4 Pareto frontiers of different algorithms for the IEEE 30-bus system
从表1也可以看出,在IEEE 30节点电力系统的算例中,本文算法与ISPEA2(improved strength Pareto evolutionary algorithm)、NSGAII、GA等七种优化算法相比较,当燃料花费为865.49$/h时,污染物排放量为0.222 7t/h,从而可以验证在低维多目标OPF的优化过程中,本文算法所得出的运行模式与其他算法所得出的相比完全占优。
为了证明寻优操作在本文算法中的作用,通过在S-MODE算法中添加寻优操作和不添加寻优操作进行对比分析,虽然最终结果一样,但将寻优操作加入算法中,只需要迭代50次,历时43.42s,而不加时,需要迭代60次才能得到理想的效果,即加入寻优操作这一项可以提高运行的速度,缩短运行时间。
4.2.2 高维目标时的最优潮流
为了验证本文算法在高维目标优化和电-气互联系统优化时的有效性,将电网与天然气网互联,其中,图1中节点11和节点13分别与图5比利时天然气系统中的节点4和12相连,使用燃气轮机作为能量传输通道,形成电-气互联的综合能源系统。
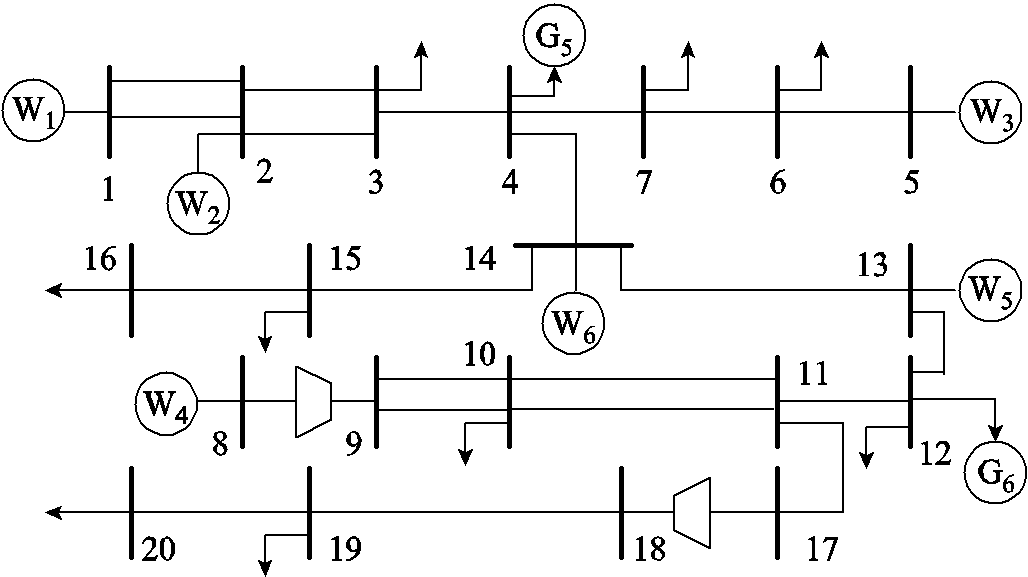
图5 比利时天然气20节点系统
Fig.5 Belgian 20-bus natural gas system
为了验证S-MODE算法在高维目标寻优中的优越性,利用S-MODE与ISPEA2I、NSGAII、PSO[32]和SFLA(shuffle frog leaping algorithm)[33]进行对比分析,其中,目标函数为发电机燃料费用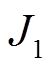 、污染物排放量
、污染物排放量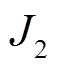 、线路间的有功损耗
、线路间的有功损耗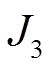 、电压波动
、电压波动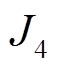 、天然气总费用
、天然气总费用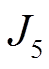 和燃气压缩机气体消耗量
和燃气压缩机气体消耗量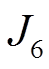 ,所有算法搜索个体
,所有算法搜索个体 均设为100,迭代次数
均设为100,迭代次数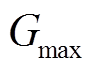 设为100,其他运行参数详见附录。由于参数较多,这里只对S-MODE与NSGAII的运行参数进行了记录。
设为100,其他运行参数详见附录。由于参数较多,这里只对S-MODE与NSGAII的运行参数进行了记录。
从表2可以看出,S-MODE算法对其他算法占优,虽然有些算法的目标函数可以达到本文算法的性能,但却以牺牲其他目标函数为代价。例如,以S-MODE和PSO为例,虽然两种算法运行后污染物排放量比较少,但是PSO优化后的电力系统运行成本比本文算法高很多,其他的目标函数也不是很理想。而且从表2中可以发现,以S-MODE和NSGAII为例,用天然气发电可以有效地减少污染物的排放,从0.222 7t/h降到了0.163 7t/h,因此可以说明,用清洁能源发电对环境的保护是非常重要的。以S-MODE和MODE为例,为了验证S-MODE算法在高维目标寻优中的优越性,使用MODE在高维目标中进行寻优操作。从MODE运行结果看,只有目标2(污染物排放量)的运行结果优于S-MODE,但优势并不明显,而且这一优势是以牺牲其他目标结果为代价的,这也能证明2.2节所说的,使用Pareto的多目标选择会使非支配排序的能力被削弱,从而使种群陷入局部最优,也就是只能保证其中任一目标结果最优,而无法满足高维目标优化时的要求。因此,利用S-MODE优化高维目标的优势是明显的。
表2 电-气互联系统不同算法结果对比
Tab.2 Results of different algorithms forintegrated electricity and gas systems

算法/(103$/h)/(t/h)/(MW /h)(pu)/()/()运行时间/s S-MODE14.390 70.163 76.293 90.443 12.468 60.132 160.77 MODE16.640 90.155 311.434 81.954 22.595 80.424 061.12 NSGAII15.713 80.204 212.211 80.615 02.509 40.693 361.82 ISPEA2I14.987 10.202 09.873 40.557 42.497 80.451 260.90 SFLA14.664 50.177 710.886 30.404 02.500 00.228 762.01 PSO15.663 60.164 112.211 90.634 52.521 10.608 360.64
为了证明使用S-MODE可以为种群带来更好的空间分布,以S-MODE和NSGA-II[24]为例进行验证,如图6所示。从图6也可以发现,利用S-MODE所得到的种群更具多样性,即搜索空间更大。这也说明,它在处理高维目标时有优势。
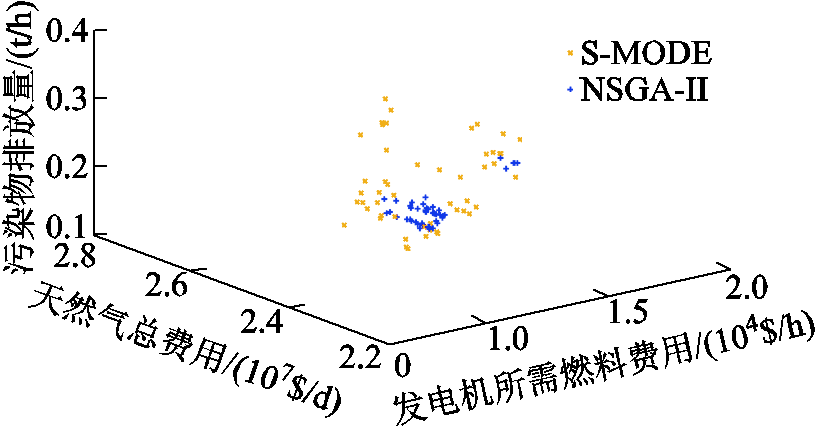
图6 三维坐标中电-气互联系统多目标最优潮流不同算法对比
Fig.6 Comparison of different algorithms for multi-objective optimal power flow of integrated electricity and gas systems in three dimensional coordinates
为了证明使用S-MODE所带来的经济性,以S-MODE和ISPEA2I[32]为例进行验证,二维坐标中电-气互联系统多目标最优潮流不同算法对比如图7所示。从柱状图中可以发现,在天然气的总费用中,本文算法的个体费用大多数比ISPEA2I的低;从折线图中可以发现,在发电机燃料总费用中,本文算法的个体费用也比ISPEA2I的低。而且可以发现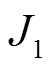 和
和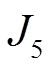 的费用成正比,即当发电机燃料总费用增加时,天然气的总费用也相应增加,这主要的原因是因为天然气价格比煤炭价格高。所以无论从图6的三维空间分布,还是从图7的二维柱状图来看,本文所提的算法都具有一定的优势。电-气互联系统中不同运行模式结果对比见表3,从优化算法的运行时间来看,本文算法也具有一定的优势。
的费用成正比,即当发电机燃料总费用增加时,天然气的总费用也相应增加,这主要的原因是因为天然气价格比煤炭价格高。所以无论从图6的三维空间分布,还是从图7的二维柱状图来看,本文所提的算法都具有一定的优势。电-气互联系统中不同运行模式结果对比见表3,从优化算法的运行时间来看,本文算法也具有一定的优势。
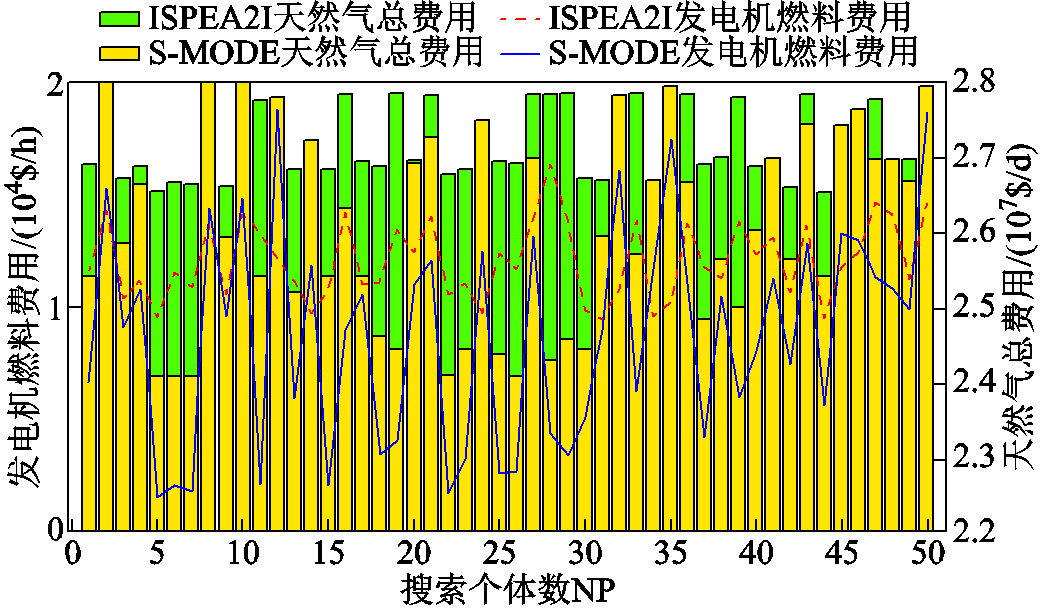
图7 二维坐标中电-气互联系统多目标最优潮流不同算法对比
Fig.7 Comparison of different algorithms for multi-objective optimal power flow of integrated electricity and gas systems in two dimensional coordinates
为了适应电-气互联系统不同工况的需求,本文将S-MODE算法的运行结果分成了五种不同的运行模式;模式1是根据加强非支配关系的多目标选择关系,对电-气互联系统不同目标函数进行综合考虑所得出的折中解;模式2则主要考虑IES运行的经济性,包括发电机所需燃料费用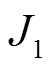 和天然气总费用
和天然气总费用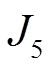 ;模式3主要考虑污染物排放和有功功率损耗;模式4主要考虑电网运行的安全性——母线节点电压的波动性;模式5主要考虑气网中压缩机的天然气用量。
;模式3主要考虑污染物排放和有功功率损耗;模式4主要考虑电网运行的安全性——母线节点电压的波动性;模式5主要考虑气网中压缩机的天然气用量。
表3 电-气互联系统中不同运行模式结果对比
Tab.3 Results of different operation modes in integrated electricity and gas systems
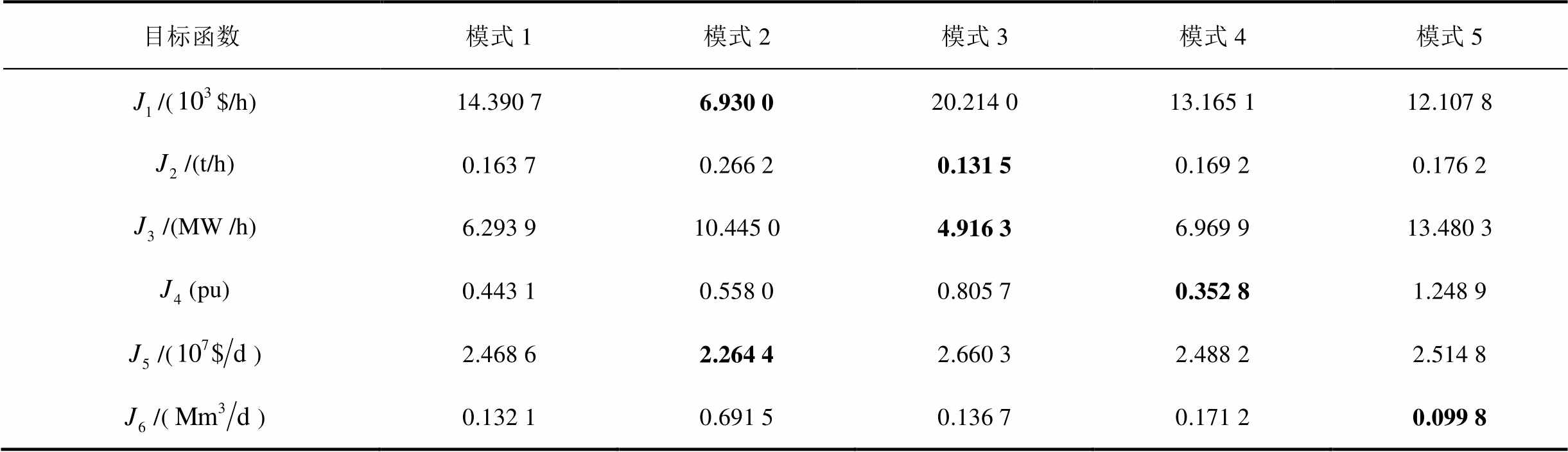
目标函数模式1模式2模式3模式4模式5 /($/h)14.390 76.930 020.214 013.165 112.107 8 /(t/h)0.163 70.266 20.131 50.169 20.176 2 /(MW /h)6.293 910.445 04.916 36.969 913.480 3 (pu)0.443 10.558 00.805 70.352 81.248 9 /()2.468 62.264 42.660 32.488 22.514 8 /()0.132 10.691 50.136 70.171 20.099 8
通过对比模式1和模式2可以发现,电网发电费用的波动性非常大,这是因为天然气的价格比煤炭高很多,这也是制约天然气发电的一个根本性问题。从表3可以发现,与其他运行模式相比,运行模式2中发电所用的燃料费用最少,也就是G5和G6的出力比较小,从而使燃气轮机的天然气消耗减少,因此在很大程度上改变了天然气系统的气体流向。由附表2可知每一个气源点的价格是不一样的,为了保证天然气按时到达用户侧,必须加大压缩机两端的压缩比,而由式(15)可知,压缩比变大会使燃料压缩机消耗的天然气流量增加,因此,最终使模式2中的压缩机的耗气量增大数倍。从模式3可以发现,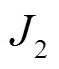 和
和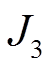 存在正比的关系,也就是随着污染物排放量的减少,电网的有功损耗也会降低。从模式4可以发现,
存在正比的关系,也就是随着污染物排放量的减少,电网的有功损耗也会降低。从模式4可以发现,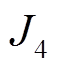 最低可以降至0.352 8,此时电网运行的安全系数最高。模式5中压缩机的天然气用量可以降至0.099 8
最低可以降至0.352 8,此时电网运行的安全系数最高。模式5中压缩机的天然气用量可以降至0.099 8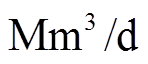 ,此时天然气的利用效率最高。
,此时天然气的利用效率最高。
为了保证电-气互联系统以安全、经济的方式运行,根据系统特性,提出了加强非支配解占优关系的多目标差分进化算法,并将它用在低维多目标和高维多目标的求解中。该算法能够对所考虑的多目标优化产生分布良好的帕累托最优前沿,而且实验结果也证明该算法可以得到更好的折中解。最优潮流算法可以实现电-气互联系统联合优化,在气源参数上、下限范围内优化选择气网运行控制参数,并同时优化发电机出力,因此具有更好的经济性、安全性、环境友好性等。
附表1 天然气网络管道参数
App.Tab.1 Pipelines parameters of natural gas network
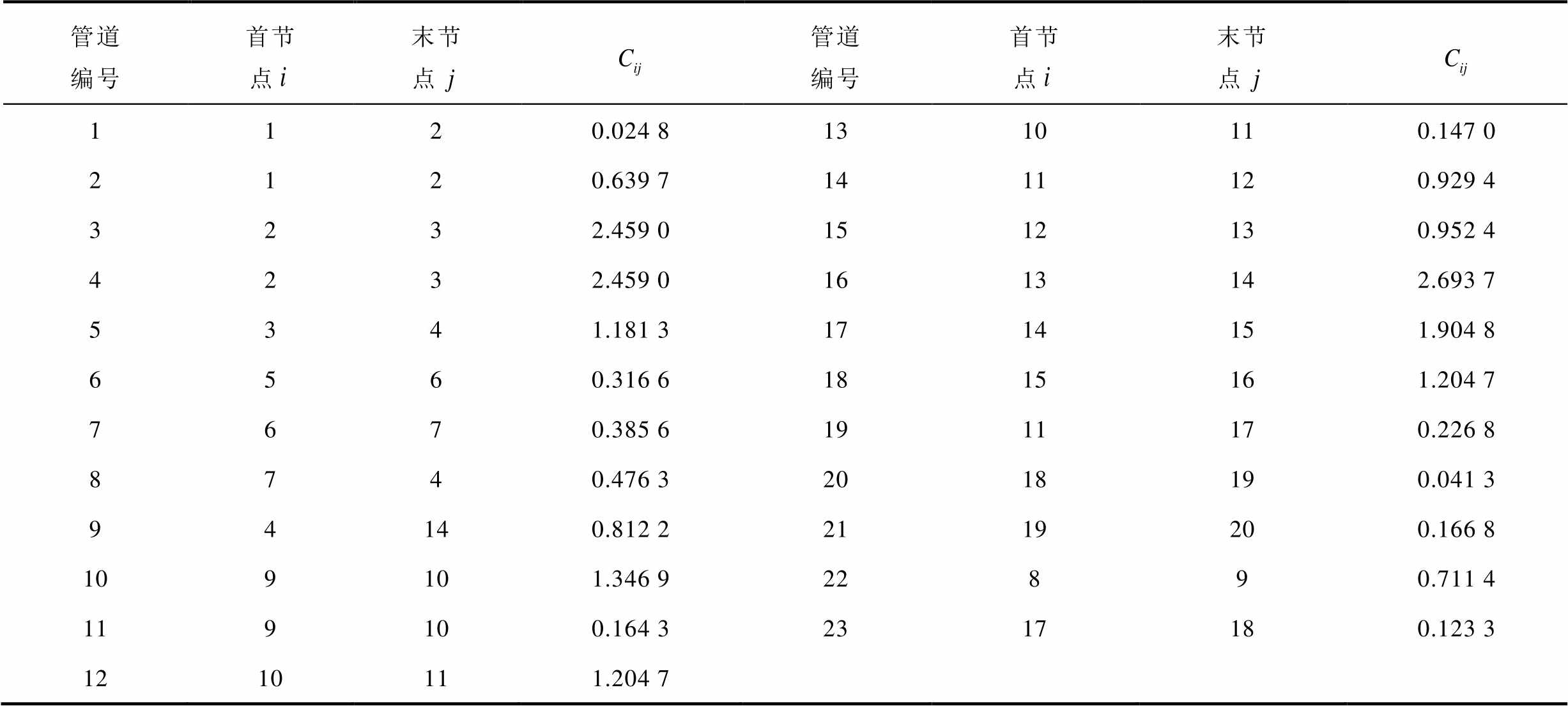
管道编号首节点末节点管道编号首节点末节点 1120.024 81310110.147 0 2120.639 71411120.929 4 3232.459 01512130.952 4 4232.459 01613142.693 7 5341.181 31714151.904 8 6560.316 61815161.204 7 7670.385 61911170.226 8 8740.476 32018190.041 3 94140.812 22119200.166 8 109101.346 922890.711 4 119100.164 32317180.123 3 1210111.204 7
附表2 天然气网络气源点参数
App.Tab.2 Parameters of gas production and storage point of natural gas network
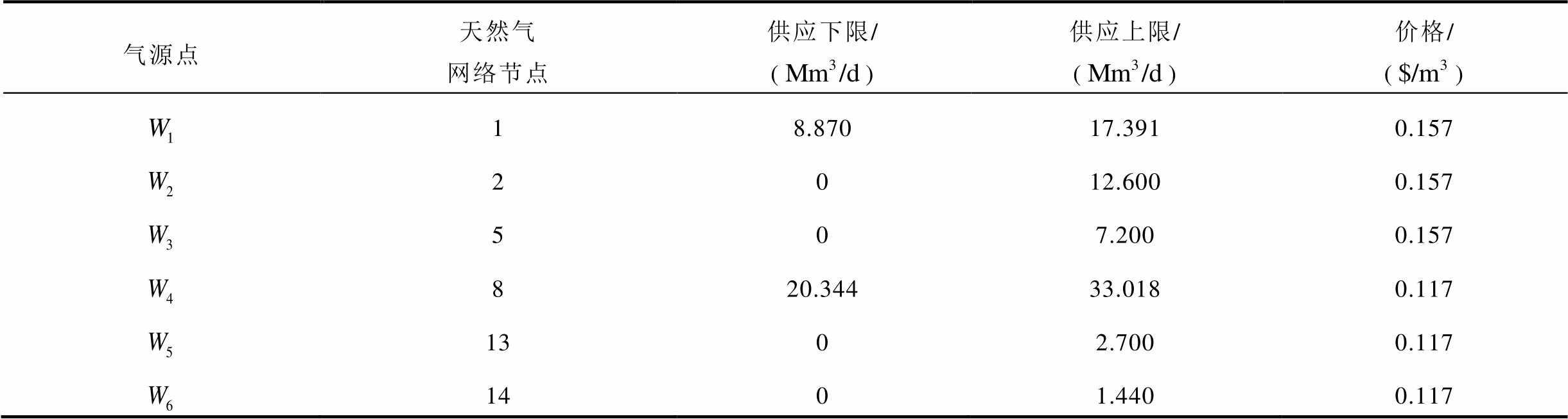
气源点天然气网络节点供应下限/ ()供应上限/ ()价格/ () 18.87017.3910.157 2012.6000.157 507.2000.157 820.34433.0180.117 1302.7000.117 1401.4400.117
附表3 电-气互联系统中天然气20节点系统不同算法结果对比
App.Tab.3 Results of natural gas 20-node system in integrated electricity and gas systems
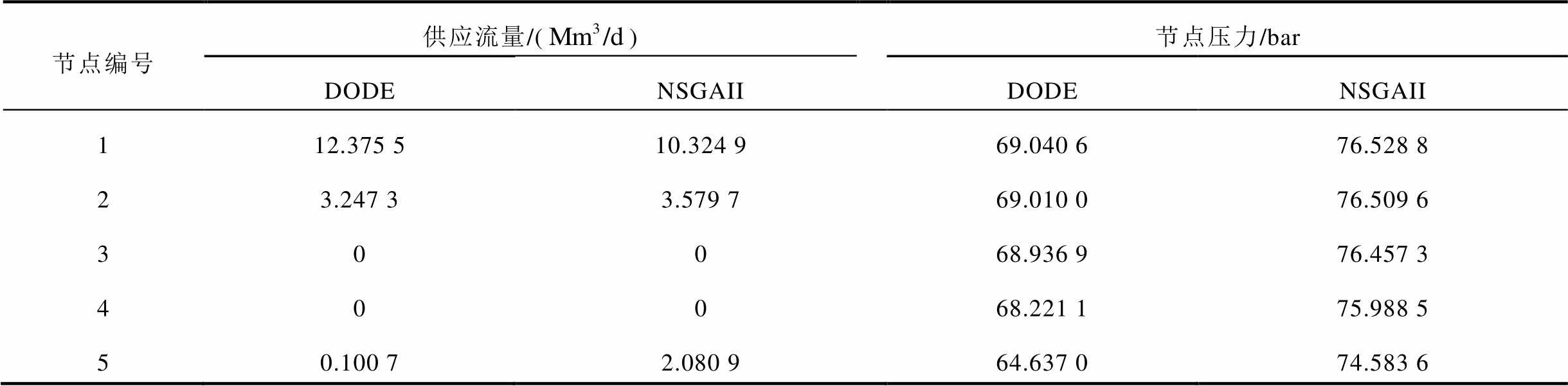
节点编号供应流量/()节点压力/bar DODENSGAIIDODENSGAII 112.375 510.324 969.040 676.528 8 23.247 33.579 769.010 076.509 6 30068.936 976.457 3 40068.221 175.988 5 50.100 72.080 964.637 074.583 6
(续)
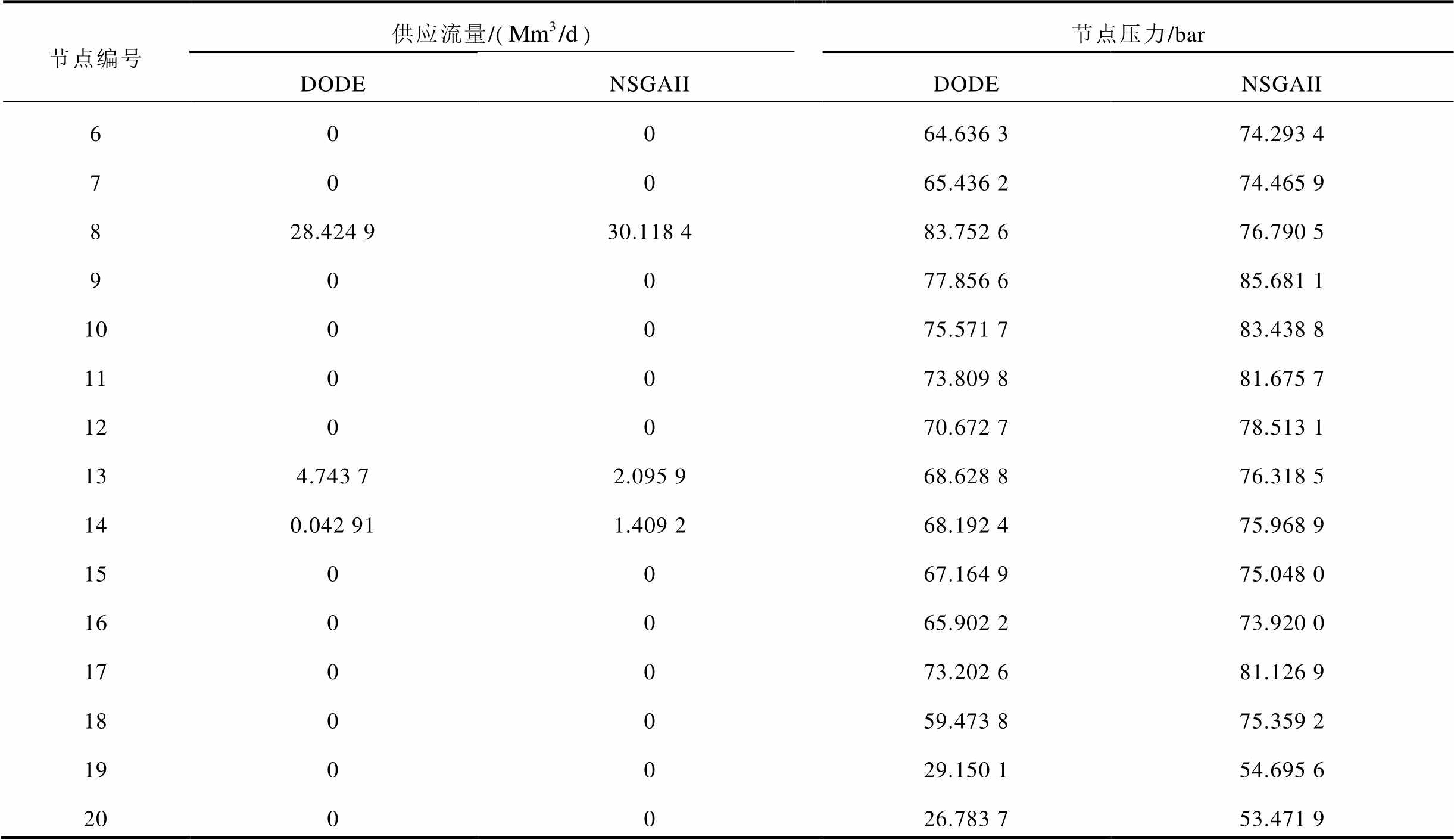
节点编号供应流量/()节点压力/bar DODENSGAIIDODENSGAII 60064.636 374.293 4 70065.436 274.465 9 828.424 930.118 483.752 676.790 5 90077.856 685.681 1 100075.571 783.438 8 110073.809 881.675 7 120070.672 778.513 1 134.743 72.095 968.628 876.318 5 140.042 911.409 268.192 475.968 9 150067.164 975.048 0 160065.902 273.920 0 170073.202 681.126 9 180059.473 875.359 2 190029.150 154.695 6 200026.783 753.471 9
注:1bar=105Pa
附表4 电-气互联系统中IEEE 30节点电力系统不同算法结果对比
App.Tab.4 Comparison of different algorithm results of IEEE 30 node power system in integrated electricity and gas systems
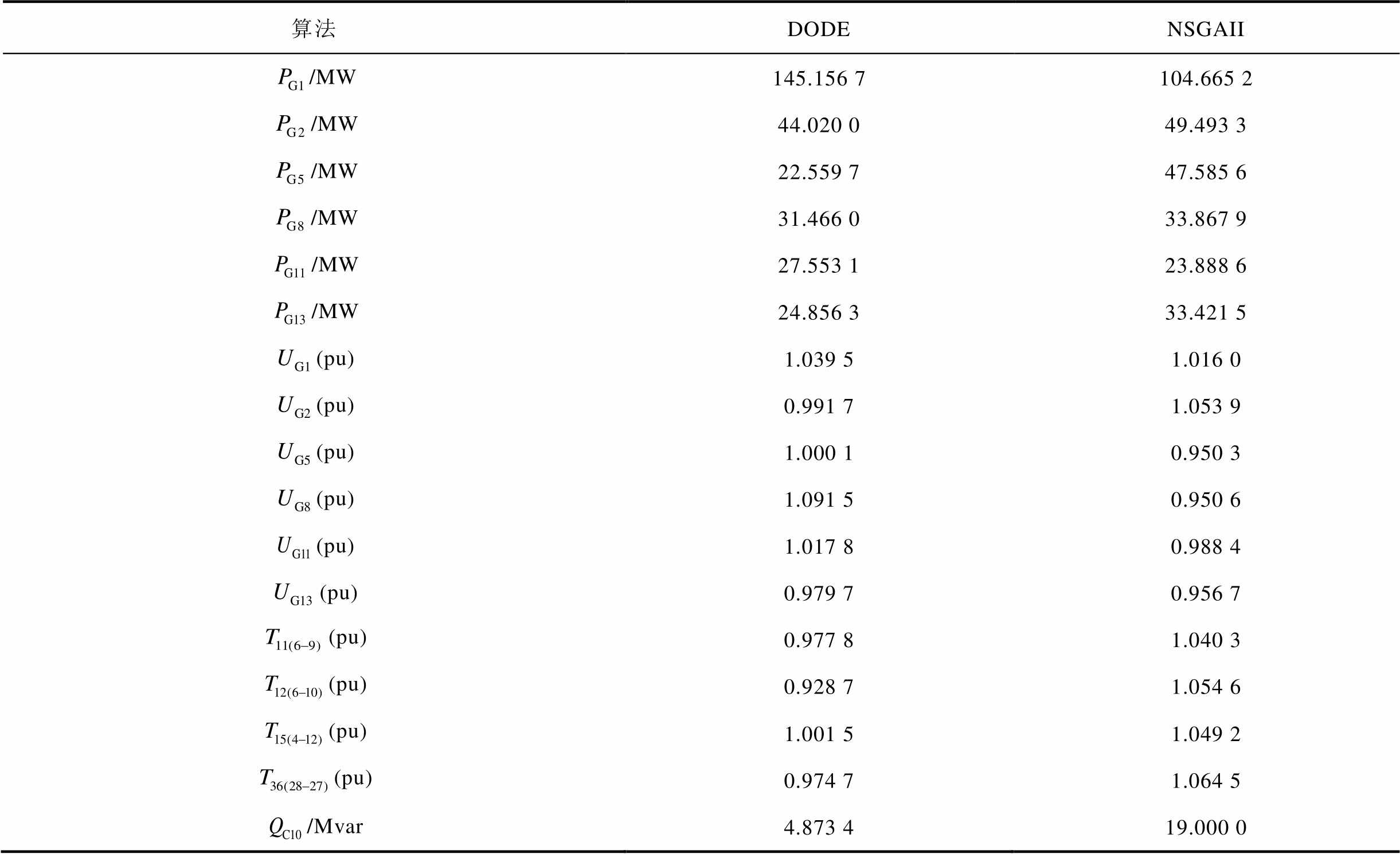
算法DODENSGAII /MW145.156 7104.665 2 /MW44.020 049.493 3 /MW22.559 747.585 6 /MW31.466 033.867 9 /MW27.553 123.888 6 /MW24.856 333.421 5 (pu)1.039 51.016 0 (pu)0.991 71.053 9 (pu)1.000 10.950 3 (pu)1.091 50.950 6 (pu)1.017 80.988 4 (pu)0.979 70.956 7 (pu)0.977 81.040 3 (pu)0.928 71.054 6 (pu)1.001 51.049 2 (pu)0.974 71.064 5 /Mvar4.873 419.000 0
(续)
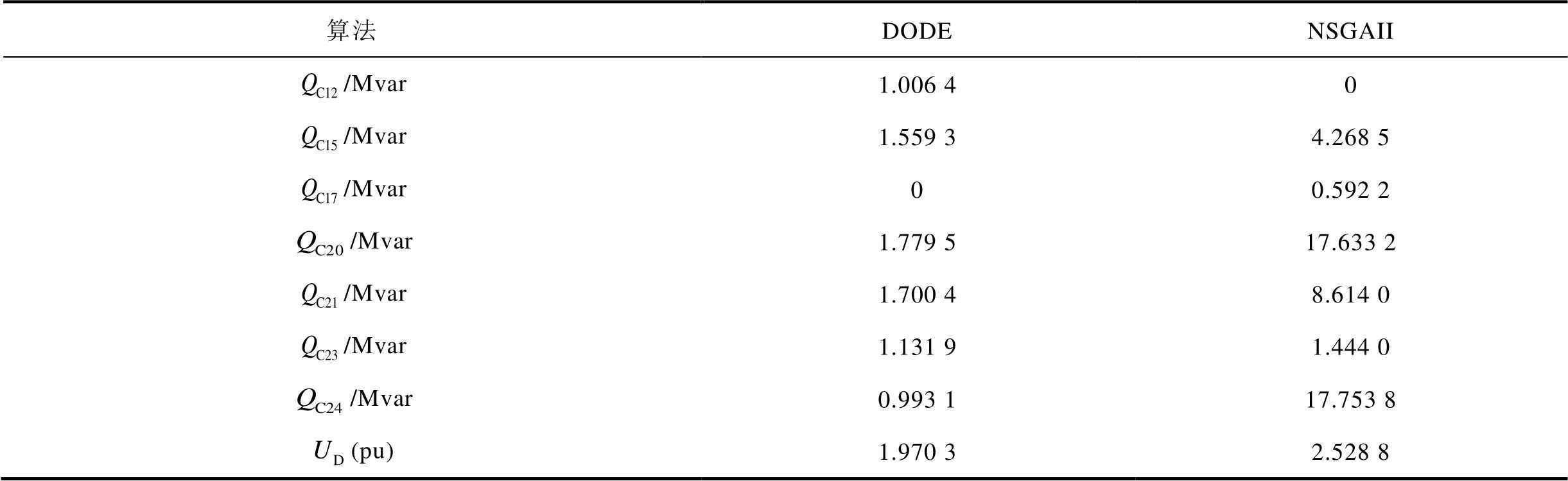
算法DODENSGAII /Mvar1.006 40 /Mvar1.559 34.268 5 /Mvar00.592 2 /Mvar1.779 517.633 2 /Mvar1.700 48.614 0 /Mvar1.131 91.444 0 /Mvar0.993 117.753 8 (pu)1.970 32.528 8
附表5 电-气互联系统中压缩机不同算法结果对比
App.Tab.5 Results of different compressor algorithms in integrated electricity and gas systems
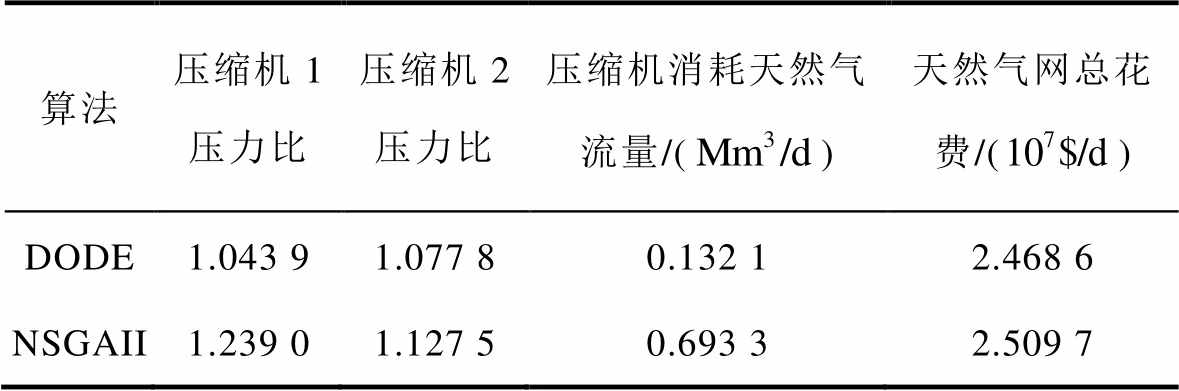
算法压缩机1压力比压缩机2压力比压缩机消耗天然气流量/()天然气网总花费/() DODE1.043 91.077 80.132 12.468 6 NSGAII1.239 01.127 50.693 32.509 7
参考文献
[1]Biswas P P, Suganthan P N, Mallipeddi R. Multi-objective optimal power flow solutions using a constraint handling technique of evolutionary algorithms[J]. Soft Computing, 2019, 24(4): 2999-3023.
[2]Li Shuijia, Gong Wenyin, Wang Ling, et al. Optimal power flow by means of improved adaptive differential evolution[J]. Energy, 2020, 198: 117314.
[3]董朝阳, 赵俊华, 文福拴, 等. 从智能电网到能源互联网:基本概念与研究框架[J]. 电力系统自动化, 2014, 38(15): 1-11. Dong Zhaoyang, Zhao Junhua, Wen Fushuan, et al. From smart grid to energy internet: basic concept and research framework[J]. Automation of Electric Power Systems, 2014, 38(15): 1-11.
[4]曾博, 胡强, 刘裕, 等. 考虑需求响应复杂不确定性的电-气互联系统动态概率能流计算[J]. 中国电机工程学报, 2020, 40(4): 1161-1171. Zeng Bo, Hu Qiang, Liu Yu, et al. Dynamic probabilistic energy flow calculation for interconnected electricity-gas system considering complex uncertainties of demand response[J]. Proceeding of the CSEE, 2020, 40(4): 1161-1171.
[5]王震, 薛庆. 充分发挥天然气在我国现代能源体系构建中的主力作用——对《天然气发展“十三五”规划》的解读[J]. 天然气工业, 2017, 37(3): 1-8.Wang Zhen, Xue Qing. To fully exert the important role of natural gas in building a modern energy security system in China: an understanding of China’s National 13th Five-Year Plan for natural gas development[J]. Natural Gas Industry, 2017, 37(3): 1-8.
[6]余晓丹, 徐宪东, 陈硕翼, 等. 综合能源系统与能源互联网简述[J]. 电工技术学报, 2016, 31(1): 1-13. Yu Xiaodan, Xu Xiandong, Chen Shuoyi, et al. A brief review to integrated energy system and energy internet[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 1-13.
[7]廖小兵, 刘开培, 张亚超, 等. 基于区间泰勒展开的不确定性潮流分析[J]. 电工技术学报, 2018, 33(4): 750-758. Liao Xiaobing, Liu Kaipei, Zhang Yachao, et al. Uncertain power flow analysis based on interval taylor expansion[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 750-758.
[8]王英瑞, 曾博, 郭经, 等. 电-热-气综合能源系统多能流计算方法[J]. 电网技术, 2016, 40(10): 2942-2950. Wang YingRui, Zeng Bo, Guo Jing, et al. Multi-energy flow calculation method for integrated energy system containing electricity, heat and gas[J]. Power System Technology, 2016, 40(10): 2942-2950.
[9]Shabanpour-Haghighi A, Seifi A R. An integrated steady-state operation assessment of electrical natural gas, and district heating networks[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3636- 3647.
[10]张刚, 张峰, 张利, 等. 考虑多种耦合单元的电气热联合系统潮流分布式计算方法[J]. 中国电机工程学报, 2018, 38(22): 6594-6604.Zhang Gang, Zhang Feng, Zhang Li, et al. Distributed algorithm for the power flow calculation of integrated electrical, gas, and heating network considering various coupling units[J]. Proceedings of the CSEE, 2018, 38(22): 6594-6604.
[11]韩佶, 苗世洪, 李超, 等. 计及相关性的电-气-热综合能源系统概率最优能量流[J]. 电工技术学报, 2019, 34(5): 1055-1067. Han Ji, Miao Shihong, Li Chao, et al. Probabilistic optimal energy flow electricity-gas-heat integrated energy system considering correlation[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1055-1067.
[12]卫志农, 张思德, 孙国强, 等. 基于碳交易机制的电-气互联综合能源系统低碳经济运行[J]. 电力系统自动化, 2016, 40(15): 9-16. Wei Zhinong, Zhang Side, Sun Guoqiang, et al, Carbon trading based low-carbon economic operation for integrated electricity and natural gas energy system[J]. Automation of Electric Power Systems, 2016, 40(15): 9-16.
[13]胡健, 秦玉杰, 焦提操, 等. 泛在电力物联网环境下考虑碳排放权约束的VPP理性调峰模型[J]. 电力系统保护与控制, 2020, 48(3): 49-57. Hu Jian, Qin Yujie, Jiao Ticao, et al. Rational peak shaving model of VPP considering carbon emission rights constraints in ubiquitous power internet of things environment[J]. Power System Protection and Control, 2020, 48(3): 49-57.
[14]王泽森, 唐艳梅, 乔宝榆, 等. 气–电综合能源系统最优潮流及其环境增效研究[J]. 中国电机工程报, 2018, 38(增刊1): 111-120. Wang Zesen, Tang Yanmei, Qiao Baoyu, et al, Research on integrated natural gas and electric power system optimal power flow and its environmental synergy[J]. Proceedings of the CSEE, 2018, 38(S1): 111-120.
[15]陈聪, 沈欣炜, 夏天, 等. 计及㶲效率的综合能源系统多目标优化调度方法[J]. 电力系统自动化, 2019, 43(12): 60-67, 121. Chen Cong, Shen Xinwei, Xia Tian, et al, Multi-objective optimal dispatch method for integrated energy system considering exergy efficiency[J]. Automation of Electric Power Systems, 2019, 43(12): 60-67, 121.
[16]Panda A, Tripathy M, Barisal A K, et al. A modified bacteria foraging based optimal power flow framework for hydro-thermal-wind generation system in the presence of STATCOM[J]. Energy, 2017, 124: 720-740.
[17]方红伟, 宋如楠, 冯郁竹, 等. 基于差分进化的波浪能转换装置阵列优化[J]. 电工技术学报, 2019, 34(12): 2597-2605. Fang Hongwei, Song Runan, Feng Yuzhu, et al. Array optimization of wave energy converters by differential evolution algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2597- 2605.
[18]刘巍, 李锰, 李秋燕, 等. 基于改进遗传算法的电网投资组合预测方法[J]. 电力系统保护与控制, 2020, 48(8): 78-85. Liu Wei, Li Meng, Li Qiuyan, et al. Power grid portfolio forcasting method based on an improved genetic algorithm[J]. Power System Protection and Control, 2020, 48(8): 78-85.
[19]白顺明, 陈磊, 姜飞, 等. 考虑风电最大化消纳的电力系统多目标优化[J]. 电气技术, 2020, 21(1): 7-11. Bai Shunming, Chen Lei, Jiang Fei, et al. Multi-objective optimal model for power system considering wind power maximum accommodation[J]. Electrical Engineering, 2020, 21(1): 7-11.
[20]王子琪, 陈金富, 张国芳, 等. 基于飞蛾扑火优化算法的电力系统最优潮流计算[J]. 电网技术, 2017, 41(11): 3641-3647. Wang Ziqi, Chen Jinfu, Zhang Guofang, et al, Optimal power flow calculation with moth-flame optimization algorithm[J]. Power System Technology, 2017, 41(11): 3641-3647.
[21]Trivedi I N, Jangir P, Parmar S A, et al. Optimal power flow with voltage stability improvement and loss reduction in power system using moth-flame optimizer[J]. Neural Computing and Applications, 2018, 30(6): 1889-1904.
[22]商立群, 朱伟伟. 基于全局学习自适应细菌觅食算法的光伏系统全局最大功率点跟踪方法[J]. 电工技术学报, 2019, 34(12): 2606-2614. Shang Liqun, Zhu Weiwei. Photovoltaic system global maximum power point tracking method based on the global learning adaptive bacteria foraging algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2606-2614.
[23]Yuan Xiaohui, Zhang Binqiao, Wang Pengtao, et al. Multi-objective optimal power flow based on improved strength pareto evolutionary algorithm[J]. Energy, 2017, 122: 70-82.
[24]Hu Yuan, Bie Zhaohong, Ding Tao, et al. An NSGA-II based multi-objective optimization for combined gas and electricity network expansion planning[J]. Applied Energy, 2015, 167: 280-293.
[25]张涛, 王成, 王凌云, 等. 偏差电量考核机制下含DG的售电公司多目标优化调度模型[J]. 电工技术学报, 2019, 34(15): 3265-3274. Zhang Tao, Wang Chen, Wang Lingyun, et al. Multi-objective optimal dispatching model of electricity retailers with distributed generator under energy deviation penalty[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3265-3274.
[26]巩敦卫, 刘益萍, 孙晓燕, 等. 基于目标分解的高维多目标并行进化优化方法[J]. 自动化学报, 2015, 41(8): 1438-1451. Gong Dunwei, Liu Yiping, Sun Xiaoyan, et al. Parallel many-objective evolutionary optimization using objectives decomposition[J]. Acta Automatica Sinica, 2015, 41(8): 1438-1451.
[27]王锡凡. 现代电力系统分析[M]. 北京: 科学出版社, 2009.
[28]高乐, 赵连琢, 蒋万荣, 等. 天然气输气压力对管道的影响分析[J]. 中国石油和化工标准与质量, 2013(15): 261.Gao Le, Zhao Lianzhuo, Jiang Wanrong, et al. Analysis of the influence of gas pressure on pipeline[J].China Petroleum and Chemical Standard and Quality, 2013(15): 261.
[29]廖宪国. 天然气输气压力对管道的影响研究[J]. 中国石油和化工标准与质量, 2014 (6): 78. Liao Xianguo. Study on the Influence of gas pressure on pipeline[J]. China Petroleum and Chemical Standard and Quality, 2014(6): 78.
[30]陈振兴, 严宣辉, 吴坤安, 等. 融合张角拥挤控制策略的高维多目标优化[J]. 自动化学报, 2015, 41(6): 1145-1158. Chen Zhenxing, Yan Xuanhui, Wu Kun’an, et al, Many-objective optimization integrating open angle based congestion control strategy[J]. Acta Automatica Sinica, 2015, 41(6): 1145-1158.
[31]Lee K Y, Park Y M, Ortiz J L. A united approach to optimal real and reactive power dispatch[J]. Power Engineering Review, IEEE, 1985, PAS-104(5): 1147 -1153.
[32]Niknam T, Mojarrad H D, Nayeripour M. A new fuzzy adaptive particle swarm optimization for non-smooth economic dispatch[J]. Energy, 2010, 35(4): 1764-1778.
[33]Niknam T, Narimani M R, Jabbari M, et al. A modified shuffle frog leaping algorithm for multi-objective optimal power flow[J]. Energy, 2011, 36(11): 6420-6432.
Enhanced Multi-Objective Differential Evolutionary Algorithm Based Optimal Power Flow Calculation for Integrated Electricity and Gas Systems
Abstract With the development of integrated energy system, the connection between power grid and natural gas network is getting closer. In order to ensure the safety and economic operation of the integrated electricity and gas systems, it is necessary to carry out the joint planning for the system. Therefore, firstly, a multi-objective optimal scheduling model of the electricity-gas energy interconnection system is proposed according to the system's large-scale, multi-dimensional, non-convex, and nonlinear characteristics. Secondly, in order to deal with the problem of poor population convergence in the solving algorithm of high-dimensional objective function, an enhanced multi-objective differential evolution algorithm is proposed to strengthen the dominant relation of non-dominant solutions. Finally, IEEE 30-node power system and Belgium 20-node natural gas system are used to show the effectiveness of the proposed algorithm. The simulations show that the present algorithm can produce a better distribution of Pareto optimal front of the objective function under consideration. Meanwhile, a set of better optimization solutions can be obtained from the high-dimensional target solving, which can meet the operating requirements of the system under different working conditions.
keywords:Optimal power flow, integrated energy system, multi-objective optimization, enhanced dominant relationship of non-dominant solution, differential evolution
中图分类号:TM73
DOI:10.19595/j.cnki.1000-6753.tces.200405
国家自然科学基金(61973070)、兴辽英才计划(XLYC1802010)和流程工业国家重点实验室基本研究项目(2018ZCX22)资助。
收稿日期 2020-04-23
改稿日期 2020-06-26
刘明凯 男,1996年生,硕士研究生,研究方向为综合能源潮流分析和最优潮流。E-mail:liumk_0124@163.com
王占山 男,1971年生,教授,博士生导师,研究方向为电力系统自动化、故障诊断和稳定性。E-mail:zhanshan_wang@163.com(通信作者)
(编辑 赫蕾)