图1 多因素动态内阻模型构建流程
Fig.1 The flow chart of multiple factors dynamic internal resistance model is constructed
摘要 锂离子电池内阻建模对研究电池热管理具有重要意义。充电内阻受温度、充电倍率等众多因素的影响，该文分析电池的内阻变化特性与多种影响因素（充电倍率、荷电状态以及温度）之间的关系，采用最小二乘法的二元多项式和三次样条插值算法对不同充电倍率、荷电状态以及温度下的电池充电内阻进行建模，并采用所建立的多因素动态内阻模型对不同状态下的充电内阻进行估算。实验结果表明，所建立的动态内阻模型获得的内阻估算值与实验值的最大误差不超过6mW，证明所提出的电池充电内阻建模方法的有效性。
关键词：充电内阻 多因素 内阻模型 最小二乘 二元多项式 三次样条
锂离子电池作为电动汽车的主要储能装置，是电动汽车的重要组成部分[1-4]。电动汽车的储能装置由上千个锂离子电池单体组成，在大电流快速充电过程中电池会释放出大量的热量，电池组积聚热量导致电池外部工作环境温度过高，这将会加速电池性能衰退，甚至引发“热失控”现象[5-6]。电池充电内阻是电池在充电工作时影响产热量大小的关键参数，对电池充电内阻准确建模能为电动汽车的安全性和热管理系统提供有效的决策参考[7]。
国内外学者对锂离子电池充电内阻研究主要集中在充电内阻影响因素与充电内阻模型两方面，采用充电脉冲电流电压的变化或等效电路模型来描述电池特性并获取充电内阻[8]。林春景等采用混合脉冲功率特性法对不同温度区间下的内阻进行实验分析，验证电池阻抗对荷电状态（State of Charge, SOC）和温度的依赖关系[9]。B. V. Ratnakumar等采用直流阻抗法分别对锂离子电池在25℃、0℃及-20℃不同SOC和充放电倍率下的内阻进行测试，并对温度、SOC及倍率进行分析研究，获取内阻关于温度的阿伦尼乌斯图[10]。Liu Xingtao等对不同温度和SOC下内阻进行测试，详细描述了电池内阻、SOC和温度之间的关系，建立了基于温度的一元三次多项式模型[11]。W. Wang等采用电化学阻抗谱（Electrochemical Impedance Spectroscopy, EIS）和电流脉冲技术对新旧状态下的电池阻抗特性进行全面的描述，明确指出，电池的阻抗特性在很大程度上取决于电池的状态，如SOC、温度及电流，并基于阿伦尼乌斯方程给出一个温度-内阻模型[12]。姜久春等测试了磷酸铁锂电池在充放电条件下的阻抗特性，并进行了实验研究，得到不同SOC下的阻抗谱，获得的阻抗谱曲线能以特高精度测量电荷转移阻抗和扩散阻抗，很好地验证了锂离子质量分数、电极材料的电化学特性所引起的电极极化和浓差极化的显著变化[13]。对基于阿伦尼乌斯方程10%SOC、50%SOC和90%SOC下的电荷转移阻抗特性进行了分析，表明电池阻抗与温度、SOC及充放电倍率存在着直接关系。总体而言，现有的多数方法多侧重于通过算法改进或融合来描述各个因素（温度、SOC及放电倍率）与内阻的独立建模，虽然有重要的研究价值，但在实际情况下电池内阻建模需要整合所有的影响因素进行准确的建模。
由于实际情况中电池充电倍率、温度及SOC对电池充电内阻均有影响[14]，只考虑一种或两种因素建模会导致构建模型误差较大，而如何从在线可测量参数（温度、SOC及充电倍率）中寻求与内阻的整体关联，并基于构建电池多因素动态内阻模型进行内阻的准确估算是电池热管理系统亟待解决的问题。针对此问题，提出融合充电倍率、温度以及SOC三个因素的动态内阻模型。采用18650车用动力三元锂离子电池作为研究对象，对不同充放电倍率、温度及SOC下的充电内阻进行测试并对其特性进行分析，最终，以上述三个因素为自变量、内阻为因变量，构建多因素动态充电内阻模型，从而避免了对电池进行测量实现对充电内阻的在线估算，为电池热管理系统提供理论基础。
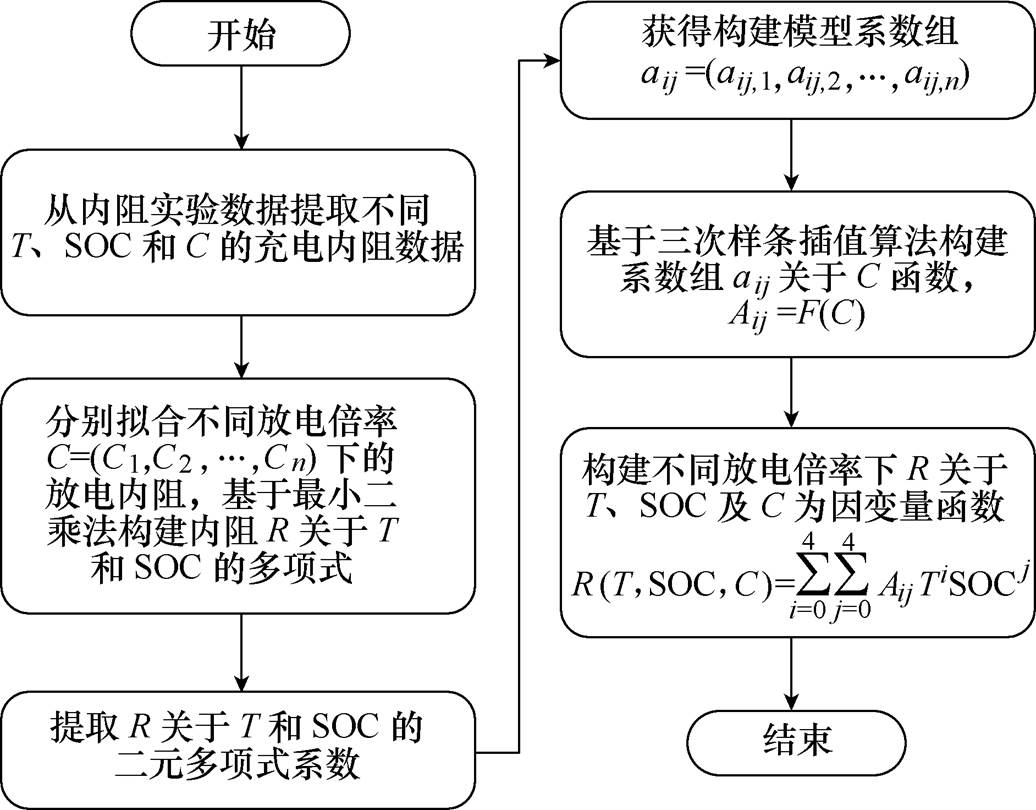
电池充电内阻R受温度T、SOC和充电倍率C的影响，采用最小二乘法的二元多项式拟合构建内阻R关于T和SOC的函数关系，得到内阻R关于T和SOC拟合的二元多项式函数系数。引进三次样条插值算法将充电倍率与二元多项式系数建立函数关系，构建以T、SOC及充电倍率C三个因素为自变量、内阻R为因变量的多因素动态充电内阻模型。多因素动态内阻模型构建流程如图1所示，具体步骤如下：
图1 多因素动态内阻模型构建流程
Fig.1 The flow chart of multiple factors dynamic internal resistance model is constructed
（1）根据实验记录的电池数据计算充电内阻。
（2）建立R关于T和SOC的函数拟合，对给定充电倍率下的内阻R均可由T和SOC唯一确定，采用最小二乘法的二元多项式函数拟合因变量R与自变量T和SOC之间函数关系，此处选二元多项式的阶数为4阶。该拟合方法拓展到其他充电倍率下的拟合为
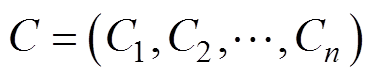（1）
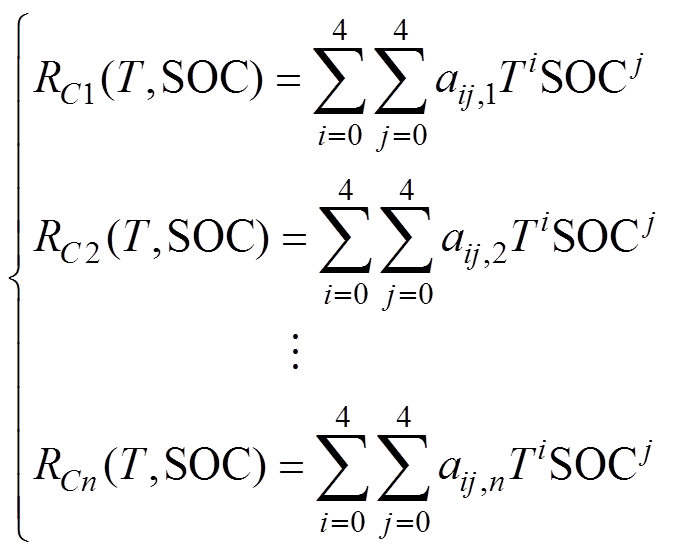（2）
式中，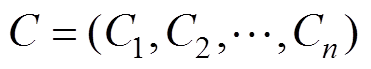
为测量不同充电倍率数组；
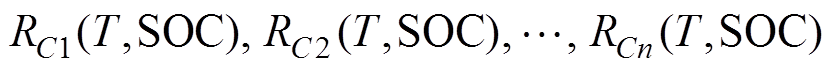分别为R在给定充电倍率C1,C2,…,Cn下关于T和SOC的二元多项式拟合函数；aij,1,aij,2,…,aij,n为在该充电倍率下的二元多项式系数。
（3）分别提取不同充电倍率下的R关于T和SOC拟合的二元多项式函数系数组为
（3）（4）为了寻求aij与充电倍率C之间内在的函数关系，将第（3）步提取的不同充电倍率下的二元多项式函数系数组aij，基于三次样条插值法在倍率数组区间上取m+1个节点，分割成m段；并将每一段倍率数据点之间进行分段，构建出一个三次样条函数；最后得到一个整体连续的关于以充电倍率C为自变量的三次样条插值函数为
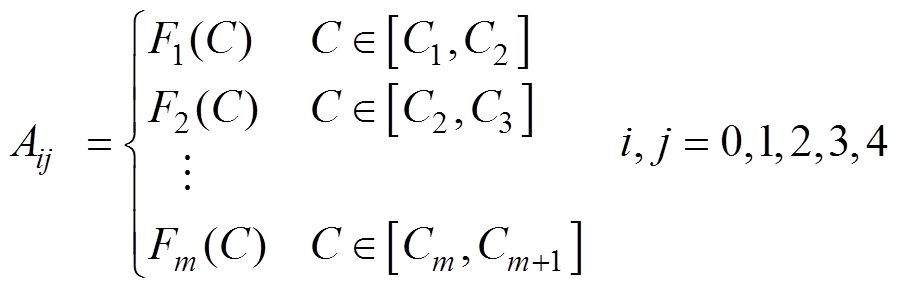（4）
式中，Aij为充电倍率C关于系数组aij的三次样条拟合函数；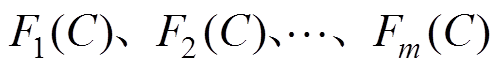
为充电倍率在对应区间
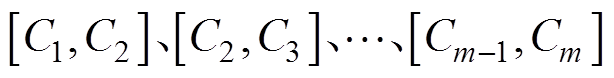关于系数组aij的三次样条分段拟合函数。
（5）将式（4）代入式（2）中获得以充电倍率为自变量、R关于T和SOC二元多项式函数的系数为因变量的函数关系，即构建R关于T、SOC和充电倍率C的多因素动态充电内阻模型为
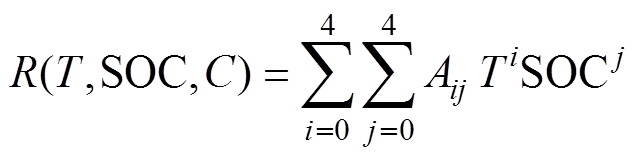（5）式中，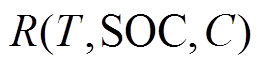
为以内阻为因变量关于T、SOC及充电倍率为自变量的构造函数。
实验测试平台由电池充放电系统、恒温箱和锂离子电池三部分组成。充放电系统主要包括直流电源、电子负载仪和上位机等，充放电系统设备精度，主要参数见表1；恒温箱用于控制电池实验的环境温度，其温度的测量误差值小于±0.5℃，测试电池为某商业18650车用动力三元锂离子电池，具体参数见表2。
表1 直流电源及电子负载仪主要参数
Tab.1 Main parameters of DC power supply and electronic load meter
参数直流电源电子负载仪 最大电压(160±0.2%)V(量程)(120±0.05%)V(量程) 最大电流(120±0.2%)A(量程)(30±0.1%)A(量程) 电压采集精度±(5+0.05%)mV±(0.05%+0.02%)(量程) 电流采集精度±(10+0.1%)mA±(0.05%+0.05)(量程)
表2 电池参数
Tab.2 Battery parameters
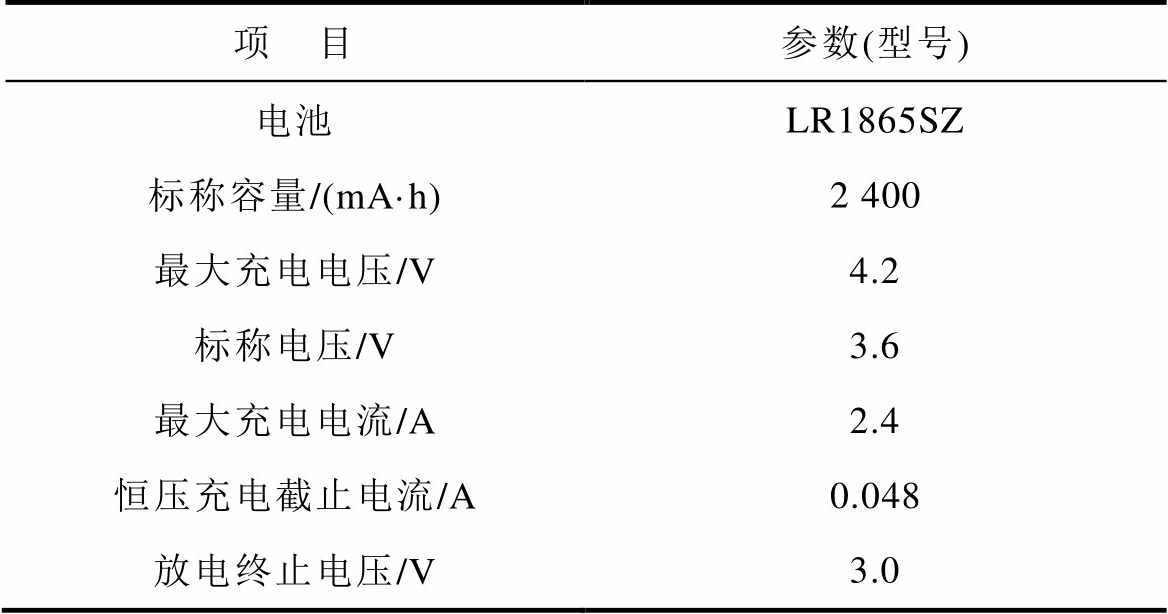
项 目参数(型号) 电池LR1865SZ 标称容量/(mA·h)2 400 最大充电电压/V4.2 标称电压/V3.6 最大充电电流/A2.4 恒压充电截止电流/A0.048 放电终止电压/V3.0
鉴于国内外相关标准中规定的电池内阻测试方法时间成本高，实验测试采用本课题组提出的Multi- rate HPPC法测量电池的充电内阻[15]。Multi-rate HPPC电压电流波形如图2所示。该方法在完成每个充放电脉冲测试后增加一个容量补损的回充阶段，避免传统HPPC法充放电脉冲过程中容量的损失，既能对每一阶段电池的SOC精确计算，又能完成多个倍率的充放电脉冲测试实验。
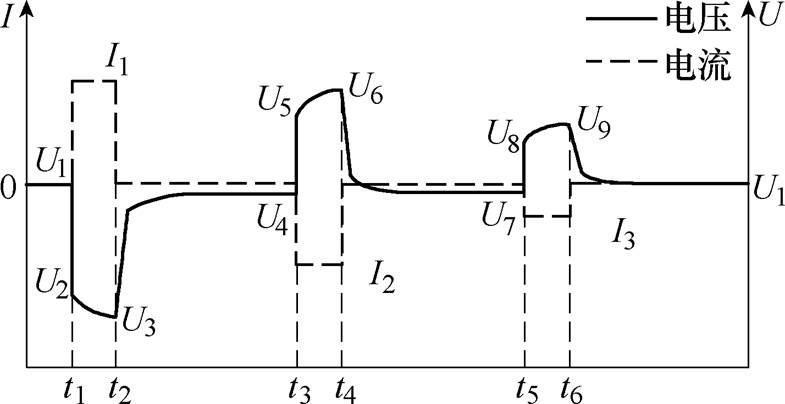
图2 Multi-rate HPPC电压电流波形
Fig.2 Voltage and current waveforms of Multi-rate HPPC
实验测试电池在多温度（5℃、15℃、25℃、35℃、45℃）、不同SOC及多种充电倍率下的充电内阻特性变化，步骤如下：
（1）将电池以标准恒压-恒流（Constant Voltage- Constant Current, CV-CC）充电直至电池满充，计此时荷电状态SOC为100%，并静置1h。
（2）将电池置于恒温箱内，并设置第一个温度测量点为5℃，以1C恒流放电至SOC减少10%，静置1h。
（3）Multi-rate HPPC测试。先将电池I1以C倍率放电10s，搁置40s，I2再以C倍率充电10s，搁置40s，最后I3以C倍率充电10s，用于对电池短暂回充实现容量补损，搁置40s；其中I1的初始值为0.25C，I1、I2、I3三者之间的固定比例关系为：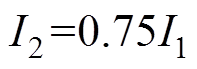
，
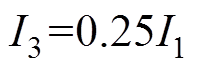，具体的电压电流波形如图2所示。重复进行Multi-rate HPPC充放电测试，并将I1电流增加0.25C，I2和I3根据固定比例而改变，直至达到电池最大的充放电倍率。
（4）九种SOC状态下的内阻测试。分别调整电池SOC至0.9、0.8、0.7、0.6、0.5、0.4、0.3、0.2、0.1，重复上述步骤（2）、步骤（3），测量出电池在这九种SOC状态下的响应电压数据。
（5）四种温度点下的内阻测试。将步骤（2）中的温度测量点依次调整为15℃、25℃、35℃和45℃，重复步骤（1）、步骤（4），分别测量出电池在这四种温度条件下的响应电压数据。
（6）计算充电内阻。根据步骤（1）～步骤（5）得到电池在不同温度、不同百分比SOC及不同倍率下响应电压数据，计算出电池在不同温度及不同百分比SOC下的多倍率充电内阻。
根据Multi-rate HPPC实验获取电池在不同充电倍率、温度以及SOC下的内阻数据，从锂离子电池在实际充电过程中电池荷电状态、温度和充电倍率对电池内阻的影响展开分析。
电池在多温度（5℃、15℃、25℃、35℃和45℃）下充电倍率均为0.25C工况时的内阻随SOC变化的平面图如图3a所示，不同温度、SOC和内阻变化的三维立体图如图3b所示。由图3整体可见，电池在充电过程中，当测量电池的环境温度逐渐升高（由5℃升到45℃）时，各个SOC状态下的电池充电内阻均减小，即温度与充电内阻呈明显的负相关。在低温（5℃）下相较于常温（25℃）和高温（45℃）时电池内阻随SOC的变化波动更为明显，呈现出典型的非线性特征。当电池的环境温度由15℃降低到5℃时，内阻值的增长幅度要远大于由45℃降低到35℃。电池在低SOC（0.1～0.2）时，在低温（5℃）和高温（45℃）下测量出来的电池内阻值相差高达近60mW，这是因为温度通过影响锂离子在正负极脱嵌与嵌入速度以及电解液黏度等，进而影响电池内阻的阻值[16-17]。因此，温度是影响电池内阻的关键因素之一。
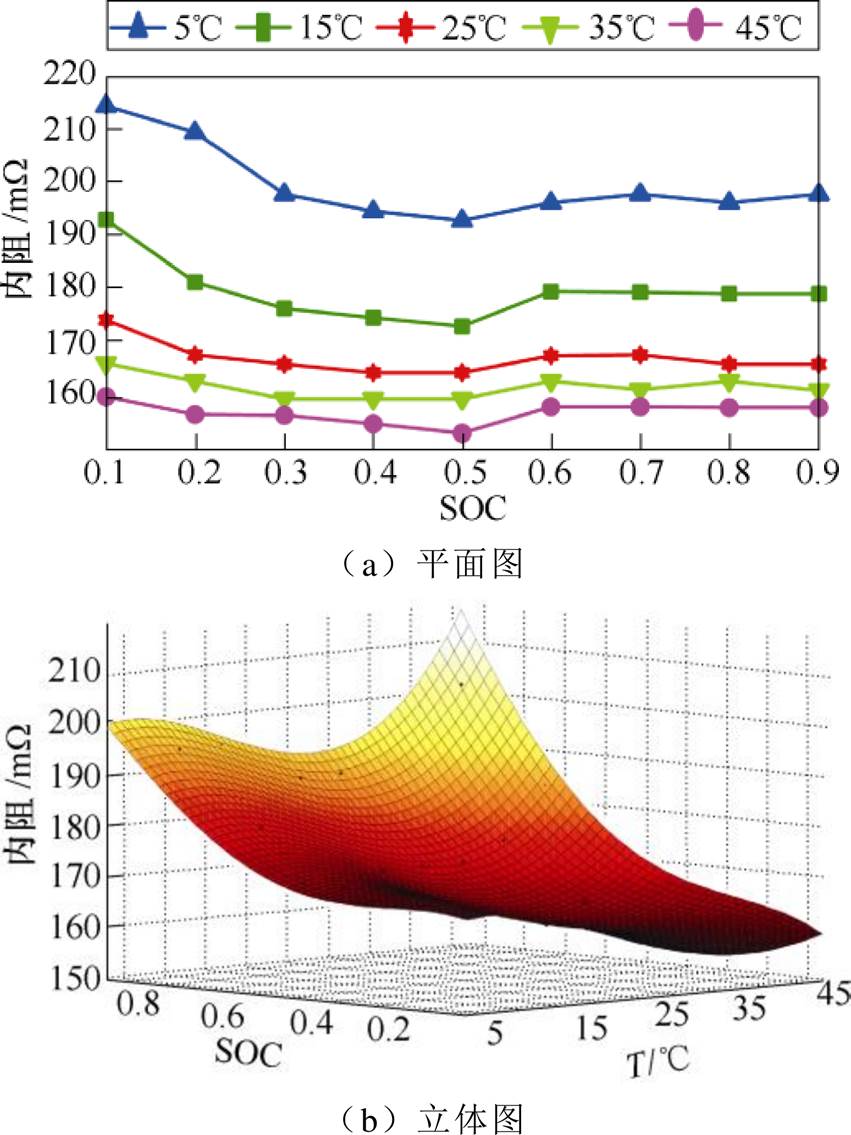
图3 不同温度和SOC下的充电内阻
Fig.3 Charge resistance under different temperature and SOC
电池在5℃和15℃下的内阻随SOC呈现相同的变化规律（见图3a），当SOC由0.1增大到0.5时，内阻值降低；但是，当SOC由0.5增长到0.6时，内阻值上升；SOC继续由0.6增长到0.9时，内阻值基本不变。而在其他25℃、35℃及45℃温度下，充电内阻随SOC（0.1～0.9）的变化幅度很小。从高温（45℃和35℃）、常温（25℃）和低温（5℃和15℃）时整体内阻值随SOC变化曲线来看，当SOC在大于30%且小于80%范围内时，充电内阻较小；当SOC＜30%或SOC＞80%时，充电内阻较大。此外，不同温度下的电池内阻随SOC变化曲线的具体数值也存在差异。在低温（5℃）条件下，SOC变化对电池内阻影响较大，内阻波动高达35mW，因此在进行低温内阻建模时，应该重点考虑SOC对内阻的影响。
选择电池在低温5℃、常温25℃和高温45℃下不同充电倍率的充电内阻进行分析，其不同充电倍率下的充电内阻如图4所示。从图4可知，电池在低温（5℃）、常温（25℃）及高温（45℃）下，充电倍率大小对电池内阻阻值均有影响。特别在低温下电池内阻随着充电倍率的增加大致呈现为下降的规律，图4a中内阻在充电倍率为0.75C和0.125C的变化最大为16.5mW。在常温及高温下，内阻随着充电倍率的增加表现为上升趋势，图4b和图4c中充电内阻在倍率为1C和0.125C下测量出来的内阻值分别相差近5mW 和7mW。虽然充电倍率相较于T和SOC对内阻的影响较小，但是，要建立准确的电池充电内阻模型，需要考虑电池充电内阻随充电倍率的变化关系。
图4 不同充电倍率下的充电内阻
Fig.4 Charge resistance at different rates
根据图1的模型构建方法，结合Multi-rate HPPC法测量的实验数据，采用Matlab对内阻与温度和SOC进行拟合，并提取拟合后的二元多项式函数的系数；然后，采用三次样条插值算法构建所提取的二元多项式函数的系数与电池充电倍率的函数关系式。具体为：
（1）采用充电倍率为0.125C、0.25C、0.375C、0.5C、0.625C、0.75C、0.875C和1C下，分别构建在充电过程中的多因素动态充电内阻模型，根据式（2）分别拟合这9个倍率，因变量R与自变量T（5～45℃，每次间隔10℃，共5个温度点）和SOC（0.1～0.9，每次间隔0.1，共9个SOC点）的二元四次多项式函数，并提取各倍率下的函数系数组，提取的不同充电倍率下二元四次多项式系数组aij见表3。
表3 不同充电倍率下二元四次多项式系数组
Tab.3 Binary quadric polynomial coefficient at different charging rates
系数0.125C0.25C0.375C0.5C0.625C0.75C0.875C1C a00260.99252.42248.64240.86231.98227.06242.94238.29 a10-4.10-3.89-4.16-3.97-3.38-3.18-3.89-3.78 a01-245.86-222.50-200.66-159.99-129.44-102.63-164.15-146.50 a20-7.9×10-32.0×10-24.8×10-26.1×10-24.3×10-25.7×10-27.9×10-28.8×10-2 a118.396.426.275.013.722.203.222.36 a02241.50303.69266.96179.64150.5894.13200.96186.62 a302.7×10-31.5×10-39.1×10-42.3×10-45.6×10-4-2.8×10-4-6.4×10-4-1.0×10-3 a21-1.2×10-1-7.9×10-2-9.7×10-2-6.2×10-2-5.8×10-2-6.3×10-3-1.7×10-2-1.2×10-2 a12-8.14-6.90-6.22-5.53-3.50-3.04-3.76-2.22 a03135.01-70.74-62.4032.617.0875.7314.62-17.32 a40-3.6×10-5-2.3×10-5-1.9×10-5-1.1×10-5-1.4×10-5-3.3×10-6-1.2×10-62.7×10-6 a318.85×10-44.43×10-48.61×10-45.43×10-45.64×10-4-4.56×10-59.58×10-51.05×10-4 a224.6×10-23.6×10-22.6×10-21.5×10-21.1×10-21.1×10-24.8×10-3-3.0×10-3 a132.332.342.262.291.321.141.510.94 a04-192.35-59.70-49.64-91.12-59.96-93.11-88.82-59.81
（2）采用三次样条插值法，根据式（4）将上一步中提取的各个倍率下的二元四次多项式系数组aij分别拟合成关于以倍率C为自变量，系数组aij为因变量的三次样条函数。表3中15个系数和倍率拟合的三次样条函数图像如图5所示。在充电倍率区间[0.15C, 1C]内，每输入一个倍率可以估算出一组与之对应的系数组（a00～a04），即可在该区间获得其他充电倍率下的内阻R关于T和SOC二元四次多项式函数的系数，再由式（5）构建充电过程中R关于T、SOC和充电倍率C的多因素动态内阻模型。
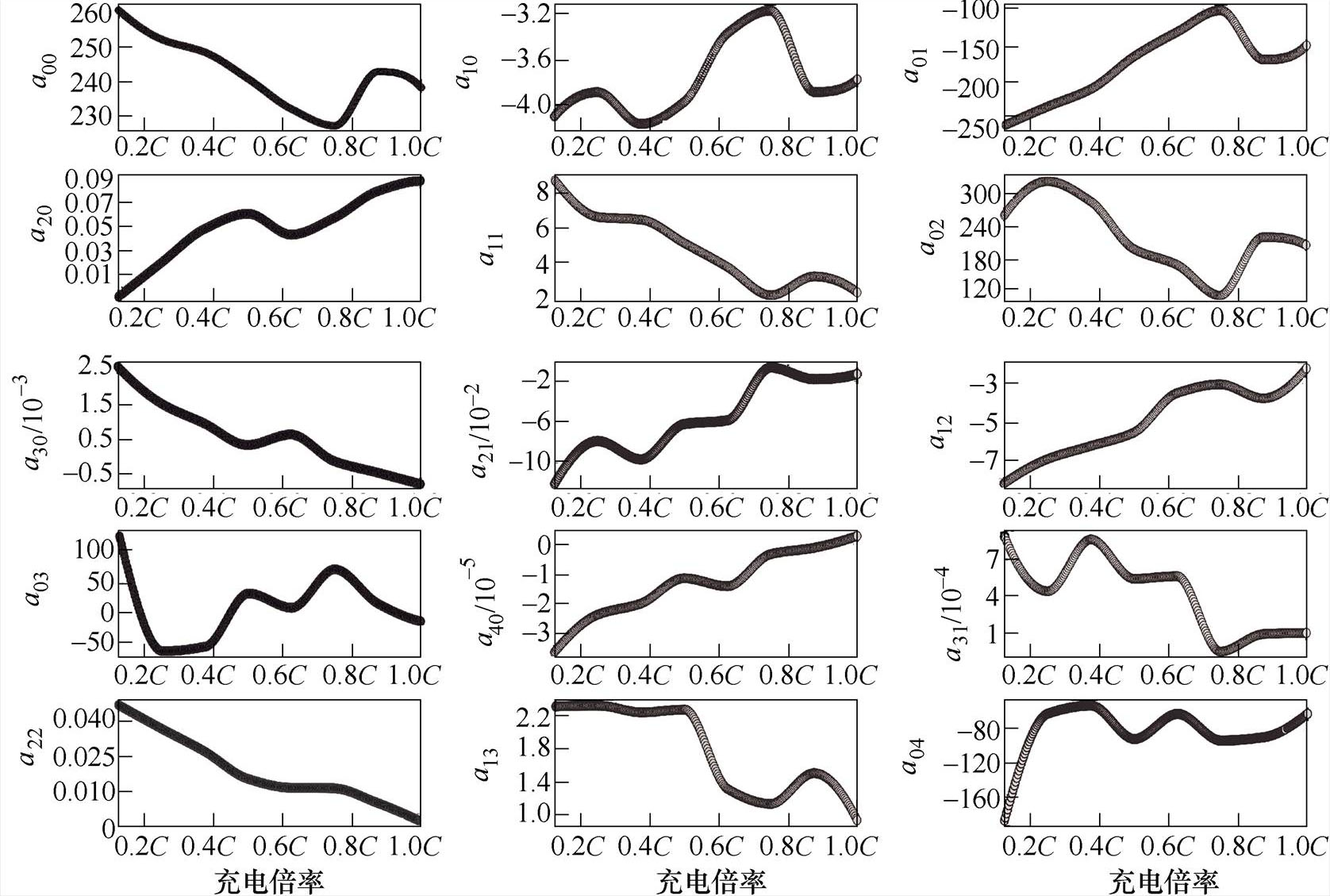
图5 15个系数和倍率拟合的三次样条函数图像
Fig.5 Image of cubic spline function fitted with 15 coefficients and multipliers
为验证模型估算的准确性，充电倍率分别选取0.187 5C、0.562 5C和0.937 5C，温度分别为5℃、25℃和45℃，SOC分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，对充电内阻的实验值与所建立的多因素动态内阻模型估算值进行比较如图6所示。从图6中可看出，内阻误差值随SOC的变化曲线具有相似的变化规律。通常估算内阻误差值在低温（5℃）和常温（25℃）下随SOC的波动幅度比在高温（45℃）工况下大，且常温内阻误差数值大体要大于高温的内阻误差值，但是内阻绝对误差的最大值却发生在常温下SOC=0.9时，倍率为0.937 5C工况中。从具体数据来看，在0.187 5C充电倍率下，5℃内阻估计误差最大且不超过4mW；在0.562 5C充电倍率下，25℃内阻估计误差最大且不超过4mW；在0.937 5C充电倍率下，25℃内阻估计误差绝对值最大且不超过6mW。这表明在不同充电倍率和SOC的变化下内阻估计值与实验值之间保持较好的一致性，验证了所提出的多因素动态充电内阻模型能够较好地估算不同温度、不同SOC及不同充电倍率的充电内阻。
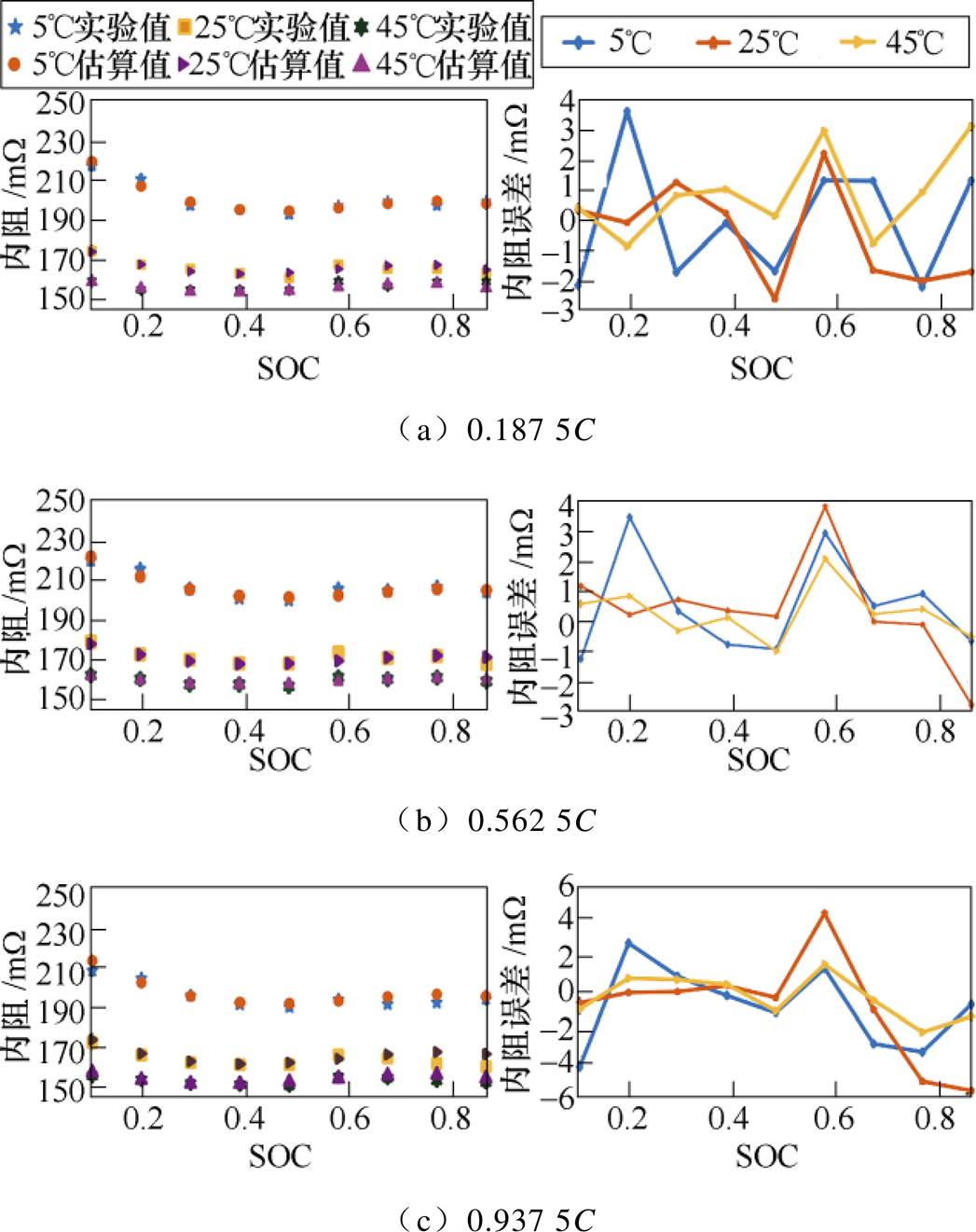
图6 充电内阻估算结果
Fig.6 Internal resistance fitting results of charging
1）通过分析锂离子电池的实际充电数据，研究电池内阻受电池SOC、温度和充电倍率的影响，并得到电池内阻和这些影响因素之间的关系。采用最小二乘法的二元多项式构建以充电内阻为因变量、温度和SOC为自变量的二元四次多项式函数描述该关系。
2）提取不同充电倍率下的二元多项式函数系数组，采用三次样条插值法拟合，构建出以温度、SOC和充电倍率为自变量，充电内阻为因变量的多因素动态内阻模型。实验验证结果表明，所建立的动态内阻模型在多种倍率和温度下能够实现准确估算电池充电内阻，估算误差不超过6mW。
参考文献
[1] 田华, 王伟光, 舒歌群, 等. 基于多尺度、电化学-热耦合模型的锂离子电池生热特性分析[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(7): 734-741.
Tian Hua, Wang Weiguang, Shu Gequn, et al. Analysis of heat generation in a Li-ion battery based on a multi-scale and electrochemical-thermal coupled model[J]. Journal of Tianjin University (Natural Science and Engineering Technology Edition), 2016, 49(7): 734-741.
[2] 孙丙香, 刘佳, 韩智强, 等. 不同区间衰退路径下锂离子电池的性能相关性及温度适用性分析[J]. 电工技术学报, 2020, 35(9): 2063-2073.
Sun Bingxiang, Liu Jia, Han Zhiqiang, et al. Per- formance correlation and temperature applicability of Li-ion batteries under different range degradation paths[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2063-2073.
[3] 潘海鸿, 吕治强, 李君子, 等. 基于灰色扩展卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2017, 32(21): 198-205.
Pan Haihong, Lü Zhiqiang, Li Junzi, et al. Estimation of state of charge of lithium ion battery based on grey extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 198-205.
[4] 何锡添, 孙丙香, 阮海军, 等. 锂离子电池变频变幅交流低温自加热策[J]. 电工技术学报, 2019, 34(9): 1798-1805.
Hen Xitian, Sun Bingxiang, Ruan Haijun, et al. A variable-frequency and variable-amplitude AC low- temperature self-heating strategy for lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1798-1805.
[5] Gümüşsu E, Ekici Ö, Köksal M. 3-D CFD modeling and experimental testing of thermal behavior of a Li-ion battery[J]. Applied Thermal Engineering, 2017, 120: 484-495.
[6] Nazari A, Farhad S. Heat generation in lithium-ion batteries with different nominal capacities and chemistries[J]. Applied Thermal Engineering, 2017, 125: 1501-1517.
[7] Waag W, Fleischer C, Sauer D U. Adaptive on-line prediction of the available power of lithium-ion batteries[J]. Journal of Power Sources, 2013, 242: 548-559.
[8] 陈英杰, 杨耕, 祖海鹏, 等. 基于恒流实验的锂离子电池开路电压与内阻估计方法[J]. 电工技术学报, 2018, 33(17): 3976-3988.
Chen Yingjie, Yang Geng, Zu Haipeng, et al. An open circuit voltage and internal resistance estimation method of lithium-ion batteries with constant current tests[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3976-3988.
[9] 林春景, 李斌, 常国峰, 等. 不同温度下磷酸铁锂电池内阻特性实验研究[J]. 电源技术, 2015, 39(1): 22-25.
Lin Chunjing, Li Bin, Chang Guofeng, et al. Experi- mental study on internal resistance of LiFePO4 batteries under different ambient temperatures[J]. Power Source Eechnology, 2015, 39(1): 22-25.
[10] Ratnakumar B V, Smart M C, Whitcanack L D, et al. The impedance characteristics of mars exploration rover Li-ion batteries[J]. Journal of Power Sources, 2006, 159(2): 1428-1439.
[11] Liu Xingtao, Chen Zonghai, Zhang Chenbin, et al. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation[J]. Applied Energy, 2014, 123: 263-272.
[12] Waag W, Käbitz S, Sauer D U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application[J]. Applied Energy, 2013, 102: 885-897.
[13] 姜久春, 时玮, 张言茹, 等. 磷酸铁锂动力电池阻抗谱参数分析[J]. 北京理工大学学报, 2014, 34(5): 470-474.
Jiang Jiuchun, Shi Wei, Zhang Yanru, et al. Impe- dance spectra investigation and parameter analysis of traction LiFePO4 battery[J]. Journal of Beijing Institute of Technology, 2014, 34(5): 470-474.
[14] 卢艳华. 车用三元锂离子动力电池内阻特性分析[J]. 电源技术, 2017, 41(5): 702-704.
Lu Yanhua. Impedance characteristics of lithium ion power battery with NCM cathode for electric vehicles[J]. Power Source Technology, 2017, 41(5): 702-704.
[15] 韦海燕, 钟腾云, 潘海鸿, 等. 基于改进HPPC锂离子电池内阻测试方法研究[J]. 电源技术, 2019, 43(8): 1309-1311.
Wei Haiyan, Zhong Tengyun, Pan Haihong, et al. Study on measurement method of internal resistance of lithium-ion battery based on improved HPPC[J]. Power Source Eechnology, 2019, 43(8): 1309-1311.
[16] Ahmed S H, Kang X, Shrestha S O B, et al. Effects of temperature on internal resistances of lithium-ion batteries[J]. Energy Resources Technology, 2015, 137(3): 1901-1905.
[17] Zhao X, De Callafon R A. Modeling of battery dynamics and hysteresis for power delivery predi- ction and SOC estimation[J]. Applied Energy, 2016, 180: 823-833.
Establishing a Dynamic Model of Lithium-Ion Battery Charging Internal Resistance Based on Multiple Factors
Abstract Modeling the internal resistance of lithium-ion batteries is of great significance for the thermal management of batteries. The internal resistance of charging is affected by many factors such as temperature and charging rate. Therefore, the relationship between the battery's internal resistance change characteristics and various influencing factors (charging rate, state of charge and temperature) is analyzed. The binary polynomial method based on the least square and the cubic spline interpolation algorithm are used to calculate the battery charging internal resistance at different charging rates, SOC, and temperature. The dynamic model of the internal resistance of multi-factor dynamic charge is established, and the charging internal resistance is estimated in different states. The results show that the maximum error between the internal resistance estimated value by the dynamic model and the experimental value does not exceed 6 mW, which proves that the proposed method for modeling battery charging internal resistance is effective.
keywords：Charging internal resistance, multiple factors, internal resistance model, least squares, binary polynomial, cubic spline
中图分类号：TM911
DOI: 10.19595/j.cnki.1000-6753.tces.200320
国家自然科学基金（51667006）和广西自然科学基金（2015GXNSFAA139287）资助项目。
收稿日期 2020-04-01
改稿日期 2020-04-29
潘海鸿 男，1966年生，教授，博士生导师，研究方向为动力电池系统信号采样及电池管理。E-mail: hustphh@163.com
陈 琳 女，1973年生，教授，博士生导师，研究方向为信号检测与处理和电池管理。E-mail: gxdxcl@163.com（通信作者）
（编辑 陈 诚）