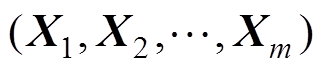 的联合分布函数[16]为
的联合分布函数[16]为摘要 锂离子电池的不一致性导致电池组的容量和寿命等指标显著小于电池单体,且该问题在梯次利用的应用场景下更为严重。电池组老化后,电池组内电池不一致性参数之间并非相互独立,而是相互耦合,因此造成电池组一致性建模困难,降低了电池组的能量利用率的估计精度。针对梯次利用电池筛选成组和成组后的状态评估,该文提出一种基于Copula理论的电池组一致性建模方法,同时实现了电池参数分布特性和参数间相关性的准确刻画。基于电池组一致性模型,提出一种电池组能量利用率估计方法,并进行实验验证,估计误差在1%以内。最后分析电池组能量利用率的影响因素,以指导电池组的优化成组和使用。
关键词:锂离子电池组 梯次利用 一致性 能量利用率
由于锂离子电池具有能量密度高、效率高和使用寿命长等优点,近年来已被广泛地应用于电动汽车和储能系统当中[1-2]。随着电动汽车数量的增长,未来将有大量的锂离子电池从电动汽车上退役,退役电池的出路逐渐成为全行业乃至全社会关注的重点。锂离子电池从电动汽车上退役后,仍然具有70%~80%的容量。若能将退役电池应用于梯次利用应用场景之中,不仅可以延长电池的使用年限,发挥出电池的剩余价值,增加锂离子电池全生命周期的经济效益;也可以大大减缓电池回收阶段的压力,带来巨大的社会效益[3-4]。因此,近年来国家相继出台了多项保障政策,以推进动力电池梯次利用的发展,梯次利用动力电池规模化工程应用于储能系统中成为技术趋势之一[5]。
由于锂离子电池单体电压和功率等级的限制,在实际使用中需要将其大量串并联成组以满足功率和能量的需求。电池单体出厂时一致性往往较好,但在电池组实际使用中,由于电池组温度场分布不均匀、电池单体在电池组中所处的位置不同等因素[6],导致电池组老化过程中电池单体的一致性参数(如容量、内阻和荷电状态(State of Charge, SOC)等)快速发散,使得电池在梯次利用场景下,其一致性不及新电池,而电池的不一致直接影响电池组的使用效率,降低电池组的经济效益[7]。因此,亟需研究梯次利用电池组的能量利用率计算方法,以指导梯次利用电池使用前的筛选成组和成组后的电池组状态评估。
电池组能量利用率的主要影响因素是电池的一致性。在实际应用中,测量每一个电池单体的参数将耗费大量人力物力,使得梯次利用电池不再具备成本上的优势。通过适当的抽样方法测量少部分电池样本,可以获得电池参数的统计特性,因此学者多研究基于概率统计的电池一致性建模。
当前,针对电池组一致性的相关研究主要集中于两方面:一方面研究电池单体参数的统计特性。S. F. Schuster等[8]通过将老化的电池组和新三元电池组进行对比,发现电池容量和内阻在新电池状态下呈现正态分布,但在电池组老化过程中,正态分布逐渐转变为Weibull分布。王震坡等[9]对不一致性的发展规律进行了研究,提出电压的不一致性分布遵循正态分布并给出了正态分布参数的计算方法。魏五星等[10]分析了110节串联电池电压的一致性,认为开路电压和极化电压都服从正态分布。程功 等[11]对两辆电动公交车电压的数据进行了长期跟踪,发现电池的开路电压(Open Circuit Voltage, OCV)服从正态分布,但随着车辆的使用,正态分布的标准差不断增大。在电池组老化的过程中,电池参数不仅呈现一定的统计规律,参数间也同时呈现出一定的相关性,因此另一方面研究关注于电池参数间的耦合机制。Zheng Yuejiu等[12]研究了电池容量衰退不一致与电池SOC不一致之间的关系,研究结果表明,锂离子在负极上的损失是电池间产生SOC差异的主要因素。Yang Fangfang等[13]研究了库仑效率与电池容量衰退之间的关系,库伦效率较低的电池不仅具有更快的容量衰退速率,也同时加大了电池间SOC的不一致。但是,当涉及电池一致性多参数联合建模时,现有的一致性刻画的方法中,多认为电池参数间相互独立[14]或服从联合分布[15],并没有同时考虑参数的统计特性和参数间的相关性。因此本文提出了一种基于Copula理论的电池一致性建模方法,基于一致性模型实现了电池组能量利用率的仿真计算,通过实验验证了方法的有效性并进一步分析了能量利用率的影响因素。
当前,电池组的不一致主要表现为电池单体容量、内阻和SOC的不一致。每个参数都有其特定的统计特征,与此同时,参数之间又存在着一定的相依性。因此,本文基于Copula理论,实现电池参数分布特性及参数间相关性的准确刻画。
Copula是一类将联合分布函数与它们各自的边缘分布函数连接在一起的函数。根据Sklar定理,每个随机向量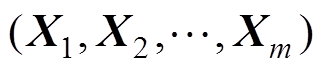 的联合分布函数[16]为
的联合分布函数[16]为
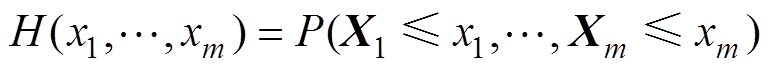 (1)
(1)都可以由随机向量的边缘分布函数
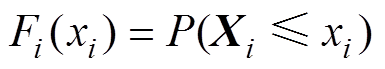 (2)
(2)
和一个Copula函数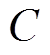 来表示,即
来表示,即
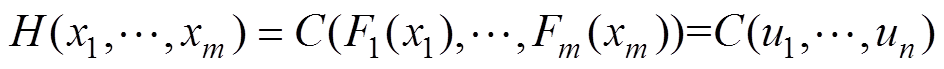 (3)
(3)式中,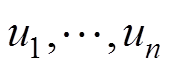 为标准均匀分布的随机变量。
为标准均匀分布的随机变量。
因此,Copula可被用于刻画随机变量之间的相依性。同样地,如果已知随机变量的边缘分布函数和对应的Copula,则可以构造出一系列与随机变量具有相同分布特性和变量间相依性的随机数。
由式(3)可知,Copula理论在应用过程中的未知参数为随机变量的边缘分布函数的相关参数和Copula模型参数。本文中采用基于非参数核密度估计的两阶段极大似然估计实现Copula参数估计,即首先利用核密度估计法获得随机变量的累积分布函数,再通过极大似然估计法估计Copula模型参数。
首先对随机变量的边缘分布函数进行核密度估计。在给定随机向量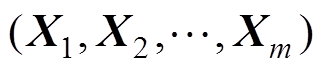 的n次观测值
的n次观测值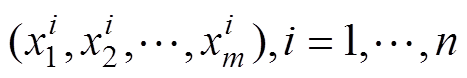 的情况下,随机变量的累积分布函数的核密度估计可表示为
的情况下,随机变量的累积分布函数的核密度估计可表示为
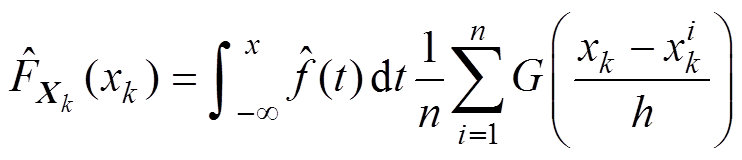 (4)
(4)其中
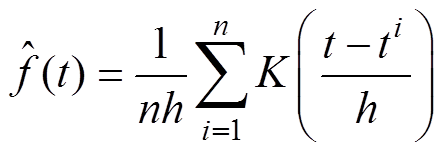 (5)
(5)
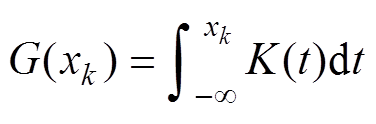 (6)
(6)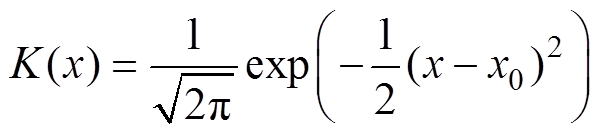 (7)
(7)
式中,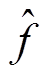 为随机变量概率密度函数的核密度估计;
为随机变量概率密度函数的核密度估计;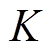 为核函数;h为带宽。本文采用高斯核函数进行核密度估计。
为核函数;h为带宽。本文采用高斯核函数进行核密度估计。
对随机变量的边缘分布函数进行核密度估计后,开展对Copula模型参数的极大似然估计。本文以三变量为例,其Copula函数及其概率密度函数可分别表示为
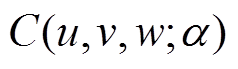 (8)
(8)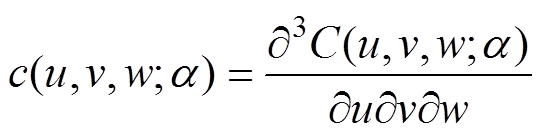 (9)
(9)
根据随机变量边缘分布函数的估计方法,其联合分布函数可表示为
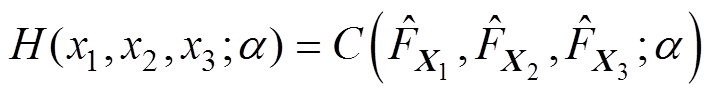 (10)
(10)对应的概率密度函数为

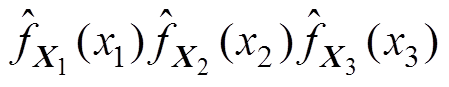 (11)
(11)样本的似然函数为
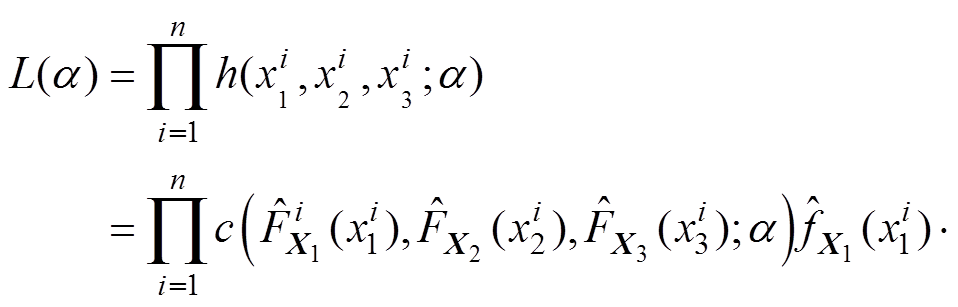
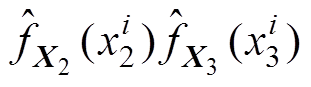 (12)
(12)对似然函数求对数可得
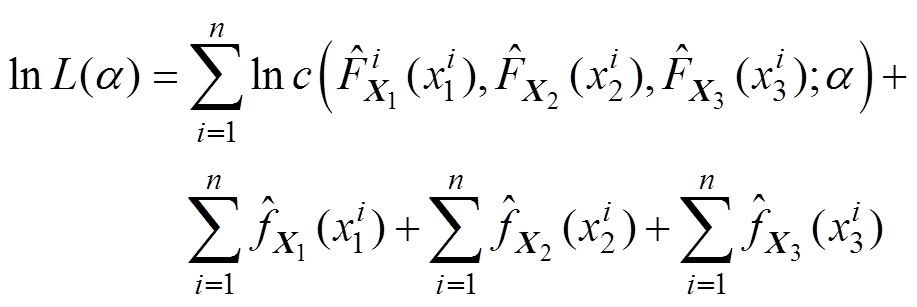 (13)
(13)
由于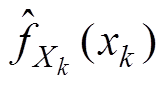 已知,因此即可通过对式(13)的第一部分对参数求导并令导数为零来获得对数似然函数的最大值点,有
已知,因此即可通过对式(13)的第一部分对参数求导并令导数为零来获得对数似然函数的最大值点,有
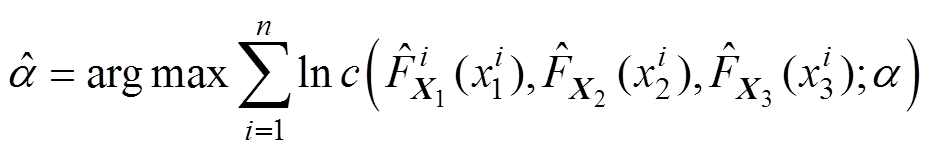 (14)
(14)尽管根据Sklar定理,任意一多元分布函数都有其对应的特定的Copula函数,但受限于相关数学理论,目前仅提出有限个类型的Copula函数,每一个类型的Copula函数适用于描述一种特定类型的变量间的相关关系。由于具备在高维空间的泛化能力,本文选取高斯Copula函数来描述变量间的相依结构。其分布函数和概率密度函数的形式分别为
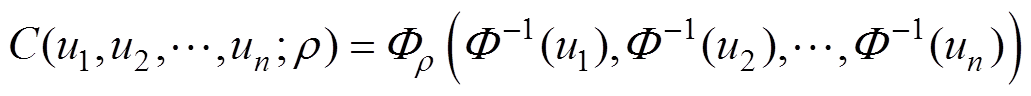 (15)
(15)
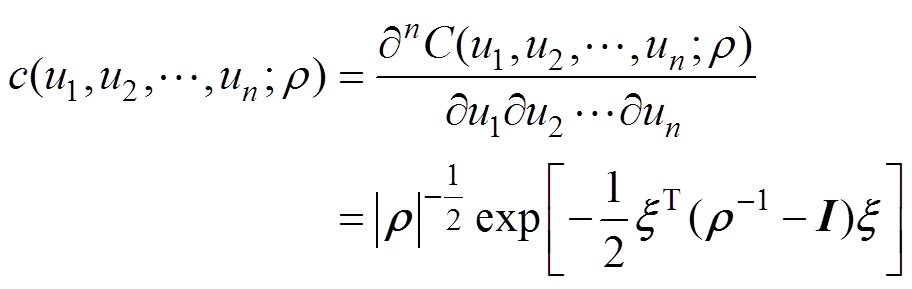 (16)
(16)式中,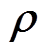 为相关系数矩阵;
为相关系数矩阵;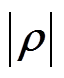 为矩阵
为矩阵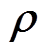 的行列式;
的行列式;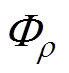 为相关系数矩阵为
为相关系数矩阵为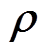 的n维标准正态分布的分布函数;
的n维标准正态分布的分布函数;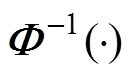 为标准正态分布的分布函数的逆函数;
为标准正态分布的分布函数的逆函数;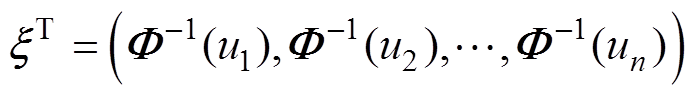 ;I为单位矩阵。
;I为单位矩阵。
在给定电池一致性参数的数据后,即可根据1.2节中介绍的方法确定最优的Copula函数。因此,便可以模拟生成一系列随机数来建立电池组一致性多元分布模型,其具体步骤如下:
(1)基于观测值,采用核密度估计方法,确定各随机变量的累积分布函数(随机变量联合分布中的边缘分布函数)。
(2)将输入随机变量(X-域)通过累积分布函数变换成Copula域内([0, 1]上均匀分布)的随变量。
(3)确定Copula函数的参数。
(4)根据Copula函数生成Copula域内的随机数。
(5)根据累积分布函数的反函数,将Copula域内的随机数变换为对应的电池一致性参数的数据。
经过变换后,新产生的随机数将与观测值具有相同的边缘分布函数和随机变量间的相依性特性。
电池组的能量利用率为电池组的放电可用能量与电池组额定能量的比值,即
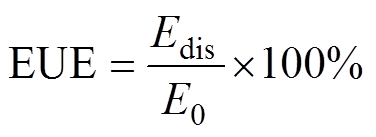 (17)
(17)式中, 为电池组的额定能量,即电池组理论上可储存的能量最大值;
为电池组的额定能量,即电池组理论上可储存的能量最大值;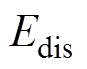 为电池组的放电可用能量,即在某一电流倍率下,电池组放电SOC从100%到0的过程中的放电能量。在放电过程中,若任意一电池单体的电压达到放电截止电压,即认为电池组SOC=0。本文以如图1所示的锂离子电池Thevenin等效电路模型为例,介绍电池组能量利用率的计算方法。
为电池组的放电可用能量,即在某一电流倍率下,电池组放电SOC从100%到0的过程中的放电能量。在放电过程中,若任意一电池单体的电压达到放电截止电压,即认为电池组SOC=0。本文以如图1所示的锂离子电池Thevenin等效电路模型为例,介绍电池组能量利用率的计算方法。
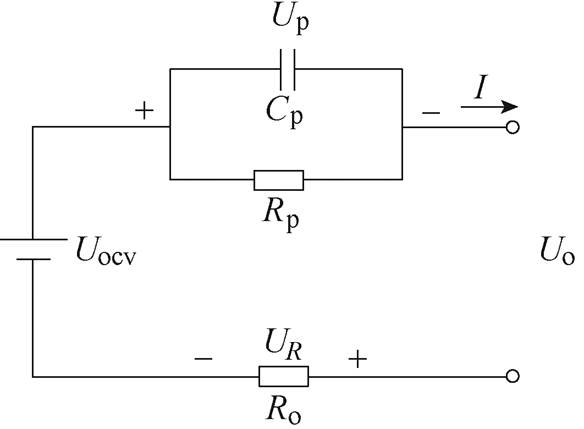
图1 锂离子电池Thevenin等效电路模型
Fig.1 Thevenin model of lithium-ion battery
图1中,Uocv为电池的开路电压;UR和Up分别为欧姆内阻Ro和极化内阻RP上的压降;I为放电电流。设R为电池欧姆内阻和极化内阻之和。若电池极化电压的动态特性可忽略不计,则电池的端电压可表示为
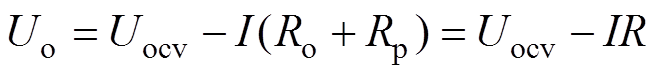 (18)
(18)当电池组对外放出能量时,一部分能量在内阻R上消耗。在一个由N个电池串联组成的电池组中,设Qi、Ri和SOCstart,i分别为电池组中第i个电池单体的容量、内阻和在放电初始时刻的SOC。则电池组的放电可用能量可进一步推导为
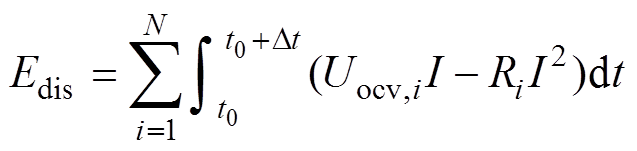 (19)
(19)
式中,Uocv,i(t)为电池OCV在放电过程中随放电时间的变化;Dt为电池组的放电时间。通常来说,可近似认为所有电池都具有相同的OCV-SOC曲线,即
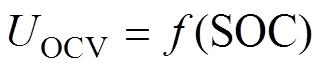 (20)
(20)由于电池组内的电池串联连接,电池组的放电时间由所有电池中具有最小放电电量的电池决定。设Qpack为电池组的容量,DSOCi和SOCend,i分别为第i个电池在以电流I放电到截止电压下限Vcutoff时SOC的变化范围和放电截止时的SOC,电池组的放电时间可表示为
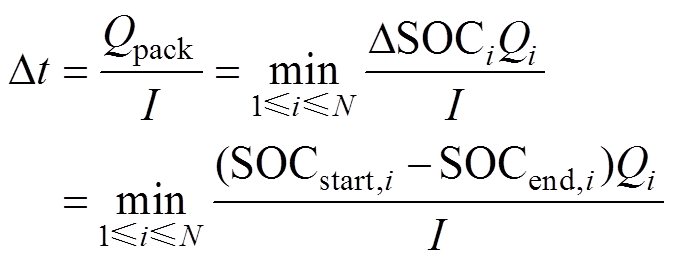 (21)
(21)
在实际应用中,可认为SOCi已知,而放电截止时刻的SOC为
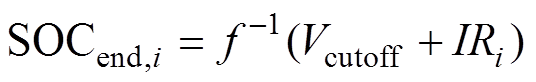 (22)
(22)电池组放电可用能量的定义,考虑了电池组放电过程中电流在内阻上的损耗。而电池组的额定容量定义为电池单体可储存的能量之和,反映了电池组储存能量的能力,因此电池组的额定能量[11]可写为
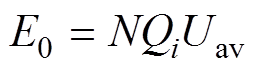 (23)
(23)
式中,Uav为电池SOC在从100%到0变化过程中开路电压OCV的平均值。因此,基于电池组放电可用能量和电池组额定能量的定义,电池组能量利用率为
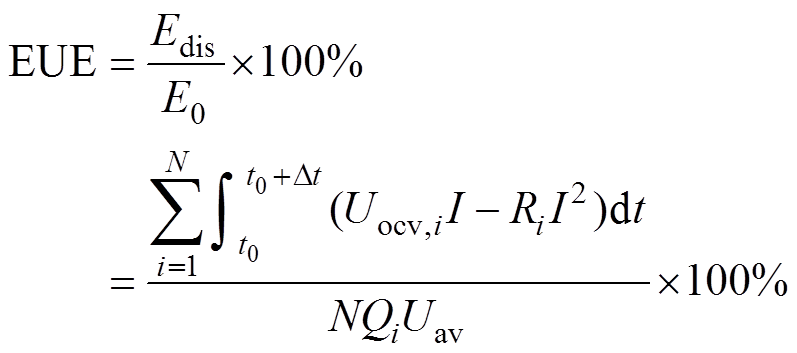 (24)
(24)需要说明的是,第1节中所述的电池一致性多元分布模型为关于电池一致性参数的概率模型,而式(24)中的EUE仍为一随机变量,且该随机变量具有复杂的概率密度函数,因此,电池组能量利用率的数值结果不能通过数学推导来解决。为了解决这一问题,本文使用蒙特卡罗模拟的方式来获得能量利用率的数值结果。蒙特卡洛的基本原理思想是通过多次重复模拟的方式来获得模型输出的统计特征。对于每次模拟中的模型输入,可根据参数的概率分布通过随机抽样的方式获得。本文以电池组能量利用率模拟仿真结果的期望值作为能量利用率的估计值,在m次模拟后,能量利用率的估计值可表示为
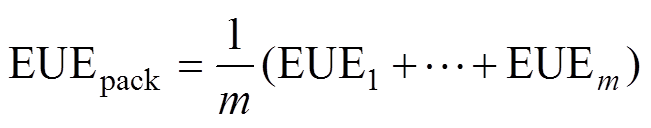 (25)
(25)
为了验证本文提出的电池组一致性建模方法的先进性以及能量利用率估计方法的准确性,本文针对磷酸铁锂电池组开展相关测试进行实验验证。该电池组在一电动乘用车上运行超过3年的时间,电池组由95块电池单体串联组成,电池单体的额定容量为60A·h,在超过3年的使用中,电池组未经过均衡维护。因此,电池间存在着容量、内阻以及SOC的差异。整个电池测试分为电池组倍率性能测试、电池单体容量测试和电池单体内阻测试三个部分:
(1)电池组倍率性能测试
在电池组倍率性能测试中,电池组以0.1C进行恒流充电,并分别以0.1C、0.3C、0.7C和1.2C进行恒流放电。在充电与放电过程之间,电池组静置2h。对于放电倍率大于0.1C的放电测试,在电池组静置过后,增加一个以0.1C放电并静置2h的过程,使得电池组在下一次充电之前处于电量完全放空的状态。整个电池组倍率性能测试过程中,电池组的充/放电截止条件分别为任意一电池单体达到充/放电截止电压(分别为3.65V和2.5V)。
(2)电池单体容量测试
在完成电池组倍率性能测试后,首先对电池组以0.1C进行恒流充电,截止条件为任一电池单体电压达到充电截止电压。然后将电池组拆解成95个电池单体,进行电池单体的容量测试。在电池单体容量测试中,将电池以0.1C进行恒流充电与恒流放电,充放电的截止电压分别为3.65V和2.5V,充电与放电过程之间,电池静置2h。将电池单体容量测试中第二次的充电容量记为电池单体的容量。
(3)电池单体内阻测试
本文采用复合脉冲电流法(Hybrid Pulse Power Characteristic, HPPC)对电池单体的内阻进行测试。首先将电池单体的SOC调至50%,静置2h后,以1C对电池进行恒流放电10s,静置40s后,再以0.5C对电池进行恒流充电10s。整个测试过程中电池的电流与电压响应如图2所示,电池的内阻可由欧姆定律计算得出。为了简化计算,在本文中以10s的放电内阻作为电池的内阻,其具体计算方法为
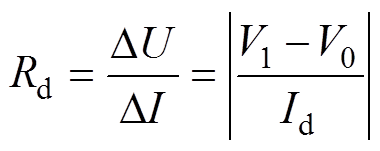 (26)
(26)式中,Rd为放电内阻;Id为放电电流;V0和V1分别为放电0s和10s时刻电池的端电压。
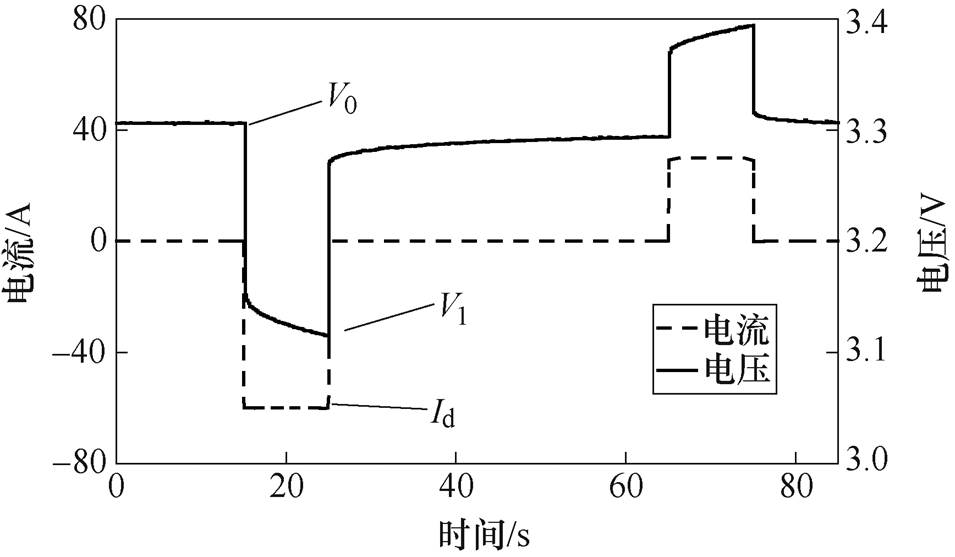
图2 内阻测试过程中电池的电压与电流响应
Fig.2 The current and voltage response during the internal resistance test
完成电池组倍率性能测试和电池单体的容量测试之后,可计算得出电池单体在电池组中SOC的差异。设电池单体容量测试中第一次循环过程中的充电容量为Qc,电池单体的容量为Q,则电池单体在电池组满电状态下的SOC为
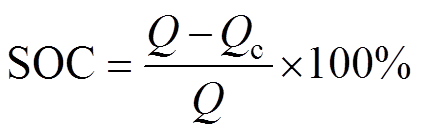 (27)
(27)图3为3.1节所述的电池测试中电池容量、内阻和电池组充满电时刻SOC的矩阵散点图。从图3中参数的直方图中可以看出,电池的容量近似正态分布,而电池内阻和SOC两个参数呈现出明显的偏态分布。与此同时,电池容量与内阻、内阻和SOC之间没有展现出明显的相关性,而容量和SOC之间显示出较强的正相关特性。
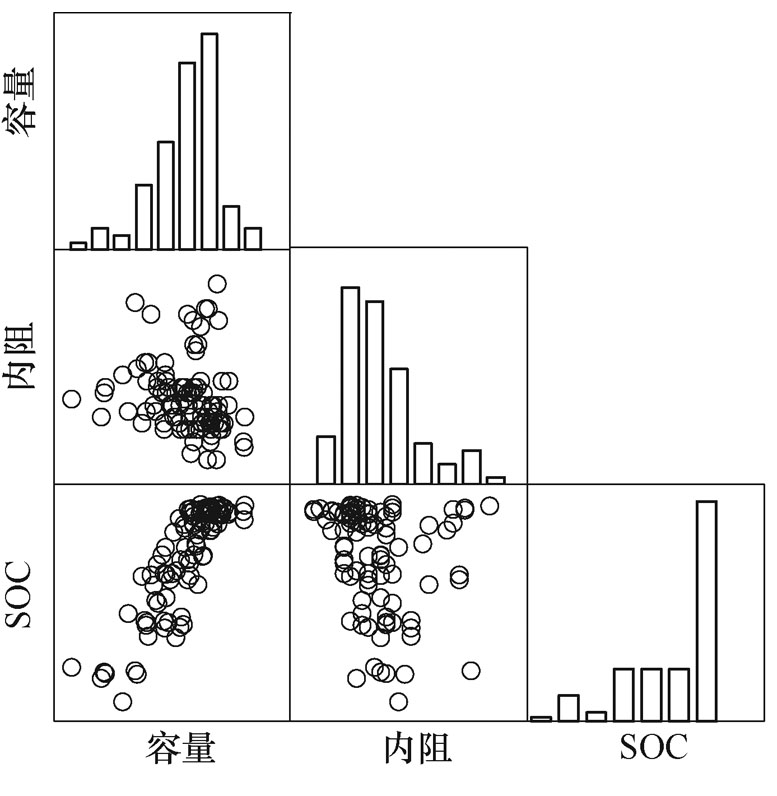
图3 电池容量、内阻和SOC的矩阵散点图
Fig.3 The scatter plot matrix of battery capacity, internal resistance and SOC
以电池的测试数据作为观测值,根据1.2节和1.3节所述的电池组一致性建模方法,在采样点数量为1 000的情况下建立的电池组一致性参数的三维散点图如图4所示。在所提出的一致性模型中,高斯Copula函数的选择保证了所建立的模型与观测值之间具有相同的相依性关系,而1.3节中所述的基于观测值累积分布函数的逆函数的变换方法保证了模型中每个随机变量都和观测值具有相同的统计特性。从图4中可以清楚地看到,SOC和容量之间存在明显的正相关关系,表明所提出的电池一致性建模方法可同时准确地刻画参数自身的统计特性和参数之间的相关性。
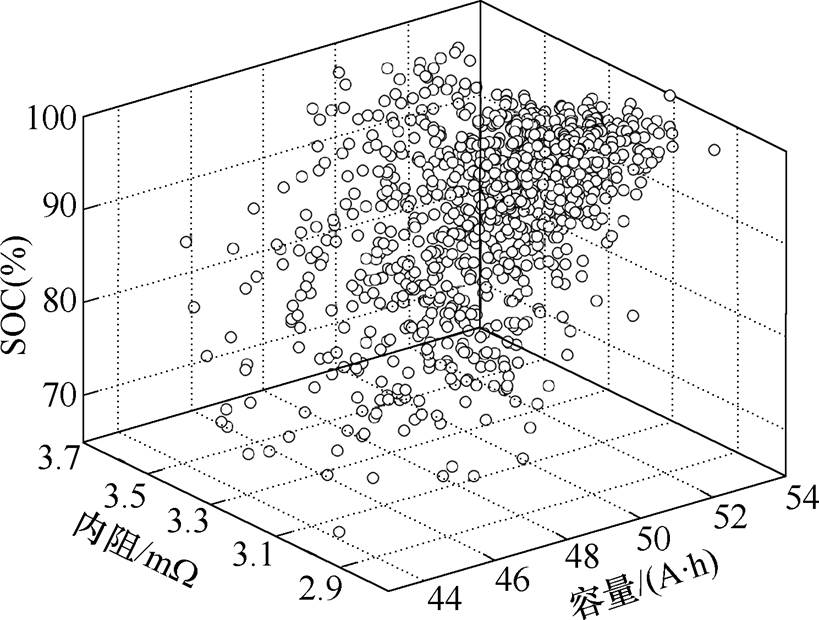
图4 电池组一致性模型
Fig.4 The proposed battery pack consistency model
根据电池组倍率性能测试和电池单体容量测试的结果,可得到电池组在不同倍率下的放电能量,进而获得电池当前状态下能量利用率的真实值。基于电池组一致性多元分布模型,根据第2节中所述的方法对电池组能量利用率进行估计,在仿真计算中,将蒙特卡洛模拟次数m设置为5 000。电池组能量利用率估计结果见表1,在4个电流倍率下,电池组能量利用率的估计结果都显示出较高的估计精度,估计误差在0.5%以内。
表1 不同放电倍率下电池组EUE估计结果
Tab.1 EUE estimation results at different discharge current rates (%)
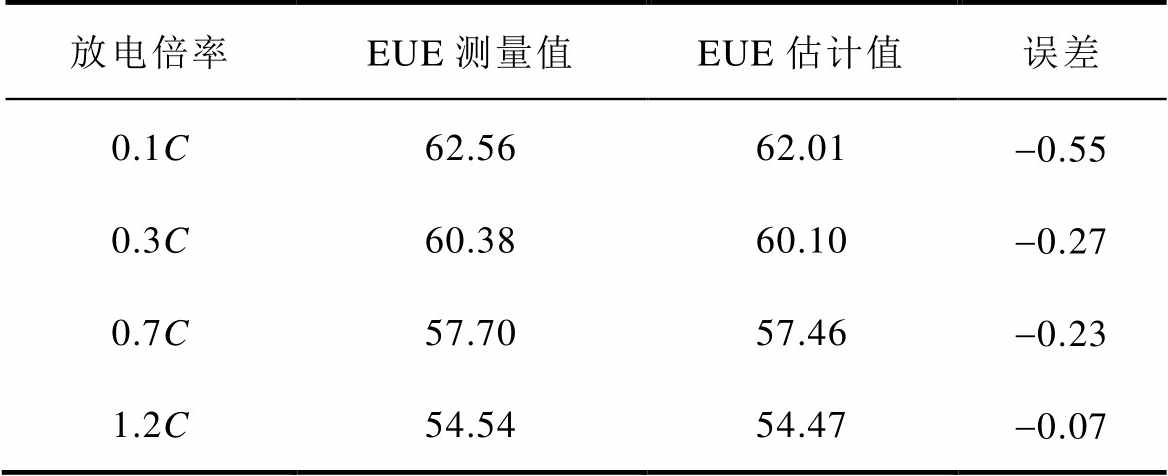
放电倍率EUE测量值EUE估计值误差 0.1C62.5662.01-0.55 0.3C60.3860.10-0.27 0.7C57.7057.46-0.23 1.2C54.5454.47-0.07
电池组的能量利用率受多种因素影响。第一,在基于电池组一致性模型的能量利用率估计中,采用了蒙特卡洛模拟的方法。蒙特卡洛模拟的次数在一定程度上影响了电池组EUE估计的精度。第二,电池组的能量利用率受电池组成组方式和使用方式的影响。当未来大量锂离子电池从电动汽车上退运后,若采用基于一致性模型的电池组能量利用率评估方法,从概率统计的角度去评估电池组在不同放电电流、不同串联数下电池组的性能,将有助于为退役锂离子电池寻找到最优的成组及使用方式。第三,电池参数的一致性也在一定程度上影响了电池组能量利用率。基于一致性模型的电池组能量利用率评估方法可定量地分析各参数的一致性对电池组能量利用率的敏感性,进而为确定电池组老化的主导因素提供理论支撑。为此,本节中将以根据3.1节中电池测试结果建立的电池组一致性模型为例,定量地分析蒙特卡洛模拟次数、电池串联数、放电倍率和电池参数一致性对电池组能量利用率的影响。
3.3.1 蒙特卡洛模拟次数的影响
基于电池组一致性模型,对电池组的能量利用率进行了5次仿真计算。在每次仿真的过程中,蒙特卡洛模拟次数m设置为10 000。图5显示了在5次仿真计算中,电池组能量利用率的估计结果随蒙特卡洛模拟次数的演变规律。在前几百次的模拟过程中电池组能量利用率估计的结果波动较大,当模拟次数达到2 500后,5次仿真的能量利用率估计结果相差不到0.1%,模拟进行到5 000次后,5次仿真的结果几乎相同。因此,在后续的仿真过程中,为了节省仿真时间,统一将蒙特卡洛模拟次数m设定为3 000。
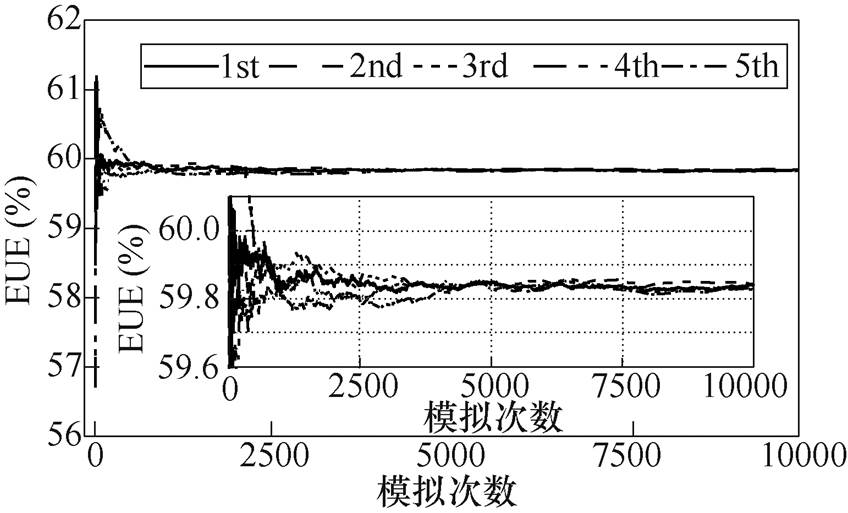
图5 电池组EUE计算结果随蒙特卡洛模拟次数的演变规律
Fig.5 The evolution of EUE with the simulation times
3.3.2 电池串联数的影响
图6显示了电池串联数从10增加到150的过程中,电池组的能量利用率在不同放电倍率下的变化情况。在不同的放电倍率下,能量利用率都表现出相似的趋势。在电池串联数从10增加到30的过程中,电池组能量利用率下降的趋势明显,各个倍率下的能量利用率都下降了5%~6%。当电池串联数继续增大后,能量利用率下降的速率逐渐变缓,能量利用率渐渐趋于稳定。这意味着从概率统计的角度看,梯次利用电池大规模串联成组后,电池组的能量利用率会最终趋近于一个稳定值,能量利用率不会因串联电池数量的继续增加而降低。
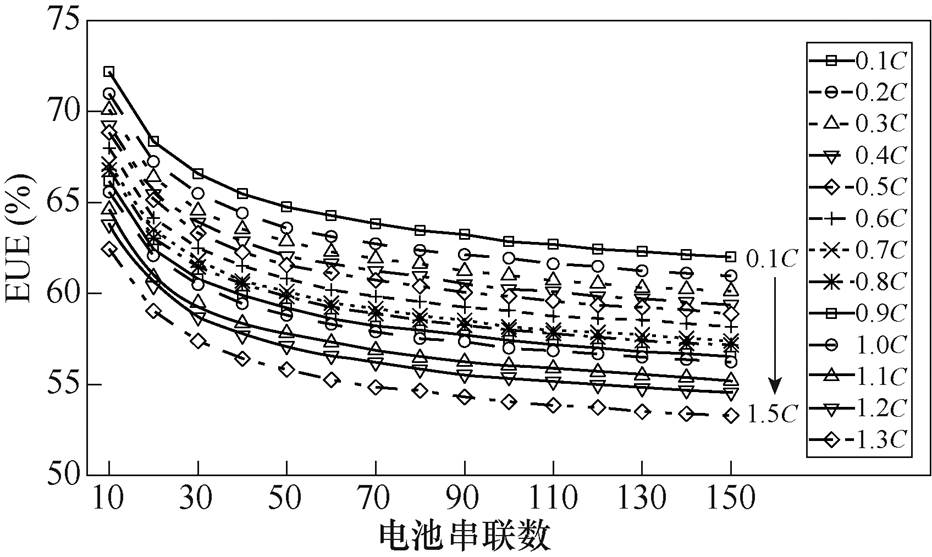
图6 在不同放电电流倍率下电池组EUE随电池串联数的演变规律
Fig.6 The evolution of EUE with the number of serial-connected battery cells at different discharge rates
3.3.3 放电倍率的影响
图7显示了放电电流倍率从0.1C逐渐增加到1.3C的过程中,电池组能量利用率在不同电池串联数下的变化情况。随着放电倍率的增加,电池组能量利用率呈现出近似线性下降的规律,并没有能量利用率迅速下降的拐点出现。当放电电流倍率从0.1C增加到1.3C时,各电池串联数下电池组的能量利用率均下降了8%~9%。
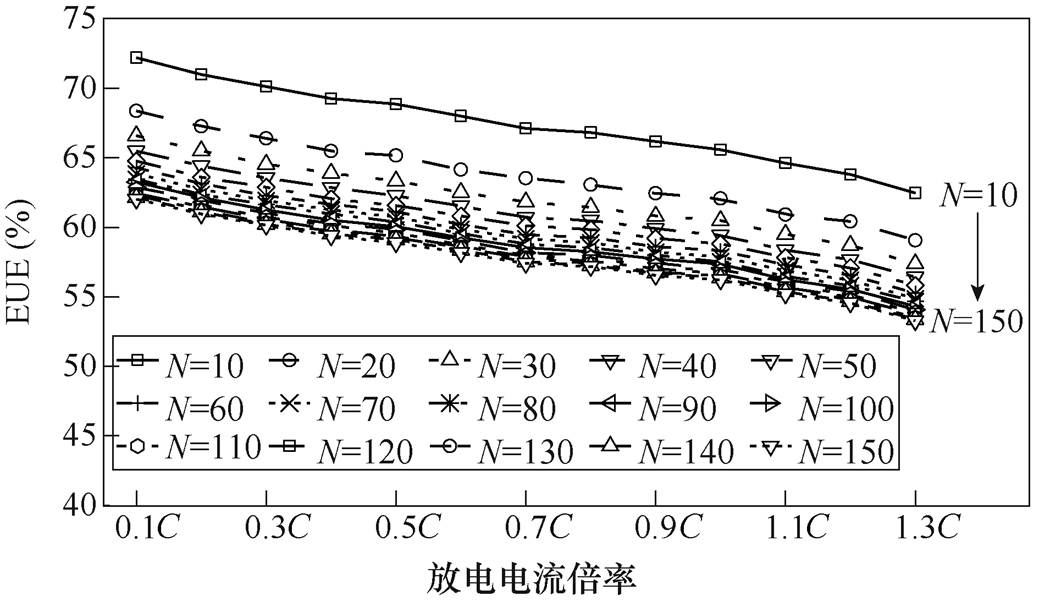
图7 在不同电池串联数下电池组EUE随放电电流倍率的演变规律
Fig.7 The evolution of EUE with discharge current rates under different number of serial-connected battery cells
综合串联电池数和放电倍率的影响分析,可建立电池组能量利用率和关于电池串联数和放电电流倍率的对应关系。基于该对应关系,可以在电池成组过程中确定最佳的电池串联数,并在后续的使用过程中优化放电电流,以达到电池组能量最大化利用的目的。
3.3.4 电池参数一致性的影响
电池组中电池各个参数的一致性同样影响了电池组的能量利用率。电池参数分布特性不同,对电池组能量利用率的影响程度也不同。为此,本文根据3.1节的测试结果,定量地分析容量、内阻和SOC三个参数的一致性对电池组能量利用率的影响。在仿真分析中,设定了四种情景。在情景1中,电池组在不同倍率下的能量利用率为表1所示的实际测试结果。而在情景2~4中,则分别消除了电池SOC、容量和内阻的不一致(情景2中所有电池SOC均为100%,情景3中所有电池的容量均取电池单体容量测试结果中的最大值,情景4中所有电池的内阻均取电池单体内阻测试结果中的最小值)。四种情景下电池组在不同放电电流倍率下的仿真结果见表2。从电池组能量利用率的仿真结果可以看出,针对本文所测试的电池组,消除电池间SOC的差异可使得电池组能量利用率增加约25%;消除容量的不一致可使电池组能量利用率增加约5%;而消除电池间内阻的不一致几乎不会提高电池组的能量利用率。电池内阻一致性对电池组能量利用率影响不明显的主要原因是,本文中所测试电池的内阻一致性较好,且仿真计算中电流倍率较小。由此可见,SOC的差异是本文所测试电池组低能量利用率的主导因素。
表2 四种情景下电池组能量利用率在不同放电倍率下的仿真结果
Tab.2 The battery pack EUE estimation simulation results of the four situations under different discharge current rates (%)
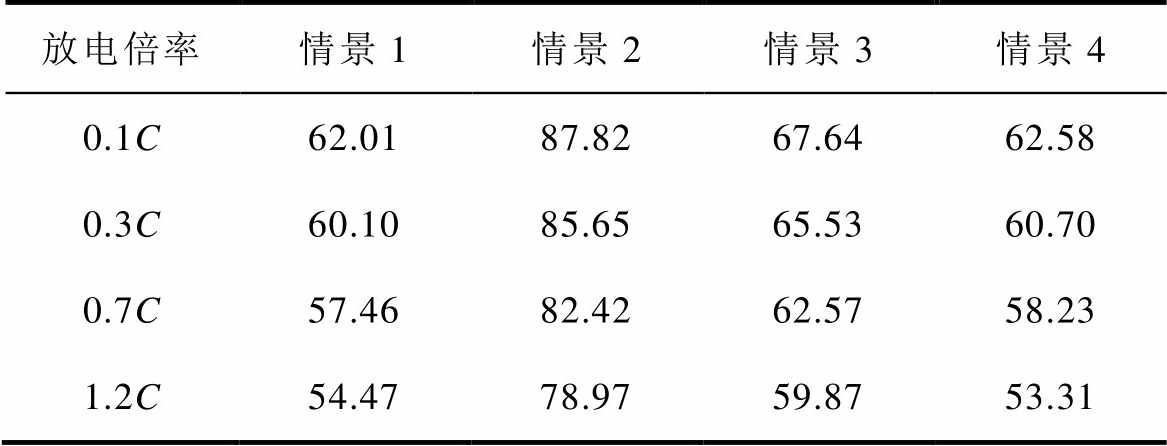
放电倍率情景1情景2情景3情景4 0.1C62.0187.8267.6462.58 0.3C60.1085.6565.5360.70 0.7C57.4682.4262.5758.23 1.2C54.4778.9759.8753.31
针对梯次利用锂离子电池组一致性较差进而导致能量利用率降低这一问题,本文提出了一种基于Copula理论的电池组一致性建模方法,基于该一致性模型,提出了电池组能量利用率的估计方法。
首先,针对一致性参数的特点,采用Copula函数来描述变量间的相关性,介绍了Copula参数估计方法和电池组一致性模型抽样方法。其次,基于电池组一致性模型和蒙特卡洛模拟的思想,提出了电池组能量利用率计算方法。根据电池组和电池单体的相关测试结果,对所提出的方法进行了精度验证,结果表明估计误差在1%以内。最后,定量地分析了蒙特卡洛模拟次数、电池串联数、放电电流倍率和电池参数一致性对电池组能量利用率的影响。结果表明,当蒙特卡洛模拟次数达到2 500后,随机模拟带来的能量利用率估计误差可降低至0.1%以内;随着电池串联数的增多,电池组能量利用率逐渐降低,但下降的速率逐渐减慢,最终能量利用率趋于稳定;随着放电电流倍率的增加,电池组能量利用率呈现出近似线性下降的规律,并没有能量利用率迅速下降的拐点出现。针对文中所测试的电池组,SOC的不一致是电池组低能量利用率的主要影响因素,消除SOC和容量的不一致,电池组能量利用率可分别提高约25%和5%,而消除电池内阻的不一致几乎不会提高电池组的能量利用率。
本文提出的基于一致性模型的电池组能量利用率估计方法和相关影响因素分析将为梯次利用锂离子电池组的优化成组与使用提供有效指导。
参考文献
[1] 焦东升, 王海云, 朱洁, 等. 基于离散Fréchet距离的电动汽车电池健康状态诊断方法[J]. 电力系统保护与控制, 2016, 44(12): 68-74.
Jiao Dongsheng, Wang Haiyun, Zhu Jie, et al. EV battery SOH diagnosis method based on discrete Fréchet distance[J]. Power System Protection and Control, 2016, 44(12): 68-74.
[2] 刘伟龙, 王丽芳, 王立业. 基于电动汽车工况识别预测的锂离子电池SOE估计[J]. 电工技术学报, 2018, 33(1): 17-25.
Liu Weilong, Wang Lifang, Wang Liye. Estimation of state-of-energy for electric vehicles based on the identification and prediction of driving condition[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 17-25.
[3] 杨若岑, 冬雷, 廖晓钟, 等. 电池剩余容量估算方法综述[J]. 电气技术, 2019, 20(10): 1-5.
Yang Ruocen, Dong Lei, Liao Xiaozhong, et al. A review on battery remaining capacity estimation[J]. Electrical Engineering, 2019, 20(10): 1-5.
[4] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948.
Yan Xiangwu, Deng Haoran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Electro- technical Society, 2019, 34(18): 3937-3948.
[5] 白恺, 李娜, 范茂松, 等. 大容量梯次利用电池储能系统工程技术路线研究[J]. 华北电力技术, 2017(3): 39-45.
Bai Kai, Li Na, Fan Maosong, et al. Research on the technical roadmap for engineering application of large-scale echelon use battery energy storage system[J]. North China Electric Poser, 2017(3): 39-45.
[6] Klein M, Tong Shijie, Park J W. In-plane nonuniform temperature effects on the performance of a large- format lithium-ion pouch cell[J]. Applied Energy, 2016, 165: 639-647.
[7] 郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J]. 电工技术学报, 2019, 34(19): 3968-3978.
Guo Yongfang, Huang Kai, Li Zhigang. Fast state of health prediction of lithium-ion battery based on terminal voltage drop during rest for short time[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3968-3978.
[8] Schuster S F, Brand M J, Berg P, et al. Lithium-ion cell-to-cell variation during battery electric vehicle operation[J]. Journal of Power Sources, 2015, 297: 242-251.
[9] 王震坡, 孙逢春, 张承宁. 电动汽车动力蓄电池组不一致性统计分析[J]. 电源技术, 2003(5): 438-441.
Wang Zhenpo, Sun Fengchun, Zhang Chengning. Study on inconsistency of electric vehicle battery pack[J]. Chinese Journal of Power Sources, 2003(5): 438-441.
[10] 魏五星. 磷酸铁锂动力电池组性能测试与分析[D]. 武汉: 武汉理工大学, 2010.
[11] 程功. 电池组一致性的统计特性与变化规律研究[D]. 北京: 北京交通大学, 2017.
[12] Zheng Yuejiu, Ouyang Minggao, Lu Languang, et al. Understanding aging mechanisms in lithium-ion battery packs: from cell capacity loss to pack capacity evolution[J]. Journal of Power Sources, 2015, 278: 287-295.
[13] Yang Fangfang, Wang Dong, Zhao Yang, et al. A study of the relationship between coulombic effici- ency and capacity degradation of commercial lithium- ion batteries[J]. Energy, 2018, 145: 486-495.
[14] Diao Weiping, Xue Nan, Bhattacharjee V, et al. Active battery cell equalization based on residual available energy maximization[J]. Applied Energy, 2018, 210: 690-698.
[15] Zhou Long, Zheng Yuejiu, Ouyang Minggao, et al. A study on parameter variation effects on battery packs for electric vehicles[J]. Journal of Power Sources, 2017, 364: 242-252.
[16] Xi Zhimin, Jing Rong, Wang Pingfeng, et al. A copula-based sampling method for data-driven pro- gnostics[J]. Reliability Engineering & System Safety, 2014, 132: 72-82.
Energy Utilization Efficiency Estimation Method for Second-Use Lithium-Ion Battery Packs Based on a Battery Consistency Model
Abstract The inconsistency of lithium-ion battery cells has caused the lifetime and capacity of the battery pack to be much smaller than that of the battery cells, and this problem is more serious in the second-use applications. Along with the aging of the battery pack, the battery consistency parameters are mutual dependent, which causes battery pack consistency modeling difficult and state of health estimation inaccurate. Aiming at the grouping and the state evaluation stages of second-use batteries, this paper proposes a Copula-based battery pack consistency modeling method. The proposed method can describe the statistical characteristics of the battery consistency parameters and the dependence structure between parameters. Based on the consistency model, a battery pack energy utilization efficiency (EUE) estimation method is put forward and verified by experiments. The estimation error is within 1%. Finally, the influencing factors of EUE is analyzed to guide the optimal grouping and operation of second-use lithium-ion battery packs.
keywords:Lithium-ion battery pack, second use, consistency, energy utilization efficiency
中图分类号:TM911
DOI: 10.19595/j.cnki.1000-6753.tces.200243
国家重点研发计划资助项目(2018YFB0905304)。
收稿日期 2020-03-10
改稿日期 2020-07-10
赵 伟 男,1981年生,博士,教授级高工,研究方向为先进电力储能集成及控制技术。E-mail: zh_solar@126.com
姜 研 男,1991年生,博士,研究方向为锂离子电池管理与成组应用技术。E-mail: jiangyan3@sunwoda.com (通信作者)
(编辑 崔文静)