
图1 电池DP模型
Fig.1 Battery DP model
摘要 建立准确合理的锂离子电池数学模型,精确估算锂离子电池(LIB)终端电压及荷电状态(SOC)对于开发高效实用的电池管理系统十分重要。首先,该文建立一种改进的环境温度依赖的锂离子电池双极化(DP)模型。然后,基于锂离子电池的动态实验数据,利用遗忘因子最小二乘法(FFLS)对该锂离子电池模型关键参数进行辨识,并将其拟合为环境温度的连续函数。同时,根据扩展卡尔曼滤波(EKF)算法,提出一种适用于不同环境温度的锂离子电池荷电状态估计方法。最后,采用-10℃、20℃和50℃下动态压力测试(DST)和US06循环工况的实验数据,对该文的锂离子电池模型进行仿真分析和验证。结果表明,该文提出的改进DP模型能够准确反映环境温度对模型参数的影响,且在电池终端电压和SOC估算方面具有较高的精度和较宽的温度适用范围。
关键词:锂离子电池 环境温度 等效电路模型 模型参数 荷电状态
锂离子电池(Lithium Ion Battery, LIB)是新能源汽车(New Energy Vehicle, NEV)的主要能量供给者,其具有轻量化、低放电率和高能量密度等诸多优点,在NEV中获得了广泛应用。需要说明的是,锂电池的精确建模和参数估计对电池荷电状态的估算至关重要,这成为开发高效的电池能量管理系统[1]最具挑战的任务和难点之一。
为此,国内外诸多研究人员对锂离子电池的数学模型开展了大量研究,主要包括电化学模型(Elec- trochemical Model, EM)[2]和等效电路模型(Equivalent Circuit Model, ECM)。与EM相比,由于ECM的模型参数少、计算简单,使其在车用锂离子电池建模中应用广泛[3]。根据文献[4]可知,常用的ECM有Rint、RC(resistance capacitor)、Thevenin以及PNGV(partnership for a new generation of vehicles)模型和双极化(Dual Polarization, DP)模型。比如,基于Thevenin模型,文献[5]提出电热耦合模型描述电池热行为和电行为之间的相互作用,通过该耦合模型,使用扩展的卡尔曼滤波器估算电池内部温度。同样,在文献[6]中,基于Thevenin模型,提出了基于AMESim-Simulink协同仿真的双滑模观测器的荷电状态(State of Charge, SOC)和健康状态(State of Health, SOH)[7]联合估算方法。尽管Thevenin模型能够对锂电池动态特性进行模拟,相比而言,常规DP模型[2]采用2个RC网络结构描述锂离子电池的电化学和浓差极化现象,能够准确地模拟电池的电化学动力学特性。
需要指出的是,锂离子电池在充放电过程中,其内部的电化学反应非常复杂[8],且具有时变性和非线性特性,其RC网络结构参数会随着不同的充放电电流、初始SOC和环境温度的不同而发生较大改变[4]。现有的锂电池建模和SOC估计中,往往忽略环境温度的影响,从而给模型参数辨识和SOC估计引入较大误差。针对温度变化下的电池建模和SOC估计,当前已有研究人员开始关注并着手研究。例如,文献[9]提出一种适用于不同温度的动力锂电池二阶RC模型及基于安时积分法的SOC估计方法,但是并没有对终端电压和不考虑环境温度的模型差异进行分析。此外,考虑到已有锂电池模型难以适应连续变化的温度环境,文献[10]基于Nernst电化学方程,提出了一种新的电池建模方法,通过在不同温度环境下模拟电动汽车实际工况,对锂电池进行放电实验,通过实验设计的方法建立电池模型,结合扩展卡尔曼滤波算法实现对锂电池SOC的动态估计。文献[10-11]建立了Thevenin模型,并以此讨论了电池内部参数测定和拟合方法,在不同温度下对电池参数进行辨识并建立电池参数与温度的函数关系,在不同环境温度下利用扩展卡尔曼滤波(Extended Kalman Filter, EKF)算法对电池进行SOC估计。在文献[12]中,基于Thevenin模型,提出一种考虑环境温度的锂离子电池模型,然后使用EKF方法估算电池SOC。上述文献中考虑环境温度影响的锂电池模型参数辨识在恒流充放电倍率下效果较好,但在动态电流下对模型精度及其SOC估计未作深入细致讨论。
为此,本文以锂电池常规DP模型为研究对象,重点考虑环境温度对模型参数的影响,提出一种环境温度依赖的改进DP模型;同时,采用遗忘因子最小二乘法(Forgetting Factor Least Square, FFLS)[13]辨识该锂电池模型参数,并应用不同环境温度下的电池实验数据[14]验证分析该改进DP模型和常规DP模型在计算电池终端电压和SOC方面的误差与精度,从而进一步分析环境温度对所提出锂离子电池模型参数及SOC估算的影响。
本文选用一种改进DP模型来描述锂离子电池的动态特性,其等效电路如图1所示。

图1 电池DP模型
Fig.1 Battery DP model
与常规DP模型不同的是,其模型参数都受到环境温度变化的影响,同时忽略SOC及电流等变量对模型参数的影响,即该改进DP模型参数只依赖环境温度而动态变化。根据基尔霍夫定律[15],图1所示的锂离子电池改进DP模型终端电压计算式为
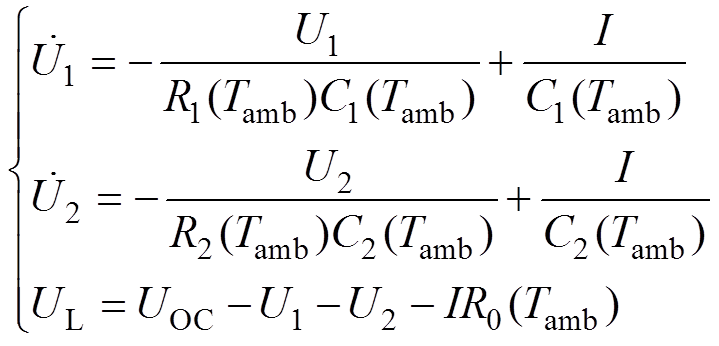 (1)
(1)式中,U1和U2分别为R1(Tamb)和R2(Tamb)两端的电压;I为电流;UL为终端电压;UOC为开路电压;R0(Tamb)为欧姆内阻;R1(Tamb)和R2(Tamb)分别为电化学极化电阻和浓度极化电阻;C1(Tamb)和C2(Tamb)分别为电化学极化电容和浓度极化电容,用于表示电池到电池或电池传输过程中的瞬态响应。改进DP模型参数R0(Tamb)、R1(Tamb)、C1(Tamb)和R2(Tamb), C2(Tamb)都被假定为依赖环境温度Tamb的待拟合多项式函数。
如文献[13]所述,准确的模型参数辨识对于锂电池SOC估算是非常重要的。锂离子电池模型参数辨识的一般步骤是利用电池充放电实验装置采集某型号电池的电流、电压数据,接着对电池可用容量的实验数据进行拟合得到电池可用容量的近似数学模型,最后利用基于遗忘因子的最小二乘法完成电池参数的辨识。
本研究中以一个A123(LiFePO4)锂离子电池作为研究对象,利用如图2所示的实验装置完成锂离子电池的动态充放电特性实验,表1列出了本文所用锂离子电池的基本规格参数。

图2 锂离子电池实验装置
Fig.2 Schematic representation of LIB test bench
表1 A123锂离子电池的基本参数
Tab.1 The specifications of A123 battery cell

A123电池标称容量/(mA·h)正极材料质量/g长度/mm 规格2 230LiFePO47665
该部分实验用于确定锂离子电池在不同环境温度下的最大可用容量和锂离子电池的UOC-SOC关系,具体实验步骤如下:①使用恒温箱将锂离子电池在目标温度-10℃、15℃、25℃、40℃、50℃下分别静置5h。②使用Arbin电池测试系统将锂离子电池单体以0.05C恒流放电至下截止电压(2.4V)。③静置半小时后再次进行恒流恒压充电至满电,恒流电流仍为0.05C。重复步骤②和步骤③3次,即可确定锂离子电池在该温度下的最大可用容量,如图3所示。④恒压充电结束后,电池的SOC为100%,恒流放电结束后电池的SOC为0,在0~100%SOC之间,由于电池存在滞后[16]特性,实验分别记录充电和放电的电压值,并将所测电压的平均值作为UOC,如图4所示,截止条件是锂离子电池最大可用容量的5%,静置2h后测量的电池端子电压即为对应的UL。另外,设定环境温度为-10℃、20℃、50℃进行电池的动态压力测试(Dynamic Stress Test, DST)和城市高速(Urban High Speed, US06)工况实验,采集获取相应的实验数据。本文所用的锂离子电池实验数据取自美国马里兰大学的CALCE电池研究小组(https://web.calce.umd.edu/batteries/index.html),这是一个开放的电池测试数据库。本实验中所得数据忽略了电池本身产热引起的温度变化。
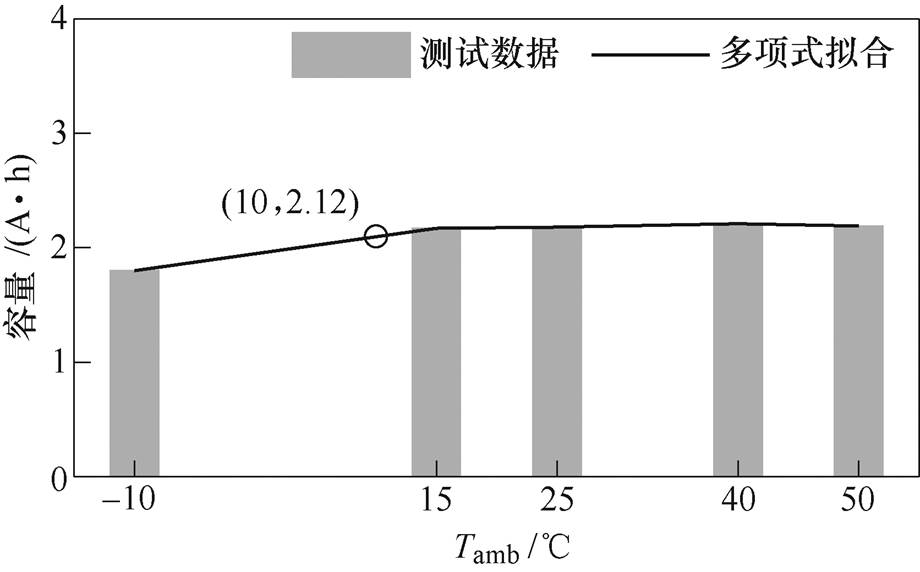
图3 锂电池容量曲线拟合
Fig.3 The fitted function of battery capacity
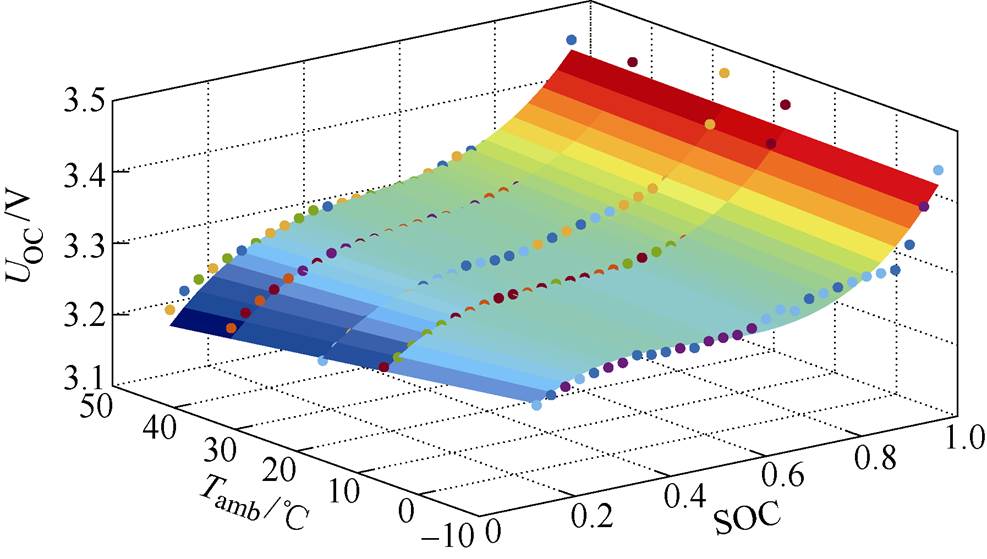
图4 UOC-SOC-Tamb的拟合三维曲面
Fig.4 The UOC-SOC-Tamb curves at various ambient temperatures
锂离子电池SOC[17]为
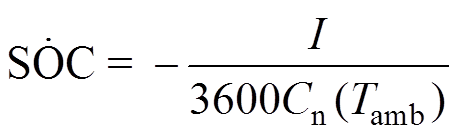 (2)
(2)式中,Cn(Tamb)为电池的实际可用容量,Cn为环境温度Tamb的函数。实验表明,锂离子电池完全放电的容量受环境温度影响[12],因此,本文通过拟合不同环境温度下电池容量实验值建立Cn-Tamb关系曲线,如图3所示,柱状图部分代表在各个温度下,锂离子电池可放电容量,黑色曲线代表拟合曲线,从曲线中可以看出,在[-10, 15]℃,锂离子电池放电容量变化明显,在[15, 50]℃,放电容量变化趋于缓和,拟合结果为
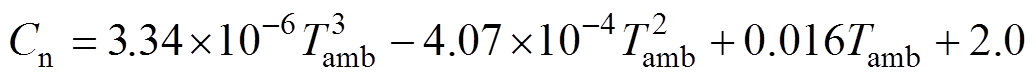 (3)
(3)
另外,其他环境温度下的锂电池容量可以由式(3)近似求出,如图3中圆圈处坐标,环境温度为10℃时,锂电池可用放电容量约为2.12A·h。
由于开路电压UOC与电池SOC的关系受环境温度影响[12-14],为使建立的开路电压模型更准确,应该同时考虑SOC和环境温度Tamb,即函数关系式UOC=f(SOC, Tamb),则基于环境温度为-10℃、15℃、25℃、40℃、50℃时的UOC-SOC实验数据,利用最小二乘法可得到如图4所示三维曲面的函数关系式。
图4中,离散点构成的曲线代表各个温度下UOC-SOC关系,曲面为采用多项式拟合得到的UOC- SOC-Tamb关系[18]。图中,三维曲面的数学关系式为
 (4)
(4)式中,SOC∈(0, 1);Tamb为环境温度。从图4可以看出,在低SOC区间[0, 0.2]及高SOC区间[0.8, 1.0]内,UOC随着SOC变化较为明显。为了进一步评估拟合曲线与实验值的相对误差,这里以平均绝对误差(Mean Absolute Error, MAE)和锂电池UOC的方均根误差(Root Mean Squared Error, RMSE)[3]为指标,其计算式分别为
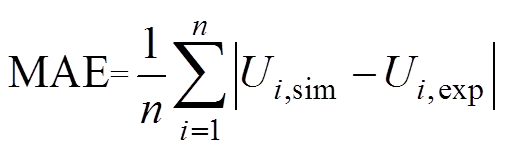 (5)
(5)
 (6)
(6)式中,Ui,exp为实验测试数据;Ui,sim为拟合曲线估算开路电压;i为在不同采样时间Dt下对应的采样点数。针对锂电池UOC拟合式(4),应用式(5)和式(6)的MAE和RMSE计算式分别计算在-10℃、15℃、25℃、50℃环境温度下拟合多项式和实验值的误差,结果见表2。
表2 锂离子电池UOC的MAE和RMSE的比较
Tab.2 The comparisons of MAE and RMSE for battery UOC

UOC/V -10℃15℃25℃50℃ MAE0.0100.0070.0080.010 RMSE0.0130.0140.0120.017
从表2中可以看出,综合各个温度下的拟合曲线与实验数据的误差计算,MAE值最大为0.010,RMSE值最大为0.017,这表明拟合的三阶多项式可以很好地逼近[-10, 50]℃范围内实际的UOC-SOC关系式,且具有较高的精度。
考虑到电池测试数据较多,容易产生较大的累积误差,本文基于-10℃、15℃、25℃、40℃、50℃环境温度下的DST和US06工况采用FFLS对融合环境温度的锂电池模型参数进行辨识,以此提高SOC估计的精度。根据文献[13],基于遗忘因子最小二乘法的电池模型参数辨识流程见表3。
应用表3中的计算流程可识别出本文所提出改进DP模型在-10℃、15℃、25℃、40℃、50℃下的参数,遗忘因子最小二乘法参数识别结果见表4,各参数与环境温度的拟合曲线及数学关系式在图5各子图中依次给出。另外,其他环境温度下的锂离子电池改进DP模型各个参数也可以由每个参数的拟合公式近似求出,如图5中黑色圆圈的坐标表示为环境温度为10℃时的各个参数估计值。观察图5可知,电池参数R0、R1和R2随Tamb的变化较小,并且随着Tamb升高,其阻抗值逐渐降低;此外,电池参数C1和C2随Tamb的变化较大,且随着Tamb升高,参数值升高幅度较大。由此可见,环境温度对锂离子电池内部化学反应性能产生一定影响,进一步影响电池的输出电压及放电性能。
本节主要从模型仿真分析的角度,讨论环境温度变化对电池终端电压和SOC估算的影响,以期获得不同环境温度下本文所提出的改进DP模型与常规DP模型的分析对比结果。
表3 应用FFLS进行电池参数识别流程
Tab.3 The battery parameters identification process of FFLS

步骤1:对终端电压计算式(1)进行拉普拉斯变换,可得 步骤2:求出系统的传递函数G(s)为 步骤3:采用双线性变换[19]离散化。 令,则。 式中,ai(i=1,2,…,5)为常数。 步骤4:将步骤3所得离散系统传递函数转化为时域差分方程为 式中,y(k)为压差,;I(k)为输入电流。 步骤5:定义 步骤6:定义采样误差为e(k), 。 步骤7:计算递归终止条件 针对 可计算出 步骤8:引入遗忘因子l,FFLS递推计算式为 步骤9:代入,可得参数ai值。 步骤10:对步骤3传递函数使用逆双线性规则[20]。 令,则 步骤11:综合对比步骤2和步骤10中相对应的系数即可得R0、R1、C1、R2和C2。
表4 遗忘因子最小二乘法参数识别结果
Tab.4 The identified parameters of FFLS

R0/WR1/WR2/WC1/FC2/F -10℃ (DST)0.240.120.144752 300 15℃ (DST)0.180.070.147234 708 25℃ (US06)0.160.060.128004 600 40℃ (DST)0.140.050.101 2005 200 50℃ (US06)0.130.040.081 8007 000
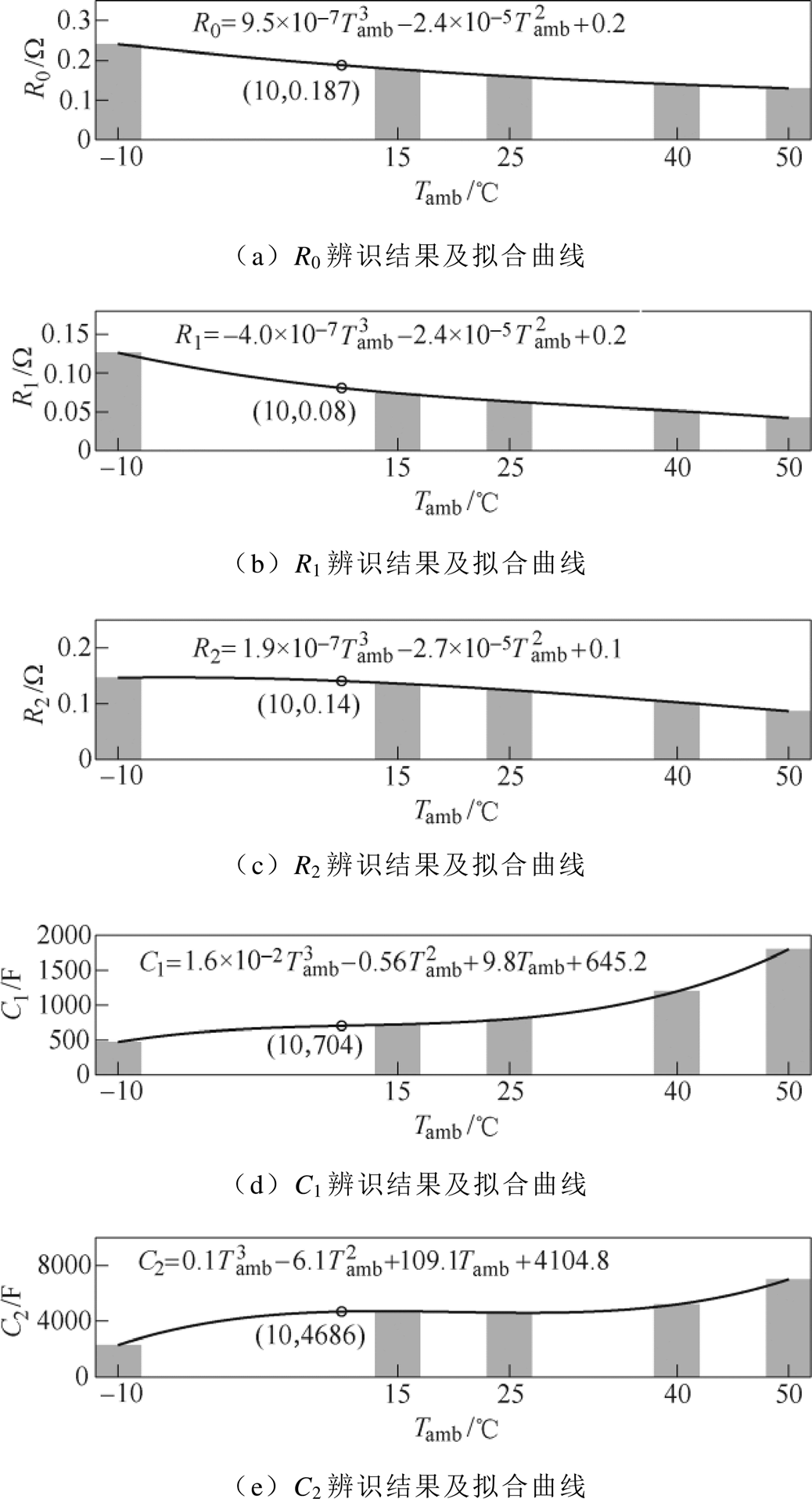
图5 模型参数识别结果及拟合曲线
Fig.5 Parameter estimation results of battery DP model
为了全面分析在较低温(-10℃)到较高温(50℃)环境下,锂离子电池终端电压的变化,分别采用常规DP模型、本文提出的改进DP模型计算的电池终端电压,并与相应工况下的实验电压曲线进行了对比。需要说明的是,常规DP模型使用的参数值取自表4中环境温度25℃时的R0、R1、R2、C3和C4。
图6~图8分别展示了两种模型在-10℃、20℃、50℃的环境温度下,在DST和US06工况中终端电压的估计值与实验数据的对比以及误差对比。需要强调的是,本文使用环境温度-10℃、15℃、40℃下DST和25℃、50℃下US06两种工况下的电池测试数据对改进DP模型参数进行了辨识;接着,不同于电池模型参数辨识所用测试数据,使用(US06, -10℃)(见图6c和图6d),(DST, 20℃),(US06, 20℃)(见图7),(DST, 50℃)(见图8a和图8b)这四组工况下测试数据对所提出改进DP模型进行验证。

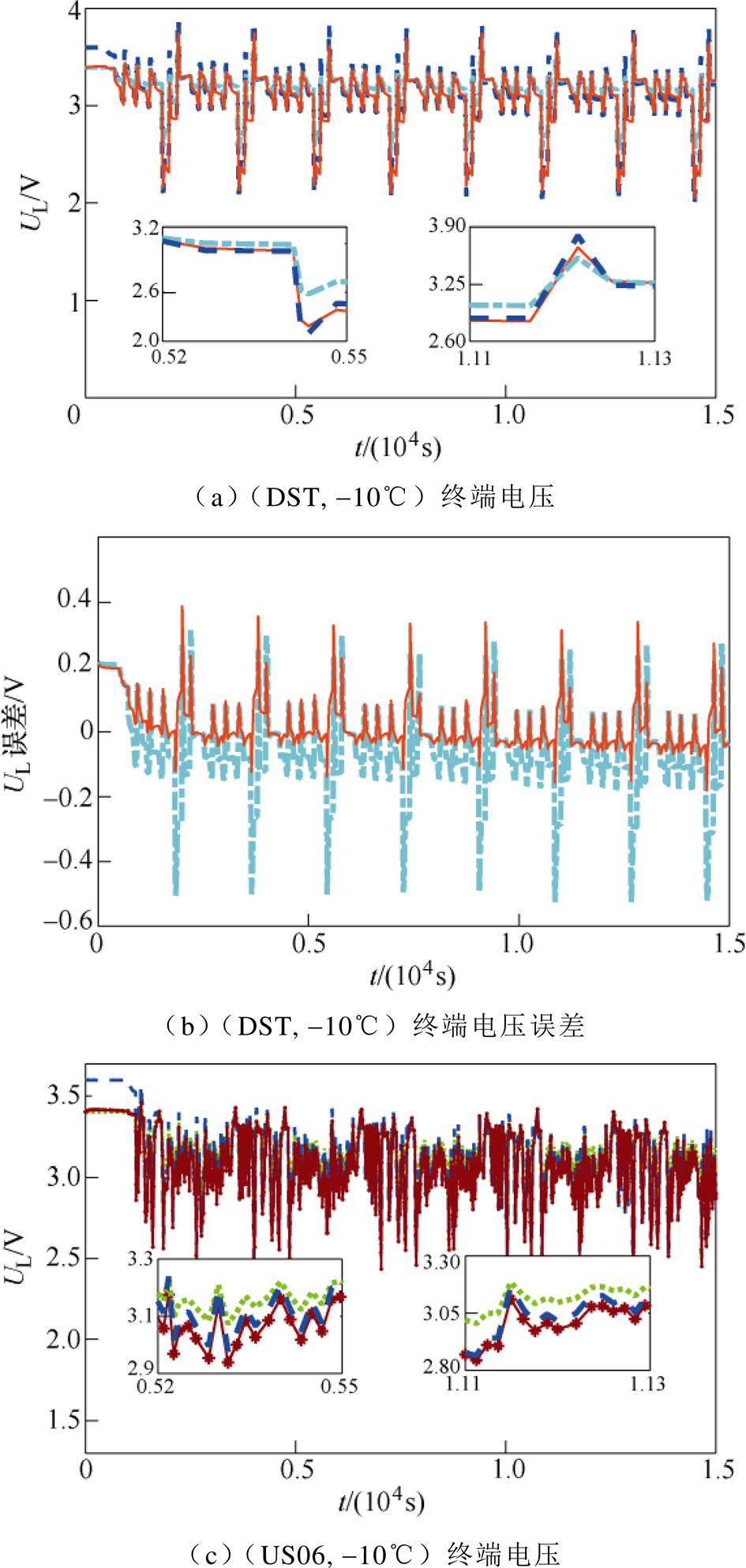
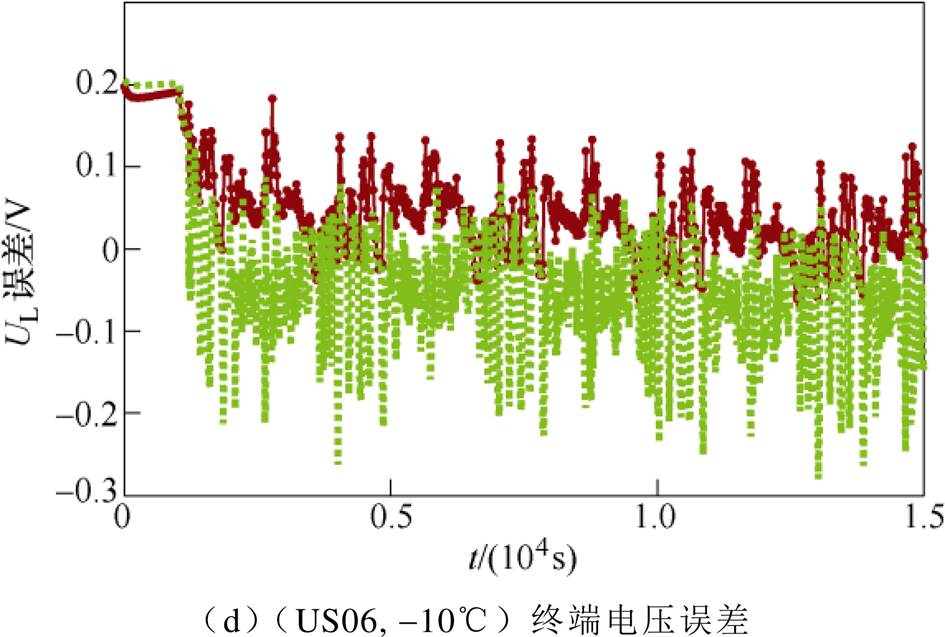
图6 两种模型在(DST, -10℃)和(US06, -10℃)下终端电压计算值及误差对比
Fig.6 Comparison of UL estimation and errors at (DST, -10℃) and (US06, -10℃)

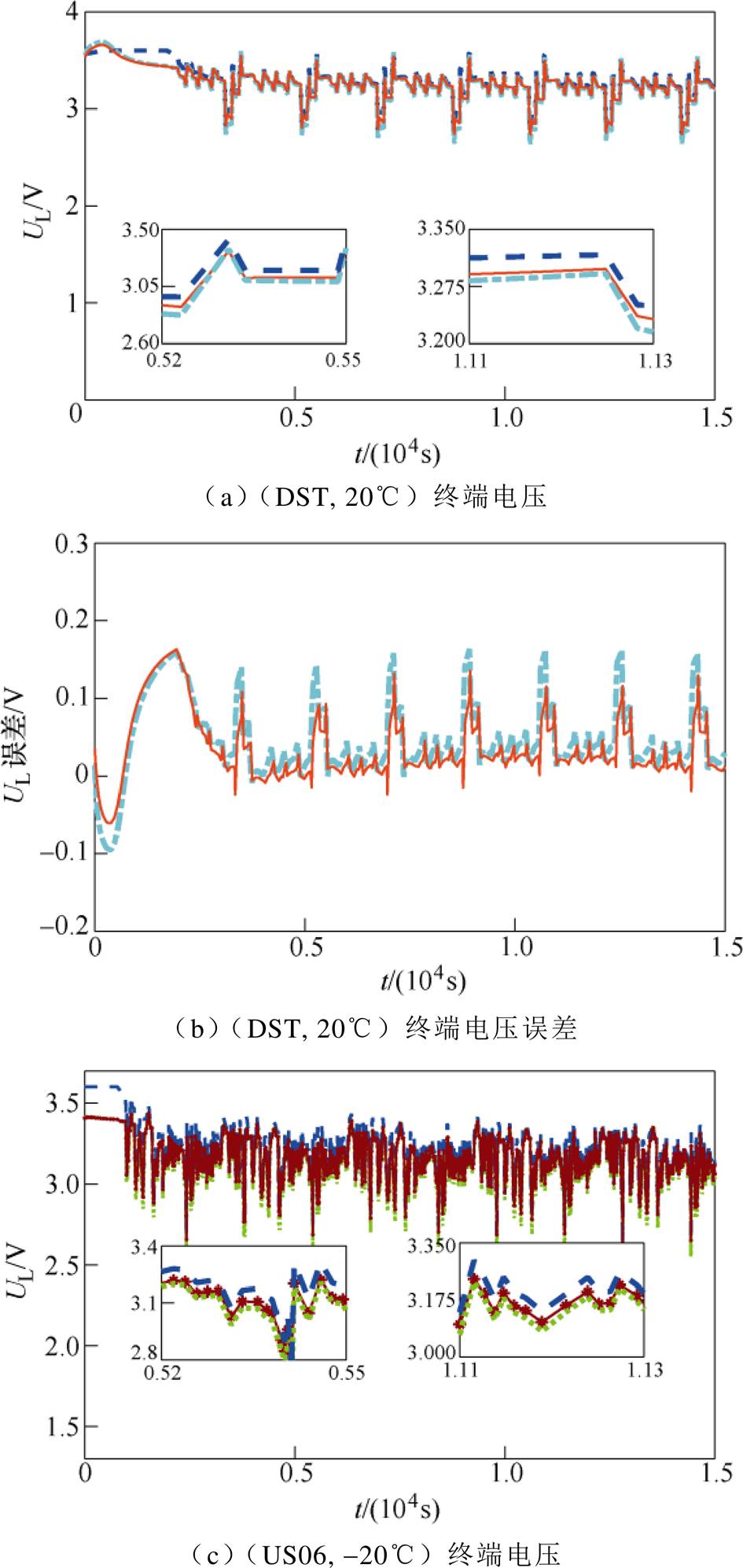
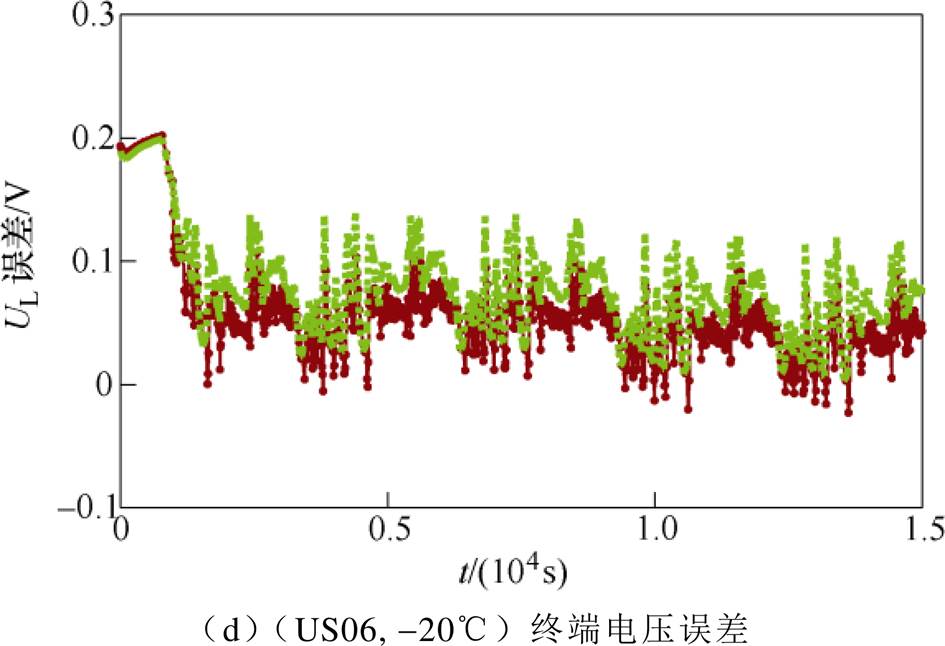
图7 两种模型在(DST, 20℃)和(US06, 20℃)下终端电压计算值及误差对比
Fig.7 Comparison of UL estimation and errors at (DST, 20℃) and (US06, 20℃)

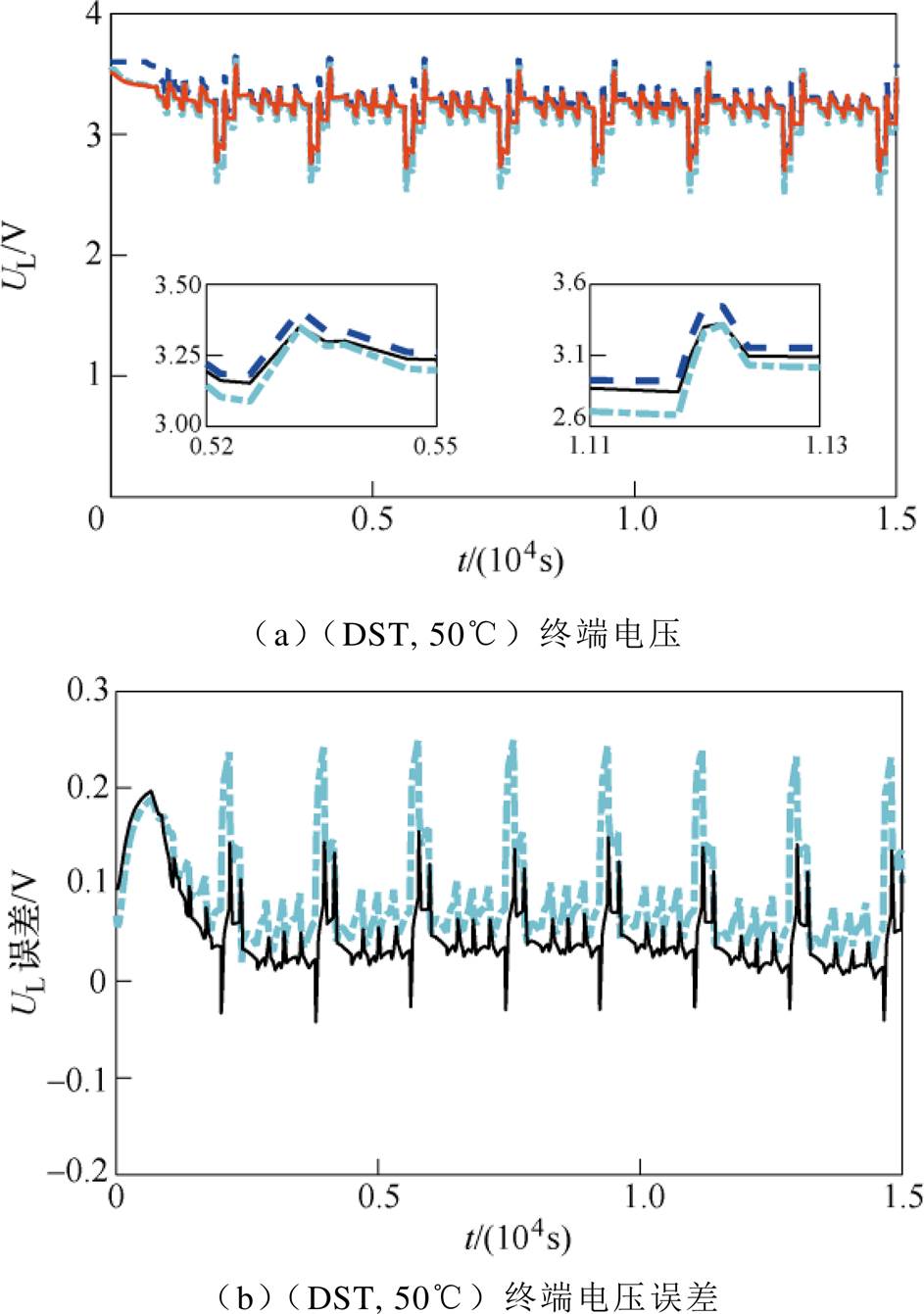
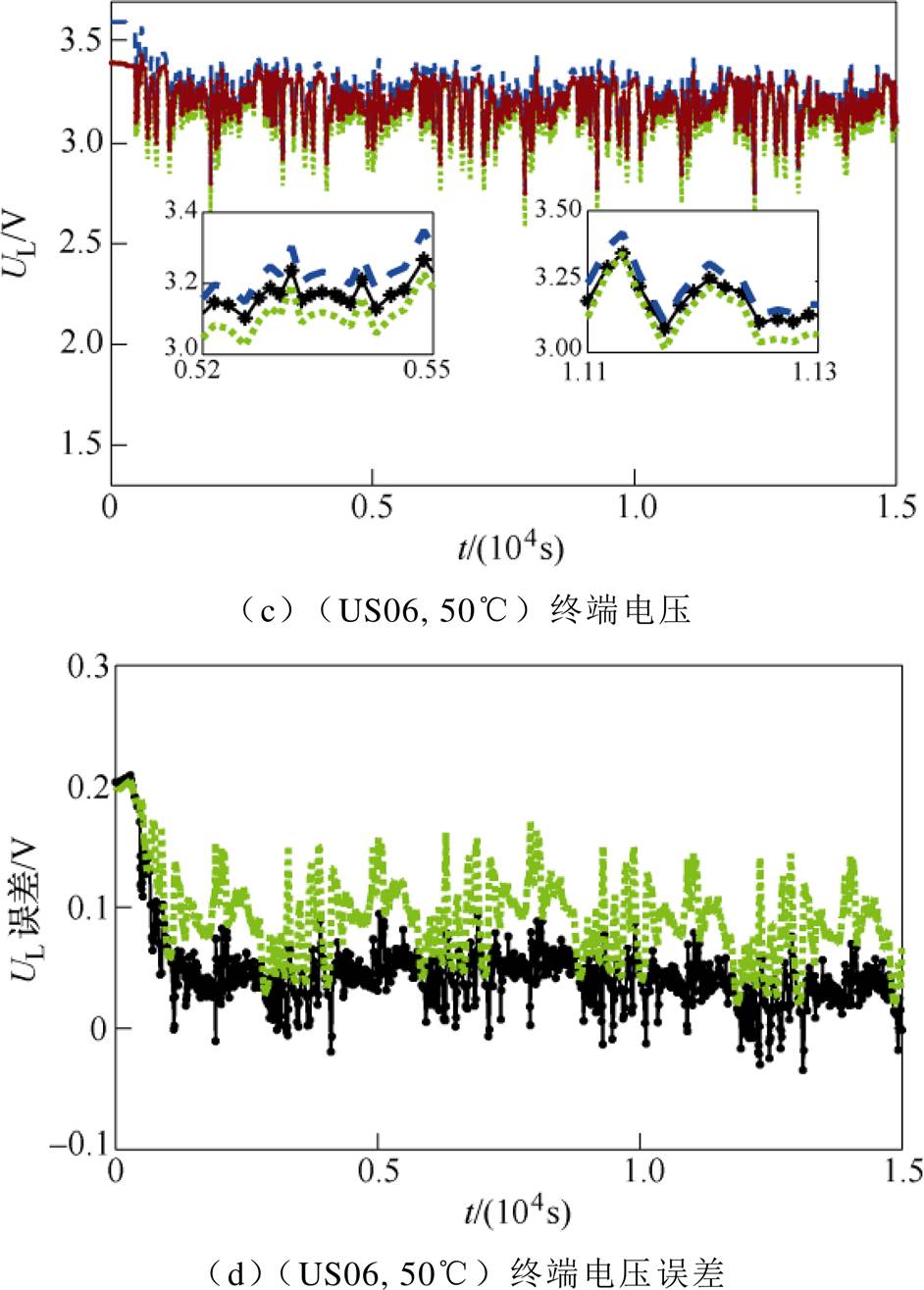
图8 两种模型在(DST, 50℃)和(US06, 50℃)下终端电压计算值及误差对比
Fig.8 Comparison of UL estimation and errors at (DST, 50℃) and (US06, 50℃)
为了更好地说明改进DP模型的准确性,这里采用平均相对误差MRE和RMSE作为电池UL仿真精度的衡量指标。
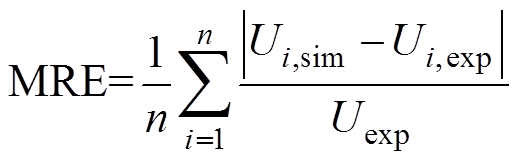 (7)
(7)表5给出了两种模型在上述给定的环境温度下在不同工况中的MRE和RMSE值对比以及改进DP模型相对常规DP模型在终端电压估计中误差降低的百分比。从表中可以看出,-10℃时MRE值最多降低了56.2%,RMSE值降低了45.1%。50℃时,MRE值最多降低了52.3%,RMSE值最多降低了45.1%,另外,在室温20℃时,MRE值最多降低了32.8%,RMSE值降低了28.2%。从模型验证的结果来看,相较于常规DP模型,本文所提出的改进DP模型具有更高的精度和适用范围。因此,环境温度在终端电压估计中是不可忽略的重要影响因素。
表5 两种模型终端电压误差的RMSE和MRE比较
Tab.5 Comparison of RMSE and MRE of UL error of two models

DP模型-10℃20℃50℃ DSTUS06DSTUS06DSTUS06 RMSE/VMRE(%)RMSE/VMRE(%)RMSE/VMRE(%)RMSE/VMRE(%)RMSE/VMRE(%)RMSE/VMRE(%) 不考虑Tamb0.1734.780.0942.520.0681.660.0852.470.1133.040.1023.00 考虑Tamb0.0952.090.0651.620.0511.140.0611.660.0661.610.0561.43 减少量(%)45.156.230.935.725.031.328.232.841.647.045.152.3
3.2.1 基于扩展卡尔曼滤波的SOC估计
扩展卡尔曼滤波算法是一种流行且有效的电池SOC估计方法,它利用泰勒级数展开的一阶或二阶项逼近非线性模型,这在文献[21-22]中得到广泛应用。对于图1所示的温度模型,采用显式欧拉方 法[23]对式(1)离散化可得
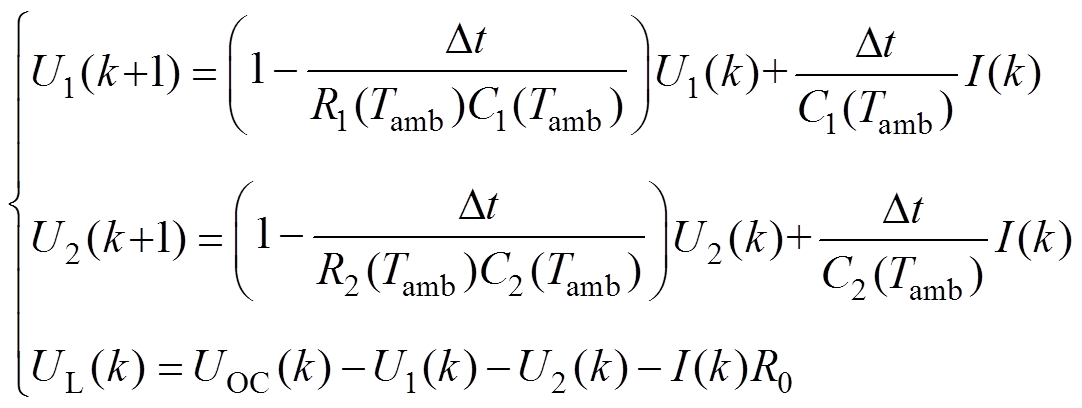 (8)
(8)式中,Dt为采样时间;I(k)为输入电流。
对式(2)采用同样方法离散化可得
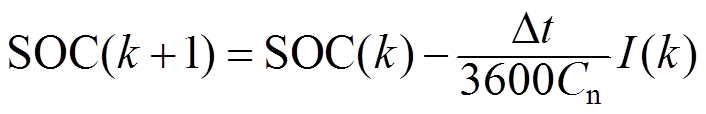 (9)
(9)定义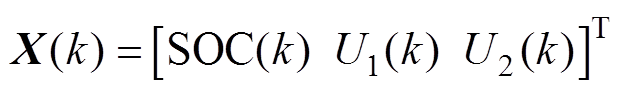 作为系统的状态变量,Y(k)为输出电压,即终端电压。
作为系统的状态变量,Y(k)为输出电压,即终端电压。
则系统的状态空间方程为
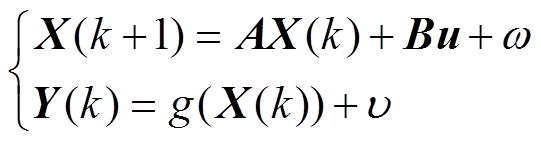 (10)
(10)其中
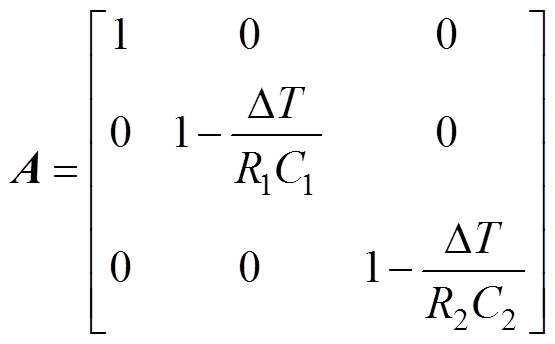
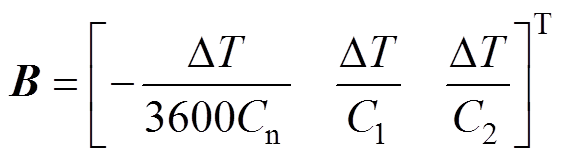
式中,w 和u 为高斯噪声;g(X(k))为电池终端电压的函数。
基于式(10)的锂电池状态空间方程,使用EKF[12]实现SOC估算的步骤如下:
(1)初始化。
状态初始化:X0=E[X(0)]
协方差初始化:
P(0)=E{[X(0)-E[X(0)]][X(0)-E[X(0)]]T}
噪声初始化:Q和R(w 和u 均为高斯噪声)
(2)状态预测。
k时刻的状态预估值可由k-1时刻的状态值计算得到,有
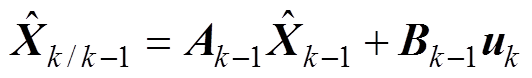 (11)
(11)式中,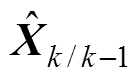 为k时刻的预测结果。
为k时刻的预测结果。
k时刻的终端电压预估值为
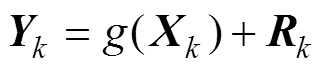 (12)
(12)k时刻的协方差预估为
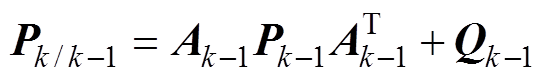 (13)
(13)
(3)更新校正。
根据实际观测电压y(k),更新系统的状态值和协方差。
①计算矩阵Hk(雅可比矩阵),Hk=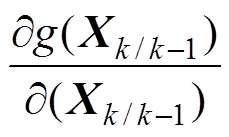 ,则
,则
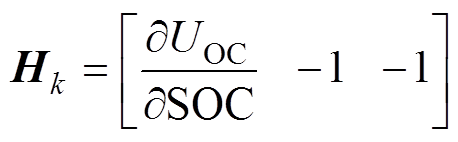 (14)
(14)式中,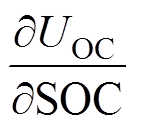 为式(4)的二阶泰勒展开对SOC的导数。
为式(4)的二阶泰勒展开对SOC的导数。
②卡尔曼增益计算。
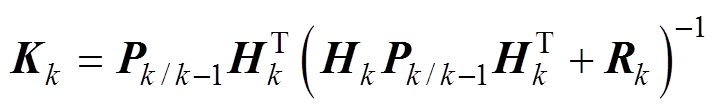 (15)
(15)③测量更新。
k时刻状态校正方程为
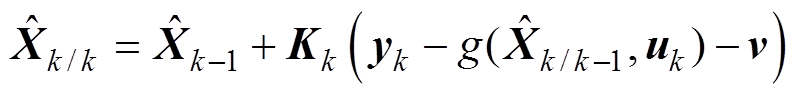 (16)
(16)k时刻的误差协方更新方程为
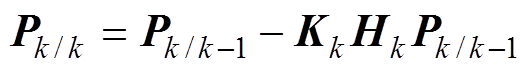 (17)
(17)
3.2.2 SOC预估和实验分析
同样地,为了评估分析环境温度变化对锂电池SOC估算的影响,分别计算了在不同环境温度、不同工况下,锂离子电池SOC值以及使用安时积分法得到的参考SOC计算值。
图9~图11分别展示了两种模型在-10℃、20℃、50℃的环境温度下,在DST和US06工况中SOC的估计值与实验数据对比以及误差对比。表6给出了两种模型在上述给定的环境温度下在两种工况中的SOC估计值和安时积分法参考数值的MRE和RMSE值对比,以及改进DP模型相对常规DP模型在终端电压估计中误差降低的百分比。从表中可以看出,在-10℃和50℃时对比更加明显,在-10℃时MRE值最多降低了53.8%,RMSE值降低了52.6%。50℃时,MRE值最多降低了53.9%,RMSE值最多降低了52.9%,另外,在室温20℃时,MRE值最多降低了33.9%,RMSE值降低了35.7%。因此,环境温度在锂离子电池SOC预估中是不可忽略的。
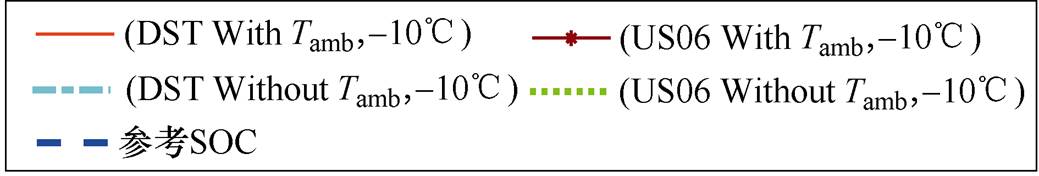
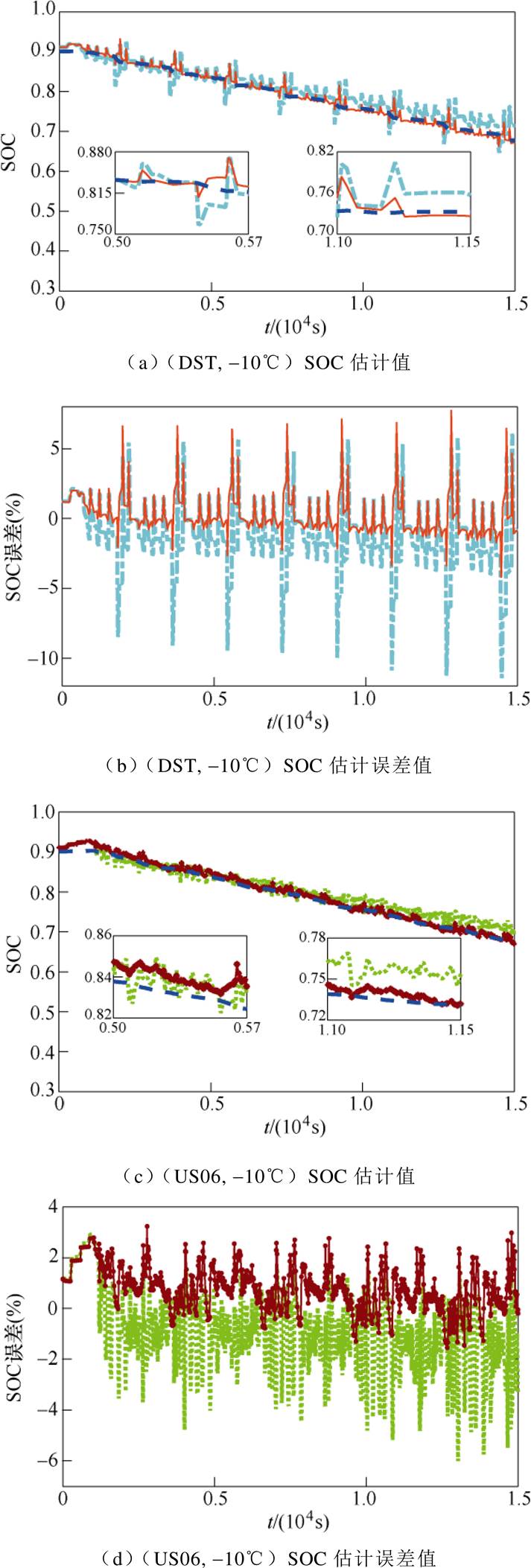
图9 两种模型在(DST, -10℃)和(US06, -10℃)下SOC预估值及误差对比
Fig.9 Comparison of SOC estimation and errors at (DST, -10℃) and (US06, -10℃)

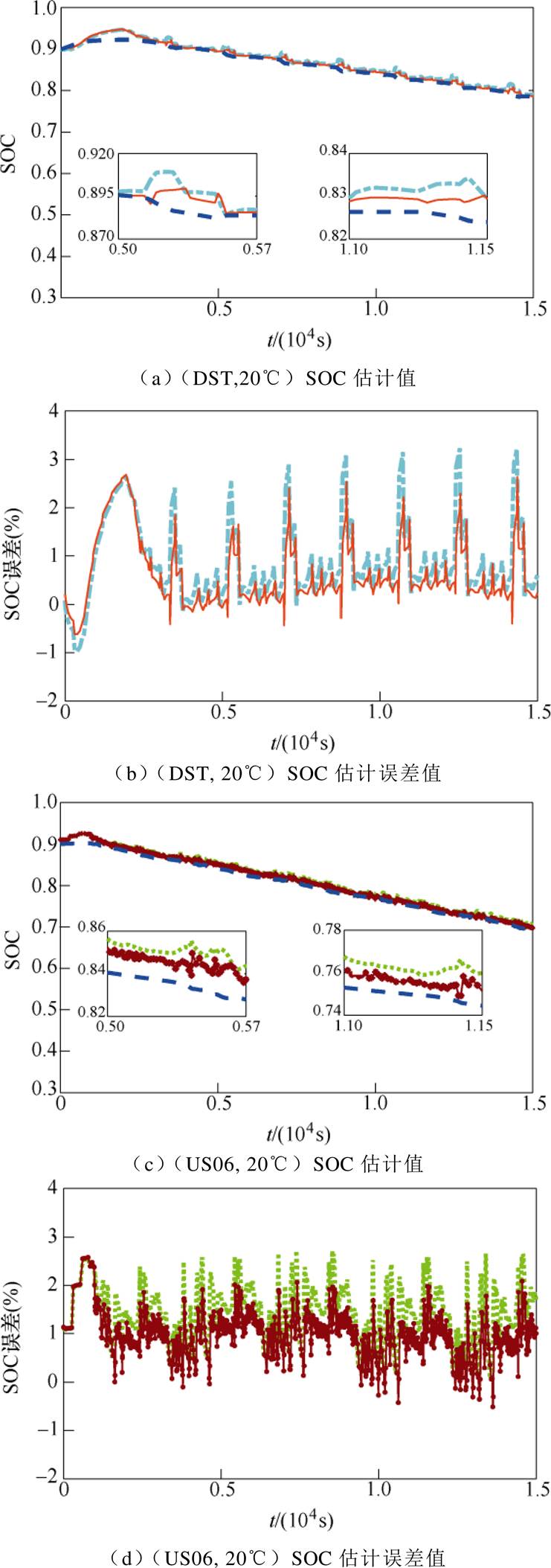
图10 两种模型在(DST, 20℃)和(US06, 20℃)下 SOC预估值及误差对比
Fig.10 Comparison of SOC estimation and errors at (DST, 20℃) and (US06, 20℃)

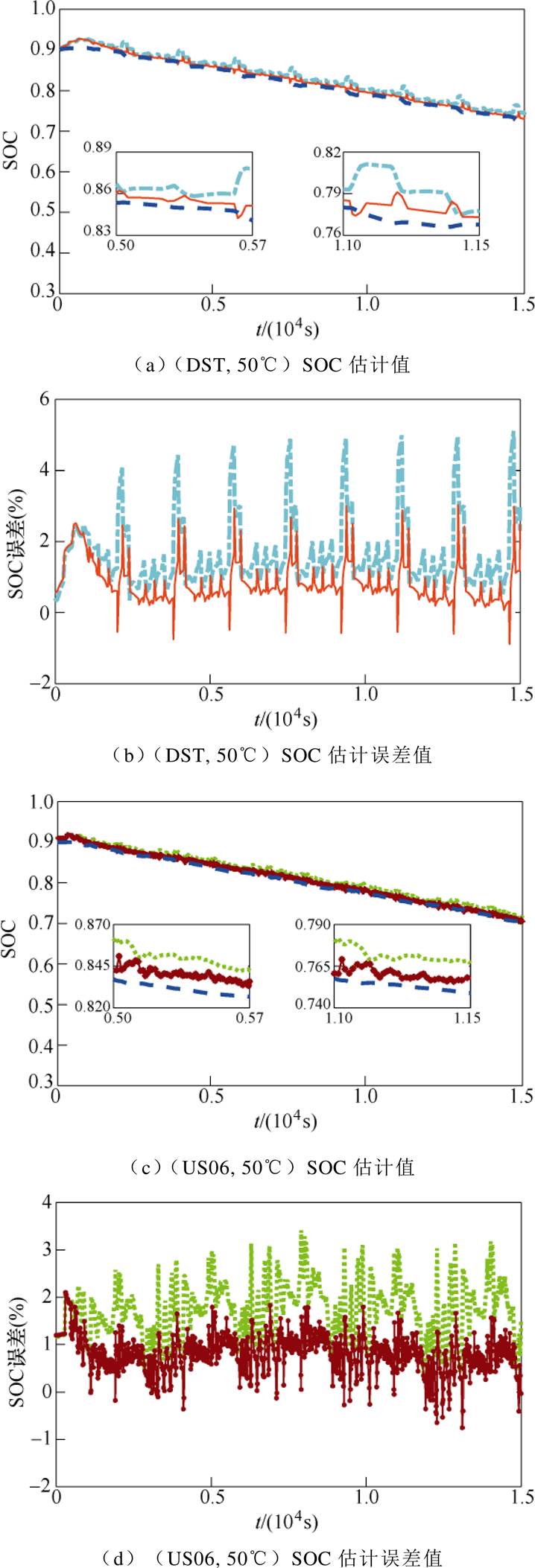
图11 两种模型在(DST, 50℃)和(US06, 50℃)下 SOC预估值及误差对比
Fig.11 Comparison of SOC estimation and errors at (DST, 50℃) and (US06, 50℃)
本文针对环境温度变化对锂离子电池模型参数和SOC的影响,在常规DP模型的基础上,引入环境温度因素,并基于电池动态实验数据建立了一种改进DP模型,进而定量分析环境温度对电池终端电压和SOC估计的影响。首先,采用改进DP模型对锂离子电池进行建模分析,并使用具有遗忘因子的递推最小二乘法在线辨识模型参数,且所识别参数均拟合为环境温度Tamb的函数。另外,通过多项式拟合得到UOC(SOC, Tamb)的曲面关系,然后基于该模型和所识别的参数函数关系并利用EKF算法估计锂电池的SOC值。接着,为了验证本文模型的有效性,在-10℃、20℃和50℃下分别计算了所提出的改进DP模型和和常规DP模型的终端电压以及基于EKF算法的电池SOC值。结果表明,相比于锂离子电池常规DP模型,在选定的三种环境温度和两种工况下,本文所提出的改进DP模型在终端电压和SOC估算方面,相应的RMSE和MRE值均较大幅度降低,尤其是在-10℃和50℃下,电池终端电压的RMSE和MRE值至少分别降低了25%和31.3%,电池SOC估算的RMSE和MRE值分布至少降低了27.3%和30.4%,这表明环境温度是重要的不可忽视的影响因素,且本文所提的电池模型具有更高的计算精度。此外,本文提出的改进DP模型能够适应连续变化的环境温度,模型所有参数均是环境温度Tamb的函数关系,这扩展了常规DP模型的使用范围,为电池终端电压和SOC估算带来方便。
表6 两种模型SOC误差的RMSE和MRE比较
Tab.6 Comparison of RMSE and MRE of SOC error of two models

DP模型-10℃20℃50℃ DSTUS06DSTUS06DSTUS06 RMSEMRE(%)RMSEMRE(%)RMSEMRE(%)RMSEMRE(%)RMSEMRE(%)RMSEMRE(%) 不考虑Tamb0.0273.290.0191.860.0111.120.0141.890.0182.230.0172.28 考虑Tamb0.0141.520.0091.180.0080.780.0091.250.0091.150.0081.05 减少量(%)48.153.852.636.627.330.435.733.950.048.452.953.9
参考文献
[1] 张振宇, 汪光森, 聂世雄, 等. 脉冲大倍率放电条件下磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2019, 34(8): 215-225.
Zhang Zhenyu, Wang Guangsen, Nie Shixiong, et al. State of charge estimation of LiFePO4: battery under the condition of high rate pulsed discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 215-225.
[2] Wang Qianqian, Wang Jiao, Zhao Pengju, et al. Correlation between the model accuracy and model- based SOC estimation[J]. Electrochimica Acta, 2017, 228: 146-159.
[3] Ali M U, Zafar A, Nengroo S H, et al. Towards a smarter battery management system for electric vehicle applications: a critical review of lithium-ion battery state of charge estimation[J]. Energies, 2019, 12(3): 446.
[4] He Hongwen, Xiong Rui, Fa Jinxin. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach[J]. Energies, 2011, 4(4): 582-598.
[5] Zhang Cheng, Li Kang, Deng Jing. Real-time esti- mation of battery internal temperature based on a simplified thermoelectric model[J]. Journal Power Sources, 2016, 302: 146-154.
[6] Chen Yang, Ma Yan, Chen Hong. State of charge and state of health estimation for lithium-ion battery through dual sliding mode observer based on AMESim- Simulink co-simulation[J]. Journal of Renewable and Sustainable Energy, 2018, 10(3): 034103.
[7] 李晓宇, 徐佳宁, 胡泽辉, 等. 磷酸铁锂电池梯次利用健康特征参数提取方法[J]. 电工技术学报, 2018, 33(1): 9-16.
Li Xiaoyu, Xu Jianing, Hu Zehui, et al. The health parameter estimation method for LiFePO4 battery echelon use[J]. Transactions of China Electrotech- nical Society, 2018, 33(1): 9-16.
[8] 刘伟, 吴海桑, 何志超, 等. 一种均衡考虑锂电池内部能量损耗和充电速度的多段恒流充电方法[J]. 电工技术学报, 2017, 32(9): 112-120.
Liu Wei, Wu Haisang, He Zhichao, et al. A multistage current charging method for Li-ion battery con- sidering balance of internal consumption and charging speed[J]. Transactions of China Electro- technical Society, 2017, 32(9): 112-120.
[9] 靳立强, 孙志祥, 刘志茹, 等. 不同温度下锂电池剩余电量估算的仿真研究[J]. 汽车工程, 2019, 41(5): 114-122.
Jin Liqiang, Sun Zhixiang, Liu Zhiru, et al. Simu- lation study on stale of charge estimation of lithium- ion battery at different temperatures[J]. Automotive Engineering, 2019, 41(5): 114-122.
[10] 刘新天, 孙张驰, 何耀, 等. 基于环境变量建模的锂电池SOC估计方法[J]. 东南大学学报: 自然科学版, 2017, 47(2): 306-312.
Liu Xintian, Sun Zhangchi, He Yao, et al. SOC estimation method based on lithium-ion cell model considering environmental factors[J]. Journal of Southeast University: Natural Science Edition, 2017, 47(2): 306-312.
[11] 华寅, 许敏. 不同温度下基于模型滤波的锂离子电池SOC估计[J]. 电源技术, 2016, 40(4): 814-817.
Hua Yin, Xu Min. SOC estimation of lithium-ion batteries by model-based filtering method under different thermal conditions[J]. Chinese Journal of Power Sources, 2016, 40(4): 814-817.
[12] Chin Cheng, Gao Zuchang, Chiew J, et al. Nonlinear temperature-dependent state model of cylindrical LiFePO4 battery for open-circuit voltage, terminal voltage and state-of-charge estimation with extended Kalman filter[J]. Energies, 2018, 11(9): 2467.
[13] Xia Bizhong, Huang Rui, Lao Zizhou, et al. Online parameter identification of lithium-ion batteries using a novel multiple forgetting factor recursive least square algorithm[J]. Energies, 2018, 11(11): 3180.
[14] Xing Yinjiao, He Wei, Pecht M, et al. State of charge estimation of lithium-ion batteries using the open- circuit voltage at various ambient temperatures[J]. Applied Energy, 2014, 113: 106-115.
[15] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019, 34(2): 221-228.
Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on com- prehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 221-228.
[16] Wang Yebin, Fang Huazhen, Zhou Lei, et al. Revisiting the state-of-charge estimation for lithium- ion batteries a methodical investigation of the extended Kalman filter approach[J]. IEEE Control Systems Magazine 2017, 37(4): 73-96.
[17] Kong S N, Chin-Sien M, Chen Yiping, et al. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries[J]. Applied Energy, 2009, 86(9): 1506-1511.
[18] Hu Xiaosong, Li Shengbo, Peng H, et al. Robus- tness analysis of state-of-charge estimation methods for two types of Li-ion batteries[J]. Journal Power Sources, 2012, 217: 209-219.
[19] Ding Feng, Chen Tongwen. Performance bounds of forgetting factor least-squares algorithms for time- varying systems with finite measurement data[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2005, 52(3): 555-566.
[20] Petr Zagalak. Discrete-time control systems[M]. Englewood Cliffs, NJ: Prentice Hall Inc., 1987.
[21] 李江, 王义伟, 魏超, 等. 卡尔曼滤波理论在电力系统中的应用综述[J]. 电力系统保护与控制, 2014, 42(6): 135-144.
Li Jiang, Wang Yiwei, Wei Chao, et al. A survey on the application of Kalman filtering method in power system[J]. Power System Protection and Control, 2014, 42(6): 135-144.
[22] 潘海鸿, 吕治强, 李君子, 等. 基于灰色扩展卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2017, 32(21): 1-8.
Pan Haihong, Lü Zhiqiang, Li Junzi, et al. Estimation of lithium-ion battery state of charge based on grey prediction model-extended Kalman filter[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(21): 1-8.
[23] Ines B, Sabeur J, Bilal M, et al. Improved OCV model of a Li-ion NMC battery for online SOC estimation using the extended Kalman filter[J]. Energies, 2017, 10(6): 764.
An Improved Dual Polarization Model of Li-Ion Battery and Its State of Charge Estimation Considering Ambient Temperature
Abstract It is very crucial to develop an efficient and practical battery management system by establishing an accurate and reasonable Li-ion battery (LIB) mathematical model to estimate battery terminal voltage and state-of-charge (SOC) with higher precision. This paper firstly builds an improved Li-ion battery cell dual polarization (DP) model that is dependent on ambient temperature. Next, based on two types of Li-ion battery dynamic test data, the key parameters of this proposed DP model are identified by forgetting factor least square (FFLS) approach and fitted as the ambient temperature- dependent functions. Meanwhile, by the extended Kalman filter (EKF) algorithm, a battery SOC estimation procedure suitable for different ambient temperatures is presented. Finally, the DST and US06 cycle test data at -10℃, 20℃ and 50℃ are used to simulate and verify the proposed battery DP model and its SOC estimation. The results show that the proposed battery DP model can accurately reflect the effects of ambient temperature on the battery model parameters, and has a higher precision and a wider ambient temperature application range in estimating the battery terminal output voltage and SOC.
keywords:Li-ion battery, ambient temperature, equivalent circuit model, model parameter, state of charge (SOC)
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.200174
国家自然科学基金资助项目(51675423)。
收稿日期 2020-02-21
改稿日期 2020-09-07
庞 辉 男,1980年生,博士,副教授,研究方向为车辆动力学与控制理论、新能源车用动力电池/超级电容管理。E-mail: huipang@163.com(通信作者)
郭 龙 男,1995年生,硕士研究生,研究方向为电池热管理及控制系统性能评价。E-mail: 774249513@qq.com
(编辑 崔文静)