
图1 关键特征参量散点示意图
Fig.1 Scatter diagrams of key characteristic parameters
摘要 风电机组数据采集与监视控制系统(SCADA)运行数据中含有大量异常数据,对风电机组健康状态预测影响严重,为此针对实测风速-功率、转速-功率数据,提出一种异常数据在线清洗方法。由于机组性能退化过程中数据特征趋于复杂,基于经验Copula-互信息(ECMI)选择关键特征参量作为数据清洗对象,并基于Copula建立置信等效功率区间描述其非线性与不确定性。针对置信边界外的堆积点和离群点,结合其时序特征与密度分布建立Copula数据清洗模型(Copula-TFDD),依次进行在线清洗。最后,基于实际数据与人工模拟数据分析模型的精度、运算效率以及对机组健康状态预测的影响表明,Copula-TFDD能准确并实时地识别各类异常数据,有效提升风电机组健康状态预测的性能。
关键词:风电机组健康状态预测 数据清洗 特征参量 互信息 Copula理论
准确可信的数据采集与监视控制系统(Super- visory Control And Data Acquisition, SCADA)运行数据[1]是风电机组发电性能预测、故障预测与健康管理等工作的基础。然而,由于机组运行环境恶劣,很多现场采集的数据质量较差,特别是因弃风限电、工况波动等原因导致的数据异常问题尤为突出。高比例异常数据对运行数据的真实规律、特征参量的相关性关系等信息的挖掘与应用影响极大,因此风电机组数据清洗工作至关重要。
风电机组数据清洗方法主要从特征空间的距离、概率和密度等角度界定异常值。文献[2-5]基于四分位法-聚类分析、最优组内方差、变点分组-四分位、Thompson tau-四分位等概率统计方法对风功率数据的空间分布位置分类以识别离群点与堆积点,但基于分类思想的方法对高比例异常数据的辨识效果不佳。文献[6]利用离群点检测算法(Density- based Local Outlier Factor, DLOF)和聚类算法(Density-Based Spatial Clustering Applications with Noise, DBSCAN)识别异常点,并指出后者更有利于风电功率预测,但内存占用大、运算效率低,影响了算法的实用性。文献[7-8]基于Copula建立风功率数据的概率功率曲线模型,利用异常点的时序特征辨识堆积点,识别效果优于传统的3-sigma概率统计法;但对于海量风功率数据,单一Copula函数对复杂数据集的适应性有限,而混合Copula函数[8]的参数拟合复杂,影响算法在线运行。上述方法均以风功率数据为清洗对象,主要研究机组发电性能预测,而数据清洗方法在机组健康状态预测中的应用研究目前仍较少。
在风电机组整机性能预测与健康状态评估的应用中,有关研究[9-12]指出,模型分析法如神经网络更适合于异常检测,而高斯混合模型、主成分分析及其改进算法等概率统计方法对机组性能退化的预测适应性更好。然而,概率统计方法对数据质量要求较高,数据清洗的应用方向不同时,清洗对象、需要清洗的异常数据以及清洗方法均会有所差别,因此有必要对风电机组健康状态预测中的异常数据清洗工作进行针对性研究。首先,选择运行数据中可反映机组性能退化的关键特征参量构成清洗对象,如风速-功率、转速-功率数据,而轴温、油温等参量作为机组健康状态预测与故障检测的重要特征依据,剔除其中的异常点反而可能造成故障信息丢失,不能轻易清洗。其次,确定待清洗的异常数据,包括堆积点与离群点。离群点可能反映了工况变化,在基于模型分析法预测发电性能或故障时可以不清洗[7],但离群点分散性较大,对其进行合理清洗将有利于基于概率统计方法预测机组的健康状态[10]。此外,不同机组的运行数据存在采样周期不同、概率分布特征呈差异化等特点,随着机组性能的逐渐退化,数据分布特征更趋复杂,这些都对数据清洗方法的通用性、精度、运算效率、稳定性以及工程适用性提出了较高要求。因此,有必要针对风电机组健康状态预测深入研究运行数据关键特征参量的选择,以及堆积点和离群点的在线清洗方法。
目前,可用于解决运行数据特征参量选择的方法有Relief、互信息、随机森林与邻域粗糙集等[13-16]。其中,Relief和互信息基于相关性度量,属于过滤法,具有快速高效、独立于预测模型的优点,但Relief为有监督法,而SCADA数据往往没有分类标签;随机森林属于封装法,可与邻域粗糙集应用于负荷预测或故障识别中对特征集的寻优与约简。因此,基于互信息选择与机组运行状态相关性强的关键特征参量有利于简单、快速地确定清洗对象,并利用Copula函数无需假设数据的分布形态即可描述其实际分布规律的特点,解决互信息计算中联合概率密度函数估计难的问题。为保证数据清洗方法的识别精度与运算效率,联合考虑关键特征参量的概率分布、时序特征与密度分布:利用单一Copula建立风速-功率、转速-功率等多元特征参量的置信等效功率区间,解决传统概率统计方法在样本分布不均、异常值较多时识别精度低的问题,同时避免采用混合Copula,确保算法的运算效率;仅考虑置信边界外的可疑数据,结合其时序特征和密度分布依次清洗堆积点与离群点,解决DBSCAN算法无法在线清洗[10-11]的问题;进一步基于Copula模拟实际异常数据,解决数据清洗模型定量分析的问题。
基于上述研究背景,本文针对风电机组健康状态预测中异常数据的在线清洗进行研究。分析风电机组性能退化过程中的数据特征,在此基础上,提出基于经验Copula-互信息(Empirical Copula-based Mutual Information, ECMI)法选择关键特征参量,并基于Copula结合异常值的时序特征与密度分布建立数据清洗模型(Copula-based data cleaning model combining Time-series Features and Density Distribution, Copula-TFDD),对堆积点和离群点等典型异常数据进行在线识别。
风电机组的风功率数据呈带状分布,非线性和不确定性明显。关键特征参量散点示意图如图1所示。依“bin法”[17]确定反映机组发电性能和运行状态的重要指标——等效风功率曲线,随着机组性能的退化该曲线逐渐下移,如图1a所示。引入置信等效功率区间描述风功率数据的非线性与不确定性,以传统的3-sigma概率统计法为例,比较机组正常运行和性能退化状态下的3-sigma曲线发现,后者发生了偏移且波动更为剧烈。由此可知,机组性能逐渐退化时有效数据会发生偏移并与异常数据相混杂,分布特征更趋复杂,而清洗异常点时置信边界波动剧烈必然会增加数据被误判与漏判的可能。
进一步分析切入、切出风速间的关键特征参量,如图1中点画线所示,机组正常运行状态下的置信边界外有三类异常点,其典型特征表现为:
(1)堆积点(类型Ⅰ、Ⅱ)。底部或中部呈水平堆积型数据,常因弃风限电、通信故障等引起。图中类型Ⅰ对应于由专家经验识别的初筛点,其输出功率很小或在一段时间内持续小于等于0。类型Ⅱ异常点的输出功率低于正常出力且在连续一段时间内不(或很少)随风速变化而变化,这类数据无法直接说明机组是否发生异常,却会影响对健康状态的预测,建立符合有效数据分布特征的置信边界决定了对该类堆积点的识别精度。

图1 关键特征参量散点示意图
Fig.1 Scatter diagrams of key characteristic parameters
(2)离群点(类型Ⅲ)。呈分散特征的离群型数据,常因传感器异常、随机噪声、工况波动等引起。离群点的波动具有随机性,虽然在一定程度上反映了实际工况,但当比例高、分散性大时会影响基于概率统计方法预测机组健康状态的精度。特别是对于机组因工况波动剧烈而频繁切换控制所产生的离群点,常表现出时序连续但关键参量随风速的变化不符合物理规律的特点,如图1b点画线中的离群点,在图1a中因落在置信边界附近而被漏判。因此,数据清洗对象除考虑风功率数据外还应考虑其他关键特征参量。
互信息[18]描述变量间的相关性,计算中利用经验Copula解决联合概率密度估计难的问题。
设随机变量(X, Y)的互信息为I(X, Y),若边缘概率分布函数FX(x)、FY(y)连续,由Skla定理[19-20]存在唯一Copula函数CX,Y(FX(x), FY(y))拟合联合累积概率分布函数FX,Y(x, y)。设FX(x)=u,FY(y)=v,则I(X,Y)可由Copula函数C的密度函数c估计为
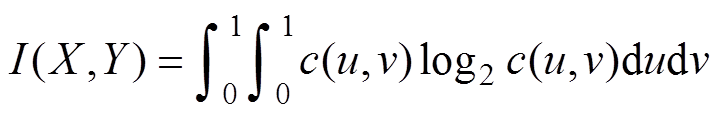 (1)
(1)计算I(X, Y)的关键是准确、快速地估计c。采用非参数核密度估计[14, 21]的方法虽然精度高但计算量大、耗时长,因此,本文基于经验Copula函数的解析法选择最优Copula函数并估计Copula密度c,兼顾计算精度和运算效率。
常用的Copula函数包括椭圆Copula函数族与阿基米德Copula函数族,依据最小距离法计算不同Copula函数与经验Copula函数的二次方欧式距离,选择距离最小的Copula函数估计I(X, Y),有
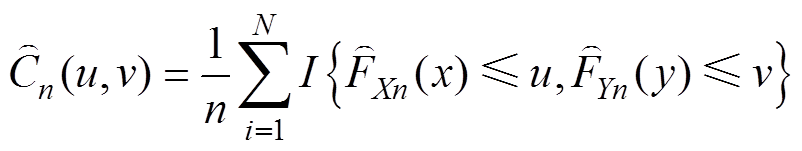 (2)
(2)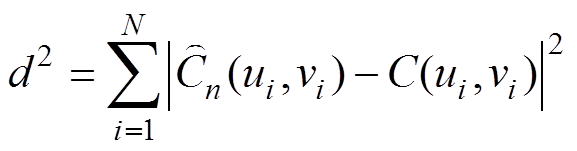 (3)
(3)
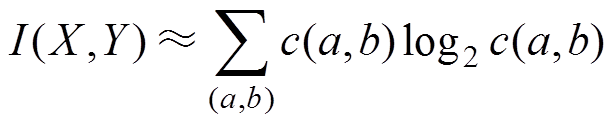 (4)
(4)
式中,N为样本数;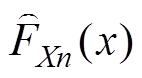 、
、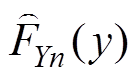 和
和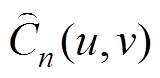 分别为X、Y的经验分布函数与经验Copula函数;当c(a, b)趋于0时,依据洛必达法则互信息为0。
分别为X、Y的经验分布函数与经验Copula函数;当c(a, b)趋于0时,依据洛必达法则互信息为0。
本文根据SCADA系统标签选出与机组运行状态相关的17个变量构成初始特征参量集,共计117 538个时刻点,对应三类特征:条件参量,如风速、机舱温度等;性能参量,如反映整机状态的输出功率、桨距角、转速等;健康参量,如反映关键部件齿轮箱运行状态的各类轴温、油温、振动等。其中,输出功率作为反映机组整机性能的重要参量,通过选择与其相关性强即互信息大的关键特征参量确定数据清洗对象。
ECMI特征参量选择策略如图2所示。①数据预处理:依专家经验剔除类型Ⅰ异常点,对新数据集按单位区间标准化。②互信息估计:将数据分箱构建经验Copula;选择最优Copula函数估计Copula 密度,采用样本的Kendall秩相关系数代替半参数法拟合参数以提高运算效率;计算各特征参量与输出功率的互信息并按等级排序,结果见表1。ECMI性能分析如下:
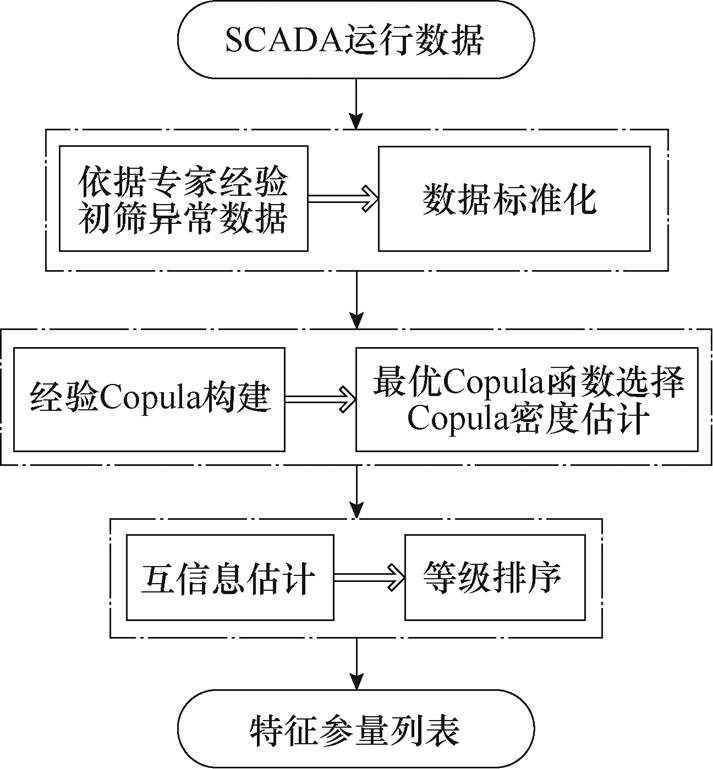
图2 ECMI特征参量选择策略
Fig.2 Selection strategy of characteristic parameters based on ECMI
表1 特征参量集等级列表
Tab.1 Rank list of characteristic parameter set
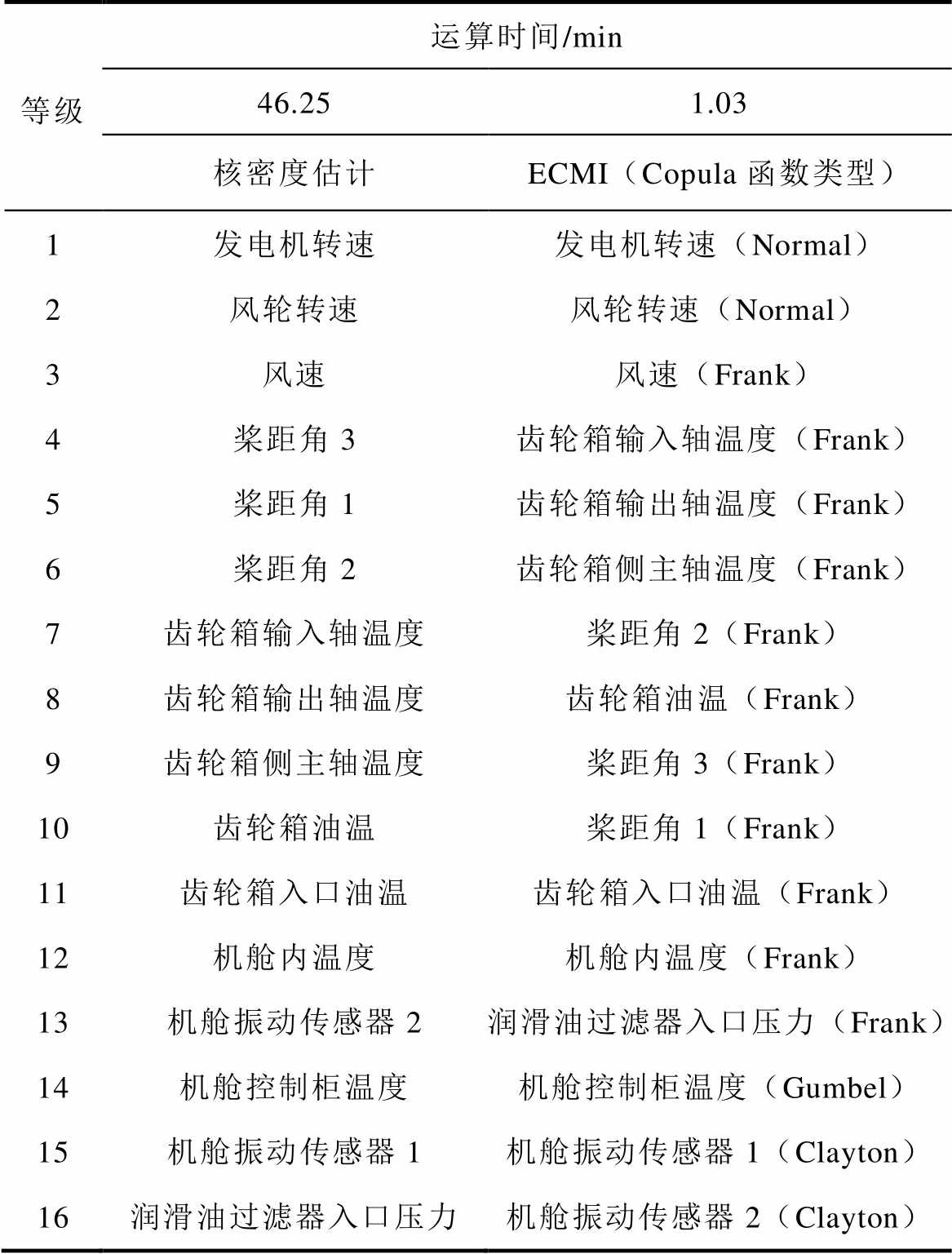
等级运算时间/min 46.251.03 核密度估计ECMI(Copula函数类型) 1发电机转速发电机转速(Normal) 2风轮转速风轮转速(Normal) 3风速风速(Frank) 4桨距角3齿轮箱输入轴温度(Frank) 5桨距角1齿轮箱输出轴温度(Frank) 6桨距角2齿轮箱侧主轴温度(Frank) 7齿轮箱输入轴温度桨距角2(Frank) 8齿轮箱输出轴温度齿轮箱油温(Frank) 9齿轮箱侧主轴温度桨距角3(Frank) 10齿轮箱油温桨距角1(Frank) 11齿轮箱入口油温齿轮箱入口油温(Frank) 12机舱内温度机舱内温度(Frank) 13机舱振动传感器2润滑油过滤器入口压力(Frank) 14机舱控制柜温度机舱控制柜温度(Gumbel) 15机舱振动传感器1机舱振动传感器1(Clayton) 16润滑油过滤器入口压力机舱振动传感器2(Clayton)
(1)可解释性。以健康参量为例,各类温度参量直接反映齿轮箱的健康状态,一旦高于报警阈值便会导致机组限功率运行或故障停机。从物理角度看,油温受温控影响变化平稳,而轴温波动较明显,变化趋势与输出功率相似,更有利于健康状态预测,机舱内温度则反映了工况的变化,也较机舱控制柜温度更有参考意义。ECMI的等级排序与上述物理知识相一致,故可解释性良好。
(2)准确性与运算效率。以风速-功率为例,最优Copula类型为Frank,主要描述对称相关结构,对上下尾部特征均不敏感,而处于中段工况子空间的数据对评估机组健康状态的贡献最大[11],可见由Frank Copula函数描述风功率数据的分布特征有利于保留有效信息。综合分析等级排序靠前的12个特征参量,其中冗余部分仅保留等级高的参量。ECMI对应的与输出功率相关性强的参量依次为发电机转速、风速、齿轮箱输入轴温度、齿轮箱侧主轴温度、桨距角2、齿轮箱油温及机舱内温度,结果与核密度估计法基本一致,主要差异在于桨距角与轴温的等级顺序,但运算效率远远高于后者。
综上分析,选择输出功率、发电机转速、风轮转速、风速和桨距角等关键特征参量构成数据清洗对象。对于轴温、油温等等级较高的健康参量,因其异常值可能反映出工况变化或关键部件有异常发生,故不能轻易剔除,但可作为机组健康状态预测与故障检测的重要特征依据。
由关键特征参量确定风速-功率、发电机转速-功率和风轮转速-功率为清洗对象后,便能建立数据清洗模型,从而实现堆积点与离群点的有效识别。
1)基于Copula建立置信等效功率区间
Copula函数无需明确数据的分布形态即可准确描述其概率分布特征,因此,基于Copula建立置信等效功率区间来描述清洗对象的非线性与不确定性,认为置信边界内的数据为符合数据真实分布规律的有效数据,边界外的数据为可疑数据。
在不同风速或转速V的条件下建立输出功率P的条件概率分布,由其上下分位数对应的概率功率曲线[22]形成置信等效功率区间。基于经验Copula函数的解析法确定最优Copula函数拟合联合分布,给定V,得条件概率分布函数为
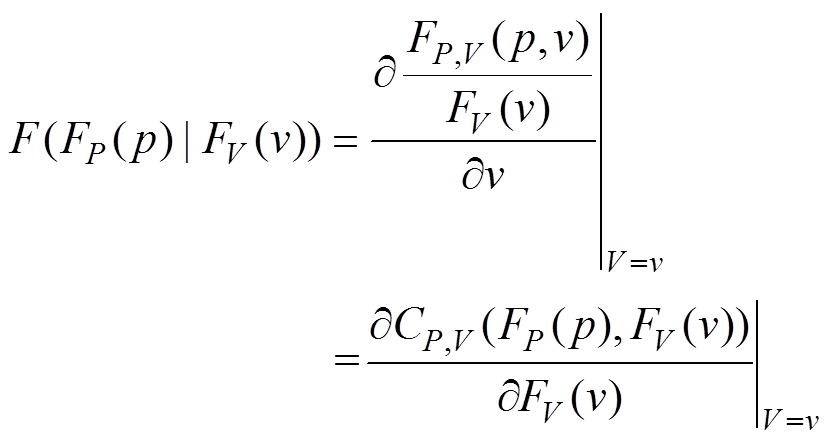 (5)
(5)设数据落在上、下置信边界外的概率分别为bup= (1-k)a、bdown=ka,对应分位数Fup、Fdown满足F(Fup|FV(v))=1-bup、F(Fdown|FV(v))=bdown,则可确定置信边界pup=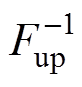 、pdown=
、pdown=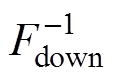 。其中,a 为显著性水平,k 为置信偏度,机组性能退化时风功率曲线会发生下移,故取k≤0.5。
。其中,a 为显著性水平,k 为置信偏度,机组性能退化时风功率曲线会发生下移,故取k≤0.5。
2)基于TFDD清洗异常数据
结合三类典型异常数据的时序特征和密度分布(Time-series Features and Density Distribution, TFDD),分别清洗堆积点与离群点。
堆积点的风速、输出功率和桨距角等关键特征参量具有典型的时序特征,结合工程经验依次识别类型Ⅰ堆积点和置信边界外的类型Ⅱ堆积点。类型Ⅲ离群点因其分散性相对于整个数据集不具有典型时序特征,但与有效数据的密度分布不同,因此利用DBSCAN算法[11, 23-24]进行甄别。若直接清洗原始数据集,需要分段处理数据[11],仅清洗数据量较小的可疑点可以克服算法本身内存占用大、运算速度慢的缺点,保证数据清洗方法的实用性。异常数据判别准则见表2。
表2 异常数据判别准则
Tab.2 Discriminant criterion of abnormal data
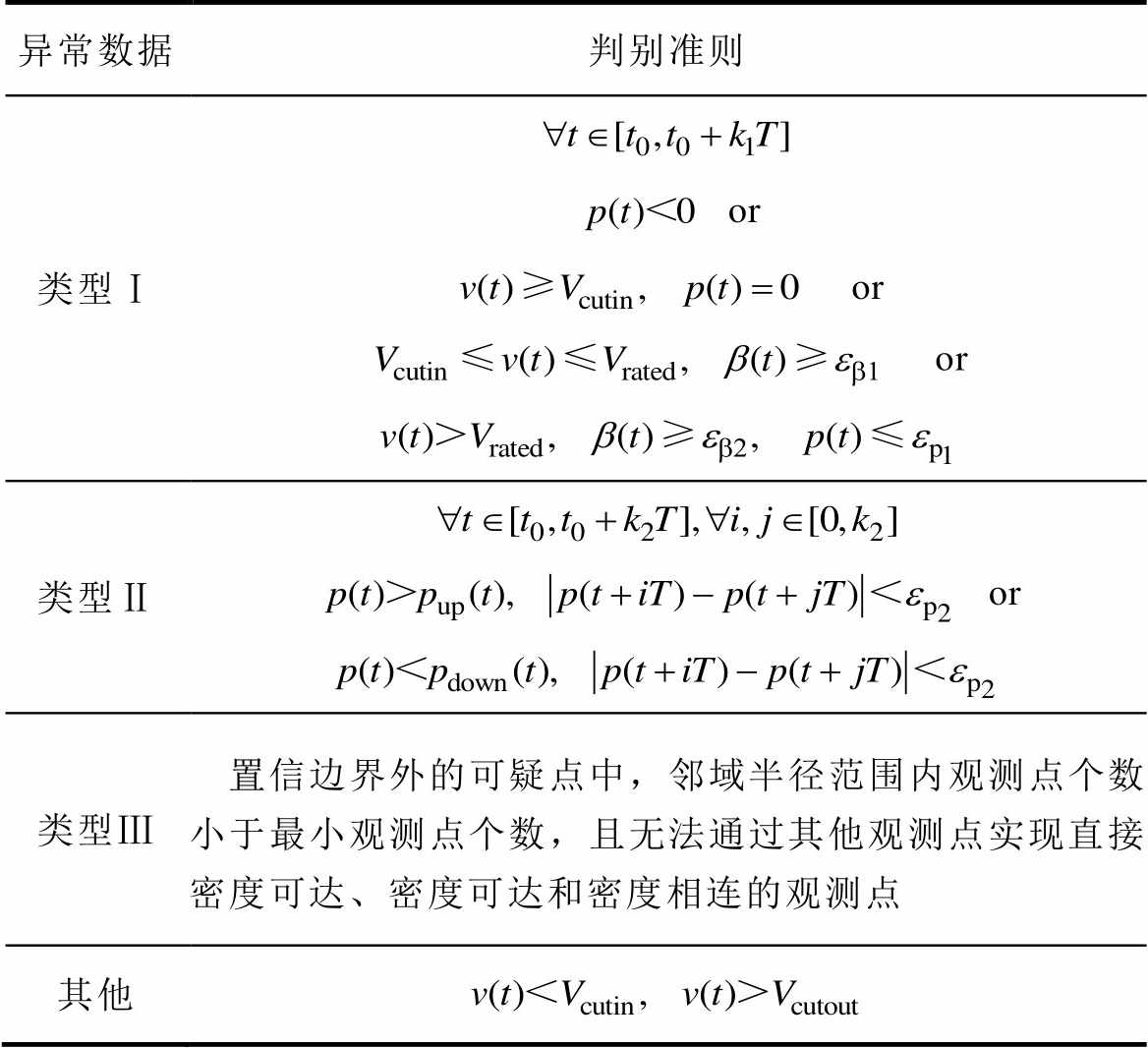
异常数据判别准则 类型Ⅰ or or or 类型Ⅱ or 类型Ⅲ置信边界外的可疑点中,邻域半径范围内观测点个数小于最小观测点个数,且无法通过其他观测点实现直接密度可达、密度可达和密度相连的观测点 其他
表2中,v(t)、p(t)、b(t)分别为风速、输出功率和桨距角;pup(t)、pdown(t)对应置信边界;Vcutin、Vrated、Vcutout分别为切入风速、额定风速和切出风速;T为单位持续时间;k11、k2、k3取整数;eb1、eb2、ep1、ep2为阈值参数,由工程经验设定。
以风速-功率、发电机转速-功率和风轮转速-功率为清洗对象,建立Copula-TFDD在线清洗流程,如图3所示,逐步清洗堆积点和离群点。
(1)模块1。识别风速-功率数据集中的堆积点。首先,基于专家经验对原始数据集进行初筛,根据机组正常运行状态下的数据确定最优Copula函数,适当设置置信概率与不对称系数,建立初始概率功率曲线;依据判别准则清洗置信边界外可疑数据中的堆积点,通过重复修正概率功率曲线自适应调整置信边界,从而提高模型对复杂数据集的适应性;最后,形成新数据集并记录数据标签。
(2)模块2。识别风速-功率数据集中的离群点。针对模块1的剩余可疑数据,利用DBSCAN算法识别离群点,形成新数据集并记录数据标签。
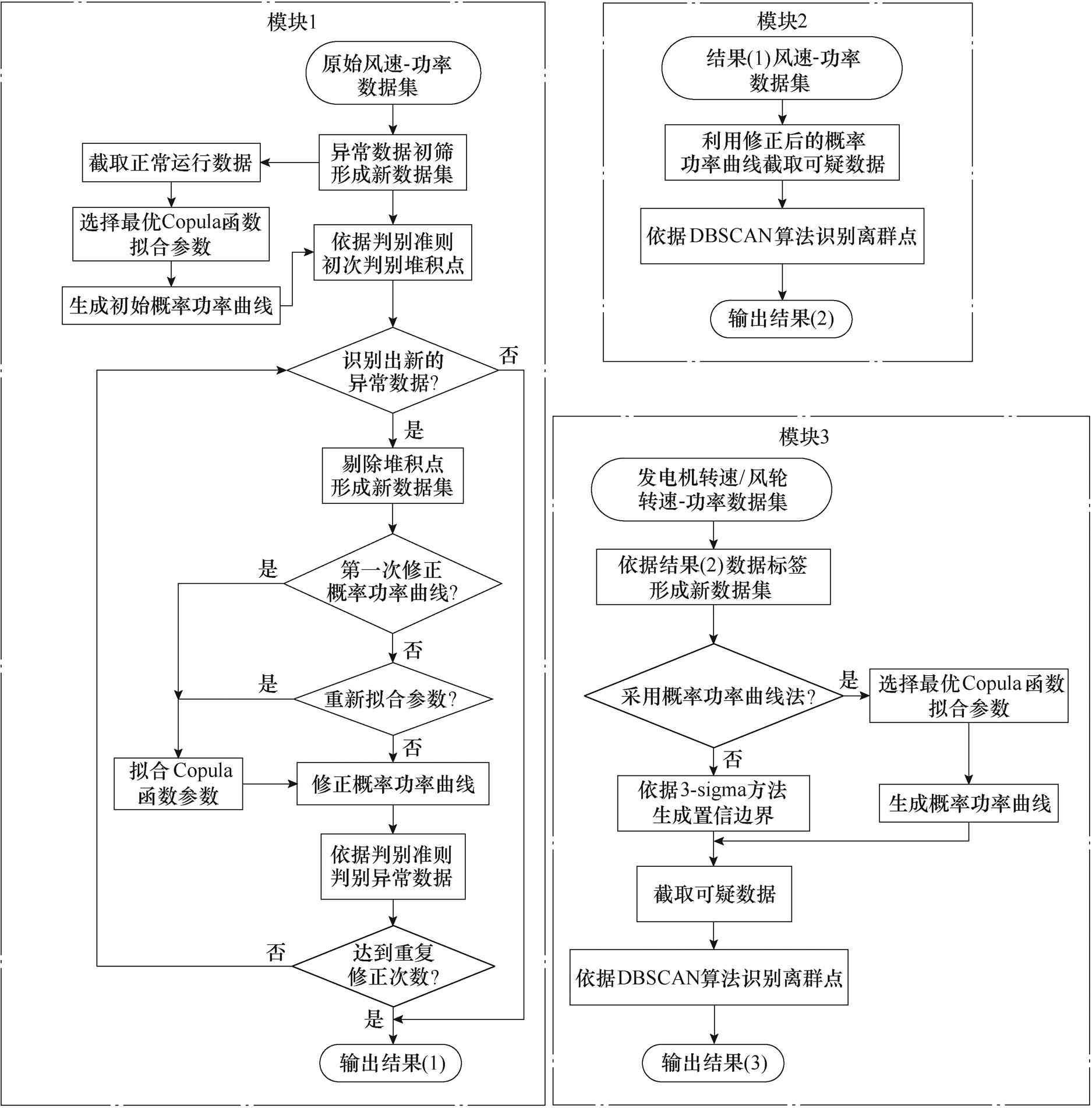
图3 Copula-TFDD数据清洗模型流程
Fig.3 Flow chart of data cleaning model based on Copula-TFDD
(3)模块3。识别发电机转速/风轮转速-功率数据集中的离群点。根据模块2的数据标签得到新的转速-功率数据集,因其离群点数量较小,且转速与功率的相关性较强,故可以利用3-sigma概率统计方法建立置信等效功率区间,以提高运算效率。
SCADA系统往往没有数据状态标签,为进一步定量分析数据清洗模型的精度与运算效率,相关文献[7, 22]普遍采用人工模拟异常数据的方法进行验证,却并未给出模拟方法。本文利用Copula理论可以模拟多元随机变量分布特征的特点,人工模拟关键特征参量中的异常数据,以定量分析Copula- TFDD的精度与运算效率。
由输出功率P和其他特征参量V构成二元随机变量,要生成服从实际分布FP,V(p, v)的随机变量(P, V),可借助条件分布函数F(FV(v)|FP(p))生成一对在(0, 1)区间上服从均匀分布且具有Copula函数CP,V(u, v)的随机变量(u, v),其中u= FP(p),v=FV(v),对u和v求逆即可得到(P, V)。
据此,以通信故障、传感器异常、弃风限电等原因引起的明显离群点和堆积点为模拟对象,人工构造各类异常数据。首先,基于经验Copula函数的解析法选择对应的最优Copula函数模拟各类异常点的分布特征,以输出功率为条件,随机生成符合实际分布特征的风速、发电机转速和风轮转速等随机变量;然后,模拟堆积点的时序特征,并以机组典型工作日数据为基础,建立带标签的混合数据集。
以实际运行数据集和人工模拟混合数据集为研究对象,利用DBSCAN算法、3-sigma-TFDD模型和Copula-TFDD模型进行异常数据清洗仿真,分析模型的精度与运算效率,并将清洗结果应用于风电机组健康状态预测,验证本文所提方法的有效性和适用性。
文中引用的实测数据分别为一台2MW(机组Ⅰ)和两台1.5MW(机组Ⅱ、Ⅲ)风电机组的SCADA运行数据集,3台机组均因主轴高温故障停机,故障部件为齿轮箱,基本参数见表3。
表3 风电机组基本参数
Tab.3 Basic parameters of wind turbine
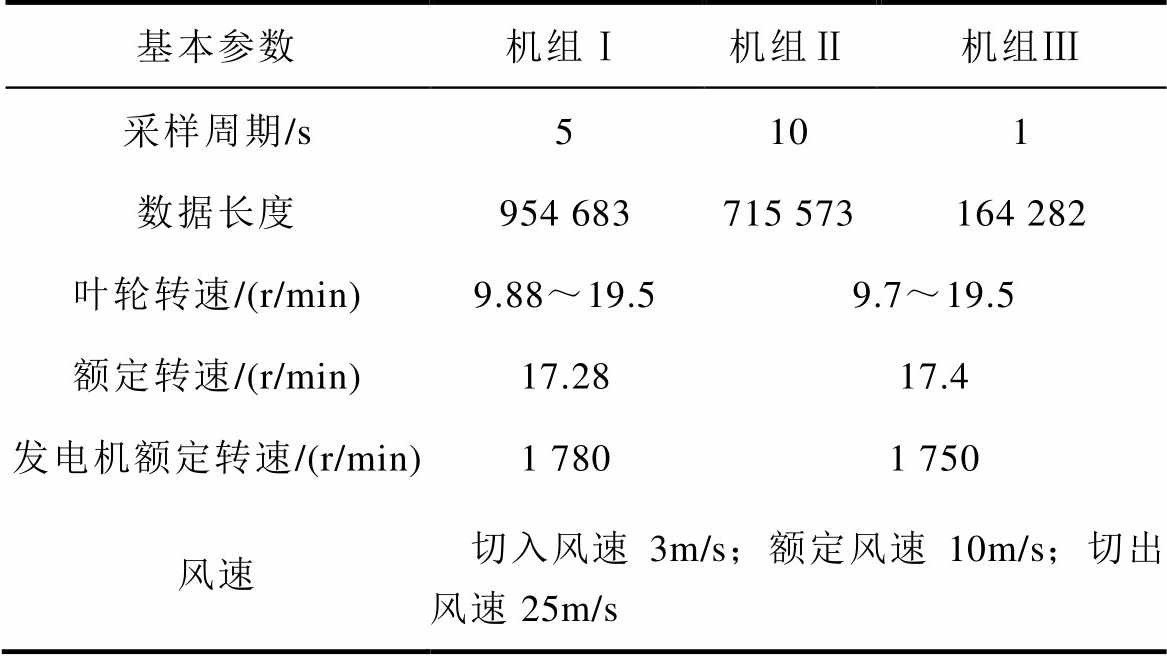
基本参数机组Ⅰ机组Ⅱ机组Ⅲ 采样周期/s5101 数据长度954 683715 573164 282 叶轮转速/(r/min)9.88~19.59.7~19.5 额定转速/(r/min)17.2817.4 发电机额定转速/(r/min)1 7801 750 风速切入风速3m/s;额定风速10m/s;切出风速25m/s
1)异常数据清洗
Copula-TFDD模型对应风速-功率的清洗结果如图4所示。以机组Ⅰ为例,对比两种置信等效功率区间发现,概率功率曲线较3-sigma曲线更接近数据的真实分布且波动较小,可知Copula-TFDD模型较3-sigma-TFDD模型(风速-功率数据的置信边界采用3-sigma曲线)更有利于减少误判与漏判。
比较3台机组的风功率曲线可知,不同机组的数据分布可能不同,机组Ⅰ、Ⅱ对应的Copula函数为反映对称相关结构的Frank型,其中,机组Ⅰ中三类异常数据均比较典型,机组Ⅱ则主要体现为离群点;机组Ⅲ虽然采样周期最短,但由于只搜集了故障前3天的数据,并未包含所有工况信息,且异常数据信息较少,对应的Copula函数类型为反映上尾特征的Gumbel型。
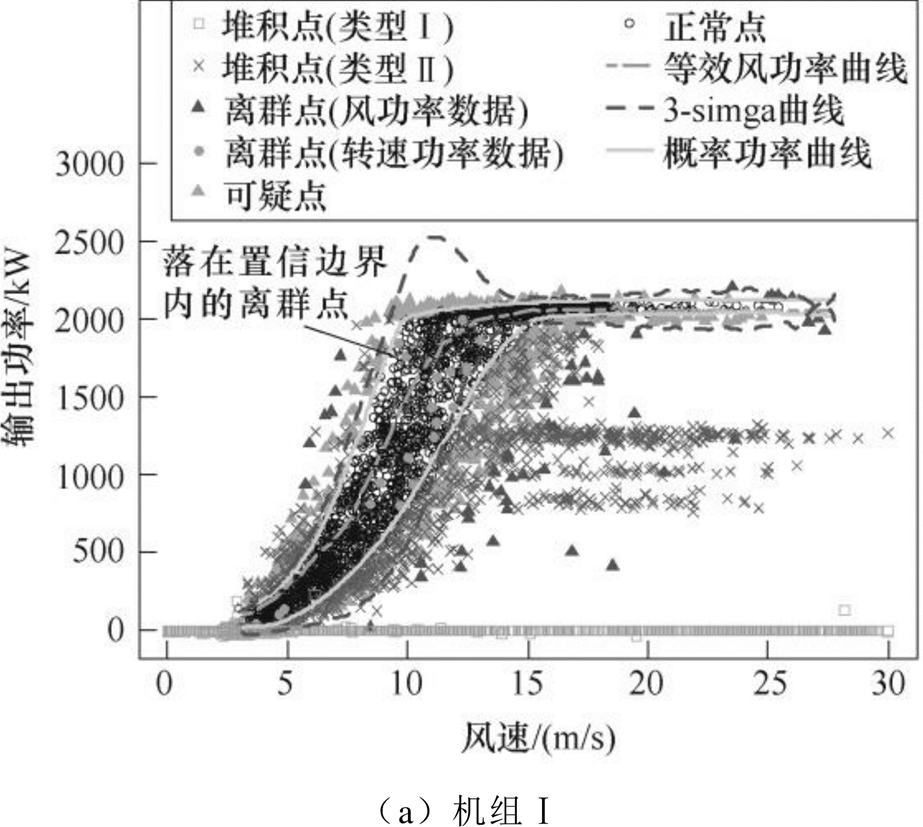

图4 实测风速-功率数据集清洗结果
Fig.4 Data cleaning result of real wind power data
进一步比较Copula-TFDD模型与DBSCAN算法,对应机组Ⅰ的发电机转速-风速-功率三维清洗结果如图5所示,图中点画线中的因频繁切换控制产生的离群点在图4a中落于置信边界内。可见,Copula-TFDD模型因同时考虑了关键特征参量中异常点的时序特征与密度分布,能有效识别落在置信边界附近的堆积点与边界内的离群点,而DBSCAN算法只清洗了风功率数据中较明显的离群点和堆积点,不仅存在漏判,还因分段清洗造成清洗效果不稳定。
分析机组Ⅰ在切入、切出风速间异常数据被剔除前后的剔除率(各风速区间内被剔除的数据占该区间内总数据的比例),DBSCAN算法、3-sigma- TFDD模型和Copula-TFDD模型在四分位间距内的剔除率分别为12.27%~25.01%、12.14%~23.44%和10.73%~22.01%,主要落在20%左右,波动范围合理。风速范围两端的剔除率偏高,存在正常数据被误判的可能,但这部分数据点较少,且对后续整机性能预测的作用较小,相对于误判的影响可忽略。
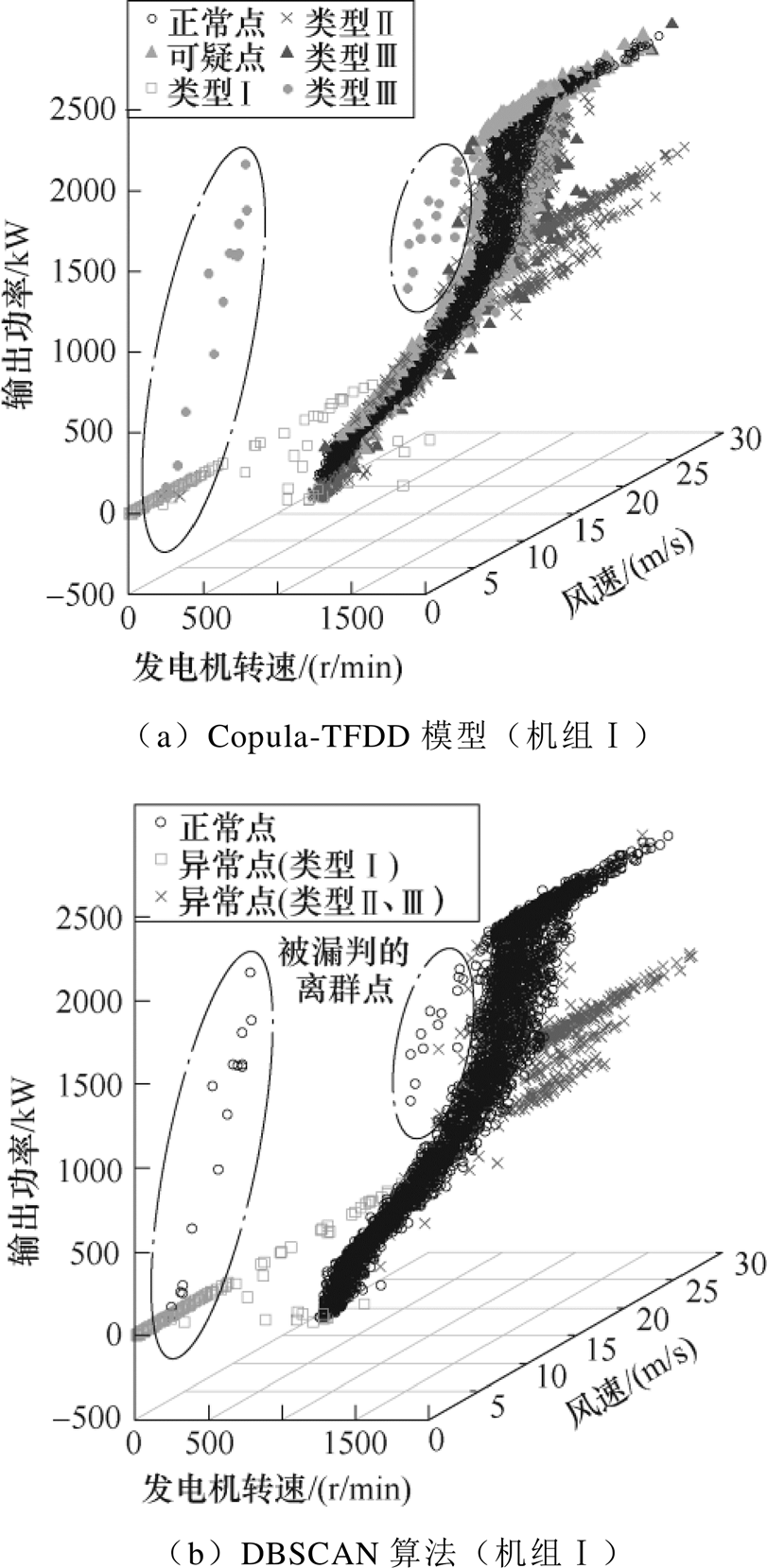
图5 实际运行数据集清洗结果
Fig.5 Data cleaning result of real SCADA data set
分析运算效率。机组Ⅰ对应3-sigma-TFDD模型和Copula-TFDD模型的清洗时间分别为1.7min和9.5min,机组Ⅱ、Ⅲ对应Copula-TFDD模型的清洗时间短于3min,两种方法均能实现在线清洗,而DBSCAN算法只能离线清洗。
2)异常数据分析
因弃风限电造成的堆积型异常点具有典型的时序特征,可以结合桨距角信息利用判别准则进行清洗,而对于离群点的清洗则需要更为谨慎。
离群点分布分散,主要因随机误差、工况波动或限电造成的控制机制频繁切换等引起,前者属于偶发,后者通常时序连续但没有典型的变化规律,因此利用基于密度聚类思想的DBSCAN算法进行清洗。图4b、图4c和图5a中点画线中的离群点分散性较大,但图4b、图4c中虚线中的离群点距离有效数据近,密度较正常运行数据低,若被过度清洗可能会误删有效数据。在风机发电性能评估中离群点通常可以不清洗[10],然而,通过合理设置参数,离群点的清洗有利于基于概率统计方法对整机性能退化过程的预测[10-11]。
3)其他关键特征参量分析
以机组Ⅰ的机舱振动与齿轮箱油温等健康参量为例,分析其他关键特征参量的数据清洗工作。机舱振动有效值-风速、齿轮箱油温-输出功率的关系分别如图6和图7所示,观察之前的数据清洗结果发现,已清洗的各类异常点特别是离群点均分布在正常范围,未超报警阈值。
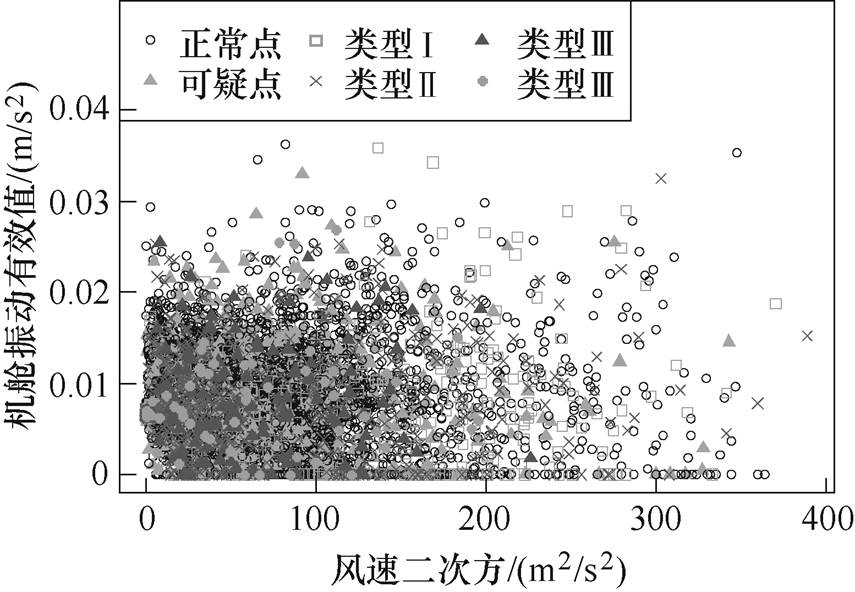
图6 机舱振动有效值与风速的关系
Fig.6 Relationship between nacelle vibration and wind speed
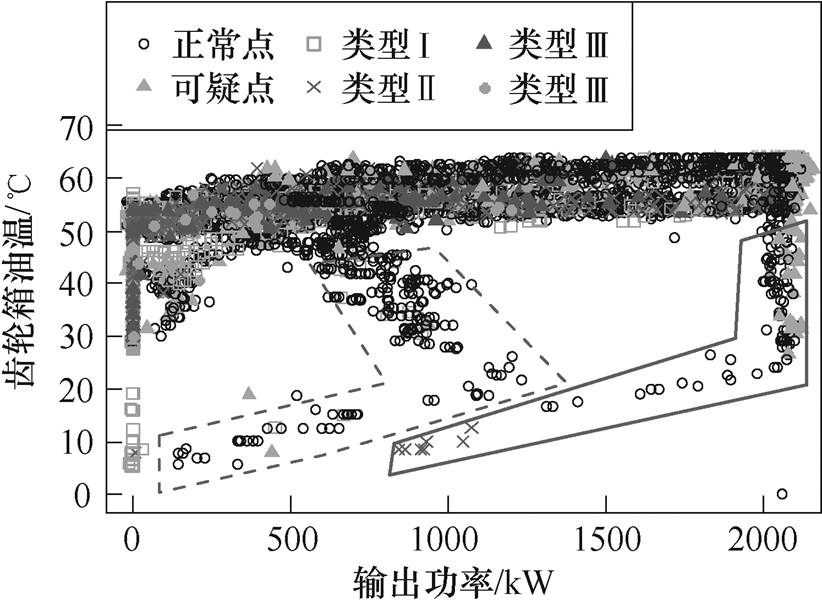
图7 齿轮箱油温与输出功率的关系
Fig.7 Relationship between gearbox oil temperature and power
图6中,机舱振动信号变化快速,随风速增大变化加剧。通常,振动信号对机械故障比较敏感,含有故障信息的振动信号常呈现出分散性较大的离群分布,故对离群点的清洗可能会隐藏故障信息。
图7中,齿轮箱油温变化平缓,由于受温控阀影响,基本不随功率变化出现明显波动。对于缓变信号,一般不会出现明显的离群点。而图中虚线和实线中的数据则分别为d6和d21两天的数据,具有典型的时序特征,且呈特殊的密集型分布,这种情况可能是受当日极端气候影响所致,不排除机组有故障发生,因此不能直接剔除。
健康参量往往反映了机组关键部件的健康状态,因此,本文不对振动与温度等参量进行清洗。
为进一步定量分析数据清洗模型的精度与运算效率,以机组Ⅰ在故障前近两个月(2.21~4.16)的数据为基础,人工模拟具有代表性的数据集。
首先,建立基础数据集。表4给出了部分工作日的风速范围和Copula-TFDD清洗结果。结合日风功率散点图发现,机组在不同工作日、不同运行工况下数据分布各异且各类异常点占比差异明显,例如,d1/d38/d45机组运行在切入、切出风速之间,异常点较少,而d4/d20几乎全部为类型Ⅰ异常点,d52~d56的异常点中类型Ⅱ、Ⅲ占比增大,故障前两日的风速范围较大,故障当天机组运行状态明显异常。因缺乏气象数据,同时要确保基础数据集覆盖全部工况,并考虑机组性能逐渐退化、气温逐渐升高等因素,本文没有直接对全部数据集抽样,而是先根据风速条件与数据分布确定各月的典型工作日(占全部数据集70%),再随机抽样构成数据集1,其中故障发生当月的数据占比较大。在此基础上,提取各类异常数据,根据3.3节中人工模拟异常数据的方法分别构造混合数据集2~4,异常数据比例见表5。以数据集2为例,散点示意图如图8所示。
表4 典型工作日异常数据比例
Tab.4 The proportion of abnormal data in typical day(%)
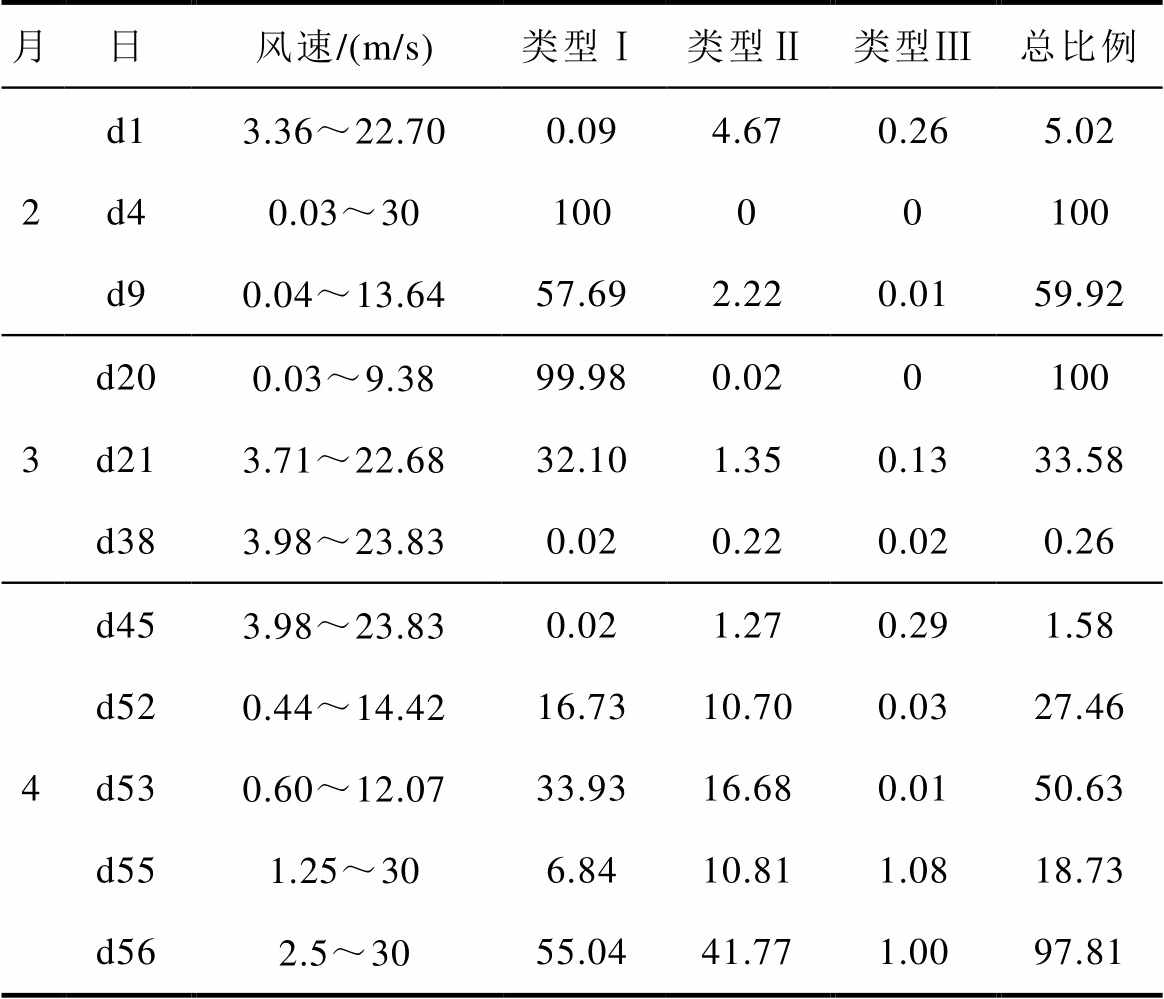
月日风速/(m/s)类型Ⅰ类型Ⅱ类型Ⅲ总比例 2d13.36~22.700.094.670.265.02 d40.03~3010000100 d90.04~13.6457.692.220.0159.92 3d200.03~9.3899.980.020100 d213.71~22.6832.101.350.1333.58 d383.98~23.830.020.220.020.26 4d453.98~23.830.021.270.291.58 d520.44~14.4216.7310.700.0327.46 d530.60~12.0733.9316.680.0150.63 d551.25~306.8410.811.0818.73 d562.5~3055.0441.771.0097.81
表5 人工模拟异常数据比例
Tab.5 The proportion of artificial abnormal data (%)
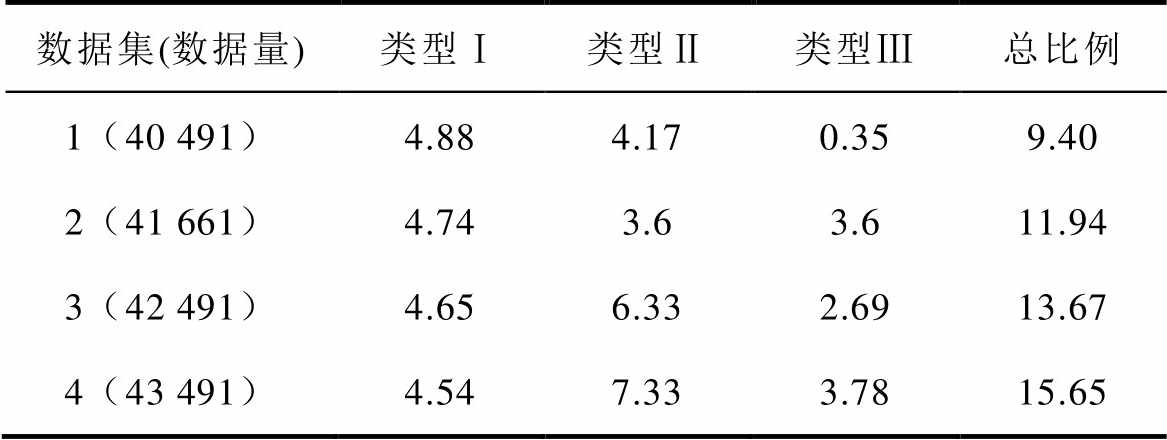
数据集(数据量)类型Ⅰ类型Ⅱ类型Ⅲ总比例 1(40 491)4.884.170.359.40 2(41 661)4.743.63.611.94 3(42 491)4.656.332.6913.67 4(43 491)4.547.333.7815.65
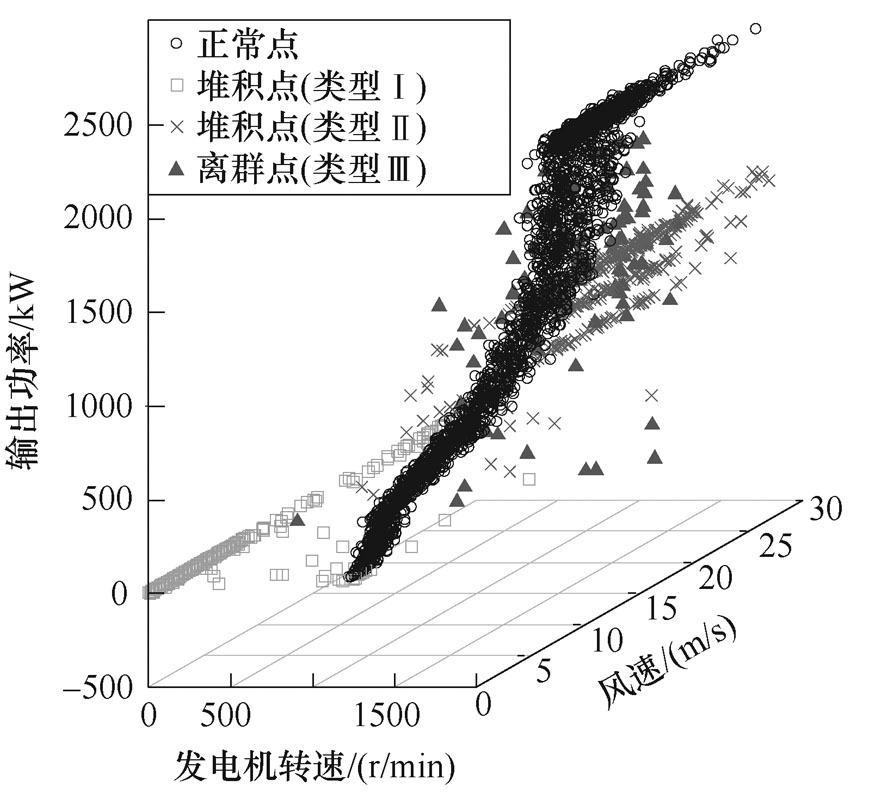
图8 人工模拟数据集2散点示意图
Fig.8 Scatter diagrams of artificially generated dataset 2
采用DBSCAN算法、3-sigma-TFDD模型和Copula-TFDD模型分别清洗数据集1~4,人工模拟混合数据集的统计识别结果见表6。
表6 人工模拟混合数据集的统计识别结果
Tab.6 Statistical identification results of artificially generated mixed datasets
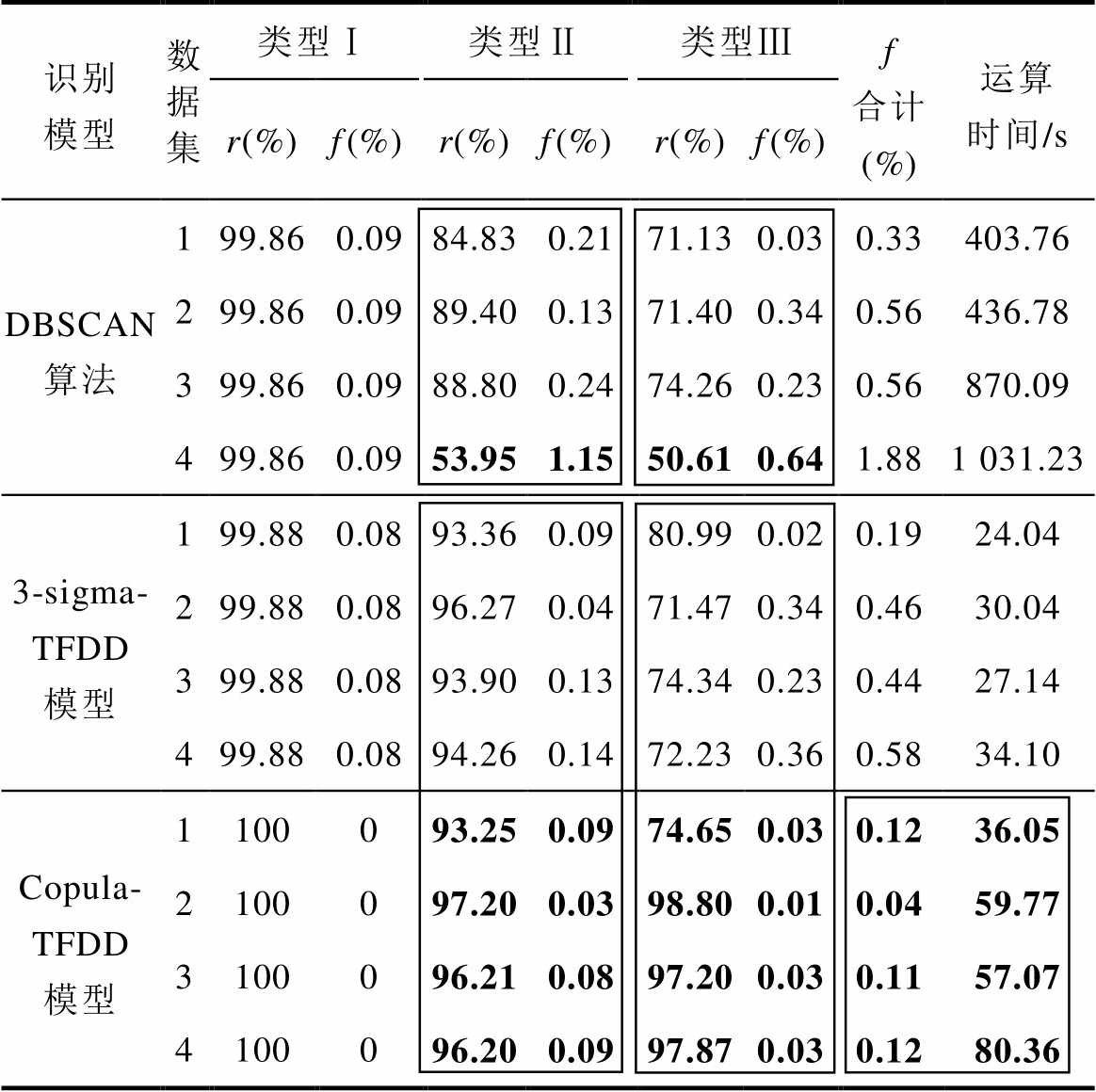
识别模型数据集类型Ⅰ类型Ⅱ类型Ⅲf合计 (%)运算时间/s r(%)f(%)r(%)f(%)r(%)f(%) DBSCAN算法199.860.0984.830.2171.130.030.33403.76 299.860.0989.400.1371.400.340.56436.78 399.860.0988.800.2474.260.230.56870.09 499.860.0953.951.1550.610.641.881 031.23 3-sigma- TFDD模型199.880.0893.360.0980.990.020.1924.04 299.880.0896.270.0471.470.340.4630.04 399.880.0893.900.1374.340.230.4427.14 499.880.0894.260.1472.230.360.5834.10 Copula- TFDD模型1100093.250.0974.650.030.1236.05 2100097.200.0398.800.010.0459.77 3100096.210.0897.200.030.1157.07 4100096.200.0997.870.030.1280.36
较高的识别率r说明模型的正确率较高,但有效的清洗模型应同时具有较低的误识别率f [22]。模型精度与运算效率定量分析如下:
(1)堆积点的识别率。三种方法对类型Ⅰ堆积点的识别率均较高;对于类型Ⅱ堆积点,两种TFDD模型因同时考虑了数据的概率分布、时序特征和密度分布,识别效果均优于DBSCAN算法,当异常点的占比增加时,后者的识别率下降明显。
(2)离群点的识别率。离群点的数量和分布位置会影响两种TFDD模型的识别效果。数据集1中离群点虽然只占0.35%,但较多离群点落在了置信边界内,Copula-TFDD模型的识别率略低于3- sigma-TFDD模型;随着数据集2~4中离群点的占比增加、概率统计特征波动变大,3-sigma-TFDD模型的识别精度明显低于Copula-TFDD模型,后者由于更符合数据的实际分布特征,保证较高识别率的同时可保持较小的波动。
(3)误识别率。三种方法针对不同数据集的误识别率均较低,因此直接剔除异常点对最终的数据应用影响不大。进一步分析,三种方法的误识别率依次降低,随着异常数据的占比增加,各模型的误识别率均有所升高,但前两者升高明显,Copula- TFDD模型的稳定性更好。
(4)运算效率。DBSCAN算法的运算时间最长,而实际运行数据的数据量很大,该方法需要依时间窗分段处理数据集,因此不利于工程应用。两种TFDD模型的运算速度均较快,虽然3-sigma-TFDD模型的算法简单、运算效率更高,但Copula-TFDD模型的识别精度更高、更稳定。
综上分析,两种TFDD模型都可以有效识别三类典型异常数据,综合考虑模型的精度、运算效率和稳定性,Copula-TFDD模型在工程应用方面的适应性更强。
将机组Ⅰ的清洗结果应用于风电机组健康状态预测,分析数据清洗方法的适用性。
利用相似性度量算法[11]预测风电机组整机性能。取前10日风功率数据作为正常样本,以1周为时间窗对剩余数据滑动截取得到46组测试样本,计算综合相似性度量指标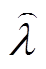 ,由机组正常运行时
,由机组正常运行时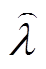 的均值m 和标准差s 确定阈值控制限,将机组运行状态分为健康、隐患和告警3个等级。
的均值m 和标准差s 确定阈值控制限,将机组运行状态分为健康、隐患和告警3个等级。
采用DBSCAN算法、3-sigma-TFDD模型、Copula- TFDD模型和Copula-TF模型(不清洗离群点)等不同方法的预测结果如图9所示。可以看出,原始数据集的概率统计指标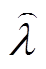 受异常点影响变化趋势不明显且波动较大,无法判断机组健康状态,而清洗后数据集对应的
受异常点影响变化趋势不明显且波动较大,无法判断机组健康状态,而清洗后数据集对应的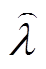 总体呈上升趋势,说明机组性能在逐渐退化。比较图9b~图9d可知,采用DBSCAN算法或3-sigma-TFDD模型均能提前一周发现机组异常,前者无法在线运行,后者
总体呈上升趋势,说明机组性能在逐渐退化。比较图9b~图9d可知,采用DBSCAN算法或3-sigma-TFDD模型均能提前一周发现机组异常,前者无法在线运行,后者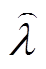 的单调性更典型;采用Copula-TFDD模型能提前8天发现异常,
的单调性更典型;采用Copula-TFDD模型能提前8天发现异常,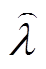 的单调性与稳定性均优于前两种方法。图9e较图9d晚一天发现机组性能恶化,可知离群点占比虽小但因其分散性大,对机组健康状态预测应用中基于概率统计方法预测整机性能的退化有不利影响,因此有必要清洗。在风电机组发电性能评估应用中,对离群点的清洗可以忽略,在做故障预测时,有必要针对时间连续但密度较低的离群点对应的关键特征参量进行深入分析,挖掘可能包含的故障信息。
的单调性与稳定性均优于前两种方法。图9e较图9d晚一天发现机组性能恶化,可知离群点占比虽小但因其分散性大,对机组健康状态预测应用中基于概率统计方法预测整机性能的退化有不利影响,因此有必要清洗。在风电机组发电性能评估应用中,对离群点的清洗可以忽略,在做故障预测时,有必要针对时间连续但密度较低的离群点对应的关键特征参量进行深入分析,挖掘可能包含的故障信息。
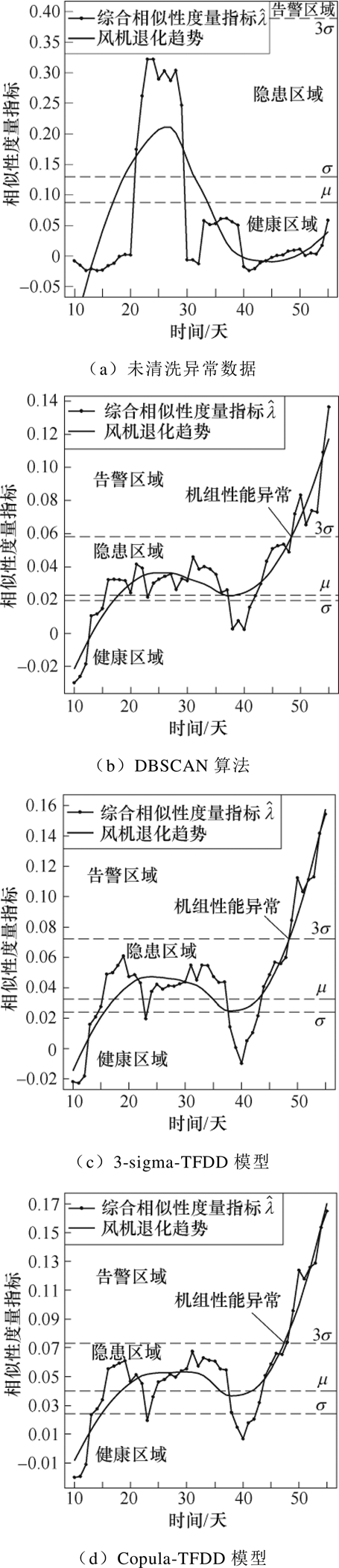
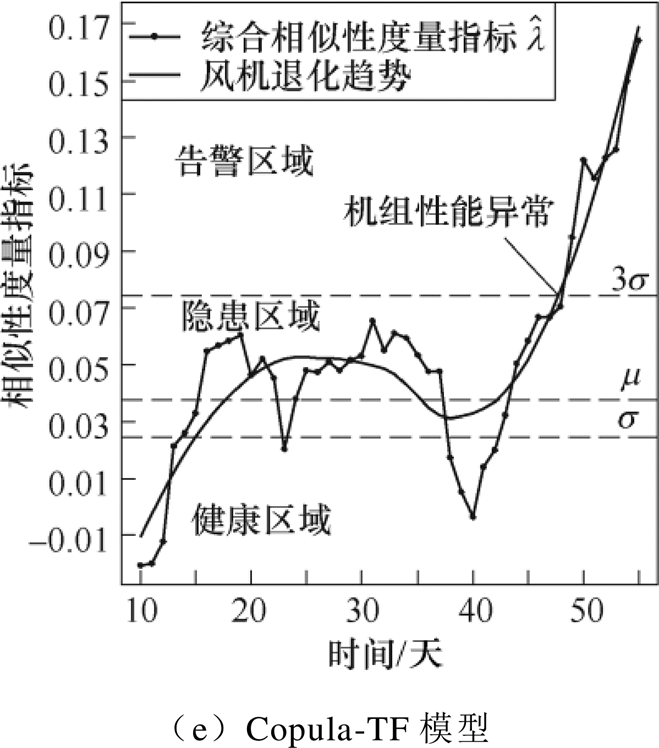
图9 风电机组整机性能指标变化趋势
Fig.9 Measurement index of wind turbine performance degradation assessment
Copula-TFDD模型能在线应用于机组健康状态预测,虽然较其他数据清洗方法仅能提前一天发现机组性能恶化,但对于风电场提前进行故障诊断、排查维修,避免如齿轮箱损坏等重大故障的发生具有重要意义。
综上分析,Copula-TFDD模型因综合考虑了关键特征参量的概率分布、时序特征和密度分布,有利于挖掘风速、转速与输出功率之间的真实物理规律,适用于风电机组健康状态预测。
针对风电机组健康状态预测中对异常数据进行在线清洗的实际需求,本文研究得出如下结论:
1)提出基于ECMI的特征参量选择方法。选择反映风电机组整机性能的关键特征参量构成清洗对象,对实测风速-功率、转速-功率数据中的堆积点和离群点等典型异常数据进行清洗。
2)基于风电机组实测运行数据的概率分布、时序特征与密度分布提出Copula-TFDD数据清洗模型。该方法可以对具有不同采样周期和差异化概率分布的运行数据实现在线清洗,且能有效提升机组健康状态预测的性能。
3)基于Copula给出了人工模拟符合实际异常数据分布特征的数据集的方法。通过对Copula- TFDD的精度、运算效率和稳定性的定量分析,验证了该数据清洗方法的工程应用性较强。
参考文献
[1] 陈俊生, 李剑, 陈伟根, 等. 采用滑动窗口及多重加噪比堆栈降噪自编码的风电机组状态异常检测方法[J]. 电工技术学报, 2020, 35(2): 346-358.
Chen Junsheng, Li Jian, Chen Weigen, et al. A method for detecting anomaly conditions of wind turbines using stacked denoising autoencoders with sliding window and multiple noise ratios[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(2): 346-358.
[2] 赵永宁, 叶林, 朱倩雯. 风电场弃风异常数据簇的特征及处理方法[J]. 电力系统自动化, 2014, 38(21): 39-46.
Zhao Yongning, Ye Lin, Zhu Qianwen. Characteristics and processing method of abnormal data clusters caused by wind curtailments in wind farms[J]. Automation of Electric Power Systems, 2014, 38(21): 39-46.
[3] 娄建楼, 胥佳, 陆恒, 等. 基于功率曲线的风电机组数据清洗算法[J]. 电力系统自动化, 2016, 40(10): 116-121.
Lou Jianlou, Xu Jia, Lu Heng, et al. Wind turbine data-cleaning algorithm based on power curve[J]. Automation of Electric Power Systems, 2016, 40(10): 116-121.
[4] 沈小军, 付雪姣, 周冲成, 等. 风电机组风速-功率异常运行数据特征及清洗方法[J]. 电工技术学报, 2018, 33(14): 3353-3361.
Shen Xiaojun, Fu Xuejiao, Zhou Chongcheng, et al. Characteristics of outliers in wind speed-power operation data of wind turbines and its cleaning method[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3353-3361.
[5] 邹同华, 高云鹏, 伊慧娟, 等. 基于Thompson tau-四分位和多点插值的风电功率异常数据处理[J]. 电力系统自动化, 2020, 44(15): 156-165.
Zou Tonghua, Gao Yunpeng, Yi Huijuan, et al. Processing of wind power abnormal data based on Thompson tau-quartile and multi-point interpo- lation[J]. Automation of Electric Power Systems, 2020, 44(15): 156-165.
[6] 范晓泉, 杜大军, 费敏锐. 风电异常测量数据智能识别方法研究[J]. 仪表技术, 2017(1): 10-14.
Fan Xiaoquan, Du Dajun, Fei Minrui. Research on the intelligent identification method for abnormal measurement data of the wind power[J]. Instru- mentation Technology, 2017(1): 10-14.
[7] 杨茂, 翟冠强, 苏欣. 基于风特征分析的风电机组异常数据识别算法[J]. 中国电机工程学报, 2017, 37(增刊1): 144-151.
Yang Mao, Zhai Guanqiang, Su Xin. An algorithm for abnormal data identification of wind turbine based on wind characteristic analysis[J]. Proceedings of the CSEE, 2017, 37(S1): 144-151.
[8] 胡阳, 乔依林. 基于置信等效边界模型的风功率数据清洗方法[J]. 电力系统自动化, 2018, 42(15): 18-23, 149.
Hu Yang, Qiao Yilin. Wind power data cleaning method based on confidence equivalent boundary model[J]. Automation of Electric Power Systems, 2018, 42(15): 18-23, 149.
[9] Edzel L, Dustin B, Hossein D A, et al. Wind turbine performance assessment using multi-regime modeling approach[J]. Renewable Energy, 2012, 45: 86-95.
[10] Jia Xiaodong, Jin Chao, Buzza M, et al. Wind turbine performance degradation assessment based on a novel similarity metric for machine performance curves[J]. Renewable Energy, 2016, 99: 1191-1201.
[11] 马然, 栗文义, 齐咏生. 基于风功率数据的风电机组性能预测与健康状态评估[J]. 可再生能源, 2019, 37(8): 1252-1259.
Ma Ran, Li Wenyi, Qi Yongsheng. Performance degradation prognostic and health assessment using wind power data for wind turbine generation unit[J]. Renewable Energy Resources, 2019, 37(8): 1252- 1259.
[12] Jia Xiaodong, Jin Chao, Buzza M, et al. A deviation based assessment methodology for multiple machine health patterns classification and fault detection[J]. Mechanical Systems and Signal Processing, 2018, 99: 244-261.
[13] 王正宇, 张扬帆, 段向阳, 等. 基于Relief算法的风电机组故障特征参数提取方法[J]. 华北电力技术, 2017(10): 57-62.
Wang Zhengyu, Zhang Yangfan, Duan Xiangyang, et al. Selection method of fault characteristic parameters for wind turbine based on Relief algorithm[J]. North China Electric Power, 2017(10): 57-62.
[14] Du Mian, Yi Jun, Peyman M, et al. A parameter selection method for wind turbine health management through SCADA data[J]. Energies, 2017, 10(2): 253.
[15] 郑睿程, 顾洁, 金之俭, 等. 数据驱动与预测误差驱动融合的短期负荷预测输入变量选择方法研究[J]. 中国电机工程学报, 2020, 40(2): 487-500.
Zheng Ruicheng, Gu Jie, Jin Zhijian, et al. Research on short-term load forecasting variable selection based on fusion of data driven method and forecast error driven method[J]. Proceedings of the CSEE, 2020, 40(2): 487-500.
[16] 王爽心, 郭婷婷, 李蒙. 风电机组变工况变桨系统异常状态在线识别[J]. 中国电机工程学报, 2019, 39(17): 5144-5152, 5295.
Wang Shuangxin, Guo Tingting, Li Meng. On-line abnormal state identification of pitch system based on transitional mode for wind turbine[J]. Proceedings of the CSEE, 2019, 39(17): 5144-5152, 5295.
[17] IEC 61400-12-1: 2017-03(en-fr). In: wind energy generation systems-part 12-1: power performance measurements of electricity producing wind tur- bines[S]. Geneva, Switzerland: International Elec- trotechnical Commission (IEC), 2017.
[18] 石访, 张林林, 胡熊伟, 等. 基于多属性决策树的电网暂态稳定规则提取方法[J]. 电工技术学报, 2019, 34(11): 2364-2374.
Shi Fang, Zhang Linlin, Hu Xiongwei, et al. Power system transient stability rules extraction based on multi-attribute decision tree[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2364-2374.
[19] 李霞. Copula方法及其应用[M]. 北京: 经济管理出版社, 2014.
[20] 沈小军, 周冲成, 吕洪. 基于运行数据的风电机组间风速相关性统计分析[J]. 电工技术学报, 2017, 32(16): 265-274.
Shen Xiaojun, Zhou Chongcheng, Lü Hong. Statistical analysis of wind speed correlation between wind turbines based on operational data[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 265- 274.
[21] 徐玉琴, 陈坤, 李俊卿, 等. Copula函数与核估计理论相结合分析风电场出力相关性的一种新方法[J]. 电工技术学报, 2016, 31(13): 92-100.
Xu Yuqin, Chen Kun, Li Junqing, et al. A new method analyzing output correlation of multi-wind farms based on combination of Copula function and kernel estimation theory[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 92-100.
[22] 龚莺飞, 鲁宗相, 乔颖, 等. 基于Copula理论的光伏功率高比例异常数据机器识别算法[J]. 电力系统自动化, 2016, 40(9): 16-22, 55.
Gong Yingfei, Lu Zongxiang, Qiao Ying, et al. Copula theory based machine identification algorithm of high proportion of outliers in photovoltaic power data[J]. Automation of Electric Power Systems, 2016, 40(9): 16-22, 55.
[23] 周贤正, 陈玮, 郭创新. 考虑供能可靠性与风光不确定性的城市多能源系统规划[J]. 电工技术学报, 2019, 34(17): 3672-3686.
Zhou Xianzheng, Chen Wei, Guo Chuangxin. An urban multi-energy system planning method incor- porating energy supply reliability and wind- photovoltaic generators uncertainty[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3672-3686.
[24] Ester M, Kriegel H P, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[J]. Proceedings of the Second International Conference on Knowledge Discovery and Datamining, 1996, 96: 226-231.
Online Cleaning of Abnormal Data for the Prediction of Wind Turbine Health Condition
Abstract Wind turbine (WT) supervisory control and data acquisition (SCADA) data contains a large number of abnormal data, which has a serious impact on the prediction of WT health condition. Therefore, an online cleaning method for abnormal data is proposed according to the measured wind-power and rotate speed-power data. Due to the complexity of data features in the process of WT performance degradation, key characteristic parameters are selected as data cleaning objects based on empirical Copula-based mutual information (ECMI), and the nonlinearity and uncertainty are described by establishing confidence equivalent power interval calculated with Copula. Accordingly, the Copula-based data cleaning model combining the time-series features and density distribution (Copula-TFDD) of abnormal points is established, and online cleaning for the stacking points and outliers outside the confidence boundary is performed in turn. Finally, through the actual data and the simulation data, the accuracy and efficiency of Copula-TFDD are analyzed, and the influence on the prediction of WT health condition is also analyzed. The results show that Copula-TFDD can accurately and real-time identify various abnormal data, effectively improving the prediction performance of WT health condition.
keywords:Prediction of wind turbine health condition, data cleaning, characteristic parameters, mutual information, Copula theory
中图分类号:TK83
DOI: 10.19595/j.cnki.1000-6753.tces.200278
国家自然科学基金项目(61763037)、内蒙古自治区高等学校科学研究项目(NJZY21305)和内蒙古自治区科技计划项目(2019,2020GG028)资助。
收稿日期 2020-03-18
改稿日期 2020-07-20
马 然 女,1982年生,讲师,博士研究生,研究方向为风电机组故障诊断与健康管理。E-mail: maran007@imut.edu.cn
栗文义 男,1963年生,教授,博士生导师,研究方向为新能源发电技术。E-mail: lwyyyll@vip.sina.com(通信作者)
(编辑 崔文静)