坐标系下对高频电流解调并构造转子位置误差信号，利用正序、负序高频电流相移等值异号的特性实现电流相移自动抵消，不仅省去复杂的位置误差补偿策略，而且将原SFAC算法的速度适用范围由零速区拓宽至非零速区。该文对SFAC算法的原理以及导致非零速区位置估计误差的原因进行分析，并介绍ISFAC算法的实现过程。最后利用RT-Lab平台对传统SFAC算法与ISFAC算法的位置估计性能进行对比验证。摘要 应用于旋转高频电压注入法的自调整轴系幅值收敛（SFAC）电流解调算法简单实用，可实现静止工况下永磁同步电机转子初始位置高精度辨识。但分析发现，由于位置估计误差随转速变化而变化，该算法不适用于非零速区间。为此，提出一种改进型SFAC（ISFAC）电流解调算法。该算法在估计坐标系下对高频电流解调并构造转子位置误差信号，利用正序、负序高频电流相移等值异号的特性实现电流相移自动抵消，不仅省去复杂的位置误差补偿策略，而且将原SFAC算法的速度适用范围由零速区拓宽至非零速区。该文对SFAC算法的原理以及导致非零速区位置估计误差的原因进行分析，并介绍ISFAC算法的实现过程。最后利用RT-Lab平台对传统SFAC算法与ISFAC算法的位置估计性能进行对比验证。
关键词：永磁同步电机 旋转高频电压注入法 电流解调 自调整轴系幅值收敛 无位置传感器控制
近年来，永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）无位置传感器控制技术由于具有成本低、实现简单以及可靠性高等优点，成为了众多学者青睐的研究课题[1-5]。按照转子速度划分，电机的运行工况可分为零低速以及中高速两种[6-7]。目前，在零低速运行工况下，旋转高频电压注入法是最常用的转子位置估计方法之一[8-10]。
旋转高频电压注入法的位置估计过程通常包含三个环节，即旋转电压注入、高频电流解调以及转子位置估计。现有文献为了获得更优的位置估计性能，不同程度地对上述三个环节进行优化。在电压注入方面，文献[8, 11]对电压注入形式进行改进，首次提出在ab 坐标中注入脉振高频电压信号，相比旋转电压信号注入，该算法的电流解调过程简单并且位置估计精度较高，严格说该算法已属于脉振高频电压注入的范畴。在位置估计方面，现有文献更加关注位置观测器的动态位置辨识性能，如文献[12-13]设计了一种零相位滞后跟踪观测器，与常用的锁相环（Phase Locked Loop, PLL）相比，该观测器利用电磁转矩反馈实现位置估计零延迟，提高了位置估计系统的快速性与稳定性[14-15]。
对于电流解调过程，其实质是对高频响应电流进行解调最终构造得到转子位置误差信号，电流解调算法的优劣将直接决定位置估计的精度以及算法复杂度。传统旋转高频电压注入法的电流解调过程采用同步轴系高通滤波器（Synchronous Frame High-pass Filter, SFHF）算法实现[16-17]。但是，受到滤波器相移和数字控制延时等因素的影响，SFHF算法容易产生位置估计误差[18-20]。文献[18]分析了不同因素对位置估计精度的影响，并提出一种统一补偿算法，实现了转子初始位置高精度辨识。但该算法应用于非零速区时容易产生较大误差[19]。文献[19]对文献[18]进行改进，在旋转坐标系对高频电流进行解调，从而消除滤波器以及转子转速等因素对位置误差的影响。但该算法为了利用正序电流的相位延迟抵消负序电流的相位延迟，需要应用两次同步轴系旋转变换以及多个滤波器分别提取正序电流与负序电流，电流解调过程较为复杂。文献[20]提出一种基于自调整轴系幅值收敛（Self-adjusting Frame Amplitude Convergence, SFAC）的电流解调算法，该算法无需区分正序电流与负序电流，仅需一次同步轴系旋转变换即实现了转子初始位置高精度辨识，不仅简化了电流解调过程，而且提高了算法的工程实践适用性。
但分析发现，当转子速度不为零时，SFAC算法的位置估计误差随转速变化而改变，难以应用于非零速区。为此，提出一种改进型SFAC（Improved SFAC, ISFAC）电流解调算法。该算法在虚拟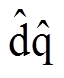坐标系下对高频电流解调并构造转子位置误差信号，然后利用正、负序高频电流相移等值异号的特性实现电流相移自动抵消，不仅消除了转速变化对位置估计精度的影响，而且将原SFAC算法的速度适用范围由零速区拓宽至非零速区。全文对传统SFAC电流解调算法的原理以及导致非零速区位置估计误差的原因进行分析，并介绍了ISFAC的实现过程，最后利用RT-Lab平台对传统SFAC算法与ISFAC算法的位置估计性能进行对比验证。
通常，为了简化分析过程，建立PMSM高频激励电压方程时作以下两个忽略：①由于注入的高频电压角频率wh远高于电机旋转角频率we，绕组中自感感抗远大于定子电阻Rs，可忽略电阻的影响； ②该方法使用于零速或低速区，可忽略电压方程中的交叉耦合项weLd和weLq以及感应电动势项weyf。此时，PMSM高频激励模型可等效为纯电感模型，d、q坐标系下电动机的电压方程可表示[5]为
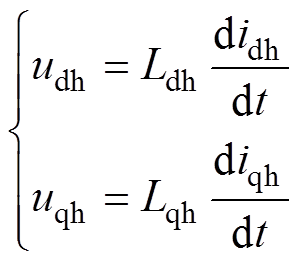（1）式中，udh和uqh分别为d、q轴的高频电压；idh和iqh分别为d、q轴的高频电流；Ldh和Lqh分别为d、q轴的高频电感。
旋转高频电压注入法的基本原理是在ab 坐标系注入一个彼此正交的高频电压激励，使电动机定子产生高频电流响应，再利用特殊的信号处理手段从中提取转子位置信息[8-10]，其原理如图1所示。实际应用时注入的高频电压可表示为
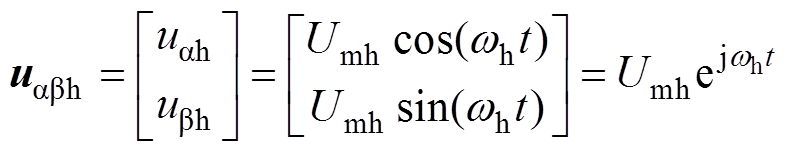（2）式中，Umh、wh分别为注入高频电压的幅值与角频率。
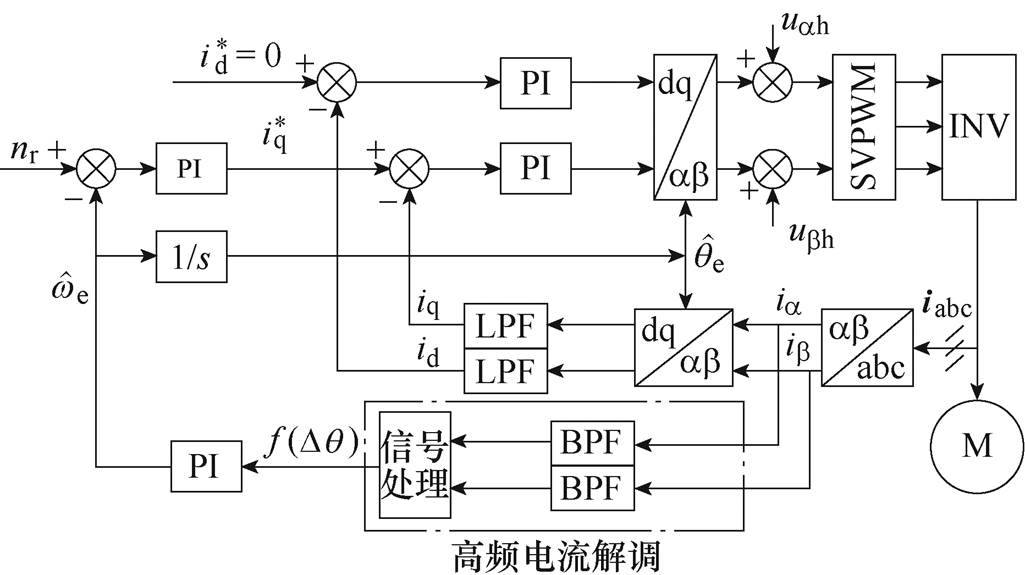
图1 旋转高频电压注入法位置估计原理
Fig.1 Block diagram of position estimation based on rotating high-frequency voltage injection method
将式（2）变换至dq坐标系中，然后代入式（1），则dq坐标系中的高频电流响应可表示[21]为
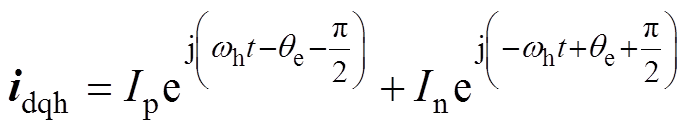（3）式中，通常将角频率等于wh与-wh的电流成分分别称为正序与负序高频电流，且Ip与In分别代表正序、负序高频电流幅值，即
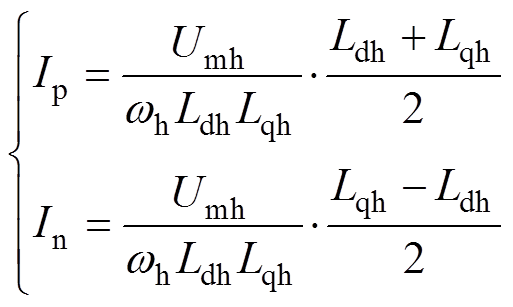（4）
对式（3）进行反Park变换，得到ab 坐标系下的高频电流响应，即
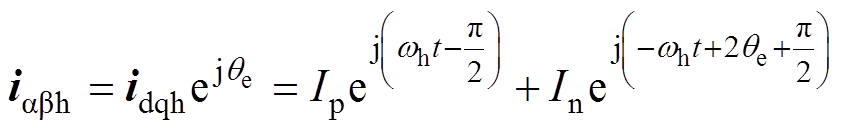（5）由式（4）可知，ab 坐标系下负序高频电流中包含转子位置信息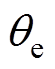
。传统旋转高频电压注入法采用SFHF算法提取负序电流并进行解调，其具体实现过程如图2所示[22]。图中，利用带通滤波器（Band Pass Filter, BPF）提取高频电流，并利用同步轴系变换使正序电流变成直流成分，负序电流变成频率为-2wh的高频成分，然后借助高通滤波器（High Pass Filter, HPF）分离负序电流，最后采用同步轴系变换得到含有转子位置信息的电流成分。图3为利用外差法构建转子位置误差信号f(Dq)的原理。外差法的数学实现原理为
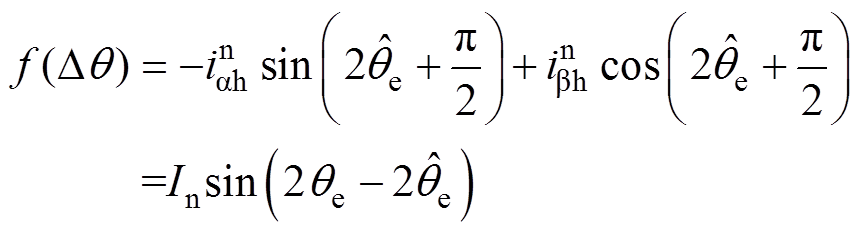（6）式中，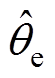
为转子位置的估计值；
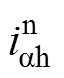为a 轴负序高频电流；
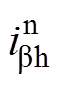为b 轴负序高频电流。获得转子位置误差信号后，利用PI调节器将其调节至零获得估计转速
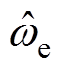，对估计转速积分后得到转子位置的估计值[21]。
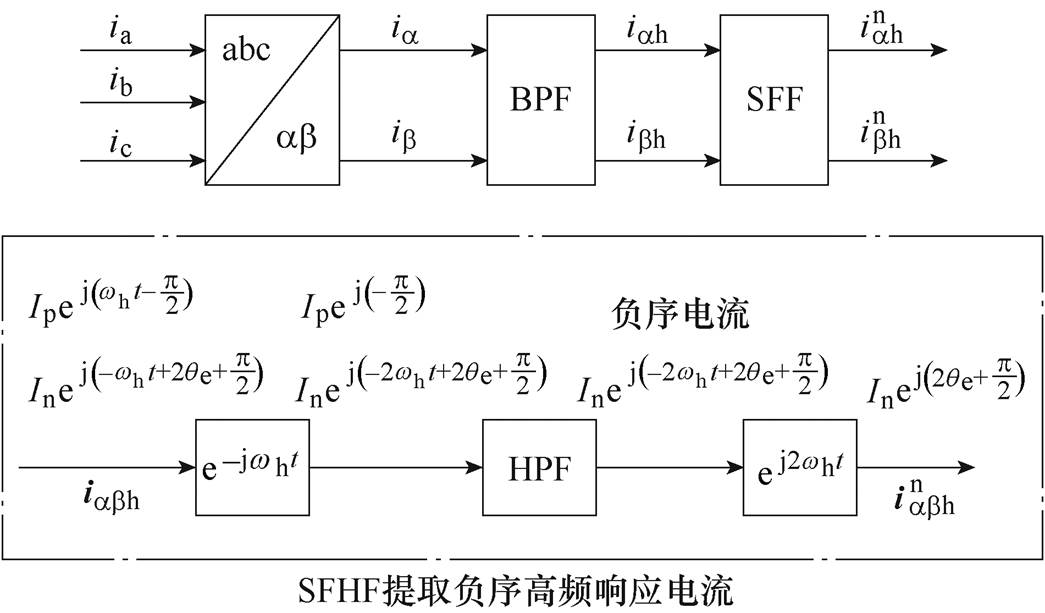
图2 基于SFHF算法的高频电流解调过程
Fig.2 HF Current demodulation based on SFHF algorithm
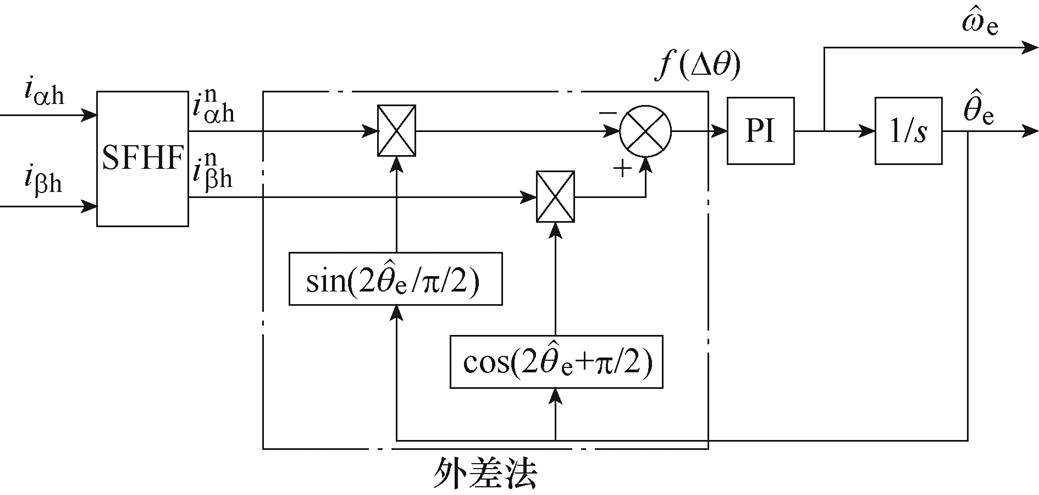
图3 基于外差法的位置误差信号构造原理
Fig.3 Block diagram of position error signal construction based on heterodyne method
旋转高频电压注入法需从负序高频电流的相位中提取转子位置信息。然而，受到高频模型建模简化、BPF以及PI电流调节器等非理想因素的影响，高频电流的相位容易发生偏移，从而产生位置估计误差[18-22]。
2.1.1 高频模型建模简化产生的相移
第1节中对PMSM高频模型建模时，忽略了定子电阻及感应电动势的影响。文献[22]详细推导了考虑定子电阻以及感应电动势后的高频电流响应表达式，指出定子电阻是造成高频电流相移的主要原因，并对理论分析结论进行了仿真验证。定子电阻对正、负序高频电流产生的相移可分别表示[22]为
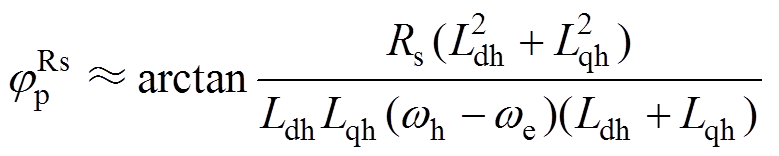（7）
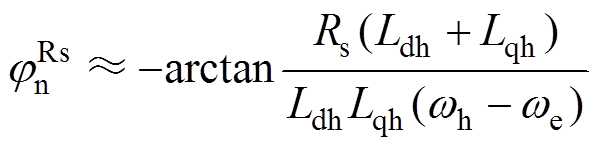（8）
根据式（6）与式（7），利用数值仿真计算不同转速下的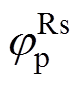
与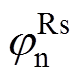
，计算结果如图4所示。仿真时高频电压信号频率为300Hz，电动机参数见表4。由图4可知，定子电阻对正、负序高频电流产生的相移与转速基本无关，二者平均值分别为0.8°与1.5°（绝对值）。
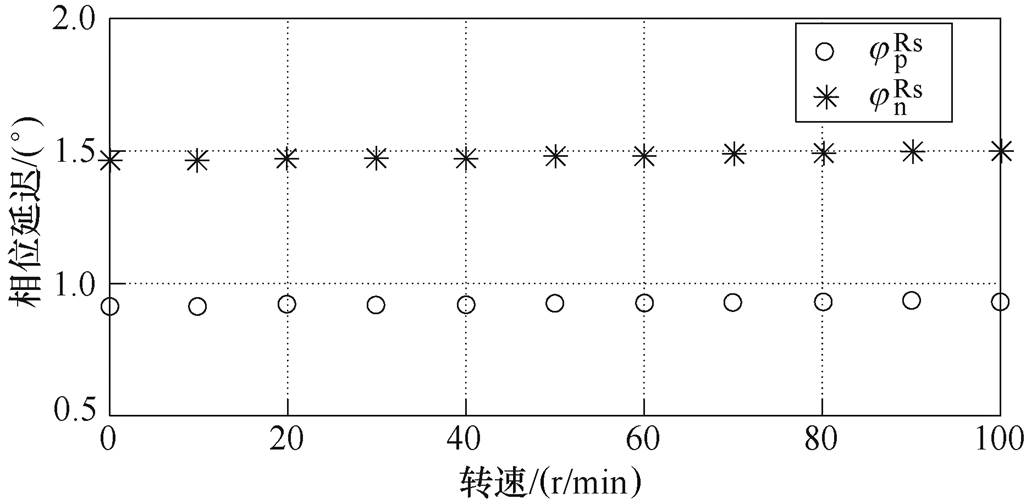
图4 不同转速下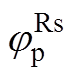
与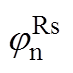
数值计算结果（绝对值）
Fig.4 Numerical calculation results (absolute) of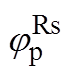 
and 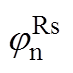under various speed
2.1.2 BPF产生的相移
高频电流需要利用BPF提取，其对不同频率的信号将产生不同的相移，记BPF对正、负序高频电流产生的相移分别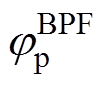
与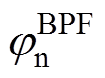
。图5代表2阶巴特沃斯BPF的频率特性仿真结果，仿真时设置采样频率为10kHz，中心频率为300Hz。
图5显示BPF对±300Hz高频信号产生的频率为±4.6°。显然，BPF产生的相移具有奇函数特性，其对频率等值异号的交流信号将产生等值异号的相位延迟。
2.1.3 PI电流调节器产生的相移
在PMSM矢量控制系统中，电流环的传递函数简化结构如图6所示。根据图6，注入高频电压到高频响应电流之间的传递函数[23]可表示为
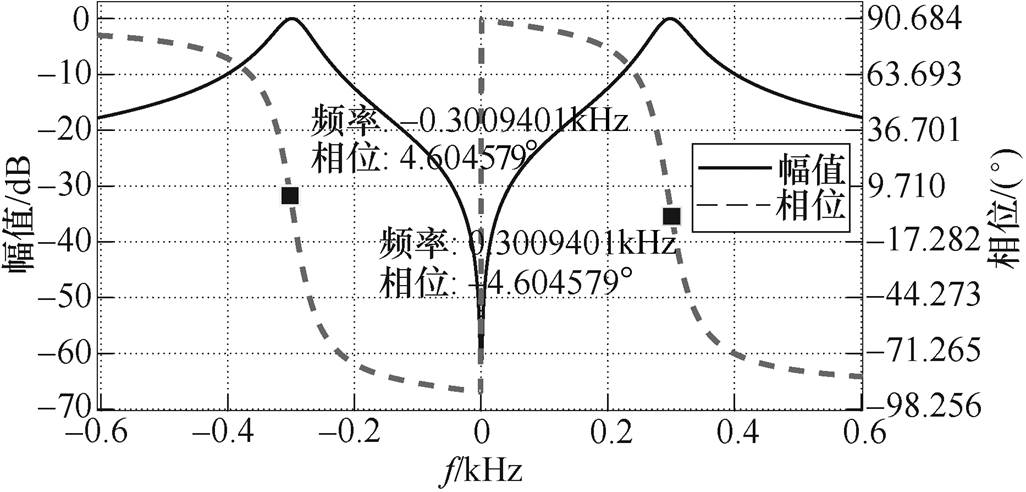
图5 二阶巴特沃斯带通滤波器频率特性
Fig.5 Frequency characteristics of second-order Butterworth band-pass filter
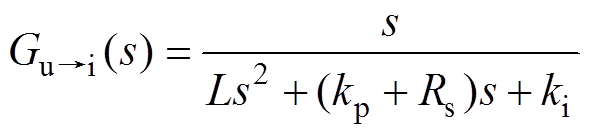（9）式中，L、Rs分别为电动机电感、定子电阻；kp、ki分别为比例积分调节器的比例、积分系数。
将s=jw 代入式（9）得到相频率性，即
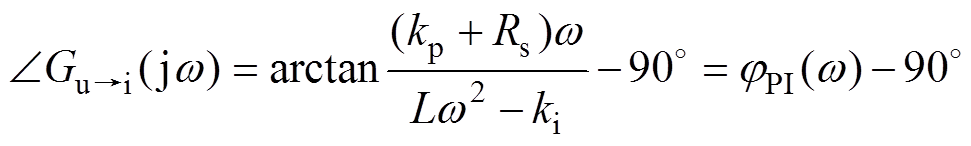（10）式中，jPI为PI调节器引起相位偏移。文献[23]指出，jPI使高频响应电流与注入的高频电压不完全正交，从而产生位置估计误差。记PI对正、负序高频电流产生的相移分别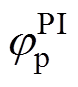
与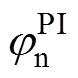
。显然，PI电流调节器产生的相移同样具有奇函数特性，其对频率等值异号的交流信号将产生等值异号的相移。
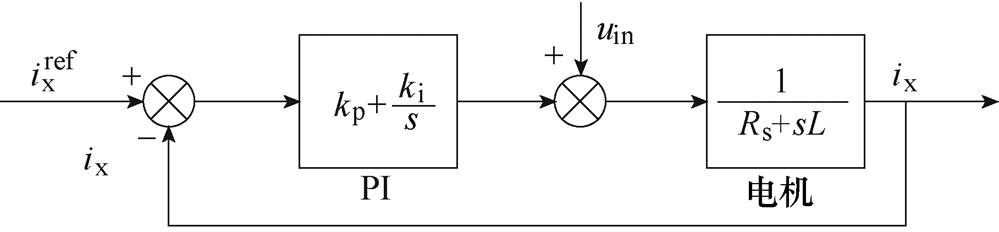
图6 电流环传递函数结构
Fig.6 Structure of current loop transfer function
综上，令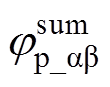
和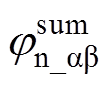
分别代表不同非理想因素对ab 坐标系中正、负序高频电流产生的总相移，则相移
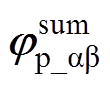和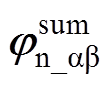
可分别表示为
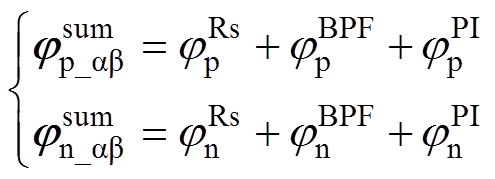（11）考虑到高频电流幅值Ip与In与转子位置无关，可依然采用与未考虑相移时一致的描述方式。那么，考虑相移后ab 坐标系下的高频电流响应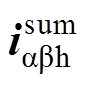
可表示为
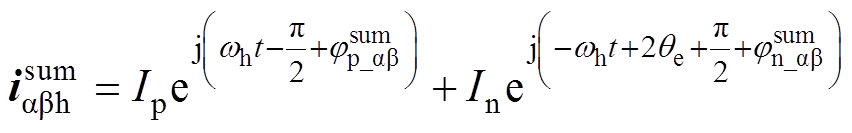（12）根据式（12）的负序高频电流表达式，考虑非理想因素后，基于SFHF电流解调算法的位置误差信号及位置估计误差分别为
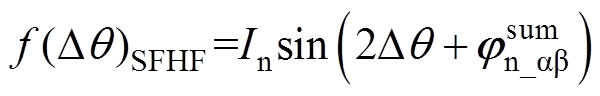（13）
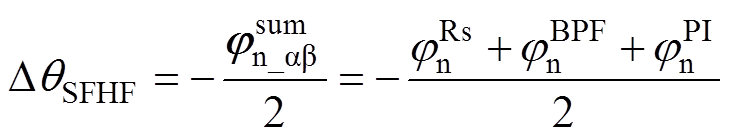（14）
可见，2.1节介绍的三种非理想因素均对SFHF电流解调算法的位置估计精度产生影响。此外，ab坐标系下负序高频电流的频率为-wh+2we，电流频率与转子电角速度we相关[22]。当we≠0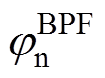，与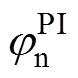均具有转速敏感性，使电流相移随转速改变而改变，SFHF电流解调算法的位置估计误差将随转速变化而变化。
为克服SFHF电流解调算法的不足，文献[20]提出SFAC电流解调算法，该算法不仅简化了电流解调过程，而且实现了零转速工况下转子初始位置的高精度估计。但分析发现，当转子速度不为零时，SFAC算法的位置估计误差同样随转速变化而改变，难以应用于非零速区。为此，本文提出一种ISFAC电流解调算法，力求克服转速对位置估计精度的影响，将原SFAC算法的速度适用范围由零速区拓宽至非零速区。
SFAC算法在ab 坐标系下同时利用正、负序高频电流构造位置误差信号，其原理如图7所示。
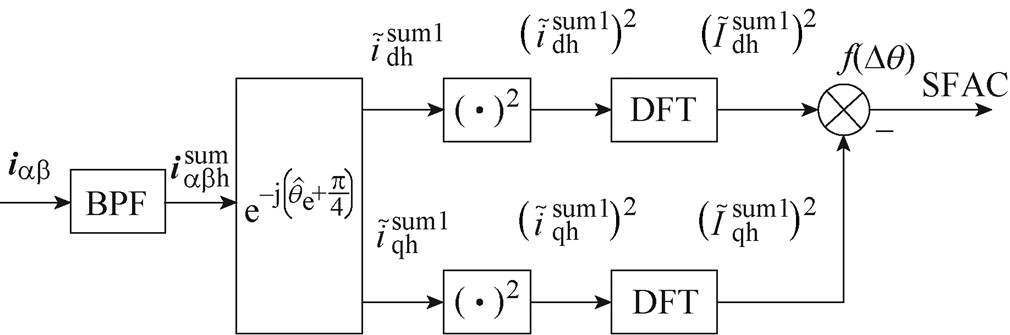
图7 基于SFAC电流解调算法的位置误差信号构造原理
Fig.7 Block diagram of position error signal construction based on SFAC current demodulation algorithm
SFAC算法的位置误差信号构造过程包含以下两个步骤：
（1）电流坐标变换。图8为各坐标系相位关系，图中，ab 代表静止坐标系、dq代表真实转子同步坐标系、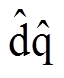代表估计转子同步坐标系；qe、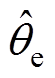分别为两个坐标系距离a 轴的角度。SFAC电流解调算法将ab 坐标系的高频电流变换至超前于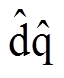坐标系p/4电角度的坐标系中，在此用
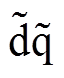表示。考虑非线性因素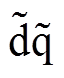，坐标系高频电流的标量形式为
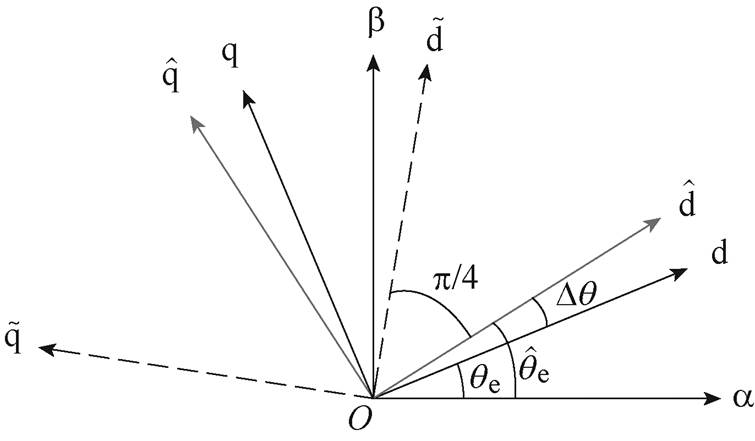
图8 不同坐标的相位关系
Fig.8 Phase relationship of different frames
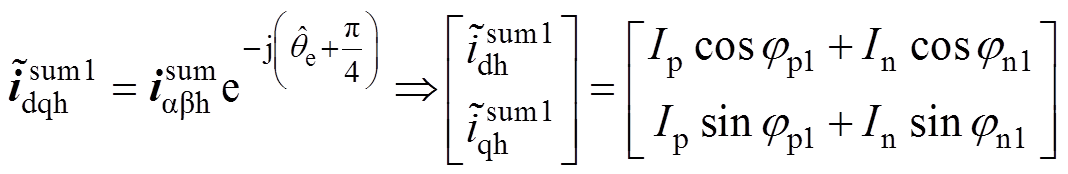（15）其中
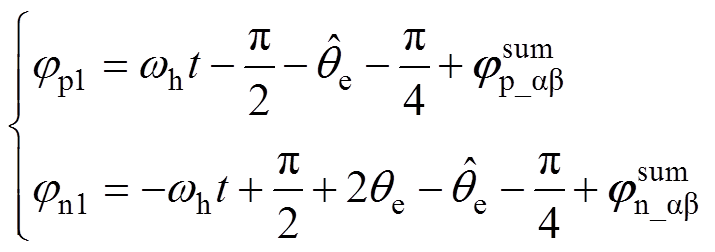（16）
式中，jp1与jn1分别为正序、负序电流的相位。
利用三角函数辅助角公式对式（15）进行化简，可得
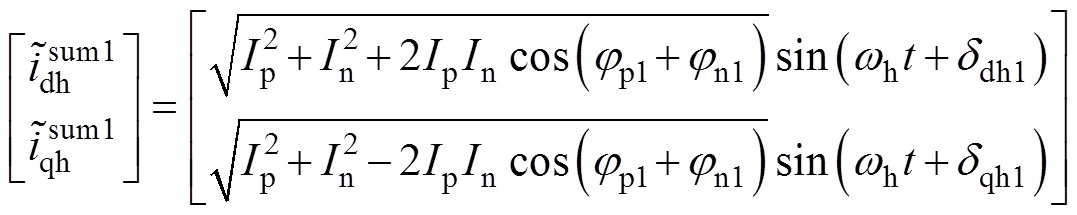（17）式中，ddh1、dqh1与Ip、In、jp1、jn1相关但与转子位置无关，在此没有给出详细表达式。
（2）提取高频电流幅值并构造位置误差信号。文献[20]利用递推离散傅里叶变换（Discrete Fourier Transform, DFT）提取式（17）电流幅值的二次方值，然后作差得到位置估计误差信号，即
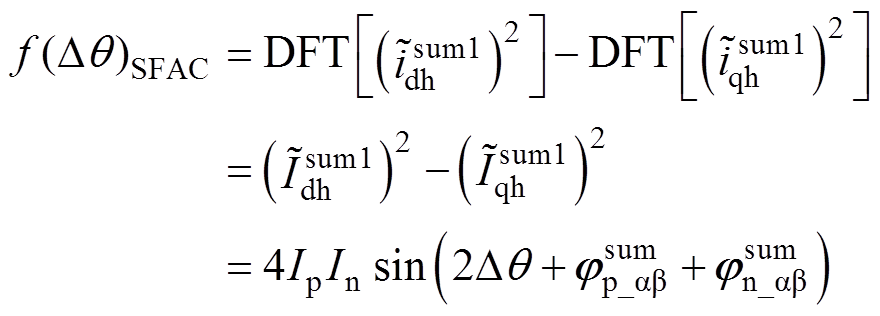（18）由式（18）可知，SFAC电流解调算法的位置估计误差可表示为
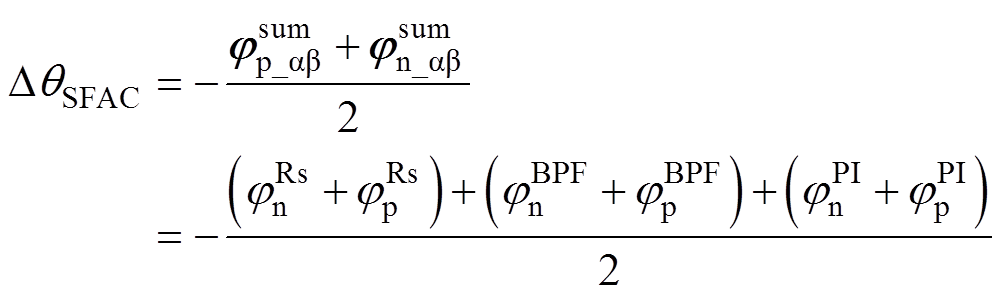（19）可见，SFAC算法的位置估计误差与正、负序高频电流相移之和相关，根据2.1节非理想因素引起的电流相移规律，其位置估计误差具有如下特性：
（1）根据图4可知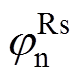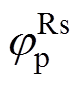，(+)/2≈0，说明高频模型建模简化引起的相移对SFAC算法位置估计误差的影响几乎可以忽略。
（2）BPF与PI引起的相移对位置估计误差的影响需分两种工况讨论。SFAC算法利用ab 坐标系的高频电流iah与ibh构造位置误差信号，根据式（4），当we=0时，正、负序高频电流频率为wh与-wh，二者具有等值异号关系，考虑到BPF与PI对交流信号产生的相移具有奇函数特性，此时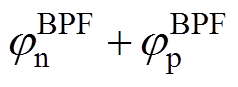
与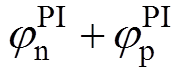
均等于0，因此SFAC算法在零转速工况下的位置估计误差较小，该结论与文献[20]的理论分析与实验结果相吻合；当we≠0时，正序高频电流的频率依然为wh，但负序高频电流的频率-wh+2we随转速改变而改变，此时
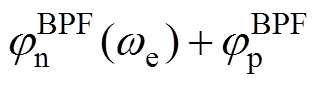与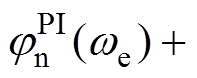
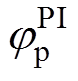均不等于0，SFAC算法的位置估计误差具有转速敏感性。为了更清楚地描述，ab 坐标系下非理想因素引起的电流相移规律见表1。
表1 ab坐标系下非理想因素引起的电流相移规律
Tab.1 Phase delay law of ab-frame caused by non-ideal factors
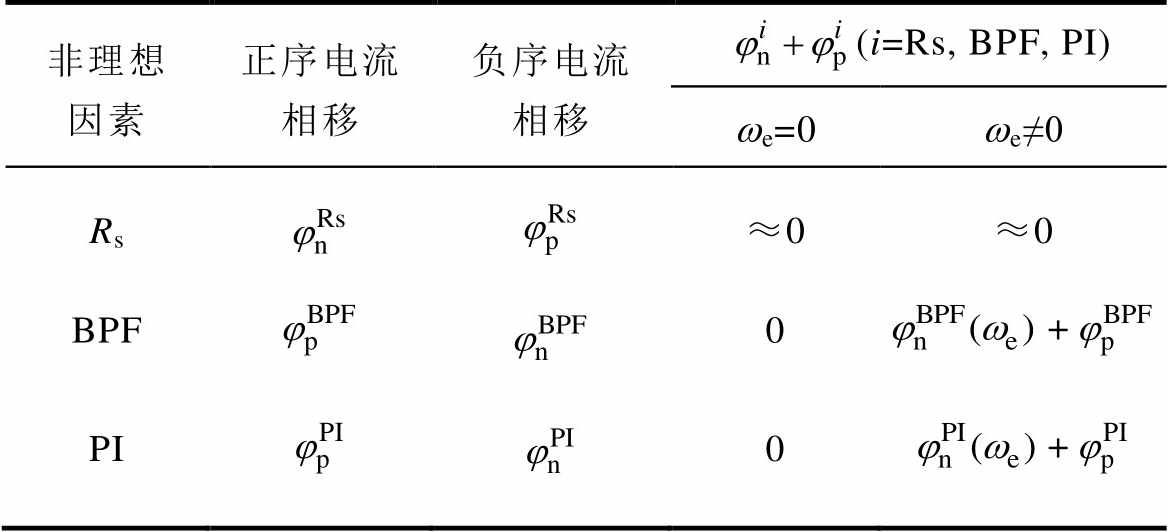
非理想因素正序电流相移负序电流相移(i=Rs, BPF, PI) we=0we≠0 Rs≈0≈0 BPF0+ PI0+
综上，SFAC算法的位置估计误差表达式可由式（19）进一步表示为
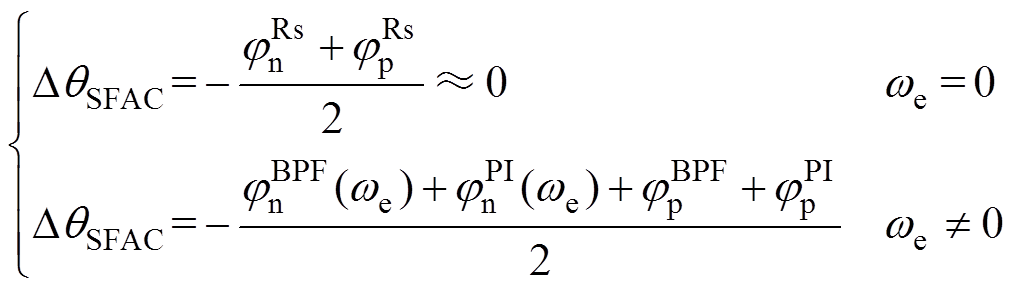（20）图9为SFAC电流解调算法在不同转速工况下的位置估计误差实验结果。由图9可知，当转速为零时，位置误差约为0.5°，而当转速由-200r/min变化至200r/min的非零速期间，位置估计误差在 ±10°以内波动，位置估计误差具有转速敏感性，图9基本验证了式（20）的理论结果。
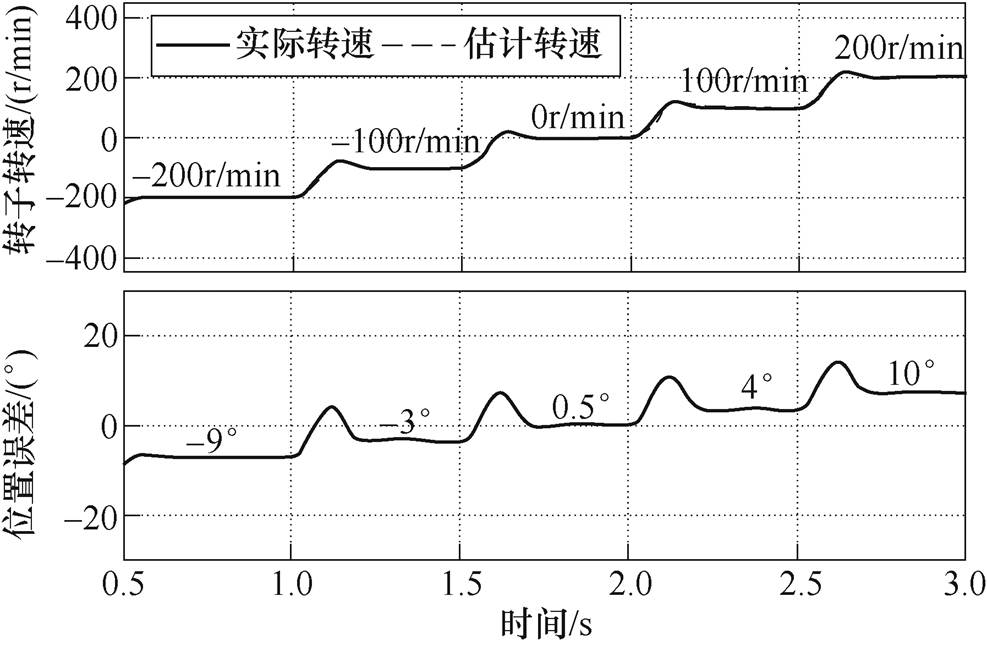
图9 SFAC算法在不同转速工况下的位置估计误差
Fig.9 Position estimation error of SFAC algorithm under various speed condition
由式（3）可知，dq坐标系下正、负序高频电流均含有转子位置信息。但由于真实转子位置未知，实际矢量控制中该坐标系应用估计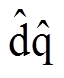坐标系表示。考虑非理想因素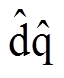，坐标系下的电流可将式（12）所示ab 坐标系的电流经过Park变换得到，即
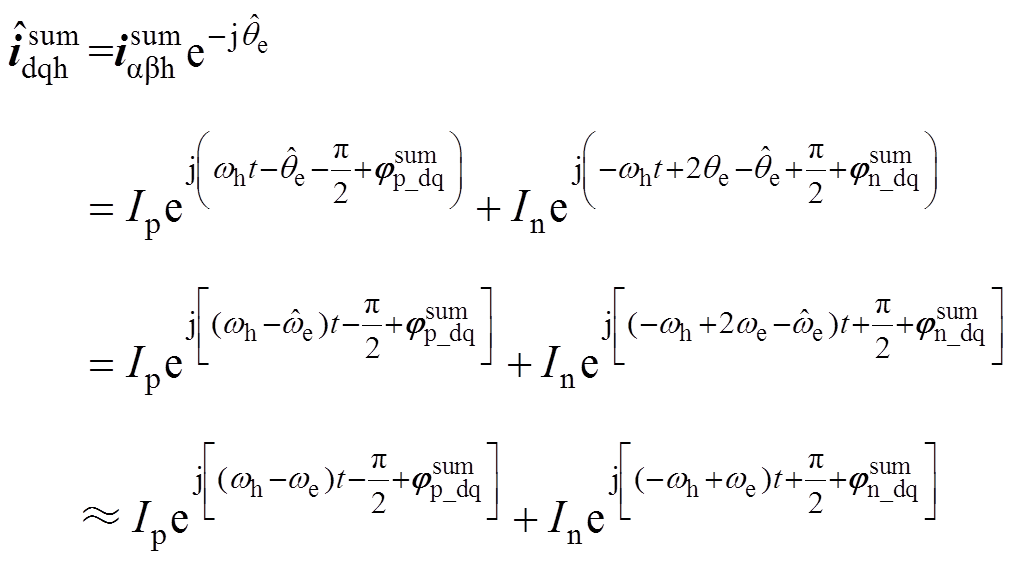（21）将估计与真实的转子位置分别表示为=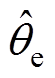
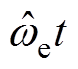、qe=wet。当位置估计过程达到稳态，转子转速估计值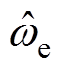与真实值we非常接近，即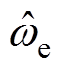≈we。此时，可认为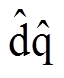坐标系下正、负序高频电流的频率为wh-we与-wh+we，二者具有等值异号关系。
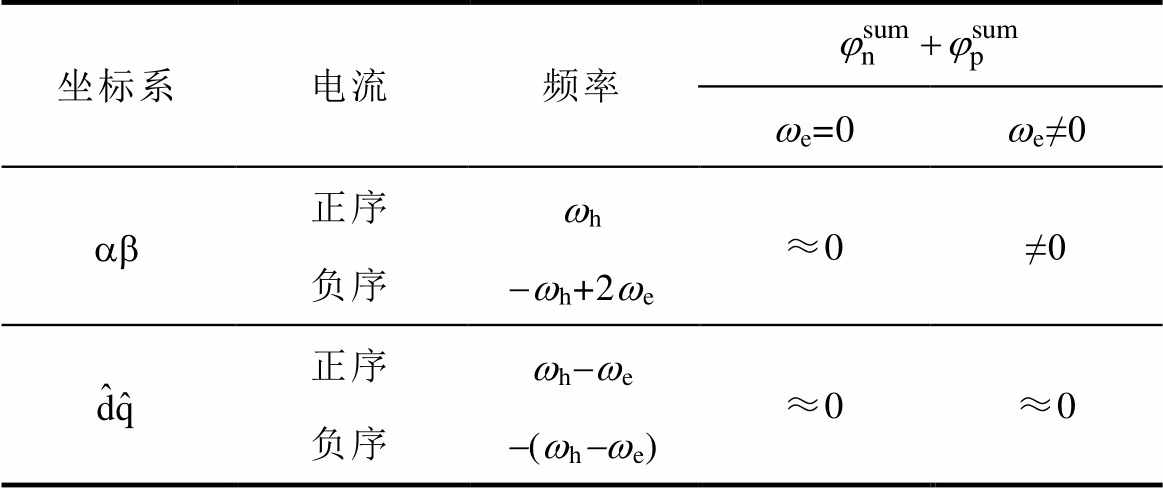
第2.1节指出，BPF及PI对频率等值异号的高频电流将产生等值异号相位延迟。根据此规律，不同坐标系下正、负序高频电流的频率特性及相移关系见表2。表2表明，在ab 坐标系中，当we=0时，正、负序高频电流的频率具有等值异号关系，非理想因素引起的正、负序高频电流的相移之和约等于零；而当we≠0时，该关系不再成立。在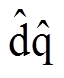坐标系，无论we是否等于零，正、负序高频电流的频率始终具有等值异号关系，非理想因素引起的正、负序高频电流相移之和始终约等于零。
表2 不同坐标系下正序与负序高频电流的频率特性及相移关系
Tab.2 Frequency characteristic and phase difference relationship of positive sequence and negative sequence HF current under various frame
坐标系电流频率 we=0we≠0 ab正序wh≈0≠0 负序-wh+2we 正序wh-we≈0≈0 负序-(wh-we)
为此，ISFAC算法选择在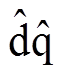
坐标系对高频响应电流进行解调，其位置误差信号构造原理框图如图10所示。对比图7与如图10可知，SFAC算法与ISFAC算法的主要区别在于BPF的施加位置不同，SFAC算法直接在ab 坐标系对iab 进行带通滤波得到高频电流
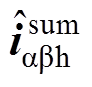，然后对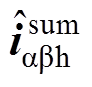处理完成位置误差信号提取；而ISFAC算法在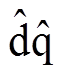坐标系对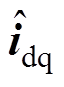
进行带通滤波得到高频电流
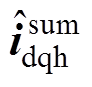，然后对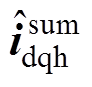处理完成位置误差信号提取。图10中，由iab 到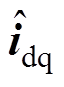的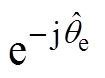
直接借助电流内环的Park变换完成，无需增加额外的运算环节。
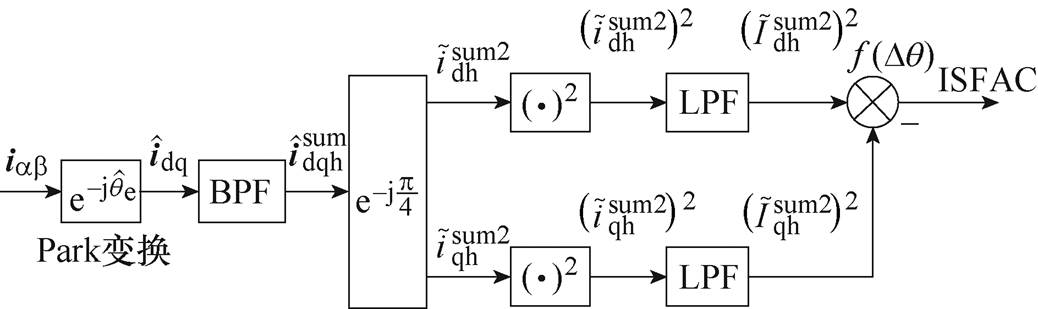
图10 基于ISFAC电流解调算法的位置误差信号构造原理框图
Fig.10 Block diagram of position error signal construction based on ISFAC current demodulation algorithm
ISFAC算法的位置误差信号构造过程包含以下两个步骤：
（1）对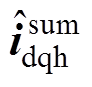变换-p/4。变换后的标量形式为
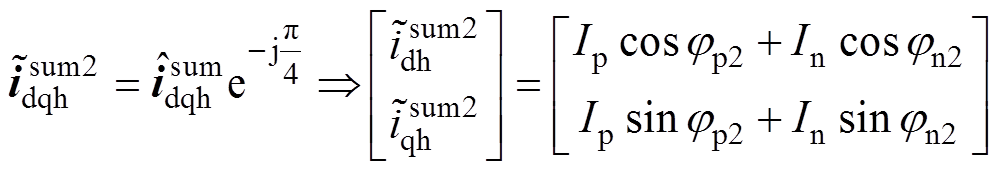（22）
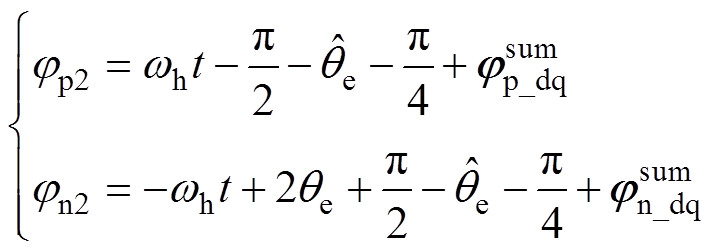（23）
式中，jp2与jn2分别为正序、负序电流的相位。
（2）提取高频电流幅值并构造位置误差信号。与文献[20]不同，本文令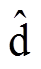
轴与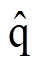
轴的高频电流自乘完成信号调制，然后采用低通滤波器将2wh高频成分直接滤除，最后将得到的低频分量作差得到位置估计误差信号，即
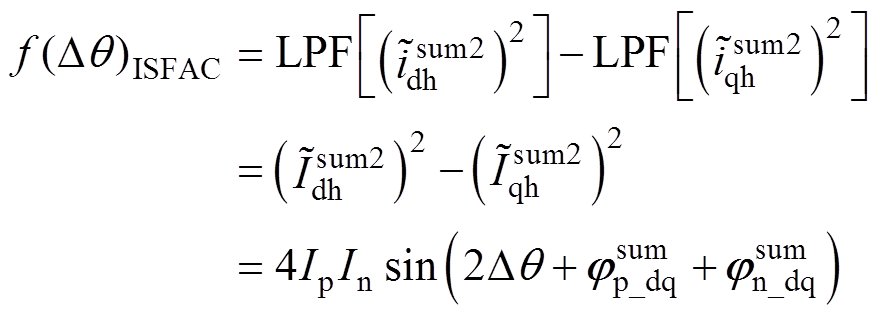（24）ISFAC电流解调算法的位置估计误差为
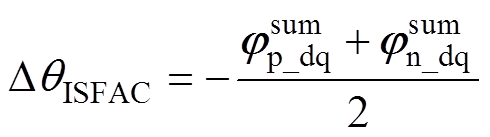（全转速） （25）
图11为ISFAC电流解调算法在不同转速工况下的位置估计误差实验结果，可见，在不同非零速工况位置估计误差的稳态值均在±2°以内，说明ISFAC算法的位置估计误差基本与转速无关。SFAC算法改进前后的转速适用区间见表3。
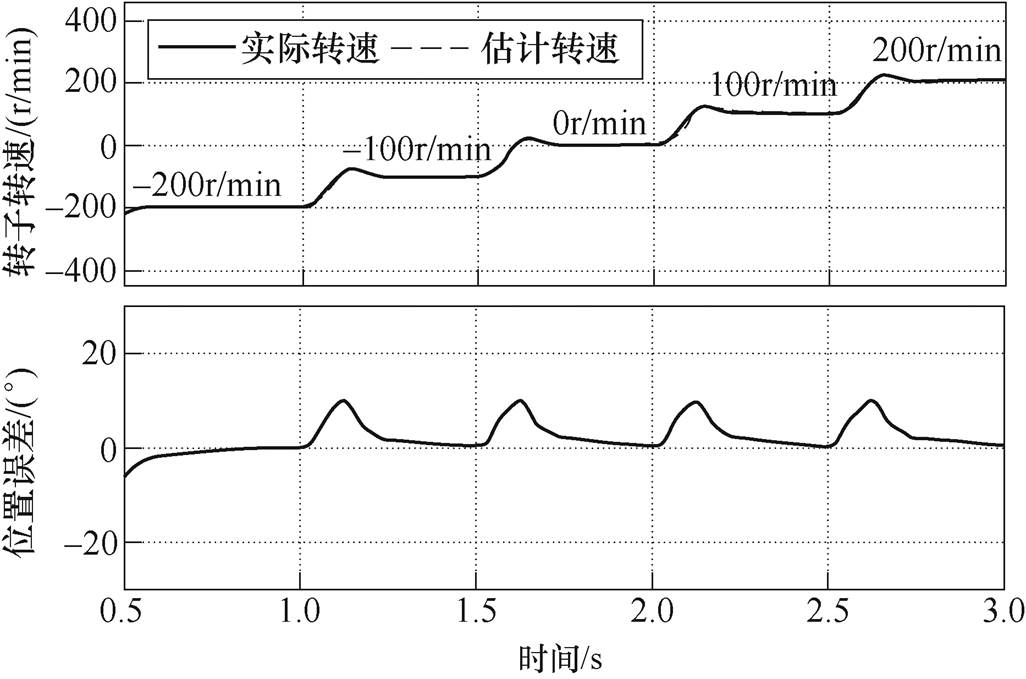
图11 ISFAC算法在不同转速工况下的位置误差
Fig.11 Position error of ISFAC algorithm under various speed condition
表3 SFAC算法改进前后的转速适用范围
Tab.3 Applicable speed range of SFAC algorithm before and after improvement
算法坐标系转速适用性 SFACab零速√ 非零速× ISFAC零速√ 非零速√
图12为基于SFAC与ISFAC电流解调算法的旋转高频电压注入法详细原理框图。可知，ISFAC算法将SFAC算法的电流解调过程由ab 坐标系转移至估计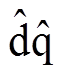坐标系，并利用LPF对高频电流的幅值进行提取，其揭示了SFAC算法在非零速区转子位置估计精度不高的本质原因，并消除了转子转速对位置估计精度的影响，将SFAC算法的转速适用范围由零速区扩展至非零速区。
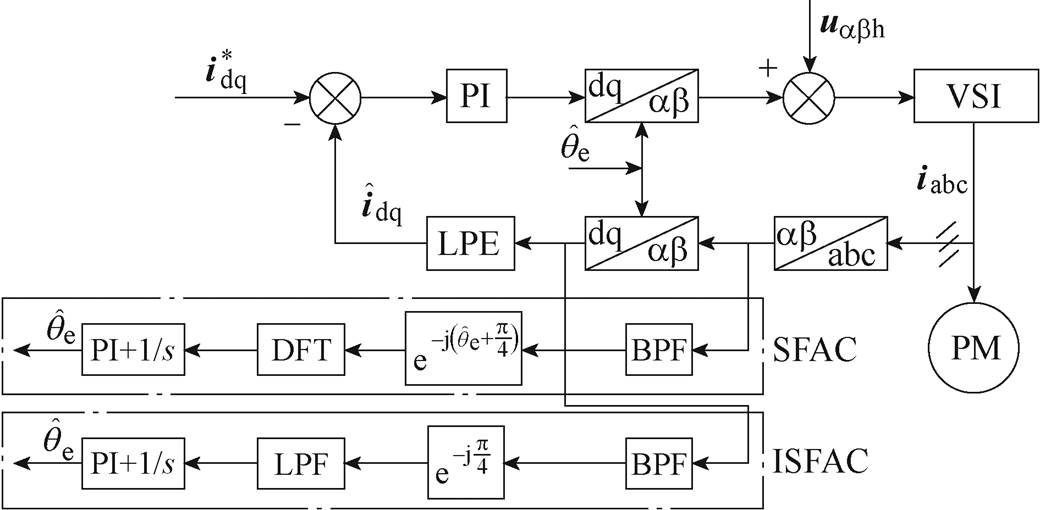
图12 基于SFAC与ISFAC电流解调算法的旋转高频电压注入法原理框图
Fig.12 Block block diagram of rotating high-frequency voltage injection method based on SFAC and ISFAC current demodulation algorithm
在图13所示的实验平台验证本文所提方法的可行性。实验时控制器完成采样及脉冲计算，电动机及逆变器主电路由实时仿真平台模拟。对于数字信号处理器（Digital Signal Processor, DSP）内部的转子位置、转速和二维坐标系下的电流信号，采用先将数据实时保存在随机存取存储器（Random Access Memory, RAM）中，停机之后再将数据导出的方式进行采集，最后采用Matlab完成数据处理。实验用电机参数见表4，开关频率为5kHz，电流采样与控制频率为10kHz。此外，高频电压的注入频率为300Hz，幅值为75V。
图13 RT-Lab实验平台
Fig.13 RT-Lab experimental platform
表4 永磁同步电机参数
Tab.4 Parameters of PMSM
参 数数 值 相数m3 极对数np2 额定转速/(r/min)2 255 额定电压/V550 额定功率/kW180 直轴电感Ld/mH2.21 交轴电感Lq/mH6.62 定子绕组电阻Rs/W0.039 永磁体磁链yf/Wb0.95
图14为转子初始位置估计实验结果。
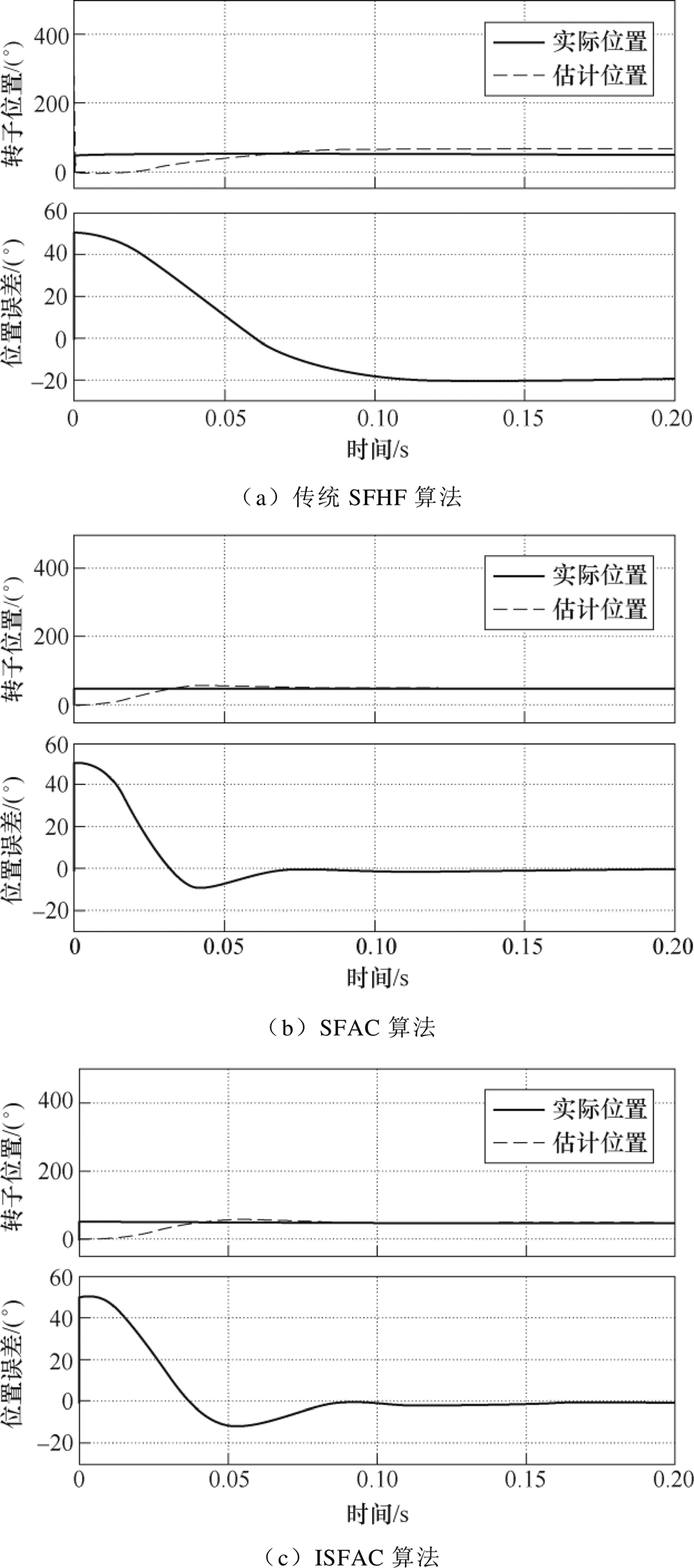
图14 转子初始位置估计实验结果
Fig.14 Experiment results of rotor initial position estimation
由图14a可以看出，传统SFHF电流解调策略受到诸多因素的影响，转子初始位置估计误差较大，稳态时约为-20°；图14b中，由于电机转速为零，原SFAC算法具有较高精度的初始位置估计效果，位置估计误差约为2°，该结论与文献[20]的实验结果基本一致；由图14c可知，ISFAC同样具有较高精度初始转子位置估计结果，保持了原SFAC算法的优点。
图15为转速突变工况位置估计性能验证结果，转速变化情况为+200～(200+200)r/min。由图15a可以看出，当转子转速不为零时，原SFAC算法对应的转子位置估计误差随转速变化而改变，在±200r/min转速工况下稳态位置误差分别为±9°；而由图15b可知，±200r/min转速工况下ISFAC算法的稳态位置误差保持在±2°以内。此外，在加速过程中，ISFAC算法的动态位置估计误差也显著小于SFAC算法，前者最大误差为5°（绝对值），后者最大误差为16°（绝对值）。实验结果证明，ISFAC电流解调算法消除了转速变化对位置估计精度的影响，将原SFAC算法的速度适用范围由零速区拓宽至非零速区。
图15 转速突变工况位置估计性能验证
Fig.15 Validation of position estimation performance under step speed condition
图16为不同坐标系下正、负序高频电流的频率分布。对于正序电流，其在ab 坐标系中的起始频率为wh，经过Park变换至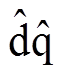坐标系，其终止频率为wh-we；对于负序电流，其在ab 坐标系中的起始频率为-wh+2we，经过Park变换至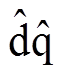坐标系，其终止频率为-wh+we。可见，经过Park变换，估计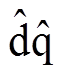坐标系下正、负序高频电流的频率具有等值异号关系。
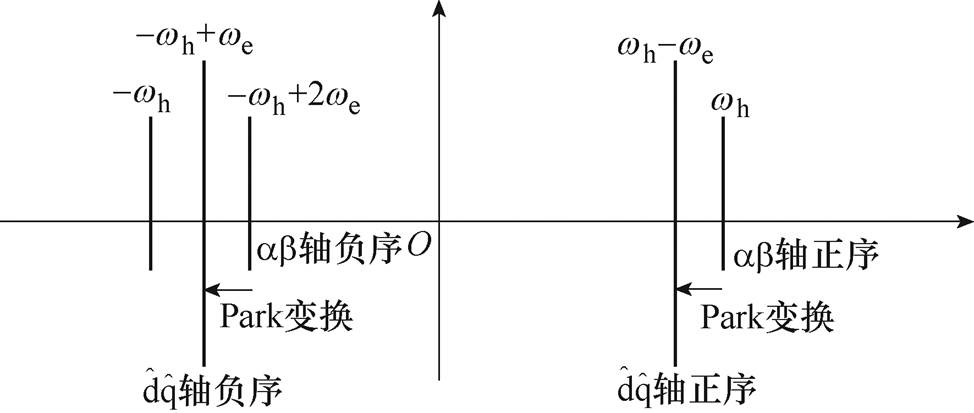
图16 不同坐标系下高频电流频率分布
Fig.16 Frequency distribution diagram of high-frequency current in different frames
为验证图16的分析结果，对a 轴及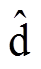轴中的高频电流
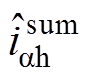与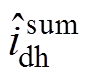
进行频谱分析，其结果如图17所示。图17中，电动机处于200r/min稳态工况。由图17a可以看出，a 轴高频电流的幅值发生正弦调制现象，频率为2倍电基频（2fe=13.34Hz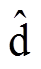），轴高频电流为标准正弦波。进一步地，从图17b展示的高频电流频谱分析结果可知，a 轴中正、负序高频电流的频率分别为300Hz与-286.7Hz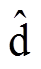；轴中正、负序高频电流的频率具有等值异号关系，分别为±293.3Hz。需要说明的是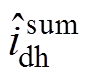，的频谱分析仅看到一个波峰，这是因为负频率的交流量实际上可表示为正频率的交流量，如sin(-wt)=-sin(wt)与cos(-wt)= cos(wt)，负序高频电流与正序高频电流同频，二者频谱分析结果产生累加，其峰值等于a 轴中正、负序高频电流峰值之和。可见，图17的实验结果验证了图16的理论分析。
图18为转矩阶跃工况下位置估计性能验证实验结果，T1瞬间负载转矩由空载阶跃至100N·m；T2瞬间负载转矩由100N·m阶跃至300N·m；T3瞬间负载转矩由300N·m阶跃至空载。由实验结果可以看出，在转矩突变瞬间SFAC与ISFAC算法的位置估计误差的阶跃量基本一致，说明对SFAC改进后ISFAC算法依然保持较强的抗负载转矩扰动能力；然而，SFAC算法产生9°的稳态位置估计误差，而ISFAC算法的稳态位置估计误差依然在±2°以内。
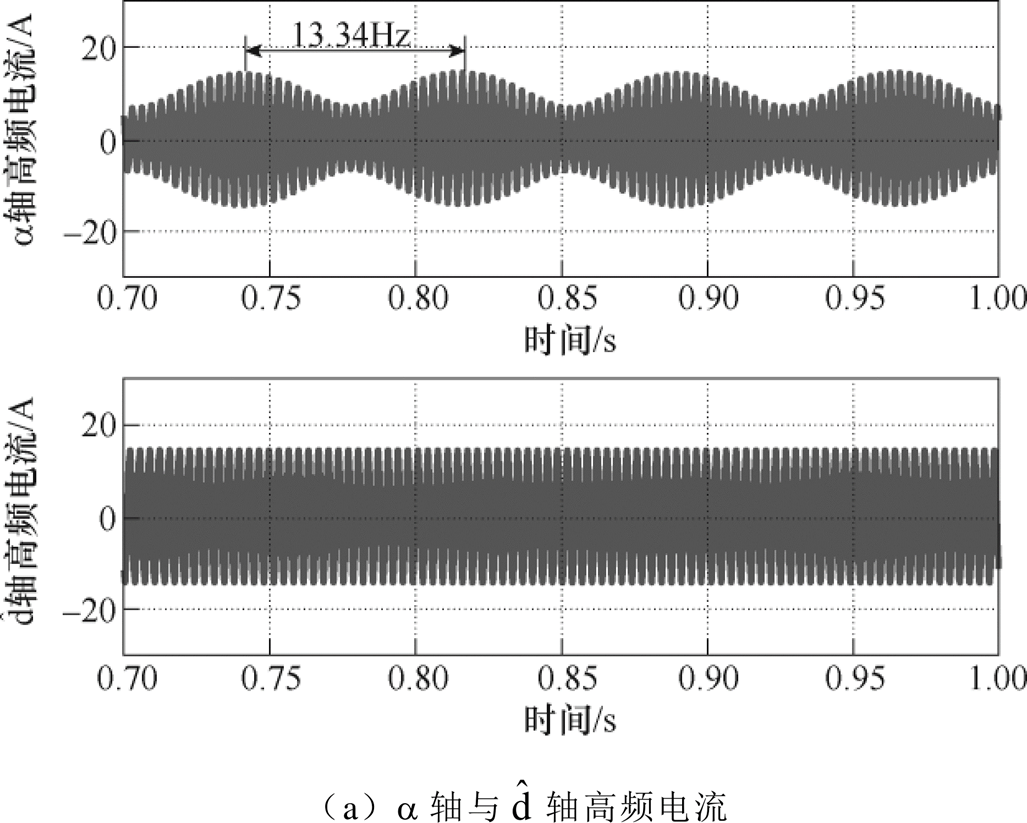
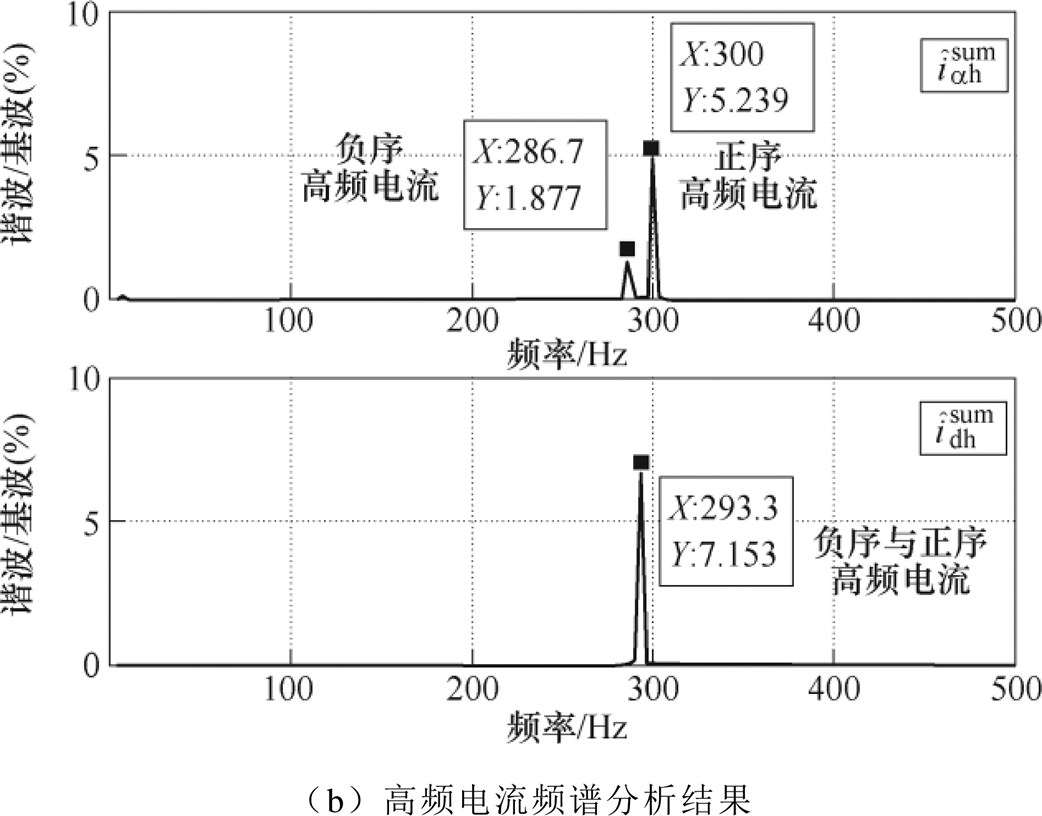
图17 200r/min工况下高频电流及频谱分析结果
Fig.17 Results of HF current and spectrum under 200r/min condition
图18 负载转矩阶跃工况位置估计实验结果
Fig.18 Experiment result of position estimation under step torque condition
本文介绍了旋转高频电压注入法的位置辨识原理以及SFAC电流解调算法的实现过程。重点分析了SFAC算法在非零速区产生位置估计误差的原因，然后提出了一种改进型的SFAC（ISFAC）电流解调算法，并利用RT-Lab平台所提算法进行实验验证。理论分析与实验结果说明，当we≠0时，ab 坐标系中正序、负序高频电流频率不满足等值异号的条件，而估计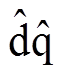坐标系中的则满足要求；并且SFAC算法的位置估计误差随转速变化而变化，而ISFAC算法的位置估计误差始终与转速无关。ISFAC算法消除了转速变化对位置估计精度的影响，不仅省去了复杂的位置误差补偿策略，而且将原SFAC算法的速度适用范围由零速区拓宽至非零速区，一定程度改善了旋转高频电压注入法的位置辨识性能。
参考文献
[1] Liang Donglai, Li Jian, Qu Ronghai, et al. Adaptive second-order sliding-mode observer for PMSM sensor- less control considering VSI nonlinearity[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 420-429.
[2] Ni Ronggang, Xu Dianguo, Wang Gaolin, et al. Efficiency enhancement of general AC drive system by remanufacturing induction motor with interior permanent-magnet rotor[J]. IEEE Transactions on Industrial Electronics, 2015, 60(2): 808-820.
[3] Song Xinda, Fang Jiancheng, Han Bangcheng, et al. Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error[J]. IEEE Transactions Power Elec- tronics, 2015, 31(2): 1438-1449.
[4] 吴春, 董士帆, 钟德刚, 等. 基于电流过采样的永磁同步电机电压脉冲注入无位置传感器控制[J]. 电工技术学报, 2018, 33(24): 5679-5687.
Wu Chun, Dong Shifan, Zhong Degang, et al. Voltage pulse injection based sensorless control for permanent magnet synchronous machine with current oversampling method[J]. Transactions of China Elec- trotechnical Society, 2018, 33(24): 5679-5687.
[5] 王海兵, 赵荣祥, 汤胜清, 等. 永磁同步电机位置检测偏差对驱动系统性能的影响研究[J]. 电工技术学报, 2018, 33(4): 911-918.
Wang Haibing, Zhao Rongxiang, Tang Shengqing, et al. Research on the influence of the position detection error to the PMSM drive system[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 911-918.
[6] 刘毅, 贺益康, 秦峰, 等. 基于转子凸极跟踪的无位置传感器永磁同步电机矢量控制研究[J]. 中国电机工程学报, 2005, 25(17): 121-126.
Liu Yi, He Yikang, Qin Feng, et al. Investigation of rotor saliency-tracking based sensorless vector control drive for PMSM[J]. Proceedings of the CSEE, 2005, 25(17): 121-126.
[7] Bernardes T, Montagner V F, Gründling H A, et al. Discrete-time sliding mode observer for sensorless vector control of permanent magnet synchronous machine[J]. IEEE Transactions on Industrial Elec- tronics, 2013, 61(4): 1679-1691.
[8] Liu Jiaming, Zhu Zhiqiang. Novel sensorless control strategy with injection of high-frequency pulsating carrier signal into stationary reference frame[J]. IEEE Transactions on Industrial Applications, 2013, 50(4): 2574-2583.
[9] Zhu Zhiqiang, Gong Liming. Investigation of effectiveness of sensorless operation in carrier- signal-injection-based sensorless-control methods[J]. IEEE Transactions on Industrial Electronics, 2010, 58(8): 3431-3439.
[10] Zhang Xing, Li Haoyuan, Yang Shuying, et al. Improved initial rotor position estimation for PMSM drives based on HF pulsating voltage signal injection[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4702-4713.
[11] 吕晓源, 刘刚, 毛琨, 等. 基于虚拟脉振高频注入法的永磁电机初始位置检测[J]. 电工技术学报, 2017, 32(23): 34-41.
Lü Xiaoyuan, Liu Gang, Mao Kun, et al. Initial position detection of permanent magnet motor based on virtual pulsating high-frequency injection method[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 34-41.
[12] Briz F, Degner M W, Garcia P, et al. Comparison of saliency-based sensorless control techniques for AC machines[J]. IEEE Transactions on Industrial Appli- cations, 2004, 40(4): 1107-1115.
[13] Kim H, Lorenz R D. Carrier signal injection based sensorless control methods for IPM synchronous machine drives[C]//39th IEEE Industry Applications Conference, Seattle, 2004, 977-984.
[14] Jansen P L, Lorenz R D. Transducerless position and velocity estimation in induction and salient AC machines[J]. IEEE Transactions on Industry Appli- cations, 1995, 31(2): 240-247.
[15] Raca D, Harke M C, Lorenz R D. Robust magnet polarity estimation for initialization of PM synchronous machines with near-zero saliency[J]. IEEE Transa- ctions on Industry Applications, 2008, 44(4): 1199- 1209.
[16] Liu Jiaming, Zhu Zhiqiang. Sensorless control strategy by square-waveform high-frequency pulsating signal injection into stationary reference frame[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2014, 2(2): 171-180.
[17] Tang Qipeng, Shen Anwen, Luo Xin, et al. IPMSM sensorless control by injecting bidirectional rotating HF carrier signals[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10698-10707.
[18] 杨健, 杨淑英, 李浩源, 等. 基于旋转高频电压注入的永磁同步电机转子初始位置估计方法[J]. 电工技术学报, 2018, 33(15): 3547-3555.
Yang Jian, Yang Shuying, Li Haoyuan, et al. Initial rotor position estimation for IPMSM based on high frequency rotating voltage injection[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3547-3555.
[19] 刘善宏, 杨淑英, 李浩源, 等. 基于旋转坐标系解调的内置式永磁同步电机旋转高频注入法位置观测[J]. 电工技术学报, 2020, 35(4): 709-716.
Liu Shanhong, Yang Shuying, Li Haoyuan, et al. Rotating high frequency signal injection based on interior permanent magnet synchronous motor rotor position estimation with the demodulation imple- mented on the synchronous reference frame[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 709-716.
[20] 李浩源, 张兴, 杨淑英, 等. 基于旋转高频注入的内置式永磁同步电机初始位置检测算法[J]. 电工技术学报, 2018, 33(8): 1724-1731.
Li Haoyuan, Zhang Xing, Yang Shuying, et al. A detecting algorithm for initial position of interior permanent magnet synchronous motor based on rotating high frequency injection[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1724- 1731.
[21] 田士侠. 高频注入法永磁同步电机转子位置检测方法研究[D]. 济南: 山东大学, 2010.
[22] 高健伟. 基于高频注入法的永磁同步电机转子位置估计误差的分析[D]. 济南: 山东大学, 2012.
[23] 孟淑平, 郭宏, 徐金全. 基于基波电流观测器和旋转高频注入法的IPMSM无传感器控制[J]. 航空学报, 2016, 37(4): 1336-1351.
Meng Shuping, Guo Hong, Xu Jinquan. A new sensorless control strategy combing a fundamental current observer with rotating high-frequency voltage injection method for interior permanent magnet synchronous motor[J]. Acta Aeronautica et Astro- nautica Sinica, 2016, 37(4): 1336-1351.
Rotating High-Frequency Voltage Injection Method Based on Improved Self-Adjusting Frame Amplitude Convergence Current Demodulation Algorithm
Abstract The self-adjusting frame amplitude convergence (SFAC) algorithm applied to the rotating high-frequency (HF) voltage injection method is simple and practical, and achieves high-precision identification of the initial rotor position of permanent magnet synchronous motor (PMSM) under standstill conditions. However, it is found that the SFAC algorithm is not suitable for non-zero speed zone because the position estimation error changes with the speed. To this end, an improved SFAC (ISFAC) current demodulation algorithm is proposed. In ISFAC algorithm, the HF current is demodulated in the estimated 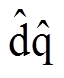-frame to construct the rotor position error signal. Utilizing the current phase delay characteristics of positive and negative HF current that are equal in magnitude and opposite in direction, the phase delay is eliminated automatically. The improved algorithm not only eliminates the complicated position error compensation strategy, but also extends the speed applicable range of the traditional SFAC algorithm from zero speed zone to non-zero speed zone. The mechanism of SFAC algorithm and the reasons leading to position estimation error in the non-zero speed zone are analyzed. Moreover, the implementation of ISFAC algorithm is introduced. The position estimation performance of traditional SFAC and ISFAC algorithm is compared and verified on a RT-Lab platform.
keywords：Permanent magnet synchronous motor (PMSM), rotating high-frequency (HF) voltage injection method, current demodulation, self-adjusting frame amplitude convergence (SFAC), sensorless control
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.200261
国防科技卓越青年基金（2018-JCJQ-ZQ-002）和国家自然科学基金青年基金（51807200）资助项目。
收稿日期 2020-03-14
改稿日期 2020-05-26
麦志勤 男，1992年生，博士研究生，研究方向为永磁同步电机无位置传感器控制技术。E-mail: 827239136@qq.com
刘计龙 男，1988年生，副研究员，硕士生导师, 研究方向为大容量电能变换技术、永磁同步电机驱动控制技术。E-mail: 66976@163.com（通信作者）
（编辑 崔文静）