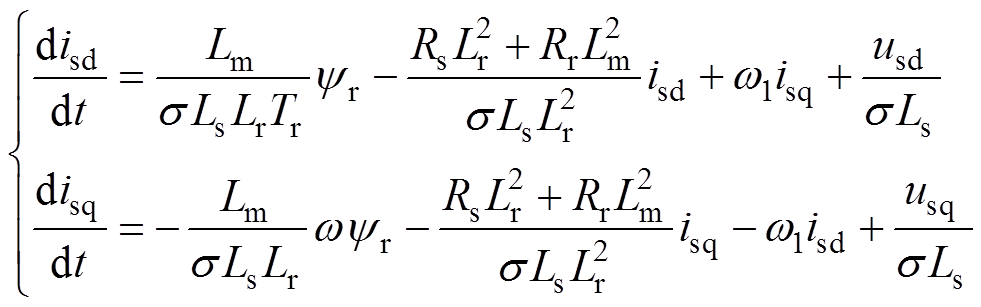（1）摘要 滑模控制器能有效提升感应电机电流环鲁棒性，然而传统滑模控制存在严重的抖振问题，虽然通过引入趋近律能有效降低系统抖振，但仍无法实现系统在有限时间内收敛。为此，该文提出一种感应电机非线性积分滑模电流控制器，在削弱系统抖振的同时，实现了定子电流误差在有限时间内收敛。首先，设计非线性积分滑模面，有效避免了传统积分滑模面中初始误差大而导致的积分饱和问题。其次，通过将滑模面的信息引入幂次趋近律，实现控制器对系统状态的自适应收敛，有效地削弱了系统抖振。最后，对比实验结果验证了所提出算法的有效性。
关键词：感应电机 电流环 积分滑模控制 有限时间内收敛 抖振
感应电机（Induction Motor, IM）矢量控制系统已广泛应用于先进制造、交通运输、采矿冶金、家用电器等诸多领域[1-2]。矢量控制通常采用级联双闭环结构，包括转速环和电流环。其中，电流环作为控制系统内环，能够使定子电流实际值跟踪给定值，其快速响应能力和鲁棒性是转速外环性能提升的基础[3-5]。
目前，电流环控制策略可分为线性控制和非线性控制两大类。线性控制以PI控制为典型代表，具有结构简单、无稳态误差、便于理论分析等优点[5]。然而传统PI控制器参数设计依赖电机数学模型。在实际运行过程中，电机参数受环境温度、磁场饱和程度等影响会发生摄动，导致电流控制性能降低，甚至不稳定。非线性控制包括滞环控制[6]、预测控制[7]、智能控制[8]、滑模控制[9]（Sliding Mode Control, SMC）等。其中，滑模控制无需系统精确模型，具有响应快速、鲁棒性强等优点[10-11]。但滑模控制存在由高频切换控制导致的抖振问题，且系统状态变量难以在有限时间内收敛[12]。
针对抖振问题，文献[13]提出了将滑模切换控制函数连续化的方法，但该方法牺牲了滑模控制的强鲁棒性。文献[14]采用边界层法来削弱系统抖振，但该方法仅能保证系统状态收敛到以滑模面为中心的较窄边界层内，只能无限接近而不能收敛到滑模面。文献[15]提出利用幂次趋近律滑模控制来削弱系统抖振，但未分对收敛时间。文献[16]提出了一种高阶滑模控制，使滑模变量高阶导数为零，在理论上消除了抖振，但并未应用到实际系统中。
针对状态变量无法在有限时间内收敛的问题，文献[17]提出了一种积分滑模控制，并将其应用于永磁直线同步电机直接推力控制，但其滑模面中包含在实际应用过程中难以直接获取的状态误差微分项。文献[18]根据Super-Twisting理论设计了永磁同步电机滑模观测器，利用二阶控制律有效削弱传统滑模观测器的固有抖振，消除了反电动势的跟踪误差，但并未用于控制器设计。文献[19]将积分滑模应用于感应电机无速度传感器带速重投控制，实现了系统在有限时间内收敛，但该方法仍沿用边界层法削弱系统抖振，牺牲了系统鲁棒性。
因此，抖振与无法在有限时间收敛问题仍是限制滑模控制在感应电机电流环应用的关键因素。为此，本文提出了一种非线性积分滑模电流环控制器，创新点主要体现在以下两方面：①设计基于非线性积分函数的滑模面，实现系统状态变量的有限时间收敛；②基于非线性积分滑模面，设计幂次趋近律削弱系统抖振。最终，在2.2kW实验平台上进行对比实验，实验结果验证了该算法的有效性。
基于转子磁场定向（Rotor Field-Oriented Control, RFOC）的感应电机状态方程可表示为
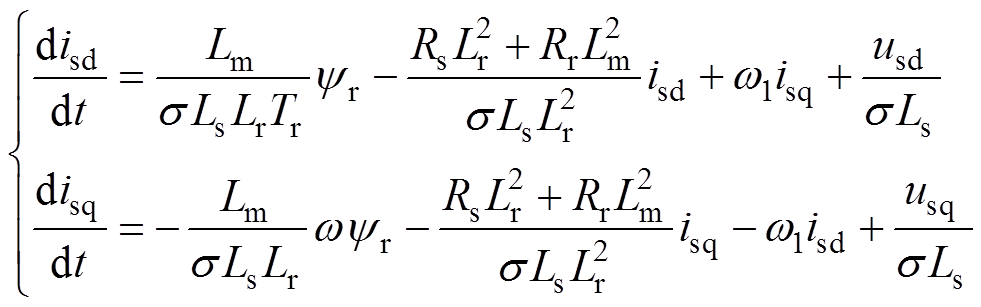（1）式中，isd、isq为定子电流d、q轴分量；usd、usq为定子电压d、q轴分量；Rs、Rr为定子、转子电阻；Ls、Lr、Lm为定、转子电感与互感；yr为转子磁链；w1为电机同步转速；w 为转子转速；Tr为转子时间常数，Tr=Lr/Rr；s 为漏感系数，s =1-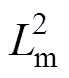
/(LsLr)。
进一步将式（1）用矩阵形式表示为
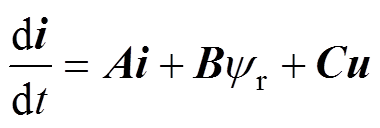（2）其中
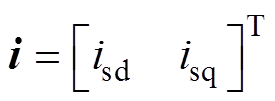
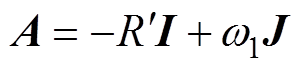
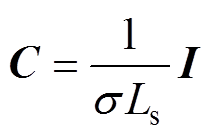
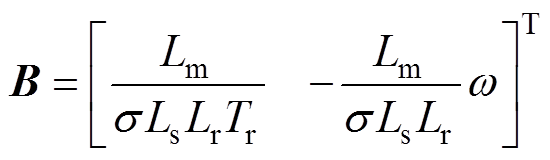
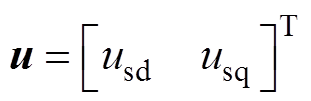
图1是基于RFOC的感应电机矢量控制系统框图。整个系统包括感应电机、整流器和逆变器、控制单元。其中，控制单元采用级联双闭环矢量控制结构，外环为转速环，采用PI控制；内环为电流环，采用本文所提出的非线性积分滑模控制，其输入为转矩电流参考值isq,ref和励磁电流参考值isd,ref，其输出为d、q轴指令电压usq与usd。
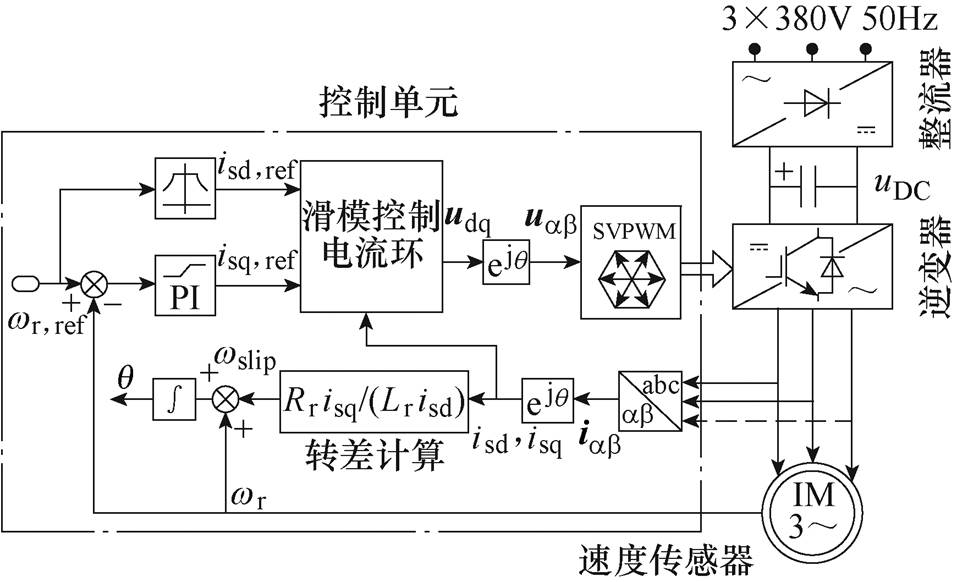
图1 基于RFOC的感应电机矢量控制系统框图
Fig.1 Block diagram of RFOC-based IM drive
PI控制作为电流环最常用的控制策略，能够实现定子电流无稳态误差收敛，但电流环PI控制器设计多采用零极点对消的方法，这导致其依赖精确的电机模型[1]。在实际应用中，由于环境温度变化和磁场饱和效应，电机的电阻和电感都将产生摄动，导致系统模型不匹配，使电流控制性能降低。
相比于PI电流环控制，滑模控制无需系统精确模型，具有对模型不敏感、抗扰动能力强等优点，是一种强鲁棒性控制策略[20-24]。本节将给出传统滑模与幂次趋近律滑模电流控制器设计，并分别对两种控制下系统状态收敛时间进行分析。
传统滑模电流控制的思想是通过切换控制使电流误差在零附近达到滑动模态，实现定子电流收敛。为此，需要建立定子电流误差的状态方程，首先，将参考电流代入式（2）得参考系统为
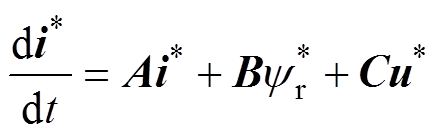（3）式中，* 为对应变量的参考值；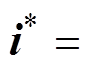
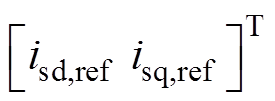；磁链参考值由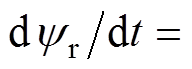
来计算[3]。
由式（3）与式（2）做差得误差系统为
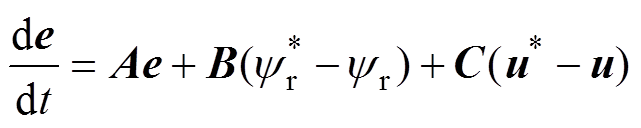（4）式中，e为定子电流误差，e=i*-i。
滑模控制设计包括滑模面的选取与控制律的设计两步。选取线性滑模面S为
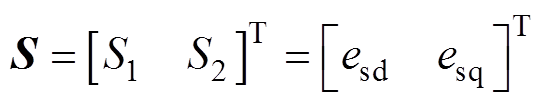（5）设计滑模控制律u为
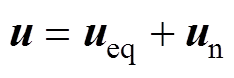（6）
其中
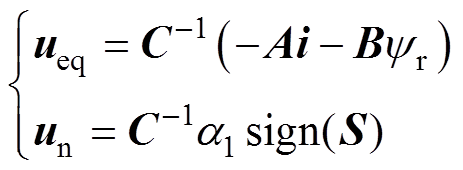（7）式中，ueq为等效控制项，用于补偿电机状态方程中可直接求得的反电动势项；un为滑模控制项，使系统状态变量在滑模面上达到滑动模态。un中控制增益a1＞0，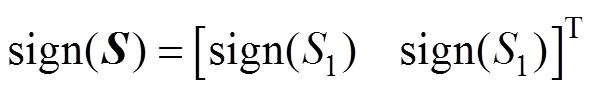
，sign()为开关函数，有
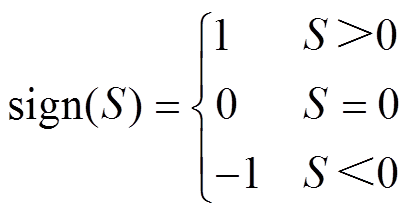（8）
可见，由于控制律u中存在切换函数，当系统处于滑模面滑动时会存在严重的抖振。
对收敛时间分析，将式（7）中的控制律与式（3）中的u*同时代入式（4），可得
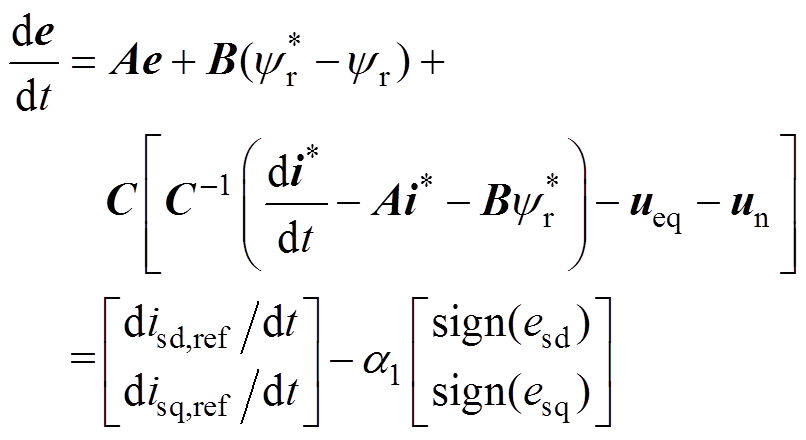（9）在电机处于暂态过程中，isd,ref保持不变，isq,ref为时变量。根据文献[25-26]，为了保证系统稳定性和鲁棒性，滑模增益a1的取值需明显大于
，因此，这里可以忽略disd,ref/dt与disq,ref/dt对收敛时间的影响。将式（9）整理为
（10）以d轴电流误差为例进行分析，q轴电流误差分析方法相同。设初始状态为esd(0)＞0。由于定子电流误差的收敛速度为恒定值，可计算出定子电流误差第一次收敛到零的时间为
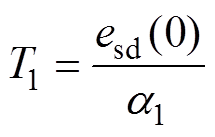（11）
可见，T1大小与系统初始状态以及增益a1有关。若a1取值较小，则会导致系统到达时间长，甚至无法收敛。若a1取值较大，虽然可以减小系统到达时间，但会增加系统抖振。
幂次趋近律法是一种有效地削弱抖振和优化系统收敛轨迹方法[13]。电流环幂次趋近律滑模控制律为
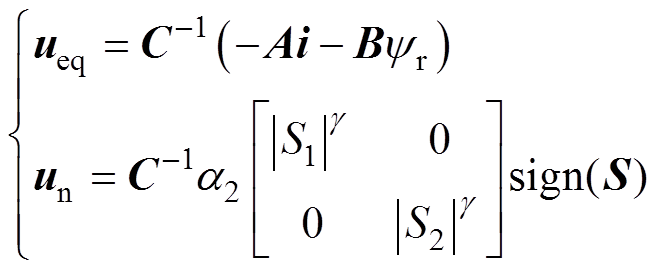a2＞0，g ≠1（12）图2为基于幂次趋近律的滑模电流控制器框图。由式（12）可见，幂次趋近律法在传统开关函数的增益中引入定子电流误差信息，使抖振随电流误差减小而减小，有效地削弱了系统抖振。文献[15, 22]已通过选择李雅普洛夫函数对幂次趋近律滑模控制的稳定性进行证明。
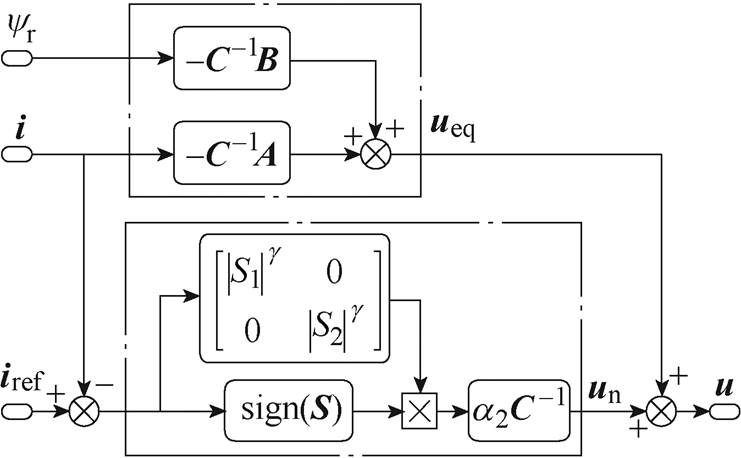
图2 基于幂次趋近律的滑模电流控制器框图
Fig.2 Block diagram of the slide mode current controller based on the power reaching law
对收敛时间分析，将式（12）中的控制律代入式（4），可得
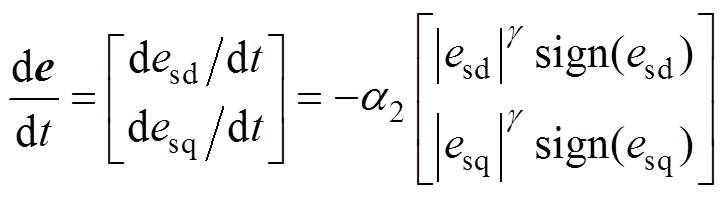（13）同样以d轴电流误差为例进行分析，假设esd的初始值为esd(0)，解微分方程式（13），可得
（14）
由式（14）可得，当g＞1时，定子电流误差esd(t)在理论上随时间的增加而无限趋近于零；当g＜1时，esd(t)随时间的增加而发散。因此，幂次趋近律无法保证系统误差在有限时间内收敛到零，即存在有限时间不收敛问题。实质上，虽然通过引入幂次趋近律能够使控制律连续化，削弱系统抖振，但其本质上仍类似Kp控制，因此在理论上无法实现有限时间收敛，最终导致系统存在稳态电流误差。
针对幂次趋近律滑模控制存在的有限时间不收敛问题，本节将提出一种非线性积分滑模电流控制器，通过将所设计的非线性积分函数引入滑模面，并以幂次趋近律结合设计控制律，实现系统状态在有限时间内收敛，最终消除稳态电流误差。
传统积分滑模面[19]可表示为
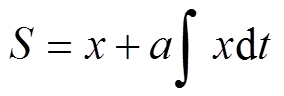（15）式中，x为状态变量的误差；a为积分项系数，a＞0。
由式（15）可见，滑模面中的积分项能够累计误差信息，使系统状态变量在有限时间内收敛。然而，在系统初始状态时，若实际定子电流与其参考值存在较大误差，则积分作用会导致滑模面的值突增，产生很大的冲击，使暂态性能恶化。
为此，本文提出了一种非线性积分滑模面，有
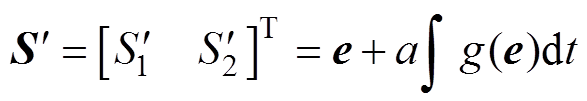（16）式中，g(e)为所设计的非线性积分函数，有
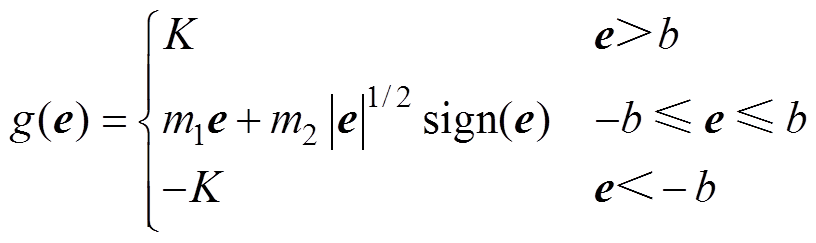（17）
式中，K=m1b+m2b0.5，且
，m1、m2为正常数。
图3为g(e)的函数图像，可见，g(e)具有“小误差放大、大误差饱和”的特点。因此，所设计的非线性积分滑模面能够在保证状态变量有限时间收敛的同时，解决系统暂态性能恶化的问题。
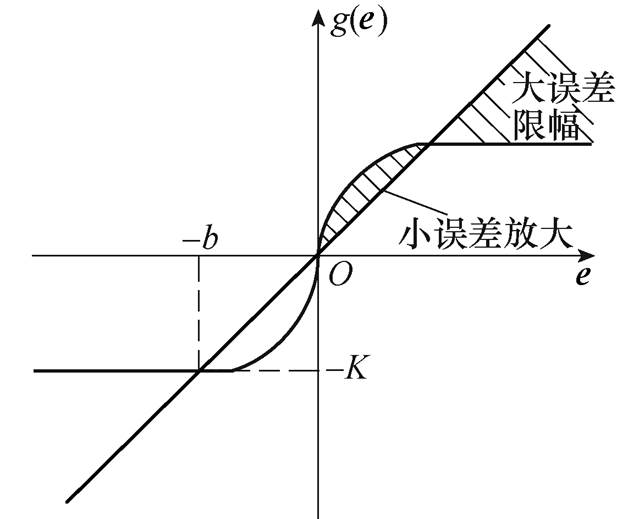
图3 g(e)函数图像
Fig.3 Graph of the function g(e)
基于非线性积分滑模面式（16），设计控制律u为
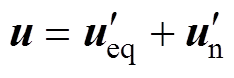（18）
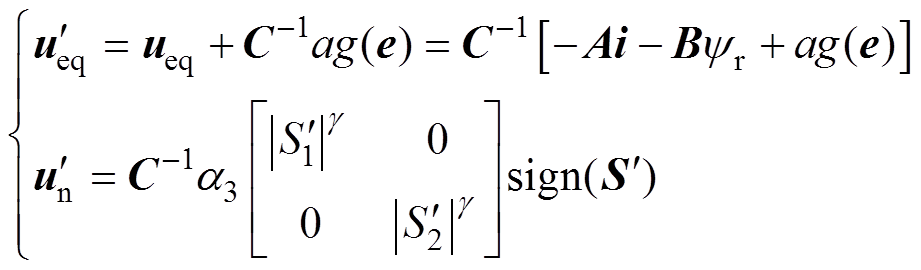（19）
由式（19）可见，所设计的控制律通过将非线性积分滑模面
的信息引入控制律，使控制律随系统状态趋近于滑模面而减小，从而有效降低系统抖振。图4为所提出的非线性积分滑模电流控制器框图。
稳定性证明，选取李雅普诺夫函数，有
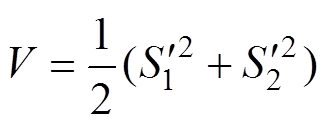（20）则函数V的导数为
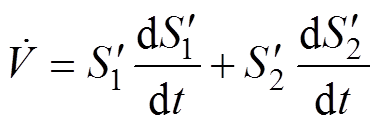（21）
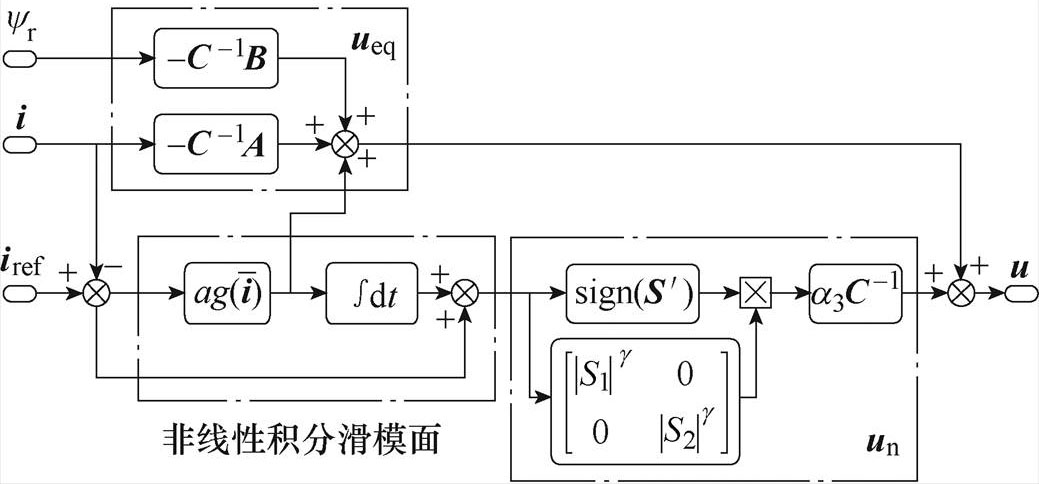
图4 非线性积分滑模电流控制器框图
Fig.4 Block diagram of nonlinear integral slide mode current controller
将如式（16）所示的滑模面关于时间t求导可得
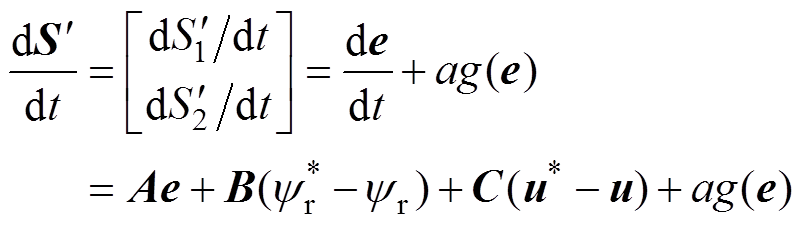（22）将式（3）中u*与式（19）所设计的控制律u代入到式（22）中可得
（23）
同理，在电机稳定运行时，disd,ref/dt=0,disq,ref/dt=0。将式（23）进一步代入式（21）中可整理得
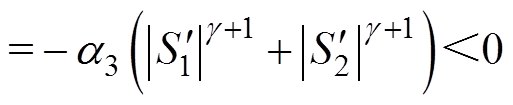（24）
此时，V的导数一定为负定，因此该有界系统是稳定的。证明完毕。
由于d、q轴收敛分析情况相同，本文以d轴电流误差收敛性为例进行分析。设初始状态为esd(0)，则：
（1）当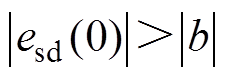
时，此时对应在图3中为大误差限幅状态，此时对式（16）求导得
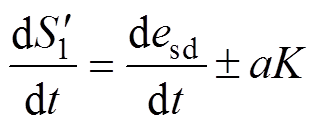（25）将式（23）进行整理，可得
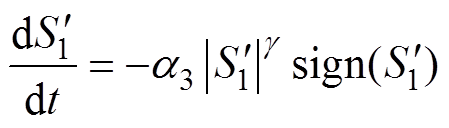（26）
式中，等式右侧可以写成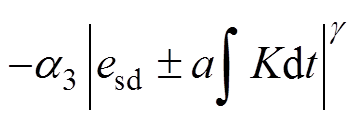
。将式（26）与式（25）进行移相整理，可得d轴电流误差微分为
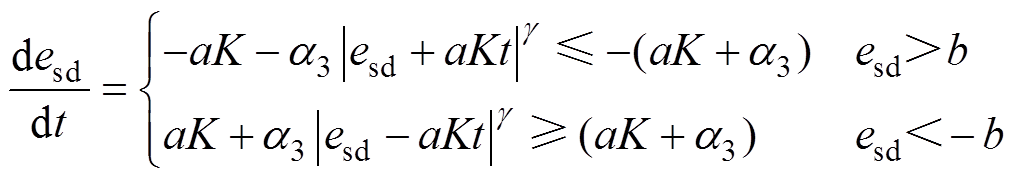
所以，电流误差可在最大时间tr内收敛到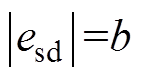
，tr的表达式为
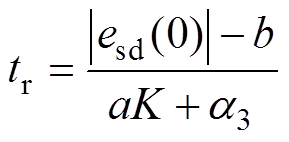（27）
（2）当收敛到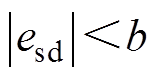
，此时对应在图3中为小误差放大状态，此时对式（16）求导得
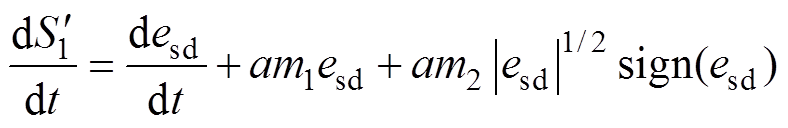（28）根据文献[21]求解式（28），可得经过ts时间，电流误差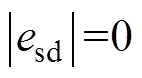
，且ts可表示为
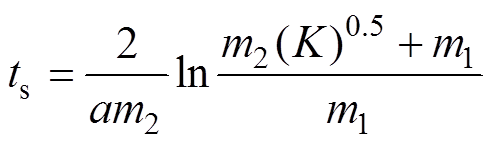（29）
根据上述推导，系统经过小于tr+ts的时间可使d、q轴电流误差均收敛到零。因此，非线性积分滑模控制能够实现系统有限时间收敛，消除稳态电流误差。
本文采用基于STM32F103 ARM的2.2kW感应电机对拖平台验证所提出的算法，实验平台如图5所示，采用两台相同规格的感应电机，参数见表1，其中，测试电机用于算法验证，加载电机用于提供负载转矩。本文采用双闭环矢量控制作为基本控制策略，电流环为所提出的非线性积分滑模控制算法。设定励磁电流isd的参考值为2.5A（50%额定电流），变频器脉冲宽度调制开关频率为6kHz。
速度环PI控制器系数选取为：Kp=2.0，Ki=450。电流环的参数选取由雅普诺夫稳定性以及收敛速度共同决定的。首先，选取非线性积分滑模面的具体参数a, b, m1, m2，步骤如下：根据式（27）与式（29），为了尽可能减小定子电流收敛时间，应尽可能增大a。但a同时决定了控制律中积分项的大小，当a取值过大时，容易造成控制超调。因此，参数a的选取应同时考虑系统收敛时间与超调量。为了简化参数整定过程，选择b=1代入式（17），可得K=m1+m2，其中，K为非线性积分函数的限幅值，其选取需同时考虑系统收敛时间与电流误差，因此选取1≤K≤1.5。最后，根据文献[21]，考虑非线性积分函数的收敛轨迹和速度，最终合理选取参数m1和m2。
图5 实验平台
Fig.5 Experimental setup
表1 感应电机参数
Tab.1 Parameters of induction motor
参 数数 值 额定功率/kW2.2 额定电压/V380 额定电流/A5 额定转速/(r/min)1 500 极对数2 定子电阻/Ω2.665 转子电阻/Ω1.580 定子电感/mH248.8 转子电感/mH240.3 互感/mH225.8
其次，通过李雅普诺夫稳定性以及抖振大小来确定滑模增益a1、a2与a3的取值。最终实验中电流环的参数选取如下：非线性积分滑模面中，a=18，b=1，m1=0.4，m2=0.8，K=1.2。滑模控制增益选取为a1=a2=a3=150。
图6为分别采用传统滑模控制、幂次趋近律法与所提出非线性积分滑模控制的全速范围运行对比实验结果。实验中，电机在空载下从零速阶梯加速到1 500r/min，再阶梯降速，并分别给出转速wfbk、指令电压Us和定子电流误差e波形。
由图6a可见，传统滑模控制指令电压存在严重抖振，幅值达0.07(pu)，这是由传统滑模控制中切换函数所导致，并且电流误差e存在随着转速升高而增大，最大误差为1.42A。在图6b中，采用幂次趋近律滑模控制的指令电压抖振幅值降低至0.03(pu)，且定子电流稳态误差减少，但仍未完全消除，最大达到0.76A。对应在图6c中，采用所提出的非线性积分滑模控制时，抖振幅值降低至0.01(pu)内，并消除了稳态电流误差。因此，所提出的非线性积分滑模控制能有效削弱系统抖振，并消除稳态电流误差。
图7为额定负载工况下上述三种不同方法的加速运行对比实验结果。实验中，电机在满载时从零速加速到900r/min，并给出指令电压Us、定子电流误差e和相电流ia的实验波形。由图7a和图7b可见，采用传统滑模控制和幂次趋近律时，系统存在明显的稳态电流误差，误差分别为1.37A与1.29A。对应在图7c中，所提出非线性积分滑模控制能有效消除稳态电流误差，且降低了指令电压中的抖振幅值。
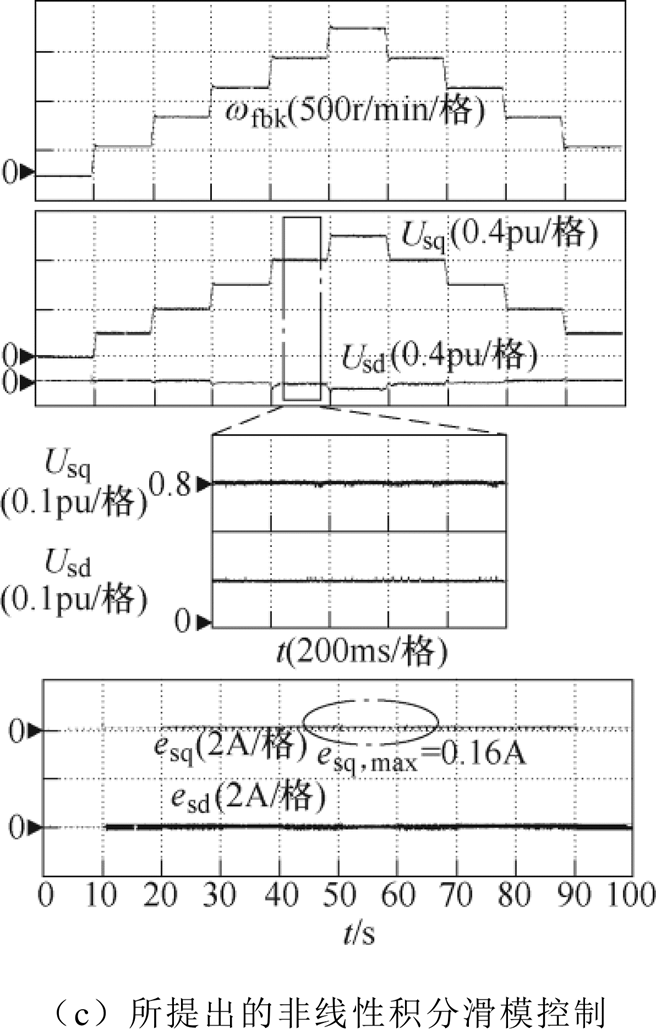
图6 三种方法不同速度下空载实验结果
Fig.6 Experimental results of three methods at different speeds without load
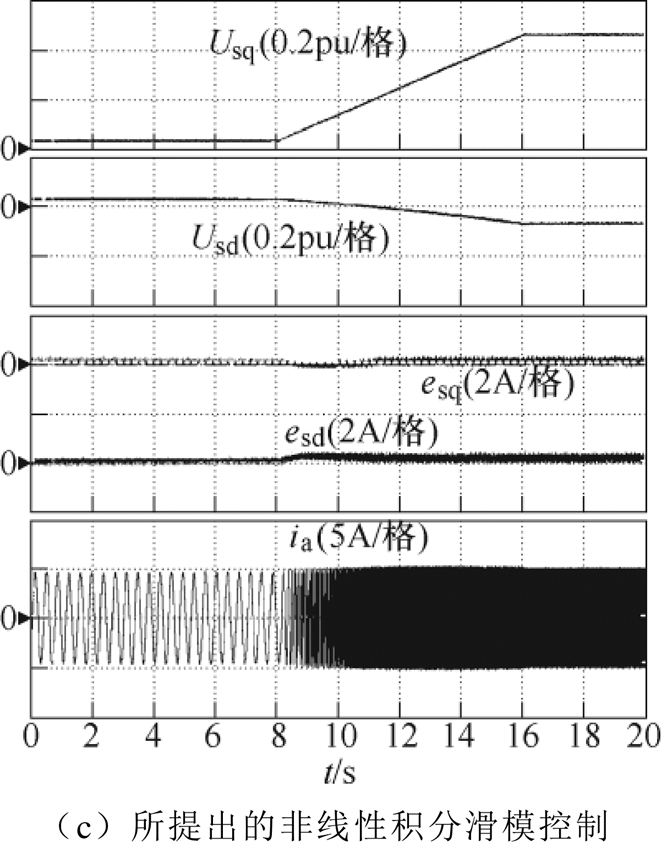
图7 三种方法额定负载下加速实验结果
Fig.7 Experimental results of three methods during acceleration with rated load
图8为分别采用传统积分滑模控制与所提出非线性积分滑模控制的系统加速对比实验结果。该实验条件为，电机在空载下转速由0加速到额定转速1 500r/min。实验结果表明，两种方法均能够实现定子电流有限时间收敛和稳态误差消除。但如图8a所示，传统积分滑模中在暂态过程中滑模面突增，导致系统收敛性能恶化。相比而言，如图8b所示，所提出的非线性积分滑模面能够有效解决滑模面突增问题，改善电流环的暂态性能。
图8 两种方法空载加速实验结果
Fig.8 Experimental results of two methods during acceleration without load
图9为所提出算法在电机参数摄动时的系统响应。在实际运行过程中，电机参数将随环境温度和磁场饱和而改变。根据式（1），电机互感摄动是影响电流环性能的主要因素[9]，为此，本文以互感变化作为参数摄动来验证所提出方法的鲁棒性。为了满足电机实际运行中互感的最大变化范围，这里选取0.5Lm～2.0Lm作为测试条件。图9为电机在600r/min工况下互感由0.5Lm阶梯变化至2.0Lm时系统的响应波形。可见，在电机互感变化过程中，定子电流d、q轴分量出现明显波动，但该波动能够很快被抑制。因此，所提出的算法能够有效抑制互感变化的影响，证明了所提出的非线性积分滑模控制具有良好的参数鲁棒性。
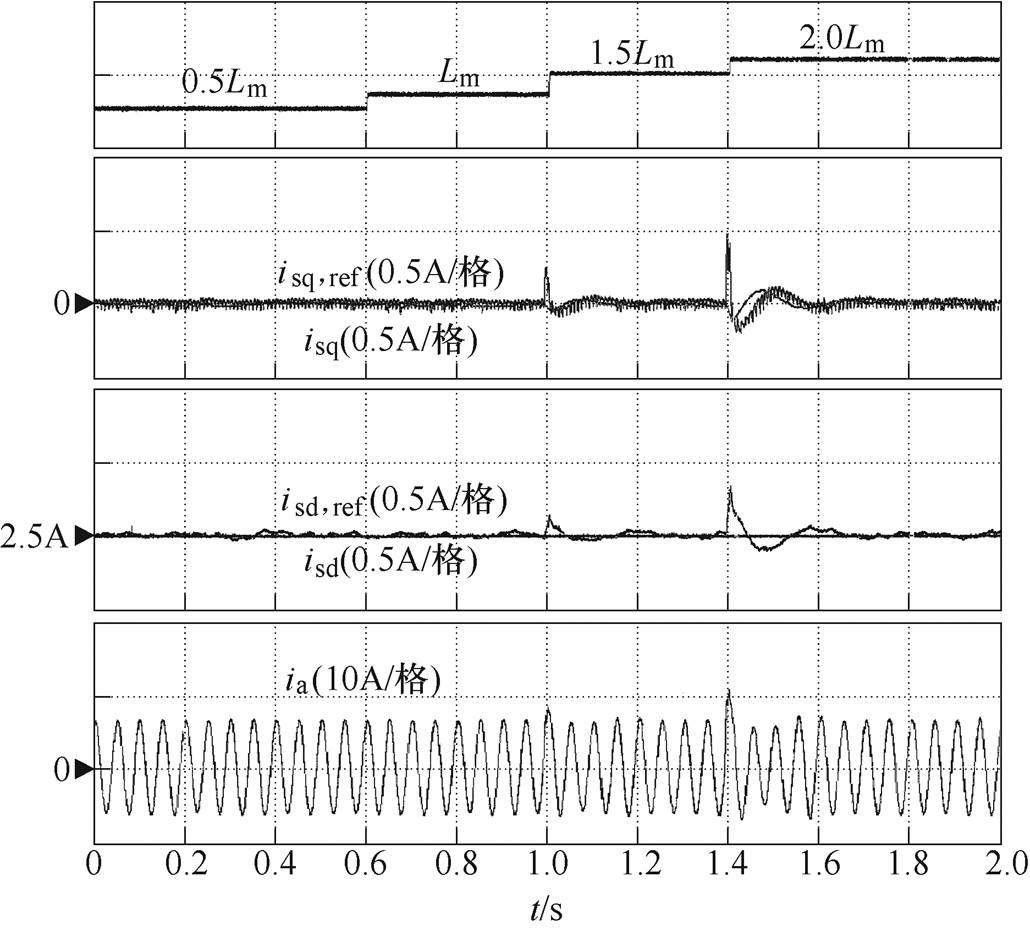
图9 所提出算法鲁棒性测试实验结果
Fig.9 Experimental results of robust test with the proposed method
本文所提出的非线性积分滑模有效地解决了传统滑模控制导致的抖振严重问题，实现了定子电流在有限时间内收敛。非线性积分滑模面能够避免传统积分滑模面由于初始误差过大导致的饱和问题，并实现定子电流在有限时间内收敛。所设计的控制律通过结合滑模面与趋近律，能够有效削弱系统抖振。对比实验结果证明，所提出的非线性积分滑模控制能够实现感应电机系统在空载和带载工况下的无稳态误差电流控制，并对电机参数摄动具有强鲁棒性。
参考文献
[1] Mishra J, Wang Liuping, Zhu Yuankang, et al. A novel mixed cascade finite-time switching control design for induction motor[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1172-1181.
[2] Yin Zhonggang, Gao Fengtao, Zhang Yanqing, et al. A review of nonlinear Kalman filter appling to sensorless control for AC motor drives[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 351-362.
[3] Fang Xiaochun, Tian Zhongbei, Li Hua, et al. Current closed-loop control and field orientation analysis of an induction motor in six-step operation for railway applications[J]. IET Power Electronics, 2019, 12(6): 1462-1469.
[4] 贺虎成, 孙磊, 张玉峰, 等. 基于矢量控制的异步电机自抗扰控制[J]. 电机与控制学报, 2019, 23(4): 120-125.
He Hucheng, Sun Lei, Zhang Yufeng, et al. Asyn- ronous motor active disturbance rejection control based on vector control[J]. Electric Machines and Control, 2019, 23(4): 120-125.
[5] 齐丽英, 王琛琛, 周明磊, 等. 一种异步电机的电流环解耦控制方法[J]. 电工技术学报, 2014, 29(5): 174-180.
Qi Liying, Wang Chenchen, Zhou Minglei, et al. A decoupling current control scheme for induction machine controllers[J]. Transactions of China Elec- trotechnical Society, 2014, 29(5): 174-180.
[6] Gauri A, Vinod B, Shiny G. Vector control method for induction motor drive based on hysteresis controller and pi controller comparative study[C]// 2019 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 2019: 1-6.
[7] 齐昕, 吴文昊, 吴琳, 等. 基于时间辅助信息的感应电机预测电流控制[J]. 中国电机工程学报, 2019, 39(16): 4927-4934, 4995.
Qi Xin, Wu Wenhao, Wu Lin, et al. Predictive current control of induction machines based on time auxiliary information[J]. Proceedings of the CSEE, 2019, 39(16): 4927-4934, 4995.
[8] 金鸿雁, 赵希梅. 基于Sugeno型模糊神经网络和互补滑模控制器的双直线电机伺服系统同步控制[J]. 电工技术学报, 2019, 34(13): 2726-2733.
Jin Hongyan, Zhao Ximei. Dual linear motors servo system synchronization control based on Sugeno type fuzzy neural and complementary sliding mode controller[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2726-2733.
[9] Wang Bo, Dong Zhen, Yu Yong, et al. Static- errorless deadbeat predictive current control using second-order sliding-mode disturbance observer for induction machine drives[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2395-2403.
[10] Chalanga A, Kamal S, Fridman L, et al. Implementation of super-twisting control: super-twisting and higher order sliding-mode observer-based approaches[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3677-3685.
[11] Meng Zhiqiang, Shao Wu, Tang Jie, et al. Sliding- mode control based on index control law for MPPT in photovoltaic systems[J]. CES Transactions on Elec- trical Machines and Systems, 2018, 2(3): 303-311.
[12] 王建美. 不确定非线性系统的滑模控制及其在永磁同步电机中的应用[D]. 秦皇岛: 燕山大学, 2018.
[13] Yin Zhonggang, Zhang Yanqing, Tong Xiangqian, et al. Model predictive control using globe exponential reaching law sliding mode design method for induction motor drives[C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 2559-2563.
[14] 张希, 陈宗祥, 潘俊民, 等. 永磁直线同步电机的固定边界层滑模控制[J]. 中国电机工程学报, 2006, 26(22): 115-121.
Zhang Xi, Chen Zongxiang, Pan Junmin, et al. Fixed boundary layer sliding mode control of permanent magnet linear synchronous motor[J]. Proceedings of the CSEE, 2006, 26(22): 115-121.
[15] Bartoszewicz A, Leśniewski P. New switching and nonswitching type reaching laws for SMC of discrete time systems[J]. IEEE Transactions on Control Systems Technology, 2016, 24(2): 670-677.
[16] Jin Jianzhao, Ge Suoliang. Finite-time active disturbance rejection control based on high-order sliding mode[C]//2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 2019: 1974-1979.
[17] 原浩, 赵希梅. 基于积分滑模的永磁直线同步电动机直接推力控制[J]. 电工技术学报, 2019, 34(3): 483-488.
Yuan Hao, Zhao Ximei. Direct thrust force control based on integral sliding mode for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 483-488.
[18] 张懿, 吴嘉欣, 韦汉培, 等. 离散型变增益永磁同步电机超螺旋滑模观测器[J]. 电工技术学报, 2018, 33(21): 4962-4970.
Zhang Yi, Wu Jiaxin, Wei Hanpei, et al. Discrete variable gain super-twisting sliding mode observer for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(21): 4962-4970.
[19] 苟立峰, 王琛琛, 游小杰, 等. 基于积分滑模的感应电机无速度传感器带速重投控制策略[J]. 电工技术学报, 2018, 33(24): 5700-5710.
Gou Lifeng, Wang Chenchen, You Xiaojie, et al. A restart method based on integral sliding mode for speed sensorless controlled induction motor[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5700-5710.
[20] Sun Dong, Hu Songyu, Shao Xiaoyin, et al. Global stability of a saturated nonlinear PID controller for robot manipulators[J]. IEEE Transactions on Control Systems Technology, 2009, 17(4): 892-899.
[21] Wang Bo, Luo Cheng, Yu Yong, et al. Antidistur- bance speed control for induction machine drives using high-order fast terminal sliding-mode load torque observer[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7927-7937.
[22] 李鹏. 传统和高阶滑模控制研究及其应用[D]. 长沙: 国防科学技术大学, 2011.
[23] 张国荣, 侯立凯, 彭勃, 等. 柔性多状态开关反馈线性化滑模控制[J]. 电力系统自动化, 2020, 44(1): 126-133.
Zhang Guorong, Hou Likai, Peng Bo, et al. Feedback linearization sliding mode control strategy for soft open point[J]. Automation of Electric Power Systems, 2020, 44(1): 126-133.
[24] 赵希梅, 刘超, 朱国昕. 永磁直线同步电机自适应非线性滑模控制[J]. 电机与控制学报, 2020, 24(7): 39-47.
Zhao Ximei, Liu Chao, Zhu Guoxin. Adaptive nonlinear sliding mode control for permanent magnet linear synchronous motor[J]. Electric Machines and Control, 2020, 24(7): 39-47.
[25] Teja A V R, Chakraborty C, Pal B C. Disturbance rejection analysis and FPGA-based implementation of a second-order sliding mode controller fed induction motor drive[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 1453-1462.
[26] Wang Liuping, Mishra J, Zhu Yuankang, et al. An improved sliding-mode current control of induction machine in presence of voltage constraints[J]. IEEE Transactions on Industrial Informatics, 2020, 16(2): 1182-1191.
Nonlinear Integral Sliding Mode Control Strategy for Current Loop of Induction Motor Drives
Abstract The sliding mode controller can effectively improve the robustness of induction motor (IM) current loop. However, the conventional sliding mode controller has serious chattering problems. Although the chattering can be effectively suppressed by introducing the reaching law, the system state variable cannot achieve finite-time convergence. To address this problem, this paper proposes a nonlinear integral sliding mode current controller for IM drives. The proposed approach can suppress the system chattering and achieve finite-time convergence simultaneously. Firstly, a nonlinear integral sliding surface is designed to avoid the integral saturation problem caused by large initial error. Secondly, the adaptive convergence of state variable can be achieved by introducing the information of sliding surface into the control law, which effectively weakens the system chattering. The experimental results verify the effectiveness of the proposed method.
keywords：Induction motor, current loop, integral sliding mode control, finite-time convergence, chattering
中图分类号：TM341
DOI: 10.19595/j.cnki.1000-6753.tces.200250
国国家科学基金（51690182, 51807038）、黑龙江省自然科学基金（YQ2020E018）、中国博士后科学基金（2018M630354, 2019T120267）、黑龙江省博士后（YQ2020E018）和中央高校基本科研业务费专项资金（HIT.NSRIF.2019025）资助项目。
收稿日期 2020-03-11
改稿日期 2020-08-14
王 勃 男，1987年生，副教授，博士生导师，研究方向为交流电机控制、现代控制理论及应用等。E-mail: wangbohit@hit.edu.cn
于 泳 男，1974年生，教授，博士生导师，研究方向为交流电机控制、故障诊断及容错控制等。E-mail: yuyong@hit.edu.cn（通信作者）
（编辑 崔文静）