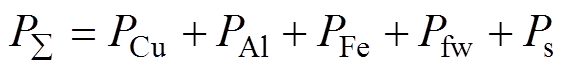 (1)
(1)摘要 针对交流牵引电机转子导条等多边形柱状热分析模型结构化网格划分质量不高的问题,提出一种结构化网格优化划分方法。建立交流牵引电机热分析的求解域模型,确定交流牵引电机多边形柱状模型的四边形区域质量计算方法,提出一种基于内置四边形的多边形柱状模型四边形区域划分方法,并采用果蝇优化算法(FOA)对各分区方式的综合质量进行优化以获得相应的最佳分区方式,再通过有限元法对其效果进行仿真验证,同时与传统结构化网格划分法进行对比仿真分析,最后通过实验对上述分析作进一步的实验验证,结果表明,该文所提出的结构化网格优化划分方法较传统结构化网格划分法显著提升了交流牵引电机多边形柱状模型的网格划分质量,从而有效提高了交流牵引电机热分析的准确性,具有较好的应用价值。
关键词:交流牵引电机 多边形柱状热分析模型 结构化网格 优化划分方法 果蝇优化算法
交流牵引电机因具有结构简单、成本低、维护方便等优点而得到了广泛应用[1]。然而由于电机在运行中会因各种损耗而使温度迅速升高[2],如果温升过高,则可能会引起转子导条断裂、绕组绝缘损坏等故障[3],因此开展交流牵引电机热分析研究以降低其温升将具有重要意义。
目前在有关交流牵引电机热分析方面已开展了大量研究,提出多种分析方法[4-6]。其中,有限元法以具有边界适应性好、准确度高等优点而得到了广泛应用。然而在采用限元法对交流牵引电机进行热分析时,需对其分析模型进行网格划分,而网格划分质量则是影响分析结果准确性的一个重要因素。
而在如何提高交流牵引电机热分析模型的网格划分质量方面,目前也已提出多种方法[7-9],其中,结构化网格划分法因具有网格质量好、计算速度快等优点而得到了普遍重视。然而该方法只适于规则模型的网格划分,对于交流牵引电机转子导条等多边形柱状模型来说,该方法难以达到满意的网格划分结果。
为此,本文针对交流牵引电机转子导条等多边形柱状分析模型,提出一种基于果蝇优化算法(Fruit Fly Optimization Algorithm, FOA)的结构化网格优化划分方法。介绍了该网格划分法的基本原理与具体实现方法,并对其效果进行验证,同时与传统结构化网格划分法进行对比分析,结果证明了该方法的有效性。
交流牵引电机运行时会产生包括定子铜耗、转子铝耗、铁耗、机械损耗及杂散损耗等多种损耗[10],其总损耗可表示为
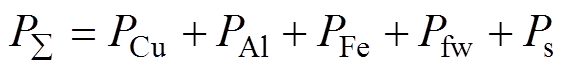 (1)
(1)式中,PCu为定子铜耗;PAl为转子铝耗;PFe为铁耗;Pfw为机械损耗;Ps为杂散损耗。
1.1.1 定子铜耗
定子铜耗计算公式[11]为
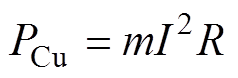 (2)
(2)式中,m为电机相数;I为定子绕组相电流有效值;R为定子绕组相电阻。
1.1.2 转子铝耗
转子铝耗计算公式[12]为
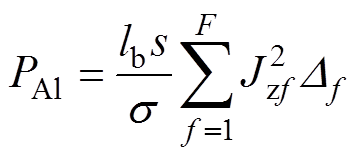 (3)
(3)式中,lb为转子导条长度;s为电机转差率;s 为转子导条电导率;F为转子槽内总单元数;Jzf为转子槽内各单元的感应电流密度;Df为转子槽内各单元的面积。
1.1.3 铁耗
铁耗常用Bertotti铁耗三项式计算[13],有
 (4)
(4)式中,Ph、Pc和Pe分别为磁滞损耗、涡流损耗与异常损耗;Bm为磁通密度幅值;f为磁场频率;Kh、Kc及Ke分别为磁滞损耗系数、涡流损耗系数及异常损耗系数。
1.1.4 机械损耗
机械损耗计算公式[11]为
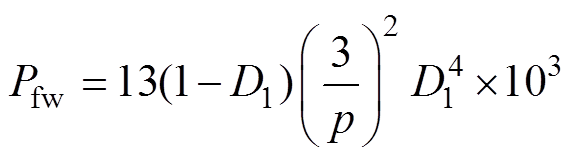 (5)
(5)式中,D1为定子外径;p为电机极对数。
1.1.5 杂散损耗
交流电机杂散损耗一般按其额定输入功率的 0.5%计算[14]。
电机运行中产生的热能将通过机壳与周围空气进行热交换,并最终达到动态平衡,其三类边界条件的数学表达式[15]为
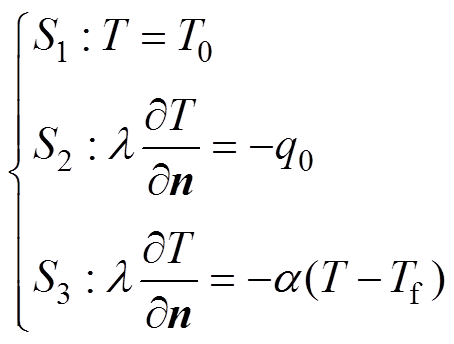 (6)
(6)式中,T为电机温度;T0为边界温度;l 为导热系数;n为边界法向量;q0为边界热流密度;a 为边界传热系数;Tf为环境温度。
其中,边界传热系数a 的计算公式[16]为
 (7)
(7)式中,v为机壳表面的风速。
而对于定转子间气隙的导热系数l 来说,则需先计算出气隙的雷诺数Reg及其临界雷诺数Recr,再根据两者的大小来确定其导热系数[17],具体为:
(1)分别计算气隙的雷诺数与临界雷诺数[18],有
 (8)
(8)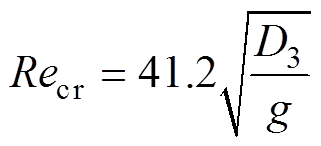 (9)
(9)
式中,D2为转子外径;D3为定子内径;g为气隙宽度;n为电机转速;g 为空气运动粘度系数。
(2)根据雷诺数Reg与临界雷诺数Recr的大小,来确定相应的导热系数,具体为:当Reg<Recr时,气隙中的空气为层流,其导热系数取空气的导热系数;当Reg≥Recr时,气隙中的空气为湍流,其导热系数的计算公式[18]为
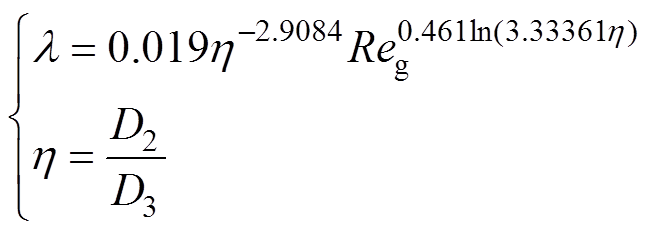 (10)
(10)在进行交流牵引电机热分析时,首先需建立其求解域模型,包括热传导方程与有限元模型。
在直角坐标系下,交流牵引电机热传导方程[19]为
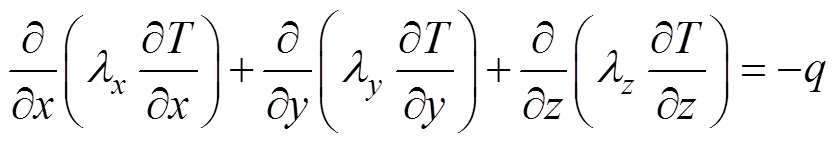 (11)
(11)式中,lx、ly、lz分别为x、y、z方向上的导热系数;q为热源密度。
由于交流牵引电机轴向对称,故可只取轴向一半且定、转子各取一槽来建立其有限元模型;同时为简化模型结构,根据文献[20],将定子绕组多匝导线等效为单一导体,因而所得交流牵引电机三维有限元模型如图1所示。
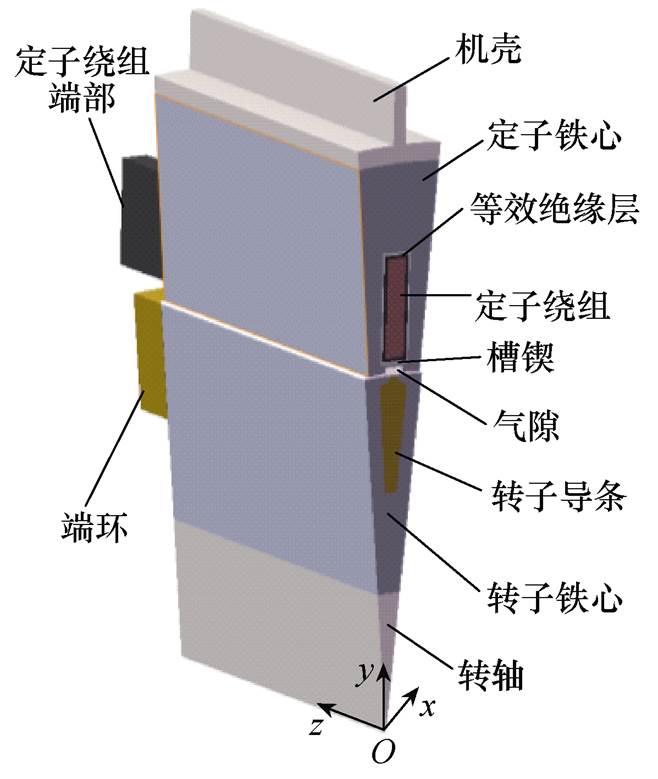
图1 交流牵引电机三维有限元模型
Fig.1 Three-dimensional finite element model of AC traction motor
在采用结构化网格划分法对交流牵引电机转子导条等多边形柱状模型进行网格划分前,首先需对其多边形顶面进行四边形分区,且分区质量直接影响网格划分质量;而要获得高的分区质量,首先需明确相应的分区质量计算方法。
对于单个四边形区域,本文拟采用雅克比比率法计算其质量[21]。基本原理是:首先由四边形各顶点坐标分别计算出该四边形各积分点所对应的雅克比行列式值,分别为
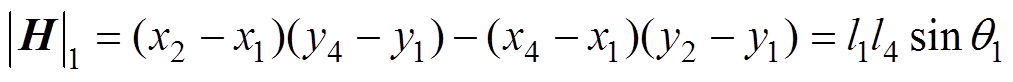 (12)
(12)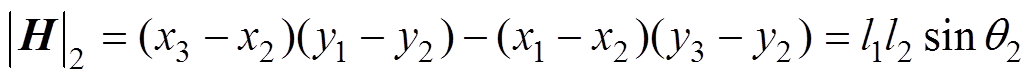 (13)
(13)
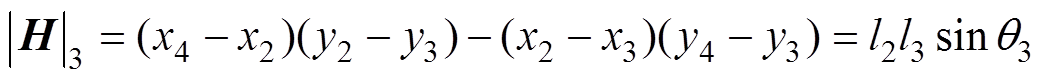 (14)
(14)
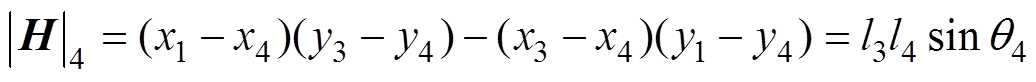 (15)
(15)式中,x1~x4为四边形各顶点的横坐标;y1~y4为四边形各顶点的纵坐标;l1~l4为四边形四边长;q1~q4为四边形的四个内角,各参数示意图如图2所示。
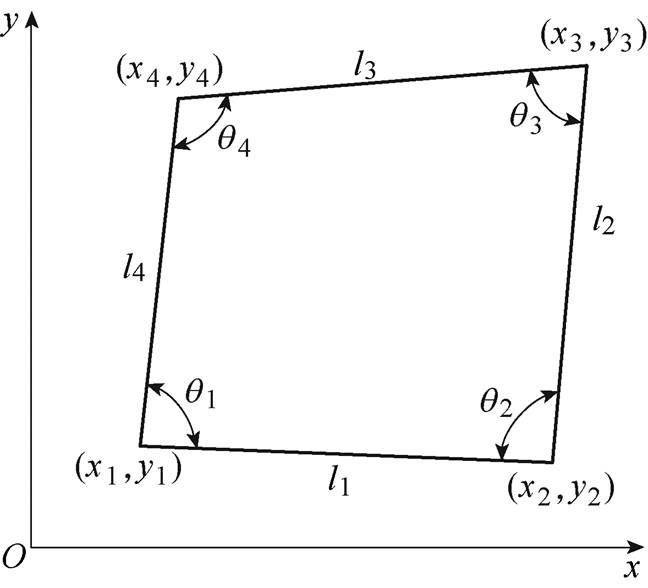
图2 四边形各参数示意图
Fig.2 Schematic diagram of quadrilateral parameters
再根据上述所得各雅克比行列式中的最小值和最大值,即可得到该四边形的雅克比比率值,其计算公式为
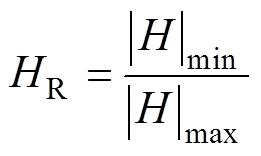 (16)
(16)式中,HR为四边形雅克比比率值;|H|min和|H|max分别为四边形雅克比行列式的最小值和最大值。
根据文献[21],四边形雅克比比率值HR越大,则表明该四边形的质量越好。
由于雅克比比率法只适于凸四边形的质量计算,即该四边形各顶点角度均应小于180°;然而实际在对多边形柱状模型的多边形顶面进行四边形分区时,却难以保证所得各四边形区域均为凸四边形。为此,在针对各四边形区域质量进行计算前,有必要首先对所得各四边形区域的形状进行判断。为此,提出采用混合积法对各四边形区域形状进行判定,具体如下:
(1)令四边形各顶点编号依次为1、2、3、4,由于混合积计算中各向量均为三维向量,因此设四边形各顶点竖坐标均为0,即z=0。计算混合积a、b、c分别[22]为
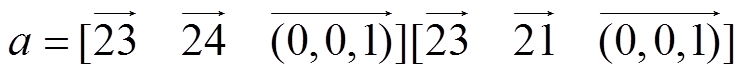 (17)
(17)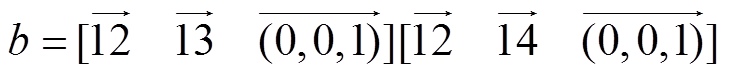 (18)
(18)
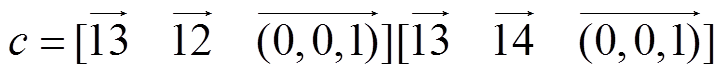 (19)
(19)
式中,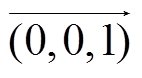 为z方向上的单位向量。
为z方向上的单位向量。
(2)根据上述所得各混合积a、b、c的值,即可判定四边形各顶点的位置关系,进而判定出该四边形的形状,混合积判定示意图如图3所示。
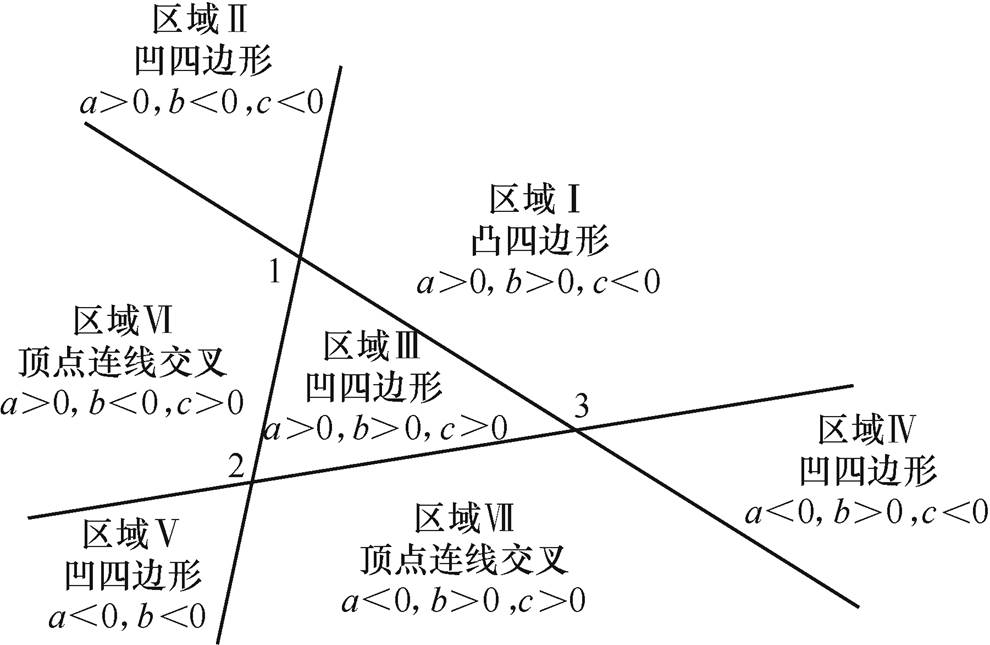
图3 混合积判定示意图
Fig.3 Schematic diagram of mixed product determination
图3中,顶点1、2、3为四边形的3个顶点,将每个顶点的两条边延长,可将平面分为7个区域,即区域Ⅰ~区域Ⅶ;再根据混合积a、b、c的值,即可确定四边形的第4个顶点处在哪个区域。根据第4个顶点所处不同区域,对应的四边形有三种形状,分别为:①若a>0, b>0, c<0,顶点4落在区域Ⅰ中,此时四边形为凸四边形;②若a>0, b<0, c<0或a>0, b>0, c>0或a<0, b>0, c<0或a<0, b<0,则顶点4分别落在区域Ⅱ~区域Ⅴ中,此时四边形均为凹四边形;③若a>0, b<0, c>0或 a<0, b>0, c>0,则顶点4分别落在区域Ⅵ和区域Ⅶ中,此时4个顶点的连线产生交叉。
如以顶点4落在区域Ⅱ中为例,即在区域Ⅱ中任取一点作为顶点4,再将4个顶点依次相连,所得四边形如图4所示,可见此时为一个凹四边形。
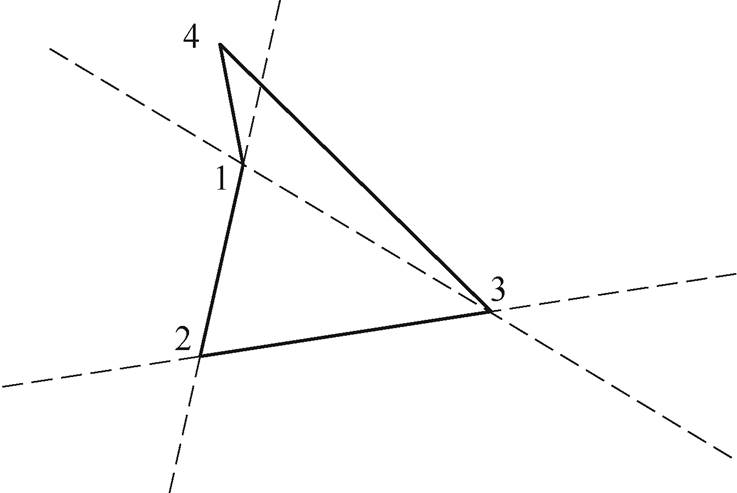
图4 顶点4落在区域Ⅱ时的四边形示意图
Fig.4 Schematic diagram of quadrilateral when vertex 4 is in region Ⅱ
通过4个顶点连线来确定相应的四边形时可能存在上述三种类型,分别为凸四边形、凹四边形和连线交叉。
如上所述,在由4个顶点通过连线来确定相应的四边形时可能存在上述三种类型。然而在针对多边形柱状模型的多边形顶面进行四边形分区时,只希望得到凸四边形,而另外两种则是不希望出现的。为此,在进行四边形区域质量计算时,对于所不希望出现的四边形类型,将通过设置相应的惩戒系数来作为其质量,以避免该类型四边形的出现。因此,有关各种四边形区域质量的计算方法,概括为
 (20)
(20)式中,Qr为第r个四边形区域的质量;x、y为设置的惩戒系数,且y<x<0。
对于多四边形区域的综合质量,本文提出取各四边形区域的平均质量作为其综合质量,即
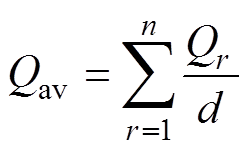 (21)
(21)式中,Qav为四边形区域的平均质量;d为四边形区域的个数。
如上所述,在采用结构化网格划分法对交流牵引电机转子导条等多边形柱状模型进行网格划分前,首先需对该模型的多边形顶面进行四边形分区。下面首先介绍其四边形的分区方式,再阐述对相应分区方式进行优化的方法。
为将多边形顶面划分为若干个四边形区域,本文提出一种基于内置四边形的区域划分法。其基本原理是:在多边形顶面内任意添加一个四边形,并由该四边形各顶点分别向顶面各顶点或顶面各边上所选取的点引线,由此将多边形顶面划分成若干个四边形区域。其中,所添加的四边形称为内置四边形,为方便分析,将内置四边形各顶点称为内点,顶面多边形各顶点称为角点,而在顶面多边形各边上所选取的点称为边点。
下面首先介绍边点数的确定方法,再阐述四边形分区方式的具体实现方法。
4.1.1 边点数确定方法
在将多边形顶面划分为若干个四边形区域过程中,为使所获得的各四边形区域尺寸基本均衡,本文提出按多边形顶面各边边长来确定其边点数的方法。其基本原理是:以多边形顶面最短边为基准,并规定最短边不设边点,再将其他各边边长分别与之比较,其比值在大于1后按每增加50%,则在该边上增加1个边点的方法来确定其边点数,且规定其上限为3个。
根据上述方法,则如果某边边长超过最短边50%而不足100%时,将在该边上设一个边点;同样,如果某边边长超过最短边100%而不足150%时,则在该边上设两个边点;而如果某边边长超过最短边150%及以上时,则在该边上设3个边点,由此可确定多边形顶面各边上的边点数。
4.1.2 多边形顶面的四边形分区方法
针对多边形顶面进行四边形分区,多边形顶面的四边形分区流程如图5所示。
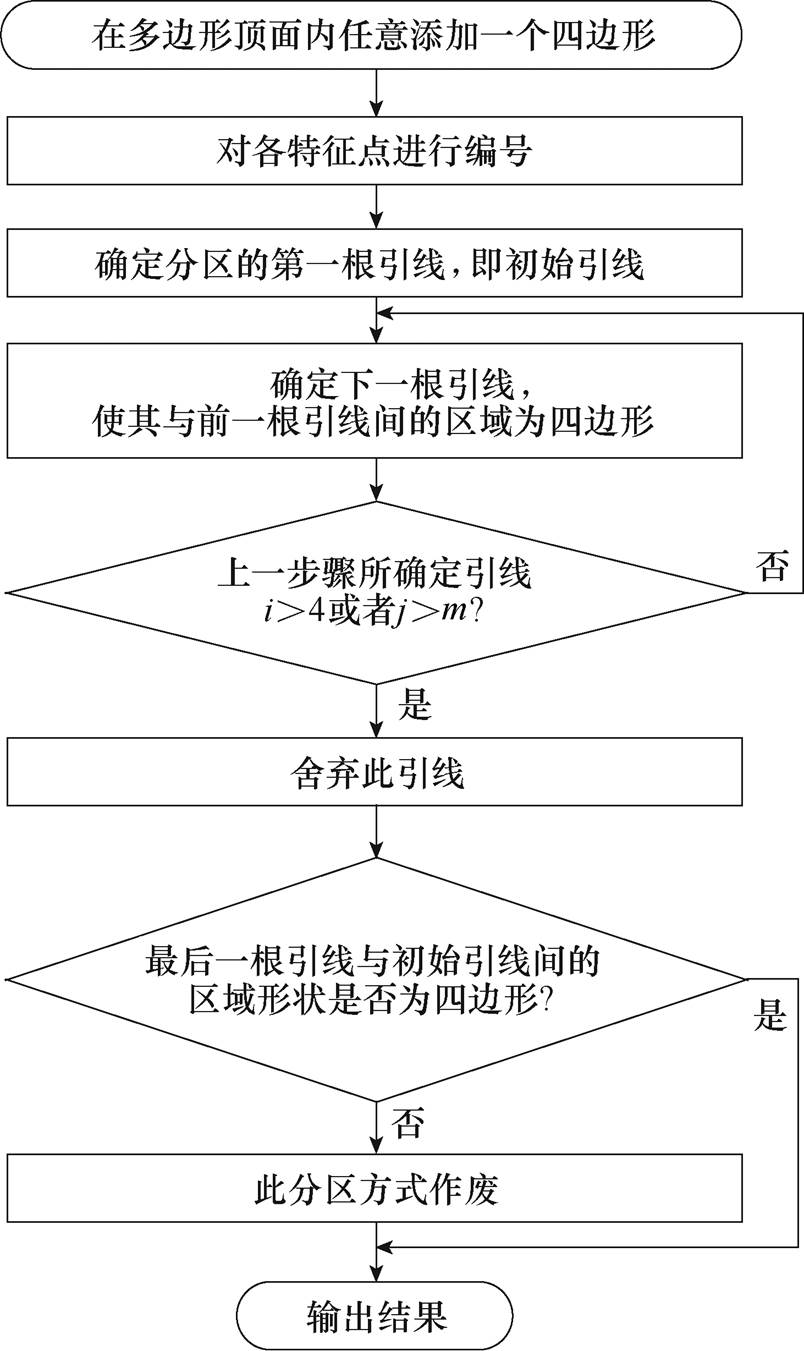
图5 多边形顶面的四边形分区流程
Fig.5 Flow chart of quadrilateral partition of polygon
具体介绍如下:
(1)在多边形顶面内任意添加一个四边形。
(2)对各特征点进行编号,特征点包括内点、角点和边点,其编号规则如下:
设内点用Ni(i=1, 2, 3, 4)表示,并设多边形顶面有m个角点,各角点用Jj(j=1, 2,…, m)表示,同时规定以多边形顶面最短边两侧角点中任取一个为J1,并由J1开始沿其另一侧角点方向依次对其他各角点编号;另外,顶面各边上的边点用Bjk(j=1, 2,…, m;k=1, 2, 3)表示,其下标j表示以第j个角点为起点所对应的第j条边,k表示该边上的第k个边点。
(3)确定分区的第一根引线,即初始引线。为方便说明,规定初始引线为N1与J1间连线。
(4)确定下一根引线,使此引线与其前一根引线之间的区域为四边形。
前一根引线包括内点与角点间连线与内点与边点间连线两种情况,引线确定示意图如图6所示。

图6 引线确定示意图
Fig.6 Schematic ram of lead determination
图6a~图6d表示当前引线为内点Ni与角点Jj间连线的情况,下一根引线可取Ni与Jj+2间连线或Ni+1与Jj+1间连线,详见图6a与图6b;同时如果第j条边或第j+1条边上有边点,则下一根引线还可取Ni+1与Bjk间连线或Ni与B(j+1)k间连线,详见图6c与图6d,其中,Bjk与B(j+1)k分别表示相应边上第k个边点。
图6e~图6h表示当前引线为内点Ni与边点Bjk间连线的情况,下一根引线可取Ni与Jj+2间连线或Ni+1与Jj+1间连线,详见图6e与6f;同时如果第j条边的边点总数l大于当前引线对应边点Bjk的序号k时,则下一根引线还可取Ni+1与Bjp间连线,详见图6g,其中:k<p≤l;此外,如果第j+1条边上有边点,则下一根引线还可取Ni与B(j+1)q间连线,详见图6h,B(j+1)q表示第j+1条边上第q个边点。
(5)对上述确定的引线进行判断,若出现了i>4或者j>m的情况,则此引线必与初始引线相交,因此需要舍弃此引线,否则返回步骤(4)。
(6)判断每种分区方式最后一根引线与第一根引线间的区域形状是否为四边形,若为四边形,则输出该分区方式,否则此分区方式作废。
对于上述所确定的四边形分区方式,因各角点坐标是固定的,而各内点和边点坐标则可进行优化调节;因此以各内点和边点坐标为优化对象,以各四边形区域的综合质量为优化目标,采用果蝇算法对其进行优化,得到该分区方式下最大综合质量所对应的各内点和边点坐标,从而获得多边形顶面所对应的最佳四边形分区方式。相应的优化设计流程如图7所示。
具体介绍如下:
(1)初始化算法参数,包括果蝇飞行半径R、果蝇种群规模Popsize、最大迭代次数Maxgen,并设果蝇个体味道浓度极大值smell_best的初始值为0。
(2)随机赋予果蝇个体位置坐标,即内点、边点坐标,使初代果蝇个体坐标分布在顶面边线和顶面内部的随机位置,使非初代果蝇个体坐标分布在以保留的内点、边点为圆心,以果蝇飞行半径R为半径的圆内随机位置。
(3)计算果蝇个体味道浓度值,即各四边形区域的综合质量Qav,具体步骤为:①首先根据各四边形区域的顶点坐标及式(17)~式(19),计算得到混合积a、b、c,再根据所得混合积判定出各四边形区域的形状;②根据各四边形区域形状并结合式(20)及式(12)~式(16),计算得到各四边形区域的质量;③再根据所得各四边形区域质量及式(21),即可计算出各四边形区域的平均质量Qav,并以该平均质量作为果蝇个体的味道浓度值。
(4)比较果蝇个体味道浓度值Qav,获得此次迭代中果蝇个体味道浓度值的最大值max_smell。
(5)判断此次迭代中果蝇个体味道浓度最大值max_smell是否优于所保留的果蝇个体味道浓度极大值smell_best;若是,则将max_smell值取代smell_best值作为新的果蝇个体味道浓度极大值,并保留其对应的果蝇个体位置坐标;否则,执行步骤(6)。
(6)进入迭代寻优,判断迭代次数是否达到最大迭代次数Maxgen;若是,则进入步骤(7);否则,返回步骤(2)。
(7)输出结果,即输出果蝇个体味道浓度极大值smell_best所对应的各内点、边点坐标。
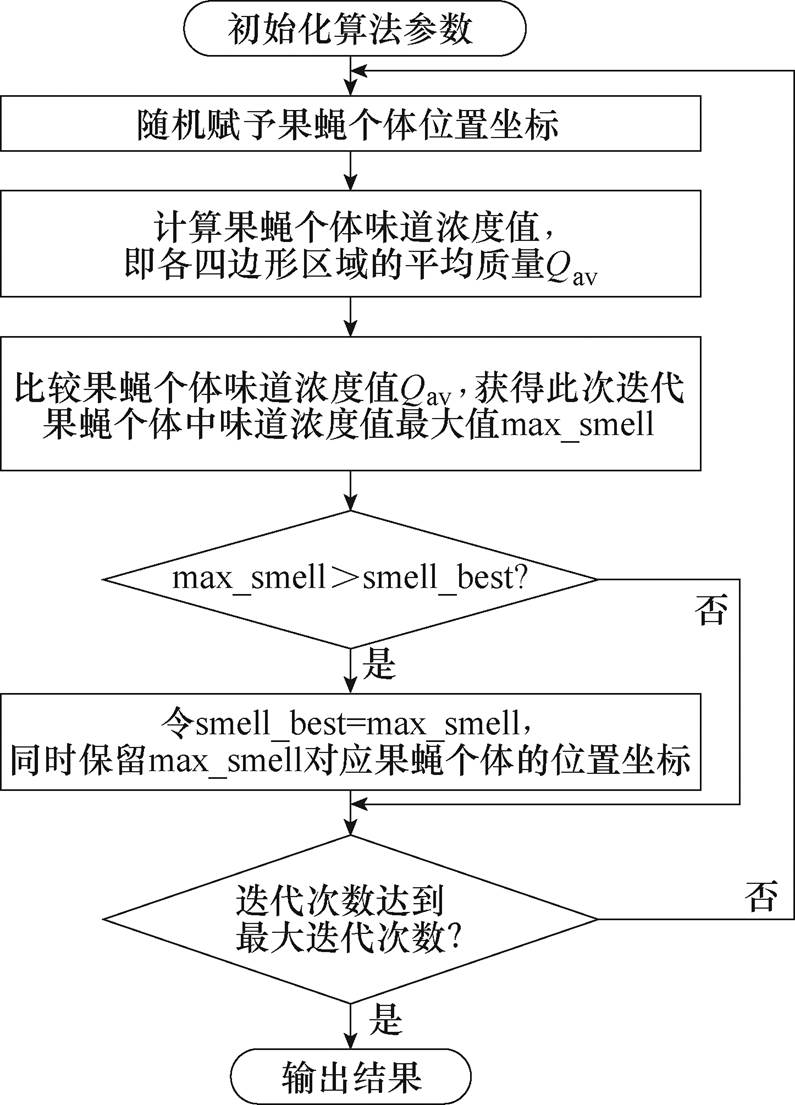
图7 四边形分区优化设计流程
Fig.7 Quadrilateral partition optimization design flow chart
为验证上述多边形柱状模型结构化网格优化划分方法的效果,以Y100L2-4型交流牵引电机为例,采用有限元法对其进行温度场分析,其主要结构参数见表1,转子导条顶面示意图如图8所示。
在针对交流牵引电机有限元法模型进行网格划分时,其转子导条采用结构化网格优化划分方法,其余部位则采用传统网格划分法;并设置转子导条优化划分的相关参数为:果蝇飞行半径取0.2,果蝇个体数设为2 000,迭代次数取300。所得转子导条结构化网格优化划分结果如图9所示,对应的交流牵引电机三维温度场分布如图10所示。
表1 Y100L2-4型电机主要结构参数
Tab.1 Main structural parameters of Y100L2-4 motor
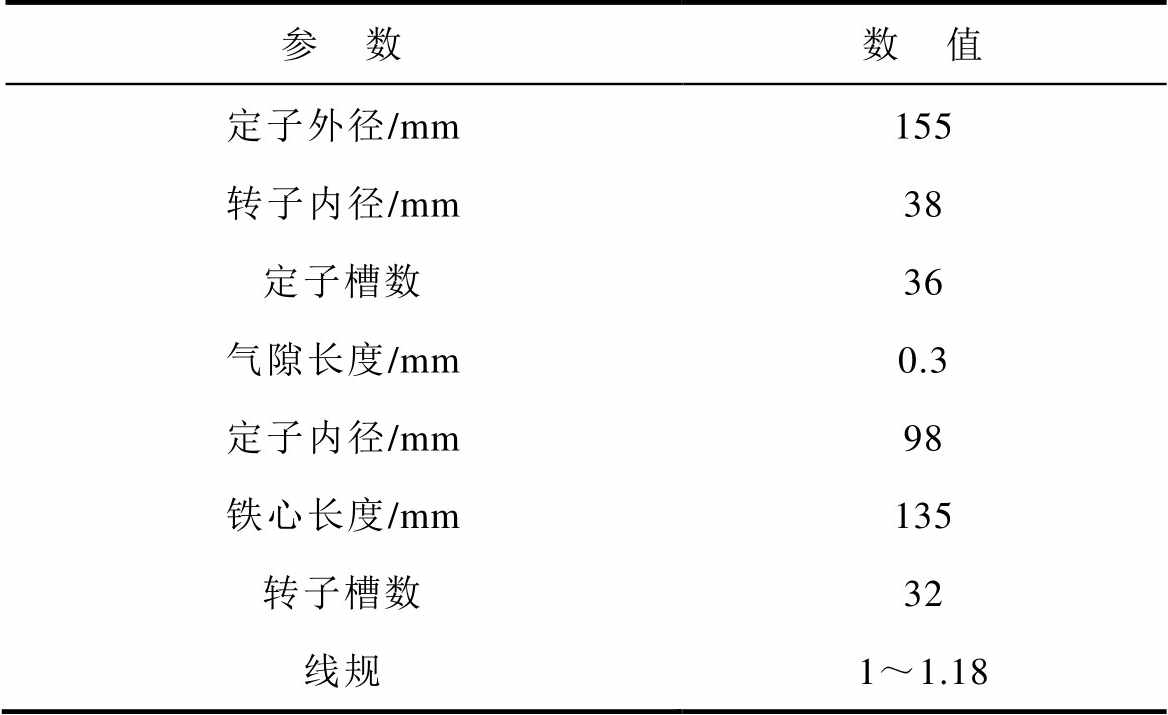
参 数数 值 定子外径/mm155 转子内径/mm38 定子槽数36 气隙长度/mm0.3 定子内径/mm98 铁心长度/mm135 转子槽数32 线规1~1.18
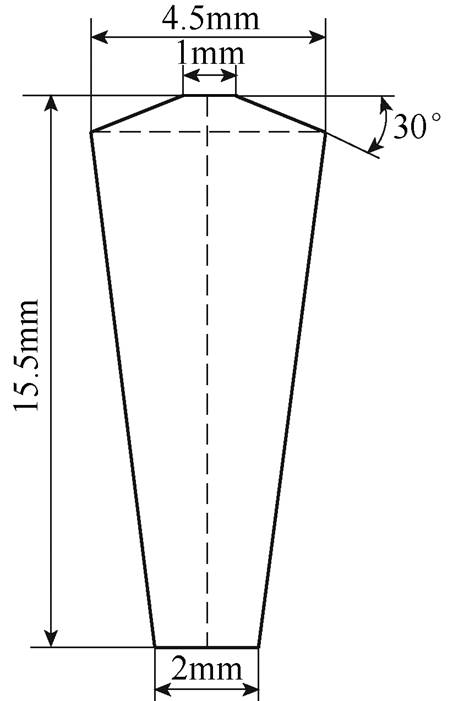
图8 转子导条顶面示意图
Fig.8 Schematic diagram of top surface of rotor guide bar

图9 转子导条结构化网格优化划分结果
Fig.9 Results of structural mesh optimization of rotor guide bar
同时,为便于说明本文提出的结构化网格优化划分方法的效果,再针对上述转子导条采用传统结构化网格划分,其余部位网格划分方法不变,则得到相应的转子导条网格划分结果及电机三维温度场分布分别如图11和图12所示。
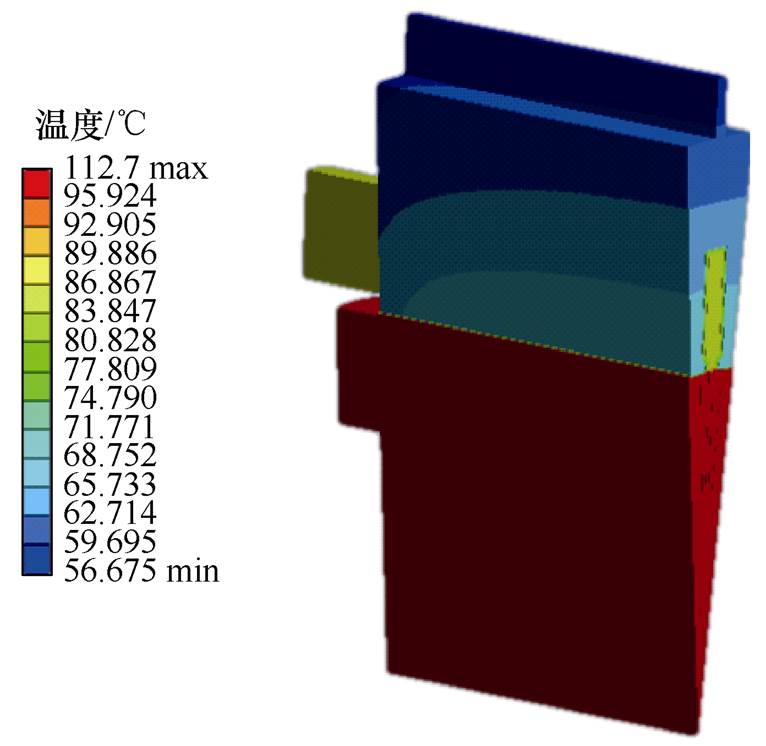
图10 转子导条结构化网格优化划分对应的电机温度场分析仿真
Fig.10 Simulation diagram of motor temperature field analysis corresponding to structural grid optimization of rotor guide bar

图11 转子导条传统结构化网格划分结果
Fig.11 Results of traditional structured mesh generation for rotor guide bar
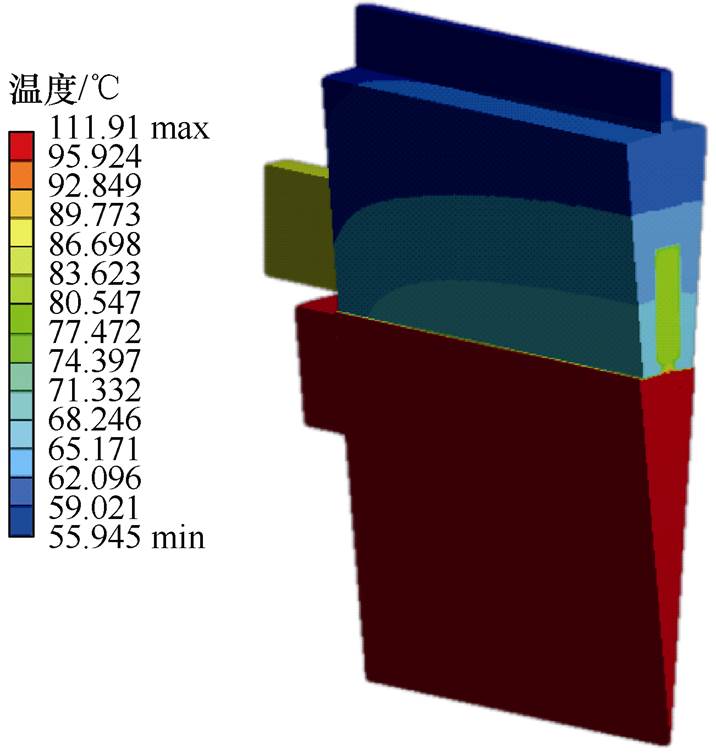
图12 传统结构化网格划分后电机温度场分析仿真
Fig.12 Simulation diagram of motor temperature field analysis after traditional structured grid division
对应于上述两种网格划分方法所得转子导条网格划分质量见表2,而对应电机温度场分析所得各主要部位的温度则见表3。
表2 两种网格划分法对应的转子导条网格划分质量
Tab.2 The meshing quality of rotor guide bar corresponding to two meshing methods
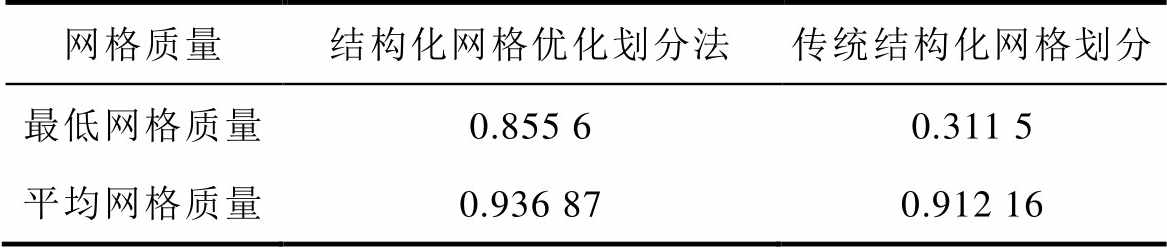
网格质量结构化网格优化划分法传统结构化网格划分 最低网格质量0.855 60.311 5 平均网格质量0.936 870.912 16
表3 电机主要部位温度
Tab.3 Temperature of main parts of motor (单位: ℃)
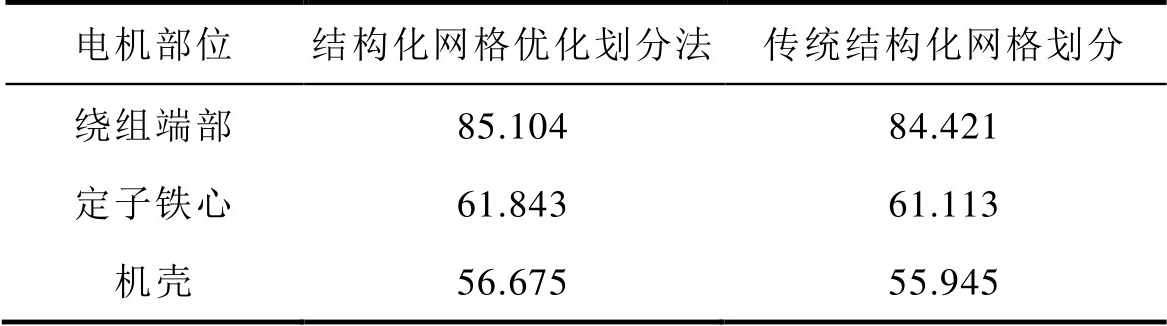
电机部位结构化网格优化划分法传统结构化网格划分 绕组端部85.10484.421 定子铁心61.84361.113 机壳56.67555.945
由表2可见,相较于传统结构化网格划分方 法,本文提出的结构化网格优化划法所得网格的平均质量虽然只提高了0.024 71,但最低网格质量却由0.311 5提高到0.855 6,相当于提高了1.74倍。由于温度场分析误差主要受低质量网格的影响,因而低质量网格的质量得到提升后,将会显著改善分析结果的准确性。同时由表3可见,采用结构化网格优化划法所得各主要部位的温度场分析结果,相对于传统结构化网格划分法,其偏差均达到了0.6℃以上,说明两种方法的效果存在较大差异。
为进一步验证本文提出的多边形柱状模型结构化网格优化划分方法的效果,构建交流牵引电机实验装置进行验证,如图13所示。该实验装置选用Y100L2-4型交流牵引电机,其主要参数见表4,除此之外还有控制器、磁粉制动器、张力控制器、温度传感器、温度显示器、转矩转速测量仪等。其中,定子绕组端部、定子铁心温度采用温度传感器检测,而电机机壳温度则采用红外测温仪测量。
实验时电机以额定工况运行,当电机各部分温度显示稳定后,分别读取相应的温度值,见表5。其中,电机机壳温度因采用红外测温仪测量,存在一定的误差,故对其进行了相应的补偿[23]。
对照表3与表5,得到在电机温度场分析中两种网格划分法所得电机各主要部件温度相对于其实测温度的相对误差,见表6。可见,采用结构化网格优化划分方法,使电机各主要部件温度相对于其实测温度的偏差有了明显的下降,从而验证了该方法的有效性。

图13 电机温升实验平台
Fig.13 Motor temperature rise test platform
表4 电机主要参数
Tab.4 Main parameters of motor

参 数数 值 额定功率/kW3 额定电压/V220 额定转速/(r/min)1 430 额定电流/A6.6
表5 电机温度实验值
Tab.5 Experimental value of motor temperature

电机部位稳态温度/℃ 定子绕组端部86.00 定子铁心62.80 机壳57.31
表6 仿真结果相对实验结果的偏差比较
Tab.6 Comparison of deviation between simulation results and experimental results

部位相对误差(%) 结构化网格优化划分方法传统结构化网格划分 绕组端部1.041.84 定子铁心1.522.69 机壳1.112.34
针对交流牵引电机转子导条等多边形柱状热分析模型结构化网格划分质量不高的问题,提出一种结构化网格优化划分方法。建立了交流牵引电机热分析的求解域模型,确定了交流牵引电机多边形柱状模型的四边形区域质量计算方法,提出一种基于内置四边形的多边形柱状模型四边形区域划分方法,并采用果蝇算法对各分区方式的综合质量进行优化以获得相应的最佳分区方式,最后通过仿真和实验对所提出的网格划分方法进行验证,同时与传统结构化网格划分方法进行对比分析。结果表明,本文所提出的结构化网格优化划分法较传统结构化网格划分法显著提高了交流牵引电机多边形柱状模型的网格划分质量,由此有效地提高了交流电机热分析的准确性,对于指导交流牵引电机的优化设计具有重要意义。
参考文献
[1] Shafighy M, Khoo S, Kouzani A Z. Modelling and simulation of regeneration in AC traction propulsion system of electrified railway[J]. IET Electrical Systems in Transportation, 2015, 5(4): 145-155.
[2] Jurkovic S, Rahman K M, Morgante J C, et al. Induction machine design and analysis for general motors e-assist electrification technology[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 631-639.
[3] 佟文明, 孙静阳, 舒圣浪. 不同数值方法在自扇冷永磁同步电机三维热分析中的应用[J]. 电工技术学报, 2017, 32(1): 151-159.
Tong Wenming, Sun Jingyang, Shu Shenglang. Appli- cation of different numerical methods in three dimensional thermal analysis of self-fan-cooled permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(1): 151-159.
[4] 上官璇峰, 蒋思远, 周敬乐, 等. 双转子双鼠笼永磁感应电机三维全域温度场分析[J]. 电机与控制学报, 2018, 22(11): 58-66.
Shangguan Xuanfeng, Jiang Siyuan, Zhou Jingle, et al. Analysis on 3-D temperature field of dual-rotor permanent magnet induction motor with double squirrel cage[J]. Electric Machines and Control, 2018, 22(11): 58-66.
[5] Cai Xiuhua, Cheng Ming, Zhu Sa, et al. Thermal modeling of flux-switching permanent-magnet machines considering anisotropic conductivity and thermal contact resistance[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3355-3365.
[6] 陈剑, 刘春明, 王茂海, 等. 广义有限差分法在静态电磁场计算中的应用[J]. 电工技术学报, 2018, 33(7): 1579-1587.
Chen Jian, Liu Chunming, Wang Maohai, et al. Application of the generalized finite difference method to static electromagnetic problems[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1579- 1587.
[7] 刘小梅. 封闭式小型异步电机的温度场研究[D]. 焦作: 河南理工大学, 2014.
[8] Zhang Yujiao, Ruan Jiangjun, Huang Tao, et al. Calculation of temperature rise in air-cooled induction motors through 3-D coupled electromagnetic fluid- dynamical and thermal finite-element analysis[J]. IEEE Transactions on Magnetics, 2012, 48(2): 1047- 1050.
[9] 石晶. 汽车发电机温度场有限元分析与计算[J]. 微电机, 2015, 48(5): 41-46.
Shi Jing. Finite element analysis and calculation of temperature field of automobile generator[J]. Micro- motors, 2015, 48(5): 41-46.
[10] 谢颖, 王泽, 单雪婷. 基于多场量的笼型感应电机三维瞬态磁热固耦合计算分析[J]. 中国电机工程学报, 2016, 36(11): 3076-3084.
Xie Ying, Wang Ze, Shan Xueting. Calculation and analysis of three-dimensional transient magneto thermo mechanical coupling of cage induction motor based on multi field[J]. Proceedings of the CSEE, 2016, 36(11): 3076-3084.
[11] 谢颖, 黎志伟, 郭金鹏. 电动汽车用高功率密度感应电机的设计与研究[J]. 电机与控制学报, 2020, 24(2): 46-54.
Xie Ying, Li Zhiwei, Guo Jinpeng. Design and research on high power density induction motor in electric vehicle[J]. Electric Machines and Control, 2020, 24(2): 46-54.
[12] 邰永. 感应电机全域三维瞬态温度场分析[J]. 中国电机工程学报, 2010, 30(30): 114-120.
Tai Yong. Three dimensional transient temperature field analysis of induction motor[J]. Proceedings of the CSEE, 2010, 30(30): 114-120.
[13] 刘刚, 孙立鹏, 王雪刚, 等. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报, 2018, 33(21): 4909-4918.
Liu Gang, Sun Lipeng, Wang Xuegang, et al. Improve- ment of core loss calculation method and simulation application under sinusoidal and harmonic excita- tions[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.
[14] 刘伟亮. 电动车用感应电机损耗及热系统的研究[D]. 哈尔滨: 哈尔滨工业大学, 2006.
[15] 吴柏禧, 万珍平, 张昆, 等. 考虑温度场和流场的永磁同步电机折返型冷却水道设计[J]. 电工技术学报, 2019, 34(11): 2306-2314.
Wu Boxi, Wan Zhenping, Zhang Kun, et al. Design of reentrant cooling channel in permanent magnet synchronous motor considering temperature field and flow field[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2306-2314.
[16] Li Weili, Cao Junci, Zhang Xiaochen. Electrothermal analysis of induction motor with compound cage rotor used for PHEV[J]. IEEE Transactions on Industrial Electronics, 2010, 57(2): 660-668.
[17] 李伟力. 感应电动机定转子全域温度场数值计算及相关因素敏感性分析[J]. 中国电机工程学报, 2007, 27(24): 85-91.
Li Weili. Numerical calculation of temperature field of stator and rotor of induction motor and sensitivity analysis of related factors[J]. Proceedings of the CSEE, 2007, 27(24): 85-91.
[18] Hatziathanassiou V, Xypteras J, Archontoulakis G. Electrical-thermal coupled calculation of an asy- nchronous machine[J]. Archiv für Elektrotechnik, 1994, 77(2): 117-122.
[19] 吴胜男, 李文杰, 安忠良, 等. 变速恒压混合励磁风力发电机的热分析[J]. 电工技术学报, 2019, 34(9): 1857-1864.
Wu Shengnan, Li Wenjie, An Zhongliang, et al. Thermal analysis of variable-speed constant-voltage hybrid excited wind generators[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1857- 1864.
[20] 王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报, 2019, 34(增刊1): 22-29.
Wang Xiaofei, Dai Ying, Luo Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.
[21] 李海峰, 吴冀川, 刘建波. 有限元网格剖分与网格质量判定指标[J]. 中国机械工程, 2012, 23(3): 368- 377.
Li Haifeng, Wu Jichuan, Liu Jianbo. Finite element mesh generation and mesh quality criteria[J]. China Mechanical Engineering, 2012, 23(3): 368-377.
[22] 张青春. 基于四叉树的复杂边界四边形网格自适应生成方法研究[D]. 沈阳: 东北大学, 2012.
[23] 廖盼盼, 张佳民. 红外测温精度的影响因素及补偿方法的研究[J]. 红外技术, 2017, 39(2): 173-177.
Liao Panpan, Zhang Jiamin. Research on the influence factors and compensation methods of infrared tem- perature measurement accuracy[J]. Infrared Tech- nology, 2017, 39(2): 173-177.
A Structured Mesh Optimization Method for Polygonal Columnar Thermal Analysis Model Based on Drosophila Algorithm
Abstract The structured mesh generation in polygonal cylindrical thermal analysis model has low quality, such as rotor guide bar of AC traction motor. Therefore, an optimized method of structured mesh generation is proposed. In this paper, the solution domain model of AC traction motor thermal analysis is established, and the quadrilateral region mass calculation method of AC traction motor polygonal cylinder model is determined. Then, a quadrilateral region division method of polygonal cylinder model based on built-in quadrilateral is proposed, and the fruit fly optimization algorithm (FOA) is used to optimize the comprehensive quality of each partition mode to obtain the corresponding optimal partition mode. Through the finite element method, the proposed method is compared with the traditional structured mesh generation method, and its effect is verified. Finally, the above analysis is further verified by experiments. The results show that compared with the traditional structured mesh generation method, the method proposed in this paper greatly improves the mesh generation of the polygon cylinder model of AC traction motor, thereby improving the accuracy of thermal analysis of AC traction motor, which has good application value.
keywords:AC traction motor, polygonal columnar thermal analysis model, structured grid, optimized partition method, fruit fly optimization algorithm (FOA)
中图分类号:TM343+.2
DOI: 10.19595/j.cnki.1000-6753.tces.200353
长株潭国家自主创新示范区专项资助项目(2017XK2303)。
收稿日期 2020-04-09
改稿日期 2020-06-16
郭宇轩 男,1994年生,硕士研究生,研究方向为电力电子与电力传动。E-mail: 453877764@qq.com
张小平 男,1966年生,博士,教授,硕士生导师,研究方向为电力电子与电力传动、智能控制等。E-mail: zxp836@163.com(通信作者)
(编辑 崔文静)