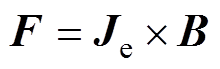（1）摘要 电磁成形是利用脉冲电磁力实现轻质合金快速塑性成形的一种高能率加工技术，可显著提高材料的成形极限并改善成形性能。吸引式电磁成形则是其中的一种独特应用，利用两种不同脉宽的电流驱动同一线圈来产生吸引式电磁力，适用于板件凹痕修复、微小管件成形等领域。单线圈结构对两种电流的参数匹配要求非常严格，且能量利用效率极低。为解决这一问题，该文提出两种电流各自驱动一个线圈的双线圈结构吸引式电磁成形方案，并进行仿真验证。然而研究过程中发现，双线圈结构带来新的涡流密度竞争现象，将会引起成形缺陷。为了消除这一缺陷，该文进一步研究涡流竞争产生的原因和机制，最终通过调整线圈的结构参数，在直径200mm的AA1060-H28铝合金板件双线圈吸引式电磁成形方案中，消除成形缺陷。相关研究结果能够加深对吸引式板件电磁成形过程的理解，对于拓展电磁成形技术在板件加工上的应用具有重要意义。
关键词：电磁成形 双线圈 板件 吸引力 涡流竞争
电磁成形（Electromagnetic Forming, EMF）是一种在线圈中通以脉冲大电流来产生脉冲磁场，进而在金属材料中感应涡流密度，涡流密度和磁场共同作用产生洛伦兹力，从而驱动工件发生塑性变形的一种高速率成形方法。该技术能显著提高铝、镁等轻质合金的成形极限，抑制起皱，减小回弹，在轻质合金的加工上具有巨大潜力[1-3]。目前，这一技术广泛地应用于金属管件和板件的电磁胀形[4-5]、电磁压缩[6-7]、电磁冲压[8-9]和电磁焊接[10-12]等工艺。
通常，电磁成形使用螺线管线圈作为驱动线圈，由其产生的脉冲磁场和在工件上产生的感应涡流密度共同作用产生电磁力。理论上，电磁力的方向及大小可通过仅改变驱动电流参数进行调控，灵活性远胜于传统机械力。但是目前大量的研究[4-13]仍普遍专注于排斥式电磁力成形。这主要是由于现有的电磁成形电流加载方式非常单一，工件上的涡流密度和磁场高度耦合，在楞次定律作用下，其产生的电磁力几乎都为排斥力。这种局限性既没有发挥出电磁力灵活调控的特点，也极大地制约了电磁成形技术的应用场景。因此，邓将华等研究了平板线圈放电波形对工件上电磁力的影响，提出了采用缓慢上升沿、加速下降沿的脉冲电流波形来产生吸引式电磁力的方案[14]。基于这一研究，曹全梁等[15]和熊奇等[16]相继开展了板件和小管件的电磁吸引力成形研究。他们通过双电源系统分别产生长、短脉宽的电流，驱动同一线圈，产生出符合上述特点的电流波形，进而将产生的吸引式电磁力用于铝合金成形，并通过实验验证了其可行性。这些研究充分体现了电磁成形灵活调控的特点，拓展了电磁成形在凹痕修复和微小管件成形领域的应用。
然而，单线圈方案要求两套电源的放电参数严格匹配，否则难以产生符合要求的合成电流波形。同时，其能量利用效率也较低。Ouyang Shaowei等提出采用内、外同轴放置的双线圈模型来改善这一问题[17]。两个线圈分别接入两套电源，并通以不同脉宽的电流，以长脉宽电流来提供变化相对缓慢的背景磁场，以短脉宽电流所产生的快速变化的磁场来提供所需的感应涡流密度，进而产生需要的吸引力，并通过仿真及实验验证了管件吸引力胀形的可 行性。
双线圈方案相对于单线圈方案更加灵活，然而也带来了新的问题。在单线圈方案中，工件上产生的感应涡流密度方向在同一时间是保持一致的。然而，在双线圈方案中，则会同一时间在工件的不同位置存在方向相反的感应涡流密度，进而导致电磁力分布不一致，在工件整体区域受吸引力作用时，其局部区域仍然存在排斥力并最终导致成形件上产生凹痕。这种涡流竞争现象是双线圈方案的固有属性，无法忽略，如何消除其对成形效果的影响也亟待研究。
因此，为了解决这一问题，本文系统性研究了涡流竞争产生的原因和机制，通过建立双线圈方案下的板件吸引力电磁成形仿真模型，对多种结构参数的线圈所产生的涡流密度现象进行了研究，力图阐明涡流密度与线圈结构间的关系，并分析了其对成形效果的影响。最后发现，通过改变线圈L（通入长脉宽电流）的层数可以降低涡流竞争对成形形状的影响，可有效提高板件的轴向位移，并最终消除板件凹痕，改善成形效果。
在电磁成形过程中，由电容器电源提供的脉冲电流流经驱动线圈产生磁场，同时在板件上产生感应涡流密度，涡流密度和磁场相互作用产生洛伦兹力驱动板件变形。作用在板件上的洛伦兹力密度可以表示为
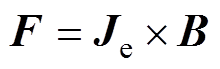（1）式中，Je和B分别为板件上感应涡流密度和磁通密度。在忽略螺线管线圈的渐近线影响时，螺线管线圈可以视作若干个轴向分布的同轴闭合圆环。故由于其结构影响，涡流密度Je只有环向分量Jephi，因此，根据洛伦兹力公式，洛伦兹力F可以表示为
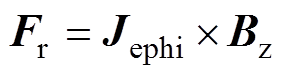（2）
（3）式中，Bz和Br分别为磁通密度B的轴向分量和径向分量；Fr和Fz则分别为板件所受到的洛伦兹力径向分量和轴向分量；负号表示该力为排斥力。而轴向分量Fz是板件成形的主要作用力，但是其方向却难以改变，这主要是因为涡流密度Je与磁通密度B是耦合的。要将Fz的方向从排斥变为吸引，一种可行的方式就是将涡流密度和磁通密度相互解耦，使涡流密度或磁通密度的方向发生反向。但是，单脉冲电源系统无法有效实现解耦，因此，就需要两套电源装置通过电流的时延控制分别产生如图1所示的高频（短脉宽）和低频（长脉宽）的电流来调控涡流密度和磁通密度的方向和大小（电流和磁通密度的变化率呈正相关）。长、短脉宽电流在板件上产生的感应涡流密度如图2所示。
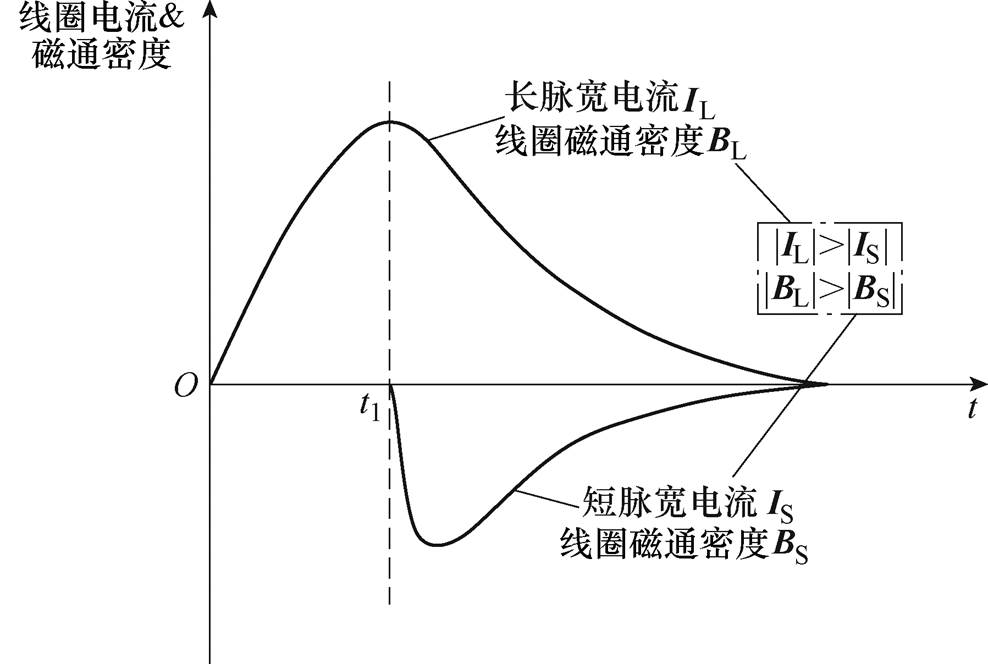
图1 长、短脉宽的电流和磁通密度波形
Fig.1 Current and magnetic field waveforms with long and short pulse widths
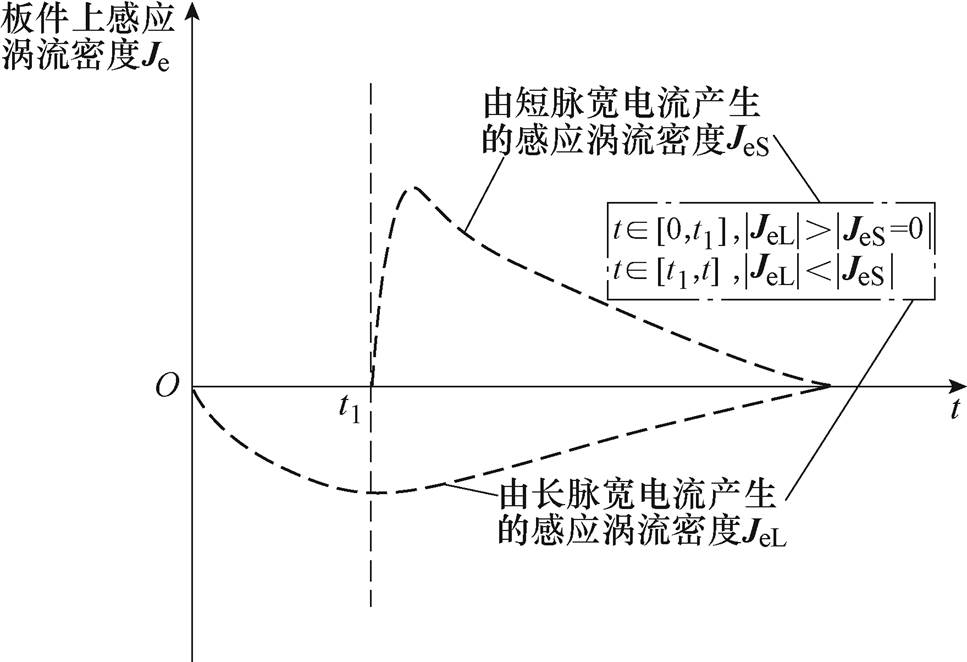
图2 长、短脉宽电流在板件上产生的感应涡流密度
Fig.2 Induced eddy currents density produced by long and short pulse width currents on a plate
根据式（3）可知，当涡流密度或磁通密度其中之一的方向发生改变时，板件上电磁力的方向也发生改变。因此，本文拟采用双线圈-双电源系统在板件上产生如图1和图2所示的磁通密度和涡流密度。此时，板件上的轴向电磁力可以表示为
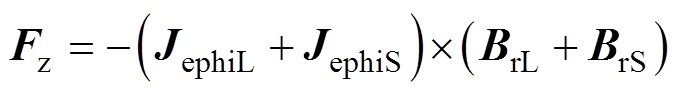（4）式中，JephiL和JephiS分别为长脉宽和短脉宽电流在板件上产生的环向感应涡流密度，且在这里规定涡流密度的顺时针方向为正；BrL和BrS则分别为长脉宽和短脉宽电流所产生的磁通密度的径向分量，且规定磁通密度BrL的方向为正方向。令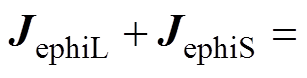
，
，则JC为合成（竞争）涡流密度，BrC为合成磁通密度，且|BL|＞|BS|，|BrL|＞|BrS|，BrC的方向为正方向。
进而从式（4）中可以推导出，当感应涡流密度的和为负值时，那么电磁力就发生了反向，即从排斥力变为吸引力，则板件上的轴向电磁力可以表 示为
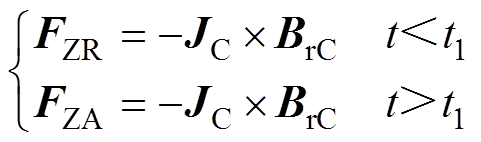（5）式中，短脉宽电流在t1时刻导通；FZR和FZA分别为随时间变化板件上受到的排斥力和吸引力，即双线圈吸引式板件的成形方法，板件上的涡流密度竞争是实现吸引力的最重要环节之一，其主旨就是利用如图3所示电流导通后，板件上的磁通密度和感应涡流密度分布中，相互叠加的合成磁通密度BrC与在t1时刻后反向的合成涡流密度JC共同作用产生吸引式电磁力。
文献[18]中提出的双线圈吸引式板件的成形方法，主要将线圈L和S内外同轴放置于板件上方，利用长、短脉宽电流通入线圈L和S中分别产生涡流密度和磁通密度。但是由于线圈L的位置，在同一时刻使板件上存在方向相反的涡流密度（涡流密度反向区域），最终导致板件成形产生凹痕缺陷。因此，本文拟通过调整线圈的结构、与板件的相对位置，消除或减小涡流密度反向区域的感应涡流密度，进而优化板件上电磁力的分布，减小其在该区域受到的排斥力。长、短脉宽电流放电系统示意图如图4所示，双线圈吸引式板件成形系统图5所示[18-19]。图4和图5中，双线圈吸引式板件电磁成形系统，涉及到外电路、线圈、压边等模块，且线圈L和S的放电电流分别由图4所示的长、短脉宽电流系统产生。且图4中的外电路放电参数见表1。其具体实施方案主要如图5所示。
图3 电流导通后，板件上的磁通密度和感应涡流密度分布
Fig.3 After the current conduction, the magnetic flux density and induced eddy current density distribution on the plate
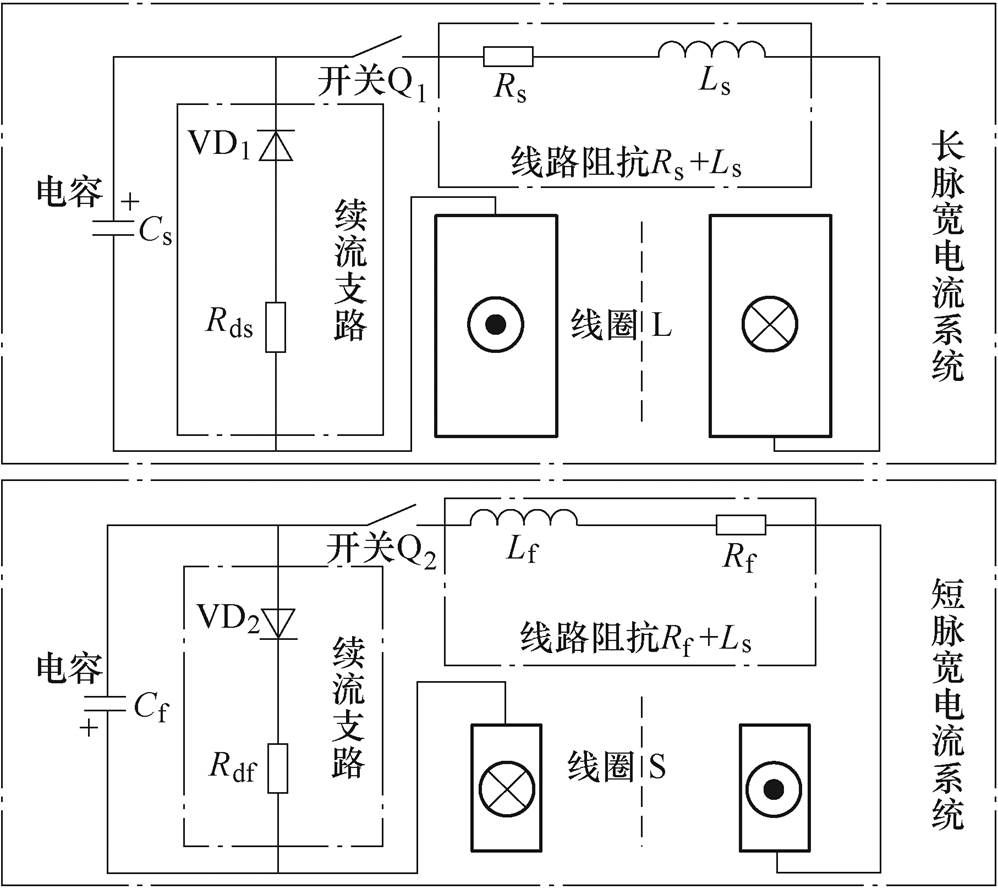
图4 长、短脉宽电流放电系统示意图
Fig.4 Long and short pulse width current discharge system
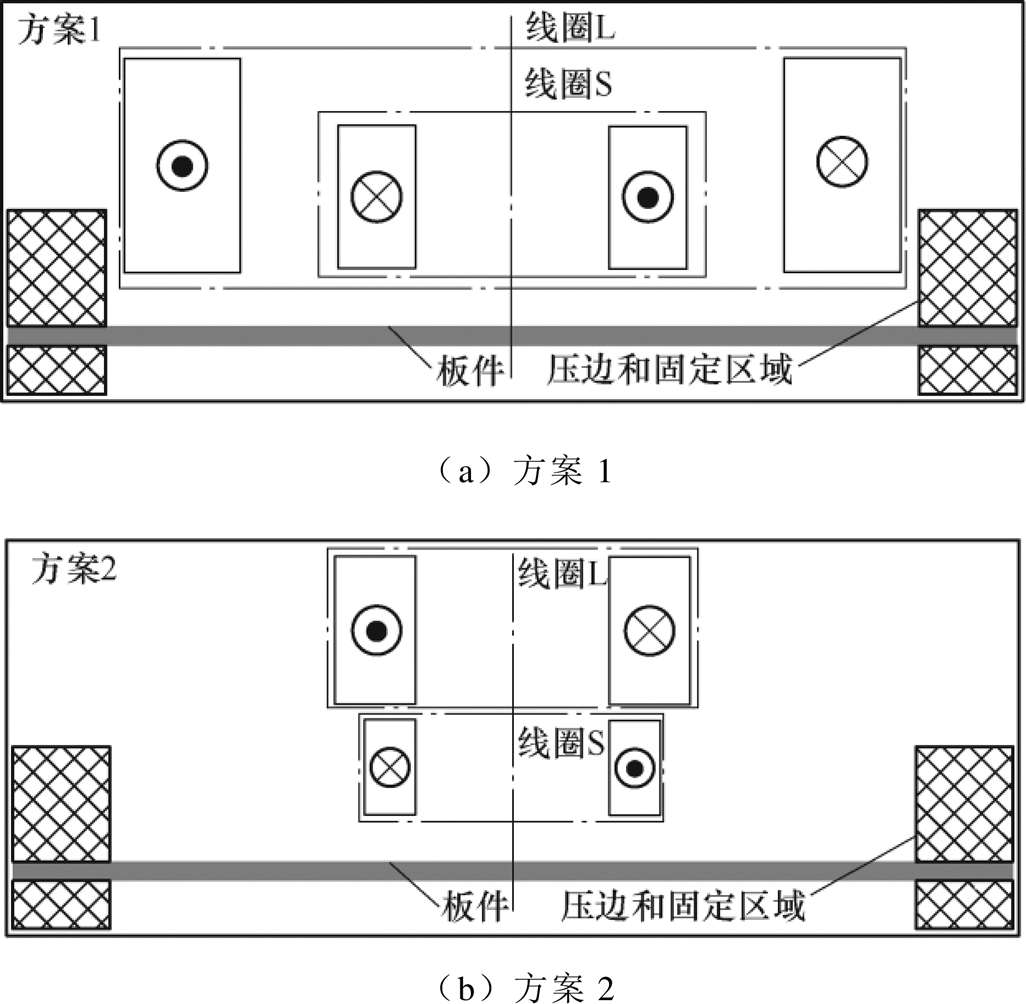
图5 双线圈吸引式板件成形系统
Fig.5 Double-coil attraction plate forming system
表1 外电路放电参数
Tab.1 External circuit discharge parameters
放电参数长脉宽电流系统短脉宽电流系统 参数数值参数数值 放电电压Us/kV10Uf/kV8.8 电容Cs/mF5.6Cf/mF120 线路电阻Rs/W0.35Rf/mW8 线路电感Ls/mH0.5Lf/mH10 续流电阻Rds/W0.2Rdf/mW10
短脉宽电流导通后，板件上的感应涡流密度分布如图6所示。板件成形区域的合成涡流密度以JephiS为主，但由于线圈S的尺寸和位置，局部（涡流密度反向区域）就会存在以涡流密度JephiL为主的现象。而涡流密度反向区域形成的原因，主要是由于该区域的涡流密度|JephiL|＞|JephiS|，且两者方向相反，导致合成涡流密度方向与JephiL一致。方案1中由于线圈L和S内外同轴放置，会造成线圈L下方区域的反向涡流密度区域面积更大，使板件在该区域受到较大的排斥力，形成凹痕缺陷。
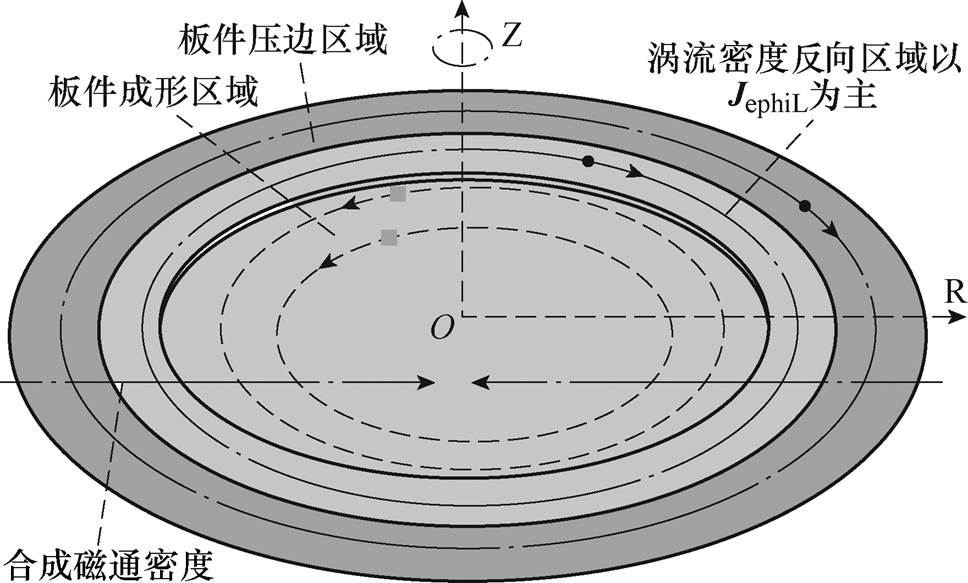
图6 短脉宽电流导通后，板件上的感应涡流密度分布
Fig.6 After the short pulse current conduction, the induced eddy current density distribution on the plate
因此，本文主要研究在放电参数一定时，方案2中线圈L的结构、尺寸及位置对于板件上感应涡流密度分布和磁通密度的影响，进而讨论其对于板件吸引式成形的影响。
由式（2）、式（3）可知，电磁力的分布与板件上的涡流密度和磁通密度密切相关，而板件上的涡流密度分布又主要取决于线圈电流的变化率，板件上的磁通密度取决于线圈电流的脉宽。因此，在放电参数一定时，为了使线圈L在板件上产生的感应涡流密度小于线圈S，则通过增大线圈L的匝数，进而增大其电感，减小线圈L电流变化率。在方案2中，为了使线圈所产生的磁通密度能满足成形要求，线圈的间距不能过大，而线圈间的间距又直接影响了线圈的工装设计。因此，基于这一考虑，本文也相应地对线圈的结构进行了设计。
2.2.1 线圈设计
由于方案2中线圈为上、下同轴放置，其间距直接影响到板件上的磁通密度，故对于如何设计线圈L和S的出线及鼻子的是必须考虑的。因此，在本文中将线圈L设计为从上端出线，且鼻子安装在线圈L上端；线圈S则设计为从下端出线，且鼻子安装在线圈S下端，线圈L和S的接线及出线设计示意图如图7所示。此外，考虑到两个线圈之间需要预留的工装空间，本文将线圈之间间距设为5mm。
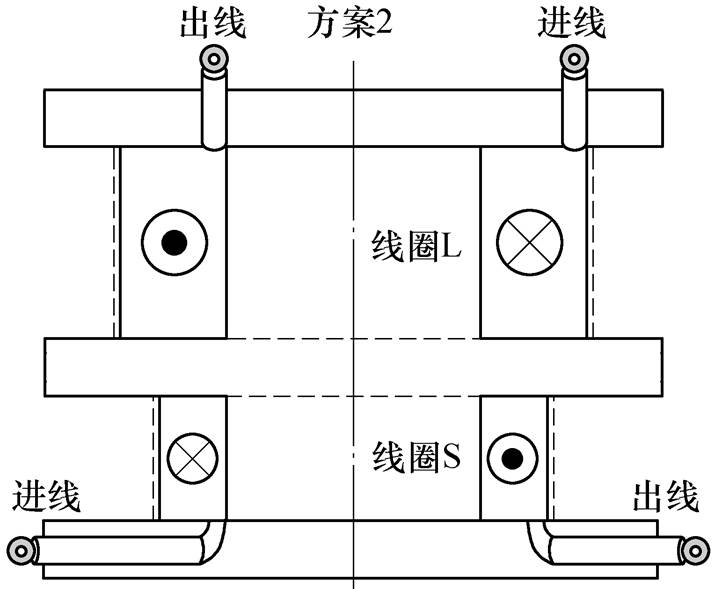
图7 线圈L和S的接线及出线设计示意图
Fig.7 Schematic diagram of wiring and outlet of coils L and S
2.2.2 线圈布局
本文建立了如图8所示双线圈吸引式板件成形仿真模型。图中，线圈L的匝数为45匝，内径为30mm，外径为52mm；线圈S的匝数为18匝，内径为30mm，外径为44.5mm。线圈L和S均为纯铜材料绕制而成，并采用0.5mm厚度的柴龙纤维进行层间加固，以确保线圈的结构稳定性。选用文献[15]中所采用的型号为AA1060-H28的铝合金板件作为研究对象，其材料属性主要包含密度（2.71g/cm3）、电导率（3.72×107S/m）、杨氏模量（69GPa）、泊松比（0.33）和初始屈服应力（98MPa）。且该板件半径为100mm，厚度为1mm，并采用电导率为0的柴龙纤维材料对板件进行压边及固定。
图8 双线圈吸引式板件成形仿真模型
Fig.8 Simulation model of double-coil attraction plate forming
由于电磁成形中板件的应变率很高，对最终成形效果有很大的影响，故本文采用文献[20]中提出的Cowper-Symonds本构模型对板件的变形过程进行分析，故其应力d -应变e 可表示为
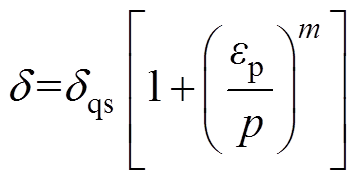（6）式中，dqs为准静态应力，dqs=98MPa；ep为塑性应变率；而对于铝合金板件，p=6 500s-1，m=0.25。
电磁成形是一个涉及电路、电磁通密度和固体力学场的多物理场耦合过程。因此大量文献[21-23]均采用有限元法分析电磁成形的物理过程。故在本节中由COMSOL Multiphysics有限元软件建立了如图8所示的考虑了板件位移和形变速率影响的全耦合数值仿真模型，板件吸引式成形仿真算法流程[24-25]如图9所示。
根据对式（3）的分析可知，当板件上感应涡流密度发生反向、但磁通密度方向不变时，轴向电磁力方向将会改变，即可实现板件的吸引式成形。而线圈L和S中的电流波形如图10所示，线圈L的电流在2.2ms时到达峰值14.4kA，而线圈S的电流在t1=2.2ms时导通，在2.26ms时就到达了峰值20.02kA。
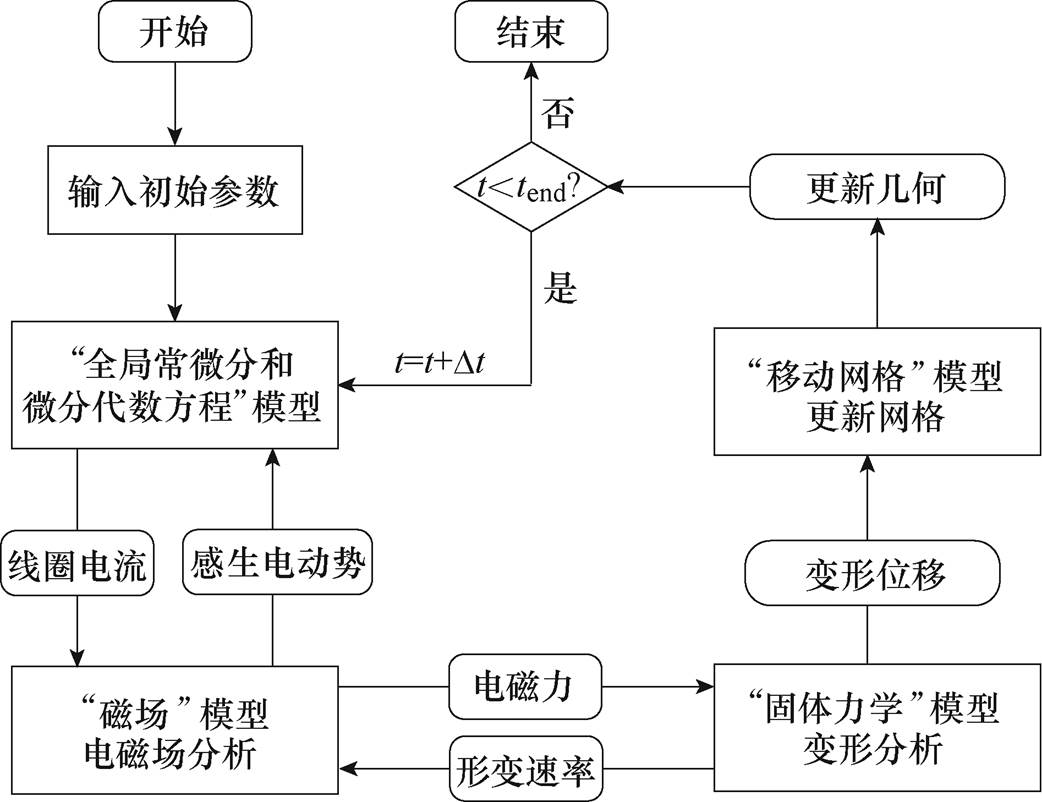
图9 板件吸引式成形仿真算法流程
Fig.9 Flow chart of simulation algorithm for sheet metal attractive forming
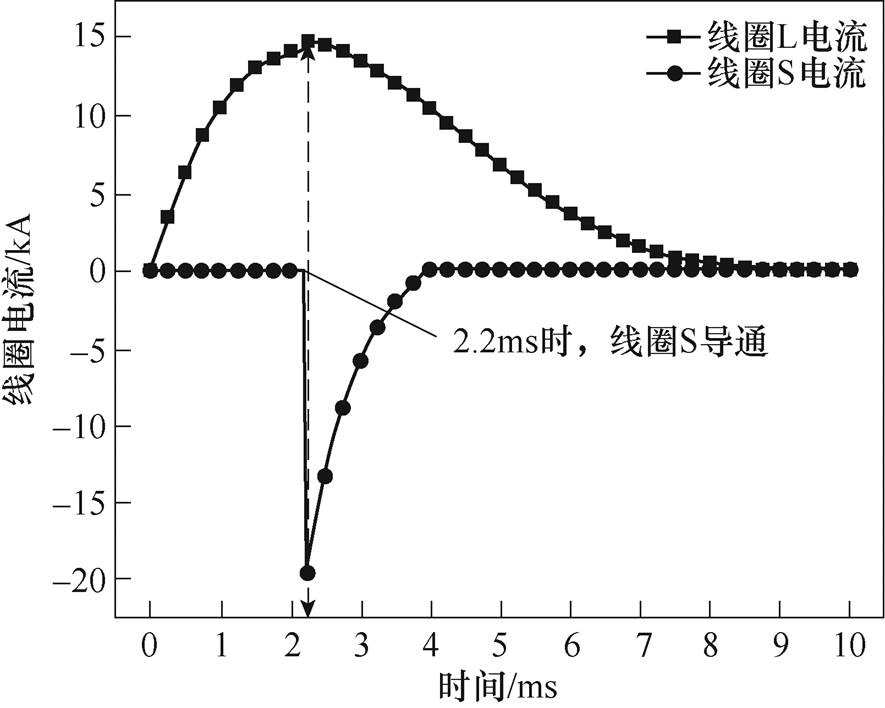
图10 线圈L和S中的电流波形
Fig.10 Current waveforms in coils L and S
电流峰值时，板件上的磁通密度分布如图11所示。由图11可知，在线圈L的电流到达峰值时，板件上的磁通密度达到了最大值5.35T；而在线圈S导通后，由于线圈L、S的电流方向相反，导致两个线圈所产生的磁通密度方向是相反的，故最终板件上的合成磁通密度数值在2.2～2.26ms的范围内是逐渐减小的，并在2.26ms（线圈S的峰值时刻）时降到了4.92T。但是由于线圈L的匝数远远大于线圈S（线圈L的感抗值大于线圈S，且Cs
Cf），这就使线圈L中的电流脉宽远远大于线圈S，线圈L的磁通密度远远大于线圈S。故可认为板件上的磁通密度方向在整个成形过程中都基本保持不变。
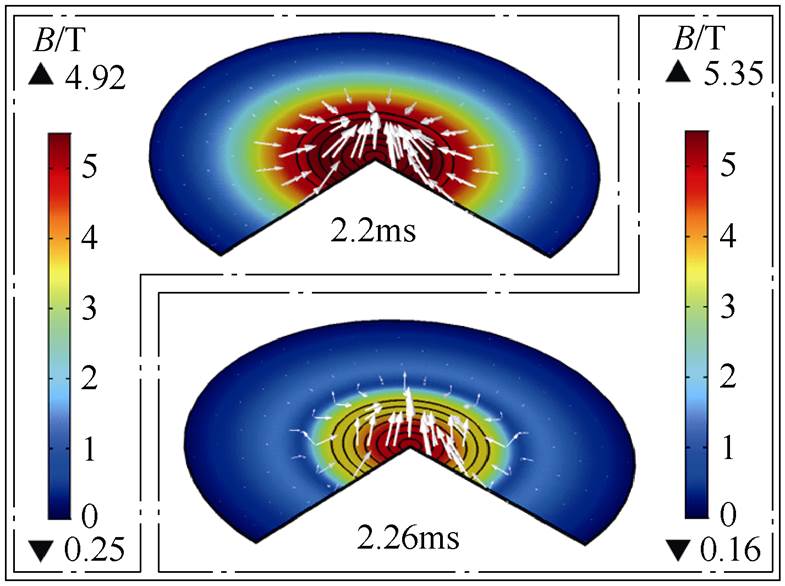
图11 电流峰值时，板件上的磁通密度分布
Fig.11 At peak current, the magnetic flux density distribution on the plate
电流峰值时，板件上的感应涡流密度分布如图12所示，板件上的感应涡流密度分布同图6分析的一样，当仅有线圈L中的长脉宽电流导通时，以线圈L在板件上所产生的顺时针方向的感应涡流密度为主，且在线圈L中的电流到达峰值时，板件上的最大感应涡流密度值仅为-7.23×108A/m2（负号表示其为顺时针方向）。但当线圈S中的短脉宽电流导通时，板件上同时分布着顺时针和逆时针方向的感应涡流密度，且在板件成形区域上，主要以线圈S在板件上所产生的逆时针方向感应涡流密度为主，并在线圈S中的电流到达峰值时，板件上的最大感应涡流密度值为4.26×109A/m2。
图12 电流峰值时，板件上的感应涡流密度分布
Fig.12 At peak current, the induced eddy current density distribution on the plate
结合图11和图12可知，板件上的磁通密度和涡流密度均符合式（4）中磁通密度分布的分析，故板件会先受到排斥式电磁力，向下凹，再受到吸引式电磁力（线圈S的电流导通后），向上凸，最终实现吸引力成形。因此，以板件中心点为零点，以5mm距离为半径，依次选取6个点（0～30mm），分析板件不同位置处的轴向位移。
板件上不同位置点处的最终轴向位移如图13所示，板件上不同点处的轴向位移从0～30mm的范围内依次递减，且在0mm处的轴向位移达到最大值8.83mm，在30mm处的轴向位移仅为1.08mm。此时，板件上未出现涡流密度竞争失败的现象，导致部分区域存在凹痕缺陷，且最终获得了较好的成形均匀度。
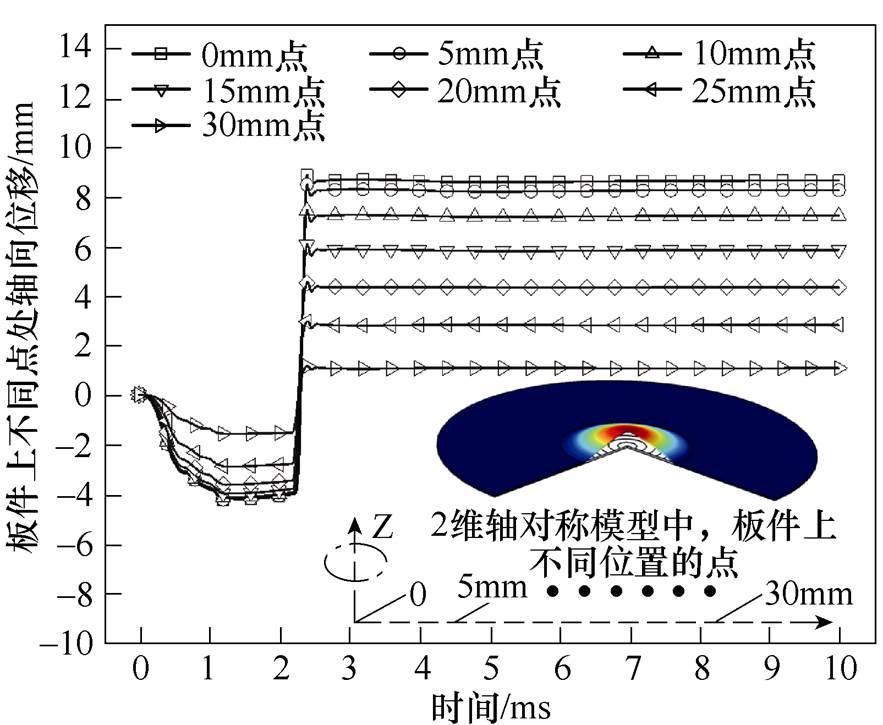
图13 板件上不同位置点处的最终轴向位移
Fig.13 The final axial displacement distribution at different positions on the plate
在本文中，方案1中的参数和仿真结果如文献[18]中所述，由此可知，当方案1和方案2中板件的最大轴向位移均为2.57mm时，方案1中外围线圈的放电电路参数UL=10kV，CL=5.6mF，内线圈的放电电路参数US=6.8kV，CS=120mF；方案2中线圈L的放电电路参数UL=6.15kV，CL=5.6mF，线圈S的放电电路参数UL=6.8kV，CL=120mF。
因此，由总能量计算公式W=WL+WS（WL=1/2CL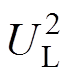
,WS=1/2CS
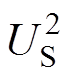）可得，方案1中所用放电总能量为282 774.4J，方案2中所用放电总能量为108 677.4J。由此可见，在板件的相同成形能力下，方案2中的能耗仅为方案1所消耗能量的38.43%。方案1中，板件会存在局部的凹痕缺陷这一问题，因此方案2对于优化板件的成形效果，具有显著的降低能耗作用。
根据式（4）中的分析可知，板件成形主要取决于磁通密度和涡流密度的大小和方向，而改变线圈的安匝数，可以调节板件上的磁通密度和涡流密度的大小。因此，本文在不改变外电路放电参数的情况下，通过改变线圈L的轴、径向层数，对板件的成形效果进行分析。
3.3.1 线圈L轴向匝数对板件成形效果的影响
在仅改变线圈L的轴向匝数时，线圈电流峰值时刻，板件上磁通密度和感应涡流密度的变化主要参数见表2。由表2可知，当线圈轴向层数增多时（匝数增多），线圈L的电流峰值减小，板件上的磁通密度相应地增大。仅在线圈L的轴向层数为3层时，板件成形区域出现凹痕，且最大的凹痕位移仅为0.02mm（分布在32.3～35mm范围内），仅为板件厚度的2%。
表2 改变线圈L的轴向层数时，线圈电流峰值时刻板件成形的主要参数
Tab.2 When changing the number of axial layers of the coil L, the main parameter value of the plate forming at the time of the peak of the coil current
L的轴向层数线圈峰值电流/kA板件上磁通密度最大值/T板件上主要感应涡流密度峰值/ (108A/m2)是否出现凹痕 LSLSLS 315.318.893.793.72-5.2142.9是 414.819.234.664.29-6.0139.8否 514.420.025.354.92-7.2342.6否 613.620.25.785.38-9.7640.2否 712.919.456.055.64-11.433.8否
改变线圈L轴向层数时，板件上的感应涡流密度分布如图14所示，线圈L在不同轴向层数下，板件上感应涡流密度分布，且随着层数增多，板件上涡流密度在减小，且涡流密度分布在逐渐保持均匀。这就保证了板件上不会产生因涡流密度竞争而出现的凹痕区域了。
改变线圈L轴向层数时，板件上不同位置点处的最终轴向位移分布如图15所示，此时，板件上不同点处的轴向位移随着线圈L轴向层数的增加而逐渐增大，但是板件的成形均匀度在减小。
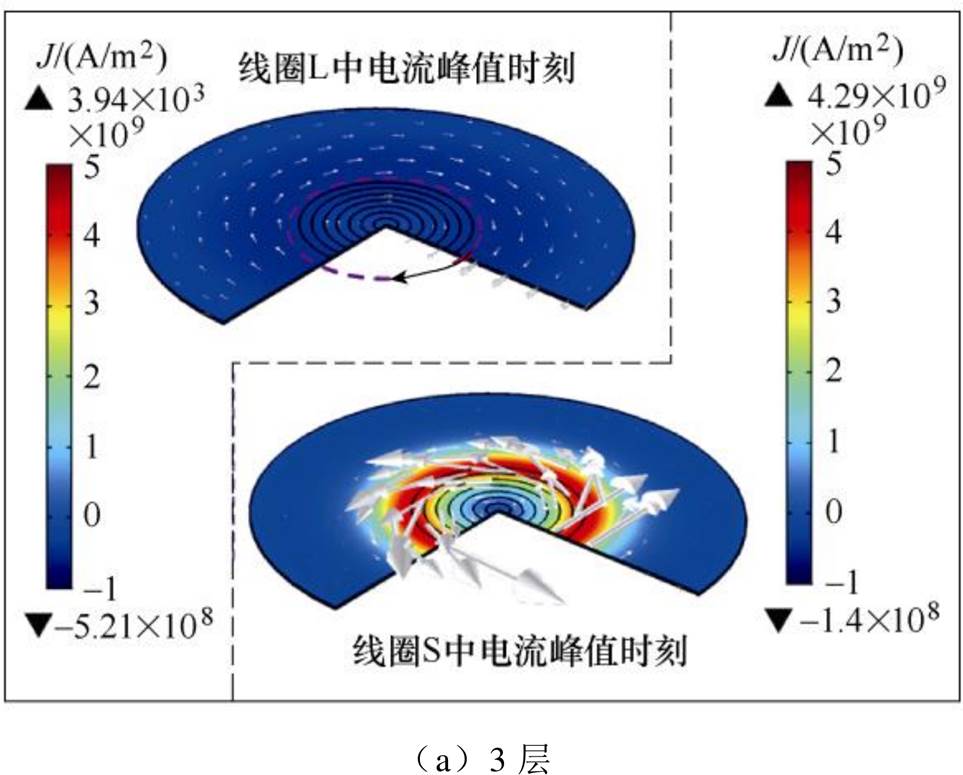
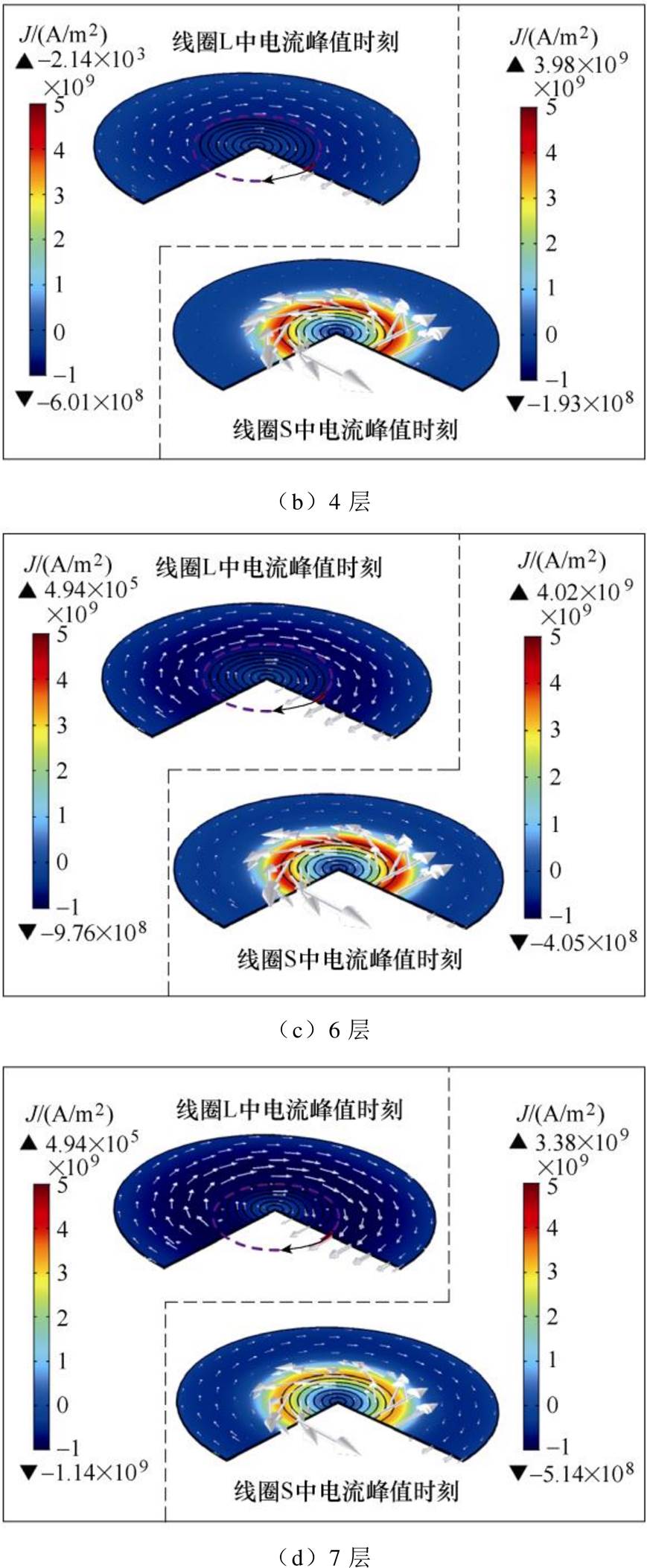
图14 改变线圈L轴向层数时，板件上的感应涡流密度分布
Fig.14 When changing the number of axial layers of coil L, the distribution of induced eddy current density on the plate
3.3.2 线圈L径向匝数对板件成形效果的影响
在改变线圈L的径向层数时，线圈电流峰值时刻影响板件成形的主要参数见表3。随着线圈L径向层数的增加，线圈L的峰值电流在逐渐减小，线圈S的峰值电流基本不变。而板件上的磁通密度在逐渐增大，且随着径向层数的增加，板件上顺时针方向的涡流密度在增加。
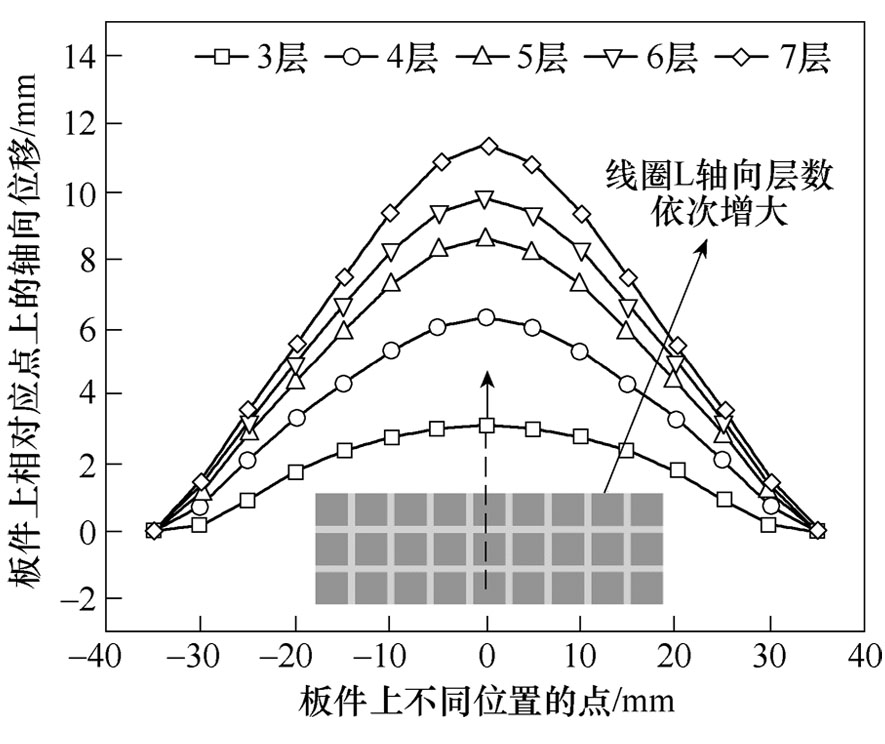
图15 改变线圈L轴向层数时，板件上不同位置点处的最终轴向位移分布
Fig.15 When changing the number of axial layers of the coil L, the final axial displacement distribution at different positions on the plate
表3 改变线圈L的径向层数时，线圈电流峰值时刻板件成形的主要参数
Tab.3 When changing the number of radial layers of the coil L, the main parameter value of the plate forming at the time of the peak of the coil current
L的径向层数线圈峰值电流/kA板件上磁通密度最大值/T板件上主要感应涡流密度峰值/ (108A/m2)是否出现凹痕 LSLSLS 615.320.283.853.73-5.3744.8是 71520.24.424.16-6.6139.8否 814.319.35.385.02-7.438.1否 914.420.025.354.92-7.2342.6否 1013.920.265.755.27-8.2341.1否
改变线圈L径向层数时，板件上不同位置点处的最终轴向位移分布如图16所示。这就最终导致了板件的轴向位移在径向层数为6层时，板件上出现了凹痕缺陷。而当径向层数达到8层时，板件的轴向位移就达到了最大，再进一步增加线圈的径向层数对于增大板件的轴向位移有相反的作用。
进一步结合图15和图16可知，在增大线圈L的层数时，相应地增大了线圈的感抗值（线圈L的峰值电流波动幅度较小），同时增大了线圈L的电流脉宽，进而增大了磁通密度，导致板件的轴向位移量增大，则线圈层数的增加可有效避免凹痕区域的出现。
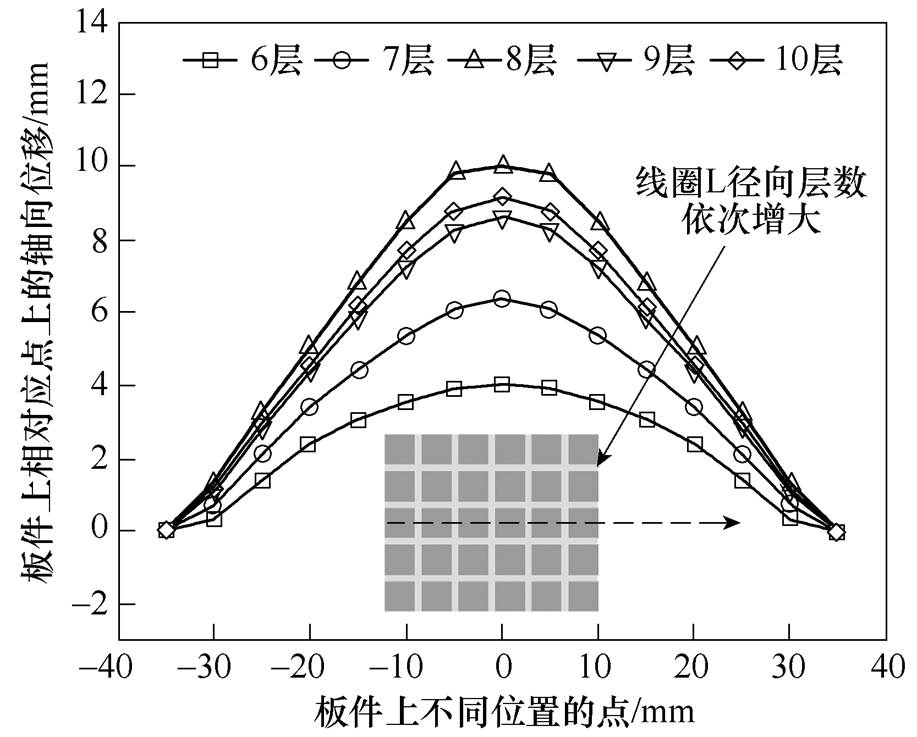
图16 改变线圈L径向层数时，板件上不同位置点处的最终轴向位移分布
Fig.16 When changing the number of radial layers of coil L, the final axial displacement distribution at different positions on the plate
由于线圈L和S之间的间距直接影响板件上的涡流密度和磁通密度分布，因此，本文在不改变外电路放电参数以及线圈S位置的情况下，通过改变线圈间距对板件的成形效果进行分析，改变线圈L和S的间距时，板件上不同位置处的最终轴向位移分布如图17所示。
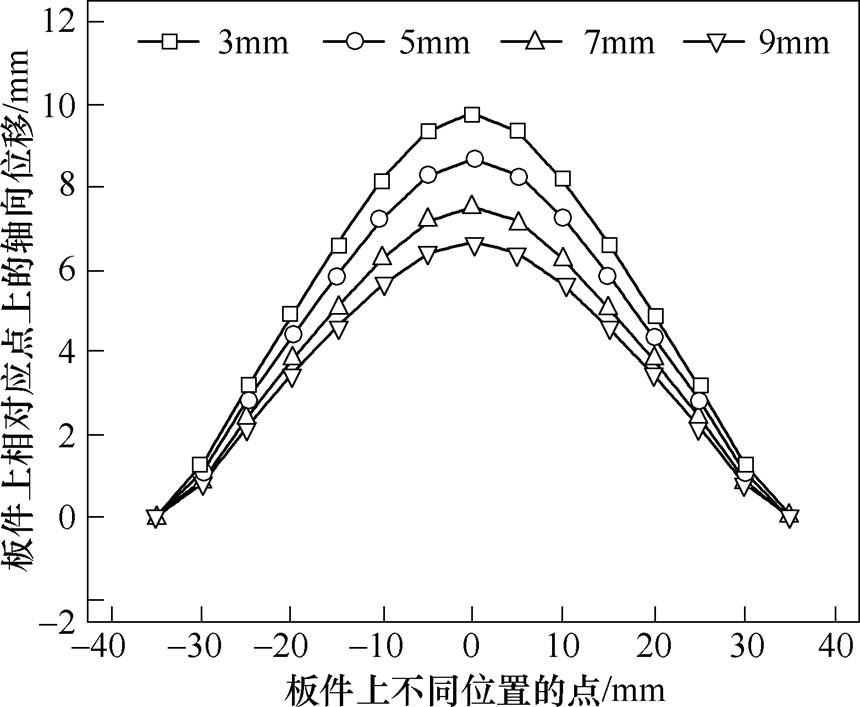
图17 改变线圈L和S的间距时，板件上不同位置处的最终轴向位移分布
Fig.17 When changing the distance between the coils L and S, the final axial displacement distribution at different positions on the plate
由图17可以看出，当线圈S的位置保持不变时，逐渐增大线圈L和S的间距，板件的轴向位移呈现为逐渐减小的趋势；当线圈L和S的间距为3mm时，板件的轴向位移达到最大，但是此时，板件上出现了0.01mm的最大轴向凹痕变形，故线圈的间距设计应不小于5mm。
在双线圈吸引式板件电磁成形过程中，存在涡流密度竞争现象，可能导致成形出现凹痕缺陷。在不改变外电路放电参数的情况下，对线圈结构进行合理的设计可以规避这种情况：
1）增大线圈L的层数，可有效增大板件上的磁通密度，进而增大板件的轴向位移，有效避免板件上凹痕区域的出现。
2）线圈L的轴向层数要大于线圈S的轴向层数，或增大线圈L的电流，才能使板件上的磁通密度满足吸引力成形的要求。
3）线圈L的径向层数要稍大于线圈S的径向层数，能较好地优化板件吸引力成形的均匀度。
本文证实了方案2可有效避免双线圈吸引式板件电磁成形由于涡流密度竞争而引起的凹痕现象，为双线圈吸引式板件电磁成形提供了更佳的实施方案。但需要注意的是，本文方案中用到的脉冲电流脉宽较长，其带来的焦耳热不可忽略，因此在实际应用时需要对线圈的温升加以考虑以免影响使用寿命。同时，由于线圈温升还会随环境因素、使用情况以及材料热力学性能等参数的变化而变化，其影响因素较多，未来将对这部分内容做进一步研究。
参考文献
[1] 熊奇, 唐红涛, 王沐雪, 等. 2011年以来电磁成形研究进展[J]. 高电压技术, 2019, 45(4): 1171-1181.
Xiong Qi, Tang Hongtao, Wang Muxue, et al. Research progress of electromagnetic forming tech- nique since 2011[J]. High Voltage Engineering, 2019, 45(4): 1171-1181.
[2] Psyk V, Risch D, Kinsey B L, et al. Electromagnetic forming-a review[J]. Journal of Materials Processing Technology, 2011, 211(5): 787-829.
[3] 邱立, 李彦涛, 苏攀, 等. 电磁成形中电磁技术问题研究进展[J]. 电工技术学报, 2019, 34(11): 2247- 2259.
Qiu Li, Li Yantao, Su Pan, et al. Research on electromagnetic problems in electromagnetic forming process[J]. Transactions on China Electrotechnical Society, 2019, 34(11): 2247-2259.
[4] Xiong Qi, Tang Hongtao, Deng Changzheng, et al. Electromagnetic attraction-based bulge forming in small tubes: fundamentals and simulations[J]. IEEE Transactions on Applied Superconductivity, 2017, 28(3): 1-5.
[5] Qiu Li, Li Yantao, Yu Yijie, et al. Numerical and experimental investigation in electromagnetic tube expansion with axial compression[J]. The Inter- national Journal of Advanced Manufacturing Tech- nology, 2019, 104(5-8): 3045-3051.
[6] 邱立, 杨新森, 常鹏, 等. 双线圈轴向压缩式管件电磁胀形电磁力分布规律与管件成形性能研究[J]. 电工技术学报, 2019, 34(14): 2855-2862.
Qiu Li, Yang Xinsen, Chang Peng, et al. Electro- magnetic force distribution and forming performance in electromagnetic tube expansion process with two coils[J]. Transactions on China Electrotechnical Society, 2019, 34(14): 2855-2862.
[7] Yu Haiping, Li ChunFeng, Deng JiangHua. Sequential coupling simulation for electromagnetic-mechanical tube compression by finite element analysis[J]. Journal of materials processing technology, 2009, 209(2): 707-713.
[8] Xu Junrui, Xie Xueyun, Wen Zhisheng, et al. Deformation behaviour of AZ31 magnesium alloy sheet hybrid actuating with Al driver sheet and temperature in magnetic pulse forming[J]. Journal of Manufacturing Processes, 2019, 37: 402-412.
[9] Cao Quanliang, Du Limeng, Li Zhenhao, et al. Investigation of the lorentz-force-driven sheet metal stamping process for cylindrical cup forming[J]. Journal of Materials Processing Technology, 2019, 271: 532-541.
[10] Kumar S, Khan M R, Saroj P C, et al. Experimental investigation of driver material on electromagnetic welding of alloy D9 SS tube to SS316L (N) plug[J]. The International Journal of Advanced Manufacturing Technology, 2019, 105(10): 4225-4235.
[11] Deng Fangxiong, Cao Quanliang, Han Xiaotao, et al. Electromagnetic pulse spot welding of aluminum to stainless steel sheets with a field shaper[J]. The International Journal of Advanced Manufacturing Technology, 2018, 98(5-8): 1903-1911.
[12] 周纹霆, 董守龙, 王晓雨, 等. 电磁脉冲焊接电缆接头的装置的研制及测试[J]. 电工技术学报, 2019, 34(11): 2424-2434.
Zhou Wenting, Dong Shoulong, Wang Xiaoyu, et al. Development and test of electromagnetic pulse welding cable joint device[J]. Transactions on China Electrotechnical Society, 2019, 34(11): 2424-2434.
[13] Lai Zhipeng, Cao Quanliang, Han Xiaotao, et al. Investigation on plastic deformation behavior of sheet workpiece during radial lorentz force augmented deep drawing process[J]. Journal of Materials Processing Technology, 2017, 245: 193-206.
[14] Deng Jianghua, Li Chunfeng, Zhao Zhiheng, et al. Numerical simulation of magnetic flux and force in electromagnetic forming with attractive force[J]. Journal of Materials Processing Technology, 2007, 184(1-3): 190-194.
[15] Cao Quanliang, Lai Zhipeng, Xiong Qi, et al. Elec- tromagnetic attractive forming of sheet metals by means of a dual-frequency discharge current: design and implementation[J]. The International Journal of Advanced Manufacturing Technology, 2017, 90(1-4): 309-316.
[16] Xiong Qi, Tang Hongtao, Wang Muxue, et al. Design and implementation of tube bulging by an attractive electromagnetic force[J]. Journal of Materials Pro- cessing Technology, 2019, 273: 116240.
[17] Ouyang Shaowei, Li Xiaoxiang, Li Changxing, et al. Investigation of the electromagnetic attractive forming utilizing a dual-coil system for tube bulging[J]. Journal of Manufacturing Processes, 2020, 49: 102-115.
[18] Xiong Qi, Yang Meng, Liu Xin, et al. A dual-coil method for electromagnetic attraction forming of sheet metals[J]. IEEE Access, 2020, 8: 92708-92717.
[19] 熊奇. 采用双线圈的金属板件吸引式成形方法及成形装置[P]. 中国: CN110899452A, 2020-03-24.
[20] Mamalis A G, Manolakos D E, Kladas A G, et al. Electromagnetic forming tools and processing con- ditions: numerical simulation[J]. Materials and Manufacturing Processes, 2006, 21(4): 411-423.
[21] 黎镇浩, 曹全梁, 赖智鹏, 等. 电流丝法在电磁成形线圈电流和工件电磁力计算中的应用[J]. 电工技术学报, 2018, 33(18): 4181-4190.
Li Zhenhao, Cao Quanliang, Lai Zhipeng, et al. Application of current filament method on the calculation of current and force in electromagnetic forming[J]. Transactions on China Electrotechnical Society, 2018, 33(18): 4181-4190.
[22] Xiong Qi, Huang Hao, Xia Liangyu, et al. A research based on advance dual-coil electromagnetic forming method on flanging of small-size tubes[J]. The Inter- national Journal of Advanced Manufacturing Techno- logy, 2019, 102(9-12): 4087-4094.
[23] 邱立, 余一杰, 聂小鹏, 等. 管件电磁胀形过程中的材料变形性能问题与电磁力加载方案[J]. 电工技术学报, 2019, 34(2): 212-218.
Qiu Li, Yu Yijie, Nie Xiaopeng, et al. Study on material deformation performance and electromagnetic force loading in electromagnetic tube expansion process[J]. Transactions on China Electrotechnical Society, 2019, 34(2): 212-218.
[24] Cao Quanliang, Li Liang, Lai Zhipeng, et al. Dynamic analysis of electromagnetic sheet metal forming process using finite element method[J]. The Inter- national Journal of Advanced Manufacturing Tech- nology, 2014, 74(1-4): 361-368.
[25] Cao Quanliang, Han Xiaotao, Lai Zhipeng, et al. Analysis and reduction of coil temperature rise in electromagnetic forming[J]. Journal of Materials Pro- cessing Technology, 2015, 225: 185-194.
Eddy Currents Competition in Electromagnetic Forming Process of Plates by Double-Coil Attraction
Abstract Electromagnetic forming (EMF) is a kind of high energy processing technology that realizes rapid plastic forming of light alloy pieces by the pulsed electromagnetic force. Attraction electromagnetic forming is one of the unique applications. It uses two different pulse width currents to drive one coil to generate an attractive electromagnetic force, which is suitable for plate dent repairment and micro-tube forming. However, the single-coil structure has very strict requirements for parameter matching of the two currents, and the energy utilization efficiency is extremely low. Therefore, this paper puts forward a double-coil structure attracting electromagnetic scheme, that is, two kinds of current are used to drive a coil each. However, the double-coil structure brings new eddy current competition phenomenon, which will cause forming defects. Thus, this paper further studies the cause and mechanism of eddy current competition, and finally eliminates the forming defects by adjusting the coil structural parameters in the scheme of AA1060-H28 aluminum alloy plate with a diameter of 200 mm. This paper provides a better understanding of the attractive EMF process, and has significance for expanding the application of the EMF technology in plate processing.
keywords：Electromagnetic forming, double-coil, sheet metals, attraction force, eddy current competition
中图分类号：TM154
DOI: 10.19595/j.cnki.1000-6753.tces.200692
国家自然科学基金（51707104）、国家公派留学奖学金（201908420196）和三峡大学学位论文培优基金（2020SSPY054）资助项目。
收稿日期 2020-06-22
改稿日期 2020-09-10
熊 奇 男，1990年生，博士，副教授，研究方向为电磁场工业应用。E-mail: pandaqi0218@gmail.com（通信作者）
杨 猛 男，1996年生，硕士研究生，研究方向为电磁场分析及应用。E-mail: ymmifaith@163.com
（编辑 陈 诚）