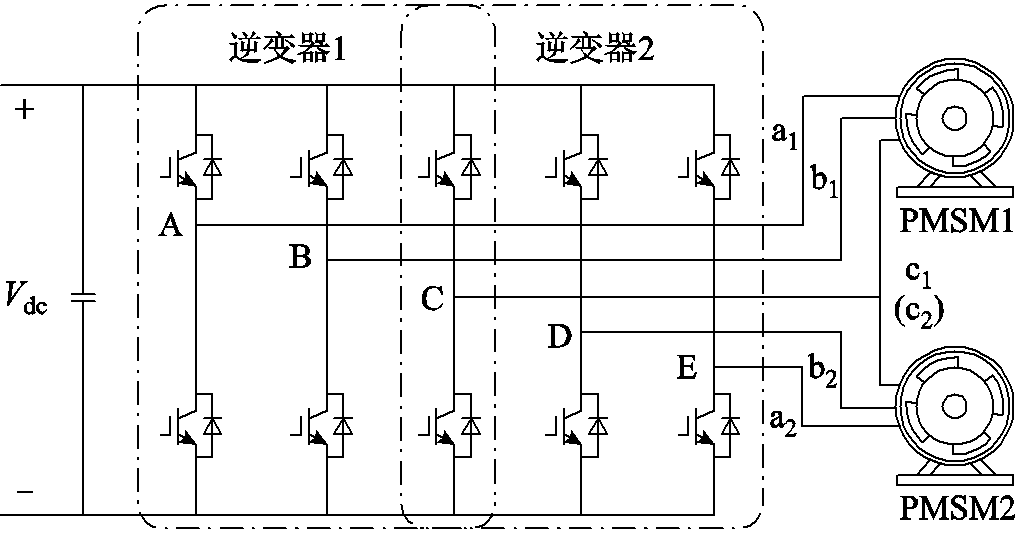
图1 五桥臂逆变器双永磁电机拓扑结构图
Fig.1 Topology diagram of dual-PMSM fed by a five-leg inverter
摘要 在五桥臂逆变器双永磁电机系统中，传统预测控制策略是一个控制周期内每台电机上等效于只作用一个幅值、方向均固定的矢量，矢量调节范围有限，系统运行时电流波动较大。为减小双电机系统中电机电流波动，采用一种三矢量预测控制策略，该策略在每个控制周期内作用两个有效矢量和一个零矢量。首先依据两个有效矢量所对应公共桥臂的开关状态将其分组，然后通过两台电机各自独立的价值函数筛选出每组中最优的矢量组合，最后比较不同组的矢量组合，从中进一步选择系统最优矢量组合，并按规则合成五桥臂电压矢量作用于双电机系统。对矢量进行分组后，该策略每个控制周期只需要计算30次价值函数，有效减小了多矢量预测控制的计算次数。实验结果表明，与传统预测控制策略相比，该策略在保持动态响应快等优点的同时，有效减小了电流波动，并具备一定的抗参数扰动性，提高了系统的稳态性能。
关键词：永磁同步电机 三矢量 预测控制 五桥臂逆变器
近年来随着工业技术的迅速发展，永磁同步电机因其自身优势在电动汽车、造纸、采矿等领域得到了广泛应用[1-5]。双永磁电机系统多采用两台三相电压源逆变器共用直流母线的拓扑结构，每台逆变器独立驱动一台电机运行。该系统半导体功率器件多、成本高、可靠性低。为了降低成本，提高系统的可靠性，近年来五桥臂逆变器双永磁电机（Permanent Magnet Synchronous Motor, PMSM）系统作为一种较好的容错方案得到了国内外学者的广泛研究[6-10]。
在五桥臂逆变器中，两台电机（负载）共用一个桥臂，公共桥臂的开关状态有时会产生冲突。为实现双电机（负载）的独立控制，很多学者在原有单电机（负载）控制策略的基础上提出了新的控制策略。文献[11]提出一种用于五桥臂双电机系统的主从直接转矩控制策略，当公共桥臂开关状态发生冲突时，选择合适的零矢量作用于从电机，最大限度地降低系统偏差。文献[12]针对五桥臂双负载系统，推导出包含公共桥臂开关特性的输出电压数学表达式，并提出新的调制方法，在实现两负载独立控制的同时增加了输出电压。文献[13]基于电流滞环控制提出一种主从电机确定原则，将相电流误差绝对值较大的电机确定为主电机，并将公共桥臂的开关状态设置为主电机的开关状态，有效避免了公共桥臂开关状态的冲突，该方法在运行过程中对电机参数依赖性低，系统鲁棒性高。
在多电机控制系统中，为保证整个控制系统处于最优运行状态，需要兼顾多种控制目标，增加了控制器的设计难度。模型预测控制因其具有内部解耦、易于实现系统多目标优化和引入非线性约束的优点，近年来被引入五桥臂双电机控制系统中。文献[14]将模型预测控制技术应用于五桥臂逆变器双电机系统。同矢量控制相比，该方法无需电流内环的参数整定，可直接产生驱动信号作用于电压源逆变器且无需脉宽调制，将调制和控制集于一身，原理简单，易于实现。文献[15]中首先针对一台电机选出最优矢量，并依此确定公共桥臂开关状态，缩小了第二台电机矢量的选择范围。文献[16]基于无差拍控制理论提出一种基于零矢量交错的预测控制策略，提高了系统的稳态性能。文献[17]针对传统模型预测控制中存在的采样延迟，提出一种两步预测控制策略，消除了程序执行延迟的影响。文献[18]在一个周期内，对每台电机采用双矢量预测控制，仿真结果表明该策略可以有效地降低转矩波动，但该策略中每台电机的输出矢量为六个相角固定、幅值可调的矢量，矢量调节范围有限，系统性能还有进一步提升的空间。
由于五桥臂逆变器公共桥臂开关状态必须一致，传统模型预测控制中将五桥臂电压矢量作为一个整体代入价值函数中，筛选出一个最优矢量作用于逆变器。一个控制周期内每台电机上等效于只作用一个幅值、方向均固定的矢量，矢量调节范围有限，系统运行时电流波动较大。
本文针对传统预测控制中存在的问题，提出一种五桥臂逆变器驱动双永磁电机三矢量预测控制方案，首先每个周期内会有两个有效矢量作用于一台电机，根据两个有效矢量作用于公共桥臂时的开关状态，对每台电机的6个有效矢量两两组合并进行分组，可以分为三组，然后通过每台电机的价值函数分别得出三组中最优矢量组合，接着从这三组中求出两台电机的最优矢量组合，最后将得到的最优矢量组合合成为五桥臂电压矢量并输出。实验结果证明了该方法的正确性和有效性。
五桥臂逆变器双永磁电机系统的拓扑结构如图1所示。系统共包含五个桥臂，分别为A、B、C、D、E。其中A、B、C三个桥臂连接至永磁同步电机1（PMSM1）的定子三相绕组a1、b1、c1，E、D、C三个桥臂连接至永磁同步电机2（PMSM2）的定子三相绕组a2、b2、c2，C桥臂为两台永磁电机的公共桥臂。该拓扑结构的开关模型与文献[18]相同，系统电压矢量如图2所示。图中，u1m(m=1,×××,6)、u1n(n=0, 7)分别为PMSM1的基本有效电压矢量和零矢量；u2m(m=1,×××,6)、u2n(n=0, 7)分别为PMSM2的基本有效电压矢量和零矢量。
图1 五桥臂逆变器双永磁电机拓扑结构图
Fig.1 Topology diagram of dual-PMSM fed by a five-leg inverter
图2 五桥臂逆变器双永磁电机电压矢量分布图
Fig.2 Vector distribution of dual-PMSM fed by a five-leg inverter
对于表贴式永磁同步电机，在忽略磁饱和与铁耗的情况下，dq旋转坐标系下的定子电流变化率为
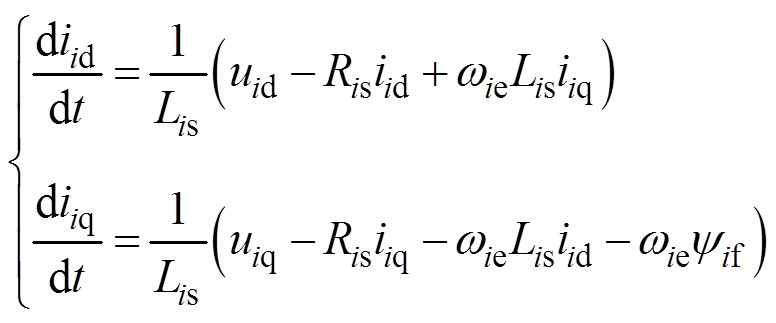（1）式中，下标i=1, 2分别为电机1和电机2；uid、uiq分别为d、q轴的电压分量；iid、iiq分别为d、q轴的电流分量；Lis为定子电感；Ris为定子电阻；ωie为转子电角速度；ψif为永磁体磁链。
采用一阶欧拉法对式（1）进行离散化可得k+1时刻d、q轴电流的预测值为
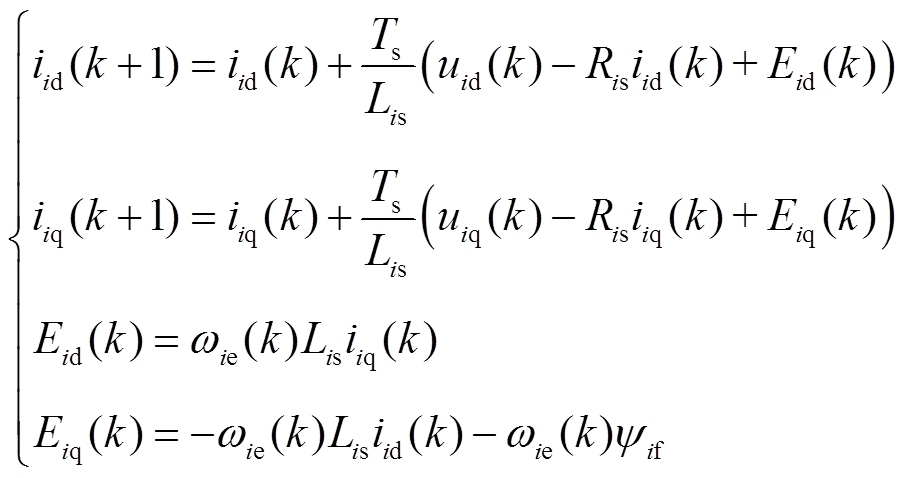（2）式中，uid(k)、uiq(k)分别为当前控制周期d、q轴电压；iid(k)、iiq(k)分别为当前控制周期d、q轴电流实际值；iid(k+1)、iiq(k+1)分别为下一个控制周期d、q轴电流预测值；Ts为采样周期；Eid(k)、Eiq(k)分别为当前控制周期d、q轴反电动势。
传统单矢量五桥臂逆变器预测控制中用模型预测控制器替代电流环的PI控制器，保留了速度环PI控制器。速度环PI控制器利用参考转速与实际转速的差值产生q轴参考电流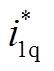
，令d轴参考电流
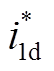=0。传统五桥臂预测控制价值函数为
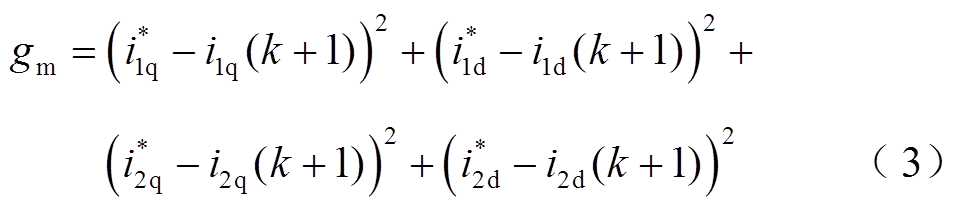
式中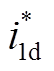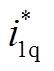，、和
、
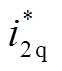分别为电机1和电机2的d、q轴电流参考值。
考虑到同一桥臂开关管开关状态的互补性，五桥臂逆变器共存在32种开关状态，可将其视为32个五桥臂电压矢量。每个五桥臂电压矢量都包含了2个单电机的三桥臂电压矢量。传统方法将每个五桥臂电压矢量对应的单电机电压矢量代入式（2），计算出k+1控制周期时d、q轴的电流值iid(k+1)、iiq(k+1)，然后将其代入式（3），选择使价值函数最小的电压矢量为系统最优电压矢量，并作用于双电机。由上述分析可知，传统方法中一个控制周期内仅有一个电压矢量作用于单台电机，矢量调节范围有限，电流波动较大，系统稳态运行效果较差。
针对传统方法的问题，在五桥臂逆变器双永磁电机系统中采用三矢量预测控制策略。该策略在一个控制周期内，针对每台电机筛选出三个电压矢量，包括两个有效电压矢量和一个零矢量。因此，在一个控制周期内作用在每台电机上的电压矢量不再局限于单一的电压矢量，扩大了电压矢量的调节范围。
设每个周期内会有两个有效矢量作用于一台电机，依据两个有效矢量作用于公共桥臂时的开关状态，对每台电机的6个有效矢量两两组合并进行分组，具体分组如下：第Ⅰ组，每台电机两个有效矢量使公共桥臂的开关状态均为0，即作用于每台电机的两个有效矢量都使公共桥臂的下桥臂导通；第Ⅱ组，每台电机两个有效矢量使公共桥臂的开关状态均为1，即作用于每台电机的两个有效矢量都使公共桥臂的上桥臂导通；第Ⅲ组，每台电机的第一个有效矢量使公共桥臂的开关状态为0，第二个有效矢量使公共桥臂的开关状态为1，即作用于每台电机的两个有效矢量一个使公共桥臂的上桥臂导通，另一个使公共桥臂的下桥臂导通。
设u11、u12分别为第1台电机的第1个有效矢量和第2个有效矢量；u21、u22分别为第2台电机的第1个有效矢量和第2个有效矢量，具体分组见表1。
表1 有效矢量的分组
Tab.1 Groups of the effective vectors
组号编号PMSM1PMSM2 u11u12u21u22 Ⅰ1100110100110 2100010100010 3110010110010 Ⅱ4011001011001 5011101011101 6001101001101 Ⅲ17100011100011 8100001100001 9100101100101 210110011110011 11110001110001 12110101110101 313010011010011 14010001010001 15010101010101
由表1可得每组矢量的调节范围，如图3所示。
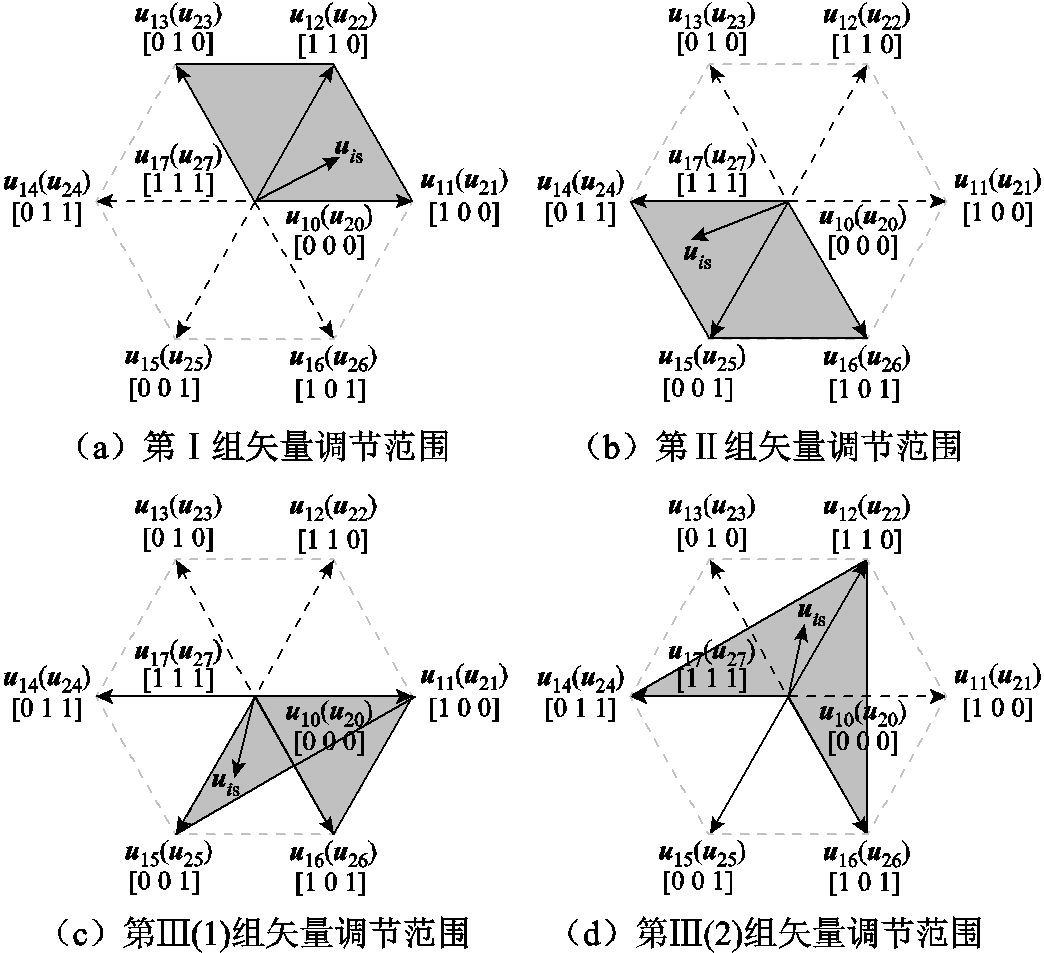
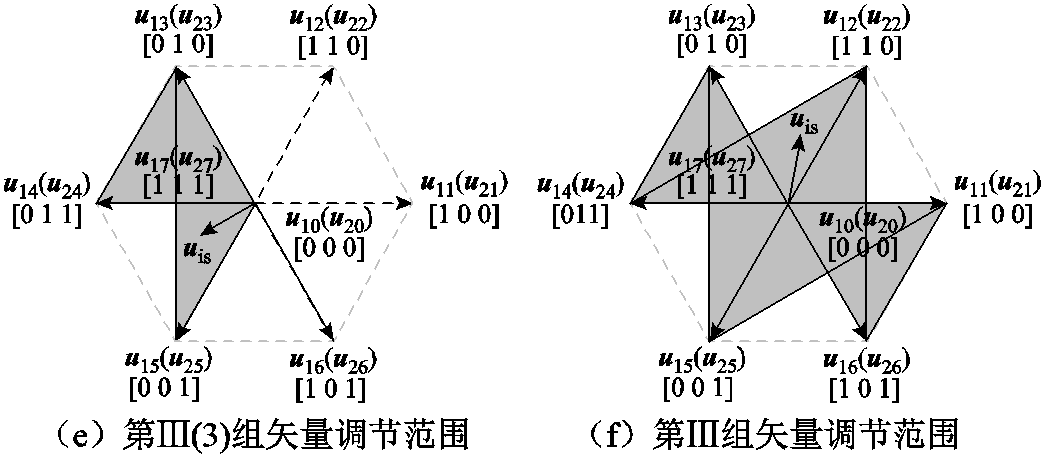
图3 每组矢量的调节范围
Fig.3 Adjustment range of each group of vectors
在电压矢量分组的基础上，针对每台电机在每组矢量中任选一种组合，可得电流方程为
（4）式中，sid1、sid2、sid0和siq1、siq2、siq0分别为两台电机两个有效矢量、零矢量作用下d轴和q轴电流斜率；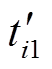
、
、
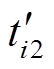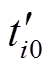分别为两个有效矢量和零矢量对单台电机作用时间的中间值。
基于无差拍理论，同时使d、q轴电流的预测值等于参考值，由式（2）可得单个矢量作用时对应的d、q轴电流斜率为
（5）式中，uid1(k)、uiq1(k)、uid2(k)、uiq2(k)分别为当前控制周期第i台电机两个有效矢量的d、q轴电压分量。
令三个矢量的作用时间和为Ts，则联立式（4）、式（5）可得三个矢量的作用时间中间值分别为
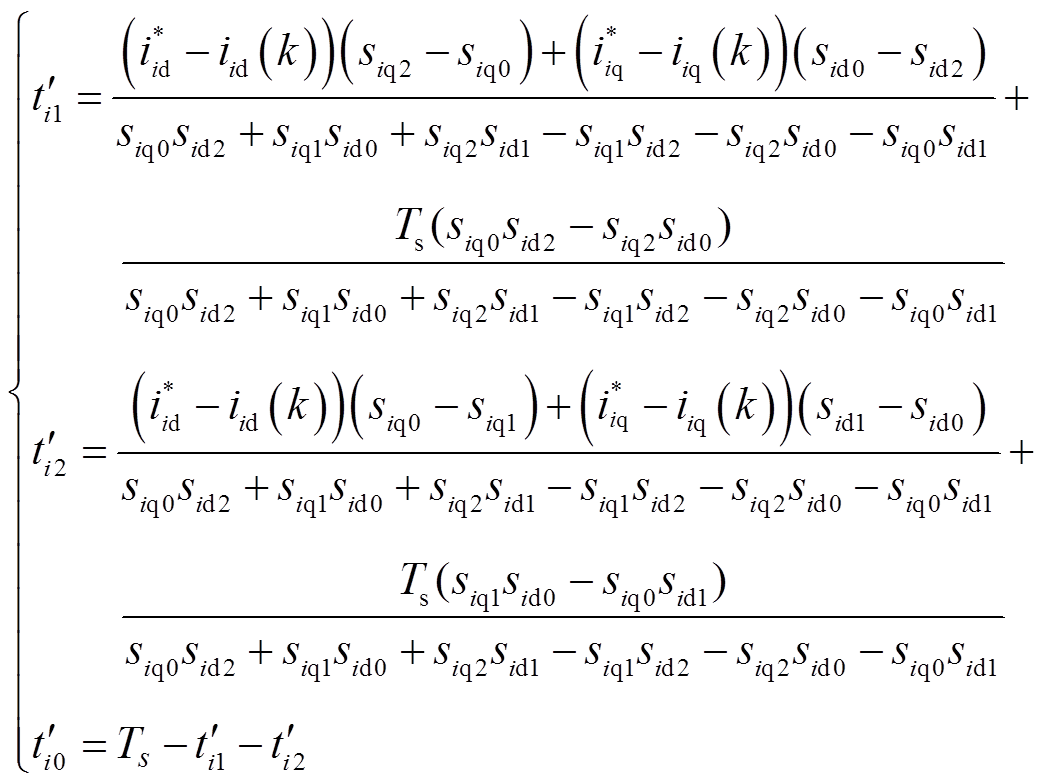（6）由式（6）求出的单个矢量作用时间有可能会出现负值，因此还需进一步对矢量作用时间在0~Ts范围内进行合理化取值，令单个矢量对单台电机作用时间的最终值分别为ti1、ti2和ti0。
（1）当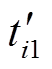≤0或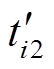≤0时，则最终值为0，即ti1=0或ti2=0。
（2）当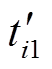≥Ts或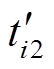≥Ts时，则最终值为Ts，即ti1=Ts或ti2=Ts。
（3）当0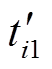＜＜Ts、0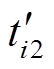＜＜Ts且0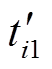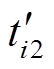＜+＜Ts时，则最终值等于中间值，此时一个周期内作用2个有效矢量和1个零矢量。
（4）当0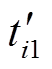＜＜Ts、0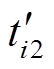＜＜Ts但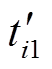+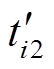＞Ts时，则需要对最终值进行归一化处理，此时零矢量作用时间为0，最终值为
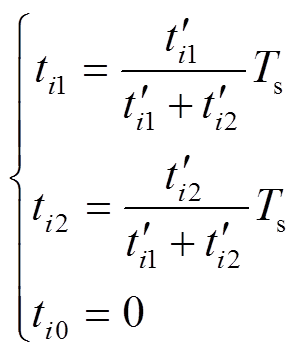（7）作用于单台电机的d、q轴电压分别为
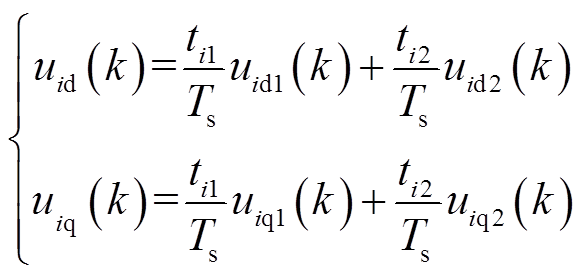（8）将其代入式（2），即可求出在不同电压矢量组合作用下，单台电机在下一个控制周期的电流预测值iid(k+1)、iiq(k+1)。
针对每台电机，构造独立的价值函数g1、g2为
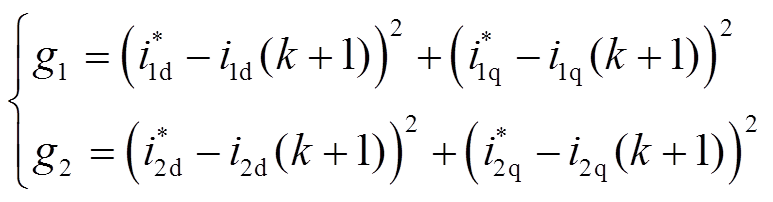（9）按照表1的分组，首先利用式（10）分别计算出每台电机在15种矢量组合作用下的价值函数并相加；然后在每组中分别选出价值函数和值最小的矢量组合，即得到3个矢量组合；最后进一步比较3个矢量组合对应的价值函数和值，和值最小的矢量组合即为最优矢量组合。当两台电机参考矢量均处于重叠区域时，有可能会出现多种矢量组合对应的价值函数和值相等的情况，此时选第一种矢量组合调制输出即可。
得到两台电机的最优电压矢量组合后，还需将其合成为五桥臂电压矢量并输出，根据表1内不同的分组，五桥臂电压矢量的合成方式如下：
1）第Ⅰ组。假设第Ⅰ组内电机1的1组合与电机2的3组合的价值函数之和最小，即该矢量组合为系统最优矢量组合。根据五桥臂逆变器中公共桥臂开关状态必须一致的原则，可以有两种方式合成五桥臂电压矢量，为尽可能地接近单台电机预期的电压矢量，可采用矢量作用时间差值最小的方法确定矢量合成方式。
（1）当
时，将电机1的第1个矢量与电机2的第1个矢量合成为第1个五桥臂电压矢量，即输出矢量10011；将电机1的第2个矢量与电机2的第2个矢量合成为第2个五桥臂电压矢量，即输出矢量11010。
（2）当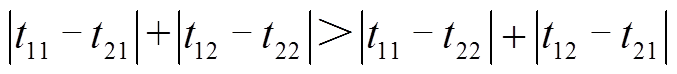
时，将电机1的第1个矢量与电机2的第2个矢量合成为第1个五桥臂电压矢量，即输出矢量10010；将电机1的第2个矢量与电机2的第1个矢量合成为第2个五桥臂电压矢量，即输出矢量11011。
2）第Ⅱ组。第Ⅱ组矢量合成方式与上述第I组矢量合成方式类似。
3）第Ⅲ组。假设第Ⅲ组内电机1的7号组合与电机2的13号组合价值函数之和最小，即该矢量组合为系统最优矢量组合。此时合成五桥臂电压矢量的方式只有一种，将电机1的第1个矢量与电机2的第1个矢量合成为第1个五桥臂电压矢量，即输出矢量10010；将电机1的第2个矢量与电机2的第2个矢量合成为第2个五桥臂电压矢量，即输出矢量01110。
确定五桥臂电压矢量合成方式后，还要对其作用时间进行计算。假设电机1的第1个矢量与电机2的第1个矢量合成为第1个五桥臂电压矢量，则单个有效矢量对单台电机的作用时间分别为t11、t21；电机1的第2个矢量与电机2的第2个矢量合成为第2个五桥臂电压矢量，则单个有效矢量对单台电机的作用时间分别为t12、t22。可按式（10）求出两个五桥臂电压矢量作用时间的中间值。
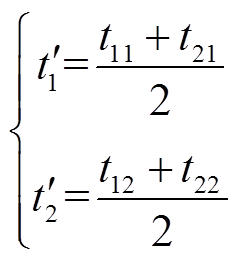（10）式中，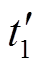
、
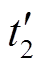分别为第1个五桥臂电压矢量和第2个五桥臂电压矢量作用时间的中间值。
当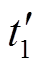+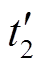≤Ts时，五桥臂电压矢量作用时间为
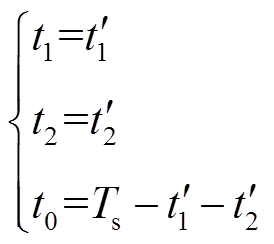（11）式中，t1、t2、t0分别为第1个五桥臂电压矢量、第2个五桥臂电压矢量和五桥臂零电压矢量作用时间的最终值。
当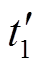+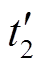＞Ts时，五桥臂电压矢量作用时间为
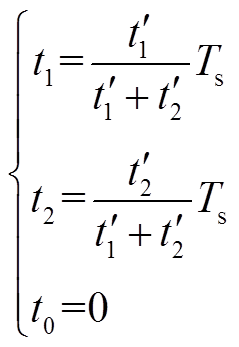（12）按式（12）求出矢量作用时间后，再结合五桥臂电压矢量的合成方式，即可调制输出电压矢量，驱动电机运行，控制策略的整体框图如图4所示。
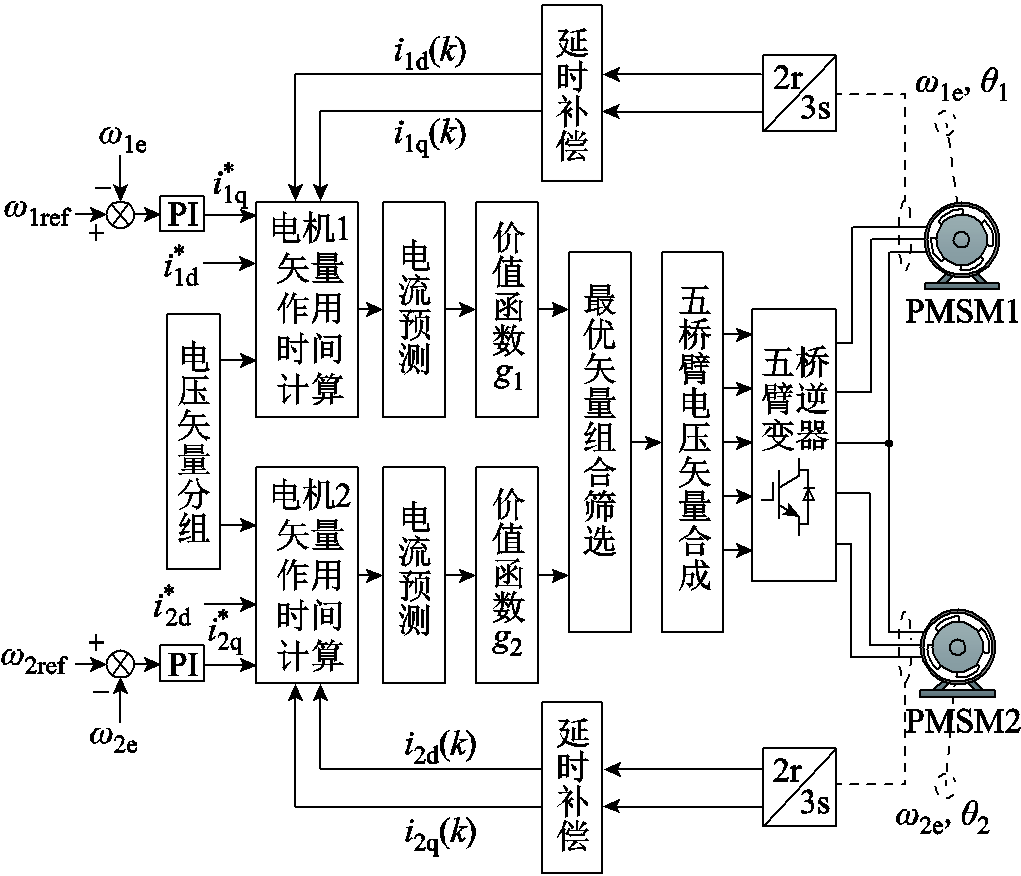
图4 控制策略框图
Fig.4 The block diagram of control strategy
所提三矢量控制策略在控制思想上等效于独立的控制两台电压源逆变器驱动双电机系统。经过对矢量进行分组后，每个控制周期系统只需要计算30次价值函数，有效减小了多矢量预测控制的计算次数，为缩短系统控制周期奠定了基础。
为验证所提五桥臂逆变器双永磁电机三矢量预测控制策略的有效性和可行性，搭建了实验平台，如图5所示。平台中包括两台参数相同的2.3kW永磁电机，电机的具体参数见表2，数字控制器采用TI公司生产的TMS320F28335。实验中，控制频率和采样频率均设定为10kHz。
图5 实验平台
Fig.5 Experiment platform
表2 电机1和2参数
Tab.2 Parameters of the two motors
参数数值 绕组线电阻/Ω1.27 绕组线电感/mH8.05 极对数2 转子磁链峰值/Wb0.5 转动惯量/(kg×cm2)27.2 额定功率/kW2.3 母线额定电压/V320 额定电流/A10 额定转矩/(N∙m)15 额定转速/(r/min)1 500 电机额定电压/V220
图6a为两电机空载、电机1参考转速突变时，传统预测控制策略与所提三矢量预测控制策略下两电机转速、q轴电流、电机1电磁转矩对比波形。图中n1、n2表示电机1和电机2转速，电机2参考转速一直保持100r/min不变；电机1初始参考转速为200r/min，在2s时将参考转速突加到300r/min，3s时将参考转速突加到500r/min。图6b为两电机空载起动、电机1突加负载时，两种控制策略下两电机转速及q轴电流对比波形。图中，电机1在3s时突加5 N∙m负载，电机2保持空载运行。
图6 动态实验波形
Fig.6 The waveforms of dynamic experiment
由图6a可以看出，电机1参考转速由300r/min突加至500r/min时，两种控制策略均能快速跟随参考值并达到稳态。由图6b可以看出，当电机1突加5N∙m负载时，两种控制策略下电机1转速均能快速调整并跟随参考值，电机2转速基本不受影响。由实验结果可知，所提三矢量预测控制策略保持了传统预测控制策略动态响应快的优点。
图7为两台电机空载稳态运行时，传统预测控制策略与所提三矢量预测控制策略下两台电机的d、q轴电流对比波形。图中，电机1转速为500r/min，电机2转速为100r/min。
图7 空载稳态实验波形
Fig.7 The waveforms of steady experiment with no load
图8为电机1带5N∙m负载，电机2空载运行时，两种控制策略下两台电机的d、q轴稳态电流和电机定子A相电流对比波形。图中，两台电机转速均为300r/min。
图8 带载稳态实验波形
Fig.8 The waveforms of steady experiment with load
由图7与图8可以看出，稳态运行时采用三矢量预测控制策略的两电机d、q轴电流波动明显小于传统控制策略，相电流谐波含量更低，所提策略有效地改善了系统稳态运行性能。
为了验证所提控制策略的参数抗扰性，在程序中将预测模型中电机电感值分别设定为额定电感0.8倍（3.22mH）和1.2倍（4.83mH），图9为所提控制策略两电机转速及q轴电流波形。图中，电机1在3s时突加5N∙m负载，电机2保持空载。
图9 参数抗扰性实验波形
Fig.9 Experimental waveforms of parametric immunity
由图9可以看出，电机1突加负载条件下，将预测模型中电感参数相对于电机电感额定值上下调节20%时，所提控制策略仍能实现对参考转速的准确稳定的跟踪，且q轴电流波动小。验证了所提控制策略具有良好的参数抗扰动性能。
为减小传统预测控制下双电机系统中电机电流波动，针对五桥臂逆变器，采用了一种三矢量预测控制策略。该策略通过对两台电机的有效矢量进行分组，首先单独求出每组中最优矢量，进而求出五桥臂逆变器所需最优矢量，该方法通过矢量分组分方法，每个控制周期系统只需要计算30次价值函数，并且增加了一个控制周期内有效矢量的个数。实验结果表明，所提三矢量预测控制策略在兼顾传统预测控制策略良好动态效果的同时有效减小了系统稳态时的电流波动，明显改善了五桥臂逆变器双永磁电机系统的稳态性能。
参考文献
[1] Longfei Li, Jie Xiao, Yun Zhao, et al. Robust position anti-interference control for PMSM servo system with uncertain disturbance[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2):151-160.
[2] 耿强, 王少炜, 周湛清, 等. 改进型偏差耦合多电机转速同步控制[J]. 电工技术学报, 2019, 34(3): 474-482.Geng Qiang, Wang Shaowei, Zhou Zhanqing, et al. Multi-motor speed synchronous control based on improved relative coupling structure[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 474-482.
[3] 肖雄, 王健翔, 张勇军, 等. 一种优化的双电机主-从模型转矩预测控制策略[J]. 电工技术学报, 2018, 33(24): 5720-5730. Xiao Xiong, Wang Jianxiang, Zhang Yongjun, et al. An optimized master-slave model predictive direct torque control scheme for the dual motor[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5720-5730.
[4] Yu Yang, Cong Leyao, Tian Xia, et al. A stator current vector orientation based multi-objective integrative suppressions of flexible load vibration and torque ripple for PMSM considering electrical loss[J].CES Transactions on Electrical Machines and Systems, 2020, 4(3):161-171.
[5] He Chengyuan, Wu Thomas. Analysis and design of surface permanent magnet synchronous motor and generator[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 94-100.
[6] 魏永清, 康军, 曾海燕, 等. 十二相永磁电机驱动系统的容错控制策略[J]. 电工技术学报, 2019, 34(21): 4467-4473. Wei Yongqing, Kang Jun, Zeng Haiyan, et al. Fault-tolerant control strategy for twelve-phase permanent magnet synchronous motor propulsion system[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4467-4473.
[7] 周长攀, 杨贵杰, 苏健勇. 五桥臂逆变器驱动双三相永磁同步电机系统双零序电压注入PWM策略[J]. 中国电机工程学报, 2016, 36(18): 5043-5052, 5129. Zhou Changpan, Yang Changjie, Su Jianyong. A double zero-sequence voltage injection PWM strategy for a five-leg inverter supplying dual three-phase permanent magnetic synchronous motor[J]. Proceedings of the CSEE, 2016, 36(18): 5043-5052, 5129.
[8] 孟云平, 周新秀, 李红, 等. 基于四桥臂拓扑的永磁同步电机断相容错控制策略[J]. 电工技术学报, 2019, 34(15): 3158-3166. Meng Yunping, Zhou Xinxiu, Li Hong, et al. Fault tolerant strategy of four-leg for permanent magnet synchronous motor in case of open circuit fault[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3158-3166.
[9] 梅杨, 黄伟超, 冯帅伟. 一种基于零矢量调节的五桥臂逆变器调制方法[J]. 电工技术学报, 2017, 32(增刊2): 96-102. Mei Yang, Huang Weichao, Feng Shuaiwei. A modulation method for a five-leg-inverter based on the zero vector adjustment[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 96-102.
[10] Hu Yashan, Huang Shoudao, Wu Xuan, et al. Control of dual three-phase permanent magnet synchronous machine based on five-leg inverter[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11071-11079.
[11] Wang Wei, Zhang Jinghao, Cheng Ming, et al. Direct torque control of five-leg dual-PMSM drive systems for fault-tolerant purposes[J]. IEEE Transactions on Power Electronics, 2017, 17(1): 161-171.
[12] Mahmoud H, Handy Fortin B, Kamal A. A hybrid modulation scheme for dual-output five-leg indirect matrix converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7299-7309．
[13] Wang Wei, Zhang Jinghao, Cheng Ming. A dual-level hystersis current control for one five-leg VSI to control two PMSMs[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 804-814.
[14] Mei Yang, Yi Zichen, Li Zhengxi. Restrained search predictive control method for five-leg inverter fed dual induction motor drives[C]//2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 2015: 1524-1529.
[15] Young-Seol L, June-Seok L, Kyo-Beum L. Improved model predictive control method for two induction motor fed by five-leg inverter system[C]//2018 IEEE Energy Conversion Congress and Exposition(ECCE), Portland, USA, 2018: 4552-4557.
[16] 梅杨, 冯帅伟. 五桥臂逆变器-双异步电机调速系统的零矢量交错模型预测控制[J]. 电工技术学报, 2017, 32(10): 214-221. Mei Yang, Feng Shuaiwei. Model predictive control based on zero vectors interleave for dual induction motor drives system fed by five-leg inverter[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 214-221.
[17] Mei Yang, Yi Zichen, Li Zhengxi. A two-step model predictive control strategy for dual induction motor drive system fed by five-leg inverter[C]//2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 2015: 137-142.
[18] 王亮, 耿强, 周湛清. 五桥臂双永磁同步电机系统双矢量模型预测电流控制[J]. 电机与控制应用, 2020, 47(2): 27-33, 41. Wang Liang, Geng Qiang, Zhou Zhanqing. Double-vector model predictive current control of five-leg dual permanent magnet synchronous motor system[J]. Electric Machines and Control Application, 2020, 47(2): 27-33, 41.
Abstract In the dual permanent magnet synchronous motors system fed by the five-leg inverter, only one voltage vector with fixed amplitude and direction is applied on each motor in a control cycle in the traditional predictive control strategy. The vector regulation range is limited and the motor currents fluctuate greatly. To reduce the motor current fluctuation in the dual-motor system, a three-vector-based predictive control strategy was adopted. In this method, two effective voltage vectors and one zero voltage vector were applied in each control period. Firstly, the two effective vectors were grouped according to their switch states. And then the optimal vector set of each group was selected by the cost function of each motor. Finally, the selected vector sets of different groups were compared, and the optimal vector set of the system was further selected from them. Based the optimal vector set, the five-leg voltage vector was synthesized and applied on the dual motors system. After grouping vectors, the strategy only needs to calculate the value of cost function 30 times per control cycle, which effectively reduces the number of calculations of multi-vector predictive control. Compared with the traditional predictive control strategy, the experimental results show that the strategy can effectively reduce the current fluctuations while maintaining the advantages of fast dynamic response, and has a certain resistance to parameter disturbance, which improves the steady-state performance of the system.
keywords：Permanent magnet synchronous motor, three-vector, predictive control, five-leg inverter
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.200348
国家自然科学基金（51907142）、天津市自然科学基金（18JCQNJC74400）、天津市教委科研计划重点项目（2019ZD09）和天津市教委科研计划项目（2018KJ208）资助。
收稿日期2020-04-09
改稿日期 2020-09-18
耿 强 男，1978年生，博士，教授，博士生导师，研究方向为电机系统及其控制。E-mail：gengqiang@tju.edu.cn
周湛清 男，1989年生，博士，副教授，研究方向为电机系统及其控制。E-mail：zhzhq@tju.edu.cn（通信作者）
（编辑 郭丽军）