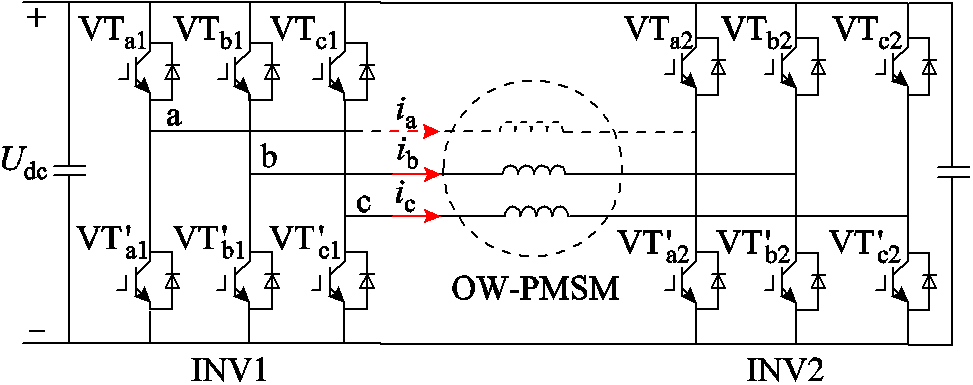
图1 共直流母线开绕组永磁同步电机系统拓扑
Fig.1 OW-PMSM system with common DC bus
摘要 共直流母线型开绕组永磁同步电机系统由于双逆变器供电且存在零序回路,具有一定的容错能力,但控制中需考虑零序电流的影响。然而当永磁同步电机发生单相断相故障后,原电机模型不再适用,若继续沿用断相前控制策略,将导致电机转矩脉动变大、控制性能变差。该文根据开绕组永磁同步电机断相后的系统特性,重新设计坐标变换矩阵,得到新坐标变换下的dq轴电机数学模型。新的转矩方程表达简洁、转矩控制方便,同时新的电压方程也相互解耦,因此电流预测计算量小,且控制更加准确。为提高电流控制性能,断相前后均采用三矢量模型预测控制策略。考虑到断相后的基本电压矢量将发生变化,重新构建了断相系统拓扑下新的电压矢量平面并基于新的基本电压矢量计算电压矢量占空比。实验结果证明了所提方法的有效性和优越性。
关键词:开绕组永磁同步电机 模型预测控制 断相故障 容错控制
永磁同步电机(Permanent MagnetSynchronous Machine, PMSM)具有高效率、高功率密度等优点,被广泛应用于军工、国防、现代工业中[1-2]。然而,在一些恶劣的工作环境下,电机会出现多种故障。其中,由绕组端部断线、供电不稳等问题造成的电机断相是最常见的故障之一[3-4]。一旦电机单相绕组断开,三相电流不再对称,若不改变控制策略会引起转矩脉动增大,控制性能下降,甚至危及系统安全,因此必须采用合适的容错控制策略[5-6]。
三相电机断相后系统仅剩单个控制自由度,无法同时控制两相电流。因此若想保证电机稳定运行,需将电机中性点接至一新引入的桥臂形成四桥臂拓扑结构,以增加电流控制自由度,实现对剩余两相电流的有效控制[6-7]。共直流母线开绕组(Open Winding, OW)PMSM系统由于采用双逆变器供电并存在零序回路,断相后无需改变系统拓扑即可实现容错控制。除容错能力外,OW-PMSM系统还具有多电平、控制灵活等优点[8-9]。但由于OW-PMSM系统存在零序回路,在正常运行时必须考虑零序电流和三次谐波磁链的影响。
在共直流母线OW-PMSM系统中采用矢量控制(Vector Control, VC)和直接转矩控制(Direct Torque Control, DTC)时,通常需加入一个额外控制环来实现零序电流的控制[10-11],增加了控制系统复杂度。模型预测控制(Model Predictive Control, MPC)由于可以实现多变量的灵活控制而在近年得到了广泛关注[12-13]。在共直流母线OW-PMSM系统中,只需修改MPC的代价函数即可灵活方便地实现对零序回路的控制[14]。然而故障后由于电机系统结构发生变化,电机系统模型和系统参数将发生变化,若继续沿用断相前的MPC策略会严重影响性能,此时电机系统需要重新建模并修改控制策略,而此内容却鲜有文献研究。
三相电机出现断相故障后,为保证转速稳定,恒定的输出转矩是最重要的控制目标,因此剩余两相电流的分配必须做出相应的改变[15]。针对三相电机系统,由于可获得断相后电流的瞬时值,因此文献[8,15]采用滞环控制器来实现两相电流的独立控制。然而这种控制方法开关频率不固定,且由于滞环控制器的固有缺陷,无法保证电流控制的精度。
为提高控制性能,文献[16]采用基于传统坐标变换的改进矢量控制策略对断相OW-PMSM系统进行控制,抑制了断相故障下d、q轴电流的谐波分量。然而由于系统建模不准确,转矩的表达式与电角度有关,同时dq轴电压方程并未实现完全解耦,因此转矩脉动抑制效果并不理想。
为进一步提高系统的容错性能,有学者提出在断相后采用新的坐标变换进行重新建模,并采用与新模型相对应的控制策略实现断相后的解耦控制[17-18]。文献[17]以断相前后d、q轴电流不变为标准得到新的坐标变换,以保证断相瞬间的转矩不变,但无法保证后续转矩脉动的抑制效果。文献[18]构造了三个新的坐标变换并推导了内嵌式PMSM断相后的数学模型,但忽略了断相后必须考虑的三次谐波磁链的影响,且坐标变换不直接,较为繁琐。
文献[13]根据表贴式PMSM断相前后电机数学模型的特点,设计了断相后的有限集MPC。然而此方法只能应用于表贴式PMSM,且单矢量MPC具有转矩脉动大、电流谐波大等问题。文献[19]采用MPC预测abc三相电流,但是未经坐标变换的abc坐标系电机数学模型较为复杂,增加了预测计算的复杂度,且依旧无法避免单矢量MPC带来的问题。
本文根据断相后OW-PMSM数学模型,设计新型坐标变换矩阵,得到共直流母线OW-PMSM故障后的dq轴电压解耦方程和简洁的转矩方程。基于新的转矩方程,进一步修正q轴电流参考值以减小三次谐波磁链产生的转矩脉动。然后根据断相后系统拓扑重新构建基本电压矢量,采用三矢量MPC来提高电流控制性能。后续电压矢量占空比和开关信号通过新电压矢量平面快速计算得到。实验结果证明了所提方法的可行性和有效性。
本文研究的共直流母线OW-PMSM系统如图1所示,图中PMSM的绕组端部被打开,由两个逆变器(INV1和INV2)通过一个直流电压源Udc供电。
由INV1和INV2提供的电压可表示为

图1 共直流母线开绕组永磁同步电机系统拓扑
Fig.1 OW-PMSM system with common DC bus
 (1)
(1)式中,Ua1、Ub1、Uc1和Ua2、Ub2、Uc3分别为INV1和INV2提供的定子三相电压;Sa1、Sb1、Sc1和Sa2、Sb2、Sc2分别为INV1和INV2的开关信号。S=1表示上桥臂开关打开,下桥臂开关关闭;S=0反之。
假设PMSM三相绕组对称,在OW-PMSM系统三相稳定运行时三相绕组电压、磁链方程可写为
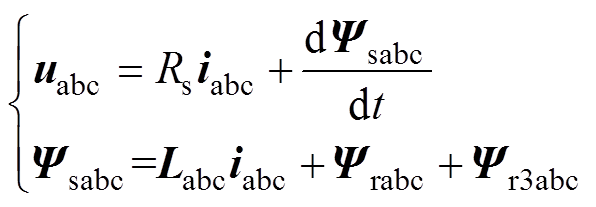 (2)
(2)式中,uabc、iabc分别为三相绕组相电压和相电流;Ψsabc为三相绕组定子磁链;Rs为绕组电阻;Labc为电感矩阵;Ψrabc和Ψr3abc分别为转子磁链的基波分量和三次谐波分量。
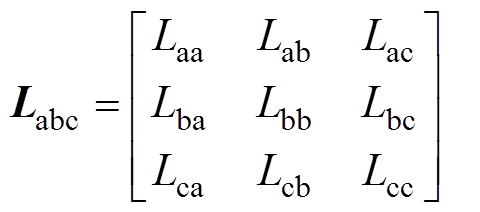 (3)
(3)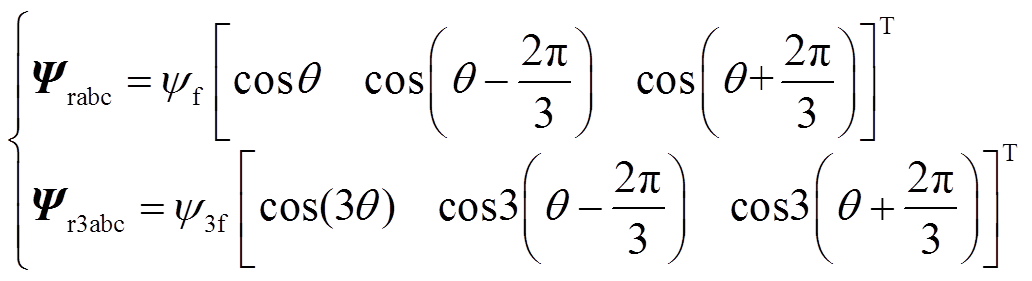 (4)
(4)式中,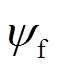 和
和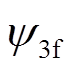 分别为转子永磁体磁链基波和三次谐波分量;θ为转子电角度;Lii(i=a,b,c)为绕组自感,Lii=Lls+L1-L2cos(2θ+2α),α=(0, -2π/3, 2π/3)分别对应a,b,c;Lij(i, j=a,b,c且i≠j)为绕组互感,Lij=-L1/2-L2cos(2θ+2β),β=(-π/3,π,π/3)分别对应Lab、Lbc、Lca;Lls为电机漏感;L1与L2表达式分别为
分别为转子永磁体磁链基波和三次谐波分量;θ为转子电角度;Lii(i=a,b,c)为绕组自感,Lii=Lls+L1-L2cos(2θ+2α),α=(0, -2π/3, 2π/3)分别对应a,b,c;Lij(i, j=a,b,c且i≠j)为绕组互感,Lij=-L1/2-L2cos(2θ+2β),β=(-π/3,π,π/3)分别对应Lab、Lbc、Lca;Lls为电机漏感;L1与L2表达式分别为
 (5)
(5)通过虚位移法[16]可得到PMSM转矩方程为
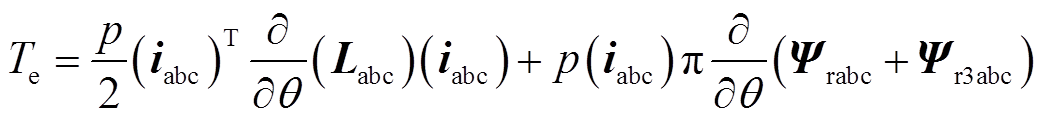 (6)
(6)式中,p为极对数。
电机三相正常运行时常用abc-dq0坐标变换矩阵为
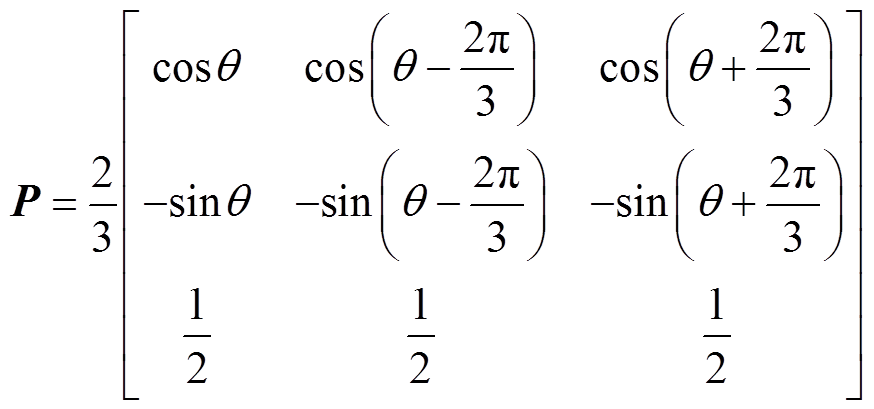 (7)
(7)结合式(2)和式(7),dq0坐标系下的电压和磁链方程可表示为
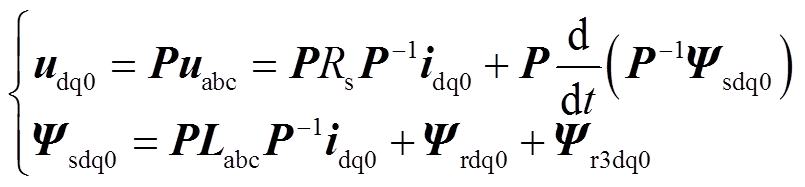 (8)
(8)此时,应用式(8)可以实现dq0轴下的电流预测计算。且此时式(8)中PLabcP-1为对角矩阵,因此dq0轴上的电流预测更加准确且计算更加简单。
利用式(7),可得dq0坐标系下的转矩方程为
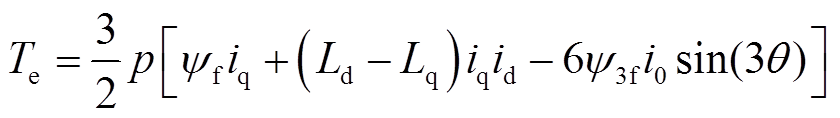 (9)
(9)可见,三次谐波磁链分量会与零轴电流作用产生脉动电磁转矩,因此控制中需抑制零轴电流以减少转矩脉动[14]。
当PMSM发生断相故障(以a相为例),坐标变换需修改。文献[16]直接将矩阵P的bc相分量作为新的变换矩阵
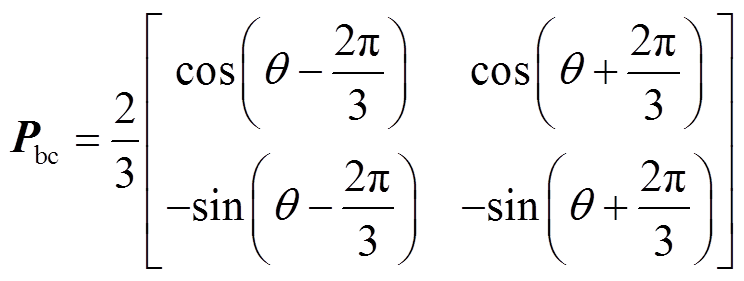 (10)
(10)然而当采用式(10)为变换矩阵时,故障后的转矩将包含电角度项,且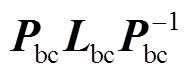 也不再为对角矩阵。dq轴下的数学模型将变得非常复杂,此时应用MPC策略将会使预测计算复杂化,电机控制性能下降。因此有必要寻求新的坐标变换矩阵修改模型预测控制策略。
也不再为对角矩阵。dq轴下的数学模型将变得非常复杂,此时应用MPC策略将会使预测计算复杂化,电机控制性能下降。因此有必要寻求新的坐标变换矩阵修改模型预测控制策略。
假设电机断相前三相电流对称
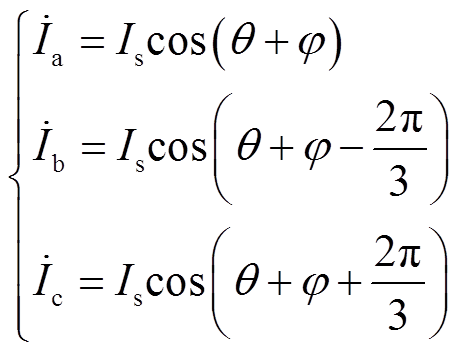 (11)
(11)式中,φ为电流矢量和q轴的夹角。
以a相断相为例,为保证输出转矩不变,bc相电流相位差变为60°,相电流幅值需增大到正常运行时的 倍[15],即
倍[15],即
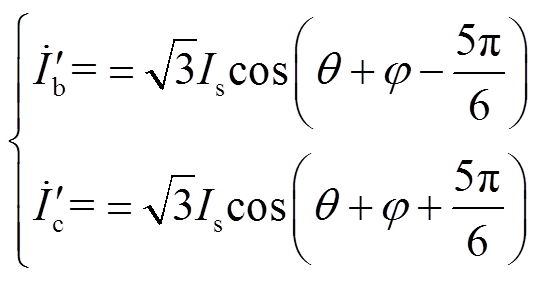 (12)
(12)将a相位置定向为α轴位置,则新的αβ坐标系位置如图2所示。
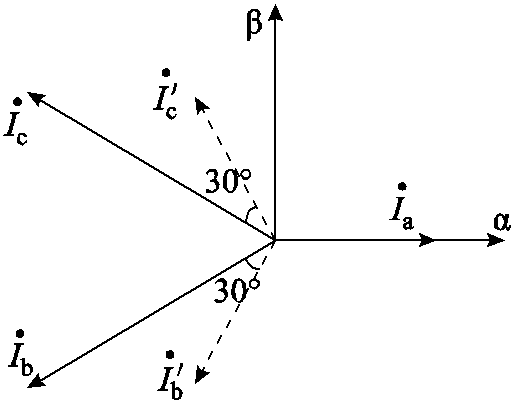
图2 a相断相后bc-αβ新坐标系
Fig.2 bc-αβ coordinate after phase ais open
由图2可得故障后(bc-αβ)坐标变换矩阵C为
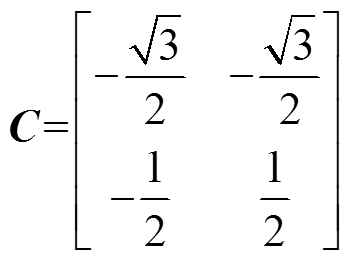 (13)
(13)故障后电磁转矩是式(6)的两相形式,将新的电流旋转坐标变换矩阵(αβ-dq)记为Pi,再将故障后的转矩转化为dq轴形式,并进一步分成三部分,即
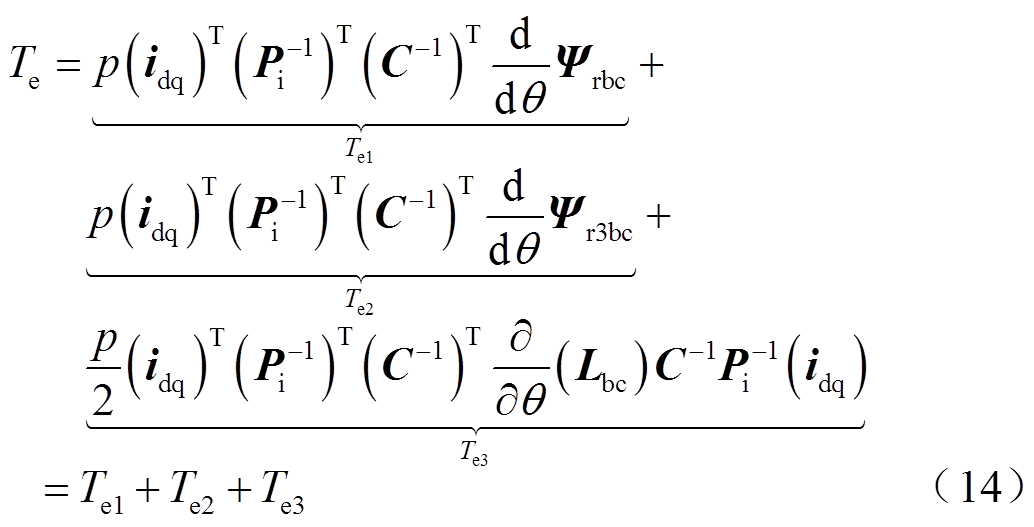
式中,Te1为永磁基波磁链产生的转矩;Te2为永磁三次谐波磁链产生的转矩;Te3为磁阻转矩。
为得到与式(9)类似的简明转矩表达式,将Pi逆矩阵的转置设为
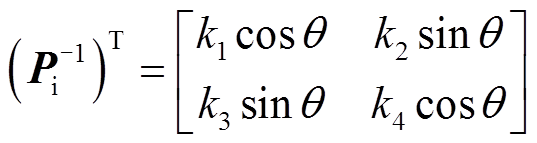 (15)
(15)式中,k1、k2、k3、k4为待定矩阵系数。
令Te1=1.5piq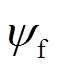 ,可得
,可得
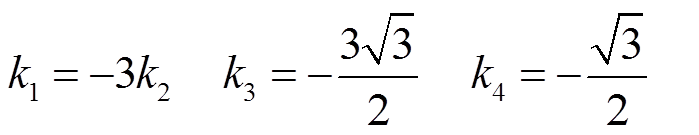 (16)
(16)令Te3=1.5p(Ld-Lq)idiq,可得
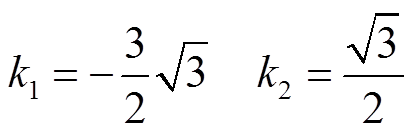 (17)
(17)因此,变换矩阵Pi可写为
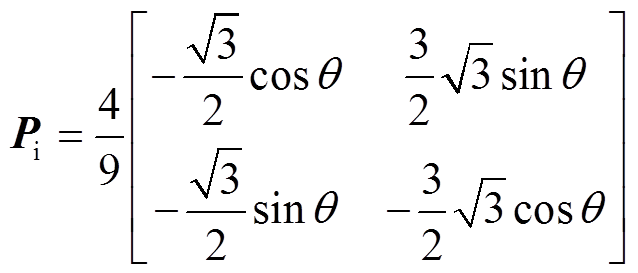 (18)
(18)将式(18)代入式(14)并进一步推导后,可得dq轴电磁转矩为
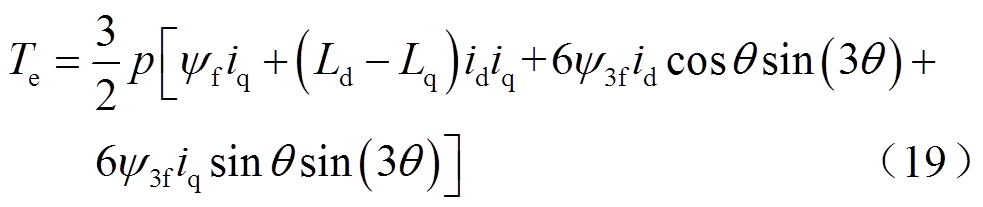
与式(9)对比可知,故障后的电磁转矩不再包含零轴分量,但三次谐波磁链将与dq轴电流相互作用形成脉动转矩。因此在系统发生断相故障后,无法通过抑制零轴电流来降低转矩脉动,需要对故障后系统的控制策略进行进一步修改。
为保证电流控制的准确性,dq轴电压方程需解耦,即dq电感矩阵为对角阵。然而Pi作为电压的旋转变换矩阵时,无法得到解耦电感矩阵。为优化系统控制性能,需为电压方程设计不同的旋转变换矩阵Pv,新的电压旋转变换矩阵定义为
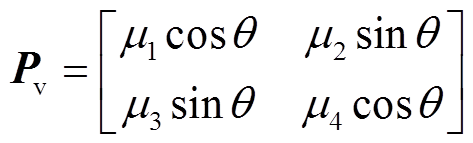 (20)
(20)式中,μ1、μ2、μ3、μ4为待定矩阵系数。则dq轴下的电机电压方程可写为
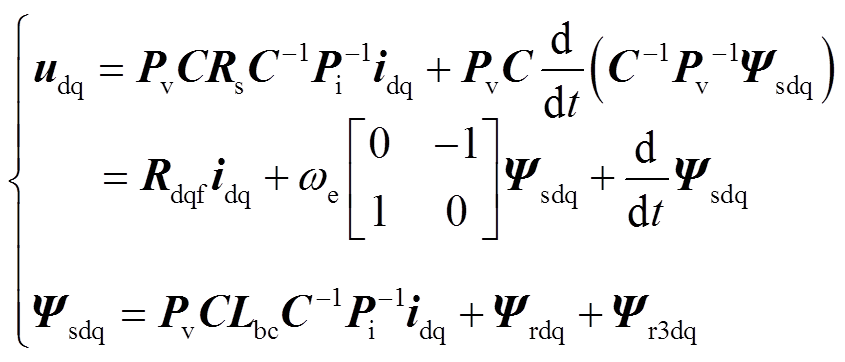 (21)
(21)由式(21)可知,坐标变换后的电感矩阵为
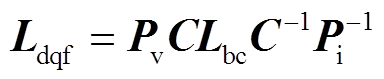 (22)
(22)将Pv、Pi、C矩阵代入式(22)中,可得
 (23)
(23)由于PMSM的漏感和dq轴电感相比可忽略不计,忽略L1中的漏感后,令Ldqf为对角阵,可得
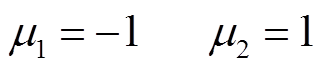 (24)
(24)再令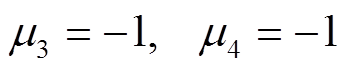 ,可得dq轴电感矩阵
,可得dq轴电感矩阵
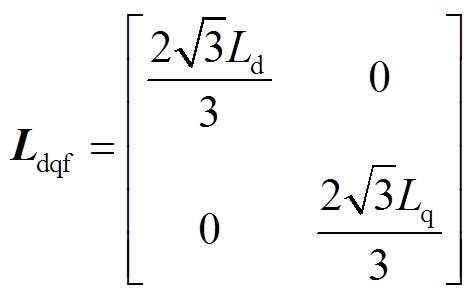 (25)
(25)因此电压旋转坐标变换矩阵为
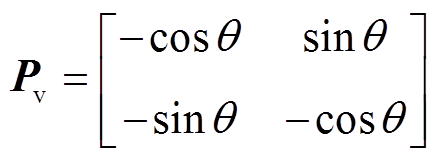 (26)
(26)将式(26)代入式(21)中,可得使用新坐标变换后的dq坐标系下的断相电机电压方程为
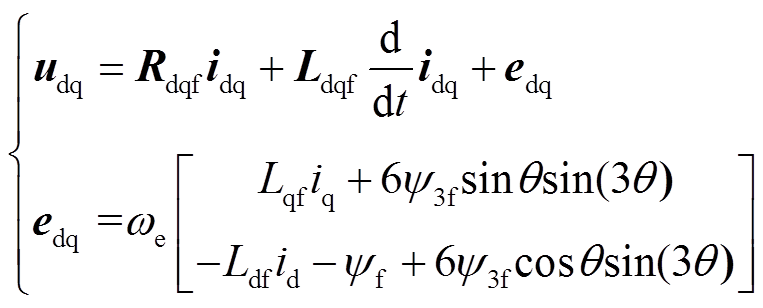 (27)
(27)式中, 为电机角速度。其中dq坐标系下的电阻矩阵为
为电机角速度。其中dq坐标系下的电阻矩阵为
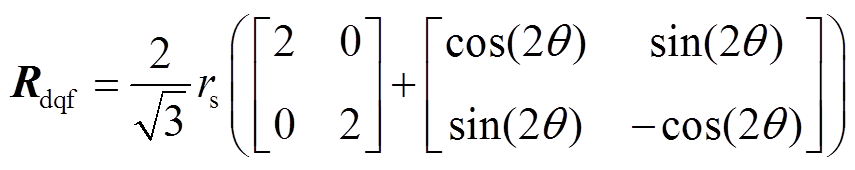 (28)
(28)由式(28)可知,利用Pv可得到相互解耦的电机dq轴电压方程,dq轴电感矩阵与电角度无关。同时新的电压方程保持了断相前的简洁形式。
为简化控制过程,本文采用id=0的控制方式,则断相故障后的转矩表达式(19)可简化为
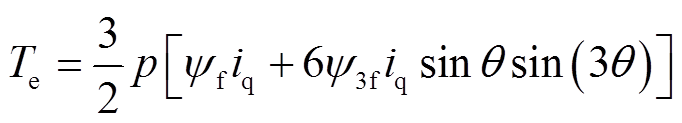 (29)
(29)为了抑制转矩脉动,应根据式(30)将dq轴电流参考值设置为
 (30)
(30)q轴电流参考值可进一步表示为
 (31)
(31)从式(31)可看出,q轴参考电流不再是直流量,而是一个包含二次和四次谐波分量的交流量。
若式(30)作为q轴电流参考值,则bc相电流不再是正弦的。如需得到正弦电流,则dq轴电流参考值可选择为式(32),然而此时不能保证转矩脉动最小。
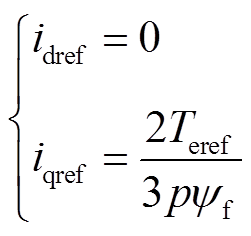 (32)
(32)经过新的坐标变换后,dq轴电压方程相互解耦。其形式简单,电感矩阵也已常数化,从而简化了整个预测计算。
用一阶前向欧拉离散法将式(27)离散化,得到OW-PMSM离散状态方程为
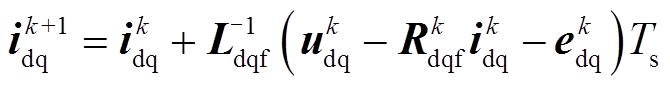 (33)
(33)由式(33)可以看出,在阶系统状态下,预测电流ik+1由电压信号uk控制,由于实际控制系统会产生一拍延时,在考虑一拍补偿[16]后,预测电流ik+2可进一步表示为
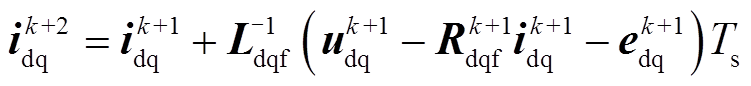 (34)
(34)式中, 为通过k时刻采样的电流电压预测模型得到的k+1时刻的电流值,而
为通过k时刻采样的电流电压预测模型得到的k+1时刻的电流值,而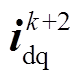 是对下个控制周期的预测值。因采样周期很短,相邻控制周期中的转速和电角度可视作常数,即
是对下个控制周期的预测值。因采样周期很短,相邻控制周期中的转速和电角度可视作常数,即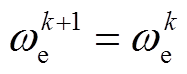 ,θk+1=θk。
,θk+1=θk。
根据无差拍MPC思想,即在下一时刻电流矢量的预测值和电流矢量参考值相同。将式(34)中的k+2时刻电流值改为电流参考值,则得到k+1时刻电压矢量的参考值为
 (35)
(35)由于断相后OW-PMSM系统只有四个桥臂工作,b、c相相电压可表示成
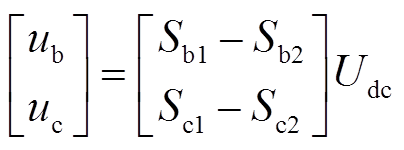 (36)
(36)由于Si1-Si2(i=b,c)取值范围为{1,0,-1},因此断相后双逆变器系统能够产生9个不同的电压矢量。bc坐标下电压矢量通过坐标变换C-1能够得到9个αβ坐标系下的基本电压矢量为
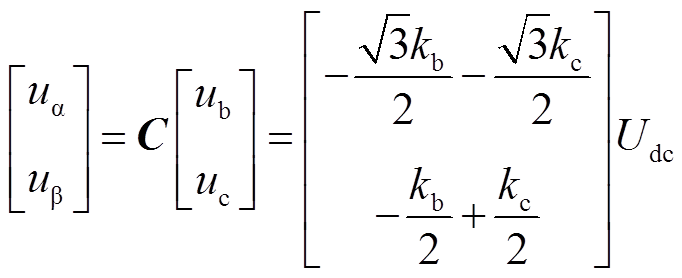 (37)
(37)式中,kb=Sb1-Sb2;kc=Sc1-Sc2。则此时基本电压矢量可通过kb、kc表示为ui=[kb kc]。
9个基本电压矢量在αβ平面上的位置如图3所示,由于u7与u8超出了线性调制范围,所以在断相后的调制中,可只考虑u0~u6共7个电压矢量。
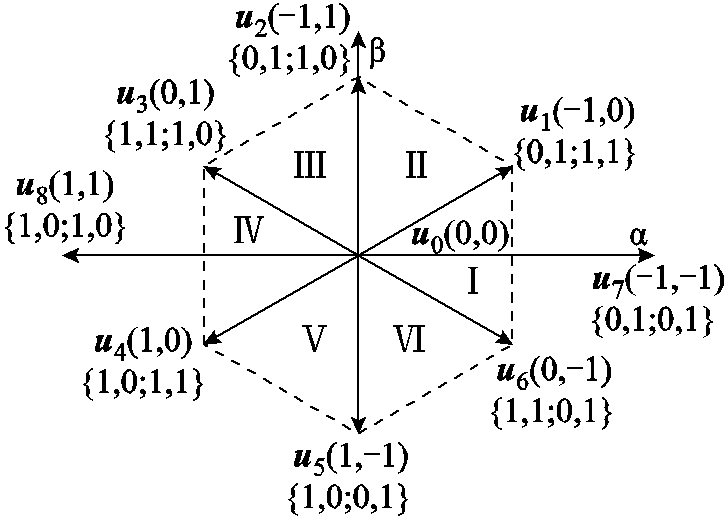
图3 断相后电压矢量平面
Fig.3 Voltage vector plane after open phase fault
参考电压矢量可由三矢量合成并表示为
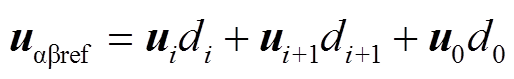 (38)
(38)dq轴参考电压矢量经电压旋转变换矩阵Pv后可得到αβ轴下的电压矢量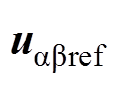 ,进一步得到电压矢量在电压矢量平面的角度
,进一步得到电压矢量在电压矢量平面的角度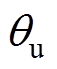 ,即
,即
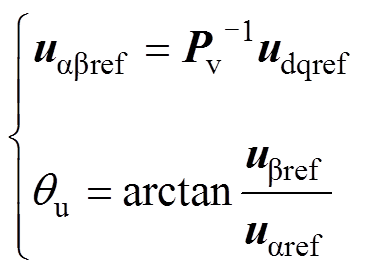 (39)
(39)根据θu的大小可判断参考电压矢量所在的电压矢量平面扇区。假设参考电压矢量位于扇区Ⅱ,则此时选择的有效电压矢量为u1、u2,参考电压矢量在扇区Ⅱ的电压矢量合成。
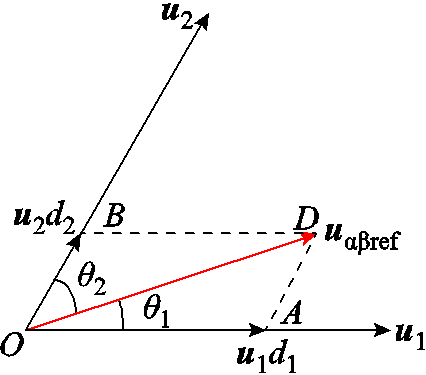
图4 参考电压矢量在扇区Ⅱ的电压矢量合成
Fig.4 Voltage vector synthesis when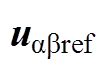 in sectorⅡ
in sectorⅡ
由正弦定理可得
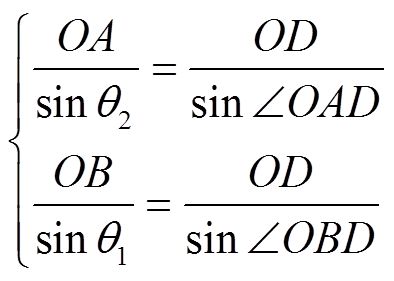 (40)
(40)由式(40)及叉乘的定义可得u1、u2、u0的作用时间分别为
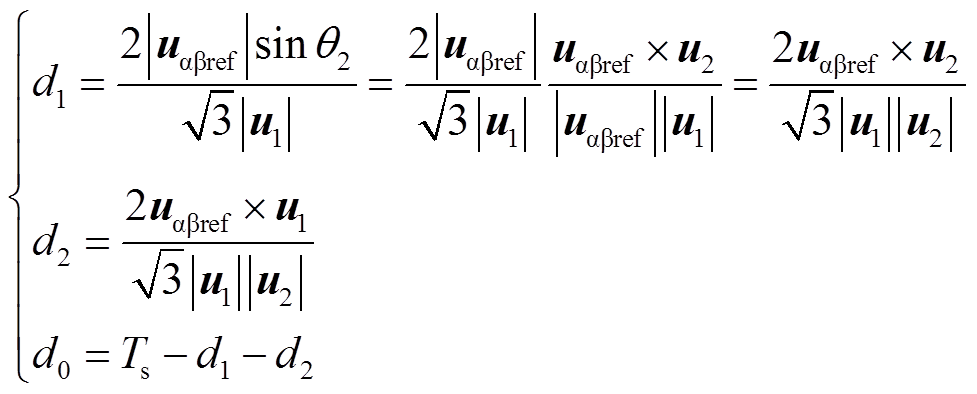 (41)
(41)当参考电压矢量在其他扇区时,可以通过类似的方法计算各个电压矢量的占空比。在计算得到三矢量的占空比后,需选取零矢量插入两有效矢量之间,零矢量的选取以系统开关次数最小为原则。为简化开关选择过程,除了非零矢量,当Si1-Si2=0时,总是选择开关状态{1, 1}。以u1与u2为例,其对应到Sb1、Sb2、Sc1、Sc2上的开关状态上为:{0,1,1,1},{0,1,1,0}。观察到Sc1相一直是开通的,为了保持Sc1在一个开关周期内不动作,则有{Sc1,Sc2}={1,1},进一步选择{Sb1,Sb2}={1,1}。此时一个周期内的开关状态如图5所示。
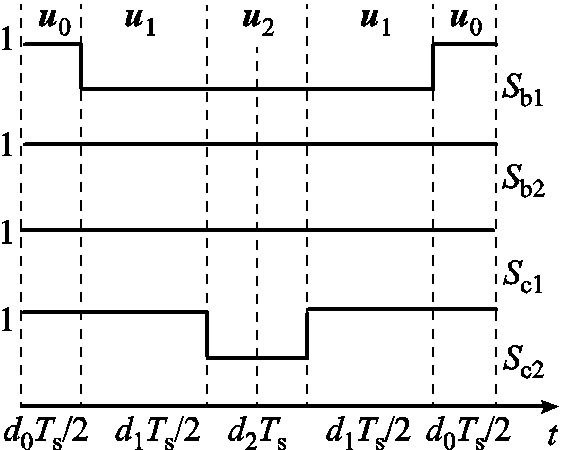
图5 开关信号示意图(电压矢量为u1, u2, u0)
Fig.5 Switch states with u1, u2, u0 applied
本文所研究的OW-PMSM系统MPC容错策略框图如图6所示,整个框图包括断相故障发生前后的控制部分。当OW-PMSM正常工作时,采用文献[14]中的MPC策略得到参考电压并进一步采用文献[20]提出的三相调制方法;当故障发生后,采用本文所提的MPC容错策略。断相故障后,故障相的电流将衰减到0。在一个控制周期内,如果一个相电流的采样值满足式(42),则计数器加1。当计数器值达到设定的阈值,故障检测程序便可认为故障已发生,然后切换至故障后控制方法。本文计数器设置为1 000,开关周期为0.1ms,因此切换控制策略时间间隔可计算为1000×0.1ms=0.1s。
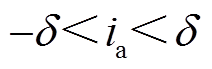 (42)
(42)式中,δ为大于0的量,本文取0.3。
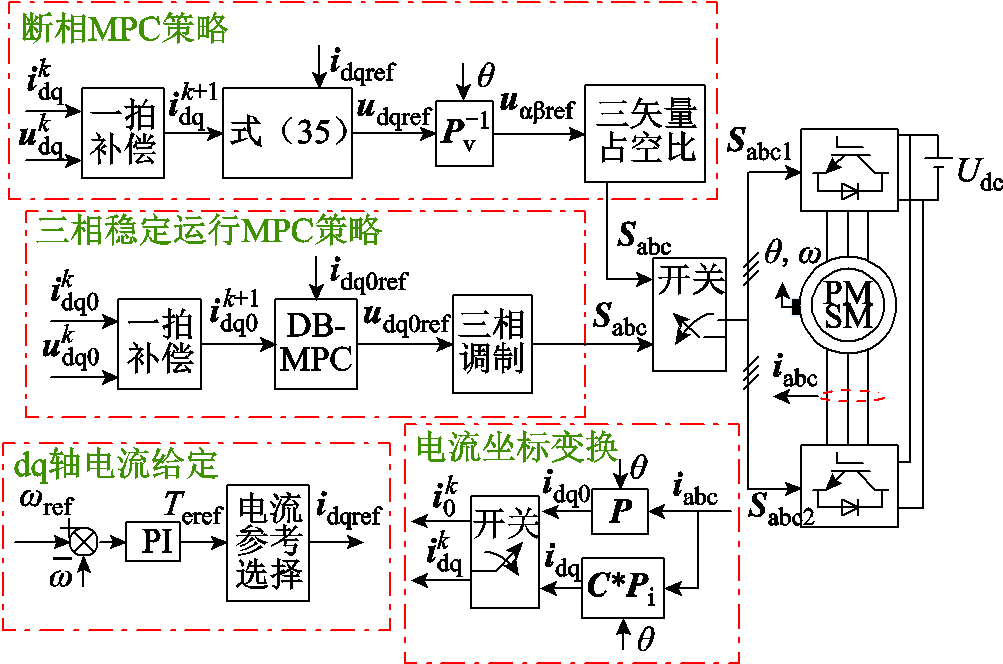
图6 共直流母线开绕组永磁同步电机系统容错控制框图
Fig.6 Control block diagram of the proposed fault-tolerant control strategy for OW-PMSM
本文通过实验研究比较了传统变换矩阵的容错策略[16](策略Ⅰ),采用新型变换矩阵且不考虑三次谐波磁链的MPC容错策略(策略Ⅱ)和考虑三次磁链的MPC容错策略(策略Ⅲ)。实验中直流母线电压Udc=90V,PMSM参数Rs=2Ω,Ld=8mH,Lq=12.7mH,ψf=0.48Wb,ψ3f=0.025Wb,极对数p=3,系统采样周期为100μs。实验结果如图7~图9所示。
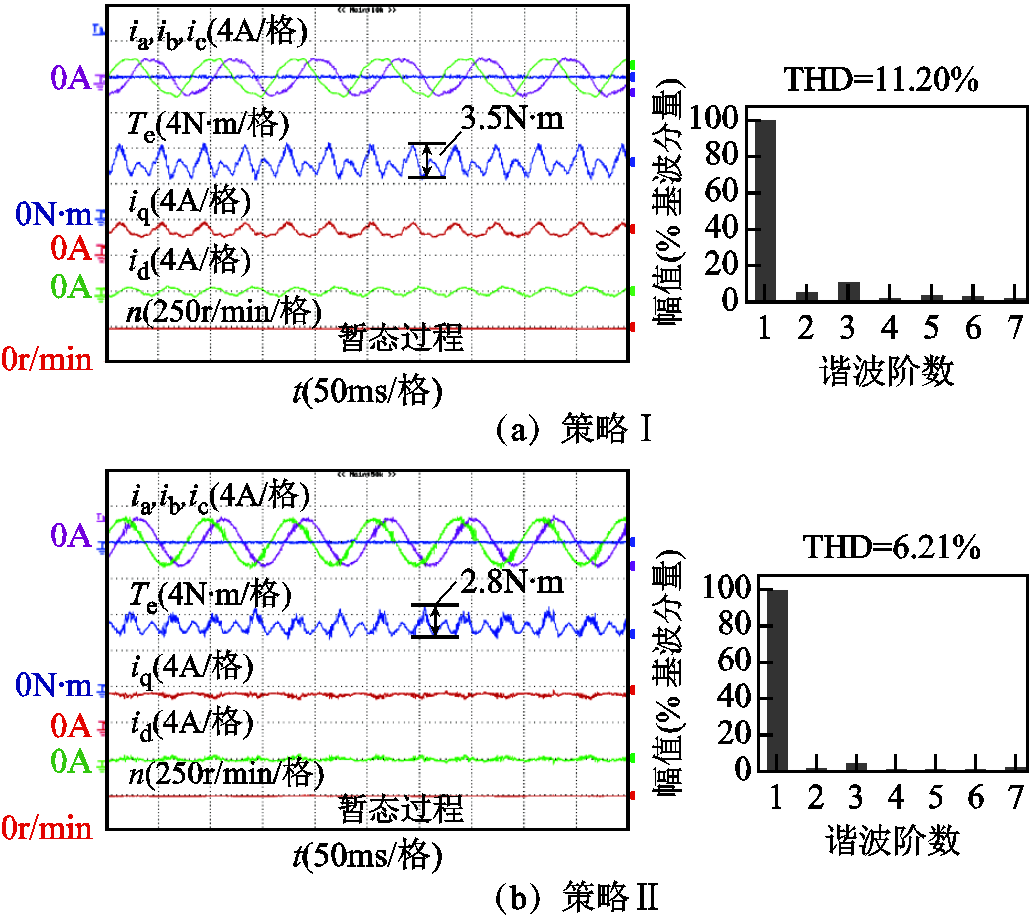

图7 转速为250r/min时的稳态实验结果与电流FFT分析
Fig.7 The steady-state experimental results when speed is 250 r/min and FFT analysis of stator current

图8 转速从250r/min到400 r/min的动态性能实验结果
Fig.8 The dynamic performances experimental results when speed changes from 250 r/min to 400 r/min
图7比较了三种策略在故障后参考转速设定为250r/min,负载转矩为6N×m时的稳态性能和电流FFT分析。从图7a左图可看出剩余两相电流畸变,转矩脉动明显增大,这是因为传统坐标变换后得到的数学模型不精确导致的。从图7b左图中可看出,与策略Ⅰ相比,转矩脉动从3.5N·m减小到2.8N·m,转矩脉动没有明显降低。这进一步表明,坐标变换矩阵对剩余两相电流的正弦度有影响,三次谐波磁链与转矩脉动有关。图7c左图为新坐标变换下考虑三次谐波磁链的结果,此时转矩脉动降低到1.5N×m,可看出该方法能有效抑制转矩脉动。从图7a和图7b可看到,在采用本文提出的坐标变换建模后,总谐波失真(Total Harmonic Distortion,THD)从11.2%降低到6.21%,定子电流的正弦性得到很大的改善。在考虑三次谐波磁链后,由于二次和四次谐波分量被注入到q轴电流基准中用以减少转矩脉动,因此bc相电流中含有3次谐波和5次谐波,从图7c看出,电流不再完全正弦,THD增加到14.51%,但是转矩脉动得到了有效的抑制。

图9 断相故障时的动态性能实验结果
Fig.9 The dynamic performances experimental results when open phase fault occurs.
图8比较了三种策略在6N×m负载转矩下参考转速从250r/min变为400r/min的动态性能。可以看出,策略Ⅰ的暂态过程为0.25s且存在超调。而策略Ⅱ和策略Ⅲ暂态过程为0.3s没有超调。这是因为策略Ⅰ的电机建模不准确,使得转速控制性能下降,出现超调现象。此时暂态过程的输出转矩要大于转矩限幅值,因此其加速过程相比另外两种策略要更快。然而暂态过程转矩超出PMSM的限幅转矩有可能会损害系统的安全性,因此必须采用更精准的转矩控制策略。从图8b可以看出,虽然策略Ⅱ中电机建模准确,然而由于未采用转矩脉动抑制,因此转矩也会周期性地超过转矩限幅值。而加入了转矩脉动抑制的策略Ⅲ暂态过程中转矩依然平稳,因此从系统安全上考虑,策略Ⅲ相比于另外两种策略更好。
图9展示了断相故障发生时的控制策略切换过程。首先,系统运行在三相运行状态(区域Ⅰ),然后强制断开a相。在t1~t2(区域Ⅱ)的0.1s切换过程中,a相电流的采样信号虽然为零,但此时故障判断模块还不能确定a相已发生断相故障,因此仍然采用三相正常运行时的控制方案。在故障检测模块检测到a相发生断相故障后,切换至不同的容错控制策略(区域Ⅲ)。
由图9可知,三种策略都能顺利地从正常运行状态切换到断相故障运行状态。由于策略Ⅰ断相前后的坐标变换保持不变,因此与策略Ⅱ和策略Ⅲ相比,策略Ⅰ的瞬态过程(t2~t3)最短为0.04s。而策略Ⅱ和策略Ⅲ两种策略的坐标变换和控制结构相同,所以它们的暂态过程时间均为0.06s。
从图9a和图9b可以发现,与切换过程(区域Ⅱ)中的情况相比,区域Ⅲ中的转矩脉动都有相应的减小,并且策略Ⅱ优于策略Ⅰ,但是转矩脉动抑制都有限。在考虑了三次谐波磁链后,从图9c可发现,和其他两种策略相比,策略Ⅲ的转矩脉动进一步减小,电机转速波形最为平滑。
表1列出了三种控制策略的控制性能对比。分析其稳态性能,策略Ⅱ有最低的THD,策略Ⅲ有最低的转矩脉动,但由于注入了谐波电流来抑制转矩脉动,其电流谐波THD含量最大。策略Ⅱ和Ⅲ有相似的动态性能,基本无超调。但由于转矩的限幅更加精确,其动态过程相比于策略Ⅰ更长。考虑断相前后的切换过程,策略Ⅱ和策略Ⅲ要比策略Ⅰ切换时间更长,这是因为坐标变换变化导致控制结构改变而引起的。可以看出,采用新型坐标变换与后续的容错模型预测控制后,在保持动态性能基本不变的情况下,策略Ⅱ和Ⅲ的稳态性能有了很大的提升。在考虑三次谐波磁链的影响后,转矩脉动将被进一步抑制。
表1 三种策略的性能比较
Tab.1 Comparisons of three methods’ performances
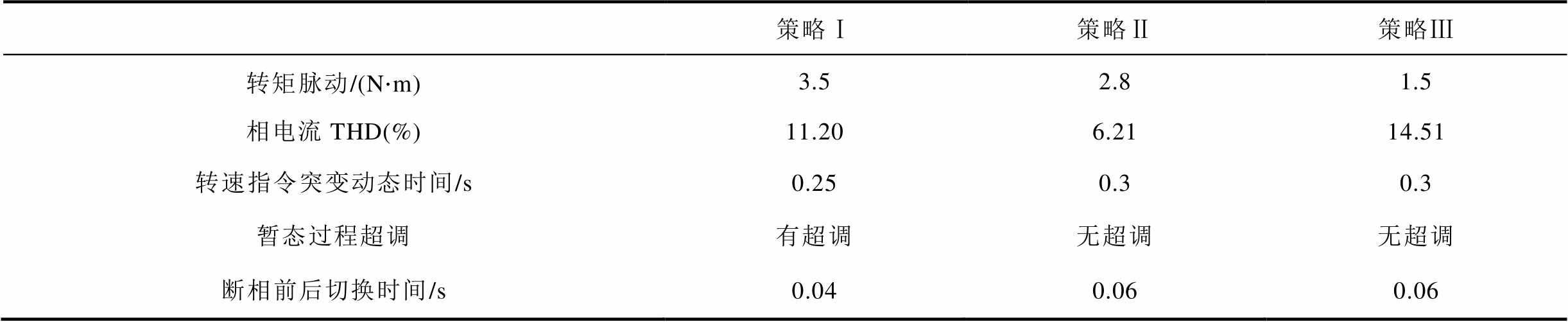
策略Ⅰ策略Ⅱ策略Ⅲ 转矩脉动/(N×m)3.52.81.5 相电流THD(%)11.206.2114.51 转速指令突变动态时间/s0.250.30.3 暂态过程超调有超调无超调无超调 断相前后切换时间/s0.040.060.06
本文提出了一种考虑三次谐波磁链的共直流母线型开绕组永磁同步电动机模型预测控制容错策略。根据断相故障后系统状态方程,重构新的坐标变换矩阵进而得到了dq轴上的简洁转矩表达式和相互解耦的电压方程。新的dq轴电压方程参数均为常数,因此简化了三矢量模型预测计算过程。根据断相后的系统开关状态和电压矢量关系,重新构建电压矢量平面,快速得到了所作用电压矢量的占空比和开关状态。实验结果验证了所提共直流母线型永磁同步电动机系统容错控制策略对断相后出现的谐波控制量具有良好的控制效果,实现了断相后转矩脉动的有效抑制。
参考文献
[1] Sun Yuanxiang, Li Zhen, Zhang Zhenbin. Hybrid predictive control with simple linear control based circulating current suppression for modular multilevel converters[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 335-341.
[2] 刘珅, 高琳. 永磁同步电机的改进模型预测直接转矩控制[J]. 电机与控制学报, 2020, 24(1): 10-17. Liu Shen, Gao Lin. Improved model of predictive direct torque control for permanent magnet synchronous motor[J]. Electric Machines and Control, 2020, 24(1): 10-17.
[3] 孟云平, 周新秀, 李红, 等. 基于四桥臂拓扑的永磁同步电机断相容错控制策略[J]. 电工技术学报, 2019, 34(15): 3158-3166.Meng Yunping, Zhou Xinxiu, Li Hong, et al. Fault tolerant strategy of four-leg for permanent magnet synchronous motor in case of open circuit fault[J].Transactions of China Electrotechnical Society, 2019, 34(15): 3158-3166.
[4] 吕康飞, 董新伟, 刘丽丽, 等.考虑零序电流抑制的开绕组永磁同步电机断相故障下统一调制策略[J].电工技术学报, 2020, 35(11): 2387-2395. Lü Kangfei, Dong Xinwei, Liu Lili, et al. The unified modulation scheme of open-end winding PMSM with common dc bus under the open-phase fault considering the suppression of zero-sequence current[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2387-2395.
[5] 方敏, 周新秀, 刘刚. 三相永磁同步电机断相容错控制[J]. 电工技术学报, 2018, 33(13): 2972-2981. Fang Min Zhou Xinxiu, Liu Gang. Fault-tolerant control strategy for three-phase permanent magnet synchronous motor in case of one phase open-circuit[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2972-2981.
[6] 彭忠, 郑泽东, 刘自程, 等. 基于虚拟绕组和全阶观测器的五相感应电机无速度传感器容错控制策略[J]. 电工技术学报, 2018, 33(21): 4949-4961. Peng Zhong, Zheng Zedong, Liu Zicheng, et al. A novel sensorless fault-tolerant control of five-phase induction machine using virtual winding and full-order observer[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4949-4961.
[7] Xu Jinquan, Zhang Boyi, Fang Hao, et al. Guaranteeing the fault transient performance of aerospace multiphase permanent magnet motor system: an adaptive robust speed control approach[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2020, 4(2): 114-122.
[8] Cheng Yifei, Sun Dan, ChenWenhan, et al. Model predictive current control for an open-winding pmsm system with a common DC bus in 3-D space[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9599-9609.
[9] 年珩, 阮晨辉, 何峪嵩, 等. 基于Z源逆变器的共直流母线开绕组永磁同步电机系统控制策略[J]. 中国电机工程学报, 2019, 39(18): 5509-5519, 5599. Nian Heng, Ruan Chenhui, He Yusong, et al. Control strategy for open-winding PMSM system with common DC bus based on Z-source inverters[J]. Proceedings of the CSEE, 2019,39(18): 5509-5519, 5599.
[10] Zhan Hanlin, Zhu Z Q, Milijana Odavic. Analysis and suppression of zero sequence circulating current in open winding PMSM drives with common DC bus[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3609-3620.
[11] Lin Xiaogang, Huang Wenxin, Jiang Wen, et al. Direct torque control for three-phase open-end winding PMSM with common DC bus based on duty ratio modulation[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4216-4232.
[12] 秦艳忠, 阎彦, 陈炜, 等. 永磁同步电机参数误差补偿-三矢量模型预测电流控制[J]. 电工技术学报, 2020, 35(2): 255-265. Qin Yanzhong, Yan Yan, Chen Wei, et al. Three-vector-based model predictive current control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 255-265.
[13] Wang Wei,Zhang Jinghao,Cheng Ming. Common model predictive control for permanent-magnet synchronous machine drives considering single-phase open-circuit fault[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5862-5872.
[14] Zhang Xiaoguang, Wang Keqin. Current prediction based zero sequence current suppression strategy for the semicontrolled open-winding PMSM generation system with a common DC bus[J]. IEEE Transactions on Industrial Electronics, 2018, 65(8): 6066-6076.
[15] Liu Tianhua, Fu Jen Ren, Lipo T A. A strategy for improving reliability of field-oriented controlled induction motor drives[J]. IEEE Transactions on Industry Applications, 1993, 29(5): 910-918.
[16] Hu Wei, Ruan Chenhui, Nian Heng, et al. Simplified modulation scheme for open-end winding PMSM system with common DC bus under open-phase fault based on circulating current suppression[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 10-14.
[17] Zhou Xinxiu, Sun Jun, Li Haitao, et al. High performance three-phase PMSM open-phase fault-tolerant method based on reference frame transformation[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7571-7580.
[18] Gaeta A, Scelba G, Consoli A. Modeling and control of three-phase pmsms under open-phase fault[J]. IEEE Transactions on Industry Applications, 2013, 49(1): 74-83.
[19] Kiselev A, Catuogno G R, Kuznietsov A, et al. Finite-control-set MPC for open-phase fault-tolerant control of PM synchronous motor drives[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 4444-4452.
[20] Hu Wei, Nian Heng, Sun Dan. Zero-sequence current suppression strategy with reduced switching frequency for open-end winding PMSM drives with common DC bus[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7613-7623.
Research on Fault-Tolerance Strategy Based on Model Predictive Control for Open-Winding PMSM System under Open-Phase Fault
Abstract Due to characteristic of dual-inverter power supplying and existence of zero sequence loop, the open wingding permanent magnet synchronous machine (OW-PMSM) system with common DC bus has certain fault tolerance ability. And the influence of zero sequence current should be considered because of the zero sequence loop. However, when open phase fault occurs, the original mathematical model is no longer applicable. Thus, the torque ripple will become larger and the control performance will worse if the control strategy before fault occurrence is adopted. In this paper, according to the characteristics of OW-PMSM, the coordinate transformation was redesigned and a new mathematical model in dq-axis was obtained. The new torque equation has concise form which makes the torque control more convenient. At meantime, the dq-axis voltage equation is decoupled based on new coordinate transformation so that the calculation burden is reduced and control performance is improved. In order to further improve the current control performance, three vector based model predictive control (MPC) strategy was adopted. Then the voltage vector plane after open phase fault is reconstructed and the duty cycle can be calculated according to the new basic voltage vectors. The experimental results verify the effectiveness and superiority of the proposed method.
keywords:Open-wingding permanent magnet synchronous machine, model predictive control, open-phase fault, fault tolerant control
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.200704
国家自然科学基金资助项目(51877197)。
收稿日期 2020-06-24
改稿日期 2020-09-12
陈文汉 男,1996年生,硕士,研究方向为开绕组电机高性能控制。E-mail:sorachen@zju.edu.cn
孙 丹 女,1975年生,教授,博士生导师,研究方向为交流电机高性能控制策略和双馈风力发电技术。E-mail:sundan@zju.edu.cn(通信作者)
(编辑 郭丽军)